1. Introduction
With the advancement of high-traffic mobile broadband services, the amount of mobile data has increased sharply. It has been estimated that mobile data will grow tenfold in the next five years [
1]. The upcoming 3GPP 5G standard is designed to provide several gigabits per second throughput to users [
2]. Therefore, limited spectrum resources need to be utilized more efficiently. However, it is reported that 20% popular video services produce 80% data [
3], which causes the frequency band to be occupied by the same service repeatedly. Spectrum resources cannot be fully utilized. Fortunately, with the multicast technology, when multiple users request the same service, they are accessed to the same time-frequency resource. Therefore, it is worthwhile to confirm that multicast technology is effective in solving this problem.
The two-stage cooperative multicast (CM) that can jointly solve the bottleneck problem (In conventional multicast, system throughput is limited by the user with the worst channel condition.) of conventional multicast and the low coverage ratio problem of opportunistic multicast scheme (OMS) has been extensively researched in recent years. In the first stage, with OMS, BS only successfully transmits data to those multicast group (MG) users who own good channel conditions (termed as successful users (SUs)). Remaining MG users with bad channel conditions are termed as unsuccessful users (USUs). In the second stage, user-to-user collaboration is carried out. Through the UR selection scheme, some SUs are selected as user relays (URs) to forward their reception signals to USUs using device-to-device (D2D) technology. It is worth mentioning that when the first-stage coverage ratio is fixed, the performance improvement of CM is mainly decided by the UR selection scheme in the second stage.
Current researches on CM are mainly based on two access technologies, orthogonal frequency division multiple access (OFDMA) and non-orthogonal multiple access (NOMA). In the OFDMA-based CM (termed as CM-OFDMA) [
4,
5,
6,
7,
8,
9], user-to-user collaboration is carried out only in a single MG. Users in a single MG are sparsely distributed in the cell. To ensure the cooperation between users who are far apart, the small efficient transmission range (ETR) of user’s device in D2D technology is not considered as a restriction to perform UR selection.
In [
4], all of the SUs are selected as URs to serve USUs. When one UR is far away from USU, due to the large path loss, he/she contributes little to the reception signal-to-noise ratio (SNR) of the USU. This causes a waste of energy. A try-best UR selection scheme is proposed in [
5]. Every USU selects the nearest SU as his (her) UR. Under the assumption that SU should be closer to the BS than USU, those SUs with low average SNR are closer to USUs. They are selected as URs [
6]. Several URs are placed on the fixed positions in the cell. In order to minimize system average outage probability, optimal locations are found to place these URs in the proposed genie-aided CM scheme [
7]. A user-autonomous relay selection scheme is proposed in [
8], in which users decide whether to participate in relay transmission in the second stage. In [
9], a location-aware relay selection scheme is proposed. In order to select the least URs to achieve greater system coverage ratio than the threshold, each USU selects UR from the SUs in a certain probability. However, the method that makes USU choose UR according to the probability is not given.
Above researches only take the requirement of USU into consideration. In the second-stage D2D transmission, the small ETR restricts the cooperation among users. The UR far away from the USU can not guarantee successful reception. It results in UR redundancy. This point is neglected.
An NOMA-based CM is investigated in [
10] (termed as COM-NOMA), in which with NOMA technology two MG are regarded as one quasi-MG to implement OMS in the first stage. Inter-group cooperation and intra-group cooperation are realized in the second stage. Thus, SU can be selected as UR by USU in either MG. UR selection probability increases. At the same time, the efficient relay selection range (ERSR) is set to maximal value, i.e., ETR. The SU density in the vicinity of USU is not taken into consideration.
When one USU locates in the range near the BS, where the density of SU is high, the largest ERSR covers maximum number of SU. Besides, owing to the small path loss, almost all of the SUs in the ETR of USU can be selected as UR. According to the condition of UR selection, each UR ensures that USU he (she) serves receives successfully. So the UR redundancy exists in this range. It is more serious in COM-NOMA than that in CM-OFDMA. The coverage efficiency (coverage efficiency is defined as the ratio of successful users to URs) performance is deteriorated. But in the range near the edge of the cell, where the density of SU is low, there is even no SU in the vicinity of USU, the maxmal ERSR is necessary to cover as many SUs as possible. According the different ranges where the USU locates, it is resaonable to adjust the ERSR. However, in COM-NOMA, the ERSR is fixed and equal to ETR.
Besides, when UR forwards data in the manner of D2D, the cooperative users with non-cooperative behavior, such as the selfishness of user, may lead to a sharp decline in network performance [
11]. However, one assumption made by all above researches is that every MG user is accommodating. USU can be served by as many URs as requirement. Therefore, from the perspective of system, under this assumption, it is essential to reduce UR redundancy. Especially for wireless sensors network, when sensors are arranged in physical environment, power supply for them is insufficient [
12,
13].
Aiming at reducing UR redundancy, we propose a region-division UR selection scheme (termed as RDUR) as an enhanced scheme in COM-NOMA systems. To maximize its coverage efficiency performance, different ERSRs are allocated to different ranges where USU locates. Firstly, the circular coverage area of the cellular is divided into continuous annular areas (AAs). Different ERSRs are assigned to AAs. USUs in the same AA have the same ERSR. Secondly, the ERSR radius set of cellular which maximizes the coverage efficiency is taken to perform UR selection.
The main contributions of this paper are summarized as follows:
Under the influence of large-scale fading, from cell edge to center, the density of SU experiences a gradual upturn. Considering this, RDUR supplies optional radius for USU’s ERSR to reduce the number of unnecessary URs. Simulation results shows that the coverage efficiency increases by at least 14% in comparision to the original UR selection scheme of COM-NOMA systems. The capacity efficiency of the second-stage D2MD has been improved. RDUR can motivate that smaller ERSRs is allocated to the cell-center AAs in high probability to reduce UR redundancy and larger ERSRs are allocated to the cell-edge AAs in high probability to ensure successful receive.
The number of UR in the ERSR of USU after the first stage of COM-NOMA follows Poisson distribution. The parameter of Poisson distribution is derived. Simulation results show that the analytic result matches well with the simulated one. It verifies that UR redundancy exists in COM-NOMA with original UR selection scheme, when the number of MG user is high (more than 100).
Under different ERSR radius sets, by utilizing the characteristics of Poisson distribution that its parameter is equal to its mathematical expectation, the expressions of UR selection ratio is derived. In this paper, after RDUR, the coverage ratio of the second stage is also given. Through simulation, it is supported that different ERSR assignments can effect the UR selection ratio and coverage ratio. The analytic result accurately reflects simulated one.
The rest of this paper is organized as follows. We describe the two-stage COM-NOMA in
Section 2. In
Section 3, RDUR is proposed. Performance analysis for different ERSR radius sets is in
Section 4. Numerical simulation results and analysis are given in
Section 5. Finally, we conclude this paper and highlight our findings in
Section 6. Notations: Throughout the paper, the notations of mathematical variables are summarized in
Table 1.
2. System Model
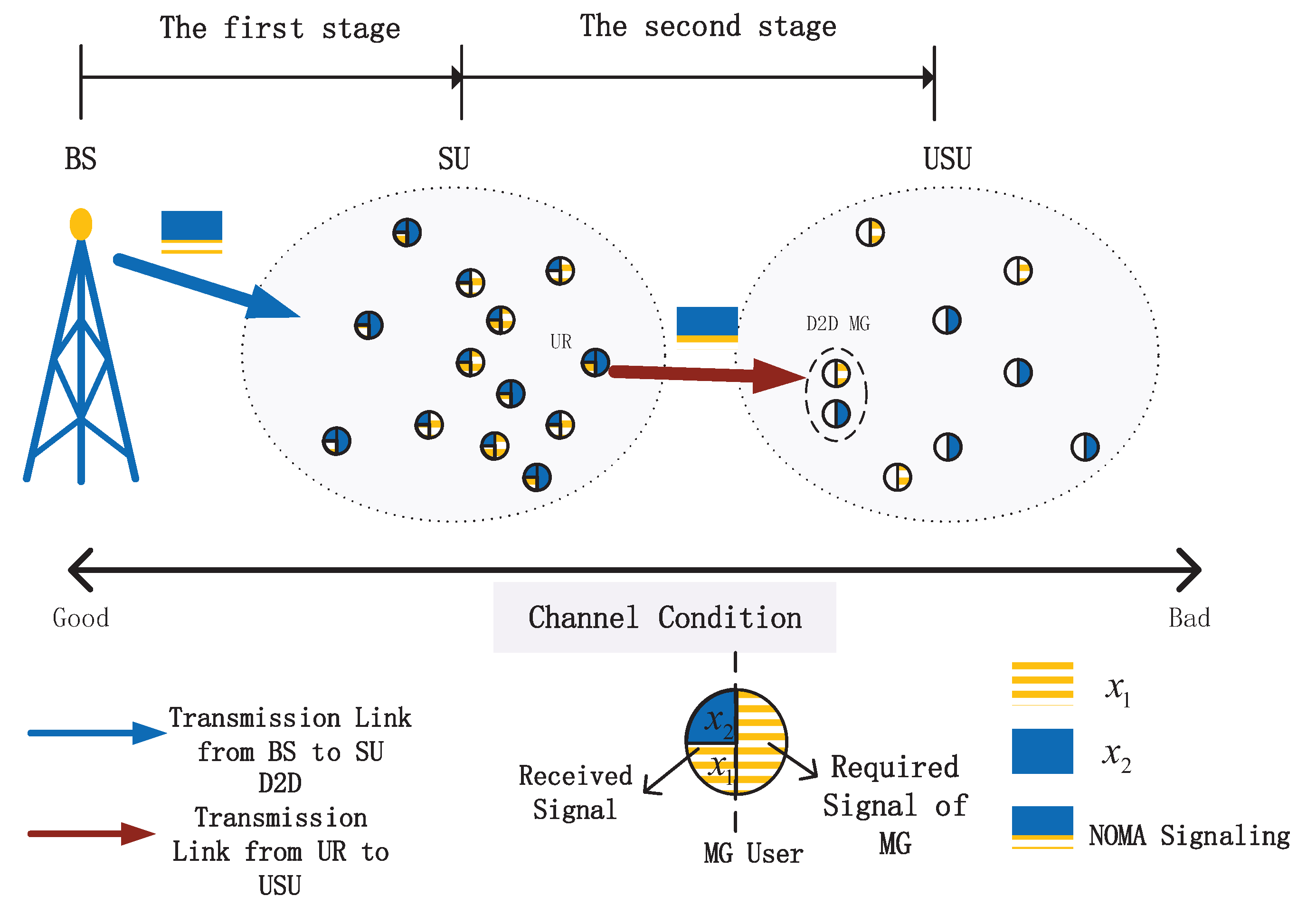
We consider a COM-NOMA system, which is shown in
Figure 1, constituted by a BS with coverage radius
R and two MGs
,
. In each MG,
users are uniformly distributed in the cellular. The probability density function of user’s distance from the BS is
,
. Time slot
T is divided into two equal sub-slots to conduct data transmission.
In order to reduce the burden of networks on keeping track of the data, especially when the number of user is large, the rateless code, such as the fountain code [
14], is employed throughout the content delivery process [
15].
In the first stage, two MGs are regarded as one quasi-MG. BS multicasts NOMA superposition signaling to the quasi-MG at coverage ratio . The SU set of is denoted by , where denotes the -th SU from , and . The corresponding channel gain set is , where . Elements in are ranged in descending order. represents small scale channel fading. is path loss. is the distance from BS to . is path loss parameter. The smallest channel gain of is . Without loss of generality, is assumed. represents the worst channel gain subset of . The corresponding user set is denoted by . Therefore, . and constitute a subgroup pair.
The required signals of two subgroups are superimposed and transmitted on the system frequency band by NOMA technology. The transmission signal of BS in the first sub-slot is
where
P is the transmission power of BS.
is the required signal of
.
and
are the power allocation factors (PAFs) of the paired subgroups,
. Because
,
.
In OMS, in order to guarantee successful reception, for two required signals, the modulation and coding schemes (MCSs) of BS are both selected according to the least channel gain of subgroup pair, i.e.,
. In the receiving end, after the signal allocated with large PAF is decoded successfully, the required signal can be achieved directly (corresponding to
) or after successive interference cancellation (SIC) (corresponding to
). Therefore, the signal-and-interference-plus-noise ratio (SINR) threshold is
where
is the power of additive white Gaussian noise (AWGN) with variance
, and
.
B is the bandwidth originally allocated to each MG in OFDMA. Because COM-NOMA occupies the bandwidth allocated to two MGs, the power of AWGN is
.
Since users in own better channel conditions than those in , they can decode , too. Simultaneously, it is assumed that the reception signal is abandoned by the remaining users (i.e., USUs), if only it is failed to be received. To sum up, after the first stage of COM-NOMA, each user in obtains the NOMA signalling.
In the second stage, SU as candidate UR is selected by USU. UR conveys the NOMA signalling to USU. The transmission signal is
where
is the tansmission power of UR. The MCSs are the same as the first stage.
D2D multicast (D2MD) transmission mode is introduced into the second stage. Hence, UR must locate within the ETR of USU. To make sure that the USU served by UR can successfully receive, even if USU only has one UR, SINR of signal
provided by UR should be larger than threshold
[
10], and
. The UR set of USU is denoted by
.
is the distance from
to USU
u.
is the reception SINR of
from
.
is the radius of ETR.
When multiple USUs select the same one UR, they comprise a D2D MG.
3. The Proposed Range-Division User Relay Selection Scheme
In COM-NOMA, the density of SU is larger than the conventional CM-OFDMA scheme. Moreover, USU chooses UR from SUs who are within his/her ETR. When USU is near the cell center, the density of SU in his/her vicinity is high; otherwise, it is low. At the same time, every UR is able to provide larger SINR than
for the USU served by him (her). Therefore, near the cell center, the probability that multiple URs serve the same one USU is high, when
is large. This is also verified by simulation in
Section 5. To reduce UR redundancy and improve coverage efficiency, RDUR scheme is proposed in this section.
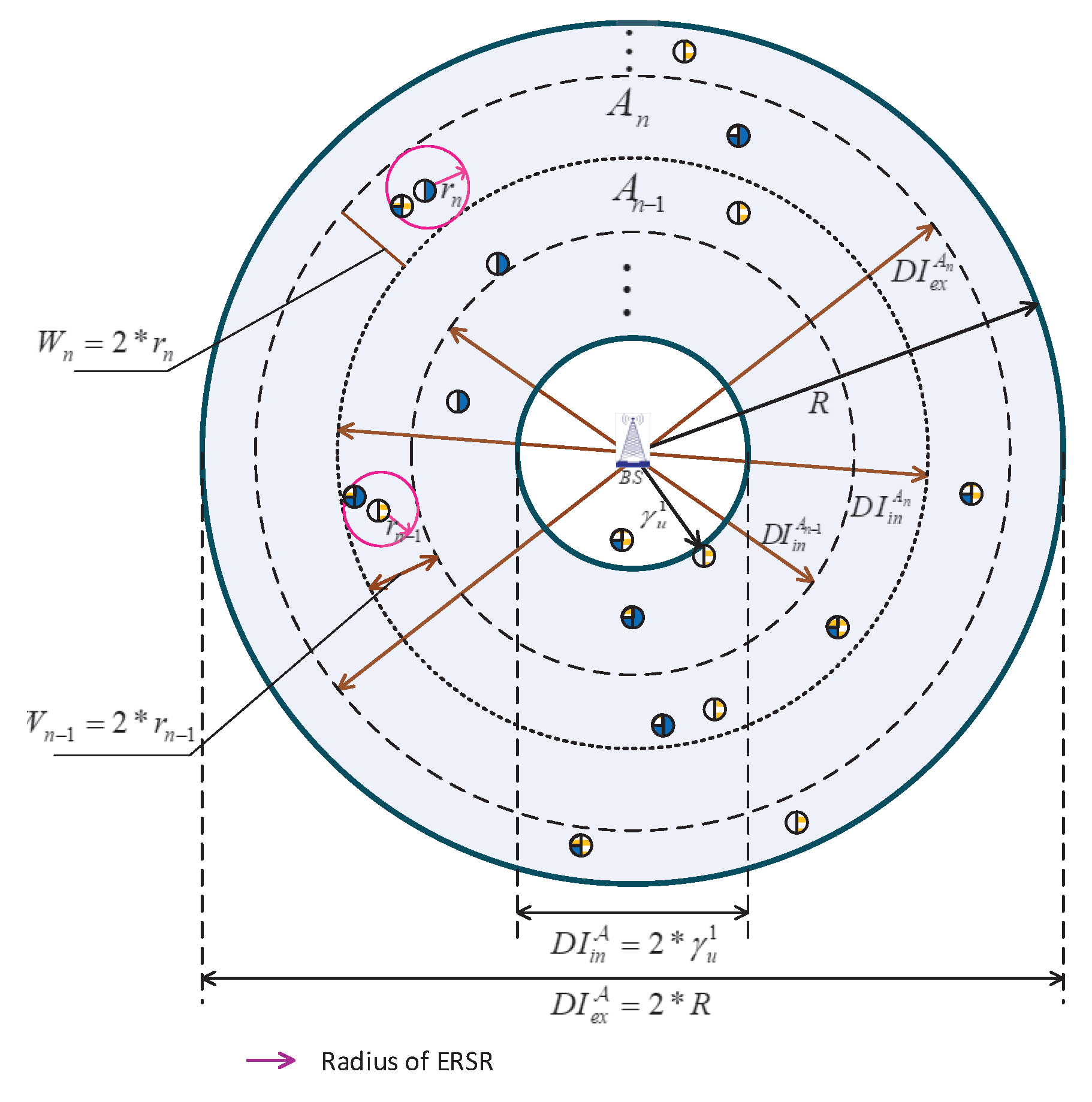
In RDUR, the circular coverage area of BS is divided into continuous AAs. The width of AA is decided by the optional radius of ERSR, which is no longer a fixed value
. RDUR is composed by three steps and shown in
Figure 2:
- (1)
Find the starting inner diameter of RDUR.
- (2)
Allocate radius of ERSR to AA.
- (3)
Determine the ERSR radius set.
3.1. Starting Inner Diameter of RDUR
Since the path loss is a key factor in determining whether MG user can successfully receive in the first stage, it is important to notice that exists. In the circular area, which is centered on BS and with as radius, MG users are all SUs. denotes the set of distance from BS to each USU, . Without loss of generality, it is assumed that elements in are ranged in ascending order.
From the analysis above, when , there is no need to implement UR selection scheme. Hence, RDUR scheme is conducted by USUs within the annular range with inner diameter and external diameter . In summary, the starting inner diameter of RDUR is .
3.2. Allocation of ERSR Radius
In D2D technology, USU uses global positioning system (GPS) location information and interacts with the information server (i.e., SU) [
16]. ETR of a user’s device is the upper bound of transmission range. Location information and training signaling of USU can be received by the SU who locates within the ETR.
For the USU who is near the cell edge, there may be no SU in the ETR. However, for the USU who is near the cell centre, several SUs may be in the vicinity. Based on this situation and the location of USU, ERSR with optional radius should be utilized to adjust the number of URs. For USU in different AAs, radius of the ERSR is different.
According to the distance between USU and BS,
is divided into
N AAs in the order from cell center to edge,
,
and
. It is obvious that
, where the inner diameter of
is denoted by
, and the external diameter is denoted by
. From the analysis of last
Section 3.1,
,
.
RDUR is intended to reduce the amount of URs of cell-center USUs through narrowing the receive range of location information and training signaling. Different ERSRs are separately allocated to the USUs within
N AAs. The radius of ERSR allocated to
is represented by
. The radius set for
is
. Actually, no more than
distance between users’ devices can be efficient in D2D technology [
17]. Therefore,
,
(In this paper,
takes discrete values less than 100 m to reduce system complexity.).
is the optional radius set of ERSR. The available
set is
.
For the ERSR set
, the relationship between the inner diameter and external diameter of
is expressed by
where
is the width of
and
.
In summary, the relationships between inner diameters and external diameters of
N AAs are expressed by
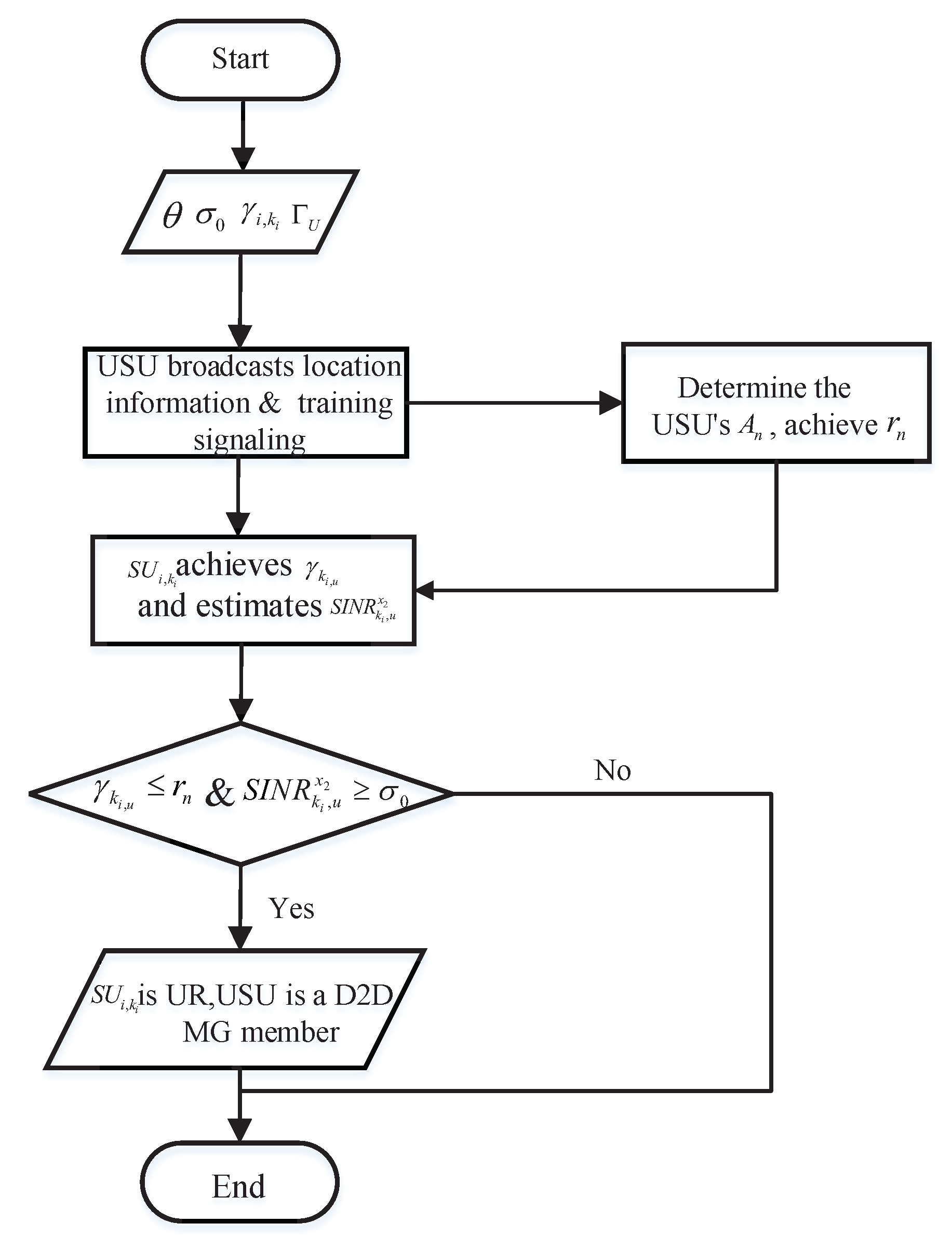
The UR selection process is shown in Algorithm 1. Its flow chat is shown in
Figure 3.
3.3. Determination of ERSR Radius Set
Corresponding to
, the total number of URs is denoted by
. The number of MG users who can successfully receive is
. The coverage efficiency is
In RDUR, the
, which maximize
, is selected to perform RDUR. The system coverage efficiency given by
| Algorithm 1 User relay (UR) selection process. |
- 1:
Every MG user achieves location information. - 2:
Every USU broadcasts location information and a training signaling. - 3:
receives location information the training signaling. The distances from to BS and USU u are measured. They are denoted by and . Simultaneously, the channel state information of USU is also obtained by . - 4:
detects the AA he (she) locates in (e.g., ) and estimates the reception SINR of each USU. If USU u can satisfy and the reception SINR of is greater than , this SU is selected as UR and the USU is a D2D MG member. - 5:
Every selected UR forwards reception signal in D2MD.
|
5. Simulation Results
Simulation results and analysis of the proposed RDUR scheme are shown in this section. Simulation parameters are shown in
Table 2.
influents the performance of COM-NOMA systems. When
was less than 0.5, there was not enough SU to be selected as UR by USU, especially when USU was near the cell edge. MG users cannot fully cooperate with each other. However, when
increased and approached to 1, the minimal channel gain of SUs who were served by BS
became smaller. In multicast technology, reception rates of all SUs were limited by
. It was more unfair to the SU with good channel condition. Therefore, we set
in the simulation. In addition, because the radius of ETR was the maxmum of
,
m. In order to reduce the complexity of simulation, we gave three optional radii of ERSR. Therefore,
. To simplify simulation, it was assumed that two MGs have the same number of users,
. This paper mainly focuses on the scenario where there is high-density MG users in the cellular. As with COM-NOMA, it was considered as high-density scenario when
.
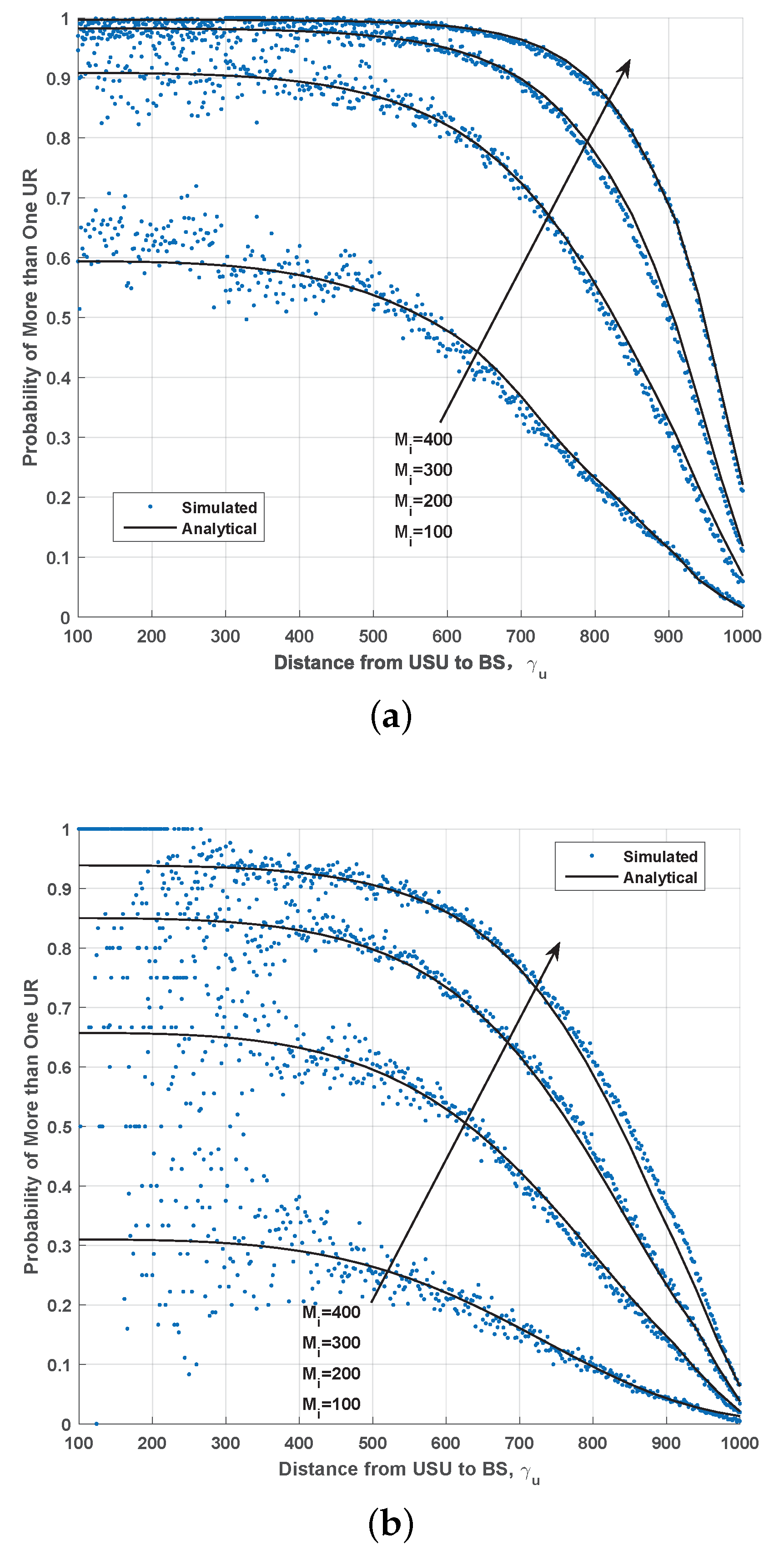
In the original UR selection scheme of COM-NOMA, which makes ETR as the ERSR of USU, i.e.,
m,
, the probability that USU selects multiple URs is shown in
Figure 4a. From the simulated results, when the distance from USU to BS was smaller than 500 m, the probability was no less than 50%. It verifies that an efficient UR selection scheme with optional ERSR to reduce UR redundancy was necessary.
In
Figure 4a,b, the analytical result was calculated from the Poisson distribution of UR in the ERSR. Poisson distribution parameter is
. Analytical probability that USU selects multiple URs is equal to
. It matched well with the simulated one. Therefore, when
, it was reasonable to use the average number of UR of
u,
, to analyze the total number of UR.
In
Figure 4b, when
is less than 500 m, simulated results are scattered. It was because that the number of USU near BS was small. In addition, the small ERSR leds to less URs. This results in the simulated probability value fluctuates greatly in the Monte Carlo simulation method.
From the simulated result, the closer the USU was to BS, the greater the probability was. The probability increases as rises. The reason is as follows. In the first stage of COM-NOMA, path loss determined whether or not MG user can succesfully receive. Therefore, the location of SU presents a trend of gathering towards BS, and the density of SU decreased as distance increased. In the second stage of COM-NOMA, the small path loss ensures that SU within USU’s ERSR can provide greater reception SINR than for USU. Therefore, the number of URs, who have been selected by an USU, is mainly decided by the density of SU. When rose, more SUs were located within the ERSR of USU. The probability that one USU was served by more than one UR rose.
5.1. Verification of Performance Analysis
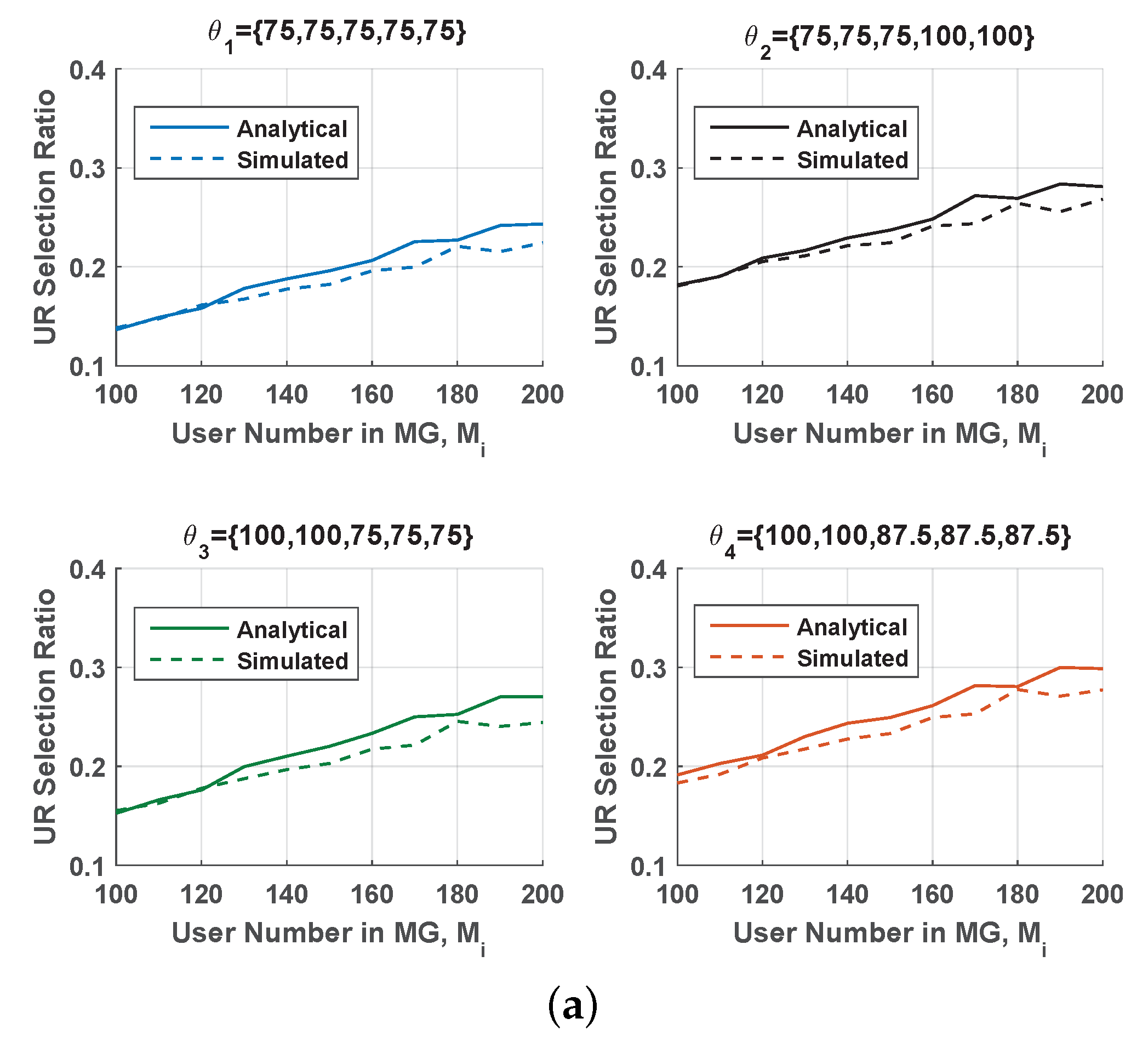
In RDUR, the ERSR radius in each AA affects the number of URs. Under different ERSR radius sets, the ratio that MG user was selected as RU is plotted in
Figure 5a. It shows that the analytical UR selection ratio was closed to the simulated one under different ERSR radius sets. When
was greater than about 120, the analytical result (
23) was bigger than the simulated one. Because in the AAs near the BS the number of SU was large,
is larger than 1. Even though ARR was introduced to reduce the number of repeated UR, in these AAs some URs are repeatedly calculated. Besides, UR selection ratio increased as
increased. This was because that the density of candidate UR in the ERSR of USU becomes large.
Obviously, as a result of small ERSR, the UR selection ratio under was smaller than that under the other three sets. It can be seen that the UR selection ratio under was larger than that under . When large ERSR was allocated to those AAs close to cell edge (e.g., m), owing to the fact that there were more USUs than cell-center AAs, the large ERSR contributes to select more URs than the situation that large ERSR is allocated to the cell-center AAs (e.g., m). Furthermore, after a thorough comparison between and , it was found that UR selection ratios were almost equal. This also verifies that different ERSR allocations can influence the number of UR.
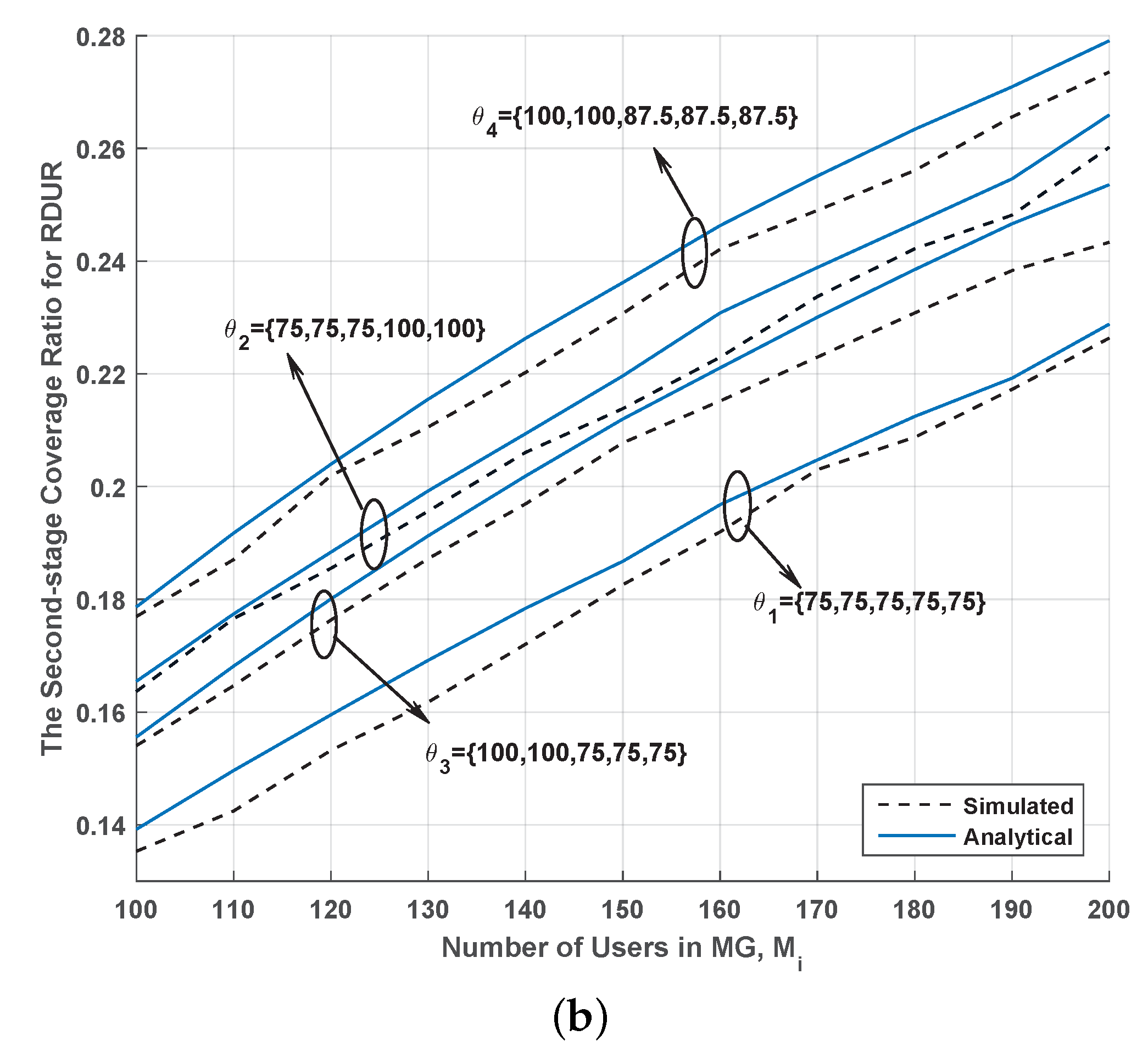
The second-stage coverage ratio performance is presented in
Figure 5b. As expected, the analytical result matches well with simulated result. The the gap between them was less than 1%, i.e., the maximum difference between the two results was less than two SUs. Furthermore, the coverage ratio under
was is smaller than that under
. The reason was that more USU locate near the cell edge. Large ERSR was allocated to
and
to select UR. It better guarantees successful reception of USU. In addition, the second-stage coverage ratio also increased with the increase of
.
5.2. Performance of RDUR Scheme
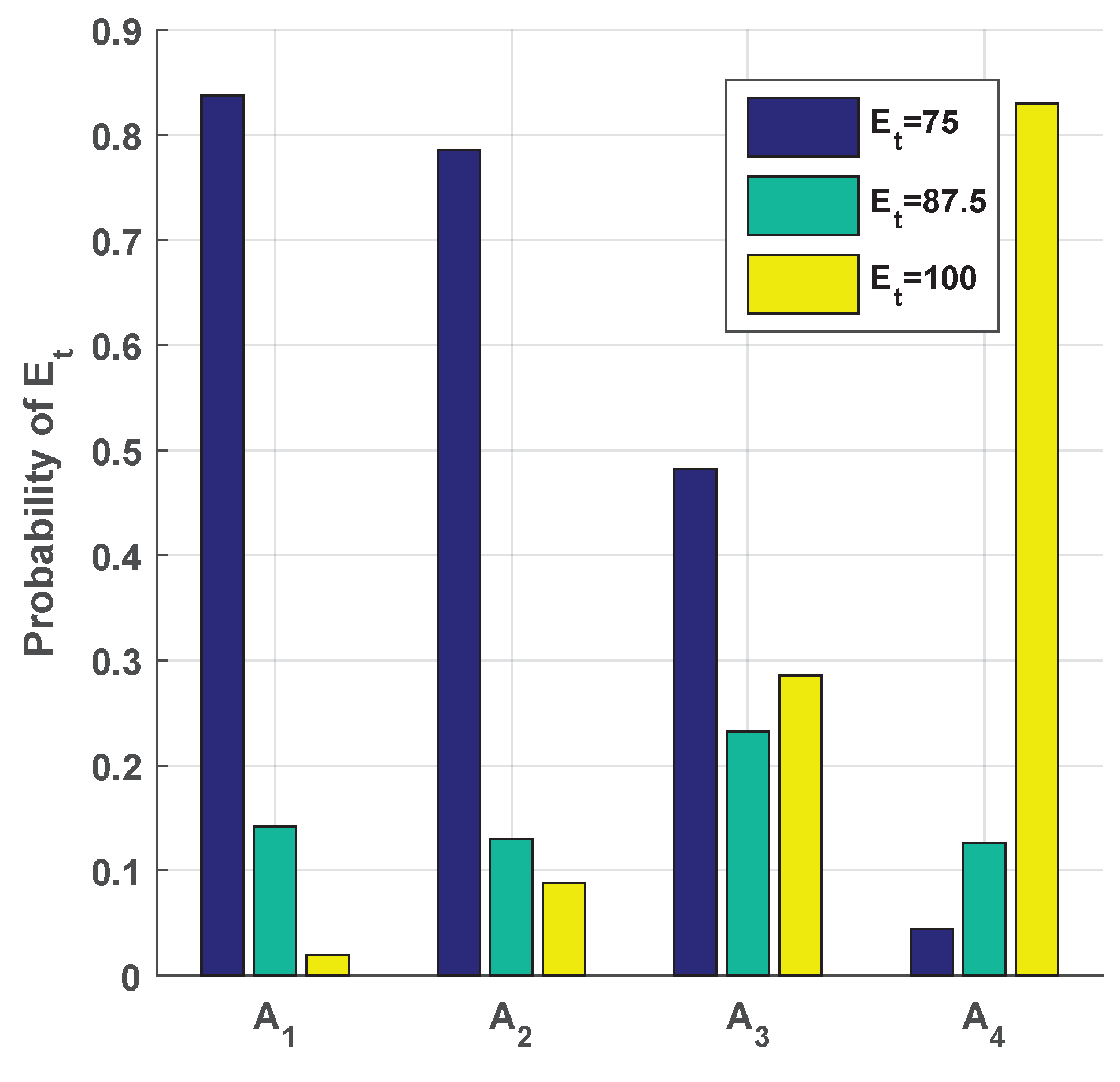
In RDUR, the probability that each optional radius of ERSR
is allocated to AA is illustrated in
Figure 6 (In
Figure 6, only the case when
is displayed. Those cases when
is equal to other values were similar to that when
, so they were not shown in this paper.). When the circular area covered by BS was divided into four AAs, in order from cell center to cell edge, four AAs are
,
,
,
and shown on the horizontal axis. Across 2000 Monte Carlo runs, it was found that a small radius of ERSR,
m, was allocated to the AA nearest to the BS,
, with the most probability 84%. A large radius of ERSR,
m, was most likely to be allocated to the cell-edge AA,
. The probability reached to 83%. It increased as the distance from BS increased. As expected, to reduce unnecessary UR, after RDUR, small ERSR should be allocated to the AA with high density of SU. To ensure that USU can select more URs and had more chances to receive successfully, large ERSR was allocated to the AA with low density of SU.
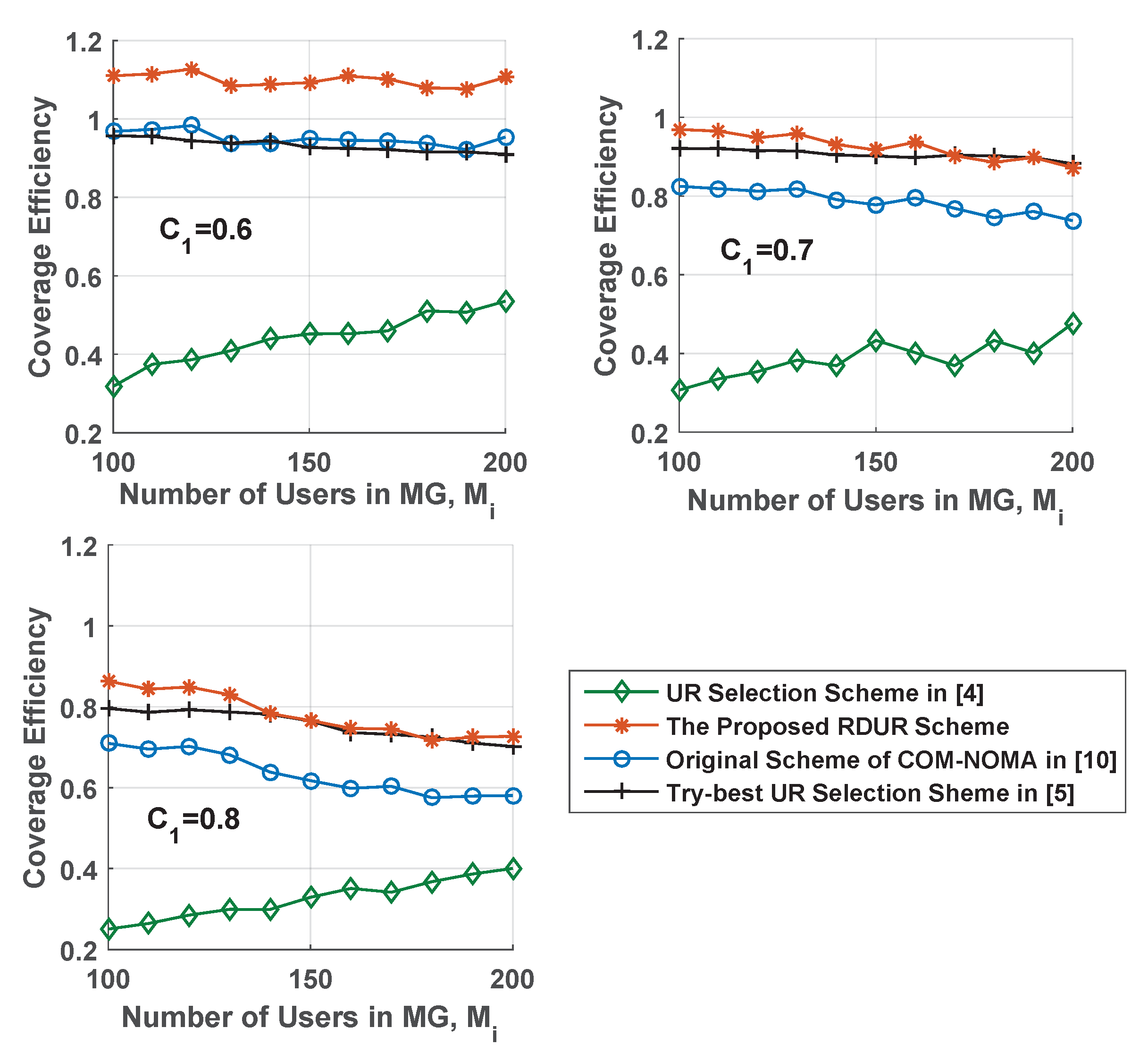
Because the proposed RDUR was an enhanced relay selection scheme aiming at NOMA-based cooperative multicast system, and the other UR selection schemes working for OFDMA-based cooperative multicast system do not make the ETR of user’s device as a restriction, which results in that no matter how far the SU is from the USU, it can be selected as UR. We compared RDUR with the original UR selection scheme of COM-NOMA systems and two other UR selection schemes in
Figure 7 and
Figure 8. The UR selection scheme proposed in [
4] made all SUs as URs to forward data for USUs. In the try-best UR selection scheme [
5], the nearest SU to each USU was selected as UR. In these two schemes, the ETR of user’s device was not taken into consideration. But it indeed impacted the performance of system. Therefore, for fairness, in the simulation, the same as RDUR scheme and original scheme of COM-NOMA systems, ETR was also a restriction for these two schemes. We made the second stage as the focus of performance simulations. Because
was a fixed value, after the first stage there are
SUs. The total number of successful users was decided by UR selection scheme in the second stage. The comparison of coverage efficiency was conducted in
Figure 7.
In comparison to the original scheme of COM-NOMA systems, via RDUR scheme, the coverage efficiency increased by at least about 14% under the same
. This is because USU selects URs with changeable ERSR. When the density of SU near the BS was large, the appropriate radius of ERSR was selected from
unlike the original UR selection scheme in COM-NOMA. In COM-NOMA, those SUs within the ETR were selected as URs. The area of relay selection was smaller in RDUR than that in COM-NOMA. Some SUs who were URs in COM-NOMA were not selected in RDUR. The number of URs reduced. In comparision to the try-best scheme, when
, the coverage efficiency enhances. However, when
, the coverage efficiency gap between the two schemes is small. This was because when
became larger, the distance between SU and USU decreased relatively, and the nearest SU to USU was also within his/her ERSR. Hence, via these two schemes, there was little difference in the number of URs or the number of USUs that can be successfully received. All of the SUs were selected as UEs in the scheme proposed in [
4], the advantage of RDUR was obvious.
For the RDUR scheme, the coverage efficiency decreases with the increase of . The reason is that when is not large enough, large means a small number of USU and high density of SU. The number of second-stage successful user is small and that of candidate UR is large. Correspondingly, the coverage efficiency becomes small. This also explains that why the coverage efficiency decreases with the increase of .
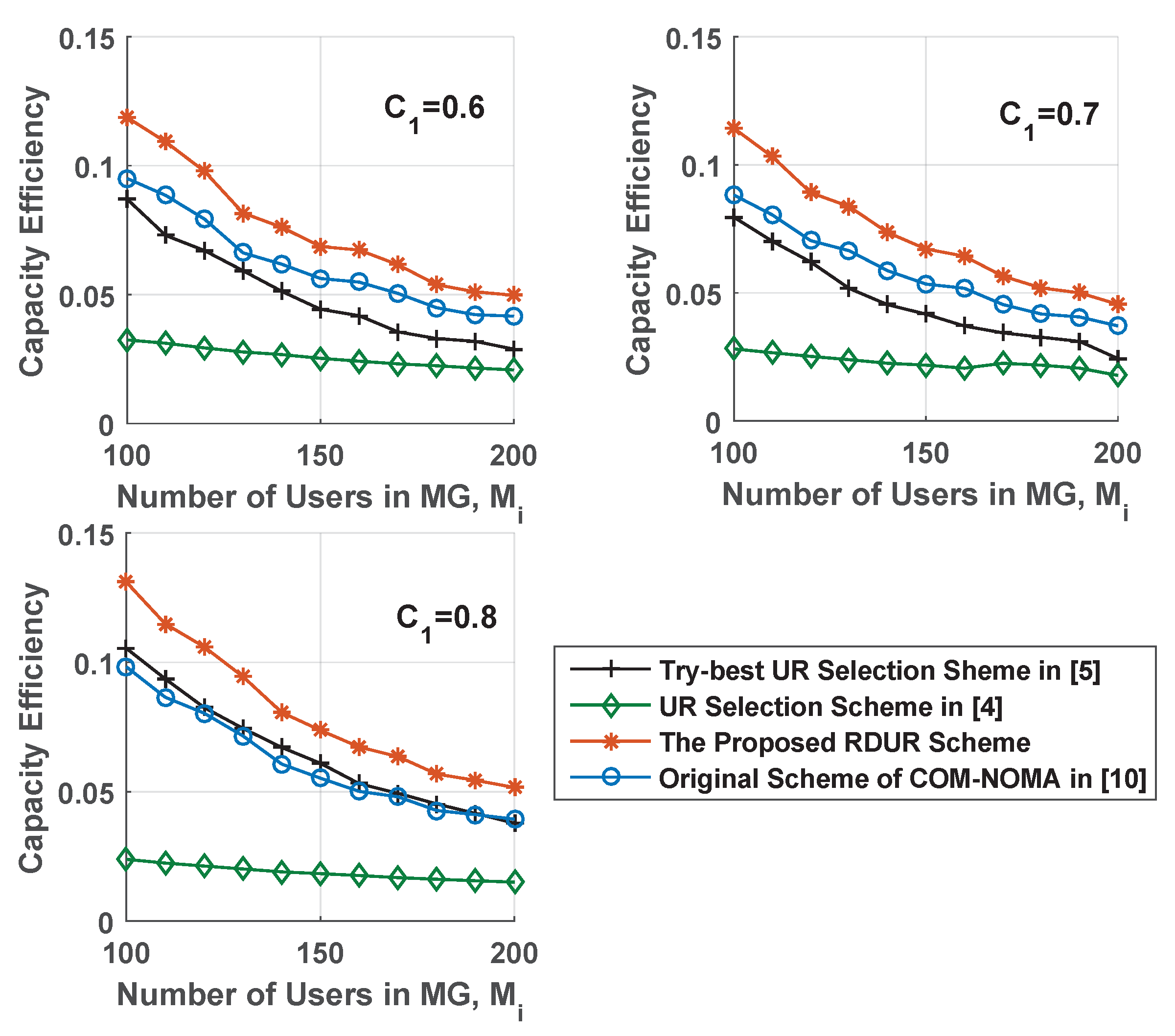
To investigate the performance of RDUR further, the capacity efficiency is simulated in
Figure 8. Capacity efficiency was to describe the contribution of a single UR to multicast capacity. It equalled to the ratio of the second-stage D2MD capacity (The second-stage D2MD capacity is calculated by the same method as [
10].) to the total number of URs. From the simulation result, the capacity efficiency after RDUR was larger than that after the original scheme of COM-NOMA and the other two schemes. After RDUR, even though the quantity of URs was smaller than that in COM-NOMA, multicast capacity of the second stage is the sum capacity of each D2MD group, which employs UR as sender. When small ERSR was used to select URs, the distance between senders and USUs in each D2MD group decreased. In the influence of smaller loss path than original scheme, the transmission rate of D2MD is higher. The total capacity of the second stage will not decrease too much. At the same time, the number of UR was smaller than the original scheme. Thus, the capacity efficiency after RDUR scheme enhances in comparision to the original scheme. With the increase of
, the density of users became large. Via the same UR selection scheme, more URs taking part in cooperation impaired the capacity efficiency. Therefore, capacity efficiency decreased with
.
Even though there was little difference in coverage efficiency between RDUR scheme and the try-best scheme under , the capacity efficiency performance of RDUR was better. It is because that USU can receive data from multiple URs who are within his/her ERSR. In the try-best scheme, USU only receives data from the USU nearest to him (her). The multicast capacity of the second stage after RDUR scheme is larger than that after try-best scheme.
6. Conclusions and Future Work
The two-stage COM-NOMA realizing the inter-cooperation between two MGs had improved coverage performance. However, in the second stage, some SUs were selected as URs with fixed ERSR, which is equal to the ETR of D2D. It resulted in low coverage efficiency. RDUR was proposed to solve this problem. The circular coverage range of BS was divided into several continuous AAs. Each AA was allocated corresponding ERSR. Expressions of UR selection ratio and coverage ratio are derived. The ERSR radius set that optimized system coverage efficiency was selected to perform UR selection. Main simulation results showed that for different ERSR radius sets, the analytical results of UR selection ratio and coverage ratio matched well with their simulated results. In comparision to other UR selection schemes, via RDUR, the capacity efficiency of the second-stage D2MD had been improved. The coverage efficiency was at least 14% higher than the original UR selection scheme of COM-NOMA systems.
Through RDUR, the coverage efficiency of COM-NOMA systems was improved. However, the radius of ERSR could only be chosen from several fixed values. It diminishes coverage efficiency of COM-NOMA system. In fact, in oder to maximize the coverage efficiency, USU should adaptively achieve the radius of ERSR according to his(her) own location information. In the future, a UR selection scheme with adaptive ERSR will be researched. Any distance smaller than 100 m can be chosen as the ERSR radius by USU.