To fully verify the effectiveness of the proposed DSGE algorithm, we conducted extensive experiments on two categories of face databases. One includes the AR database [
49] and the Extended Yale B database [
50] which are captured in strictly controlled environments, the other contains the LFW database [
46] and the PubFig database [
51] which are collected in real environments. PCA [
10] was applied as a preprocessing step for avoiding matrix singularity, and 98% of the image energy is retained.
4.1. Experiments on the AR Database
The AR database contains over 4000 frontal-view face images of 126 individuals with different facial expressions, lighting conditions, and occlusions (including sunglasses and scarves). These images were collected under strictly controlled experimental conditions. In this section, we selected 3120 images of 120 individuals (65 males and 55 females) which were taken in two sessions (separated by two weeks), and each session of one individual contains 13 face images in which the first four images are interfered by expression, the fifth to seventh images are influenced by light conditions, and the remaining six images have occlusion interference factors (three images with sunglass and three images with scarf).
Figure 3 provides some samples of one individual in two sessions and the face portion of each image was normalized to 50 × 40 pixels. In this section, we do three experiments for proving the effectiveness of DSGE on the AR database.
Experiment 1: We first evaluated the effectiveness of DSGE against the interference of expression change and light condition of facial images on the AR database. In this experiment, we selected seven images without occlusions in session one for training, and choose the corresponding seven images in session two for testing. Since the training samples and testing samples were selected from two different sessions, the influence of time variation residing in facial images still needs to be considered. We respectively used LDA [
11], LPP [
22], NPE [
23], SPP [
33], DSNPE [
39], DP-NFL [
52], SRC-DP [
53] and the proposed DSGE for dimensionality reduction respectively, and exploited SRC classifier for face recognition, in which L1-Ls [
54] was adopted to calculate the sparse representation coefficients. The recognition rate of each method and the corresponding dimension are listed in
Table 1. In detail DSGE achieved the best performance with 12.74%, 10.24%, 8.69%, 9.17%, 1.31%, 5.58% and 2.18% improvements over LDA, LPP, NPE, SPP, DSNPE, DP-NFL and SRC-DP, respectively. Thus it can be seen that DSGE was not only unaffected by the interference of facial expression and light condition, but also effectively overcame the influence of time variation on human face.
Meanwhile, we randomly selected the total seven images without occlusions in session one and session two for training, and the remaining seven images for testing.
Figure 4 gives the maximal recognition rate versus the variation of dimension. From it, we can see that DSGE outperformed other methods when the dimension is larger than 30. Therefore DSGE is insensitive to variations of dimension and can well characterize the discriminative structure of facial images disturbed by facial expression, light condition and time variation.
Experiment 2: We further demonstrated the effectiveness of DSGE against the interference of real occlusion on the AR database. In this experiment, we assessed it from three aspects. (1) Sunglass occlusion. We selected seven images without occlusion and one image with sunglass in session one for training, and choose seven images without occlusion in session two and the remaining five images with sunglass in session one and session two for testing. (2) Scarf occlusion. The selection of samples is similar to the above. We selected seven images without occlusion and one image with scarf in session one for training, and choose seven images without occlusion in session two and the remaining five images with scarf in session one and session two for testing. (3) Mixed occlusion of sunglass and scarf. We selected seven images without occlusion and one image with sunglass and one image with scarf in session one for training, and choose the remaining images in session one and the whole images in session two for testing.
Table 2 presents the recognition rate of these methods under three real occlusion conditions. Although the performance of DSGE is slightly lower than that of SRC-DP under sunglass occlusion and scarf occlusion, it outperforms all the other methods by more than 2% under the mixed occlusion. Therefore it can be seen that DSGE is more conducive to obtaining the intrinsic manifold structure embedded in the mixed occlusion images.
Experiment 3: We comprehensively assessed the performance of DSGE against all the interference including facial expression, light condition, real occlusion and time variation on the AR database. In this experiment we randomly selected the total 13 images in session one and session two for training, and choose the remaining 13 images for testing. We repeated this process 10 times by using 1NN classifier and SVM classifier respectively, and then obtained the experimental results as shown in
Table 3. From it, we can see that DSGE was still superior to other methods which means that the proposed DSGE was free from the influence of mixed interference factors, and can well characterize the underlying manifold structure of data.
4.2. Experiments on the Extended Yale B Database
The Extended Yale B database contains 2414 frontal-face images of 38 individuals with different light conditions. Each individual had about 64 images. These images were resized to 32 × 32 pixels, and some samples of one person are shown in
Figure 5. In this section, we did two experiments for evaluating the performance of DSGE on the Extended Yale B database.
Experiment 1: First, for proving the effectiveness of DSGE against the interference of illumination with different degrees on the Extended Yale B database, we randomly selected N images of each individual as training samples, and the remaining 64–N images were used as test samples. In this experiment, the value of N is 10, 20 or 30. In order to facilitate the comparison with the state-of-the-art algorithm named GRSDA [
41], we adopted the nearest neighbor classifier with the identical settings as GRSDA to conduct experiments. The best recognition rate of each method and the corresponding dimension are listed in
Table 4. It should be noted that the experimental results of methods except for DSGE in
Table 4 are all cited from Ref [
41]. From it, we observed that whether the number of training samples is 10, 20 or 30, DSGE was always superior to the other methods and it outperformed GRSDA by 6.58%, 6.25% and 4.79% respectively. This demonstrates that the proposed DSGE has the ability of eliminating the interference of light change and is insensitive to the number of training samples.
Experiment 2: For further demonstrating the effectiveness of DSGE against occlusion on the Extended Yale B database, we randomly selected 14 images of each individual and added noise occlusion block with black and white dots with random distribution. The location of noise occlusion block was random and the ratio of size between noise occlusion block and original image was also random where the ratio parameter ranged from 0.05 to 0.15. Some occlusion samples of one person are depicted in
Figure 6. In this section, we did the following experiments by two cases. (1) We randomly selected 32 images per person which included 14 images with noise occlusion block, and the remaining images for testing. (2) We randomly selected 32 images per person which contained seven images with noise occlusion block, and the remaining images for testing. All experiments in each case were conducted by 1NN classifier and SVM classifier respectively, and were repeated 10 times. The experimental results are shown in
Table 5. From it, we observed that despite the location and size of noise occlusion block in facial images being random, the performance of DSGE was still not affected. By using the 1NN classifier and SVM classifier in the first case, the average accuracy and standard deviation of DSGE were 94.84 ± 1.82% and 95.96 ± 0.87%, respectively, which ranked the highest. When reducing the number of occlusion images, such as in case two, the recognition accuracy of DSGE also increased and still preserved optimal performance. Therefore, DSGE had the superior capacity against the interference of occlusion block whether on the 1NN classifier or SVM classifier.
4.3. Experiments on the LFW and PubFig Databases
The Labeled Faces in the Wild database (LFW database) [
46] is a challenging unconstrained face database which is collected from the Internet. It has a total of 13,233 facial images from 5749 different individuals, of which 4069 individuals only have a single image. To perform face recognition, in this section we constructed a new subset by gathering the subjects which had more than 20 samples from the original LFW database. The new subset had a total of 3023 facial images. Since these images are taken in completely real environments with non-cooperative subjects, there were complex backgrounds and some non-target subjects in the captured images. We adopted the face detection algorithm proposed in [
58] to remove the interference of background and non-target subjects and croped images into 128 × 128 pixels. Some samples of one person are illustrated in
Figure 7.
The PubFig database [
51] is similar to the LFW database which is also collected from the Internet including 58,797 images of 200 different individuals. In our experiments, we randomly selected 99 individuals from the original database and chose 20 images of each individual to construct a new subset, of which 10 images were for training and the remaining images for testing. Similarly we also exploited the face detection method proposed in [
58] to preprocess images and the size of cropped facial image was 128 × 128 pixels as shown in
Figure 8.
In this section, we also conducted three experiments to further demonstrate the effectiveness of DSGE on two challenging facial databases. On the LFW and PubFig databases, we all randomly selected 10 images for training and reserved the remaining images for testing.
Experiment 1: We adopted PCA [
10], LDA [
11], NPE [
23], LSDA [
59], SPP [
33], DSNPE [
30] and our proposed DSGE for dimension reduction and exploit the SRC classifier for recognition. The recognition rate curve of each method versus the variation of dimensions is presented in
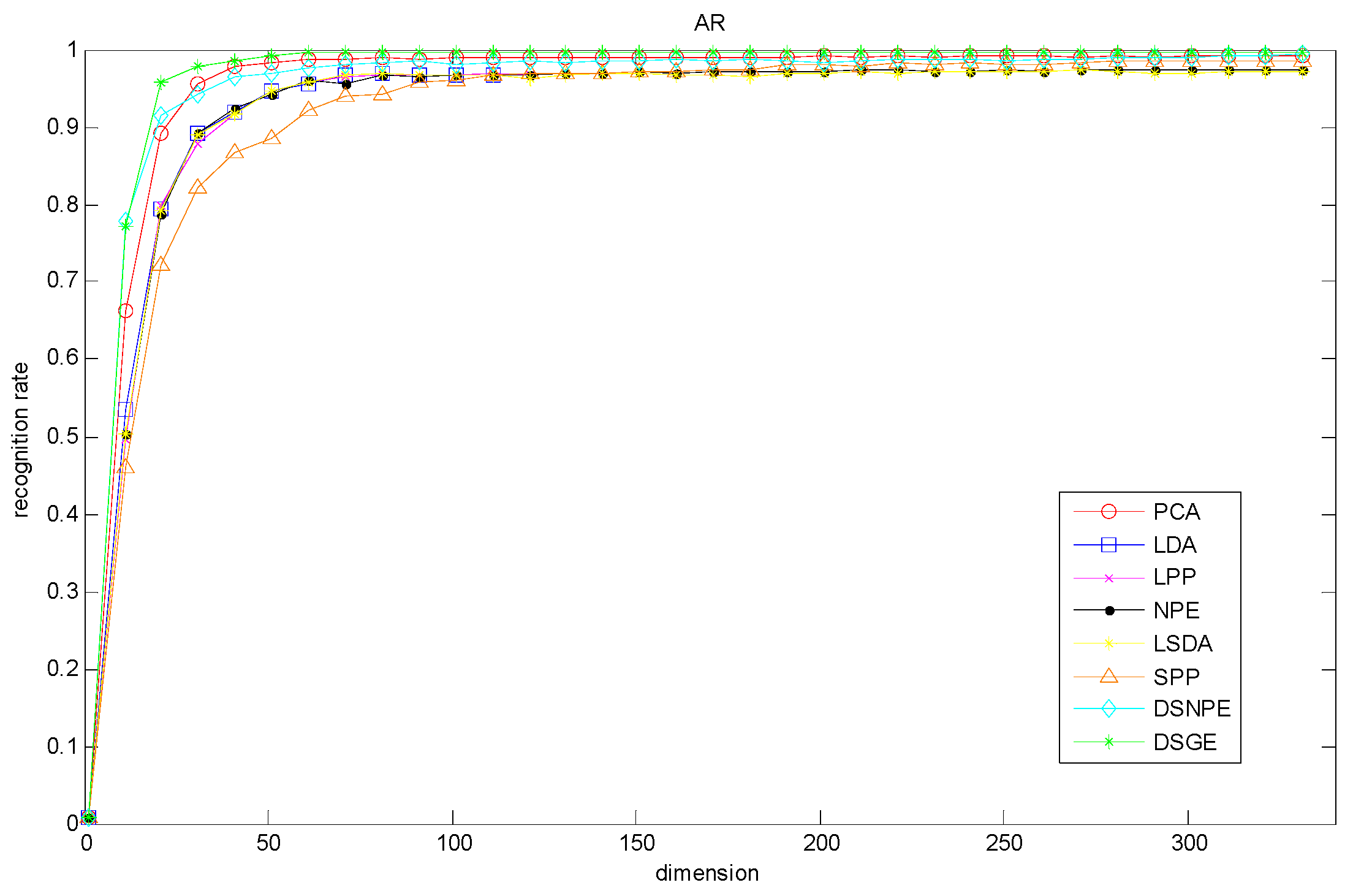
Figure 9, and
Table 6 lists the optimum accuracy of each method and the corresponding dimension. From them, we made observations that DSGE was always superior to the other methods regardless of the variation of dimension. More precisely, on the basis of the optimal dimension, the maximal recognition rates of DSGE on the LFW database and PubFig database were 64.84% and 37.88% respectively. It outperformed the second-placed LSDA (or LPP) by 8.54% on the LFW database, and surpassed the second-placed DSNPE by 3.53% on the PubFig database. Thus it can be seen that the performance of DSGE was not influenced by the variations of dimension and has absolute advantage in characterizing the discriminative manifold structure of unconstrained face images which are collected from completely real environments.
Experiment 2: For further evaluating the performance of DSGE on different classifiers, we also repeated the above experiment by 1NN classifier and SVM classifier respectively, in which the selected dimension of each method was identical with that in the SRC classifier as depicted in
Table 6. The corresponding experimental results are presented in
Table 7 and
Table 8. From them, we made two observations:
(1) The recognition rates of DSGE were respectively 48.94%, 60.55% and 64.84 by successively adopting 1NN classifier, SVM classifier and SRC classifier on the LFW database, which were consistently higher than those of other methods. In the same way, DSGE still outperformed the other methods regardless of which classifier is used on the PubFig database. Thereby we make conclusion that on the two challenging unconstrained face databases the performance of DSGE is not affected by the selection of classifier. Meanwhile whichever classifier is exploited, DSGE still maintains the best performance.
(2) The average value and standard deviation of recognition rates on three classifiers are shown in the last columns of
Table 7 and
Table 8, which can evaluate the adaptability and stability of methods on different classifiers. From them, we can see that the average recognition rate of DSGE on the LFW database is 58.11% which was the maximum, and the standard deviation of recognition rate of DSGE is 8.23% which was the minimum. Similarly, the average recognition rate of DSGE on the PubFig database is still maximal, while the standard deviation of recognition rate of DSGE is slightly higher than that of SPP. Since the average value is larger, the performance of method is more superior, conversely, the smaller the standard deviation is, the more stable the performance of method is. In view of the above results, we conclude that the performance of DSGE is not only unaffected by the selected classifier but also has better stability which does not greatly fluctuate with the classifier.
Experiment 3: Apart from the accuracy of face recognition, the computational cost is also another important issue for each method. Since these methods belonging to Sparse Graph Embedding Framework (SGEF), such as SPP, DSNPE and the proposed DSGE algorithm are all needed to construct adjacent graphs by using sparse regularization optimization algorithms [
54], their computational cost is much larger than that of the classical dimensional reduction algorithms, for example PCA, LDA, LSDA, LPP and NPE. Therefore in this section we mainly discuss the computational cost of SSP, DSNPE and our proposed DSGE algorithm which include the sparse adjacent graph construction time t
C and the low-dimensional projection time t
P. All the experiments were conducted by using Matlab R2013a software on the 2.50 GHz Intel (R) Core (TM) i5-2450M CPU with 4GB RAM. The experimental results on the LFW database and PubFig database are listed in
Table 9 respectively. We made the following observations:
(1) As shown in
Table 9, the low-dimensional projection time t
P of SPP, DSNPE and DSGE on the LFW database and PubFig database is far less than the sparse adjacent graph construction time t
C of them. For example, on the LFW database, the sparse adjacent graph construction time of SPP is 507.04 s, while the low-dimensional projection time is only 0.05 s. The value of t
C is about 10,000 times as long as that of t
P by SPP algorithm. Meanwhile the t
C and t
P of other methods also present the similar relationship. Therefore we consider that the computational complexity of SPP, DSNPE and DSGE mainly concentrates on the stage of sparse adjacent graph construction, while the running time of low-dimensional projection can be neglected.
(2) As illustrated in the last row of
Table 9, the low-dimensional projection time t
P of SPP, DSNPE and DSGE are fairly close, with values that fluctuate around 0.1 s on the two databases. This explains that no matter how different the theories of methods are, the running time of low-dimensional projection is similar. Hence, it is appropriate to exploit the running time of sparse adjacent graph construction to measure the computational cost of methods.
(3) Further analyzing the experimental results illustrated in the first row of
Table 9, we find that the sparse adjacent graph construction time t
C of DSGE is about 13 times faster than that of SPP, and is about five times faster than that of DSNPE on the LFW database. Similarly on the PubFig database, DSGE also provides the least computational complexity. The main reason is that SPP constructs the sparse adjacent graph based on the whole training samples, whereas those of DSNPE and DSGE are respectively constructed by the intra-class training samples and the inter-class training samples. Hence SPP consumes more time in contrast to DSNPE and DSGE. Meanwhile, in this paper we respectively adopt the intra-class reconstruction weight optimization algorithm and the inter-class reconstruction weight optimization algorithm (described in
Section 3.1) to directly calculate the intra-class reconstruction weight and the inter-class reconstruction weight of DSGE which greatly reduces the running time of sparse adjacent graph construction. Therefore compared to DSNPE, DSGE still has competitive advantage in computational cost. In conclusion our proposed DSGE algorithm greatly reduces the computational complexity without sacrificing accuracy or quality and provides a new research idea for the following practical application.
4.4. Comparison with Deep Learning Algorithms
In the above sections we have carried out many experiments on the unconstrained face databases to demonstrate the effectiveness of our proposed method compared to the traditional subspace learning algorithms, such as LPP [
22], NPE [
23], SPP [
33] and DSNPE [
39] etc. However, as we all know, in recent years Deep Learning (DL) technology has already attracted widespread attentions due to its superior performance in many practical applications, such as face recognition [
6,
7], object tracking [
60,
61], image restoration [
62,
63], pose estimation [
64,
65], etc. Hence, in this section we also further compare the performance between DL-based algorithms and our proposed DSGE method, and analyze the advantages of using DSGE algorithm in the unconstrained face recognition. The experiments were still conducted on two challenging unconstrained face databases, i.e., LFW database and PubFig database, and the selections of training samples were identical to those in
Section 4.3.
Experiment 1: For comparing with the experimental results of DL-based algorithms presented in [
5] conveniently, we conducted the experiment on the PubFig 83 dataset [
66] which was used in [
5]. In detail, PubFig 83 dataset is the subset of PubFig database and has 13,002 face images (8720 training samples and 4282 testing samples) representing 83 individuals. In this experiment, the input data of DSGE method is the 1536-dimensional features [
66] which are identical with the experimental settings of [
5].
Table 10 lists the corresponding experimental results, in which the recognition rates of DeepLDA [
67], Alexnet [
68], VGG [
69], MPDA [
70] and LDA [
71] are all directly quoted from [
5]. We make observations that:
(1) It is obvious that VGG achieves the highest accuracy compared to the non-DL-based algorithms, as well as the other two DL-based algorithms, i.e., Alexnet and DeepLDA. Alexnet and DeepLDA are directly trained by 8720 images, while VGG is conducted with a pre-trained model, which result in a better performance. Thus we find that DL-based algorithms need massive training samples or pre-trained model to achieve superior performance.
(2) As shown in
Table 10, Alexnet and DeepLDA also perform worse than the non-deep learning methods, such as MDPA, LDA and our proposed DSGE. Especially, the recognition rate of Alexnet is 17.13% lower than that of DSGE, and the recognition rate of DeepLDA is 36.78% lower than that of DSGE. This further demonstrates that in the case of small-sample learning, DL-based algorithms have limitations. In the same way, without regard to DL-based algorithms, compared with the other two subspace learning methods, i.e., MDPA and LDA, our proposed DSGE method can still obtain the highest accuracy on the PubFig 83 dataset. Thus we conclude that our proposed DSGE method is more conducive to obtaining the discriminative manifold structure of unconstrained face images based on its improvements. Furthermore, in the condition of limited samples and limited computing resources, DSGE also can present certain advantages compared to DL-based algorithms.
Experiment 2: For further evaluating the effectiveness of DL-based features, we first adopted Histograms of Oriented Gradients (HOG) descriptor [
72] and VGG [
69] to extract image features of LFW and PubFig databases respectively, and then employed them into sparse graph embedding methods for unconstrained face recognition. The corresponding experimental results are shown in
Table 11. From it we can see that:
(1) Whether adopting the hand-craft features (HOG features) or the DL-based features (VGG features) into sparse graph embedding methods, i.e., SPP, DSNPE and our proposed DSGE, their recognition performances all have been significantly improved. For example, on the LFW database, the recognition rates of pixel-based methods do not exceed 70%, while those of feature-based methods all exceed 80%. Thus we conclude that the features of images are more discriminative than the original images. It is more conductive to improve the unconstrained face recognition accuracy by combining feature representations with sparse graph embedding methods.
(2) As mentioned above, the feature-based methods outperform the pixel-based methods, but there is still some performance difference between them. For example, on the PubFig database, the recognition rate of DSGE-HOG is far lower than that of DSGE-VGG, despite that it outperforms DSGE-pixels by 13.64%. Thus we find that compared to the hand-craft features, DL-based features are more accurate and more discriminative.
(3) Finally, as shown in
Table 11, in the condition of adopting VGG features, our proposed DSGE still outperforms other methods. In detail, DSGE-VGG outperforms SPP-VGG and DSNPE-VGG by 0.04% and 0.37% on the LFW database, and it outperforms SPP-VGG and DSNPE-VGG by 3.43% and 0.91% on the PubFig database. Thus we conclude that DSGE still has the optimal performance.