On Secrecy Performance of the Strong User in MISO-NOMA Visible Light Communication System

Abstract

Since successive interference cancellation in non-orthogonal multiple access (NOMA) is enabled at the strong user to remove the signal of the weak user, if the information safety of the strong user cannot be ensured, neither can the weak user. The physical-layer security of the strong user in a two-user multiple-input single-output (MISO)-NOMA visible light communication (VLC) system in the presence of a passive eavesdropper was studied, with multiple light-emitting diodes (LEDs) transmitting and a photodiode (PD) receiver receiving. To demonstrate the superiority of the MISO-NOMA VLC system over the SISO-NOMA VLC system, numerical simulations were made, and results show that the secrecy outage probability (SOP) performance of the strong user in the MISO-NOMA VLC system is superior to that in the SISO-NOMA VLC system. Furthermore, the SOP of the strong user depends highly on the room arrangement, the difference between the legitimate channel and eavesdropper channel, and the properties of the LEDs and PD.

1. Introduction

As a promising alternative complementary to current radio frequency (RF) wireless communications, visible light communication (VLC) can simultaneously provide illumination and data communication by exploiting the existing lighting infrastructure, and it has been regarded as a potential technology for indoor 5G communications, Internet of Things (IoTs), and device-to-device communications [1].

Due to the broadcasting nature, VLC is especially applicable for massive connectivity, supporting multiple users to access the same wireless resource. Non-orthogonal multiple access (NOMA) as a novel multiple access protocol where multiple users are multiplexed in the power domain via superposition coding at the transmitter and de-multiplexed by successive interference cancellation (SIC) at the receiver is particularly suitable for VLC systems. The throughput [2], coverage probability [3], reliability [4], spectral-energy efficiency [5], and users’ fairness [6] of NOMA VLC systems have been well investigated. Meanwhile, the security problem of NOMA VLC systems has become increasingly important [7]. If eavesdroppers appear at the same region illuminated by light-emitting diodes (LEDs) as the NOMA legitimate users, the useful information is inevitably susceptible to eavesdropping. Physical-layer security [8] has emerged as a promising approach to protect information from eavesdropping and has drawn much attention in recent years of those who aim to achieve secure transmission at the physical layer.

With the development of multi-antenna technology, optical multiple-input multiple-output (MIMO) or multiple-input single-output (MISO) VLC systems can greatly enhance physical-layer security by fully exploiting the spatial degree of freedom. Meanwhile, to satisfy the requirement of massive connectivity for the next wireless communication, there is an urgent need for multiple users to access the communication system. However, existing work on the security problem of MISO (or MIMO) VLC systems focused mainly on a single legitimate user suffering security threats from one or multiple eavesdroppers [9,10]. As to the existing MISO-VLC systems with multi-user [11,12], although precoding has been used to improve secrecy performance, multiple users access the system in the conventional orthogonal multiple access (OMA) scheme, which greatly limits the accessed number of users. Applying NOMA to a multi-user MISO VLC system can not only take advantage of the potential of NOMA to really support multiple users, but can also enhance the physical-layer security via multi-antenna technology, such as beamforming/precoding, artificial noise and transmit antenna selection technology, etc. However, thus far, the secrecy performance of a MISO-NOMA VLC system has not yet been studied. It is necessary to investigate the physical layer security of MISO-NOMA VLC systems. This is due to the fact that: (1) to effectively support massive connectivity, which is important for ensuring the forthcoming 5G network to support the IoTs functionalities, it is necessary to study on NOMA VLC systems; (2) in practical application, multiple LEDs are often deployed to meet the lighting requirements. Multiple LEDs assignment enables the MISO or MIMO transmission scheme and also constructs a multi-antenna transmitting system. To meet the practical LEDs assignment and further improve the physical-layer security performance of multiple NOMA users, multi-antenna technology with multiple LEDs at the transmitter could be adopted.

In this paper, we investigate the physical-layer security of a two-user MISO-NOMA VLC system, where multiple LEDs serve two legitimate users via downlink NOMA in the presence of a passive eavesdropper. All the LEDs are utilized to transmit signals with equal power. Both the legitimate users and the eavesdropper employ a photodiode (PD) receiver to detect and receive the optical signal. Selection combination technology is utilized at the legitimate users and the eavesdropper. The optical signal radiated from LED to the user with weak channel gain (called a weak user) should be first decoded by the user with strong channel gain (called a strong user) so as to enable SIC at the strong user. Therefore, the secrecy performance of the weak user is conditioned on the fact that the strong user does not release any information about the weak user [13]. Hence, the physical-layer security of the strong user in a two-user MISO-NOMA VLC system is analyzed and measured by the secrecy outage probability (SOP) performance criteria. To demonstrate the superiority of the MISO-NOMA VLC system over the single-input single-output (SISO) NOMA VLC system, numerical simulations are made based on typical parameters of indoor LED transmitters and PD receivers, and results show that the SOP performance of the strong user in the MISO-NOMA VLC system is superior to that in the SISO-NOMA VLC system. In addition, the SOP of the strong user depends highly on the room arrangement, the difference between the legitimate channel and the eavesdropper channel, and the properties of the LEDs and the PD.

It should be noted that in the proposed two-user MISO-NOMA VLC system, each of the legitimate users and the eavesdropper is with a single PD receiver, which is the most common case until now. As to a MIMO-NOMA VLC system where the legitimate users and/or the eavesdropper are with multiple PD receivers, it is necessary to take more factors into consideration, such as the geometric layout of the PD receivers and the complicated channel estimation [14,15] for the MIMO case, which would increase the difficulty of the system implementation and make the computational complexity high. However, MIMO technique is an efficient way to increase system capacity and extend system coverage, as will be studied in our future work.

The rest of this paper is organized as follows. In Section 2, the MISO-NOMA VLC system model is proposed, and the statistical characteristics of the intensity modulation direct detection (IM/DD) channel and the signal-to-noise ratio (SNR) is also investigated. In Section 3, the physical-layer security performance of the strong NOMA user is analyzed. Numerical results are presented in Section 4 to verify the theoretical analysis. Finally, conclusions are given in Section 5.

2. System Model

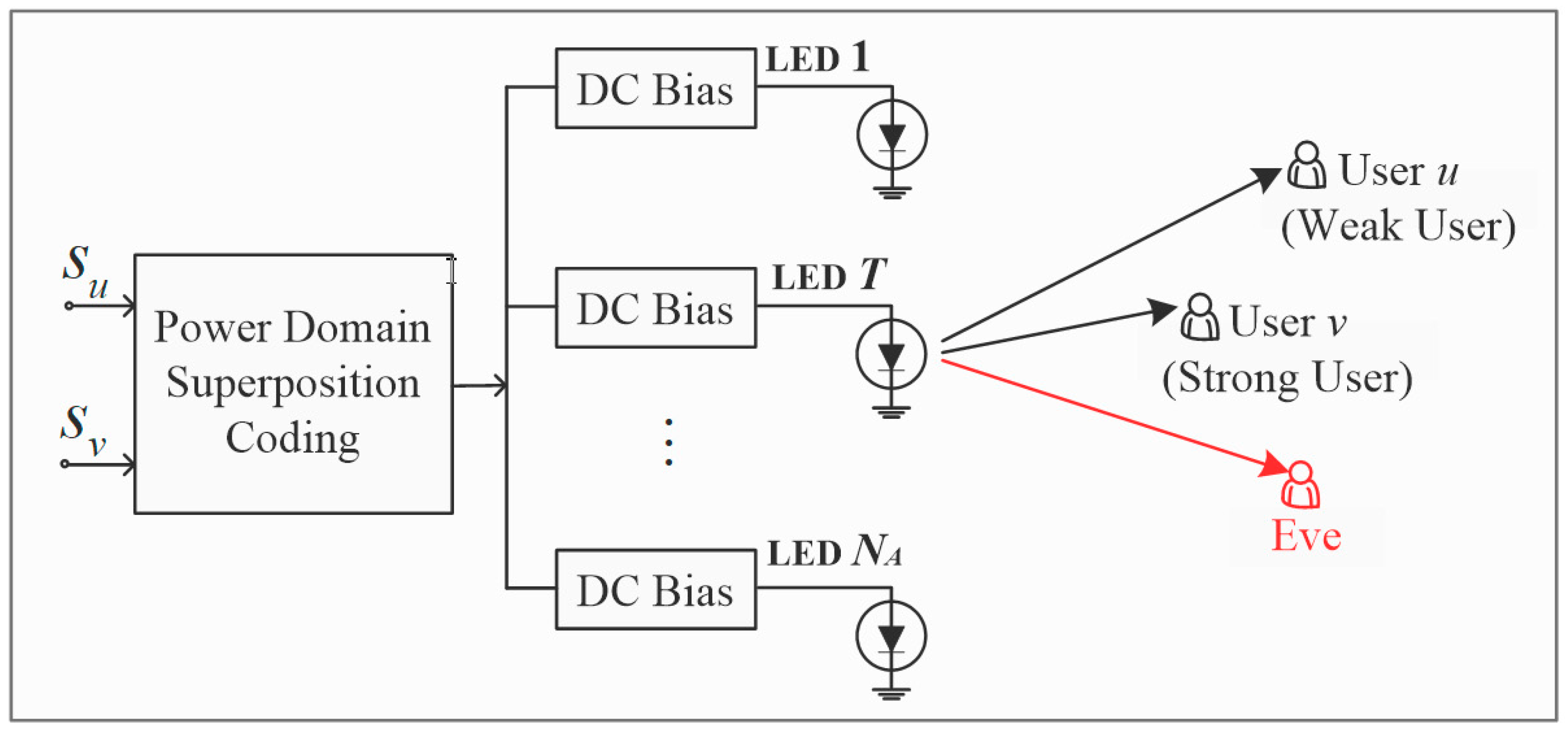
The MISO-NOMA VLC system is shown in Figure 1, where N_A LEDs serves user u and user v via downlink NOMA in the presence of a passive Eve (eavesdropper). Each of the legitimate users and Eve is with a PD receiver (Series 5T, Centronic Silicon PD, Croydon, London, UK). All the PD receivers are within the illuminating region of LED (BXRA-56C5300-H-00, Bridgelux LED, Fremont, CA, USA), and selection combination is utilized at the legitimate users and Eve. Since the secrecy performance of the weak user is conditioned on the fact that the strong user does not release any information about the weak user, we put emphasis on the physical-layer security of the strong user.

At the transmitting terminal, the signals of the two NOMA legitimate users are first superposed in power in an electrical domain. Then, a direct current (DC) bias is added to the superposition coding signal to satisfy a certain requirement of illumination before the electrical-to-optical conversion of LED. Hence, the signal from the T-th LED, T ∈{1, …, N_A}, can be expressed as $x=a_{T,u}\sqrt{P/N_A}{s}_u+a_{T,v}\sqrt{P/N_A}{s}_v+I_{\mathrm{DC}}$, where $I_{\mathrm{DC}}$ is the DC bias, which is utilized to set the average radiated optical power of LED and adjust the indoor illumination level; $P$ is the total electrical power of the signal in the electrical domain, and each LED transmits signal with equal power of $P/N_A$; $s_i$ represents the signal of the i-th legitimate user, $i\in \left\{u,v\right\}$, which is assumed to be with zero mean and $0\le \left|s_i\right|\le 1$; and $a_{T,i}$ is the power allocation coefficient of the T-th LED for the i-th legitimate user. Assuming the fixed power allocation scheme is used, then $a_{T,u}$ and $a_{T,v}$ remains constant for each LED and is respectively expressed as $a_u$ and $a_v$ below for simplicity. According to the NOMA principle, more power will be allocated to the weak user, while less power is allocated to the strong user for any LED, i.e., $a_u\ge a_v$. Since there exist only two NOMA users in the system, the coefficients should also satisfy $a_u^2+a_v^2=1$ and $0<a_u\le 1$, $0<a_v\le 1$. Due to the expectation $\mathbb{E}\left\{{{\displaystyle \sum }}_{i\in \left\{u,v\right\}}{a}_i\sqrt{P/N_A}{s}_i\right\}=0$, the superposition coding signal ${{\displaystyle \sum }}_{i\in \left\{u,v\right\}}{a}_i\sqrt{P/N_A}{s}_i$ does not contribute to the average optical power and therefore does not influence the illumination level. Due to the limited dynamic range and the linear electrical-to-optical conversion characteristics of LED, constraint $\left|{{\displaystyle \sum }}_{i\in \left\{u,v\right\}}{a}_i\sqrt{P/N_A}{s}_i\right|\le I_{DC}$ should also be satisfied, thus the signal at the input of the IM/DD channel can be a non-negative real signal.

At the receiving terminal, the arrived optical intensity signal is first converted into a current signal via photo-electric conversion of the PD receiver, and then the constant DC offset is removed, and noise is added in the electrical domain. For the NOMA legitimate user i, the received signal can be given by $y_i=h_{T,i}x+n_{T,i}$, where $h_{T,i}$ is the DC gain of the IM/DD channel between the T-th LED and the user i; $n_{T,i}$ is the additive white Gaussian noise of the channel and is assumed to be with zero mean and variance ${\sigma }^2$. Without loss of generality, it is assumed that the channel power gain satisfies $0<h_{T,u}^2\le h_{T,v}^2$, where $h_{T,u}^2$, $h_{T,v}^2$ is respectively the channel power gain of the weak user and the strong user. According to the NOMA principle, the strong user can perform SIC while the weak user cannot. Therefore, in the two-user MISO-NOMA VLC system, the peak SNR [10] in the channel from the T-th LED to the strong user v can be given by:

$$Q_{T,v}=\frac{h_{T,v}^2{a}_v^2\rho }{N_A}$$

(1)

While the peak signal-to-interference-plus-noise ratio (SINR) in the channel from the T-th LED to the weak user u is:

$$Q_{T,u}=\frac{h_{T,u}^2{a}_u^2}{h_{T,u}^2{a}_v^2+N_A/\rho }$$

(2)

where $\rho =P/{\sigma }^2$ is defined as the transmission SNR of the LED transmitter to the NOMA legitimate user.

Eve is assumed to be aware of the decoding orders and power allocation coefficients, and by adopting the multi-user detection technique, it can distinguish the multi-user signal and subtract the interference generated by the superposed signals from each other. This is a common assumption in analyzing the secrecy performance of the NOMA system [16,17]. The SNR for Eve to detect the message of user $i,i\in \left\{u,v\right\}$ can be given by $Q_{T,e\to i}=$ $h_{T,e}^2{a}_i^2{\rho }_e/N_A$, where ${\rho }_e=P/{\sigma }_e^2$ and ${\sigma }_e^2$ is the noise variance of the eavesdropper channel.

2.1. Statistical Characteristics of the IM/DD Channel

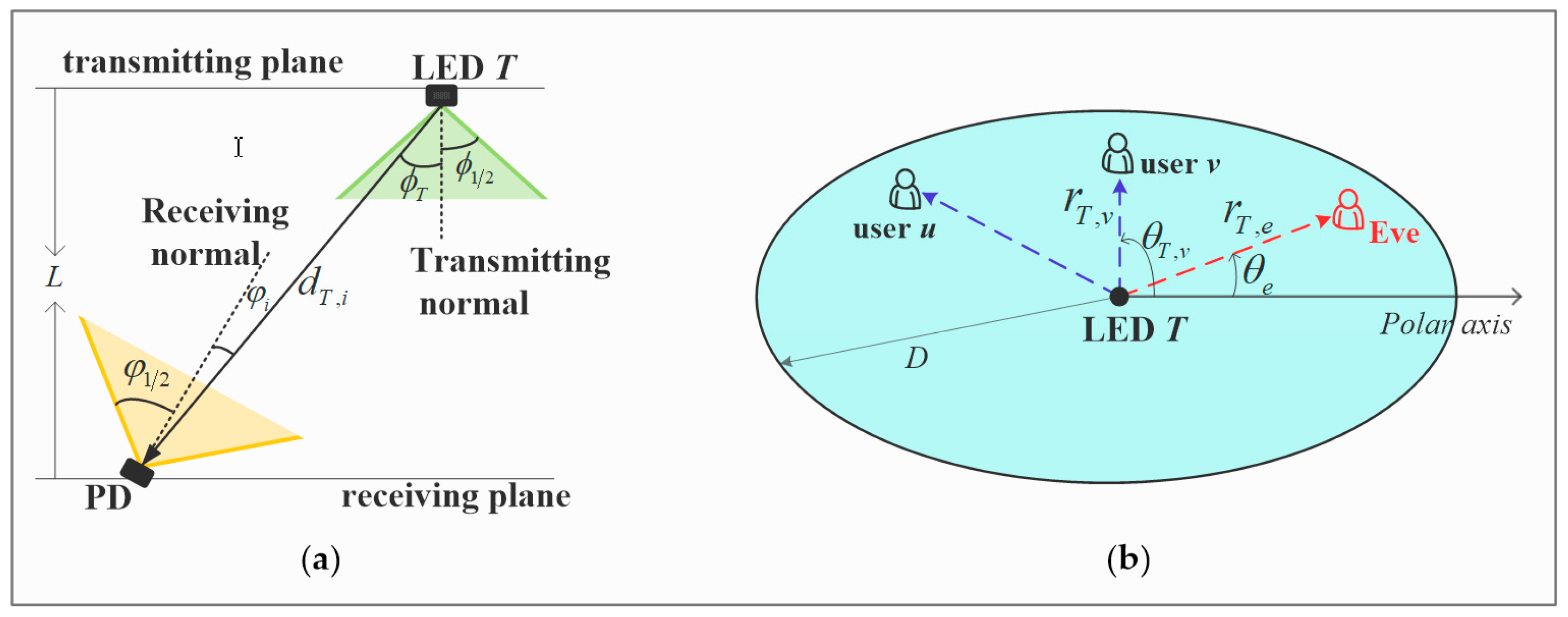
In the IM/DD channel, information is carried by the optical intensity. The light from the LED is successively concentrated and filtered by an optical concentrator and a filter in front of the PD receiver. In general, the received signals at the PD receiver include both the line-of-sight (LOS) and the diffuse component. However, it has been demonstrated by Zeng et al. [18] that even the strongest diffuse component is at least 7 dB lower than the weakest LOS component. Hence, only the LOS path is taken into account in this paper. The cross-section and the top view of the IM/DD channel are shown in Figure 2.

If the LED works in a generalized Lambertian radiation pattern, the DC gain of the IM/DD channel from the T-th LED to user i can be described as $h_{T,i}=S\eta \left(m+1\right){\cos }^m\left({\varphi }_T\right)\cos \left({\phi }_i\right)$ $rect\left({\phi }_i/{\phi }_{1/2}\right)g_{oc}\left({\phi }_i\right)g_{of}\left({\phi }_i\right)/(2\pi d_{T,i}^2)$, where ${\varphi }_T$ is the angle of irradiance with respect to the transmitting normal of the T-th LED plane; ${\phi }_i$ is the angle of incidence with respect to the receiving normal of the i-th PD receiver plane; ${\phi }_{1/2}$ is the field of view (FOV) of the PD receiver; $rect(·)$ is a rectangular function and is equal to 1 only if ${\phi }_i\le {\phi }_{1/2}$, and the FOV of both the legitimate users and Eve is assumed to be wide enough to receive signal from LED; d_T,i is the transmission distance between the T-th LED and the i-th PD receiver; $m$ is the order of Lambertian radiation, and $m=-ln2/ln\left(cos{\varphi }_{1/2}\right)$; ${\varphi }_{1/2}$ is the semi-angle at half illuminance of the LED; $g_{oc}$ is the optical concentrator gain and $g_{oc}\left({\phi }_i\right)=n^2/{\sin }^2\left({\phi }_{1/2}\right)$, where $n$ is the refractive index of the optical concentrator utilized at the PD receiver front-end and $g_{of}$ is the optical filter coefficient; S and η are the effective physical detecting area and the responsivity of the PD receiver, respectively.

For simplicity, it is assumed that $g_{oc}=g_{of}=1$ and the PD receiver has strong adaptive adjustment ability, which is easy to implement in practical application, since various sensors such as the gyroscope sensor, the accelerometer sensor, and the electronic compass sensor are embedded in people’s hand phone, and then the incidence angle can be adjusted to be zero [19]. The two-dimensional illuminated region of the T-th LED on the PD receiver plane is assumed to be a circle with a radius of D, and the projection of the T-th LED on the PD receiver plane is located at the center, then we can get $d_{T,i}^2=r_{T,i}^2+L^2$, where L is the vertical distance between the LED plane and the PD plane in three-dimensional space, and $r_{T,i}$ is the distance between the T-th LED projection and user i, as shown in Figure 2b. We can also get $\cos \left({\varphi }_T\right)=L/d_{T,i}$ from Figure 2a. Therefore, the channel power gain of the channel from the T-th LED to user i can be written as $h_{T,i}^2={\left[S\eta \left(m+1\right)L^m/2\pi \right]}^2{\left(r_{T,i}^2+L^2\right)}^{-\left(m+2\right)}\triangleq \hslash {\left(r_{T,i}^2+L^2\right)}^{-\left(m+2\right)}$, where $\hslash ={\left[S\eta \left(m+1\right)L^m/2\pi \right]}^2$ is often a constant.

Conditioned on the fact that the NOMA legitimate users $i,i\in \left\{u,v\right\}$ are uniformly located in this disc, the probability density function (PDF) of $r_{T,i}$ is given by $f(r_{T,i})=2r_{T,i}/D^2$. Utilizing the method of calculating the function of random variables, the PDF of the unordered channel power gain can be given by:

$$\stackrel{⌣}{f}\left(h_{T,i}^2\right)=\left|\frac{\partial r_{T,i}}{\partial h_{T,i}^2}\right|f\left(r_{T,i}\right)=\frac{1}{m+2}{\hslash }^{\frac{1}{m+2}}\frac{1}{D^2}{\left(h_{T,i}^2\right)}^{-\frac{1}{m+2}-1}$$

(3)

and the cumulative distribution function (CDF) of the unordered channel power gain can be given by:

$$\begin{array}{cc}\hfill {\stackrel{⌣}{F}}_{h_{T,i}^2}\left(x\right)& ={\displaystyle {\int }_{-\infty }^x{\stackrel{⌣}{f}}_{h_{T,i}^2}\left(y\right)}dy={\displaystyle {\int }_{-\infty }^{{\kappa }_{\min }}0}dy+{\displaystyle {\int }_{{\kappa }_{\min }}^x{\stackrel{⌣}{f}}_{h_{T,i}^2}\left(y\right)}dy\hfill \\ & =-{\hslash }^{\frac{1}{m+2}}\frac{1}{D^2}{x}^{-\frac{1}{m+2}}+\frac{D^2+L^2}{D^2}\hfill \end{array}$$

(4)

where ${\kappa }_{\min }\le h_{T,i}^2\le {\kappa }_{\max }$ and ${\kappa }_{\min }=\hslash {\left(D^2+L^2\right)}^{-\left(m+2\right)},{\kappa }_{\max }=\hslash {\left(L^2\right)}^{-\left(m+2\right)}$.

Adopting order statistics [20], the CDF of the ordered channel power gain for the two-user MISO-NOMA VLC system can be given by:

$$F_{h_{T,i}^2}\left(x\right)=\frac{1}{2}{\left(-{\hslash }^{\frac{1}{m+2}}\frac{1}{D^2}{x}^{-\frac{1}{m+2}}+\frac{D^2+L^2}{D^2}\right)}^2,i\in \left\{u,v\right\}$$

(5)

2.2. Statistical Characteristic of the SNR

With the statistical characteristic of the channel, the CDF of the SNR of the strong user v can be given by:

$$\begin{array}{cc}\hfill F_{Q_{T,v}}\left(x\right)& =\mathbb{P}\left(Q_{T,v}\le x\right)\hfill \\ & =F_{h_{T,v}^2}\left(\frac{x}{a_v^2\rho }\right)=\frac{1}{2}{\left[\tilde{\hslash }{\left(a_v^2\right)}^{-\tilde{m}}{x}^{\tilde{m}}+\tilde{D}\right]}^2\hfill \end{array}$$

(6)

and the CDF of the SINR of the weak user u can be given by:

$$F_{Q_{T,u}}\left(x\right)=\{\begin{array}{ll}\frac{1}{2}{\left[\tilde{\hslash }{\left(a_u^2-x{a}_v^2\right)}^{-\tilde{m}}{x}^{\tilde{m}}+\tilde{D}\right]}^2,& x<a_u^2/a_v^2\\ 1,& x\ge a_u^2/a_v^2\end{array}$$

(7)

where $\tilde{D}=\left(D^2+L^2\right)/D^2,\tilde{\hslash }=-{\left(\hslash \rho \right)}^{\frac{1}{m+2}}/D^2,\tilde{m}=-1/\left(m+2\right)$.

Since the channel power gain of the eavesdropper channel is $h_{T,e}^2=\hslash {\left(r_{T,e}^2+L^2\right)}^{-\left(m+2\right)}$ where $r_{T,e}$ is the distance between the T-th LED projection on the PD plane and Eve, the CDF of the SNR for Eve to detect the message of user i is given by $F_{Q_{T,e\to i}}\left(x\right)=\mathbb{P}\left(Q_{T,e\to i}\le x\right)={\tilde{\hslash }}_e{\left(a_i^2\right)}^{-\tilde{m}}{x}^{\tilde{m}}+\tilde{D}$, and the PDF of the SNR for Eve to detect the message of user i is given by:

$$f_{Q_{T,e\to i}}\left(x\right)={\tilde{\hslash }}_e\tilde{m}{\left(a_i^2\right)}^{-\tilde{m}}{x}^{\tilde{m}-1},i\in \left\{u,v\right\}$$

(8)

where ${\tilde{\hslash }}_e=-{\left(\hslash {\rho }_e\right)}^{\frac{1}{m+2}}/D^2$.

With these statistical characteristics known, it is suitable to use SOP to measure the secrecy performance. A secrecy outage event occurs when the secrecy rate of user k (k ∈{u, v}) is lower than the target rate, which can be written as $P_k=\mathbb{P}\left(C_k<R_{th}\right)$, where $\mathbb{P}\left(x\right)$ is the probability of the occurrence of an event $x$; $C_k$ is the secrecy rate of user k and is given by $C_k={\left[R_k-R_e\right]}^{+}$, where $R_k$ and $R_e$ are respectively the achievable rate of the legitimate user and the eavesdropper, and [x]⁺ = max{x, 0}; R_th is the predefined target rate.

3. Secrecy Performance Analysis

The selection combination strategy is utilized at the PD receiver of the legitimate user and Eve. Then, the CDF of the SNR of the strong user v is given by:

$$\begin{array}{cc}\hfill F_{Q_{T,v}}\left(x\right)& =\mathrm{P}\left(\underset{1\le T\le N_A}{max}{Q}_{T,v}<x\right)={\left[\mathrm{P}\left(Q_{T,v}<x\right)\right]}^{N_A}\hfill \\ & ={\left[\frac{1}{2}{\left(N_A^{\tilde{m}}\tilde{\hslash }{\left(a_v^2\right)}^{-\tilde{m}}{x}^{\tilde{m}}+\tilde{D}\right)}^2\right]}^{N_A}\hfill \end{array}$$

(9)

and the CDF of the SNR of the weak user u is given by:

$$\begin{array}{cc}\hfill F_{Q_{T,u}}\left(x\right)& =\mathrm{P}(\underset{1\le T\le N_A}{\max }{Q}_{T,u}<x)={\left[\mathrm{P}\left(Q_{T,u}<x\right)\right]}^{N_A}\hfill \\ & =\{\begin{array}{cc}{\left[\frac{1}{2}{\left(N_A^{\tilde{m}}\tilde{\hslash }{\left(a_u^2-x{a}_v^2\right)}^{-\tilde{m}}{x}^{\tilde{m}}+\tilde{D}\right)}^2\right]}^{N_A},& x<a_u^2/a_v^2\hfill \\ 1,& x\ge a_u^2/a_v^2\hfill \end{array}\hfill \end{array}$$

(10)

and the CDF of the SNR for Eve to detect the message of user i, i ∈{u, v} is given by:

$$F_{Q_{T,e\to i}}\left(x\right)=\mathrm{P}\left(\underset{1\le T\le N_A}{max}{Q}_{T,e\to i}<x\right)={\left[N_A^{\tilde{m}}{\tilde{\hslash }}_e{\left(a_i^2\right)}^{-\tilde{m}}{x}^{\tilde{m}}+\tilde{D}\right]}^{N_A}$$

(11)

and the PDF of the SNR for Eve to detect the message of user i, i ∈{u, v} is given by:

$$f_{Q_{T,e\to i}}\left(x\right)=N_A^{\tilde{m}+1}{\tilde{\hslash }}_e\tilde{m}{\left(a_i^2\right)}^{-\tilde{m}}{\left[N_A^{\tilde{m}}{\tilde{\hslash }}_e{\left(a_i^2\right)}^{-\tilde{m}}{x}^{\tilde{m}}+\tilde{D}\right]}^{N_A-1}{x}^{\tilde{m}-1}$$

(12)

For the MISO-NOMA VLC system, where two NOMA users are in the presence of a single eavesdropper, all LEDs are utilized to transmit signals with equal power, and the selection combination scheme is employed at the PD receiver for both the NOMA legitimate users and the eavesdropper. Then, the SOP of the strong user in the system can be given by:

$$\begin{array}{cc}\hfill P_v& =\mathrm{P}\left[\frac{1}{2}{\log }_2\left(1+\underset{1\le T\le N_A}{max}{Q}_{T,v}\right)-\frac{1}{2}{\log }_2\left(1+\underset{1\le T\le N_A}{max}{Q}_{T,e\to v}\right)<R_{th}\right]\hfill \\ & ={\displaystyle {\int }_0^{+\infty }{F}_{Q_{T,v}}\left(2^{2R_{th}}\left(1+x\right)-1\right)f_{Q_{T,e\to v}}\left(x\right)dx}\hfill \end{array}$$

(13)

Substituting (9) and (12) into (13), we get the SOP of the strong user, which is given by:

$$\begin{array}{ll}\hfill P_v=& {\tilde{D}}^{3N_A-1}{2}^{-N_A}{N}_A^{\tilde{m}+1}{\tilde{\hslash }}_e\tilde{m}{\left(a_v^2\right)}^{-\tilde{m}}{\displaystyle \sum _{k=0}^{2N_A}{\displaystyle \sum _{w=0}^{N_A-1}}}\hfill \\ & \left(\begin{array}{l}2N_A\\ k\end{array}\right)\left(\begin{array}{l}{N}_A-1\\ w\end{array}\right){\left[{\left(-1\right)}^{\tilde{m}}{\tilde{D}}^{-1}{N}_A^{\tilde{m}}\tilde{\hslash }{\left(a_v^2\right)}^{-\tilde{m}}\right]}^k{\left[{\tilde{D}}^{-1}{N}_A^{\tilde{m}}{\tilde{\hslash }}_e{\left(a_v^2\right)}^{-\tilde{m}}\right]}^w\mho \left(k\right)\hfill \end{array}$$

(14)

where $\mho \left(k\right)={\displaystyle {\int }_0^{+\infty }{\left[1-2^{2R_{th}}\left(1+x\right)\right]}^{\tilde{m}}{}^k}{x}^{\tilde{m}-1}{x}^{\tilde{m}w}dx$. First, utilizing the power series expansion formula in [21] [Equation (1.110)] to expand ${\left[1-2^{2R_{th}}\left(1+x\right)\right]}^{\tilde{m}}{}^k$, then keeping the first two terms and neglecting the higher order terms, we get:

$$\begin{array}{cc}\hfill \mho \left(k\right)& ={\displaystyle {\int }_0^{+\infty }\left[1-2^{2R_{th}}\tilde{m}k\left(1+x\right)\right]x^{\tilde{m}+\tilde{m}w-1}dx}\hfill \\ & ={\frac{1-2^{2R_{th}}\tilde{m}k}{\tilde{m}+\tilde{m}w}{x}^{\tilde{m}+\tilde{m}w}|}_{Q_{\min }/N_A}^{Q_{\max }/N_A}{-\frac{2^{2R_{th}}\tilde{m}k}{\tilde{m}+\tilde{m}w+1}{x}^{\tilde{m}+\tilde{m}w+1}|}_{Q_{\min }/N_A}^{Q_{\max }/N_A}\hfill \end{array}$$

(15)

where $Q_{\min }\le Q_{T,e\to v}\le Q_{\max },Q_{\min }=a_v^2{\rho }_e\hslash {\left(D^2+L^2\right)}^{-\left(m+2\right)},Q_{\max }=a_v^2{\rho }_e\hslash {\left(L^2\right)}^{-\left(m+2\right)}.$

4. Numerical Results

In this section, we present insightful numerical results to disclose the SOP performance of the strong NOMA user.

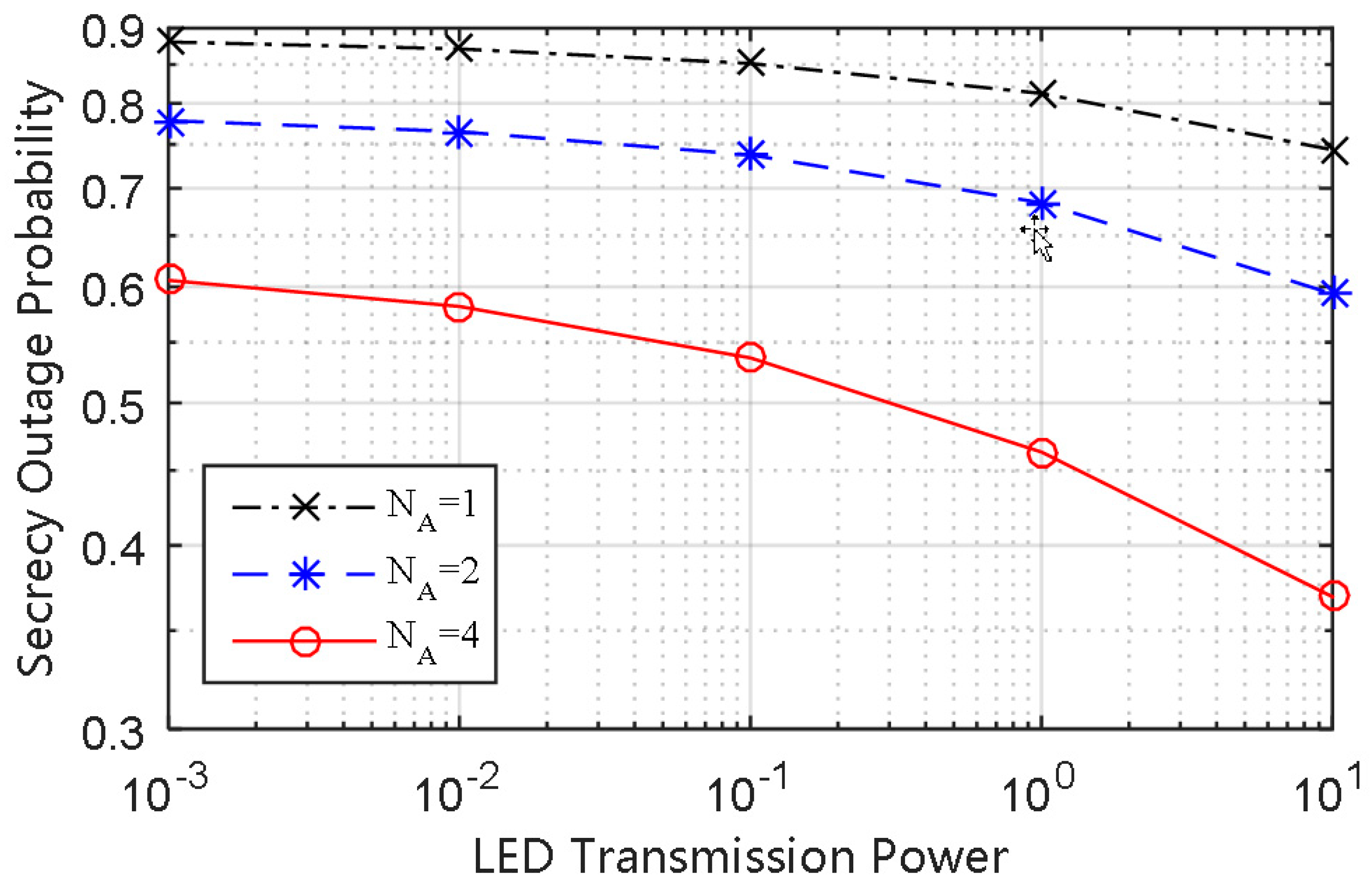
The SOP performance of the strong user versus a different number of LEDs is plotted in Figure 3. It can be seen that the SOP performance of the MISO-NOMA VLC system (N_A > 1) is superior to that of the SISO-NOMA VLC system (N_A = 1). The SOP in the case of N_A = 1 is consistent with the result of [7], where only a single LED is used, and multi-antenna technology has not been adopted.

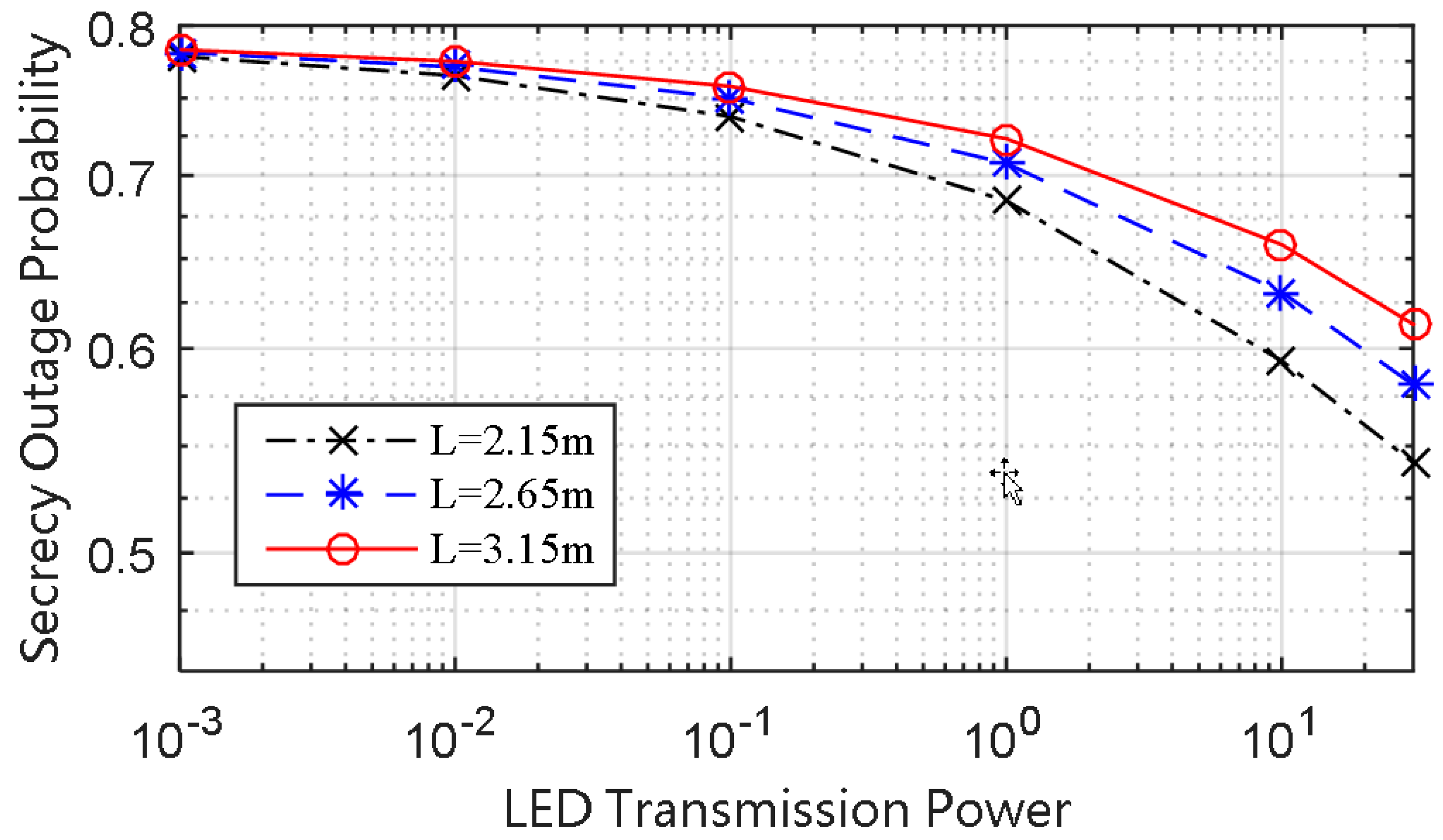
It can be seen from Figure 4 that reducing the distance from the LED transmitting plane to the PD receiving plane can reduce the SOP, and this is due to the fact that the condition of the main channel gets better at a shorter relative distance between the LED transmitting plane to the PD receiving plane. Thus, we come to the conclusion that room arrangement has great influence on the secrecy performance with the location of the receiving plane remaining unchanged.

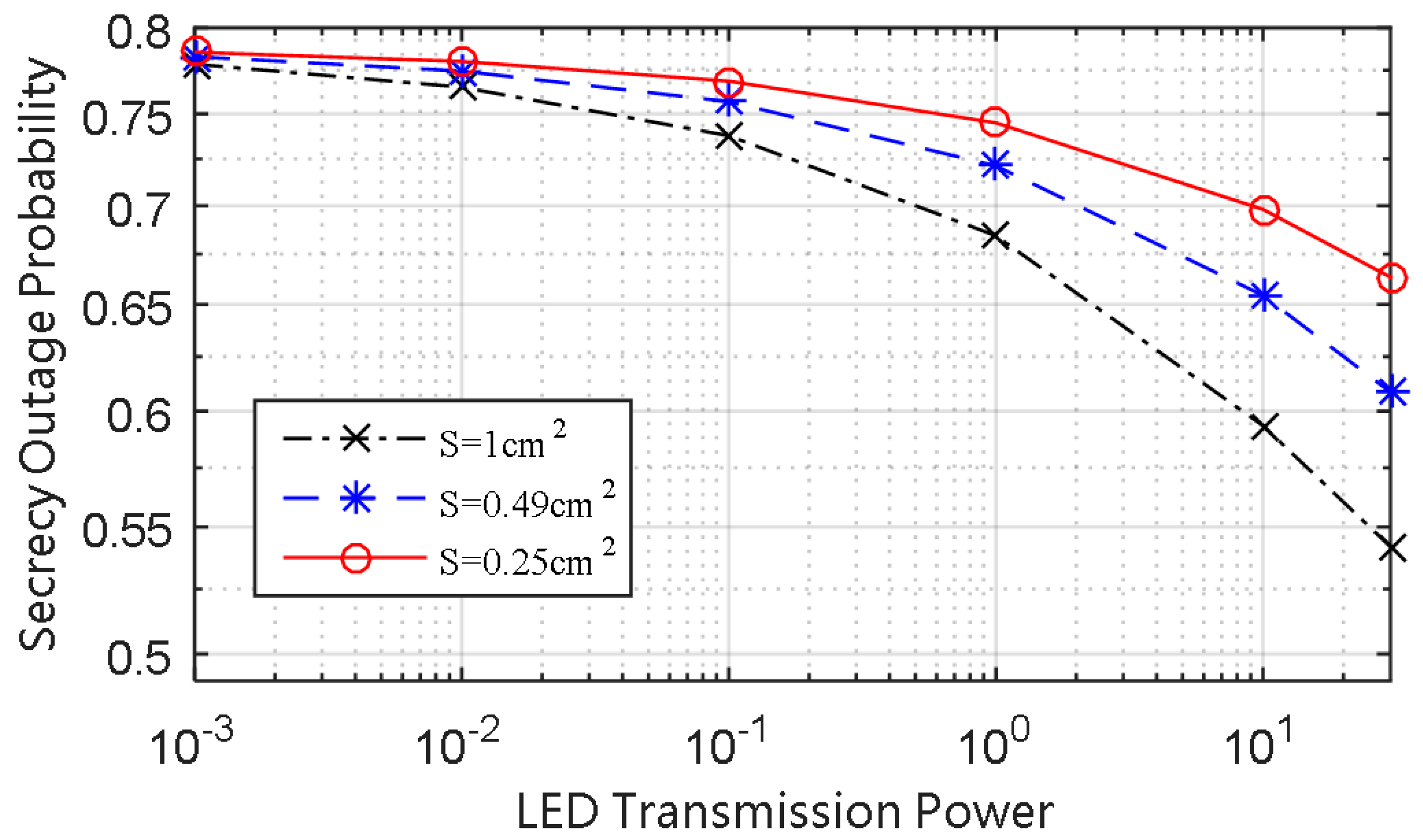
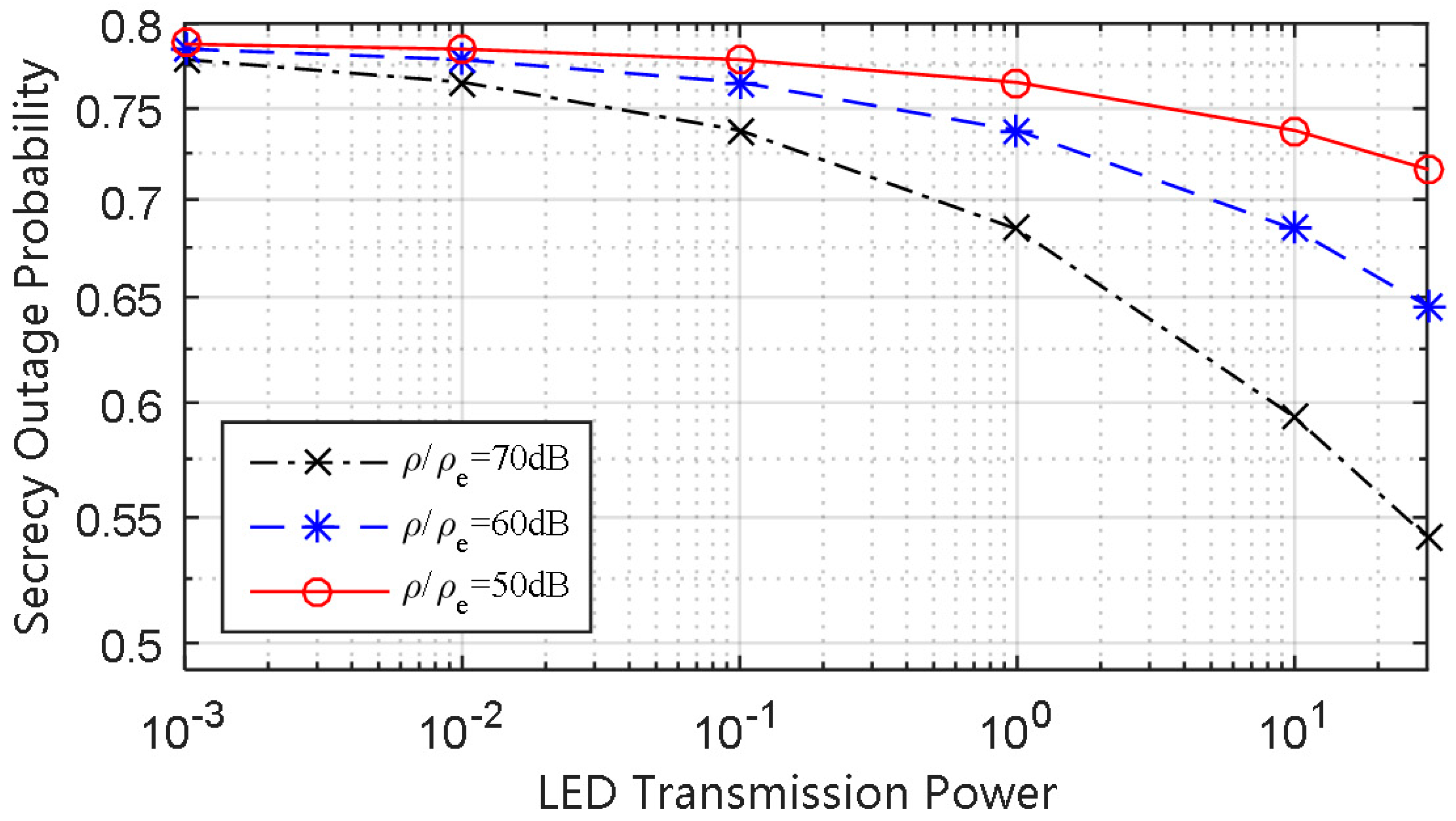
The SOP performance of the strong user versus different physical detecting areas of PD is plotted in Figure 5, and we can see that enlarging the physical detecting area of PD can reduce the SOP. It can be seen from Figure 6 that when the LED transmission power is given, increasing the ratio of $\rho$ to ${\rho }_e$ can make the SOP of the strong user decrease. This is because the channel difference is enlarged between the strong legitimate channel and the eavesdropper channel with the increase of the ratio. Hence, in practical application, if the strong user could be far enough from the eavesdropper, the SOP of the strong user would remain at a moderate level.

Extending the approaches of the paper to a MIMO-NOMA VLC system with multiple LEDs transmitting and multiple PDs receiving would be of interest as a future direction. For a MIMO-NOMA VLC system, in addition to the above mentioned factors, how the geometric layout of the PD receivers, such as the respective orientation and the relative distance from each other, affects the security performance of the system should also be taken into account. Additionally, the complexity of various channel estimation algorithms for the MIMO case, such as the zero forcing, the least mean square, and the recursive least square algorithm, should also be compared and analyzed.

5. Conclusions

In this paper, we specifically consider the physical-layer security performance of the strong user in a MISO-NOMA VLC system with two legitimate users in the presence of a passive eavesdropper. All the LEDs are utilized to transmit signal, while a PD receiver with the selection combination approach is used at the two legitimate users and Eve. Numerical results show that the SOP performance of the strong user in the MISO-NOMA VLC system is superior to that in the SISO case. In addition, the SOP of the strong user in the MISO-NOMA VLC system depends highly on the room arrangement, the difference between the legitimate channel and the eavesdropper channel, and the properties of the LEDs and the PD.