Narrowband Interference Separation for Synthetic Aperture Radar via Sensing Matrix Optimization-Based Block Sparse Bayesian Learning
Abstract
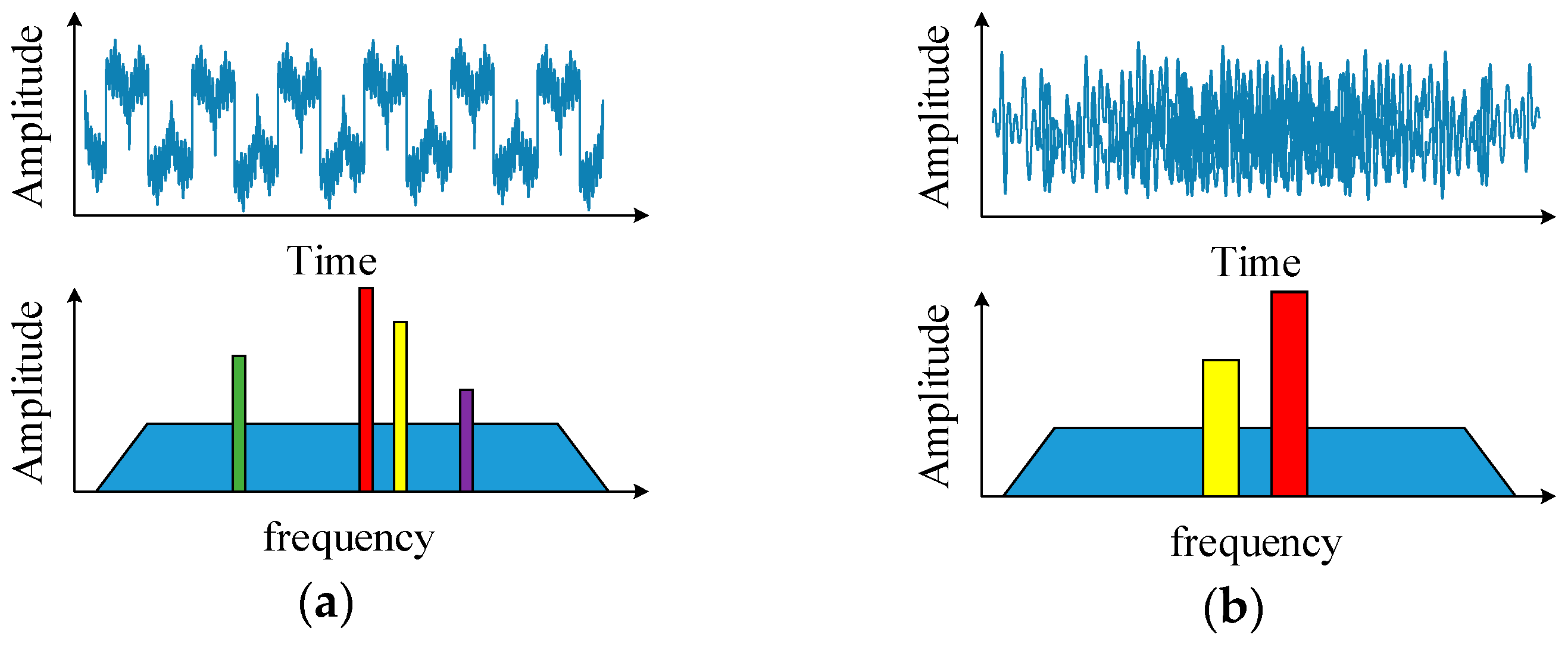
1. Introduction
2. Problem Formulation
2.1. Sparse Model and Joint Recovery
2.2. Complex BSBL Framework
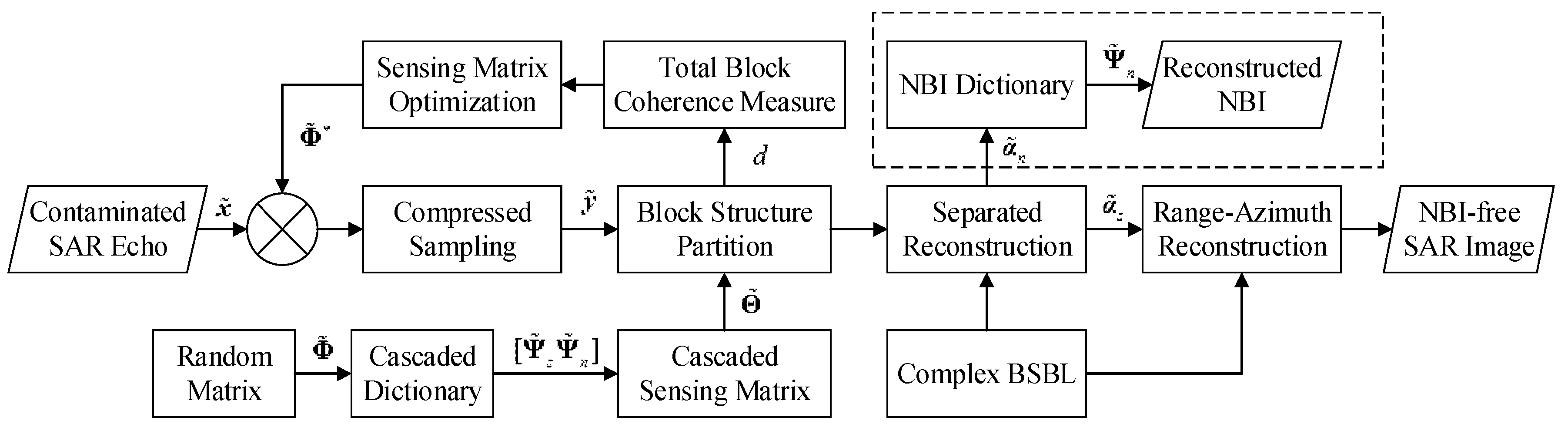
3. NBI Separation Based on SMO-BSBL
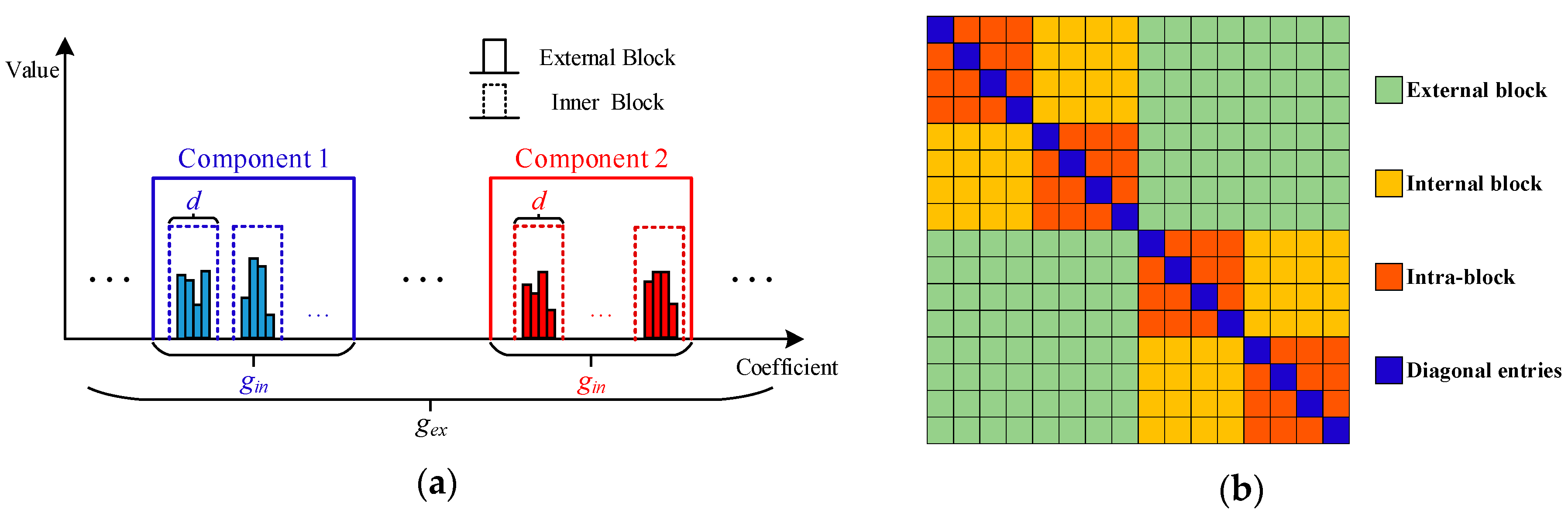
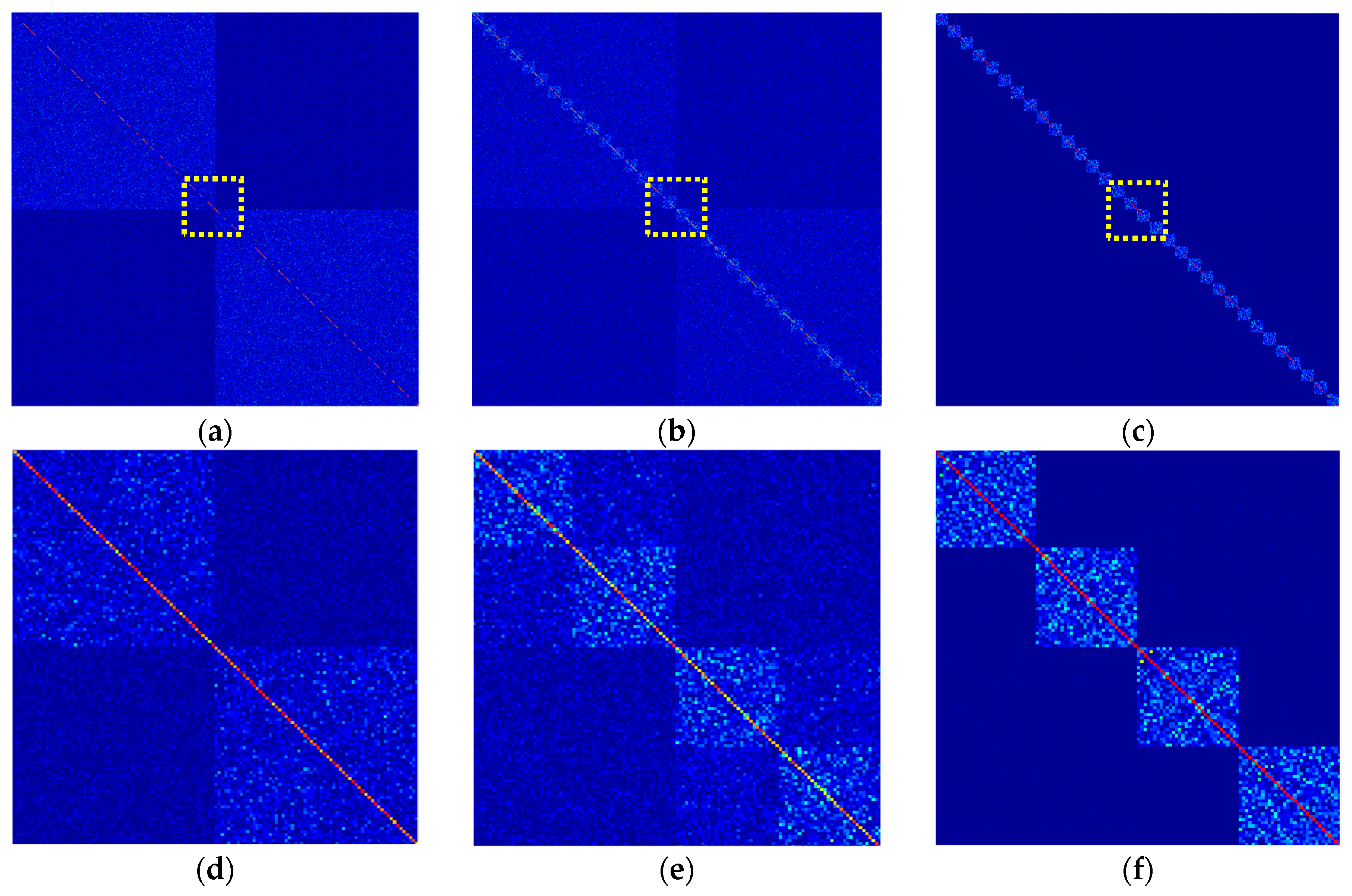
3.1. Block Coherence Measure
3.2. Sensing Matrix Optimization
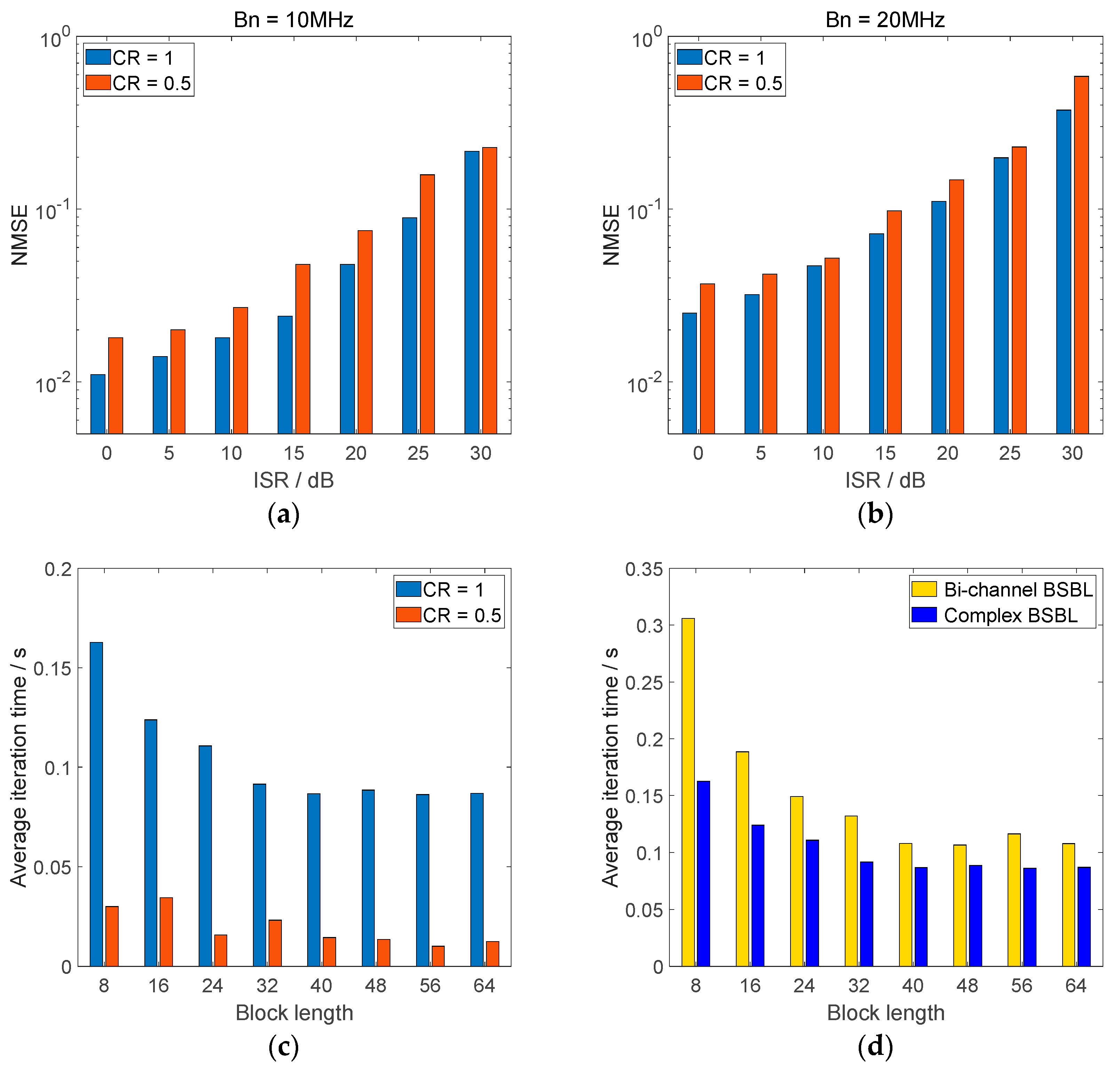
3.3. SMO-BSBL Algorithm
3.4. SAR Imaging Procedure with NBI Separation
4. Experiments
4.1. Experiment Setup
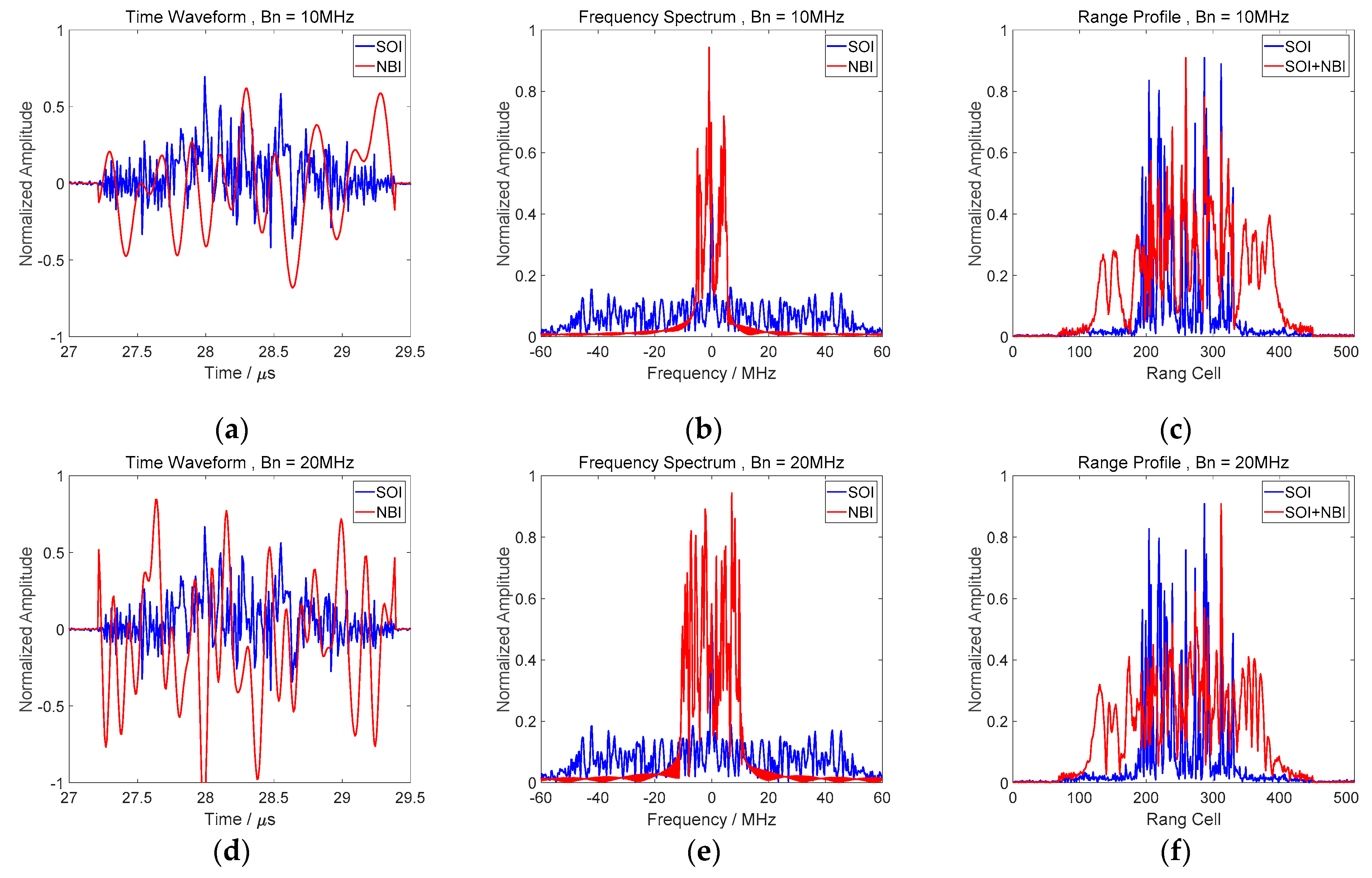
4.1.1. Simulation Specification
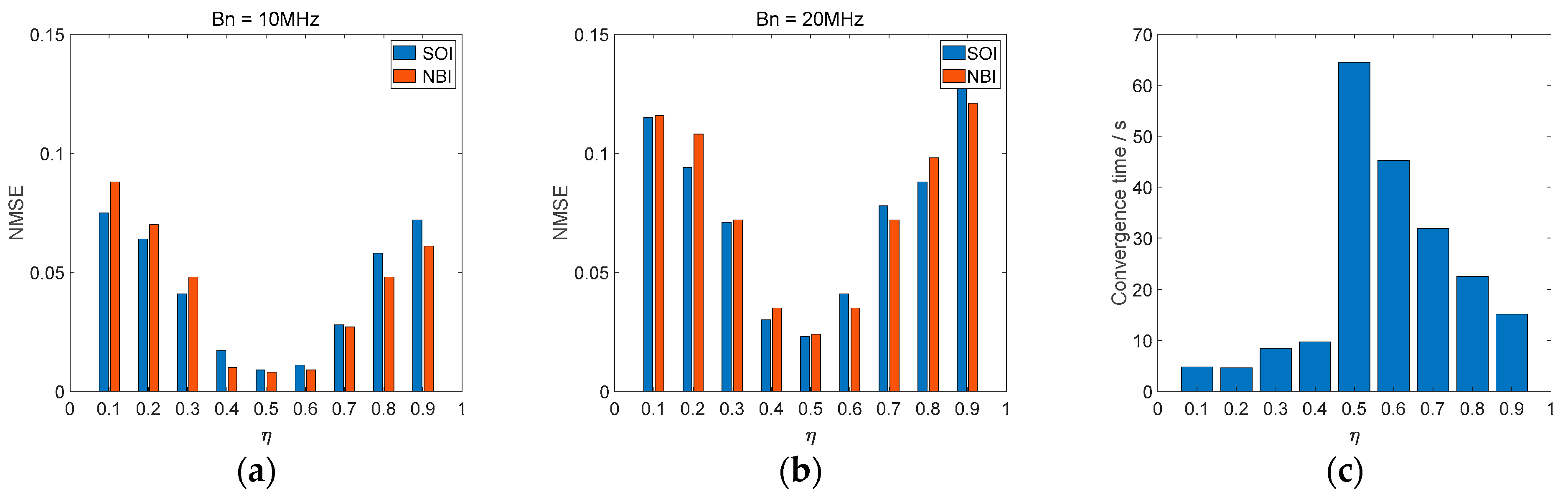
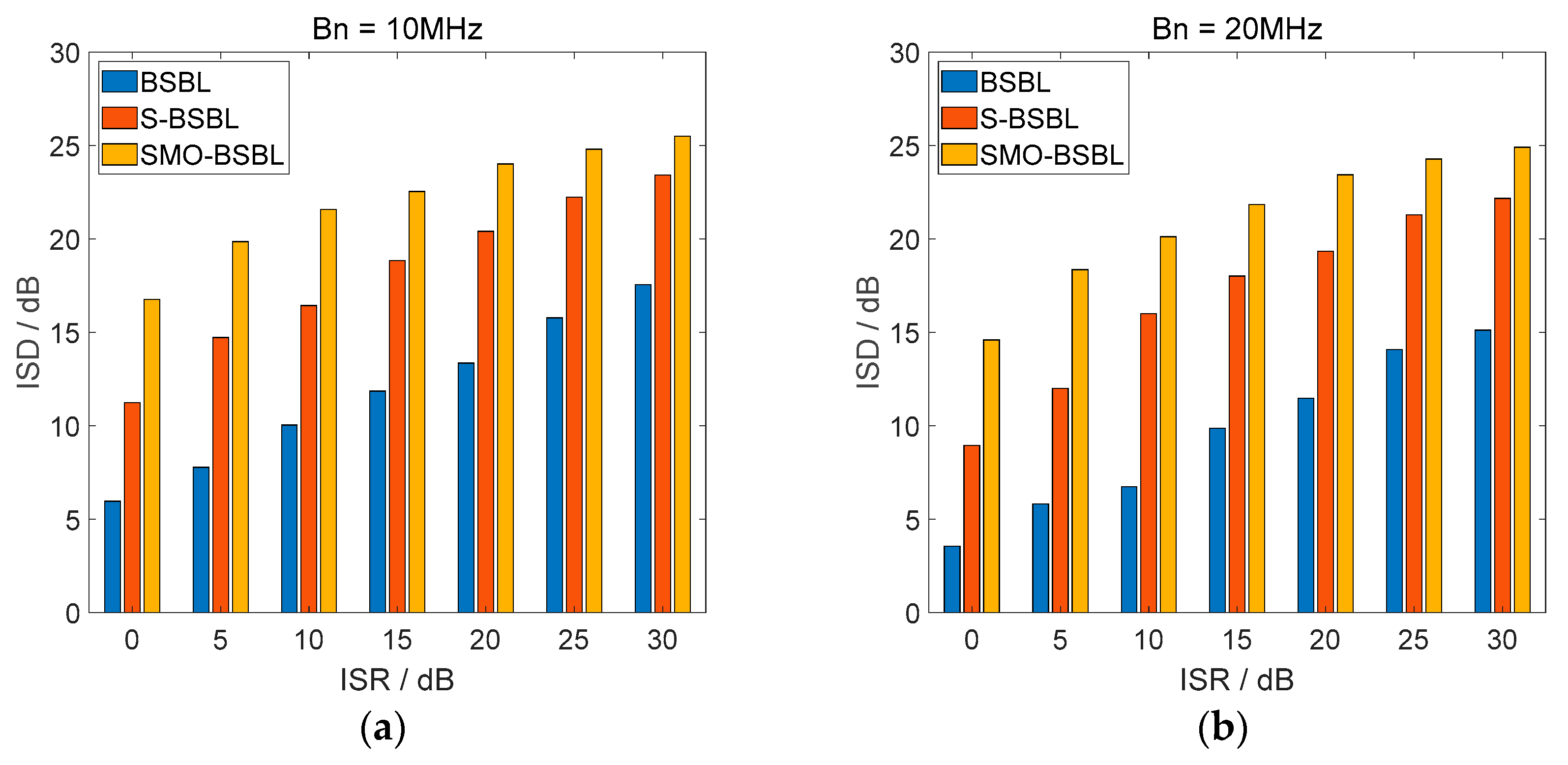
4.1.2. Performance Indicators
4.2. Simulation and Analysis
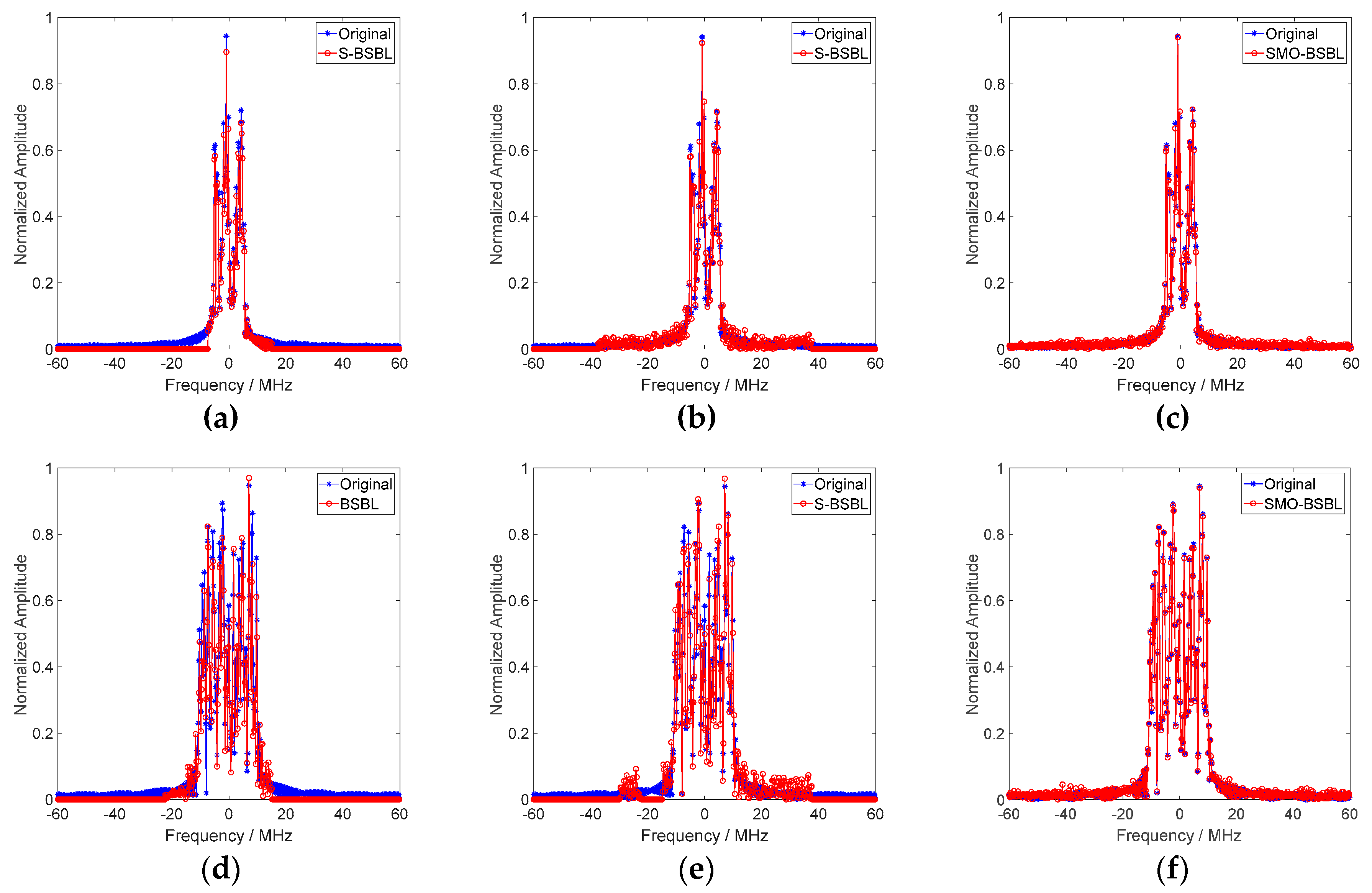
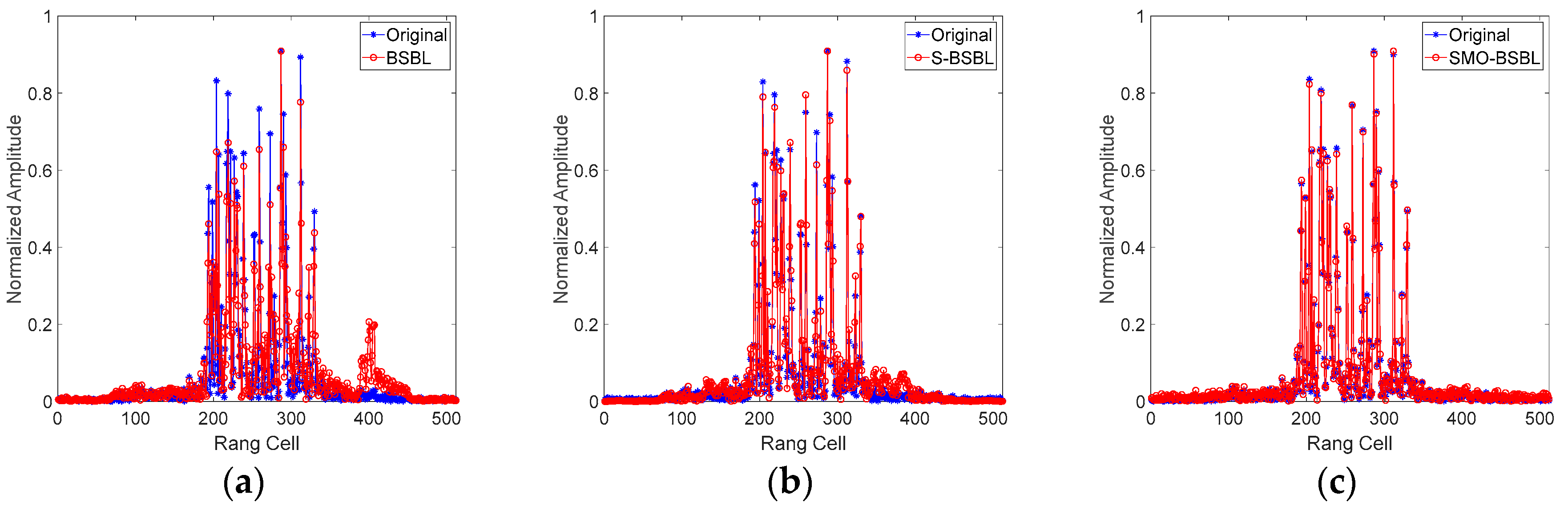
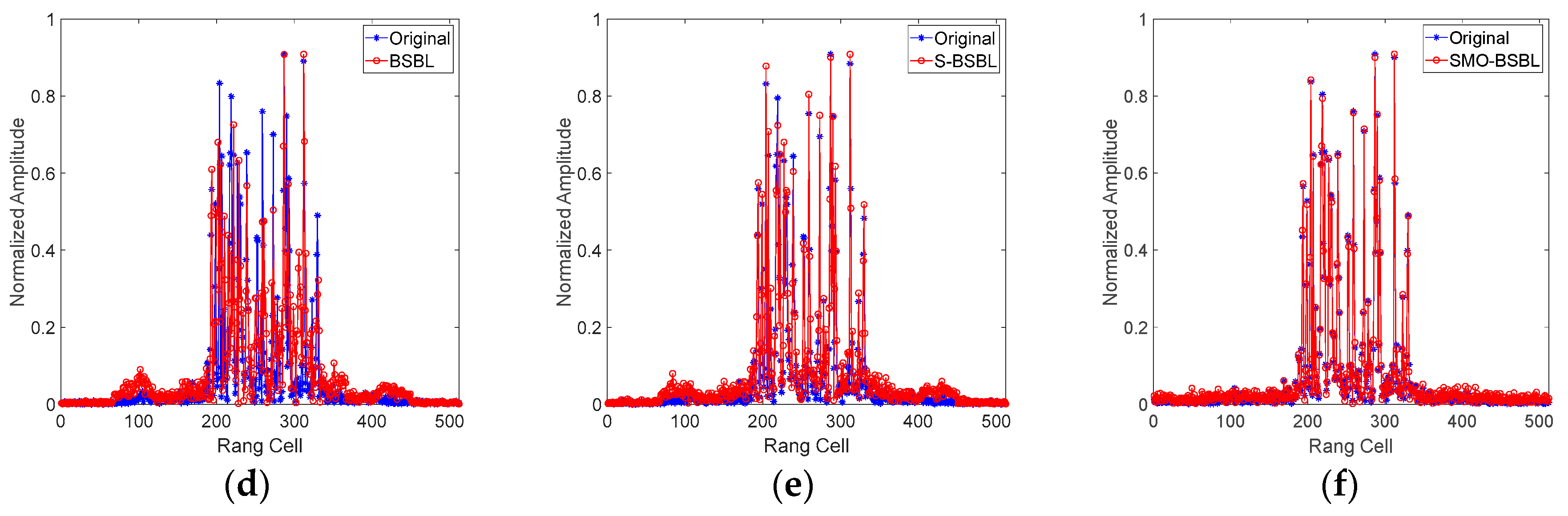
4.2.1. Range Profile Imaging
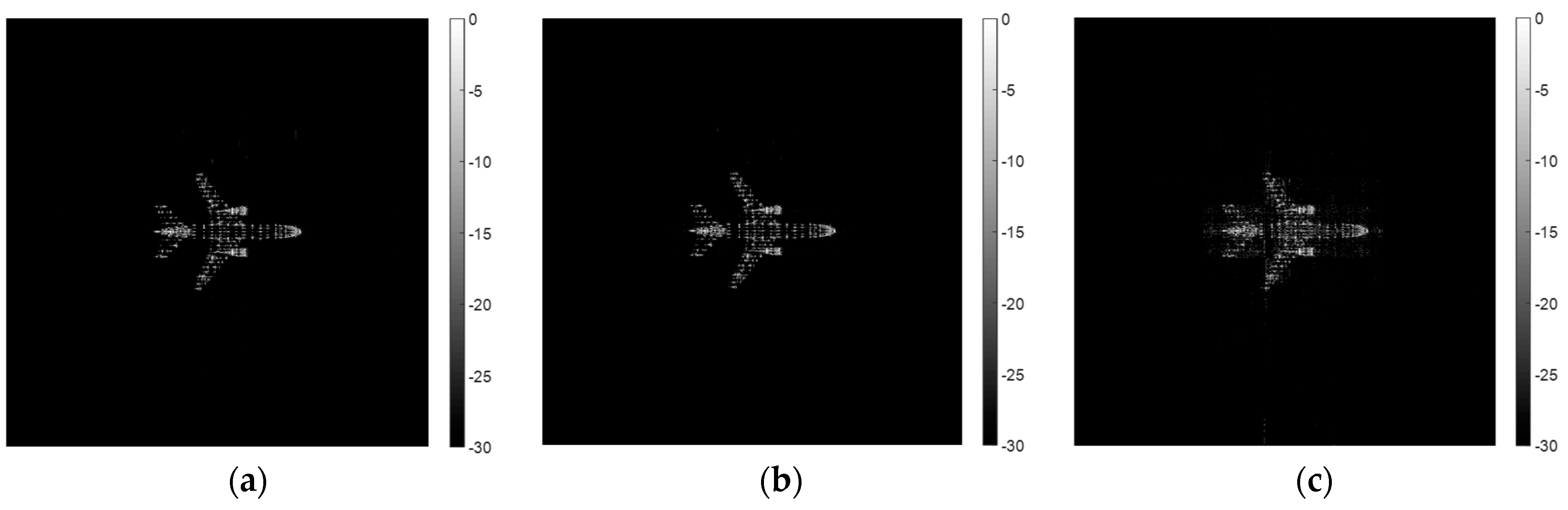
4.2.2. Range-Azimuth Imaging
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lin, X.; Li, X.; Man, X.; Tian, W. Narrow-band interference suppression method in multichannel SAR based on beamforming technique and sparse recovery. Electron. Lett. 2018, 54, 1189–1191. [Google Scholar] [CrossRef]
- Meller, M.; Niedźwiecki, M. Multichannel self-optimizing narrowband interference canceller. Signal Process 2014, 98, 396–409. [Google Scholar] [CrossRef]
- Djukanovic, S.; Popovic, V. A Parametric Method for Multicomponent Interference Suppression in Noise Radars. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2730–2738. [Google Scholar] [CrossRef]
- Zhou, F.; Xing, M.; Bai, X.; Sun, G.; Bao, Z. Narrow-Band interference suppression for SAR based on complex empirical mode decomposition. IEEE Geosci. Remote S. 2009, 6, 423–427. [Google Scholar] [CrossRef]
- Lamont-Smith, T.; Hill, R.D.; Hayward, S.D.; Yates, G.; Blake, A. Filtering approaches for interference suppression in low-frequency SAR. IEEE Proc. Radar Sonar. Navig. 2006, 153, 338–344. [Google Scholar] [CrossRef]
- Wu, P.; Yang, L.; Zhang, Y. A modified notch filter for suppressing radio-frequency-interference in P-band SAR data. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016. [Google Scholar]
- Lord, R.T.; Inggs, M.R. Efficient RFI suppression in SAR using LMS adaptive filter integrated with range/Doppler algorithm. Electron. Lett. 1999, 35, 629–630. [Google Scholar] [CrossRef]
- Zhou, F.; Wu, R.; Xing, M.; Bao, Z. Eigensubspace-Based filtering with application in Narrow-Band interference suppression for SAR. IEEE Geosci. Remote S. 2007, 4, 75–79. [Google Scholar] [CrossRef]
- Zhou, F.; Tao, M.; Bai, X.; Liu, J. Narrow-Band interference suppression for SAR based on independent component analysis. IEEE Trans. Geosci. Remote 2013, 51, 4952–4960. [Google Scholar] [CrossRef]
- Tao, M.; Zhou, F.; Liu, J.; Liu, Y.; Zhang, Z.; Bao, Z. Narrow-Band interference mitigation for SAR using independent subspace analysis. IEEE Trans. Geosci. Remote 2014, 52, 5289–5301. [Google Scholar]
- Zhou, F.; Tao, M. Research on methods for narrow-band interference suppression in synthetic aperture radar data. IEEE J.-STARS 2015, 8, 3476–3485. [Google Scholar] [CrossRef]
- Su, J.; Tao, H.; Tao, M.; Wang, L.; Xie, J. Narrow-Band interference suppression via RPCA-Based signal separation in time–frequency domain. IEEE J.-STARS 5016, 10, 5016–5025. [Google Scholar] [CrossRef]
- Nguyen, L.H.; Tran, T.D. Efficient and robust RFI extraction via sparse recovery. IEEE J.-STARS 2016, 9, 2104–2117. [Google Scholar] [CrossRef]
- Huang, Y.; Liao, G.; Li, J.; Xu, J. Narrowband RFI suppression for SAR system via fast implementation of joint sparsity and Low-Rank property. IEEE Trans. Geosci. Remote 2018, 56, 2748–2761. [Google Scholar] [CrossRef]
- Huang, Y.; Liao, G.; Zhang, Z.; Xiang, Y.; Li, J.; Nehorai, A. Fast narrowband RFI suppression algorithms for SAR systems via Matrix-Factorization techniques. IEEE Trans. Geosci. Remote 2019, 57, 250–262. [Google Scholar] [CrossRef]
- Li, G.; Liu, G.; Ye, W. RFI mitigation for SAR based on compressed sensing and morphological component analysis. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 22–25 October 2017. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed Optimization and Satistical Learning via the Alternating Direction Method of Mmultipliers; Now Publishers Inc.: Hanover, MA, USA, 2011; pp. 13–24. [Google Scholar]
- Liu, H.; Li, D. RFI suppression based on sparse frequency estimation for SAR imaging. IEEE Geosci. Remote Sens. 2016, 13, 63–67. [Google Scholar] [CrossRef]
- Donoho, D. Compressed sensing. IEEE Trans. Inform. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inform. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Eldar, Y.C.; Kuppinger, P.; Bolcskei, H. Block-Sparse signals: Uncertainty relations and efficient recovery. IEEE Trans. Signal Proces. 2010, 58, 3042–3054. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Zhang, Z.; Rao, B.D. Sparse signal recovery with temporally correlated source vectors using sparse bayesian learning. IEEE J.-STSP 2011, 5, 912–926. [Google Scholar] [CrossRef]
- Zhang, Z.; Rao, B.D. Extension of SBL algorithms for the recovery of block sparse signals with Intra-Block correlation. IEEE Trans. Signal Proces. 2013, 61, 2009–2015. [Google Scholar] [CrossRef]
- Lu, X.; Su, W.; Yang, J.; Gu, H.; Zhang, H.; Yu, W.; Yeo, T.S. Radio frequency interference suppression for SAR via block sparse Bayesian learning. IEEE J.-STARS 2018, 11, 4835–4847. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Publishing House of Electronics Industry: Beijing, China, 2012; pp. 75–104. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1993; p. 504. [Google Scholar]
- Mahler, R. Statistical Multisource-Multitarget Information Fusion; Artech House: Norwood, MA, USA, 2007; pp. 699–703. [Google Scholar]
- Hj∅rungnes, A. Complex-Valued Matrix Derivatives: With Applications in Signal Processing and Communications; Cambridge University Press: New York, NY, USA, 2011; pp. 43–59. [Google Scholar]
- Zelnik-Manor, L.; Rosenblum, K.; Eldar, Y.C. Sensing matrix optimization for Block-Sparse decoding. IEEE Trans. Signal Proces. 2011, 59, 4300–4312. [Google Scholar] [CrossRef]
- Zelnik-Manor, L.; Rosenblum, K.; Eldar, Y.C. Dictionary optimization for Block-Sparse representations. IEEE Trans. Signal Proces. 2012, 60, 2386–2395. [Google Scholar] [CrossRef]
- Elad, M.; Bruckstein, A.M. A generalized uncertainty principle and sparse representation in pairs of bases. IEEE Trans. Inform. Theory 2002, 48, 2558–2567. [Google Scholar] [CrossRef]
- Duarte-Carvajalino, J.M.; Sapiro, G. Learning to sense sparse signals: Simultaneous sensing matrix and sparsifying dictionary optimization. IEEE Trans. Image Process. 2009, 18, 1395–1408. [Google Scholar] [CrossRef] [PubMed]
- Gandhi, P.; Kassam, S. Analysis of CFAR processors in nonhomogeneous background. IEEE Trans. Aerosp. Electron. Syst. 1988, 24, 427–445. [Google Scholar] [CrossRef]
- Fang, J.; Xu, Z.; Zhang, B.; Hong, W.; Wu, Y. Fast Compressed Sensing SAR Imaging Based on Approximated Observation. IEEE J.-STARS 2014, 7, 352–363. [Google Scholar]
- Lao, G.; Ye, W.; Li, G.; Zhang, W. A quality evaluation method of SAR image based on grayscale image and electromagnetic scattering characteristics. In Proceedings of the 8th International Conference on Digital Image Processing, Chengdu, China, 29 August 2016; Society of Photo-Optical Instrumentation Engineers (SPIE): Bellingham, WA, USA, 2016. [Google Scholar] [CrossRef]

| Task: Find an Optimal Observation Matrix to Improve NBI Separation and SOI Reconstruction Based on Block Sparse Bayesian Learning. |
|---|
| Inputs: |
| 1. Random observation matrix ; |
| 2. Compressed measurement ; |
| 3. Cascaded dictionary ; |
| 4. Block size ; |
| 5. Number of external and internal blocks ; |
| 6. Coherence weight ; |
| Outputs: |
| 1. Optimal observation matrix ; |
| 2. Reconstructed NBI-free signal ; |
| Initialization: |
| 1. Initialize as an M×N Gaussian random matrix; |
| 2. Initialize the maximum number of optimizing iterations as Nmax = 500; |
| 3. Initialize the public parameters to be estimated as ; |
| 4. Initialize the parameters for separation as , ; |
| 5. Initialize the threshold for pruning out as ; |
| 6. Initialize the iteration stop condition as ; |
| 7. Initialize the maximum number of reconstructive iterations as Kmax = 1000; |
| A. Sensing matrix optimizing stage |
| 1. Calculate the total block coherence by Equations (29)–(31); |
| 2. Build objective function for optimizing by Equation (32); |
| 3. Calculate a new initialized observation matrix by Equations (33)–(34); |
| Repeat from n = 0 until n = Nmax − 1 |
| (1) Calculate the Gram matrix by ; |
| (2) Build the equivalent objective function by Equations (35)–(36); |
| (3) Update the optimal by Equation (37); |
| (4) n = n + 1; |
| 4. Set ; |
| B. Separation and reconstruction stage: |
| 1. Reset the sensing matrix by ; |
| Repeat from k = 1 until Kmax or ; |
| (1) Update the prior covariance matrix by Equation (11); |
| (2) Update the covariance matrix by ; |
| (3) Update the expectation by ; |
| (4) Update the parameters by Equations (20)–(24); |
| (5) Update the threshold of by Equation (38) |
| (6) k = k + 1 |
| 2. Calculate coefficient by ; |
| 3. Reconstruct the NBI-free signal by . |
| Pfa = 10−1 | Pfa = 10−2 | Pfa = 10−3 | Pfa = 10−4 | |
|---|---|---|---|---|
| Nc = 4 | 3.11 | 8.65 | 18.49 | 36.00 |
| Nc = 8 | 2.69 | 6.23 | 10.97 | 17.30 |
| Nc = 16 | 2.48 | 5.34 | 8.64 | 12.45 |
| Nc = 32 | 2.39 | 4.95 | 7.71 | 10.67 |
| Parameter Class | Parameter Name | Parameter Value |
|---|---|---|
| Platform | Platform height | 3000 m |
| Pitch angle | 45° | |
| Squint Angle | 0° | |
| Target | Number of points | 1932 |
| Scene vertical range | −128 to 128 m | |
| Scene parallel range | −128 to 128 m | |
| Signal | Carrier frequency | 3 GHz |
| Bandwidth | 100 MHz | |
| Pulse width | 1 μs | |
| Pulse repetition frequency | 125 Hz | |
| Oversampling coefficient | 1.2 | |
| Size of Range-Azimuth Cells | 512×512 |
| Original | Bn | Contaminated | BSBL | S-BSBL | SMO-BSBL | |
|---|---|---|---|---|---|---|
| PSNR (dB) | 18.809 | 10 MHz | 10.489 | 11.441 | 15.617 | 16.322 |
| 20 MHz | 10.479 | 11.319 | 12.770 | 14.915 | ||
| ENL (dB) | 1.537 | 10 MHz | 3.840 | 2.950 | 2.366 | 2.140 |
| 20 MHz | 3.681 | 2.941 | 3.463 | 2.636 | ||
| Entropy | 3.902 | 10 MHz | 6.006 | 5.404 | 4.435 | 4.292 |
| 20 MHz | 5.877 | 5.122 | 4.950 | 4.577 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Ye, W.; Lao, G.; Kong, S.; Yan, D. Narrowband Interference Separation for Synthetic Aperture Radar via Sensing Matrix Optimization-Based Block Sparse Bayesian Learning. Electronics 2019, 8, 458. https://doi.org/10.3390/electronics8040458
Li G, Ye W, Lao G, Kong S, Yan D. Narrowband Interference Separation for Synthetic Aperture Radar via Sensing Matrix Optimization-Based Block Sparse Bayesian Learning. Electronics. 2019; 8(4):458. https://doi.org/10.3390/electronics8040458
Chicago/Turabian StyleLi, Guojing, Wei Ye, Guochao Lao, Shuya Kong, and Di Yan. 2019. "Narrowband Interference Separation for Synthetic Aperture Radar via Sensing Matrix Optimization-Based Block Sparse Bayesian Learning" Electronics 8, no. 4: 458. https://doi.org/10.3390/electronics8040458
APA StyleLi, G., Ye, W., Lao, G., Kong, S., & Yan, D. (2019). Narrowband Interference Separation for Synthetic Aperture Radar via Sensing Matrix Optimization-Based Block Sparse Bayesian Learning. Electronics, 8(4), 458. https://doi.org/10.3390/electronics8040458




