Transmission Capacity Characterization in VANETs with Enhanced Distributed Channel Access
Abstract
1. Introduction
- The transmission scheme is modeled to mimic EDCA protocol from the perspective of the spatial geometric relationship among transmitters, in which the division of priorities takes into account both the data type and the transmission distance requirement. and the transmission opportunity under EDCA protocol is calculated and compared with that of CSMA/CA.
- More realistic characteristics of the VANET are considered, for instance, the moving pattern of vehicles is described as the classic car-following model, and the propagation channel is modeled as the combination of path-loss and Rayleigh fading.
- With the theoretical results obtained from the analysis on spatial transmission opportunity and outage probability, the network transmission capacity of VANETs is thereby calculated and also verified by simulations.
2. Related Works
3. System Model
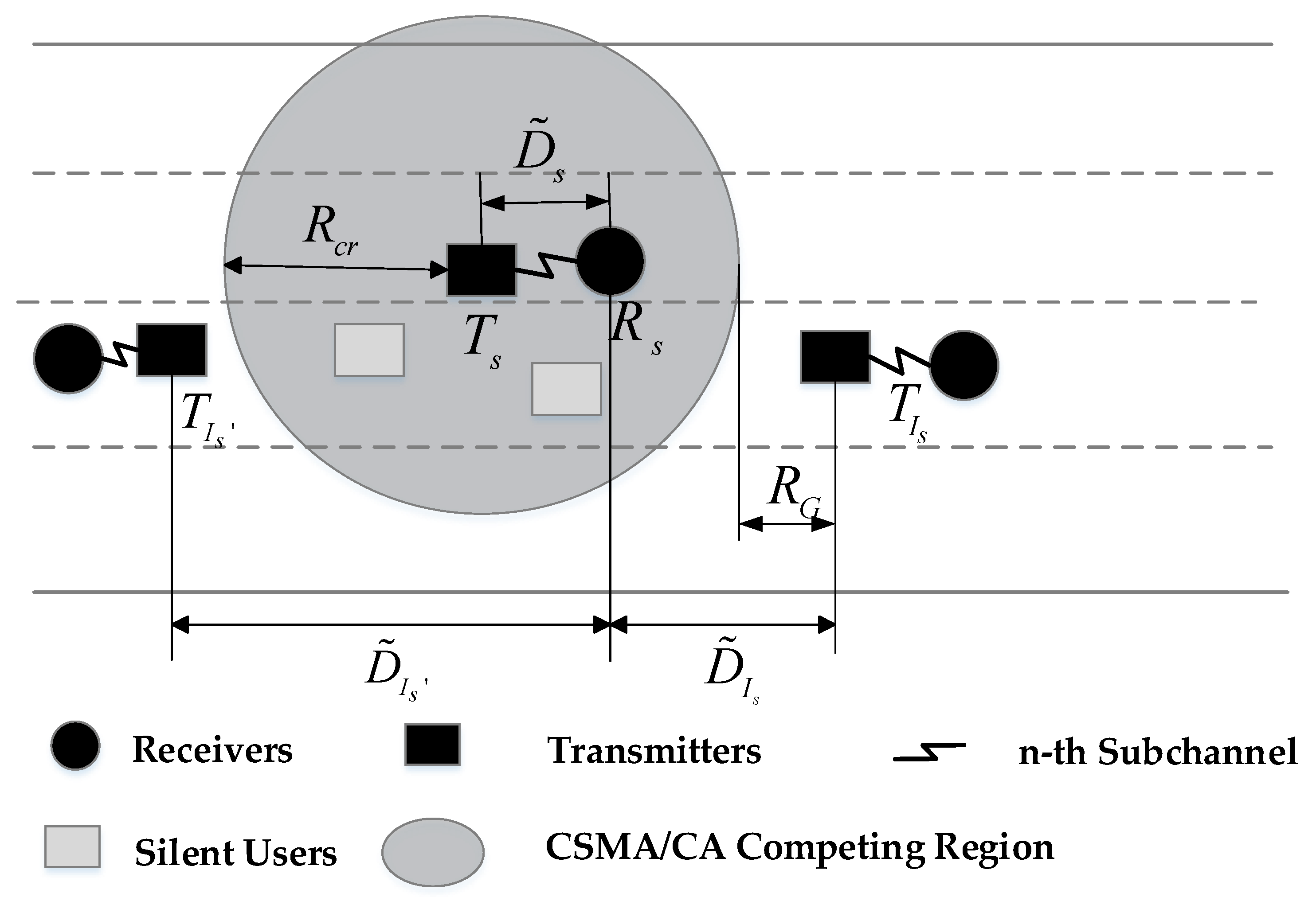
3.1. 1-Dimensional VANET Model
3.2. Slotted Medium Access Protocol Model
3.3. Performance Metric
4. Transmission Capacity Analysis
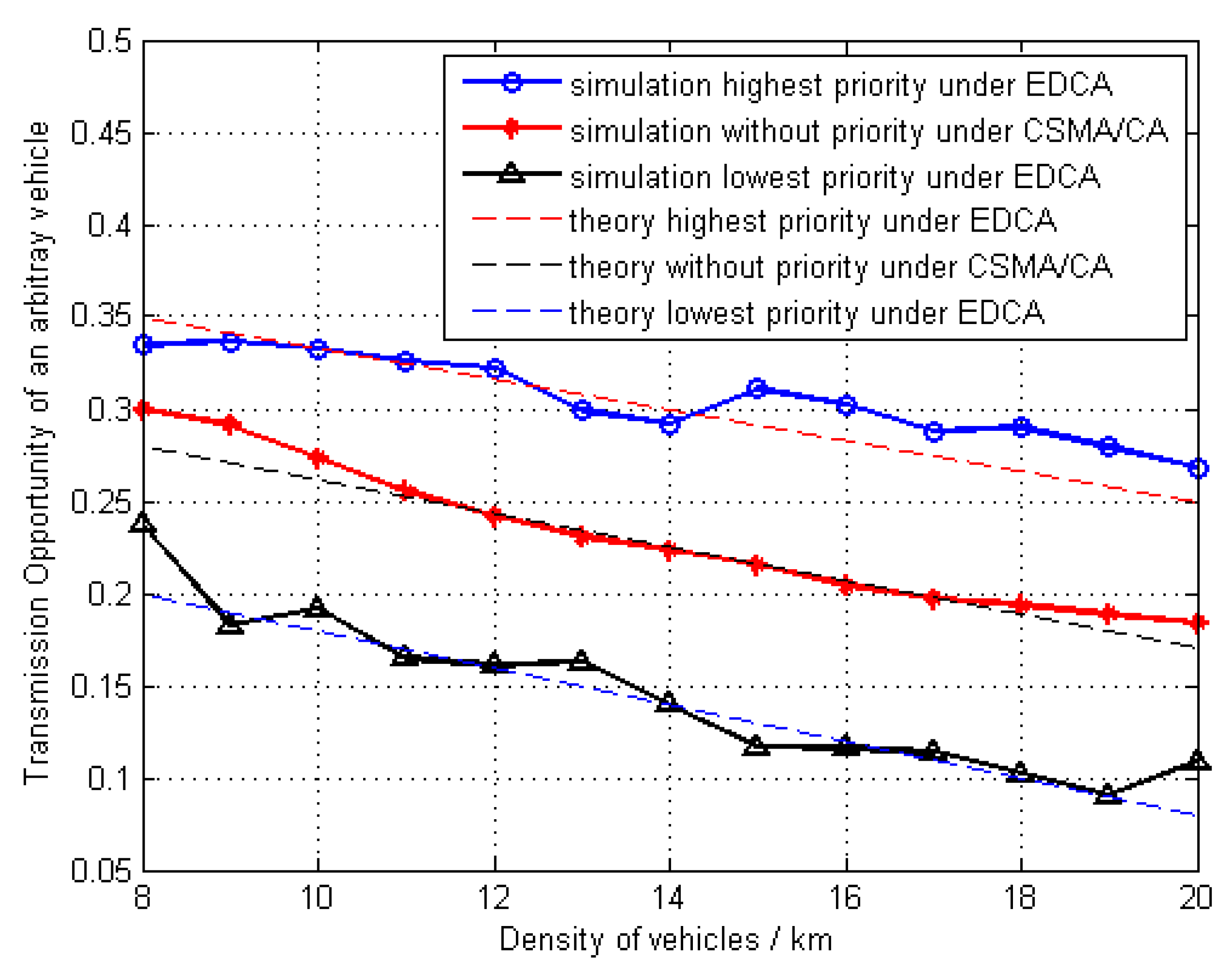
4.1. Subsection Transmission Opportunity Under EDCA
4.2. Transmission Opportunity Under CSMA/CA
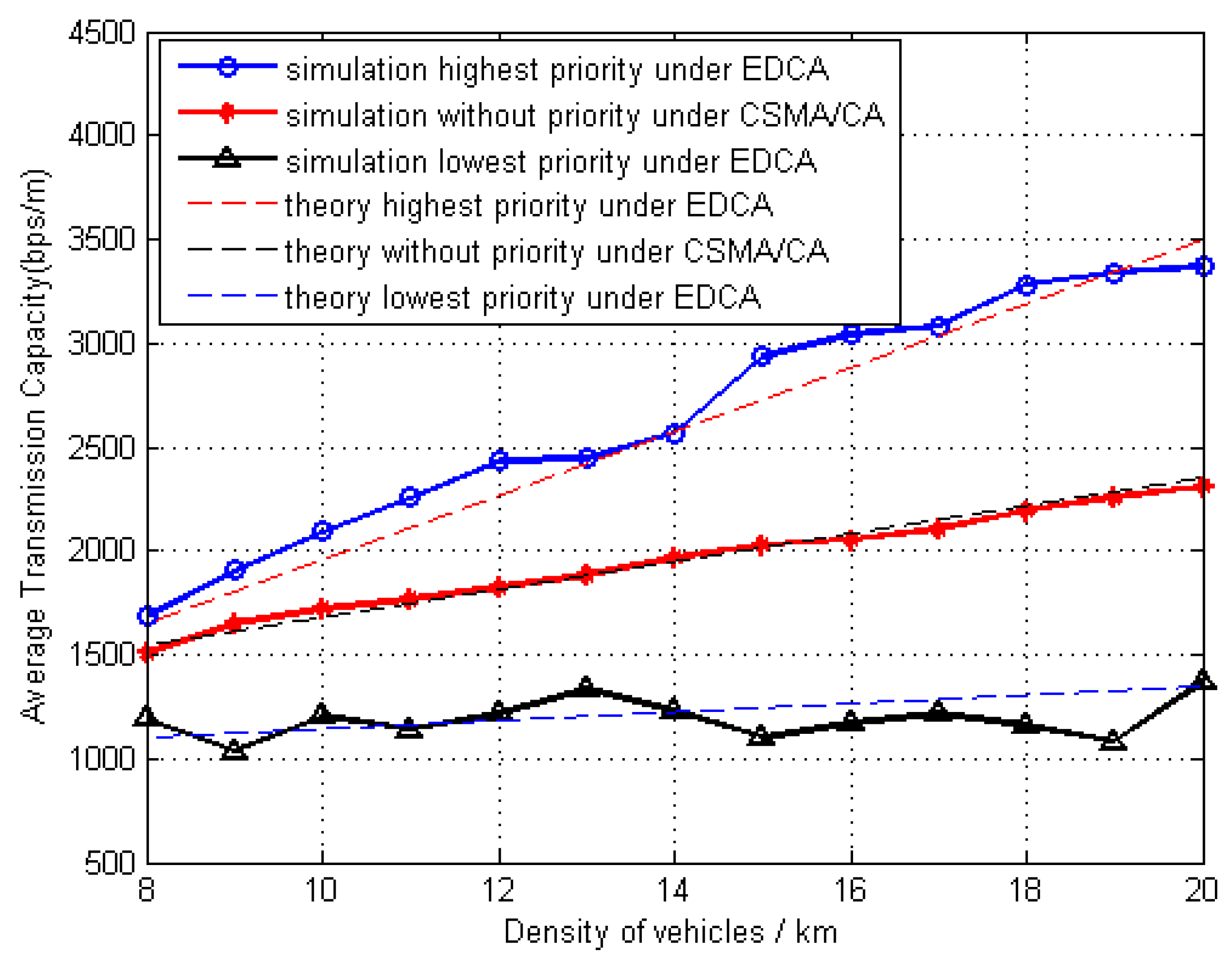
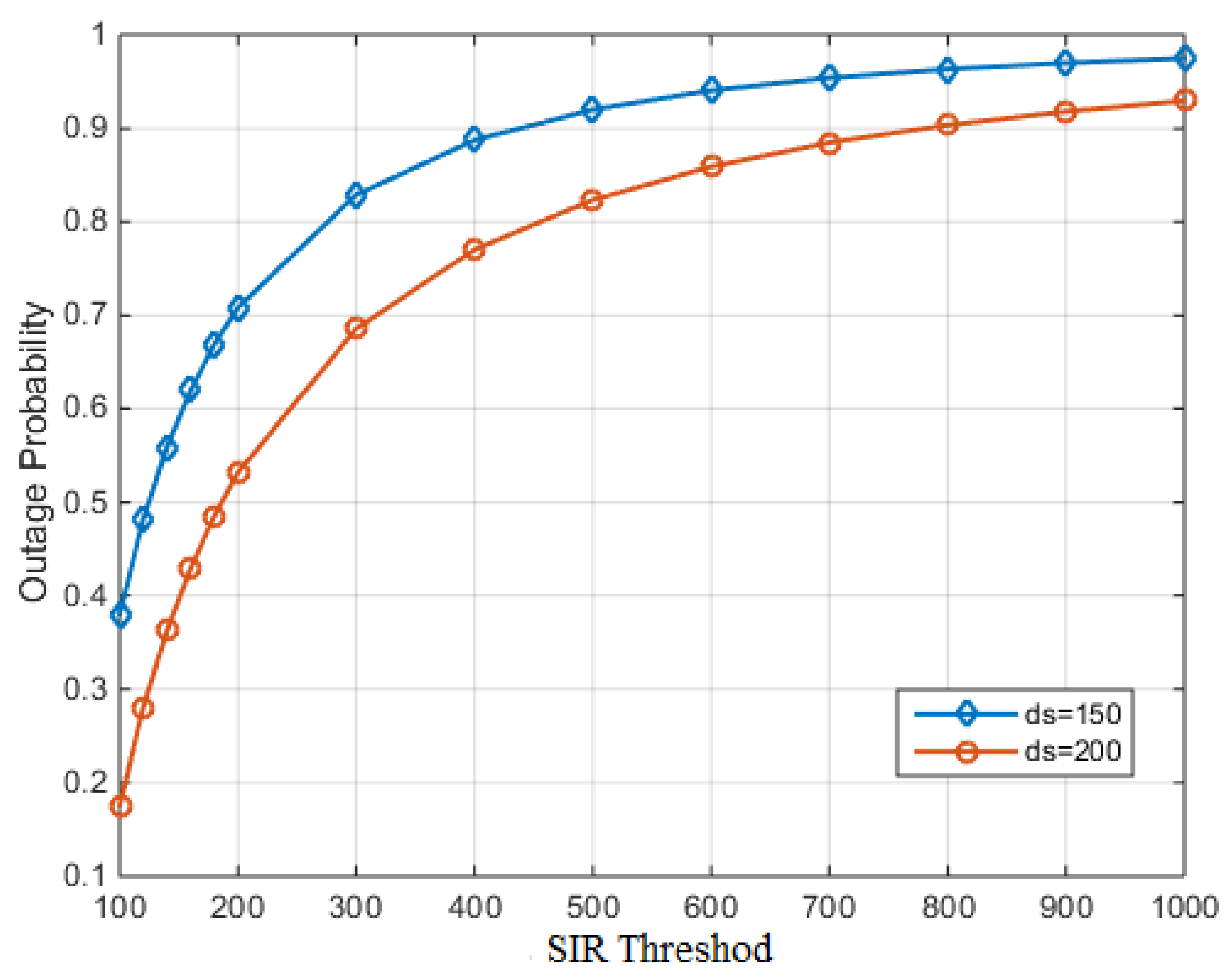
4.3. Outage Probability
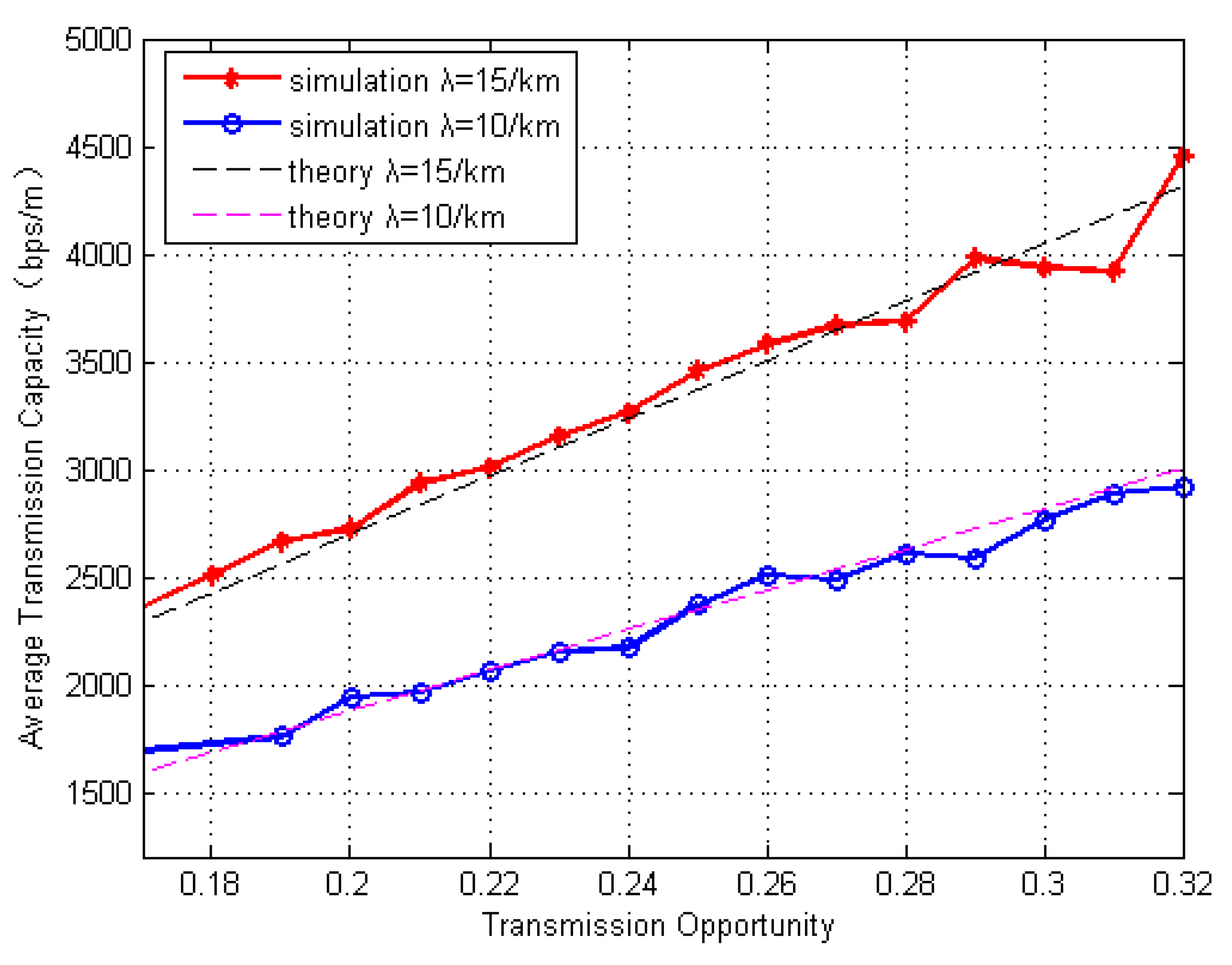
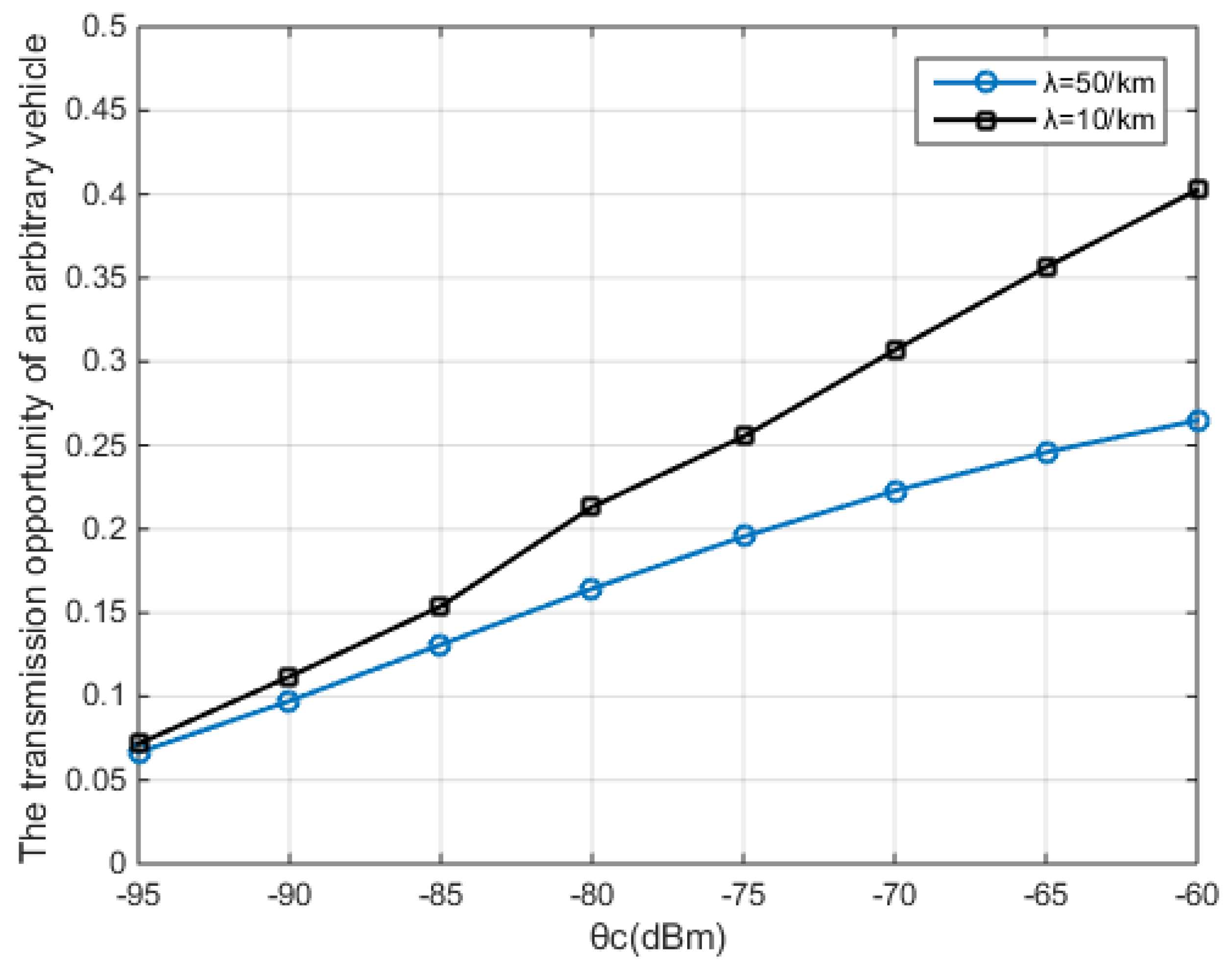
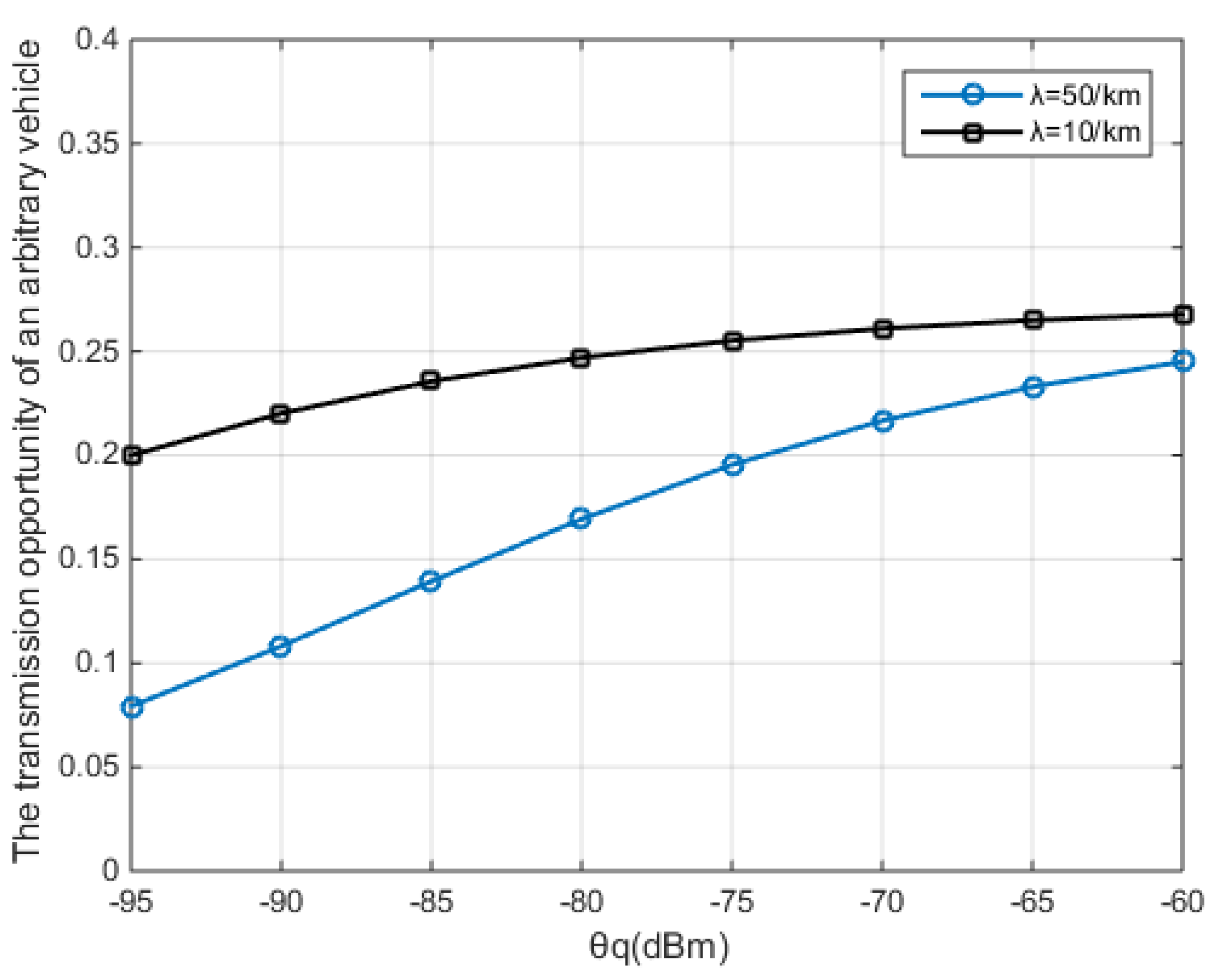
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sheet, D.K.; Kaiwartya, O.; Abdullah, A.H.; Cao, Y.; Hassan, N.S.; Kumar, S. Location information verification using transferable belief model for geographic routing in vehicular ad hoc networks. IET Intell. Transp. Syst. 2017, 11, 53–60. [Google Scholar] [CrossRef]
- Kaiwartya, O.; Abdullah, A.H.; Cao, Y.; Altameem, A.; Prasad, M.; Lin, C.T.; Liu, X. Internet of vehicles: Motivation, layered architecture, network model, challenges, and future aspects. IEEE Access 2016, 4, 5356–5373. [Google Scholar] [CrossRef]
- Qureshi, K.N.; Abdullah, A.H.; Kaiwartya, O.; Iqbal, S.; Butt, R.A.; Bashir, F. A dynamic congestion control scheme for safety applications in vehicular ad hoc networks. Comput. Electr. Eng. 2018, 72, 774–788. [Google Scholar] [CrossRef]
- Aliyu, A.; Abdullah, H.; Kaiwartya, O.; Cao, Y.; Usman, M.J.; Kumar, S.; Lobiyal, D.K.; Raw, R.S. Cloud computing in VANETs architecture, taxonomy, and challenges. IETE Tech. Rev. 2018, 35, 523–547. [Google Scholar] [CrossRef]
- Xia, Y.; Chen, W.; Liu, X.; Zhang, L.; Li, X.; Xiang, Y. Adaptive multimedia data forwarding for privacy preservation in Vehicular Ad-Hoc Networks. IEEE Trans. Intell. Transp. 2017, 18, 2629–2641. [Google Scholar] [CrossRef]
- Gupta, P.; Kumar, P.R. The capacity of wireless networks. IEEE Trans. Inf. Theory 2000, 46, 388–404. [Google Scholar] [CrossRef]
- Baccelli, F.; Blaszczyszyn, B.; Muhlethaler, P. An Aloha protocol for multihop mobile wireless networks. IEEE Trans. Inf. Theory 2006, 2, 421–436. [Google Scholar] [CrossRef]
- Weber, S.; Andrews, J.G.; Jindal, N. The effect of fading, channel inversion, and threshold scheduling on ad hoc networks. IEEE Trans. Inf. Theory 2007, 11, 4127–4149. [Google Scholar] [CrossRef]
- Baccelli, F.; Btaszczyszyn, B. Stochastic Geometry and Wireless Networks. NOW Found. Trends Netw. 2010, 4, 1–312. [Google Scholar]
- Haenggi, M.; Andrews, J.G.; Baccelli, F.; Dousse, O.; Franceschetti, M. Stochastic geometry and random graphs for the analysis and design of wireless networks. IEEE J. Sel. Areas Commun. 2009, 7, 1029–1046. [Google Scholar] [CrossRef]
- Weber, S.; Andrews, J.G. Transmission capacity of wireless networks. Found. Trends Netw. 2012, 5, 3593–3604. [Google Scholar] [CrossRef]
- Kasana, R.; Kumar, S.; Kaiwartya, O.; Kharel, R.; Lloret, J.; Aslam, N.; Wang, T. Fuzzy-based channel selection for location oriented services in multichannel VCPS environments. IEEE Internet Things 2018, 5, 4642–4651. [Google Scholar] [CrossRef]
- Hassan, A.N.; Kaiwartya, O.; Abdullah, A.H.; Sheet, D.H.; Raw, R.S. Inter-vehicle distance based connectivity aware routing in vehicular adhoc networks. Wirel. Pers. Commun. 2018, 98, 33–54. [Google Scholar] [CrossRef]
- Lu, N.; Luan, T.H.; Wang, M.; Shen, X.; Bai, F. Capacity and delay analysis for social-proximity urban vehicular networks. In Proceedings of the IEEE INFOCOM, Orlando, FL, USA, 25–30 March 2012; pp. 1476–1484. [Google Scholar]
- Huang, Y.; Chen, M.; Cai, Z.; Guan, X.; Ohtsuki, T.; Zhang, Y. Graph Theory Based Capacity Analysis for Vehicular Ad Hoc Networks. In Proceedings of the 2015 IEEE Global Communications Conference, San Diego, CA, USA, 6–10 December 2015. [Google Scholar] [CrossRef]
- Wang, M.; Shan, H.; Luan, T.H.; Lu, N.; Zhang, R.; Shen, X.; Bai, F. Asymptotic Throughput Capacity Analysis of VANETs Exploiting Mobility Diversity. IEEE Trans. Veh. Technol. 2015, 64, 4187–4202. [Google Scholar] [CrossRef]
- Jacquet, P.; Muhlethaler, P. Mean Number of Transmissions with CSMA in a Linear Network. In Proceedings of the Vehicular Technology Conference, Ottawa, ON, Canada, 6–9 September 2010. [Google Scholar] [CrossRef]
- Giang, A.T.; Busson, A.; Lambert, A.; Gruyer, D. An upper bound for capacity of VANET. In Proceedings of the 2012 International Conference on Advanced Technologies for Communications, Hanoi, Vietnam, 10–12 October 2012. [Google Scholar] [CrossRef]
- Ozturk, S.; Mi, J.; Mi, V.B. Capacity limits in a variable duty cycle IEEE 802.11p-based VANET. Wirel. Commun. Mob. Comput. 2012, 12, 1672–1684. [Google Scholar] [CrossRef]
- Giang, A.T.; Busson, A.; Gruyer, D.; Lambert, A. A packing model to estimate VANET capacity. In Proceedings of the Wireless Communications and Mobile Computing Conference (IWCMC), Limassol, Cyprus, 27–31 August 2012; pp. 1119–1124. [Google Scholar]
- Ni, M.; Pan, J.; Cai, L.; Yu, J.; Wu, H.; Zhong, Z. Interference-Based Capacity Analysis for Vehicular Ad Hoc Networks. IEEE Commun. Lett. 2015, 19, 621–624. [Google Scholar] [CrossRef]
- Donadee, J.; Marija, D. Stochastic Optimization of Grid to Vehicle Frequency Regulation Capacity Bids. IEEE Trans. Smart Grid 2014, 5, 1061–1069. [Google Scholar] [CrossRef]
- Luan, T.H.; Ling, X.; Shen, X. MAC in Motion: Impact of Mobility on the MAC of Drive-Thru Internet. IEEE Trans. Mob. Comput. 2011, 11, 305–319. [Google Scholar] [CrossRef]
- He, X.; Shi, W.; Luo, T. Transmission Capacity Analysis for Vehicular Ad Hoc Networks. IEEE Access 2018, 6, 30333–30341. [Google Scholar] [CrossRef]
- Le, D.T. A Priority-Based Multichannel Mac to Support the Non-Safety Applications in SCH Interval at RSU in V2I Communication. Transp. Telecommun. J. 2018, 19, 269–283. [Google Scholar] [CrossRef]
- Brackstone, M.; McDonald, M. Car-following: A historical review. Transportation Research Part F. Traffic Psychol. Behav. 1999, 2, 181–196. [Google Scholar] [CrossRef]
- Shiraki, Y.; Ohyama, T.; Nakabayashi, S. Development of an Inter-Vehicle communications system. IEEE Trans. Intell. Transp. Syst. 2001, 68, 11–13. [Google Scholar]
- Lu, N.; Zhang, N.; Cheng, N.; Shen, X. Vehicles meet infrastructure: Toward capacity cost tradeoffs for vehicular access networks. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1266–1277. [Google Scholar] [CrossRef]
- Ni, M.; Zhang, L.; Pan, J.; Cai, L.; Rutagemwa, H.; Li, L.; Wei, T. Connectivity in mobile tactical networks. In Proceedings of the 2014 IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 4400–4405. [Google Scholar]
- Ji, Y.; Zhang, J.; Wang, X.; Yu, H. Towards converged, collaborative and co-automatic (3C) optical networks. Sci. China Inf. Sci. 2018, 61, 121301. [Google Scholar] [CrossRef]
- Ucar, S.; Ergen, S.C.; Ozkasap, O. IEEE 802.11p and Visible Light Hybrid Communication based Secure Autonomous Platoon. IEEE Trans. Veh. Technol. 2018, 67, 8667–8681. [Google Scholar] [CrossRef]



| Transmitting data-rate of the vehicle | |
| Transmitting power of the vehicle | |
| The received power of the vehicle | |
| Propagation distance between the transmitter and the receiver | |
| Path-loss exponent | |
| Rayleigh fading factor | |
| The threshold of the transmission range between the transmitter and the receiver | |
| The total transmission opportunity under EDCA protocol | |
| The probability that a vehicle is preselected | |
| The probability that the preselected vehicle successfully transmits | |
| Transmission capacity | |
| The density of the potential transmitters | |
| The CCA threshold in sensing period | |
| Predefined carrier sensing threshold in the contention period | |
| The density of the active transmitters which occupied the channel at the same time | |
| The density of the eligible transmitters after the sensing period | |
| The backoff time | |
| The total time that the eligible vehicle in the contention period needs to wait | |
| Outage probability | |
| The threshold of SIR |
| Priority Level | Data Type | Distance Level | CWmin | CWmax | AIFSN |
|---|---|---|---|---|---|
| P1 | AC_VO | N | (CWBKmin+1)/16-1 | (CWBKmin+1)/8-1 | (AIFS+1)/2-3 |
| P2 | AC_VO | F | (CWBKmin+1)/8-1 | (CWBKmin+1)/4-1 | (AIFS+1)/2-3 |
| P3 | AC_VI | N | (CWBKmin+1)/4-1 | (CWBKmin+1)/2-1 | (AIFS+1)/2-3 |
| P4 | AC_VI | F | (CWBKmin+1)/4-1 | (CWBKmin+1)/2-1 | (AIFS+1)/2-2 |
| P5 | AC_BE | N | (CWBKmin+1)/2-1 | CWBKmin | (AIFS+1)/2-2 |
| P6 | AC_BE | F | (CWBKmin+1)/2-1 | CWBKmin | (AIFS+1)/2-1 |
| P7 | AC_BK | N | CWBKmin | CWBKmax | (AIFS+1)/2-1 |
| P8 | AC_BK | F | CWBKmin | CWBKmax | AIFS |
| Simulation Parameter | Numerical Value | Simulation Parameter | Numerical Value |
|---|---|---|---|
| IEEE 802.11std | 802.11p | Transmission Gain Gt | 34 dBm |
| CCA mode | CCA mode 1 | Receiving Gain Gr | 33 dBm |
| Carrier Wavelength λ | 0.051 m | CCA Threshold | −75 dBm |
| Packet Length | 2048 byte | Exponent α | 2 |
| Slot-time | 20 μs | Outage Probability | 0 |
| [CWmin, CWmax] | [140 μs, 300 μs] | Transmission Data-rate R | 2 Mbps |
| Arbitration Inter-Frame Space (AIFS) | 50 μs | Effective Transmission Radium D | 500 m |
| Short Inter-frame Space (SIFS) | 10 μs | Road Length L | 4 km |
| Transmission Power Pt | 33 dBm | Duration of Simulation ts | 3 s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; He, X.; Huang, Z.; Ji, Y. Transmission Capacity Characterization in VANETs with Enhanced Distributed Channel Access. Electronics 2019, 8, 340. https://doi.org/10.3390/electronics8030340
Liu W, He X, Huang Z, Ji Y. Transmission Capacity Characterization in VANETs with Enhanced Distributed Channel Access. Electronics. 2019; 8(3):340. https://doi.org/10.3390/electronics8030340
Chicago/Turabian StyleLiu, Wei, Xinxin He, Zhitong Huang, and Yuefeng Ji. 2019. "Transmission Capacity Characterization in VANETs with Enhanced Distributed Channel Access" Electronics 8, no. 3: 340. https://doi.org/10.3390/electronics8030340
APA StyleLiu, W., He, X., Huang, Z., & Ji, Y. (2019). Transmission Capacity Characterization in VANETs with Enhanced Distributed Channel Access. Electronics, 8(3), 340. https://doi.org/10.3390/electronics8030340




