Analytical Modeling of Metamaterial Differential Transmission Line Using Corrugated Ground Planes in High-Speed Printed Circuit Boards

Abstract

An analytical model for metamaterial differential transmission lines (MTM-DTLs) with a corrugated ground-plane electromagnetic bandgap (CGP-EBG) structure in high-speed printed circuit boards is proposed. The proposed model aims to efficiently and accurately predict the suppression of common-mode noise and differential signal transmission characteristics. Analytical expressions for the four-port impedance matrix of the CGP-EBG MTM-DTL are derived using coupled-line theory and a segmentation method. Converting the impedance matrix into mixed-mode scattering parameters enables obtaining common-mode noise suppression and differential signal transmission characteristics. The comprehensive evaluations of the CGP-EBG MTM-DTL using the proposed analytical model are also reported, which is validated by comparing mixed-mode scattering parameters S_cc21 and S_dd21 with those obtained from full-wave simulations and measurements. The proposed analytical model provides a drastic reduction of computation time and accurate results compared to full-wave simulation.

1. Introduction

In high-speed printed circuit boards (PCBs) for digital communication systems, such as USB, HDMI, and PCI-Express technologies, electromagnetic interference during data transmission is a serious problem because the data rate of digital interfaces and the switching speed of processors continuously increase, but the voltage level continuously decreases. In recent high-speed PCB designs, simultaneous switching output noise in power delivery networks and near-field coupling noise in high-speed transmission lines notably undermine digital data transmission. To mitigate the electromagnetic interference effects, differential signaling is usually adopted. Given its balanced transmission, differential signaling is tolerant to both simultaneous switching output noise and near-field coupling noise. Hence, differential signaling is being increasingly adopted in high-speed PCBs by implementing a scheme using three conductor systems, namely positive signal line, negative signal line, and ground plane. Maintaining symmetry of those signal lines over the ground plane in high-speed PCBs is critical, because the noise robustness of differential signaling depends on the balanced scheme. However, it is difficult to prevent asymmetries in practical PCB designs. For instance, the unbalanced structures of meander delay lines, ball–grid–array escape routing, and asymmetric ground via configurations frequently occur during the practical design of high-speed PCBs. Moreover, current-strength mismatch of output driver circuits and trace-length mismatch in cables lead to unbalance in the differential scheme even if the PCB is symmetrical. Consequently, imbalance in differential signaling is inevitable in practical PCBs.

Unbalanced differential lines result in severe common-mode (CM) noise generation in high-speed PCBs [1,2,3,4]. Specifically, skewed signals in unbalanced differential lines generate wideband CM noise with high-order harmonics in the range of gigahertz and related electromagnetic interference problems. For intra-system electromagnetic interference, CM noise coupled to power delivery networks degrades the noise margin and timing budget of circuits mounted on the same board. Additionally, serious radio-frequency interference is produced when the CM noise flows into cables attached to PCBs. A practical example of radio-frequency interference induced by CM noise is presented in Reference [5], where experimental results show severe interference between a USB device and a 2.4-GHz wireless LAN device. Hence, CM noise caused by unbalanced differential structures should be mitigated in high-speed PCBs.

To suppress wideband and high-frequency CM noise in high-speed PCBs, metamaterial (MTM)-based techniques were proposed [6,7,8,9,10,11]. In Reference [6], differential transmission lines (DTLs), using a mushroom-type electromagnetic bandgap (EBG) structure with LTCC process technology, are presented. This type of EBG structure provides a wide stopband for even-mode propagation to suppress CM noise flowing along the differential lines, and the passband characteristics of odd-mode propagation ensure good differential-signal integrity during transmission. Then, CM noise suppression is predicted using dispersion analysis based on a lumped circuit model assuming a periodic structure, but prediction for differential signal transmission is not provided. In Reference [7], a complementary split ring resonator (CSRR) is employed to suppress CM noise of differential lines in high-speed PCBs. The CSRR etched in a ground plane forms an LC resonator to prevent even-mode propagation and behaves as an LC ladder network for odd-mode propagation. To predict selective CM noise suppression, a dispersion relationship is established from a lumped circuit model. However, the differential transmission characteristics are not estimated before performing full-wave simulations and measurements. As reported in References [8,9,10,11], a stepped impedance resonator is favorable for MTM-DTLs. In Reference [8], a stepped impedance resonator is implemented using various sizes for planar patches. A large patch and a narrow branch correspond to low and high characteristic impedances, respectively. CM noise suppression and differential signal quality are examined through full-wave simulations and experiments. In Reference [9], dual-type transmission lines are proposed to realize an MTM-DTLs. Impedance variations are implemented by alternating microstrip and strip lines, and a dispersion equation based on a periodic condition is derived, but it only predicts CM noise suppression. In References [10,11], a technique with ground planes vertically distributed in PCBs is proposed. The stepped impedance for odd-mode propagation is realized by variations of the vertical distances from differential lines to ground planes, representing a corrugated ground-plane electromagnetic bandgap (CGP-EBG) structure. Dispersion equations for odd-mode propagation are extracted to predict CM noise suppression only.

Therefore, recent research mainly focused on MTM-DTLs for CM noise suppression. It demonstrated wideband and high-frequency CM noise suppression with good differential signal integrity, simple implementation, and rigorous analysis based on dispersion relations. The key idea behind the development of MTM-DTLs is to provide structures handling different characteristics in the propagation modes of CM noise and differential-mode (DM) signal. To efficiently design and optimize MTM-DTLs, predicting and examining CM and DM characteristics of MTM-DTLs before their fabrication is needed. Although electromagnetic full-wave simulations can be employed, their prediction is computationally intensive in time and resources, thus being unsuitable for rapid design, testing, and prototyping of MTM-DTLs.

To overcome this problem, dispersion analysis with Floquet theory was adopted to estimate CM noise suppression. However, this analysis is limited to periodic structures, hindering the estimation of noise suppression characteristics when MTM-DTLs include a finite and small number of unit cells (UCs). Moreover, the periodicity of an MTM-DTL is not ensured in practical PCB applications. Likewise, dispersion analysis does not allow to accurately predict the suppression level, as its results only indicate whether a sufficient suppression will be provided in a stopband without retrieving a quantitative prediction. In addition, CM noise suppression characteristics in regions outside the stopband are not obtained, despite this information being critical in certain MTM-DTL applications. Moreover, the DM propagation associated with differential signaling characteristics was not estimated with a fast and simple approach in previous works. In Reference [12], the analytical method for the EBG structure employed in power delivery networks is presented. However, it is difficult to apply the method to DTLs because the segment model and recombined Z-parameter are limited to power delivery networks. Consequently, an efficient and accurate method to predict both CM noise and differential signaling characteristics of MTM-DTLs is still required for practical research and development of high-speed PCBs.

In this paper, an analytical model focusing on the MTM-DTL using a CGP-EBG structure is presented. In previous research [11], the CGP-EBG MTM-DTL was not fully characterized due to a limited method of CM noise prediction and a lack of estimation of differential transmission characteristics. Therefore, the research of the CGP-EBG MTM-DTL is extended by proposing an analytical model that efficiently provides rapid and accurate results for a nonperiodic array of CGP-EBG MTM-DTLs. The contribution of this paper is developing and verifying the analytical model, which simultaneously and quantitatively estimates the CM and DM propagation characteristics for the CGP-EBG MTM-DTL with a finite number of UCs.

2. Analytical Model of CGP-EBG MTM-DTL

2.1. Description of CGP-EBG MTM-DTL

In this section, a CGP-EBG MTM-DTL is briefly described, and the method for its analytical modeling is developed. Figure 1 shows a UC with its geometric parameters and the top and side views of the CGP-EBG MTM-DTL with a finite array size (three UCs). This CGP-EBG technique forms a stepped impedance resonator for even-mode propagation associated with CM noise and a constant impedance for odd-mode propagation associated with differential signal transmission by using the original distribution of ground planes. Basically, the characteristic impedances for odd- (Z_oo) and even-mode (Z_oe) propagations are determined by combining various geometric parameters of signal lines and ground plane. However, the CGP-EBG technique retrieves the desired Z_oe and Z_oo by only adjusting the vertical distance between signal lines and ground plane. The specific arrangement of ground patches, which are distributed in the different layers, provides varying Z_oe but the same Z_oo given in References [10,11]. The vertical distribution of ground planes efficiently achieves the decomposition of CM noise and differential signal propagation. The bandgap characteristics of the periodic CGP-EBG MTM-DTL were analyzed in References [10,11].

As shown in Figure 1, the UC of the CGP-EBG MTM-DTL consists of three parts, namely two DTLs with low Z_oe (LZ-DTL) and length d_L/2, and one DTL with high Z_oe (HZ-DTL) and length d_H. The vertical distance h_L between signal transmission lines and a ground patch for LZ-DTL is relatively short compared to h_H of HZ-DTL for obtaining low Z_oe for LZ-DTL and high Z_oe for HZ-DTL. Those ground planes are connected using plated-through-hole or blind vias for DC continuity. The via is separated from the center of the differential line by distance S_v.

2.2. Analytical Model

The proposed model is based on an analytical expression for the impedance matrix (Z-matrix) of LZ- and HZ-DTLs and a segmentation method for recombining the Z-matrices. The procedure of the proposed method mainly consists of two steps, namely segment modeling and segment recombination, as illustrated in Figure 2. During segment modeling, analytical expressions for the Z-parameters of HZ- and LZ-DTLs are extracted using coupled-line theory. Moreover, an analytical model of the via, which is used for reference plane transition between HZ- and LZ-DTLs, is derived.

The Z-parameters of the HZ- and LZ-DTLs are extracted using microwave theory for the four-port parallel-coupled lines that are represented in Figure 3a. The coupled line can be characterized by characteristic impedances of even and odd modes, a propagation constant, and a line length. In the parallel-coupled line for the HZ- and LZ-DTLs, the odd- and even-mode characteristic impedances at the i-th segment for recombination are denoted as Z_oo(i) and Z_oe(i), respectively, whereas the propagation constant and length are denoted as β_i and d_i, respectively. The voltage–current relationship for the parallel-coupled line of the i-th segment is given by

$$\left(\begin{array}{c}{V}_{1,\mathrm{seg}\left(i\right)}\\ V_{2,\mathrm{seg}\left(i\right)}\\ V_{3,\mathrm{seg}\left(i\right)}\\ V_{4,\mathrm{seg}\left(i\right)}\end{array}\right)=\left(\begin{array}{cccc}{Z}_{11,\mathrm{seg}\left(i\right)}& Z_{12,\mathrm{seg}\left(i\right)}& Z_{13,\mathrm{seg}\left(i\right)}& Z_{14,\mathrm{seg}\left(i\right)}\\ Z_{21,\mathrm{seg}\left(i\right)}& Z_{22,\mathrm{seg}\left(i\right)}& Z_{23,\mathrm{seg}\left(i\right)}& Z_{24,\mathrm{seg}\left(i\right)}\\ Z_{31,\mathrm{seg}\left(i\right)}& Z_{32,\mathrm{seg}\left(i\right)}& Z_{33,\mathrm{seg}\left(i\right)}& Z_{34,\mathrm{seg}\left(i\right)}\\ Z_{41,\mathrm{seg}\left(i\right)}& Z_{42,\mathrm{seg}\left(i\right)}& Z_{43,\mathrm{seg}\left(i\right)}& Z_{44,\mathrm{seg}\left(i\right)}\end{array}\right)\left(\begin{array}{c}{I}_{1,\mathrm{seg}\left(i\right)}\\ I_{2,\mathrm{seg}\left(i\right)}\\ I_{3,\mathrm{seg}\left(i\right)}\\ I_{4,\mathrm{seg}\left(i\right)}\end{array}\right)$$

(1)

where

$$Z_{11,\mathrm{seg}\left(i\right)}=Z_{11,\mathrm{seg}\left(i\right)}=Z_{11,\mathrm{seg}\left(i\right)}=Z_{11,\mathrm{seg}\left(i\right)}=-j/2\left(Z_{\mathrm{oe}\left(i\right)}+Z_{\mathrm{oo}\left(i\right)}\right)\cot \left({\beta }_i{d}_i\right),$$

(2a)

$$Z_{12,\mathrm{seg}\left(i\right)}=Z_{21,\mathrm{seg}\left(i\right)}=Z_{34,\mathrm{seg}\left(i\right)}=Z_{43,\mathrm{seg}\left(i\right)}=-j/2\left(Z_{\mathrm{oe}\left(i\right)}-Z_{\mathrm{oo}\left(i\right)}\right)\cot \left({\beta }_i{d}_i\right),$$

(2b)

$$Z_{13,\mathrm{seg}\left(i\right)}=Z_{31,\mathrm{seg}\left(i\right)}=Z_{24,\mathrm{seg}\left(i\right)}=Z_{42,\mathrm{seg}\left(i\right)}=-j/2\left(Z_{\mathrm{oe}\left(i\right)}-Z_{\mathrm{oo}\left(i\right)}\right)\csc \left({\beta }_i{d}_i\right),$$

(2c)

$$Z_{14,\mathrm{seg}\left(i\right)}=Z_{41,\mathrm{seg}\left(i\right)}=Z_{23,\mathrm{seg}\left(i\right)}=Z_{32,\mathrm{seg}\left(i\right)}=-j/2\left(Z_{\mathrm{oe}\left(i\right)}+Z_{\mathrm{oo}\left(i\right)}\right)\csc \left({\beta }_i{d}_i\right).$$

(2d)

The analytical expressions for the Z-parameter of the i-th segment in Equation (2) are obtained from References [13,14]. The Z-parameter of the HZ- and LZ-DTLs are extracted by letting (Z_oe(i) = Z_oe,H, Z_oo(i) = Z_oo,H) and (Z_oe(i) = Z_oe,L, Z_oo(i) = Z_oo,L), respectively. The analytical expressions for the HZ- and LZ-DTLs at the i-th segment are obtained from Equations (2a)–(2d).

The physical transition from the HZ-DTL to the LZ-DTL is modeled to capture its inductive effect on return current. In particular, the return path for even-mode propagation is considered because the physical transition mainly contributes this propagation, as described in Reference [11]. The return path effect can be modeled as an effective partial inductance determined by the via diameter and length, the pitch between the via and the center of the signal transmission line, and the number of vias. In the proposed analytical method, only the via diameter and length are considered because they are the major parameters determining the effective inductance for the transitions. The inductive effect of the physical transition is analytically expressed as

$$L_{\mathrm{v}}=\{\begin{array}{l}{\mu }_0\frac{h_{\mathrm{v}}}{2\pi }\left[\ln \left(\frac{2h_{\mathrm{v}}}{r}+\sqrt{1+{\left(\frac{2h_{\mathrm{v}}}{r}\right)}^2}\right)-\sqrt{1+{\left(\frac{2h_{\mathrm{v}}}{r}\right)}^{-2}}+{\left(\frac{2h_{\mathrm{v}}}{r}\right)}^{-1}+\frac{1}{4}\right] \mathrm{for}\mathrm{even}\mathrm{mode},\hfill \\ 0 \mathrm{for}\mathrm{odd}\mathrm{mode},\hfill \end{array}$$

(3)

where μ₀ is the permeability of free space, and h_v and r are the via length and radius, respectively, with h_v = h_H − h_L. The analytical expression for the via inductance in Equation (3) is extracted from Reference [15].

Next, segment recombination for the proposed model is applied. In this step, a technique is presented for merging the Z-matrices of HZ- and LZ-DTLs connected to each other through a via inductance to obtain the Z-matrix of a finite array of CGP-EBG MTM-DTLs. Segment recombination consists of three parts, namely derivation of recombined Z-matrix, iterative recombination, and parameter conversion. To extract the recombined Z-matrix, the block diagram of the segmentation method is illustrated in Figure 4. Two segments are connected through via inductances. For the sake of generality, the segments are denoted as the i-th and (i + 1)-th segments. Each segment includes four ports, P_{1_seg} to P_{4_seg}. The Z-parameters of the segments are Z_seg(i) and Z_seg(i+1). Port P_{3_seg} of the i-th segment is connected to port P_{1_seg} of the (i + 1)-th segment through the via with inductance L_v. Similarly, the other ports are connected through the via. Then, the recombined segment is conformed of Z-parameter and ports represented as Z_rec(i), P_{1_rec(i)}, P_{2_rec(i)}, P_{3_rec(i)}, and P_{4_rec(i)}. Ports P_{1_rec(i)} and P_{2_rec(i)} of the recombined segment are associated with ports P_{1_seg(i)} and P_{2_seg(i)} of the i-th segment, whereas ports P_{3_rec} and P_{4_rec} of the recombined segment are associated with ports P_{1_seg(i+1)} and P_{2_seg(i+1)} of the (i + 1)-th segment. Using the segmentation method in Reference [16], recombined matrix Z_rec(i) is extracted in terms of Z_seg(i), Z_seg(i+1), and L_v with operator $\oplus$ representing Z-parameter recombination.

$$\begin{array}{ll}{Z}_{\mathrm{rec}\left(i\right)}& =Z_{\mathrm{seg}\left(i\right)}\oplus Z_{\mathrm{via}}\oplus Z_{\mathrm{seg}\left(i+1\right)}\\ & =Z_{\mathrm{pp}}+\left(Z_{\mathrm{pq}}-Z_{\mathrm{pr}}\right){\left(Z_{\mathrm{qq}}-Z_{\mathrm{qr}}-Z_{\mathrm{rq}}+Z_{\mathrm{rr}}+Z_{\mathrm{via}}\right)}^{-1}\left(Z_{\mathrm{rp}}-Z_{\mathrm{qp}}\right),\end{array}$$

(4)

where

$$Z_{\mathrm{pp}}=\left(\begin{array}{cccc}{Z}_{11,\mathrm{seg}\left(i\right)}& Z_{12,\mathrm{seg}\left(i\right)}& 0& 0\\ Z_{21,\mathrm{seg}\left(i\right)}& Z_{22,\mathrm{seg}\left(i\right)}& 0& 0\\ 0& 0& Z_{33,\mathrm{seg}\left(i+1\right)}& Z_{34,\mathrm{seg}\left(i+1\right)}\\ 0& 0& Z_{43,\mathrm{seg}\left(i+1\right)}& Z_{44,\mathrm{seg}\left(i+1\right)}\end{array}\right),$$

(5a)

$$Z_{\mathrm{pq}}=\left(\begin{array}{cc}{Z}_{13,\mathrm{seg}\left(i\right)}& Z_{14,\mathrm{seg}\left(i\right)}\\ Z_{23,\mathrm{seg}\left(i\right)}& Z_{24,\mathrm{seg}\left(i\right)}\\ 0& 0\\ 0& 0\end{array}\right),$$

(5b)

$$Z_{\mathrm{pr}}=\left(\begin{array}{cc}0& 0\\ 0& 0\\ Z_{31,\mathrm{seg}\left(i+1\right)}& Z_{32,\mathrm{seg}\left(i+1\right)}0\\ Z_{41,\mathrm{seg}\left(i+1\right)}& Z_{42,\mathrm{seg}\left(i+1\right)}\end{array}\right),$$

(5c)

$$Z_{\mathrm{qq}}=\left(\begin{array}{cc}{Z}_{33,\mathrm{seg}\left(i\right)}& Z_{34,\mathrm{seg}\left(i\right)}\\ Z_{43,\mathrm{seg}\left(i\right)}& Z_{44,\mathrm{seg}\left(i\right)}\end{array}\right),$$

(5d)

$$Z_{\mathrm{qr}}=Z_{\mathrm{rq}}=\left(\begin{array}{cc}0& 0\\ 0& 0\end{array}\right),$$

(5e)

$$Z_{\mathrm{rr}}=\left(\begin{array}{cc}{Z}_{11,\mathrm{seg}\left(i+1\right)}& Z_{12,\mathrm{seg}\left(i+1\right)}\\ Z_{21,\mathrm{seg}\left(i+1\right)}& Z_{22,\mathrm{seg}\left(i+1\right)}\end{array}\right),$$

(5f)

$$Z_{\mathrm{via}}=\left(\begin{array}{cc}j\omega L_{\mathrm{v}}& 0\\ 0& j\omega L_{\mathrm{v}}\end{array}\right),$$

(5g)

$$Z_{\mathrm{rp}}=\left(\begin{array}{cccc}0& 0& Z_{13,\mathrm{seg}\left(i+1\right)}& Z_{14,\mathrm{seg}\left(i+1\right)}\\ 0& 0& Z_{23,\mathrm{seg}\left(i+1\right)}& Z_{24,\mathrm{seg}\left(i+1\right)}\end{array}\right),$$

(5h)

$$Z_{\mathrm{qp}}=\left(\begin{array}{cccc}{Z}_{31,\mathrm{seg}\left(i\right)}& Z_{32,\mathrm{seg}\left(i\right)}& 0& 0\\ Z_{41,\mathrm{seg}\left(i\right)}& Z_{42,\mathrm{seg}\left(i\right)}& 0& 0\end{array}\right).$$

(5i)

In the next part, recombination of the Z-parameter is iteratively applied. Suppose that a CGP-EBG MTM-DTL containing N UCs is given. The original problem of the MTM-DTL is replaced with subdomain problems constituting the N UCs further divided into HZ-DTLs, LZ-DTLs, and via transitions. The solutions of the subdomains are obtained using the expressions in Equations (1)–(3). Applying the recombined Z-parameter method iteratively, the subdomain solutions are updated to finally obtain the Z-parameter of the CGP-EBG MTM-DTLs with N UCs as

$$Z_{\mathrm{rec}\left(1\right)}=Z_{\mathrm{DTL}}\left(Z_{\mathrm{oe},\mathrm{L}}, Z_{\mathrm{oo}},d_{\mathrm{L}}/2\right)\oplus Z_{\mathrm{via}}\oplus Z_{\mathrm{DTL}}\left(Z_{\mathrm{oe},\mathrm{H}}, Z_{\mathrm{oo}},d_{\mathrm{H}}\right),$$

(6a)

$$Z_{\mathrm{rec}\left(2\right)}=Z_{\mathrm{rec}\left(1\right)}\oplus Z_{\mathrm{via}}\oplus Z_{\mathrm{DTL}}\left(Z_{\mathrm{oe},\mathrm{L}}, Z_{\mathrm{oo}},d_{\mathrm{L}}\right),$$

(6b)

$$Z_{\mathrm{rec}\left(2\left(N-1\right)\right)}=Z_{\mathrm{rec}\left(2\left(N-1\right)-1\right)}\oplus Z_{\mathrm{via}}\oplus Z_{\mathrm{DTL}}\left(Z_{\mathrm{oe},\mathrm{H}}, Z_{\mathrm{oo}},d_{\mathrm{H}}\right),$$

(6c)

$$Z_{\mathrm{MTM}-\mathrm{DTL}}=Z_{\mathrm{rec}\left(2\left(N-1\right)+1\right)}\oplus Z_{\mathrm{via}}\oplus Z_{\mathrm{DTL}}\left(Z_{\mathrm{oe},\mathrm{L}}, Z_{\mathrm{oo}},\frac{d_{\mathrm{L}}}{2}\right),$$

(6d)

where Z_DTL(Z_oe,L, Z_oo, d_L/2) denotes a four-port Z-parameter of the LZ-DTL with the length being half of d_L. The first and last segments of the CGP-EBG MTM-DTL, presented herein, are supposed to be the LZ-DTLs with length d_L/2. Still, note that the proposed analytical model for the MTM DTL is not limited to this configuration. From the four-port Z-parameter of the CGP-EBG MTM-DTL, the S-parameter is given as

$$S_{\mathrm{MTM}-\mathrm{DTL}}={\left(Z_{\mathrm{MTM}-\mathrm{DTL}}+Z_{0}E\right)}^{-1}\left(Z_{\mathrm{MTM}-\mathrm{DTL}}-Z_{0}E\right),$$

(7)

where Z₀ is the reference characteristic impedance, commonly taken as 50 Ω, and E is the identity matrix. The CM and differential characteristics are finally obtained using mixed-mode S-parameter theory [17]. Only the analytical expressions for S_cc21 and S_dd21 are presented due to the focus on CM noise suppression and differential transmission characteristics.

$$S_{\mathrm{cc}21}= \frac{1}{2}\left(S_{31,\mathrm{MTM}-\mathrm{DTL}}+S_{41,\mathrm{MTM}-\mathrm{DTL}}+S_{32,\mathrm{MTM}-\mathrm{DTL}}+S_{42,\mathrm{MTM}-\mathrm{DTL}}\right),$$

(8)

$$S_{\mathrm{dd}21}= \frac{1}{2}\left(S_{31,\mathrm{MTM}-\mathrm{DTL}}-S_{41,\mathrm{MTM}-\mathrm{DTL}}-S_{32,\mathrm{MTM}-\mathrm{DTL}}+S_{42,\mathrm{MTM}-\mathrm{DTL}}\right).$$

(9)

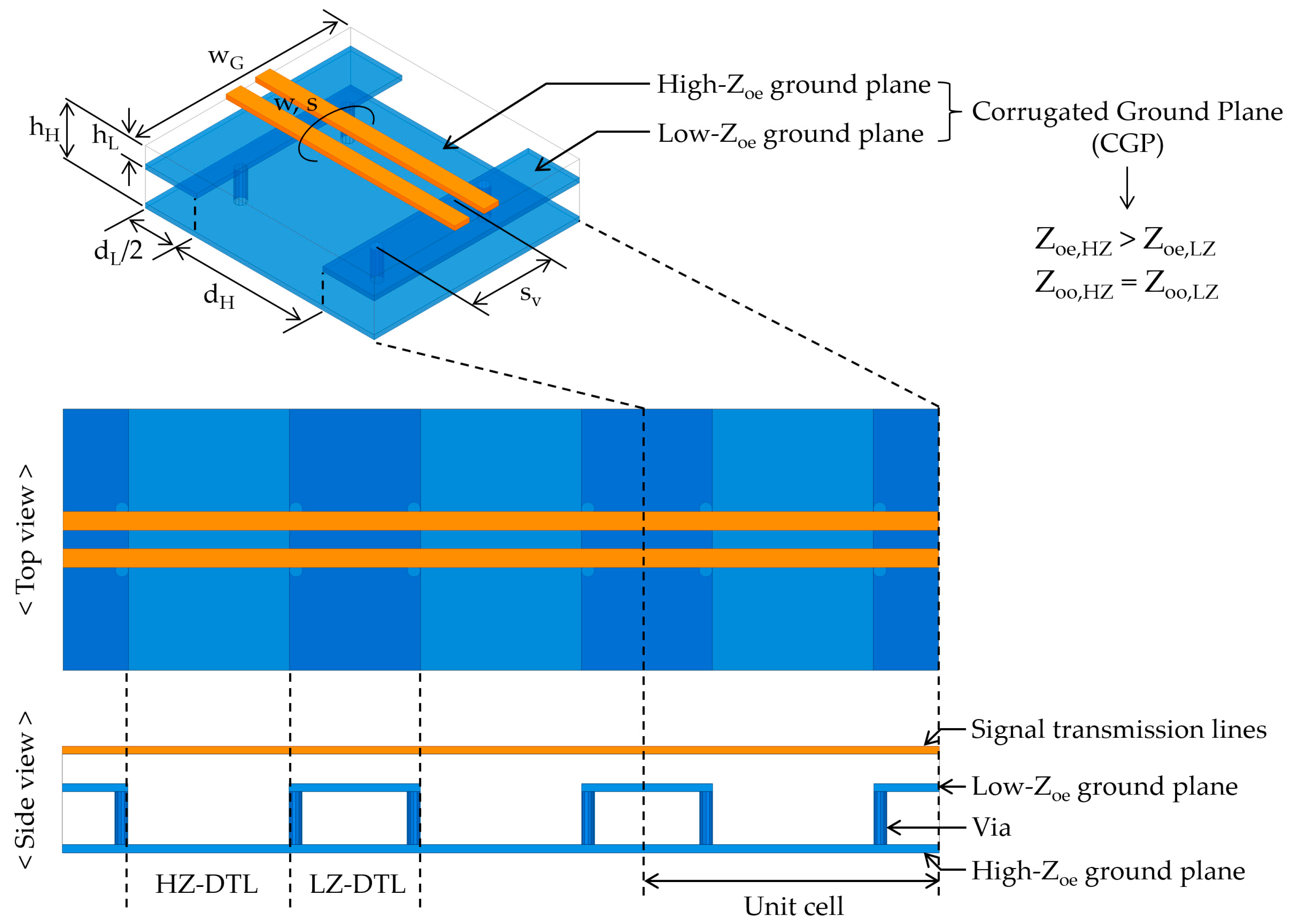
3. Results

To verify the proposed analytical model of CGP-EBG MTM-DTLs, it is compared to full-wave simulations based on the finite element method (FEM) [18] and measurements. Comprehensive validations were performed considering various cases. Firstly, the CM characteristics of the CGP-EBG MTM-DTLs between the proposed model and full-wave simulations are compared. For the full-wave simulation model, geometrical parameters d_H, h_H, d_L, h_L, w, s, w_G, and s_v are set to 10, 1.0, 10, 0.08, 0.1, 0.1, 10, and 1.3 mm, respectively. The values were determined considering a commercial PCB process. FR-4 and copper (35 μm thick) were used as a dielectric material and conductor, respectively. The physical dimensions of the CGP-EBG MTM-DTL present Z_oe,H, Z_oo,H, Z_oe,L, and Z_oo,L of 218, 66.3, 66, and 52 Ω, respectively. The dimensions and parameters for this validation are listed in

Table 1. Parameters for verification of the proposed analytical model. DTL—differential transmission line; HZ—high Z_oe; LZ—low Z_oe; UC—unit cell; CM—common mode; DM—differential mode.

Parameter	Figure	HZ-DTL				LZ-DTL				No. of UCs
		Zoe,H	Zoo,H	dH	hH	Zoe,L	Zoo,L	dL	hL
No. of UCs effect on CM, DM	6 (CM) 8 (DM)	218	66.3	10	1.0	66	52	10	0.08	1
		218	66.3	10	1.0	66	52	10	0.08	2
		218	66.3	10	1.0	66	52	10	0.08	3
		218	66.3	10	1.0	66	52	10	0.08	4
Zoe effect on CM	7	113	66.3	10	0.2	66	52	10	0.08	4
		171	66.3	10	0.5	66	52	10	0.08	4
		218	66.3	10	1.0	66	52	10	0.08	4

.

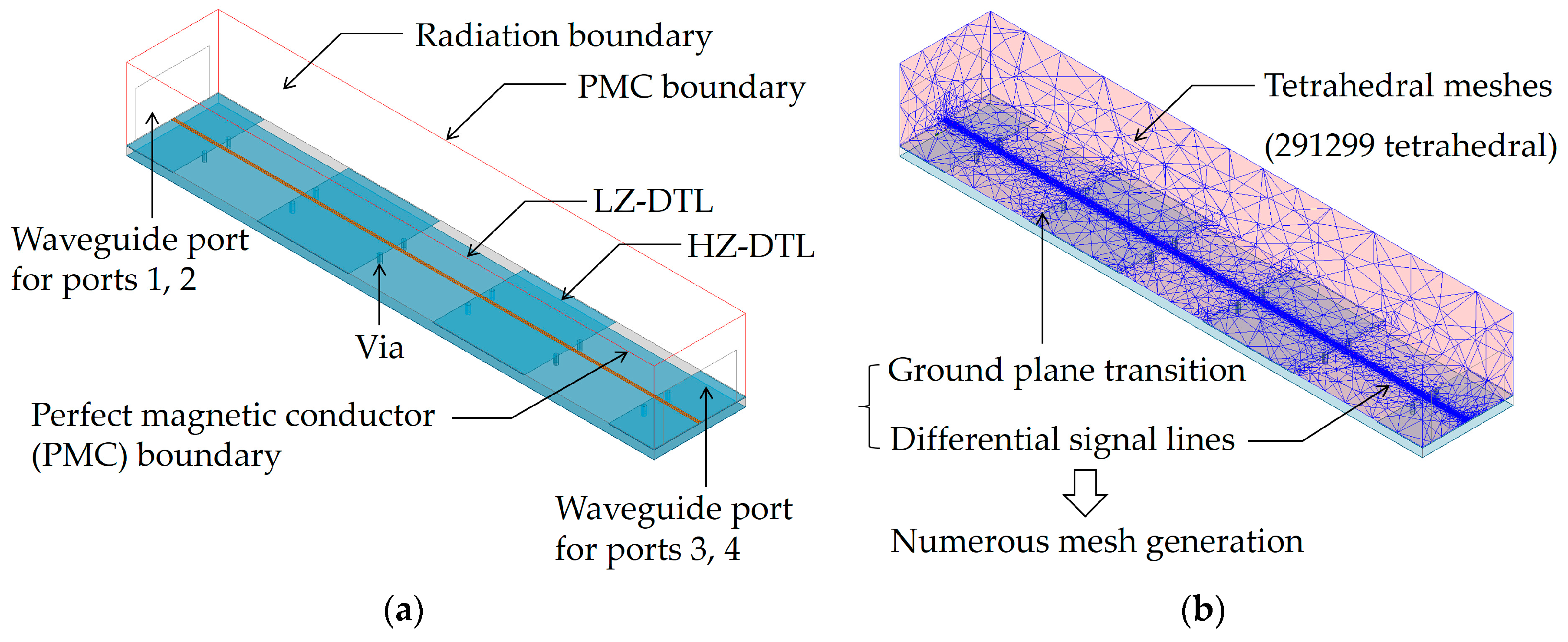
The FEM simulation model for the CGP-EBG MTM-DTLs including three unit cells and their mesh generation result are shown in Figure 5. The waveguide ports are adopted for the excitation of the CM and DM waves at ports 1, 2, 3, and 4 of the differential signal lines. The perfect magnetic conductor and radiation boundaries are assigned at the sides and top of the vacuum box, which is shown as a red box in the Figure 5a. The dielectric constant and loss tangent of FR-4 are 4.4 and 0.02, respectively. The via in the FEM model is modeled using a polyhedron with 12 segments. Its radius and height are 0.2 and 0.9 mm, respectively. The meshes are generated with the solution frequency of 10 GHz, which is the maximum frequency of interest. As can be seen in Figure 5b, most meshes are placed in differential signal lines and ground plane transition.

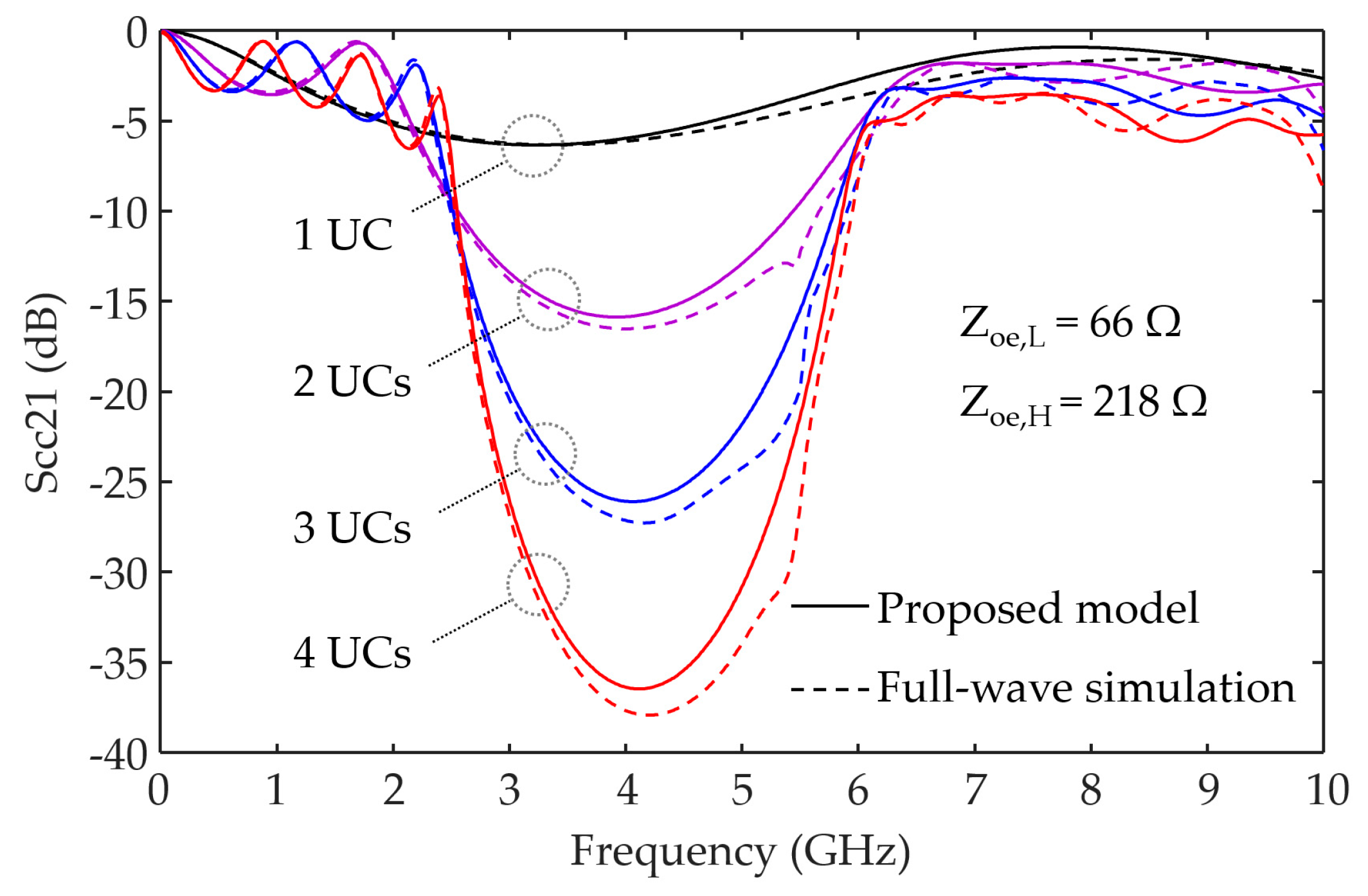
Figure 6 depicts the eight curves of parameter S_cc21 from the CGP-EBG MTM-DTLs considering one to four UCs, using the proposed analytical model (solid lines) and full-wave simulations (dashed lines). The proposed model suitably agrees with the full-wave simulations in the four cases. From the proposed model, the minimum values of CM noise suppression from one to four UCs are −6.1, −15.6, −25.9, and −36.3 dB, respectively. Overall, CM noise suppression improves as the number of UCs increases.

Examining the suppression levels where the suppression bandwidth of 3 GHz is ensured, the values for two to four UCs are −10.1, −14.1, and −18.6 dB, respectively. The value of 3 GHz was selected because it corresponds to the suppression bandwidth predicted by the dispersion analysis based on Floquet theory. The high and low cut-off frequencies from Floquet theory were obtained as 2.7 and 5.7 GHz, respectively. The periodic analysis only estimates the cut-off frequencies, but not the suppression level. As seen in Figure 6, the suppression level corresponding to Floquet theory notably varies according to the number of UCs. In the practical use of MTM-DTLs for high-speed PCBs, a periodic condition is not commonly ensured, thus requiring the development of approaches such as the proposed model considering MTM DTLs with a finite and small number of UCs.

Remarkably, the proposed analytical model achieves a drastic reduction in computation time compared to the full-wave simulation. For instance, the time for determining S_cc21 of the CGP-EBG MTM-DTL with four UCs using the proposed model was 0.3 s, whereas that using the full-wave simulation was 18,257 s. Hence, the proposed model substantially reduces the computation time while providing a suitable accuracy compared to the full-wave simulation. The time reduction results are listed in

Table 2. Computation time for estimating CM and differential transmission characteristics of the corrugated ground-plane electromagnetic bandgap (CGP-EBG) metamaterial (MTM)-DTL.

	1 UC	2 UCs	3 UCs	4 UCs
Proposed model	0.13 s	0.19 s	0.24 s	0.32 s
Full-wave simulation	120 s	1830 s	5903 s	18,257 s

Computation platform: Intel Xeon processor (3.2 GHz), 512 GB RAM (E5-2667 v4 @3.20 GHz, Intel, Santa Clara, CA, USA).

.

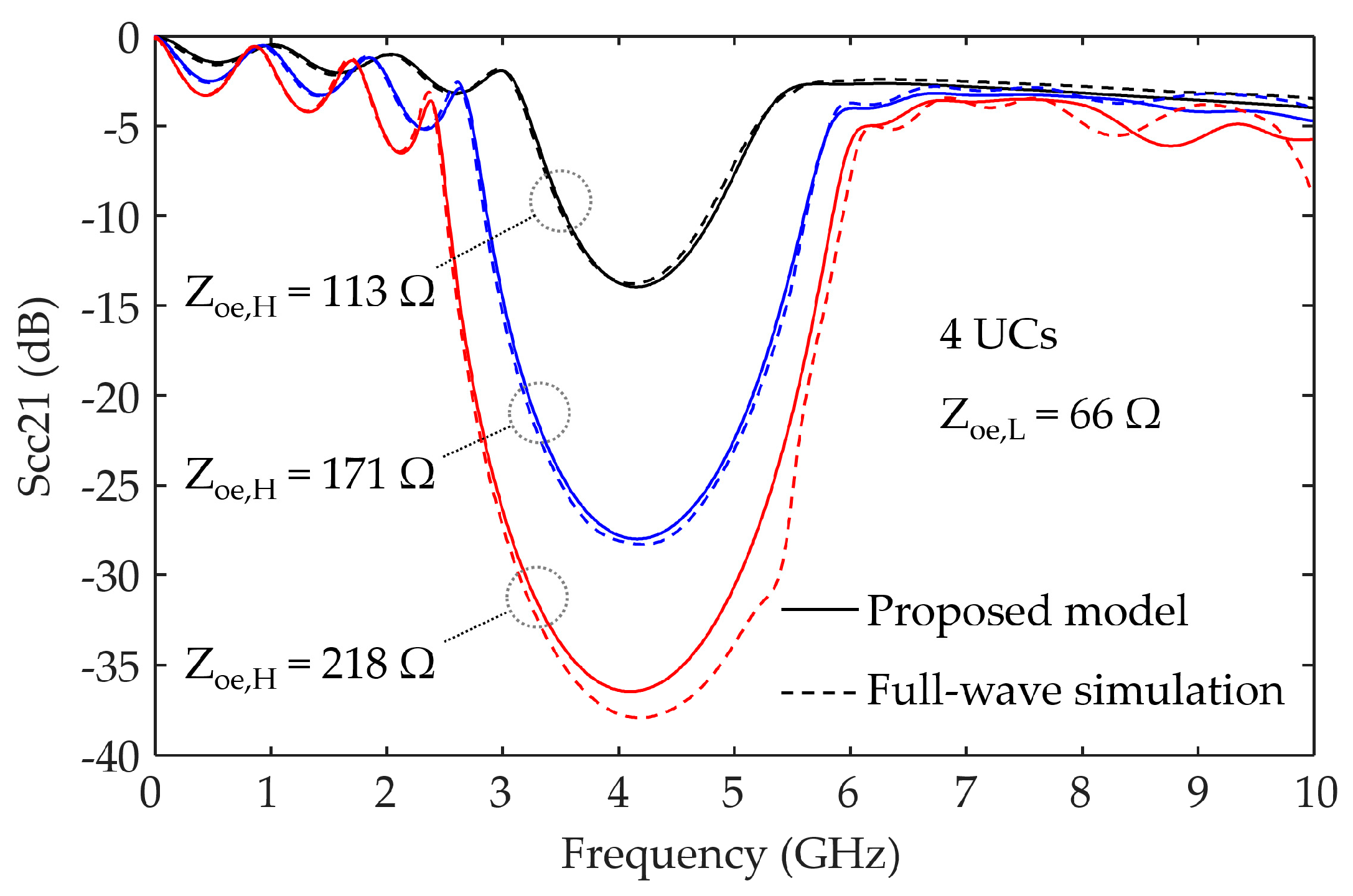
The effect of Z_oe on parameter S_cc21 is further examined by comparing the proposed analytical model and full-wave simulations, as shown in Figure 7. For the CGP-EBG MTM-DTL with four UCs, Z_oe,H changes to 113, 171, and 218 Ω by adjusting h_H to 0.2, 0.5, and 1.0 mm, respectively. The corresponding changes in the ratio of Z_oe,H to Z_oe,L are approximately 1.7, 2.6, and 3.3. The low and high cut-off frequencies with a suppression level of −10 dB were also investigated. The corresponding (high, low) cut-off frequencies for Z_oe,H of 113, 171, and 218 Ω are (3.56, 4.85 GHz), (2.94, 5.72 GHz), and (2.65, 6.09 GHz), respectively. Hence, the suppression bandwidth and level improve as the ratio of Z_oe,H to Z_oe,L increases. Again, the results of the proposed analytical model are consistent with those of the full-wave simulation.

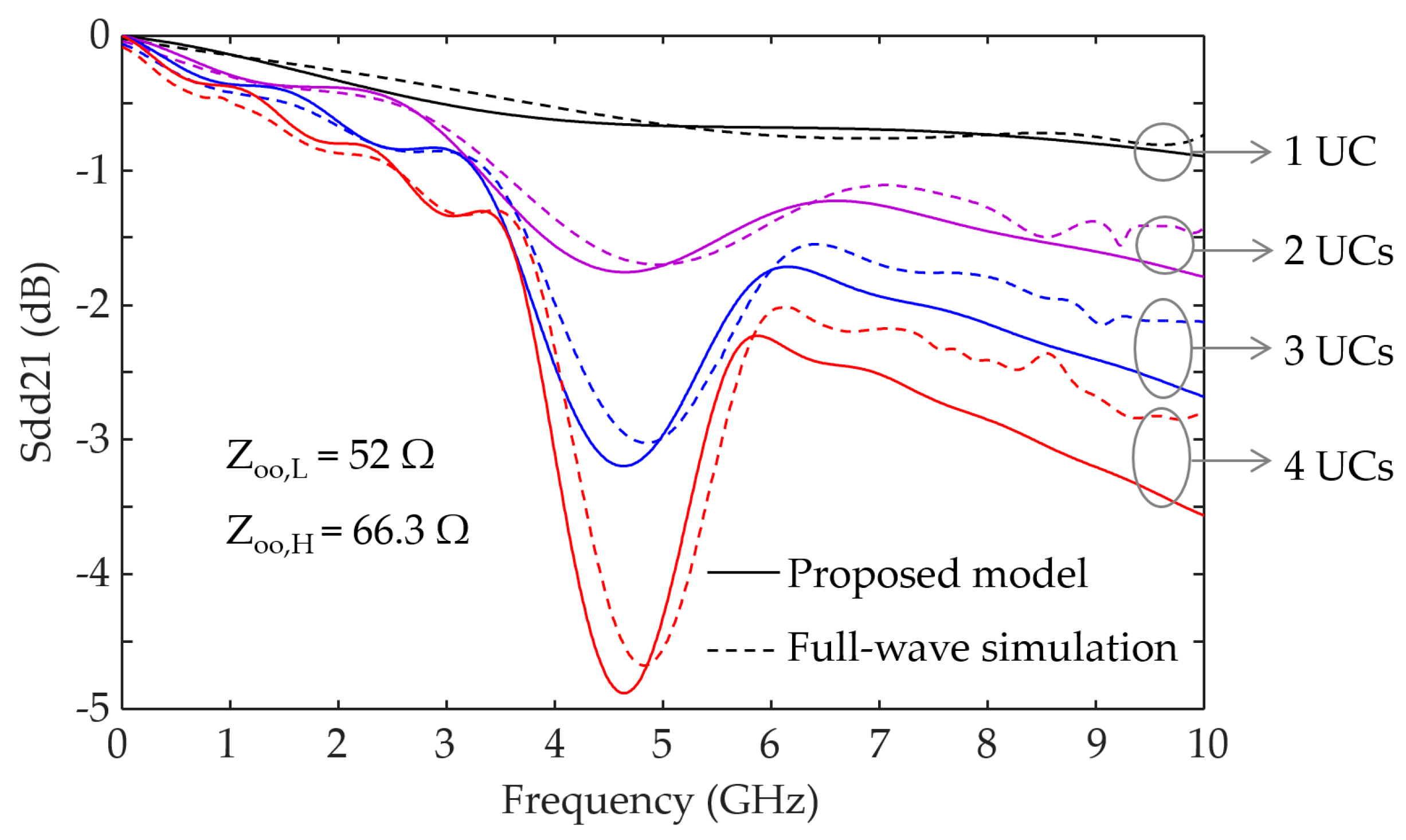
In addition to CM noise suppression, the differential transmission characteristics of the CGP-EBG MTM-DTLs were investigated. Figure 8 shows parameter S_dd21 for differential transmission using the proposed model and full-wave simulations. The design parameters and dimensions are those listed in Table 1. The values of Z_oo,L and Z_oo,H associated with differential transmission are 52 and 66.3 Ω, respectively. For ideal differential characteristics, the same values of Z_oo between the HZ- and LZ-DTLs are preferred. However, this condition is commonly limited by the design rules of commercial PCB processes, thus making it difficult to avoid different Z_oo values for HZ- and LZ-DTLs in practical high-speed PCBs. The effect of the Z_oo difference on the differential characteristics is shown in Figure 8. The small difference in the Z_oo values between HZ- and LZ-DTLs degrades differential transmission characteristics. This effect increases with the number of UCs. This phenomenon can be inferred considering the theory of a stepped impedance resonator. However, it is important to obtain the exact degradation of parameter S_dd21 for measuring and quantitating its impact on differential signal transmission.

The accuracy and efficiency of the proposed analytical model for CGP-EBG MTM-DTLs are verified from comparisons to full-wave simulations based on FEM. The CM noise and differential signal transmission results of the proposed model suitably agree with those of full-wave simulations, but the computation time for obtaining the characteristics of the nonperiodic array of MTM-DTLs was substantially reduced using the proposed four-port analytical model.

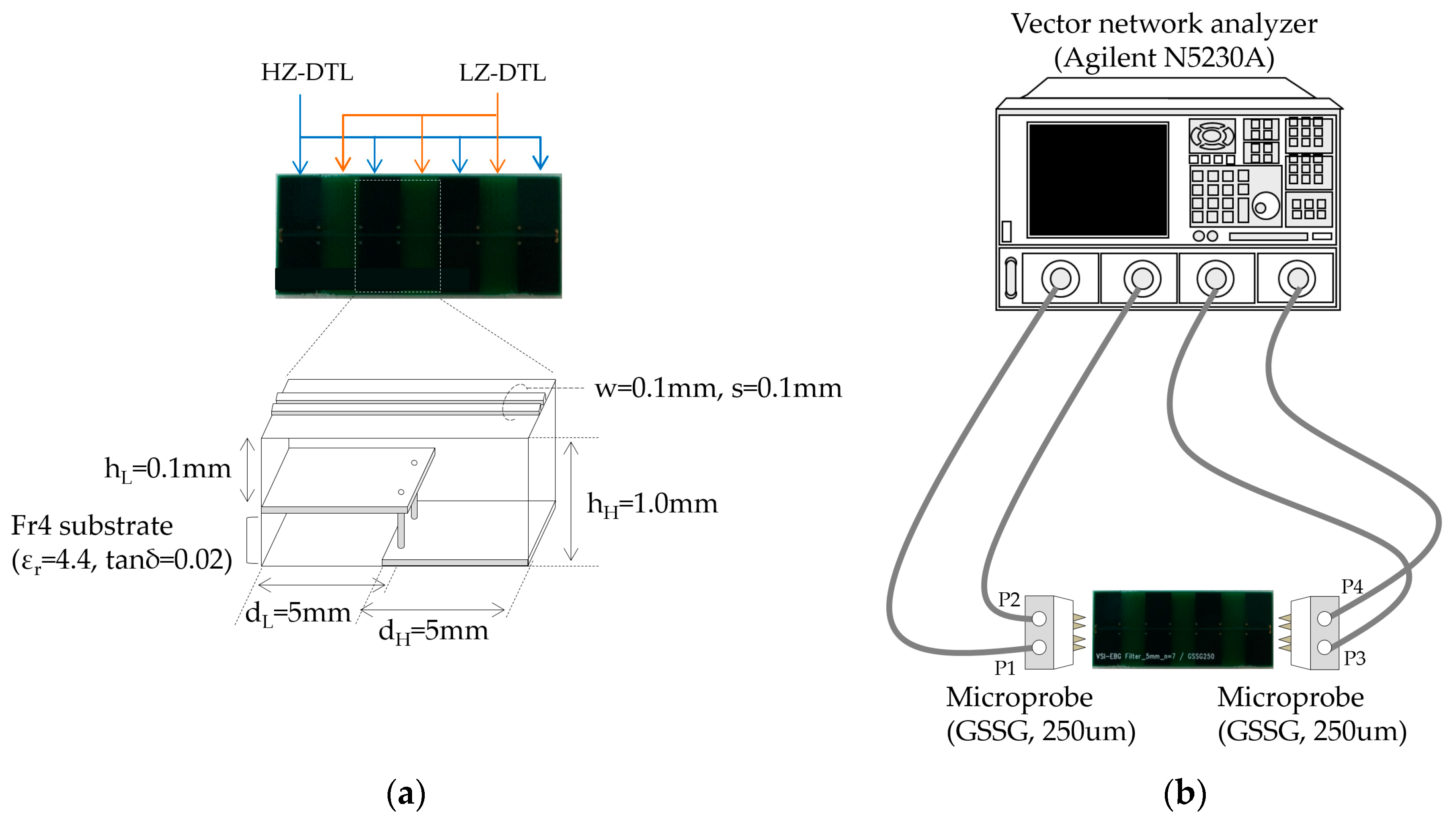
To further validate the proposed model of the CGP-EBG MTM-DTL, the correlations between the proposed model, full-wave simulations, and measurements are examined using the fabricated PCB pattern of the CGP-EBG MTM-DTL. The fabricated PCB pattern and the measurement set-up for S_cc21 and S_dd21 are shown in Figure 9. The low-cost PCB process employs the FR-4 dielectric and copper metal layers. The dielectric constant and loss tangent of the FR-4 substrate are 4.4 and 0.02, respectively. The PCB pattern contains four HZ-DTLs and three LZ-DTLs. The geometric dimensions are shown in Figure 9a. To obtain the S_cc21 and S_dd21, four-port S-parameters of the PCB pattern are measured using a vector network analyzer and high-frequency microprobes. 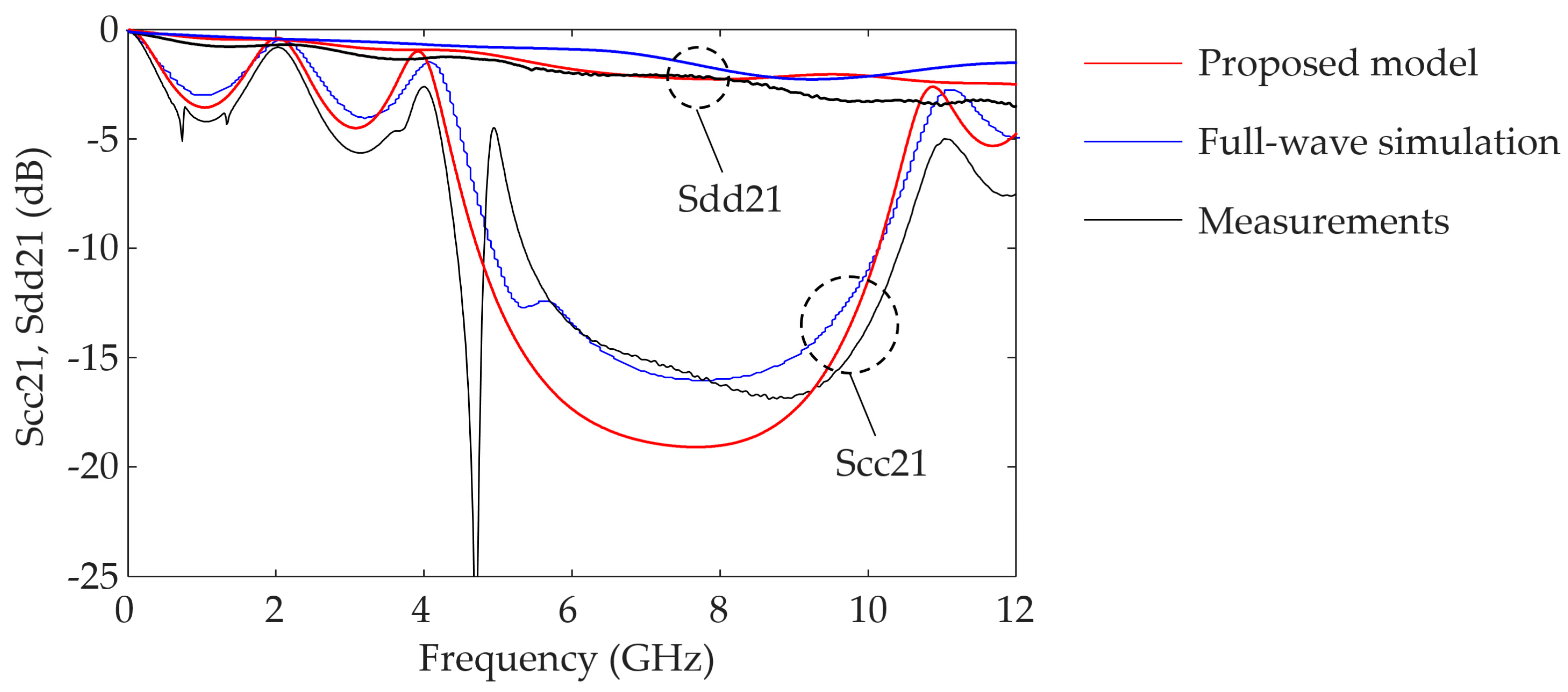Figure 10 depicts the comparison of S_cc21 and S_dd21 between the proposed model, full-wave simulations, and measurements. The proposed model agrees well with the measurements. As can be seen in the results, CM noise is successfully suppressed, while good differential data transmission is achieved. In the S_cc21 of the measurements, discrepancy is observed around the frequency of 5 GHz. This defect is caused by PCB manufacturing tolerances because it is not observed in the full-wave simulations.

4. Conclusions

An efficient and accurate approach to evaluate CGP-EBG MTM-DTLs using an analytical model and segmentation method was proposed. The four-port model of the CGP-EBG segments was extracted using coupled-line theory and an analytical via model. For a finite array of CGP-EBG MTM-DTLs, the method of Z-parameter recombination was presented. The proposed analytical model was thoroughly validated by comparisons with full-wave simulations based on FEM. The CM noise suppression and differential signal transmission results of the CGP-EBG MTM-DTL variants were consistent between the proposed model and full-wave simulations. However, the computation time for estimating the characteristics of the CGP-EBG MTM-DTL was drastically reduced when using the proposed model. Moreover, the proposed model can be easily combined with other types of circuit and electromagnetic models, thus enabling system-level simulations for high-speed PCB applications. Overall, the assessment of CGP-EBG MTM-DTLs in early design stages and simulation-based verification can be efficiently and accurately conducted using the proposed analytical model. In this paper, the CGP-EBG MTM-DTL for one pair of differential lines was explored. For further research, the CGP-EBG MTM-DTL and its analytical model of multiple pairs of differential lines for emerging technologies of high-speed differential signaling can be examined.