Compressed Sensing-Based DOA Estimation with Antenna Phase Errors
Abstract
:1. Introduction
- The sparse-based system model with unknown phase errors: A system model using a diagonal matrix with phase errors among antennas is formulated, and converts the DOA estimation problem into a sparse reconstruction problem.
- The CS-based DOA estimation method with unknown phase errors: A novel CS-based DOA estimation method is proposed to estimate both the phase errors and DOA, iteratively. The proposed method is cost-effective and can achieve a better performance than state-of-the-art methods regarding the DOA estimation with unknown phase errors.
- The theoretical expressions of the gradient descent method: In the proposed method, the phase errors are estimated by a gradient descent method iteratively with the theoretical expressions.
2. System Model for DOA Estimation with Phase Errors
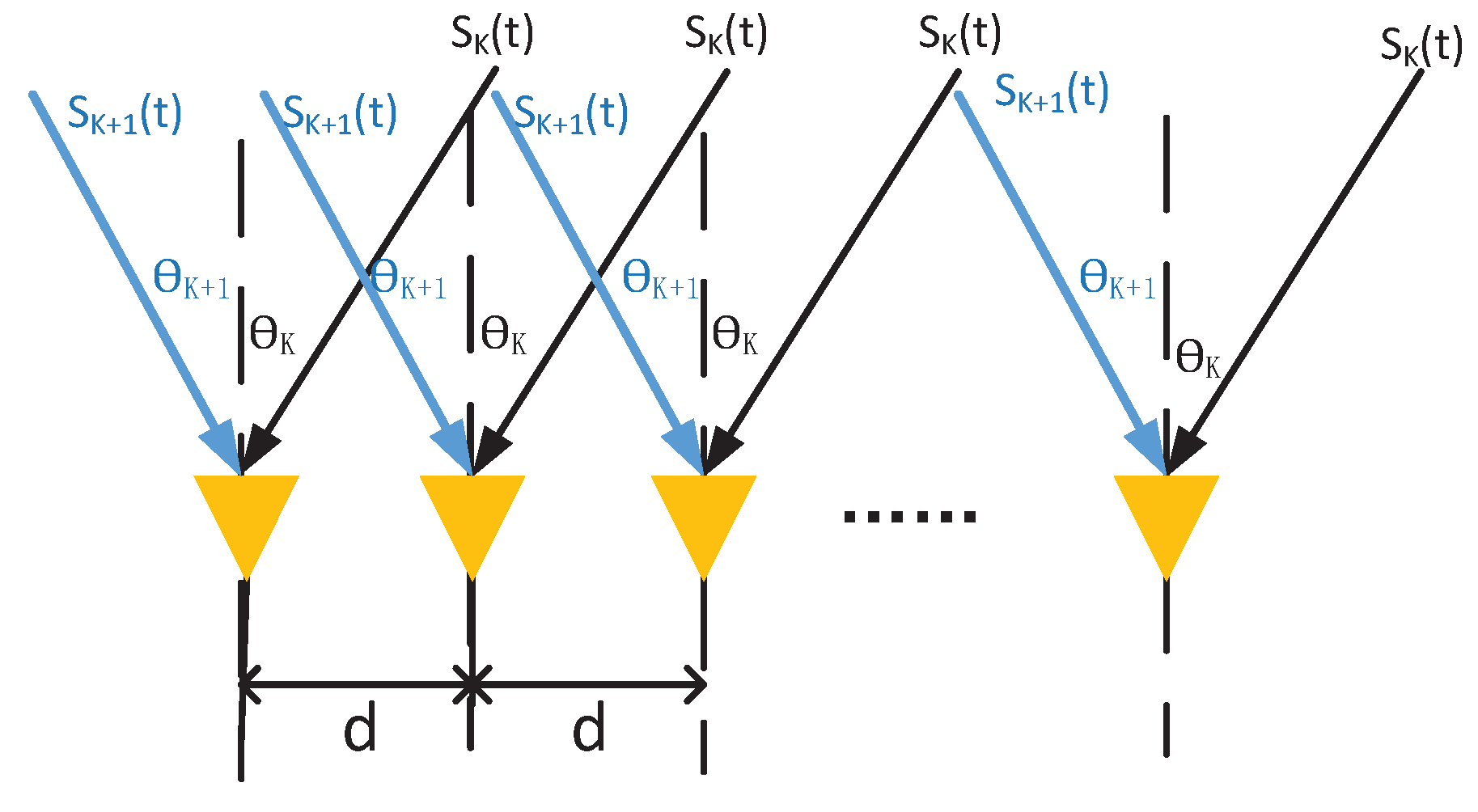
2.1. Ideal System without Phase Errors
2.2. System Model with Phase Errors
3. Sparse-Based Algorithm for DOA Estimation
| Algorithm 1 The proposed algorithm to estimate the DOAs in the scenario with phase errors among the antennas. |
|
| Algorithm 2 SOMP algorithm to estimate the DOAs |
|
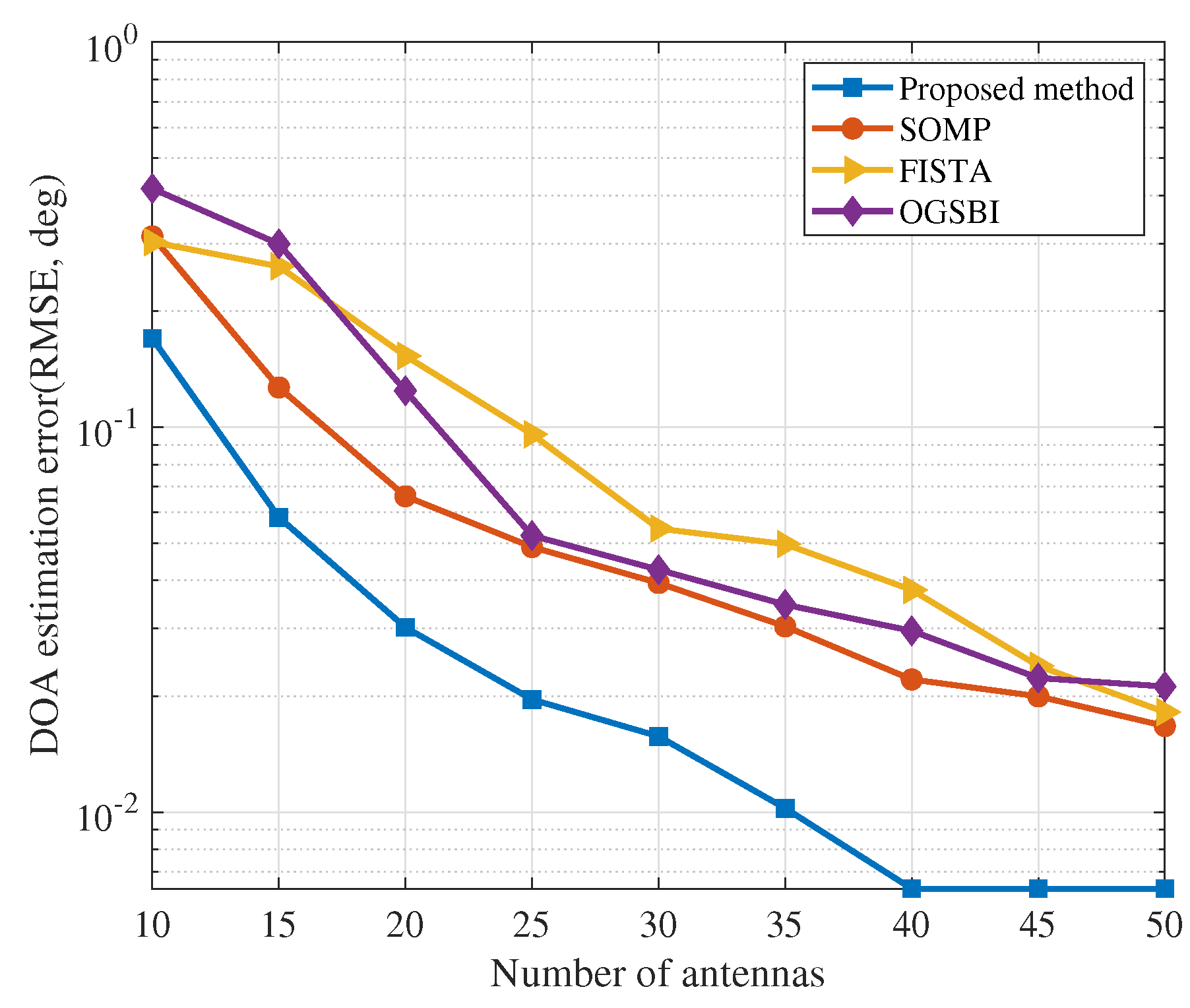
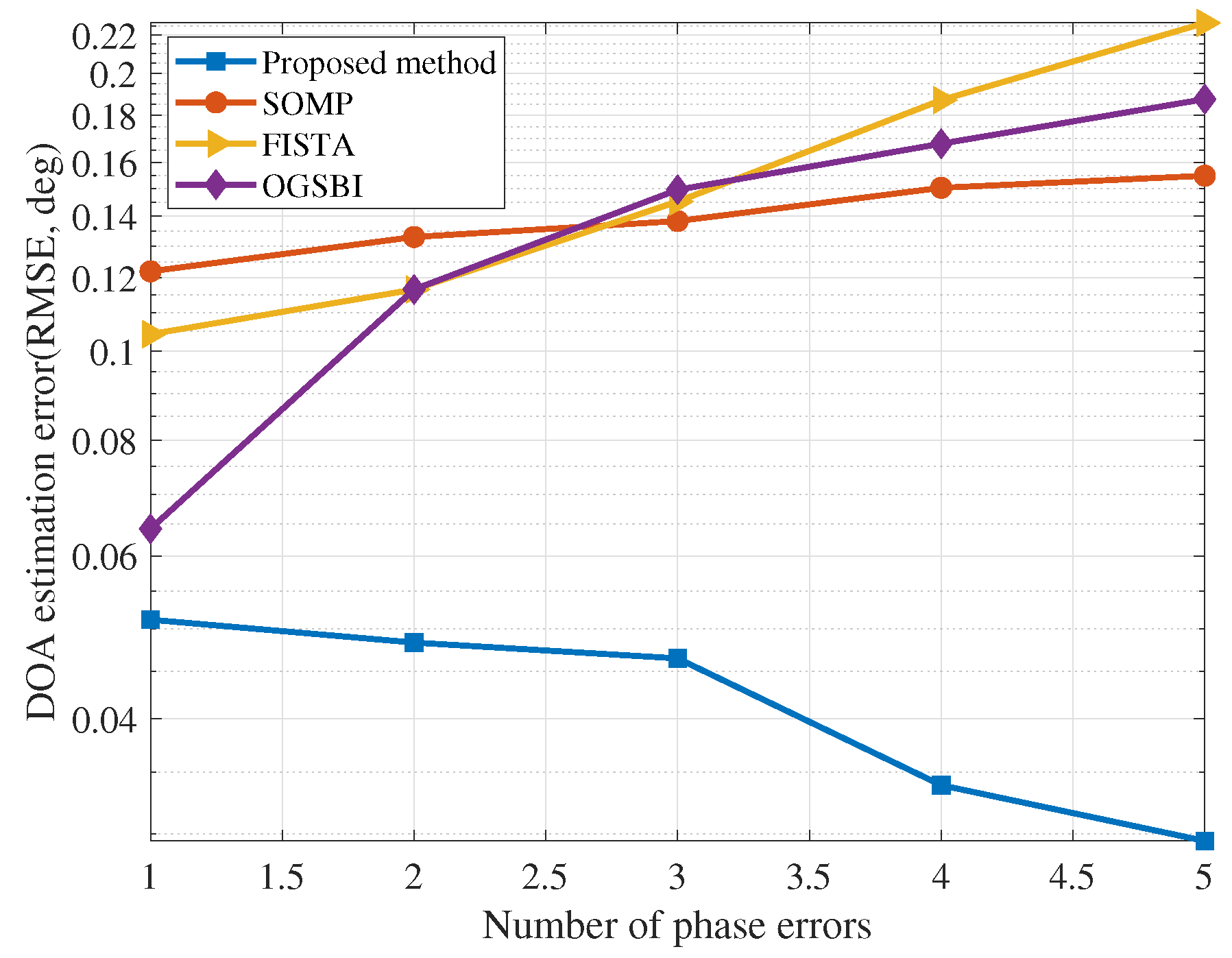
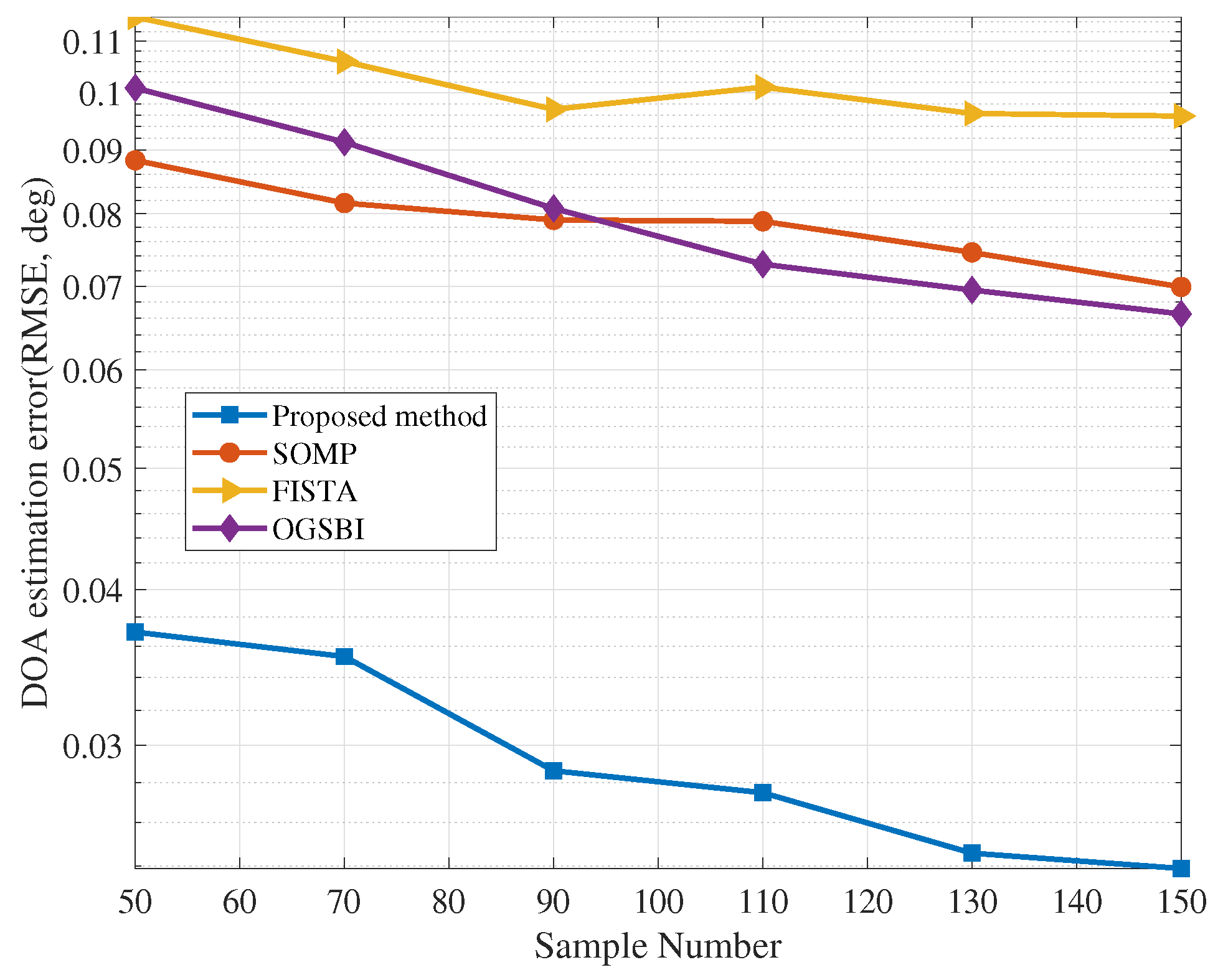
4. Simulation Results
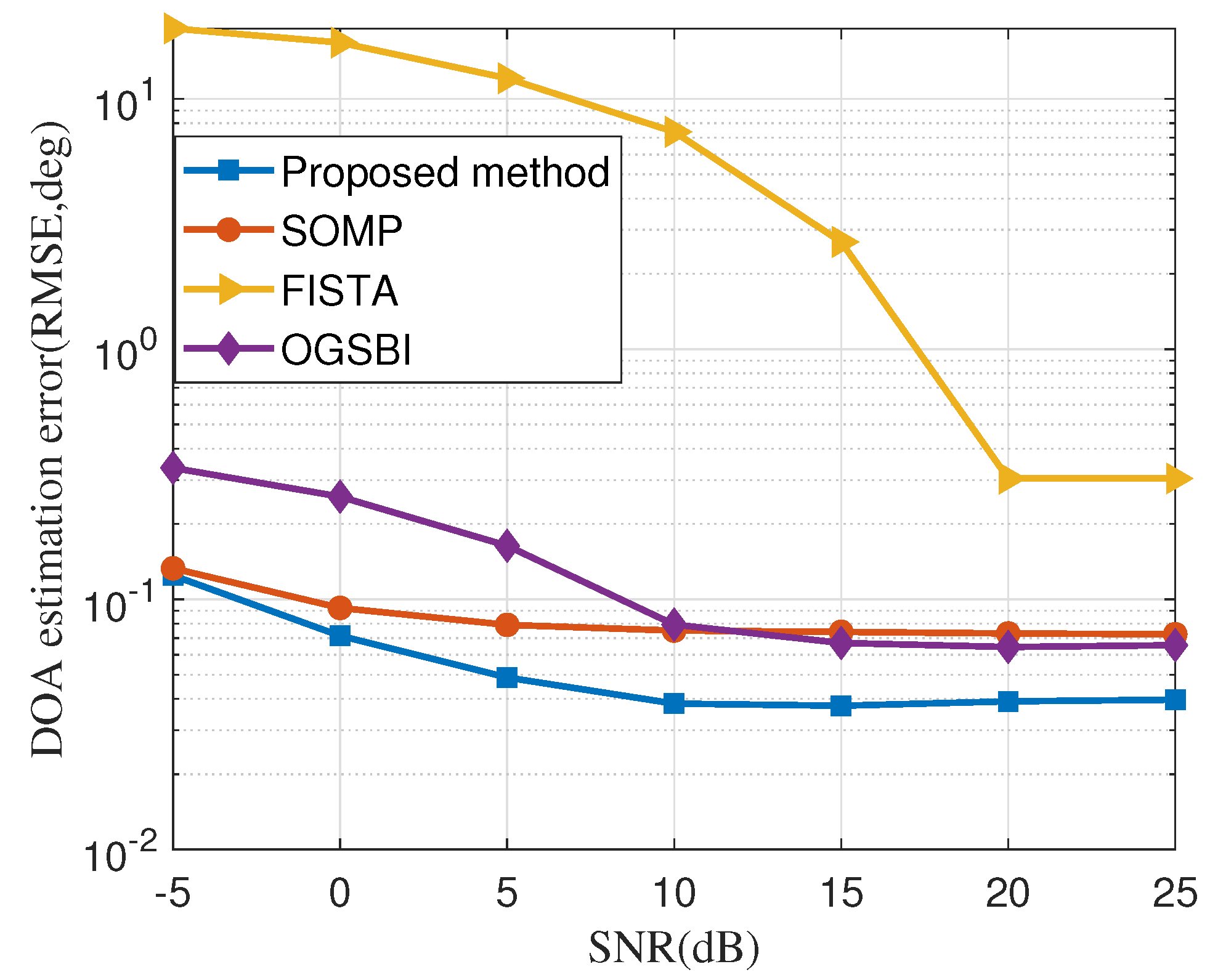
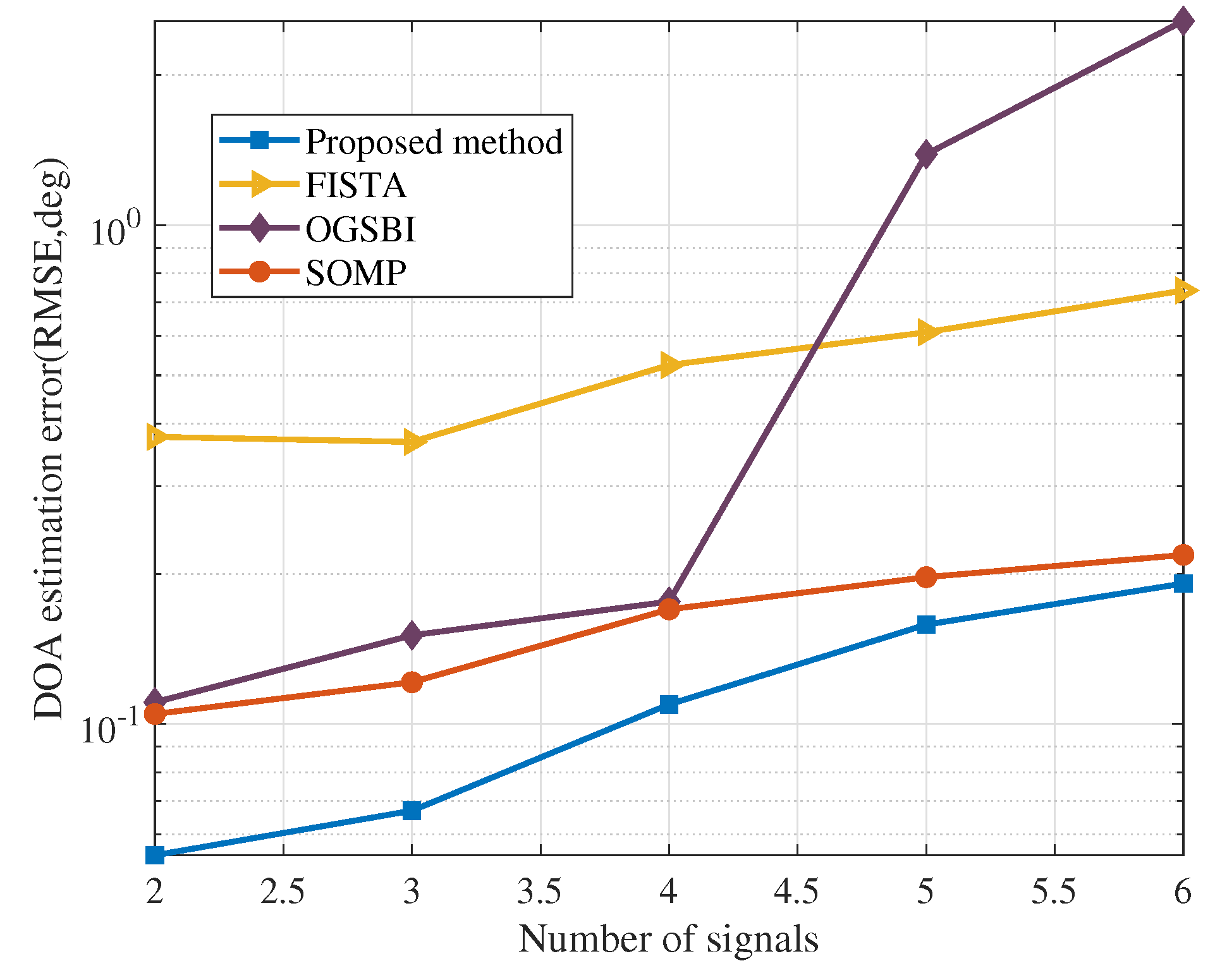
- FISTA: fast iterative shrinkage-thresholding algorithm method proposed in [43]. FISTA provided a new resolution to realize the forward-backward splitting method (also known as the proximal gradient method) splitting to a broad range of problems appearing in sparse recovery, MMV problems, and many other aspects. Whether the problem solved is simple or complex, FISTA simplifies it efficiently by handling issues like stepsize selection, acceleration, and stopping conditions.
- OGSBI: the off-grid sparse Bayesian inference method proposed in [44]. The OGSBI method deals with the off-grid DOA estimation problem and uses an iterative algorithm based on the off-grid model from a Bayesian perspective, while joint sparsity among different snapshots is exploited by assuming a Laplace prior for signals at all snapshots. The OGSBI method applies to both single-snapshot and multi-snapshot cases and has high estimation accuracy, even under a very coarse sampling grid.
- SOMP: for compressed sensing, the critical thing is to extend from the single-measurement vector (SMV) problem to the MMV problem.SOMP, which can recover signals by increasing the number of measurement vectors, is an MMV extension of OMP.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, L.; Zhao, L.; Bi, G.; Wan, C.; Zhang, L.; Zhang, H. Novel Wideband DOA Estimation Based on Sparse Bayesian Learning with Dirichlet Process Priors. IEEE Trans. Signal Process. 2016, 64, 275–289. [Google Scholar] [CrossRef]
- Cao, Z.; Chen, P.; Chen, Z.; He, X. Maximum likelihood-based methods for target velocity estimation with distributed MIMO radar. Electronics 2018, 7, 29. [Google Scholar] [CrossRef]
- Chen, P.; Qi, C.; Wu, L.; Wang, X. Waveform design for Kalman filter-based target scattering coefficient estimation in adaptive radar system. IEEE Trans. Veh. Technol. 2018, 67, 11805–11817. [Google Scholar] [CrossRef]
- Krim, H.; Viberg, M. Two decades of array signal processing research: the parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- BURG, J.P. Maximum entropy spectral analysis. In Proceedings of the 37th Annual International Meeting, Oklahoma City, OK, USA, 31 October 1967. [Google Scholar]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Chen, J.; Huo, X. Theoretical Results on Sparse Representations of Multiple-Measurement Vectors. IEEE Trans. Signal Process. 2006, 54, 4634–4643. [Google Scholar] [CrossRef]
- Ren, Q.S.; Willis, A.J. Fast ROOT-MUSIC algorithm. Electron. Lett. 1997, 33, 450–451. [Google Scholar] [CrossRef]
- Rao, B.D.; Hari, K.V.S. Performance analysis of ROOT-MUSIC. IEEE Transa. Acoust. Speech Signal Process. 1989, 37, 1939–1949. [Google Scholar] [CrossRef]
- Roy, R.H.; Paulraj, A.; Kailath, T. Comparative performance of ESPRIT and MUSIC for direction-of-arrival estimation. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Dallas, TX, USA, 6–9 April 1987; Volume 12, pp. 2344–2347. [Google Scholar]
- Roy, R.H.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. Opt. Eng. 1990, 29, 369–411. [Google Scholar]
- Roy, R.H.; Paulraj, A.; Kailath, T. ESPRIT—A subspace rotation approach to estimation of parameters of cisoids in noise. IEEE Trans. Acoust. Speech Signal Process. 1986, 34, 1340–1342. [Google Scholar] [CrossRef]
- Stoica, P.; Arye, N. MUSIC, maximum likelihood, and Cramer-Rao bound. IEEE Transa. Acoust. Speech Signal Process. 1989, 37, 720–741. [Google Scholar] [CrossRef]
- Ottersten, B.; Viberg, M.; Stoica, P.; Nehorai, A. Exact and Large Sample Maximum Likelihood Techniques for Parameter Estimation and Detection in Array Processing; Springer: Berlin/Heidelberg, Germany, 1993; pp. 99–151. [Google Scholar]
- Cadzow, J.A. A high resolution direction-of-arrival algorithm for narrow-band coherent and incoherent sources. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 965–979. [Google Scholar] [CrossRef]
- Clergeot, H.; Tressens, S.; Ouamri, A. Performance of high resolution frequencies estimation methods compared to the cramer-rao bounds. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 1703–1720. [Google Scholar] [CrossRef]
- Ziskind, I.; Wax, M. Maximum likelihood localization of multiple sources by alternating projection. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 1553–1560. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theor. 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Gilbert, A.C.; Indyk, P. Sparse recovery using sparse matrices. Proc. IEEE 2010, 98, 937–947. [Google Scholar] [CrossRef]
- Donoho, D.L.; Elad, M. Optimally sparse representation in general (nonorthogonal) dictionaries via ℓ1 minimization. Proc. Natl. Acad. Sci. USA 2003, 100, 2197–2202. [Google Scholar] [CrossRef]
- Baraniuk, R.G.; Cevher, V.; Duarte, M.F.; Hegde, C. Model-based compressive sensing. IEEE Trans. Inf. Theory 2010, 56, 1982–2001. [Google Scholar] [CrossRef]
- Baraniuk, R.G. Compressive sensing [lecture notes]. IEEE Signal Process. Mag. 2007, 24, 118–121. [Google Scholar] [CrossRef]
- Chen, P.; Qi, C.; Wu, L.; Wang, X. Estimation of Extended Targets Based on Compressed Sensing in Cognitive Radar System. IEEE Trans. Veh. Technol. 2017, 66, 941–951. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Chen, P.; Chen, Z.; Zhang, X.; Liu, L. SBL-based direction finding method with imperfect array. Electronics 2018, 7, 426. [Google Scholar] [CrossRef]
- Chen, P.; Cao, Z.; Chen, Z.; Wang, X. Off-Grid DOA estimation using sparse Bayesian learning in MIMO radar with unknown mutual coupling. IEEE Trans. Signal Process. 2019, 67, 208–220. [Google Scholar] [CrossRef]
- Bishop, C.M.; Tipping, M.E. Variational relevance vector machines. In Uncertainty in Artificial Intelligence; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 2000; pp. 46–53. [Google Scholar]
- Yardibi, T.; Li, J.; Stoica, P. Nonparametric and sparse signal representations in array processing via iterative adaptive approaches. In Proceedings of the 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 26–29 October 2008; pp. 278–282. [Google Scholar]
- Li, J.; Zhu, X.; Stoica, P.; Rangaswamy, M. Iterative Space-Time Adaptive Processing. In Proceedings of the IEEE 13th Digital Signal Processing Workshop and 5th IEEE Signal Processing Education, Marco Island, FL, USA, 4–7 January 2009; pp. 440–445. [Google Scholar]
- Xue, M.; Zhu, X.; Li, J.; Vu, D.; Stoica, P. MIMO radar angle-doppler imaging via iterative space-time adaptive processing. In Proceedings of the IEEE nternational Waveform Diversity and Design Conference, Kissimmee, FL, USA, 8–13 February 2009; pp. 129–133. [Google Scholar]
- Xue, M.; Roberts, W.; Li, J.; Tan, X.; Stoica, P. MIMO radar sparse angle-Doppler imaging for ground moving target indication. In Proceedings of the IEEE Radar Conference, Washington, DC, USA, 10–14 May 2010; pp. 553–558. [Google Scholar]
- Malioutov, D.M.; Cetin, M.; Willsky, A.S. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef]
- Cetin, M.; Malioutov, D.M.; Willsky, A.S. A variational technique for source localization based on a sparse signal reconstruction perspective. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, FL, USA, 13–17 May 2002; Volume 3, pp. 2965–2968. [Google Scholar]
- Malioutov, D.M.; Cetin, M.; Willsky, A.S. Source localization by enforcing sparsity through a Laplacian prior: An SVD-based approach. In Proceedings of the IEEE Workshop on Statistical Signal Processing, St. Louis, MO, USA, 28 September–1 October 2003. [Google Scholar]
- Rebolloneira, L.; Lowe, D. Optimized orthogonal matching pursuit Approach. IEEE Signal Process. Lett. 2002, 9, 137–140. [Google Scholar] [CrossRef]
- Ng, B.C.; See, C.M.S. Sensor-array calibration using a maximum-likelihood approach. IEEE Trans. Antennas Propag. 1996, 44, 827–835. [Google Scholar]
- Friedlander, B.; Weiss, A.J. Eigenstructure methods for direction finding with sensor gain and phase uncertainties. Circuits Syst. Signal Process. 1988, 9, 271–300. [Google Scholar]
- Cao, S.; Ye, Z.; Xu, D.; Xu, X. A Hadamard Product Based Method for DOA Estimation and Gain-Phase Error Calibration. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1224–1233. [Google Scholar] [CrossRef]
- Liu, A.; Liao, G.; Zeng, C.; Yang, Z.; Xu, Q. An Eigenstructure Method for Estimating DOA and Sensor Gain-Phase Errors. IEEE Trans. Signal Process. 2011, 59, 5944–5956. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C.; Strauss, M. Algorithms for simultaneous sparse approximation: Part I: Greedy pursuit. Signal Process. 2006, 86, 572–588. [Google Scholar] [CrossRef]
- Goldstein, T.; Studer, C.; Baraniuk, R.G. A field guide to forward-backward splitting with a FASTA implementation. arXiv, 2014; arXiv:1411.3406. [Google Scholar]
- Yang, Z.; Xie, L.; Zhang, C. Off-grid direction of arrival estimation using sparse bayesian inference. IEEE Trans. Signal Process. 2011, 61, 08. [Google Scholar] [CrossRef]
- Chen, P.; Cao, Z.; Chen, Z.; Liu, L.; Feng, M. Compressed sensing-based DOA estimation with unknown mutual coupling effect. Electronics 2018, 7, 424. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| The signal-to-noise ratio (SNR) of the received signal | 20 dB |
| The number of samples M | 100 |
| The number of antennas N | 20 |
| The number of signals K | 2 |
| The space between antennas | wavelength |
| The grid size | ° |
| The detection DOA range | [−30°, 30°] |
| The minimum DOA space between signals | 10° |
| Method | FISTA | SOMP | OGSBI | Proposed Method |
|---|---|---|---|---|
| Time(s) | 0.1470 | 0.0910 | 12.3063 | 0.1548 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Zhang, X.; Chen, P. Compressed Sensing-Based DOA Estimation with Antenna Phase Errors. Electronics 2019, 8, 294. https://doi.org/10.3390/electronics8030294
Liu L, Zhang X, Chen P. Compressed Sensing-Based DOA Estimation with Antenna Phase Errors. Electronics. 2019; 8(3):294. https://doi.org/10.3390/electronics8030294
Chicago/Turabian StyleLiu, Linxi, Xuan Zhang, and Peng Chen. 2019. "Compressed Sensing-Based DOA Estimation with Antenna Phase Errors" Electronics 8, no. 3: 294. https://doi.org/10.3390/electronics8030294
APA StyleLiu, L., Zhang, X., & Chen, P. (2019). Compressed Sensing-Based DOA Estimation with Antenna Phase Errors. Electronics, 8(3), 294. https://doi.org/10.3390/electronics8030294






