Ultra-Short Pulsed Laser Annealing Effects on MoS2 Transistors with Asymmetric and Symmetric Contacts
Abstract
1. Introduction
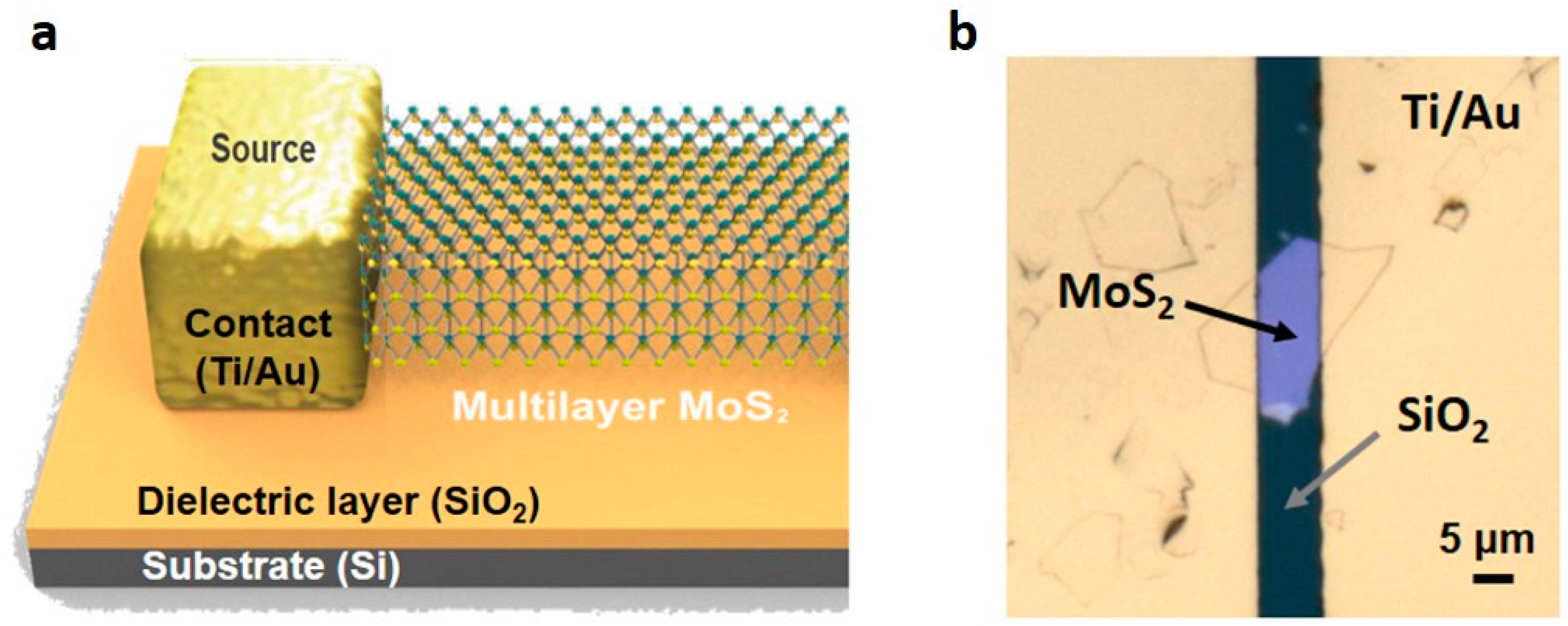
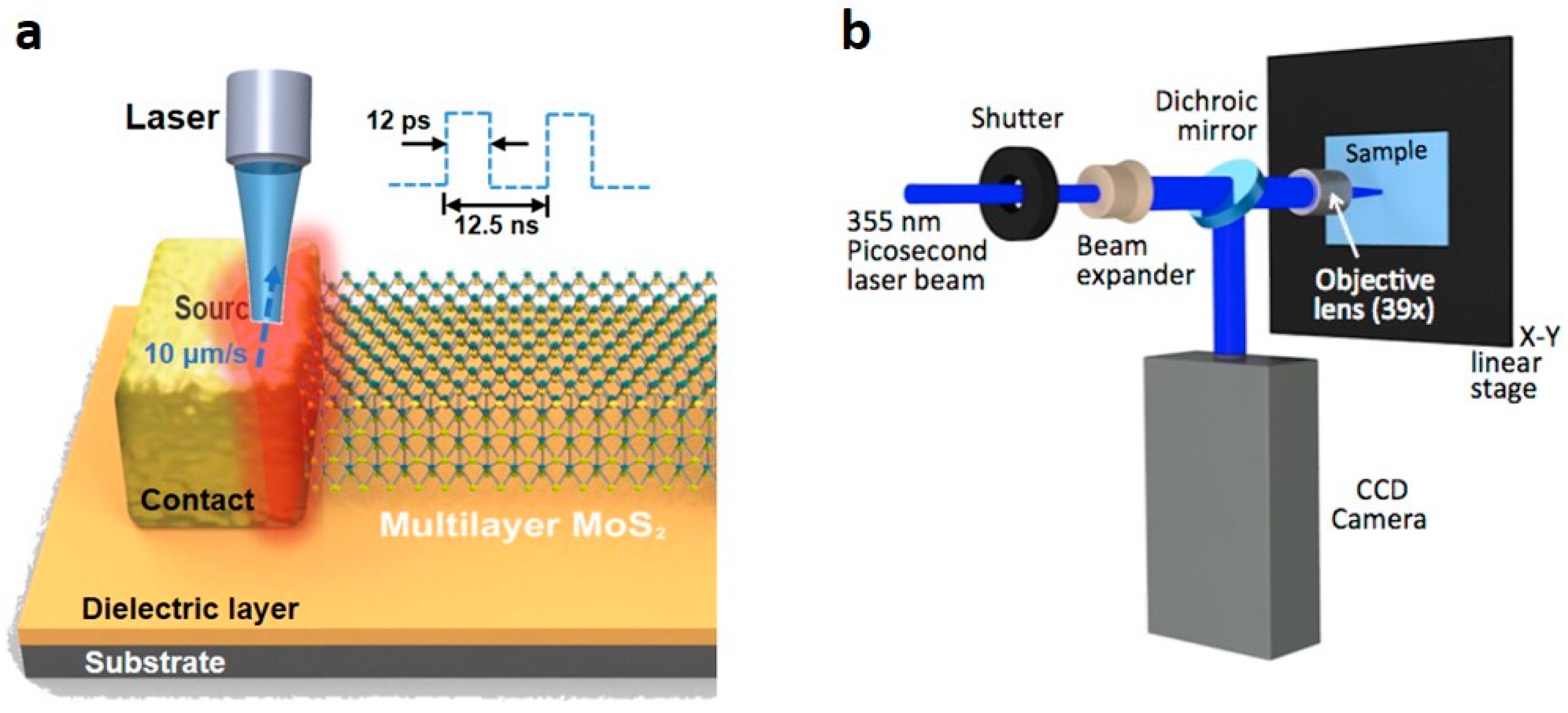
2. Experiments and Setup
3. Results and Discussion
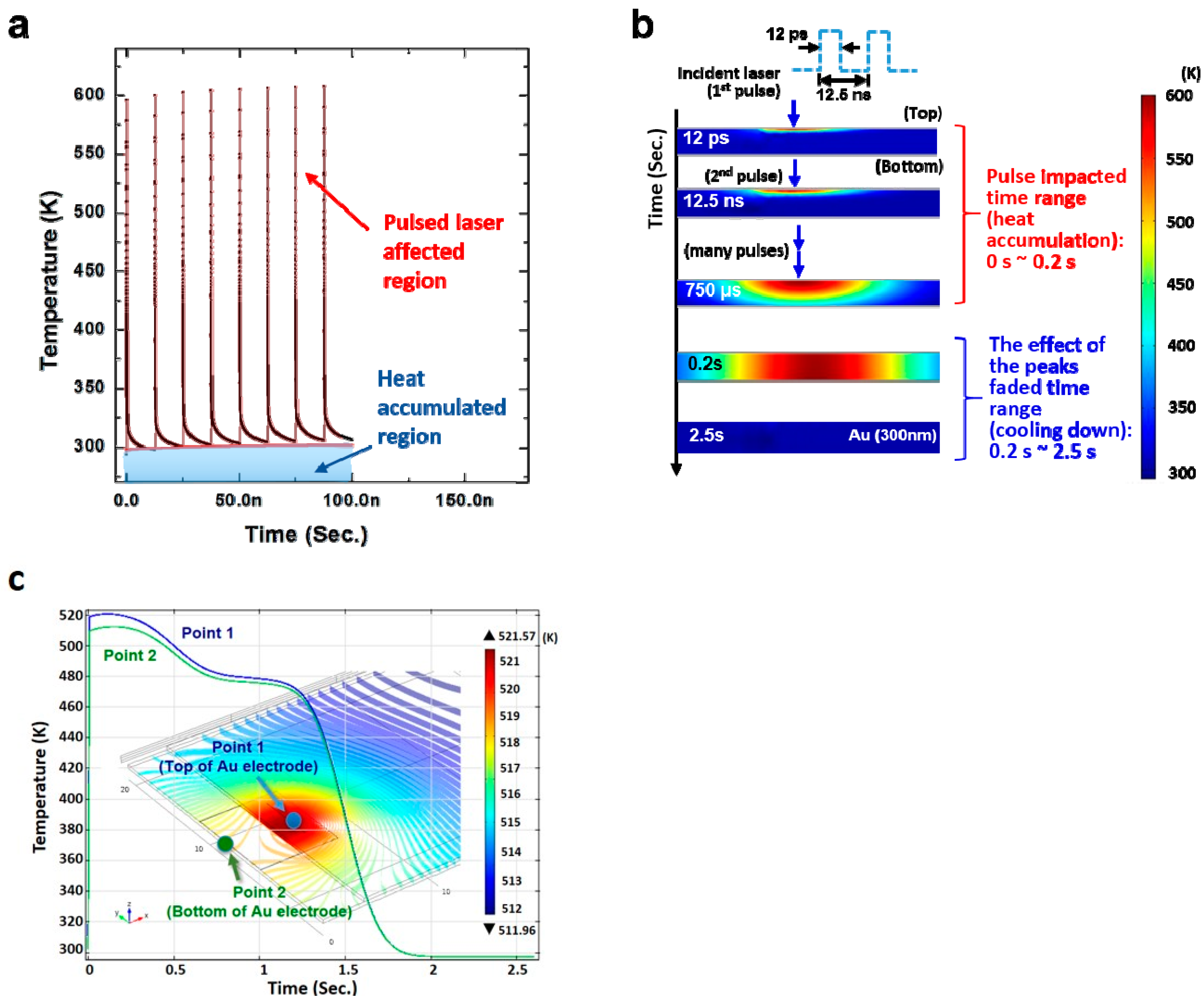
3.1. Thermal Analysis
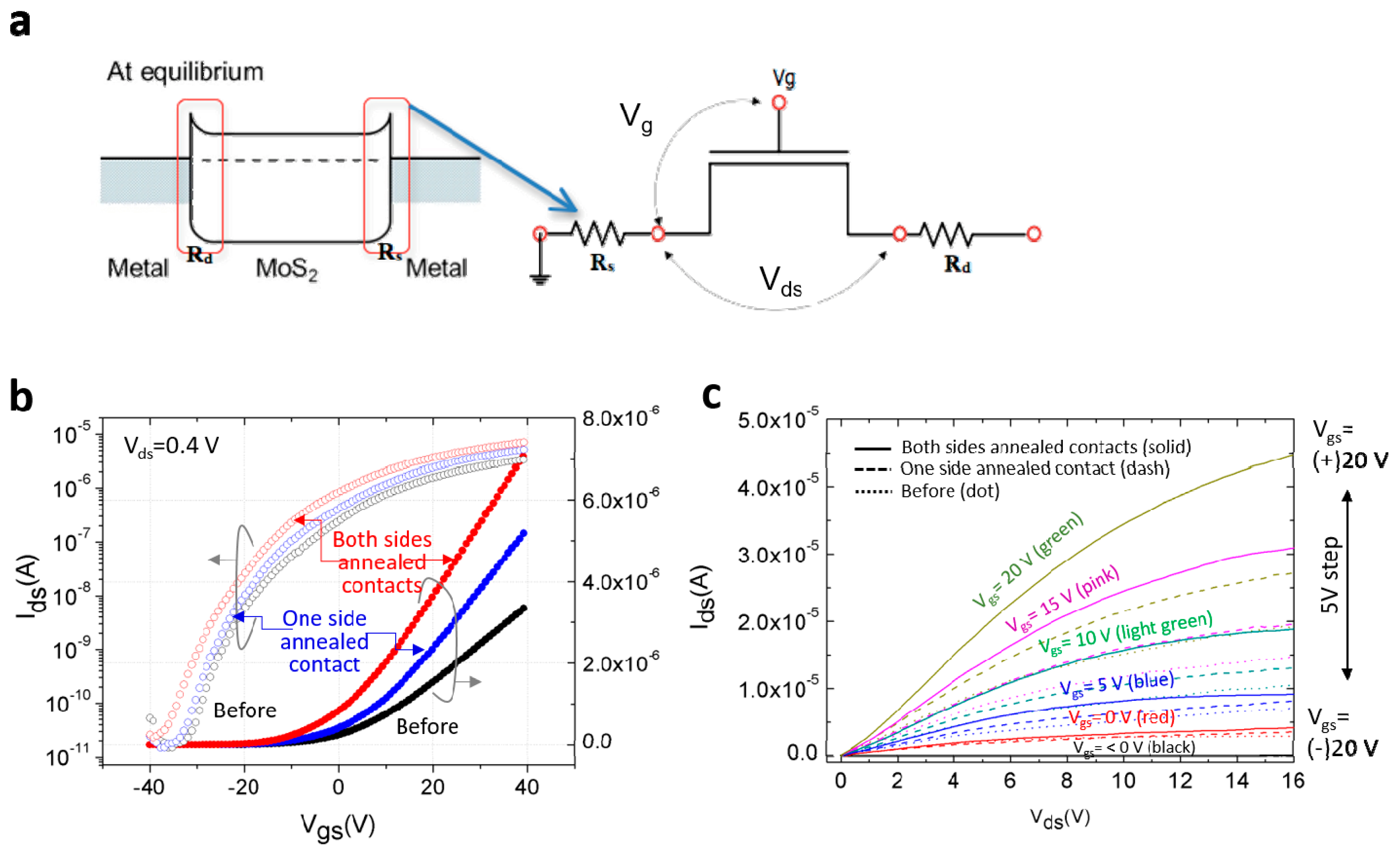
3.2. Electrical Characteristics
4. Summary and Outlook
Author Contributions
Funding
Conflicts of Interest
Appendix A

References
- MacDonald, W.A.; Looney, M.; MacKerron, D.; Eveson, R.; Adam, R.; Hashimoto, K.; Rakos, K. Latest advances in substrates for flexible electronics. J. Soc. Inf. Disp. 2007, 15, 1075–1083. [Google Scholar] [CrossRef]
- Kim, D.-H.; Lu, N.; Ma, R.; Kim, Y.-S.; Kim, R.-H.; Wang, S.; Wu, J.; Won, S.M.; Tao, H.; Islam, A. Epidermal electronics. Science 2011, 333, 838–843. [Google Scholar] [CrossRef] [PubMed]
- Akinwande, D.; Petrone, N.; Hone, J. Two-dimensional flexible nanoelectronics. Nat. Commun. 2014, 5, 5678. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J.N.; Strano, M.S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotech. 2012, 7, 699. [Google Scholar] [CrossRef] [PubMed]
- Splendiani, A.; Sun, L.; Zhang, Y.; Li, T.; Kim, J.; Chim, C.-Y.; Galli, G.; Wang, F. Emerging photoluminescence in monolayer MoS2. Nano. Lett. 2010, 10, 1271–1275. [Google Scholar] [CrossRef] [PubMed]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically thin MoS2: A new direct-gap semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef] [PubMed]
- Radisavljevic, B.; Radenovic, A.; Brivio, J.; Giacometti, I.V.; Kis, A. Single-layer MoS2 transistors. Nat. Nanotech. 2011, 6, 147. [Google Scholar] [CrossRef]
- Ganatra, R.; Zhang, Q. Few-layer MoS2: A promising layered semiconductor. ACS Nano. 2014, 8, 4074–4099. [Google Scholar] [CrossRef]
- Castellanos-Gomez, A.; Poot, M.; Steele, G.A.; van der Zant, H.S.; Agraït, N.; Rubio-Bollinger, G. Elastic properties of freely suspended MoS2 nanosheets. Adv. Mater. 2012, 24, 772–775. [Google Scholar] [CrossRef]
- Bertolazzi, S.; Brivio, J.; Kis, A. Stretching and breaking of ultrathin MoS2. ACS Nano. 2011, 5, 9703–9709. [Google Scholar] [CrossRef]
- Pu, J.; Yomogida, Y.; Liu, K.-K.; Li, L.-J.; Iwasa, Y.; Takenobu, T. Highly flexible MoS2 thin-film transistors with ion gel dielectrics. Nano. Lett. 2012, 12, 4013–4017. [Google Scholar] [CrossRef] [PubMed]
- Duerloo, K.-A.N.; Ong, M.T.; Reed, E.J. Intrinsic piezoelectricity in two-dimensional materials. J. Phys. Chem. Lett. 2012, 3, 2871–2876. [Google Scholar] [CrossRef]
- Popov, I.; Seifert, G.; Tománek, D. Designing electrical contacts to MoS2 monolayers: a computational study. Phys. Rev. Lwtt. 2012, 108, 156802. [Google Scholar]
- Fang, H.; Chuang, S.; Chang, T.C.; Takei, K.; Takahashi, T.; Javey, A. High-performance single layered WSe2 p-FETs with chemically doped contacts. Nano Lett. 2012, 12, 3788–3792. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Chen, H.-Y.; Penumatcha, A.V.; Appenzeller, J. High performance multilayer MoS2 transistors with scandium contacts. Nano Lett. 2012, 13, 100–105. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Ding, S.; Araki, T.; Jiu, J.; Sugahara, T.; Wang, J.; Vanfleteren, J.; Sekitani, T.; Suganuma, K. Facile fabrication of stretchable Ag nanowire/polyurethane electrodes using high intensity pulsed light. Nano. Res. 2016, 9, 401–414. [Google Scholar] [CrossRef]
- Kwon, H.; Choi, W.; Lee, D.; Lee, Y.; Kwon, J.; Yoo, B.; Grigoropoulos, C.P.; Kim, S. Selective and localized laser annealing effect for high-performance flexible multilayer MoS2 thin-film transistors. Nano Res. 2014, 7, 1137–1145. [Google Scholar] [CrossRef]
- Kwon, H.-J.; Jang, J.; Kim, S.; Subramanian, V.; Grigoropoulos, C.P. Electrical characteristics of multilayer MoS2 transistors at real operating temperatures with different ambient conditions. Appl. Phys. Lett. 2014, 105, 152105. [Google Scholar] [CrossRef]
- Yeh, P.-C.; Jin, W.; Zaki, N.; Kunstmann, J.; Chenet, D.; Arefe, G.; Sadowski, J.T.; Dadap, J.I.; Sutter, P.; Hone, J. Direct measurement of the tunable electronic structure of bilayer MoS2 by interlayer twist. Nano. Lett. 2016, 16, 953–959. [Google Scholar] [CrossRef]
- Py, M.; Haering, R. Structural destabilization induced by lithium intercalation in MoS2 and related compounds. Can. J. Phys. 1983, 61, 76–84. [Google Scholar] [CrossRef]
- Di Bartolomeo, A.; Genovese, L.; Giubileo, F.; Iemmo, L.; Luongo, G.; Foller, T.; Schleberger, M. Hysteresis in the transfer characteristics of MoS2 transistors. 2D Mater. 2017, 5, 015014. [Google Scholar] [CrossRef]
- Léonard, F.; Talin, A.A. Electrical contacts to one-and two-dimensional nanomaterials. Nat. Nanotech. 2011, 6, 773. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wang, T.; Liu, L.; Du, K.; Liu, W.; Zhu, Z.; Li, M. Molybdenum disulfide and Au ultrasmall nanohybrids as highly active electrocatalysts for hydrogen evolution reaction. J. Mater. Chem. A 2017, 5, 4122–4128. [Google Scholar] [CrossRef]
- Eaton, S.M.; Zhang, H.; Herman, P.R.; Yoshino, F.; Shah, L.; Bovatsek, J.; Arai, A.Y. Heat accumulation effects in femtosecond laser-written waveguides with variable repetition rate. Opt. Express 2005, 13, 4708–4716. [Google Scholar] [CrossRef] [PubMed]
- Di Bartolomeo, A.; Grillo, A.; Urban, F.; Iemmo, L.; Giubileo, F.; Luongo, G.; Amato, G.; Croin, L.; Sun, L.; Liang, S.J. Asymmetric Schottky Contacts in Bilayer MoS2 Field Effect Transistors. Adv. Funct. Mater. 2018, 1800657. [Google Scholar] [CrossRef]
- Xu, Y.; Minari, T.; Tsukagoshi, K.; Chroboczek, J.; Ghibaudo, G. Direct evaluation of low-field mobility and access resistance in pentacene field-effect transistors. J. Appl. Phys. 2010, 107, 114507. [Google Scholar] [CrossRef]
- Ghibaudo, G. New method for the extraction of MOSFET parameters. Electron. Lett. 1988, 24, 543–545. [Google Scholar] [CrossRef]
- Chang, H.-Y.; Zhu, W.; Akinwande, D. On the mobility and contact resistance evaluation for transistors based on MoS2 or two-dimensional semiconducting atomic crystals. Appl. Phys. Lett. 2014, 104, 113504. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwon, H.; Baik, S.; Jang, J.E.; Jang, J.; Kim, S.; Grigoropoulos, C.P.; Kwon, H.-J. Ultra-Short Pulsed Laser Annealing Effects on MoS2 Transistors with Asymmetric and Symmetric Contacts. Electronics 2019, 8, 222. https://doi.org/10.3390/electronics8020222
Kwon H, Baik S, Jang JE, Jang J, Kim S, Grigoropoulos CP, Kwon H-J. Ultra-Short Pulsed Laser Annealing Effects on MoS2 Transistors with Asymmetric and Symmetric Contacts. Electronics. 2019; 8(2):222. https://doi.org/10.3390/electronics8020222
Chicago/Turabian StyleKwon, Hyeokjin, Seunghun Baik, Jae Eun Jang, Jaewon Jang, Sunkook Kim, Costas P. Grigoropoulos, and Hyuk-Jun Kwon. 2019. "Ultra-Short Pulsed Laser Annealing Effects on MoS2 Transistors with Asymmetric and Symmetric Contacts" Electronics 8, no. 2: 222. https://doi.org/10.3390/electronics8020222
APA StyleKwon, H., Baik, S., Jang, J. E., Jang, J., Kim, S., Grigoropoulos, C. P., & Kwon, H.-J. (2019). Ultra-Short Pulsed Laser Annealing Effects on MoS2 Transistors with Asymmetric and Symmetric Contacts. Electronics, 8(2), 222. https://doi.org/10.3390/electronics8020222





