Design of A Series Resonant Converter GMAW Welding Machine by Using the Harmonic Current Technique for Power Transfer

Abstract

This paper proposes the use of a control algorithm that can yield soft switching both at turn-on and turn-off of the inverter of series resonance converter (SRC) gas metal arc welding (GMAW) machines. The technique takes advantage of the band-pass filter characteristics of the SRC and controls the power by using switching frequencies that are subharmonics of the resonance frequency. The design and the experimental results for a 5 kW prototype system are given to prove that the algorithm can be used in GMAW systems.

1. Introduction

Flexibility, high speed, and capability of employing different types and thicknesses of materials make gas metal arc welding (GMAW) one of the most widely used processes in industrial and manufacturing operations. Commercial arc welders can be made in smaller sizes with the same capability by reducing the volume of the passive components such as transformers and filter inductors, and cooling parts such as heatsinks [1,2,3]. This can be achieved by increasing the switching frequency and utilizing soft switching techniques to decrease the losses. The power level in traditional welders is usually up to several kilowatts and they are more likely to use Insulated Gate Bipolar Transistor (IGBT) devices. The high current IGBTs usually can be switched at about 20 kHz [4] with a hard switching method. Resonant converters such as the LLC and the series resonant converter (SRC) achieve soft switching-like lossless switching transitions, pushing the switching frequency and efficiency to higher values and reducing the electromagnetic interference (EMI). They also have a wide operating frequency range and thus do not need filter inductors so that the volume and weight are comparatively reduced. On the other hand, resonant converters produce higher RMS current values than their square waveform counterparts, causing increased conduction losses [5].

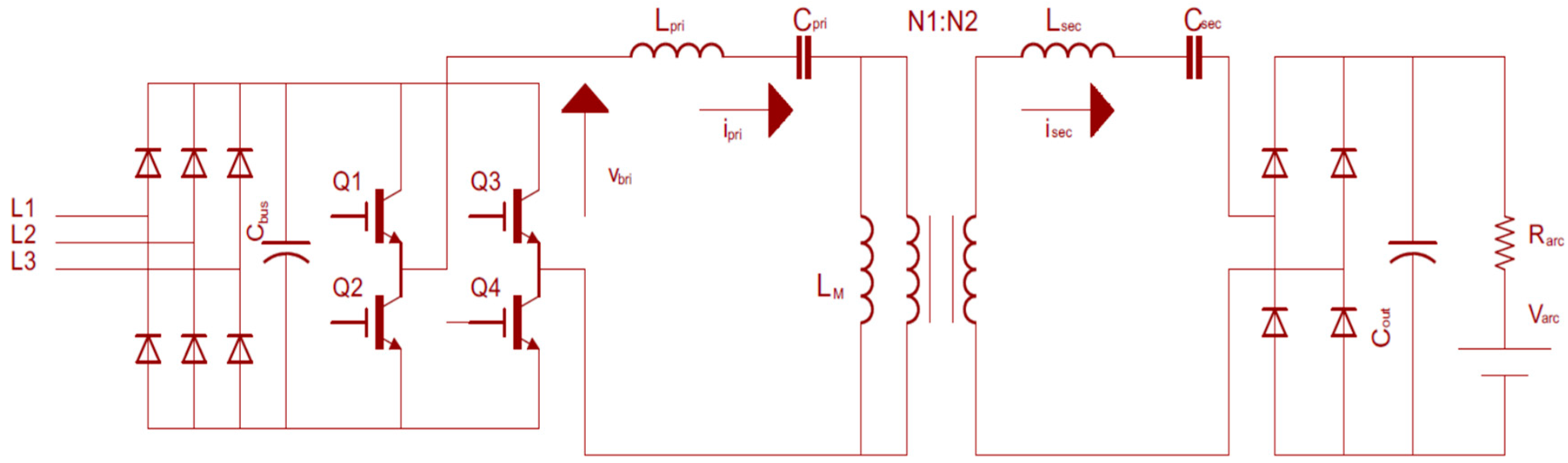
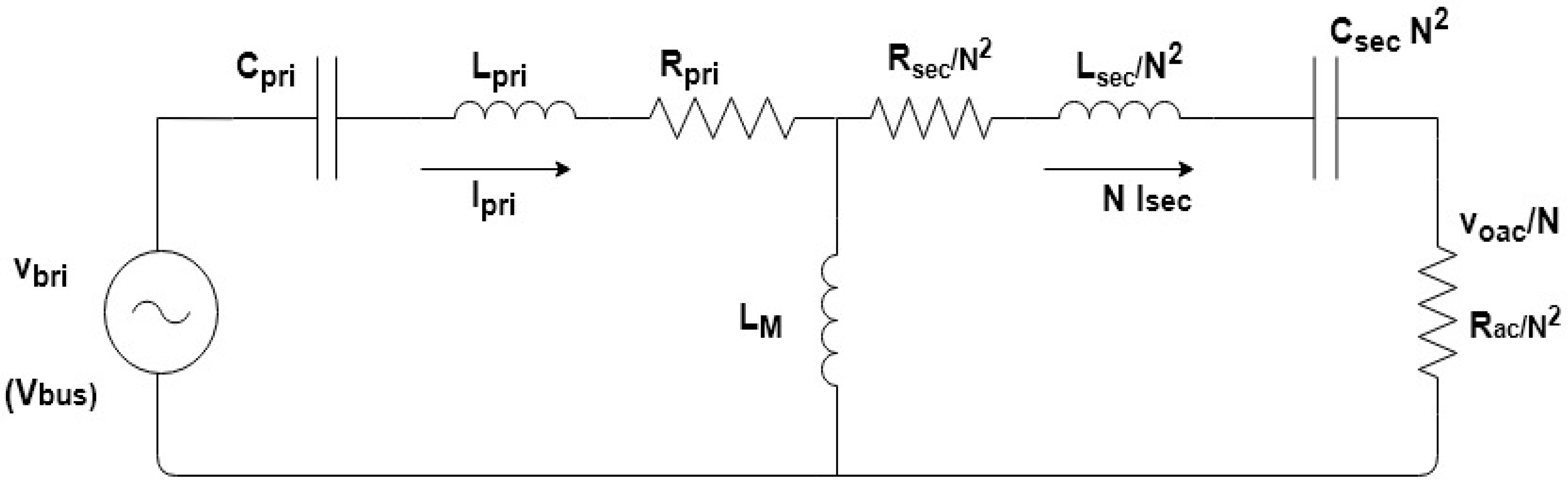
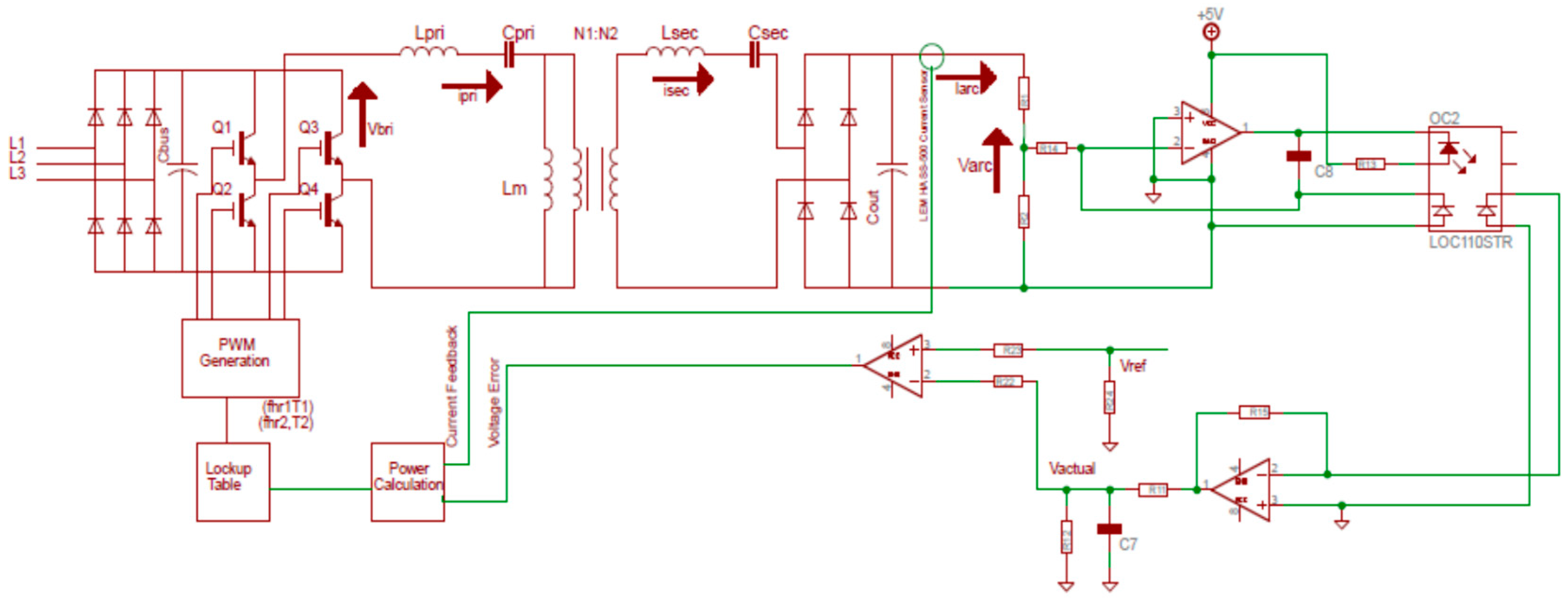
The frequency response of the SRC is that of the band-pass filters in that it allows only the resonant frequency component of the current to pass through while significantly attenuating the other order harmonics [4,6]. Figure 1 shows the circuit diagram of a welding machine including a full-bridge SRC. The welding arc is modeled with a series connected resistor and voltage source [5]. The three-phase rectifier converts the AC power from grid to DC voltage, which is then converted to high-frequency ac voltage by an H-bridge inverter, feeding a resonant network. The resonant frequency of the system is determined by $L_{pri}$ and $C_{pri}$. The other components make up the band-pass filter. These passive components can be optimized with simple equations.

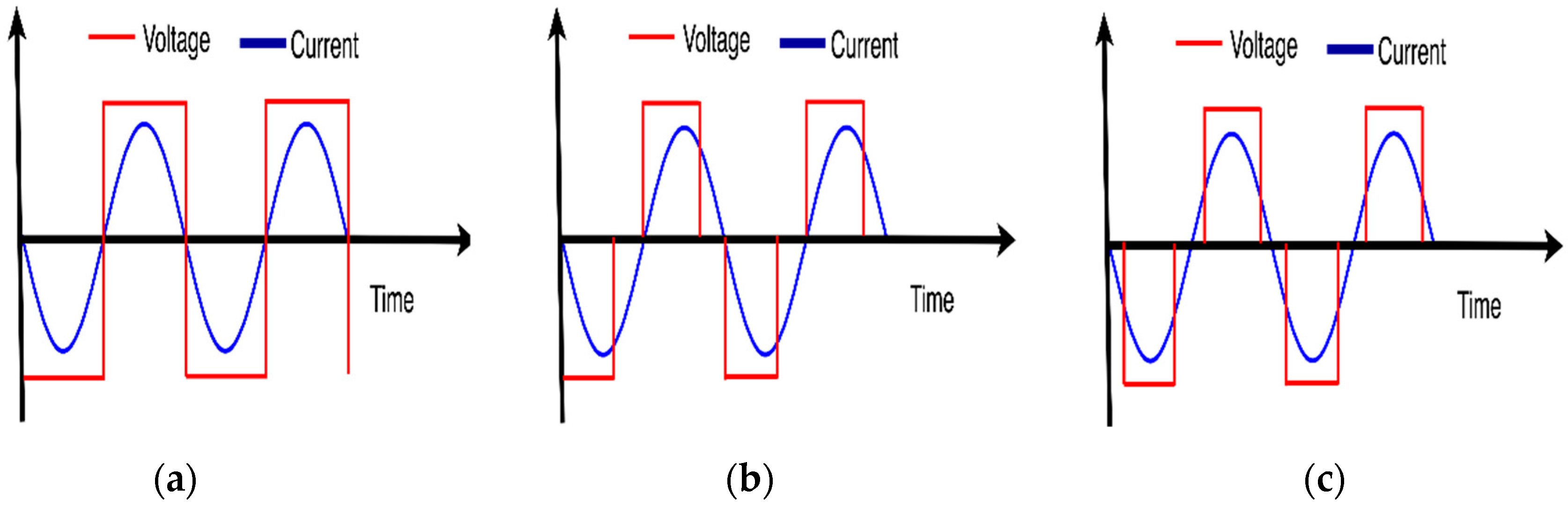
Although the efficiency of the SRC is high around full load conditions, it deteriorates at light loads for which the switching frequency needs to be increased above the resonance frequency, increasing the switching losses. Many methods have been proposed to achieve higher efficiency at low load conditions [7,8]. However, all these methods suffer from a similar problem: losing the soft switching property at turn-on, or at turn-off, or both, nullifies the advantages of soft switching. These cases are illustrated in Figure 2. When the converter operates at full load (Figure 2a) voltage transitions and current transitions occur at the same time leading to soft switching. When the converter operates at partial load, the turn-on may use zero-current switching but turn-off may use hard switching as shown in Figure 2b, or both turn-on and turn-off may use hard switching as shown in Figure 2c.

Power transfer via harmonic currents is a technique that utilizes different current harmonics such as 3rd, 5th, 7th, 9th, etc., successively at one period to regulate output power to achieve soft switching. In [4,6] this technique was proposed for electrical vehicle charging systems as an application of wireless power transfer with an efficiency of 83% for a 1 kW system. A similar concept called burst mode or bang-bang control was used to improve the efficiency of the resonance converter at light load [9,10,11]. However, they do not present results for a wide load range.

This paper presents the design and application of a 5 kW SRC GMAW welding machine utilizing the harmonic currents technique for power transfer. The soft switching is achieved both at turn-on and turn-off for a wide range of load. It has been observed that the efficiency of the machine has been improved and the size has been reduced.

The remainder of the paper is structured as follows. In the next section the GMAW system is explained and its model is presented. In Section 3 the full bridge SRC and its band-pass filter behavior are discussed. Then, the proposed method is explained in Section 4. Section 5 is about the design of the converter and its controller. Results obtained at the prototype set-up are presented in Section 6.

2. Load Behavior of the GMAW System

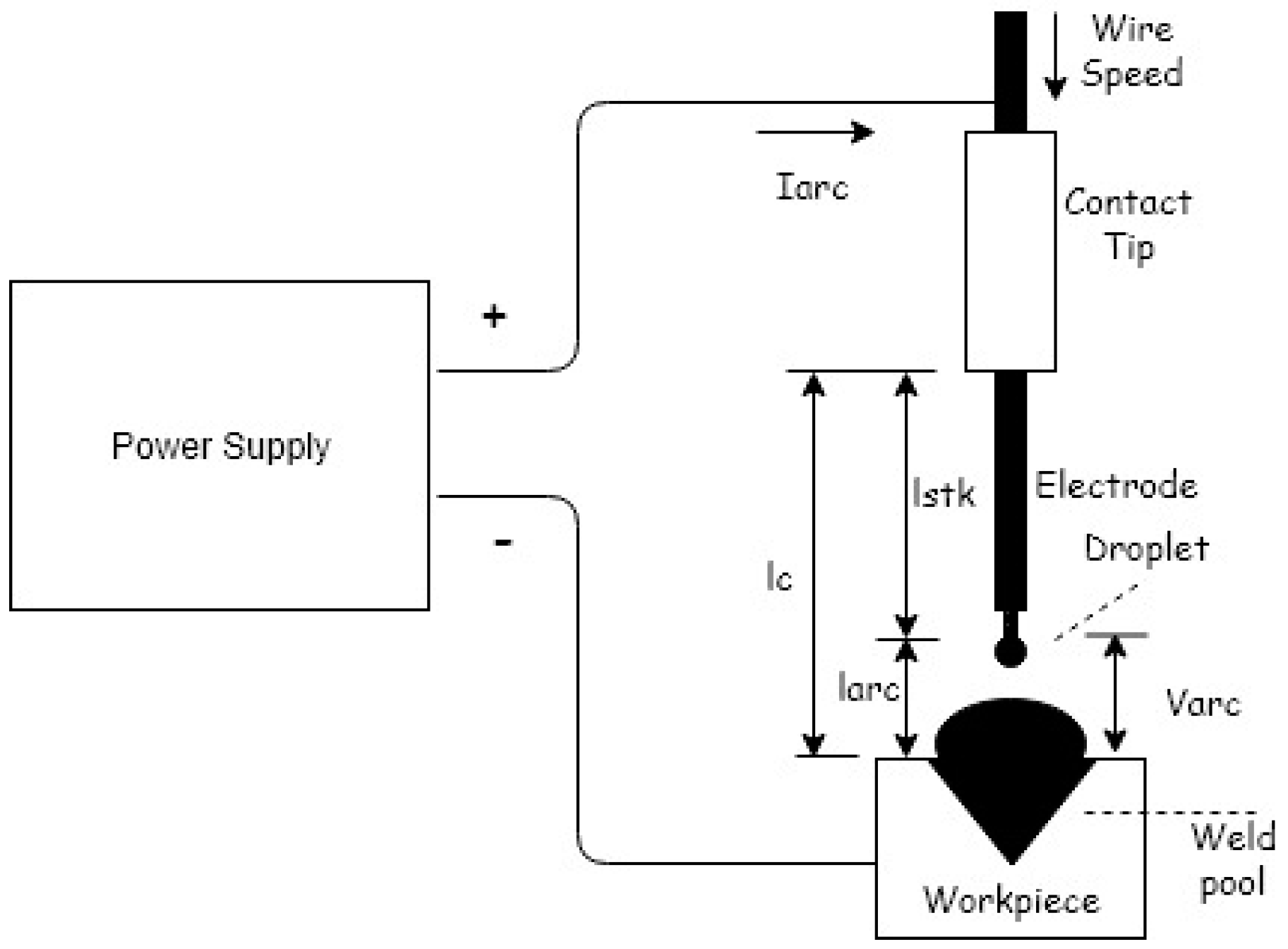
GMAW is one of several types of welding methods. It is highly efficient and it can be used to weld any material of any thickness in any position with the possibility of automatic implementation. GMAW nowadays is considered the most popular type of arc welding process [3,12,13]. Figure 3 shows a schematic that represents the GMAW process.

2.1. Modeling of the GMAW Process

The welding machine for GMAW includes a DC power source. The positive terminal of this power source is connected to the welding electrode while the negative one is connected to the workpiece or vice versa. At the steady state when the arc current $\left(I_{arc}\right)$ and the arc length ($l_{arc})$ are positive, the arc voltage ($V_{arc}$) and arc power functions that generate arc energy for making a metal joint can be expressed as follows [3,12,13,14]:

$$V_{arc}=V_{ccz}+E_{arc}{l}_{arc}+R_{arc}{I}_{arc}=V_{ccz}+E_{arc}\left(l_c-l_{stk}\right)+R_{arc}{I}_{arc}$$

(1)

The power arc ($P_{arc}$) can be expressed as:

$$P_{arc}=V_{ccz}{I}_{arc}+\left(E_{arc}{l}_{arc}+R_{arc}{I}_{arc}\right)I_{arc}=V_{ccz}{I}_{arc}+\left(E_{arc}\left(l_c-l_{stk}\right)+R_{arc}{I}_{arc}\right)I_{arc}$$

(2)

The four distinct parameters of an arc are the constant charge zone voltage ($V_{ccz}$), which is the sum of cathode and anode drop voltages that are considered constant, the arc length ($l_{arc}$), the arc length factor ($E_{arc}$), and the arc resistance ($R_{arc}$). The distance between the contact tube and base plate ($l_c$) is the sum of the arc length ($l_{arc}$) and stick out distance ($l_{stk}$) as shown in Figure 3.

To define the load voltage and power of the system the electrode resistivity ($\rho$) needs to be known. The load voltage ($V_{load}$) and load power ($P_{load}$) are given as follows [12,14]:

$$V_{load}=V_{ccz}+E_{arc}{l}_{arc}+\left(R_{arc}+\rho l_{stk}\right)I_{arc}$$

(3)

$$P_{load}=\rho l_{stk}{I}_{arc}+P_{arc}$$

(4)

To define the wire feed speed ($v_{fsd}$), the electrode melting rate ($v_{mr}$) and the rate of change of electrode stick out should be known.

$$v_{fsd}=\frac{d{l}_{stk}}{dt}+v_{mr}$$

(5)

$$v_{mr}=\frac{4000}{q_m\pi {\rho }_d{d}^2}p{l}_{stk}{I}_{arc}+{\eta }_{arc}{V}_{ccz}{I}_{arc}$$

(6)

where $q_m$ is quantity of heat needed to melt one gram of weld metal, ${\rho }_d$ is the density, $d$ is the dimeter of the wire, and ${\eta }_{arc}$ is the heat transfer efficiency of the process. Equation (6) can be re-written as:

$$v_{mr}=k_1{I}_{arc}+k_2{l}_{stk}{I}_{arc}^2$$

(7)

where $k_1$ and $k_2$ are constant for a specific operating set up.

2.2. Conventional Load Regulation

In general, there are two types of regulations in welding machines: constant voltage (CV) and constant current (CC) mode regulations. In CC mode machines the current affects the melt-off rate or consumption rate of the electrode, whether it is a stick electrode or wire electrode. The higher the current level, the faster the electrode melts or the higher the melt-off rate. In CV mode machines, the voltage controls the length of the welding arc, and the resulting width and volume of the arc cone. As the voltage increases, the arc length gets longer.

Table 1. Recommended power source output type by arc welding process [15].

Welding Process	SMAW (Shielded Metal Arc Welding)	GTAW (Gas Tungsten Arc Welding)	GMAW (Gas Metal Arc Welding)	FCAW (Flux Cored Arc Welding)
Output type	CC	CC	CV	CC

summarizes the recommended output types by welding process [12,15].

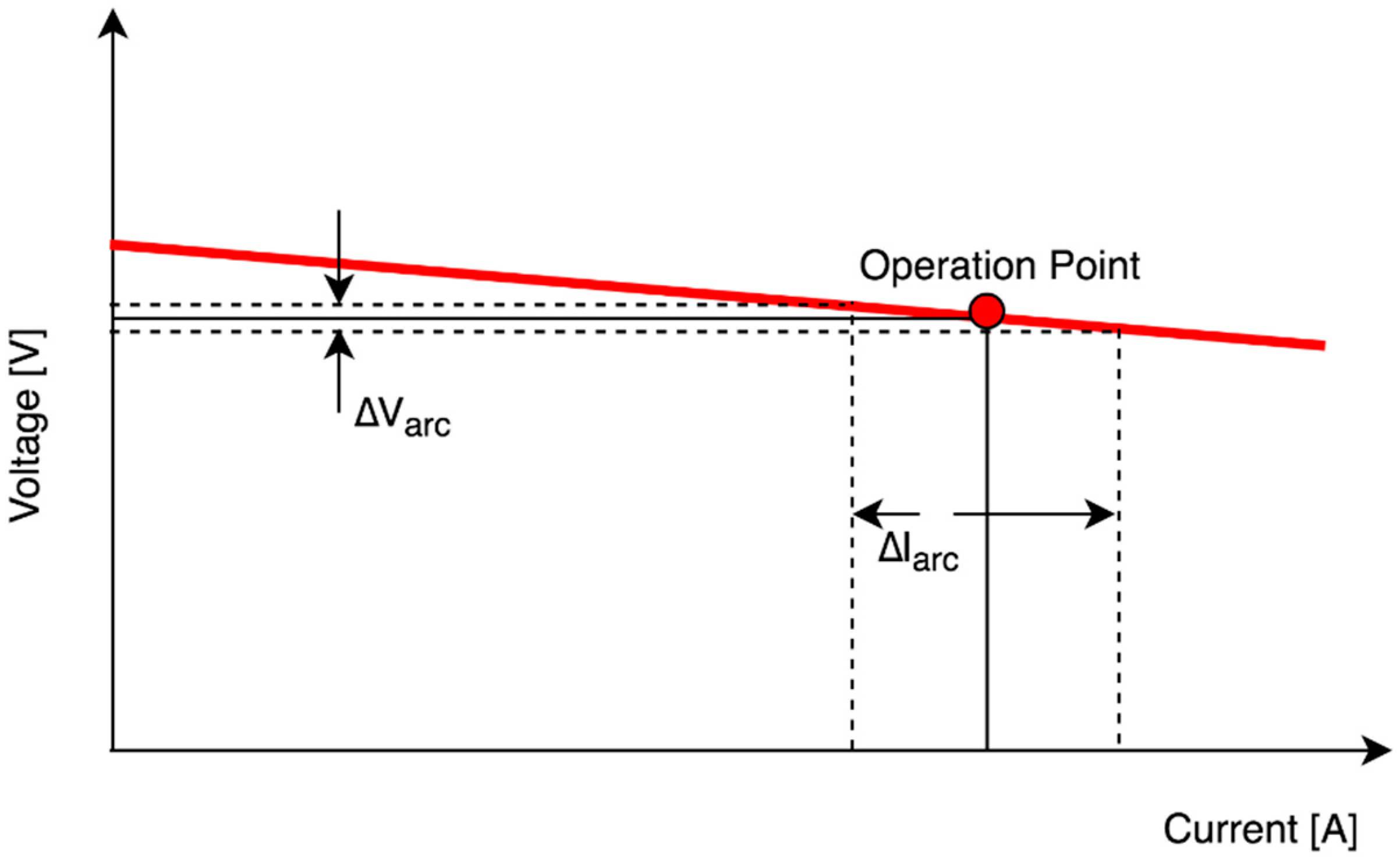
Figure 4 shows the typical output curves of a CV GMAW which is chosen in this work. The voltage stays in a narrow band although the current may vary by a large range.

3. Basic Operation Principles of a Series Resonant Circuit

3.1. Band-Pass Filter Characteristic of the SRC

The SRC H-bridge inverter in Figure 1 can be reduced to an equivalent circuit shown in Figure 5.

In this equivalent circuit the input AC voltage source ($v_{bri}$) represents the output voltage of the full bridge and $R_{ac}$ is the equivalent AC resistance of the load ($R_L$) seen from the input side of the output rectifier, and it is given as follows:

$$R_{ac}=\frac{8}{{\pi }^2}{R}_L$$

(8)

$N=N_2/N_1$ is the turns ratio of the transformer, $R_{pri}$ is the primary coil AC resistance, and $R_{sec}$ is the secondary coil AC resistance. $N=1$ and $R_{pri}=R_{sec}=0$ are assumed in this analysis. $C_{pri}$ and $C_{sec}$ are the compensation capacitances that determine the resonant frequency by compensating for the leakage inductance. All parameters on the secondary side of the transformer are reflected in the primary. The analysis of the SRC can be performed using this equivalent circuit [16].

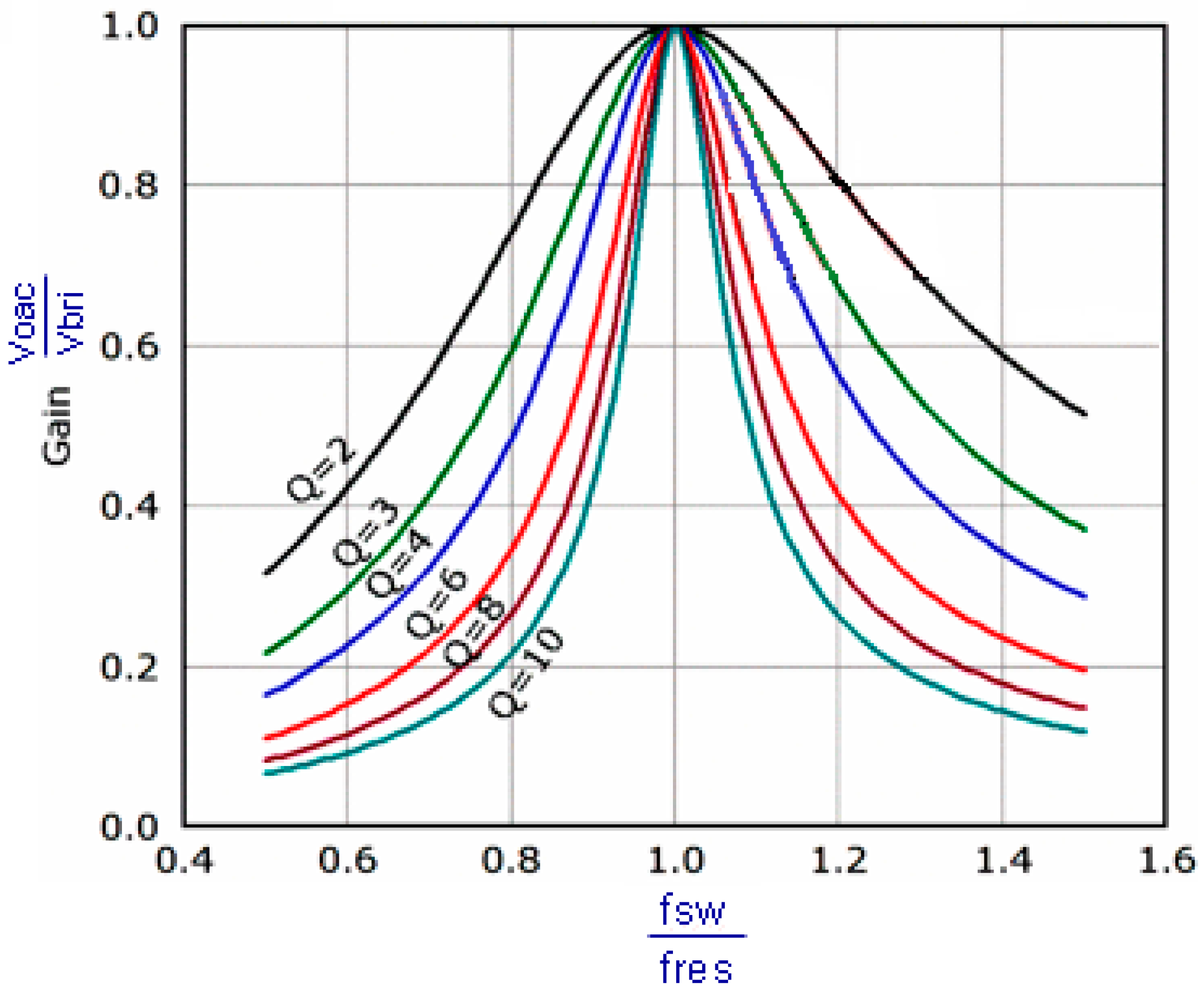
The maximum transfer gain is achieved when the input switching frequency ($f_{sw}$) is equal to the resonant frequency ($f_{res}$) where the $v_{bri}$ voltage appears across the load ($R_{ac}$). The voltage gain then can be defined in terms of the RMS voltages of the output and input as:

$$VG=\frac{V_{oac}}{V_{bri}}$$

(9)

In this equation, $Q$ is the quality factor and is defined as:

$$Q=\omega \times \frac{Totalenergystored\left(E\right)inpassiveelements}{Powerdissipated}$$

(10)

For the SRC this equation can be written as follows:

$$Q=\omega \times \frac{E\left({\mathrm{L}}_{pri}\right)+\mathrm{E}\left(C_{pri}\right)+\mathrm{E}\left({\mathrm{L}}_m\right)+\mathrm{E}\left(L_{sec}\right)+\mathrm{E}\left(C_{sec}\right)}{V_{oac}2/R_{ac}}$$

(11)

where $\omega =2\pi f$.

Figure 6 shows the voltage gain frequency variation with the quality factor used as a parameter [16,17].

3.2. Control of Power Through Harmonic Components

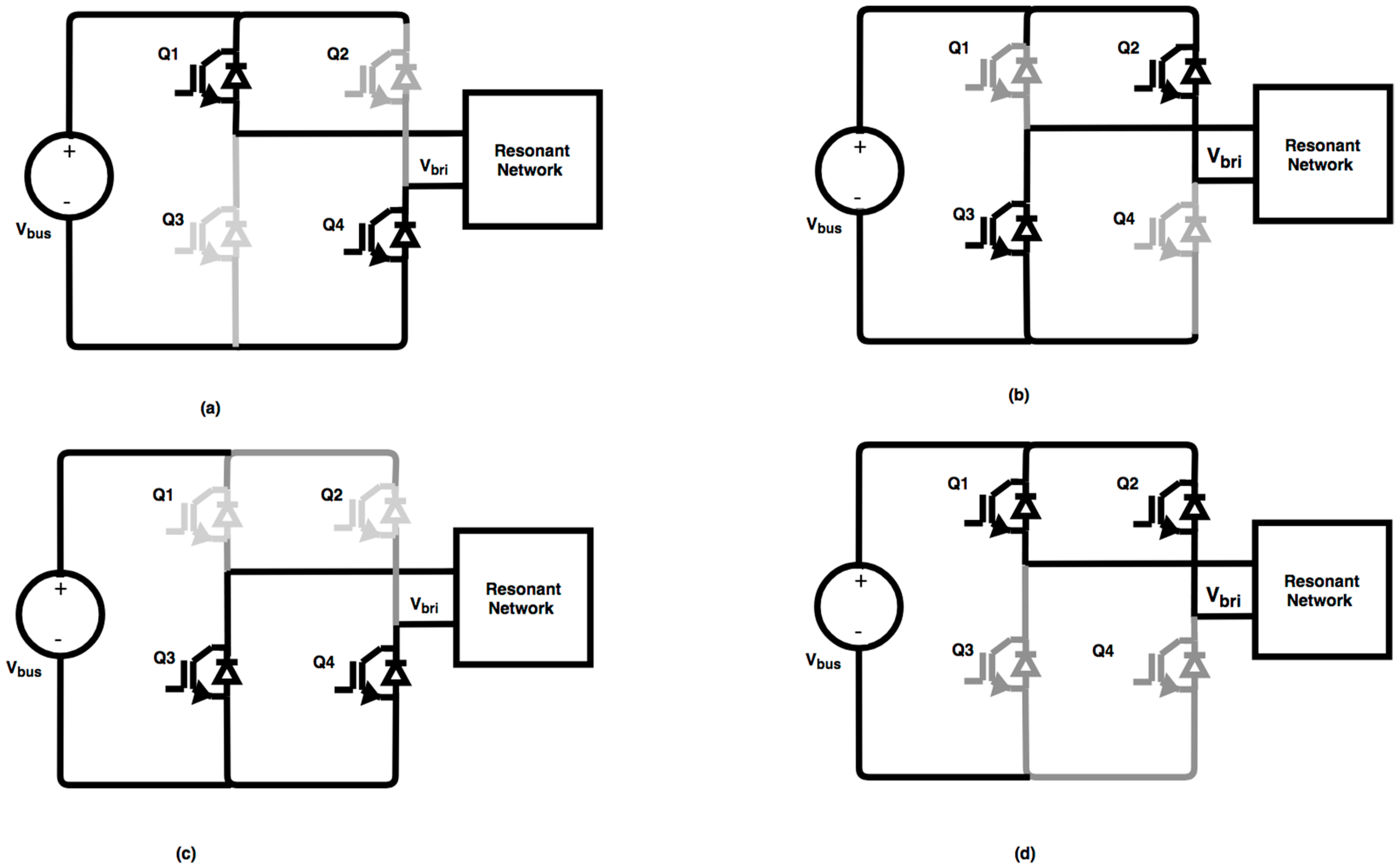
As shown in Figure 7, the H-bridge inverter has three modes of operation: it generates positive voltage ($v_{bri}=V_{bus}$) when Q1 and Q4 are on, negative voltage ($v_{bri}=-V_{bus}$) when Q2 and Q3 are on, and zero voltage ($v_{bri}=0$) when either Q1 and Q3 or Q2 and Q4 pairs are on. The last two modes can be called the circulation modes. The first two modes are initiated when diagonal switches are turned on creating a resonant pulse train. At the end of the first pulses these modes end, and circulation modes start. In circulation modes pulses continue to flow through the load [18].

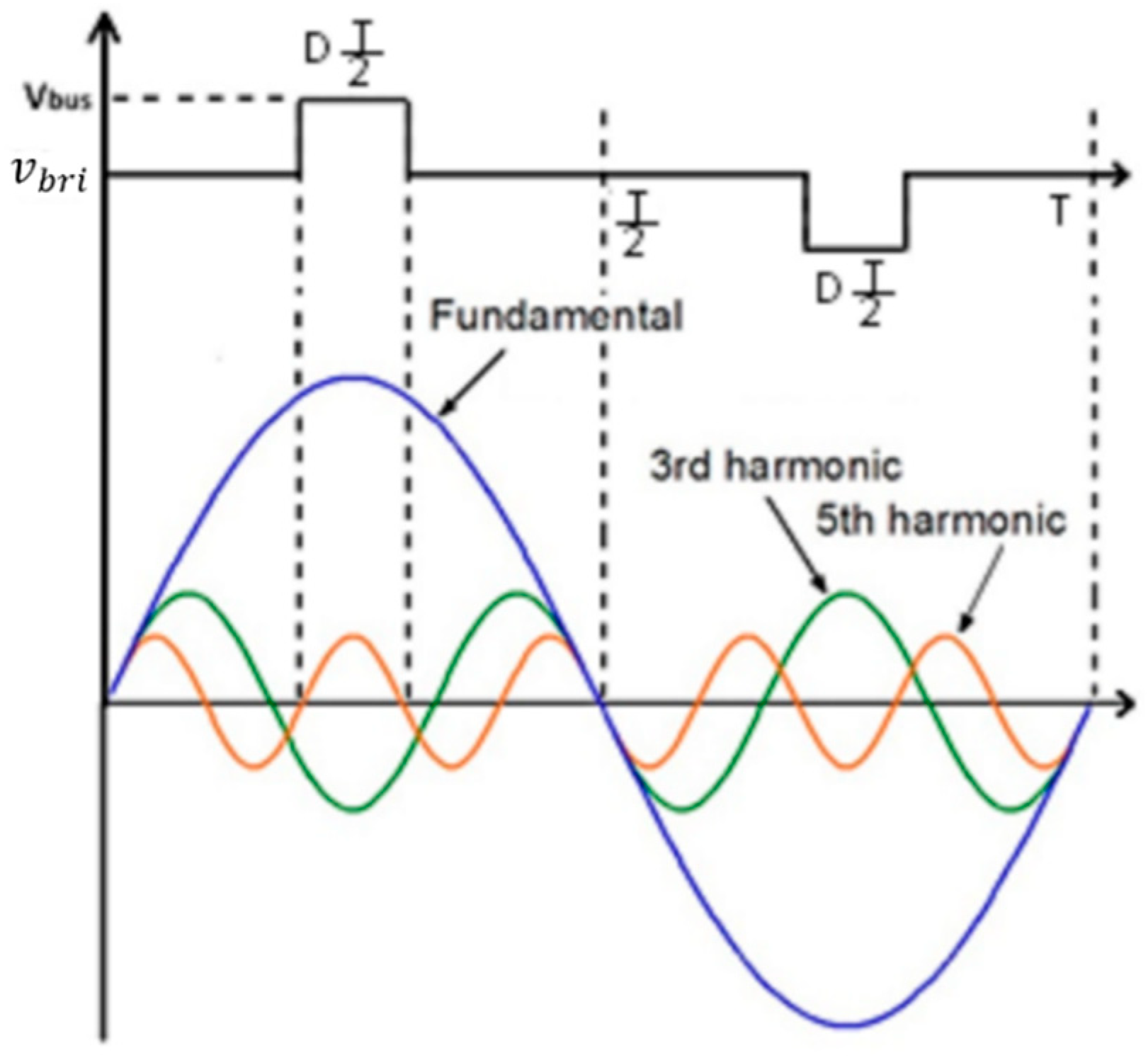
Figure 8 shows the output voltage waveforms of the H-bridge ($v_{bri}$) and its harmonic components. D is the duty cycle defined as the ratio of the on time switches to the half period (D$\frac{T}{2}$). The phase shift between the two legs controls the RMS output voltage of $v_{bri}$. Fourier series expansion of this voltage is given as [1]:

$$v_{bri}={\displaystyle \sum }_{n=1}^{\infty }\frac{4V_{bus}}{n\pi }\sin \left(Dn\pi \right)\sin \left(n\omega t\right)$$

(12)

Due to the band-pass filter feature of the resonant network, only the resonant frequency component of $i_{pri}$ can pass to the secondary side of the converter, with all other frequency components filtered out by the large impedance.

The power control in this circuit is achieved by changing the switching frequency of the SRC in such a way that it is equal to $\frac{f_{res}}{3},\frac{f_{res}}{5}$, $\frac{f_{res}}{7}$, etc. If the required power is low, the switching frequency is adjusted to a lower value so that a very high order of harmonic is at the resonant frequency. In this case, the value of the voltage harmonic at the resonance frequency is low, generating low power. 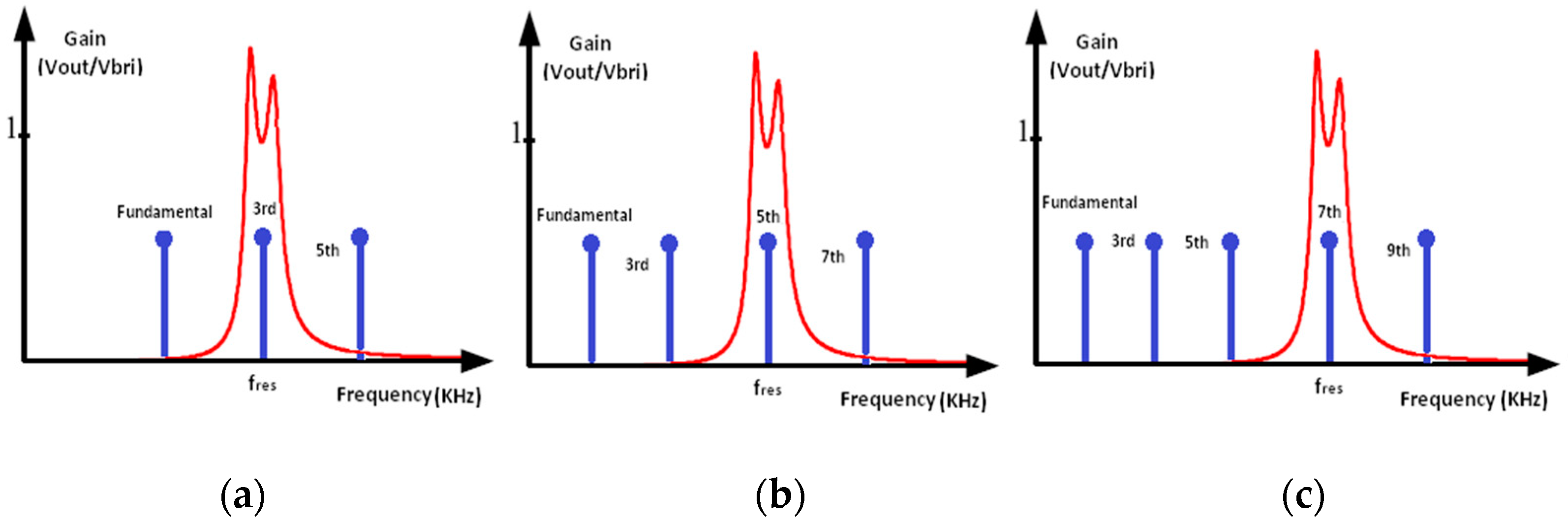For full power, the highest possible switching frequency ($\frac{f_{res}}{3}$) is selected. In this case, the third harmonic of the voltage determines the power. This concept is depicted in Figure 9 for a system using three different switching frequencies for three specific power levels. Figure 9a shows the case for the highest power for which the switching frequency is equal to 1/3rd of the resonant frequency. In Figure 9b, a lower power is required and switching at 1/5th of the resonant frequency produces a 5th harmonic voltage whose RMS value is 1/5th of that of the fundamental. Figure 9c shows the case when the power demand is the lowest. Switching at 1/7th of the resonant frequency produces a 7th harmonic voltage whose RMS value is 1/7th of that of the fundamental.

If a power level between the specific levels is required, then switching frequencies corresponding to the two neighboring levels are alternately used for a calculated length of time. For example, for a power level between the medium power and the full power, a number of pulses is applied for $f_{sw}=\frac{f_{res}}{3}$ and a number of pulses is applied for $f_{sw}=\frac{f_{res}}{5}$. The required numbers should be calculated by the controller.

For fine power control, the number of switching frequencies can be increased and much lower switching frequencies can be used.

4. Design of the SRC Converter and its Controller

Nowadays GMAW welding machines have new technology called “smart MIG (Metal Inert Gas)”. With smart MIG technology, users choose variables such as material thickness, material type, welding wire diameter, isolated gas used, and the value of arc voltage ($V_{arc}$), arc current, and the speed of wire feeding ($v_{fsd}$) are determined automatically by using a look-up table.

A 5 kW GMAW welder utilizing an SRC converter has been designed for this work. The input is a 380 Vrms, 50 Hz AC source. The output voltage can be adjusted between 18 and 30 V. Technical specifications of the designed system are given in

Table 2. Parameters of the designed GMAW machine.

Name	Value	Name	Value/Model no
DC input voltage (Vdc)	560 V	Full bridge switches	IGBT SKM200GB125D
Max. output voltage	30 V	Output rectifier	STTH200W06TV1
Switching frequency (fsw)	15/6.4/5 kHz	Main controller	DSPIC33EP128GS806
Resonant frequency ($f_{res}$)	45 kHz

.

The control circuit of the system was designed to achieve constant voltage by charging the output capacitor C_out by using the harmonics-based control method. Figure 10 shows which harmonic order is used for which required power level.

5. Simulation Results

Simulations have been carried out in PSIM to see the operation of the system.

Table 3. Parameters and some variables of the GMAW process model used in the simulations for carbon steel [13].

Nomenclature	Symbol	Value (unit)
Arc resistance	Rarc	0.0237 (Ω)
Arc length factor	Earc	400 (vm−1)
Constant charge zone	Vccz	12 (V)
Resistive of the electrode	$\rho$	0.43 (Ω m−1)
Density of the liquid electrode material (steel)	${\rho }_d$	7850 (kg m−3)
Electrode dimeter	D	0.01 (m2)
Melting rate constant 1	k1	3.3 × 10−10 (m3 S−1 A−1)
Melting rate constant 2	k2	0.78 × 10−10 (m3 S−1 A−1)
Quantity of heat needed to melt one gram of weld metal (steel)	Qm	≈1430 (J/gm)
Open circuit voltage	Voc	22 (V)
Constant distance between contact tube and base plate	lc	23.5 (mm)
Stick out distance	lstk	11 (mm)
Arc length distance	larc	12.5 (mm)

shows the parameters of the welding components used in the system modeling.

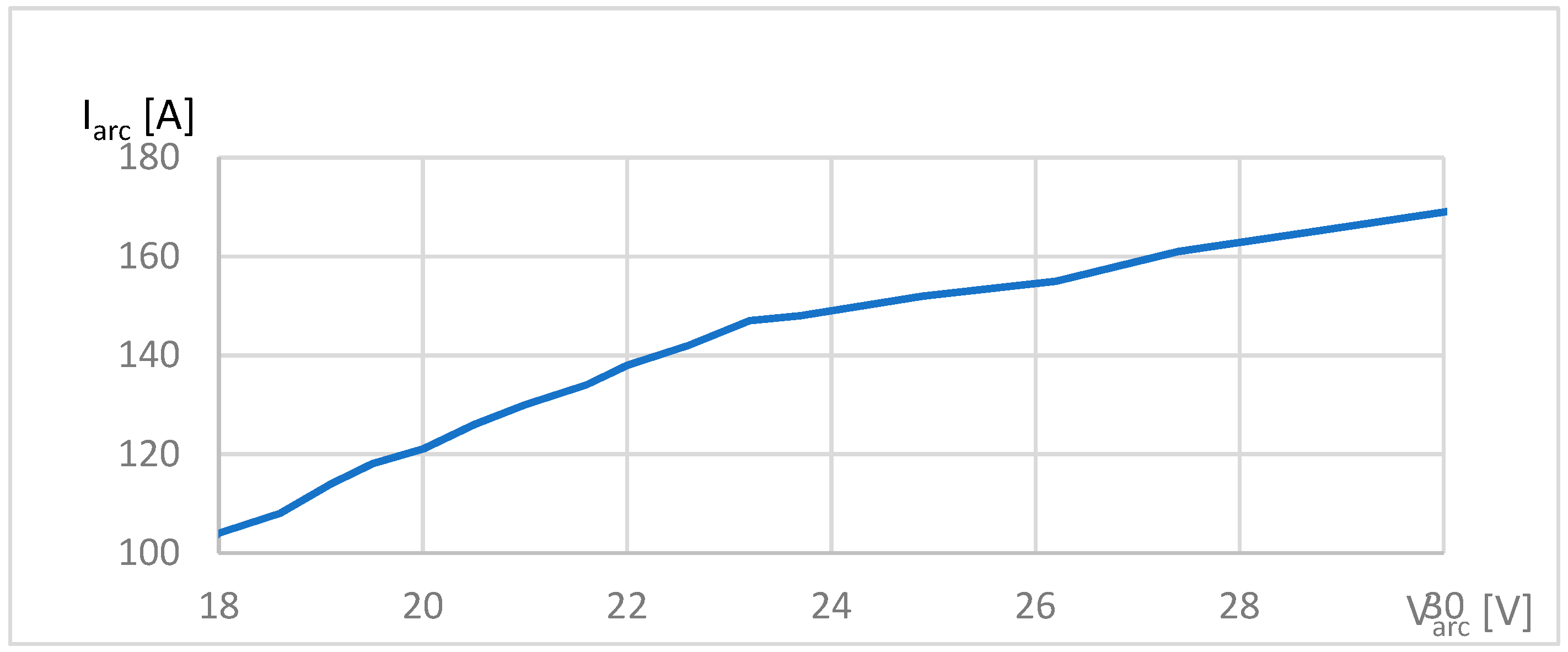
The arc current–arc voltage relationship has been obtained for these parameters as shown in Figure 11. As seen in the graph the variation is linear in the designed operation range.

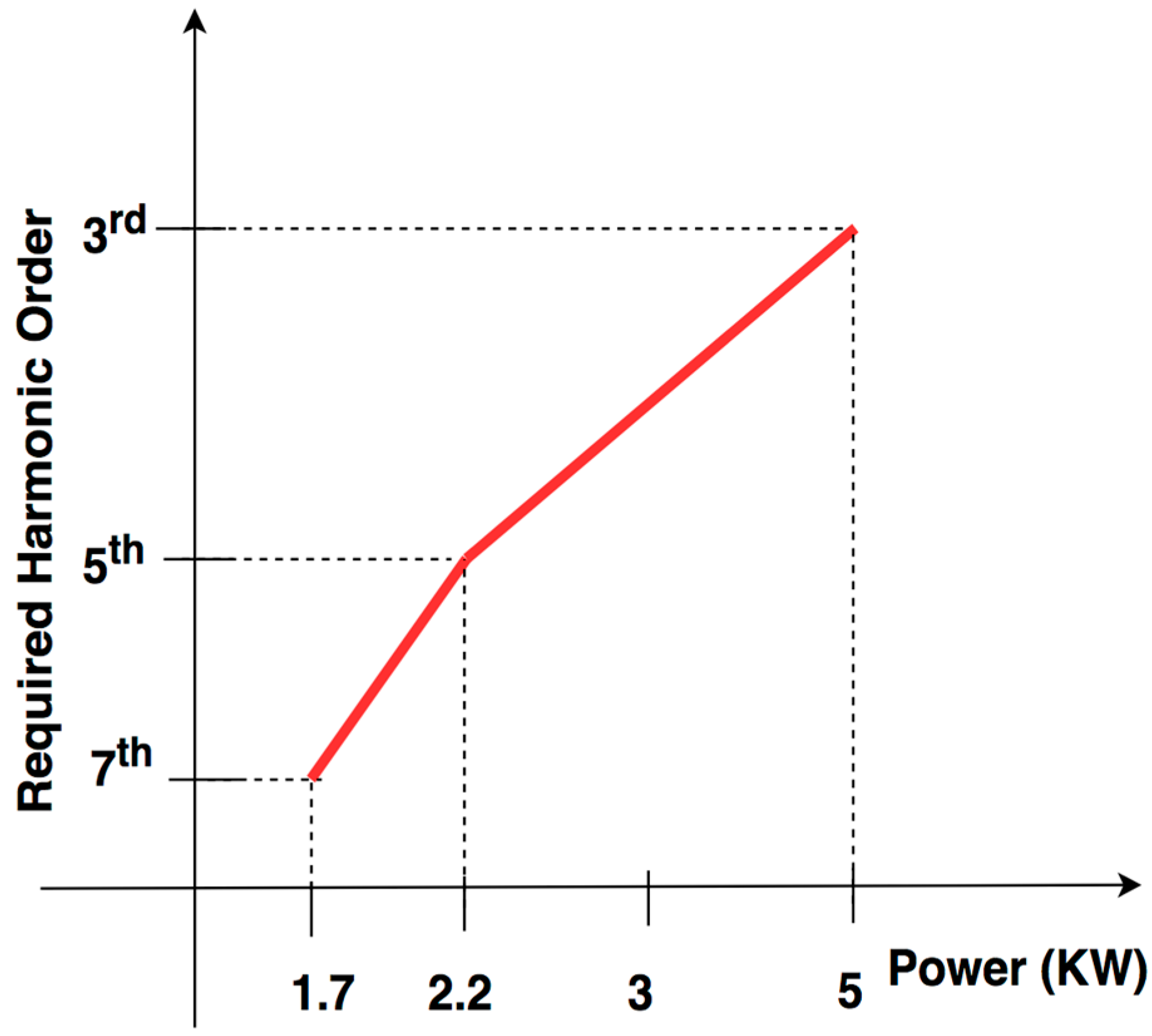
The system has been designed to have the harmonic order–power profile as shown in Figure 12. For full power the third harmonics (5 kW), for medium power (2.2 kW) the fifth harmonics, and for low power (1.7 kW) the seventh harmonics are used.

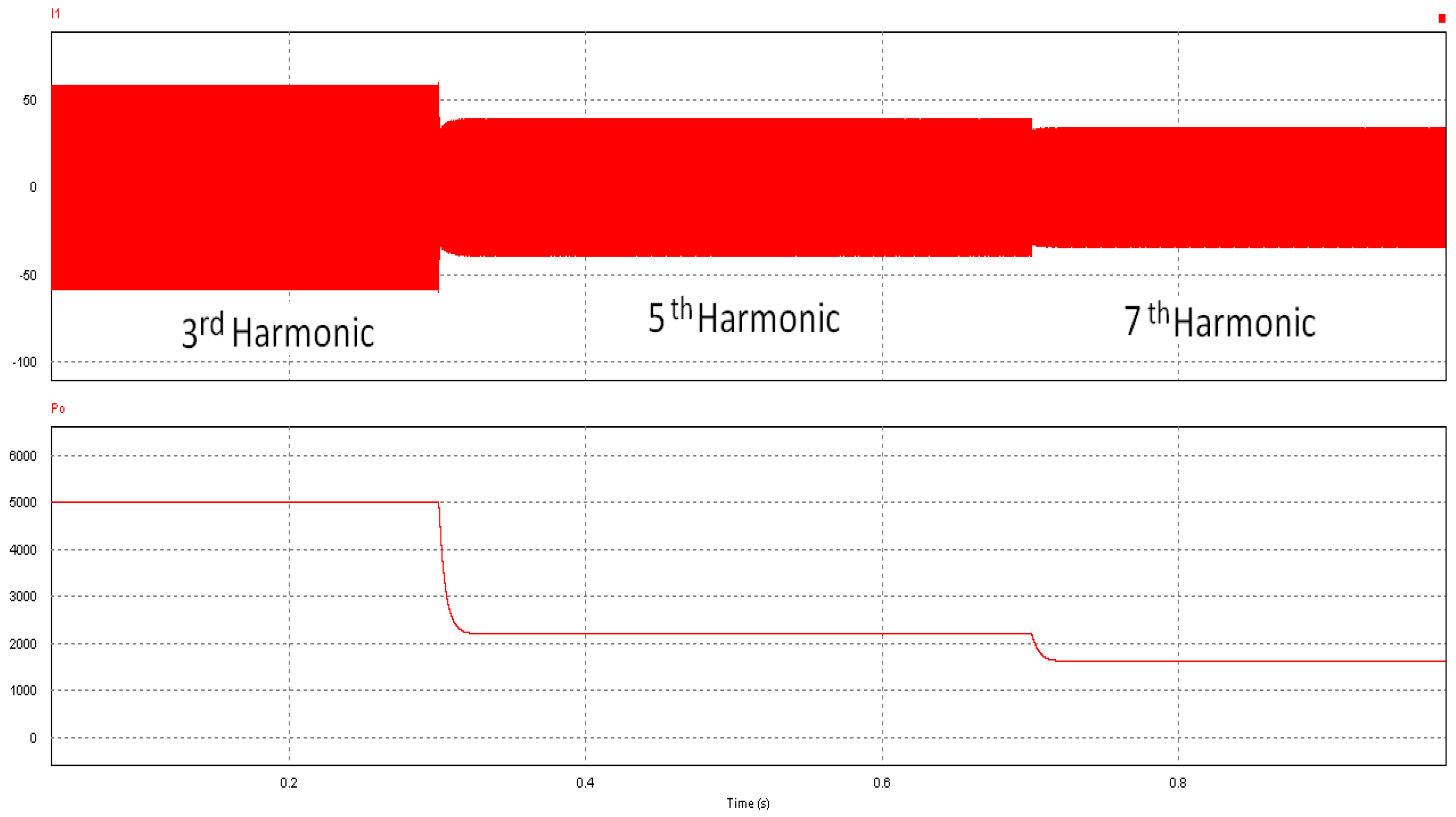
Figure 13 shows the bridge output voltage and current pulses. First, the switching frequency is 1/3rd of the resonant frequency and therefore the 3rd harmonic current passes through. Then 1/5th and 1/7th of resonant frequency are used for switching, respectively, yielding the 5th and 7th harmonic currents to transfer the power. Soft switching is achieved at each turn-on and turn-off.

The resonant frequency depends on the value of the passive components. The time that $i_{pri}$ needs to return to zero is half of the resonant period ($T_{res}/2$). In order to achieve soft switching, the switch on time $T_{on}=T_{res}/2$ condition has to be met. This is adjusted by the duty cycle of the switch as the switching frequency is changed.

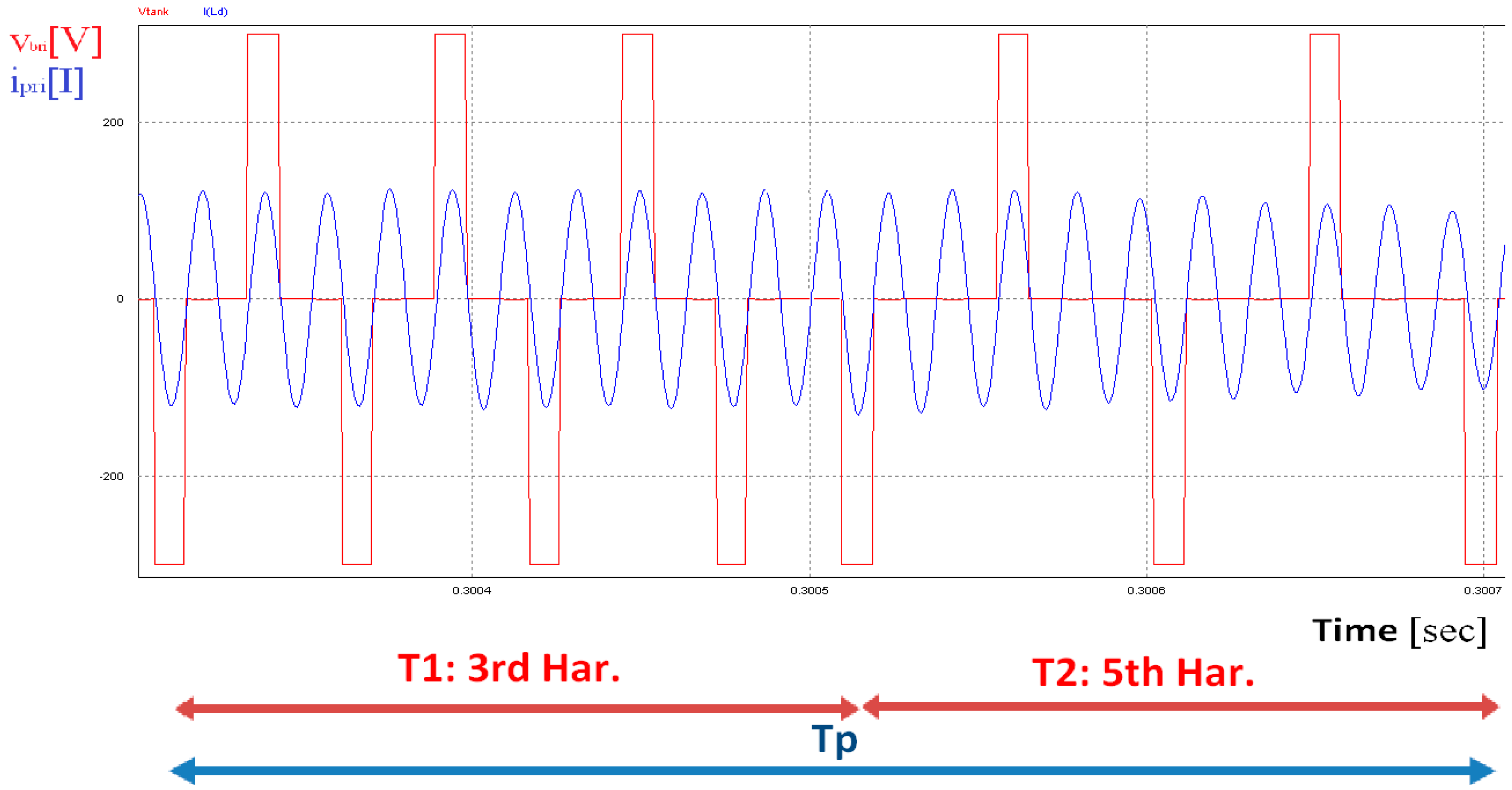
Figure 14 shows how the power is regulated. If a power level other than the specified levels is required, two different switching frequencies are used alternately in a period of regulation ($T_p=T_1+T_2$) where $T_1$ and $T_2$ are the corresponding application times of each frequency generating the desired harmonics at the resonant frequency. $T_p$ should be significantly larger than the switching frequency, and smaller than the system response frequency. In this figure, the 3rd harmonic and 5th harmonic currents are generated to obtain the required power.

6. Loss Analysis

6.1. Transformer Loss Calculations

There are two kinds of losses in the magnetic components like the inductors and the transformers: core losses ($P_{core}$) and copper losses ($P_{Cu}$). The total losses for a transformer can be calculated as [19,20]:

$$P_{total}=P_{core}+P_{Cu}$$

(13)

6.1.1. Copper Losses

If the primary and secondary currents are known copper losses can be calculated using the following equation:

$$P_{Cu}=I_{pri}^2{R}_{pri}+I_{sec}^2{R}_{sec}$$

(14)

As the load becomes lighter the copper losses decrease.

6.1.2. Core Losses

The Steinmetz equation is used to determine the core losses of magnetic components [19,20].

$$P_{core}=J_1{f}_{res}^{J_2}{B}^{J_3}$$

(15)

$B$ is the peak flux density and $J_1$, $J_2$, and $J_3$ are material parameters. In this work a ferrite EE80 core is used and the material parameters are taken from the manufacturer’s material specifications.

The parameters for the magnetic components of the system are given in

Table 4. Parameters of the magnetic components.

Name	Value
LM	8 µH
Lpri	76 µH
Lsec	1.2 µH
Rpri	0.1 mΩ
Rsec	1.3 mΩ
J1	0.47
J2	1.43
J3	2.83
B	370 mT

.

It should be mentioned that as the core losses depend on the applied voltage, they are almost constant at constant-voltage, constant-frequency applications. However, in the application described in this paper, as the load becomes lighter, the switching frequency is reduced leading to lower voltages across the transformer. While the frequency is constant at the resonance frequency, the reduced voltage leads to reduced flux and therefore core losses are lower at light load.

6.2. Semiconductor Losses

The semiconductor losses can be calculated by using the technical information given in manufacturers datasheets. The designed circuit in the primary stage has six line-rectifier diodes and four inverter IGBTs. The secondary stage has four high frequency rectifier diodes.

There are two types of losses in an IGBT: conduction losses ($P_{cond}$) and switching losses ($P_{sw}$). The total loss equation is given in (16).

$$P_{IGBT}=\frac{1}{2}{f}_{sw}{V}_{off}{I}_{on}\left(t_r+t_f\right)+d{V}_{CE\left(sat\right)}{I}_{on}$$

(16)

where $V_{off}$ is the voltage across the device at the off state, $I_{on}$ is the current level at the on state, $V_{CE\left(sat\right)}$ is the voltage across the device at the on state, $t_r$ is the rise time of the current, $t_f$ is the fall time of the current, and $d$ is the duty cycle ratio of the switch. If the inverter is operating at resonance conditions, the switching losses can be ignored.

Primary diodes rectify at 50 Hz, and therefore reverse recovery losses can be ignored. Total loss from primary diodes can be calculated as:

$$P_{D,primary}=V_F{I}_{pri}$$

(17)

Secondary side rectification diodes rectify at high frequency so reverse recovery losses are dominant.

$$P_{D,secondary}=\frac{1}{2}{f}_{sw}{V}_{off}{I}_{sec}{t}_{rr}$$

(18)

In this equation $t_{rr}$ is the diode reverse recovery time.

The device parameters are listed in

Table 5. Parameters of the semiconductor devices.

Name	Value
$V_{CE\left(sat\right)}$	3.3 V
$t_r$	36 ns
$t_f$	25 ns
$V_F$	1.5 V
$t_{rr}$	55 ns

.

It should be mentioned that while the switching losses are reduced as the load becomes lighter at constant-voltage, constant-frequency applications, they are almost ignorable in this application due to near zero-voltage-switching (ZVS) switching as well as reduced switching frequency.

6.3. Other Losses

Other parasitic losses exist within the system, like capacitor equivalent series resistor (ESR), particularly for high current systems. Capacitors are important for maintaining waveform quality and reducing voltage spikes and ripples and ESR losses can become significant when the current is large.

Another type of loss that is difficult to estimate is due to the parasitic inductance of cables, wires, etc. Parasitic inductance can cause excessive voltage spikes during switching. Switching the waveforms affected will result in larger losses in addition to higher voltage stress. Termination and mechanical connections are another major parasitic loss, especially for high current situations.

7. Experimental Results

The designed system has been built and tested. The experimental 5 kW set-up is shown in Figure 15. DSPIC33EP128GS806 has been used as the core of the control circuit. The full-bridge is composed of four IGBTs (Semikron SKM200GB125D) that work with the resonant converter up to 100 kHz, and a Ferroxcube E80/38/20 (3C94) ferrite core for high frequency transformers and the two resonant inductors.

Figure 16 shows the complete control diagram of the resonant welding machine. The output voltage is fed back by using an isolated voltage sensor. $V_{ref}$ is the value of the arc voltage that is set by users according to the welding parameters between 18 V and 30 V. The look-up table data is calculated offline and every value of power has harmonics data (frequencies, time of harmonics).

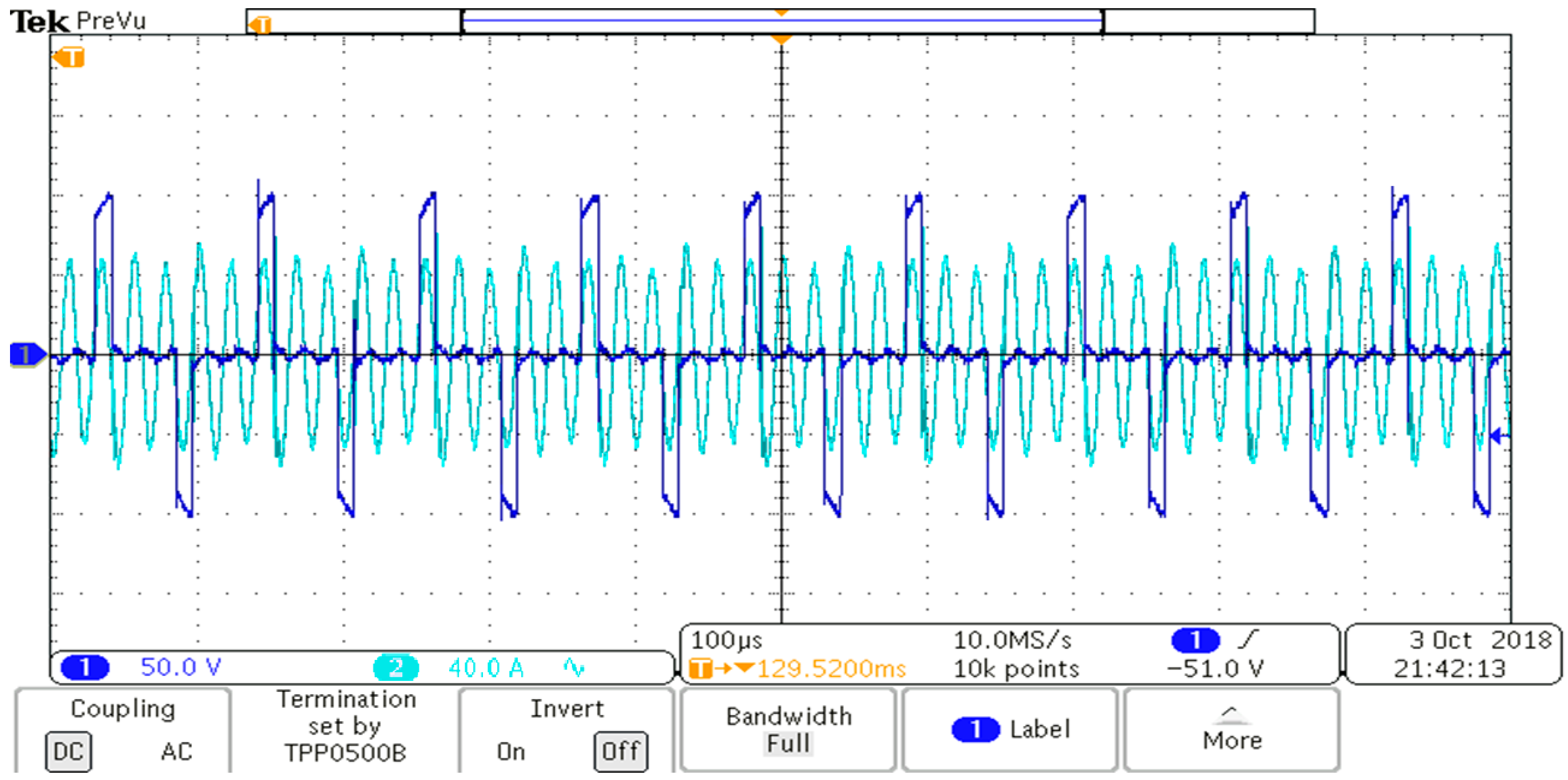
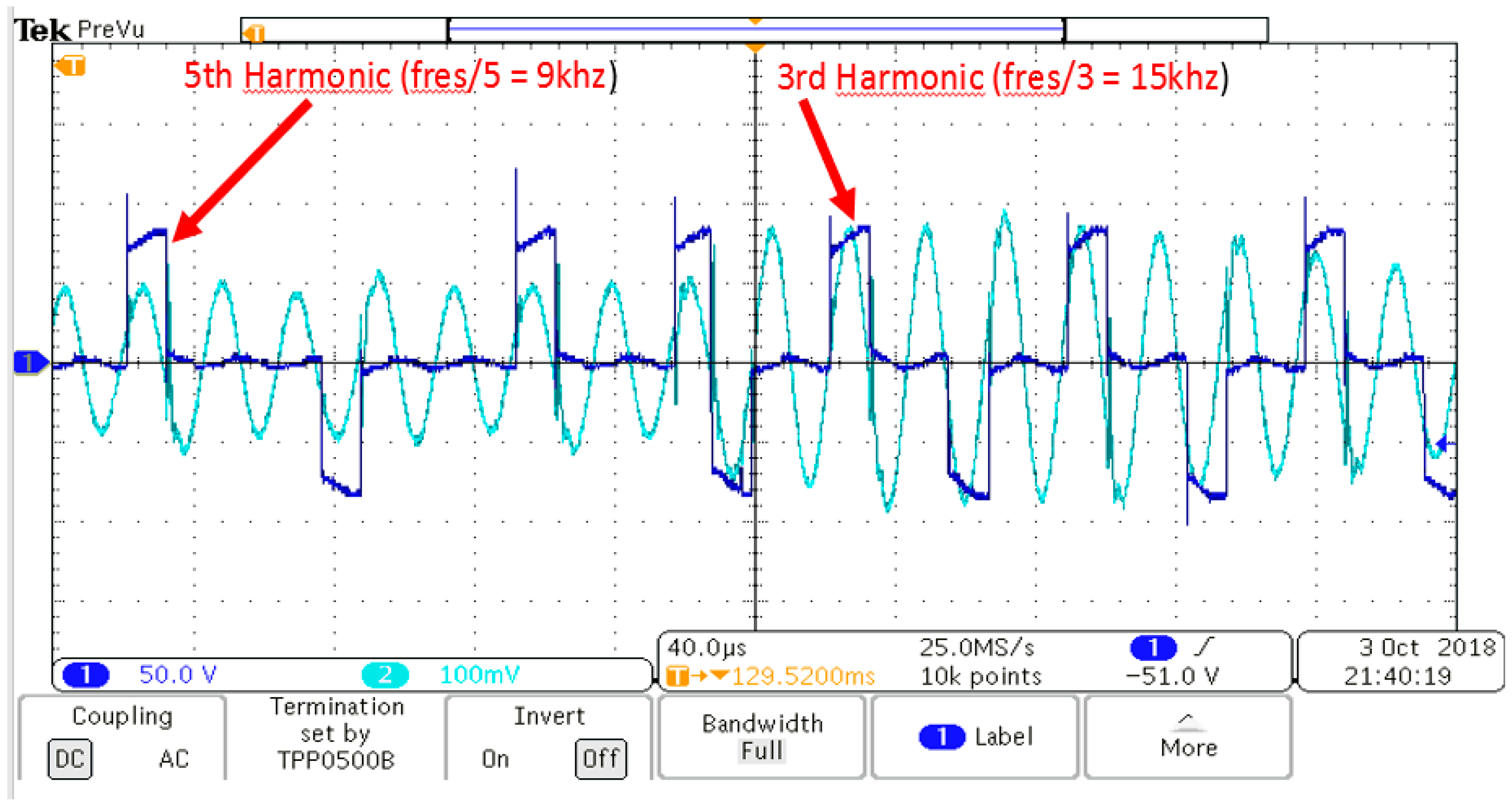
Figure 17 shows the output voltage of the bridge $v_{bri}$ and primary resonant current $i_{pri}$ waveforms when the converter is controlled by the harmonic current at full load. Soft switching is obvious at both turn-ons and turn-offs. The output voltage is constant at 30V ± 1V and the current is around 165 A.

Figure 18 shows the output voltage of the bridge $v_{bri}$ and primary resonant current $i_{pri}$ waveforms at 60% load. Waveforms have the 3rd and 5th harmonics as expected. The power is estimated by the feedback of the current and voltage and the required percentages of each harmonic (switching frequency) for one full period ($T_{\mathrm{p}}$) is determined by using the look-up table.

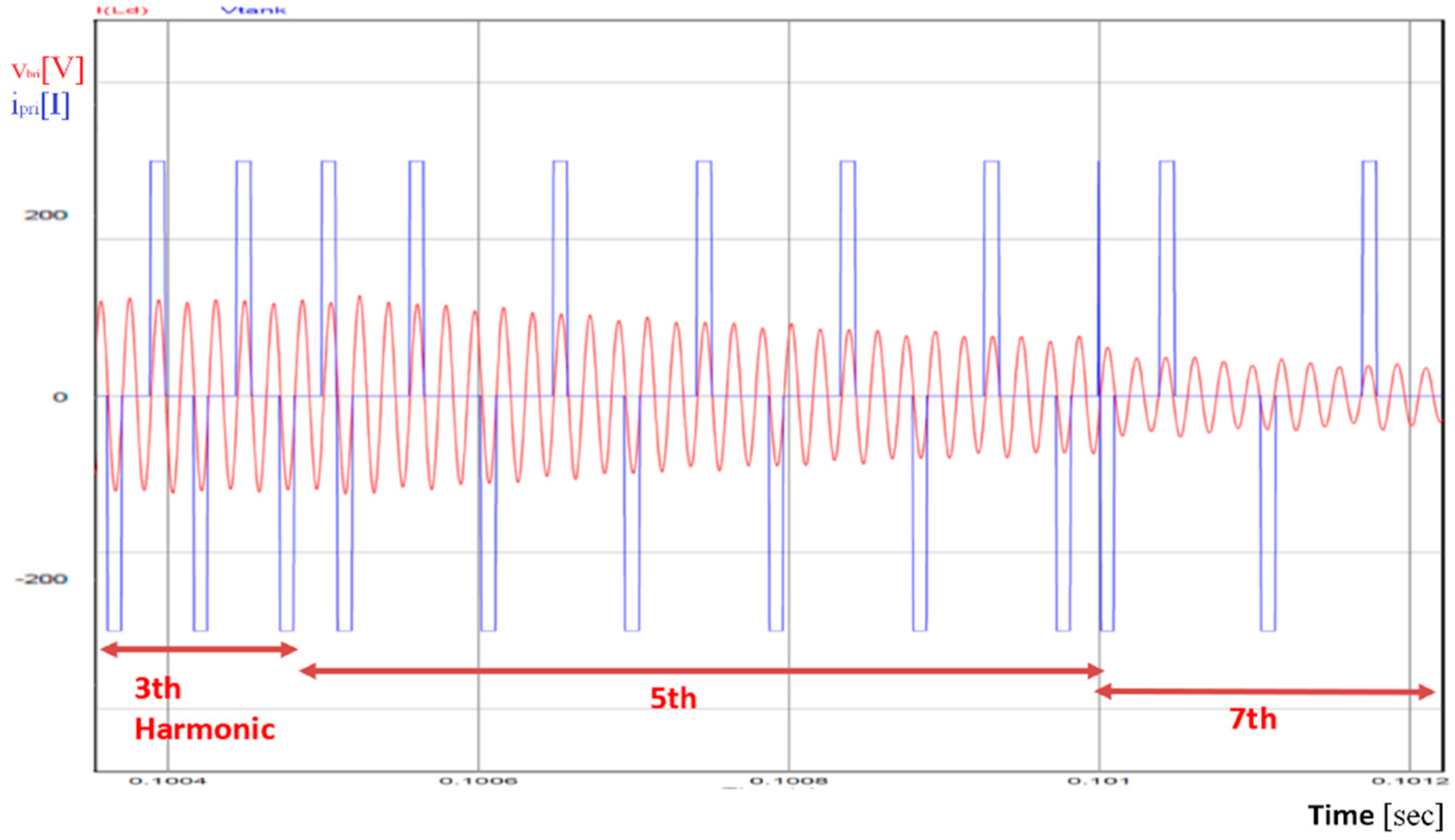
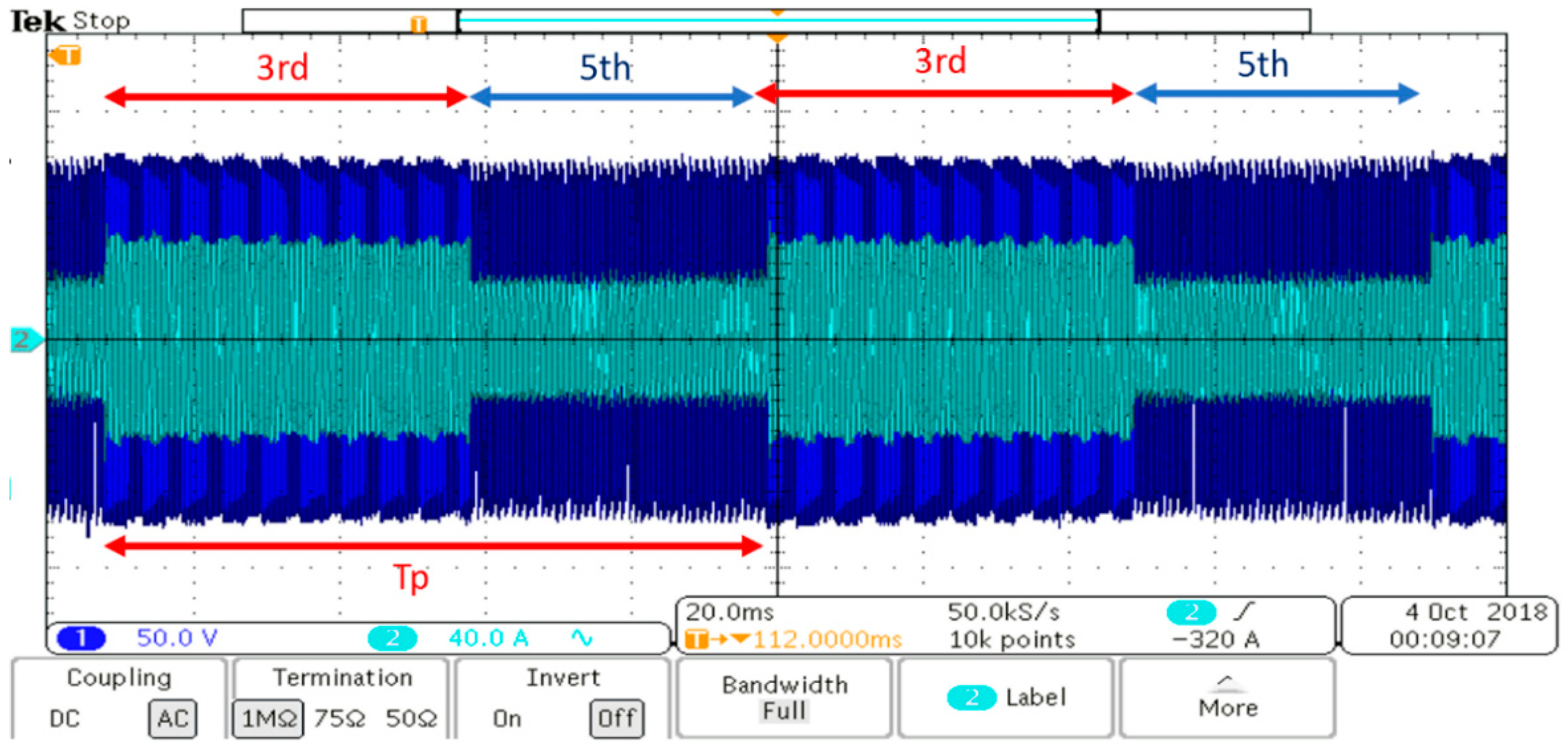
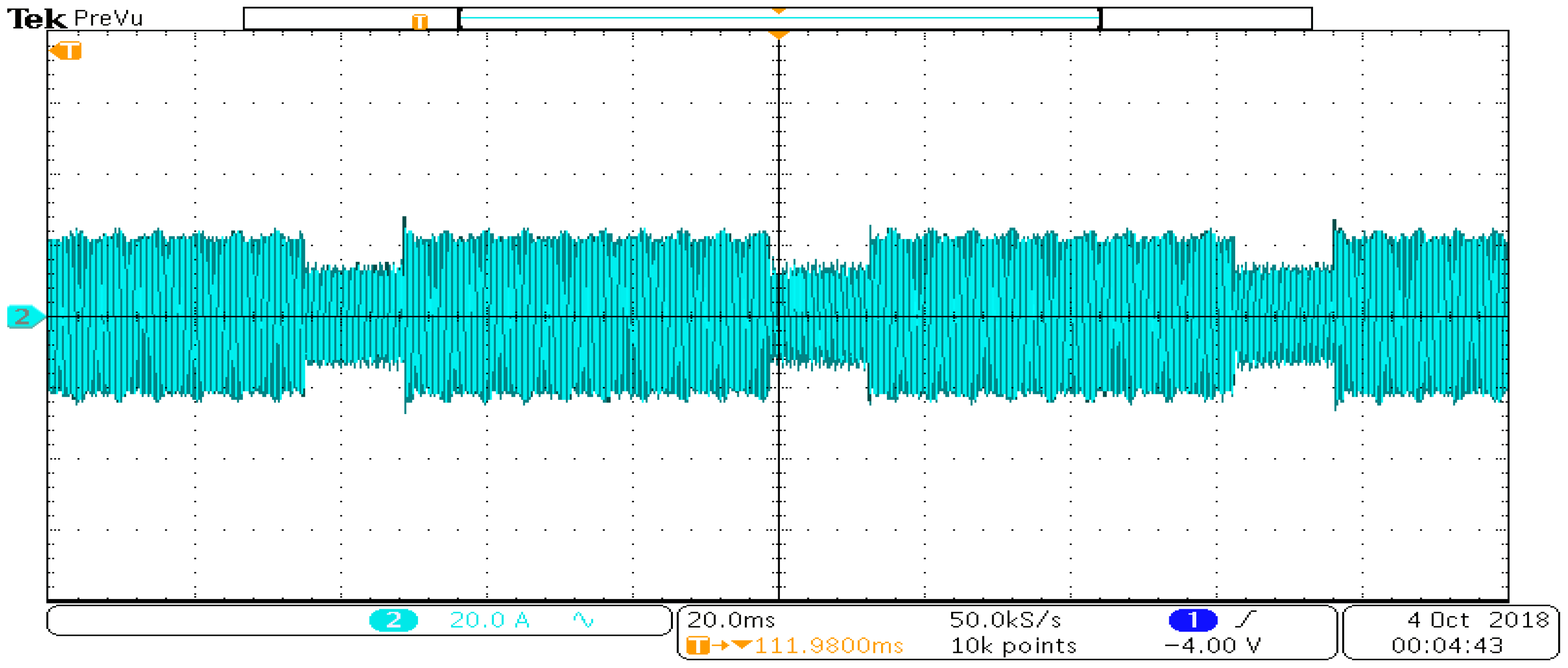
Figure 19 shows operation at 60% load for the full period $(T_p)$ for the waveforms in Figure 18. A combination of the 3rd and 5th harmonics is used to meet this load demand. The percentage of each harmonic changes as the load demand changes. Figure 20 shows the operation at 40% load for which a combination of the 5th and 7th harmonics is used.

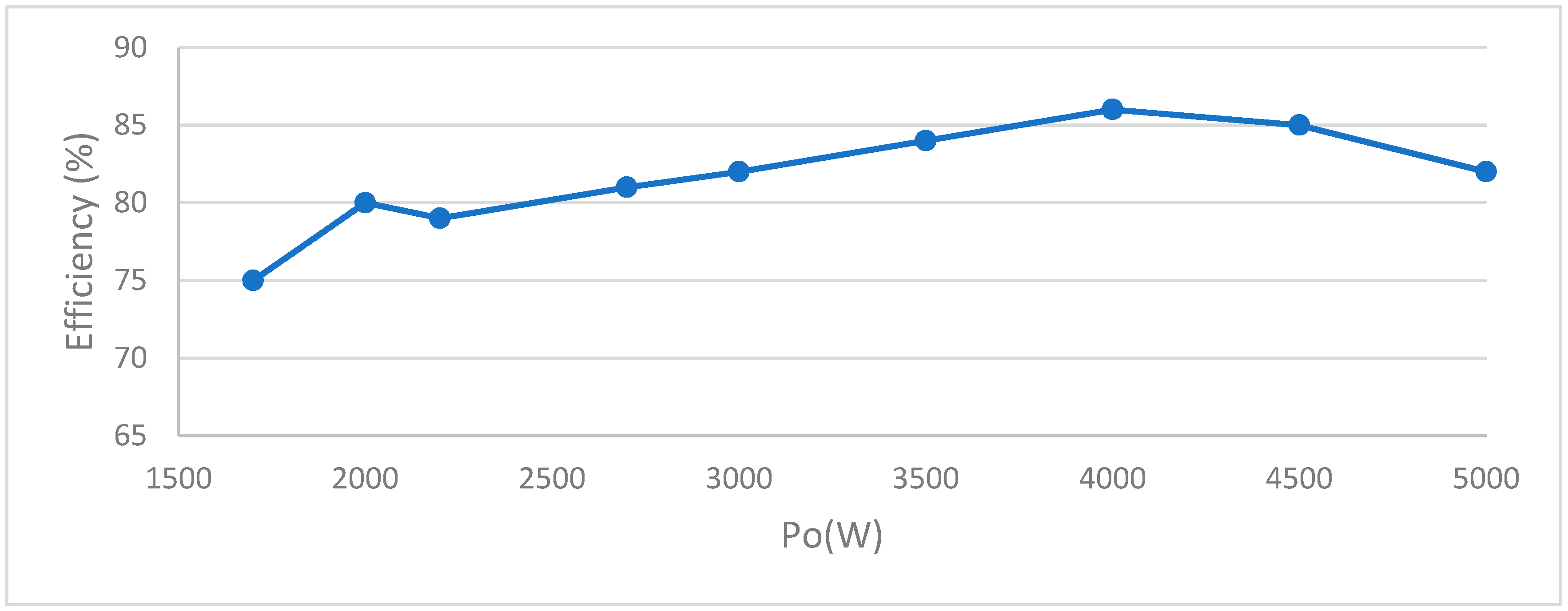
The efficiency of the designed system of the SRC converter welding machine with the proposed control technique was measured practically by a three phase power quality analyzer (Fluke 435) at different values of the output power. The maximum efficiency was obtained at 80% to approximately 86% load as shown in Figure 21.

Table 6. Losses cause by system at 86% efficiency.

Element Name	Calculated Loss Value (W)	Measured Loss Value (W)
Transformer and inductor losses	70	153
IGBTs losses	71.5	118
Primary diodes (3 phase rectifier)	30	25
Secondary diodes	223	254

shows the measured losses as well as the calculated ones. For welding machine efficiencies, around 80% is acceptable in industry applications [21,22].

Compared to the constant switching frequency of hard switched cases, the advantages of this technique come from two different areas: (a) soft switching at both turn-on and turn-off, and (b) reduced core losses at light load as the switching frequency has to be reduced. However, the efficiency can be improved further by optimizing the remaining system, especially the transformer. Thermal losses especially at parts that handle high current like secondary diodes need to be handled better. Since this paper focuses on the control technique, the system was not optimized yet.

8. Conclusions

GMAW welding machines are very commonly used in industry. Reducing the size and weight of these machines requires high switching frequencies. However, the switching frequency is limited by the losses of the devices used in the inverter. This paper proposes a control algorithm that can be used in GMAW machines along with series resonance converters. The technique takes advantage of the band-pass filter-like nature of the converter and uses switching frequencies that are 1/3rd, 1/5th, 1/7th, etc., of the resonance frequency. The switching frequency varies between these discrete values to meet the load demand.