Multi-Sensor Optimization Scheduling for Target Tracking Based on PCRLB and a Novel Intercept Probability Factor
Abstract
1. Introduction
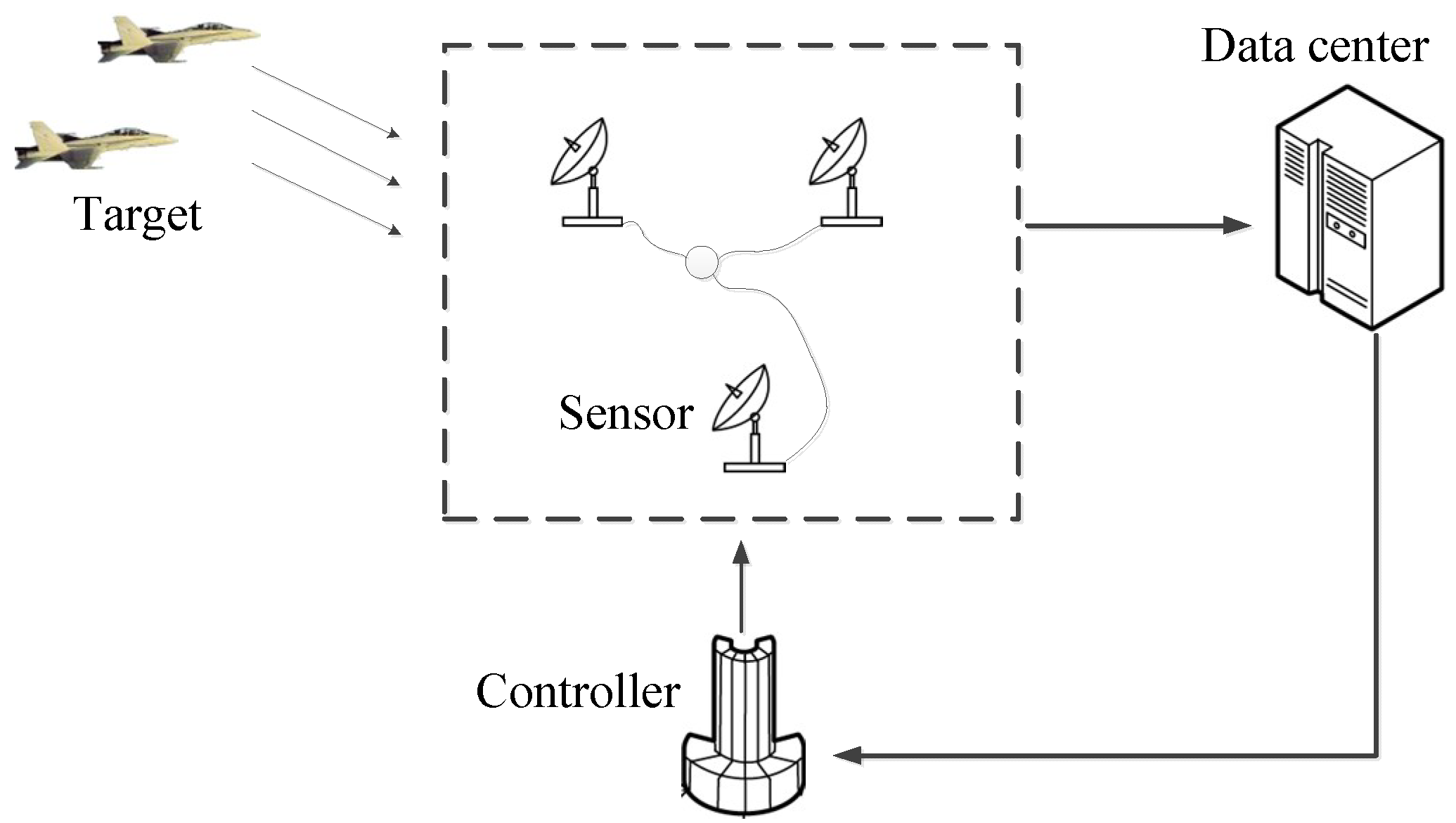
2. Problem Formulation
2.1. Target Tracking Model
2.2. PCRLB of Target State
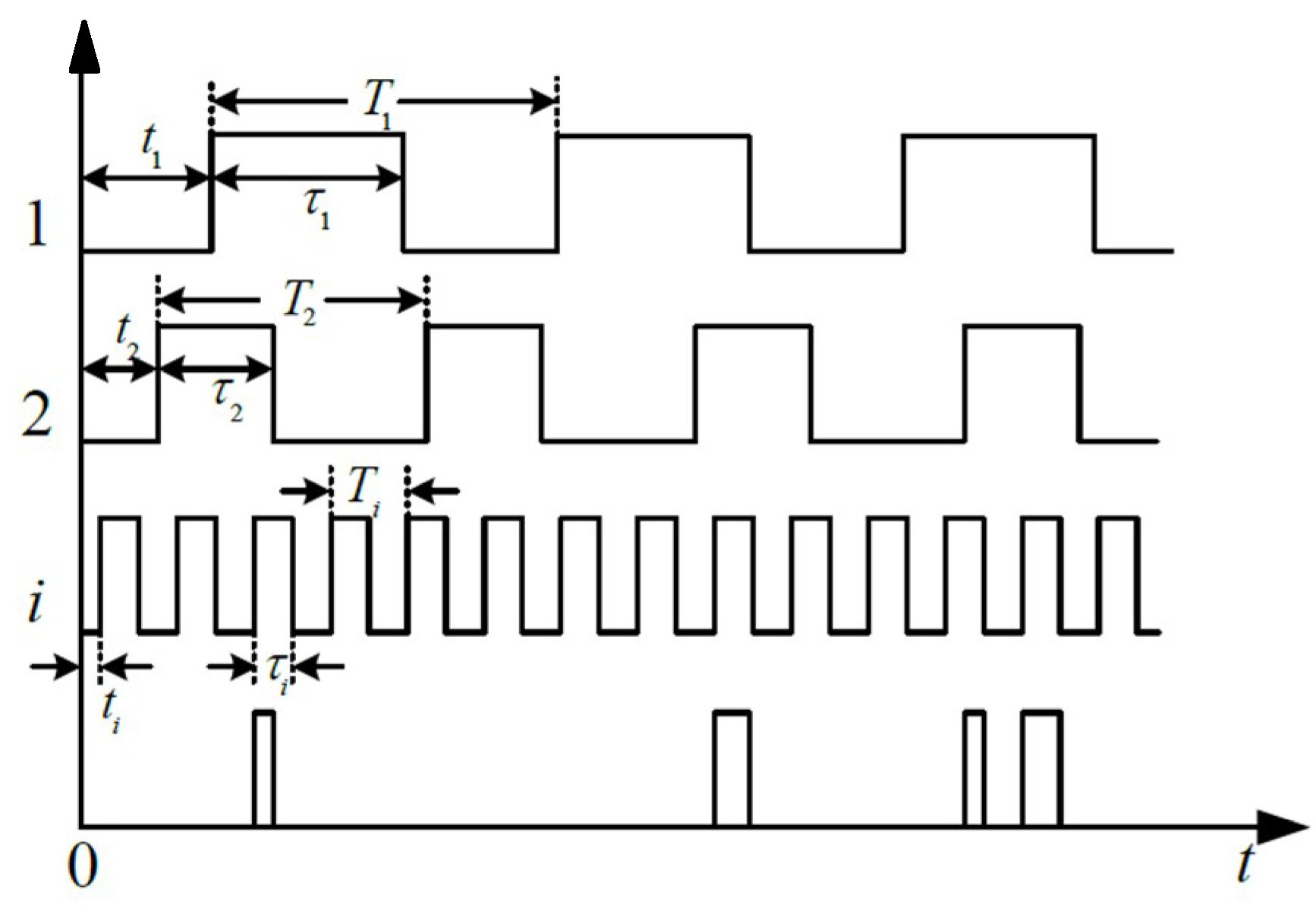
3. Novel Intercept Probability Factor
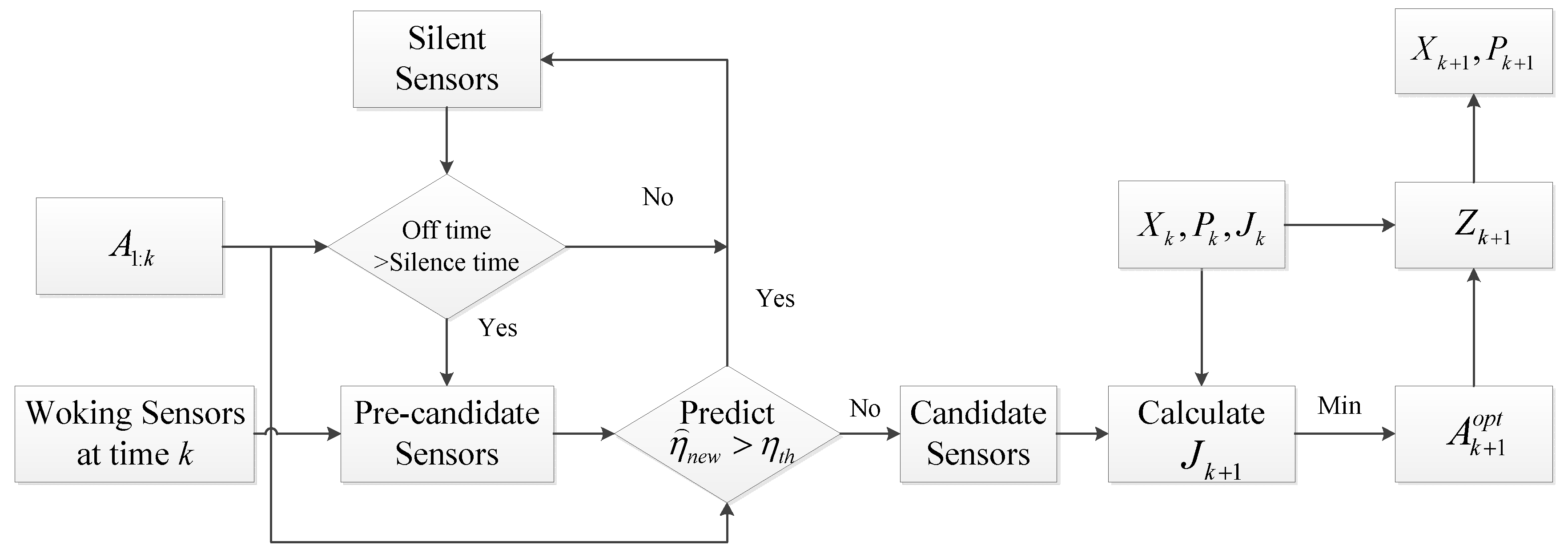
4. Multi-Sensor Scheduling Model
| Algorithm 1 Multi-sensor scheduling algorithm |
| Input: target state , sensor scheduling actions Output: sensor scheduling actions |
| Determine whether the silent sensors have reached the silence time For (sensor in silent group) If (off-time> silence time) silent sensors start work else silent sensors keep silence End End Predict the IPF of sensors which do not keep silence For (sensor which don’t keep silence) IF (Predictive IPF > ) Sensor will be not selected and turn to silence End End Select the sensor-target combination which has the smallest PCRLB Use particle swarm optimization (PSO) algorithm to search the optimal scheduling actions Output sensor scheduling actions |
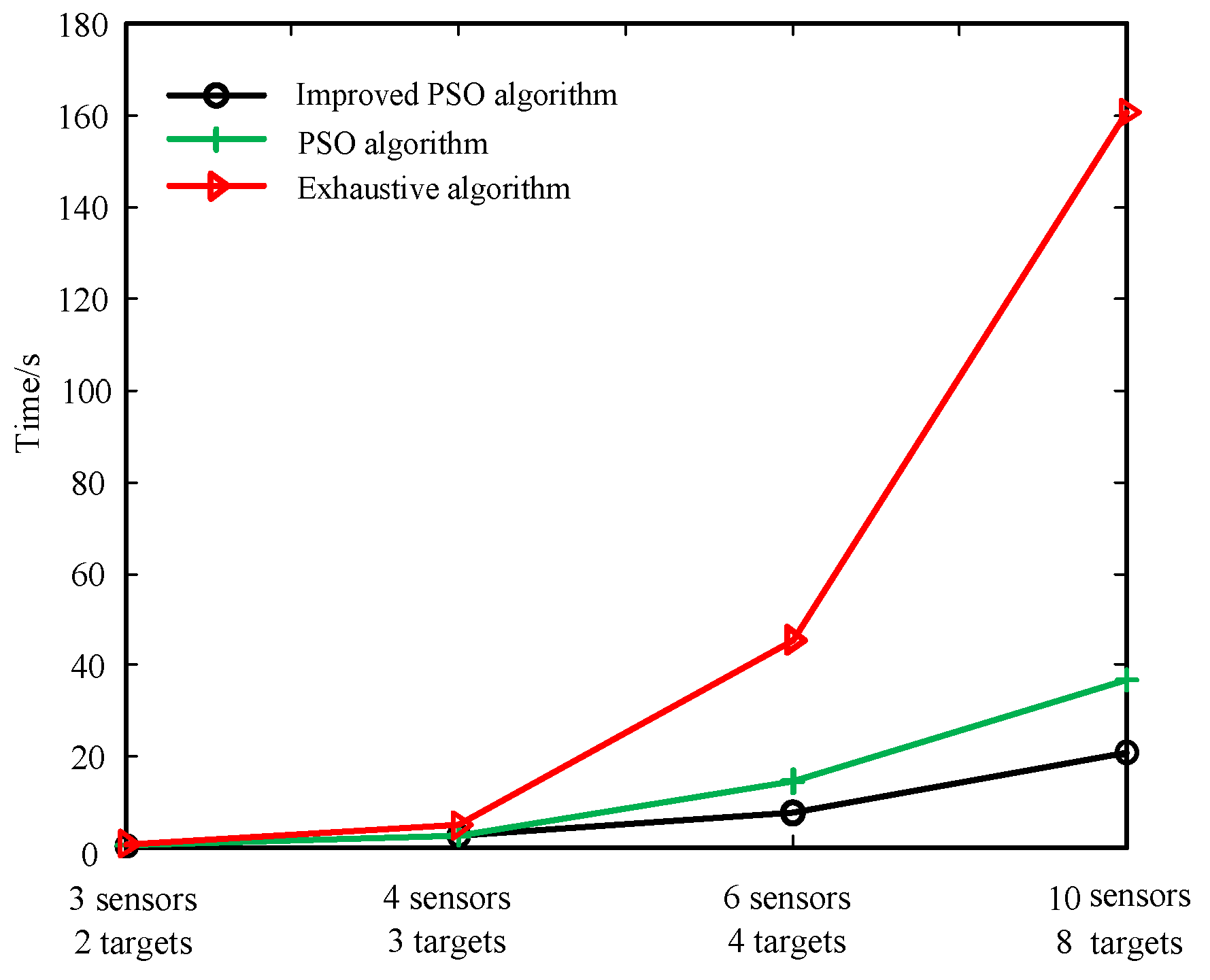
5. Solution Algorithm of Multi-Sensor Scheduling Problem
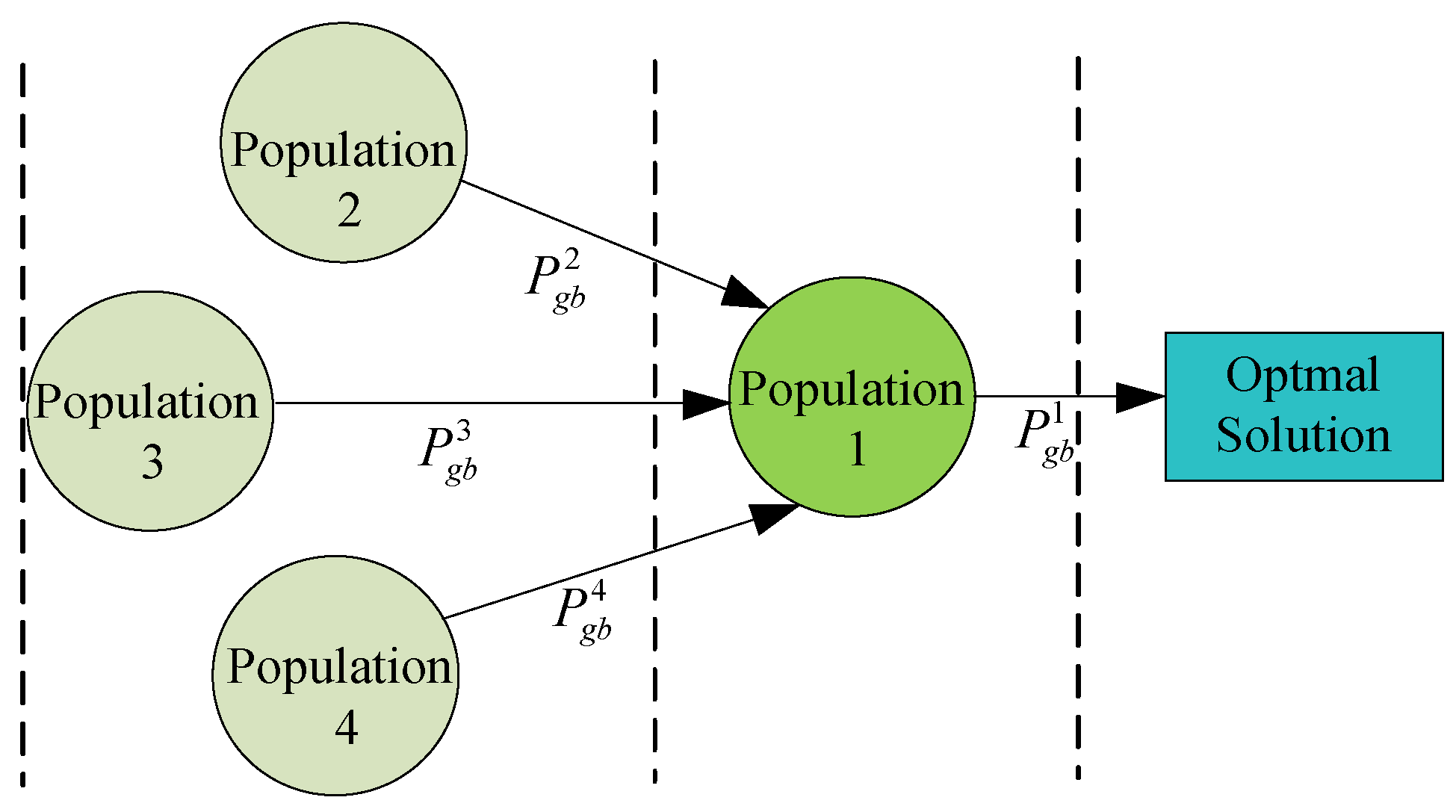
5.1. Solution Algorithm Based on Improved PSO Algorithm
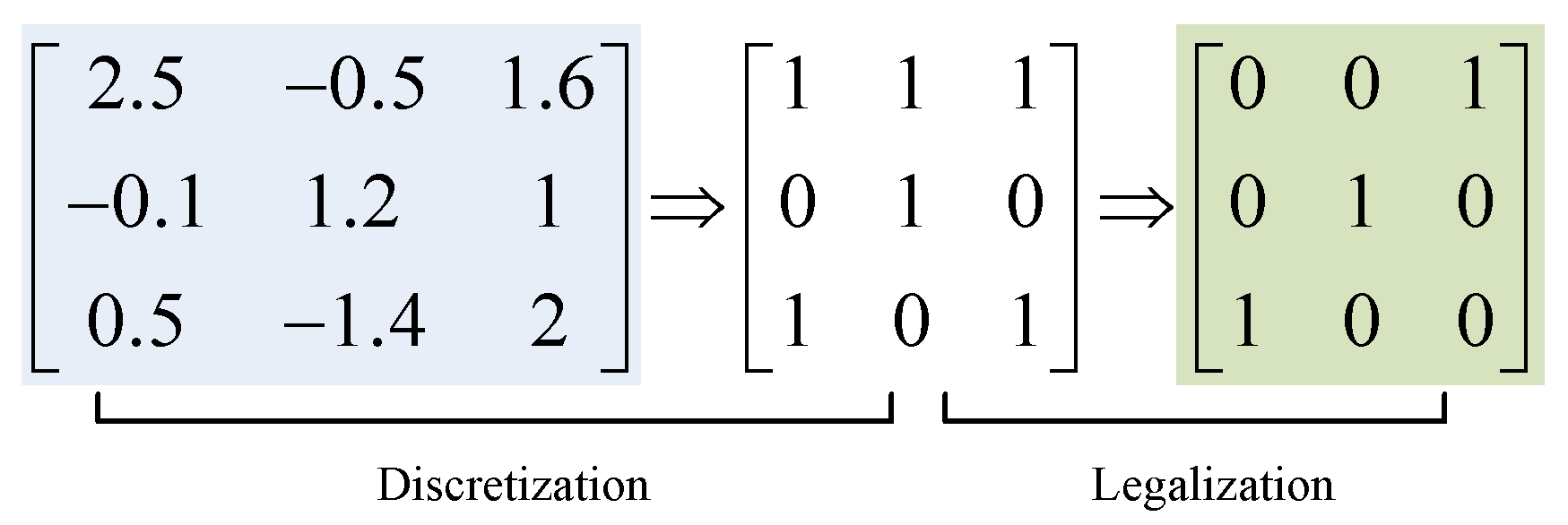
5.2. Particle Encoding in Improved PSO Algorithm
| Algorithm 2 Multi-sensor scheduling algorithm |
| Input: illegal Output: legal |
| For (each column of ) Sort elements in each column of the scheduling actions matrix from great to small. Select the previous elements and then change the element value to 1 Change the rest elements value to 0 End For (each row of ) Calculate the number of the elements whose value is 1 in each row If ( > ) Randomly select elements and then change the element value from 1 to 0 End End Output legal scheduling actions matrix |
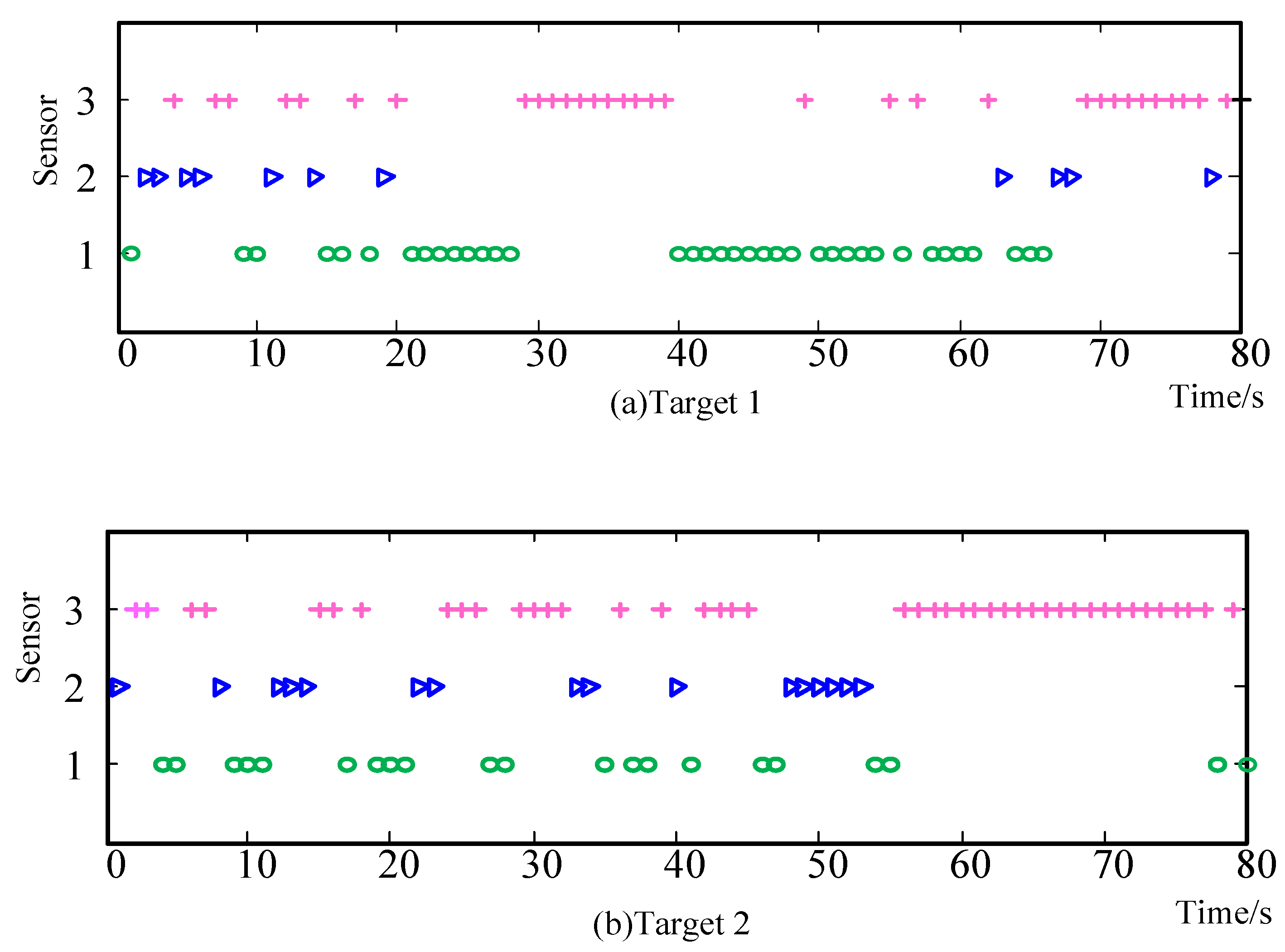
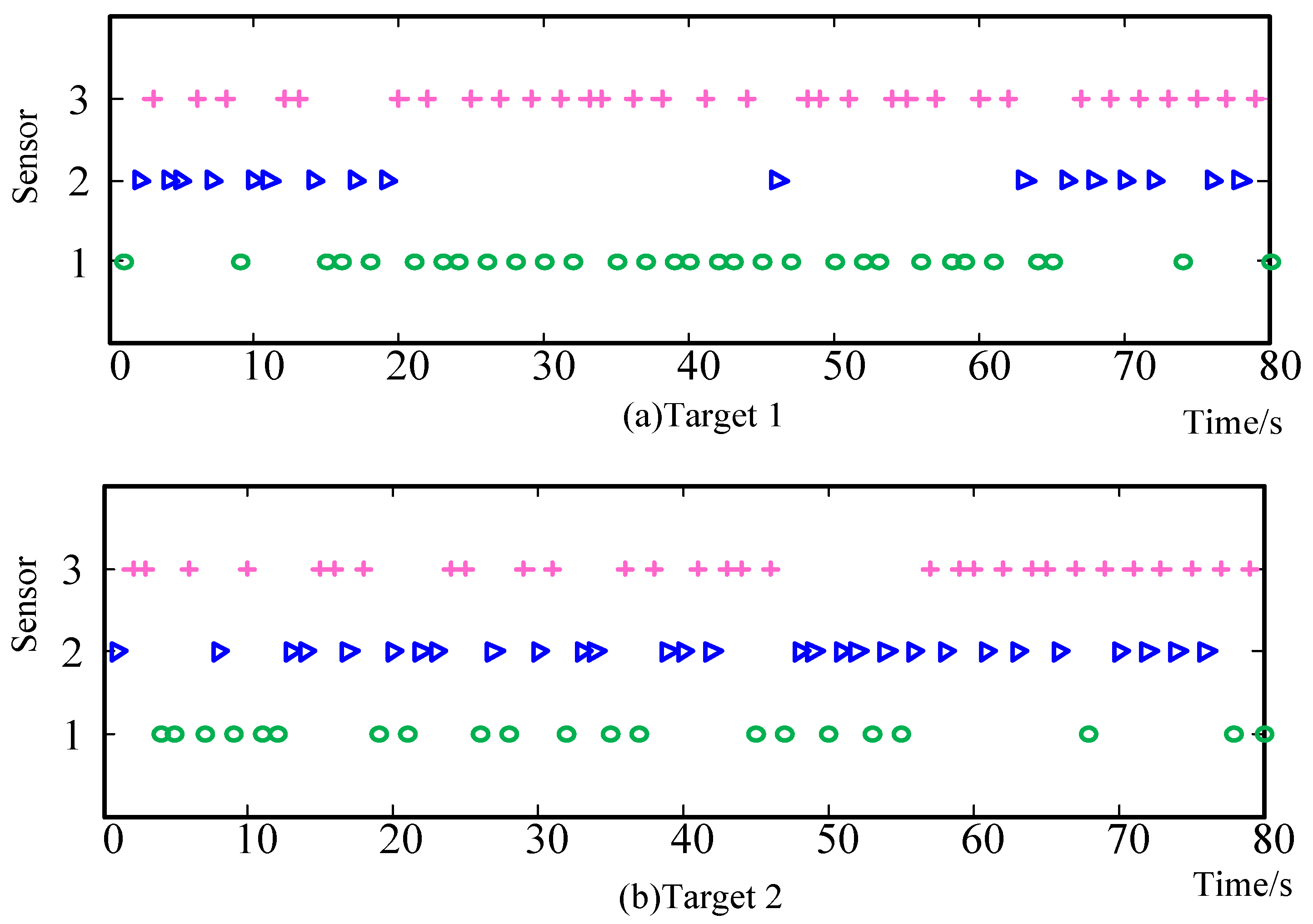
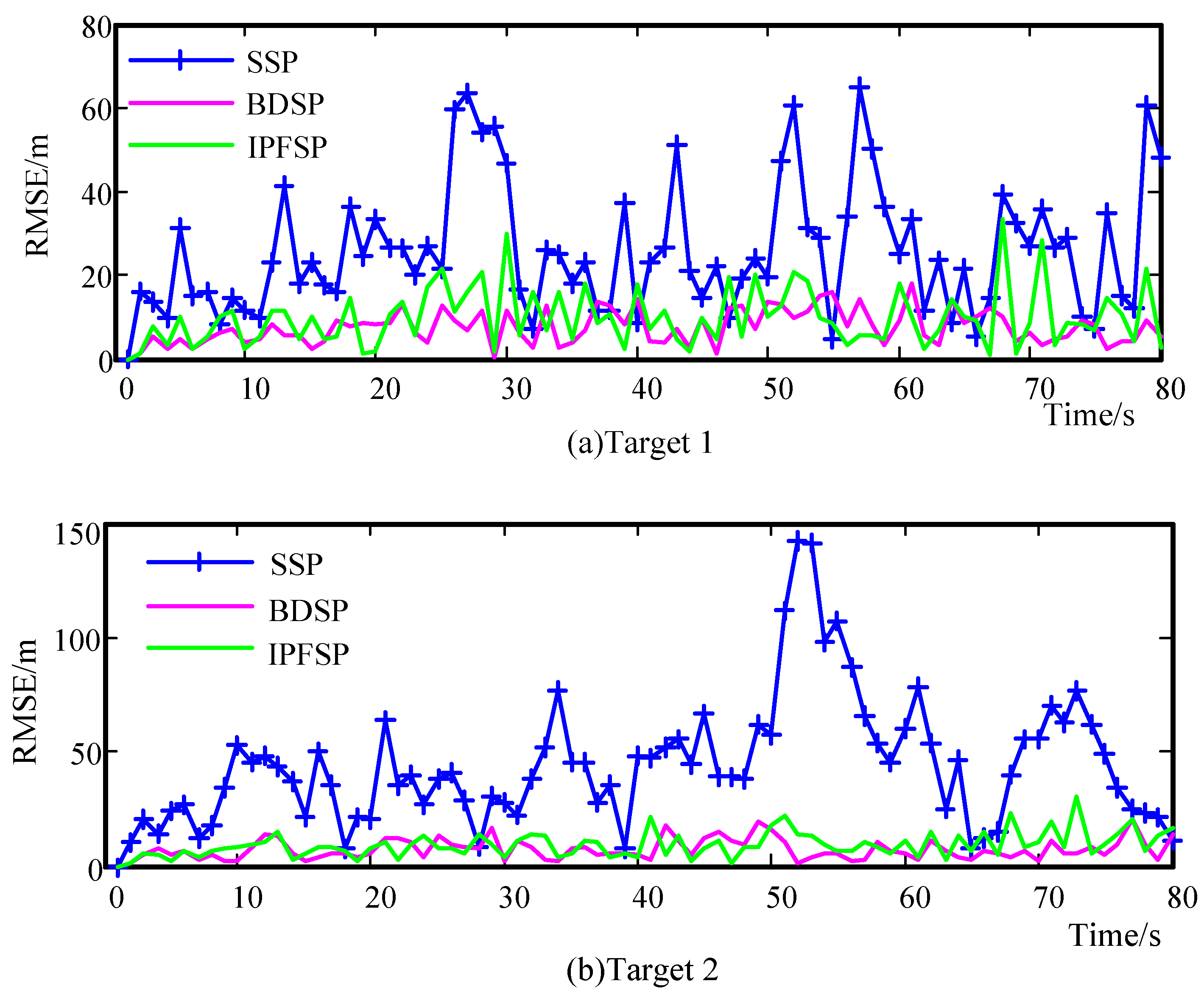
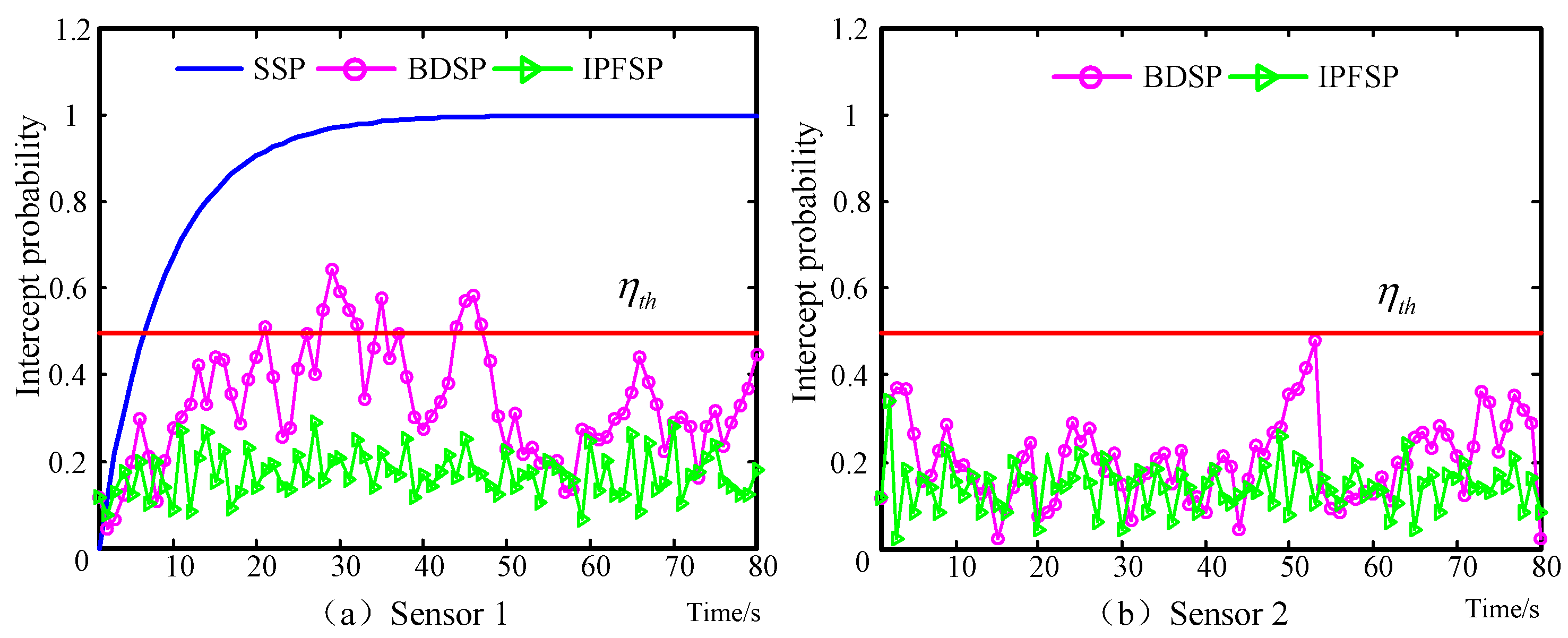
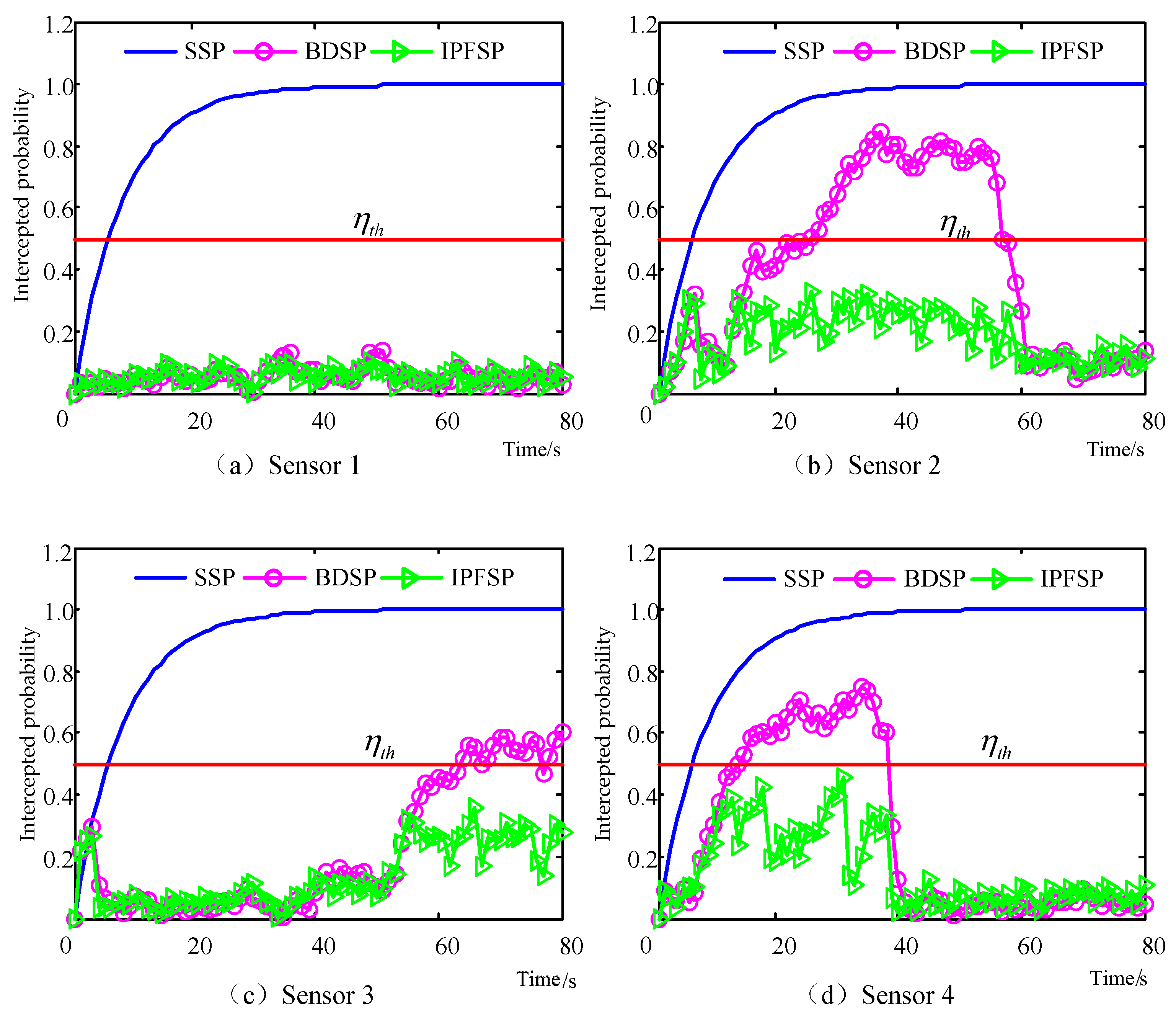
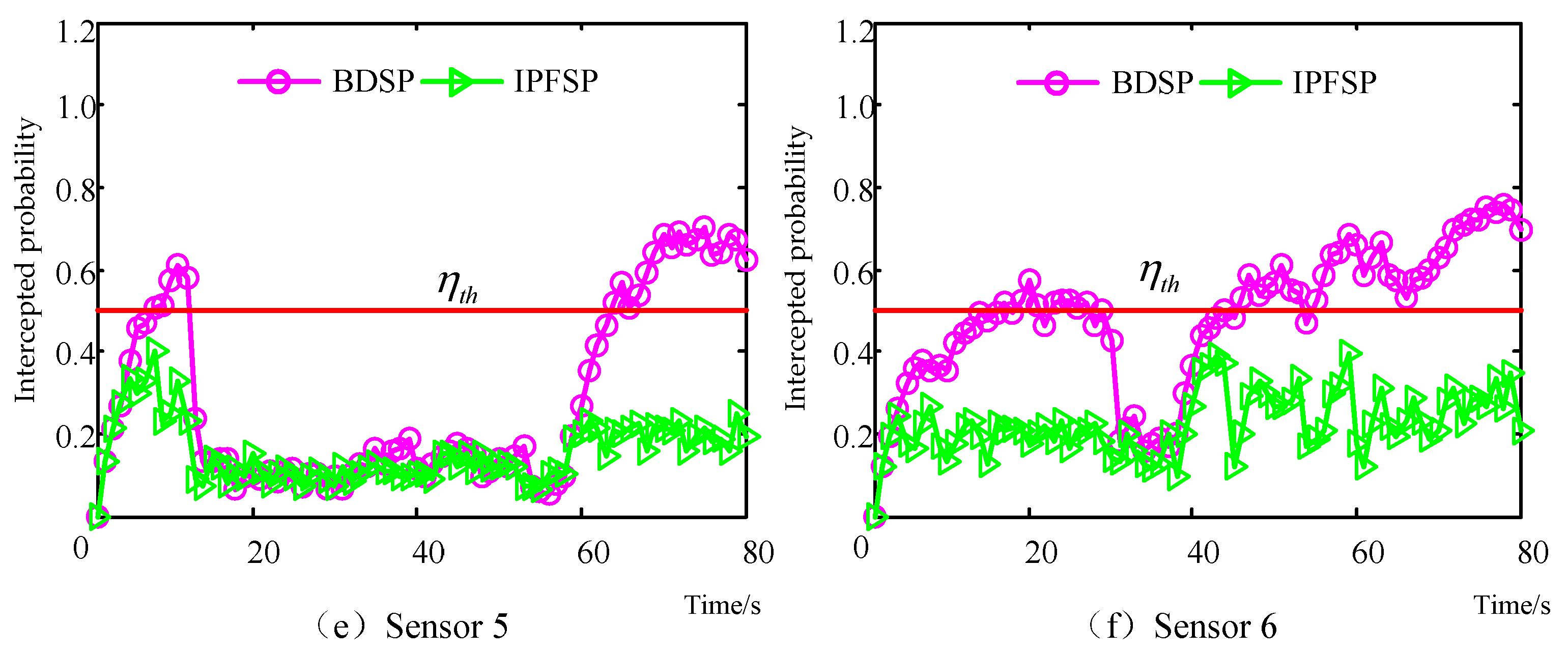
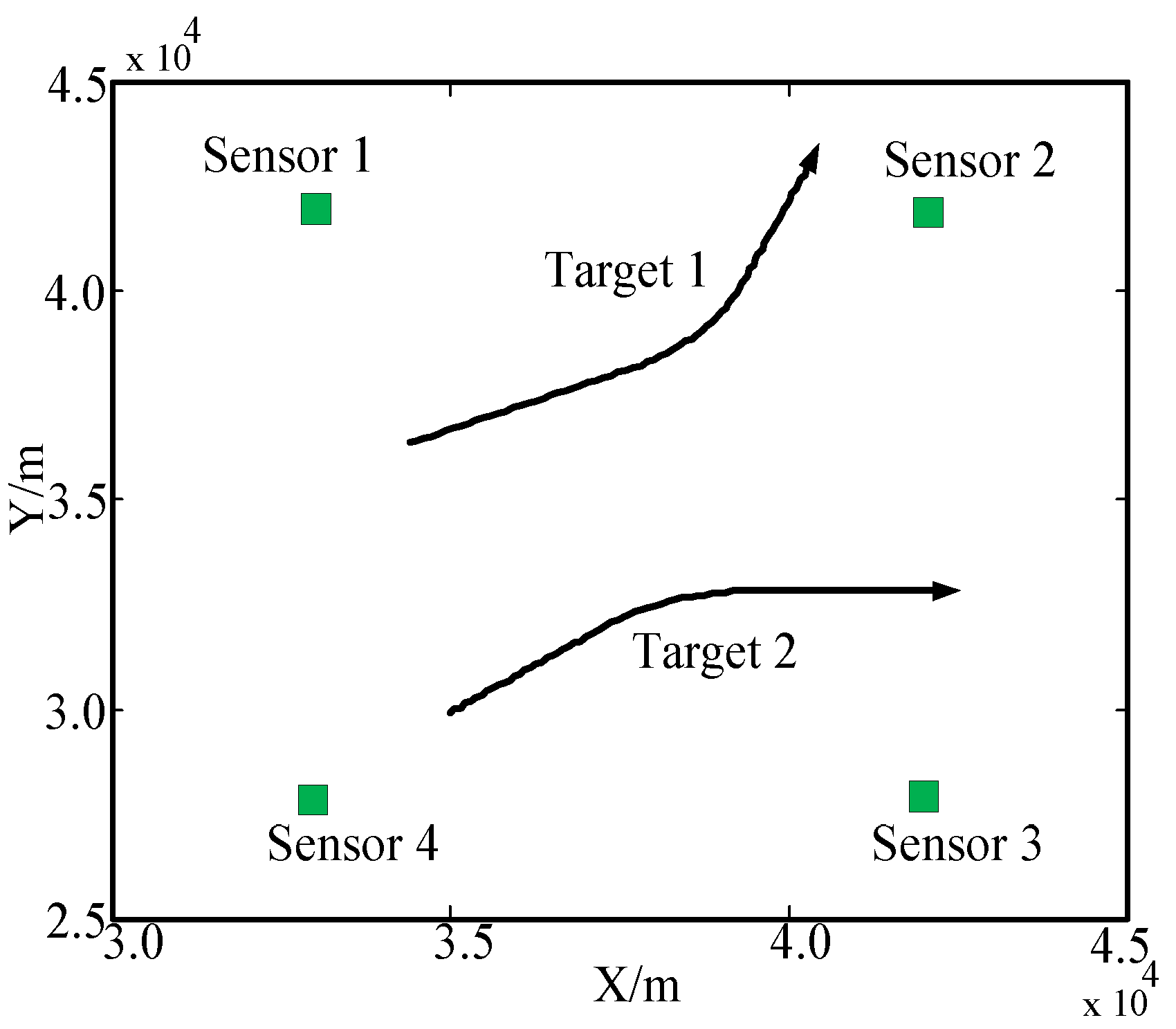
6. Simulations
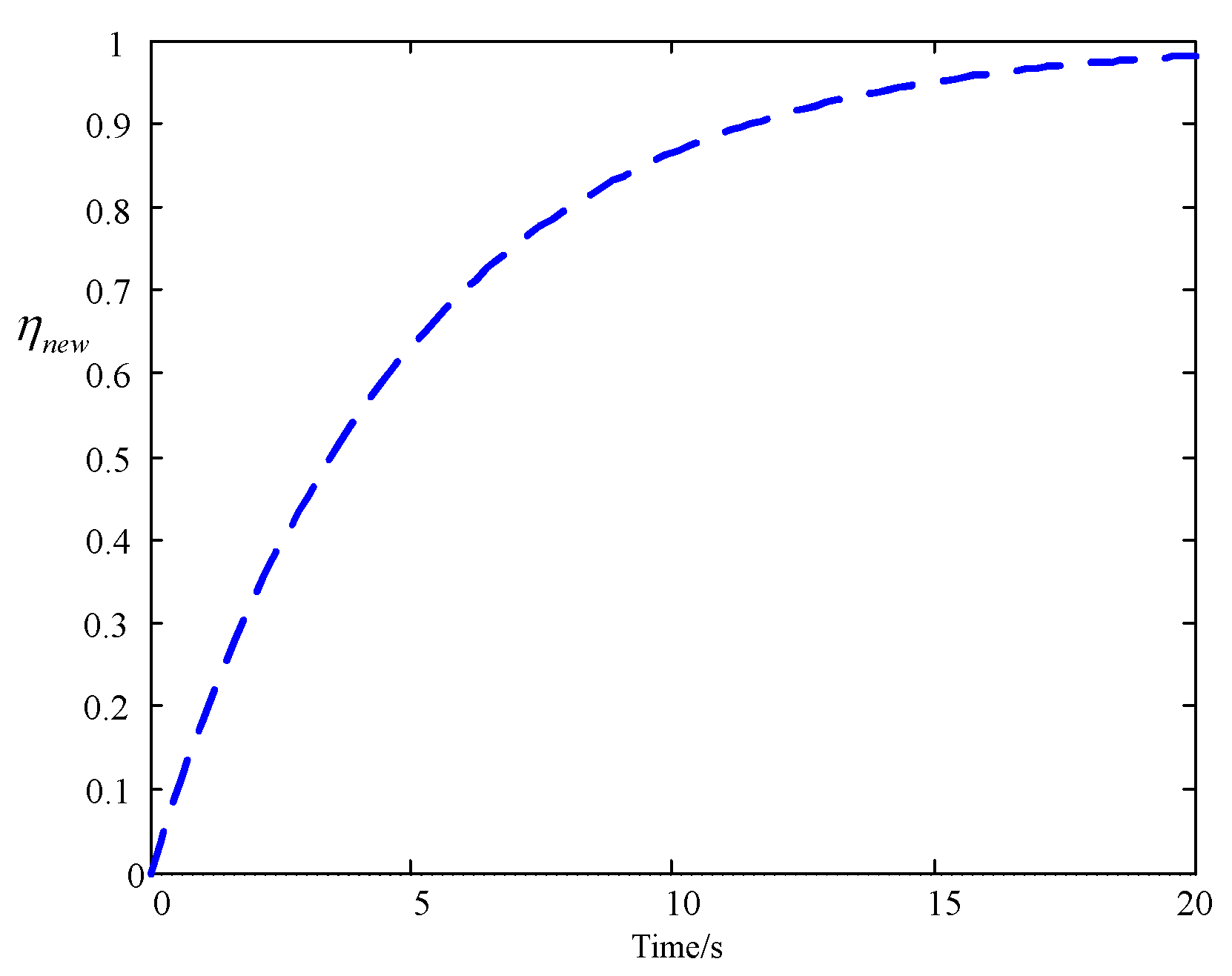
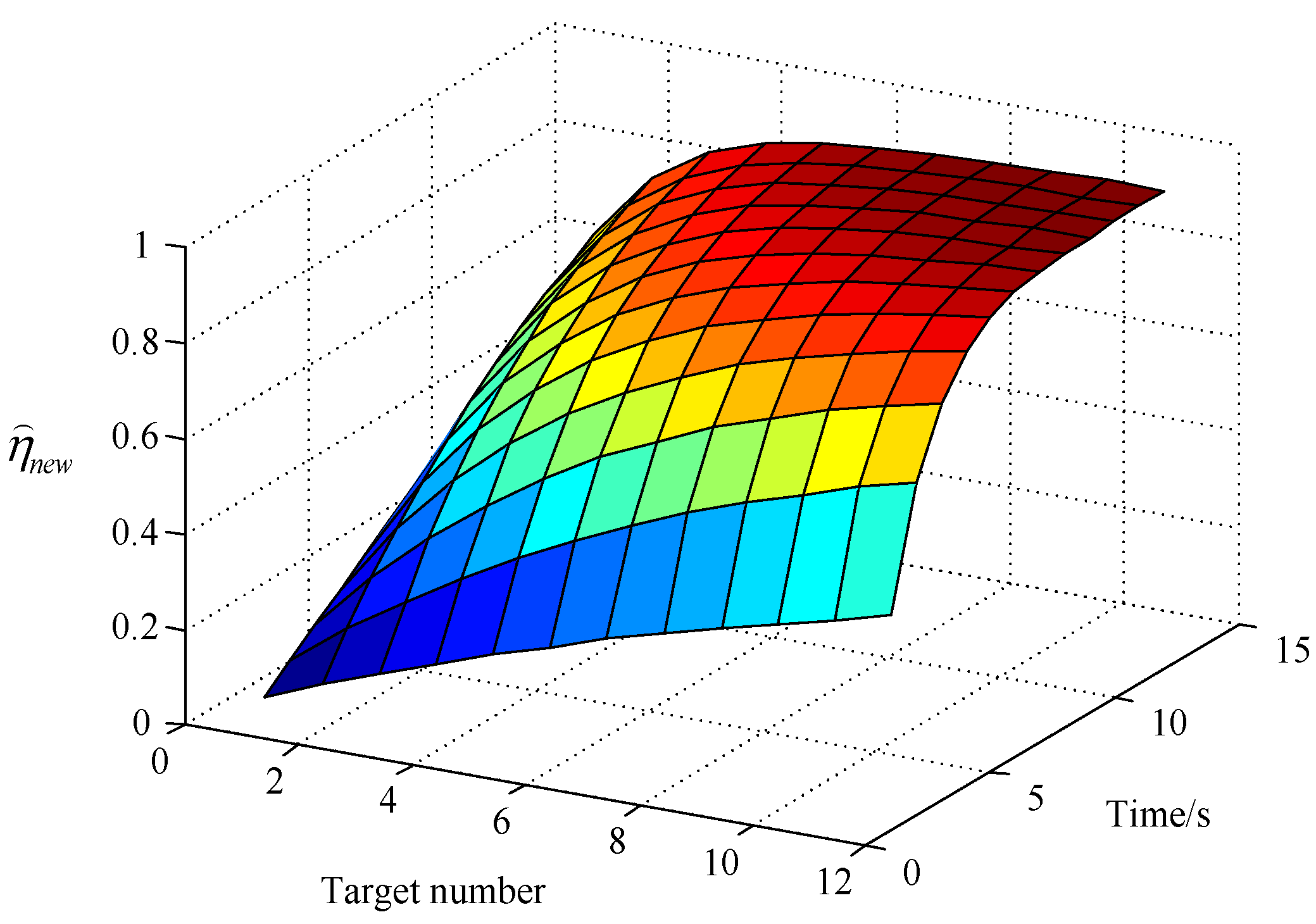
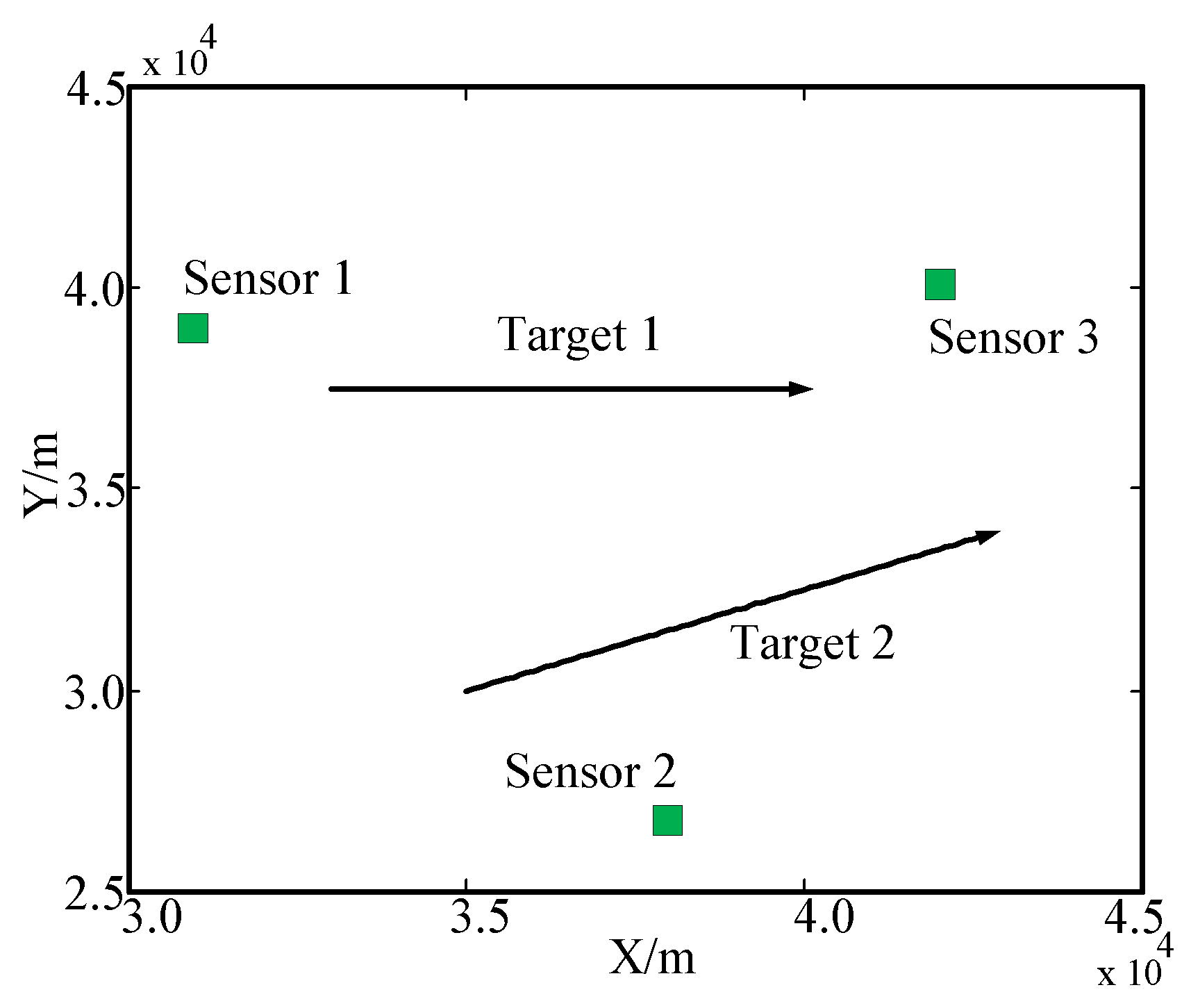
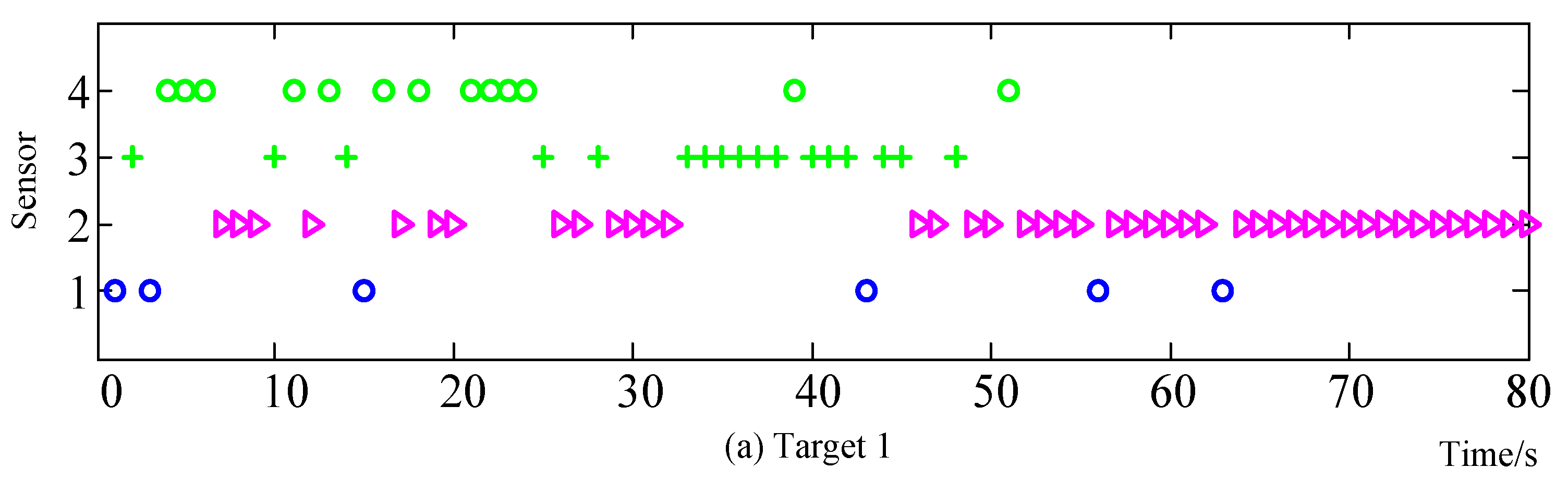
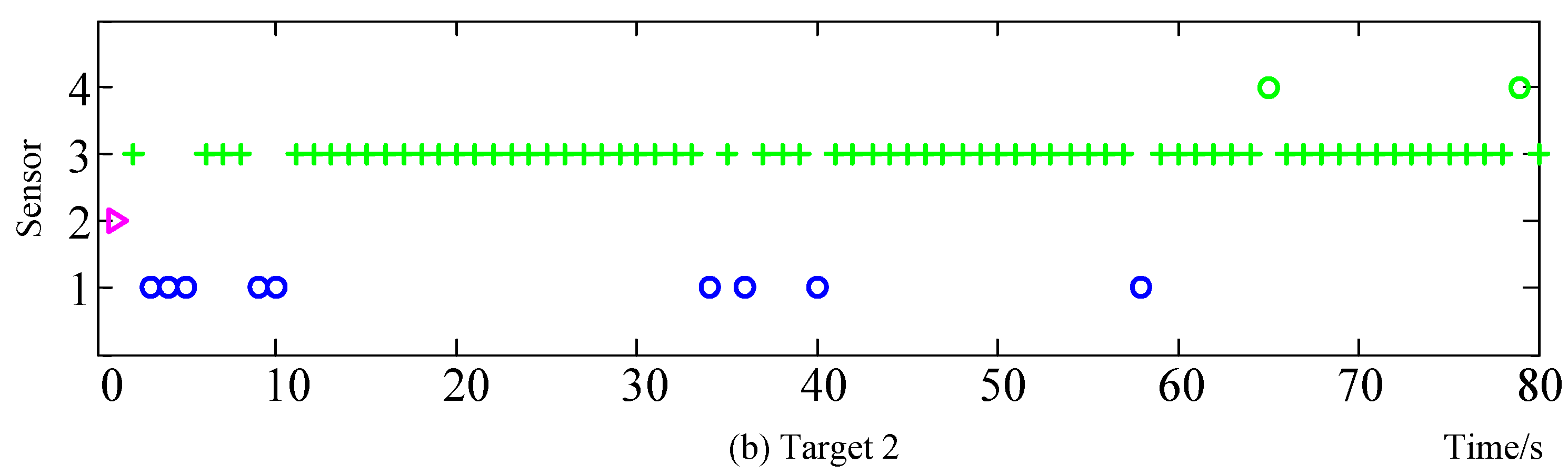
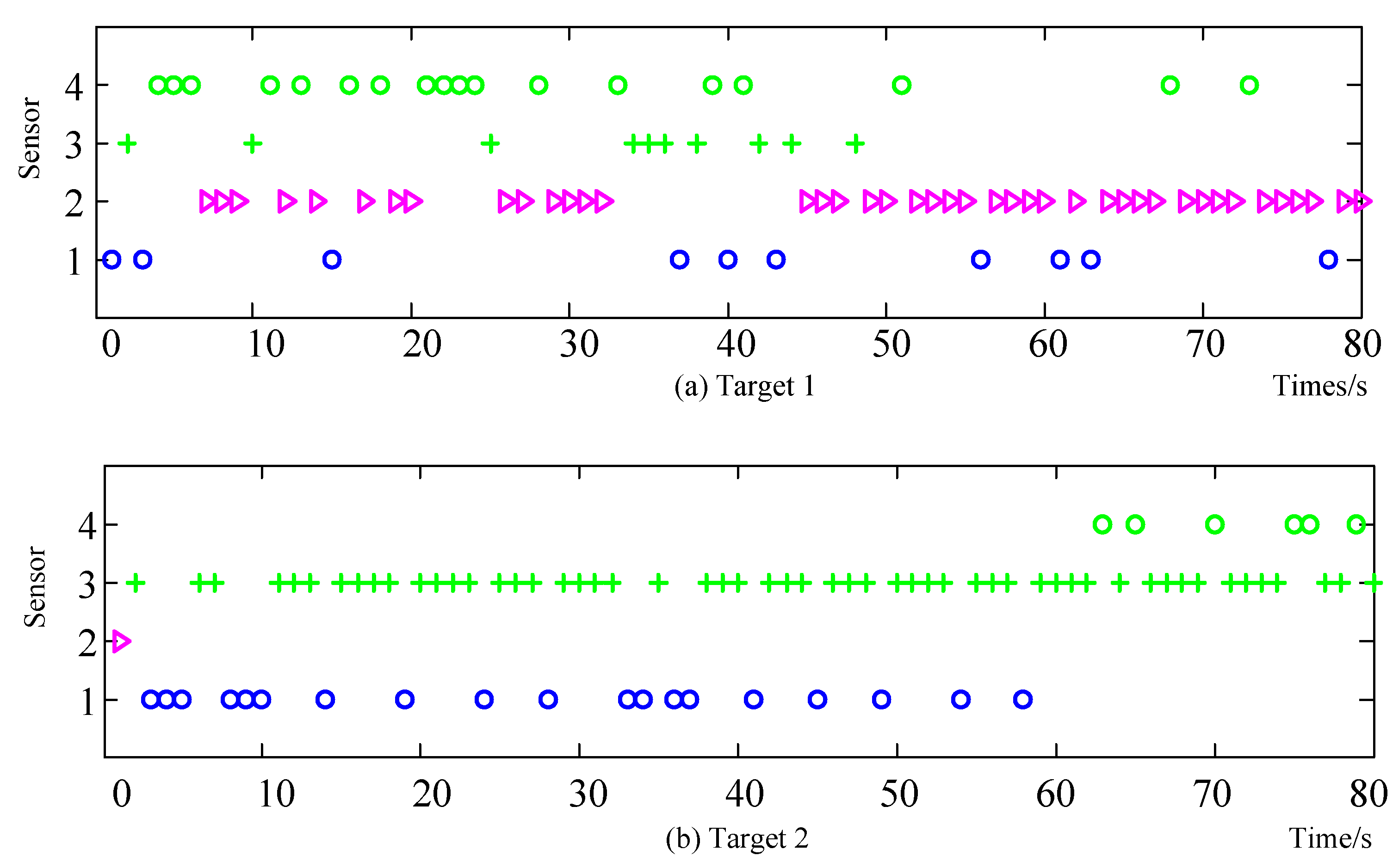
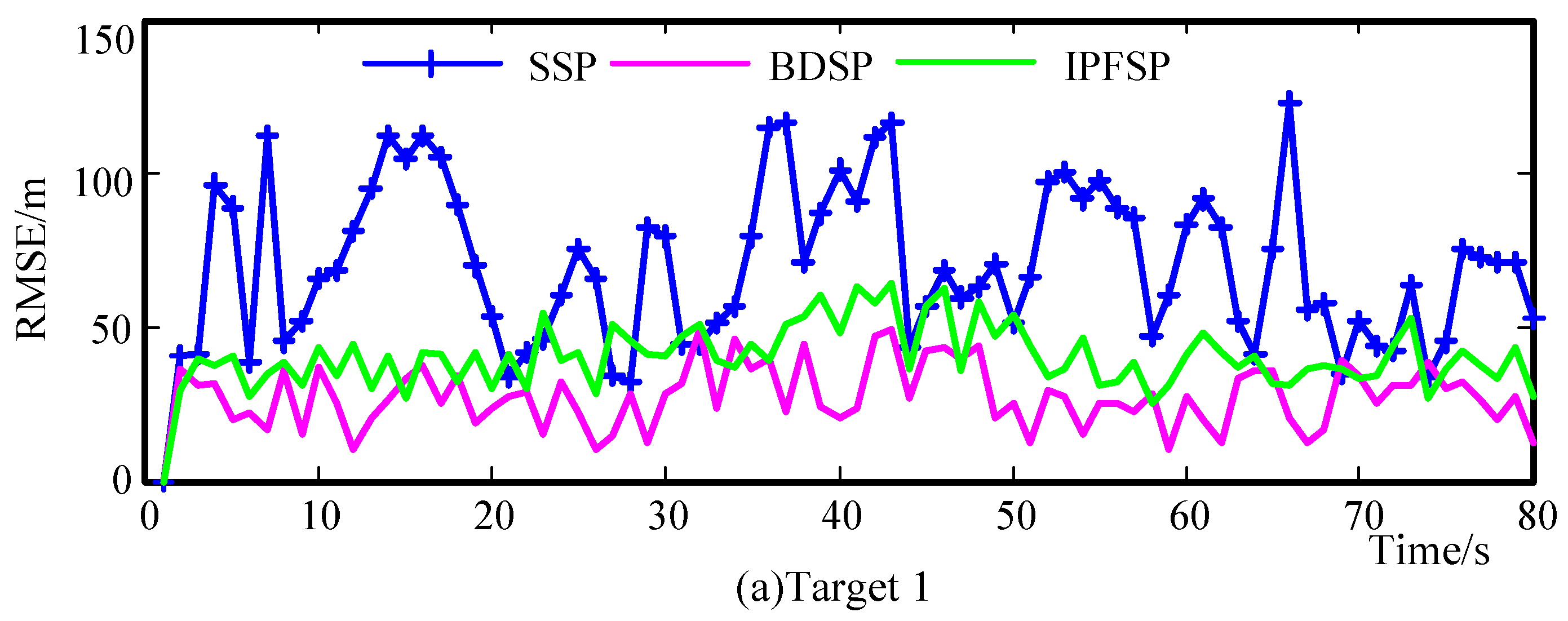
6.1. Scenario 1
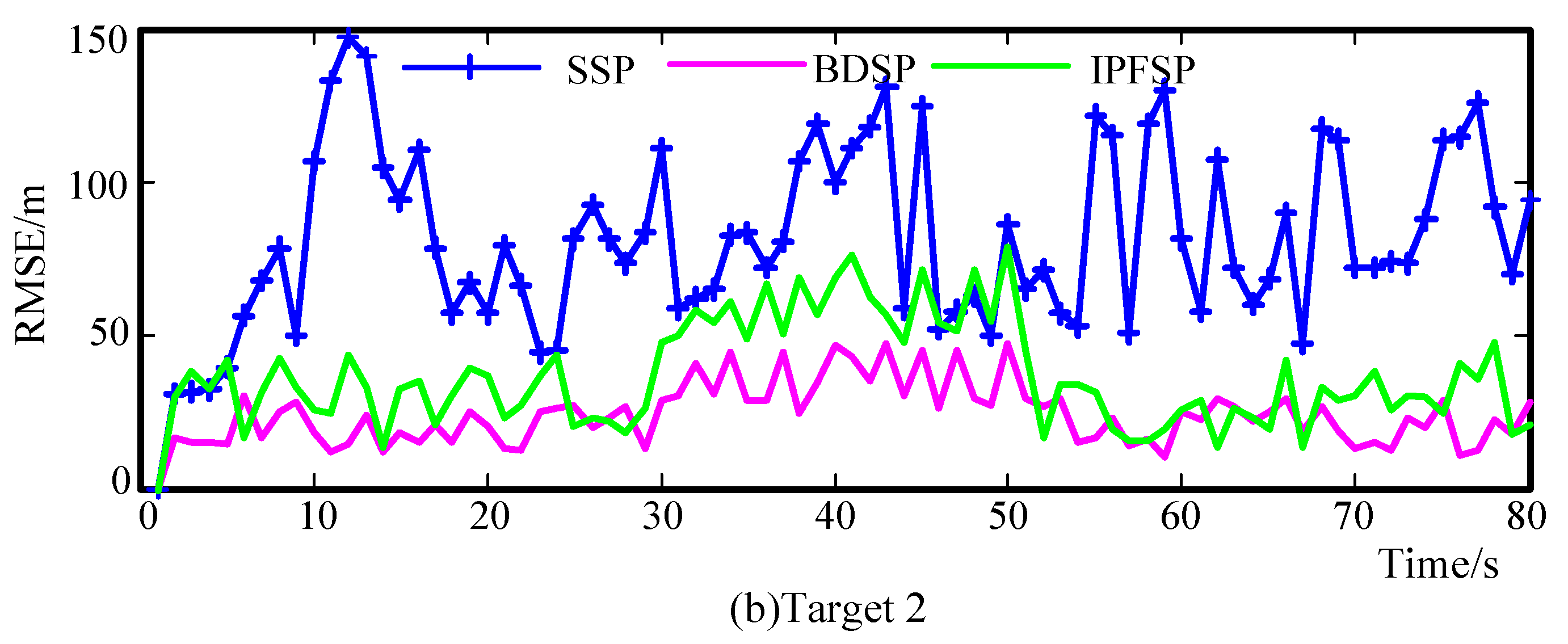
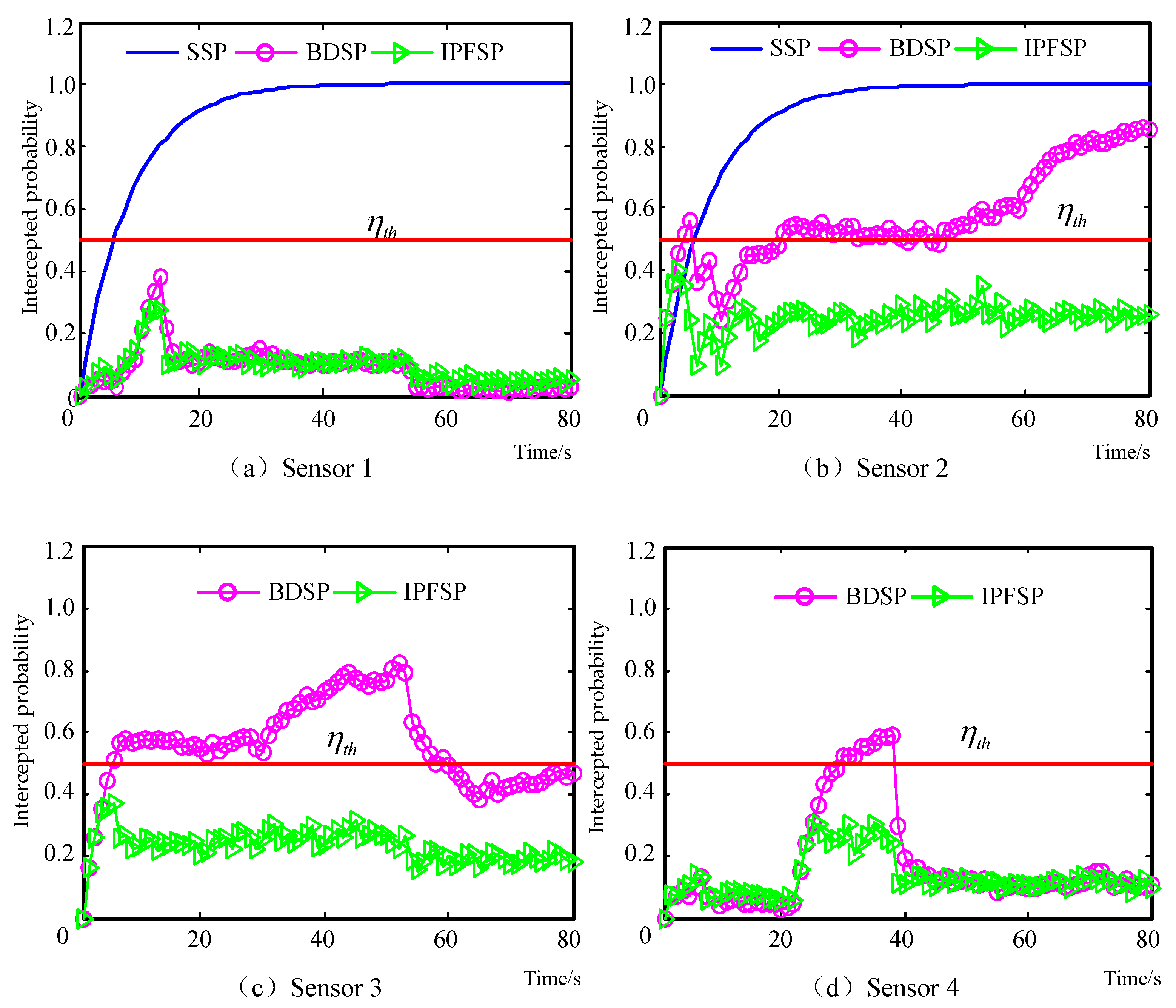
6.2. Scenario 2
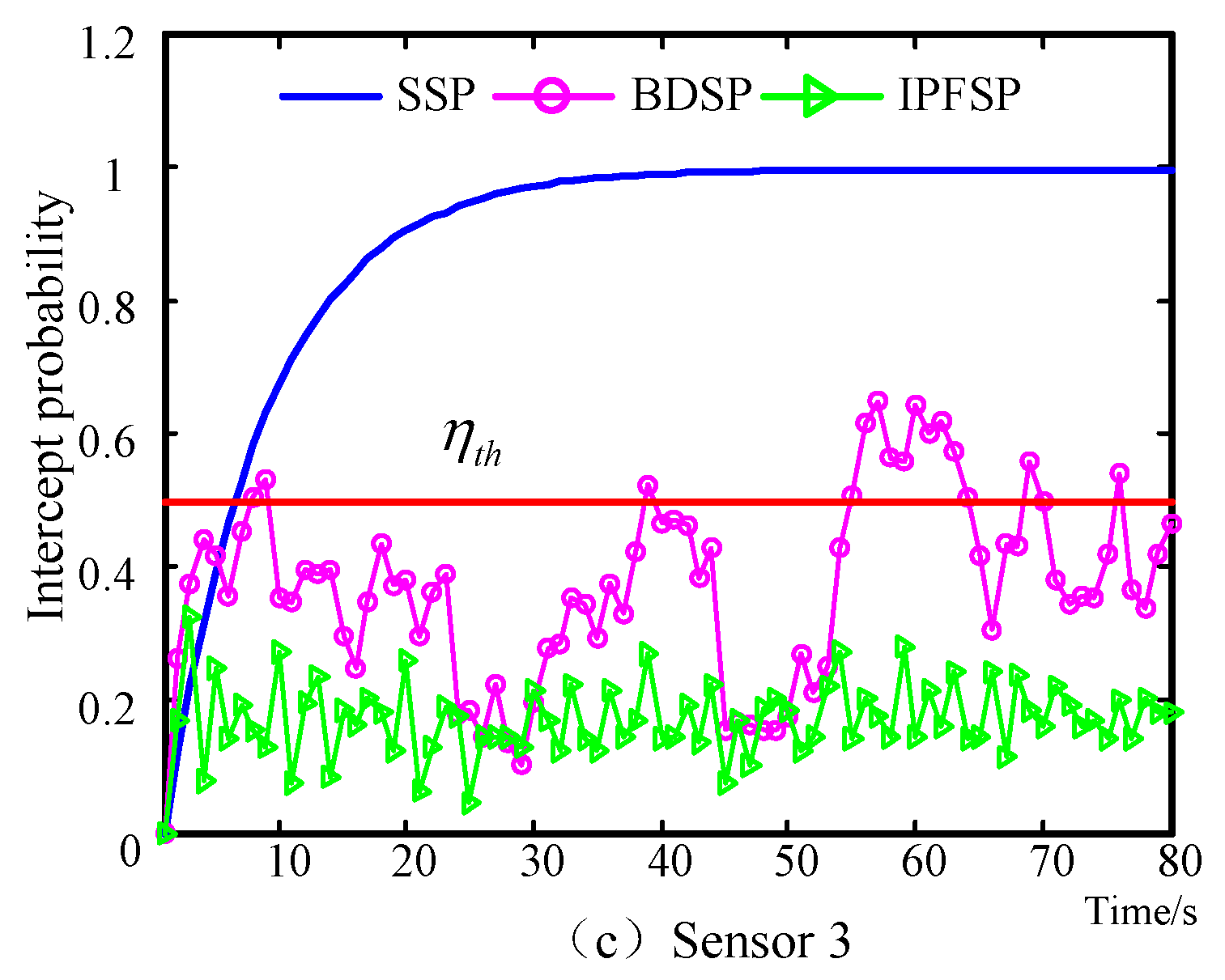
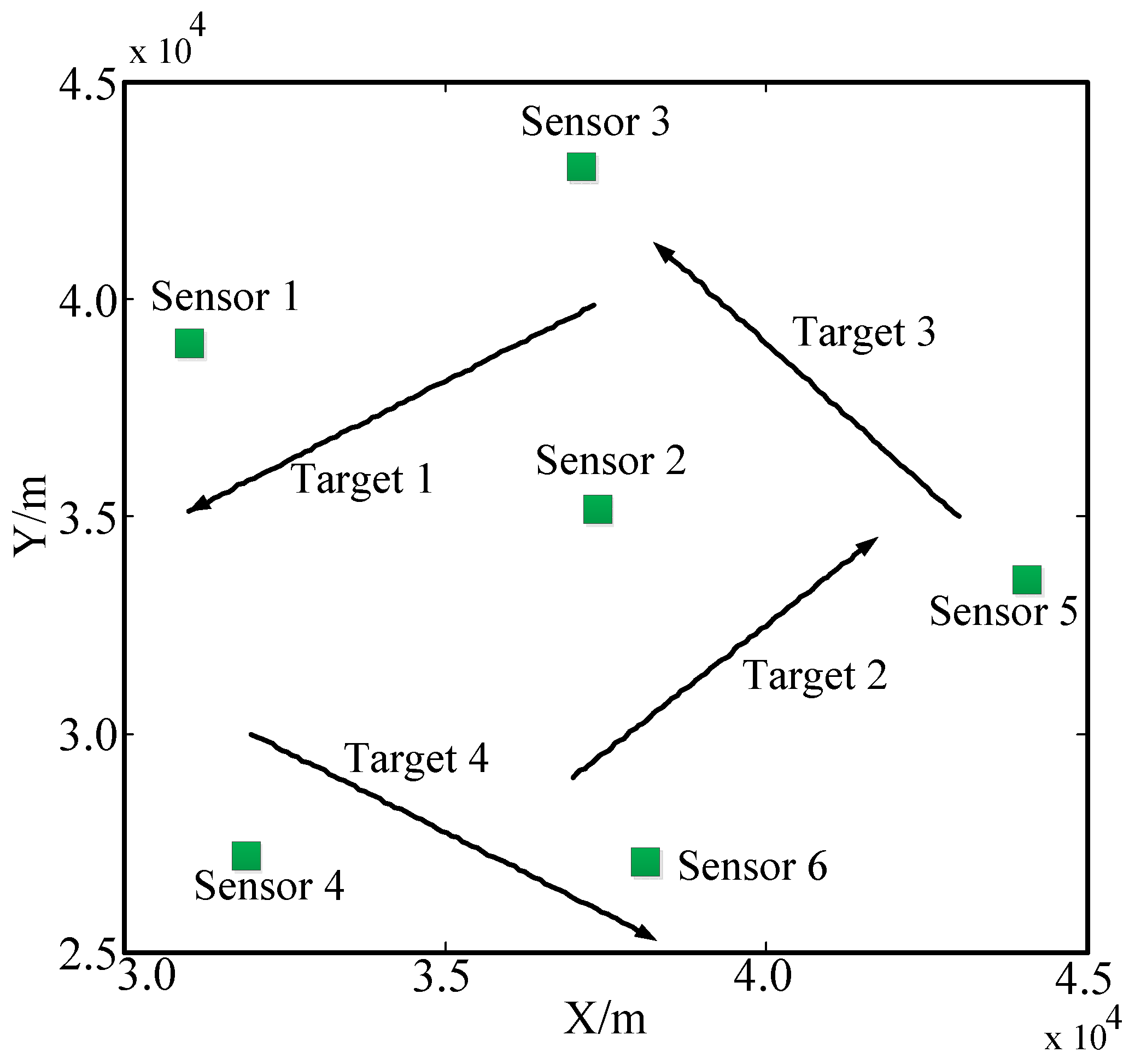
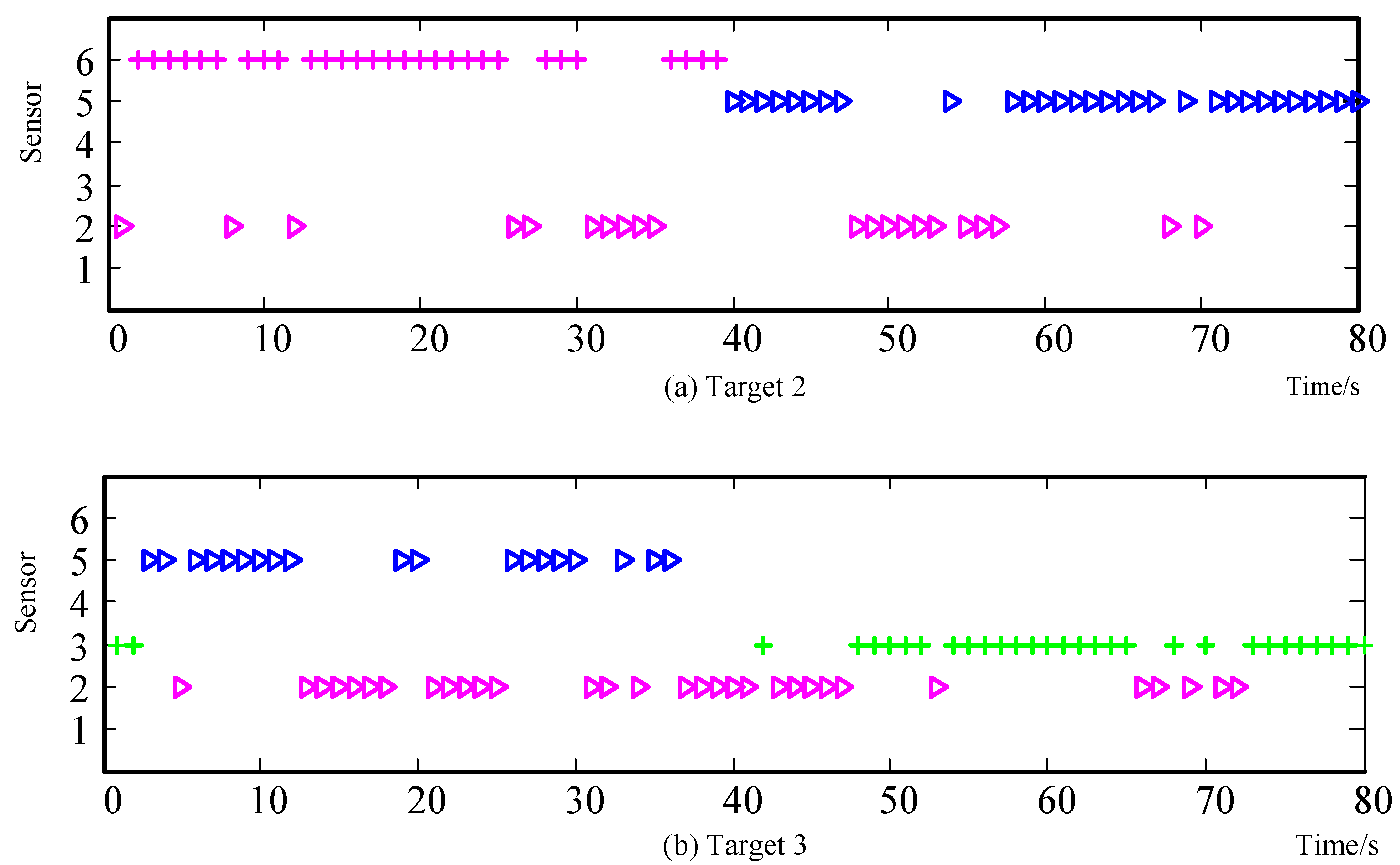
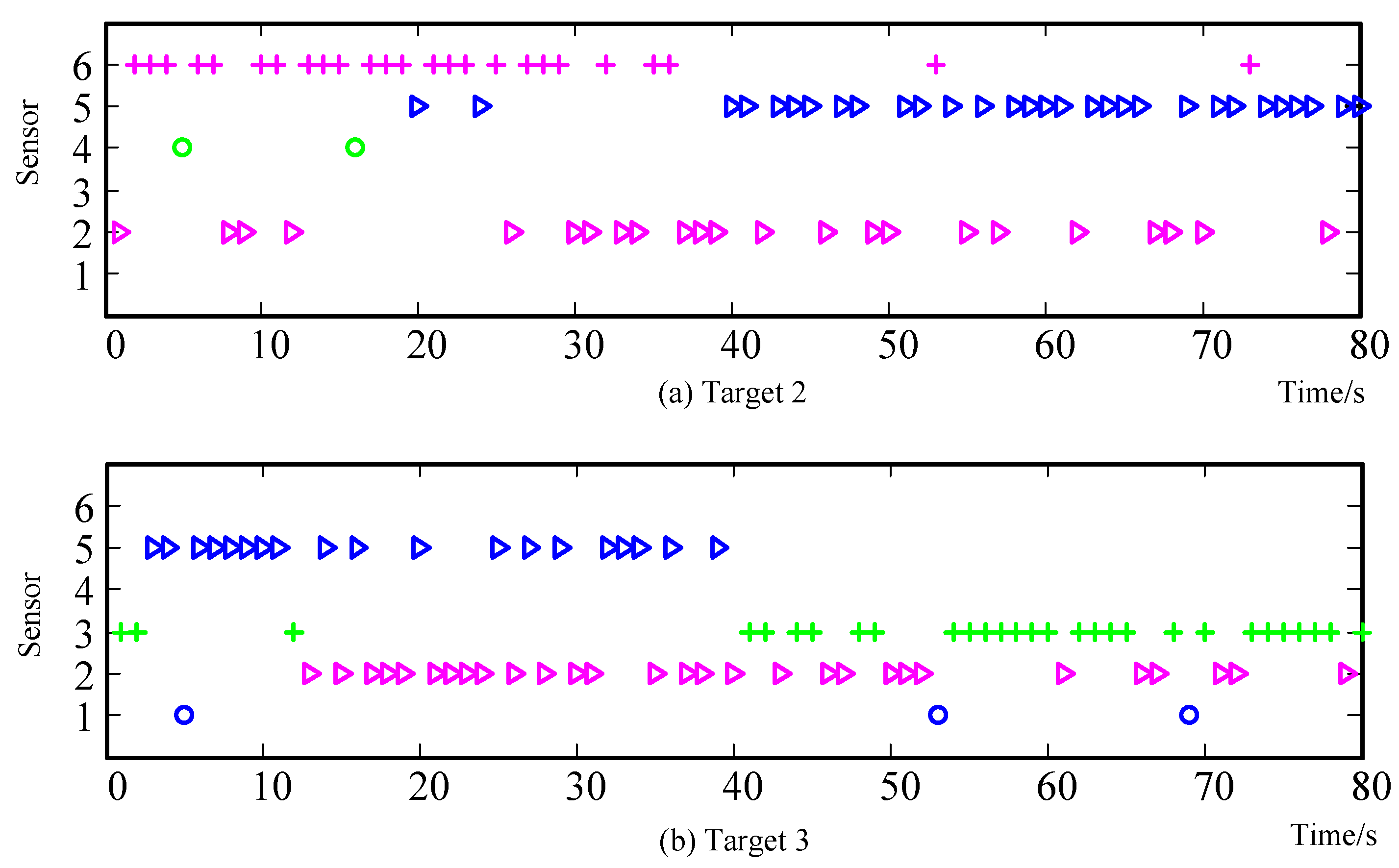
6.3. Scenario 3
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. A survey on sensor networks. IEEE Commun. Mag. 2002, 40, 102–105. [Google Scholar] [CrossRef]
- Salvagnini, P.; Pernici, F.; Cristani, M.; Lisanti, G.; Del Bimbo, A.; Murino, V. Non-myopic information theoretic sensor management of a single pan-tilt-zoom camera for multiple object detection and tracking. Comput. Vis. Image Underst. 2015, 134, 74–88. [Google Scholar] [CrossRef]
- Zhang, Z.N.; Shan, G.L. Non-myopic sensor scheduling to track multiple reactive targets. Signal Process. IET 2015, 9, 37–47. [Google Scholar] [CrossRef]
- Gupta, R.; Sultania, K.; Singh, P.; Gupta, A. Security for wireless sensor networks in military operations. In Proceedings of the IEEE Fourth International Conference on Computing, Communications and Networking Technologies, Tiruchengode, India, 4–6 July 2013; pp. 1–6. [Google Scholar]
- Collotta, M.; Bello, L.L.; Pau, G. A novel approach for dynamic traffic lights management based on wireless sensor networks and multiple fuzzy logic controllers. Expert Syst. Appl. 2015, 42, 5403–5415. [Google Scholar] [CrossRef]
- Wu, H.; Shi, Z.Y.; Shen, W.D.; Wang, J.S.; Wang, W.Z. Design of LPI radar waveform based on chaos theory. Comput. Eng. Appl. 2017, 53, 241–244. [Google Scholar]
- Deng, H. Waveform design for MIMO radar with low probability of intercept (LPI) property. In Proceedings of the IEEE International Symposium on Antennas and Propagation, Spokane, WA, USA, 3–8 July 2011; pp. 305–308. [Google Scholar]
- Chen, J.; Wang, F.; Zhou, J. Information Content Based Optimal Radar Waveform Design: LPI’s Purpose. Entropy 2017, 19, 210. [Google Scholar] [CrossRef]
- Angley, D.; Ristic, B.; Suvorova, S.; Moran, B.; Fletcher, F.; Gaetjens, H.; Simakov, S. Non-myopic sensor scheduling for multi-static sonobuoy fields. IET Radar Sonar Navig. 2017, 11, 1770–1775. [Google Scholar] [CrossRef]
- Shi, C.; Wang, F.; Salous, S.; Zhou, J. Optimal Power Allocation Strategy in a Joint Bistatic Radar and Communication System Based on Low Probability of Intercept. Sensors 2017, 17, 2731. [Google Scholar] [CrossRef]
- Rim, J.W.; Jung, K.H.; Koh, I.S.; Baek, C.; Lee, S.; Choi, S.H. Simulation of Dynamic EADs Jamming Performance against Tracking Radar in Presence of Airborne Platform. Int. J. Aeronaut. Space Sci. 2015, 16, 475–483. [Google Scholar] [CrossRef]
- She, J.; Zhou, J.; Wang, F.; Li, H. LPI optimization framework for radar network based on Minimum mean-square error estimation. Entropy 2017, 19, 397. [Google Scholar] [CrossRef]
- Shi, C.; Wang, F.; Sellathurai, M.; Zhou, J. LPI optimization framework for target tracking in radar network architectures using information theoretic criteria. Int. J. Antennas Propag. 2014, 2014. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, J.; Salous, S. A novel dwelling time design method for low probability of intercept in a complex radar network. Int. J. Des. Nat. Ecodyn. 2015, 10, 309–318. [Google Scholar] [CrossRef]
- Krishnamurthy, V. Emission management for low probability intercept sensors in network centric warfare. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 133–151. [Google Scholar] [CrossRef]
- Shan, G.L.; Zhang, Z.N. Non-myopic sensor scheduling for low radiation risk tracking using mixed POMDP. Trans. Inst. Meas. Control 2015, 39. [Google Scholar] [CrossRef]
- Tichavsky, P.; Muravchik, C.H.; Nehorai, A. Posterior Cramer-Rao bounds for discrete-time nonlinear filtering. IEEE Trans.Signal Process. 1998, 46, 1386–1396. [Google Scholar] [CrossRef]
- Stein, S.; Johansen, D. A Statistical Description of Coincidences among Random Pulse Trains. Proc. IRE 2007, 46, 827–830. [Google Scholar] [CrossRef]
- Self, A.G.; Smith, B.G. Intercept time and its prediction. IEE Proc. F Commun. Radar Signal Process. 2008, 132, 215–220. [Google Scholar] [CrossRef]
- Masdari, M.; Salehi, F.; Jalali, M.; Bidaki, M. A Survey of PSO-Based Scheduling Algorithms in Cloud Computing. J. Netw. Syst. Manag. 2017, 25, 122–158. [Google Scholar] [CrossRef]
- Geng, J.C.; Cui, Z.; Gu, X.S. Scatter search based particle swarm optimization algorithm for earliness/tardiness flow shop scheduling with uncertainty. Int. J. Autom. Comput. 2016, 13, 285–295. [Google Scholar] [CrossRef]
- Trelea, I.C. The particle swarm optimization algorithm: Convergence analysis and parameter selection. Inf. Process. Lett. 2003, 85, 317–325. [Google Scholar] [CrossRef]
- Naidu, Y.R.; Ojha, A.K. Solving Multi-objective Optimization Problems Using Hybrid Cooperative Invasive Weed Optimization With Multiple Populations. IEEE Trans. Syst. Man Cybern. Syst. 2016, 48, 821–832. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, G.; Pang, C.; Duan, X.; Shan, G. Multi-Sensor Optimization Scheduling for Target Tracking Based on PCRLB and a Novel Intercept Probability Factor. Electronics 2019, 8, 140. https://doi.org/10.3390/electronics8020140
Xu G, Pang C, Duan X, Shan G. Multi-Sensor Optimization Scheduling for Target Tracking Based on PCRLB and a Novel Intercept Probability Factor. Electronics. 2019; 8(2):140. https://doi.org/10.3390/electronics8020140
Chicago/Turabian StyleXu, Gongguo, Ce Pang, Xiusheng Duan, and Ganlin Shan. 2019. "Multi-Sensor Optimization Scheduling for Target Tracking Based on PCRLB and a Novel Intercept Probability Factor" Electronics 8, no. 2: 140. https://doi.org/10.3390/electronics8020140
APA StyleXu, G., Pang, C., Duan, X., & Shan, G. (2019). Multi-Sensor Optimization Scheduling for Target Tracking Based on PCRLB and a Novel Intercept Probability Factor. Electronics, 8(2), 140. https://doi.org/10.3390/electronics8020140




