DC-Microgrid System Design, Control, and Analysis
Abstract
:1. Introduction
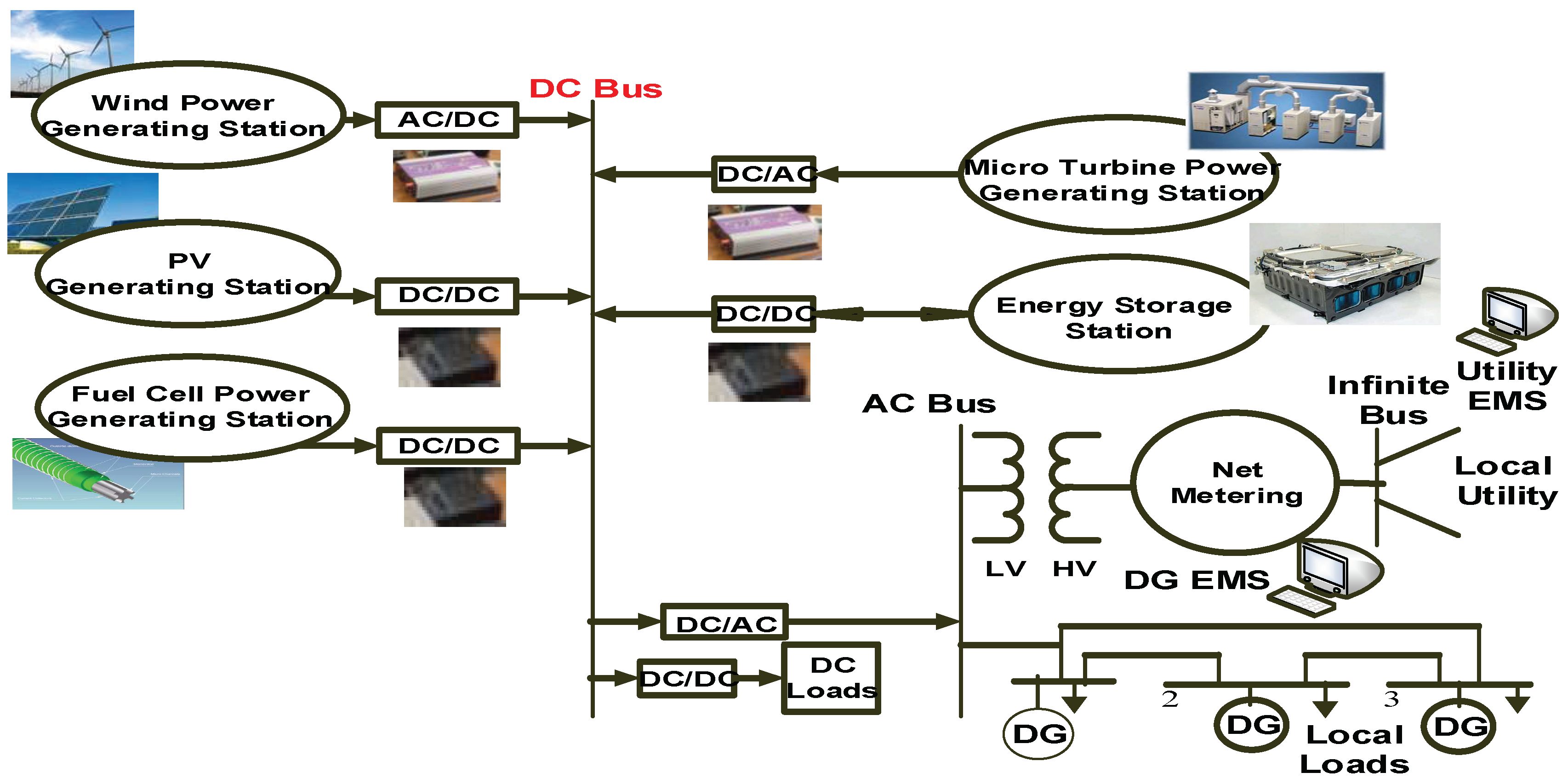
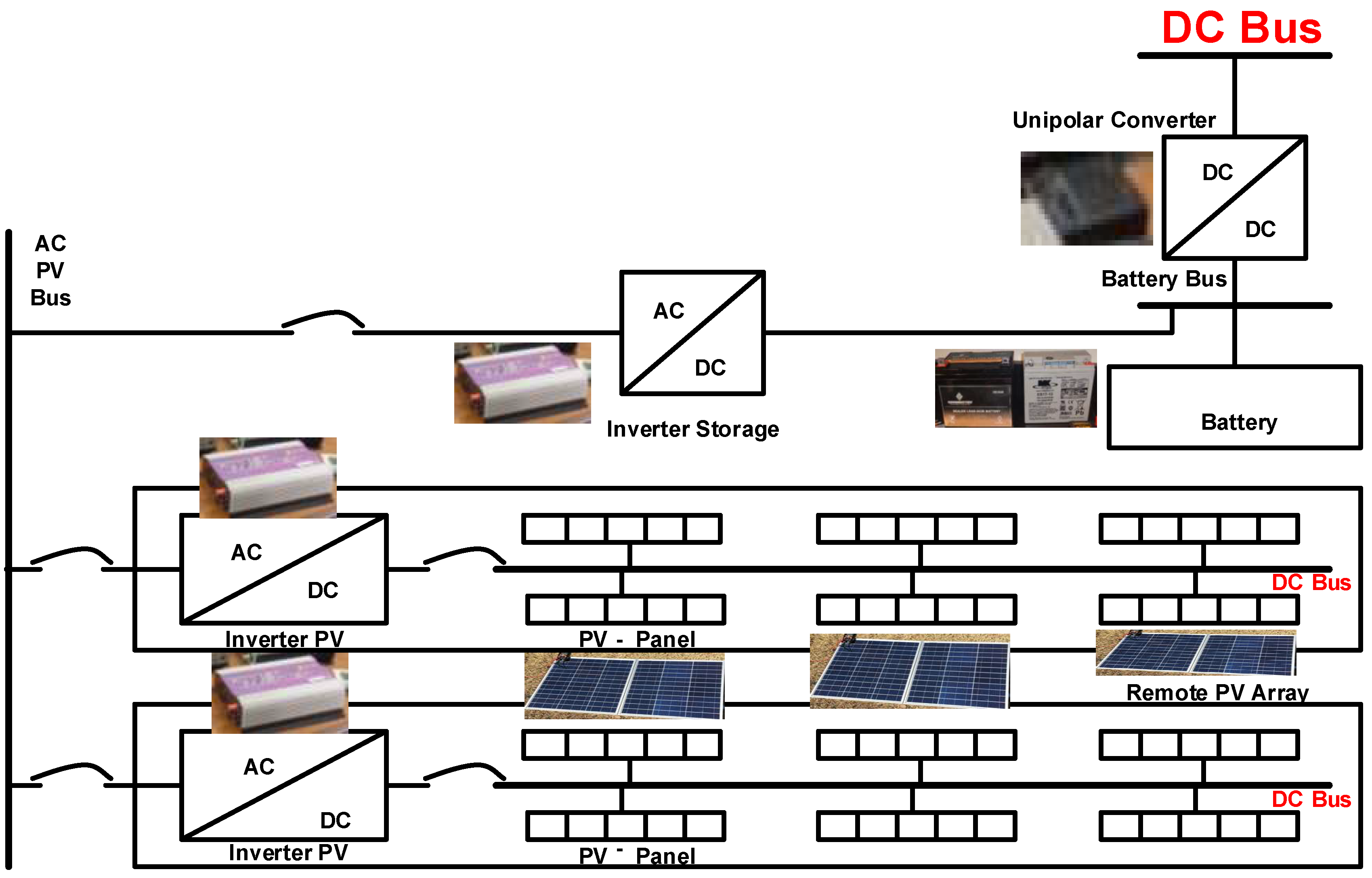
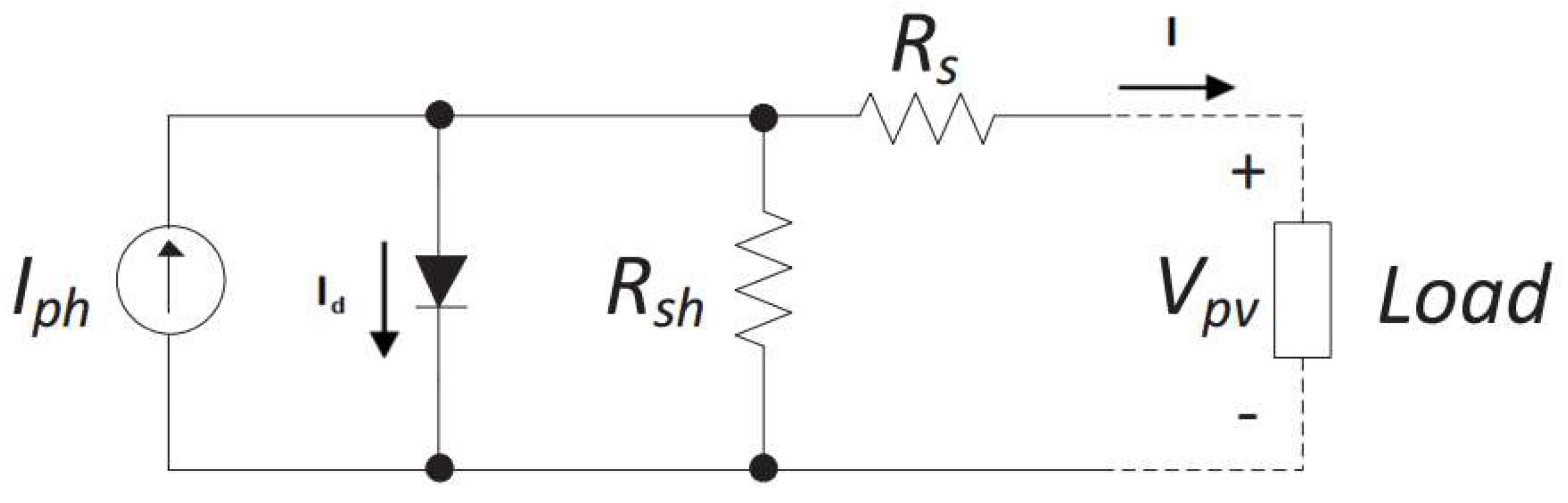
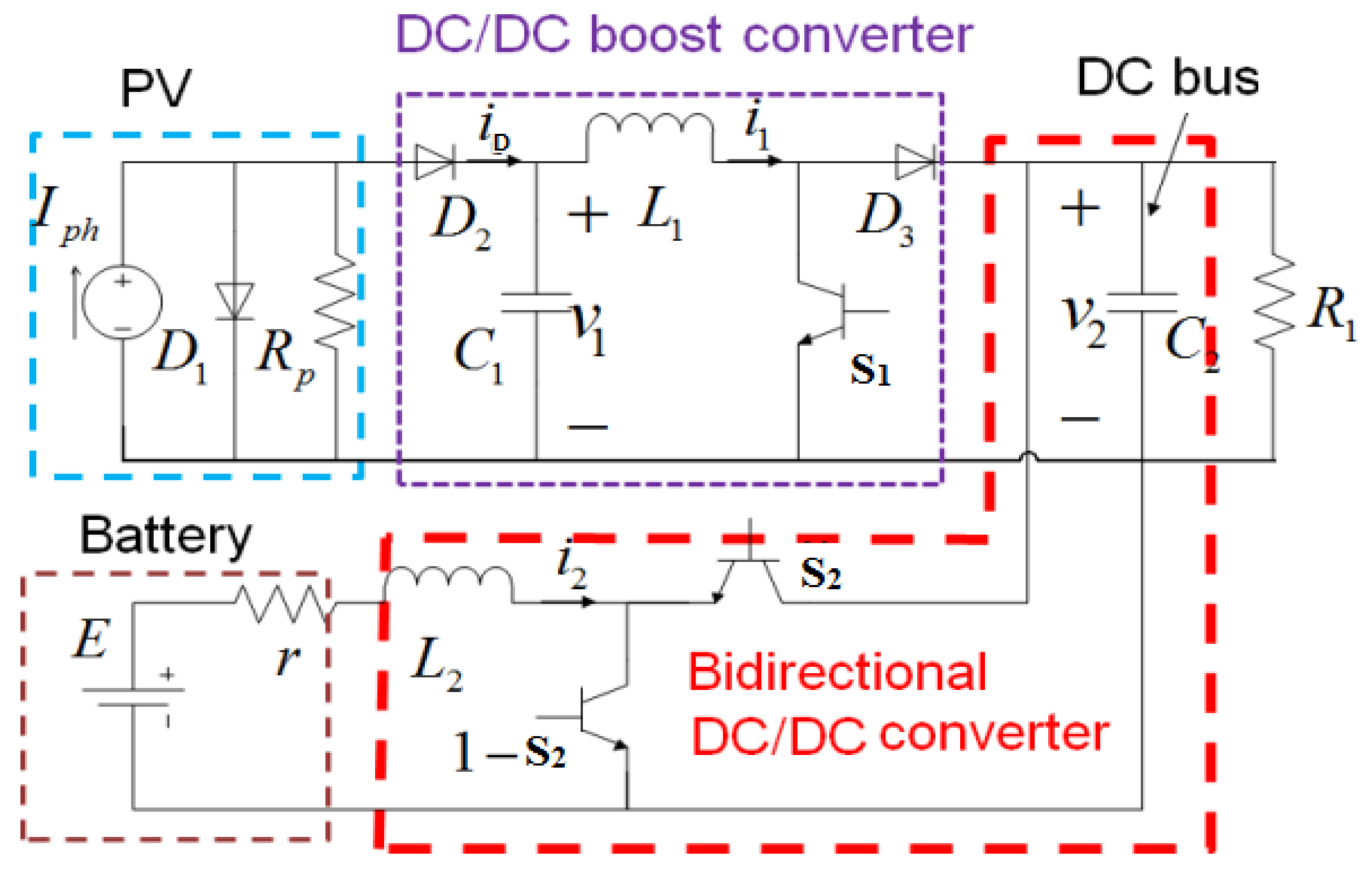
2. Photovoltaic DC Microgrid System
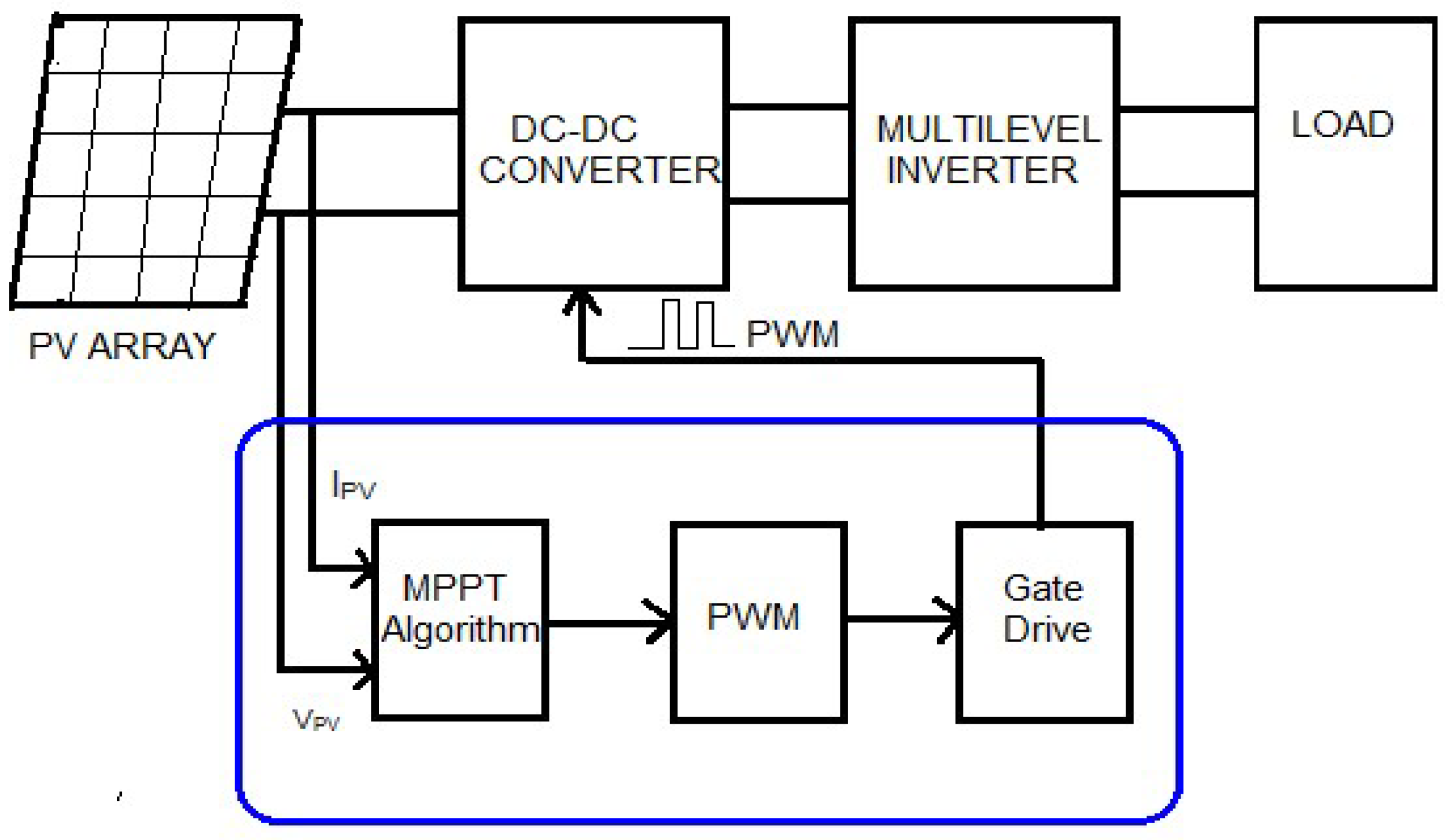
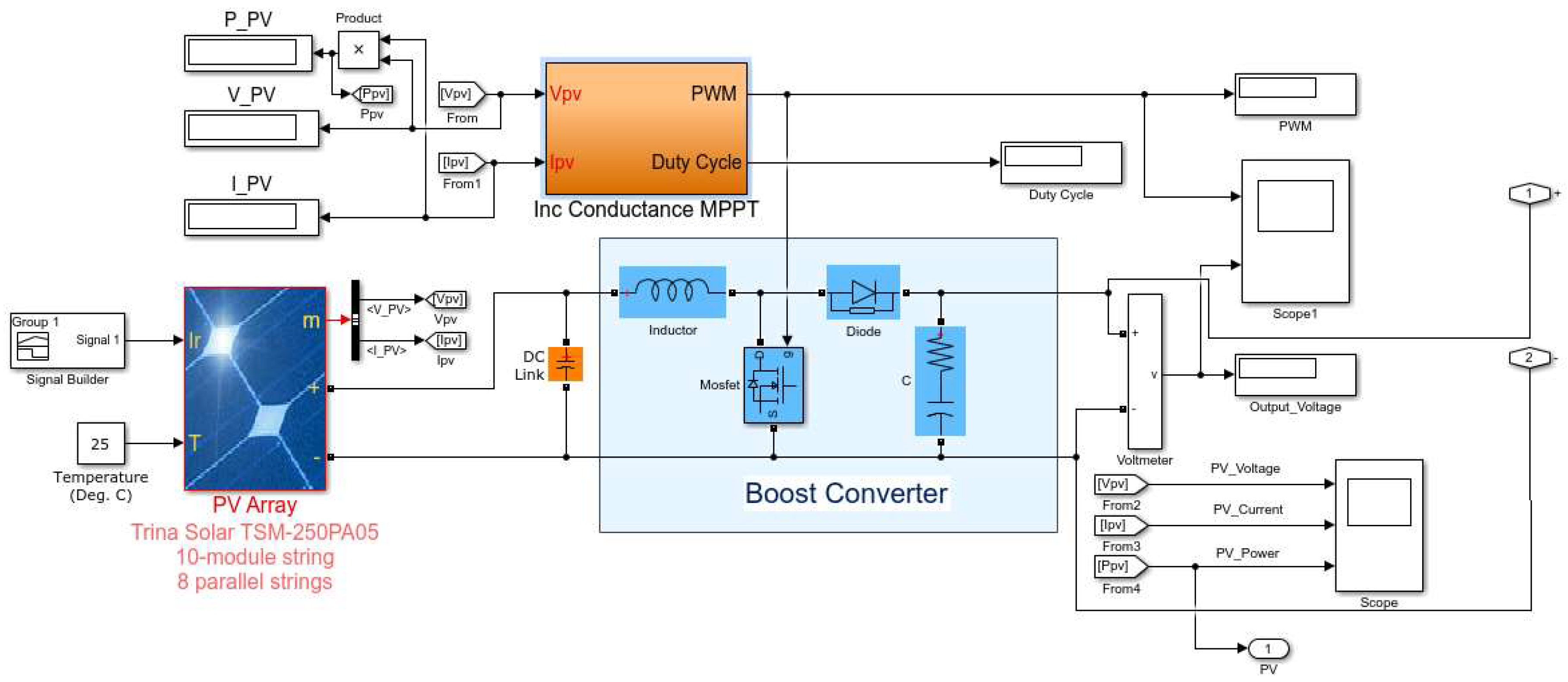
3. Simulink Representation of the Complete PV System and the Proposed MPPT Techniques
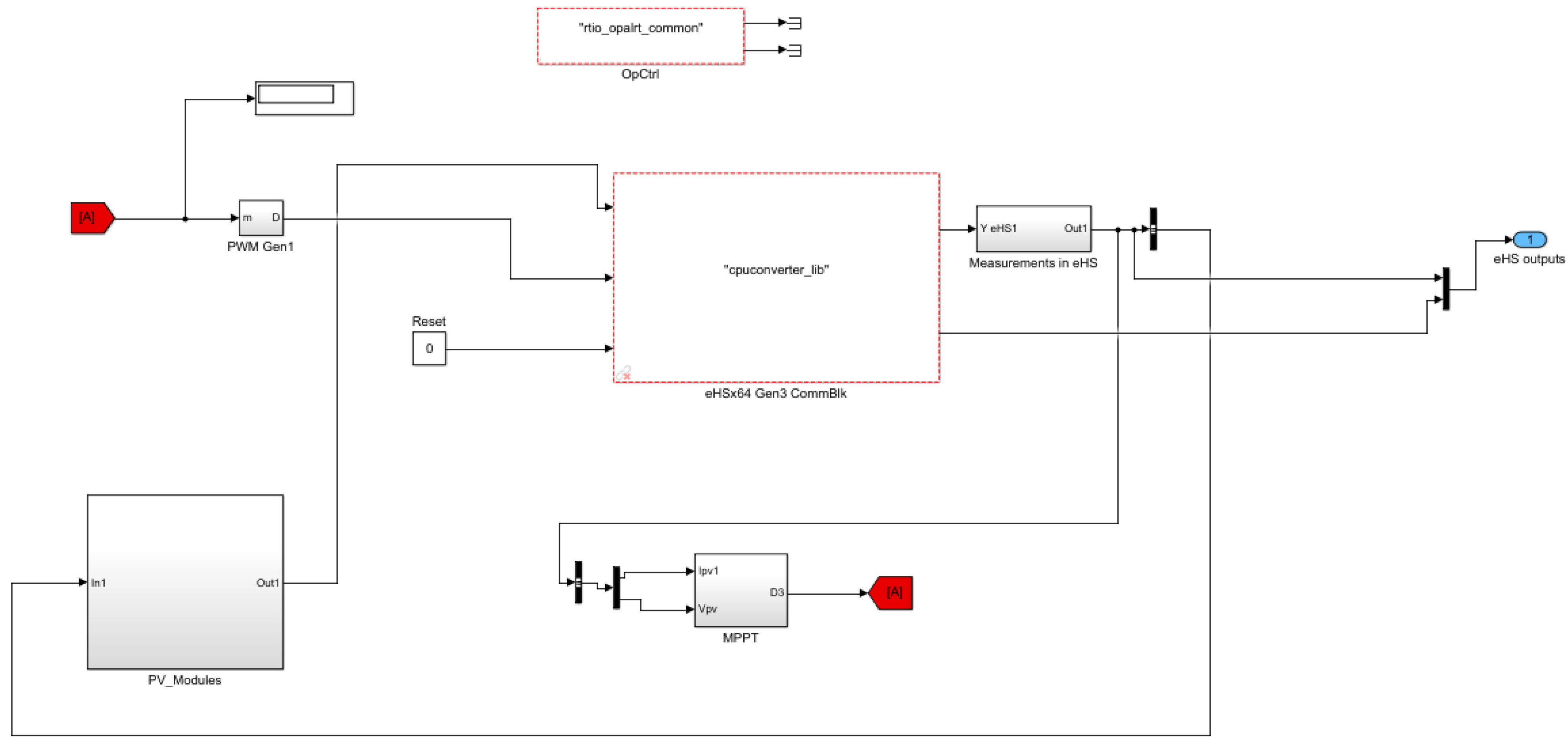
3.1. Modeling of the Solar PV System
3.2. Modeling and Simulation of the Boost Converter
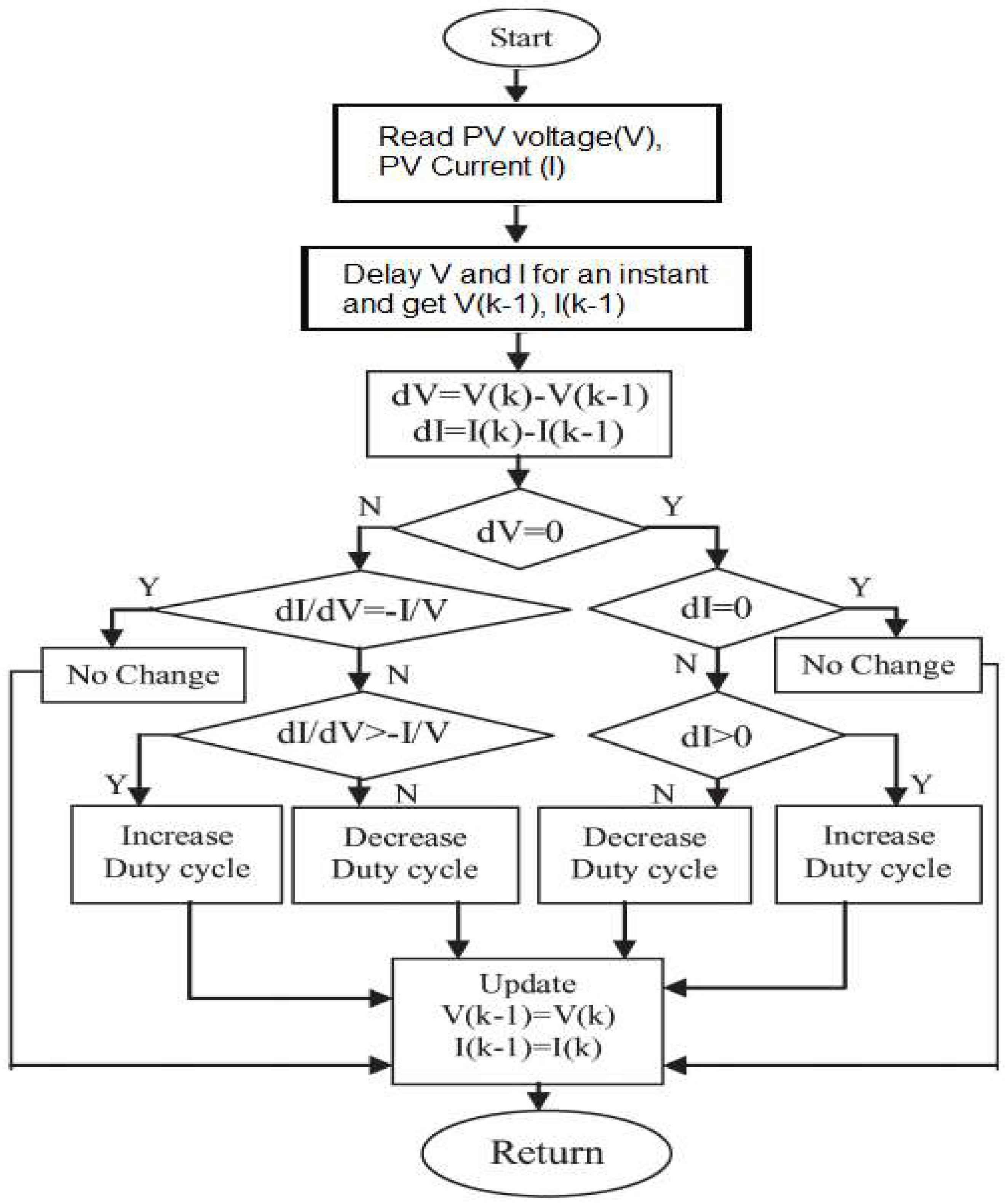
3.3. Incremental Conductance MPPT
3.4. Perturb and Observe Algorithm
3.5. Practical Swarm Optimisation for MPPT
- Step 1. (Parameter Selection): As far as the planned MPPT algorithm is concerned, the converter’s duty cycle is described as the particle position; the derived output power being considered to operate as the fitness vale assessment function; with each particle’s initial 99 velocity and position being initialized at random and in a consistent distribution within the search space.
- Step 2. (Fitness Evaluation): The fitness value of particle i, is calculated subsequent to the controller issuing the duty cycle directive, symbolizing the location of particle i.
- Step 3. (Update Individual and Global Best Data): pbest, i and gbest positions and values are revised by evaluating the freshly computed fitness values with those obtained previously, plus having pbest, i, and gbest and their resultant positions replaced accordingly.
- Step 4. (Update Individual and Global Best Data): Updating fitness values, gbest (global best fitness values) and pbest (individual best positions), of each particle is achieved by having the fresh computed fitness values with the preceding examples as well as substituting the gbest and pbest equivalent to their positions as needed.
- Step 5. (Update Velocity and Position of Each Particle): By engaging the assessment of all particles, each particle’s positions and velocities in the swarm are updated via engaging PSO equations.
- Step 6. (Convergence Determination): The converge criterion are located either to the optimal solution or reach the maximum number of iterations. If the convergence criterion is met, the process will terminate; otherwise, rerun Steps 2 through to 7.
- Step 7: (Re-initialization): By considering the PSO technique, the convergence technique is either to establish the most favorable solution, or attain the maximum number of iterations. However, the fitness value in PV systems does not remain constant, since it varies respective of the applied load as well as the atmospheric conditions. For that reason, there is the need to reinitialize PSO while a search recommenced for a novel method of identifying the novel MPP upon having the output of the PV module varied.
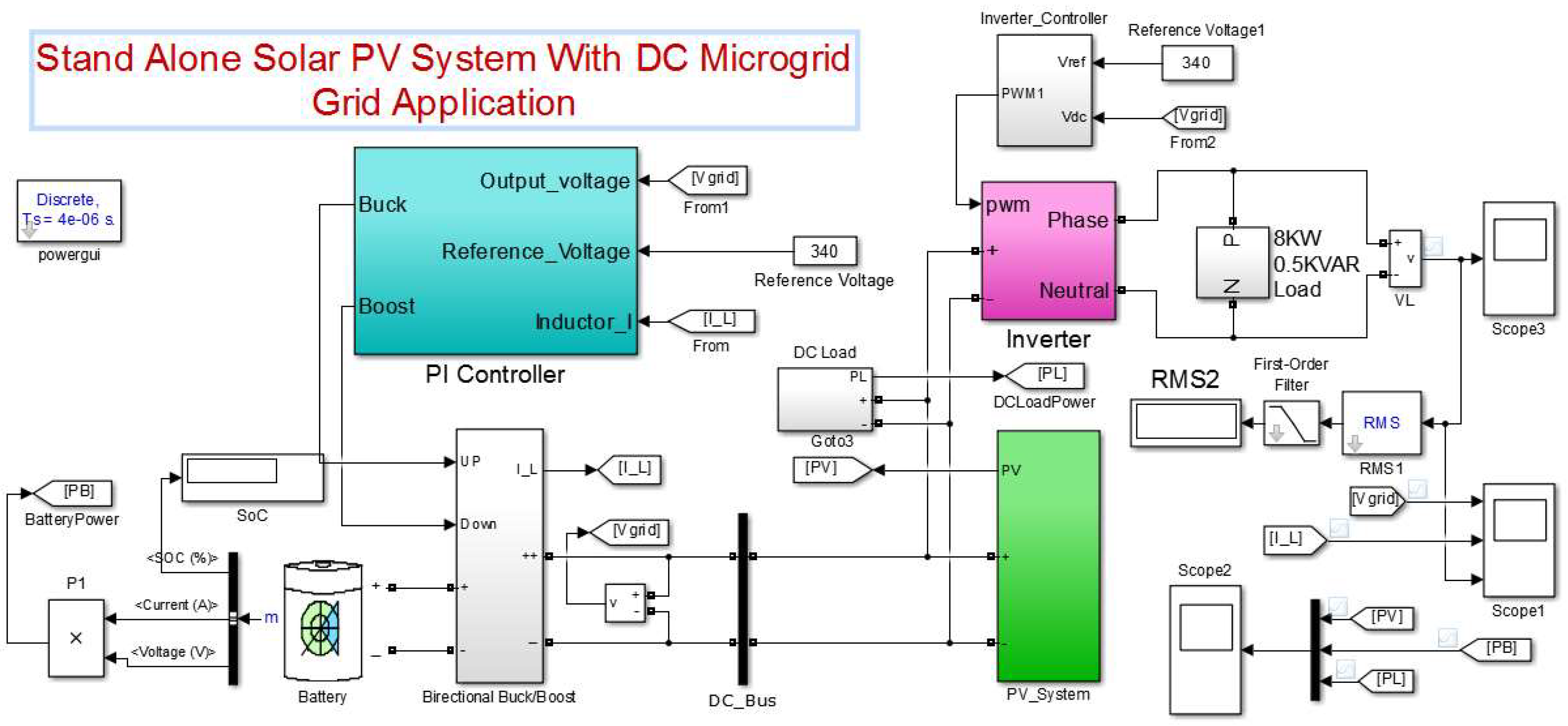
3.6. PV Simulink Model
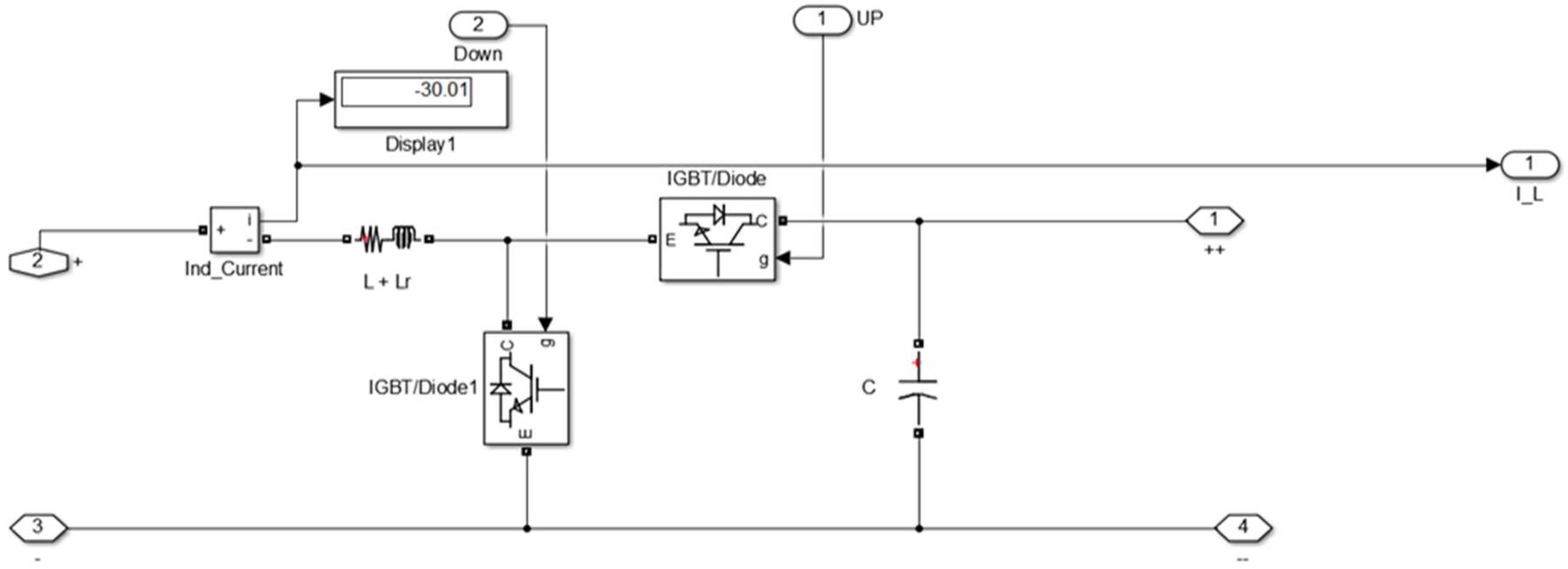
3.7. Modeling of Bidirectional Buck-boost Converter
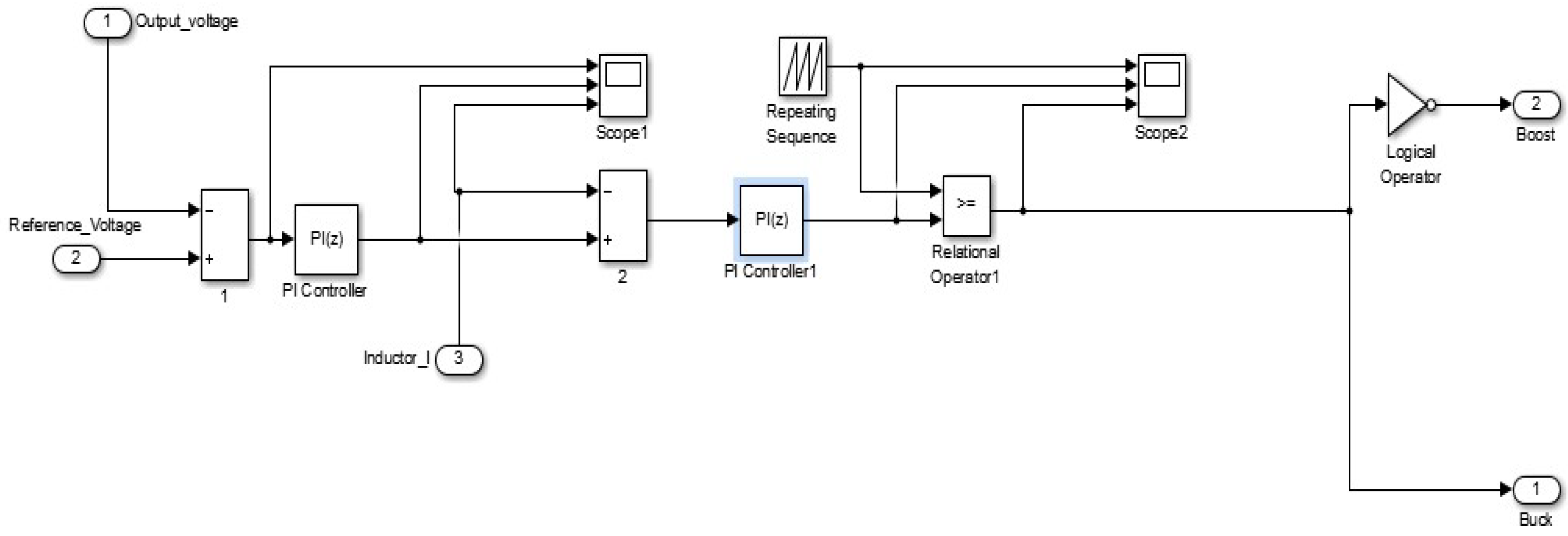
3.8. Bidirectional Buck-Boost Converter Controller
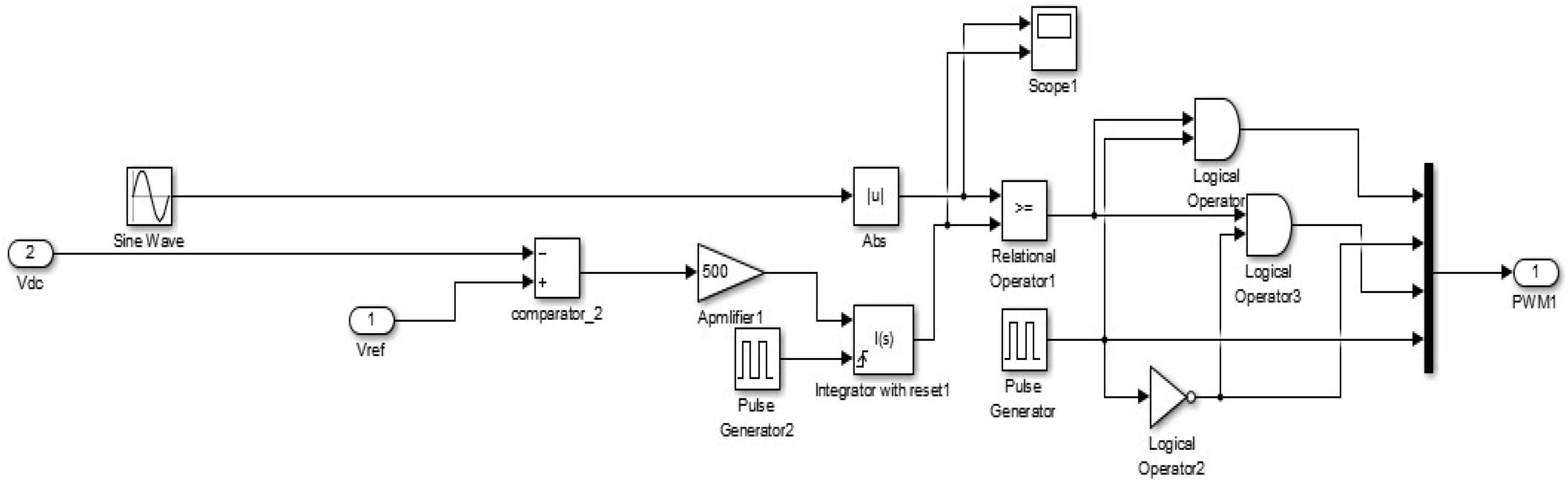
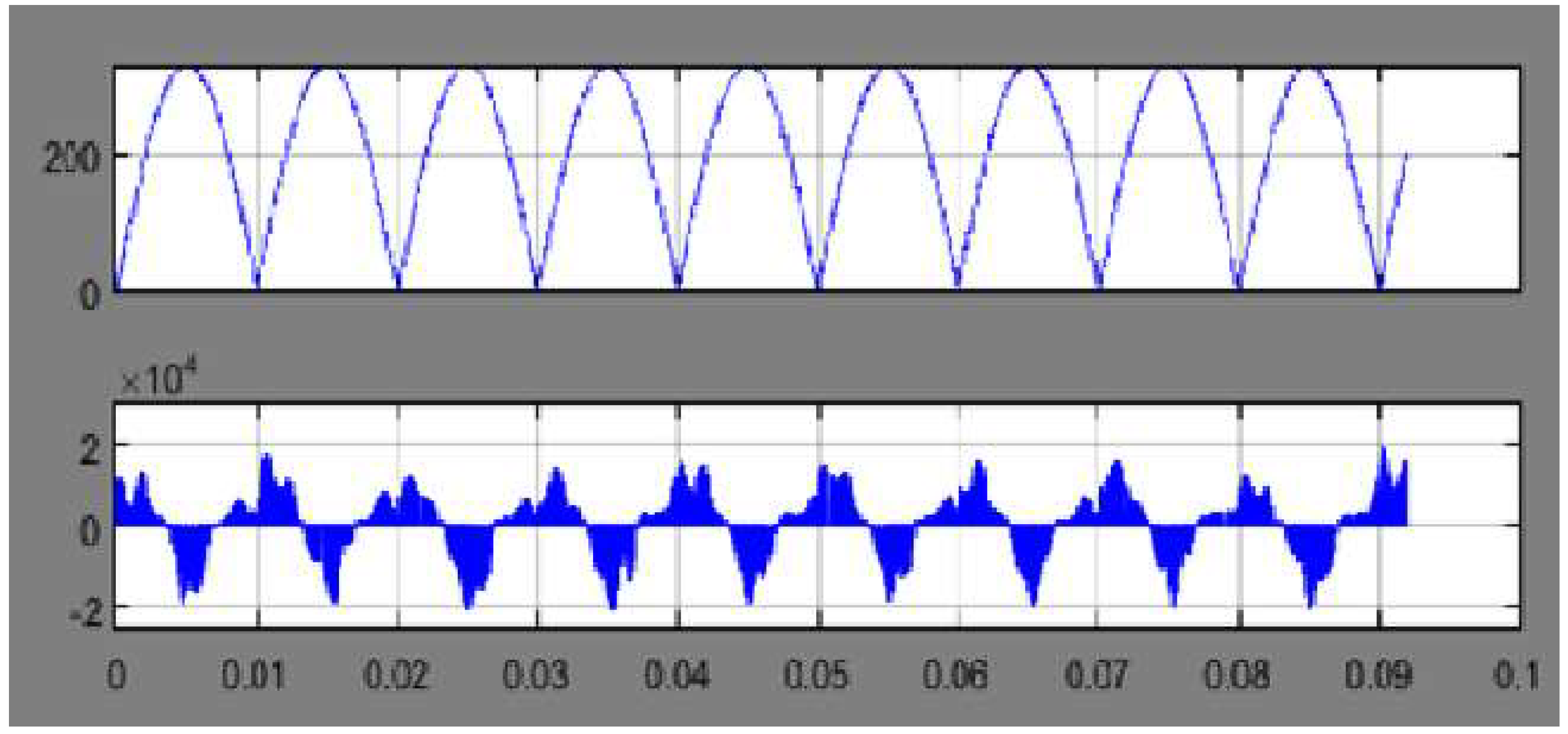
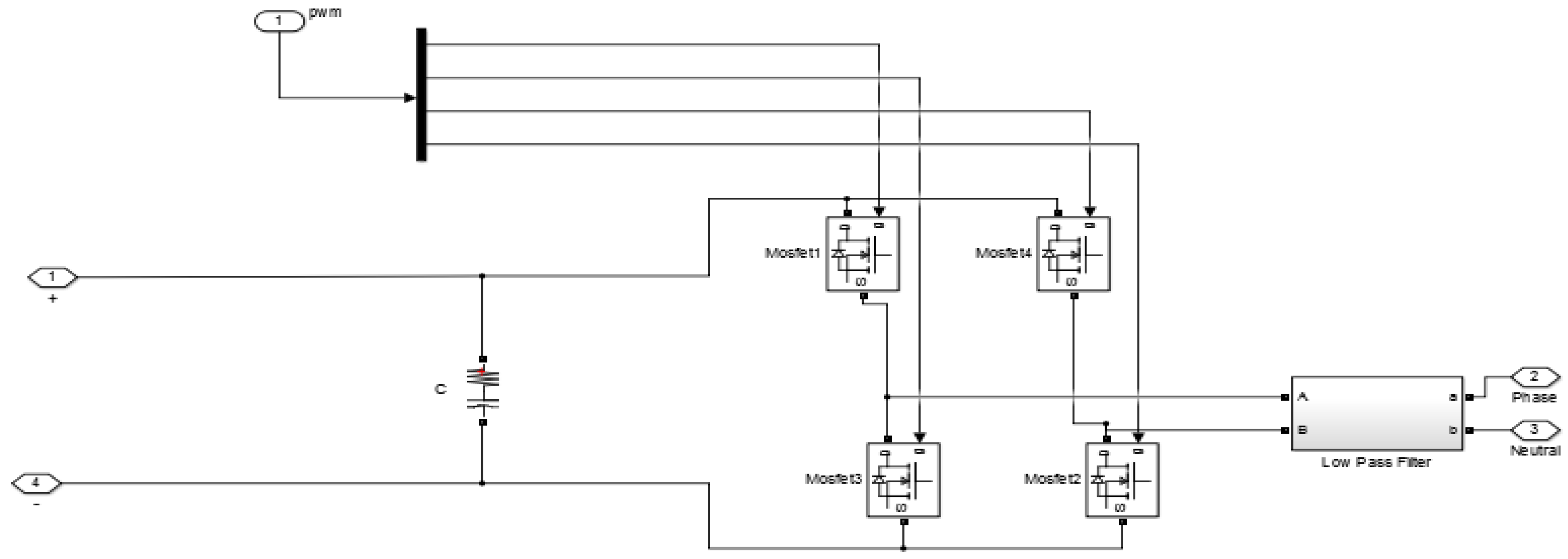
3.9. Modeling of the Inverter and Inverter Controller
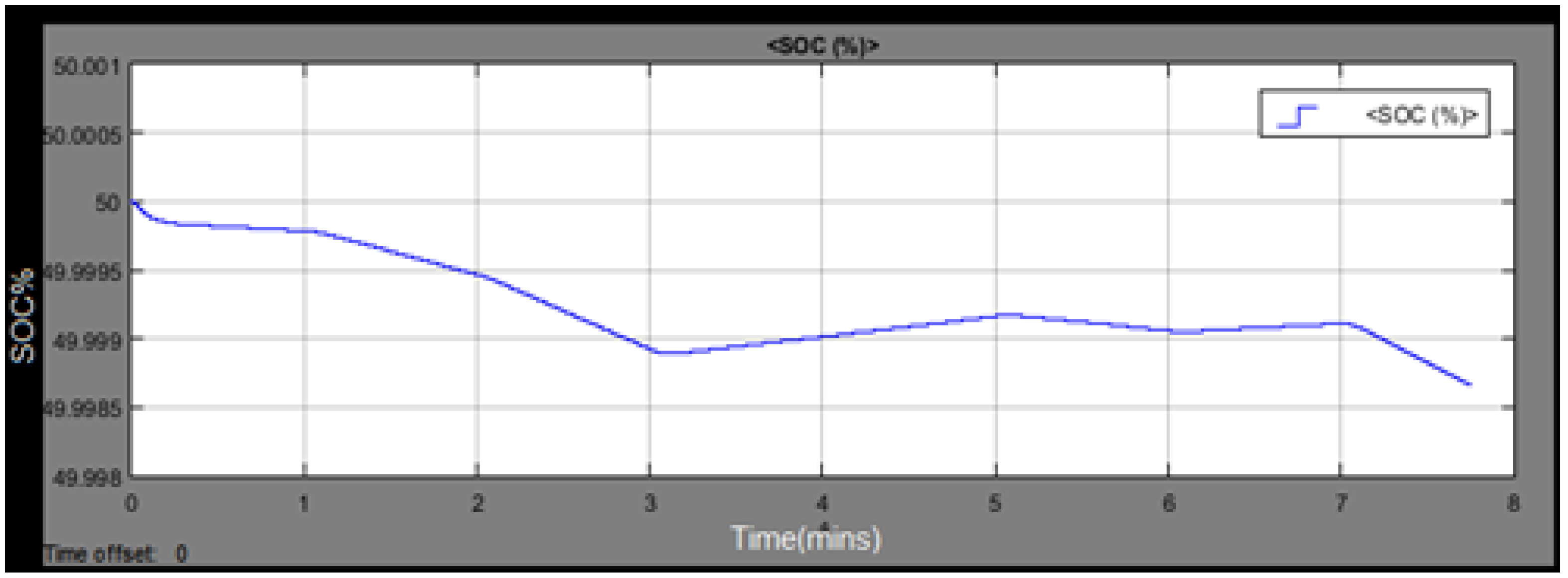
3.10. Modeling of the Battery
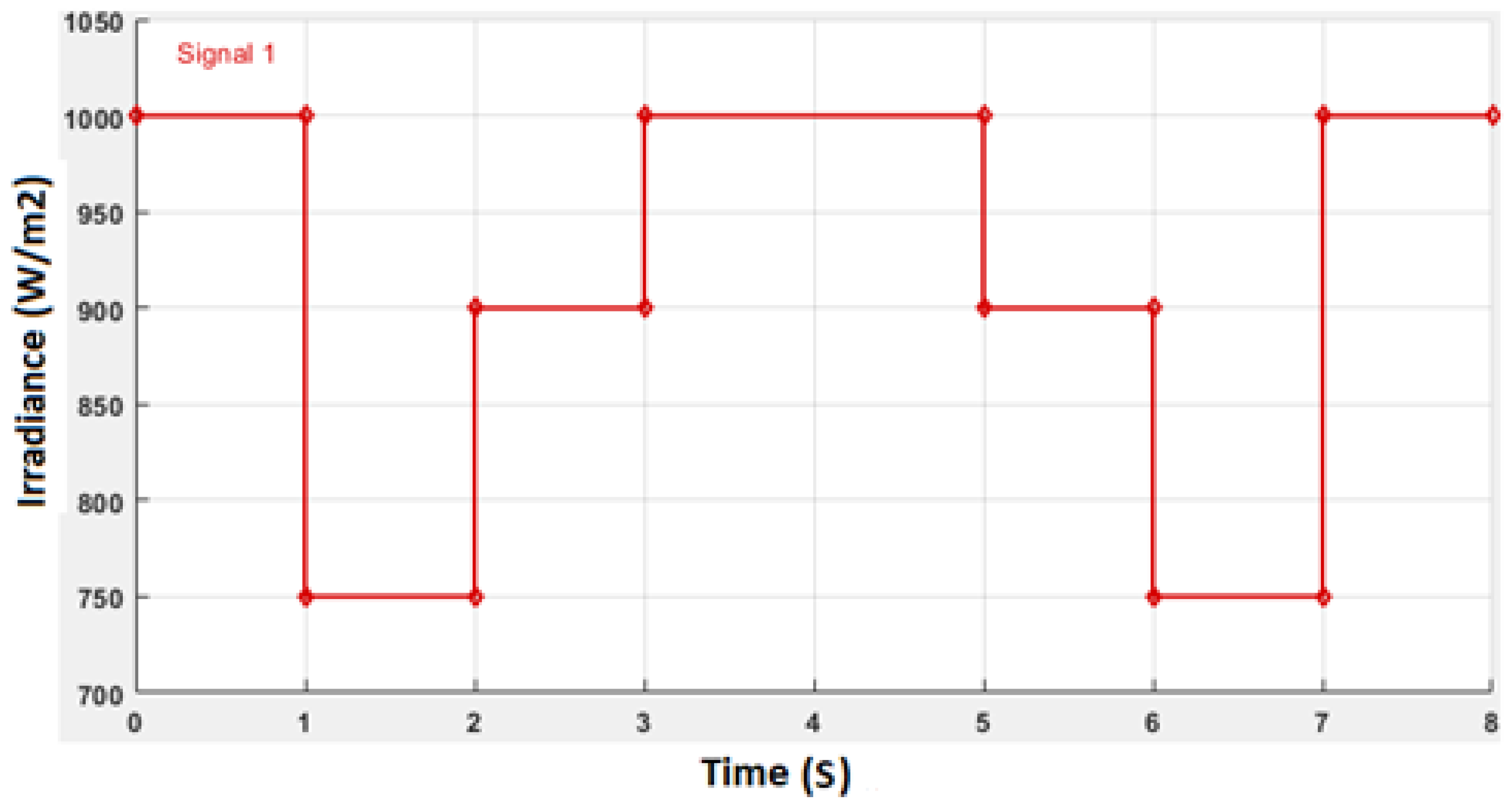
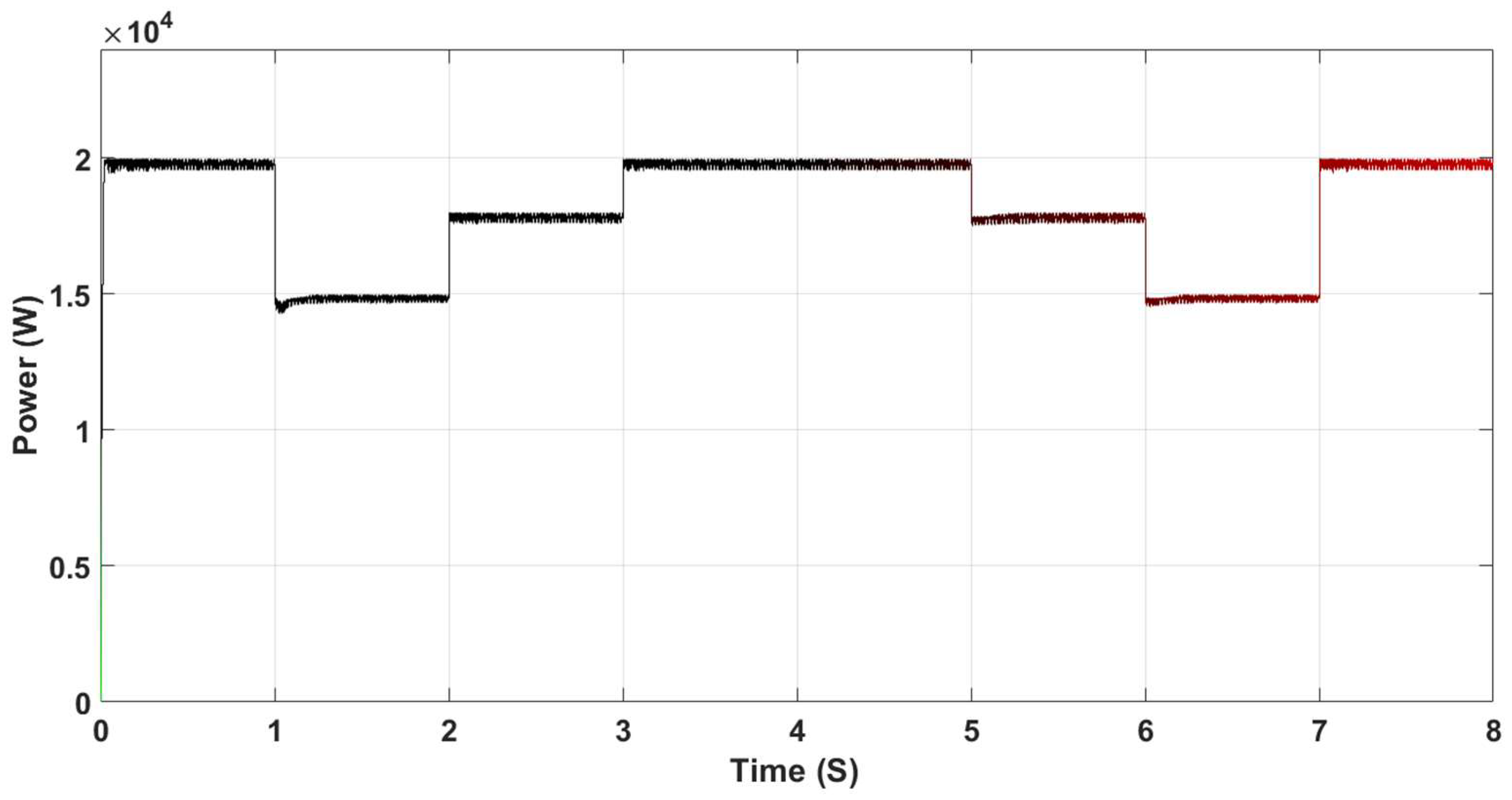
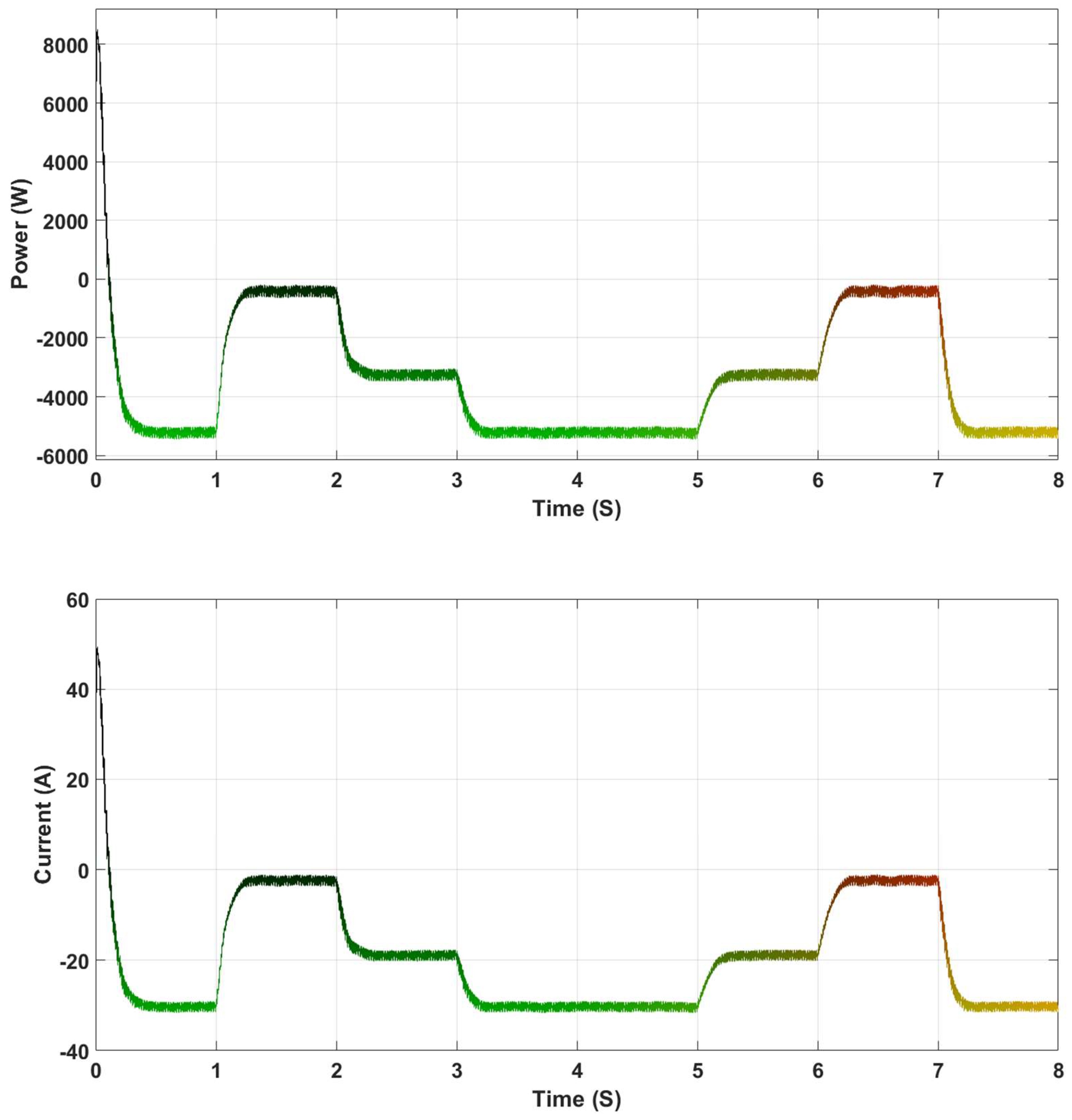
4. Input Irradiance Variation Effect
5. Stability Analysis Investigation
- Set A: Set of the states x within an arbitrary “radius” (in other word, satisfying the inequality p(x) < β, where p(x) has an arbitrary shape)
- Set B: Set of the states x for which an arbitrary is an upper bound of the Lyapunov function V(x);
- Set C: Set of the states x for which is negative. It should be noted that this the only set that depends directly on F(x);
- Step 1: “To start the VS iteration, a first estimation of the LF is determined using the linear approximation of (3) in the vicinity of the equilibrium point yielding the following”;where “A is the Jacobian of F(x). Once A has been determined, if all of its eigenvalues are found to have negative real parts, then there exists a positive-definite matrix P (where Q must be positive definite) that satisfies the following condition”The corresponding LF is determined using:
- Step 2: “In this step, V(x) is held fixed while and are determined using Equations (15) and (17), using the bisection method to iteratively determine the biggest value of ;”
- Step 3: “In this step, V(x) is held fixed while both and are determined using Equation (16). However, Equation (10) is bilinear in and , bisection is used to obtain while keeping fixed”
- Step 4: “In this step , , , and are held fixed while V(x) is determined using Equations (14) through (17) and normalized with respect to to avoid numerical problem”;
- Step 5a: “If the value of converges, the iteration process is stopped; otherwise, the process flow restarts at step 2”;
- Step 5b: “Determine the variation in the shaping function following”
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Haque, A.; Rahman, M.A.; Ahsan, Q. Building integrated photovoltaic system: Cost effectiveness. In Proceedings of the 2012 7th International Conference on Electrical and Computer Engineering, Dhaka, Bangladesh, 20–22 December 2012; pp. 904–907. [Google Scholar]
- Haque, A.; Rahman, M.A. Study of a solar PV-powered mini-grid pumped hydroelectric storage & its comparison with battery storage. In Proceedings of the IEEE Electrical & Computer Engineering (ICECE) 7th International Conference, Dhaka, Bangladesh, 28–30 December 2012; pp. 626–629. [Google Scholar]
- Li, C.; de Bosio, F.; Chaudhary, S.K.; Graells, M.; Vasquez, J.C.; Guerrero, J.M. Operation cost minimization of droop-controlled DC microgrids based on real-time pricing and optimal power flow. In Proceedings of the IECON 2015-41st Annual Conference IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 003905–003909. [Google Scholar]
- Arifin, M.S.; Khan, M.M.S.; Haque, A. Improvement of load-margin and bus voltage of Bangladesh power system with the penetration of PV based generation. In Proceedings of the 2013 International Conference IEEE Informatics, Electronics & Vision (ICIEV), Dhaka, Bangladesh, 17–18 May 2013; pp. 1–5. [Google Scholar]
- Islam, M.; Mekhilef, S. High efficiency transformerless MOSFET inverter for grid-tied photovoltaic system. In Proceedings of the 2014 Twenty-Ninth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Fort Worth, TX, USA, 16–20 March 2014; pp. 3356–3361. [Google Scholar]
- Hasan, K.N.; Haque, M.E.; Negnevitsky, M.; Muttaqi, K.M. Control of energy storage interface with a bidirectional converter for photovoltaic systems. In Proceedings of the IEEE Power Engineering Conference, Australasian Universities, Sydney, Australia, 14–17 December 2008; pp. 1–6. [Google Scholar]
- Boujemaa, M.; Rachid, C. Different methods of modeling a photovoltaic cell using Matlab/Simulink/Simscape. Int. J. Sci. Eng. Res. 2014, 5, 671–677. [Google Scholar]
- Chafle, S.R.; Vaidya, U.B. Incremental conductance MPPT technique for PV system. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2013, 2, 2720–2726. [Google Scholar]
- Putri, R.I.; Wibowo, S.; Rifa’i, M. Maximum power point tracking for photovoltaic using incremental conductance method. Energy Procedia 2015, 68, 22–30. [Google Scholar] [CrossRef]
- Safari, A.; Mekhilef, S. Simulation and hardware implementation of incremental conductance MPPT with direct control method using Cuk converter. IEEE Trans. Ind. Electron. 2011, 58, 1154–1161. [Google Scholar] [CrossRef]
- Setyawan, L.; Peng, W.; Jianfang, X. Implementation of sliding mode control in DC Microgrids. In Proceedings of the 2014 IEEE 9th Conference IEEE Industrial Electronics and Applications (ICIEA), Hangzhou, China, 9–11 June 2014; pp. 578–583. [Google Scholar]
- Teodorescu, R.; Liserre, M.; Rodriguez, P. Grid Converters for Photovoltaic and Wind Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 29. [Google Scholar]
- Vijayaragavan, K.P. Feasibility of DC Microgrids for Rural Electrification; Dalarna University: Falun, Sweden, 2017. [Google Scholar]
- Garg, A.; Nayak, R.S.; Gupta, S. Comparison of P & O and Fuzzy Logic Controller in MPPT for Photovoltaic (PV) Applications by Using MATLAB/Simulink. IOSR J. Electr. Electron. Eng. 2015, 4, 53–62. [Google Scholar]
- Solaredge. 2016. Available online: https://www.solaredge.com/sites/default/files/monitoring_performance_ratio_calculation (accessed on 2 April 2018).
- Takun, P.; Kaitwanidvilai, S.; Jettanasen, C. Maximum power point tracking using fuzzy logic control for photovoltaic systems. In Proceedings of the International MultiConference of Engineers and Computer Scientists, Hongkong, China, 16–18 March 2011. [Google Scholar]
- Sun, J. Voltage Regulation of DC-microgrid with PV and Battery. Ph.D. Thesis, Case Western Reserve University, Cleveland, OH, USA, 2017. [Google Scholar]
- Ahamed, M.F.; Dissanayake, U.D.; De Silva, H.P.; Kumara, H.P.; Lidula, N.A. Designing and simulation of a DC microgrid in PSCAD. In Proceedings of the 2016 IEEE International Conference on Power System Technology (POWERCON), Wollongong, Australia, 28 September–1 October 2016; pp. 1–6. [Google Scholar]
- Boroyevich, D.; Cvetkovic, I.; Burgos, R.; Dong, D. Intergrid: A Future Electronic Energy Network? IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 127–138. [Google Scholar] [CrossRef]
- Patterson, B.T. Come Home: DC Microgrids and the Birth of the ‘Enernet’. IEEE Power Energy Mag. 2012, 10, 60–69. [Google Scholar] [CrossRef]
- Singh, R.; Shenai, K. DC Microgrids and the Virtues of Local Electricity; IEEE Spectrum: New York, NY, USA, 2014. [Google Scholar]
- Abdelaziz, M.M.A.; Farag, H.E.; El-Saadany, E.F.; Mohamed, Y.A.R.I. A novel and generalized three-phase power flow algorithm for islanded microgrids using a newton trust region method. IEEE Trans. Power Syst. 2013, 28, 190–201. [Google Scholar] [CrossRef]
- Mahmood, H.; Michaelson, D.; Jin, J. Accurate Reactive Power Sharing in an Islanded Microgrid Using Adaptive Virtual Impedances. IEEE Trans. Power Electron. 2015, 30, 1605–1617. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, W.; Burgos, R.; Boroyevich, D. Droop voltage range design in DC micro-grids considering cable resistance. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 770–777. [Google Scholar]
- Ali, A.; Saied, M.; Mostafa, M.; Abdel-Moneim, T. A survey of maximum PPT techniques of PV systems. In Proceedings of the IEEE Energytech, Cleveland, OH, USA, 29–31 May 2012. [Google Scholar]
- Abouobaida, H.; Cherkaoui, M. Comparative study of maximum power point trackers for fast changing environmental conditions. In Proceedings of the 2012 International Conference on Multimedia Computing and Systems (ICMCS), Tangiers, Morocco, 10–12 May 2012; pp. 1131–1136. [Google Scholar]
- Subudhi, B.; Pradhan, R. A comparative study on maximum power point tracking techniques for photovoltaic power systems. IEEE Trans. Sustain. Energy 2013, 4, 89–98. [Google Scholar] [CrossRef]
- El-Shahat, A. PV Module Optimum Operation Modeling. J. Power Technol. 2014, 94, 50–66. [Google Scholar]
- El-Shahat, A. Maximum Power Point Genetic Identification Function for Photovoltaic System. Int. J. Res. Rev. Appl. Sci. 2010, 3, 264–273. [Google Scholar]
- El-Shahat, A. PV Cell Module Modeling & ANN Simulation for Smart Grid Applications. J. Theor. Appl. Inf. Technol. 2010, 16, 9–20. [Google Scholar]
- El-Shahat, A. DC-DC Converter Duty Cycle ANN Estimation for DG Applications. J. Electr. Syst. 2013, 9, 1112–5209. [Google Scholar]
- El-Shahat, A. Stand-alone PV System Simulation for DG Applications, Part I: PV Module Modeling and Inverters. J. Autom. Syst. Eng. 2012, 6, 36–54. [Google Scholar]
- El-Shahat, A. Stand-alone PV System Simulation for DG Applications, Part II: DC-DC Converter feeding Maximum Power to Resistive Load. J. Autom. Syst. Eng. 2012, 6, 55–72. [Google Scholar]
- Abidi, H.; Abdelghani, A.; Montesinos-Miracle, D. MPPT algorithm and photovoltaic array emulator using DC/DC converters. In Proceedings of the 2012 16th IEEE Mediterranean Electro Technical Conference, Hammamet, Tunisia, 25–28 March 2012; pp. 567–572. [Google Scholar]
- Potnuru, S.; Pattabiraman, D.; Ganesan, S.; Chilakapati, N. Positioning of PV panels for reduction in line losses and mismatch losses in PV array. Renew. Energy 2015, 78, 264–275. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Lauss, G. The performance of perturb and observe and incremental conductance maximum power point tracking method under dynamic weather conditions. Appl. Energy 2014, 119, 228–236. [Google Scholar] [CrossRef]
- Lian, K.; Jhang, J.; Tian, I. A maximum power point tracking method based on perturb-and-observe combined with particle swarm optimisation. IEEE J. Photovolt. 2014, 4, 626–633. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z. A deterministic particle swarm optimization maximum power point tracker for photovoltaic system under partial shading condition. IEEE Trans. Ind. Electron. 2013, 60, 3195–3206. [Google Scholar] [CrossRef]
- Mirbagheri, S.; Aldeen, M.; Saha, S. A PSO-based MPPT re-initialised by incremental conductance method for a standalone PV system. In Proceedings of the 2015 23th Mediterranean Conference on Control and Automation (MED), Torremolinos, Spain, 16–19 June 2015. [Google Scholar]
- Benigni, A.; Monti, A. A parallel approach to real-time simulation of power electronics systems. IEEE Trans. Power Electron. 2015, 30, 5192–5206. [Google Scholar] [CrossRef]
- Jung, J. Power hardware-in-the-loop simulation (PHILS) of photovoltaic power generation using real-time simulation techniques and power interfaces. J. Power Sources 2015, 285, 137–145. [Google Scholar] [CrossRef]
- Koad, R.; Zobaa, A.; El-Shahat, A. A novel MPPT algorithm based on particle swarm optimization for photovoltaic systems. IEEE Trans. Sustain. Energy 2017, 8, 468–476. [Google Scholar] [CrossRef]
- Koad, R.; Zobaa, A. Comparison study of five maximum power point tracking techniques for photovoltaic energy systems. Int. J. Energy Convers. 2014, 2, 17–25. [Google Scholar]
- Koad, R.; Zobaa, A. Comparison between the conventional methods and PSO based MPPT algorithm for photovoltaic systems. Int. J. Electr. Comput. Energet. Electron. Commun. Eng. 2014, 8, 690–695. [Google Scholar]
- Mazumder, S.; De-la-Fuente, E. Transient stability analysis of power system using polynomial Lyapunov function based approach. In Proceedings of the 2014 IEEE PES General Meeting|Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar]
- Mazumder, S.; De-la-Fuente, E. Dynamic stability analysis of power network. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 5808–5815. [Google Scholar]
- Mazumder, S.; De-la-Fuente, E. Stability Analysis of Micro Power Network. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 2016, 6. [Google Scholar]
- Chamana, M.; Bayne, S.B. Modeling and control of directly connected and inverter interfaced sources in a microgrid. In Proceedings of the North American Power Symposium (NAPS), Boston, MA, USA, 4–6 August 2011. [Google Scholar]
- Zhang, T. Adaptive Energy Storage System Control for Microgrid Stability Enhancement. Ph.D. Thesis, Worcester Polytechnic Institute, Worcester, MA, USA, 2018. [Google Scholar]
- Alaboudy, A.; Zeineldin, H.; Kirtley, J. Microgrid stability characterization subsequent to fault-triggered islanding incidents. IEEE Trans. Power Deliv. 2012, 27, 658–669. [Google Scholar] [CrossRef]
- Bachovchin, K. Design, Modeling, and Power Electronic Control for Transient Stabilization of Power Grids Using Flywheel Energy Storage Systems. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2015. [Google Scholar]
- Kanchanaharuthai, A.; Chankong, V.; Loparo, K. Transient stability and voltage regulation in multimachine power systems vis statcom and battery energy storage. IEEE Trans. Power Syst. 2015, 30, 2404–2416. [Google Scholar] [CrossRef]
- Yu, J. Hybrid AC-High Voltage DC Grid Stability and Controls. Ph.D. Thesis, Arizona State University, Tempe, AZ, USA, 2017. [Google Scholar]
- Majumder, R. Some aspects of stability in microgrids. IEEE Trans. Power Syst. 2013, 28, 3243–3252. [Google Scholar] [CrossRef]
- Kundur, P.; Paserba, J.; Ajjarapu, V.; Andersson, G.; Bose, A.; Canizares, C.; Hatziargyriou, N.; Hill, D.; Stankovic, A.; Taylor, C.; et al. Definition and classification of power system stability IEEE/CIGRE joint task force on stability terms and definitions. IEEE Trans. Power Syst. 2004, 19, 1387–1401. [Google Scholar]
- Elizondo, J.; Kirtley, J. Effect of inverter-based dg penetration and control in hybrid microgrid dynamics and stability. In Proceedings of the 2014 Power and Energy Conference at Illinois (PECI), Champaign, IL, USA, 28 February–1 March 2014. [Google Scholar]
- Bottrell, N.; Prodanovic, M.; Green, T. Dynamic stability of a microgrid with an active load. IEEE Trans. Power Electron. 2013, 28, 5107–5119. [Google Scholar] [CrossRef]


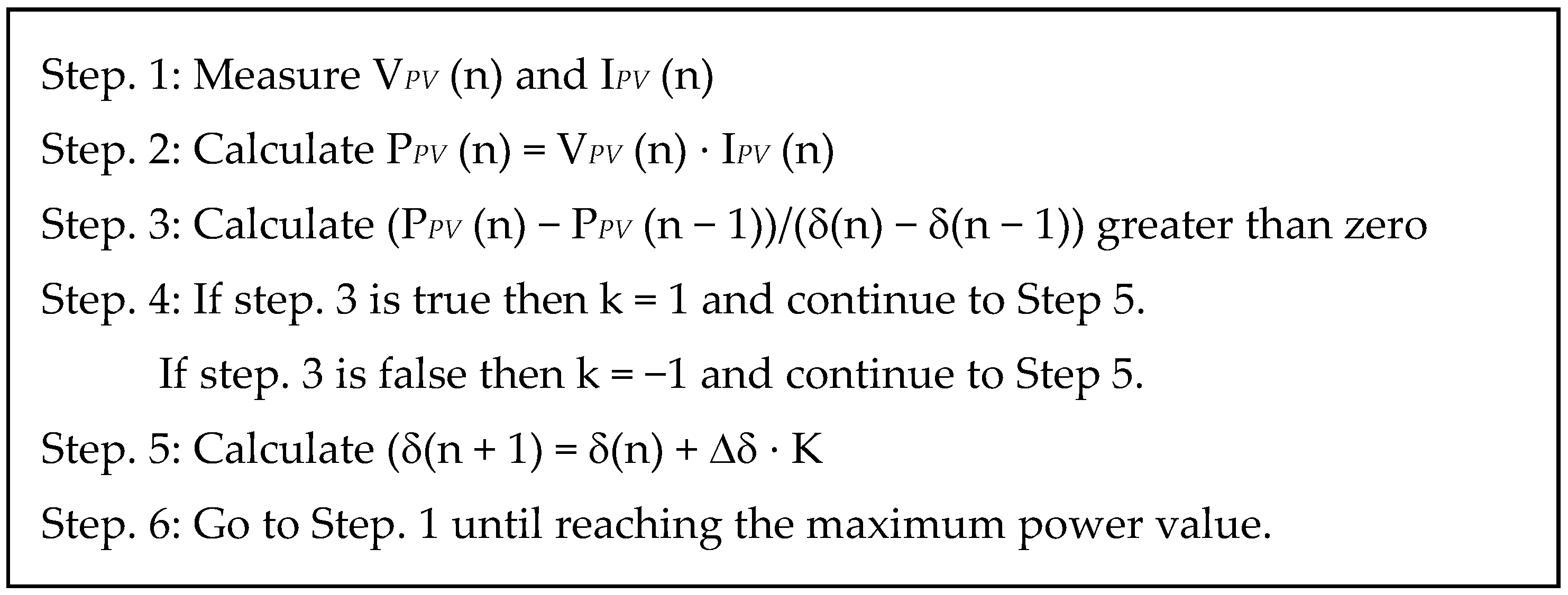

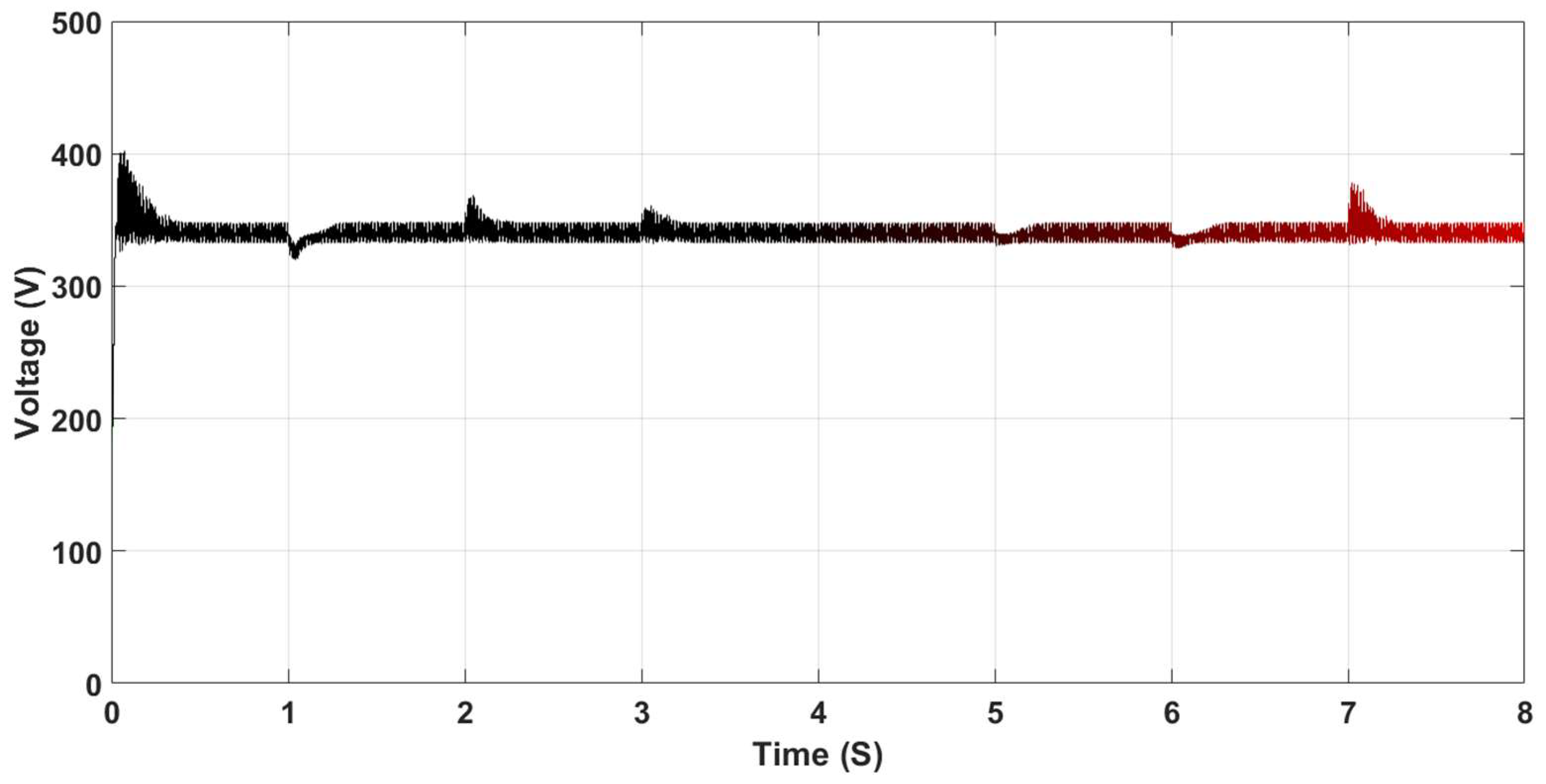
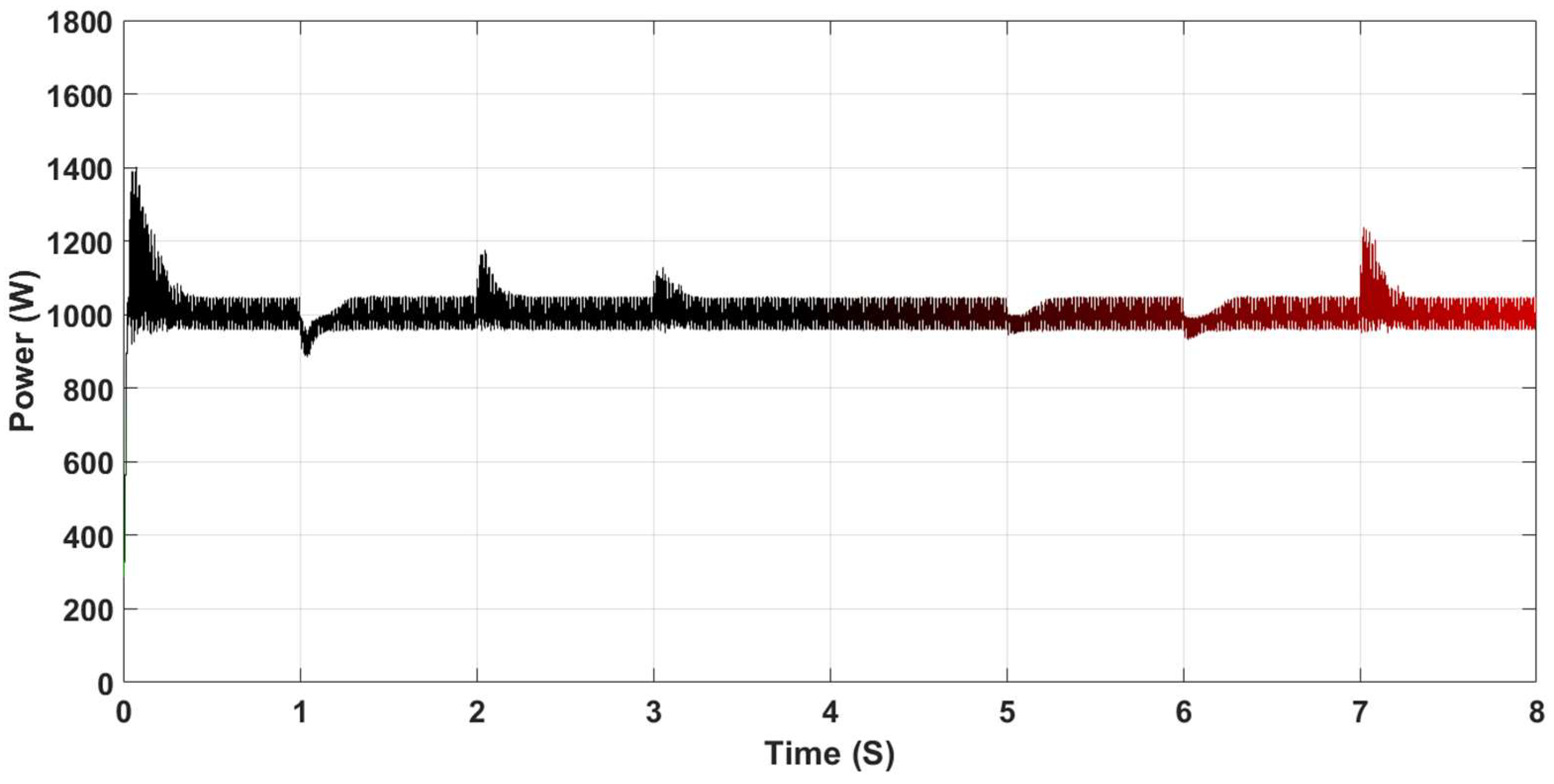
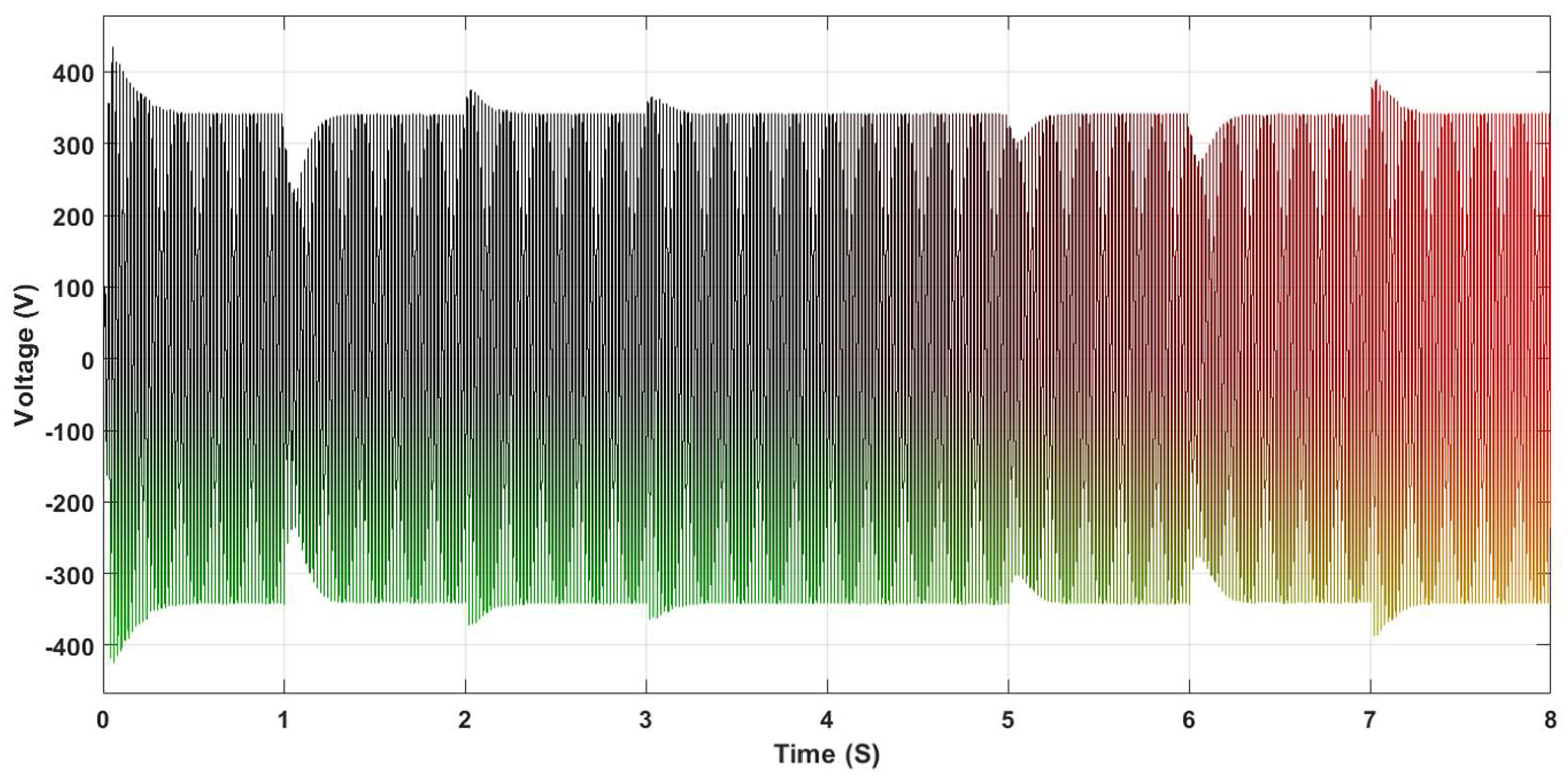
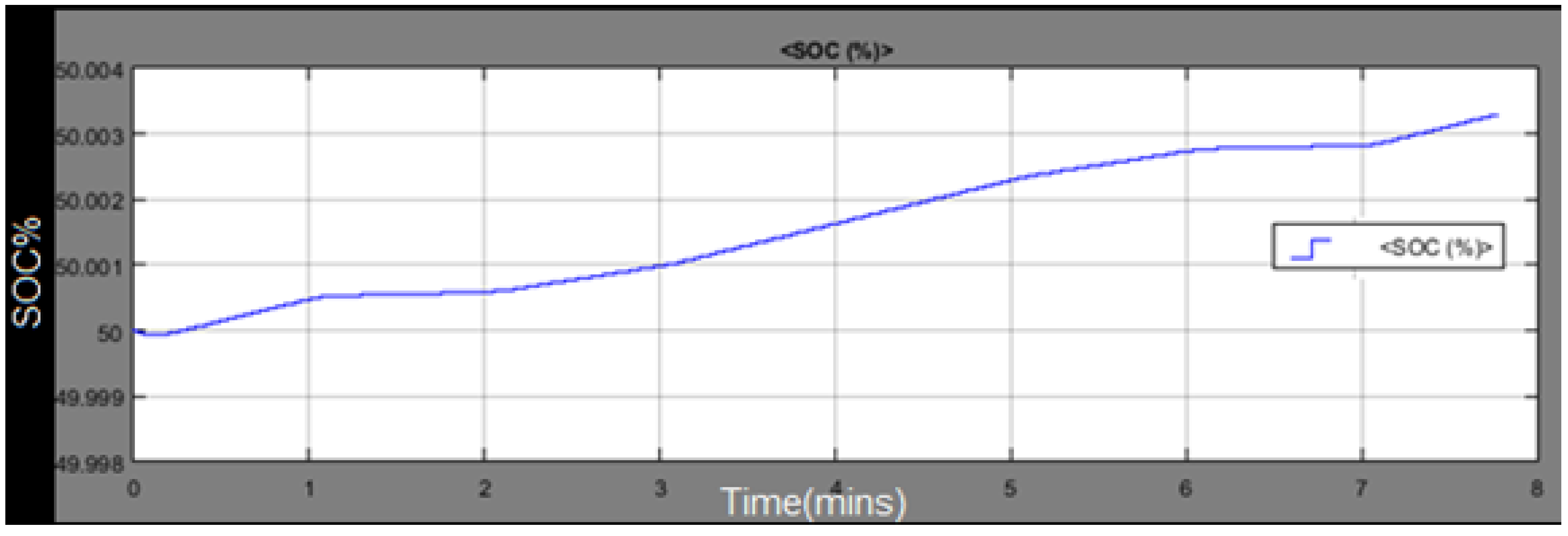

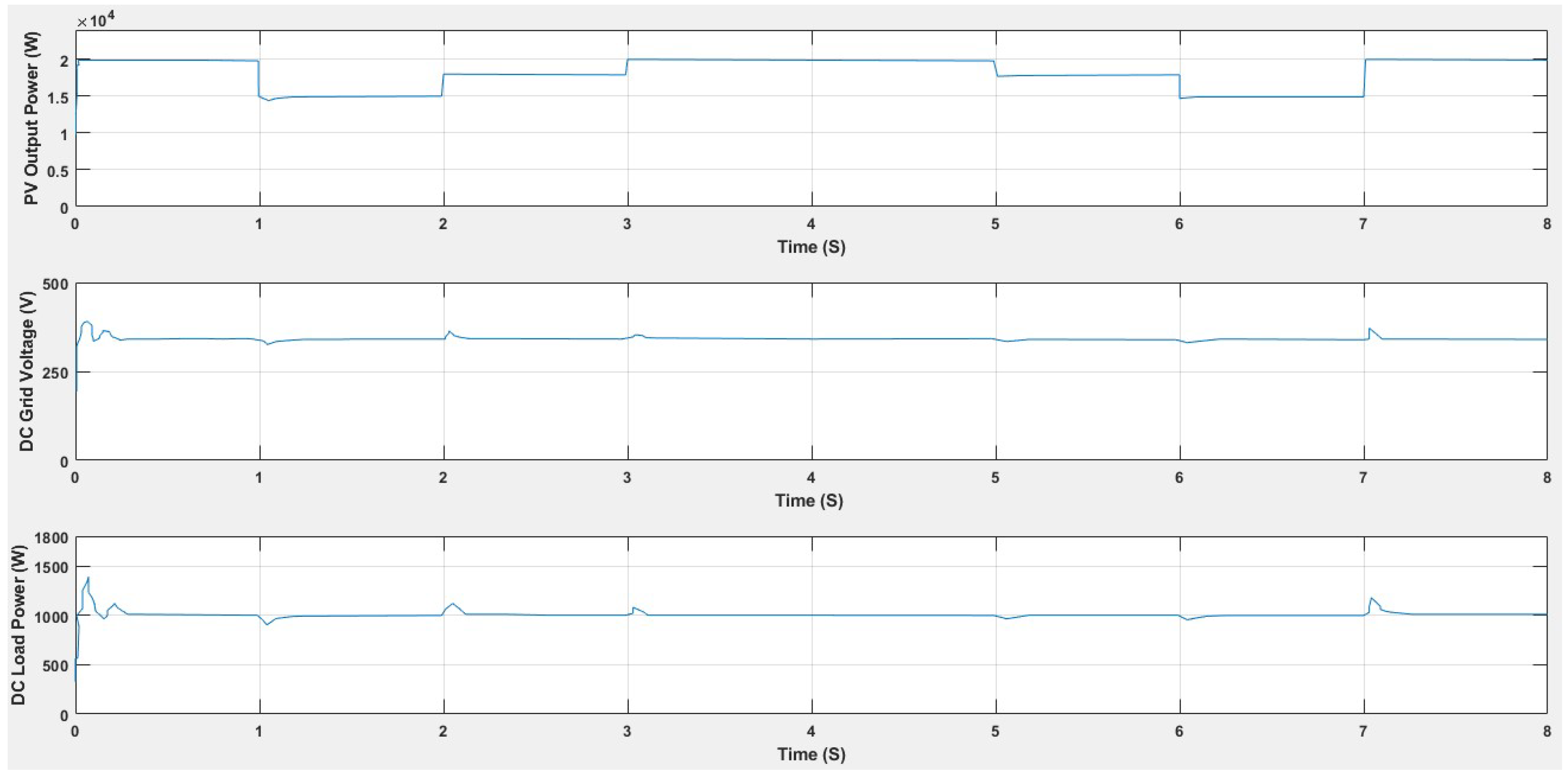
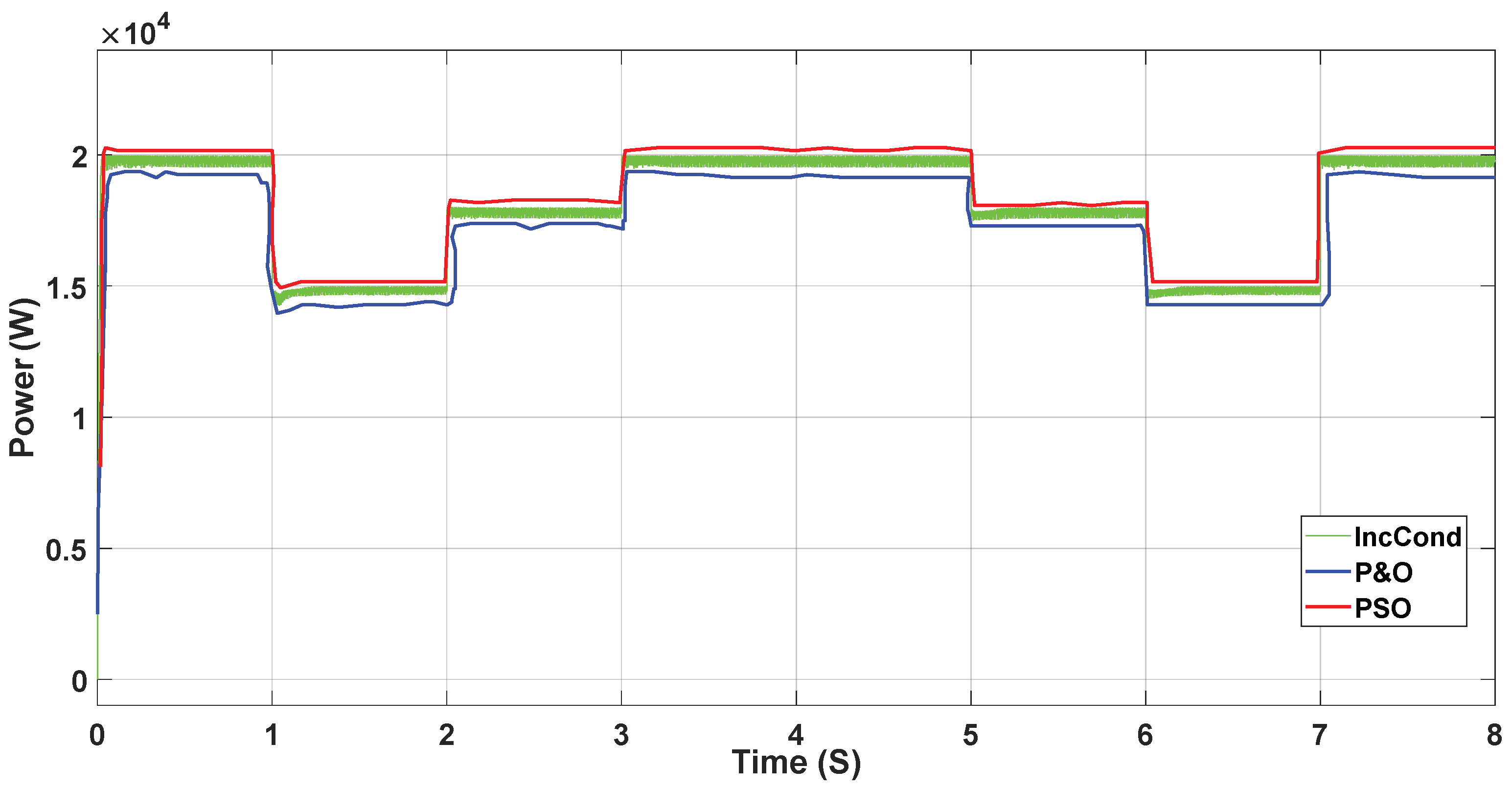

| Parameters of the Inverter | Value |
|---|---|
| Dc grid Voltage | 340 VDC |
| DC bus capacitor | 1000 µF |
| Filter capacitors | 1000 µF |
| Filter Inductor | 18 mH |
| Frequency | 50 Hz |
| Symbols | Description | Value | Unit |
|---|---|---|---|
| Q | Rated Capacity | 1150 | Ah |
| SOC | Initial State-of-Charge | 50 | % |
| V | Nominal Voltage | 160 | V |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Shahat, A.; Sumaiya, S. DC-Microgrid System Design, Control, and Analysis. Electronics 2019, 8, 124. https://doi.org/10.3390/electronics8020124
El-Shahat A, Sumaiya S. DC-Microgrid System Design, Control, and Analysis. Electronics. 2019; 8(2):124. https://doi.org/10.3390/electronics8020124
Chicago/Turabian StyleEl-Shahat, Adel, and Sharaf Sumaiya. 2019. "DC-Microgrid System Design, Control, and Analysis" Electronics 8, no. 2: 124. https://doi.org/10.3390/electronics8020124
APA StyleEl-Shahat, A., & Sumaiya, S. (2019). DC-Microgrid System Design, Control, and Analysis. Electronics, 8(2), 124. https://doi.org/10.3390/electronics8020124





