Improved RMS Delay Spread Estimation for mmWave Channels Using Savitzky–Golay Filters
Abstract
1. Introduction
2. Channel Parameter Estimation from CTF Magnitude
2.1. Channel Model and Parameter Estimation Method
2.2. Noise Influence on Parameter Estimation Accuracy
2.3. Savitzky–Golay (S-G) Filter
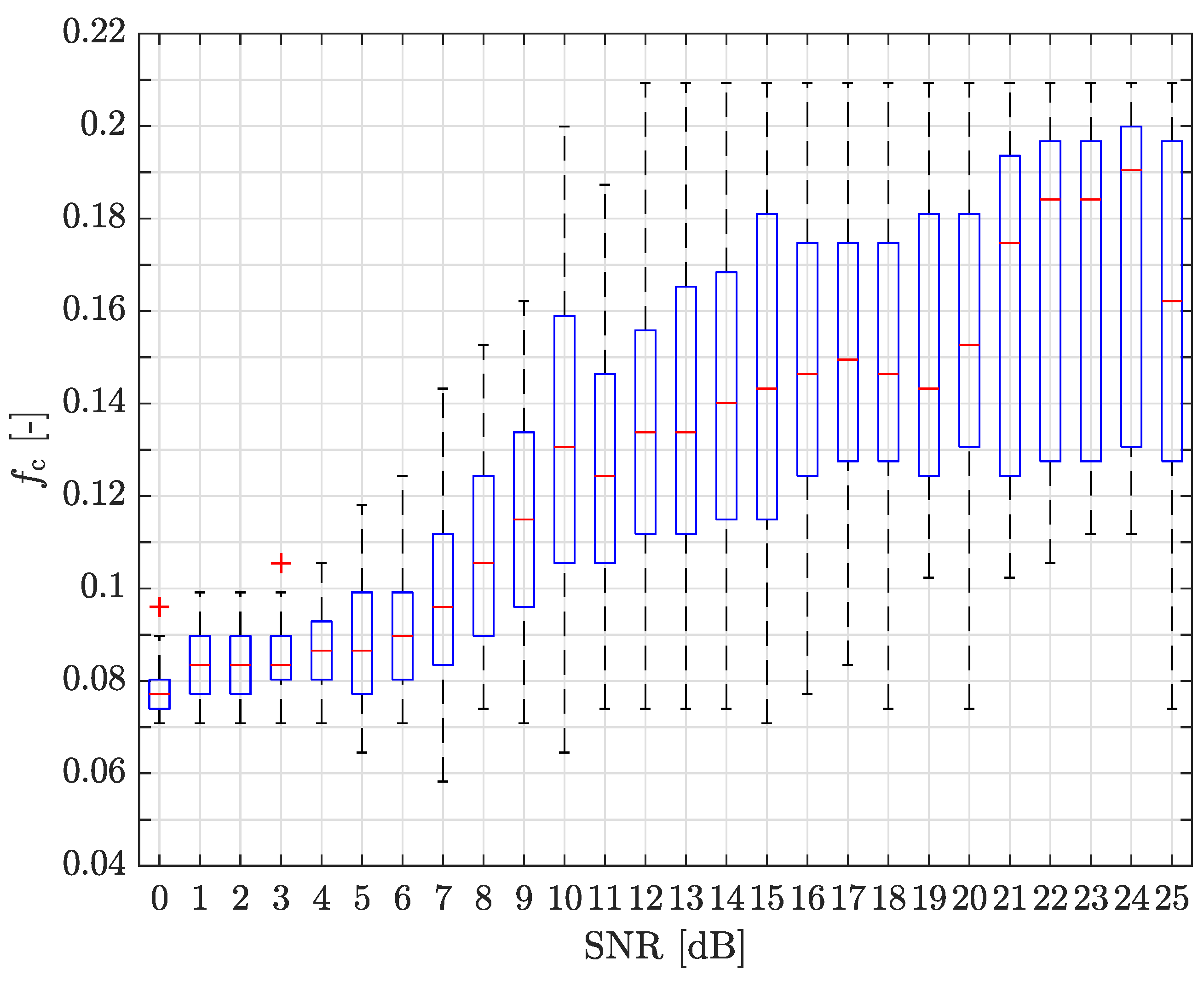
2.4. Optimal S-G Cut-Off Frequency for Application on Noisy CTF Magnitude
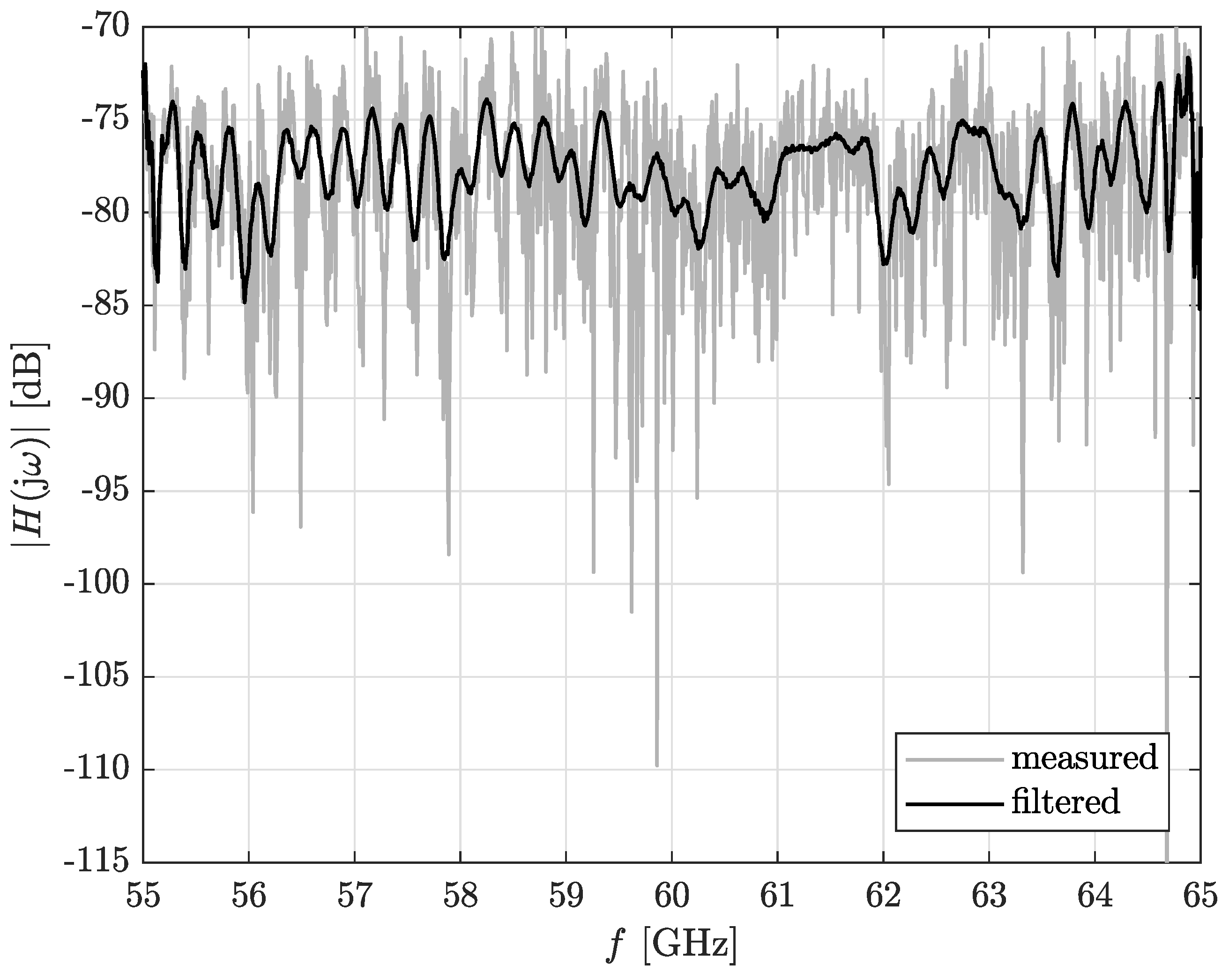
3. Application of the Savitzky–Golay Filter to the Measured CTF
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| RMS | root mean square |
| CTF | Channel Transfer Function |
| S-G filter | Savitzky–Golay filter |
| SNR | Signal-to-Noise Ratio |
| 5G | The fifth-generation networks |
| RF | Radio Frequency |
| mmWave | millimeter wave |
| OFDM | Orthogonal Frequency Division Multiplexing |
| PDP | Power Delay Profile |
| CIR | Channel Impulse Response |
| VNA | Vector Network Analyzer |
| IFFT | Inverse Fast Fourier Transform |
| TX | transmitter |
| RX | receiver |
| V2V | Vehicle-to-Vehicle |
| LCR | Level Crossing Rate |
| LOS | Line-of-Sight |
| NLOS | Non-Line-of-Sight |
| FD | frequency domain |
| ABF | Average Bandwidth Of Fades |
| CDF | Cumulative Distribution Function |
| AWGN | Additive White Gaussian Noise |
| MSE | Mean Squared Error |
| TWDP | Two-wave channel model with diffuse power fading |
References
- Molisch, A.F. Statistical properties of the RMS delay-spread of mobile radio channels with independent Rayleigh fading paths. IEEE Trans. Veh. Technol. 1996, 45, 201–204. [Google Scholar] [CrossRef]
- Witrisal, K. On estimating the RMS delay spread from the frequency-domain level crossing rate. IEEE Commun. Lett. 2001, 5, 287–289. [Google Scholar] [CrossRef]
- Chandra, A.; Prokes, A.; Mikulasek, T.; Blumenstein, J.; Kukolev, P.; Zemen, T.; Mecklenbrauker, C.F. Frequency-domain in-vehicle UWB channel modeling. IEEE Trans. Veh. Technol. 2016, 65, 3929–3940. [Google Scholar] [CrossRef]
- Muquet, B.; Wang, Z.; Giannakis, G.B.; De Courville, M.; Duhamel, P. Cyclic prefix or zero padding for wireless multicarrier transmissions? IEEE Trans. Commun. 2002, 50, 2136–2148. [Google Scholar] [CrossRef]
- Molisch, A.F. Wireless Communications, 2nd ed.; John Wiley and Sons: Chichester, UK, 2011. [Google Scholar]
- Flikkema, P.G.; Johnson, S.G. A comparison of time- and frequency-domain wireless channel sounding techniques. In Proceedings of the SOUTHEASTCON’96, Tampa, FL, USA, 11–14 April 1996; pp. 488–491. [Google Scholar]
- Witrisal, K.; Kim, Y.-H.; Prasad, R. RMS delay spread estimation technique using non-coherent channel measurements. Electron. Lett. 1998, 34, 1918–1919. [Google Scholar] [CrossRef]
- Witrisal, K.; Bohdanowicz, A. Influence of noise on a novel RMS delay spread estimation method. In Proceedings of the 11th IEEE International Symposium on Personal Indoor and Mobile Radio Communications PIMRC, London, UK, 18–21 September 2000; pp. 560–566. [Google Scholar]
- Bohdanowicz, A.; Janssen, G.J.M.; Pietrzyk, S. Wideband indoor and outdoor multipath channel measurements at 17 GHz. In Proceedings of the IEEE VTS 50th Vehicular Technology Conference (VTC 1999-Fall), Amsterdam, The Netherlands, 19–22 September 1999; pp. 1998–2003. [Google Scholar]
- Prokes, A.; Mikulasek, T.; Blumenstein, J.; Vychodil, J. Usability of Hilbert transform for complex channel transfer function calculation in 60 GHz band. In Proceedings of the Progress in Electromagnetics Research Symposium—Fall (PIERS-FALL), Singapore, 19–22 November 2017; pp. 2945–2951. [Google Scholar]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentation of data by simplified least squares procedures. Analy. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Krishnan, S.R.; Seelamantula, C.S. On the selection of optimum Savitzky-Golay filters. IEEE Trans. Signal Process. 2013, 61, 380–391. [Google Scholar] [CrossRef]
- Zöchmann, E.; Hofer, M.; Lerch, M.; Pratschner, S.; Bernado, L.; Blumenstein, J.; Prokes, A. Position-specific statistics of 60 GHz vehicular channels during overtaking. IEEE Access 2019, 7, 14216–14232. [Google Scholar] [CrossRef]
- Zöchmann, E.; Guan, K.; Rupp, M. Two-ray models in mmWave communications. In Proceedings of the IEEE 18th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Sapporo, Japan, 3–6 July 2017; pp. 1–5. [Google Scholar]
- Chen, Y.; Beaulieu, N.C. Maximum likelihood estimation of the K factor in Ricean fading channels. IEEE Commun. Lett. 2005, 9, 1040–1042. [Google Scholar] [CrossRef]
- Schafer, R.W. What is Savitzky-Golay filter? IEEE Signal Proc. Mag. 2011, 28, 111–117. [Google Scholar] [CrossRef]
- Evaluating Uncertainty Components: Type A. The NIST Reference on Constants, Units, and Uncertainity. Available online: https://physics.nist.gov/cuu/Uncertainty/typea.html (accessed on 2 November 2019).
- Garcia, D. Robust smoothing of gridded data in one and higher dimensions with missing values. Comp. Stat. Data Anal. 2010, 54, 1167–1178. [Google Scholar] [CrossRef] [PubMed]



| Parameter | Value |
|---|---|
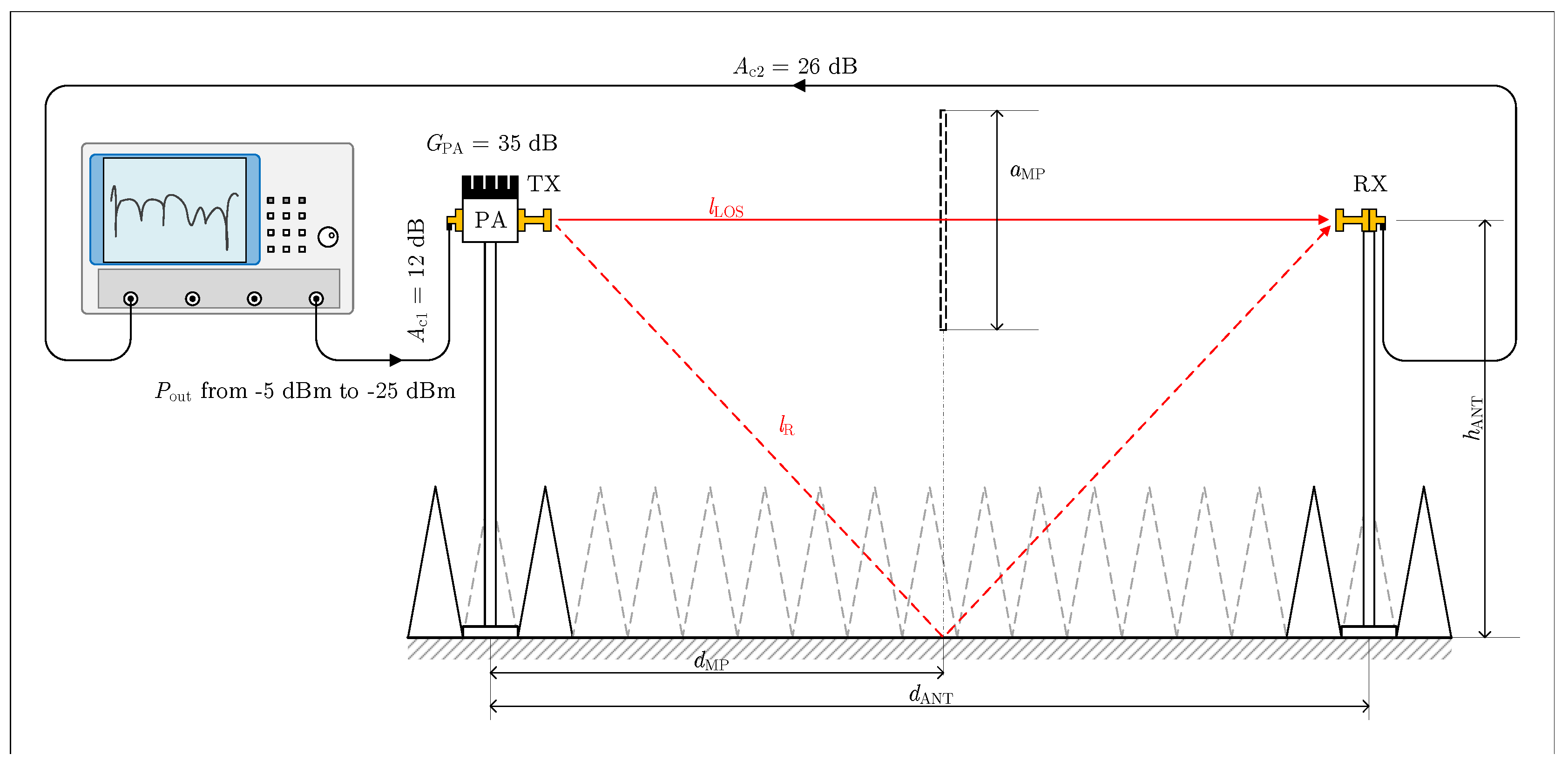
| Antenna height () | 1.245 m |
| Antenna distance () | 2.100 m |
| Meas. antenna type TX | open waveguide with power amplifier |
| Meas. antenna type RX | open waveguide |
| Antenna gain () | 9 dBi |
| TX amplifier gain () | 35 dB |
| TX cable loss () | 12 dB |
| RX cable loss () | 26 dB |
| VNA intermediate frequency bandwidth () | 100 Hz |
| Frequency range | from 55 GHz to 65 GHz |
| Observed bandwidth | 10 GHz |
| Number of points in frequency domain | 1001 |
| Measured Results without Application of S-G Filter Smoothing | |||||
| Av. | 120.4 | 178.9 | 211.0 | 212.8 | 201.3 |
| 8.8 | 27.5 | 53.9 | 55.7 | 49.0 | |
| ±0.1 ns | ±0.1 ns | ±0.2 ns | ±0.2 ns | ±0.2 ns | |
| 0.4 | 0.5 | 0.6 | 0.6 | 0.5 | |
| ±1.2 MHz | ±0.6 MHz | ±0.4 MHz | ±0.4 MHz | ± 0.4 MHz | |
| Measured Results with Application of S-G Filter Smoothing | |||||
| Av. est. SNR | 13.15 dB | 9.76 dB | 7.78 dB | 6.92 dB | 6.91 dB |
| Av. est. | 0.1344 | 0.1280 | 0.1034 | 0.0953 | 0.0954 |
| Av. | 38.3 | 49.7 | 52.6 | 44.6 | 39.4 |
| Av. | 1.49 ns | 1.47 ns | 1.33 ns | 1.44 ns | 1.80 ns |
| 0.01 | 0.01 | 0.02 | 0.05 | 0.13 | |
| 0.04 | 0.02 | 0.02 | 0.03 | 0.20 | |
| S-G Filter | Lowpass FIR Filter (Equiripple) | ||
|---|---|---|---|
 | = = = = 31 = = |  | = = = = 29 = = |
 | = = = = 29 = = |  | = = = = 62 = = |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miloš, J.; Blumenstein, J.; Prokeš, A.; Mikulášek, T.; Mecklenbräuker, C. Improved RMS Delay Spread Estimation for mmWave Channels Using Savitzky–Golay Filters. Electronics 2019, 8, 1530. https://doi.org/10.3390/electronics8121530
Miloš J, Blumenstein J, Prokeš A, Mikulášek T, Mecklenbräuker C. Improved RMS Delay Spread Estimation for mmWave Channels Using Savitzky–Golay Filters. Electronics. 2019; 8(12):1530. https://doi.org/10.3390/electronics8121530
Chicago/Turabian StyleMiloš, Jiří, Jiří Blumenstein, Aleš Prokeš, Tomáš Mikulášek, and Christoph Mecklenbräuker. 2019. "Improved RMS Delay Spread Estimation for mmWave Channels Using Savitzky–Golay Filters" Electronics 8, no. 12: 1530. https://doi.org/10.3390/electronics8121530
APA StyleMiloš, J., Blumenstein, J., Prokeš, A., Mikulášek, T., & Mecklenbräuker, C. (2019). Improved RMS Delay Spread Estimation for mmWave Channels Using Savitzky–Golay Filters. Electronics, 8(12), 1530. https://doi.org/10.3390/electronics8121530






