The P-Type Module with Virtual DC Links to Increase Levels in Multilevel Inverters
Abstract
:1. Introduction
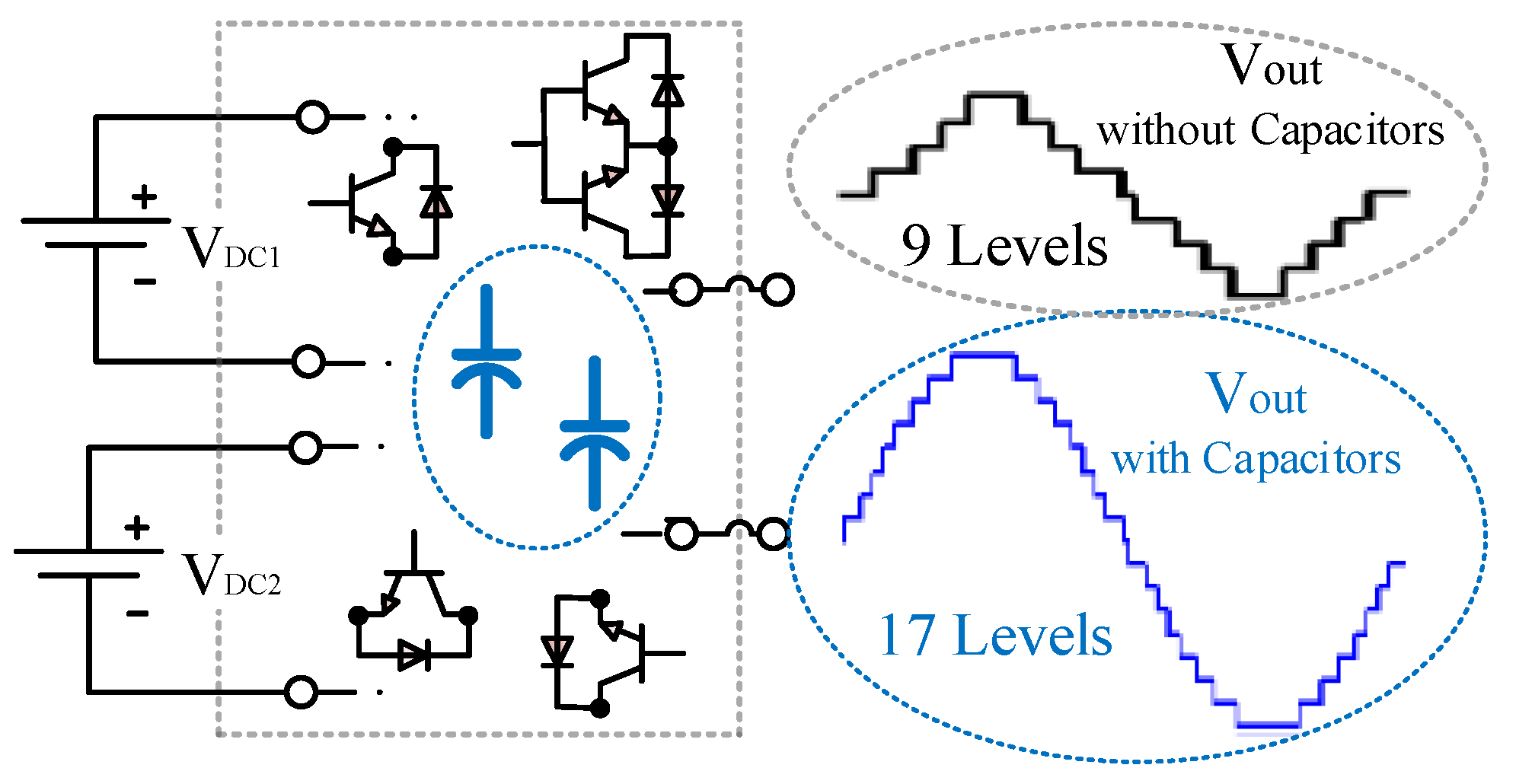
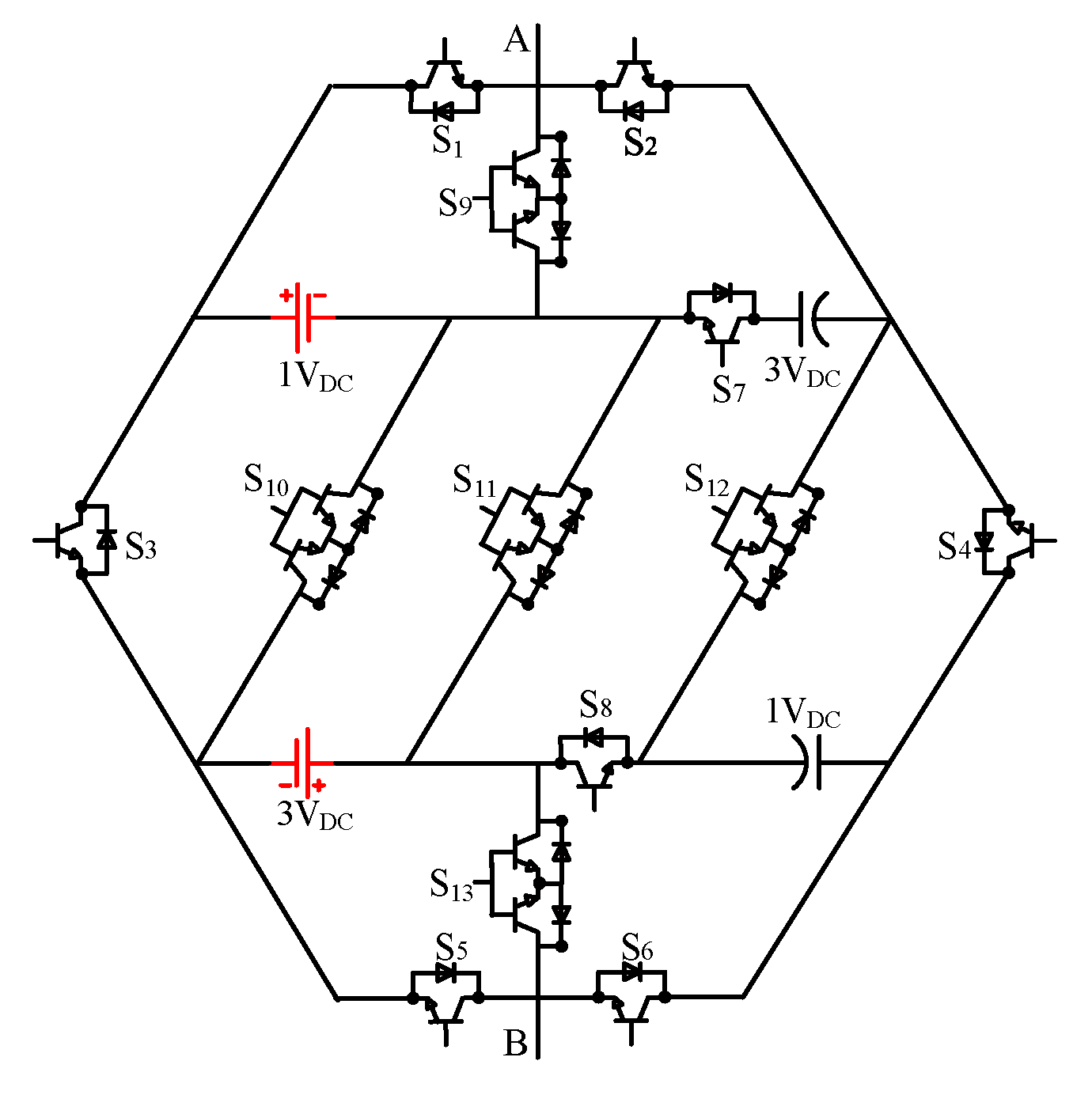
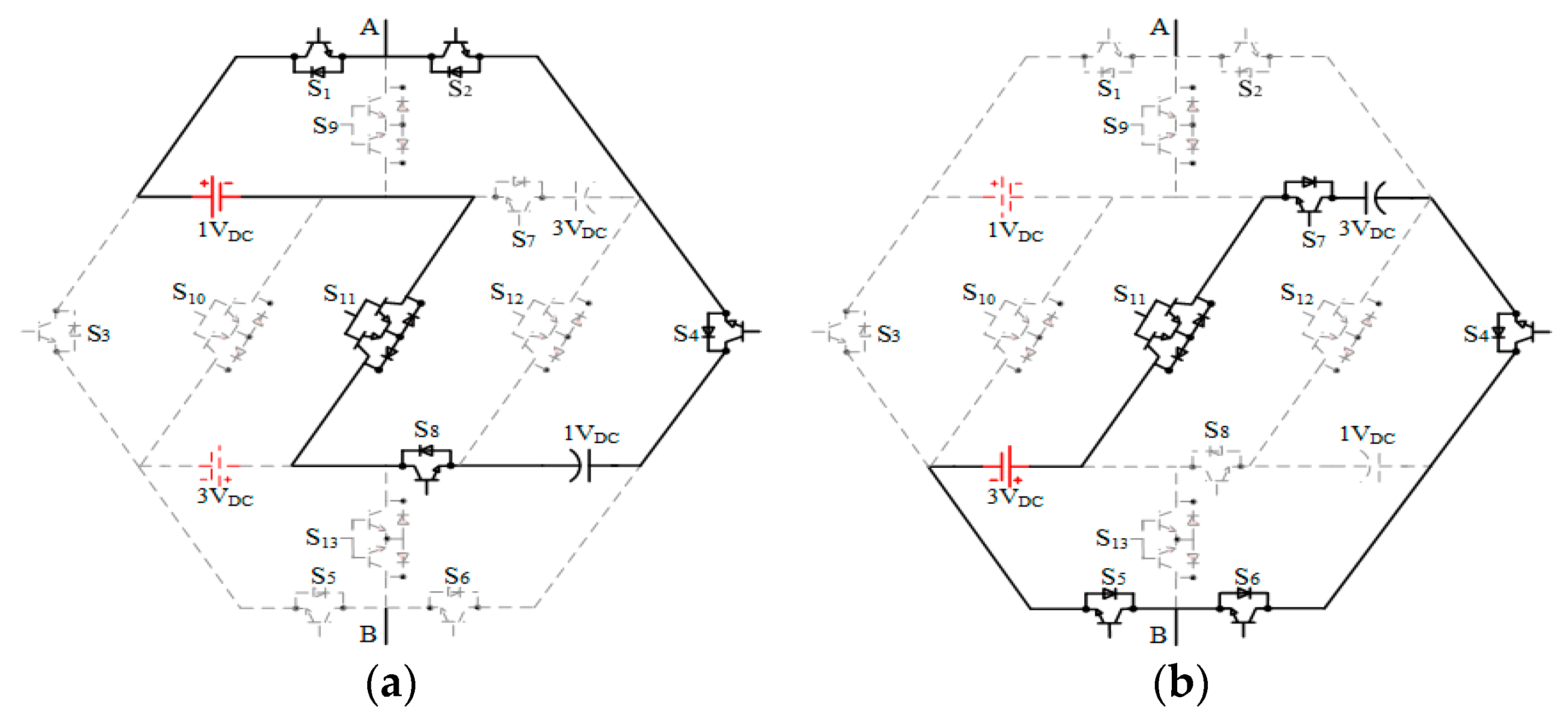
2. Proposed Module
2.1. Module Configuration
2.2. Module Extension
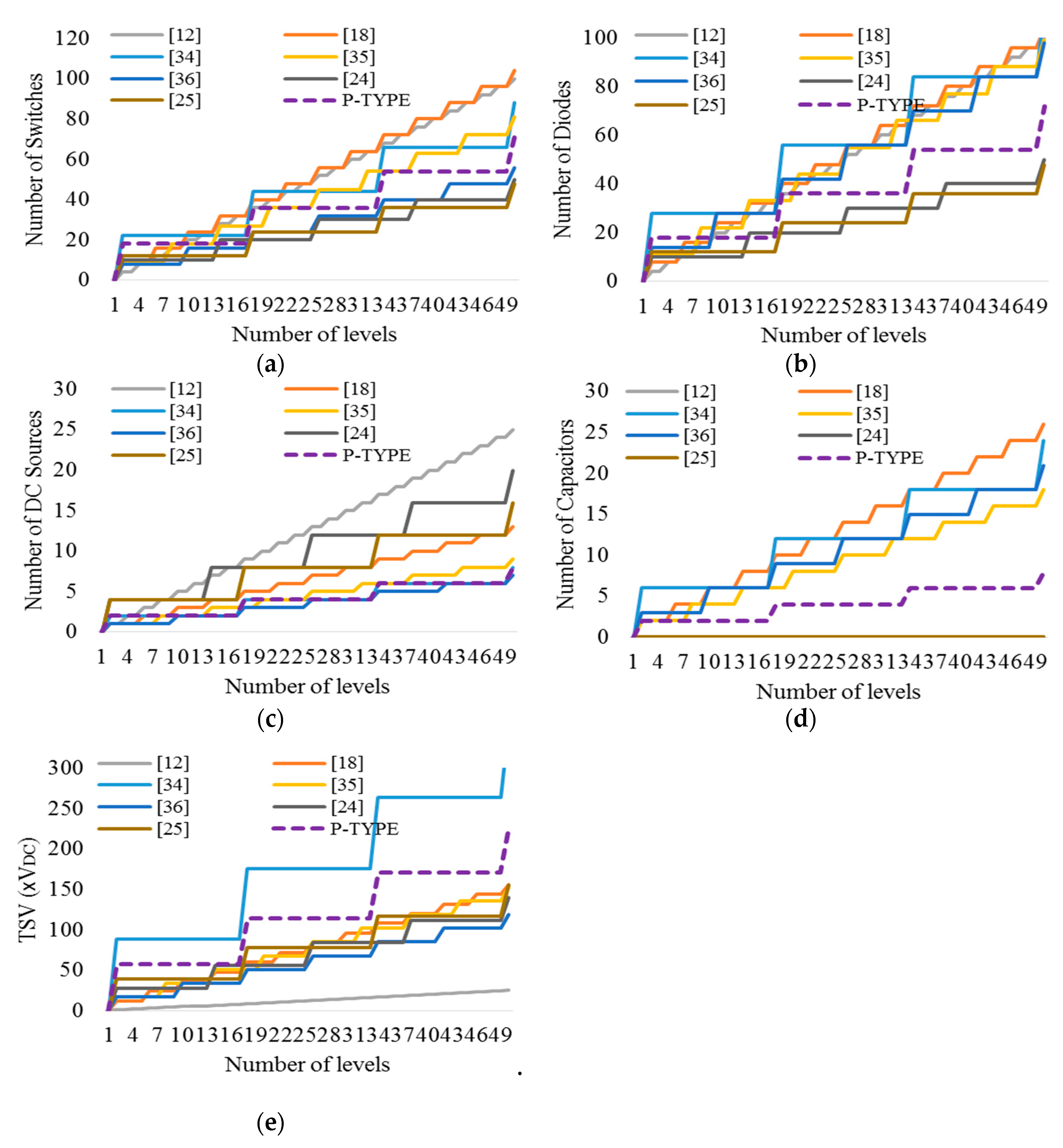
2.3. Comparative Study
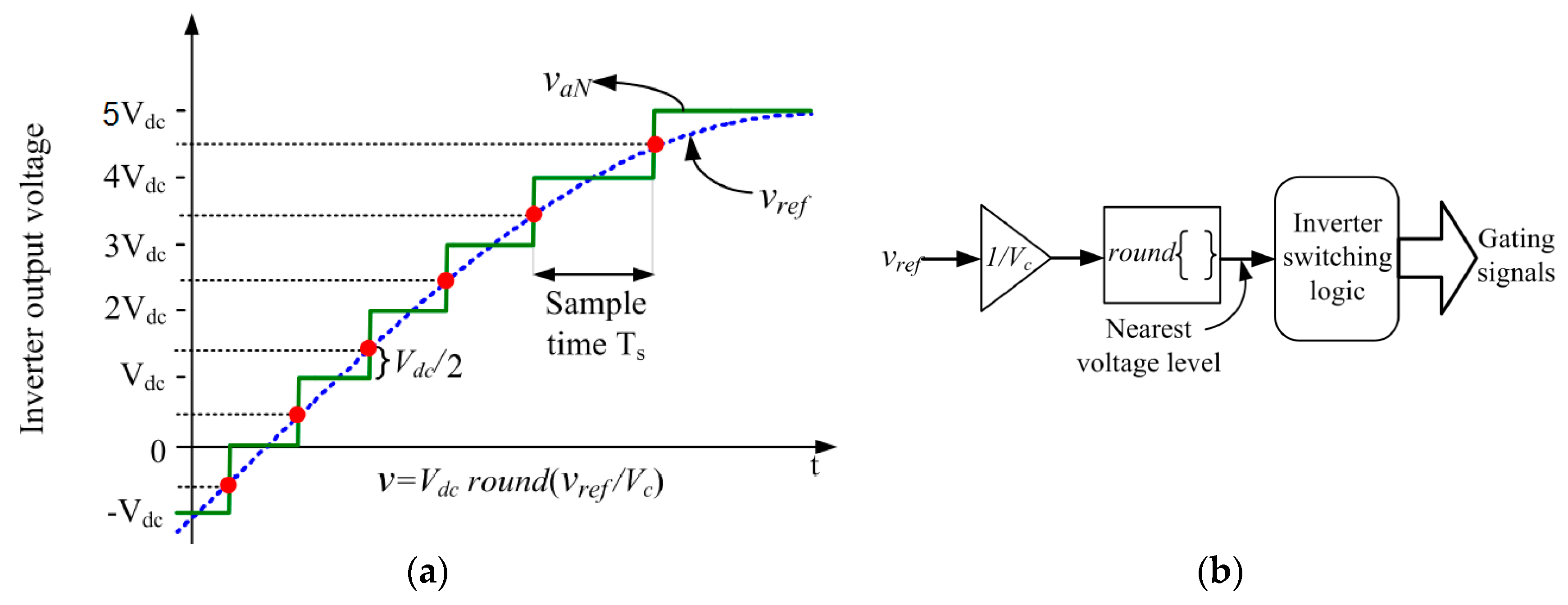
3. Nearest Level Control (NLC) Modulation Method
4. The Analysis of Capacitors Ripple
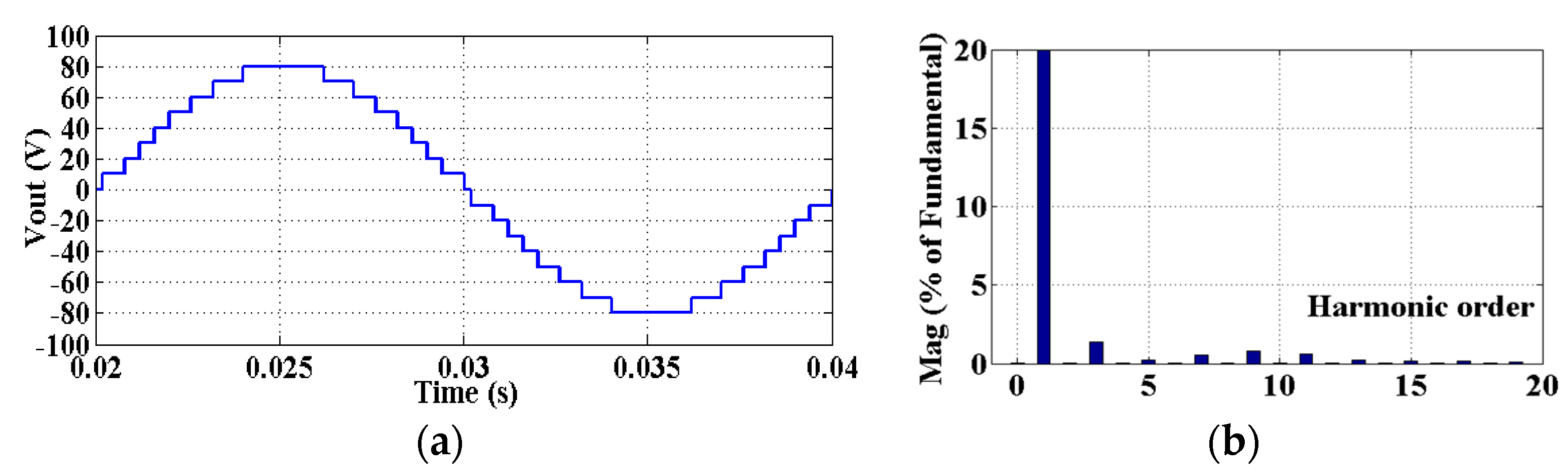
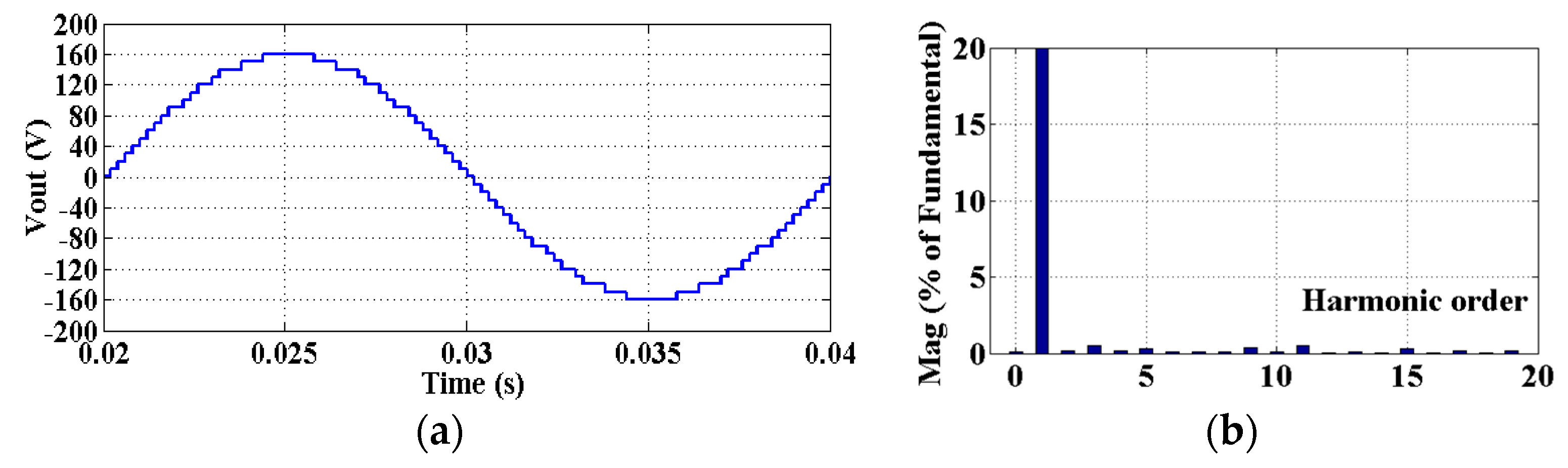
5. Simulation Results
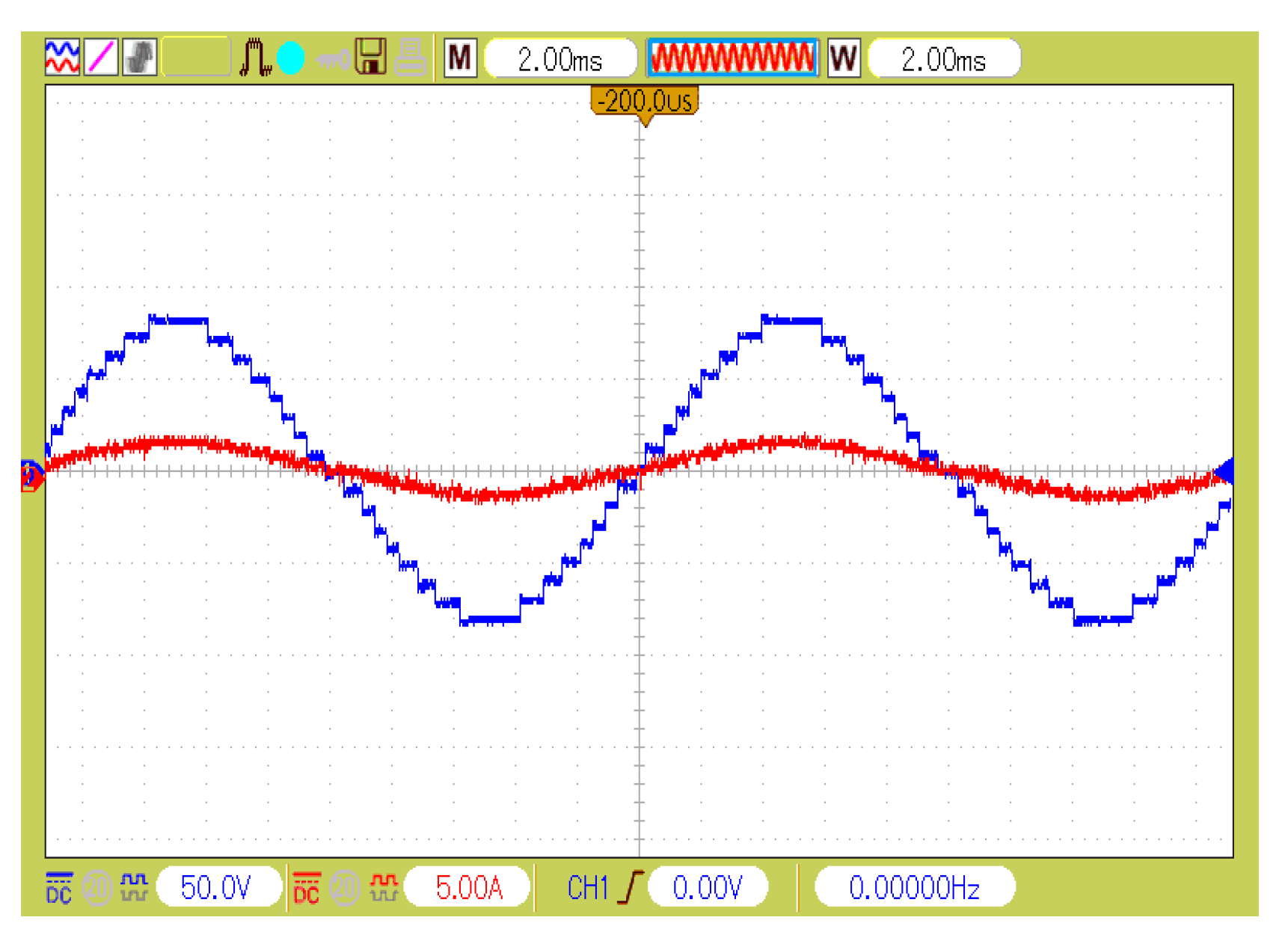
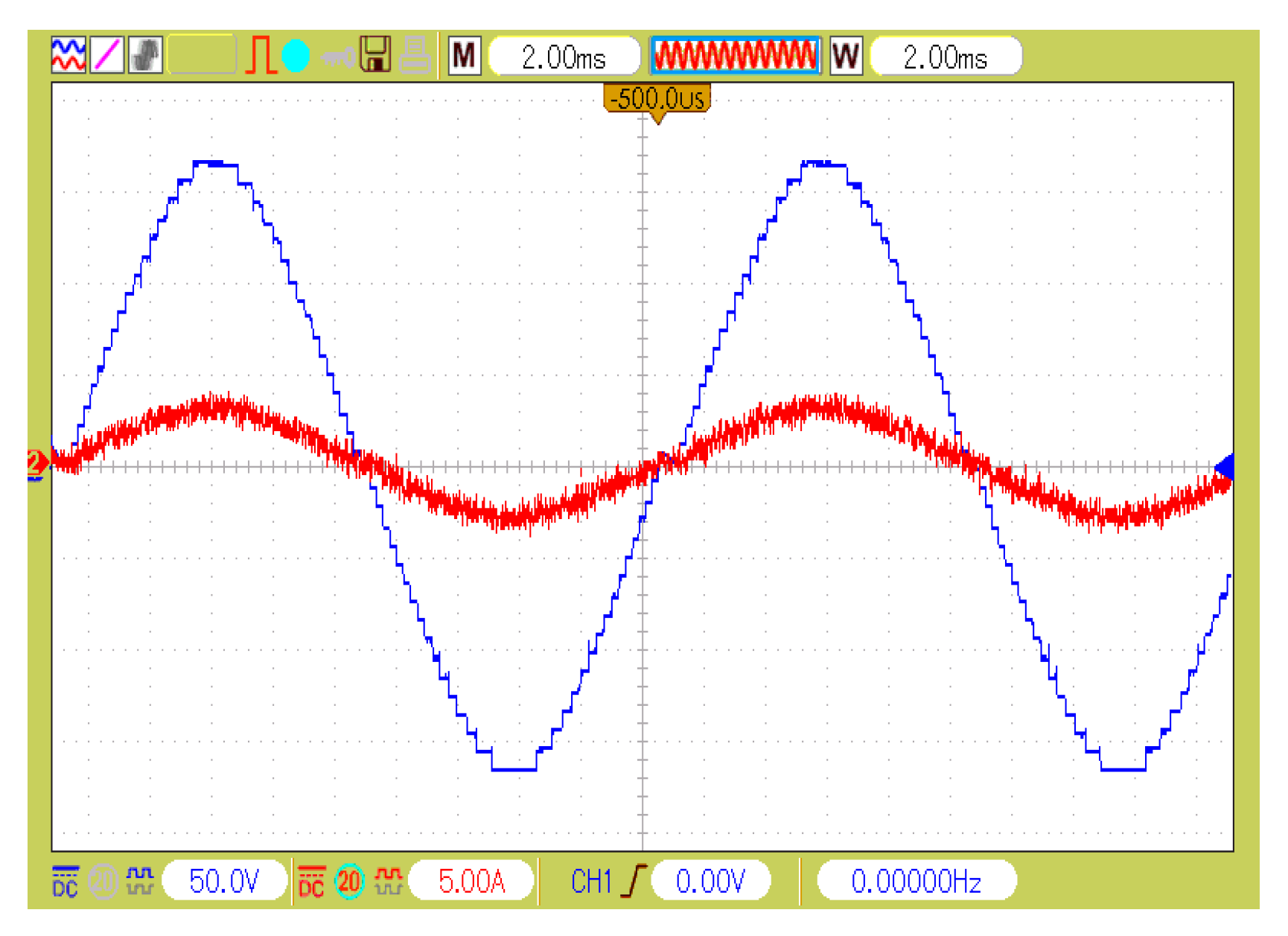
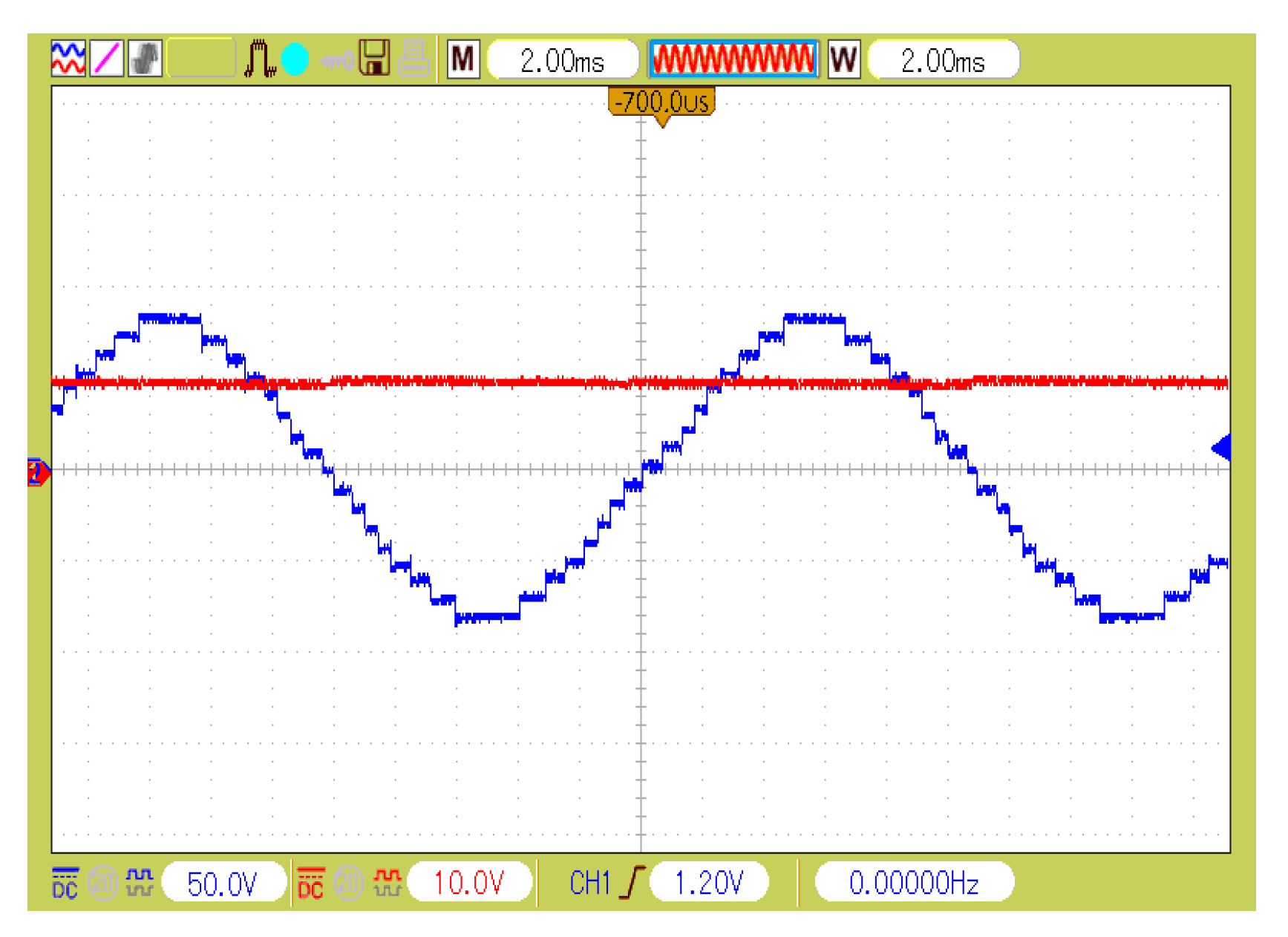
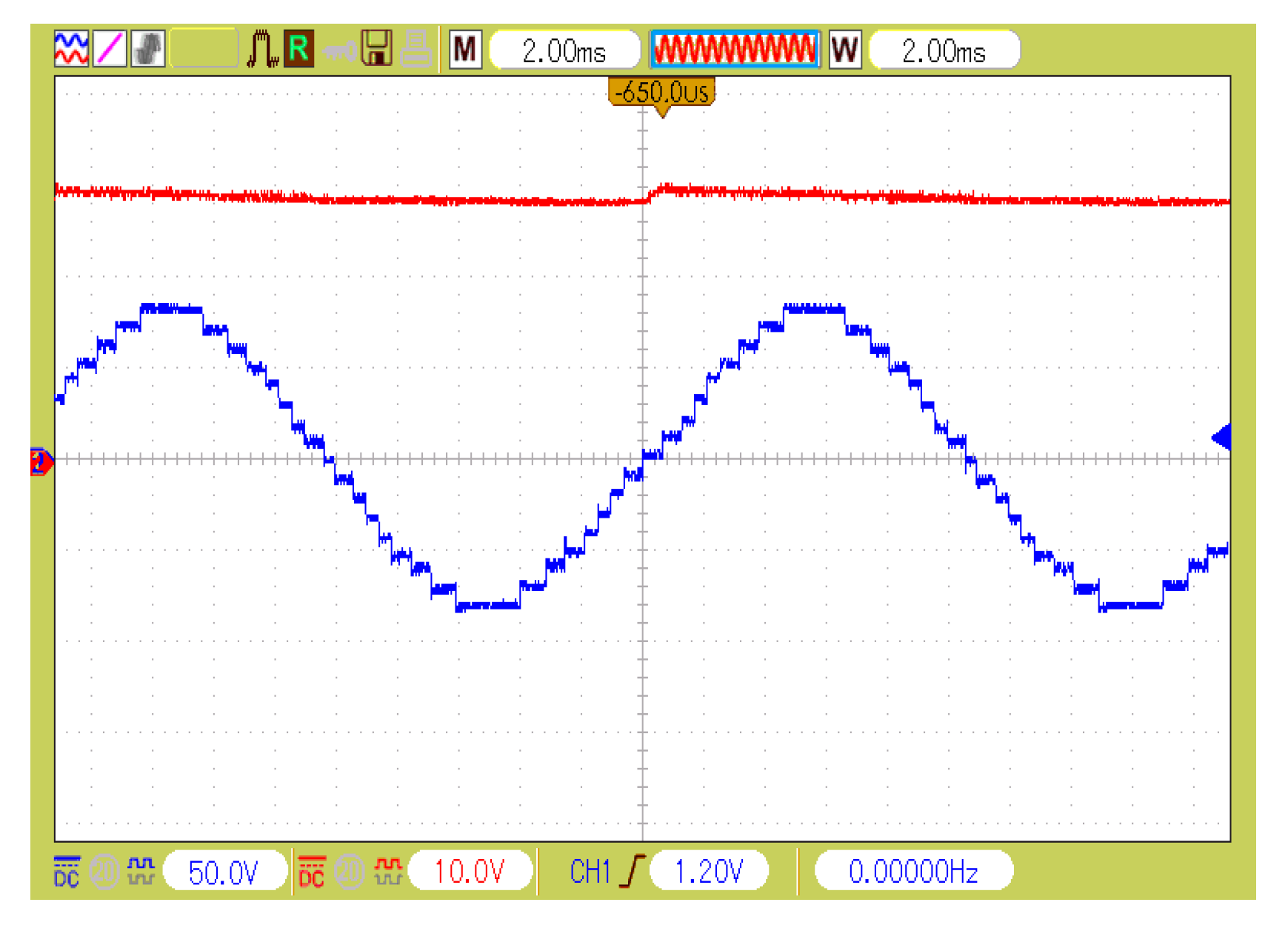
6. Experimental Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yuan, X. A Set of Multilevel Modular Medium-Voltage High Power Converters for 10-MW Wind Turbines. IEEE Trans. Sustain. Energy 2014, 5, 524–534. [Google Scholar] [CrossRef]
- Nami, A.; Liang, J.; Dijkhuizen, F.; Demetriades, G.D. Modular Multilevel Converters for HVDC Applications: Review on Converter Cells and Functionalities. IEEE Trans. Power Electron. 2015, 30, 18–36. [Google Scholar] [CrossRef]
- Gowaid, I.A.; Adam, G.P.; Massoud, A.M.; Ahmed, S.; Williams, B.W. Hybrid and Modular Multilevel Converter Designs for Isolated HVDC–DC Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 188–202. [Google Scholar] [CrossRef]
- Essakiappan, S.; Krishnamoorthy, H.S.; Enjeti, P.; Balog, R.S.; Ahmed, S. Multilevel Medium-Frequency Link Inverter for Utility Scale Photovoltaic integration. IEEE Trans. Power Electron. 2015, 30, 3674–3684. [Google Scholar] [CrossRef]
- Mathew, J.; Rajeevan, P.P.; Mathew, K.; Azeez, N.A.; Gopakumar, K. A Multilevel Inverter Scheme with Dodecagonal Voltage Space Vectors Based on Flying Capacitor Topology for Induction Motor Drives. IEEE Trans. Power Electron. 2013, 28, 516–525. [Google Scholar] [CrossRef]
- Viju Nair, R.; Arun Rahul, S.; Pramanick, S.; Gopakumar, K.; Franquelo, L.G. Novel Symmetric Six-Phase Induction Motor Drive Using Stacked Multilevel Inverters with a Single DC Link and Neutral Point Voltage Balancing. IEEE Trans. Ind. Electron. 2017, 64, 2663–2670. [Google Scholar] [CrossRef]
- Ahmadi, D.; Wang, J. Online Selective Harmonic Compensation and Power Generation with Distributed Energy Resources. IEEE Trans. Power Electron. 2014, 29, 3738–3747. [Google Scholar] [CrossRef]
- Haw, L.K.; Dahidah, M.S.A.; Almurib, H.A.F. A New Reactive Current Reference Algorithm for the STATCOM System Based on Cascaded Multilevel Inverters. IEEE Trans. Power Electron. 2015, 30, 3577–3588. [Google Scholar] [CrossRef]
- Zheng, Z.; Wang, K.; Xu, L.; Li, Y. A Hybrid Cascaded Multilevel Converter for Battery Energy Management Applied in Electric Vehicles. IEEE Trans. Power Electron. 2014, 29, 35373546. [Google Scholar] [CrossRef]
- Nabae, A.; Takahashi, I.; Akagi, H. A new neutral-point-clamped PWM inverter. IEEE Trans. Ind. Appl. 1981, IA-17, 518–523. [Google Scholar] [CrossRef]
- Meynard, T.A.; Foch, H. Multi-level choppers for high voltage applications. EPE J. 1992, 2, 45–50. [Google Scholar] [CrossRef]
- Peng, F.Z.; Lai, J.-S.H.; McKeever, J.W.; VanCoevering, J. A multilevel voltage-source inverter with separate DC sources for static VAr generation. IEEE Trans. Ind. Appl. 1996, 32, 1130–1138. [Google Scholar] [CrossRef]
- Zare, F. Power Electronics Education Electronic-Book; School of Engineering Systems, Queensland University of Technology: Brisbane, Australia, 2008. [Google Scholar]
- Gupta, K.K.; Ranjan, A.; Bhatnagar, P.; Sahu, L.K.; Jain, S. Multilevel Inverter Topologies with Reduced Device Count: A Review. IEEE Trans. Power Electron. 2016, 31, 135–151. [Google Scholar] [CrossRef]
- Debnath, S.; Qin, J.; Bahrani, B.; Saeedifard, M.; Barbosa, P. Operation, Control, and Applications of the Modular Multilevel Converter: A Review. IEEE Trans. Power Electron. 2015, 30, 37–53. [Google Scholar] [CrossRef]
- Venkataramanaiah, J.; Suresh, Y.; Panda, A.K. A review on symmetric, asymmetric, hybrid and single DC sources based multilevel inverter topologies. Renew. Sustain. Energy Rev. 2017, 76, 788–812. [Google Scholar] [CrossRef]
- Babaei, E.; Hosseini, S.H. New cascaded multilevel inverter topology with minimum number of switches. Energy Convers. Manag. 2009, 50, 2761–2767. [Google Scholar] [CrossRef]
- Babaei, E.; Kangarlu, M.F.; Sabahi, M. Extended multilevel converters: An attempt to reduce the number of independent DC voltage sources in cascaded multilevel converters. IET Power Electron. 2014, 7, 157–166. [Google Scholar] [CrossRef]
- Gupta, K.K.; Jain, S. Topology for multilevel inverters to attain maximum number of levels from given DC sources. IET Power Electron. 2012, 5, 435–446. [Google Scholar] [CrossRef]
- Farhadi Kangarlu, M.; Babaei, E. Cross-switched multilevel inverter: An innovative topology. IET Power Electron. 2013, 6, 642–651. [Google Scholar] [CrossRef]
- Babaei, E.; Laali, S.; Alilu, S. Cascaded multilevel inverter with series connection of novel H-bridge basic units. IEEE Trans. Ind. Electron. 2014, 61, 6664–6671. [Google Scholar] [CrossRef]
- Babaei, E.; Alilu, S.; Laali, S. A new general topology for cascaded multilevel inverters with reduced number of components based on developed H-bridge. IEEE Trans. Ind. Electron. 2014, 61, 3932–3939. [Google Scholar] [CrossRef]
- Shalchi Alishah, R.; Nazarpour, D.; Hosseini, S.H.; Sabahi, M. New hybrid structure for multilevel inverter with fewer number of components for high-voltage levels. IET Power Electron. 2014, 7, 96–104. [Google Scholar] [CrossRef]
- Samadaei, E.; Gholamian, S.A.; Sheikholeslami, A.; Adabi, J. An Envelope Type (E-Type) Module: Asymmetric Multilevel Inverters with Reduced Components. IEEE Trans. Ind. Electron. 2016, 63, 7148–7156. [Google Scholar] [CrossRef]
- Samadaei, E.; Sheikholeslami, A.; Gholamian, S.A.; Adabi, J. A Square T-Type (ST-Type) Module for Asymmetrical Multilevel Inverters. IEEE Trans. Power Electron. 2018, 33, 987–996. [Google Scholar] [CrossRef]
- Samadaei, E.; Kaviani, M.; Bertilsson, K. A 13-levels Module (K-Type) with two DC sources for Multilevel Inverters. IEEE Trans. Ind. Electron. 2018, 66, 5186–5196. [Google Scholar] [CrossRef]
- Vahedi, H.; Labbé, P.A.; Al-Haddad, K. Sensor-Less Five-Level Packed U-Cell (PUC5) Inverter Operating in Stand-Alone and Grid-Connected Modes. IEEE Trans. Ind. Inform. 2016, 12, 361–370. [Google Scholar] [CrossRef]
- Metri, J.I.; Vahedi, H.; Kanaan, H.Y.; Al-Haddad, K. Real-Time Implementation of Model-Predictive Control on Seven-Level Packed U-Cell Inverter. IEEE Trans. Ind. Electron. 2016, 63, 4180–4186. [Google Scholar] [CrossRef]
- Vahedi, H.; Al-Haddad, K. Real-Time Implementation of a Seven-Level Packed U-Cell Inverter with a Low-Switching-Frequency Voltage Regulator. IEEE Trans. Power Electron. 2016, 31, 5967–5973. [Google Scholar] [CrossRef]
- Sun, X.; Wang, B.; Zhou, Y.; Wang, W.; Du, H.; Lu, Z. A Single DC Source Cascaded Seven-Level Inverter Integrating Switched-Capacitor Techniques. IEEE Trans. Ind. Electron. 2016, 63, 7184–7194. [Google Scholar] [CrossRef]
- Taghvaie, A.; Adabi, J.; Rezanejad, M. A Multilevel Inverter Structure Based on a Combination of Switched-Capacitors and DC Sources. IEEE Trans. Ind. Inform. 2017, 13, 2162–2171. [Google Scholar] [CrossRef]
- Taghvaie, A.; Adabi, J.; Rezanejad, M. Circuit Topology and Operation of a Step-Up Multilevel Inverter with a Single DC Source. IEEE Trans. Ind. Electron. 2016, 63, 6643–6652. [Google Scholar] [CrossRef]
- Tang, Y.; Ran, L.; Alatise, O.; Mawby, P. Capacitor Selection for Modular Multilevel Converter. IEEE Trans. Ind. Appl. 2016, 52, 3279–3293. [Google Scholar] [CrossRef]
- Zamiri, E.; Vosoughi, N.; Hosseini, S.H.; Barzegarkhoo, R.; Sabahi, M. A New Cascaded Switched-Capacitor Multilevel Inverter Based on Improved Series–Parallel Conversion with Less Number of Components. IEEE Trans. Ind. Electron. 2016, 63, 3582–3594. [Google Scholar] [CrossRef]
- Liu, J.; Wu, J.; Zeng, J.; Guo, H. A Novel Nine-Level Inverter Employing One Voltage Source and Reduced Components as High-Frequency AC Power Source. IEEE Trans. Power Electron. 2017, 32, 2939–2947. [Google Scholar] [CrossRef]
- Ye, Y.; Cheng, K.W.E.; Liu, J.; Ding, K. A Step-Up Switched-Capacitor Multilevel Inverter with Self-Voltage Balancing. IEEE Trans. Ind. Electron. 2014, 61, 6672–6680. [Google Scholar] [CrossRef]
- Vijeh, M.; Rezanejad, M.; Samadaei, E.; Bertilsson, K. A General Review of Multilevel Inverters Based on Main Submodules: Structural Point of View. IEEE Trans. Power Electron. 2019, 34, 9479–9502. [Google Scholar] [CrossRef]
- Meshram, P.M.; Borghate, V.B. A simplified nearest level control (NLC) voltage balancing method for modular multilevel converter (MMC). IEEE Trans. Power Electron. 2015, 30, 450–462. [Google Scholar] [CrossRef]

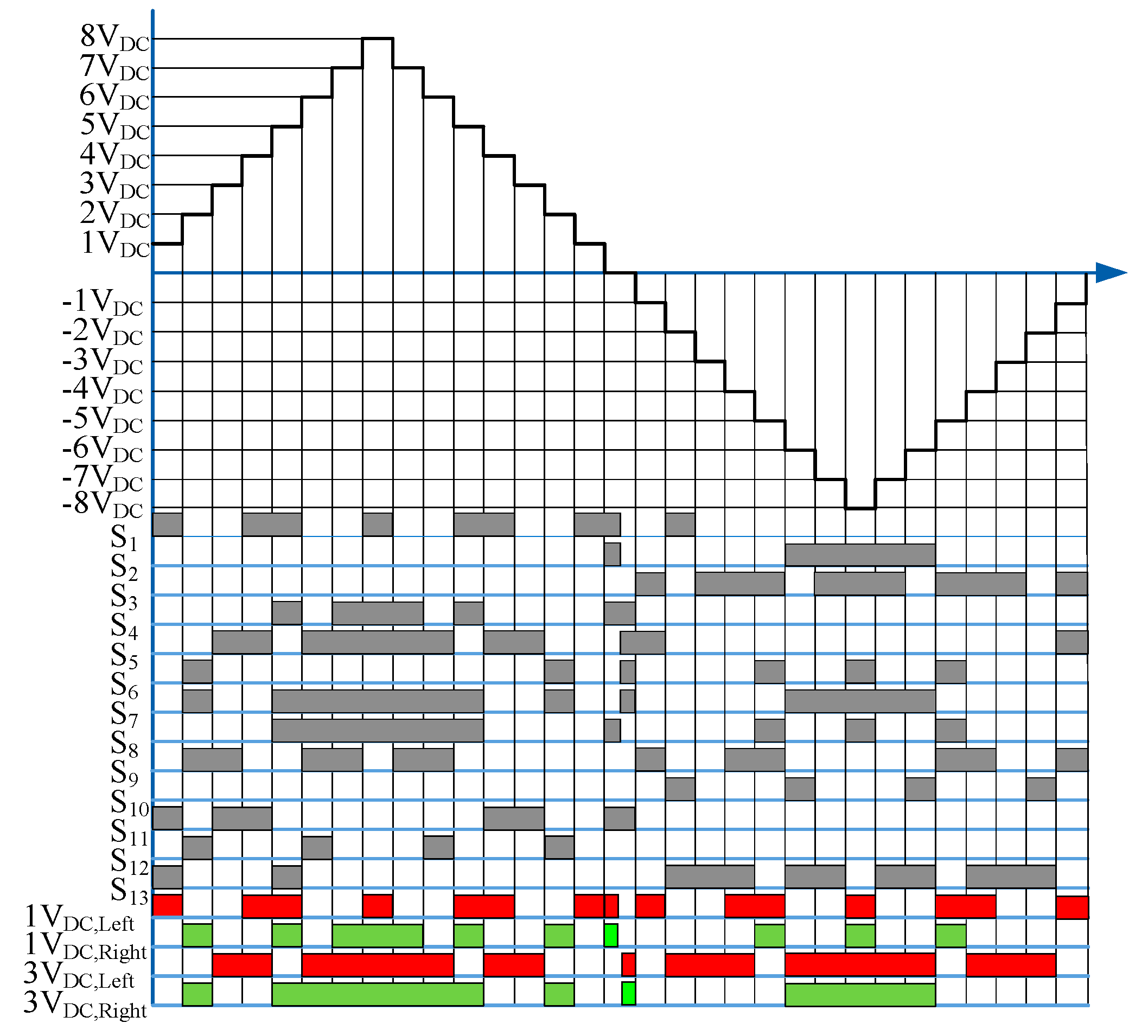
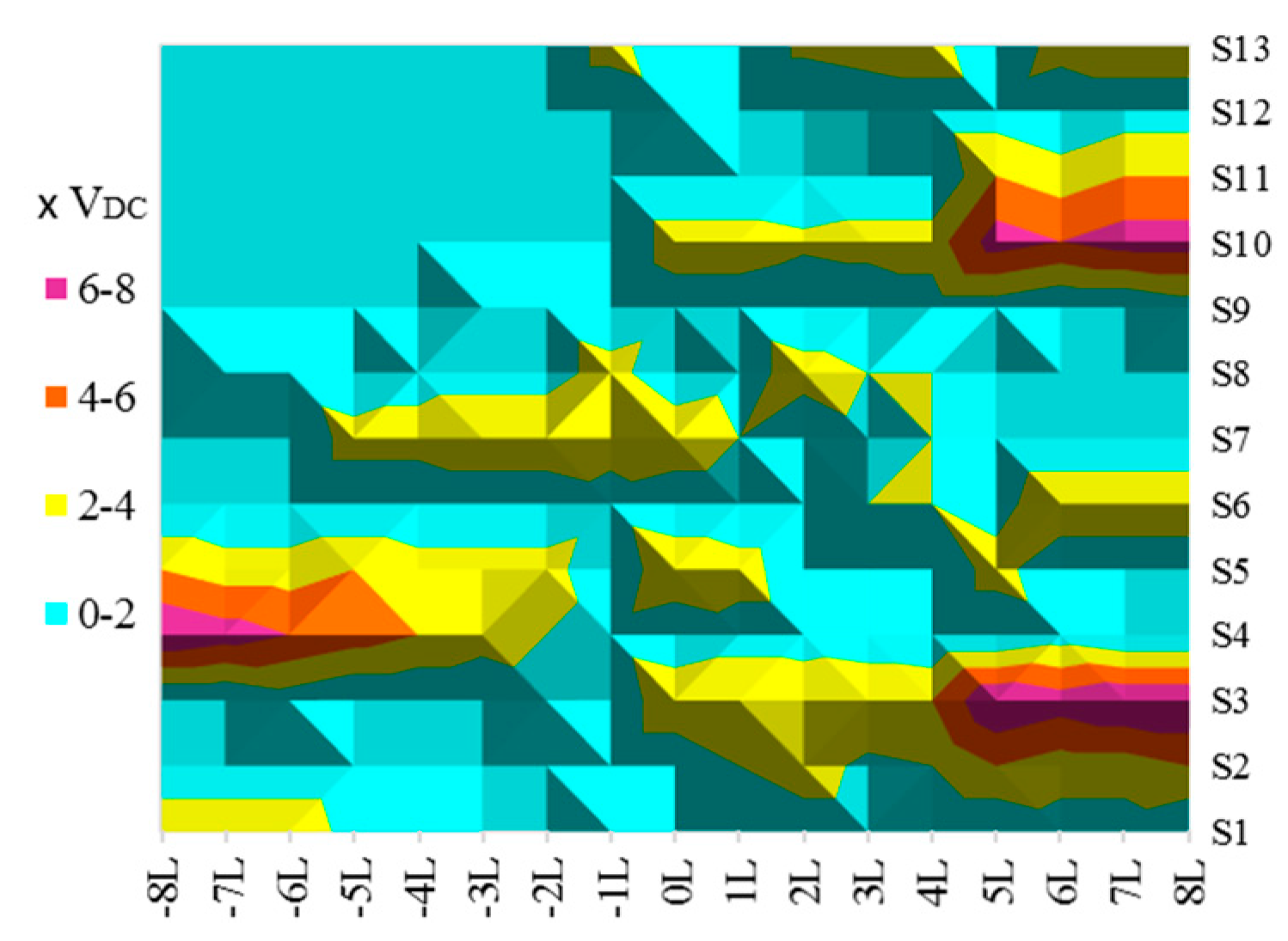
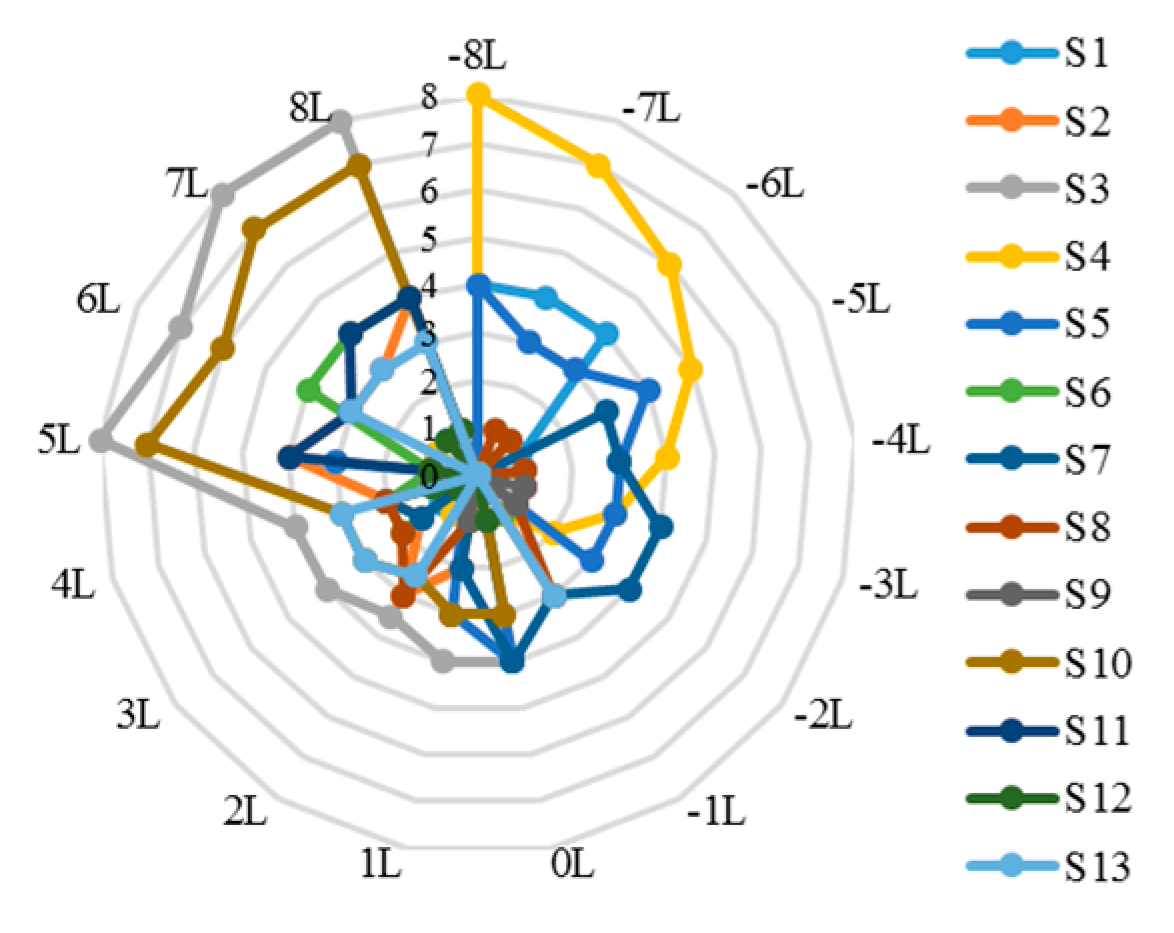
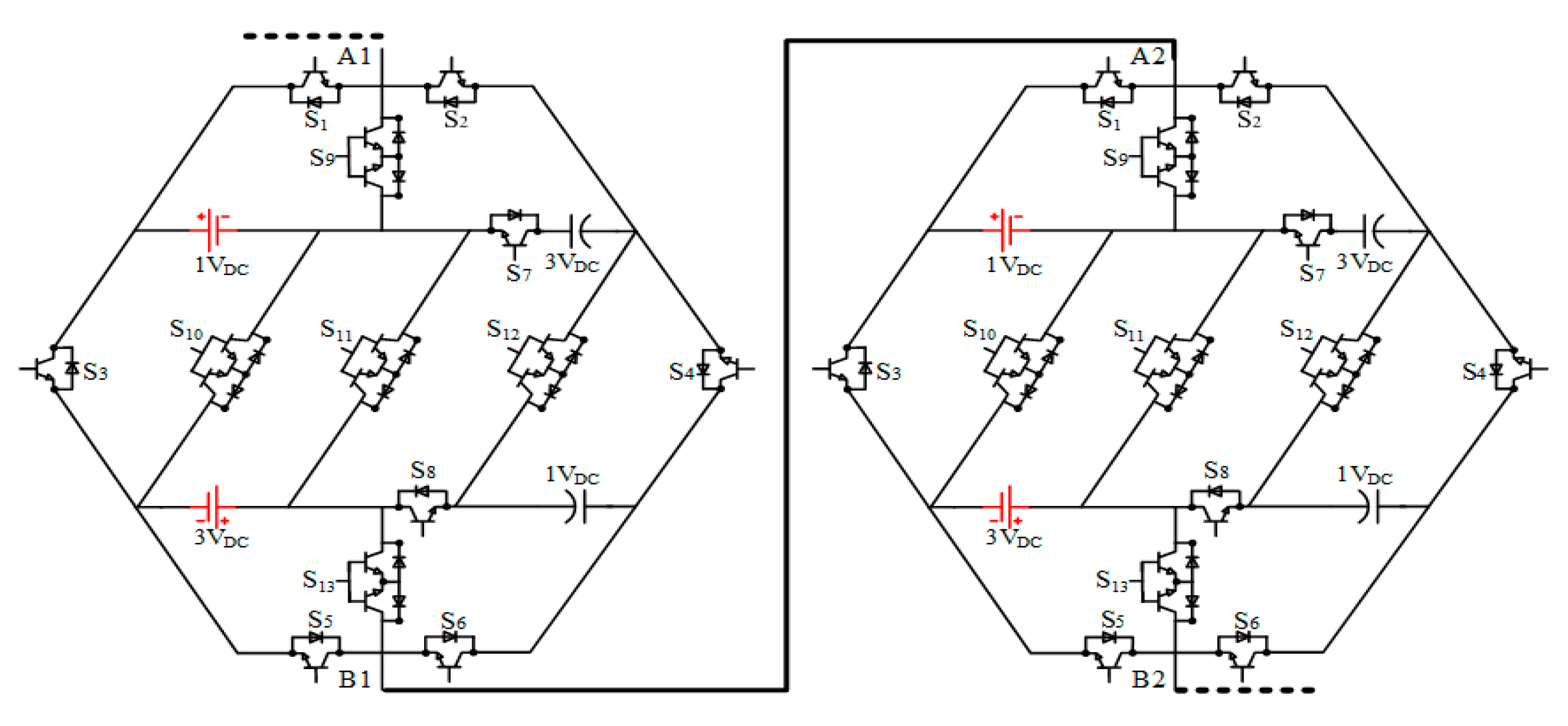

| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | S11 | S12 | S13 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Positive level | 8VDC | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 7VDC | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |
| 6VDC | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | |
| 5VDC | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | |
| 4VDC | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |
| 3VDC | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | |
| 2VDC | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | |
| 1VDC | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | |
| Negative level | −1VDC | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| −2VDC | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | |
| −3VDC | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| −4VDC | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | |
| −5VDC | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | |
| −6VDC | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | |
| −7VDC | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| −8VDC | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | |
| Num. of turning on per 1-cycle | 6 | 2 | 5 | 4 | 4 | 6 | 5 | 5 | 7 | 4 | 4 | 4 | 6 | |
| Based on the Number of Module Units | Based on the Number of Desired Levels | |
|---|---|---|
| Levels | 16n+1 | NL |
| Number of Switches | 18n | |
| Number of Diodes | 18n | |
| Driver | 13n | |
| DC sources | 2n | |
| Capacitors | 2n | |
| TSV | 57n |
| u1= | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| u2= | ||||||||||||||||||
| −8 | −16 | −15 | −14 | −13 | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | |
| −7 | −15 | −14 | −13 | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | |
| −6 | −14 | −13 | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | |
| −5 | −13 | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | |
| −4 | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | |
| −3 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | |
| −2 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| −1 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 2 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 3 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| 4 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 5 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| 6 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| 7 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 8 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| CHB [12] | [18] | [34] | [35] | [36] | [24] | [25] | Proposed Module | |
|---|---|---|---|---|---|---|---|---|
| Number of Switches | ||||||||
| Number of Diodes | ||||||||
| Number of DC sources | ||||||||
| Number of capacitors | - | - | - | |||||
| TSV 1 (xVDC) | ||||||||
| Negative level | With H-Bridge | With H-Bridge | With H-Bridge | With H-Bridge | With H-Bridge | Inherent | Inherent | Inherent |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samadaei, E.; Kaviani, M.; Iranian, M.; Pouresmaeil, E. The P-Type Module with Virtual DC Links to Increase Levels in Multilevel Inverters. Electronics 2019, 8, 1460. https://doi.org/10.3390/electronics8121460
Samadaei E, Kaviani M, Iranian M, Pouresmaeil E. The P-Type Module with Virtual DC Links to Increase Levels in Multilevel Inverters. Electronics. 2019; 8(12):1460. https://doi.org/10.3390/electronics8121460
Chicago/Turabian StyleSamadaei, Emad, Mohammad Kaviani, Mina Iranian, and Edris Pouresmaeil. 2019. "The P-Type Module with Virtual DC Links to Increase Levels in Multilevel Inverters" Electronics 8, no. 12: 1460. https://doi.org/10.3390/electronics8121460
APA StyleSamadaei, E., Kaviani, M., Iranian, M., & Pouresmaeil, E. (2019). The P-Type Module with Virtual DC Links to Increase Levels in Multilevel Inverters. Electronics, 8(12), 1460. https://doi.org/10.3390/electronics8121460






