Improved Efficiency Management Strategy for Battery-Based Energy Storage Systems

1. Introduction

Energy storage systems can support the diffusion of renewable energy sources for both off-grid and grid-tied applications, and can offer ancillary services for the distribution grid such as frequency regulation, spinning reserve and voltage control, potentially aiding the actual transition to the smart grid of the future. For these reasons, energy storage systems, and in particular battery-based storage systems, are increasingly gaining attention nowadays at the grid-scale level, but also at the commercial and residential level. Moreover, we are in a phase in which electric vehicles [1,2,3] and electric vehicles [4] diffusion is rapidly increasing, and first pilot projects in which batteries of electric vehicles are also used to inject energy into the grid when necessary (vehicle-to-grid, V2G applications) are being implemented world-wide [5,6,7,8,9,10,11,12]. In this scenario, smart battery management strategies will be required to control effectively the complex bidirectional energy flow between the distribution grid and the customers arising from a large deployment of storage systems. These strategies will have to take into account several important aspects, such as the energy efficiency of the whole storage chain. Indeed, the energy efficiency of the battery-based storage system, i.e., the overall efficiency of both batteries and inverters composing the system, plays a fundamental role in order to keep energy losses as small as possible during the energy transfer processes. In some papers dealing with charging/discharging strategies for batteries, non-unitary charging/discharging efficiency coefficients were considered, but they were assumed as constant values independent on the charging/discharging rate used to charge/discharge the batteries [5,6,7,8]. However, the charging/discharging efficiency of a battery strongly depends on the charging/discharging rate used [13,14,15,16]. Moreover, also the inverter efficiency typically depends on the delivered power level [17,18,19].

This work aims at demonstrating the importance of taking into account the dependence of the efficiency on the output power of batteries and inverters when defining management strategies for battery-based storage systems interfaced with the distribution grid.

The rest of the paper is organized as follows: In Section 2, the typical dependence of the efficiency on the output power of a battery/inverter system is analyzed; in Section 3 an optimal management strategy is proposed and analyzed in MATLAB for a distributed energy storage system used for grid flexibility services; in Section 4 an optimal management strategy is presented and tested thanks to a Hardware-in-the-Loop platform for a grid-connected PV plant equipped with a commercial energy storage system; finally conclusions are drawn.

2. Fundamentals of Proposed Management Strategy

The overall efficiency of a battery/inverter system is clearly given by the product between the battery discharging efficiency and the inverter efficiency. As previously discussed, both these parameters generally depend on the output power of the system. Obviously, the particular relationship between the efficiency and the output power depends on the specific battery/inverter system considered.

To give a quantitative idea of the impact of the efficiency on the overall performance of a battery-based storage system, the two typical realistic efficiency curves shown in Figure 1 and Figure 2 are considered for the inverter and the battery, respectively. In both the plots of Figure 1 and Figure 2, the efficiency is reported as a function of the output power normalized with respect to the maximum output.

The curve of Figure 1 was constructed by considering typical efficiency profiles of commercial inverters, in which the efficiency usually degrades at low output power levels because of switching and conducting power losses in the circuit elements of the inverter [17,18,19].

Instead, the curve of Figure 2 takes into account the typical degradation of the battery charging/discharging efficiency at high power levels due to the increase of the power losses on the internal battery resistances [16] with the discharging rate. This efficiency profile was constructed on the basis of experimental tests on a 18650 lithium ion battery (for which the maximum discharging rate is 1C), and is similar to results obtained for other battery types (for example for charging/discharging efficiencies of NiMH batteries in [13,14]).The product between the two profiles of Figure 1 and Figure 2 results in the overall charging/discharging efficiency profile reported in Figure 3, which achieves a maximum efficiency of about 90% when the output power is about 40% of the maximum power.

Thus, it appears how common values of 90% used in previous works [11] to model constant non-unitary charging/discharging efficiencies are a good starting point to take into account typical maximum efficiencies of energy storage systems in defining energy management strategies, but not efficiency variations with the charging/discharging power.

As it will be shown, taking into account the actual roundtrip efficiency profile (given by the product of charging and discharging efficiency profiles) as a function of battery charging/discharging power can be fundamental in real situations that will be analysed in the following for two different cases:

• A distributed energy storage system used to provide flexibility grid services.
• A commercial energy storage system connected to a photovoltaic plant.

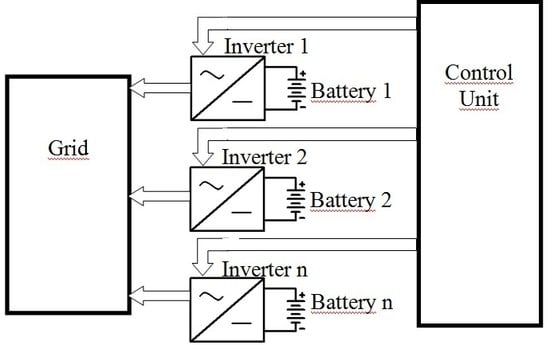
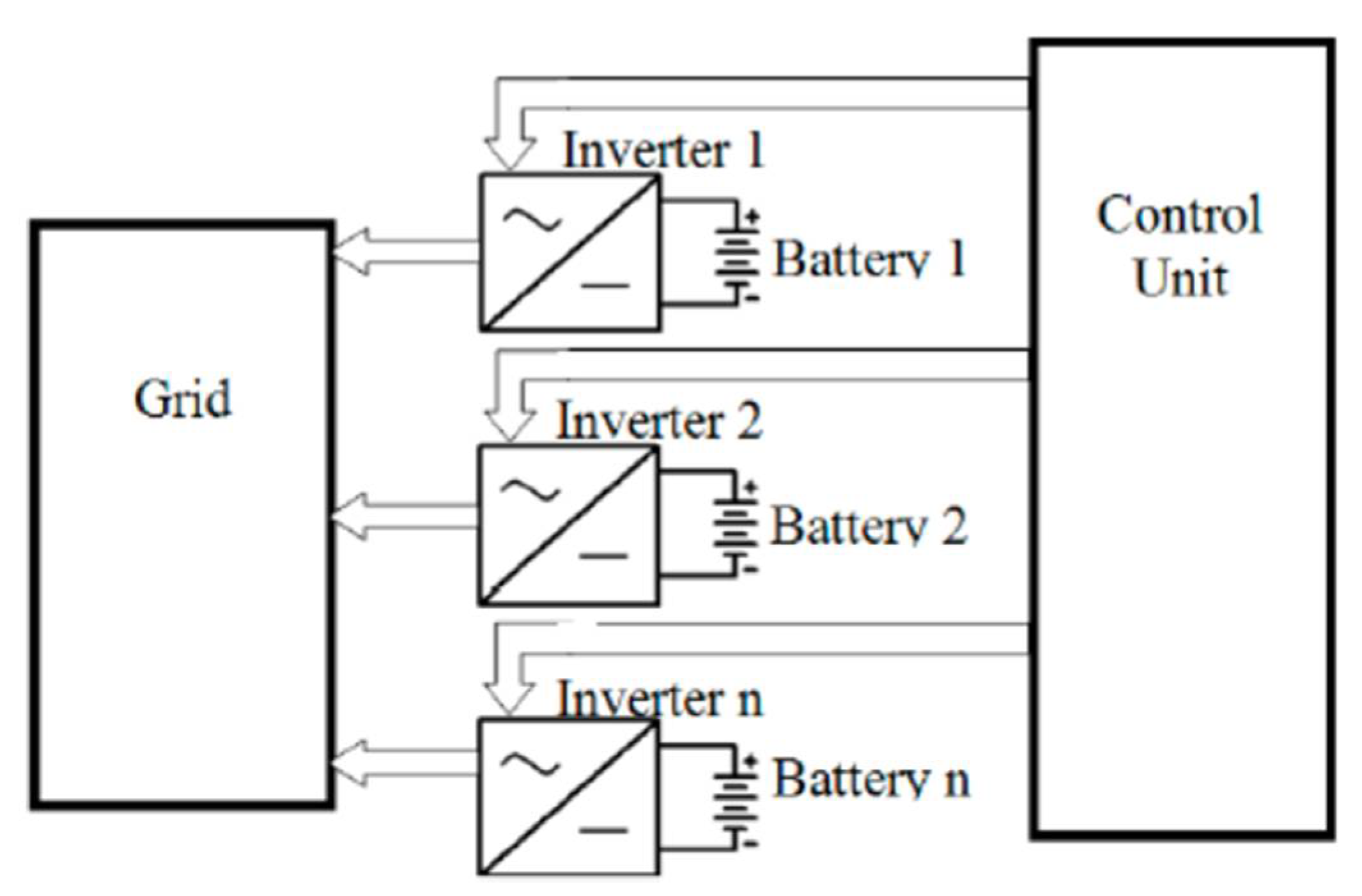
3. Proposed Management Strategy for Grid-Connected Distributed Energy Storage Systems

The proposed management strategy is first analyzed for a distributed energy storage system used for flexibility grid services, in which the energy required by the grid should be drawn from a system including different battery/inverter subsystems connected to the grid.

This is a common situation occurring in scenarios in which a given power level required to stabilize the grid (in terms of grid, frequency, load, etc.) can be achieved by aggregating:

• Different energy storage systems distributed on the grid, for example, coupled to renewable energy sources or batteries of electric vehicles used in V2G modes;
• different modules of a modular storage system sized to achieve given maximum target values of output power and energy capacity.

In these cases, some management strategies for the storage system are required to determine the discharging rate of each battery on the basis of the total power required by the grid. These strategies can be implemented by a management system such as the one shown in the principle scheme of Figure 4, in which a control unit manages each battery/inverter subsystem by setting its output power.

The basic management strategy of the storage system which can be implemented is that indicated herein as “Energy Distributed (ED)” strategy. In this approach, all the batteries of the system inject into the grid the same amount of power, i.e., the amount of power required by the grid is equally distributed between the n batteries of the system, which then have the same discharging rate. By indicating with Pb_i the power supplied by the i-th battery/inverter subsystem to the grid, and P_req the total power required by the grid, the analytical formulation of the ED approach can be expressed as follows:

$$P{b}_i=\frac{P_{req}}{n}$$

(1)

From the above discussion, it is evident that the basic ED strategy does not take the roundtrip energy efficiency into account in any way, intended as the ratio between the energy actually available from batteries and the energy globally spent to recharge them.

Therefore, in order to minimize the energy losses of the overall energy storage system, a more appropriate management strategy is needed. To this aim, the strategy indicated as “Maximum Efficiency (ME)” is proposed. Starting from the relationship between the efficiency and the output power of each battery/inverter subsystem, the proposed strategy selects the optimal number of batteries to be discharged for a given power demand, in order to make these batteries to operate at the discharging rate which allows reaching the maximum possible efficiency of the overall storage system (calculated as the ratio between the total power supplied by the energy storage to the grid and the total power consumed by the storage system during the energy transfer process).

From an analytical point of view, this means finding the solution of the following constrained problem:

$$\{\begin{array}{c}\max \frac{{\displaystyle \sum _{i=1}^{n}P{b}_i}}{{\displaystyle \sum _{i=1}^{n}P{b}_i/\eta \left(P{b}_i\right)}}\\ {\displaystyle \sum _{i=1}^{n}P{b}_i}=P_{req}\\ 0\le P{b}_i\le P{\max }_i\end{array}$$

(2)

where η(Pb_i) is the overall efficiency of the i-th battery/inverter system as a function of the power supplied by the battery, and Pmax_i is the maximum power that can be supplied by the i-th battery.

To show the importance of taking the efficiency into account, MATLAB simulations were carried out to analyze the batteries/inverters sub-systems. The 10 sub-systems were considered having the same capacity of 1 kWh, with a maximum output power of 10 kW available from the entire storage system.

The discharging efficiency profile shown in Figure 3 was considered for each battery/inverter system. Clearly, these assumptions do not limit the general validity of the analysis, which could be extended to larger storage systems comprising a greater number of batteries, and to systems characterized by different efficiency profiles.

The analysis was carried out by considering both the ED and ME strategies previously discussed. Figure 5 shows the fraction of batteries of the storage system used (i.e., the ratio between the number of batteries with a discharging rate greater than 0 and the total number of batteries available in the system) as a function of the power required by the grid (normalized with respect to the maximum output power available from the system).

It appears that the ME strategy does not use all the batteries present in the system until the power demand is less than 40% of the maximum output power of the system. From an intuitive point of view, this can be explained by considering that the ME strategy tries to satisfy all the grid power requests by using the number of batteries, which allow to have a discharging rate equal to about 40% of the maximum power of each battery, this discharging rate being the optimal one in terms of efficiency, according to Figure 3.

Obviously, when the grid power demand exceeds the 40% of the maximum output power of the system, the strategy is forced to use a larger number of batteries, by operating them at a non-optimal discharging rate. In this case, the ME tends to become equivalent to the ED strategy, which always withdraws energy from all the batteries present in the system, whatever the grid power demand. The two different approaches in selecting the batteries to be discharged result in different performances of the two strategies in terms of energy efficiency. This is shown in Figure 6, which reports the overall system efficiency as a function of the power required by the grid for both the used strategies.

As it can be easily understood, the two strategies are almost equivalent for power levels comprised in the range 40%–100% of the maximum output power of the system, because they tend to use the same number of batteries for these power levels. However, the ME strategy performs significantly better than the ED one for power levels up to the 40% of the maximum output power, allowing fully exploiting the system capabilities in terms of energy efficiency.

In fact, it is evident that the efficiency guaranteed by the ME strategy stays to the maximum possible level guaranteed by the system (0.9 according to the profile in Figure 3) for all the power levels comprised in the range 0%–40% of the maximum output power of the system. Instead, the efficiency guaranteed by the ED approach drops for the power level less than 40% of the maximum output power, even becoming more than 20% less than the efficiency guaranteed by the ME strategy for power levels less than 10% of the maximum output power. Thus, the proposed management strategy proves to be very useful to guarantee efficient energy transfer processes from distributed storage systems to the grid by limiting the energy losses as much as possible.

Obviously, it is worth pointing out that the proposed strategy can be combined in more complex algorithms taking into account other inputs such as battery state of health, in order to select the most appropriate sequence for using subsets of batteries without affecting negatively their lifetimes.

In the following it will be shown how the proposed strategy can be profitably used also for energy storage systems coupled to renewable sources.

4. Proposed Management Strategy for Grid-Connected Renewable Plants

The proposed strategy was also analyzed on a commercial energy storage system for a grid-connected PV system, composed by:

• A SMA Sunny Island battery inverter (5 kWp);
• a 48 V–185 Ah Sonneschein battery.

The system was tested thanks to the Hardware-in-the-Loop platform reported in Figure 6, comprising:

• The storage system;
• a remotely controlled load;
• a computer implementing a LabView platform for the emulation of typical PV production and load profiles, as well as for the management of charging/discharging processes of the storage system.

The system was managed according to two different strategies:

• Traditional management, in which the battery is charged using all the instantaneous power generated from the PV plant exceeding the load, as well as load demand is satisfied entirely by the battery when there is no PV production;
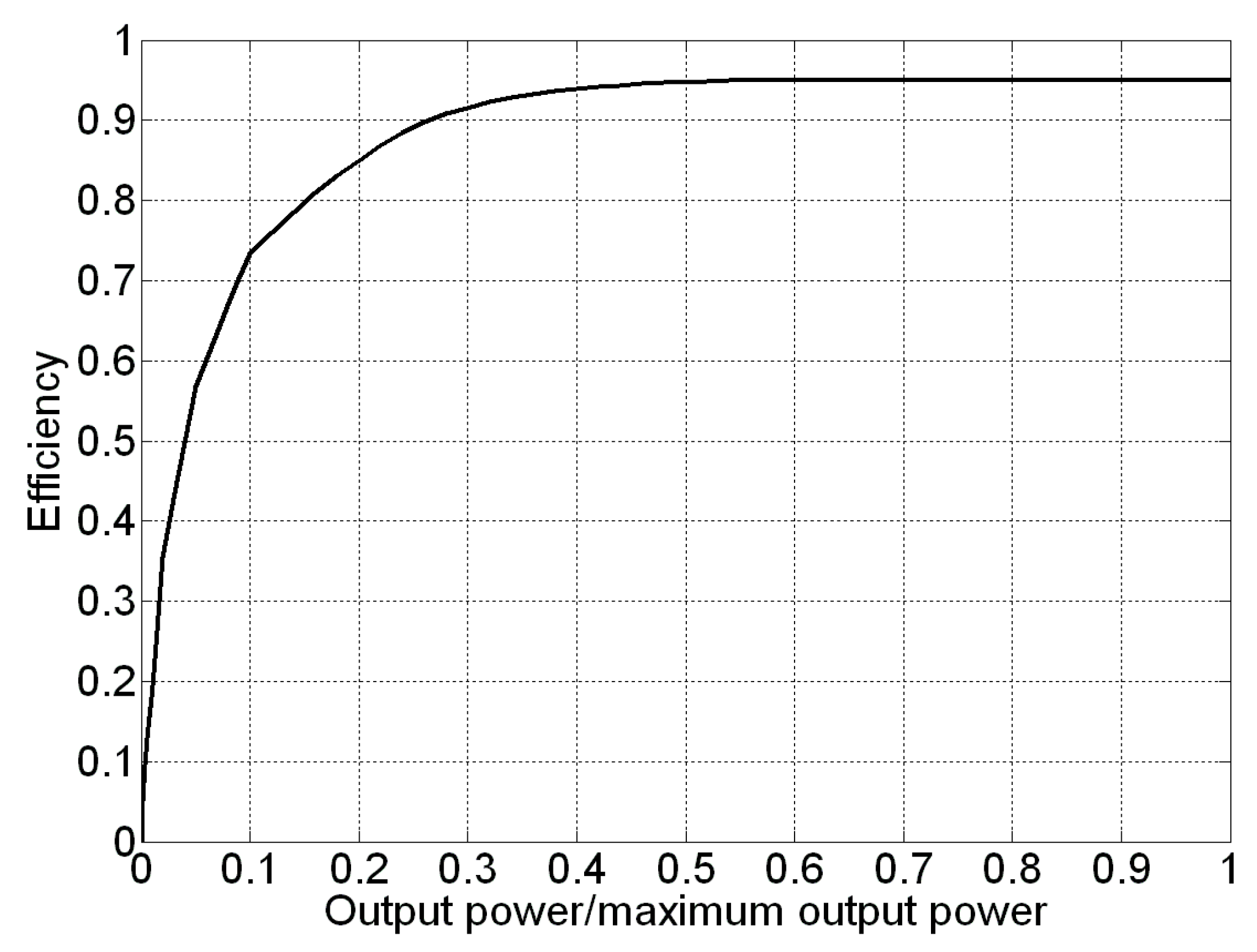
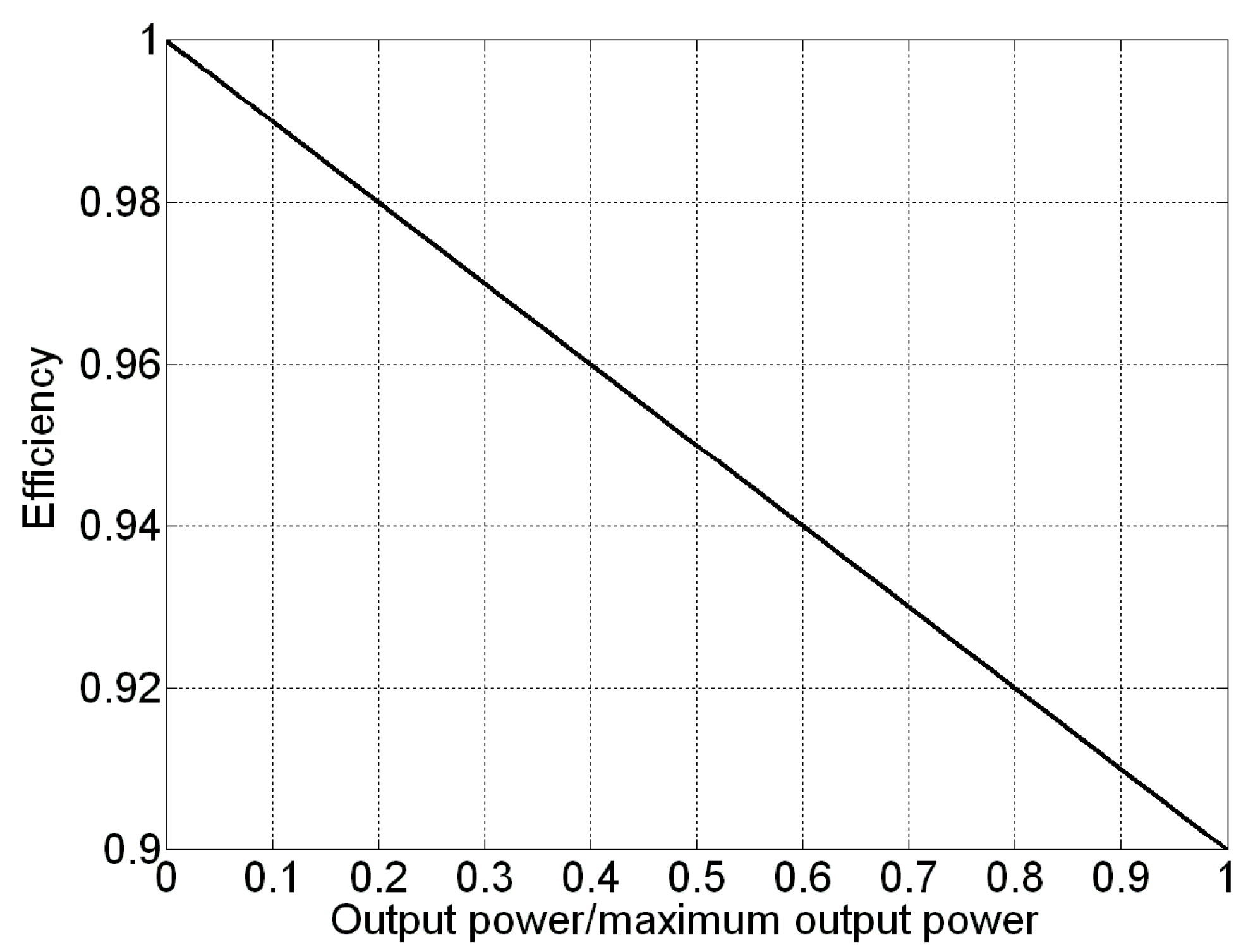
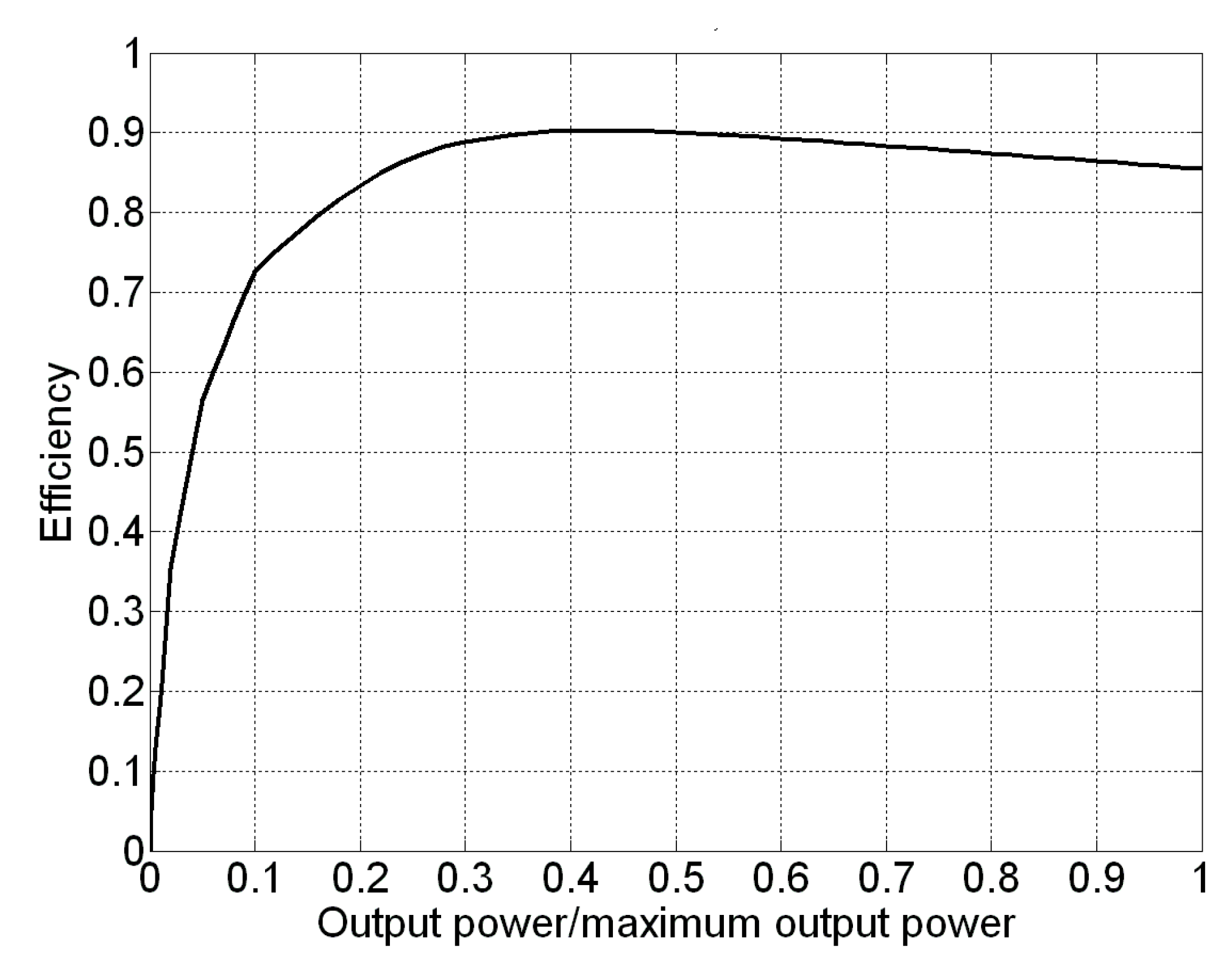
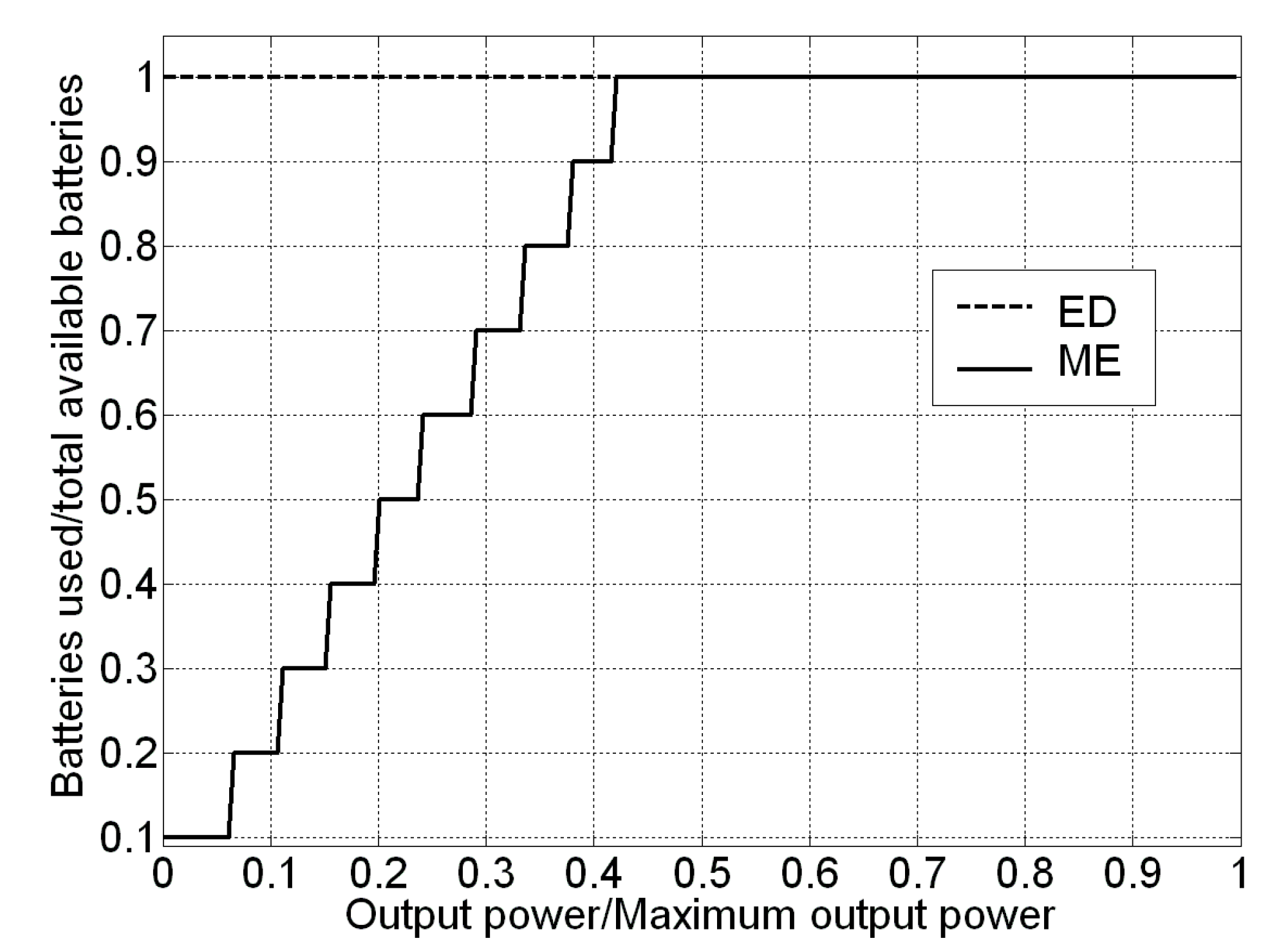
• Maximum Efficiency (ME) strategy, in which battery charging power profile is selected to achieve maximum charging efficiency, as well as load demand in the absence of renewable power is satisfied by the most convenient mix of battery and grid power allowing to maximize discharging efficiency, in order to achieve the maximum overall roundtrip efficiency of the energy storage system.

Tests were carried out by comparing traditional and ME strategies in two different scenarios:

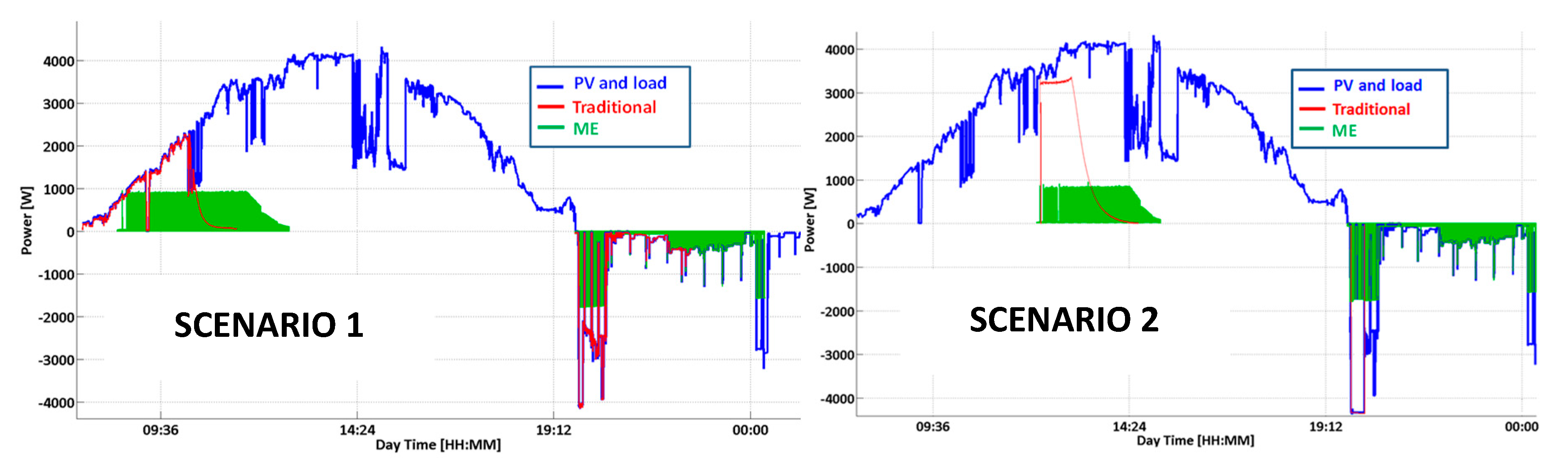
• Scenario 1, characterized by typical PV and load profiles, in which battery charging is performed at the beginning of the PV production;
• scenario 2, in which overnight load is increased (for example to perform electric vehicle charging) and battery charging is performed during peak production hours.

Figure 7 shows the charging/discharging profiles for the storage system in the two scenarios.

As shown in the figure:

• In the traditional approach, the charging power is limited only by both the PV production or the maximum absolute rating set by the manufacturer, and the charge process is carried out as soon as the PV production starts or is just shifted in time to match PV peak production and limit the PV power fed into the grid accordingly, whereas according to the ME strategy charging profiles are spread intelligently over the time taking into account also the impact of power on energy efficiency;
• in the traditional approach battery discharging profiles just follow the load profile until the battery is not fully discharged, where the ME approach allows to satisfy the instantaneous load demand with the most efficient mix of power coming from both the battery and the grid.

As reported in

Table 1. Efficiency optimization allowed by the ME strategy.

Scenario	Parameter	Traditional	Me	Variation
SCENARIO 1	Energy spent for storage charging	3.03 kWh	2.88 kWh	−5.0%
	Energy supplied during storage discharging	2.27 kWh	2.30 kWh	+1.3%
	Roundtrip efficiency	74.9%	79.9%	+6.7%
SCENARIO 2	Energy spent for storage charging	3.25 kWh	2.88 kWh	−11.4%
	Energy supplied during storage discharging	2.25 kWh	2.30 kWh	+2.2%
	Roundtrip efficiency	69.2%	79.9%	+15.5%

, the efficiency optimization allowed by the ME strategy results in energy savings in both charging and discharging phases, whose amounts depend on the scenarios considered and therefore on both PV production and load profiles.

In particular, it appears that:

• In Scenario 1, ME allows a 6.7% relative increase of the storage roundtrip efficiency, coming from a 5.0% and an 1.3% energy savings during the charging and discharging phases, respectively;
• in Scenario 2, ME allows a 15.5% relative increase of the storage roundtrip efficiency, coming from a 11.4% and a 2.2% energy savings during the charging and discharging phases, respectively.

5. Conclusions

This paper proposes an efficient management strategy for battery-based storage systems interfaced to the distribution grid. This strategy allows optimizing the overall efficiency of storage systems taking into account the dependence of the energy efficiency on the charging/discharging power of both the battery and the power conversion section of the storage system.

The performances of the proposed strategy are analyzed for both distributed energy storage systems used to perform grid services and for renewable energy plants.

For distributed energy storage, a theoretical analysis based on the MATLAB simulation shows how the proposed strategy can allow a significant improvement of the overall system efficiency with respect to traditional strategies which are not aimed at the efficiency optimization, that fix the output power of each battery/inverter subsystem by distributing equally between them the amount of power required to satisfy a given grid power request.

Experimental results for commercial energy storage systems coupled with renewable sources prove also the effectiveness of the proposed strategy in increasing the roundtrip storage efficiency with respect to traditional approaches which define battery charging/discharging profiles just taking into account PV production and load profiles and neglecting the impact of energy efficiency on the overall system performance.

Real hardware tests carried out for a small-scale prototype allow to evaluate an up to 15.5% roundtrip efficiency increase, which can be obviously scaled on a larger scale for distributed energy storage systems.

The analysis performed gives useful well-founded guidelines for the development of smart management strategies for energy storage systems, as well as for next-generation inverters and smart grid management systems.