1. Introduction
With the rapid growth of mobile terminals and multimedia services, the demand for high-rate data transmission has increased and the traffic pressure on the core network has become extremely high. Device-to-device (D2D) communication is considered a key technology to relieve the pressure of the core network effectively [
1]. It enables users to communicate with each other by reusing the resources of other users without passing through the base station, thus significantly improving spectrum utilization and system throughput. Non-orthogonal multiple access (NOMA) is also a recent research hot spot. Compared with orthogonal multiple access (OMA), it has higher spectral efficiency and can provide faster transmission rate and lower outage probability [
2].
In wireless communication, resource allocation has attracted widespread attention as it considerably affects system performance [
3,
4]. Game theory is often used to solve such problems [
5,
6]. In D2D communication, many studies focused on the resource allocation problem to improve the system performance. In Reference [
7], a joint optimization algorithm for channel and power allocation based on the Nash bargaining game was proposed. It decomposed the optimization problem into two sub-problems, which simplified the calculation and improved the system throughput. In Reference [
8], D2D power allocation was studied under cooperative and non-cooperative games, and the D2D transmit power was optimized via sub-gradient methods. In Reference [
9], a D2D power auction mechanism based on a stochastic game was proposed to reduce interference and optimize power allocation. In Reference [
10], a student-project matching model of cellular, D2D, and relay users, which improved the system throughput, was proposed. However, none of the above algorithms considers NOMA and no further improvement in system throughput was achieved.
A D2D transmitter can send messages to multiple D2D receivers simultaneously through NOMA. The distribution of D2D communication resources assisted by NOMA was studied in Reference [
11], and the D2D throughput was optimized while ensuring the quality of service (QoS) of cellular users. In Reference [
12], NOMA-based D2D resource allocation was studied as a Nash bargaining game, and the power optimization problem was solved by using the Karush–Kuhn–Tucker (KKT) conditions. In Reference [
13], a D2D-NOMA optimization algorithm combining sub-channel allocation, user matching, and power control was proposed to optimize the total transmit power by coordinating interference. However, mobile devices are carried by humans and none of the above solutions considers the influence of social factors. In a practical environment, social relationships will affect user’s decision-making and can be used to strengthen the cooperation between users, thereby effectively improving system throughput.
In this study, a cellular uplink network scenario is considered. Cellular users occupy independent sub-channels, and D2D groups, which consist of a D2D transmitter and two D2D receivers, reuse the uplink channels of the cellular users to communicate with each other. In D2D groups, NOMA is considered to make the D2D receivers demodulate the signal correctly from the mixed signal. The resource allocation is modeled as a two-stage Stackelberg game by defining the utility functions of cellular users and D2D groups. The main contributions of this paper can be summarized as follows:
The social relationship between cellular and D2D users is considered. When D2D users reuse the channel resources of cellular users for communication, their social relationship will affect the channel selection and transmit power of D2D users. Considering the social relationship can strengthen the cooperation between users, thus increasing the system throughput.
In the two-stage Stackelberg game model, the cellular user is the leader. In the first stage, maximum weight matching between cellular users and D2D groups is achieved using the Kuhn–Munkres (KM) algorithm while ensuring the QoS of all users on the sub-channel to allocate channels for D2D groups.
The D2D group is the follower. In the second stage, a penalty-function-based particle swarm optimization (PSO) algorithm is utilized to optimize the D2D transmit power. The final power allocation strategy is determined via the convergence of PSO.
The rest of this paper is organized as follows.
Section 2 presents the system model. In
Section 3, we define the utility functions of cellular users and D2D groups, establish the Stackelberg game model, and prove the convergence of the algorithm. In
Section 4, the simulation results are presented and analyzed. In
Section 5, we summarize the paper.
2. System Model
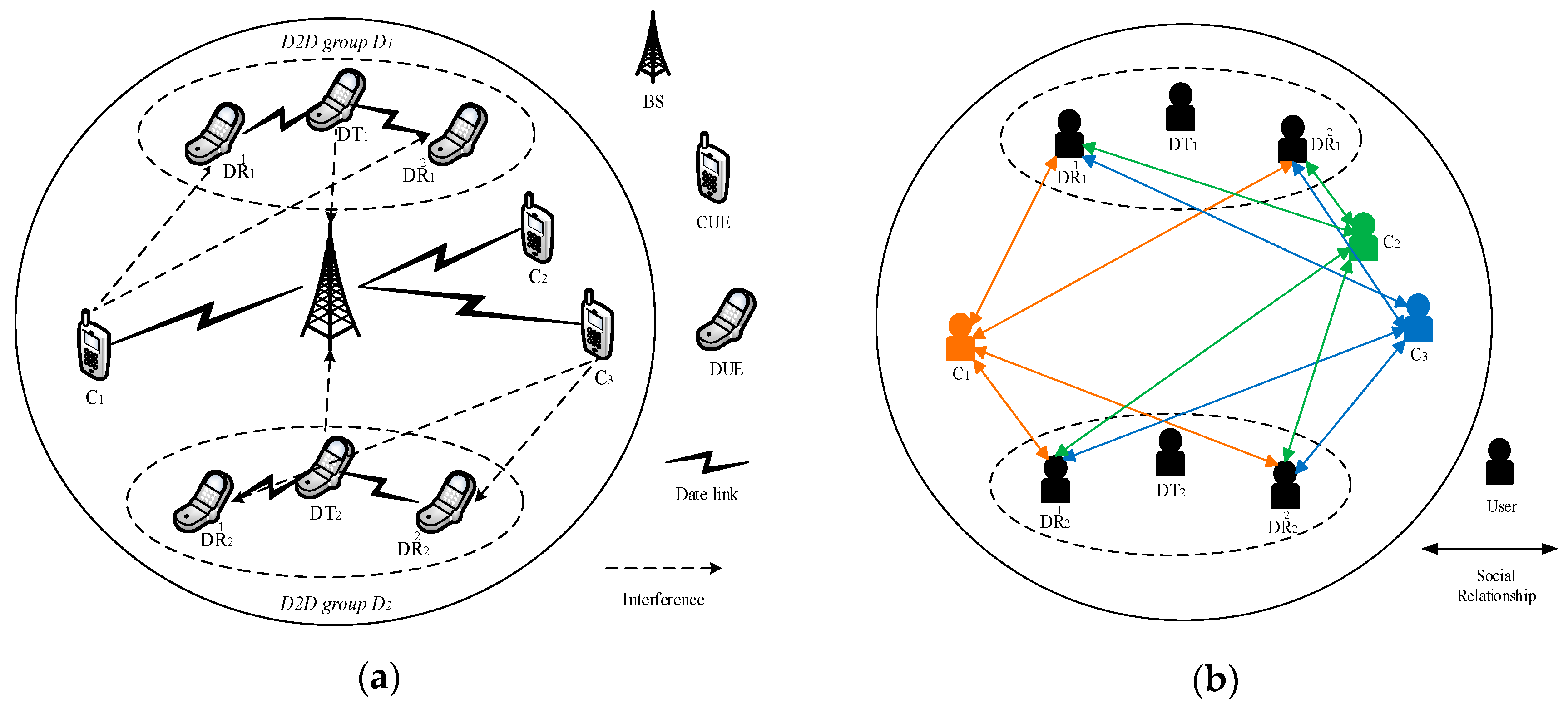
In the cellular communication system, a single-cell uplink transmission scenario is considered. As shown in
Figure 1a, we consider that
cellular users
and
D2D groups
are randomly distributed in the cell. The BS allocates a dedicated subchannel for each cellular user, and subchannels
are orthogonal with each other. We assume that the cellular user
occupies the subchannel
without loss of generality. The cellular users communicate with the BS in the traditional cellular mode. The D2D group is different from the traditional D2D pair. There are one D2D transmitter and several D2D receivers in one D2D group. We consider NOMA transmission protocol and serial interference cancellation (SIC) technology within D2D groups, so that the D2D transmitter can send messages to multiple D2D receivers simultaneously and each D2D receiver can demodulate the message which belongs to itself correctly. Considering that as the number of D2D receivers increases, series of problems such as complex interference, huge computational complexity, etc. will occur. This paper assumes that one D2D group only consists of one D2D transmitter
and two D2D receivers
,
, and each D2D receiver is randomly distributed within a disc centred on
.
Considering that mobile devices are carried by the human, social relationship between the cellular user and D2D user is taken into account. Social relationship will affect the channel selection and power allocation for D2D users and thereby strengthen the cooperation between D2D users and cellular users. Since the system model is closely associated with the social relationship between users, the following is the analysis of the physical domain and social domain, respectively.
Physical domain can be used to describe the impact of channel condition and system interference in practical network. In this paper, D2D groups communicate by reusing cellular users’ uplink channel resources. Therefore, cellular users may cause interference to D2D receivers and BS will suffer interference from D2D transmitters. The physical domain can be represented as a graph , where denotes the devices, indicates the channel quality for data transmission. The physical domain shows whether the channel can meet the communication requirements of users.
Social domain can be used to describe users’ social attributes, which is shown in
Figure 1b. Similarly, social domain can be represented as a graph
, where
denotes the users,
indicates the social relationship between cellular users and D2D receivers. Social relationship is defined as
,
,
. When two users have a very close social relationship,
should be close to one and they are more willing to cooperate with each other, which means the cellular user is more willing to let the D2D user who occupy its channel to increase the transmit power.
This paper assumes that each cellular user occupies an independent subchannel and each subchannel can be reused by only one D2D group. Meanwhile, each D2D group can only reuse one cellular user’s channel. Therefore, the signal received at the BS on the subchannel
can be expressed as
where
and
represent the transmit power of the cellular user and D2D transmitter, respectively.
and
are the channel gain between
and BS,
, and BS, respectively.
indicates whether
reuse
, i.e.,
is reused by
,
; otherwise
.
and
are the signals sent by
and
, respectively.
represents the additive white Gaussian noise (AWGN) on the channel. As a consequence, the signal-to-interference-plus -noise-ratio (SINR) and transmission rate of
at BS can be defined as
where
represents the noise power.
Considering NOMA in D2D groups, we set the power allocation coefficients of the D2D transmitter
as
and
, and
. Therefore, the signal received by the D2D receiver
can be expressed as
where
and
are the signals sent to
and
, respectively.
and
are the channel gain between
and
,
and
, respectively.
represents the AWGN at
.
If D2D receiver
need to remove
and demodulate
properly through SIC, the following condition must be met [
14], which can be represented as
where
and
are the channel gain between
and
,
and
, respectively.
Equation (5) can be simplified as
As shown in Equation (6), the inequality is unrelated to the power allocation coefficient , and is only related to the channel allocation . As a consequence, it can be expressed as a function of .
Thus, the SINR and transmission rate at D2D receiver
and
can be defined as
The above conclusions are all based on the assumption that can remove and correctly demodulate , and the corresponding other case, that is, remove and correctly demodulate , is similar to the above and will not be derived again.
3. Stackelberg Game Based Resource Allocation
According to the system model, this paper mainly studies the channel and power allocation of the D2D group under NOMA. Since the channel D2D group reuse may affect the D2D transmitter’s transmit power and the different transmit power is relative to the channel selection, the model is in accordance with the Stackelberg game. Therefore, we designed a two-stage Stackelberg game model where the leader is cellular users and the follower is D2D groups. In the first stage, we use KM algorithm to match the cellular users with D2D groups in order to allocate subchannels for D2D users. In the second stage, PSO algorithm based on penalty function will be used to optimize D2D users’ transmit power.
3.1. Utility Model
The utility functions of cellular users and D2D groups are defined on the basis of their benefit and loss. The first stage mainly solves the channel allocation problem, that is, the matching problem between cellular users and D2D groups. Considering that when D2D users reuse the channel of cellular users, they cause interference to cellular users and reduce cellular users’ throughput. Therefore, when the cellular channel is reused, the D2D user needs to pay a certain price for using the cellular channel. As a consequence, for cellular users, incentive is mainly derived from the rewards of assigning power to D2D groups based on social relationship. Meanwhile, they also sacrifice some of their throughput. Hence, the utility function of cellular users can be defined as
where
and
are the social relationships between the cellular user
and D2D receivers
,
, respectively.
represents the price of per unit power.
is the actual price of per unit power and it is related to the social relationship between two users. The closer the social relationship is, the lower the actual price is.
denotes the data rate of
when no D2D user reuses
.
can be expressed as
The second stage mainly solves the power allocation for D2D users. We do not consider optimizing the cellular users’ transmit power here and set it to a certain value. Therefore, power allocation means optimizing the D2D transmitter’s transmit power when sending messages to two D2D receivers. For D2D users, the incentive is mainly derived from the increase of data rate after reusing the cellular channels. If the data rate is not improved after reusing the cellular channel, then the utility will be less than zero, and the cellular mode will be selected for communication; if the data rate is increased, D2D users should pay for the transmit power. As a consequence, we can obtain the utility functions of
and
:
where
and
are the data rates when D2D users do not reuse the cellular channel and send messages to the BS in traditional cellular mode. They can be defined as Equation (13).
Hence, the utility function of the D2D groups is given by
3.2. Analysis of Leaders
Cellular users are the leaders in the Stackelberg game. In the first stage, we mainly solve the matching problem among cellular users and D2D groups. Based on cellular user’s utility function defined in the previous section, the channel allocation problem can be formulated as the following:
where Equation (16a) is the optimization problem we formulate to maximize the cellular users’ utility through the channel allocation. Constraint (16b) limits the interference which the D2D user brings to the cellular user and ensures the QoS of the cellular user. Constraint (16c) guarantees the QoS of D2D users. Constraint (16d) represents the requirement which must be met if using SIC. Constraint (16e) indicates that the value of
should be either 1 or 0, representing reusing
or not. Constraint (16f) indicates that the D2D group can only reuse one cellular user’s subchannel. Constraint (16g) indicates that only one D2D group can be assigned to each subchannel.
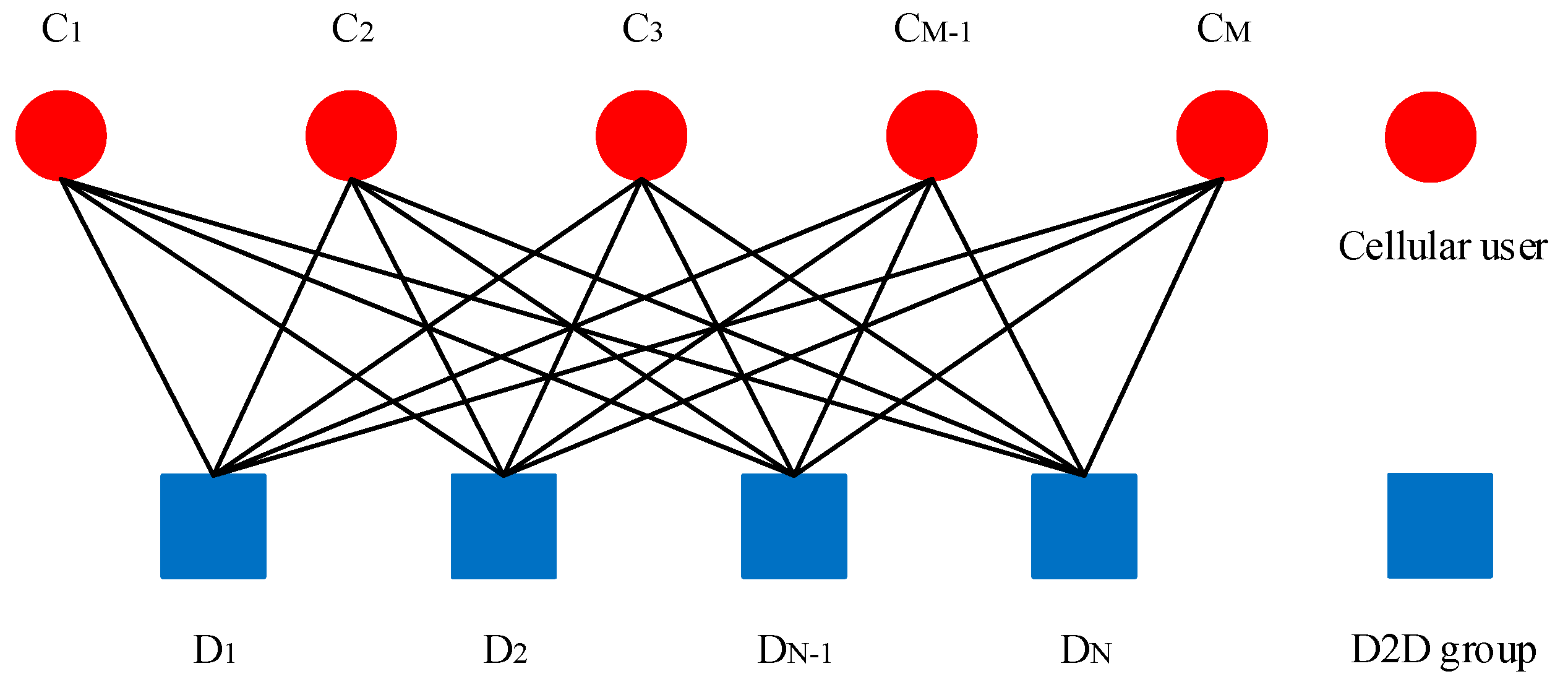
The objective function is non-convex because it is a 0–1 integer problem. It can be transformed into the optimal matching problem of the weighted bipartite graph. As we can see from
Figure 2, the cellular users and D2D groups form two sets of vertices in the bipartite graph and cellular users’ utility can represent the weight of edge
. The principle of the matching process is that each vertex can only match one vertex from the other side, and each vertex should select the vertex with the largest weight edge if possible. Therefore, the optimization problem can be converted to
.
KM algorithm can be used to solve Equation (16a) because it can solve the maximum weighted-matching problem under complete matching via the Hungarian method. Specifically, it transforms the weight of edges to the vertex and finds a perfect matching via the Hungarian method. During the matching process, it continuously adjusts the vertex value, increases the feasible edges, then uses Hungarian method to find the final matching. However, KM algorithm requires that the bipartite graph is completely symmetrical. We assume that the number of D2D groups is no more than the number of cellular users in this paper. In order to apply KM algorithm in our scenario, it is necessary to add several virtual vertices to D2D groups. In addition, in order to avoid a non-conforming match, we reset the weight of edge to zero if constraints Equation (16a–c) are not met. Furthermore, KM algorithm is inherently in compliance with the constraints Equation (16d–f). As a consequence, we can solve the channel allocation problem through KM algorithm in the first stage.
Proposition 1. KM algorithm converges to the optimal channel allocation strategy.
Proof. KM algorithm claims that, during the matching process, the total utility of all the cellular users should not reduce and at least one cellular user’s utility should increase if the match changes, which indicates that the matching is optimized to the perfect match. Since the cellular users and D2D groups participating in the match are finite, the corresponding match is also limited. As a consequence, KM is bound to converge to the optimal match after a finite number of iterations. □
Proposition 2. The computational complexity of KM is .
Proof. The computational complexity of KM is related to the number of vertices. As mentioned above, the number of vertices on both sides of our scenario is M. Hence, the computational complexity of KM is . □
3.3. Analysis of Followers
D2D groups are the followers in the Stackelberg game. In the second stage, we mainly solve the power allocation for D2D users. Based on the utility function of D2D groups defined in
Section 3.1, the power allocation problem can be formulated as the following:
where Equation (17a) is the optimization problem we formulate to maximize the D2D group’s utility through the power allocation. Constraint Equation (17b,c) ensures the QoS of all the users on
. Constraint Equation (17d,e) indicates that the D2D transmitter
’s transmit power should not exceed the power threshold, and the transmit power should not be less than zero when
sends signals to
and
, respectively.
Considering that Equation (17a) is a constrained optimization problem, we can transform it into an unconstrained optimization problem by the external penalty function method. The corresponding augmented objective function can be defined as
Based on the channel allocation in the previous section, Equation (18) mainly optimizes and . This problem is a non-convex problem and it can be solved via PSO. PSO is a parallel algorithm. The main idea of PSO is to initialize a group of random particles within the definition domain. Each particle adjusts its position according to the fitness determined by the objective function in each iteration. Two factors may affect particle’s speed and position. One is the optimal solution found by itself, and the other is the optimal solution currently found by the population. Through continuous iteration, all particles approximate the global optimal solution.
On the basis of the main idea of PSO, the position of the particle can be expressed as , where represents the particle number and represents the dimension. In this section, (18) mainly optimizes and , which means each particle represents a set of power allocation coefficients including two parameters and . Hence, it is a 2D optimization problem. can be expressed as , where represents the size of the population. Each particle constantly adjusts its speed and position to approximate the optimal value based on (18) on the joint definition domain of and .
The updated speed can be defined as
where
represents inertia weight which determines the speed of finding the optimal solution.
is non-negative.
and
are the acceleration constant used to characterize cognitive behaviour and social behaviour, respectively.
means a random number between [0, 1].
represents the individual optimal position of
in dimension
.
represents the optimal position of the population in dimension
.
The updated position can be defined as
The algorithm stops when the fitness change of the optimal position is less than the convergence threshold or reaches the maximum number of iterations. Through the continuous updating of particles’ speed and positions, the optimal value of the power allocation coefficients can be obtained. The proposed power allocation algorithm is shown in Algorithm 1.
| Algorithm 1. PSO based on penalty function |
| 1: Initialization: Population size , maximum number of iterations , number of iterations , maximum speed of the particle , search region [0, 1]. Initialize each particle’s velocity and position. |
| 2: For i = 1: |
| 3: |
| 4: For j = 1: |
| 5: Calculate the fitness according to (18) |
| 6: Compare and update and |
| 7: Update particle velocity according to (19) |
| 8: Update particle position according to (20) |
| 9: End for |
| 10: If |
| 11: Break |
| 12: End If |
| 13: End for |
| 14: Output: |
Proposition 3. PSO based on penalty function converges to the optimal power allocation strategy.
Proof. Reference [
15] proves the convergence of PSO. The parameters of the converged PSO should conform to:
. In this paper, we set
and
to satisfy the convergence requirement. In addition, although the power allocation for D2D groups involve
and
, the power allocation of each D2D group is independent with each other. D2D group only causes interference to the corresponding cellular user on the reused channel. Therefore, the power allocation problem can be decomposed into
sub-problems. Each sub-problem will converge to a stable optimal solution through PSO. As a consequence, the optimization problem in the second stage will converge to a stable optimal solution. □
Proposition 4. The computational complexity of PSO based on penalty function is .
Proof. The computational complexity of PSO is related to the number of particles and the number of iterations . It needs to perform PSO every time when optimizing transmit power for a D2D group. Therefore, the computational complexity of each execution of PSO is and the total computational complexity in the second stage is . □
3.4. Joint Channel and Power Allocation Based on Stackelberg Game
We propose a two-stage Stackelberg game, where the leader is cellular users and the follower is D2D groups. In the first stage, we find the optimal match between cellular users and D2D groups according to
Section 3.2. In the second stage, we optimize the D2D transmitter’s transmit power in each D2D group according to
Section 3.3. The two-stage Stackelberg game will finally converge to a stable solution which will be proved later. The specific two-stage Stackelberg game based joint channel and power allocation algorithm (S-JCPA) is shown in Algorithm 2.
| Algorithm 2. Stackelberg game based joint channel and power allocation (S-JCPA) |
| 1: Initialization: Set of cellular users , set of D2D groups , power allocation coefficients and , set of historical channel allocation , maximum number of iterations . |
| 2: For t=1: K |
| 3: Allocate channels for D2D groups via KM according to (12) |
| 4: If channel allocation results already exist in |
| 5: For i = 1: N |
| 6: Optimize transmit power for D2D users via PSO according to (18) |
| 7: Update and |
| 8: End for |
| 9: break |
| 10: Else |
| 11: Save the channel allocation result to |
| 12: For i = 1: N |
| 13: Optimize transmit power for D2D users via PSO according to (18) |
| 14: Update and |
| 15: End for |
| 16: End if |
| 17: End for |
| 18: Output: |
According to
Section 3.2 and
Section 3.3, it can be proved that both of the two stages can converge to the optimal solution. According to the characteristic of Stackelberg game, when the leader and follower both have an equilibrium solution, the Stackelberg equilibrium can be achieved. Through the previous analysis, we can easily achieve the network complexity in the system. Considering the computational complexity of KM and PSO, the network complexity is
.
4. Simulation and Performance Analysis
This section simulates and analyzes the proposed joint channel and power allocation algorithm based on Stackelberg game. The system model is shown in
Figure 1a. The simulation is built in a disc area with a radius of 500 m. The channel gain is subject to large-scale fading based on distance loss and small-scale fading based on Rayleigh fading [
16]. The large-scale fading can be modeled as
, where
represents the transmit distance,
and
represent the possible fading and path loss exponent, respectively. The Rayleigh fading follows the exponential distribution with a mean of 1. The simulation parameters are shown in
Table 1.
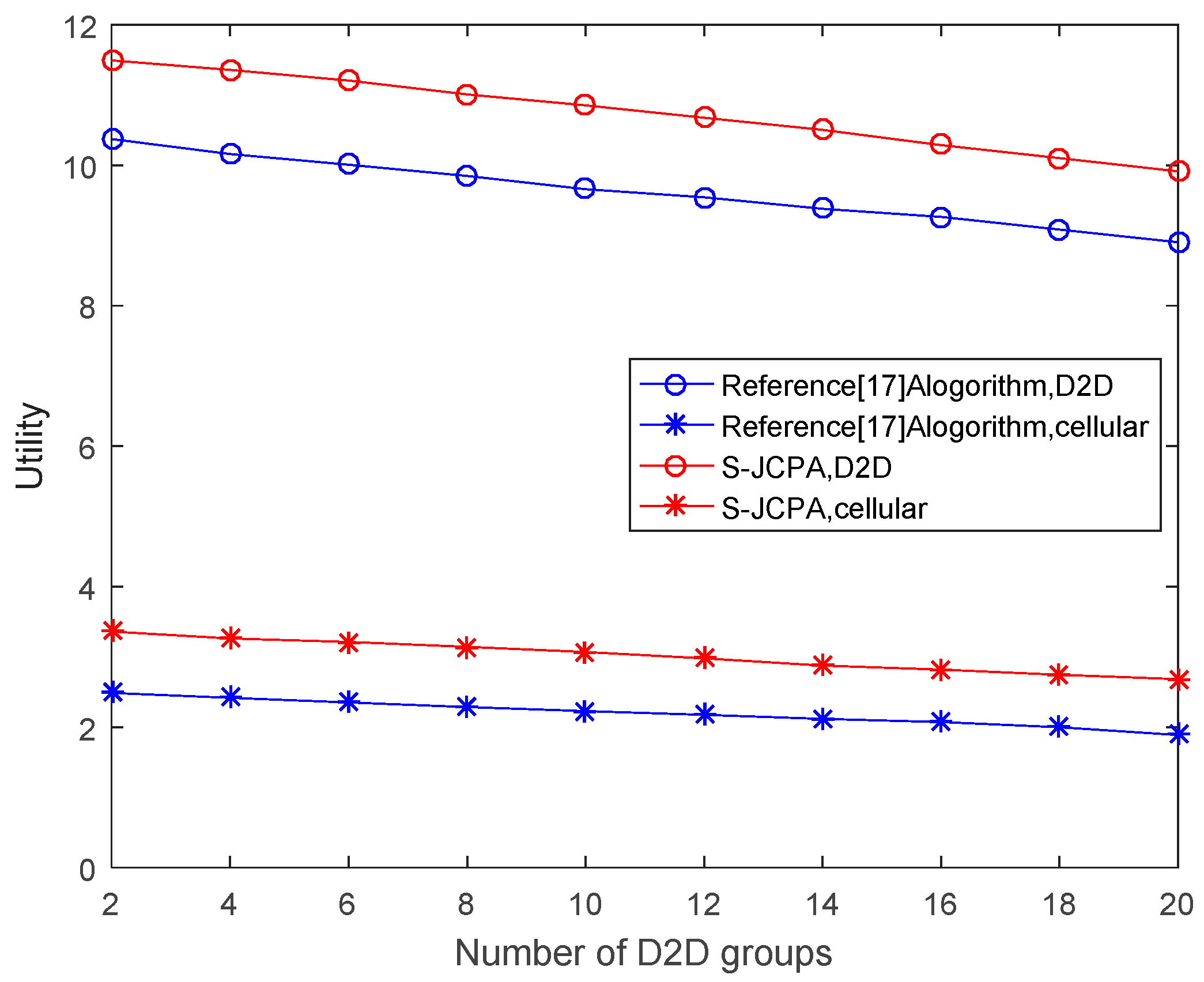
Figure 3 plots the utilities of the cellular and D2D users for different numbers of D2D groups. When the number of D2D groups increases, the utilities of both cellular and D2D users decline. This is because, as the number of D2D groups increases, the gap between the number of cellular users and the number of D2D groups is reduced. When performing channel matching, it is difficult to obtain an optimal match for each user because of the lack of channel resources. Consequently, the utilities of both cellular users and D2D users decline. In Reference [
17], a joint optimization algorithm for channel allocation and power control was proposed to optimize the throughput of D2D users. However, this study did not consider the effect of the social relationship between cellular and D2D users and did not optimize the utility function based on the social relationship. Hence, the utility obtained with the algorithm in Reference [
17] was not as high as that obtained with our algorithm.
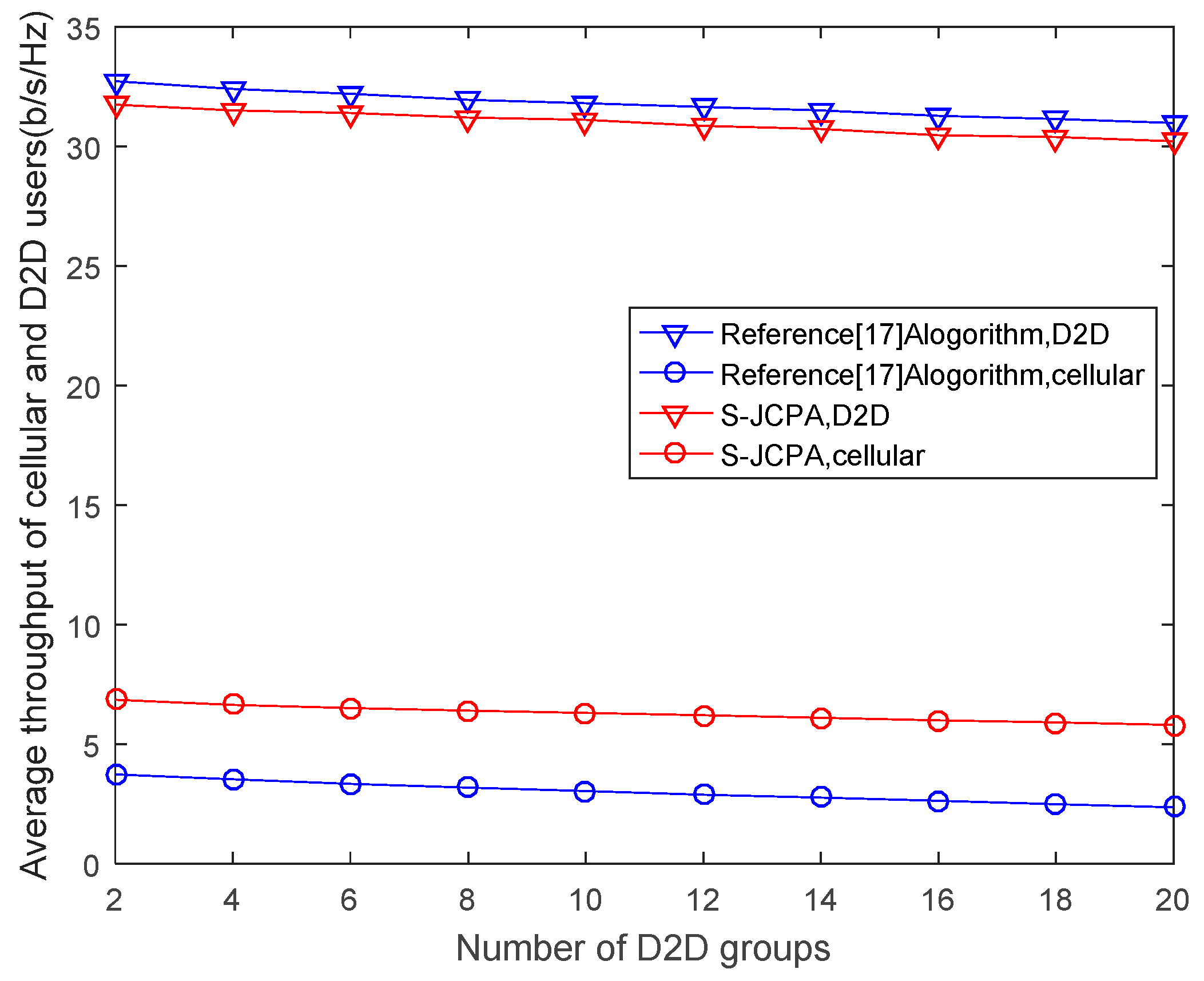
Figure 4 plots the average throughput(rate) of the cellular and D2D users for different numbers of D2D groups. As the number of D2D groups increases, the average throughput of both cellular and D2D users shows a downward trend. This is because cellular users represent subchannels available for allocation in the system. Similar to the reason in
Figure 3, the number of cellular users is unchanged whereas the number of D2D groups increases. Hence, it is difficult to obtain an optimal match for each individual because of the lack of channel resources. Consequently, the average throughput is reduced for both cellular and D2D users. Furthermore, Reference [
17] aimed at optimizing the throughput of all the D2D users without considering whether the cellular users were willing to cooperate with them. Hence, the average throughput of D2D users in Reference [
17] was higher than that obtained with our algorithm, whereas the average throughput of cellular users in Reference [
17] was lower than that obtained with our algorithm.
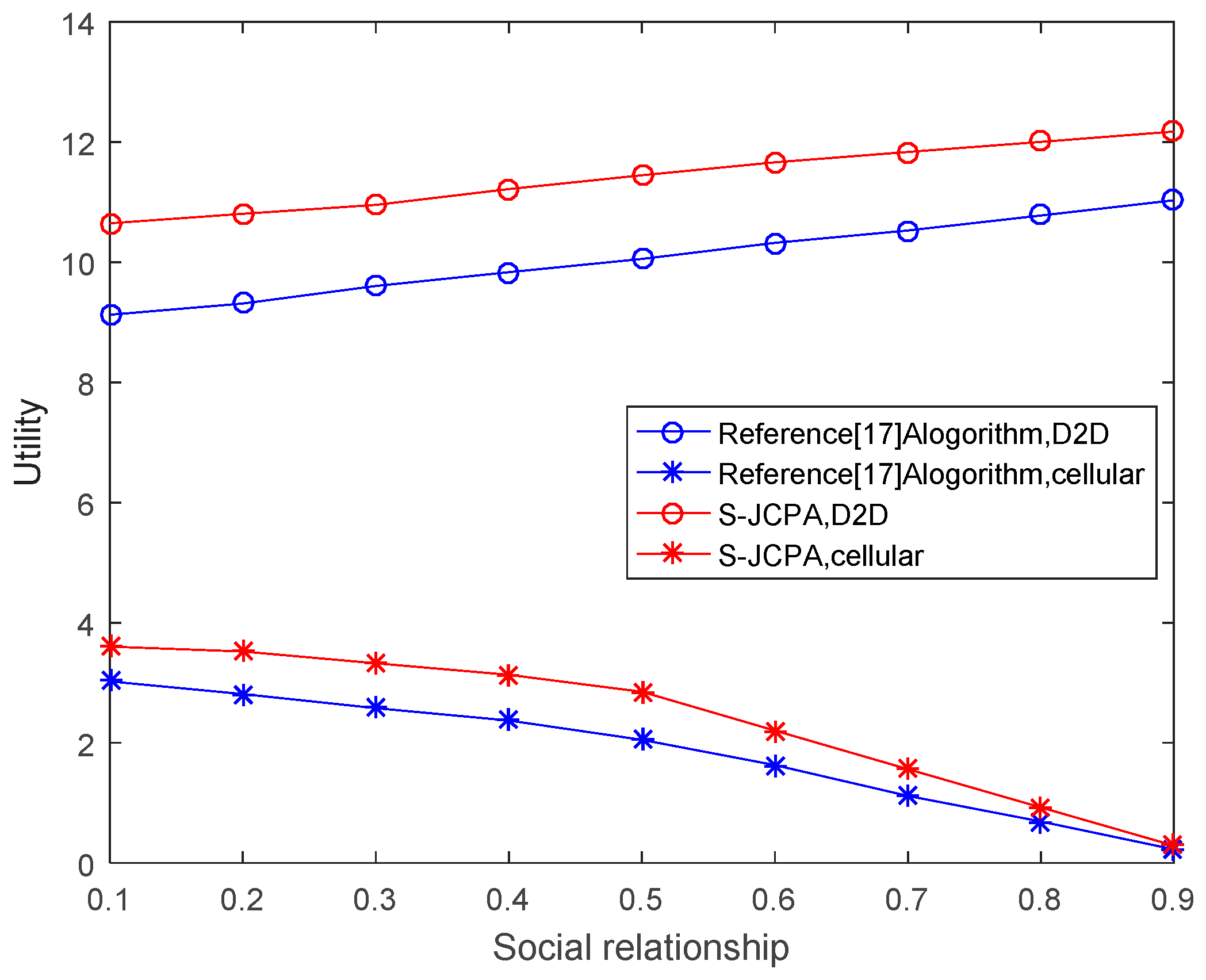
Figure 5 shows the impact of the social relationships on the utilities of the cellular and D2D users. With a closer social relationship, the utility of D2D users continues to increase and the utility of cellular users continues to decrease, which is determined by their respective utility functions. When the social relationship between D2D and cellular users is not close, cellular users are not willing to allow the D2D users who reuse their channels to increase their transmit power to improve their throughput. Hence, the cellular users have high utility whereas the D2D users have low utility. When the social relationship is close, the D2D users can increase the transmit power on the cellular channel with a small expense. Consequently, the utility of the D2D users increases, whereas the utility of the cellular users gradually decreases. As the social relationship becomes closer, the D2D users can increase their transmit power without paying an expense to the cellular users. Hence, the utility of the cellular users drops sharply, even approaching zero. However, as Reference [
17] did not consider the social relationship between cellular and D2D users, the utility function based on the social relationship was not optimized. Consequently, the utilities of both cellular and D2D users were lower than those obtained with our algorithm.
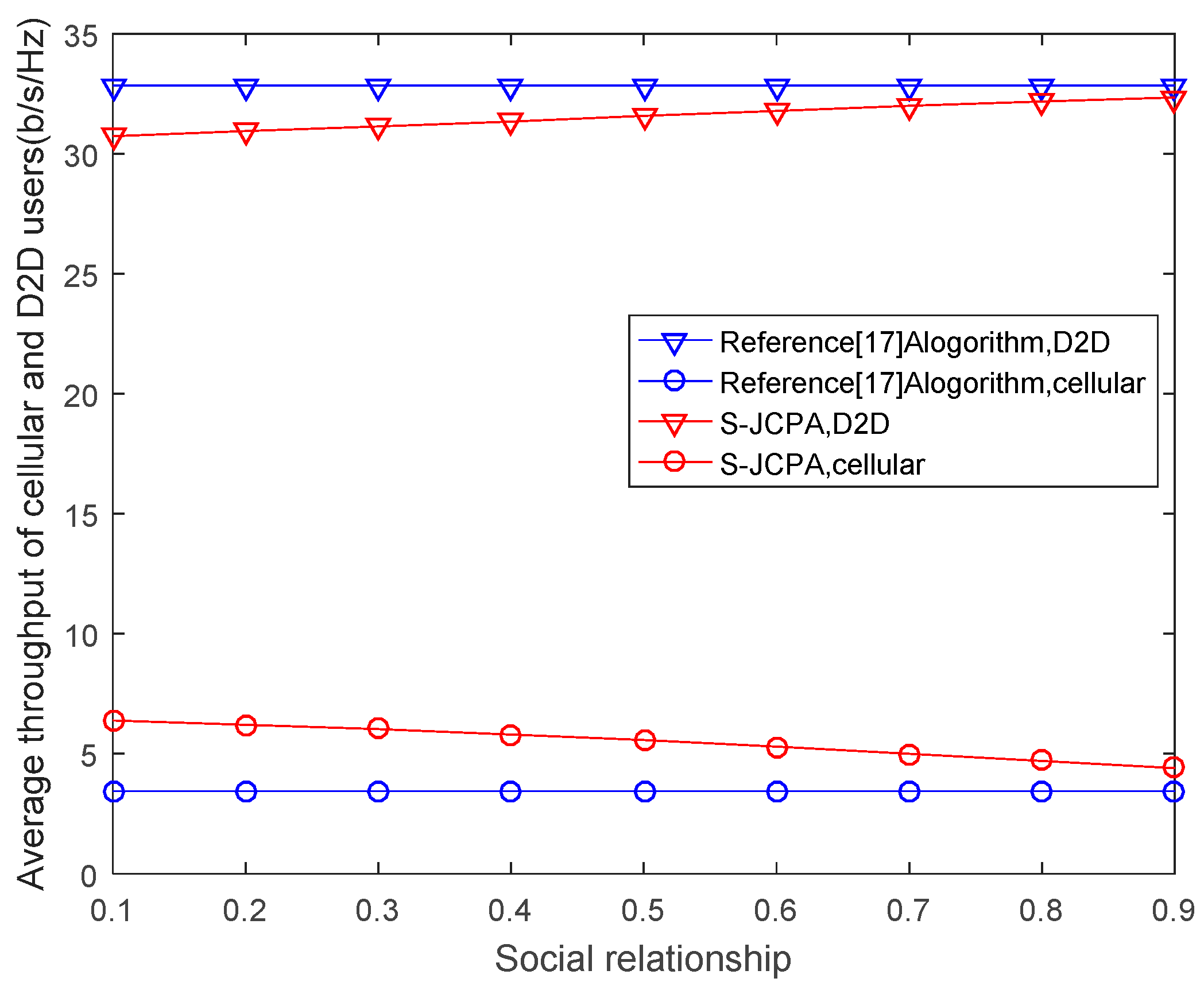
Figure 6 shows the impact of social relationships on the average throughput of the cellular and D2D users. As Reference [
17] did not consider the influence of social relationship, the average throughput of the cellular and D2D users was unchanged. However, in our algorithm, the closer the social relationship between the cellular users and D2D users, the more cellular users are willing to allow the D2D users who reuse their channels to increase their transmit power to improve their throughput. As the social relationship becomes closer, the D2D users only need to pay a small expense to achieve a high transmit power. Therefore, the average throughput of the D2D users continuously increases, whereas the average throughput of the cellular users gradually decreases. Moreover, as the social relationship becomes closer, the average throughput of the D2D group in this study approaches that in Reference [
17] and the average throughput of the cellular users becomes higher than that in Reference [
17].
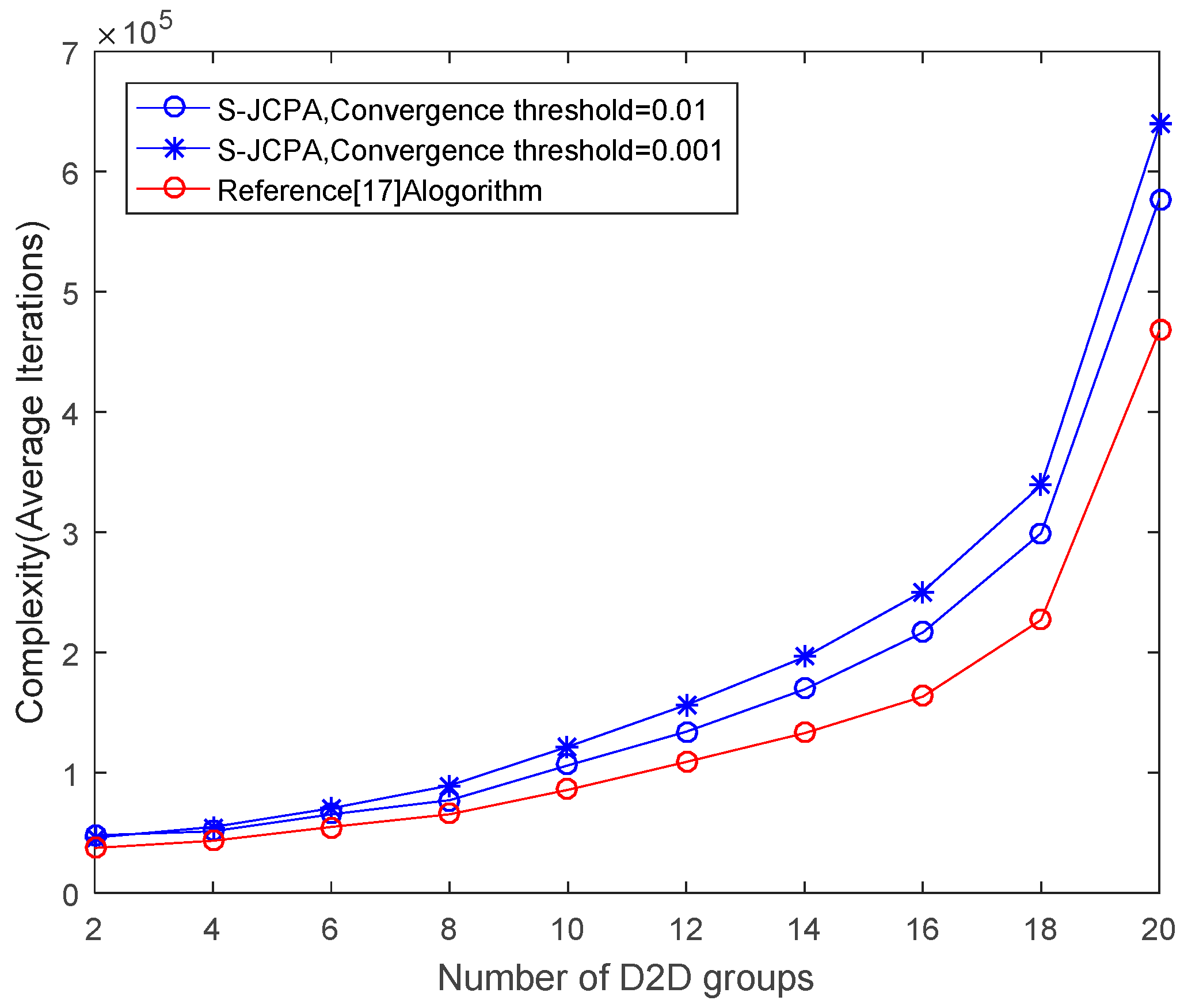
Figure 7 plots the network complexity for different numbers of D2D groups under different convergence thresholds and compares the proposed algorithm S-JCPA with the algorithm proposed in [
17].
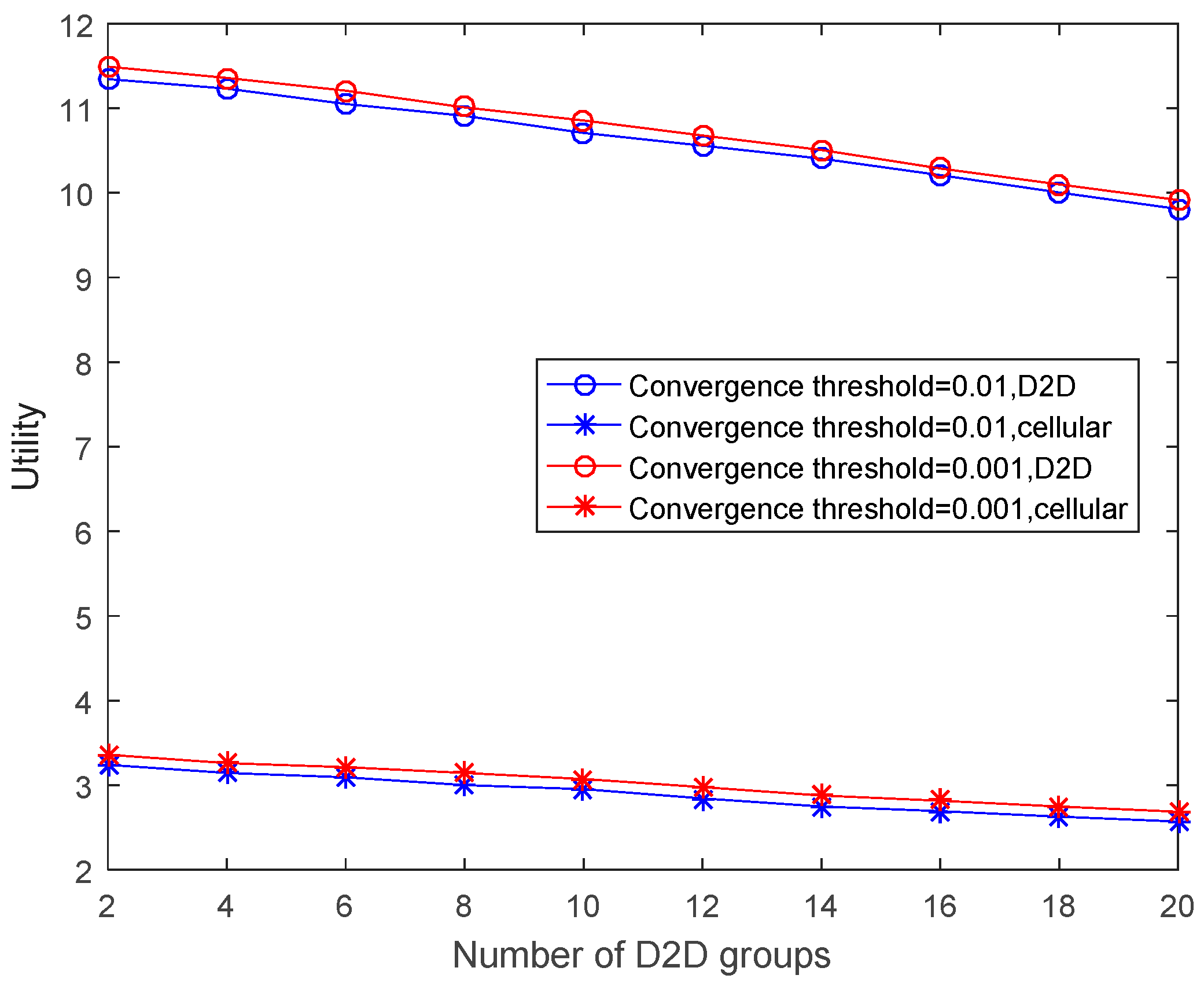
Figure 8 shows the impact of convergence threshold on the utilities of the cellular and D2D users. The study in Reference [
17] first solved the channel allocation problem with KM and then optimized the D2D transmit power with KKT. In S-JCPA, KM and PSO are used to solve the resource allocation problem. Consequently, the network complexity of the algorithm in Reference [
17] is less than that of our algorithm. We also compare the network complexity of our algorithm under different convergence thresholds. The results show that, when the convergence threshold is small, the network complexity is higher, and meanwhile, the utilities of the cellular and D2D users are higher as well because PSO can search for more accurate results. Considering that as the convergence threshold decreases, the utilities don’t change much, so we choose 0.001 as the convergence threshold instead of continuously reducing the convergence threshold.