A Survey on Application of Non-Orthogonal Multiple Access to Different Wireless Networks
Abstract
1. Introduction
- A comprehensive network model is provided for each of the considered NOMA-based CN, D2D communication, and WSN.
- In order to evaluate the performance of each considered NOMA-based network, outage probability expressions are presented.
- In addition, the sum-rate maximization problem is formulated for each type of NOMA-based network, which could serve as a good reference point for beginners and practitioners working on NOMA-based CN, D2D communication, or WSN.
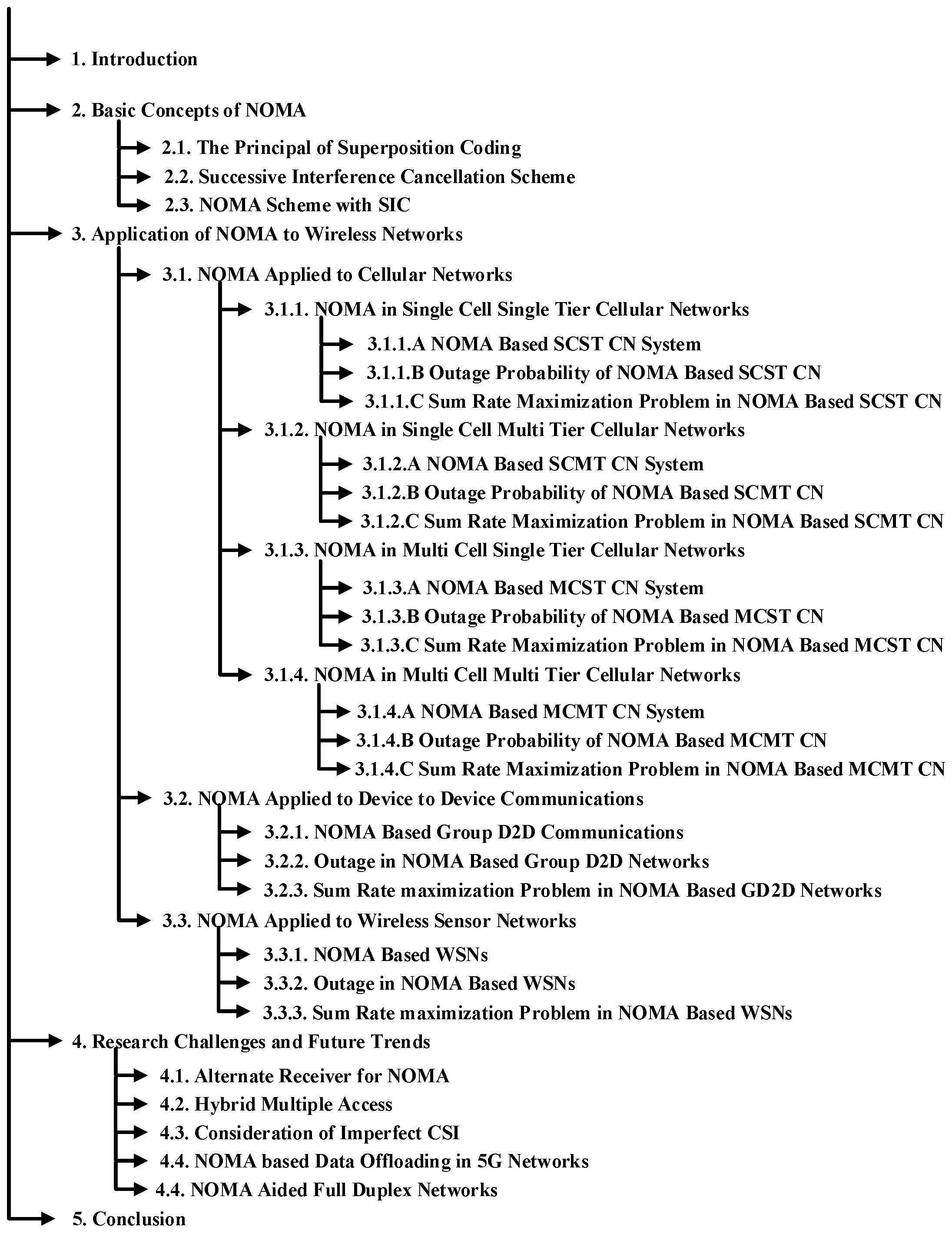
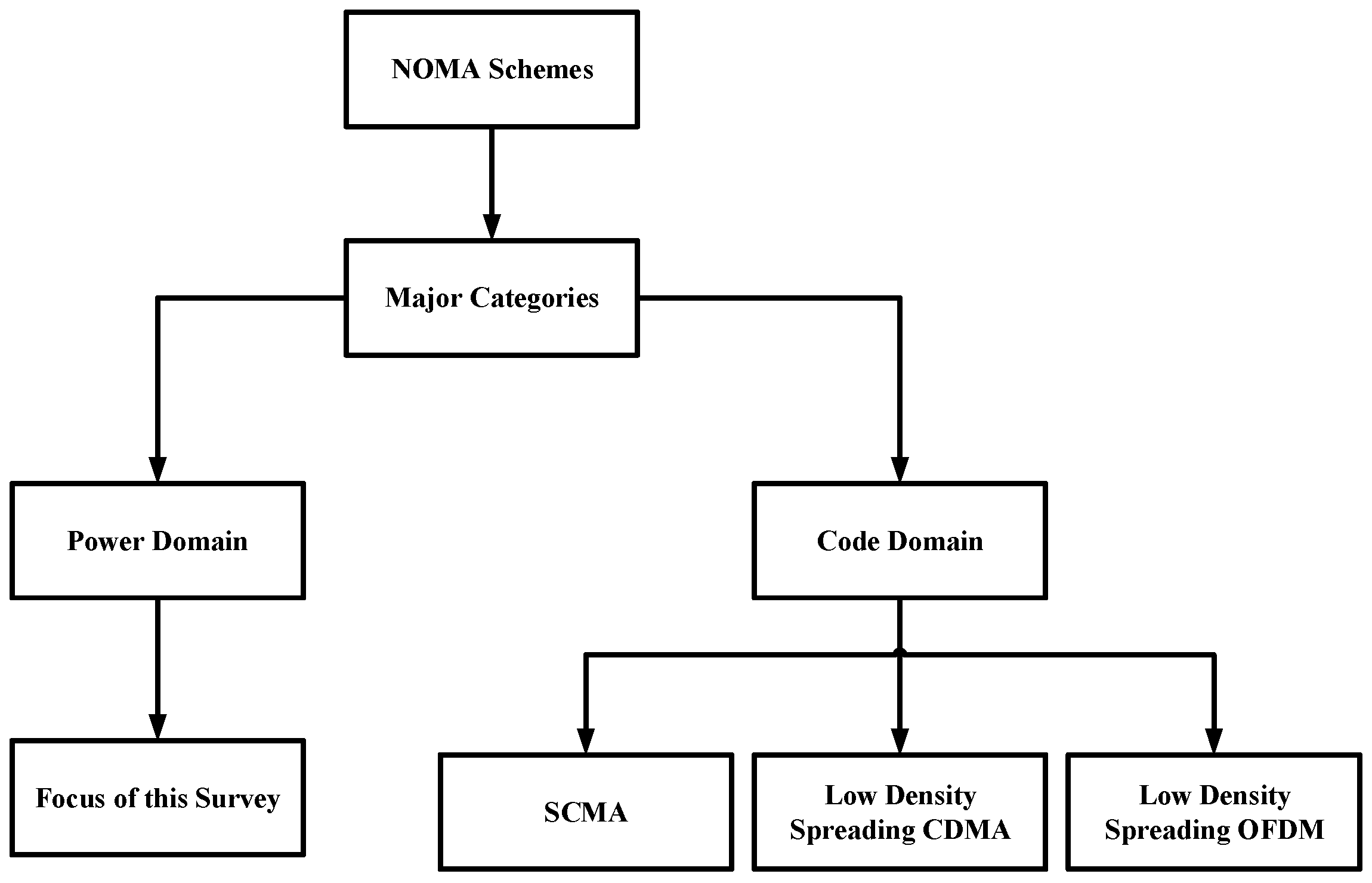
2. Basic Concepts of NOMA
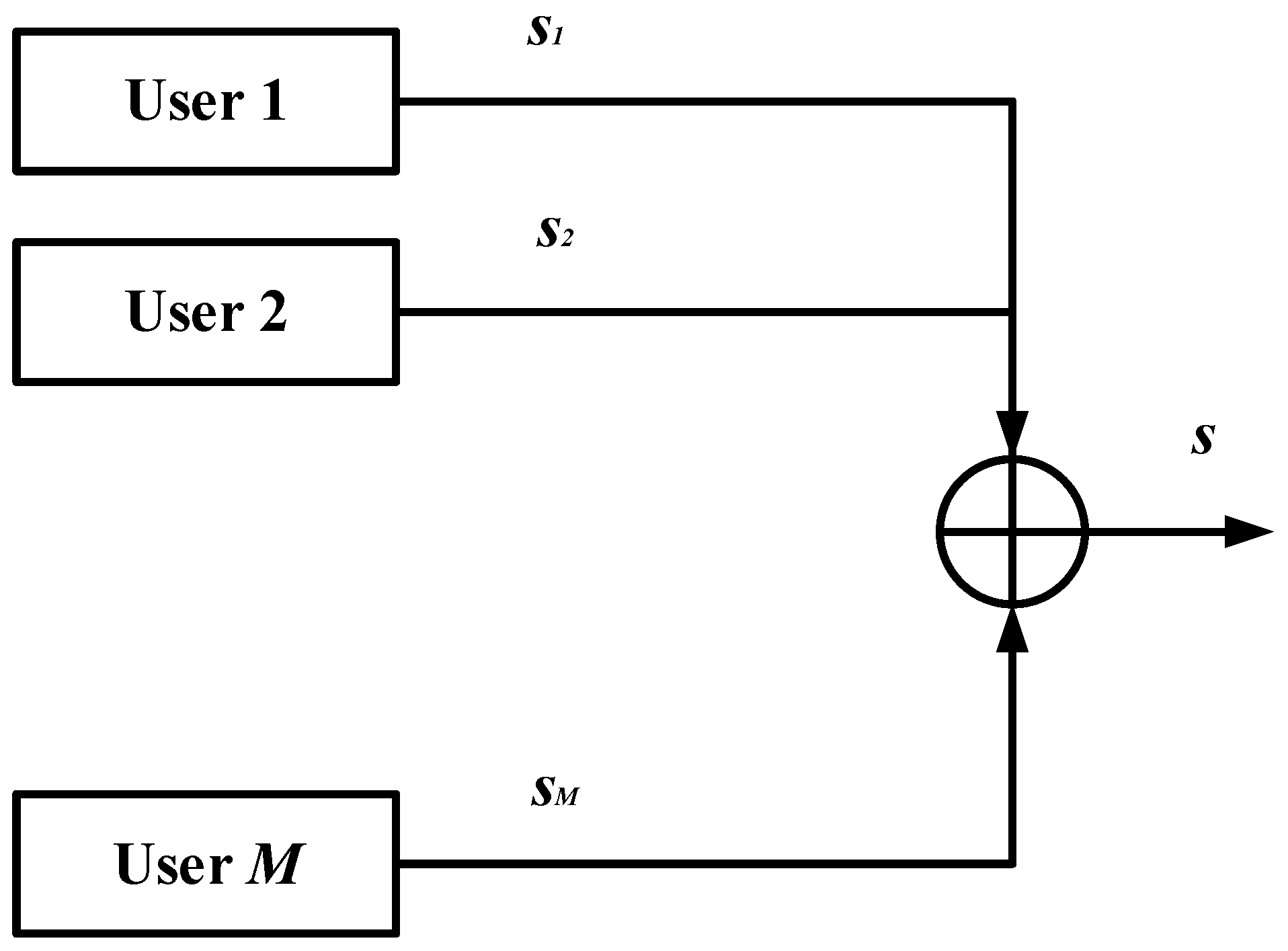
2.1. The Principle of Superposition Coding
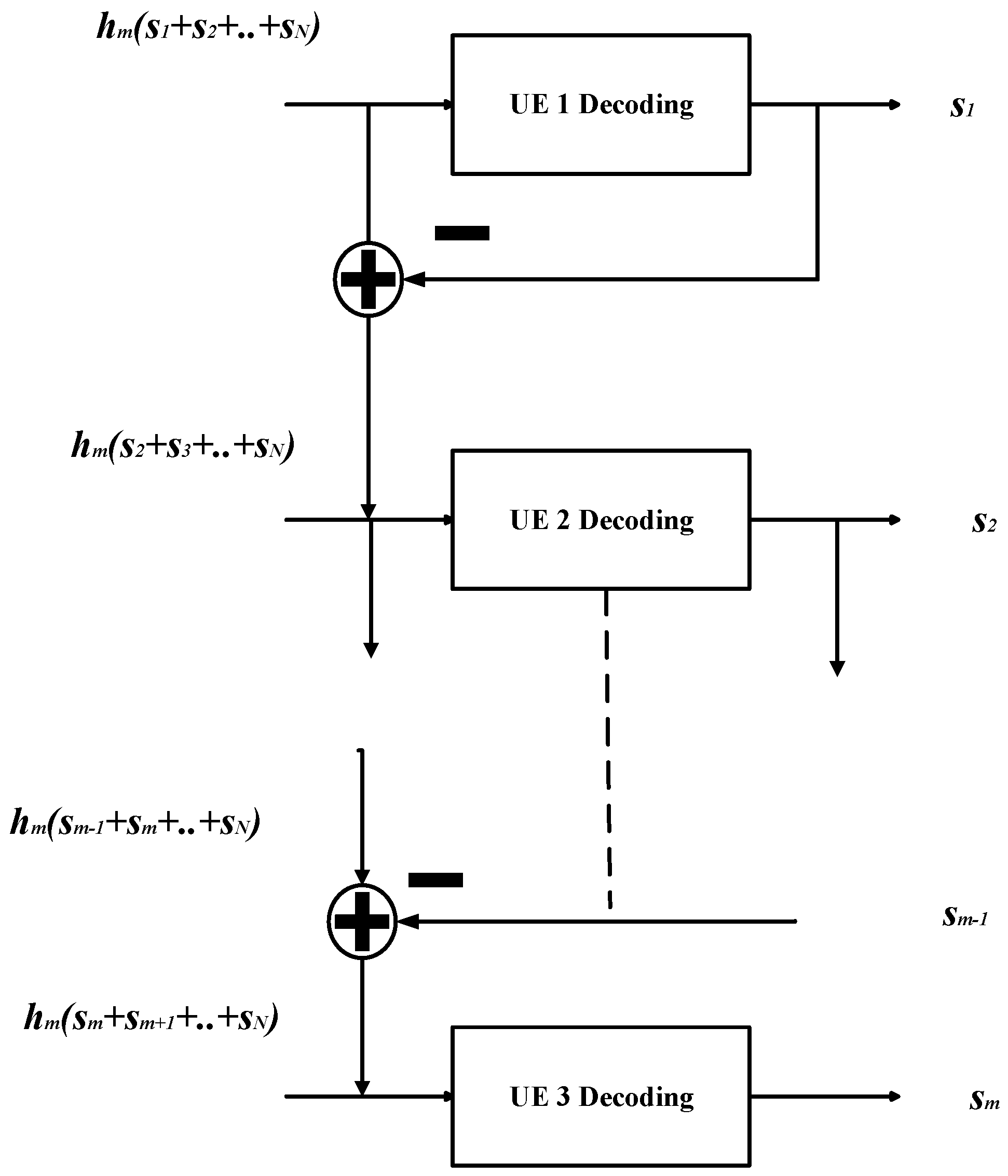
2.2. Successive Interference Cancellation Scheme
2.3. NOMA Scheme with SIC
3. Application of NOMA to Wireless Networks
3.1. NOMA Applied to Cellular Networks
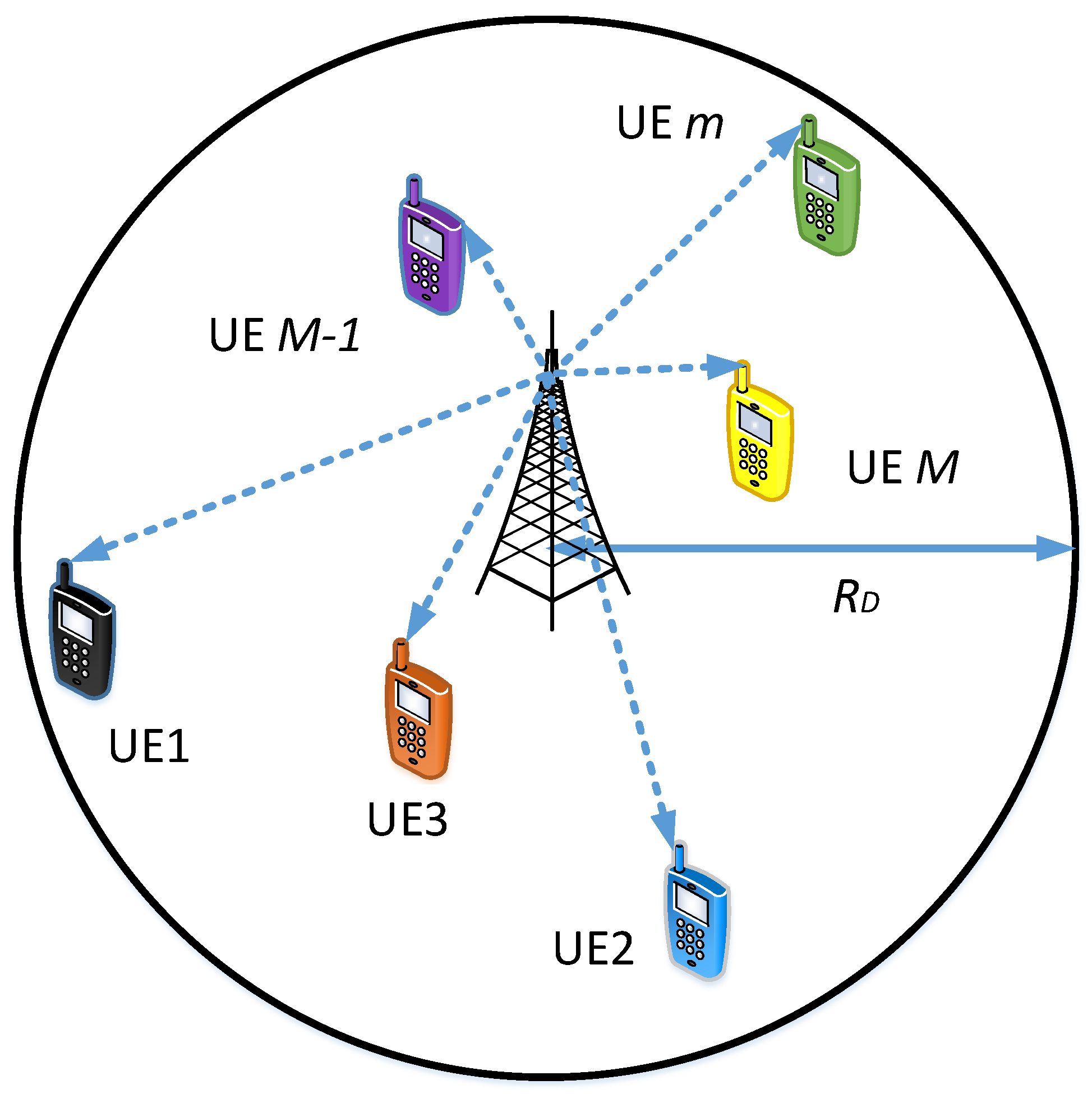
3.1.1. NOMA in Single-Cell Single-Tier Cellular Networks
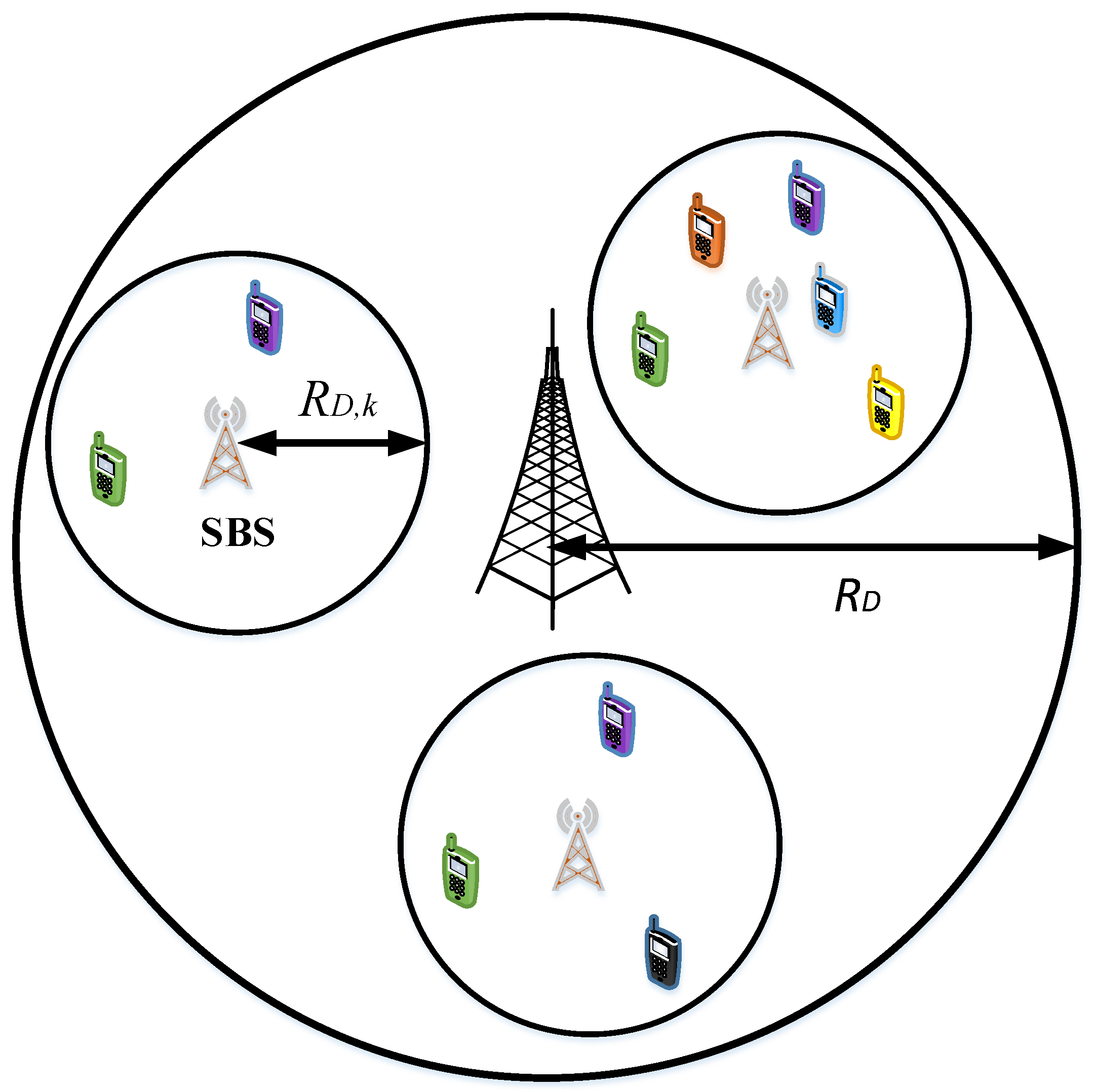
3.1.2. NOMA in Single-Cell Multi-Tier Cellular Networks
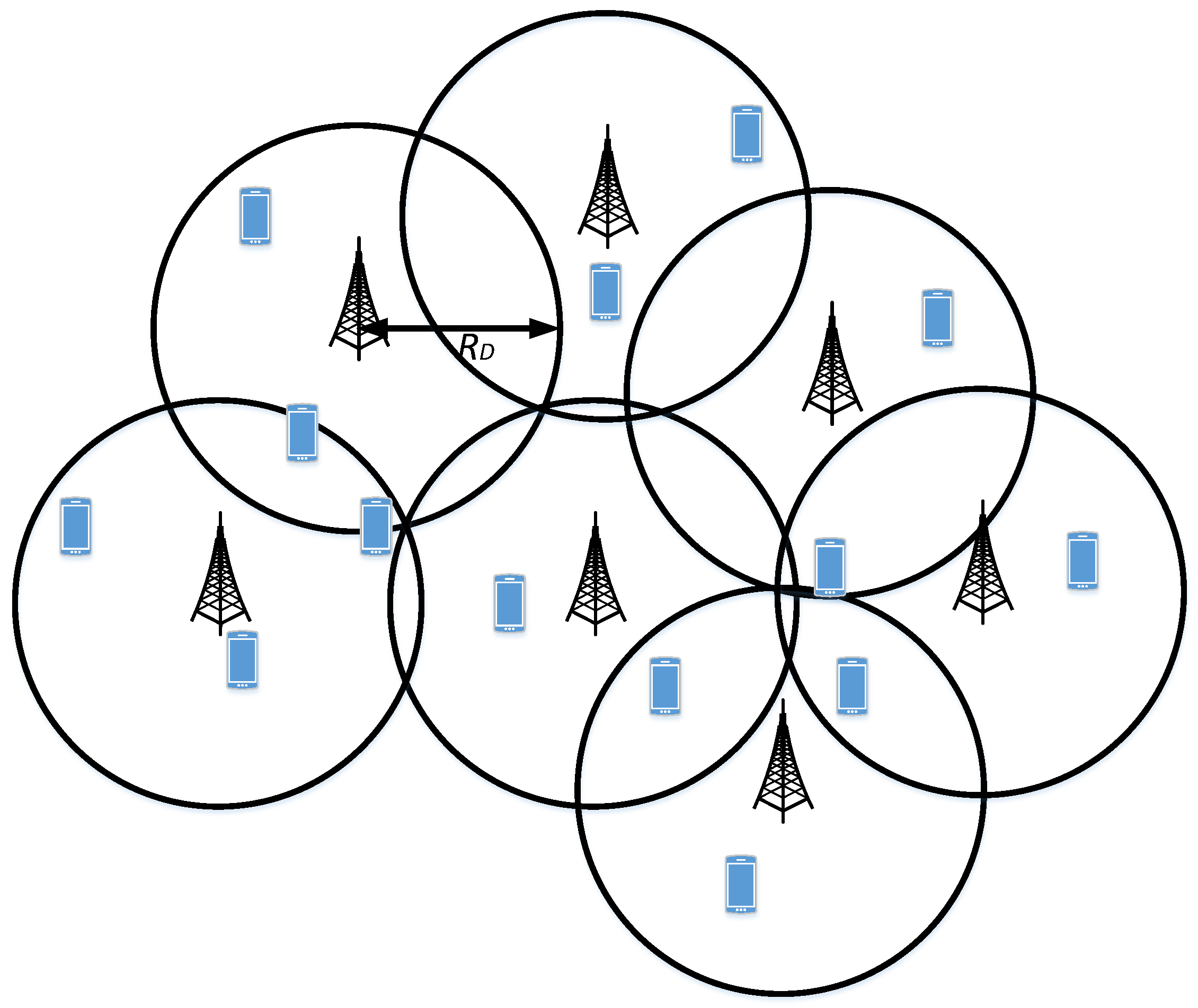
3.1.3. NOMA in Multi-Cell Single-Tier Cellular Network
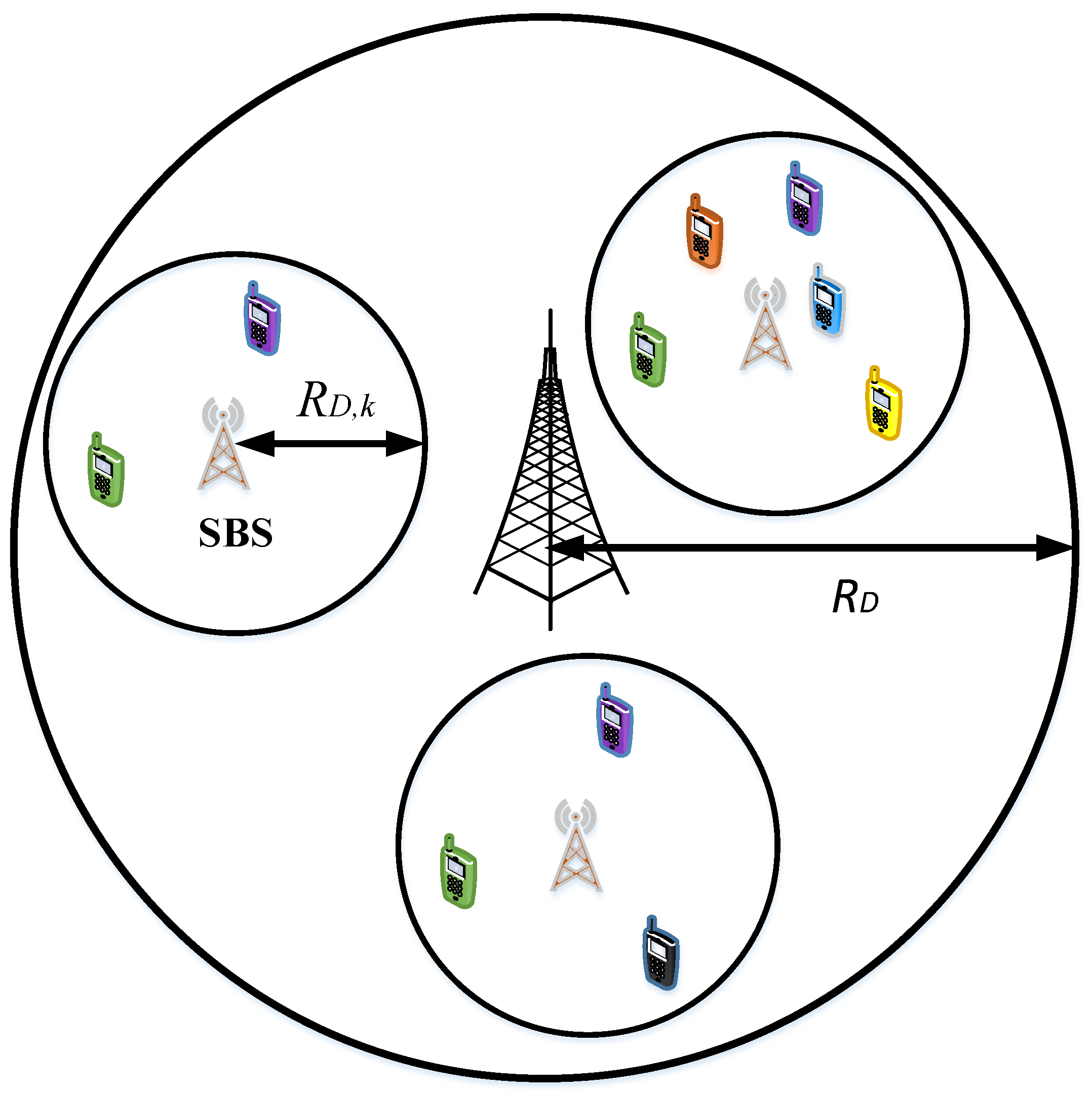
3.1.4. NOMA in Multi-Cell Multi-Tier Cellular Networks
3.2. NOMA Applied to Device-To-Device Communications
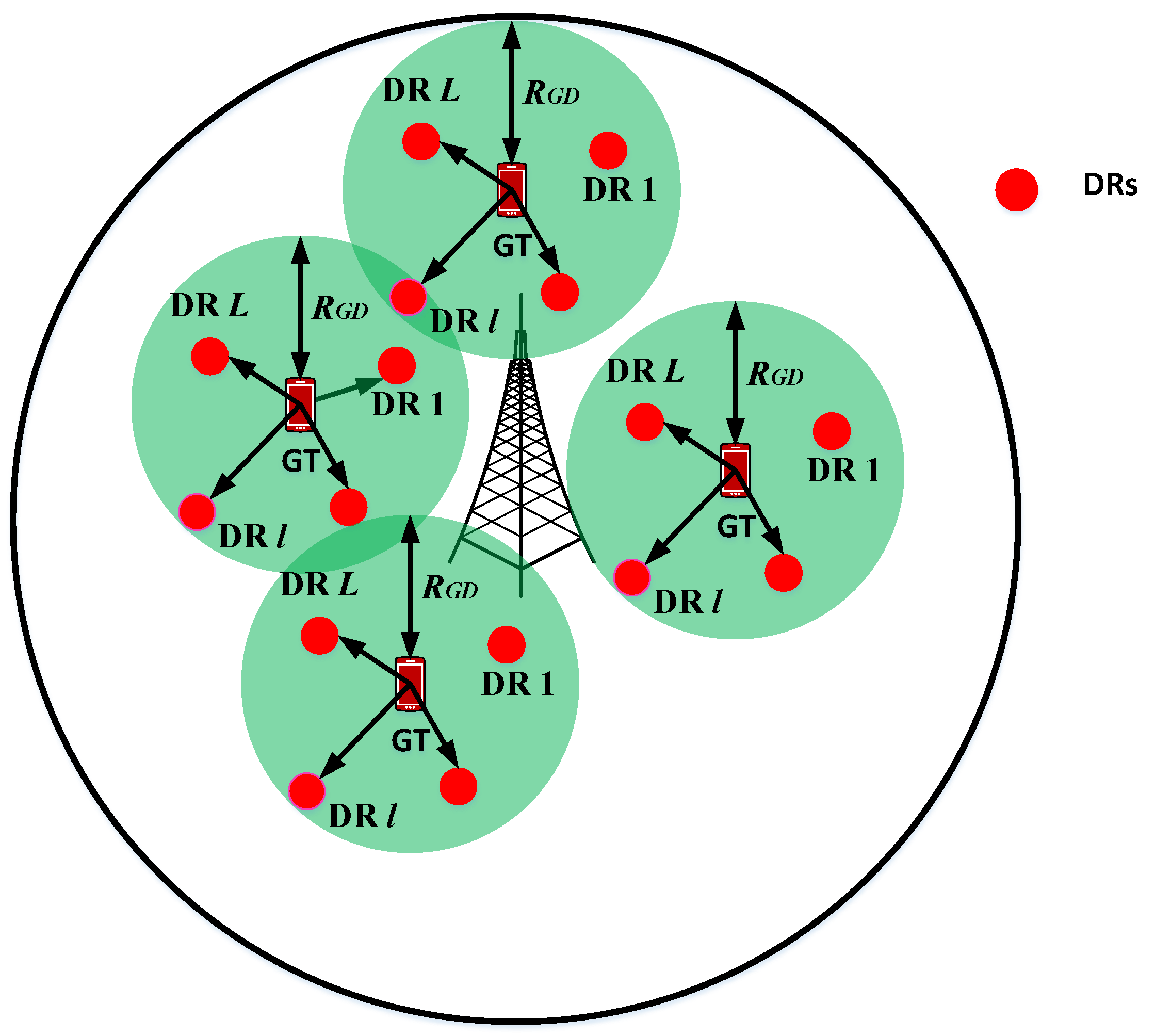
3.2.1. NOMA-Based Group D2D Communications
3.2.2. Outage in NOMA-Based Group D2D Network
3.2.3. Sum-Rate Maximization Problem in NOMA-Based GD2D Networks
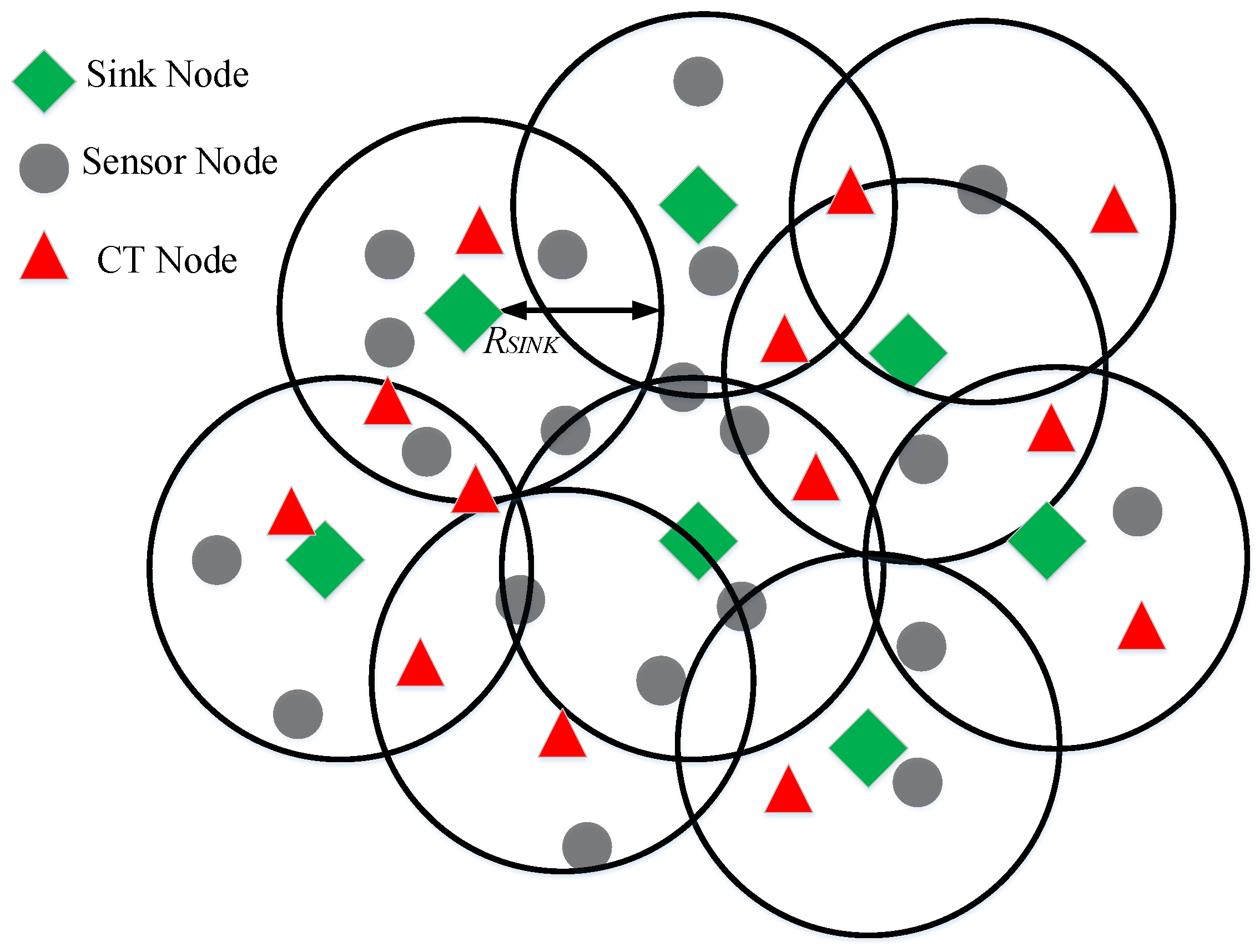
3.3. NOMA Applied to Wireless Sensor Networks
3.3.1. NOMA-Based WSNs
3.3.2. Outage in NOMA-Based WSNs
3.3.3. Sum-Rate Maximization Problem in NOMA-Based WSNs
4. Research Challenges and Future Trends
4.1. Alternate Receiver for NOMA
4.2. Hybrid Multiple Access
4.3. Consideration of Imperfect CSI
4.4. NOMA-Based Data Offloading in 5G Networks
4.5. NOMA-Aided Full Duplex Networks
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Andrews, J.G.; Buzzi, S.; Choi, W.; Hanly, S.V.; Lozano, A.; Soong, A.C.; Zhang, J.C. What will 5G be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Nie, S.; Lin, S.C.; Chandrasekaran, M. 5G roadmap: 10 key enabling technologies. Comput. Netw. 2016, 106, 17–48. [Google Scholar] [CrossRef]
- Boccardi, F.; Heath, R.W.; Lozano, A.; Marzetta, T.L.; Popovski, P. Five disruptive technology directions for 5G. IEEE Commun. Mag. 2014, 52, 74–80. [Google Scholar] [CrossRef]
- Wang, C.X.; Haider, F.; Gao, X.; You, X.H.; Yang, Y.; Yuan, D.; Aggoune, H.M.; Haas, H.; Fletcher, S.; Hepsaydir, E. Cellular architecture and key technologies for 5G wireless communication networks. IEEE Commun. Mag. 2014, 52, 122–130. [Google Scholar] [CrossRef]
- Hossain, E.; Hasan, M. 5G cellular: Key enabling technologies and research challenges. arXiv 2015, arXiv:1503.00674. [Google Scholar] [CrossRef]
- Wang, P.; Xiao, J.; Li, P. Comparison of orthogonal and non-orthogonal approaches to future wireless cellular systems. IEEE Veh. Technol. Mag. 2006, 1, 4–11. [Google Scholar] [CrossRef]
- Kadir, M.I.; Sugiura, S.; Zhang, J.; Chen, S.; Hanzo, L. OFDMA/SC-FDMA aided space–time shift keying for dispersive multiuser scenarios. IEEE Trans. Veh. Technol. 2012, 62, 408–414. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, Z.; Ding, Z.; Fan, P.; Li, H. Key techniques for 5G wireless communications: Network architecture, physical layer, and MAC layer perspectives. Sci. China Inf. Sci. 2015, 58, 1–20. [Google Scholar] [CrossRef]
- Baldemair, R.; Dahlman, E.; Fodor, G.; Mildh, G.; Parkvall, S.; Selen, Y.; Tullberg, H.; Balachandran, K. Evolving wireless communications: Addressing the challenges and expectations of the future. IEEE Veh. Technol. Mag. 2013, 8, 24–30. [Google Scholar] [CrossRef]
- Yifei, Y.; Longming, Z. Application scenarios and enabling technologies of 5G. China Commun. 2014, 11, 69–79. [Google Scholar] [CrossRef]
- Ding, Z.; Fan, P.; Poor, H.V. Impact of user pairing on 5G nonorthogonal multiple-access downlink transmissions. IEEE Trans. Veh. Technol. 2015, 65, 6010–6023. [Google Scholar] [CrossRef]
- Islam, S.R.; Avazov, N.; Dobre, O.A.; Kwak, K.S. Power-domain non-orthogonal multiple access (NOMA) in 5G systems: Potentials and challenges. IEEE Commun. Surv. Tutor. 2016, 19, 721–742. [Google Scholar] [CrossRef]
- Docomo, N. 5G Radio Access: Requirements, Concept and Technologies; NTT DOCOMO, Inc.: Tokyo, Japan, 2014. [Google Scholar]
- Tao, Y.; Liu, L.; Liu, S.; Zhang, Z. A survey: Several technologies of non-orthogonal transmission for 5G. China Commun. 2015, 12, 1–15. [Google Scholar] [CrossRef]
- Rappaport, T.S. Wireless Communications: Principles and Practice; Prentice Hall: Upper Saddle River, NJ, USA, 1996; Volume 2. [Google Scholar]
- Study on Downlink Multiuser Superposition Transmission for LTE; Technical Report; 3rd Generation Partnership Project (3GPP): 650 Route des Lucioles-Sophia Antipolis Valbonne-France. 2015. Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=2912 (accessed on 13 November 2019).
- Zhang, L.; Li, W.; Wu, Y.; Wang, X.; Park, S.I.; Kim, H.M.; Lee, J.Y.; Angueira, P.; Montalban, J. Layered-division-multiplexing: Theory and practice. IEEE Trans. Broadcast. 2016, 62, 216–232. [Google Scholar] [CrossRef]
- Benjebbour, A.; Saito, K.; Li, A.; Kishiyama, Y.; Nakamura, T. Non-orthogonal multiple access (NOMA): Concept, performance evaluation and experimental trials. In Proceedings of the IEEE International Conference on Wireless Networks and Mobile Communications (WINCOM), Marrakech, Morocco, 20–23 October 2015; pp. 1–6. [Google Scholar]
- Benjebbour, A.; Li, A.; Saito, K.; Saito, Y.; Kishiyama, Y.; Nakamura, T. NOMA: From concept to standardization. In Proceedings of the IEEE Conference on Standards for Communications and Networking (CSCN), Tokyo, Japan, 28–30 October 2015; pp. 18–23. [Google Scholar]
- Saito, Y.; Benjebbour, A.; Kishiyama, Y.; Nakamura, T. System-level performance evaluation of downlink non-orthogonal multiple access (NOMA). In Proceedings of the IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), London, UK, 8–11 September 2013; pp. 611–615. [Google Scholar]
- Saito, Y.; Benjebbour, A.; Kishiyama, Y.; Nakamura, T. System-level performance of downlink non-orthogonal multiple access (NOMA) under various environments. In Proceedings of the IEEE 81st Vehicular Technology Conference (VTC Spring), Glasgow, UK, 11–14 May 2015; pp. 1–5. [Google Scholar]
- Saito, K.; Benjebbour, A.; Harada, A.; Kishiyama, Y.; Nakamura, T. Link-level performance of downlink NOMA with SIC receiver considering error vector magnitude. In Proceedings of the IEEE 81st Vehicular Technology Conference (VTC Spring), Glasgow, UK, 11–14 May 2015; pp. 1–5. [Google Scholar]
- Saito, K.; Benjebbour, A.; Kishiyama, Y.; Okumura, Y.; Nakamura, T. Performance and design of SIC receiver for downlink NOMA with open-loop SU-MIMO. In Proceedings of the IEEE International Conference on Communication Workshop (ICCW), London, UK, 8–12 June 2015; pp. 1161–1165. [Google Scholar]
- Lu, L.; Chen, Y.; Guo, W.; Yang, H.; Wu, Y.; Xing, S. Prototype for 5G new air interface technology SCMA and performance evaluation. China Commun. 2015, 12, 38–48. [Google Scholar] [CrossRef]
- Dai, L.; Wang, B.; Ding, Z.; Wang, Z.; Chen, S.; Hanzo, L. A survey of non-orthogonal multiple access for 5G. IEEE Commun. Surv. Tutor. 2018, 20, 2294–2323. [Google Scholar] [CrossRef]
- Ding, Z.; Lei, X.; Karagiannidis, G.K.; Schober, R.; Yuan, J.; Bhargava, V.K. A survey on non-orthogonal multiple access for 5G networks: Research challenges and future trends. IEEE J. Sel. Areas Commun. 2017, 35, 2181–2195. [Google Scholar] [CrossRef]
- Ding, Z.; Liu, Y.; Choi, J.; Sun, Q.; Elkashlan, M.; Chih-Lin, I.; Poor, H.V. Application of non-orthogonal multiple access in LTE and 5G networks. IEEE Commun. Mag. 2017, 55, 185–191. [Google Scholar] [CrossRef]
- Higuchi, K.; Benjebbour, A. Non-orthogonal multiple access (NOMA) with successive interference cancellation for future radio access. IEICE Trans. Commun. 2015, 98, 403–414. [Google Scholar] [CrossRef]
- Wei, Z.; Yuan, J.; Ng, D.W.K.; Elkashlan, M.; Ding, Z. A survey of downlink non-orthogonal multiple access for 5G wireless communication networks. ZTE Commun. 2016, 14, 17–23. [Google Scholar]
- Vaezi, M.; Amarasuriya, G.; Liu, Y.; Arafa, A.; Fang, F.; Ding, Z. Interplay Between NOMA and Other Emerging Technologies: A Survey. arXiv 2019, arXiv:1903.10489. [Google Scholar] [CrossRef]
- Vaezi, M.; Ding, Z.; Poor, H.V. Multiple Access Techniques for 5G Wireless Networks and Beyond; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Islam, S.; Zeng, M.; Dobre, O.A.; Kwak, K.S. Non-Orthogonal Multiple Access (NOMA): How It Meets 5G and Beyond. arXiv 2019, arXiv:1907.10001. [Google Scholar]
- Wan, D.; Wen, M.; Cheng, X.; Mumtaz, S.; Guizani, M. A Promising Non-Orthogonal Multiple Access Based Networking Architecture: Motivation, Conception, and Evolution. IEEE Wirel. Commun. 2019, 26, 152–159. [Google Scholar] [CrossRef]
- Chen, Y.; Bayesteh, A.; Wu, Y.; Ren, B.; Kang, S.; Sun, S.; Xiong, Q.; Qian, C.; Yu, B.; Ding, Z.; et al. Toward the Standardization of Non-Orthogonal Multiple Access for Next Generation Wireless Networks. IEEE Commun. Mag. 2018, 56, 19–27. [Google Scholar] [CrossRef]
- Arachchillage, U.S.S.S.; Jayakody, D.N.K.; Biswash, S.K.; Dinis, R. Recent Advances and Future Research Challenges in Non-Orthogonal Multiple Access for 5G Networks. In Proceedings of the IEEE 87th Vehicular Technology Conference (VTC Spring), Porto, Portugal, 3–6 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Liaqat, M.; Noordin, K.A.; Abdul Latef, T.; Dimyati, K. Power-domain non orthogonal multiple access (PD-NOMA) in cooperative networks: An overview. Wirel. Netw. 2018. [Google Scholar] [CrossRef]
- Elouafadi, R.; Benjillali, M. Cooperative NOMA-based D2D communications: A survey in the 5G/IoT context. In Proceedings of the 19th IEEE Mediterranean Electrotechnical Conference (MELECON), Marrakesh, Morocco, 2–7 May 2018; pp. 132–137. [Google Scholar] [CrossRef]
- Chen, X.; Liu, G.; Ma, Z.; Zhang, X.; Fan, P.; Chen, S.; Yu, F.R. When Full Duplex Wireless Meets Non-Orthogonal Multiple Access: Opportunities and Challenges. arXiv 2019, arXiv:1905.13605. [Google Scholar] [CrossRef]
- Mohammadi, M.; Shi, X.; Chalise, B.K.; Ding, Z.; Suraweera, H.A.; Zhong, C.; Thompson, J.S. Full-Duplex Non-Orthogonal Multiple Access for Next Generation Wireless Systems. IEEE Commun. Mag. 2019, 57, 110–116. [Google Scholar] [CrossRef]
- Elbamby, M.S.; Bennis, M.; Saad, W.; Debbah, M.; Latva-Aho, M. Full-Duplex Non-Orthogonal Multiple Access Networks. In Multiple Access Techniques for 5G Wireless Networks and Beyond; Vaezi, M., Ding, Z., Poor, H.V., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 285–303. [Google Scholar] [CrossRef]
- Thakur, P.; Kumar, A.; Pandit, S.; Singh, G.; Satashia, S.N. Frameworks of non-orthogonal multiple access techniques in cognitive radio communication systems. China Commun. 2019, 16, 129–149. [Google Scholar] [CrossRef]
- Zhou, F.; Wu, Y.; Liang, Y.; Li, Z.; Wang, Y.; Wong, K. State of the Art, Taxonomy, and Open Issues on Cognitive Radio Networks with NOMA. IEEE Wirel. Commun. 2018, 25, 100–108. [Google Scholar] [CrossRef]
- Yin, L.; Haas, H. Non-Orthogonal Multiple Access in LiFi Networks. In Multiple Access Techniques for 5G Wireless Networks and Beyond; Vaezi, M., Ding, Z., Poor, H.V., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 609–638. [Google Scholar] [CrossRef]
- Van De Beek, J.; Popovic, B.M. Multiple access with low-density signatures. In Proceedings of the IEEE Global Telecommunications Conference (IEEE Globecom), Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–6. [Google Scholar]
- Razavi, R.; Hoshyar, R.; Imran, M.A.; Wang, Y. Information theoretic analysis of LDS scheme. IEEE Commun. Lett. 2011, 15, 798–800. [Google Scholar] [CrossRef]
- Mohammed, A.I.; Imran, M.A.; Tafazolli, R.; Chen, D. Performance evaluation of low density spreading multiple access. In Proceedings of the IEEE International Wireless Communications and Mobile Computing Conference (IWCMC), Limassol, Cyprus, 27–31 August 2012; pp. 383–388. [Google Scholar]
- Hoshyar, R.; Razavi, R.; Al-Imari, M. LDS-OFDM an efficient multiple access technique. In Proceedings of the IEEE 71st Vehicular Technology Conference (VTC), Taipei, Taiwan, 16–19 May 2010; pp. 1–5. [Google Scholar]
- Al-Imari, M.; Xiao, P.; Imran, M.A.; Tafazolli, R. Uplink non-orthogonal multiple access for 5G wireless networks. In Proceedings of the IEEE International Symposium on Wireless Communications Systems (ISWCS), Poznan, Poland, 20–23 September 2014; pp. 781–785. [Google Scholar]
- Du, Y.; Dong, B.; Chen, Z.; Fang, J.; Wang, X. A fast convergence multiuser detection scheme for uplink SCMA systems. IEEE Wirel. Commun. Lett. 2016, 5, 388–391. [Google Scholar] [CrossRef]
- Mu, H.; Ma, Z.; Alhaji, M.; Fan, P.; Chen, D. A fixed low complexity message pass algorithm detector for up-link SCMA system. IEEE Wirel. Commun. Lett. 2015, 4, 585–588. [Google Scholar] [CrossRef]
- Du, Y.; Dong, B.; Chen, Z.; Fang, J.; Yang, L. Shuffled multiuser detection schemes for uplink sparse code multiple access systems. IEEE Commun. Lett. 2016, 20, 1231–1234. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, X.; Lu, L.; Wu, Y.; He, G.; Chen, Y. Sparse code multiple access: An energy efficient uplink approach for 5G wireless systems. In Proceedings of the IEEE Global Communications Conference (Globecom), Austin, TX, USA, 8–12 December 2014; pp. 4782–4787. [Google Scholar]
- Wu, Y.; Zhang, S.; Chen, Y. Iterative multiuser receiver in sparse code multiple access systems. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 2918–2923. [Google Scholar]
- Au, K.; Zhang, L.; Nikopour, H.; Yi, E.; Bayesteh, A.; Vilaipornsawai, U.; Ma, J.; Zhu, P. Uplink contention based SCMA for 5G radio access. In Proceedings of the IEEE Globecom Workshops (GC Wkshps), Austin, TX, USA, 8–12 December 2014; pp. 900–905. [Google Scholar]
- Taherzadeh, M.; Nikopour, H.; Bayesteh, A.; Baligh, H. SCMA codebook design. In Proceedings of the IEEE 80th Vehicular Technology Conference (VTC2014-Fall), Vancouver, BC, Canada, 14–17 September 2014; pp. 1–5. [Google Scholar]
- Benjebbovu, A.; Li, A.; Saito, Y.; Kishiyama, Y.; Harada, A.; Nakamura, T. System-level performance of downlink NOMA for future LTE enhancements. In Proceedings of the 2013 IEEE Globecom Workshops (GC Wkshps), Atlanta, GA, USA, 9–13 December 2013; pp. 66–70. [Google Scholar]
- Saito, Y.; Kishiyama, Y.; Benjebbour, A.; Nakamura, T.; Li, A.; Higuchi, K. Non-orthogonal multiple access (NOMA) for cellular future radio access. In Proceedings of the 2013 IEEE 77th Vehicular Technology Conference (VTC Spring), Dresden, Germany, 2–5 June 2013; pp. 1–5. [Google Scholar]
- Wang, L.; Şaşoğlu, E.; Bandemer, B.; Kim, Y.H. A comparison of superposition coding schemes. In Proceedings of the 2013 IEEE International Symposium on Information Theory, Istanbul, Turkey, 7–12 July 2013; pp. 2970–2974. [Google Scholar]
- Zhang, R.; Hanzo, L. A unified treatment of superposition coding aided communications: Theory and practice. IEEE Commun. Surv. Tutor. 2010, 13, 503–520. [Google Scholar] [CrossRef]
- Zafar, A.; Shaqfeh, M.; Alouini, M.S.; Alnuweiri, H. On multiple users scheduling using superposition coding over Rayleigh fading channels. IEEE Commun. Lett. 2013, 17, 733–736. [Google Scholar] [CrossRef]
- Cover, T. Broadcast channels. IEEE Trans. Inf. Theory 1972, 18, 2–14. [Google Scholar] [CrossRef]
- Vanka, S.; Srinivasa, S.; Gong, Z.; Vizi, P.; Stamatiou, K.; Haenggi, M. Superposition coding strategies: Design and experimental evaluation. IEEE Trans. Wirel. Commun. 2012, 11, 2628–2639. [Google Scholar] [CrossRef]
- Li, L.E.; Alimi, R.; Ramjee, R.; Shi, J.; Sun, Y.; Viswanathan, H.; Yang, Y.R. Superposition coding for wireless mesh networks. In Proceedings of the ACM International Conference on Mobile Computing and Networking, Los Angeles, CA, USA, 23–29 September 2007; pp. 330–333. [Google Scholar]
- Buehrer, R.M. Code Division Multiple Access (CDMA); Morgan & Claypool Publishers: San Rafael, CA, USA, 2006; Volume 1, pp. 1–192. [Google Scholar]
- Buehrer, R.M. Equal BER performance in linear successive interference cancellation for CDMA systems. IEEE Trans. Commun. 2001, 49, 1250–1258. [Google Scholar] [CrossRef]
- Miridakis, N.I.; Vergados, D.D. A survey on the successive interference cancellation performance for single-antenna and multiple-antenna OFDM systems. IEEE Commun. Surv. Tutor. 2012, 15, 312–335. [Google Scholar] [CrossRef]
- Wildemeersch, M.; Quek, T.Q.; Kountouris, M.; Rabbachin, A.; Slump, C.H. Successive interference cancellation in heterogeneous networks. IEEE Trans. Commun. 2014, 62, 4440–4453. [Google Scholar] [CrossRef]
- Dai, L.; Wang, B.; Yuan, Y.; Han, S.; Chih-Lin, I.; Wang, Z. Non-orthogonal multiple access for 5G: Solutions, challenges, opportunities, and future research trends. IEEE Commun. Mag. 2015, 53, 74–81. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, Z.; Elkashlan, M.; Ding, Z.; Nallanathan, A.; Hanzo, L. Nonorthogonal multiple access for 5G and beyond. Proc. IEEE 2017, 105, 2347–2381. [Google Scholar] [CrossRef]
- Ding, Z.; Yang, Z.; Fan, P.; Poor, H.V. On the performance of non-orthogonal multiple access in 5G systems with randomly deployed users. IEEE Signal Process. Lett. 2014, 21, 1501–1505. [Google Scholar] [CrossRef]
- Ali, M.S.; Tabassum, H.; Hossain, E. Dynamic user clustering and power allocation for uplink and downlink non-orthogonal multiple access (NOMA) systems. IEEE Access 2016, 4, 6325–6343. [Google Scholar] [CrossRef]
- Sedaghat, M.A.; Müller, R.R. On user pairing in uplink NOMA. IEEE Trans. Wirel. Commun. 2018, 17, 3474–3486. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, D.K.; Meng, W.X.; Li, C. User pairing algorithm with SIC in non-orthogonal multiple access system. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 23–27 May 2016; pp. 1–6. [Google Scholar]
- Al-Abbasi, Z.Q.; So, D.K. User-pairing based non-orthogonal multiple access (NOMA) system. In Proceedings of the IEEE 83rd Vehicular Technology Conference (VTC Spring), Nanjing, China, 15–18 May 2016; pp. 1–5. [Google Scholar]
- Bui, V.P.; Nguyen, P.X.; Nguyen, H.V.; Nguyen, V.D.; Shin, O.S. Optimal User Pairing for Achieving Rate Fairness in Downlink NOMA Networks. In Proceedings of the IEEE International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Okinawa, Japan, 11–13 February 2019; pp. 575–578. [Google Scholar]
- Zhu, L.; Zhang, J.; Xiao, Z.; Cao, X.; Wu, D.O. Optimal user pairing for downlink non-orthogonal multiple access (NOMA). IEEE Wirel. Commun. Lett. 2018, 8, 328–331. [Google Scholar] [CrossRef]
- Shahab, M.B.; Irfan, M.; Kader, M.F.; Young Shin, S. User pairing schemes for capacity maximization in non-orthogonal multiple access systems. Wirel. Commun. Mob. Comput. 2016, 16, 2884–2894. [Google Scholar] [CrossRef]
- Liu, F.; Mähönen, P.; Petrova, M. Proportional fairness-based user pairing and power allocation for non-orthogonal multiple access. In Proceedings of the IEEE 26th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Hong Kong, China, 30 August–2 September 2015; pp. 1127–1131. [Google Scholar]
- Long, K.; Wang, P.; Li, W.; Chen, D. Spectrum Resource and Power Allocation With Adaptive Proportional Fair User Pairing for NOMA Systems. IEEE Access 2019, 7, 80043–80057. [Google Scholar] [CrossRef]
- He, J.; Tang, Z.; Che, Z. Fast and efficient user pairing and power allocation algorithm for non-orthogonal multiple access in cellular networks. Electron. Lett. 2016, 52, 2065–2067. [Google Scholar] [CrossRef]
- Mei, J.; Yao, L.; Long, H.; Zheng, K. Joint user pairing and power allocation for downlink non-orthogonal multiple access systems. In Proceedings of the IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 23–27 May 2016; pp. 1–6. [Google Scholar]
- Guo, J.; Wang, X.; Yang, J.; Zheng, J.; Zhao, B. User pairing and power allocation for downlink non-orthogonal multiple access. In Proceedings of the IEEE Globecom Workshops (GC Wkshps), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Hsiung, C.; Huang, R.; Zhou, Y.; Wong, V.W. Dynamic User Pairing and Power Allocation for Throughput Maximization in NOMA Systems. In Proceedings of the IEEE International Conference on Communications Workshops (ICC Workshops), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar]
- Timotheou, S.; Krikidis, I. Fairness for non-orthogonal multiple access in 5G systems. IEEE Signal Process. Lett. 2015, 22, 1647–1651. [Google Scholar] [CrossRef]
- Wei, Z.; Guo, J.; Ng, D.W.K.; Yuan, J. Fairness comparison of uplink NOMA and OMA. In Proceedings of the IEEE 85th Vehicular Technology Conference (VTC Spring), Sydney, Australia, 4–7 June 2017; pp. 1–6. [Google Scholar]
- Al-Wani, M.M.; Sali, A.; Ali, B.M.; Salah, A.A.; Navaie, K.; Leow, C.Y.; Noordin, N.K.; Hashim, S. On Short Term Fairness and Throughput of User Clustering for Downlink Non-Orthogonal Multiple Access System. In Proceedings of the IEEE 89th Vehicular Technology Conference (VTC2019-Spring), Kuala Lumpur, Malaysia, 28 April–1 May 2019; pp. 1–6. [Google Scholar]
- Gui, G.; Sari, H.; Biglieri, E. A New Definition of Fairness for Non-Orthogonal Multiple Access. IEEE Commun. Lett. 2019, 23, 1267–1271. [Google Scholar] [CrossRef]
- Fang, F.; Ding, Z.; Liang, W.; Zhang, H. Optimal Energy Efficient Power Allocation With User Fairness for Uplink MC-NOMA Systems. IEEE Wirel. Commun. Lett. 2019, 8, 1133–1136. [Google Scholar] [CrossRef]
- Xu, P.; Cumanan, K.; Yang, Z. Optimal Power Allocation Scheme for NOMA with Adaptive Rates and alpha-Fairness. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Xu, P.; Cumanan, K. Optimal Power Allocation Scheme for Non-Orthogonal Multiple Access With α-Fairness. IEEE J. Sel. Areas Commun. 2017, 35, 2357–2369. [Google Scholar] [CrossRef]
- Xing, H.; Liu, Y.; Nallanathan, A.; Ding, Z.; Poor, H.V. Optimal throughput fairness tradeoffs for downlink non-orthogonal multiple access over fading channels. IEEE Trans. Wirel. Commun. 2018, 17, 3556–3571. [Google Scholar] [CrossRef]
- Al-Obiedollah, H.; Cumanan, K.; Thiyagalingam, J.; Burr, A.G.; Ding, Z.; Dobre, O.A. Sum Rate Fairness Trade-off-based Resource Allocation Technique for MISO NOMA Systems. arXiv 2019, arXiv:1902.05735. [Google Scholar]
- Qi, T.; Feng, W.; Chen, Y.; Wang, Y. Optimum Fairness for Non-Orthogonal Multiple Access. In Proceedings of the IEEE/CIC International Conference on Communications in China (ICCC), Beijing, China, 16–18 August 2018; pp. 116–120. [Google Scholar]
- Zeng, M.; Yadav, A.; Dobre, O.A.; Tsiropoulos, G.I.; Poor, H.V. On the Sum Rate of MIMO-NOMA and MIMO-OMA Systems. IEEE Wirel. Commun. Lett. 2017, 6, 534–537. [Google Scholar] [CrossRef]
- Ding, Z.; Adachi, F.; Poor, H.V. The application of MIMO to non-orthogonal multiple access. IEEE Trans. Wirel. Commun. 2015, 15, 537–552. [Google Scholar] [CrossRef]
- Higuchi, K.; Kishiyama, Y. Non-orthogonal access with random beamforming and intra-beam SIC for cellular MIMO downlink. In Proceedings of the IEEE 78th Vehicular Technology Conference (VTC Fall), Las Vegas, NV, USA, 2–5 September 2013; pp. 1–5. [Google Scholar]
- Nonaka, N.; Kishiyama, Y.; Higuchi, K. Non-orthogonal multiple access using intra-beam superposition coding and SIC in base station cooperative MIMO cellular downlink. IEICE Trans. Commun. 2015, 98, 1651–1659. [Google Scholar] [CrossRef]
- Lan, Y.; Benjebboiu, A.; Chen, X.; Li, A.; Jiang, H. Considerations on downlink non-orthogonal multiple access (NOMA) combined with closed-loop SU-MIMO. In Proceedings of the IEEE International Conference on Signal Processing and Communication Systems (ICSPCS), Gold Coast, Australia, 15–17 December 2014; pp. 1–5. [Google Scholar]
- Ding, Z.; Schober, R.; Poor, H.V. A general MIMO framework for NOMA downlink and uplink transmission based on signal alignment. IEEE Trans. Wirel. Commun. 2016, 15, 4438–4454. [Google Scholar] [CrossRef]
- Ding, Z.; Peng, M.; Poor, H.V. Cooperative Non-Orthogonal Multiple Access in 5G Systems. IEEE Commun. Lett. 2015, 19, 1462–1465. [Google Scholar] [CrossRef]
- Ding, Z.; Dai, H.; Poor, H.V. Relay Selection for Cooperative NOMA. IEEE Wirel. Commun. Lett. 2016, 5, 416–419. [Google Scholar] [CrossRef]
- Liang, X.; Wu, Y.; Ng, D.W.K.; Zuo, Y.; Jin, S.; Zhu, H. Outage Performance for Cooperative NOMA Transmission with an AF Relay. IEEE Commun. Lett. 2017, 21, 2428–2431. [Google Scholar] [CrossRef]
- Yang, Z.; Ding, Z.; Wu, Y.; Fan, P. Novel Relay Selection Strategies for Cooperative NOMA. IEEE Trans. Veh. Technol. 2017, 66, 10114–10123. [Google Scholar] [CrossRef]
- Luo, S.; Teh, K.C. Adaptive Transmission for Cooperative NOMA System With Buffer-Aided Relaying. IEEE Commun. Lett. 2017, 21, 937–940. [Google Scholar] [CrossRef]
- Li, Q.; Wen, M.; Basar, E.; Poor, H.V.; Chen, F. Spatial Modulation-Aided Cooperative NOMA: Performance Analysis and Comparative Study. IEEE J. Sel. Top. Signal Process. 2019, 13, 715–728. [Google Scholar] [CrossRef]
- Zeng, M.; Yadav, A.; Dobre, O.A.; Tsiropoulos, G.I.; Poor, H.V. Capacity Comparison Between MIMO-NOMA and MIMO-OMA With Multiple Users in a Cluster. IEEE J. Sel. Areas Commun. 2017, 35, 2413–2424. [Google Scholar] [CrossRef]
- Chi, Y.; Liu, L.; Song, G.; Yuen, C.; Guan, Y.L.; Li, Y. Practical MIMO-NOMA: Low Complexity and Capacity-Approaching Solution. IEEE Trans. Wirel. Commun. 2018, 17, 6251–6264. [Google Scholar] [CrossRef]
- Sun, X.; Yang, N.; Yan, S.; Ding, Z.; Ng, D.W.K.; Shen, C.; Zhong, Z. Joint Beamforming and Power Allocation in Downlink NOMA Multiuser MIMO Networks. IEEE Trans. Wirel. Commun. 2018, 17, 5367–5381. [Google Scholar] [CrossRef]
- Wan, D.; Wen, M.; Ji, F.; Yu, H.; Chen, F. Non-Orthogonal Multiple Access for Cooperative Communications: Challenges, Opportunities, and Trends. IEEE Wirel. Commun. 2018, 25, 109–117. [Google Scholar] [CrossRef]
- Lv, L.; Chen, J.; Ni, Q.; Ding, Z.; Jiang, H. Cognitive Non-Orthogonal Multiple Access with Cooperative Relaying: A New Wireless Frontier for 5G Spectrum Sharing. IEEE Commun. Mag. 2018, 56, 188–195. [Google Scholar] [CrossRef]
- Lv, L.; Chen, J.; Ni, Q.; Ding, Z. Design of Cooperative Non-Orthogonal Multicast Cognitive Multiple Access for 5G Systems: User Scheduling and Performance Analysis. IEEE Trans. Commun. 2017, 65, 2641–2656. [Google Scholar] [CrossRef]
- Xu, Y.; Sun, H.; Hu, R.Q.; Qian, Y. Cooperative Non-Orthogonal Multiple Access in Heterogeneous Networks. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Afshang, M.; Dhillon, H.S. Poisson cluster process based analysis of HetNets with correlated user and base station locations. IEEE Trans. Wirel. Commun. 2018, 17, 2417–2431. [Google Scholar] [CrossRef]
- David, H.A.; Nagaraja, H.N. Order Statistics; Wiley Online Library: Hoboken, NJ, USA, 1970. [Google Scholar]
- Liu, Y.; Qin, Z.; Elkashlan, M.; Nallanathan, A.; McCann, J.A. Non-Orthogonal Multiple Access in Large-Scale Heterogeneous Networks. IEEE J. Sel. Areas Commun. 2017, 35, 2667–2680. [Google Scholar] [CrossRef]
- Ding, Z.; Poor, H.V. Cooperative Energy Harvesting Networks with Spatially Random Users. IEEE Signal Process. Lett. 2013, 20, 1211–1214. [Google Scholar] [CrossRef]
- Hildebrand, F.B. Introduction to Numerical Analysis; Courier Corporation: North Chelmsford, MA, USA, 1987. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Zhao, J.; Liu, Y.; Chai, K.K.; Nallanathan, A.; Chen, Y.; Han, Z. Resource allocation for non-orthogonal multiple access in heterogeneous networks. In Proceedings of the IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Zhao, J.; Liu, Y.; Chai, K.K.; Nallanathan, A.; Chen, Y.; Han, Z. Spectrum allocation and power control for non-orthogonal multiple access in HetNets. IEEE Trans. Wirel. Commun. 2017, 16, 5825–5837. [Google Scholar] [CrossRef]
- Xu, B.; Chen, Y.; Carrión, J.R.; Zhang, T. Resource allocation in energy-cooperation enabled two-tier NOMA HetNets toward green 5G. IEEE J. Sel. Areas Commun. 2017, 35, 2758–2770. [Google Scholar] [CrossRef]
- Song, X.; Dong, L.; Wang, J.; Qin, L.; Han, X. Energy Efficient Power Allocation for Downlink NOMA Heterogeneous Networks With Imperfect CSI. IEEE Access 2019, 7, 39329–39340. [Google Scholar] [CrossRef]
- Swami, P.; Bhatia, V.; Vuppala, S.; Ratnarajah, T. On user offloading in NOMA-HetNet using repulsive point process. IEEE Syst. J. 2018, 13, 1409–1420. [Google Scholar] [CrossRef]
- Swami, P.; Bhatia, V.; Vuppala, S.; Ratnarajah, T. A cooperation scheme for user fairness and performance enhancement in NOMA-HCN. IEEE Trans. Veh. Technol. 2018, 67, 11965–11978. [Google Scholar] [CrossRef]
- Xiang, L.; Chen, H. Energy-efficient and fair power allocation approach for NOMA in ultra-dense heterogeneous networks. In Proceedings of the IEEE International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery (CyberC), Nanjing, China, 12–14 October 2017; pp. 89–94. [Google Scholar]
- Zhang, S.; Zhang, N.; Kang, G.; Liu, Z. Energy and spectrum efficient power allocation with NOMA in downlink HetNets. Phys. Commun. 2018, 31, 121–132. [Google Scholar] [CrossRef]
- Zhang, H.; Fang, F.; Cheng, J.; Long, K.; Wang, W.; Leung, V.C. Energy-efficient resource allocation in NOMA heterogeneous networks. IEEE Wirel. Commun. 2018, 25, 48–53. [Google Scholar] [CrossRef]
- Song, Z.; Ni, Q.; Sun, X. Distributed power allocation for nonorthogonal multiple access heterogeneous networks. IEEE Commun. Lett. 2018, 22, 622–625. [Google Scholar] [CrossRef]
- Fang, F.; Cheng, J.; Ding, Z.; Poor, H.V. Energy efficient resource optimization for a downlink NOMA heterogeneous small-cell network. In Proceedings of the 2018 IEEE 10th Sensor Array and Multichannel Signal Processing Workshop (SAM), Sheffield, UK, 8–11 July 2018; pp. 51–55. [Google Scholar]
- Fang, F.; Cheng, J.; Ding, Z. Joint energy efficient subchannel and power optimization for a downlink NOMA heterogeneous network. IEEE Trans. Veh. Technol. 2018, 68, 1351–1364. [Google Scholar] [CrossRef]
- Khan, W.U.; Jameel, F.; Ristaniemi, T.; Khan, S.; Sidhu, G.A.S.; Liu, J. Joint Spectral and Energy Efficiency Optimization for Downlink NOMA Networks. IEEE Trans. Cogn. Commun. Netw. 2019. [Google Scholar] [CrossRef]
- Moltafet, M.; Azmi, P.; Mokari, N.; Javan, M.R.; Mokdad, A. Optimal and fair energy efficient resource allocation for energy harvesting-enabled-PD-NOMA-based HetNets. IEEE Trans. Wirel. Commun. 2018, 17, 2054–2067. [Google Scholar] [CrossRef]
- Moltafet, M.; Azmi, P.; Javan, M.R.; Mokari, N.; Mokdad, A. Optimal radio resource allocation to achieve a low BER in PD-NOMA–based heterogeneous cellular networks. Trans. Emerg. Telecommun. Technol. 2019, 30, e3572. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, B.; Ge, X.; Li, Y. Performance Analysis of Non-Orthogonal Multicast in Two-tier Heterogeneous Networks. In Proceedings of the 2018 IEEE International Conference on Communication Systems (ICCS), Chengdu, China, 19–21 December 2018; pp. 456–462. [Google Scholar]
- Ni, D.; Hao, L.; Tran, Q.T.; Qian, X. Power allocation for downlink NOMA heterogeneous networks. IEEE Access 2018, 6, 26742–26752. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.; Yang, M.; Liu, Z. Ratio fairness-based power allocation and user scheduling for downlink NOMA heterogeneous networks. In Proceedings of the ACM Turing Celebration Conference-China, Chengdu, China, 17–19 May 2019; p. 155. [Google Scholar]
- Tuncel, N.Ö.; Koca, M. Self-Organizing Networking in NOMA-Enabled Heterogeneous Networks. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–18 April 2019; pp. 1–6. [Google Scholar]
- Anwar, A.; Seet, B.C.; Hasan, S.F.; Li, X.J.; Chong, P.H.J.; Chung, M.Y. An Analytical Framework for Multi-Tier NOMA Networks With Underlay D2D Communications. IEEE Access 2018, 6, 59221–59241. [Google Scholar] [CrossRef]
- ElSawy, H.; Hossain, E.; Haenggi, M. Stochastic geometry for modeling, analysis, and design of multi-tier and cognitive cellular wireless networks: A survey. IEEE Commun. Surv. Tutor. 2013, 15, 996–1019. [Google Scholar] [CrossRef]
- Gong, Z.; Haenggi, M. Interference and outage in mobile random networks: Expectation, distribution, and correlation. IEEE Trans. Mob. Comput. 2012, 13, 337–349. [Google Scholar] [CrossRef]
- Win, M.Z.; Pinto, P.C.; Shepp, L.A. A mathematical theory of network interference and its applications. Proc. IEEE 2009, 97, 205–230. [Google Scholar] [CrossRef]
- Inaltekin, H.; Chiang, M.; Poor, H.V.; Wicker, S.B. On unbounded path-loss models: Effects of singularity on wireless network performance. IEEE J. Sel. Areas Commun. 2009, 27, 1078–1092. [Google Scholar] [CrossRef]
- Stoyan, D. Applied stochastic geometry: A survey. Biomed. J. 1979, 21, 693–715. [Google Scholar]
- Haenggi, M. Stochastic Geometry for Wireless Networks; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Li, Y.; Baccelli, F.; Dhillon, H.S.; Andrews, J.G. Statistical modeling and probabilistic analysis of cellular networks with determinantal point processes. IEEE Trans. Commun. 2015, 63, 3405–3422. [Google Scholar] [CrossRef]
- Haenggi, M. On distances in uniformly random networks. IEEE Trans. Inf. Theory 2005, 51, 3584–3586. [Google Scholar] [CrossRef]
- Tabassum, H.; Hossain, E.; Hossain, J. Modeling and analysis of uplink non-orthogonal multiple access in large-scale cellular networks using poisson cluster processes. IEEE Trans. Commun. 2017, 65, 3555–3570. [Google Scholar] [CrossRef]
- Parida, P.; Das, S.S. Power allocation in OFDM based NOMA systems: A DC programming approach. In Proceedings of the IEEE Globecom Workshops (GC Wkshps), Austin, TX, USA, 8–12 December 2014; pp. 1026–1031. [Google Scholar]
- Zhang, Z.; Sun, H.; Hu, R.Q.; Qian, Y. Stochastic geometry based performance study on 5G non-orthogonal multiple access scheme. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Shin, W.; Vaezi, M.; Lee, B.; Love, D.J.; Lee, J.; Poor, H.V. Non-orthogonal multiple access in multi-cell networks: Theory, performance, and practical challenges. IEEE Commun. Mag. 2017, 55, 176–183. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, Z.; Elkashlan, M.; Gao, Y.; Nallanathan, A. Non-orthogonal multiple access in massive MIMO aided heterogeneous networks. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Zhang, Z.; Ma, Z.; Xiao, M.; Liu, G.; Fan, P. Modeling and analysis of non-orthogonal MBMS transmission in heterogeneous networks. IEEE J. Sel. Areas Commun. 2017, 35, 2221–2237. [Google Scholar] [CrossRef]
- Liu, C.H.; Liang, D.C. Heterogeneous networks with power-domain NOMA: Coverage, throughput, and power allocation analysis. IEEE Trans. Wirel. Commun. 2018, 17, 3524–3539. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, G.; Ma, Z.; Xiao, M.; Ding, Z.; Fan, P. Heterogeneous Ultradense Networks with NOMA: System Architecture, Coordination Framework, and Performance Evaluation. IEEE Veh. Technol. Mag. 2018, 13, 110–120. [Google Scholar] [CrossRef]
- Han, T.; Gong, J.; Liu, X.; Islam, S.R.; Li, Q.; Bai, Z.; Kwak, K.S. On downlink NOMA in heterogeneous networks with non-uniform small cell deployment. IEEE Access 2018, 6, 31099–31109. [Google Scholar] [CrossRef]
- Tran, H.Q.; Truong, P.Q.; Phan, C.V.; Vien, Q.T. On the energy efficiency of NOMA for wireless backhaul in multi-tier heterogeneous CRAN. In Proceedings of the 2017 International Conference on Recent Advances in Signal Processing, Telecommunications & Computing (SigTelCom), Da Nang, Vietnam, 9–11 January 2017; pp. 229–234. [Google Scholar]
- Qin, Z.; Yue, X.; Liu, Y.; Ding, Z.; Nallanathan, A. User association and resource allocation in unified NOMA enabled heterogeneous ultra dense networks. IEEE Commun. Mag. 2018, 56, 86–92. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, Z.; Xiao, M.; Ding, Z.; Fan, P. Full-duplex device-to-device-aided cooperative nonorthogonal multiple access. IEEE Trans. Veh. Technol. 2016, 66, 4467–4471. [Google Scholar]
- Ali, K.S.; ElSawy, H.; Alouini, M.S. Modeling cellular networks with full-duplex D2D communication: A stochastic geometry approach. IEEE Trans. Commun. 2016, 64, 4409–4424. [Google Scholar] [CrossRef]
- Afshang, M.; Dhillon, H.S. Spatial modeling of device-to-device networks: Poisson cluster process meets Poisson hole process. In Proceedings of the 2015 49th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 8–11 November 2015; pp. 317–321. [Google Scholar]
- Sun, H.; Xu, Y.; Hu, R.Q. A NOMA and MU-MIMO Supported Cellular Network with Underlaid D2D Communications. In Proceedings of the 2016 IEEE 83rd Vehicular Technology Conference (VTC Spring), Nanjing, China, 15–18 May 2016; pp. 1–6. [Google Scholar]
- Pei, L.; Yang, Z.; Pan, C.; Huang, W.; Chen, M.; Elkashlan, M.; Nallanathan, A. Energy-efficient D2D communications underlaying NOMA-based networks with energy harvesting. IEEE Commun. Lett. 2018, 22, 914–917. [Google Scholar] [CrossRef]
- Pan, Y.; Pan, C.; Yang, Z.; Chen, M. Resource allocation for D2D communications underlaying a NOMA-based cellular network. IEEE Wirel. Commun. Lett. 2017, 7, 130–133. [Google Scholar] [CrossRef]
- Song, Y.B.; Kang, H.S.; Kim, D.K. 5G cellular systems with D2D assisted NOMA relay. In Proceedings of the URSI Asia-Pacific Radio Science Conference (URSI AP-RASC), Seoul, Korea, 21–25 August 2016; pp. 1–3. [Google Scholar]
- Zhao, J.; Liu, Y.; Chai, K.K.; Chen, Y.; Elkashlan, M.; Alonso-Zarate, J. NOMA-based D2D communications: Towards 5G. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Zhao, J.; Liu, Y.; Chai, K.K.; Chen, Y.; Elkashlan, M. Joint subchannel and power allocation for NOMA enhanced D2D communications. IEEE Trans. Commun. 2017, 65, 5081–5094. [Google Scholar] [CrossRef]
- Shi, Z.; Ma, S.; ElSawy, H.; Yang, G.; Alouini, M.S. Cooperative HARQ-assisted NOMA scheme in large-scale D2D networks. IEEE Trans. Commun. 2018, 66, 4286–4302. [Google Scholar] [CrossRef]
- Anwar, A.; Seet, B.C.; Li, X. Quality of service based NOMA group D2D communications. Future Internet 2017, 9, 73. [Google Scholar] [CrossRef]
- Joshi, S.; Mallik, R.K. Cooperative NOMA with AF Relaying over Nakagami-m Fading in a D2D Network. In Proceedings of the IEEE 89th Vehicular Technology Conference (VTC2019-Spring), Kuala Lumpur, Malaysia, 28 April–1 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Duan, W.; Ju, J.; Sun, Q.; Ji, Y.; Wang, Z.; Choi, J.; Zhang, G. Capacity Enhanced Cooperative D2D Systems over Rayleigh Fading Channels with NOMA. arXiv 2018, arXiv:1810.06837. [Google Scholar]
- Dai, Y.; Sheng, M.; Liu, J.; Cheng, N.; Shen, X.; Yang, Q. Joint Mode Selection and Resource Allocation for D2D-Enabled NOMA Cellular Networks. IEEE Trans. Veh. Technol. 2019, 68, 6721–6733. [Google Scholar] [CrossRef]
- Chen, J.; Jia, J.; Liu, Y.; Wang, X.; Aghvami, A.H. Optimal Resource Block Assignment and Power Allocation for D2D-Enabled NOMA Communication. IEEE Access 2019, 7, 90023–90035. [Google Scholar] [CrossRef]
- Yoon, T.; Nguyen, T.H.; Nguyen, X.T.; Yoo, D.; Jang, B.; Nguyen, V.D. Resource Allocation for NOMA-Based D2D Systems Coexisting With Cellular Networks. IEEE Access 2018, 6, 66293–66304. [Google Scholar] [CrossRef]
- Baidas, M.W.; Bahbahani, M.S.; Alsusa, E.; Hamdi, K.A.; Ding, Z. Joint D2D Group Association and Channel Assignment in Uplink Multi-Cell NOMA Networks: A Matching-Theoretic Approach. IEEE Trans. Commun. 2019. [Google Scholar] [CrossRef]
- Li, Q.; Ren, P.; Xu, D. Security Enhancement and QoS Provisioning for NOMA-Based Cooperative D2D Networks. IEEE Access 2019, 7, 129387–129401. [Google Scholar] [CrossRef]
- Alemaishat, S.; Saraereh, O.A.; Khan, I.; Choi, B.J. An Efficient Resource Allocation Algorithm for D2D Communications Based on NOMA. IEEE Access 2019, 7, 120238–120247. [Google Scholar] [CrossRef]
- Wang, Y.; Zhai, D.; Zhang, R.; Zhang, Z. Sum-Rate Maximization for D2D and Cellular Hybrid Networks Enhanced by NOMA. In Proceedings of the 2019 IEEE 20th International Conference on High Performance Switching and Routing (HPSR), Xi’an, China, 26–29 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Anwar, A.; Seet, B.C.; Ding, Z. Non-orthogonal multiple access for ubiquitous wireless sensor networks. Sensors 2018, 18, 516. [Google Scholar] [CrossRef]
- Do, D.T.; Le, C.B. Application of NOMA in wireless system with wireless power transfer scheme: Outage and ergodic capacity performance analysis. Sensors 2018, 18, 3501. [Google Scholar] [CrossRef]
- Nguyen, H.; Nguyen, T.; Tin, P.T.; Voznak, M. Outage performance of time switching energy harvesting wireless sensor networks deploying NOMA. In Proceedings of the IEEE 20th International Conference on e-Health Networking, Applications and Services (Healthcom), Ostrava, Czech Republic, 17–20 September 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Hu, Z.; Xu, L.; Cao, L.; Liu, S.; Luo, Z.; Wang, J.; Li, X.; Wang, L. Application of Non-Orthogonal Multiple Access in Wireless Sensor Networks for Smart Agriculture. IEEE Access 2019, 7, 87582–87592. [Google Scholar] [CrossRef]
- Nguyen, H.S.; Ly, T.T.; Nguyen, T.S.; Huynh, V.V.; Nguyen, T.L.; Voznak, M. Outage performance analysis and SWIPT optimization in energy-harvesting wireless sensor network deploying NOMA. Sensors 2019, 19, 613. [Google Scholar] [CrossRef]
- Li, S.; Nie, H.; Wu, H. Performance Analysis of Frequency Hopping Ad Hoc Communication System With Non-Orthogonal Multiple Access. IEEE Access 2019, 7, 113171–113181. [Google Scholar] [CrossRef]
- Buehrer, R.M.; Correal-Mendoza, N.S.; Woerner, B.D. A simulation comparison of multiuser receivers for cellular CDMA. IEEE Trans. Veh. Technol. 2000, 49, 1065–1085. [Google Scholar] [CrossRef]
- Li, A.; Benjebbour, A.; Harada, A. Performance evaluation of non-orthogonal multiple access combined with opportunistic beamforming. In Proceedings of the 2014 IEEE 79th Vehicular Technology Conference (VTC Spring), Seoul, Korea, 18–21 May 2014; pp. 1–5. [Google Scholar]
- Yamamoto, K.; Saito, Y.; Higuchi, K. System-level throughput of non-orthogonal access with SIC in cellular downlink when channel estimation error exists. In Proceedings of the IEEE 79th Vehicular Technology Conference (VTC Spring), Seoul, Korea, 18–21 May 2014; pp. 1–5. [Google Scholar]
- Tan, Y.; Zhou, J.; Qin, J. Novel channel estimation for non-orthogonal multiple access systems. IEEE Signal Process. Lett. 2016, 23, 1781–1785. [Google Scholar] [CrossRef]
- Struminsky, K.; Kruglik, S.; Vetrov, D.; Oseledets, I. A new approach for sparse Bayesian channel estimation in SCMA uplink systems. In Proceedings of the IEEE International Conference on Wireless Communications & Signal Processing (WCSP), Yangzhou, China, 13–15 October 2016; pp. 1–5. [Google Scholar]
- Ding, Z.; Fan, P.; Poor, H.V. On the coexistence between full-duplex and NOMA. IEEE Wirel. Commun. Lett. 2018, 7, 692–695. [Google Scholar] [CrossRef]
- Sun, Y.; Ng, D.W.K.; Ding, Z.; Schober, R. Optimal joint power and subcarrier allocation for full-duplex multicarrier non-orthogonal multiple access systems. IEEE Trans. Commun. 2017, 65, 1077–1091. [Google Scholar] [CrossRef]
- Sun, Y.; Ng, D.W.K.; Zhu, J.; Schober, R. Robust and secure resource allocation for full-duplex MISO multicarrier NOMA systems. IEEE Trans. Commun. 2018, 66, 4119–4137. [Google Scholar] [CrossRef]
- Abbasi, O.; Ebrahimi, A. Secrecy analysis of a NOMA system with full duplex and half duplex relay. In Proceedings of the IEEE Iran Workshop on Communication and Information Theory (IWCIT), Tehran, Iran, 3–4 May 2017; pp. 1–6. [Google Scholar]
- Lei, L.; Lagunas, E.; Chatzinotas, S.; Ottersten, B. NOMA aided interference management for full-duplex self-backhauling HetNets. IEEE Commun. Lett. 2018, 22, 1696–1699. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anwar, A.; Seet, B.-C.; Hasan, M.A.; Li, X.J. A Survey on Application of Non-Orthogonal Multiple Access to Different Wireless Networks. Electronics 2019, 8, 1355. https://doi.org/10.3390/electronics8111355
Anwar A, Seet B-C, Hasan MA, Li XJ. A Survey on Application of Non-Orthogonal Multiple Access to Different Wireless Networks. Electronics. 2019; 8(11):1355. https://doi.org/10.3390/electronics8111355
Chicago/Turabian StyleAnwar, Asim, Boon-Chong Seet, Muhammad Amish Hasan, and Xue Jun Li. 2019. "A Survey on Application of Non-Orthogonal Multiple Access to Different Wireless Networks" Electronics 8, no. 11: 1355. https://doi.org/10.3390/electronics8111355
APA StyleAnwar, A., Seet, B.-C., Hasan, M. A., & Li, X. J. (2019). A Survey on Application of Non-Orthogonal Multiple Access to Different Wireless Networks. Electronics, 8(11), 1355. https://doi.org/10.3390/electronics8111355






