A Unified Multimode Control of a DC–DC Interlinking Converter Integrated into a Hybrid Microgrid
Abstract
:1. Introduction
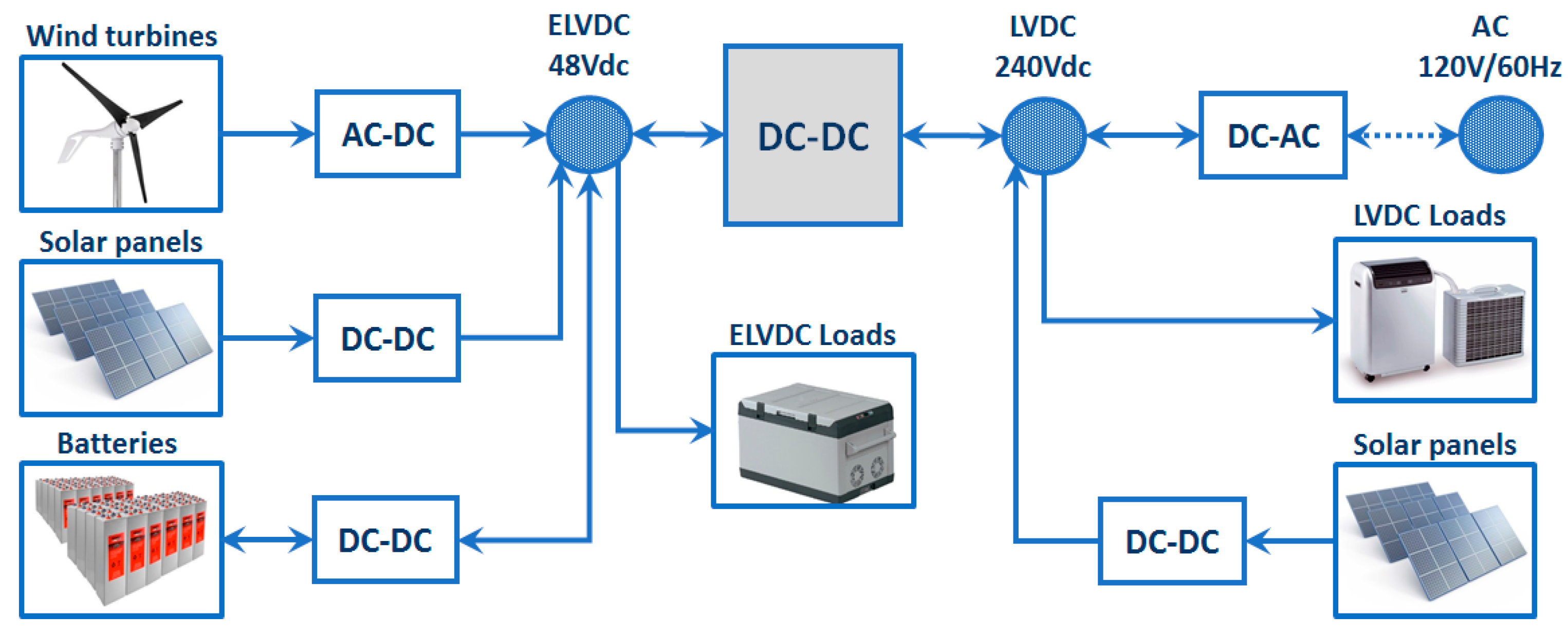
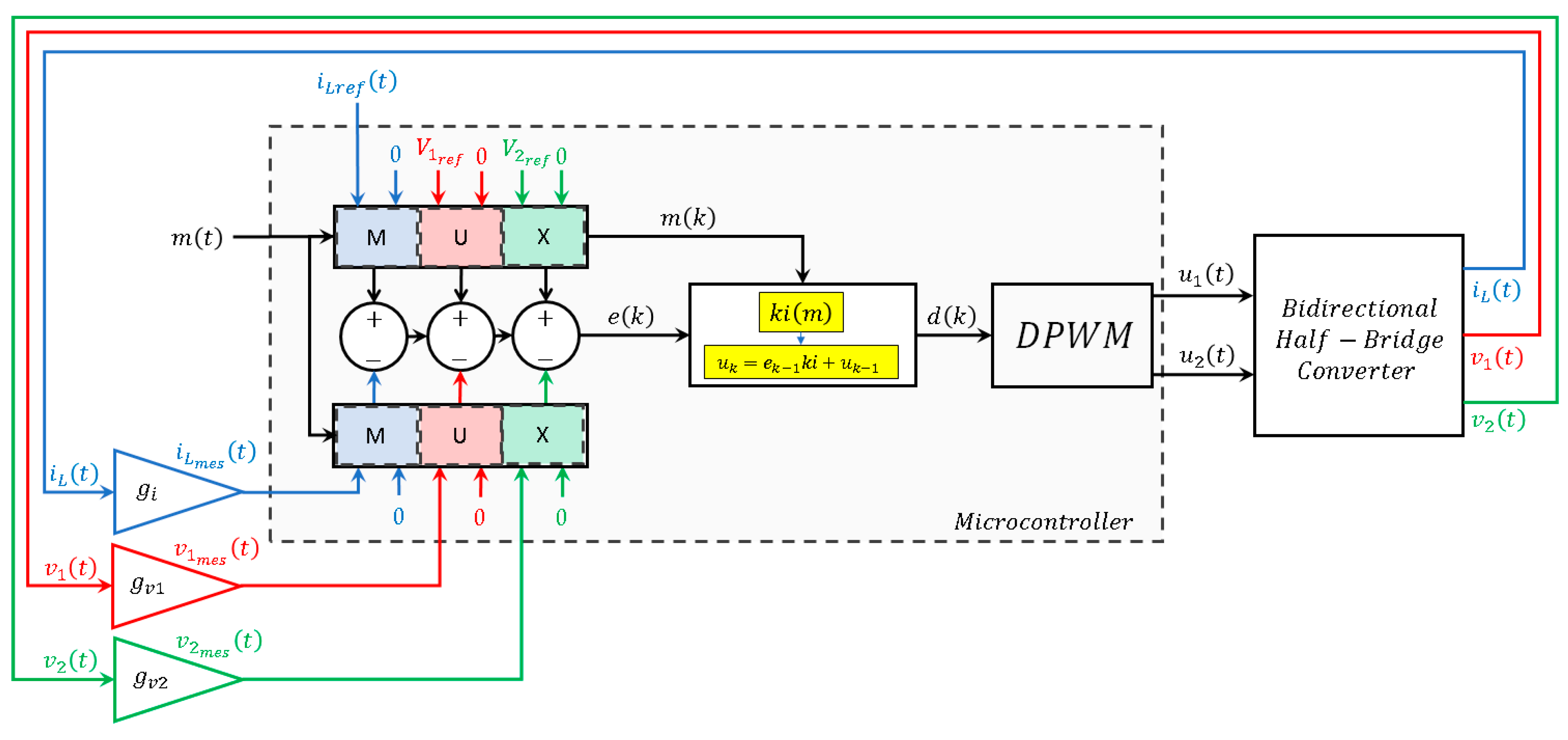
2. Interlinking DC–DC Converter in the Studied Microgrid Architecture
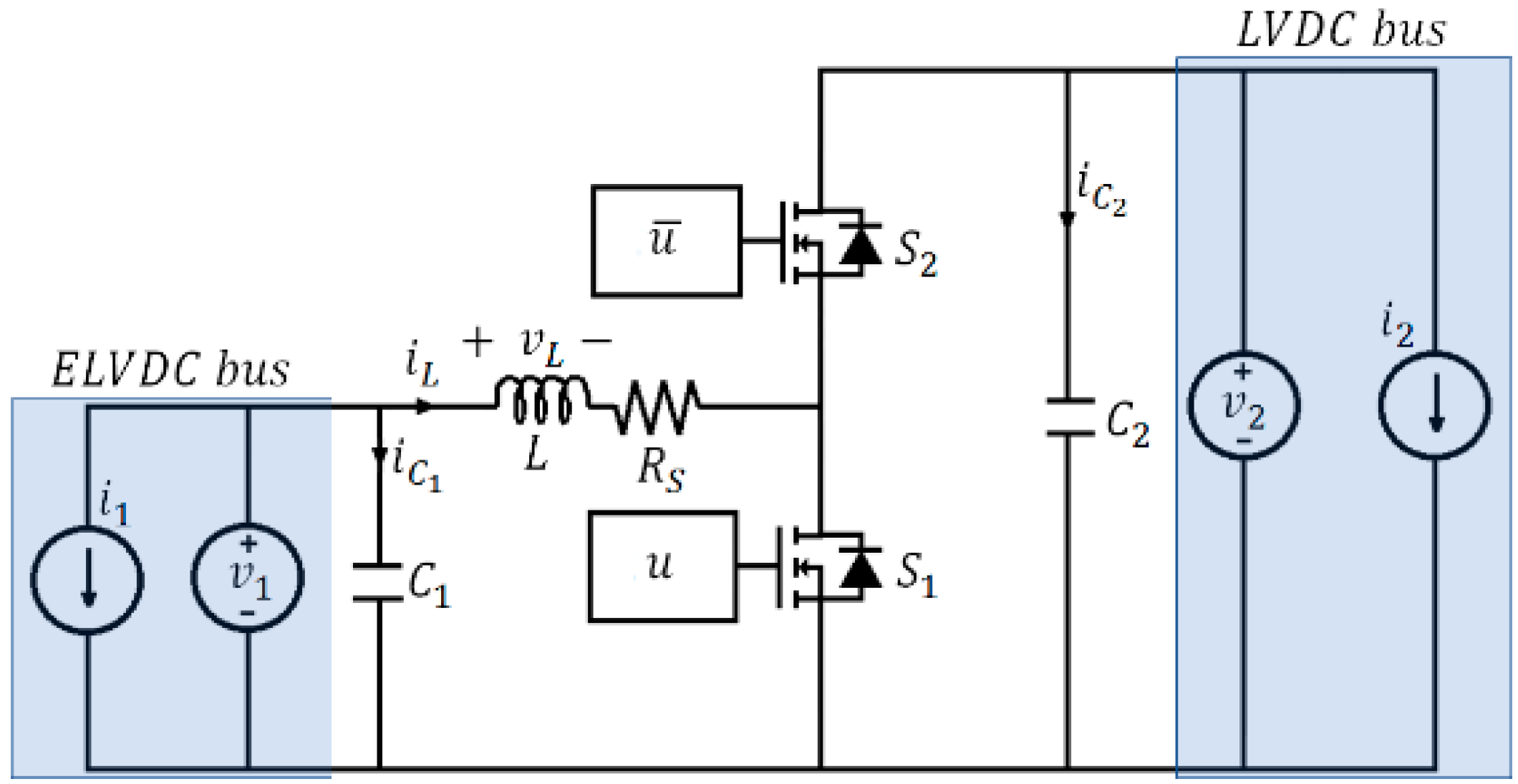
3. BHCB Converter Modeling and Control
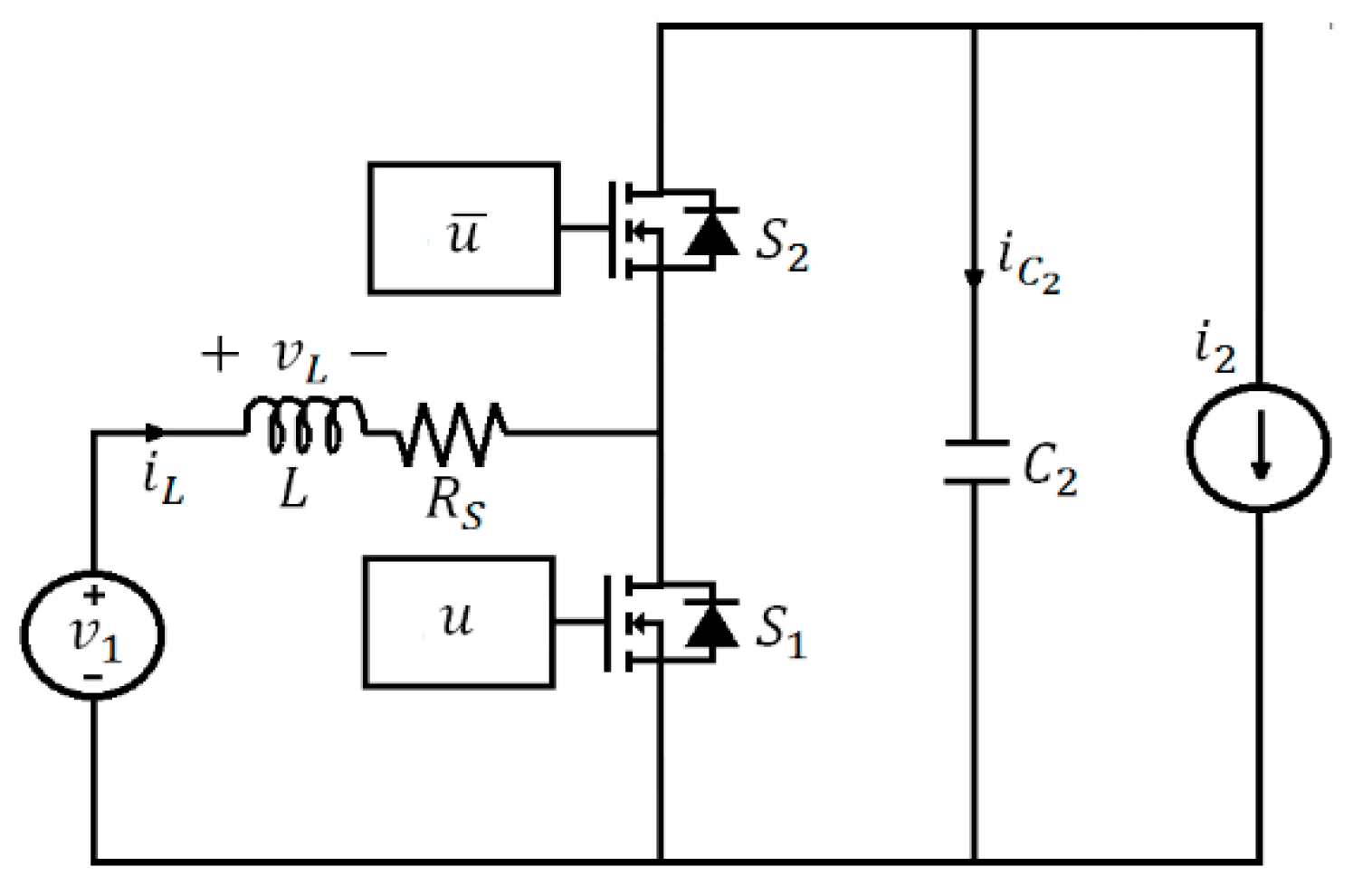
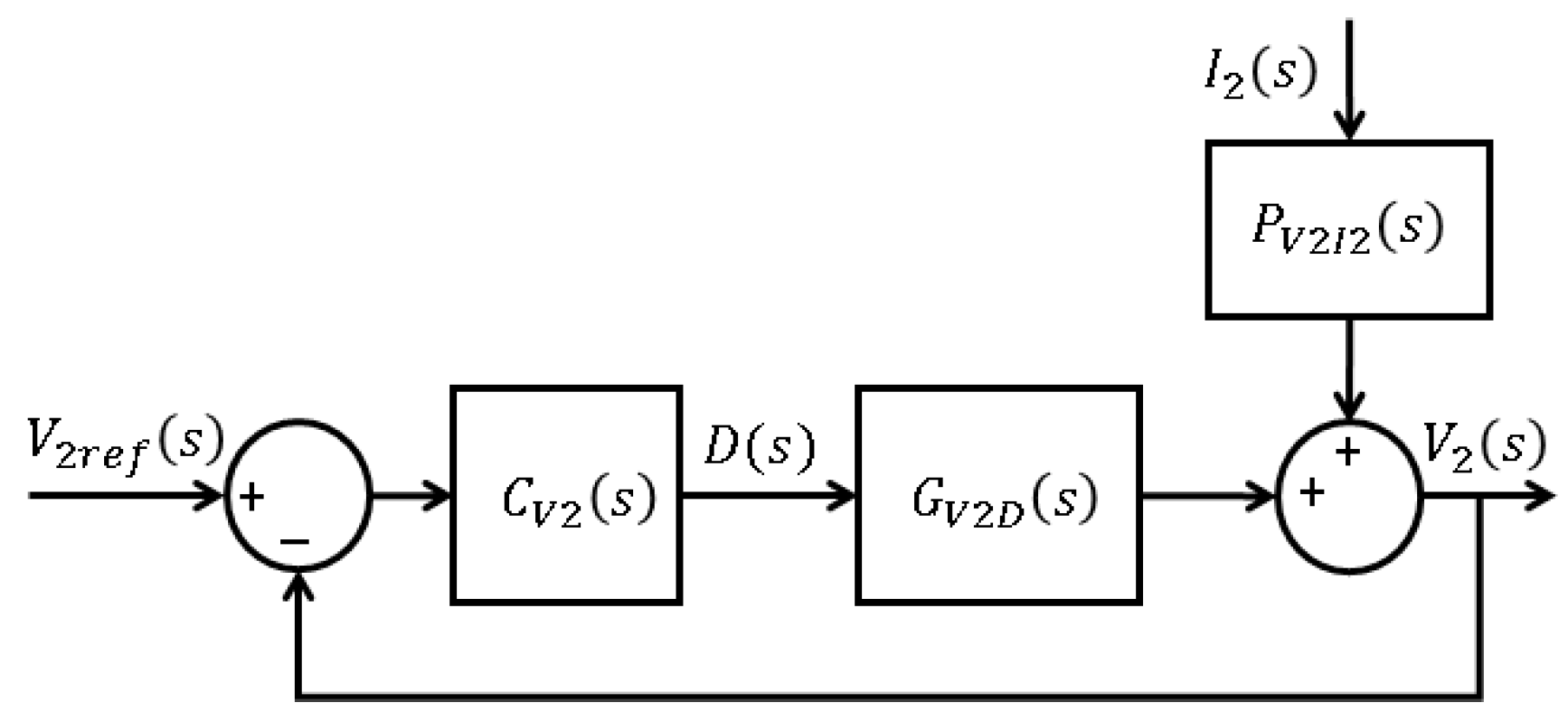
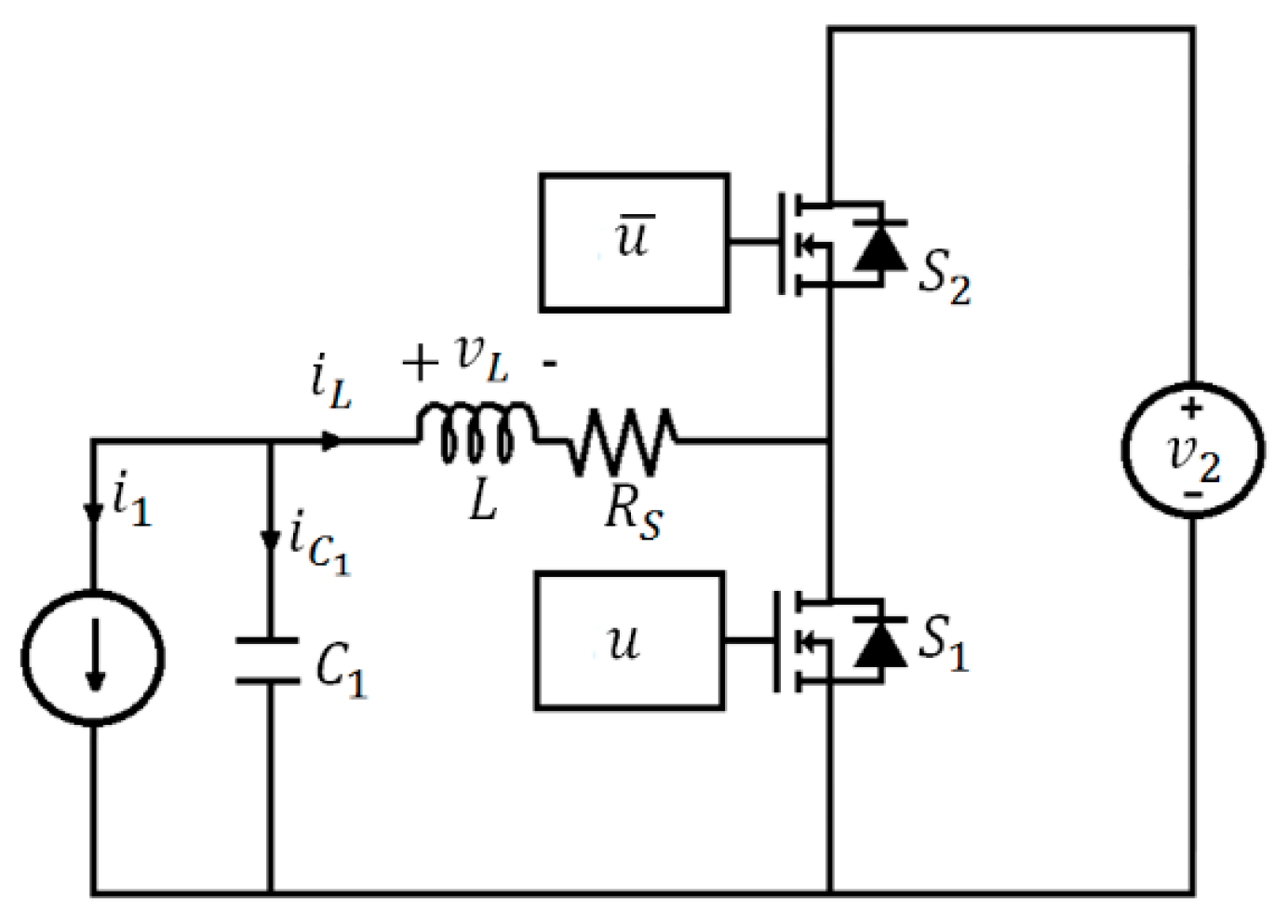
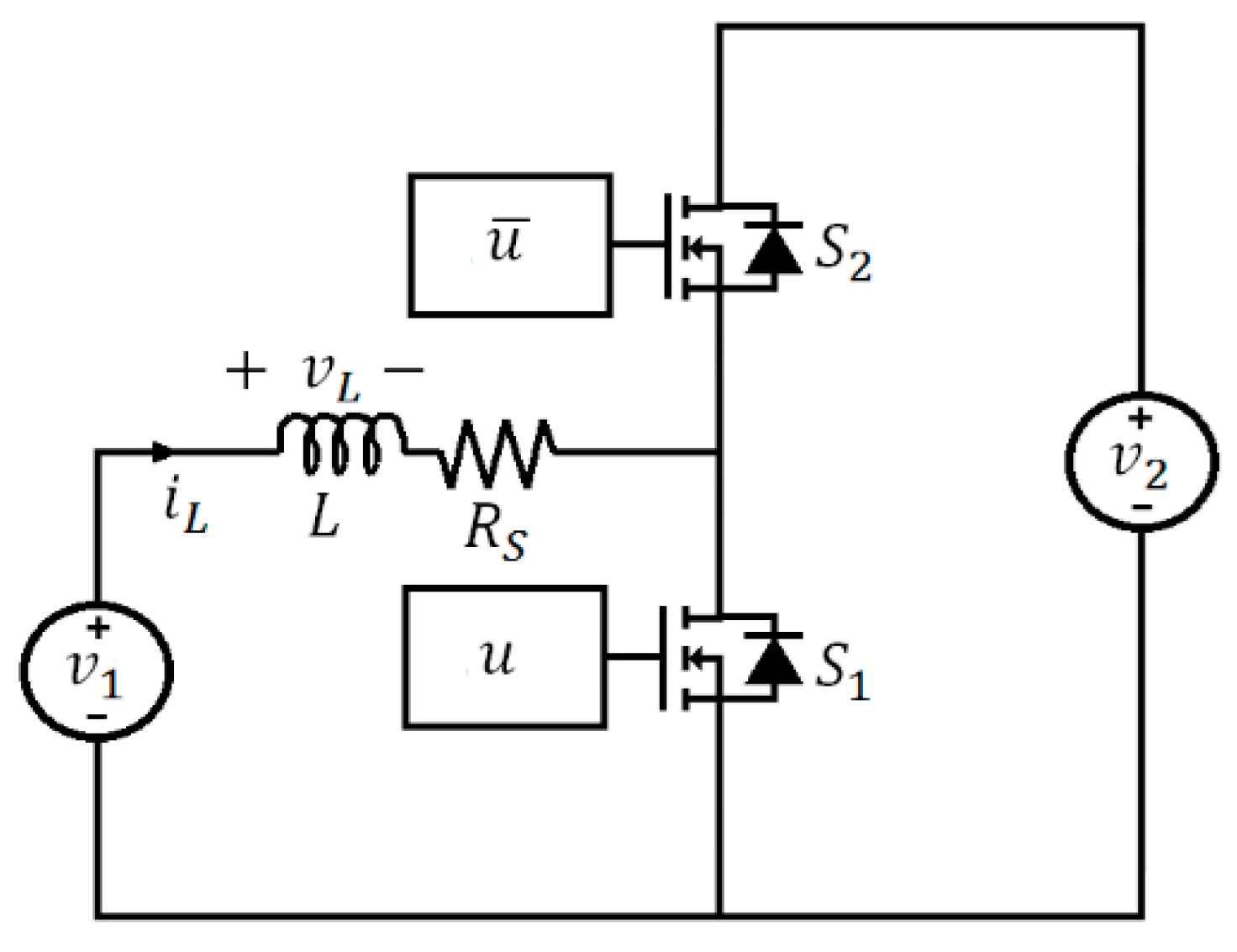
3.1. Regulation of the LVDC Bus (Boost Mode)
3.2. Regulation of the ELVDC Bus (Buck Mode)
3.3. Bidirectional Power Transfer without Voltage Regulation
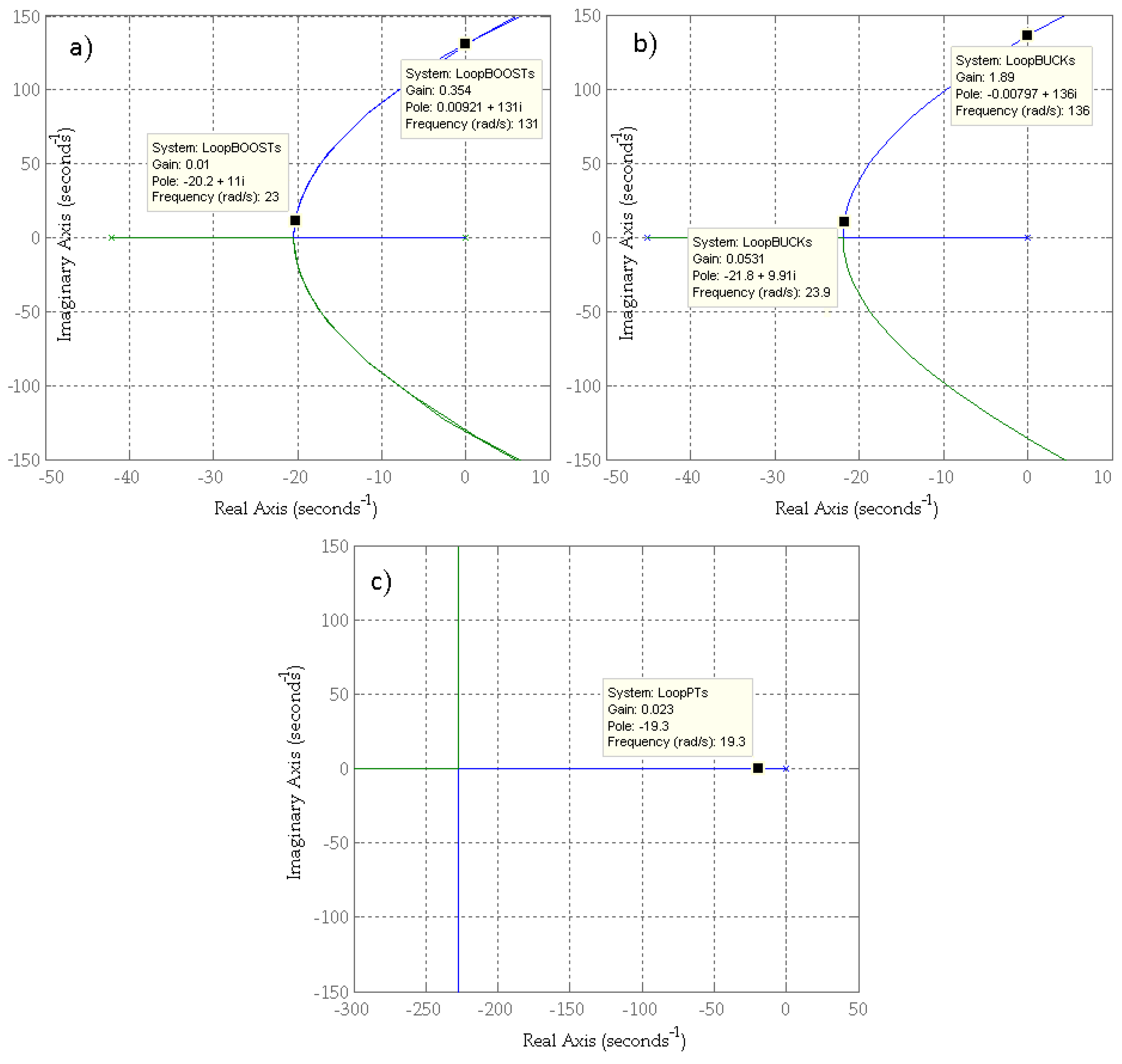
3.4. Stability Analysis
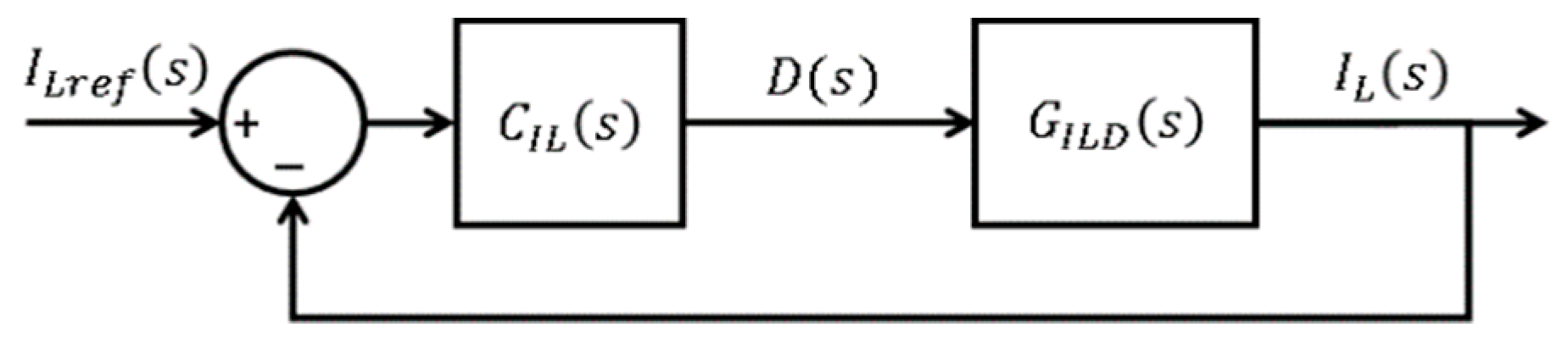
3.5. Unified Control Proposal
4. Simulation Results
4.1. Controller Design Procedure
4.2. Regulation of the LVDC Bus (Boost Mode)
4.3. Regulation of the ELVDC Bus (Buck Mode)
4.4. Bidirectional Power Transfer without Voltage Regulation
4.5. Seamless Changing between Modes
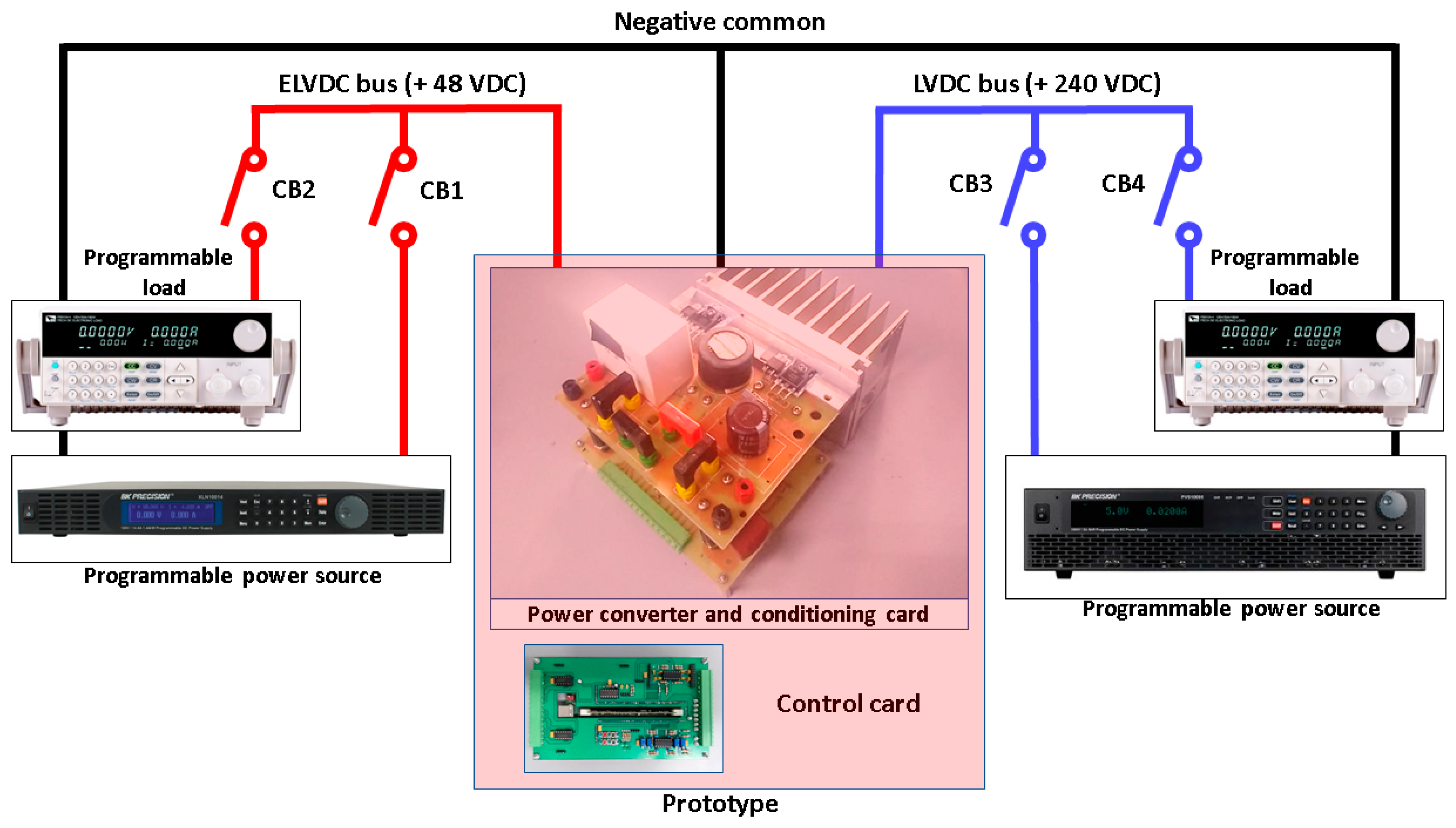
5. Experimental Results
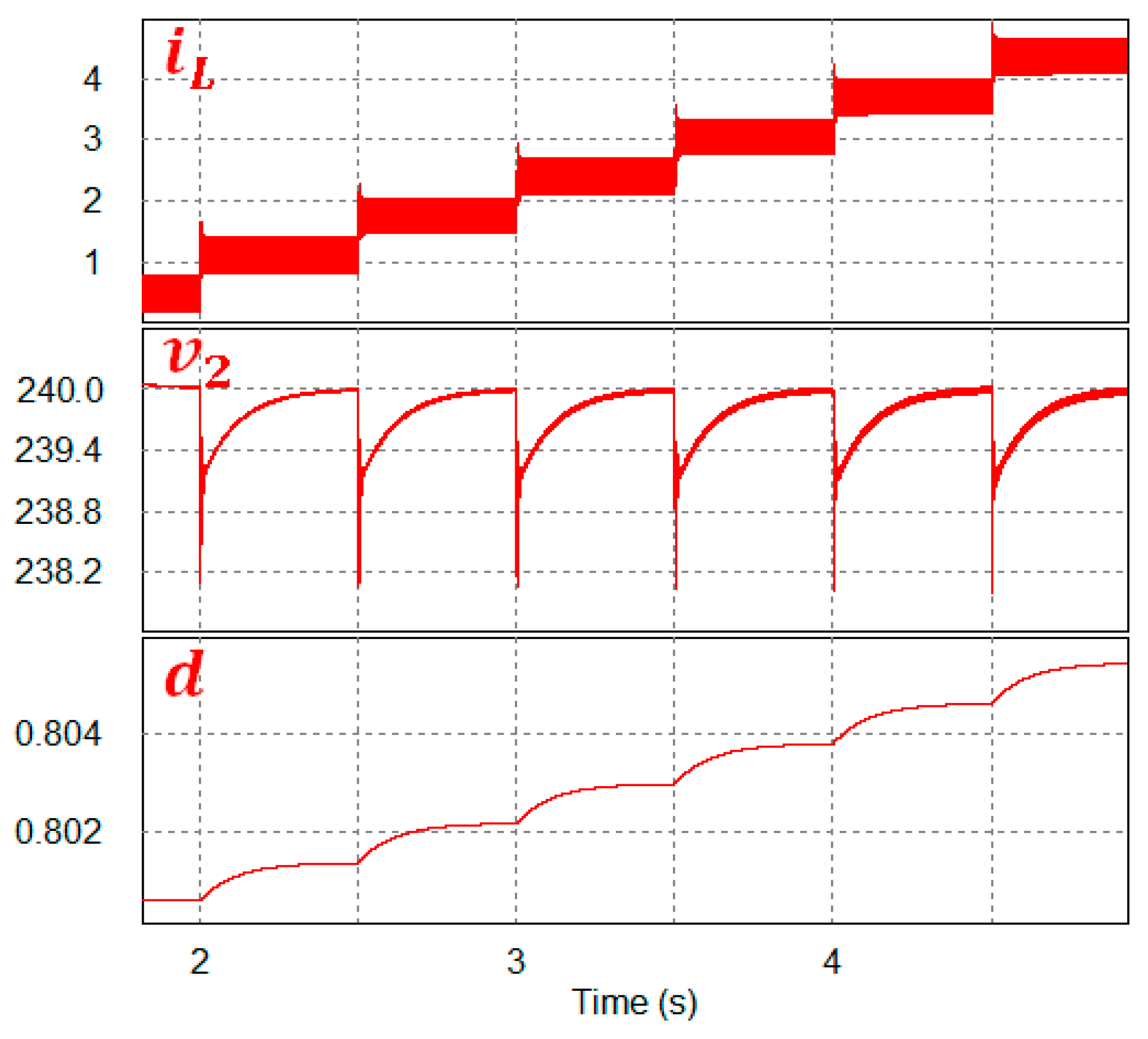
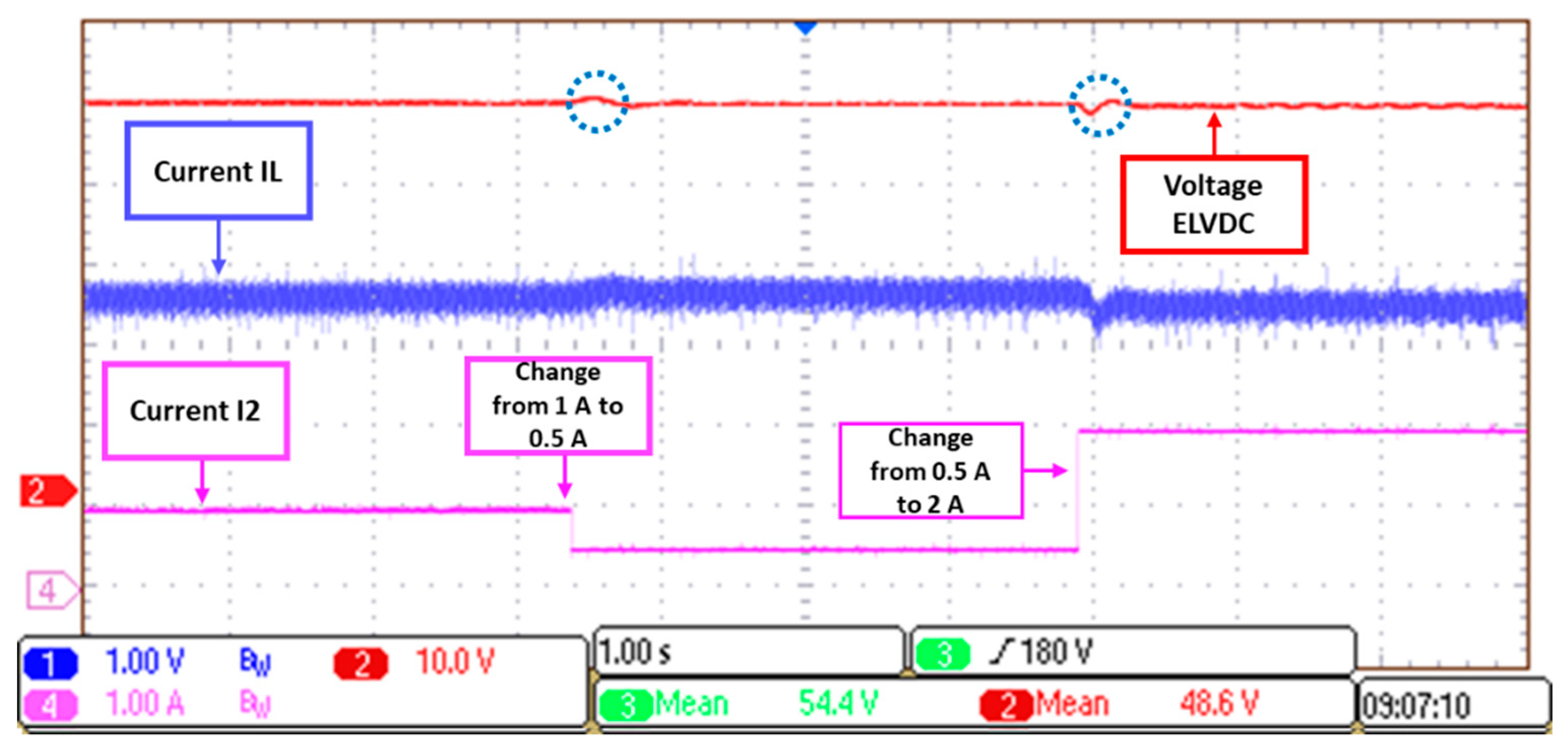
5.1. Regulation of the LVDC Bus (Boost Mode)
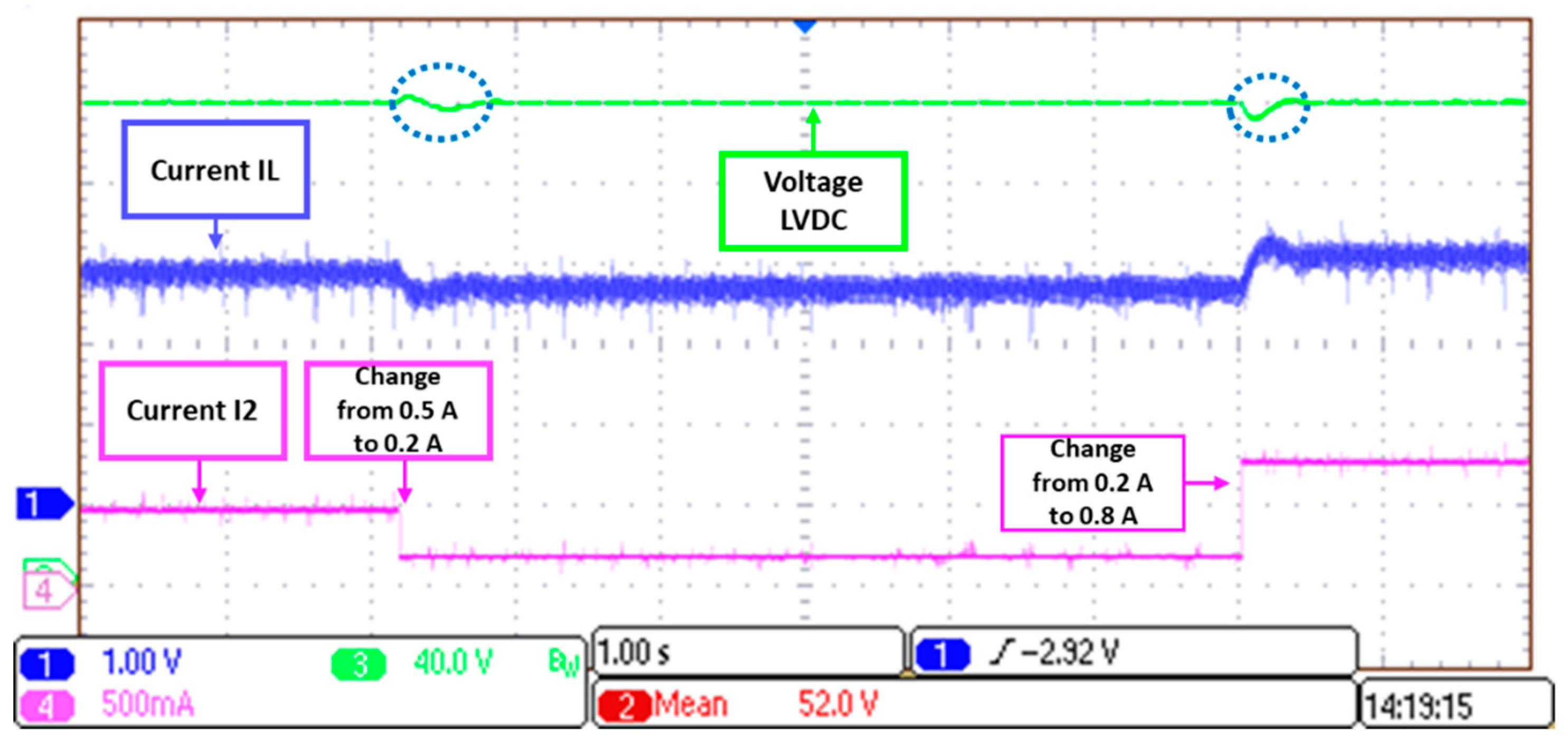
5.1.1. Load Regulation Test
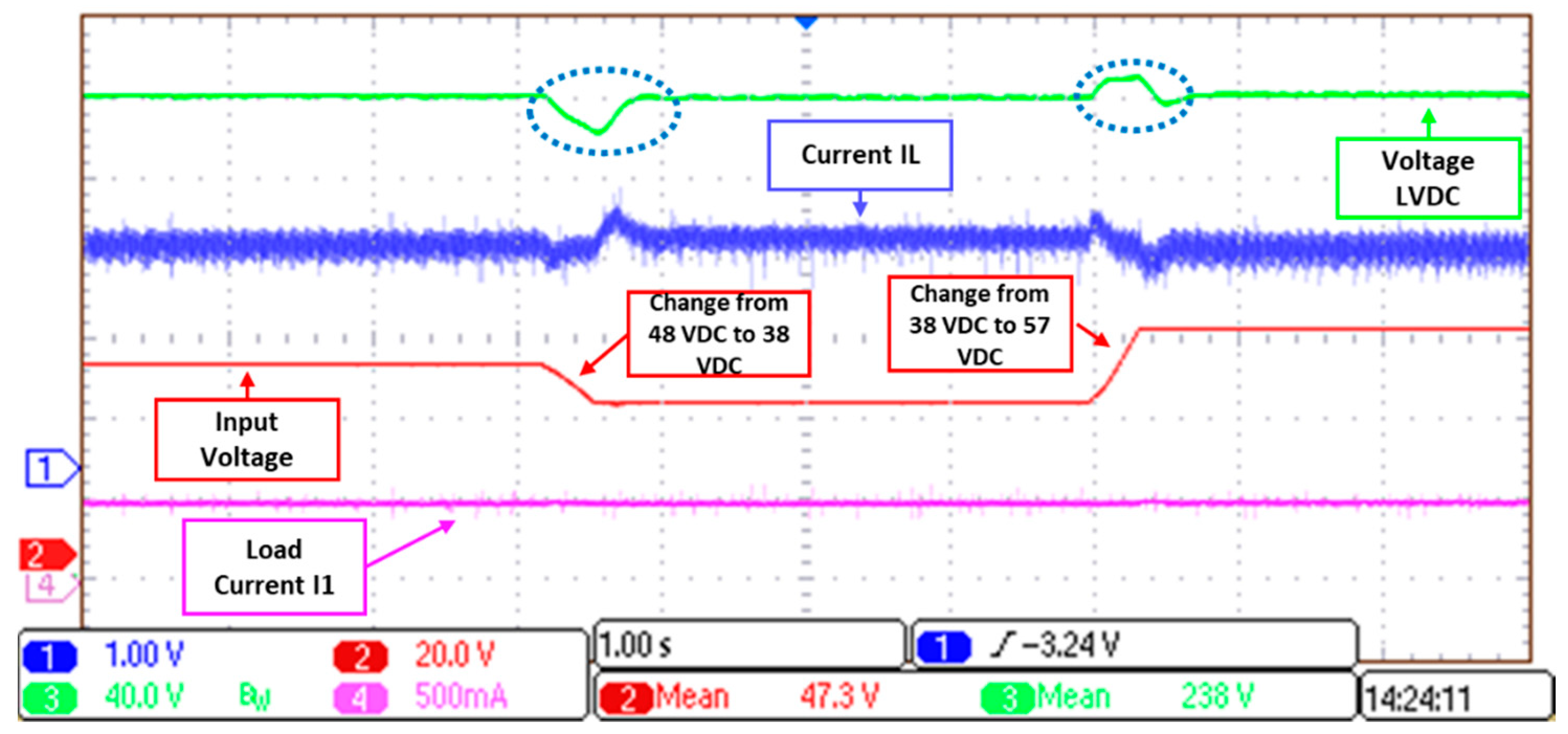
5.1.2. Line Regulation Test
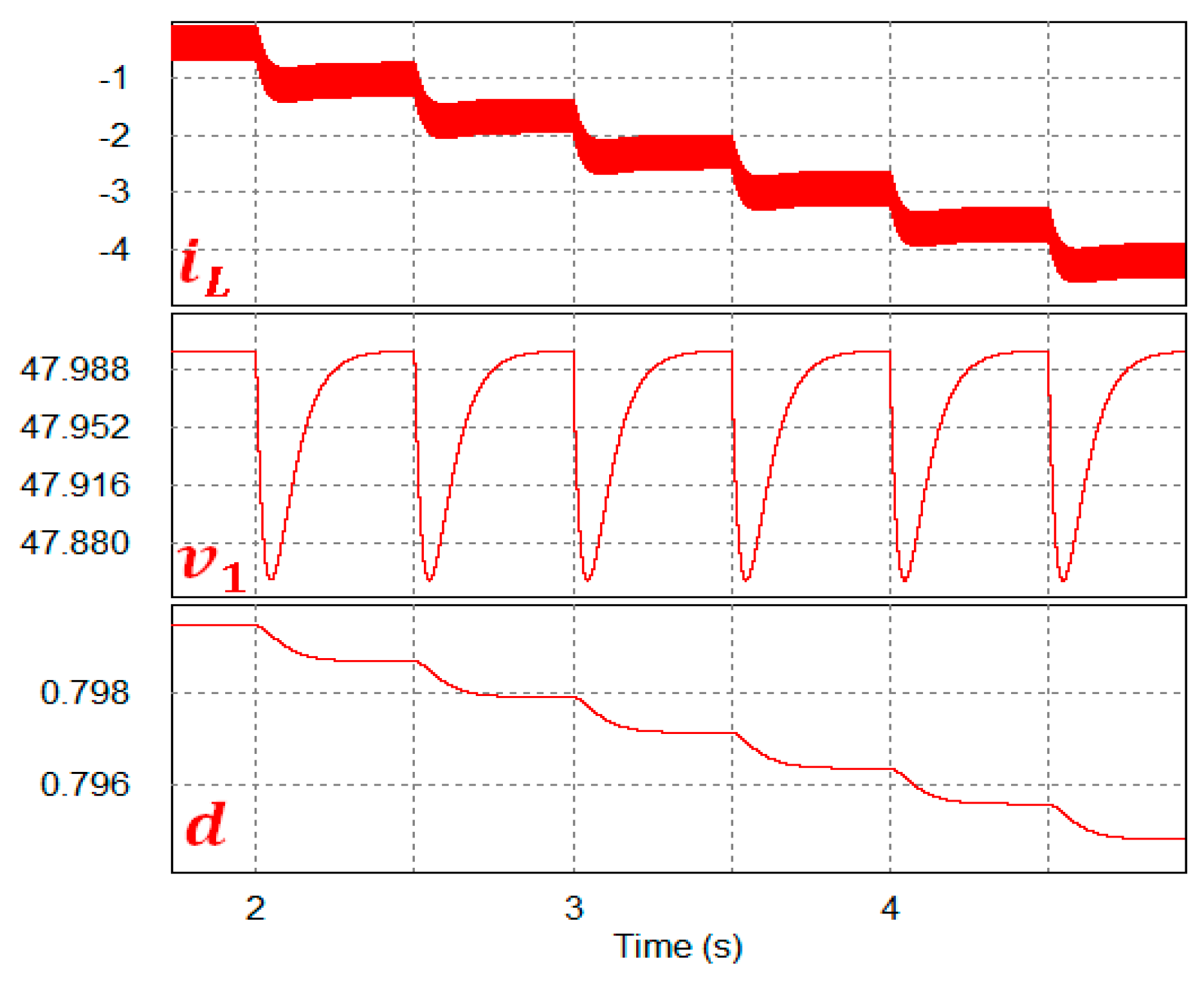
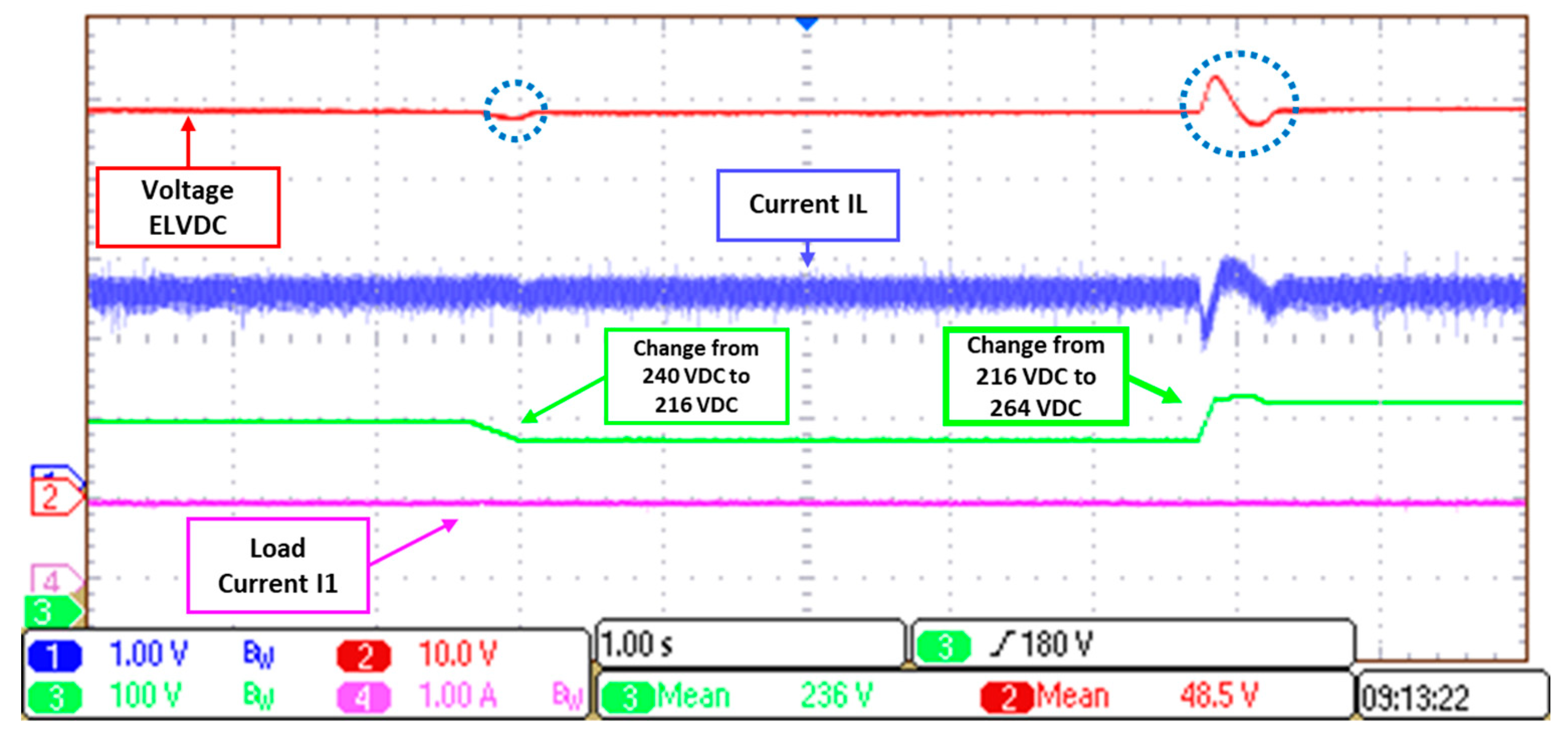
5.2. Regulation of the ELVDC Bus (Buck Mode)
5.2.1. Load Regulation Test
5.2.2. Line Regulation Test
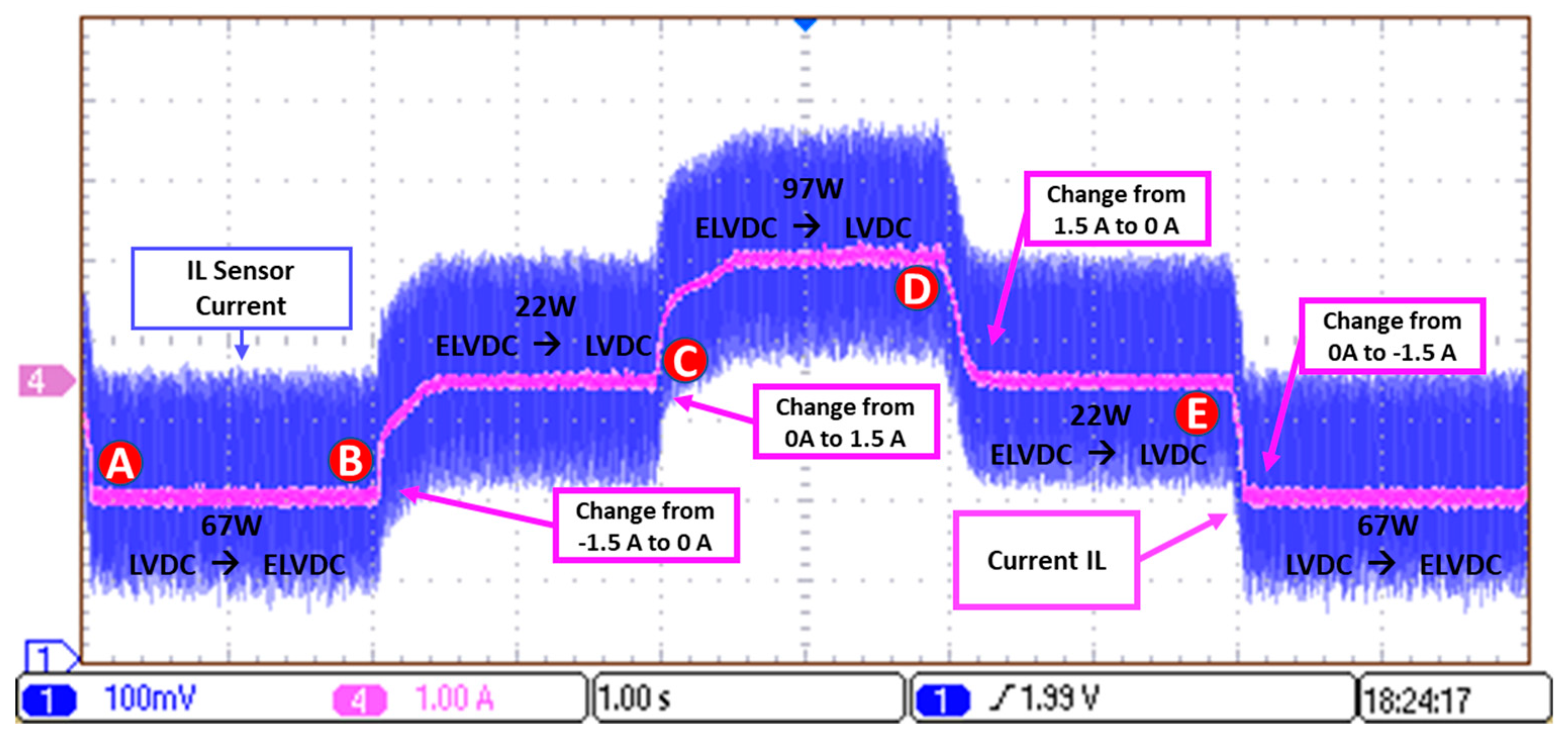
5.3. Bidirectional Power Transfer without Voltage Regulation
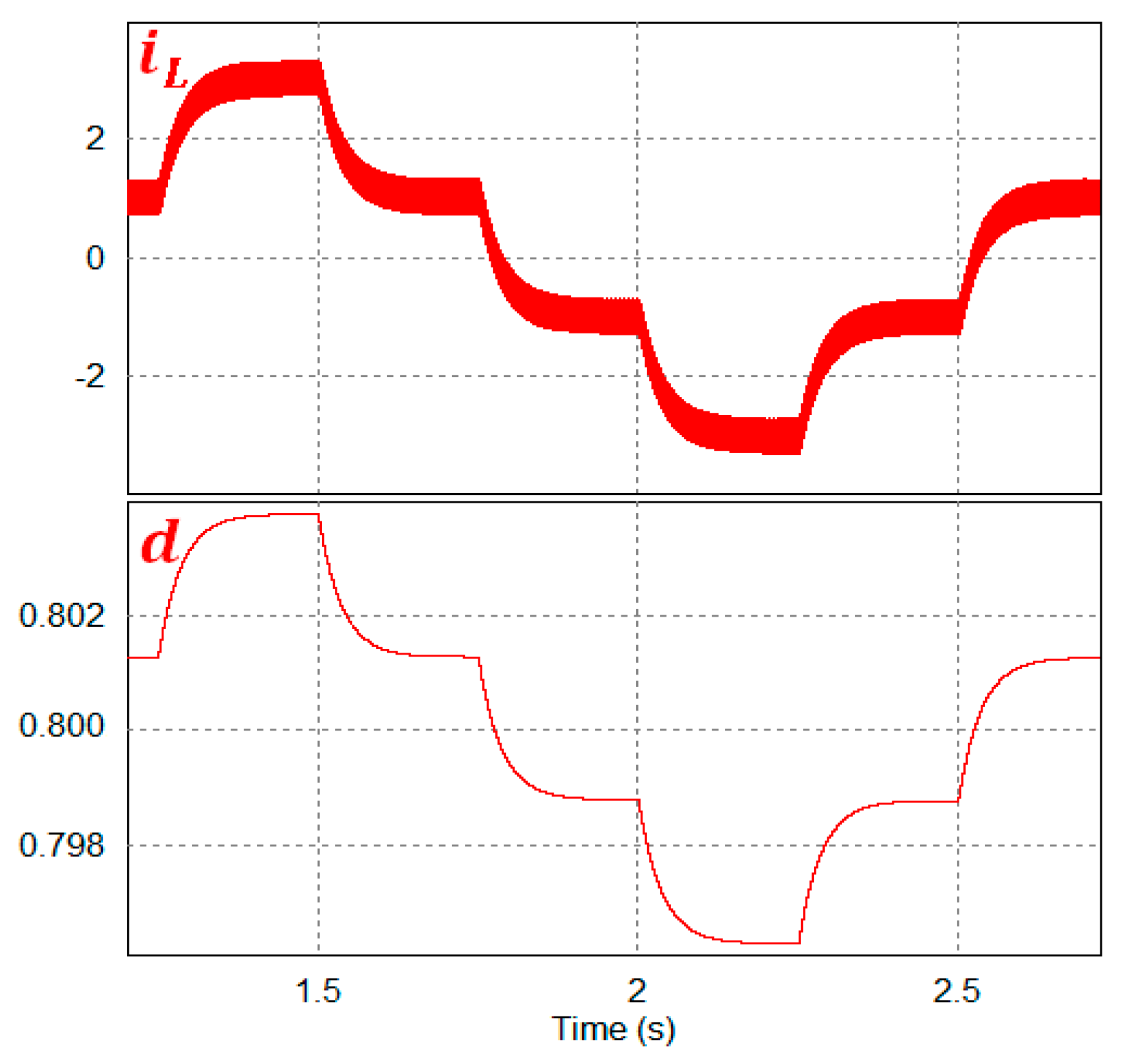
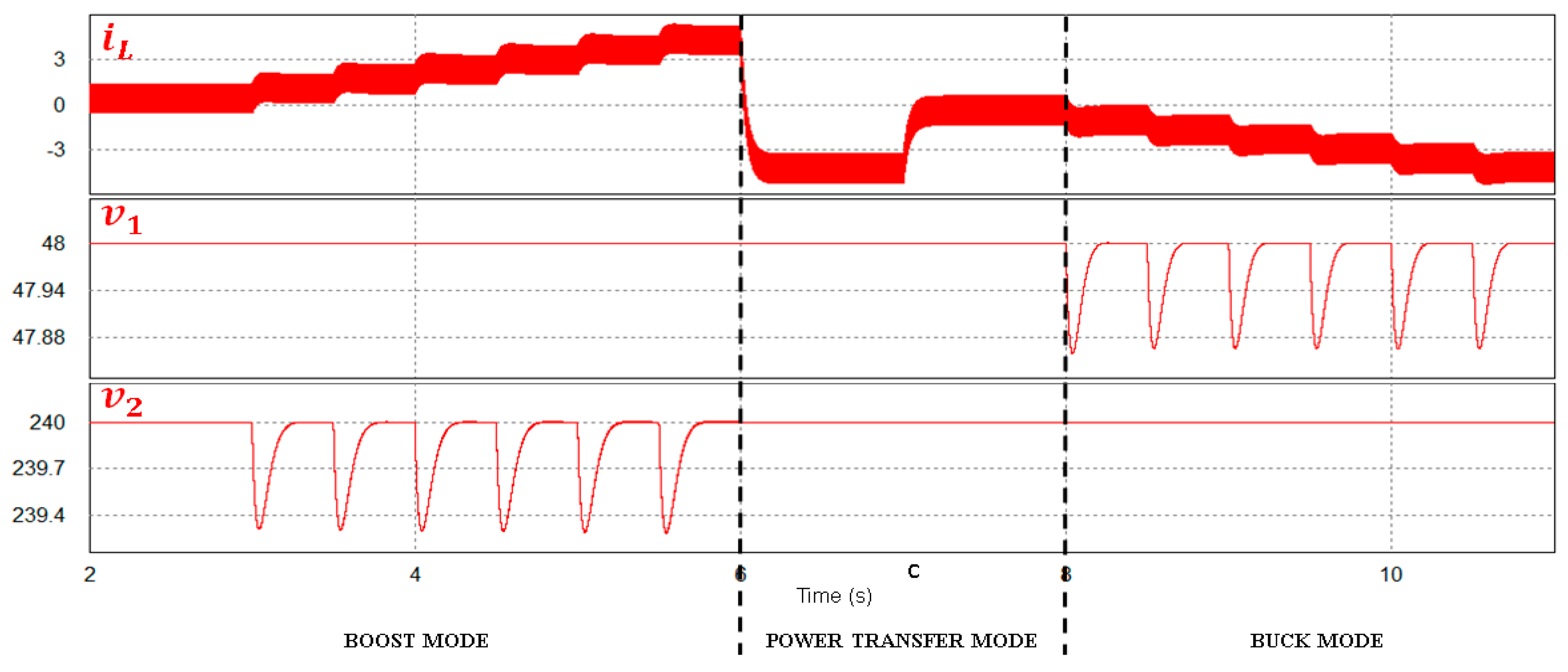
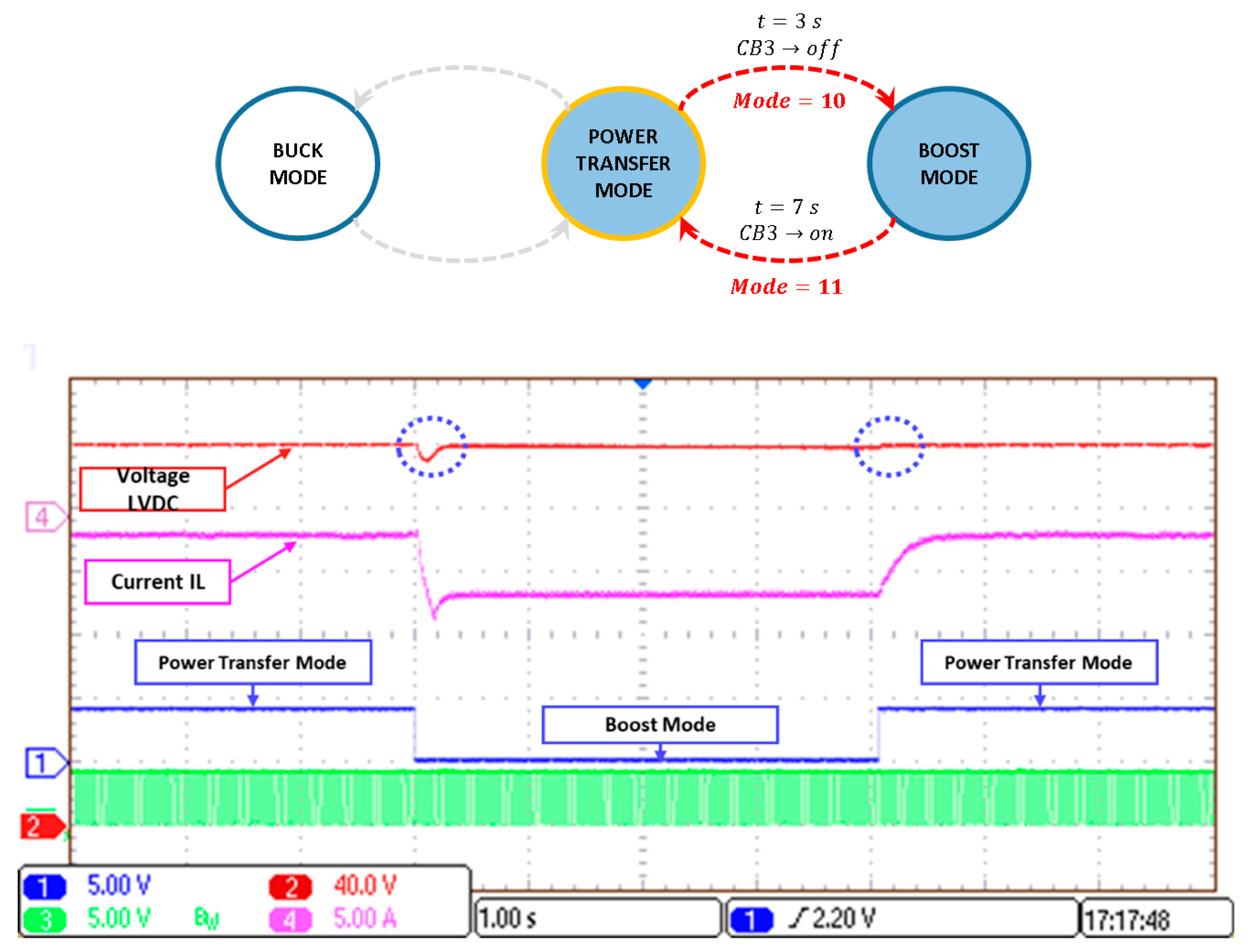
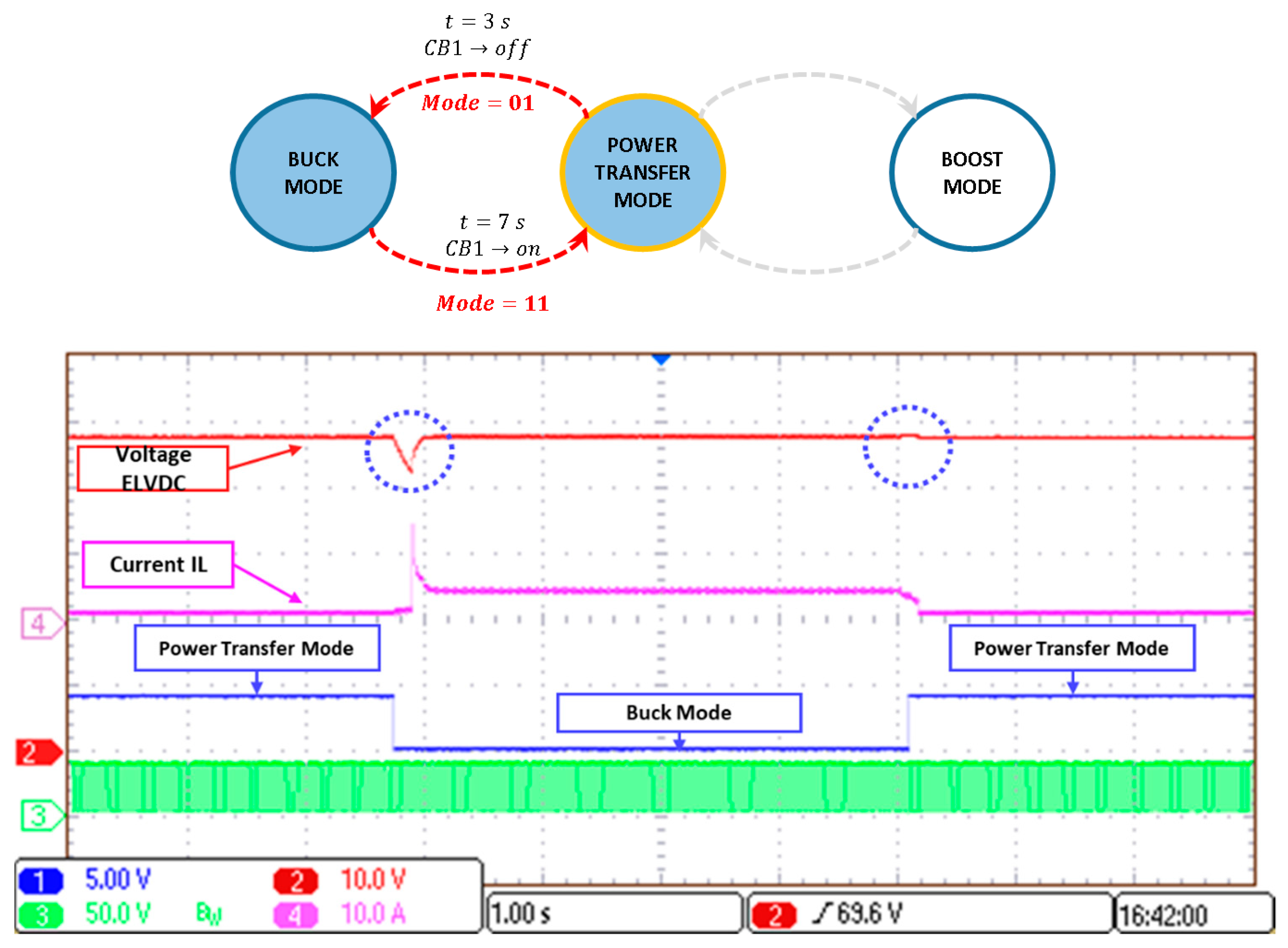
5.4. Seamless Changing between Modes
5.4.1. Transition between Power Transfer and Boost Modes
5.4.2. Transition between Power Transfer Mode and Buck Mode
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, P.; Goel, L.; Liu, X.; Choo, F.H. Harmonizing AC and DC: A hybrid AC/DC future grid solution. IEEE Power Energy Mag. 2013, 11, 76–83. [Google Scholar] [CrossRef]
- Planas, E.; Andreu, J.; Gárate, J.I.; de Alegría, I.M.; Ibarra, E. AC and DC technology in microgrids: A review. Renew. Sustain. Energy Rev. 2015, 43, 726–749. [Google Scholar] [CrossRef]
- Unamuno, E.; Barrena, J.A. Hybrid ac/dc microgrids—Part I: Review and classification of topologies. Renew. Sustain. Energy Rev. 2015, 52, 1251–1259. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Loh, P.C.; Lee, T.; Chandorkar, M. Advanced Control Architectures for Intelligent Microgrids—Part II: Power Quality, Energy Storage, and AC/DC Microgrids. IEEE Trans. Ind. Electron. 2013, 60, 1263–1270. [Google Scholar] [CrossRef]
- Martin-Martínez, F.; Sánchez-Miralles, A.; Rivier, M. A literature review of Microgrids: A functional layer based classification. Renew. Sustain. Energy Rev. 2016, 62, 1133–1153. [Google Scholar] [CrossRef]
- Khan, A.A.; Naeem, M.; Iqbal, M.; Qaisar, S.; Anpalagan, A. A compendium of optimization objectives, constraints, tools and algorithms for energy management in microgrids. Renew. Sustain. Energy Rev. 2016, 58, 1664–1683. [Google Scholar] [CrossRef]
- Nejabatkhah, F.; Li, Y.W. Overview of Power Management Strategies of Hybrid AC/DC Microgrid. IEEE Trans. Power Electron. 2015, 30, 7072–7089. [Google Scholar] [CrossRef]
- Xiao, J.; Nguyen, X.B.; Wang, P.; Huang, J.; Zhou, Q. Implementation of DC/DC converter with high frequency transformer (DHFT) in hybrid AC/DC microgrid. In Proceedings of the 2017 Asian Conference on Energy, Power and Transportation Electrification (ACEPT), Singapore, 24–26 October 2017; pp. 1–5. [Google Scholar]
- Tibola, G.; Duarte, J.L. Isolated bidirectional DC-DC converter for interfacing local storage in two-phase DC grids. In Proceedings of the IEEE 8th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Florianopolis, Brazil, 17–20 April 2017; pp. 1–8. [Google Scholar]
- Zhang, H.; Chen, Y.; Park, S.-J.; Kim, D.-H. A Family of Bidirectional DC–DC Converters for Battery Storage System with High Voltage Gain. Energies 2019, 12, 1289. [Google Scholar] [CrossRef]
- Lin, B.-R. Investigation of a Resonant dc–dc Converter for Light Rail Transportation Applications. Energies 2018, 11, 1078. [Google Scholar] [CrossRef]
- Bi, H.; Wang, P.; Wang, Z. Common Grounded H-Type Bidirectional DC-DC Converter with a Wide Voltage Conversion Ratio for a Hybrid Energy Storage System. Energies 2018, 11, 349. [Google Scholar] [CrossRef]
- Hussain, A.; Akhtar, R.; Ali, B.; Awan, S.E.; Iqbal, S. A Novel Bidirectional DC–DC Converter with Low Stress and Low Magnitude Ripples for Stand-Alone Photovoltaic Power Systems. Energies 2019, 12, 2884. [Google Scholar] [CrossRef]
- Wang, C.S.; Li, W.; Wang, Y.F.; Han, F.Q.; Meng, Z.; Li, G.D. An Isolated Three-Port Bidirectional DC-DC Converter with Enlarged ZVS Region for HESS Applications in DC Microgrids. Energies 2017, 10, 446. [Google Scholar] [CrossRef]
- Tao, H.; Kotsopoulos, A.; Duarte, J.L.; Hendrix, M.A. Family of multiport bidirectional DC–DC converters. IEE Proc. Electr. Power Appl. 2006, 153, 451–458. [Google Scholar] [CrossRef]
- Lin, C.-C.; Yang, L.-S.; Wu, G. Study of a non-isolated bidirectional DC–DC converter. IET Power Electron. 2013, 6, 30–37. [Google Scholar] [CrossRef]
- Huang, C.-C.; Tsai, T.-L.; Hsieh, Y.-C.; Chiu, H.-J. A Bilateral Zero-Voltage Switching Bidirectional DC-DC Converter with Low Switching Noise. Energies 2018, 11, 2618. [Google Scholar] [CrossRef]
- Tytelmaier, K.; Husev, O.; Veligorskyi, O.; Yershov, R. A review of non-isolated bidirectional dc-dc converters for energy storage systems. In Proceedings of the II International Young Scientists Forum on Applied Physics and Engineering (YSF), Kharkiv, Ukraine, 10–14 October 2016; pp. 22–28. [Google Scholar]
- Kondrath, N. Bidirectional DC-DC converter topologies and control strategies for interfacing energy storage systems in microgrids: An overview. In Proceedings of the IEEE International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 14–17 August 2017; pp. 341–345. [Google Scholar]
- Patel, A. A new bidirectional DC-DC converter for fuel cell, solar cell and battery systems. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 150–155. [Google Scholar]
- Xia, B.; Li, Y.; Li, Z.; Gao, F.; Wang, P.; Huang, R.; Wang, C. A modular multilevel DC/DC converter interconnecting HVDC systems. In Proceedings of the 43rd Annual Conference of the IEEE Industrial Electronics Society (IECON), Beijing, China, 29 October–1 November 2017; pp. 4477–4481. [Google Scholar]
- Ribeiro, E.; Cardoso, A.J.; Boccaletti, C. Fault diagnosis in non-isolated bidirectional half-bridge DC-DC converters. In Proceedings of the 40th Annual Conference of the IEEE Industrial Electronics Society (IECON), Dallas, TX, USA, 29 October–1 November 2014; pp. 4458–4463. [Google Scholar]
- Shan, Y.; Hu, J.; Chan, K.W.; Fu, Q.; Guerrero, J.M. Model Predictive Control of Bidirectional DC–DC Converters and AC/DC Interlinking Converters—A New Control Method for PV-Wind-Battery Microgrids. IEEE Trans. Sustain. Energy 2019, 10, 1823–1833. [Google Scholar] [CrossRef]
- SK280MB10 MOSFET Module Datasheet; Semikron: Nuremberg, Germany, 2018; pp. 1–4.
- LM5108 Robust and Compact 100-V Half-Bridge Gate Driver; Texas Instruments: Dallas, TX, USA, 2019; pp. 1–33.
- Xu, W.; Chan, N.H.L.; Or, S.W.; Ho, S.L.; Chan, K.W. A New Control Method for a Bi-Directional Phase-Shift-Controlled DC-DC Converter with an Extended Load Range. Energies 2017, 10, 1532. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Y.; Chen, B.; Han, F.; Wang, Q. Studies on a Hybrid Full-Bridge/Half-Bridge Bidirectional CLTC Multi-Resonant DC-DC Converter with a Digital Synchronous Rectification Strategy. Energies 2018, 11, 227. [Google Scholar] [CrossRef]
- Rouzbehi, K.; Miranian, A.; Escaño, J.M.; Rakhshani, E.; Shariati, N.; Pouresmaeil, E. A Data-Driven Based Voltage Control Strategy for DC-DC Converters: Application to DC Microgrid. Electronics 2019, 8, 493. [Google Scholar] [CrossRef]
- Liu, X.; Bian, Y.; Cao, M.; Zhang, Z.; Meng, Q. The Control Parameter Determination Method for Bidirectional DC-DC Power Converters Interfaced Storage Systems Based on Large Signal Stability Analysis. Electronics 2019, 8, 1018. [Google Scholar] [CrossRef]
- Barrado, J.A.; Aroudi, A.E.; Valderrama-Blavi, H.; Calvente, J.; Martinez-Salamero, L. Analysis of a Self-Oscillating Bidirectional DC–DC Converter in Battery Energy Storage Applications. IEEE Trans. Power Deliv. 2012, 27, 1292–1300. [Google Scholar] [CrossRef]
- Romero, A.; Martinez-Salamero, L.; Valderrama, H.; Pallas, O.; Alarcon, E. General purpose sliding-mode controller for bidirectional switching converters. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Monterey, CA, USA, 31 May–3 June 1998; Volume 6, pp. 466–469. [Google Scholar]
- Albiol-Tendillo, L.; Vidal-Idiarte, E.; Maixe-Altes, J.; Mendez-Prince, S.; Martinez-Salamero, L. Seamless sliding-mode control for bidirectional boost converter with output filter for electric vehicles applications. IET Power Electron. 2015, 8, 1808–1816. [Google Scholar] [CrossRef]
- Martinez-Salamero, L.; Calvente, J.; Giral, R.; Poveda, A.; Fossas, E. Analysis of a bidirectional coupled-inductor Cuk converter operating in sliding mode. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1998, 45, 355–363. [Google Scholar] [CrossRef]
- Lopez-Santos, O.; Zambrano-Prada, D.A.; Aldana-Rodriguez, Y.A.; Esquivel-Cabeza, H.A.; Garcia, G.; Martinez-Salamero, L. Control of a Bidirectional Cûk Converter Providing Charge/Discharge of a Battery Array Integrated in DC Buses of Microgrids. Commun. Comput. Inf. Sci. 2017, 742, 495–507. [Google Scholar]
- Lopez-Santos, O.; Urrego-Aponte, J.O.; Tilaguy-Lezama, S.; Almansa-López, J.D. Control of the Bidirectional Buck-Boost Converter Operating in Boundary Conduction Mode to Provide Hold-Up Time Extension. Energies 2018, 11, 2560. [Google Scholar] [CrossRef]
- Rehman, M.M.U.; Zhang, F.; Zane, R.; Maksimovic, D. Control of bidirectional DC/DC converters in reconfigurable, modular battery systems. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 1277–1283. [Google Scholar]
- IET Standards. Code of Practice for Low and Extra Low Voltage Direct Current Power Distribution in Buildings; The Institution of Engineering and Technology: London, UK, 2015. [Google Scholar]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics, 2nd ed.; Kluwer Academic Publishers: Boston, MA, USA, 2000. [Google Scholar]
- dsPIC30F Family Reference Manual: High Performance Digital Signal Controllers; Microchip Technology Incorporated: Chandler, AR, USA, 2006; pp. 1–772.


| General Operation Specifications | |||
| Parameter | Convention | Value | Units |
| Nominal power | 240 | W | |
| ELVDC bus voltage | 240 | V | |
| LVDC bus voltage | 48 | V | |
| ELVDC load current | 5 | A | |
| LVDC load current | 1 | A | |
| Converter Parameters | |||
| Parameter | Convention | Value | Units |
| LVDC bus capacitance | 3300 | µF | |
| ELVDC bus capacitance | 82,000 | µF | |
| Inductor | 660 | µH | |
| Inductor series resistance | 0.3 | Ω | |
| Switching frequency | 25 | kHz | |
| Controller Parameters | |||
| Integral gain | Convention | Value | |
| Boost mode | 0.010 | ||
| Buck mode | 0.053 | ||
| Power transfer mode | 0.023 | ||
| Parameters of the Digital Controller | ||
|---|---|---|
| Gain | Convention | Value |
| Sample time | 0.2 ms | |
| Controller gain buck mode | 12.5 × 10−6 | |
| Controller gain boost mode | 2.15 × 10−6 | |
| Controller gain power transfer mode | 6.50 × 10−6 | |
| Inductor current sensor gain | 0.1048 | |
| ELVDC bus voltage sensor gain | 0.0713 | |
| LVDC bus voltage sensor gain | 0.0112 | |
| Quantity | Equipment | Model | Manufacturer | Capacity |
|---|---|---|---|---|
| 1 | Programmable DC source | XLN6024 | BK Precision | 60 V/1.44 kW |
| 1 | Programmable DC source | PVS60085 | BK Precision | 600 V/5 kW |
| 2 | Programmable DC load | IT8512B+ | ITECH | 600 V/300 W |
| 1 | Oscilloscope | MSO2014B | Tektronix | 50 MHz |
| 1 | Current probe | TCP0020 | Tektronix | 20 A/50 MHz |
| 1 | Power source for control circuits | GPC-3030D | 30 V/3 A |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Santos, O.; Aldana-Rodríguez, Y.A.; Garcia, G.; Martínez-Salamero, L. A Unified Multimode Control of a DC–DC Interlinking Converter Integrated into a Hybrid Microgrid. Electronics 2019, 8, 1314. https://doi.org/10.3390/electronics8111314
López-Santos O, Aldana-Rodríguez YA, Garcia G, Martínez-Salamero L. A Unified Multimode Control of a DC–DC Interlinking Converter Integrated into a Hybrid Microgrid. Electronics. 2019; 8(11):1314. https://doi.org/10.3390/electronics8111314
Chicago/Turabian StyleLópez-Santos, Oswaldo, Yeison Alejandro Aldana-Rodríguez, Germain Garcia, and Luis Martínez-Salamero. 2019. "A Unified Multimode Control of a DC–DC Interlinking Converter Integrated into a Hybrid Microgrid" Electronics 8, no. 11: 1314. https://doi.org/10.3390/electronics8111314
APA StyleLópez-Santos, O., Aldana-Rodríguez, Y. A., Garcia, G., & Martínez-Salamero, L. (2019). A Unified Multimode Control of a DC–DC Interlinking Converter Integrated into a Hybrid Microgrid. Electronics, 8(11), 1314. https://doi.org/10.3390/electronics8111314






