Cell Voltage Equalizer Using a Selective Voltage Multiplier with a Reduced Selection Switch Count for Series-Connected Energy Storage Cells
Abstract
:1. Introduction
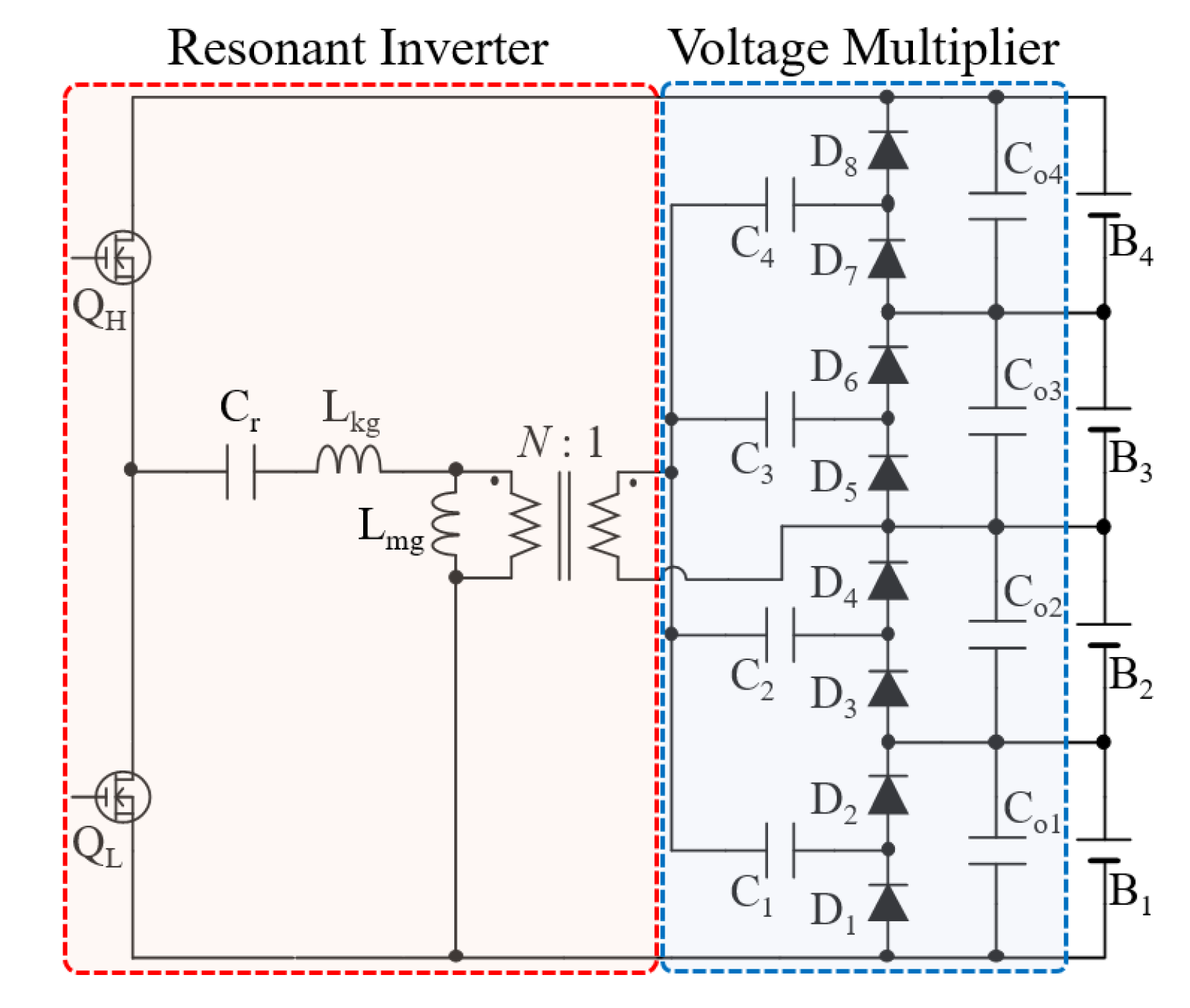
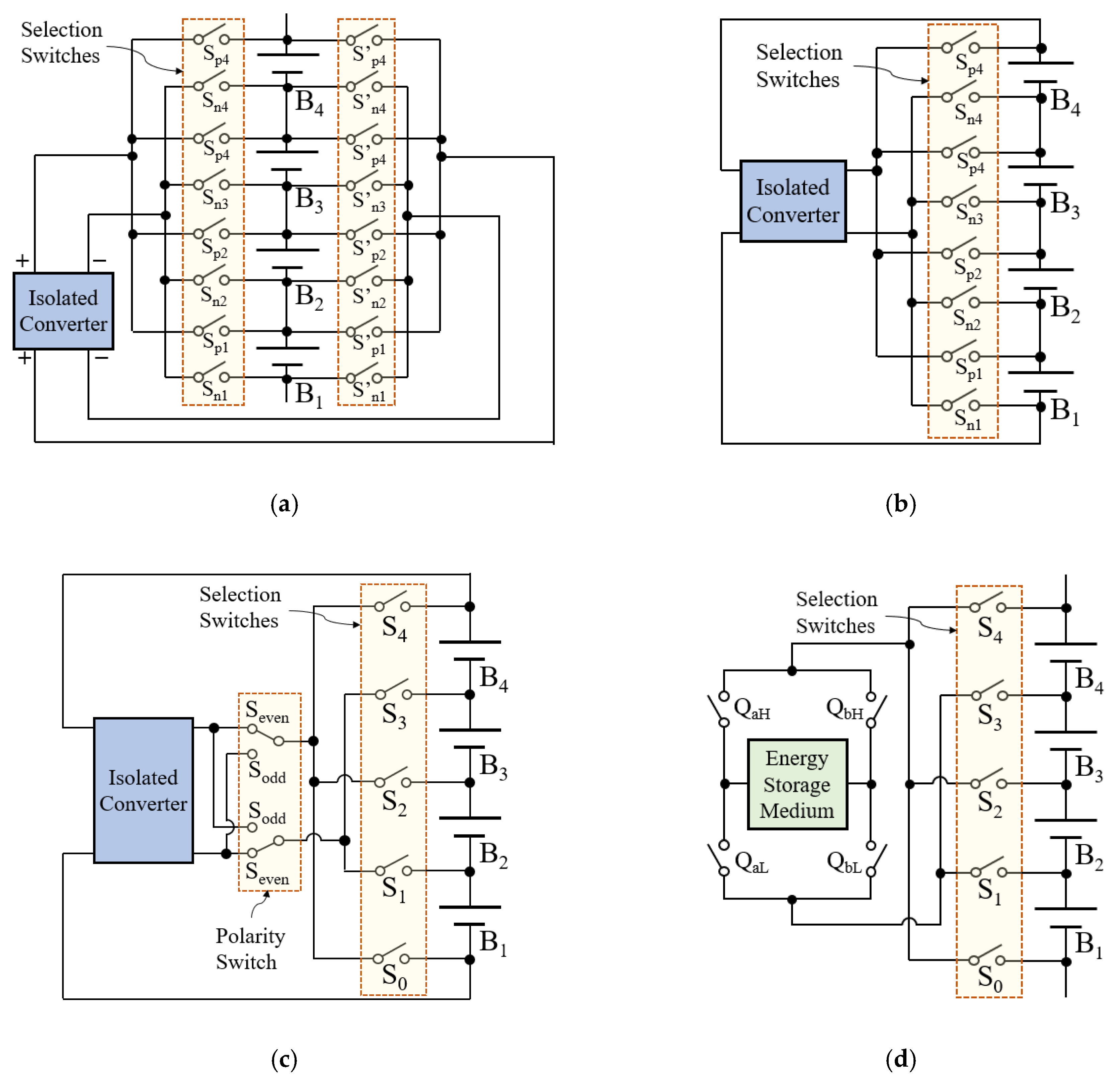
2. Proposed Cell Voltage Equalizer Using Selective Voltage Multiplier
2.1. Topology
2.2. Features
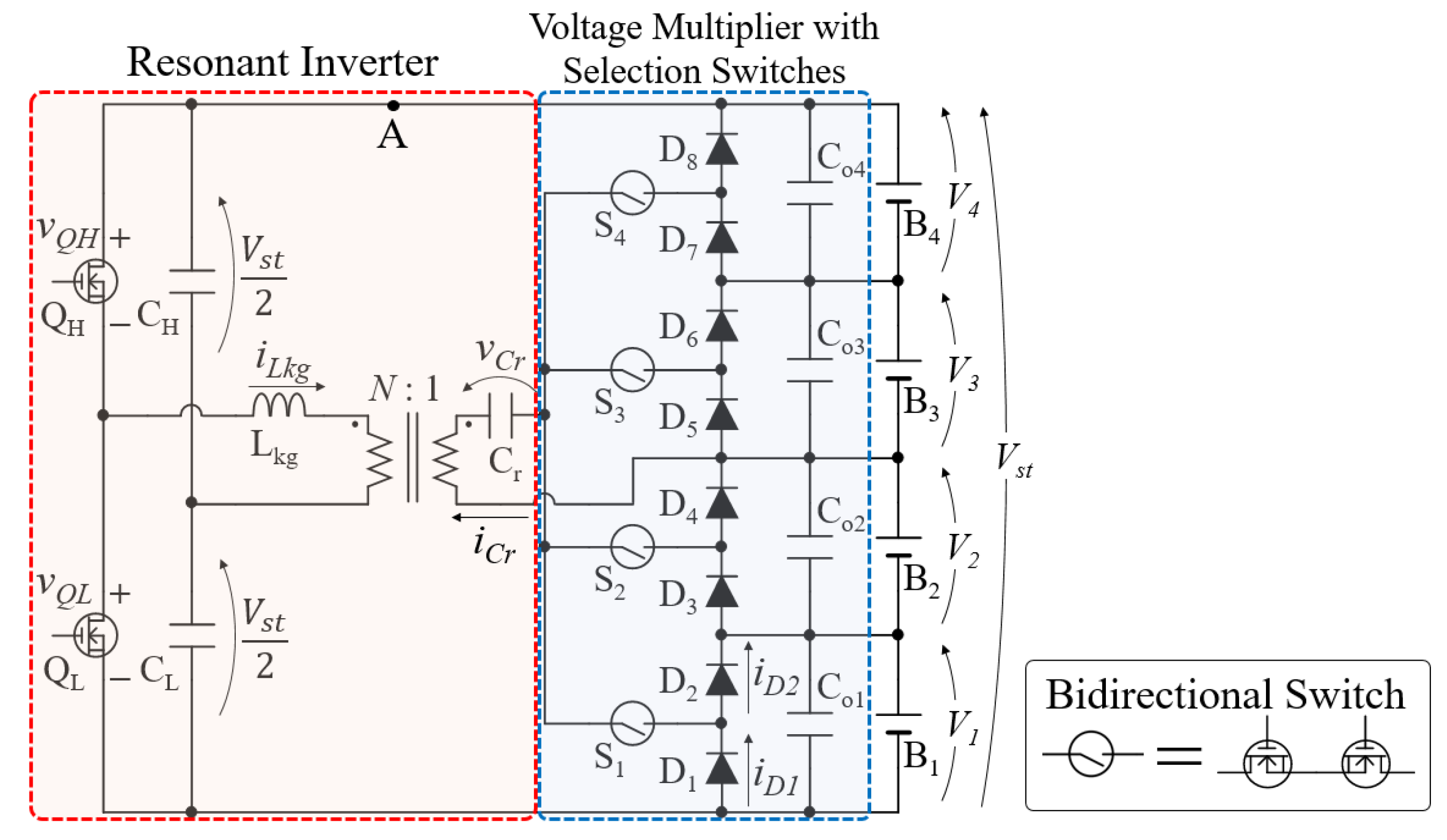
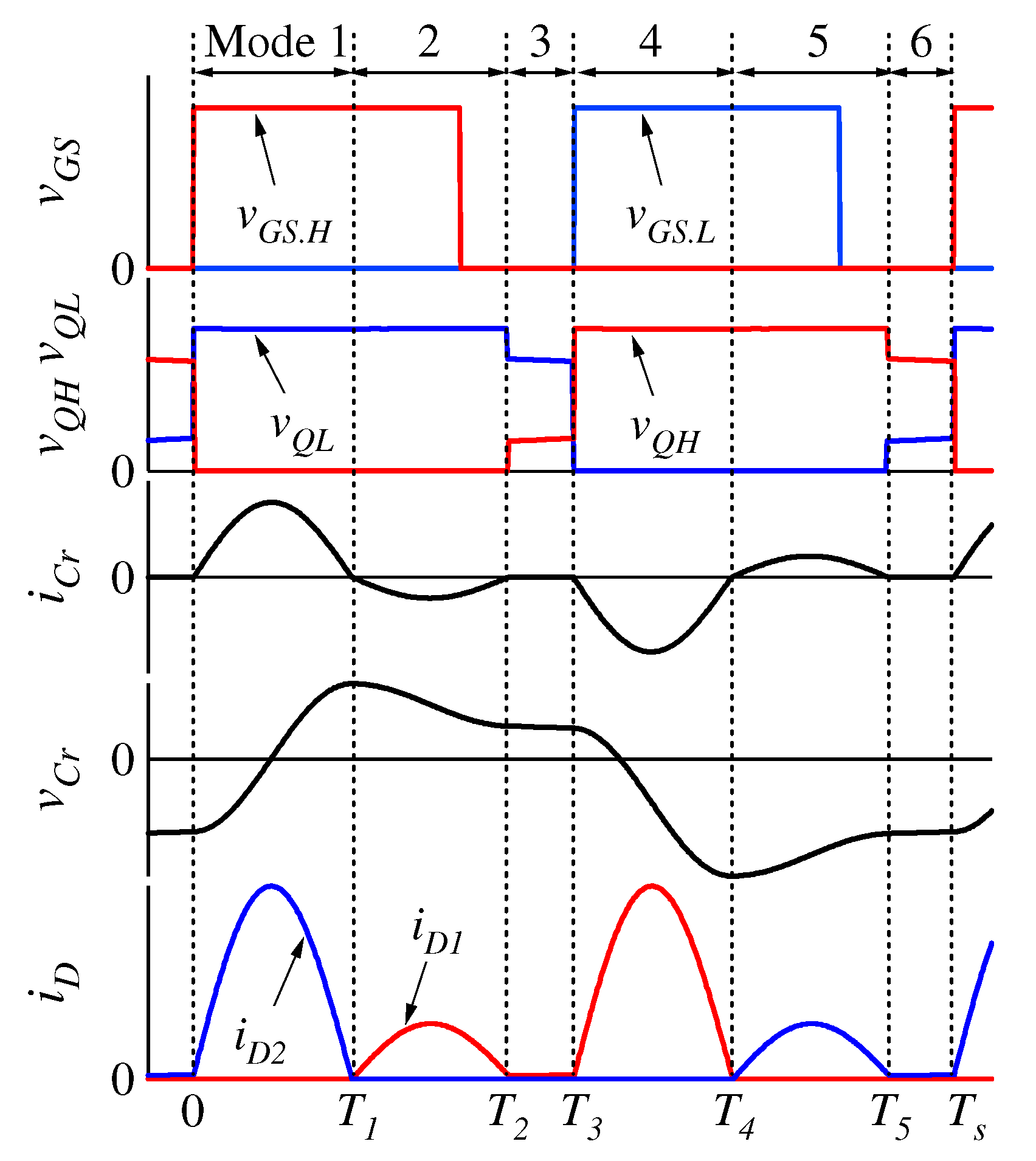
3. Operation Analysis
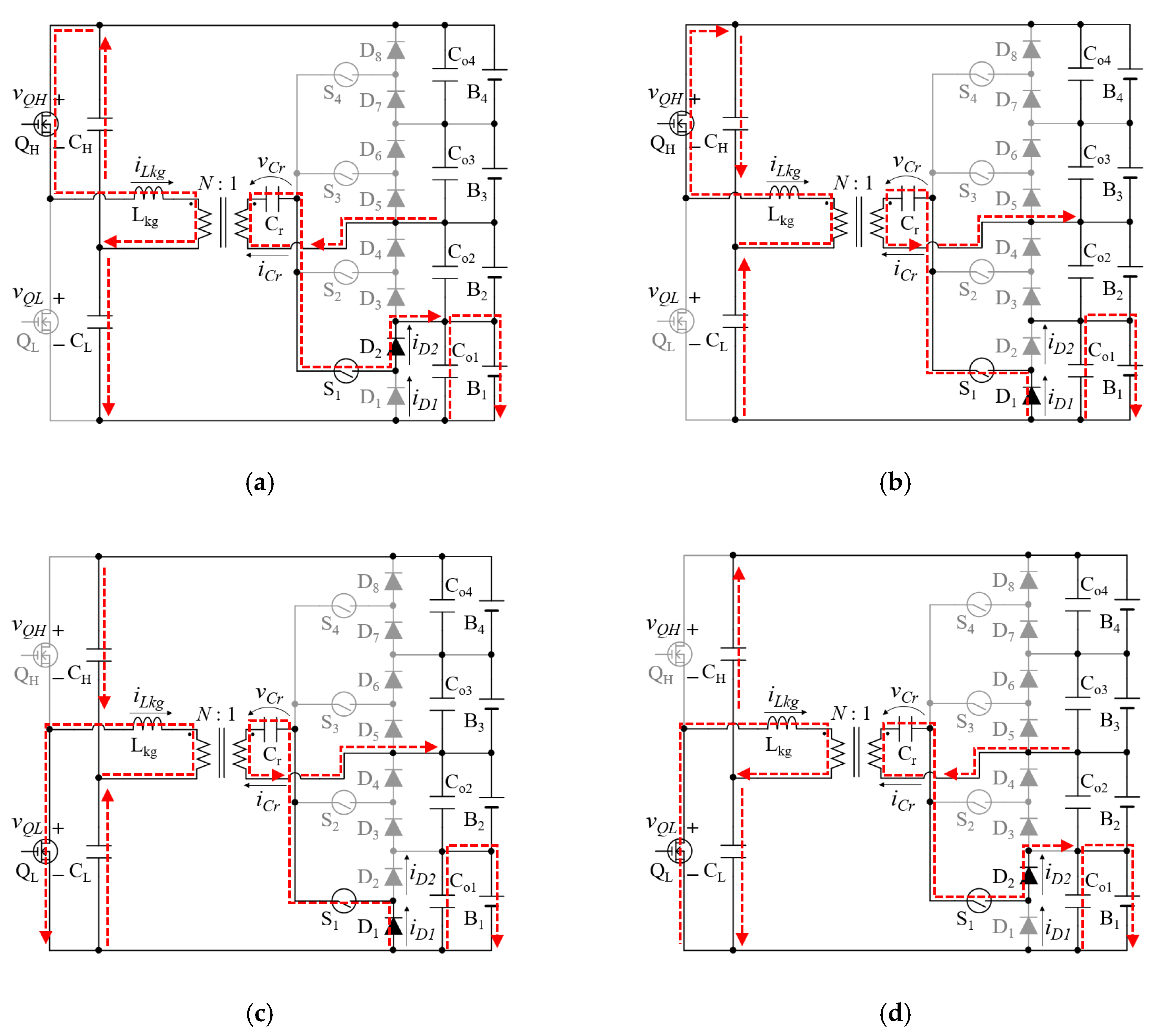
3.1. Operation Modes
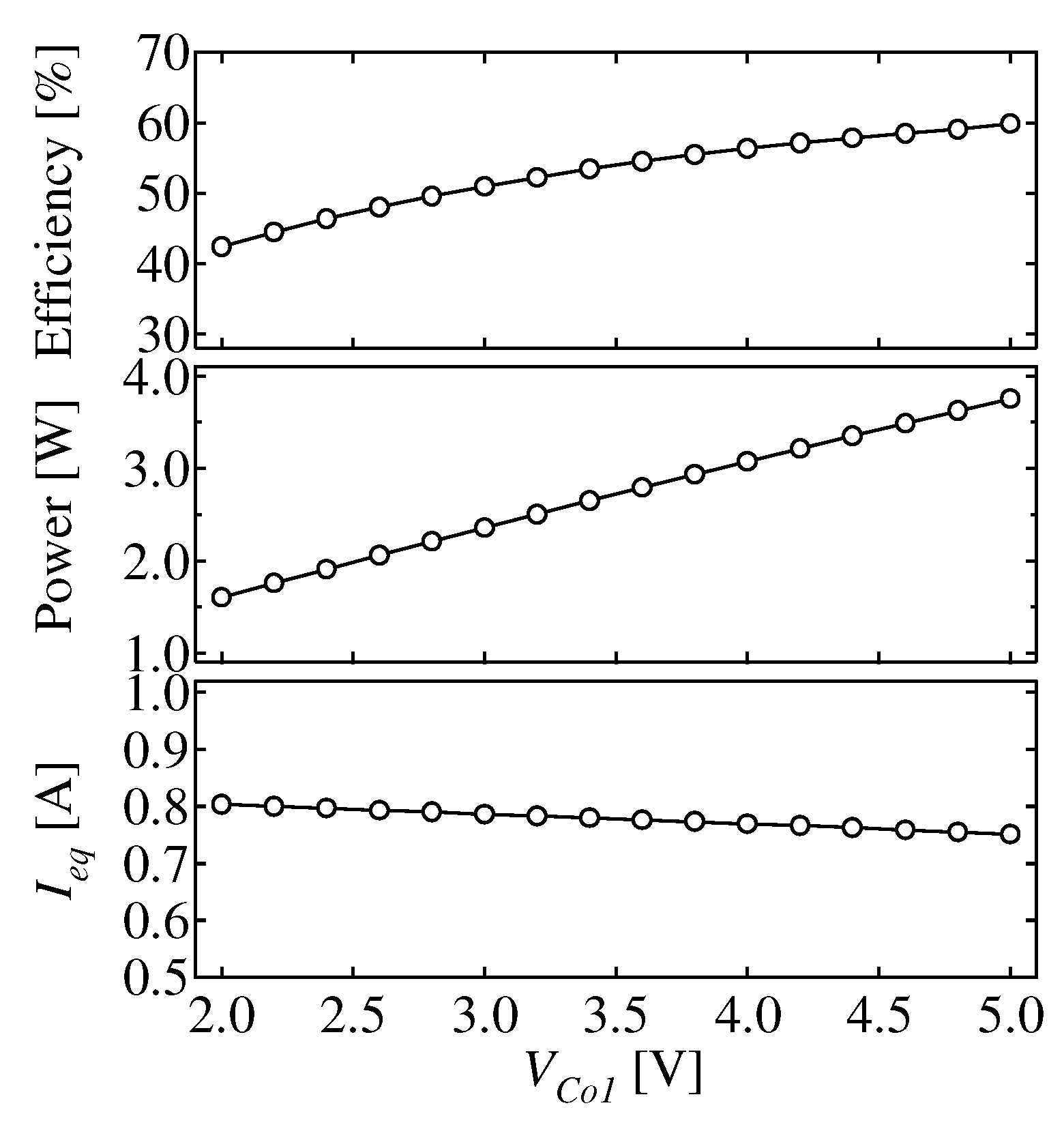
3.2. Operation Boundary and Equalization Current
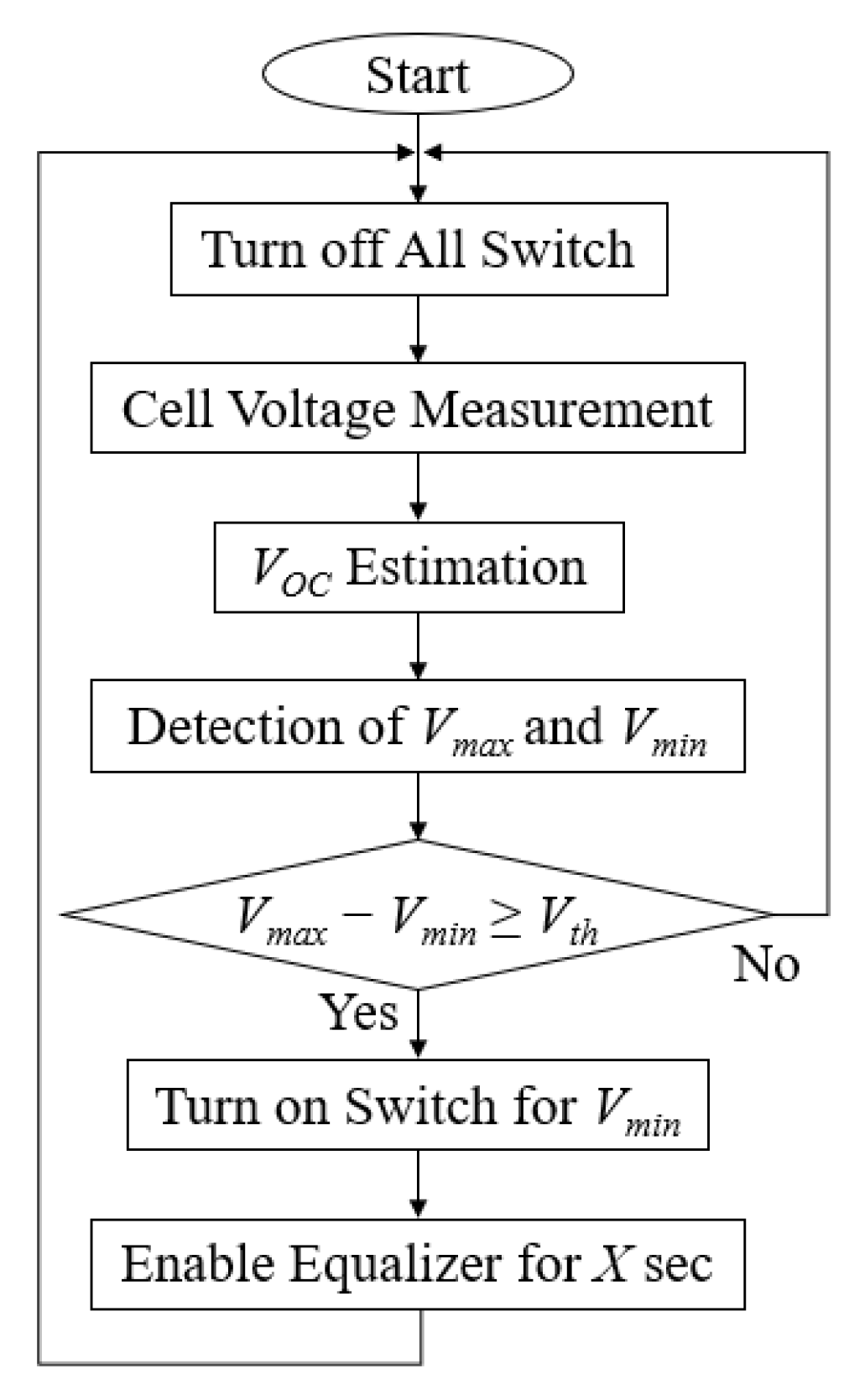
3.3. Equalization Algorithm
4. Experimental Results
4.1. Prototype
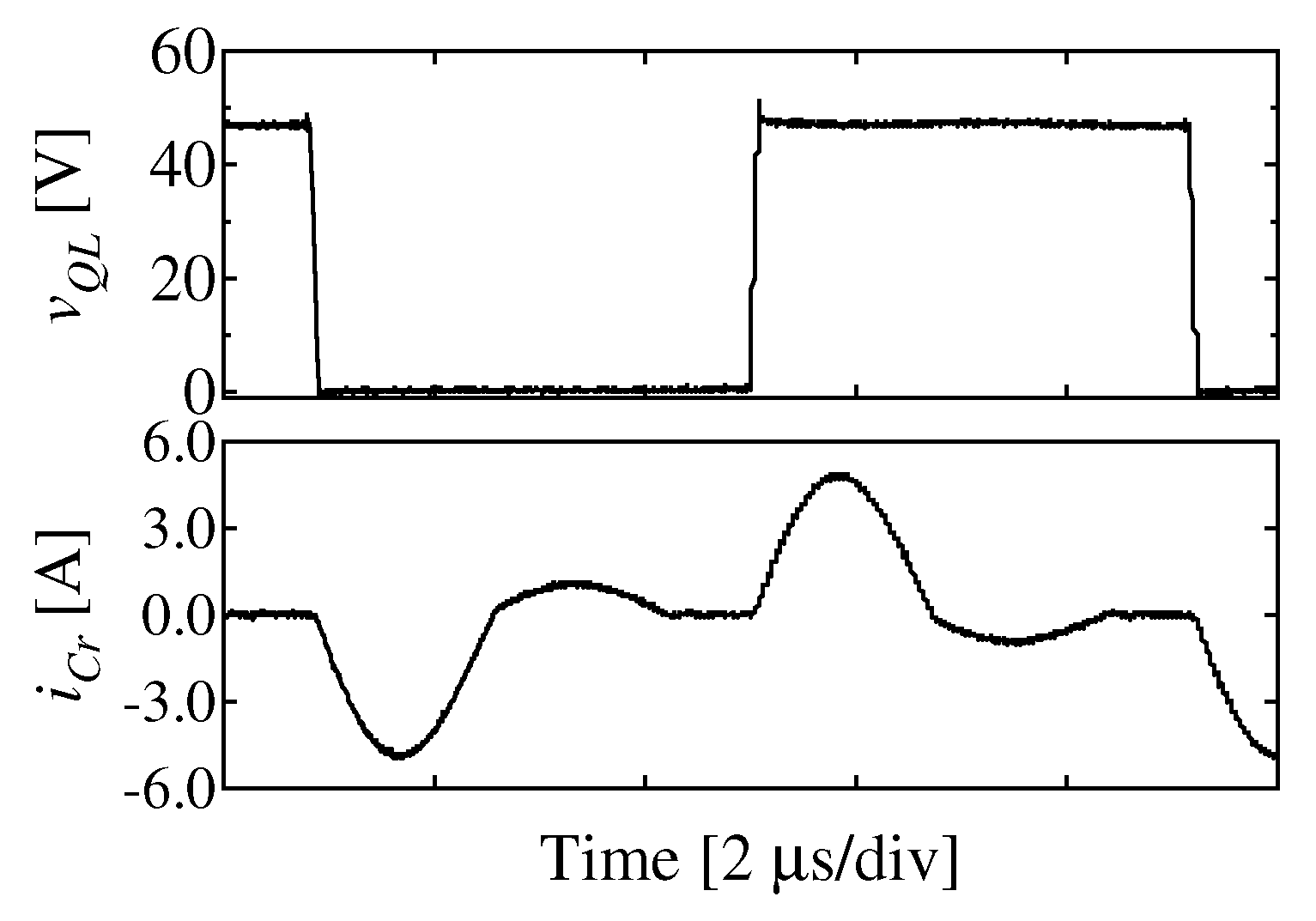
4.2. Measured Waveforms and Characteristics of Equalizer
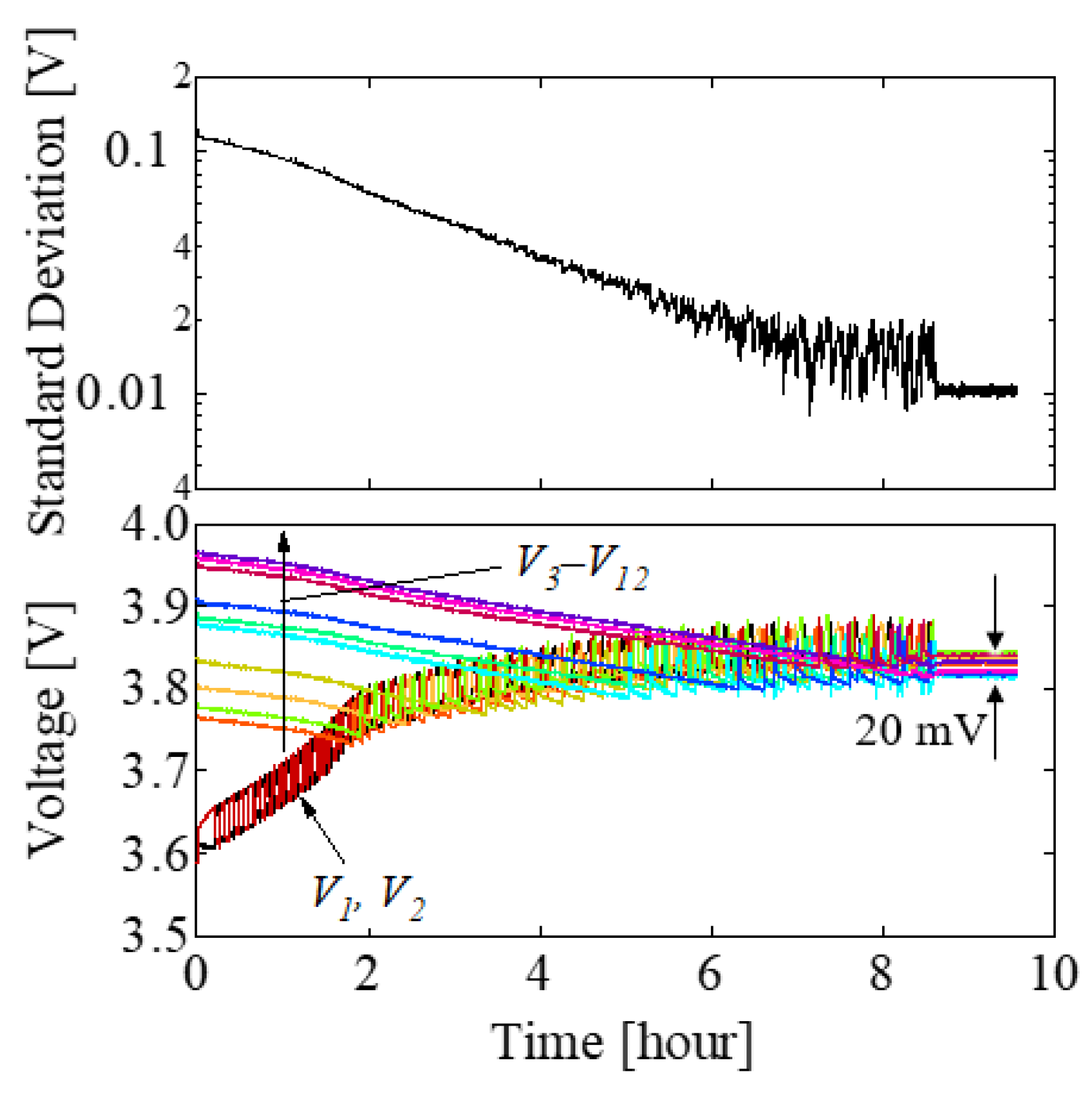
4.3. Equalization Test
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Uno, M.; Kukita, A. String-to-battery voltage equalizer based on half-bridge converter with multi-stacked current doublers for series-connected batteries. IEEE Trans. Power Electron. 2019, 34, 1286–1298. [Google Scholar] [CrossRef]
- Uno, M.; Tanaka, K. Accelerated charge-discharge cycling test and cycle life prediction model for supercapacitors in alternative battery applications. IEEE Trans. Ind. Electron. 2012, 59, 4704–4712. [Google Scholar] [CrossRef]
- Cassani, P.A.; Williamson, S.S. Design, testing, and validation of a simplified control scheme for a novel plug-in hybrid electric vehicle battery cell equalizer. IEEE Trans. Ind. Electron. 2010, 57, 3956–3962. [Google Scholar] [CrossRef]
- Phung, T.H.; Collet, A.; Crebier, J. An optimized topology for next-to-next balancing of series-connected lithium-ion cells. IEEE Trans. Power Electron. 2014, 29, 4603–4613. [Google Scholar] [CrossRef]
- Baughman, A.; Ferdowsi, M. Double-tiered switched-capacitor battery charge equalization technique. IEEE Trans. Ind. Appl. 2008, 55, 2277–2285. [Google Scholar] [CrossRef]
- Uno, M.; Tanaka, K. Influence of high-frequency charge-discharge cycling induced by cell voltage equalizers on the life performance of lithium-ion cells. IEEE Trans. Veh. Technol. 2011, 60, 1505–1515. [Google Scholar] [CrossRef]
- Kim, M.Y.; Kim, C.H.; Kim, J.H.; Moon, G.W. A chain structure of switched capacitor for improved cell balancing speed of lithium-ion batteries. IEEE Trans. Ind. Electron. 2014, 61, 3989–3999. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, K.W.E.; Fong, Y.C. Series-parallel switched capacitor balancing circuit for hybrid source package. IEEE Access 2018, 34254–34261. [Google Scholar] [CrossRef]
- Kutkut, N.H.; Divan, D.M.; Novotny, D.W. Charge equalization for series connected battery strings. IEEE Trans. Ind. Appl. 1995, 31, 562–568. [Google Scholar] [CrossRef]
- Uno, M.; Tanaka, K. Single-switch cell voltage equalizer using multistacked buck-boost converters operating in discontinuous conduction mode for series-connected energy storage cells. IEEE Trans. Veh. Technol. 2011, 60, 3635–3645. [Google Scholar] [CrossRef]
- Uno, M.; Tanaka, K. Double-switch single-transformer cell voltage equalizer using a half-bridge inverter and voltage multiplier for series-connected supercapacitors. IEEE Trans. Veh. Technol. 2012, 61, 3920–3930. [Google Scholar] [CrossRef]
- Uno, M.; Tanaka, K. Single-switch multioutput charger using voltage multiplier for series-connected lithium-ion battery/supercapacitor equalization. IEEE Trans. Ind. Electron. 2013, 60, 3227–3239. [Google Scholar] [CrossRef]
- Uno, M.; Kukita, A. Double-switch equalizer using parallel- or series-parallel-resonant inverter and voltage multiplier for series-connected supercapacitors. IEEE Trans. Power Electron. 2014, 29, 812–828. [Google Scholar] [CrossRef]
- Uno, M.; Kukita, A. Single-switch single-transformer cell voltage equalizer based on forward-flyback resonant inverter and voltage multiplier for series-connected energy storage cells. IEEE Trans. Veh. Technol. 2014, 63, 4232–4247. [Google Scholar] [CrossRef]
- Arias, M.; Sebastian, J.; Hernando, M.M.; Viscarret, U.; Gil, I. Practical application of the wave-trap concept in battery–cell equalizers. IEEE Trans. Power Electron. 2015, 30, 5616–5631. [Google Scholar] [CrossRef]
- Xu, A.; Xie, S.; Liu, X. Dynamic voltage equalization for series-connected ultracapacitors in EV/HEV applications. IEEE Trans. Veh. Technol. 2009, 58, 3981–3987. [Google Scholar]
- Li, S.; Mi, C.C.; Zhang, M. A high-efficiency active battery-balancing circuit using multiwinding transformer. IEEE Trans. Ind. Appl. 2013, 49, 198–207. [Google Scholar] [CrossRef]
- Hua, C.C.; Fang, Y.H.; Chen, Y.L. Modified rectifications for improving the charge equalisation performance of series-connected battery stack. IET Trans. Power Electron. 2016, 9, 1924–1932. [Google Scholar] [CrossRef]
- Uno, M.; Kukita, K. Bidirectional PWM converter integrating cell voltage equalizer using series-resonant voltage multiplier for series-connected energy storage cells. IEEE Trans. Power Electron. 2015, 30, 3077–3090. [Google Scholar] [CrossRef]
- Yashiro, K.; Uno, M. Transformer-less bidirectional PWM converter integrating voltage multiplier-based cell voltage equalizer for series-connected electric double-layer capacitors. IEEE Trans. Power Electron. 2019, 34, 4304–4315. [Google Scholar] [CrossRef]
- Uno, M.; Yoshino, K.; Hasegawa, K. Direct cell-to-cell voltage equalizer using capacitively-isolated parallel-resonant converter for series-connected energy storage cells. In Proceedings of the IEEE 18th International Conference on Power Electronics and Motion Control (PEMC), Budapest, Hungary, 26–30 August 2018; pp. 94–100. [Google Scholar]
- Hannan, M.A.; Hoque, M.M.; Ker, P.J.; Begumm, R.A.; Mohamed, A. Charge equalization controller algorithm for series-connected lithium-ion battery storage systems modeling and applications. Energies 2017, 10, 1390. [Google Scholar] [CrossRef]
- Park, H.S.; Kim, C.E.; Kim, C.H.; Moon, G.W.; Lee, J.H. A modularized charge equalizer for an HEV lithium-ion battery string. IEEE Trans. Ind. Electron. 2009, 56, 1464–1476. [Google Scholar] [CrossRef]
- Park, H.S.; Kim, C.H.; Park, K.B.; Moon, G.W.; Lee, J.H. Design of a charge equalizer based on battery modularization. IEEE Trans. Veh. Technol. 2009, 58, 3216–3223. [Google Scholar] [CrossRef]
- Kim, C.H.; Kim, M.Y.; Park, H.S.; Moon, G.W. A modularized two-stage charge equalizer with cell selection switches for series-connected lithium-ion battery string in a HEV. IEEE Trans. Power Electron. 2012, 27, 3764–3774. [Google Scholar] [CrossRef]
- Kim, C.H.; Kim, M.Y.; Moon, G.W. A modularized charge equalizer using a battery monitoring IC for series-connected Li-ion battery strings in electric vehicles. IEEE Trans. Power Electron. 2013, 28, 3779–3787. [Google Scholar] [CrossRef]
- Hoquea, M.M.; Hannanb, M.A.; Mohameda, A.; Ayoba, A. Battery charge equalization controller in electric vehicle applications: A review. Renew. Sustain. Energy Rev. 2017, 75, 1363–1385. [Google Scholar] [CrossRef]
- Yarlagadda, S.; Hartley, T.T.; Husain, I. A battery management system using an active charge equalization technique based on a DC/DC converter topology. IEEE Trans. Ind. Appl. 2013, 49, 2720–2729. [Google Scholar] [CrossRef]
- Lee, K.M.; Chung, Y.C.; Sung, C.H.; Kang, B. Active cell balancing of Li-ion batteries using LC series resonant circuit. IEEE Trans. Ind. Electron. 2015, 62, 5491–5501. [Google Scholar] [CrossRef]
- Shang, Y.; Zhang, C.; Cui, N.; Guerrero, J.M. A cell-to-cell battery equalizer with zero-current switching and zero-voltage gap based on quasi-resonant LC converter and boost converter. IEEE Trans. Power Electron. 2015, 30, 3731–3747. [Google Scholar] [CrossRef]
- Lee, K.M.; Lee, S.W.; Choi, Y.G.; Kang, B. Active balancing of Li-ion battery cells using transformer as energy carrier. IEEE Trans. Ind. Electron. 2017, 64, 1251–1257. [Google Scholar] [CrossRef]
- Lee, S.W.; Lee, K.M.; Choi, Y.G.; Kang, B. Modularized design of active charge equalizer for Li-ion battery pack. IEEE Trans. Power Electron. 2018, 65, 8697–8706. [Google Scholar] [CrossRef]
- Lee, S.W.; Choi, Y.G.; Kang, B. Active charge equalizer of Li-ion battery cells using double energy carriers. Energies 2019, 12, 2290. [Google Scholar] [CrossRef]
- Zhang, C.; Shang, Y.; Li, Z.; Cui, N. An interleaved equalization architecture with self-learning fuzzy logic control for series-connected battery strings. IEEE Trans. Veh. Technol. 2017, 66, 10923–10934. [Google Scholar] [CrossRef]
- Shang, Y.; Zhang, Q.; Cui, N.; Duan, B.; Zhou, Z.; Zhang, C. Multi-cell-to-multi-cell equalizers based on matrix and half-bridge LC converters for series-connected battery strings. IEEE J. Emerg. Sel. Top. Power Electron. 2019. [Google Scholar] [CrossRef]
- Andrea, D. Battery Management Systems for Large Lithium-Ion Battery Packs, Boston, 1st ed.; Artech House: Boston, MA, USA, 2010; pp. 76–79. ISBN 1608071049. [Google Scholar]
- Kimball, J.W.; Kuhn, B.T.; Krein, P.T. Increased performance of battery packs by active equalization. In Proceedings of the IEEE Vehicle Power Propulsion Conference, Arlington, TX, USA, 9–12 September 2007; pp. 323–327. [Google Scholar]


| Component | Value |
|---|---|
| QH, QL | N-Ch MOSFET, FDD390N15A, Ron = 40 mΩ |
| CH, CL | Ceramic Capacitor, GRM31CB31H106KA12L 10 μF |
| Cr | Film Capacitor, F161SP474M063V, 0.47 μF |
| Transformer | N1:N2 = 15:3, Lkg = 13.8 μH, Lmg = 100 μH |
| S1–S12 | N-Ch MOSFET, IRF7341PBF, Ron = 50 mΩ |
| Co1–Co12 | Ceramic Capacitor, JMK325ABJ277MM-P, 220 μF |
| D1–D24 | Schottky Diode, CRS04 (T5L, TEMQ), Vf = 0.49 V |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uno, M.; Ueno, T.; Yoshino, K. Cell Voltage Equalizer Using a Selective Voltage Multiplier with a Reduced Selection Switch Count for Series-Connected Energy Storage Cells. Electronics 2019, 8, 1303. https://doi.org/10.3390/electronics8111303
Uno M, Ueno T, Yoshino K. Cell Voltage Equalizer Using a Selective Voltage Multiplier with a Reduced Selection Switch Count for Series-Connected Energy Storage Cells. Electronics. 2019; 8(11):1303. https://doi.org/10.3390/electronics8111303
Chicago/Turabian StyleUno, Masatoshi, Teruhisa Ueno, and Koji Yoshino. 2019. "Cell Voltage Equalizer Using a Selective Voltage Multiplier with a Reduced Selection Switch Count for Series-Connected Energy Storage Cells" Electronics 8, no. 11: 1303. https://doi.org/10.3390/electronics8111303
APA StyleUno, M., Ueno, T., & Yoshino, K. (2019). Cell Voltage Equalizer Using a Selective Voltage Multiplier with a Reduced Selection Switch Count for Series-Connected Energy Storage Cells. Electronics, 8(11), 1303. https://doi.org/10.3390/electronics8111303





