Abstract
This paper proposes an approach to an ANN-based temperature controller design for a plastic injection moulding system. This design approach is applied to the development of a controller based on a combination of a classical ANN and integrator. The controller provides a fast temperature response and zero steady-state error for three typical heaters (bar, nozzle, and cartridge) for a plastic moulding system. The simulation results in Matlab Simulink software and in comparison to an industrial PID regulator have shown the advantages of the controller, such as significantly less overshoot and faster transient (compared to PID with autotuning) for all examined heaters. In order to verify the proposed approach, the designed ANN controller was implemented and tested using an experimental setup based on an STM32 board.
1. Introduction
Injection moulding is a fundamental industrial process in the polymer industry for plastic part manufacturing. This process is widely applied to the mass production of a large variety of plastic components, from LEGO bricks to advanced body panels for automobiles. The process comprises plastic granule movement through a barrel using a reciprocating screw, melting under the heater’s influence, injection of the molten material under high pressure into a mould for shaping the polymer into the desired form and, finally, cooling. At the end of the process, the pressure is decreased, the mould is opened, the detail is removed, and the next cycle of the process starts again. Figure 1 shows a schematic structure of a typical injection moulding machine for plastic part manufacturing.
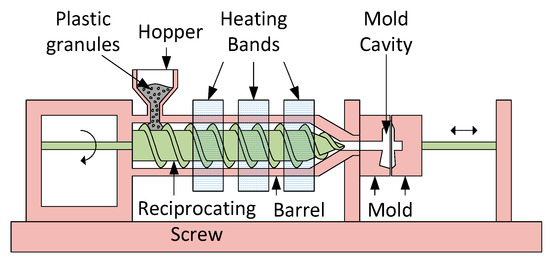
Figure 1.
Simplified schematic diagram of injection moulding machine.
There are many process parameters affecting on the microstructure, properties, and quality of the moulded parts, such as mould tolerance, pressure of molten plastic, and temperature in the melting zone. However, the temperature of the heating element is the most crucial parameter to ensure the required quality, efficiency, and productivity of the moulding process. Injection velocity, part cooling time, and cavity pressure significantly depend on the temperature in the melting zone [1,2]. Incorrect temperature of the molten plastic leads to deterioration of the overall product quality and obtaining the desired part properties. On the other hand, the dynamic properties of temperature control impact energy efficiency and moulding parts quality. If the temperature in the melting zone transients slowly to a desired value, then the productivity of the manufacturing process is decreased. In the case of fast temperature transient, a dynamic control could respond with an overshoot temperature instead of a sloping process to a steady-state condition value. Therefore, the control system has to ensure an appropriate controlling accuracy and speed of temperature setting. These parameters depend on the quality of controller tuning and heater parameter permanence [3,4]. Yao et al. [5] formulated the main requirements applied to the temperature controller design as (1) fast start-up of the system without overshot transient and (2) consistency of the temperature control under operational conduction.
The major issue of the temperature control algorithms for plastic injection moulding machines is that the melting zone heater properties, such as gain and time constants, are usually unknown to the controller. Obviously, parameters of a single heater could be easily identified and implemented into a controller structure. However, the heating elements can be replaced during the production cycle due to operational requirements or in the course of machine maintenance. In this case, the parameters of a new heater are undefined to the controller. This means that model-based control methods cannot provide sufficient accuracy of the control without additional tuning each time when the heating elements are changed [4,6]. In order to avoid additional controller tuning, a method of online parameter estimation could be involved, but this demands additional computational resources and increases execution time. It is important to note that the melting zone heater properties can vary over time in relation to the filling level of barrel, type of plastic, number of production cycles, etc. This uncertainty of heater properties also makes the model-based methods inefficient and requires the utilisation of a complex control system operating under sophisticated algorithms [3,4,7].
Apart from classical PID control, there are a variety of advanced control methods aimed to provide precise temperature management of the heaters with instable parameters. Precision temperature control can be obtained using advanced algorithms, such as an artificial neural network (ANN) [8,9,10], fuzzy-logic, or combined adaptive neuro fuzzy inference system (ANFIS) controller [11,12,13]. However, either classical or ANN-based controllers have to be tuned in the initial stage of operation.
This paper discusses the control method applied for a plastic injection moulding system based on the ANN approach. The principle of the proposed control consists of the combination of initial tuning and further behavioural performance of an ANN. According to this approach, the ANN-based controller has to be tuned off-line at the initial stage of the operation to provide the optimal control signal calculated for a set of heater parameters. Then, this trained controller uses its behavioral properties for normal operation in a system where parameters of the heating element could vary. Such an approach utilises the generalization ability of ANN. This method of control is implemented to ensure an efficient operation of the manufacturing system, providing a fast transient and minimum overshooting of the temperature in the melting zone. The closed-loop temperature control for the plastic moulding process is shown in Figure 2. It can be seen that the ANN controller is responsible for a fast temperature transient, while the integrator block holds it at the desired level under steady state condition.
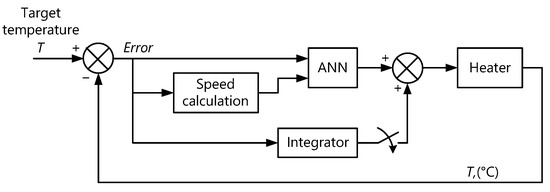
Figure 2.
Block diagram of a close-loop temperature control with an ANN (artificial neural network) controller.
The major issues of ANN controller design are the selection of an ANN structure which determines the computational complexity and generalisation efficiency; the appropriate training data set and algorithm; and reference system dynamics to be performed by the trained ANN controller. This paper proposes an approach to design an ANN-based temperature controller for a plastic moulding system to increase the performance of the manufacturing process due to a fast transient. The design approach focusing on the reference control algorithm is represented by a number of steps considered in Section 2 of the paper. Section 3 provides a discussion of the results of system simulation for various barrels and heaters in a Matlab/Simulink software environment and a comparison with experimental data.
2. ANN Controller Design
The initial design stage for the majority of control systems is the identification of the plant transfer function. For this purpose, three commonly used heater elements were investigated, tested, and analysed in [3]. The transfer functions (including the coefficients) have been identified using the practical test results. Therefore, the transfer functions for most common heaters are represented by the following equations—(1) nozzle heater, (2) bar heater, (3) cartridge heater:
These transfer functions represent the most typical plants, but their coefficients can vary due to manufacturing tolerance and operational conditions. However, the designed control system should provide an adequate transient for all of these objects and be not sensitive to their parameter change or variation. It is well-known that a digital control system can provide a fast transient without overshoot in a finite number of control steps equal to the order of the plant. The variable gain method was proposed in [14] to calculate the appropriate control steps, and as was shown in [15], this method is well suited for calculating the reference control steps for the ANN training procedure.
2.1. Reference Digital Controller Design
In order to design the digital controller, one of the three transfer function (1)–(3) should be selected for the calculation. The 2nd order transfer function with the fastest dynamics is preferred because the ANN controller must perform a transient without overshoot (or with minimum possible overshoot) for any of these plants. This is why the transfer function (3) was selected. To simplify the calculations, the transfer function should be rewritten as follows:
The transfer function (3) in terms of Equation (4) is represented as below:
The reference digital control system with the heater block diagram is shown in Figure 3. The approach to calculate the duration of the control steps for the system in Figure 3 was derived from the differential equations and transition states equations (excluding the controller), as follows:
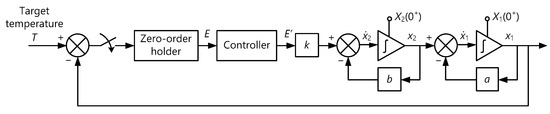
Figure 3.
Block diagram of the reference digital control system.
The set of the differential equation (6) was used to derive the state matrix A:
whereas the equations of transition states (7) were applied for development of matrix B:
The transposed extended state column vector of the system is:
The transposed vector of initial conditions is:
The state matrix of the system was used for the development of the transition matrix at the initial step of control, shown below:
where .
The modified equation representing the transition state can be applied in order to determine the state of the system at various times. However, the fact that the duration of the control steps is variable must be taken into account, according to [14]:
The transposed extended state column vector for the first, initial step of control operation can be derived from Equations (13) and (14), taking into account Equations (9), (11), and (12):
where m1 is controller output (could be described as an error at the beginning of the first control step multiplied by controller gain).
The transition matrix given below was developed for the second step of control:
where .
The extended state column vector for the second step of control process can be derived from Equations (13) and (14), taking into account Equations (16) and (17):
where m2 is controller output (could be described as an error at the beginning of the second control step multiplied by controller gain).
Since the selected transfer function was represented by the second order equation, the finite duration of control process could be realised within two control steps. In order to obtain the finite duration of the system transient process the conditions given below must be met:
Hence, a final set of equations was obtained using Equations (19) and (20):
In order to provide the fast transient, the amplitude of the first control step m1 should be equal to 1 (1 means 100% of power applied to the load). Consequently, the speed of the temperature rise at the end of the first control step will reach the maximum. The second control step should perform a stabilisation of the temperature on the given level so the inertness of the heating system could be used for this purpose. The value of m2 should be equal to 0 in this case (0 means no power applied to the load). However, a certain amount of power must be applied to the load after the end of the second control step to support the temperature at the desired level. The value of the further control steps can be calculated using the following formula:
where n = 3, 4, ….
If the parameters of control actions m1 and m2 are known, then Equation (21) has two unknown variables—h1, h2. The resolution of Equation (21) for various temperatures T(0) determines the duration of the control steps h1, h2 and, therefore, ensures the implementation of a digital controller operating under time-pulse modulation. Unfortunately, this system has no analytical solution and requires the application of a numerical method to obtain the control step durations. Figure 4 illustrates the transient of the system with the plant described by Equation (5) and control steps calculated using Equations (21) and (22).
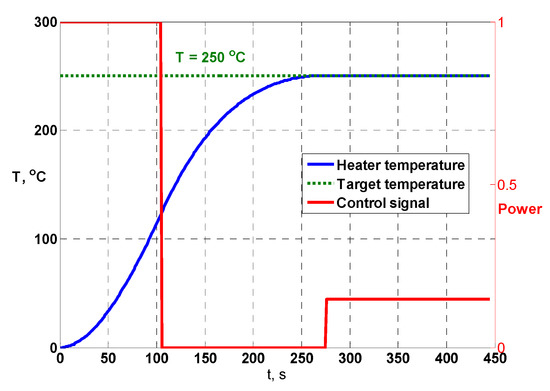
Figure 4.
Reference controller transient.
However, the uncertainty of heater parameters and complex calculations are major issues for the implementation of this algorithm for embedded application where computational resources are limited. On the other hand, this algorithm can be used for ANN controller offline training purposes.
2.2. ANN Structure and Training
ANNs simulate the behavior of biological neurons and are based on a set of artificial neurons connected to each other. The neurons in a typical ANN have fixed activation functions, however their weights can be varied. There are three main topology groups of ANN: full-mesh, weakly connected networks, and multilayer network. [16,17] recognised that the best topology for automatic control systems is a multilayer network. Other types of networks, such as radial basis function networks (RBF) and recurrent networks, are also used in control system applications, however, these networks have some disadvantages. For example, [17,18] stated that RBF networks usually have a larger quantity of neurons than feed forward networks (FFN) for the same application. Regarding the recurrent networks, [17,19] noted that the implementation of these networks in control loops requires significant computational resources due to the network dynamic properties with highly nonlinear parameters.
The multilayer FFN trained offline was selected for controller design due to its strong function approximation capability and relatively low computational complexity. As described in [17], if the FFN has two hidden layers, the approximation process can be built up easier than for a system with one hidden layer. Therefore, the structure of the proposed FNN shown in Figure 5 utilises two hidden layers. The temperature error and the speed of temperature error are the inputs of the ANN to represent the control system dynamics. The exact number of neurons in each hidden layer depends on a variety of factors, such as the number of inputs, size of training set, a character of approximated control signal. The actual number of neurons in hidden layers were chosen as the result of previous experience obtained from the modelling and simulation of various FFN structures. The proposed network consists of six neurons in the first hidden layer and three neurons in the second hidden layer. It can be seen that the activation function of the neurons in the hidden layers is a hyperbolic tangent function which provides a good learning efficiency [16]. The output layer consists of a single neuron with a linear activation function. This layer generates the output signal, which varies between 0 (no power applied to the heater) and 1 (full power applied to the heater).
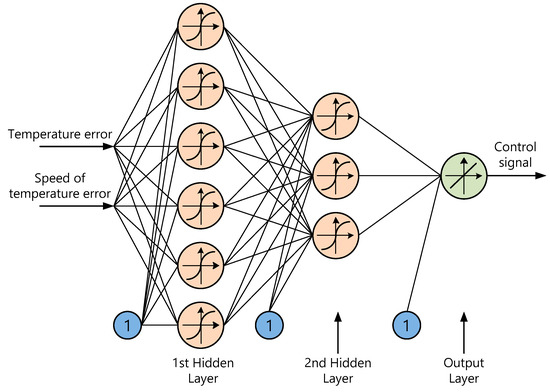
Figure 5.
ANN controller structure.
The ANN must be trained offline at the initial stage of operation in the temperature control system. In order to ensure this procedure, the training set of data should be prepared in advance. It is expected that the dataset for training is regularly distributed across the entire range of possible input values to ensure the best approximation capability of the network. Hence, the algorithm used to organise a regular data set is listed below:
- Firstly, the maximum and minimum values of temperature should be selected;
- Then, the duration of both control steps is calculated using Equation (21) for the maximum given temperature;
- The plant response is calculated using transfer Equation (5) for each sampling period of the system. The error is calculated as a difference between the given and current temperatures. The speed of the error varying is calculated as a difference between the current and previous errors (the distance between error values used for speed calculation could be bigger than one sampling period, it depends on the sampling rate and plant dynamic properties);
- The values of errors and speed are stored in two-dimensional input array. The values of control signal, which are “1” for the first control step and “0” for the second, are stored in the output array;
- The target temperature is decremented in the given amount of degrees and process repeats from stage 2 of this algorithm, but on stage 4 the data is placed at the end of the input and output arrays;
- The algorithm stops when the minimum temperature chosen at the first stage is achieved.
When the dataset was ready, the ANN was trained using the Levenberg–Marquardt algorithm. This algorithm is considered one of the most efficient back propagation algorithms based on conjugate gradient method [20,21]. As a result, the ANN controller ready to use was obtained; its control surface is shown in Figure 6. The ANN training dataset was collected with a sampling period equal to 1.3 s and the gap of five samples was used for the speed of the error varying calculation.
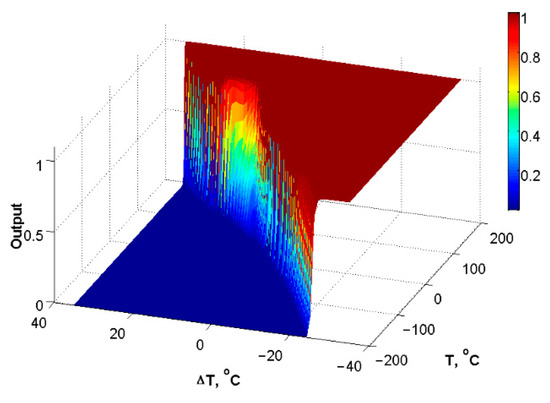
Figure 6.
Trained ANN control surface.
The dominant signal values of the ANN controller were 0 and 1, similar to the reference controller. Nevertheless, the transition between 0 and 1 was not so sharp, especially in the region of low errors and low error speed. The reason for such behaviour is the smooth activation functions, which ANN uses to approximate the reference controller dynamics. However, this issue had no crucial influence on the process in general and could be improved by using a scale gain for the error and its speed.
3. Matlab Simulation and Experimental Validation
3.1. Matlab Simulation
To evaluate the dynamics of the ANN-based temperature control system, the Simulink model shown in Figure 7 was designed. The complete transient process was virtually divided into two regions: “far region” and “near region”. The “far region” was the area where the new target temperature was established. This region was characterised by a constantly decreasing high error and by an error speed which was increasing from zero to maximum and consequently smoothly decreasing. The “near region” was the area where the temperature was close to steady state value; it was characterised by low errors and low error speed. Therefore, at the beginning of process, “Switch1” and “Switch2” were in the bottom position and the feedback signals passed through the “Error Gain” block and “Speed Gain” block to the ANN controller. “Switch3” held the integrator output disconnected from the plant input. Hence, the ANN controller performed the control assignment by itself.
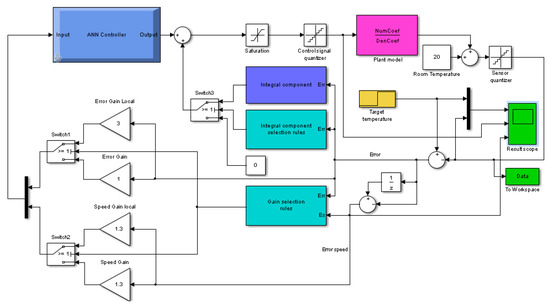
Figure 7.
Matlab-model for the parameter identification of the heater system transfer function.
When the temperature was close to target value and the speed of the error variance was close to zero, block Gain selection rules switched the error and the error speed signal gains. Block Integral component selection rules turned on the integrator output. Now, the integrator supplied a signal proportional to the power to hold the temperature on a desired level. The ANN controller’s role was to withstand the disturbances and to support the integral component if it did not have an appropriate value at the end of the “far region” of transient. The simulation of system behaviour was held for the heaters with transfer functions (1): Nozzle, (2): Bar, (3): Cartridge.
In addition, the same simulation was performed for the temperature control system with a PID regulator tuned for each heater separately. In addition, the simulation was made for the PID regulator with autotuning, which is currently used in industrial equipment. The results of these simulations are shown in Figure 8. The general parameters of transient responses are presented in Table 1 and Table 2, where (I)—PID with autotuning, (II)—PID with prior tuning, (III)—ANN with integrator.
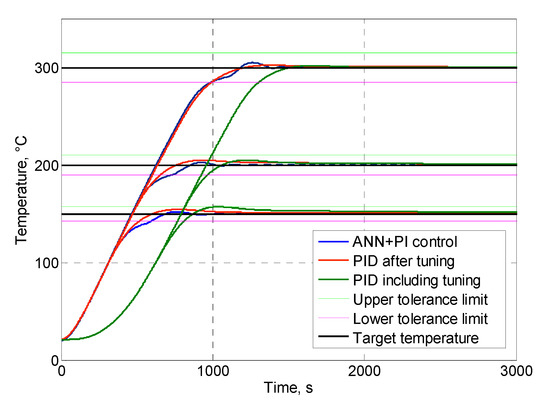
Figure 8.
Bar heating.

Table 1.
Rise time for different controllers, [s].

Table 2.
Overshoot for different controllers, [%].
The results of simulation show that PID with autotuning was the slowest algorithm among these three, because of the time used for parameter tuning at the beginning of transient (Figure 8, Figure 9 and Figure 10). PID with prior tuning showed a slightly faster transient (for 60–90 s) than ANN with integrator, but usually had higher overshoot (Table 1 and Table 2). However, the major drawback of PID with prior tuning is the requirement of individual tuning for each heater before use, which is impractical and inefficient in industrial equipment for injection moulding.
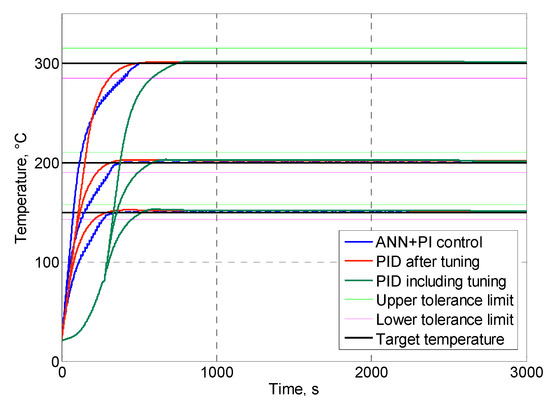
Figure 9.
Nozzle heating.
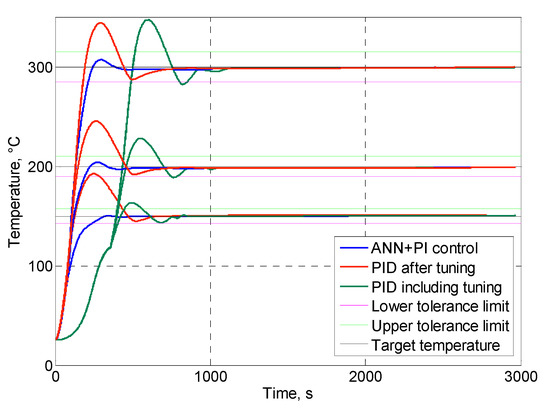
Figure 10.
Cartridge heater heating.
3.2. Experimental Validation
To verify the dynamics of the proposed controller the experimental setup was designed (Figure 11). The control algorithm was realised using a PC as a program with graphical user interface (GUI) in Matlab environment (Figure 12). This program communicated with the STM32F4DISCOVERY board via USB interface to set the PWM duty cycle and to collect the temperature data. POWER BOARD fed the CARTRIDGE heater with a desired amount of power from the AC main. THERMOCOUPLE BOARD converted the signal proportional to the temperature in a digital form and sent it via SPI to the STM32F4DISCOVERY board.
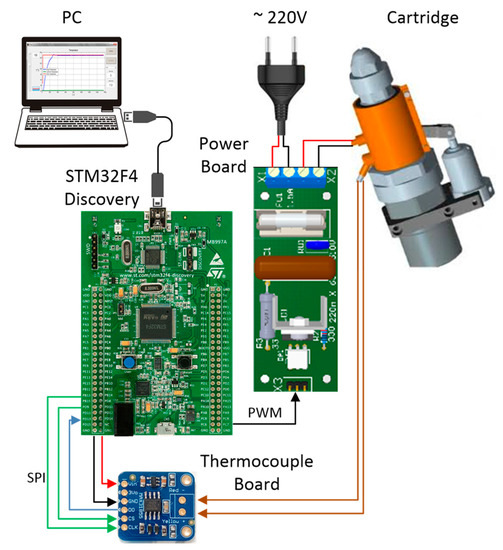
Figure 11.
Cartridge heater controller.
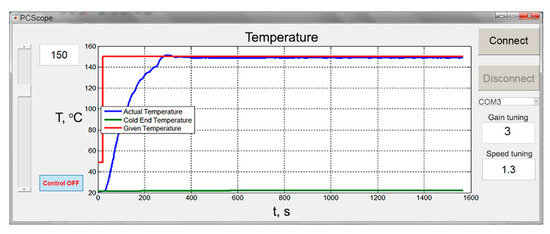
Figure 12.
GUI (graphical user interface) of the control program in Matlab.
The GUI of the control program provided an opportunity to set the desired temperature value (slider and text field in the left side of the GUI). It also provided real time monitoring of the dynamics of the heater temperature change (plot in the centre of the GUI) and observation of the values of current error and speed gains (text fields in the right corner of the GUI), including adjusting values “on the fly”.
The experimental data of the transient process for the cartridge heater with transfer function (1) are shown in Figure 13, alongside simulation results for the same object. The diagram shows nearly the same results for the experiment and simulation. The major differences between these two curves could be found in the steady state region. The experimental transient had a steady state error different from zero because of disturbances, such as an air flow that increased the speed of cooling down in the real system in contrast to the Simulink model. In addition, a steady state error shows the weakness of integral gain that could not be increased without increasing the overshoot. Hence, the solution of this issue is a subject for future research.
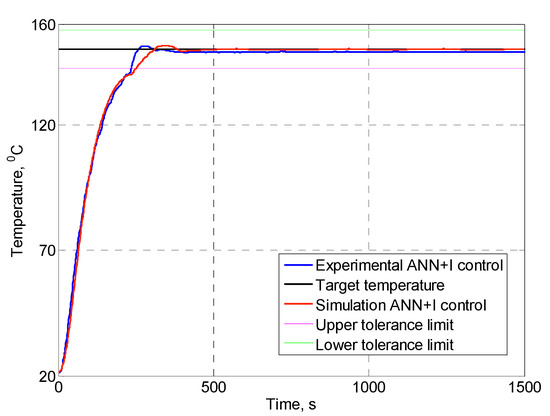
Figure 13.
Experimental data and simulation result.
4. Conclusions
This paper discussed a method of temperature controller design for a plastic injection moulding system utilising a multilayer FFN trained offline to approximate the dynamic properties of a regulator optimised by speed and overshoot.
It was proposed to divide the entire temperature transient process into two regions and apply different control structures for these regions. This approach was derived from the fact that the system should satisfy different requirements at the beginning of transient process and at the end. The main scope of this work was focused on the first region of the transient process, where the main issue is the fast set-point tracking with minimum overshoot. However, the second region, where precision and stability are the major demands, should be the subject of the future investigation.
The simulation results of the proposed design and its comparison to the PID regulator currently used in the industry have been shown. This simulation demonstrated the advantages of the proposed method, such as less overshoot and fast transient (in comparison to PID with autotuning).
Author Contributions
Conceptualization, O.V. and M.K.; methodology, O.V., M.K. and R.C.; validation, O.V., M.K. and Y.V.; writing—original draft preparation, O.V. and Y.V.; writing—review and editing, Y.V.; supervision, R.C.; project administration, R.C.
Funding
This research was supported by German Central Innovation Program for SMEs (Zentrales Innovationsprogramm Mittelstand) from Federal Ministry for Economic Affairs and Energy (Bundesministeriums für Wirtschaft und Energie), project No ZF4190302DB6.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Diduch, C.; Dubay, R.; Li, W.G. Temperature control of injection molding. Part I: Modeling and identification. Polym. Eng. Sci. 2004, 44, 2308–2317. [Google Scholar] [CrossRef]
- Spina, R.; Spekowius, M.; Dahlmann, R.; Hopmann, C. Analysis of polymer crystallization and residual stresses in injection molded parts. Int. J. Precis. Eng. Manuf. 2014, 15, 89–96. [Google Scholar] [CrossRef]
- Khomenko, M.; Velihorskyi, O.; Chakirov, R.; Vagapov, Y. Parameters identification of injection plastic moulding heaters. In Proceedings of the 2016 IEEE 36th International Conference on Electronics and Nanotechnology (ELNANO), Kiev, Ukraine, 16 June 2016; pp. 1–6. [Google Scholar]
- Chen, Z.; Turng, L.-S. A review of current developments in process and quality control for injection molding. Adv. Polym. Technol. 2005, 24, 165–182. [Google Scholar] [CrossRef]
- Yao, K.; Gao, F.; Allgower, F. Barrel temperature control during operation transition in injection molding. Control Eng. Pract. 2008, 16, 1259–1264. [Google Scholar] [CrossRef]
- Dubay, R.; Hu, B.; Hernandez, J.M.; Charest, M. Controlling process parameters during plastication in plastic injection molding using model predictive control. Adv. Polym. Technol. 2014, 33. [Google Scholar] [CrossRef]
- Park, H.S.; Phuong, D.X.; Kumar, S. AI based injection molding process for consistent product quality. Procedia Manuf. 2019, 28, 102–106. [Google Scholar] [CrossRef]
- Munoz-Barron, B.; Morales-Velazquez, L.; Romero-Troncoso, R.J.; Rodriguez-Donate, C.; Trejo-Hernandez, M.; Benitez-Rangel, J.P.; Osornio-Ri, R.A. FPGA-based multiprocessor system for injection molding control. Sensors 2012, 12, 14068–14083. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Lai, W. Control system software design of injection molding machine based on neural network. In Proceedings of the 2011 Second International Conference on Mechanic Automation and Control Engineering, Hohhot, China, 18 August 2011; pp. 1119–1122. [Google Scholar]
- Lu, C.H.; Tsai, C.C.; Liu, C.M.; Charng, Y.H. Predictive control based on recurrent neural network and application to plastic injection molding processes. In Proceedings of the IECON 2007—33rd Annual Conference of the IEEE Industrial Electronics Society, Taipei, Taiwan, 5–8 November 2007; pp. 792–797. [Google Scholar]
- Selvakarthi, D.; Prasad, S.J.S.; Meenakumari, R.; Balakrishnan, P.A. Optimized temperature controller for plastic injection molding system. In Proceedings of the 2014 International Conference on Green Computing Communication and Electrical Engineering (ICGCCEE), Coimbatore, India, 6–8 March 2014; pp. 1–5. [Google Scholar]
- Tian, D.Z. Main steam temperature control based on GA-BP optimised fuzzy neural network. Int. J. Eng. Syst. Model. Simul. 2017, 9, 150–160. [Google Scholar]
- Ravi, S.; Balakrishnan, P.A. Modelling and control of an anfis temperature controller for plastic extrusion process. In Proceedings of the 2010 International Conference on Communication Control and Computing Technologies, Ramanathapuram, India, 7–9 October 2010; pp. 314–320. [Google Scholar]
- Tou, J.T. Modern Control Theory; McGraw-Hill: New York, NY, USA, 1964. [Google Scholar]
- Khomenko, M.; Voytenko, V.; Vagapov, Y. Neural network-based optimal control of a dc motor positioning system. Int. J. Autom. Control 2013, 7, 83–104. [Google Scholar] [CrossRef]
- Cirstea, M.N.; Dinu, A.; Khor, J.G.; McCormick, M. Neural and Fuzzy Logic Control of Drives and Power Systems; Elsevier Ltd.: Newnes, Australia, 2002. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Syafaruddin, S.; Hiyama, T.; Karatepe, E. Investigation of ANN performance for tracking the optimum points of PV module under partially shaded conditions. In Proceedings of the 9th International Power and Energy Conference, Singapore, 27–29 October 2010; pp. 1186–1191. [Google Scholar]
- Prokhorov, D.V. Training recurrent neurocontrollers for real-time applications. Ieee Trans. Neural Netw. 2007, 18, 1003–1015. [Google Scholar] [CrossRef] [PubMed]
- Veligorskyi, O.; Chakirov, R.; Khomenko, M.; Vagapov, Y. Artificial neural network motor control for full-electric injection moulding machine. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT), Melbourne, Australia, 13–15 February 2019; pp. 1–5. [Google Scholar]
- Rios-Gutierrez, F.; Makableh, Y.F. Efficient position control of dc servomotor using backpropagation neural network. In Proceedings of the 7th International Conference on Natural Computation, Shanghai, China, 26–28 July 2011; pp. 653–657. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).