Control of MMC-Based STATCOM as an Effective Interface between Energy Sources and the Power Grid
Abstract
1. Introduction
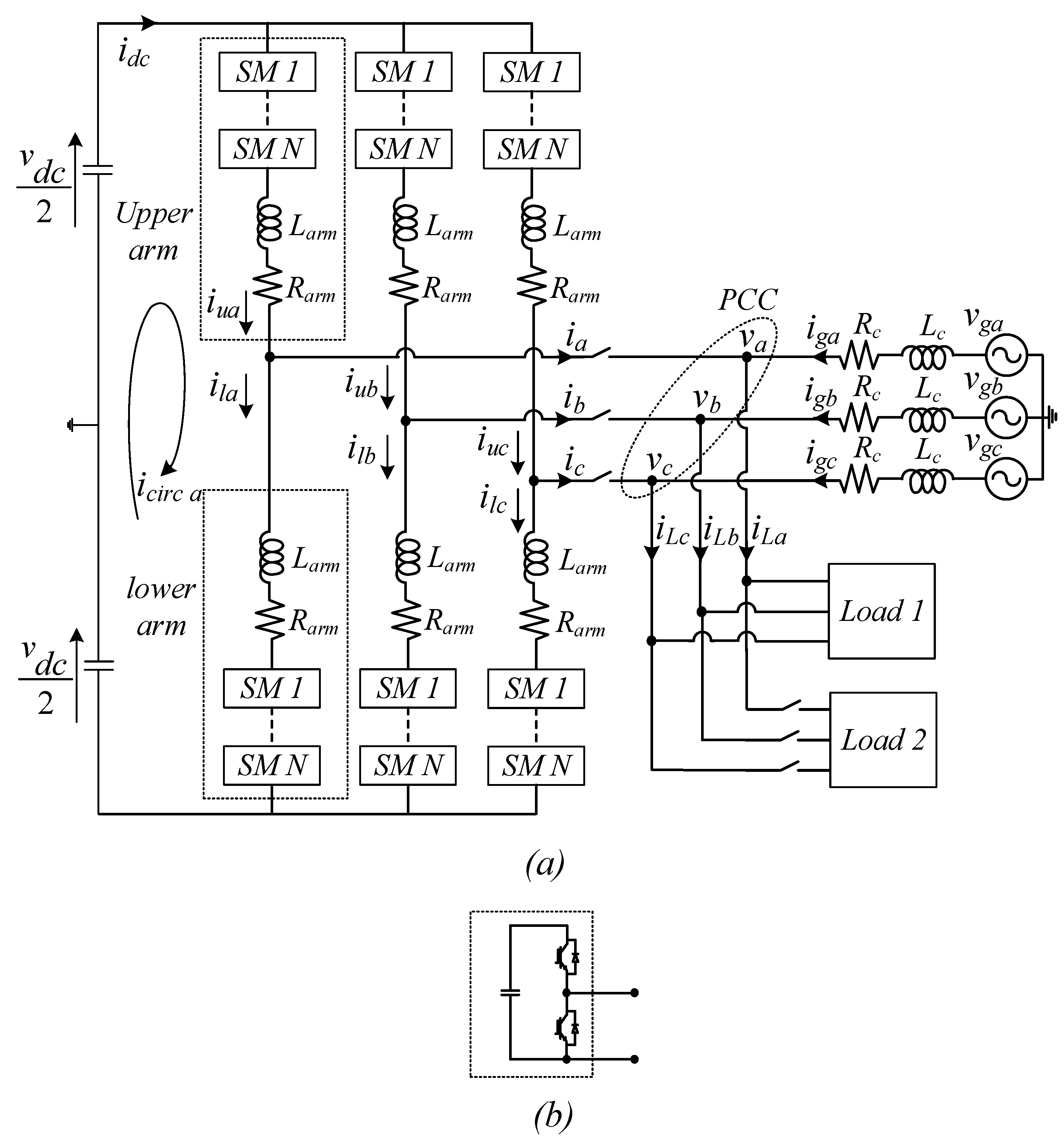
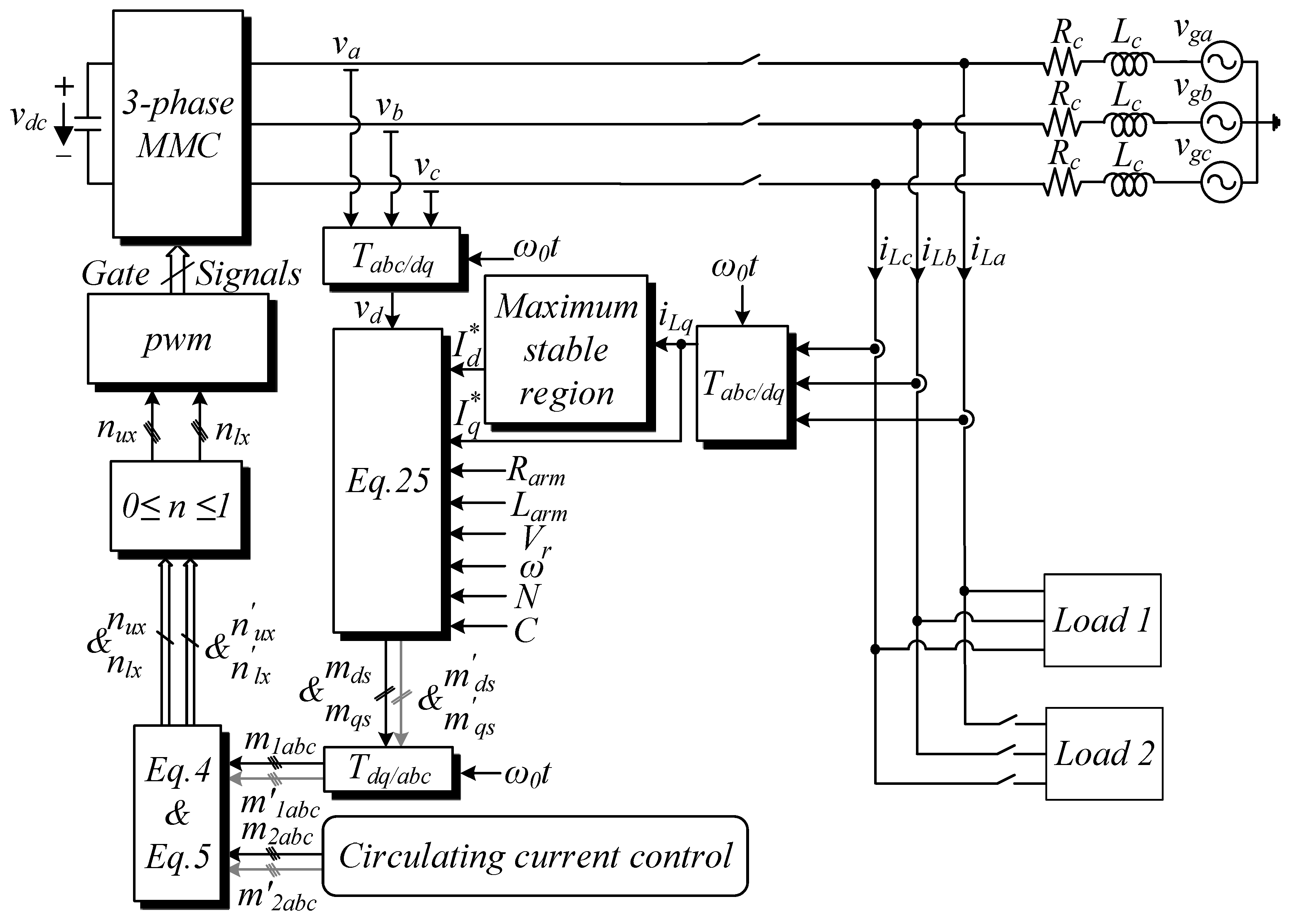
2. General Configuration and Dynamic Analysis of the Proposed Model
3. Steady-State Operation Analysis and Controller Design
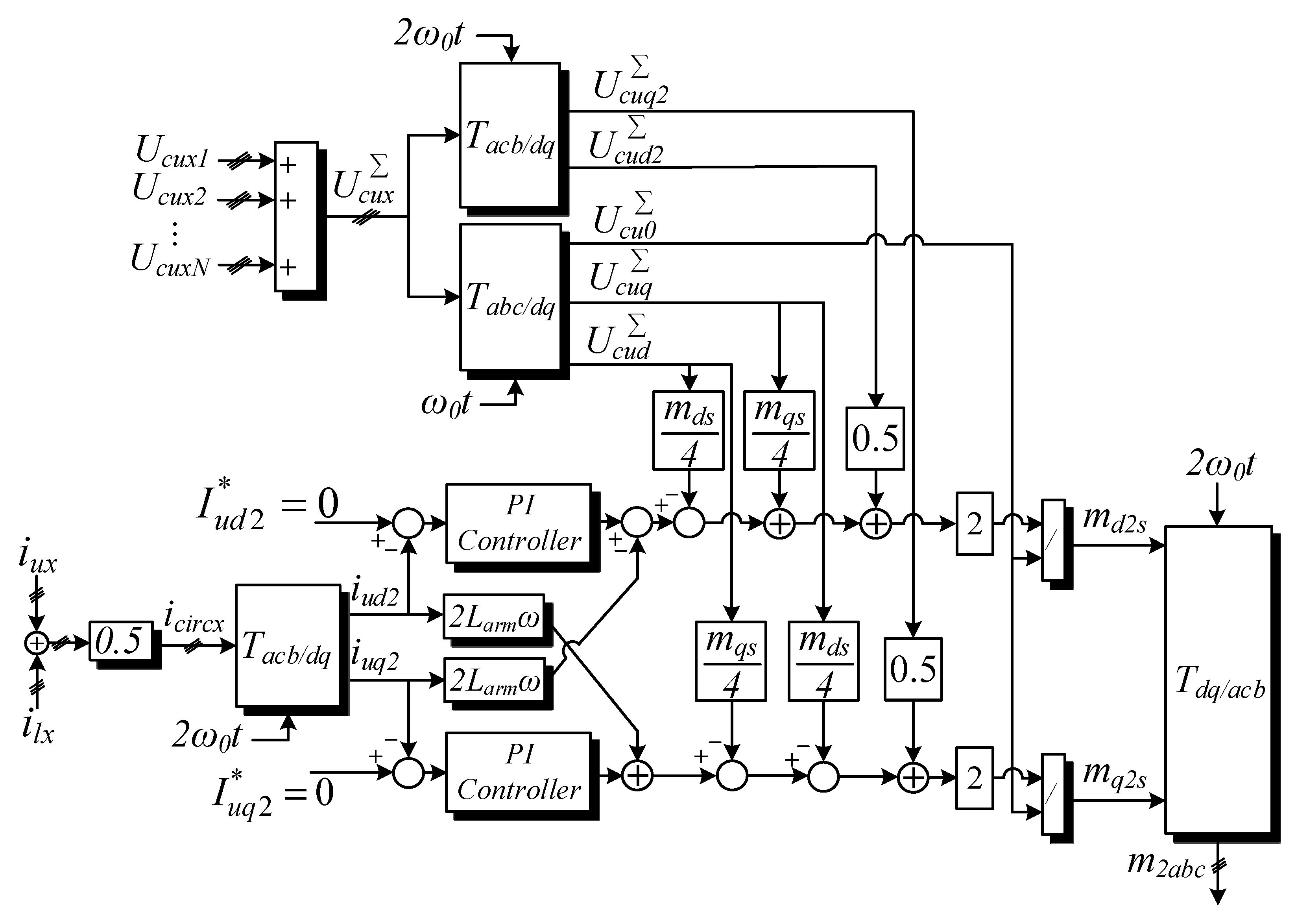
3.1. Circulating Current Control
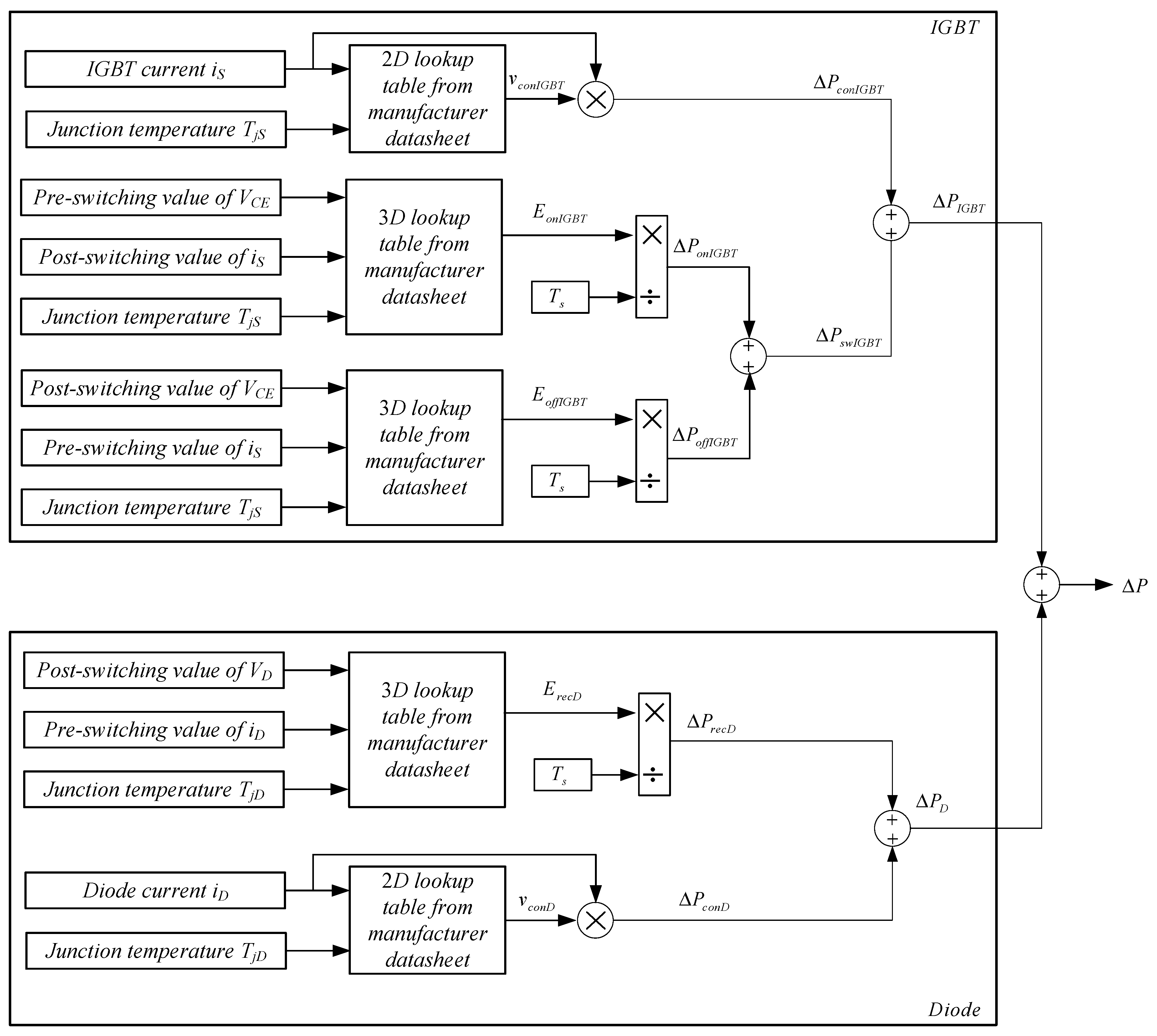
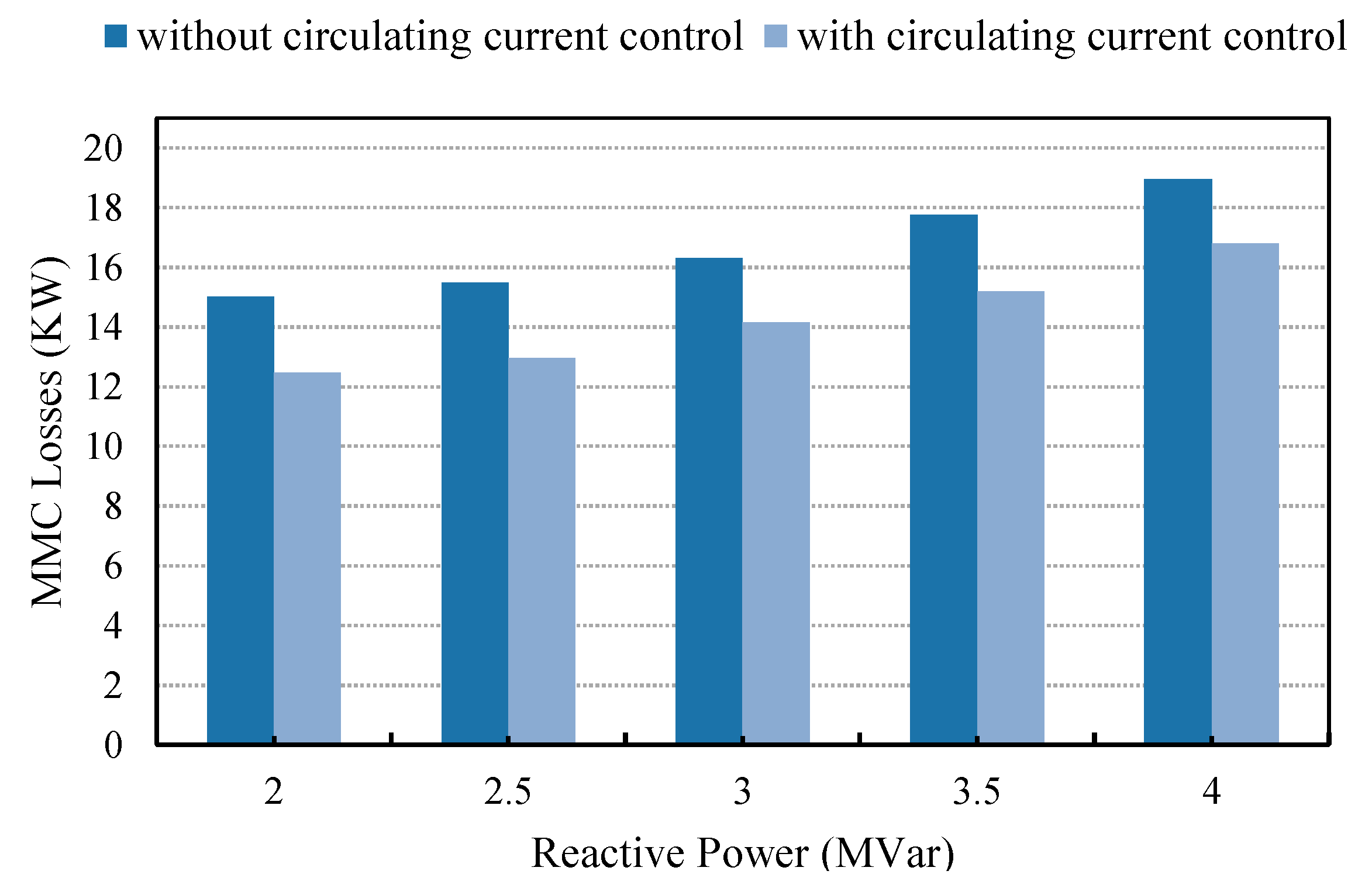
3.2. MMC Loss Evaluations
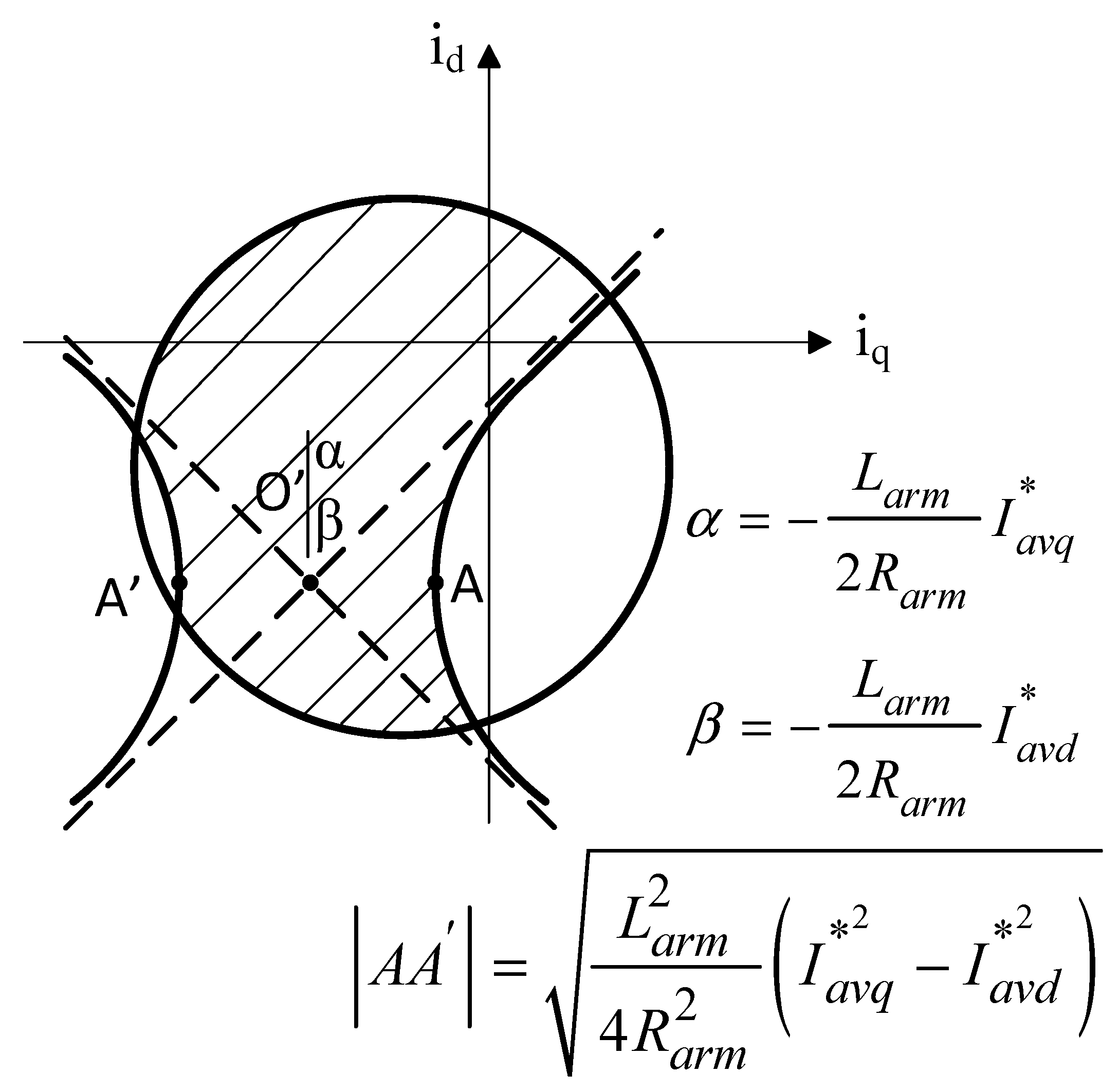
3.3. Maximum Stable Operation Range
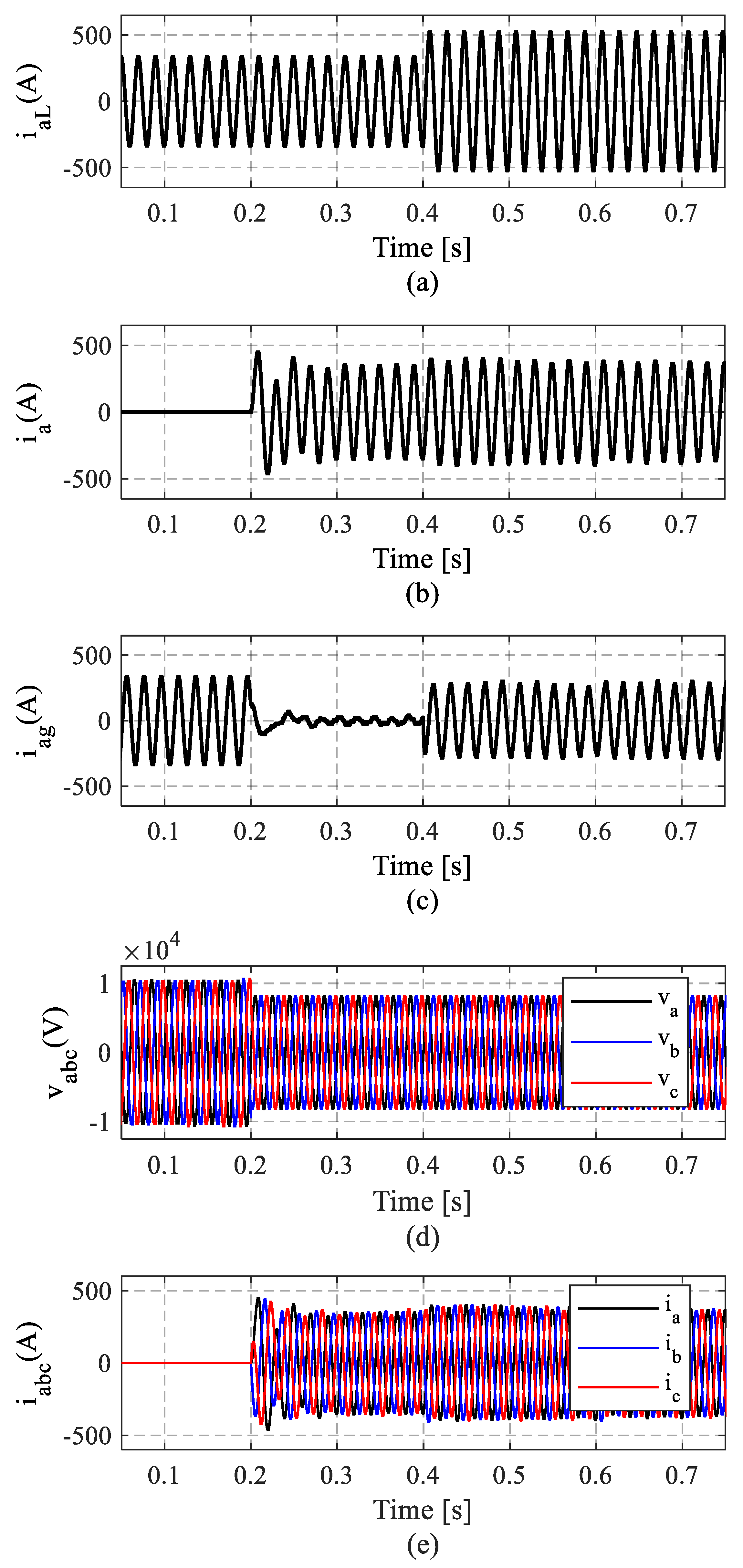
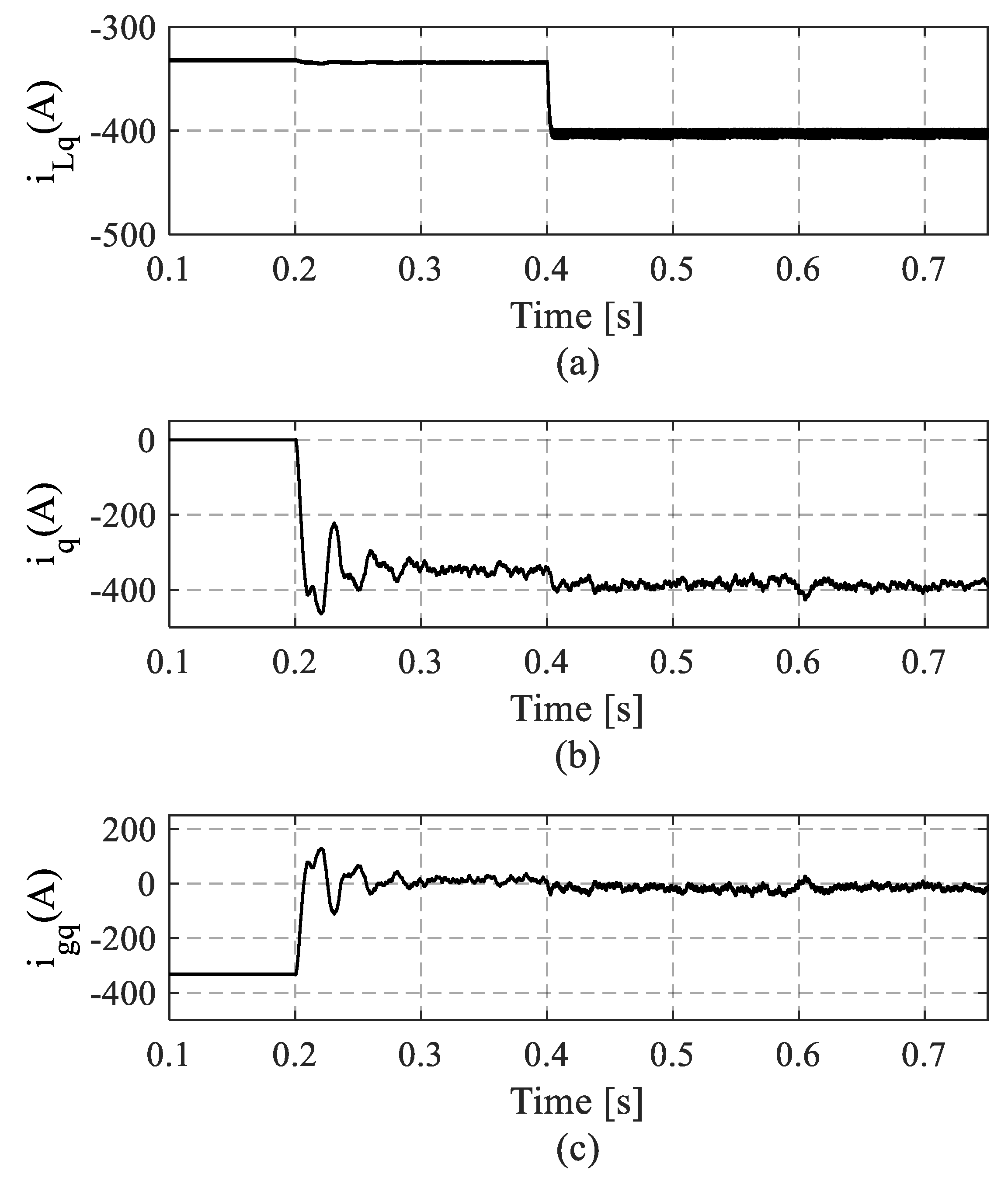
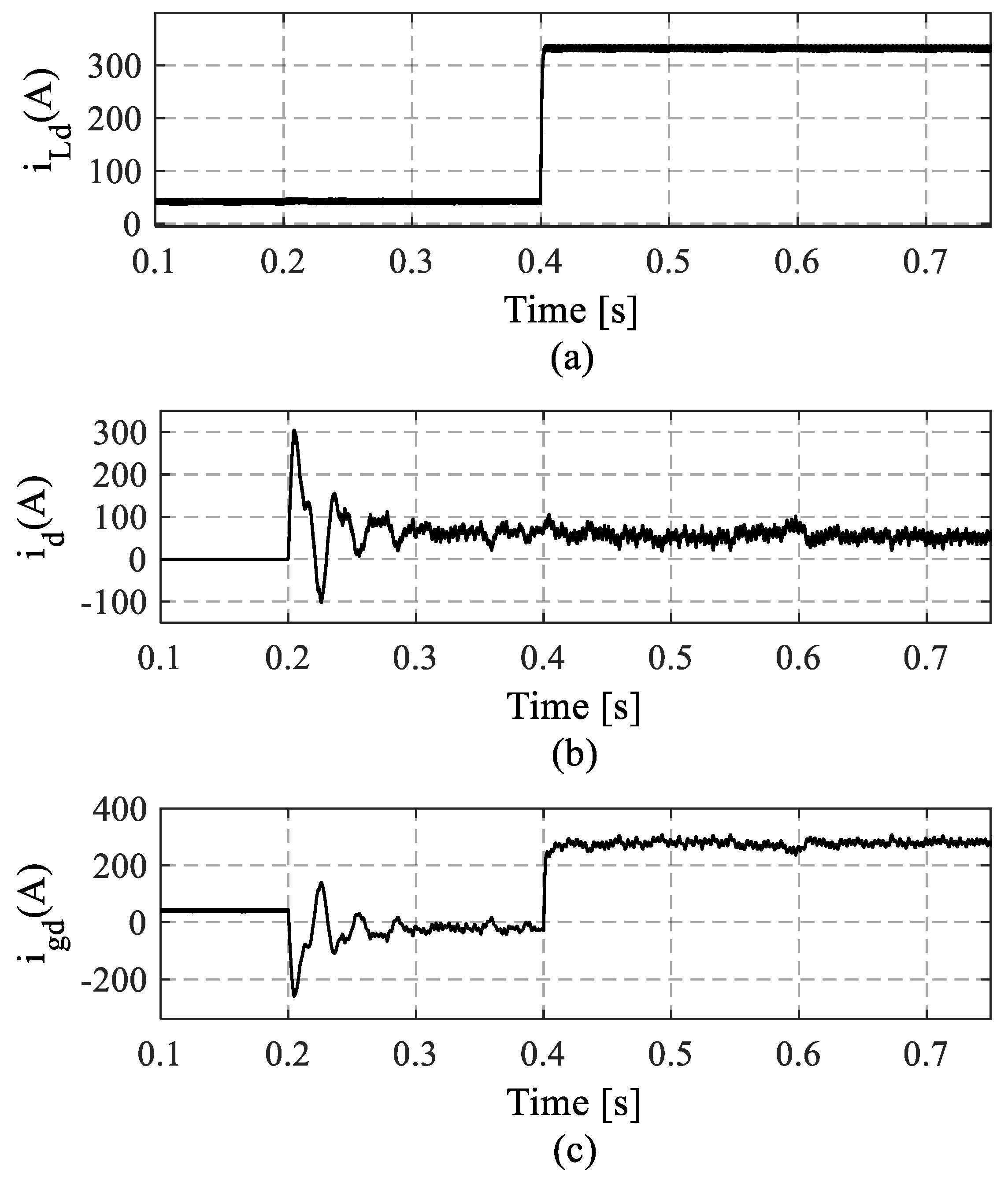
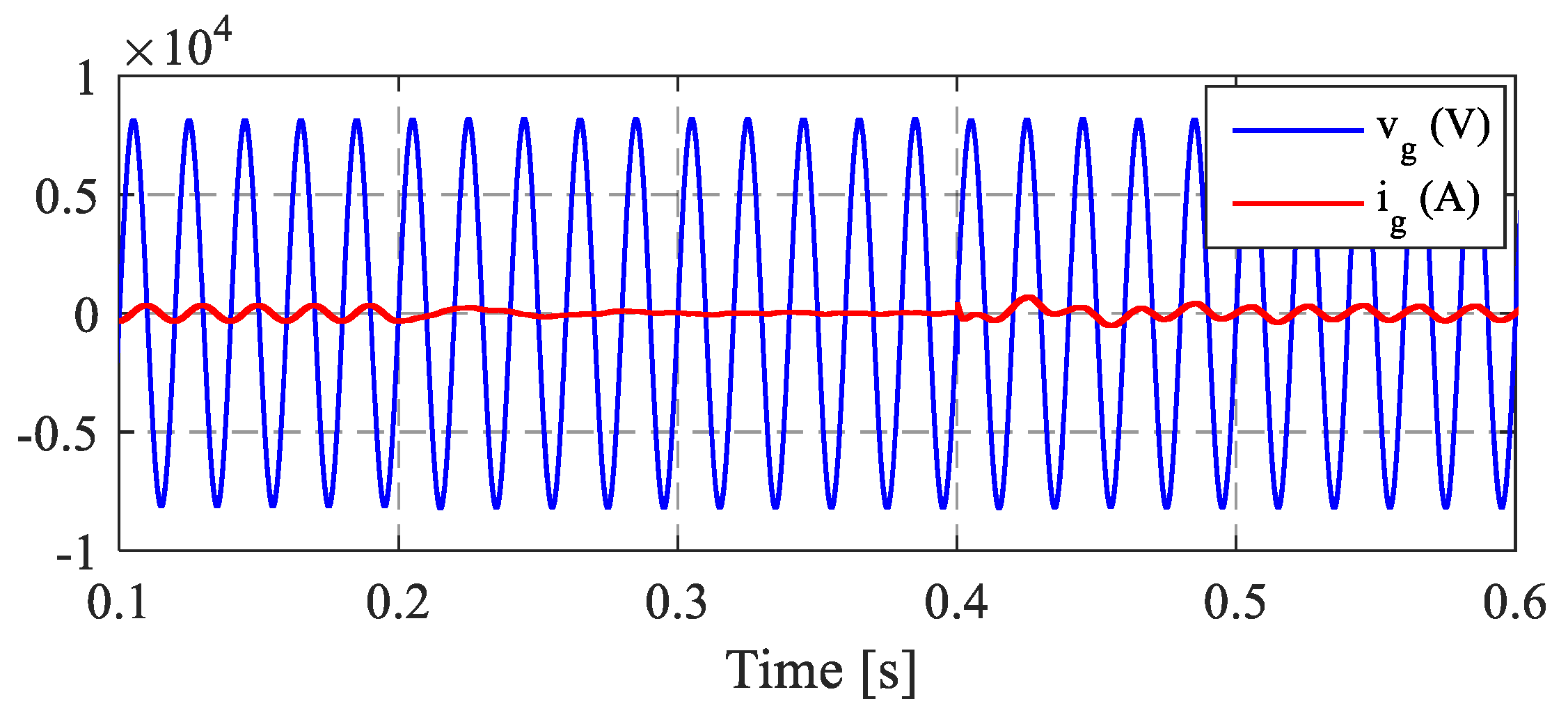
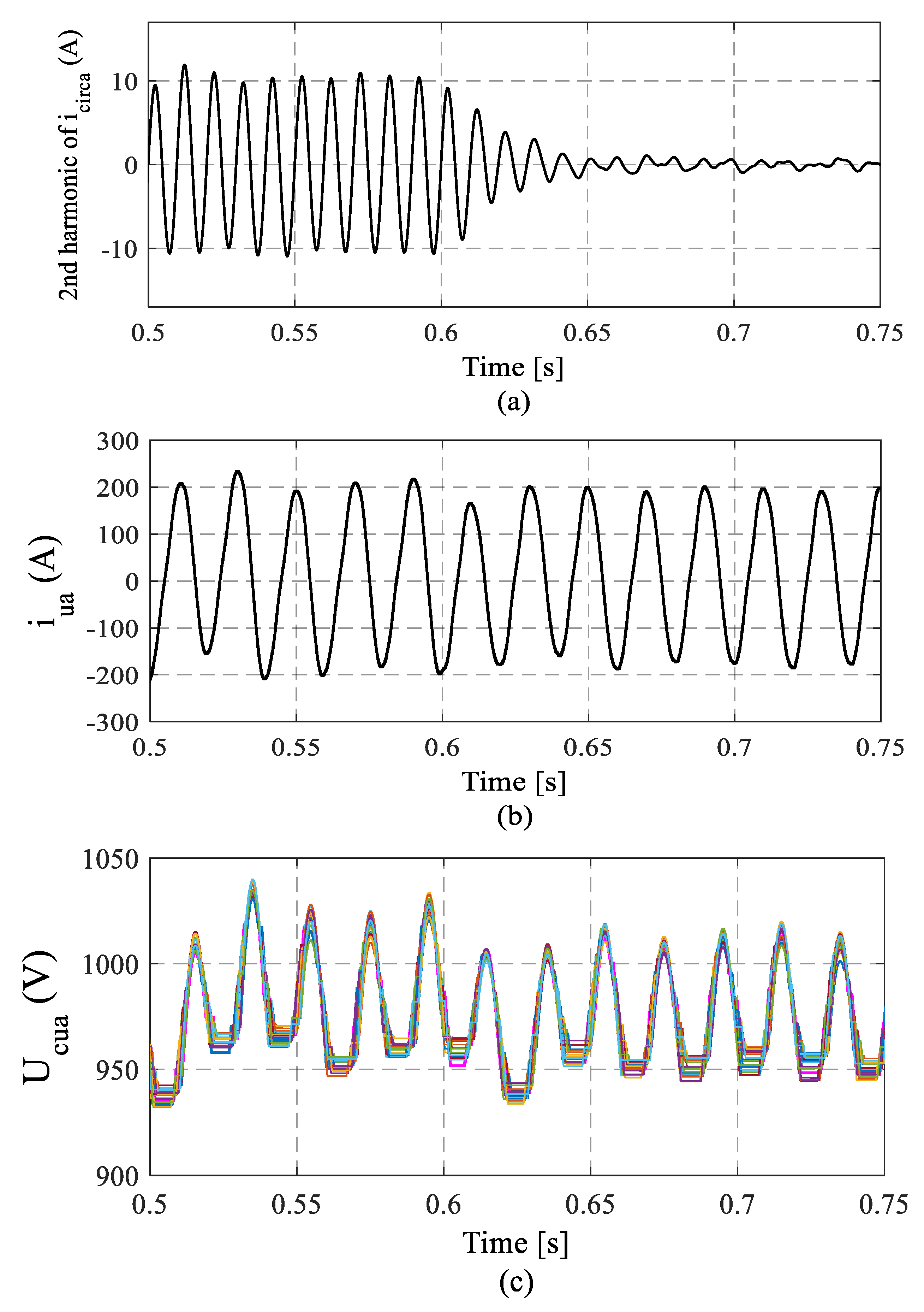
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Indices | |
| x | a, b, c |
| u, l | upper and lower arm |
| Variables | |
| , | upper and lower arm currents in abc frame |
| circulating current in abc frame | |
| converter output current in abc frame | |
| load current in abc frame | |
| , | upper and lower arm desired voltages in abc frame |
| , | upper and lower arm modulation indices in abc frame |
| , | upper and lower arm sum capacitor voltages in abc frame |
| fundamental frequency component of modulation indices in abc frame | |
| second harmonic component of modulation indices in dq0 frame | |
| , | fundamental frequency component of modulation indices in dq0 frame |
| , | second harmonic component of modulation indices in dq0 frame |
| , | DC components of upper and lower arm sum capacitor voltages in abc frame |
| , | fundamental frequency components of upper and lower arm sum capacitor voltages in abc frame |
| , | second harmonic components of upper and lower arm sum capacitor voltages in abc frame |
| ω | angular frequency |
| ω0 | reference angular frequency |
| t | time |
| , | phase angle of the fundamental frequency components of upper and lower arm sum capacitor voltages in abc frame |
| , | phase angle of the second harmonic frequency components of upper and lower arm sum capacitor voltages in abc frame |
| , | zero component of upper and lower arm sum capacitor voltages in dq0 frame |
| , | fundamental frequency components of upper arm sum capacitor voltage in dq0 frame |
| , | fundamental frequency components of lower arm sum capacitor voltage in dq0 frame |
| , | second harmonic frequency components of upper arm sum capacitor voltage in dq0 frame |
| , | second harmonic frequency components of lower arm sum capacitor voltage in dq0 frame |
| total energy stored in SM capacitors of each upper and lower arm | |
| zero component of upper arm current in dq0 frame | |
| , | fundamental frequency components of upper arm current in dq0 frame |
| , | second harmonic components of upper arm current in dq0 frame |
| DC-link voltage | |
| reference value of DC-link voltage | |
| DC-link current | |
| MMC output voltage at PCC in abc frame | |
| phase voltage of the grid in abc frame | |
| , | fundamental frequency components of MMC output voltage at PCC in dq0 frame |
| , | fundamental frequency components of grid voltage at PCC in dq0 frame |
| , | fundamental frequency components of MMC output current in dq0 frame |
| , | fundamental frequency components of grid current in dq0 frame |
| , | fundamental frequency components of load current in dq0 frame |
| , | fundamental frequency components of average MMC output current in dq0 frame |
| , | fundamental frequency components of average load current in dq0 frame |
| , | steady-state fundamental frequency components of modulation indices in dq0 frame |
| , | steady-state second harmonic frequency components of modulation indices in dq0 frame |
| , | reference values of average upper arm currents in dq0 frame |
| , | reference values of average MMC output currents in dq0 frame |
| , | reference values of instantaneous upper arm currents in dq0 frame |
| , | reference values of MMC output currents in dq0 frame |
| reference value of upper arm zero component current in dq0 frame | |
| , | reference value of MMC output voltages in dq0 frame |
| total losses in each IGBT/diode switch | |
| conduction loss for IGBT/diode | |
| voltage across IGBT/diode during conduction | |
| current passing through IGBT/diode during conduction | |
| total losses of IGBT | |
| switching losses in IGBTs | |
| turn-on switching losses of IGBTs | |
| turn-off switching losses of IGBTs | |
| turn-on energy losses of IGBTs | |
| turn-off energy losses of IGBTs | |
| turn-on commutation time | |
| turn-off commutation time | |
| voltage across IGBT | |
| voltage across diode | |
| junction temperature in IGBT and diode | |
| simulation time step | |
| total diode losses | |
| reverse recovery loss of diode | |
| reverse recovery energy loss of diode | |
| reverse recovery time of diode | |
| Parameters | |
| C | SM capacitance |
| N | total number of SMs per arm |
| Rarm | arm equivalent resistance |
| Larm | arm inductance |
| Rc | ac system resistance |
| Lc | ac system inductance |
| Abbreviation | |
| MMC | modular multilevel converter |
| STATCOM | static synchronous compensator |
| DG | distributed generation |
| HVDC | high voltage direct current |
| THD | total harmonic distortion |
| PF | power factor |
| FACTS | flexible AC transmission system |
| PI | proportional integral |
| SM | sub-modules |
| PCC | point of common coupling |
| KVL | Kirchhoff’s voltage law |
| IGBT | insulated gate bipolar transistor |
References
- Ochoa, L.F.; Harrison, G.P. Minimizing energy losses: Optimal accommodation and smart operation of renewable distributed generation. IEEE Trans. Power Syst. 2010, 26, 198–205. [Google Scholar] [CrossRef]
- Shaaban, M.F.; Atwa, Y.M.; El-Saadany, E.F. DG allocation for benefit maximization in distribution networks. IEEE Trans. Power Syst. 2012, 28, 639–649. [Google Scholar] [CrossRef]
- Debnath, S.; Qin, J.; Bahrani, B.; Saeedifard, M.; Barbosa, P. Operation, control, and applications of the modular multilevel converter: A review. IEEE Trans. Power Electron. 2014, 30, 37–53. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Otero-De-Leon, R.; Mohan, N. Review of modular multilevel converters for teaching a graduate-level course of power electronics in power systems. In Proceedings of the 2013 North American Power Symposium (NAPS), Manhattan, KS, USA, 22–24 September 2013; pp. 1–6. [Google Scholar]
- Nami, A.; Liang, J.; Dijkhuizen, F.; Demetriades, G.D. Modular multilevel converters for HVDC applications: Review on converter cells and functionalities. IEEE Trans. Power Electron. 2014, 30, 18–36. [Google Scholar] [CrossRef]
- Franquelo, L.G.; Rodriguez, J.; Leon, J.I.; Kouro, S.; Portillo, R.; Prats, M.A. The age of multilevel converters arrives. IEEE Ind. Electron. Mag. 2008, 2, 28–39. [Google Scholar] [CrossRef]
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Pou, J.; Franquelo, L.G.; Wu, B.; Rodriguez, J.; Pérez, M.A.; Leon, J.I. Recent advances and industrial applications of multilevel converters. IEEE Trans. Ind. Electron. 2010, 57, 2553–2580. [Google Scholar] [CrossRef]
- Lawan, A.U.; Abbas, H.; Khor, J.G.; Karim, A.A. Dynamic performance improvement of MMC inverter with STATCOM capability interfacing PMSG wind turbines with grid. In Proceedings of the 2015 IEEE Conference on Energy Conversion (CENCON), Johor Bahru, Malaysia, 19–20 October 2015; pp. 492–497. [Google Scholar]
- Lesnicar, A.; Marquardt, R. An innovative modular multilevel converter topology suitable for a wide power range. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003. [Google Scholar]
- Liu, Z.; Hu, X.; Liao, Y. Vehicle-Grid System Stability Analysis Based on Norm Criterion and Suppression of Low-Frequency Oscillation With MMC-STATCOM. IEEE Trans. Transp. Electr. 2018, 4, 757–766. [Google Scholar] [CrossRef]
- Farias, J.V.M.; Cupertino, A.F.; Pereira, H.A.; Junior, S.I.S.; Teodorescu, R. On the redundancy strategies of modular multilevel converters. IEEE Trans. Power Deliv. 2017, 33, 851–860. [Google Scholar] [CrossRef]
- Yue, Y.; Ma, F.; Luo, A.; Xu, Q.; Xie, L. A circulating current suppressing method of MMC based STATCOM for negative-sequence compensation. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016. [Google Scholar]
- Muñoz, J.A.; Espinoza, J.R.; Baier, C.R.; Morán, L.A.; Guzmán, J.I.; Cárdenas, V.M. Decoupled and modular harmonic compensation for multilevel STATCOMs. IEEE Trans. Ind. Electr. 2013, 61, 2743–2753. [Google Scholar] [CrossRef]
- Zhu, J.; Li, L.; Pan, M. Study of a novel STATCOM based on modular multilevel inverter. In Proceedings of the IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 1428–1432. [Google Scholar]
- Zhang, W.; Gao, Q.; Su, B.; Jin, M.; Xu, D.; Liu, J. Research on the control strategy of STATCOM based on modular multilevel converter. In Proceedings of the 2014 International Power Electronics Conference (IPEC-Hiroshima 2014-ECCE ASIA), Hiroshima, Japan, 18–21 May 2014. [Google Scholar]
- Vivas, J.H.; Bergna, G.; Boyra, M. Comparison of multilevel converter-based STATCOMs. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August–1 September 2011. [Google Scholar]
- Nwobu, C.J.; Efika, I.B.; Oghorada, O.J.K.; Zhang, L. A modular multilevel flying capacitor converter-based STATCOM for reactive power control in distribution systems. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015. [Google Scholar]
- Liu, X.; Lv, J.; Gao, C.; Chen, Z.; Chen, S. A novel STATCOM based on diode-clamped modular multilevel converters. IEEE Trans. Power Electr. 2016, 32, 5964–5977. [Google Scholar] [CrossRef]
- Yang, X.; Li, J.; Fan, W.; Wang, X.; Zheng, T.Q. Research on modular multilevel converter based STATCOM. In Proceedings of the 2011 6th IEEE Conference on Industrial Electronics and Applications, Beijing, China, 21–23 June 2011; pp. 2569–2574. [Google Scholar]
- Pereira, H.A.; Haddioui, M.R.; De Oliveira, L.O.; Mathe, L.; Bongiorno, M.; Teodorescu, R. Circulating current suppression strategies for D-STATCOM based on modular Multilevel Converters. In Proceedings of the 2015 IEEE 13th Brazilian Power Electronics Conference and 1st Southern Power Electronics Conference (COBEP/SPEC), Fortaleza, Brazil, 29 November–2 December 2015; pp. 1–6. [Google Scholar]
- Nieves, M.; Maza, J.; Mauricio, J.; Teodorescu, R.; Bongiorno, M.; Rodriguez, P. Enhanced control strategy for MMC-based STATCOM for unbalanced load compensation. In Proceedings of the 2014 16th European Conference on Power Electronics and Applications, Lappeenranta, Finland, 26–28 August 2014; pp. 1–10. [Google Scholar]
- António-Ferreira, A.; Gomis-Bellmunt, O.; Teixidó, M. HVDC-based modular multilevel converter in the statcom operation mode. In Proceedings of the 2016 18th European Conference on Power Electronics and Applications (EPE’16 ECCE Europe), Karlsruhe, Germany, 5–9 September 2016; pp. 1–10. [Google Scholar]
- Liu, L.; Li, H.; Xue, Y.; Liu, W. Decoupled active and reactive power control for large-scale grid-connected photovoltaic systems using cascaded modular multilevel converters. IEEE Trans. Power Electr. 2014, 30, 176–187. [Google Scholar]
- Mehrasa, M.; Pouresmaeil, E.; Zabihi, S.; Catalao, J.P.S. Dynamic model, control and stability analysis of MMC in HVDC transmission systems. IEEE Trans. Power Deliv. 2016, 32, 1471–1482. [Google Scholar] [CrossRef]
- Mehrasa, M.; Pouresmaeil, E.; Zabihi, S.; Vechiu, I.; Catalão, J.P.S. A multi-loop control technique for the stable operation of modular multilevel converters in HVDC transmission systems. Int. J. Electr. Power Energy Syst. 2018, 96, 194–207. [Google Scholar] [CrossRef]
- Xu, C.; Dai, K.; Kang, Y.; Liu, C. Characteristic analysis and experimental verification of a novel capacitor voltage control strategy for three-phase MMC-DSTATCOM. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015; pp. 1528–1533. [Google Scholar]
- Cupertino, A.F.; Farias, J.V.M.; Pereira, H.A.; Seleme, S.I.; Teodorescu, R. Comparison of dscc and sdbc modular multilevel converters for statcom application during negative sequence compensation. IEEE Trans. Ind. Electr. 2019, 66, 2302–2312. [Google Scholar] [CrossRef]
- Luo, F.; Wang, J.; Li, Z.; Duan, Q.; Lv, Z.; Ji, Z.; Gu, W.; Wu, Z. A circuit-oriented average-value model of modular multilevel converter based on sub-module modelling method. In Proceedings of the 2017 12th IEEE Conference on Industrial Electronics and Applications (ICIEA), Siem Reap, Cambodia, 18–20 June 2017; pp. 7–12. [Google Scholar]
- Mehrasa, M.; Pouresmaeil, E.; Taheri, S.; Vechiu, I.; Catalão, J.P.S. Novel control strategy for modular multilevel converters based on differential flatness theory. IEEE J. Emerg. Sel. Top. Power Electr. 2018, 6, 888–897. [Google Scholar] [CrossRef]
- Sun, Y.; Teixeira, C.A.; Holmes, D.G.; McGrath, B.P.; Zhao, J. Low-order circulating current suppression of PWM-based modular multilevel converters using DC-link voltage compensation. IEEE Trans. Power Electr. 2017, 33, 210–225. [Google Scholar] [CrossRef]
- Yang, S.; Wang, P.; Tang, Y.; Zagrodnik, M.; Hu, X.; Tseng, K.J. Circulating current suppression in modular multilevel converters with even-harmonic repetitive control. IEEE Trans. Ind. Appl. 2017, 54, 298–309. [Google Scholar] [CrossRef]
- Adabi, M.E.; Martinez-Velasco, J.A. MMC-based solid-state transformer model including semiconductor losses. Electr. Eng. 2018, 100, 1613–1630. [Google Scholar] [CrossRef]
- Wang, J.; Han, X.; Ma, H.; Bai, Z. Analysis and injection control of circulating current for modular multilevel converters. IEEE Trans. Ind. Electr. 2019, 66, 2280–2290. [Google Scholar] [CrossRef]
- Yang, S.; Wang, P.; Tang, Y. Feedback linearization-based current control strategy for modular multilevel converters. IEEE Trans. Power Electr. 2018, 33, 161–174. [Google Scholar] [CrossRef]
- Xiang, M.; Hu, J.; He, Z. Loss reduction analysis and control of AC voltage-boosted FBSM MMC by injecting second harmonic circulating current. J. Eng. 2018, 2019, 2328–2331. [Google Scholar] [CrossRef]
- Yang, L.; Li, Y.; Li, Z.; Wang, P.; Xu, S.; Gou, R. Loss optimization of MMC by second-order harmonic circulating current injection. IEEE Trans. Power Electr. 2018, 33, 5739–5753. [Google Scholar] [CrossRef]
| Items | Values |
|---|---|
| AC system voltage (L-L,rms) | 10 KV |
| AC system inductance Lc | 0.5 mH |
| AC system resistance Rc | 1 mΩ |
| DC bus voltage Vr | 20 KV |
| number of SMs per arm N | 20 |
| SM capacitance C | 10,000 μF |
| arm inductance Larm | 40 mH |
| arm equivalent resistance Rarm | 1.5 Ω |
| SM capacitor voltage Vcsm | 1 KV |
| carrier frequency fsw | 5 KHz |
| simulation time step Ts | 83.3 × 10−6 s |
| Load1 active power Pref1 | 0.5 MW |
| Load1 reactive power Qref1 | 4 MVar |
| Load2 active power Pref2 | 3.5 MW |
| Load2 reactive power Qref2 | 0.8 MVar |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahnazian, F.; Adabi, E.; Adabi, J.; Pouresmaeil, E.; Rouzbehi, K.; Rodrigues, E.M.G.; Catalão, J.P.S. Control of MMC-Based STATCOM as an Effective Interface between Energy Sources and the Power Grid. Electronics 2019, 8, 1264. https://doi.org/10.3390/electronics8111264
Shahnazian F, Adabi E, Adabi J, Pouresmaeil E, Rouzbehi K, Rodrigues EMG, Catalão JPS. Control of MMC-Based STATCOM as an Effective Interface between Energy Sources and the Power Grid. Electronics. 2019; 8(11):1264. https://doi.org/10.3390/electronics8111264
Chicago/Turabian StyleShahnazian, Fatemeh, Ebrahim Adabi, Jafar Adabi, Edris Pouresmaeil, Kumars Rouzbehi, Eduardo M. G. Rodrigues, and João P. S. Catalão. 2019. "Control of MMC-Based STATCOM as an Effective Interface between Energy Sources and the Power Grid" Electronics 8, no. 11: 1264. https://doi.org/10.3390/electronics8111264
APA StyleShahnazian, F., Adabi, E., Adabi, J., Pouresmaeil, E., Rouzbehi, K., Rodrigues, E. M. G., & Catalão, J. P. S. (2019). Control of MMC-Based STATCOM as an Effective Interface between Energy Sources and the Power Grid. Electronics, 8(11), 1264. https://doi.org/10.3390/electronics8111264








