Research on Linear Active Disturbance Rejection Control in DC/DC Boost Converter
Abstract
:1. Introduction
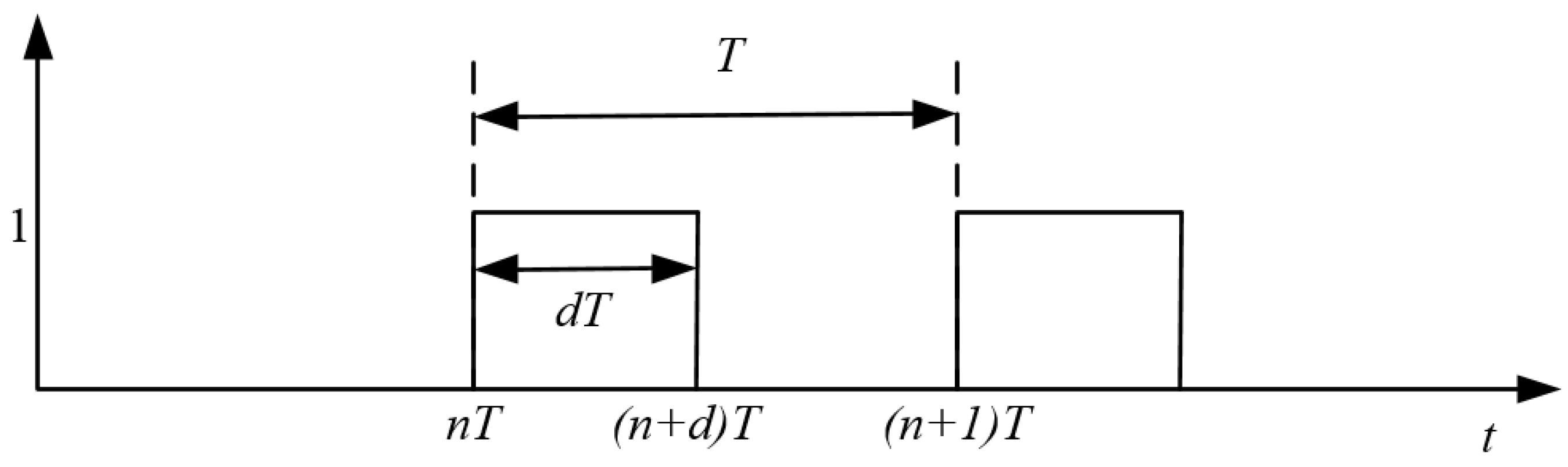
2. Modeling of DC/DC Boost Converter
3. Control Method Design
3.1. Cascade Control
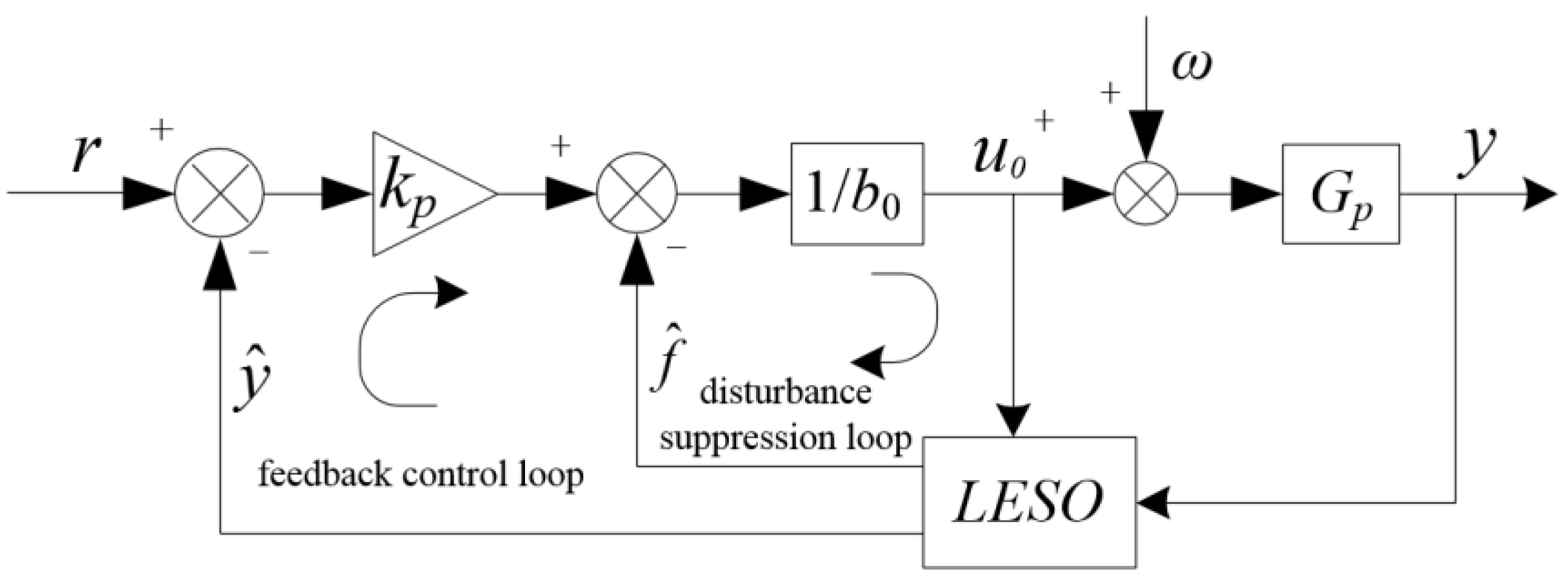
3.2. Linear Active Disturbance Rejection Control
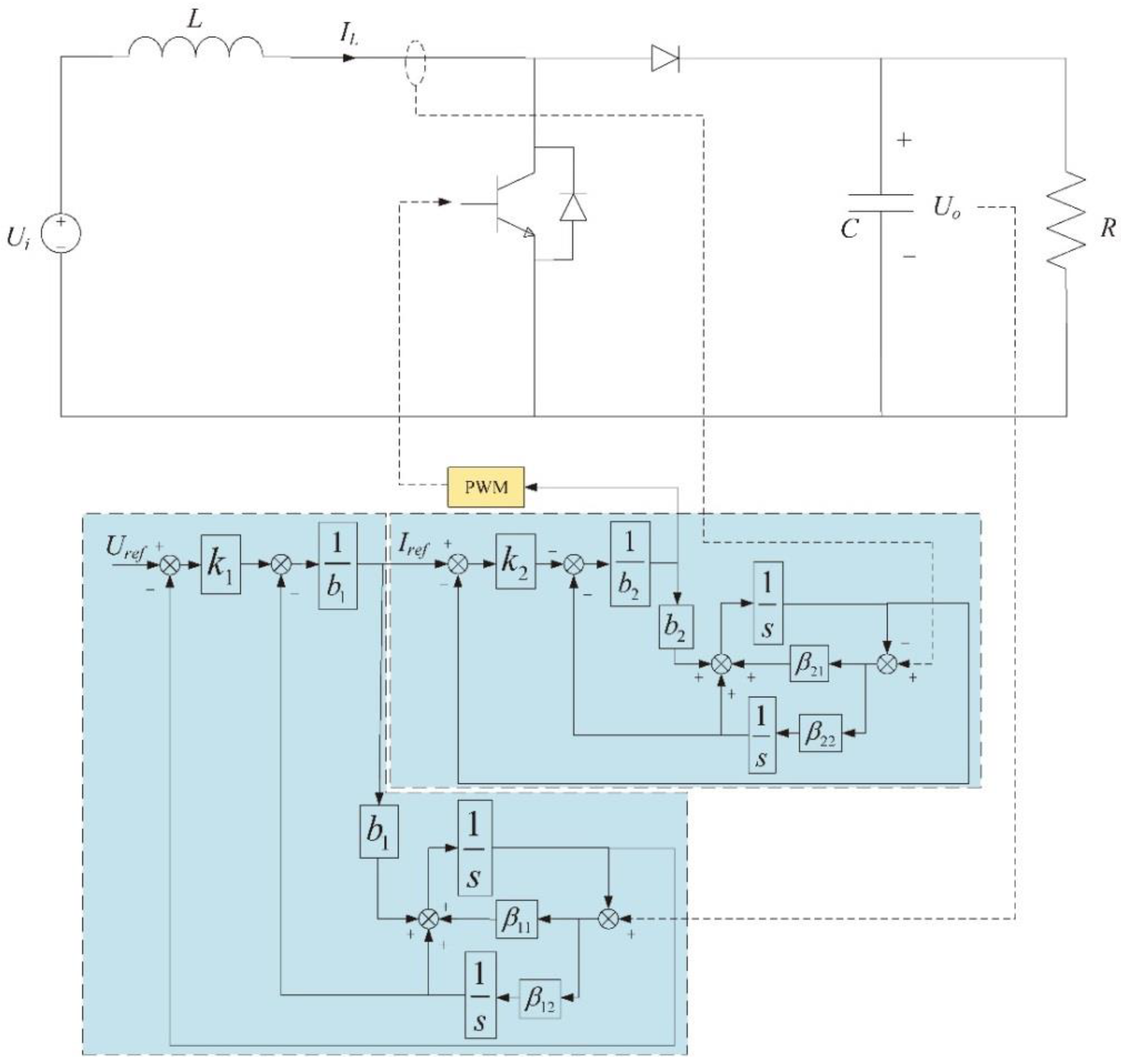
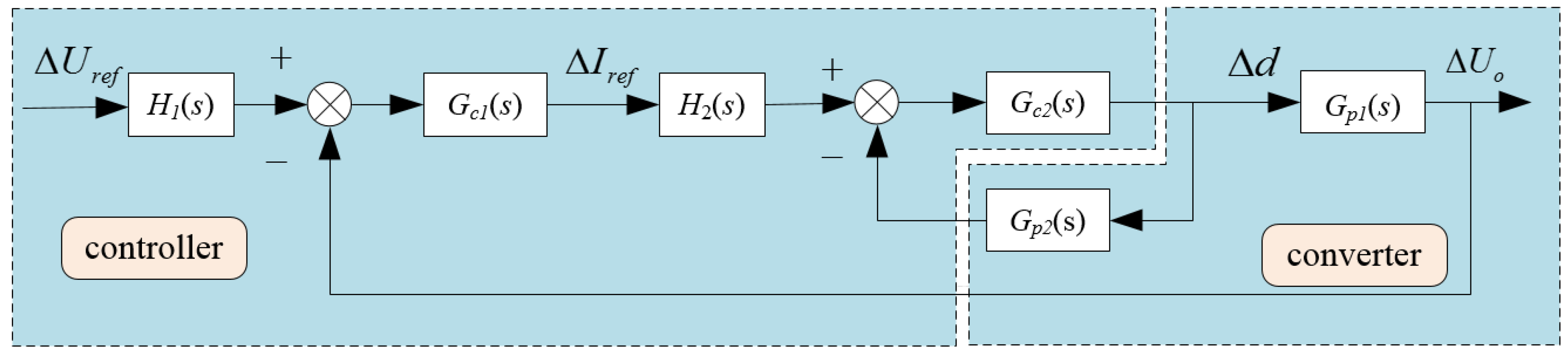
4. Controller Design
4.1. Design of Current Controller
4.2. Design of Voltage Controller
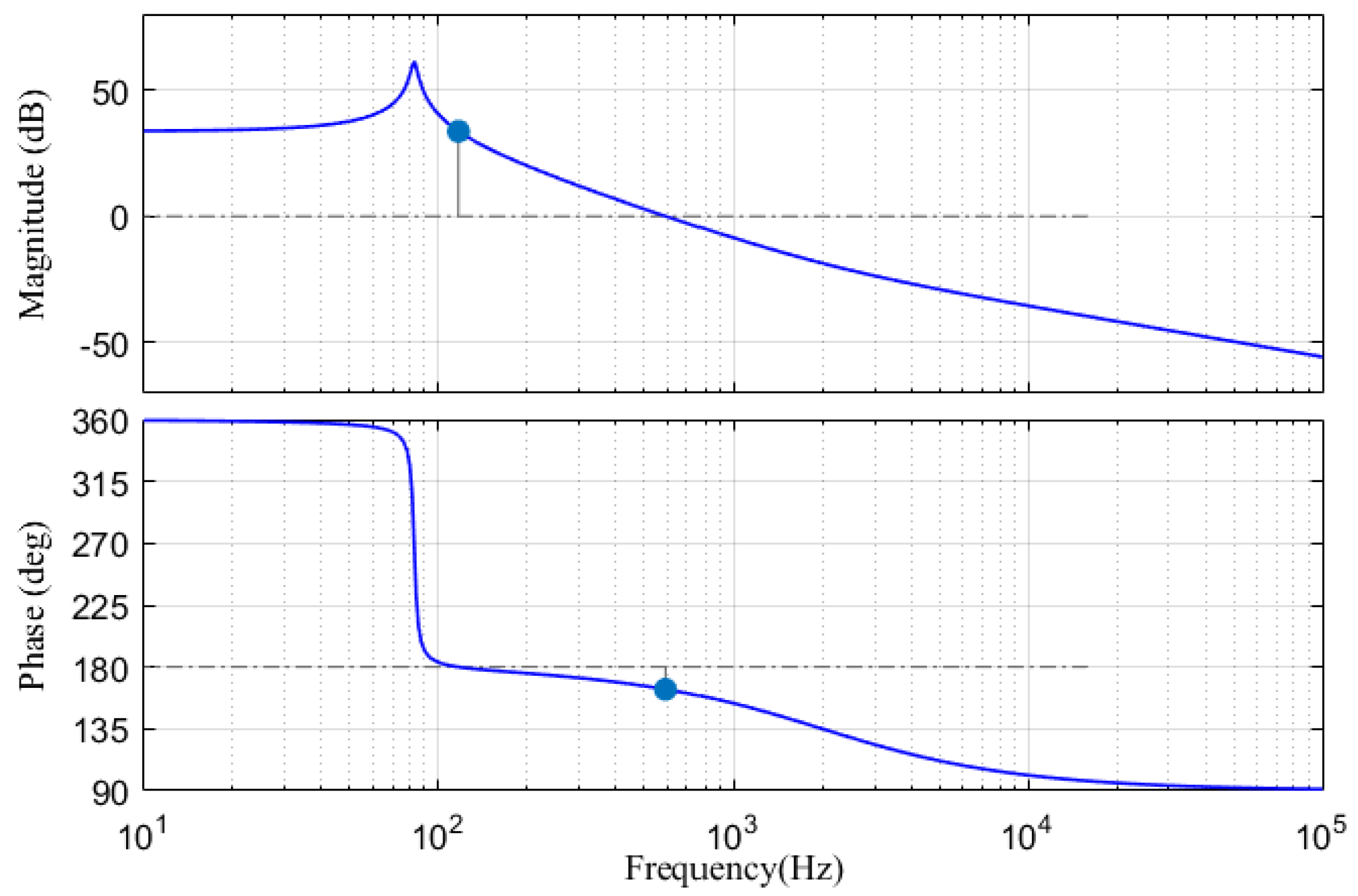
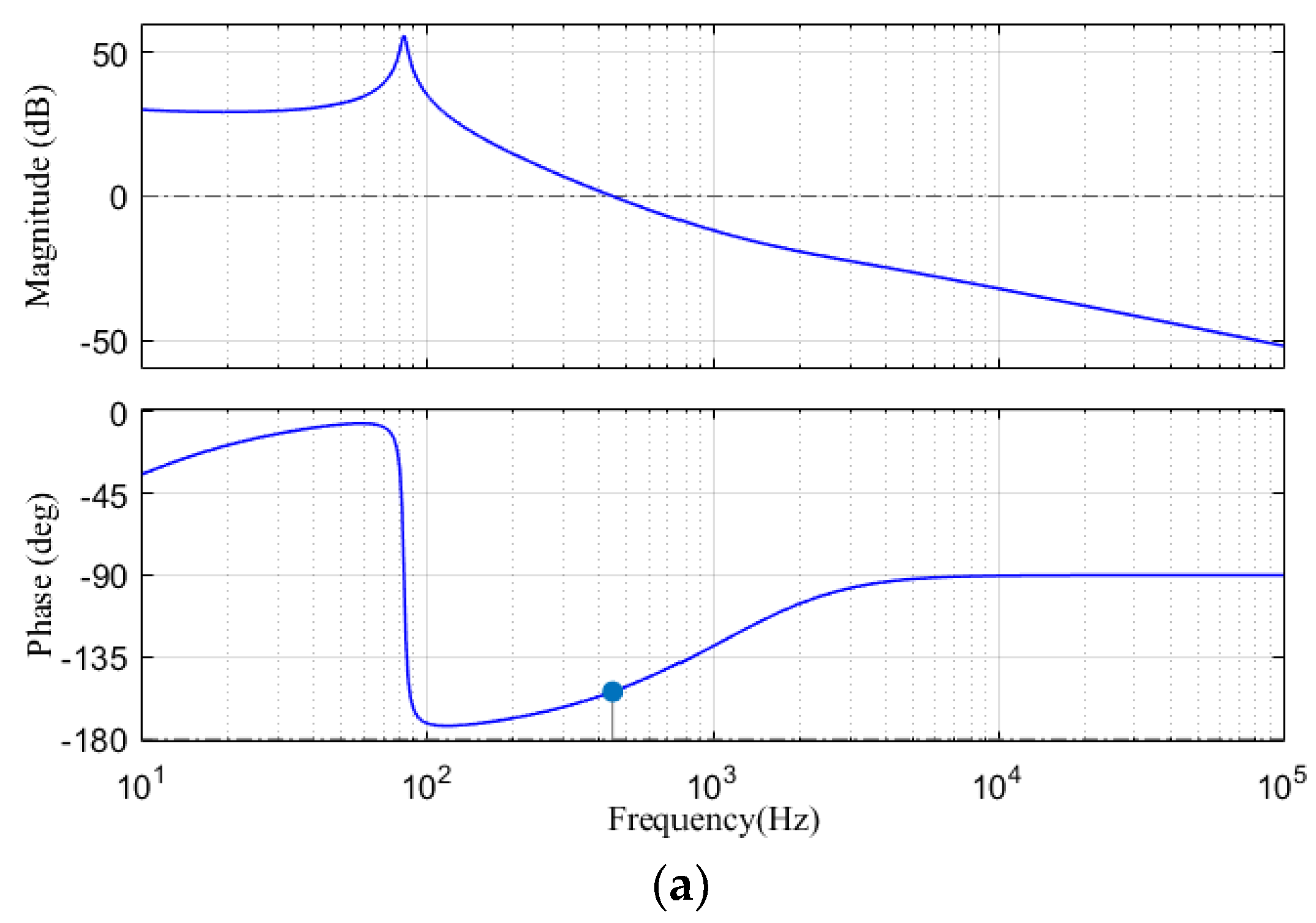
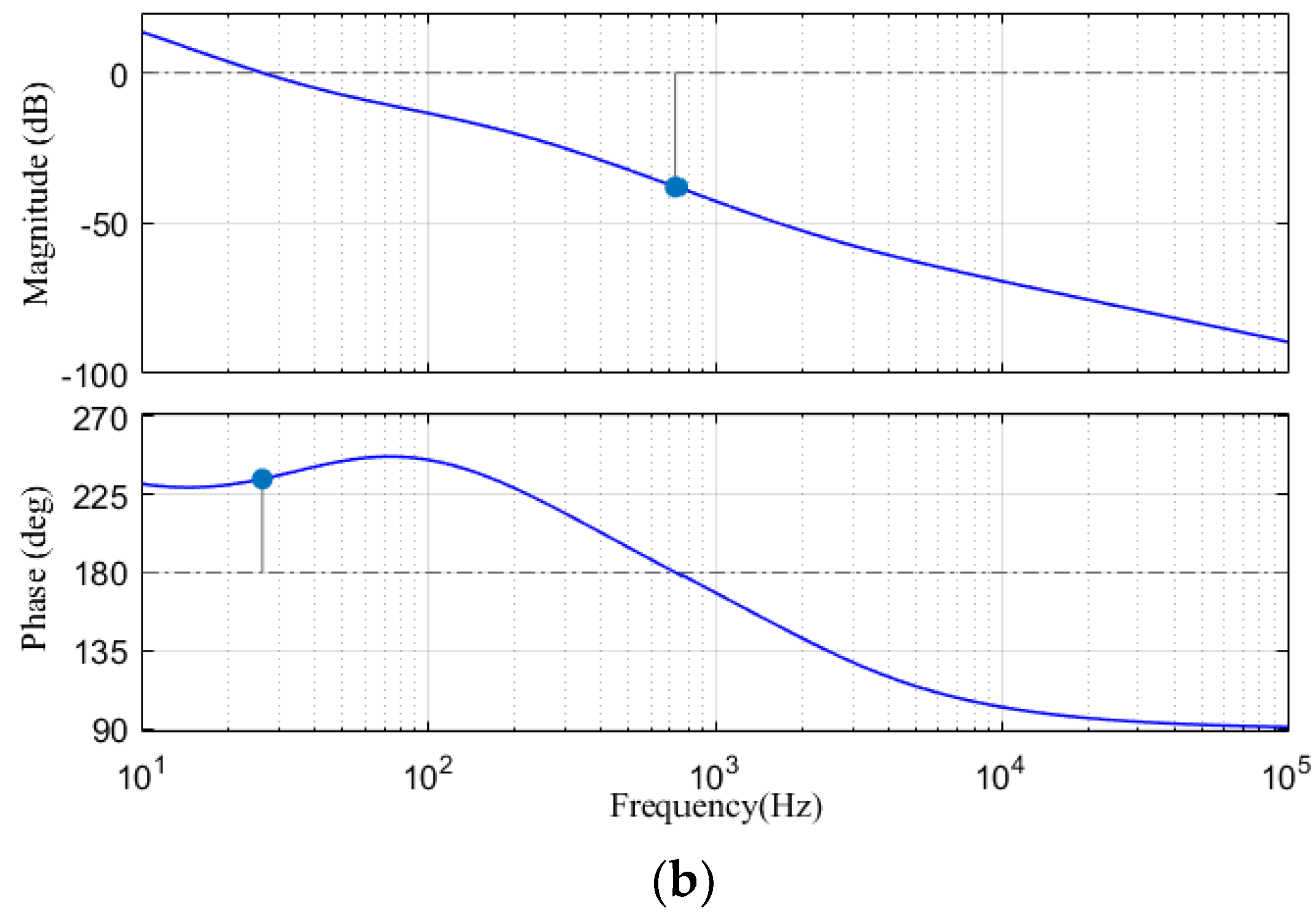
4.3. System Stability Analysis
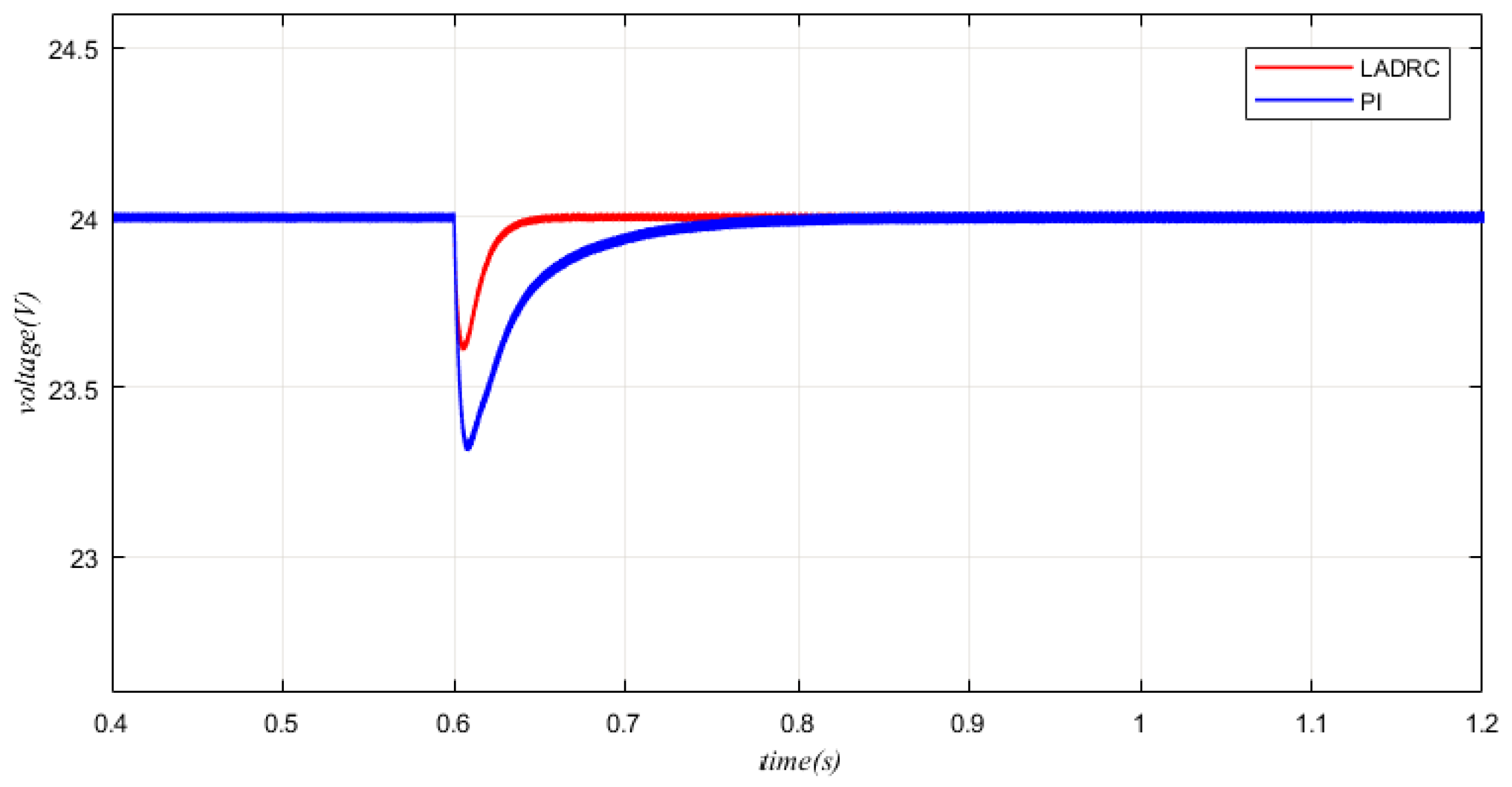
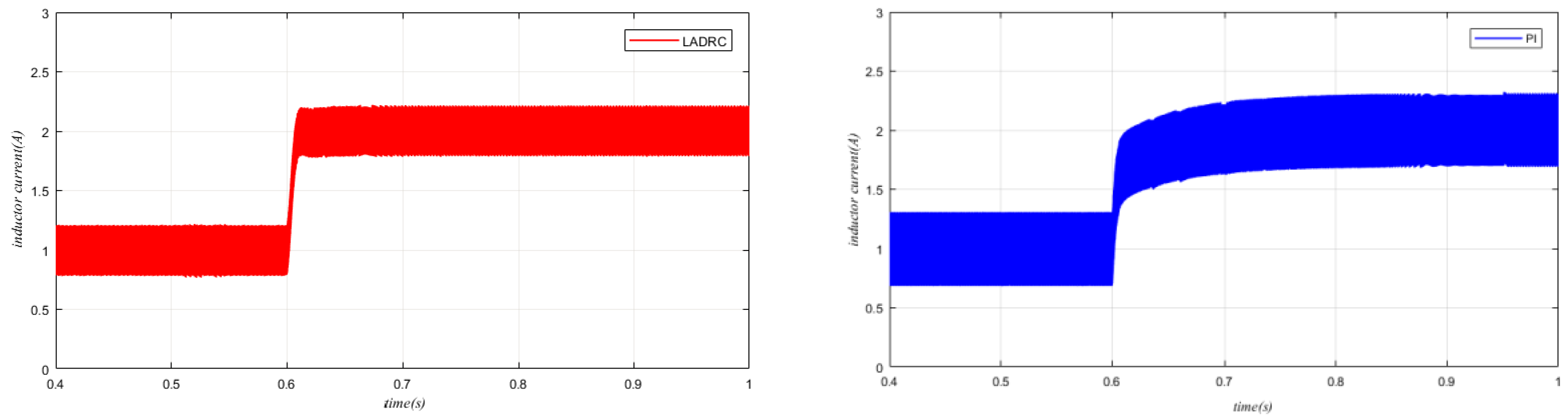
5. Simulation Results
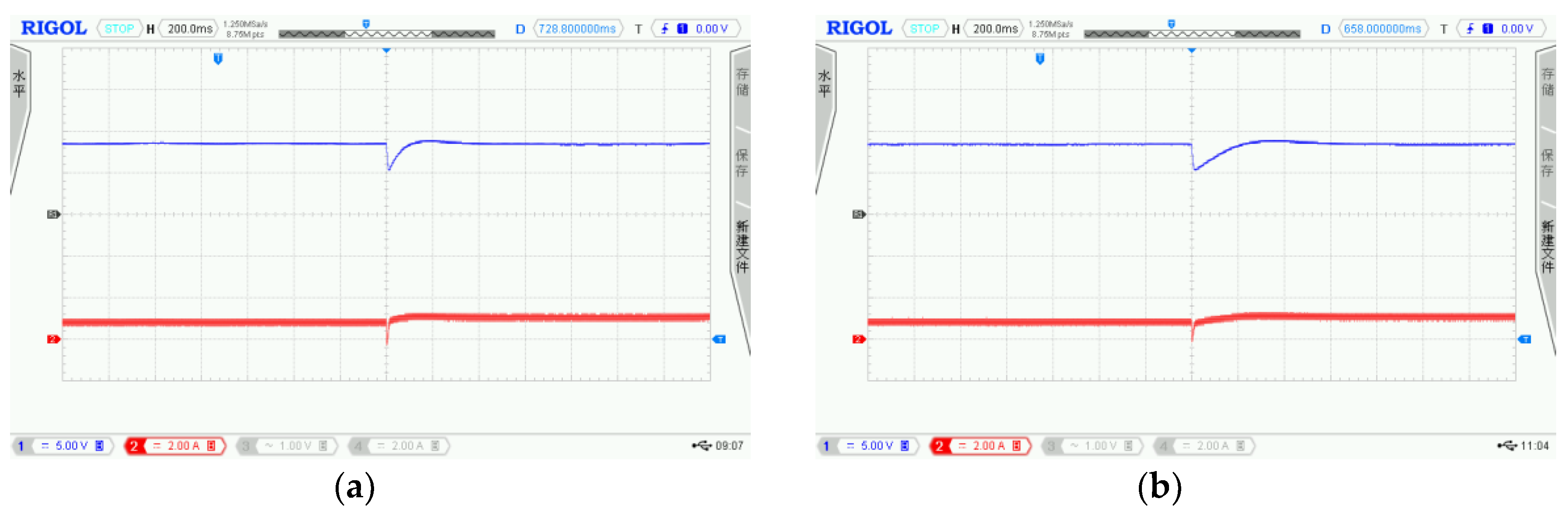
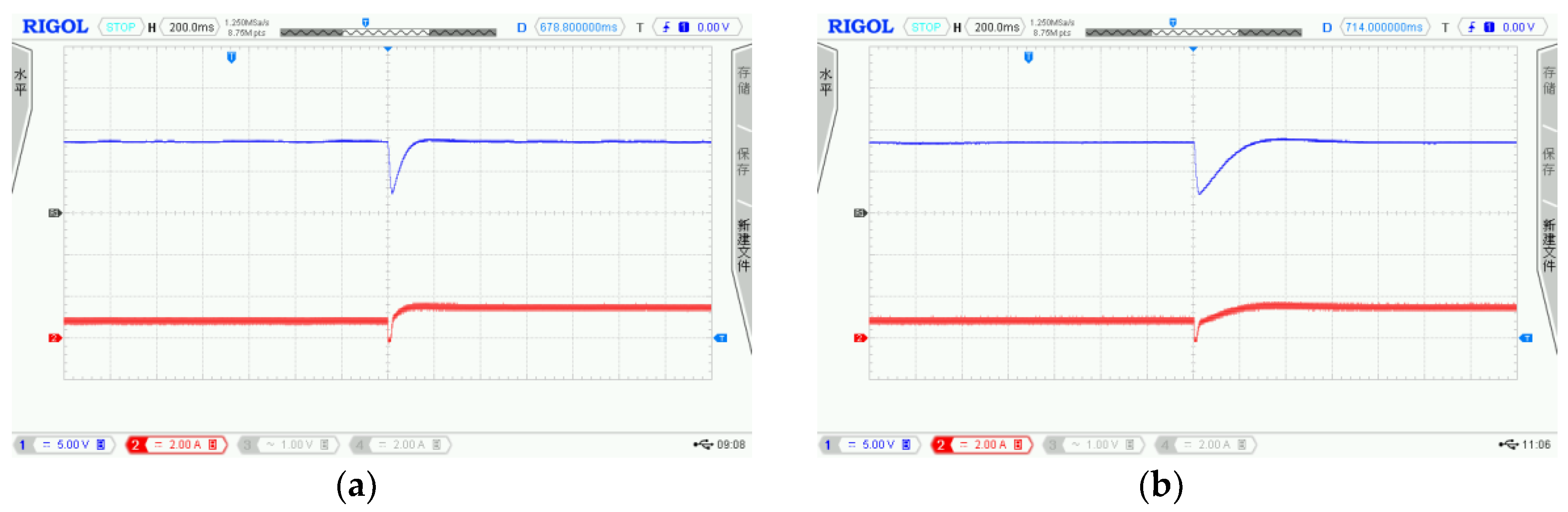
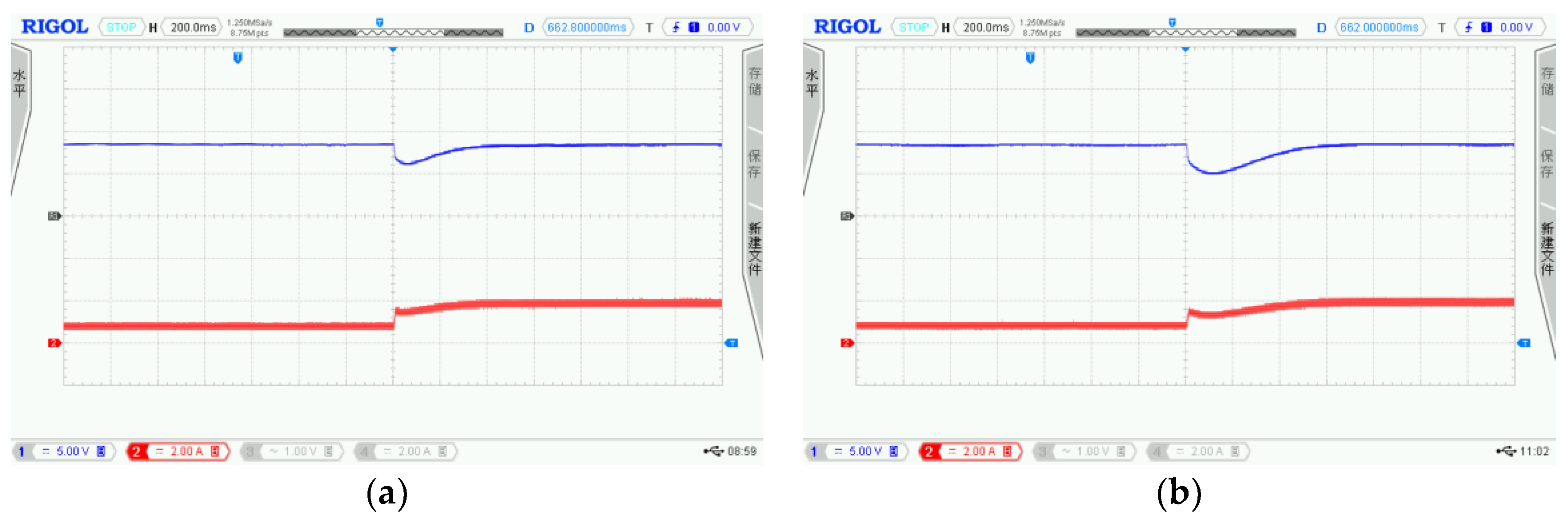
6. Hardware Experiment
7. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Symbols | Description |
| DC | direct current |
| AC | alternating current |
| LADRC | linear active disturbance rejection control |
| LSEF | linear state error feedback |
| LESO | linear extended state observer |
| ADRC | active disturbance rejection control |
| NLSEF | nonlinear state error feedback |
| ESO | extended state observer |
| TD | tracking differentiator |
| PD | proportional-derivative |
| PWM | pulse width modulation |
| Ui | input voltage of DCDC boost converter |
| Uo | output voltage of DCDC boost converter |
| IL | inductor current |
| L | inductance value |
| C | capacitance value |
| R | resistive load |
| fsw | switching frequency |
| T | switching period |
| d | duty cycle |
| μ(t) | pulse function |
| Uo(∞) | the steady state values of Uo |
| IL(∞) | the steady state values of IL |
| Uoref | reference value of output voltage |
| ILref | reference value of inductor current |
| r | first-order LADRC input reference |
| u0 | controlled quantity |
| ω | external disturbance of the system |
| Gp | controlled object |
| y | system output |
| estimated value of system output | |
| f | total disturbance of the system |
| estimated value of the total disturbance | |
| b0 | system gain |
| Kp | gain of LSEF |
| Lo | gain of LESO |
| ωo | observer’s bandwidth |
| ωc | controller’s bandwidth |
| D | 1-d |
| Gp(s) | transfer function of the DC/DC boost converter |
| Uref | reference voltage of the voltage loop |
| Iref | reference current of the current loop |
| Uo | output voltage |
| H1(s), Gc1(s) | transfer function of LADRC voltage outer loop |
| H2(s), Gc2(s) | transfer function of LADRC current inner loop |
| Gp1(s) | transfer function of the d to Uo |
| Gp2(s) | transfer function of the d(t) to the IL |
| G1(s) | transfer function of the inner loop current loop |
| G0(s) | system open loop transfer function |
| ωc1, ωo1, b1 | LADRC parameters of current control loop |
| ωc2, ωo2, b2 | LADRC parameters of voltage control loop |
| kp1, ki1 | PI parameters of voltage control loop |
| kp2, ki2 | PI parameters of current control loop |
References
- Dragicevic, T.; Lu, X.; Vasquez, J.; Guerrero, J. DC Microgrids–Part I: A Review of Control Strategies and Stabilization Techniques. IEEE Trans. Power Electron. 2016, 31, 4876–4891. [Google Scholar] [CrossRef]
- El-Shahat, A.; Sumaiya, S. DC-Microgrid System Design, Control, and Analysis. Electronics 2019, 8, 124. [Google Scholar] [CrossRef]
- Baranwal, M.; Askarian, A.; Salapaka, S.; Salapaka, M. Distributed Architecture for Robust and Optimal Control of DC Microgrids. IEEE Trans. Ind. Electron. 2018. [Google Scholar] [CrossRef]
- Kakigano, H.; Nishino, A.; Ise, T. Distribution Voltage Control for DC Microgrids Using Fuzzy Control and Gain-Scheduling Technique. IEEE Trans. Power Electron. 2013, 28, 2246–2258. [Google Scholar] [CrossRef]
- Shenai, K.; Shah, K. Smart DC micro-grid for efficient utilization of distributed renewable energy. In Proceedings of the Energytech, Cleveland, OH, USA, 25–26 May 2011. [Google Scholar]
- Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M.; Skrlec, D. Advanced LVDC Electrical Power Architectures and Microgrids: A step toward a new generation of power distribution networks. IEEE Elect. Mag. 2014, 2, 54–65. [Google Scholar] [CrossRef]
- Boujelben, N.; Masmoudi, F.; Djemel, M.; Derbel, N. Design and comparison of quadratic boost and double cascade boost converters with boost converter. In Proceedings of the 14th International Multi-Conference on Systems, Signals Devices (SSD), Marrakech, Morocco, 28–31 March 2017; pp. 245–252. [Google Scholar]
- Jou, H.; Huang, J.; Wu, J.; Wu, K. Novel Isolated Multilevel DC–DC Power Converter. IEEE Trans. Power Electron. 2016, 31, 2690–2694. [Google Scholar] [CrossRef]
- Zhang, C.; Gao, Z.; Chen, T.; Yang, J. Isolated DC/DC converter with three-level high-frequency link and bidirectional power flow ability for electric vehicles. IET Power Electron. 2019, 12, 1742–1751. [Google Scholar] [CrossRef]
- Leyva-Ramos, J.; Ortiz-Lopez, M.G.; Diaz-Saldierna, L.H.; Morales-Saldana, J.A. Switching regulator using a quadratic boost converter for wide DC conversion ratios. Power Electron. IET 2009, 2, 605–613. [Google Scholar] [CrossRef]
- Wang, Y.; Qiu, Y.; Bian, Q.; Guan, Y.; Xu, D. A Single Switch Quadratic Boost High Step up DC-DC Converter. IEEE Trans. Ind. Electron. 2018, 66, 4387–4397. [Google Scholar] [CrossRef]
- Wu, G.; Ruan, X.; Ye, Z. Non-isolated High Step-up DC-DC Converters Adopting Switched-capacitor Cell. Ind. Electron. IEEE Trans. 2015, 62, 383–393. [Google Scholar] [CrossRef]
- Chen, F.; Cai, X.S. Design of feedback control laws for switching regulators based on the bilinear large signal model. Power Electron. IEEE Trans. 1989, 5, 236–240. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, X.; Lin, P.; Liu, P.X.; Yan, Y.; Yang, J. Finite-Time Feedforward Decoupling and Precise Decentralized Control for DC Microgrids Towards Large-Signal Stability. IEEE Trans. Smart Grid 2019. [Google Scholar] [CrossRef]
- Lee, T.S. Input-output linearization and zero-dynamics control of three-phase AC/DC voltage-source converters. Power Electron. IEEE Trans. 2003, 18, 11–22. [Google Scholar]
- Viswanathan, K.; Oruganti, R.; Srinivasan, D. Dual mode control of tri-state boost converter for improved performance. In Proceedings of the IEEE Power Electronics Specialist Conference, Acapulco, Mexico, 15–19 June 2003. [Google Scholar]
- Sastry, J.; Ojo, O.; Wu, Z. High performance control of a boost AC-DC PWM rectifier-induction generator system. In Proceedings of the Industry Applications Conference, Hong Kong, China, 2–6 October 2005. [Google Scholar]
- Wei, X.; Tsang, K.M.; Chan, W.L. DC/DC Buck Converter Using Internal Model Control. Electr. Mach. Power Syst. 2009, 37, 320–330. [Google Scholar] [CrossRef]
- Shuai, D.; Xie, Y.; Wang, X. The Research of Input-Output Linearization and Stabilization Analysis of Internal Dynamics on the CCM Boost Converter. In Proceedings of the International Conference on Electrical Machines Systems, Wuhan, China, 17–20 October 2008. [Google Scholar]
- Sira-Ramírez, H.; Silva-Ortigoza, R. Control Design Techniques in Power Electronics Devices; Springer: London, UK, 2006; pp. 235–355. [Google Scholar]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906.22. [Google Scholar] [CrossRef]
- Han, J. The auto-disturbance-rejection controller (ADRC) and its application. Control Decis. 1998, 1, 19–23. [Google Scholar]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]
- Gao, Z. Active Disturbance Rejection Control: A paradigm shift in feedback control system design. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006. [Google Scholar]
- Gang, T.; Gao, Z. Benchmark tests of Active Disturbance Rejection Control on an industrial motion control platform. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 5552–5557. [Google Scholar]
- Huang, Y.; Xue, W.; Gao, Z.; Sira-Ramirez, H.; Sun, M. Active Disturbance Rejection Control: Methodology, Practice and Analysis. In Proceedings of the Control Conference, Hilton, Portland, 4–6 June 2014. [Google Scholar]
- Song, C.; Wei, C.; Yang, F.; Cui, N. High-Order Sliding Mode-Based Fixed-Time Active Disturbance Rejection Control for Quadrotor Attitude System. Electronics 2018, 7, 357. [Google Scholar] [CrossRef]
- Li, H.; Qu, Y. A Composite Strategy for Harmonic Compensation in Standalone Inverter Based on Linear Active Disturbance Rejection Control. Energies 2019, 12, 2618. [Google Scholar] [CrossRef]
- Zuo, Y.; Zhu, X.; Li, Q.; Chao, Z.; Yi, D.; Xiang, Z. Active Disturbance Rejection Controller for Speed Control of Electrical Drives Using Phase-locking Loop Observer. IEEE Trans. Ind. Electron. 2019, 66, 1748–1759. [Google Scholar] [CrossRef]
- Zheng, Q.; Dong, L.; Lee, D.H.; Gao, Z. Active disturbance rejection control for MEMS gyroscopes. In Proceedings of the American Control Conference, St. Louis, MO, USA, 10–12 June 2009. [Google Scholar]
- You, J.; Fan, W.; Yu, L.; Fu, B.; Liao, M. Disturbance Rejection Control Method of Double-Switch Buck-Boost Converter. Energies 2019, 12, 278. [Google Scholar] [CrossRef]

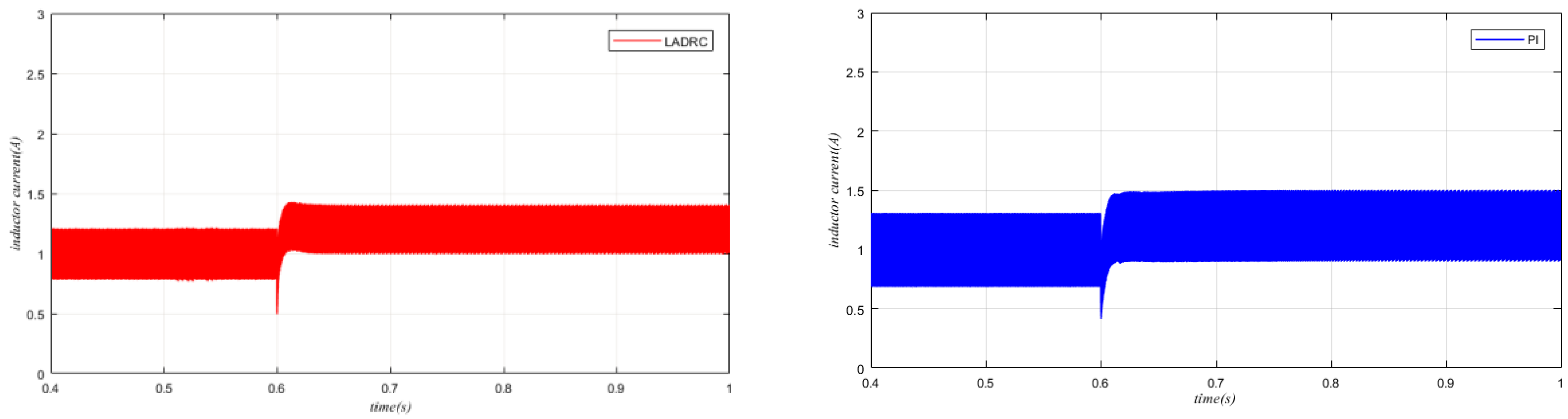
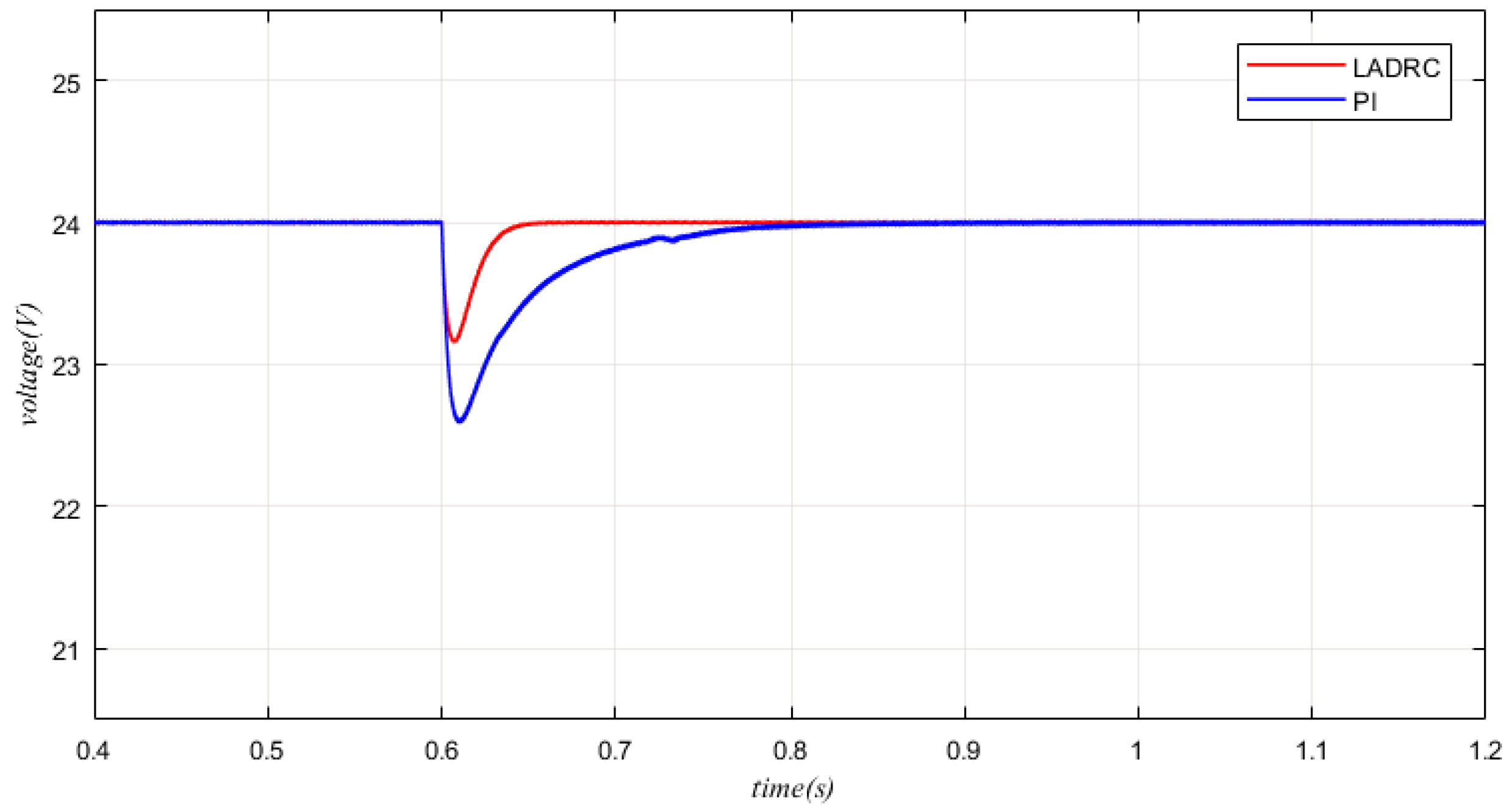
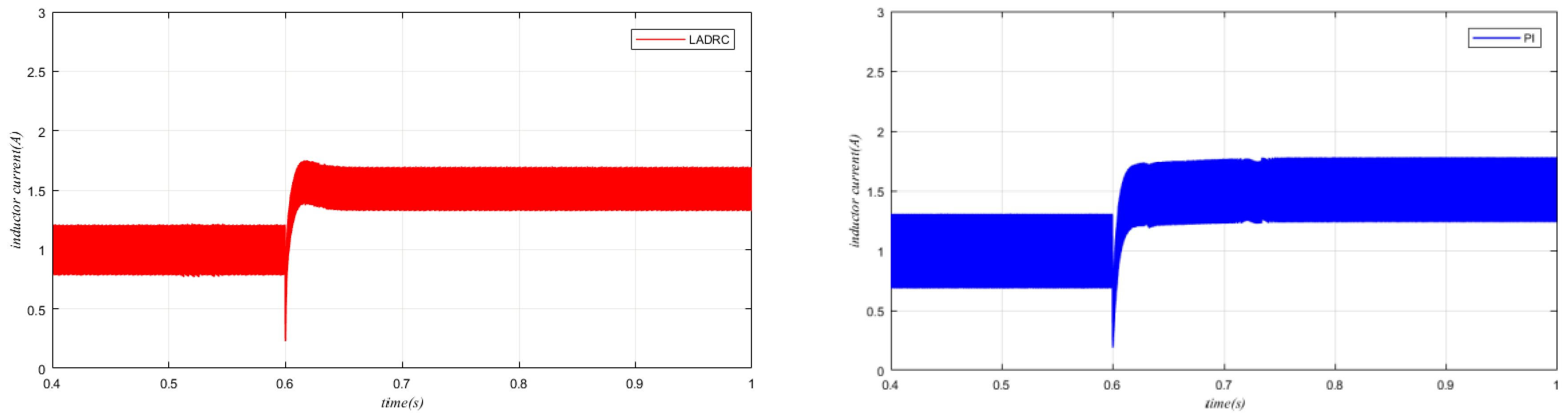
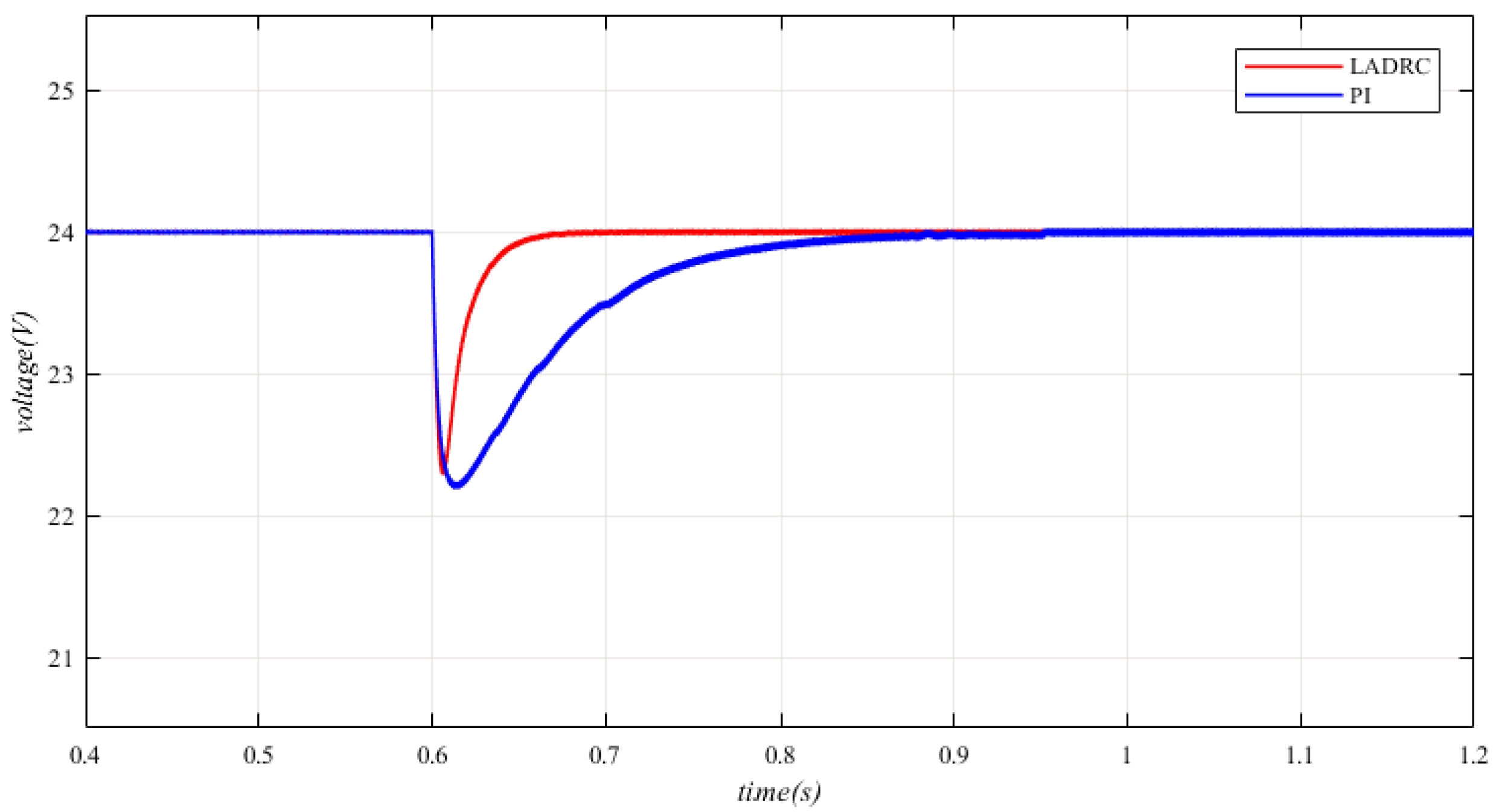

| Parameters | Description | Value |
|---|---|---|
| Uoref | Reference value of output voltage | 24 V |
| L | inductance value | 1 mH |
| C | capacitance value | 920 μF |
| fsw | switching frequency | 10 KHz |
| ωc1, ωo1,b1 | LADRC parameters of current control loop | 165, 270, 543.5 |
| ωc2, ωo2,b2 | LADRC parameters of voltage control loop | 1600, 8800, 24,000 |
| kp1, ki1 | PI parameters of voltage control loop | 0.3, 7 |
| kp2, ki2 | PI parameters of current control loop | 0.25, 30 |
| Case | Input Voltage | Load |
|---|---|---|
| 1 | 12 V→10 V | 50 Ω |
| 2 | 12 V→8 V | 50 Ω |
| 3 | 12 V | 50 Ω→25 Ω |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Liu, X.; Lu, J. Research on Linear Active Disturbance Rejection Control in DC/DC Boost Converter. Electronics 2019, 8, 1249. https://doi.org/10.3390/electronics8111249
Li H, Liu X, Lu J. Research on Linear Active Disturbance Rejection Control in DC/DC Boost Converter. Electronics. 2019; 8(11):1249. https://doi.org/10.3390/electronics8111249
Chicago/Turabian StyleLi, Hui, Xinxiu Liu, and Junwei Lu. 2019. "Research on Linear Active Disturbance Rejection Control in DC/DC Boost Converter" Electronics 8, no. 11: 1249. https://doi.org/10.3390/electronics8111249
APA StyleLi, H., Liu, X., & Lu, J. (2019). Research on Linear Active Disturbance Rejection Control in DC/DC Boost Converter. Electronics, 8(11), 1249. https://doi.org/10.3390/electronics8111249





