Unsupervised Monocular Depth Estimation Based on Residual Neural Network of Coarse–Refined Feature Extractions for Drone
Abstract
1. Introduction
2. Method
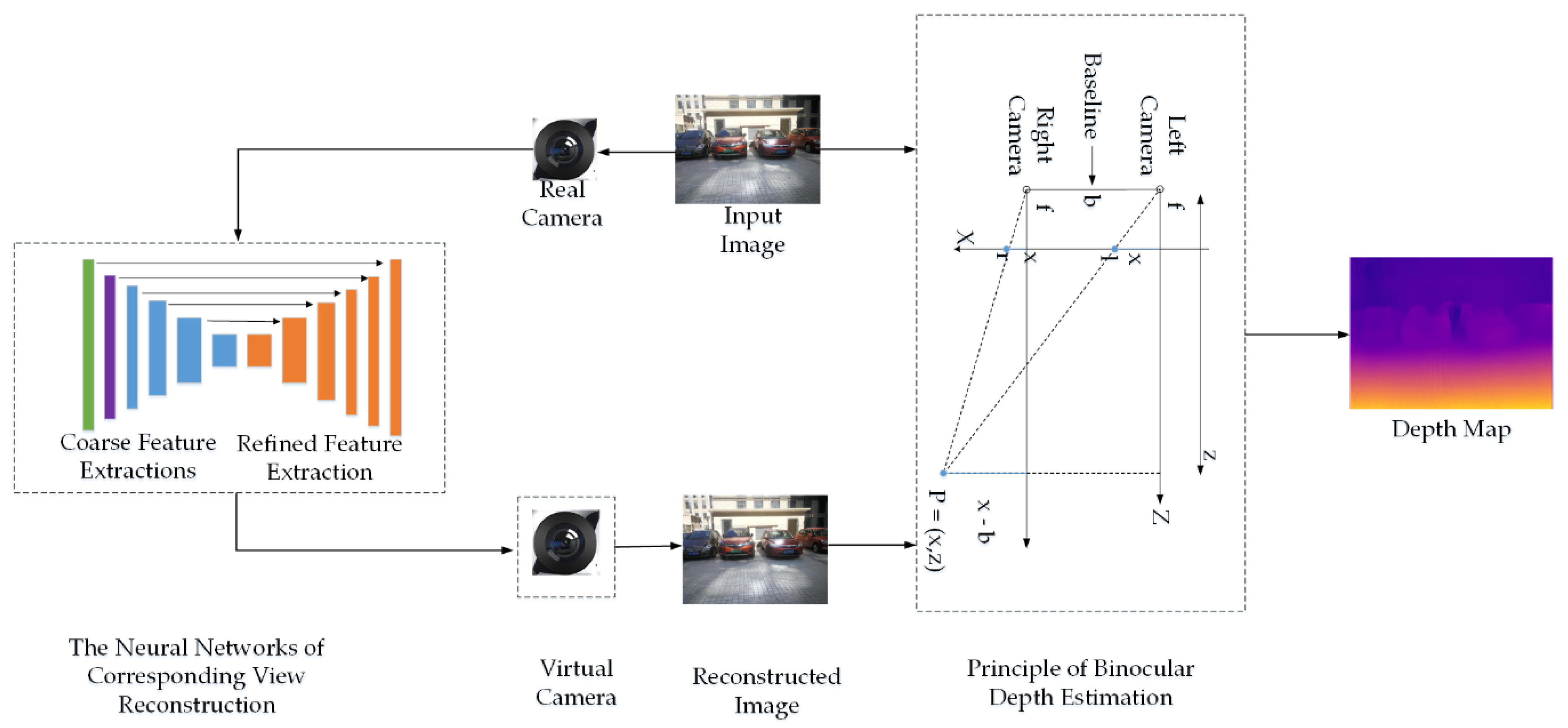
2.1. The Principle of Our Model for Monocular Depth Estimation
2.2. The Outstanding Advantages of Our Model
2.3. The Details of Our Model
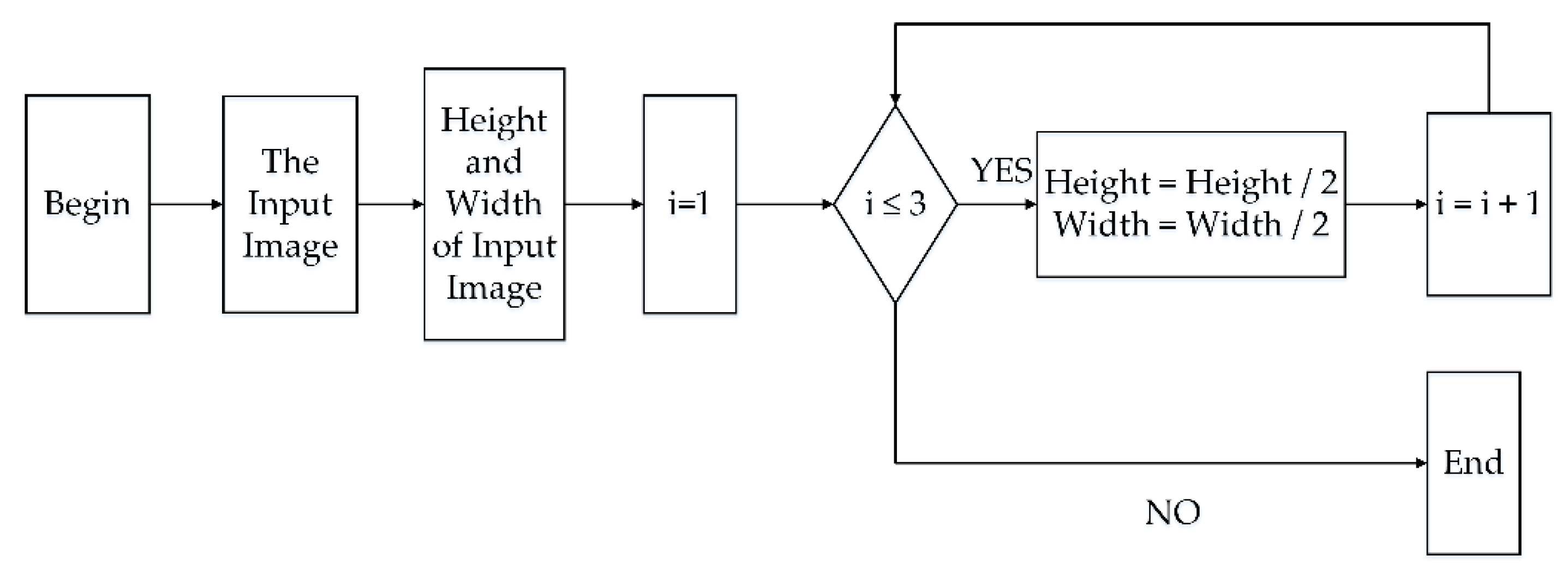
2.3.1. The Pyramid Processing for Input Image
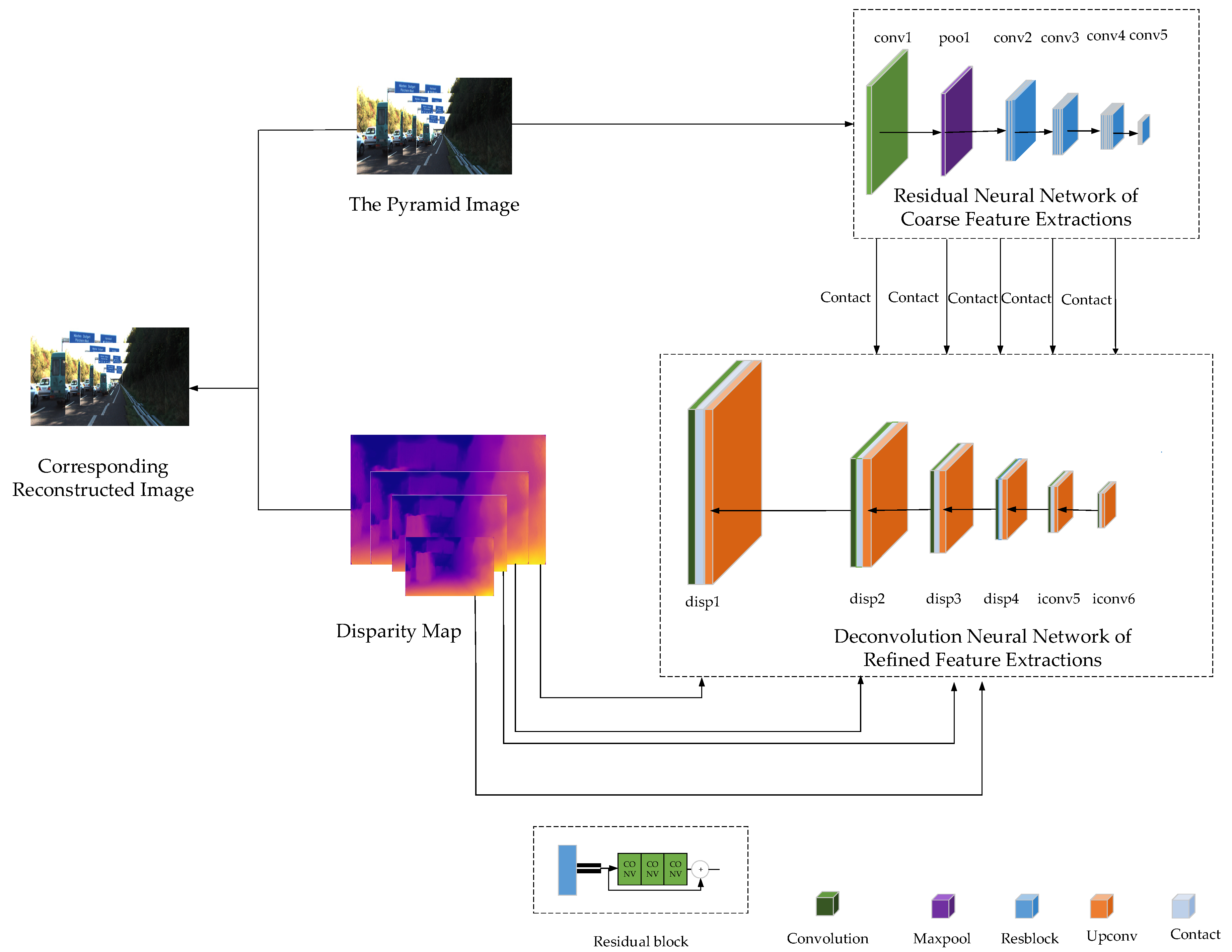
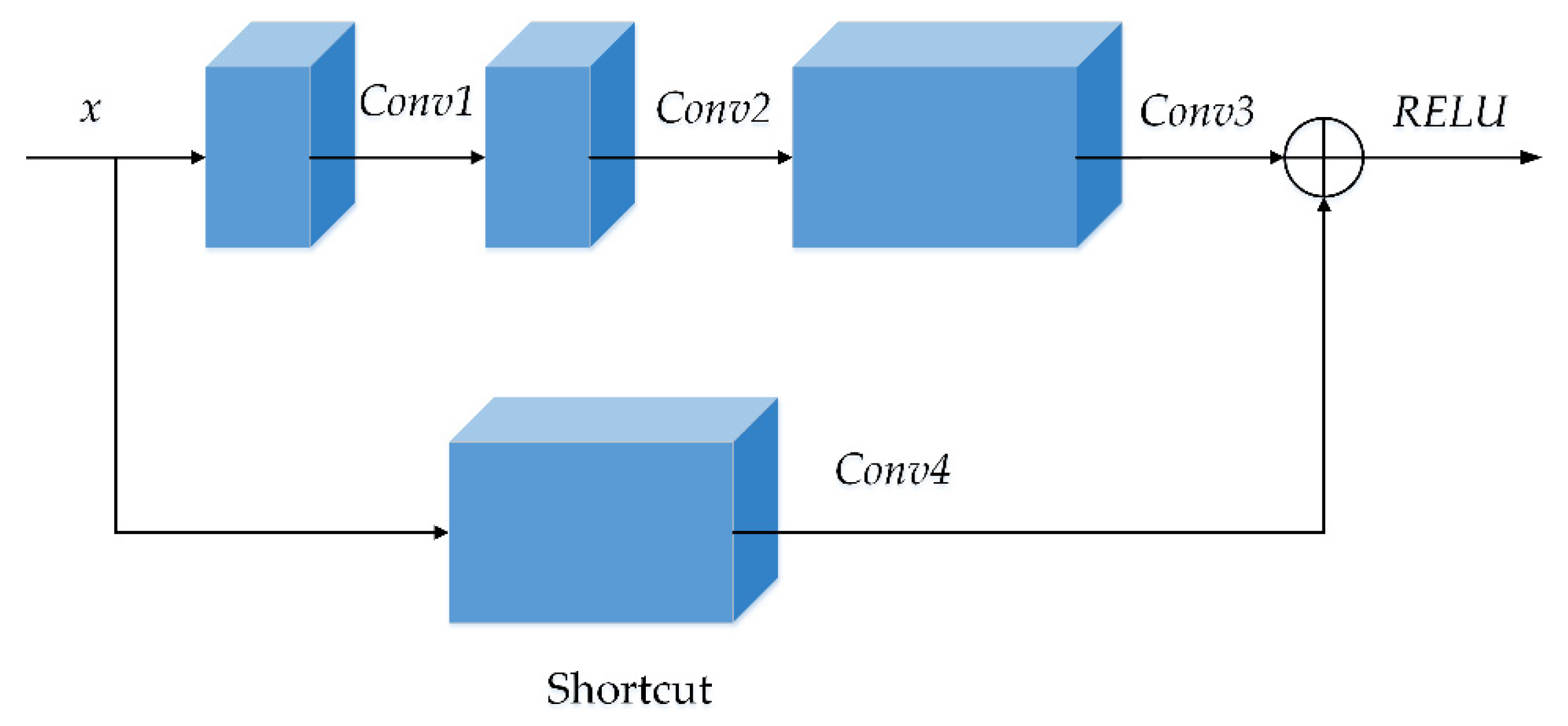
2.3.2. The Residual Neural Network of Coarse–Refined Feature Extractions for Corresponding View Reconstruction
- Step 1:
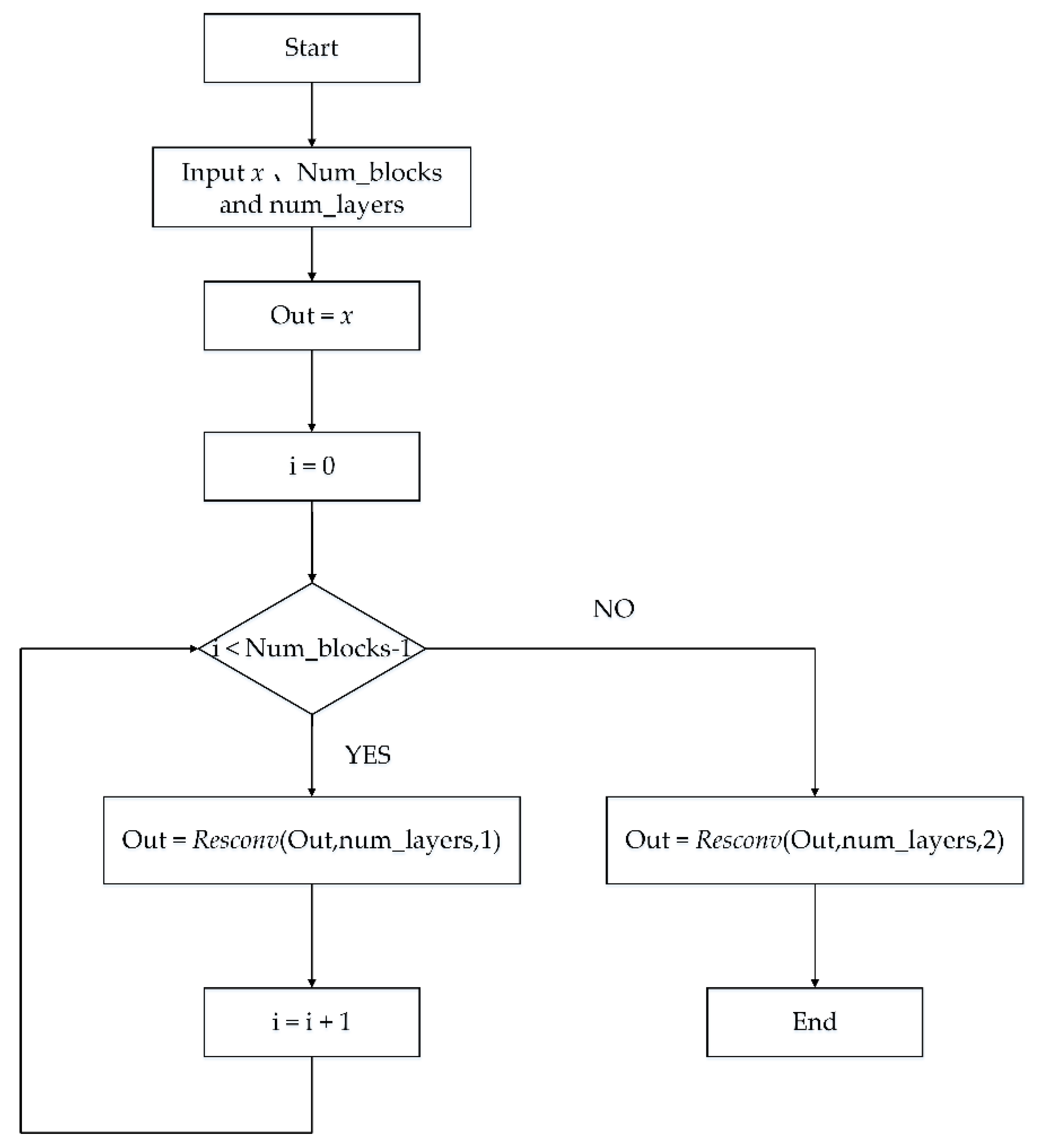
- Residual neural network-based coarse feature extractions. Input to our network was the RGB camera image of pyramid. The residual neural network based on coarse feature extractions (without the final fully connected layer) successively extracted low resolution high-dimensional features from the input image of 256 × 512. The residual neural network based on coarse feature extractions subsampled the input image in six stages: the output was 128 × 256 × 64 through Conv1; the output was 64 × 128 × 64 through Pool 1; the output was 32 × 64 × 256 through Resblock_1; the output was 16 × 32 × 512 through Resblock_2; the output was 8 × 16 × 1024 through Resblock_3; the output was 4 × 8 × 2018 through Resblock_4.
- Step 2:
- Deconvolution neural network-based refined feature extractions. Long skip connections between corresponding layers in the encoder and decoder were added to improve the performance on all metrics without affecting convergence. The deconvolution neural network based on refined feature extractions subsampled the Resblock_4 in six stages: (1) The output was 8 × 16 × 512 through Upconv5; the output was 8 × 16 × 1536 through Contact5; the output was 8 × 16 × 512 through Iconv5. (2) The output was 16 × 32 × 256 through Upconv4; the output was 16 × 32 × 768 through Contact4; the output was 16 × 32 × 256 through Iconv4. (3) The output was 32 × 64 × 128 through Upconv3; the output was 32 × 64 × 384 through Contact3; the output was 32 × 64 × 128 through Iconv3; the output was 32 × 64 × 2 through Disp3; the output was 64 × 128 × 2 through Udisp3. (4) The output was 64 × 128 × 64 through Upconv2; the output was 64 × 128 × 128 through Contact2; the output was 64 × 128 × 64 through Iconv2; the output was 64 × 128 × 2 through Disp2; the output was 128 × 256 × 2 through Udisp2. (5) The output was 128 × 256 × 32 through Upconv1; the output was 128 × 256 × 96 through Contact1; the output was 128 × 256 × 32 through Iconv1; the output was 128 × 256 × 2 through Disp1; the output was 256 × 512 × 2 through Udisp1. (6) The output was 256 × 512 × 16 through Upconv0; the output was 256 × 512 × 18 through Contact0; the output was 256 × 512 × 16 through Iconv0; the output was 256 × 512 × 2 through Disp0.
- Step 3:
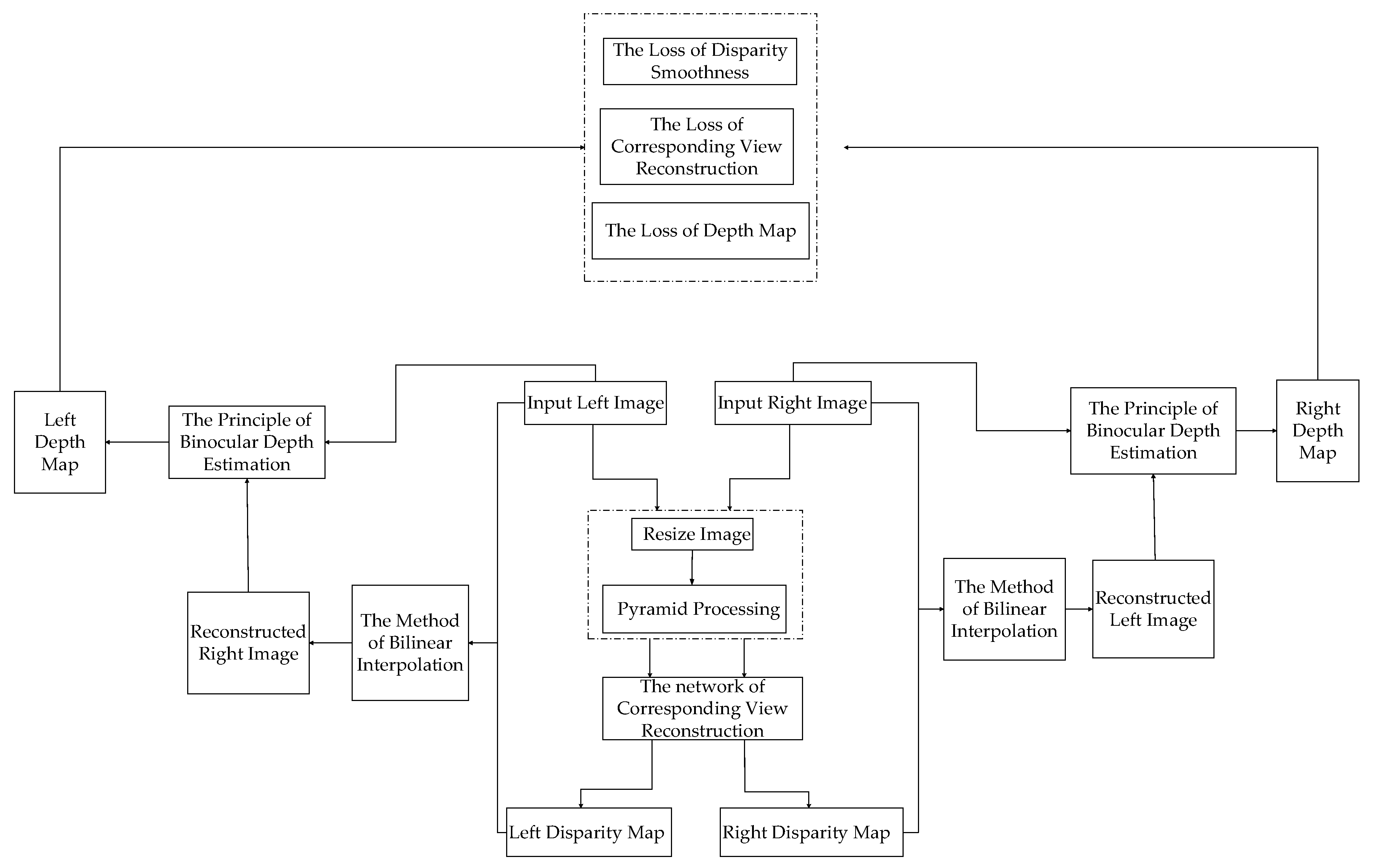
- Corresponding view reconstruction based on the method of bilinear interpolation. Right or left view was reconstructed according to the pyramid disparity map including Disp0, Disp1, Disp2, Disp4 and the corresponding input left or right image processed by the method of the pyramid.
2.3.3. The Function of Training Loss
3. Experimental Results
3.1. Experimental Setup
3.1.1. Platform of Drone Experience
3.1.2. Evaluation Metrics
3.1.3. Implementation Details
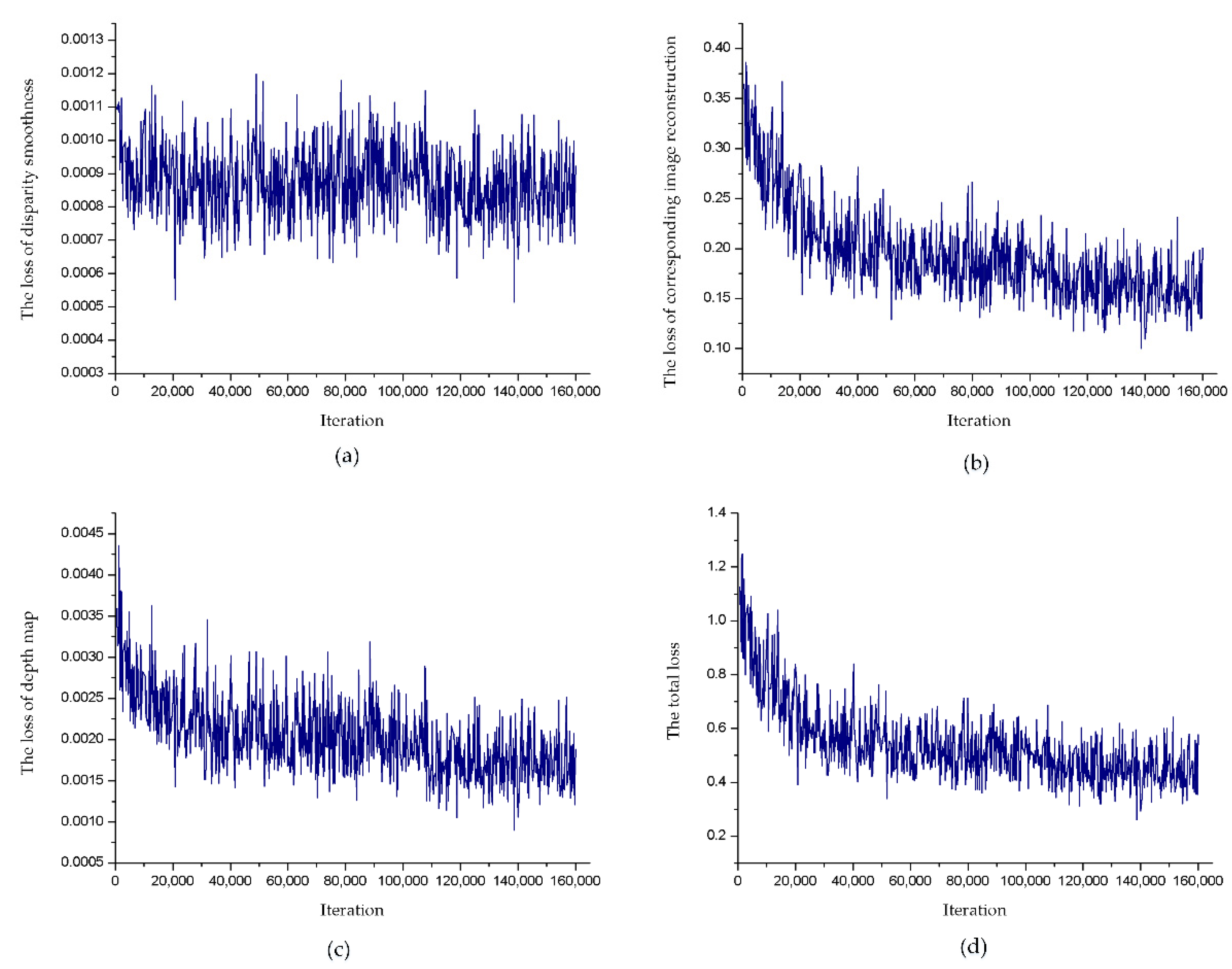
3.2. Training
3.3. Experimental Results and Analysis
3.3.1. Comparison with State-of-the-Art Method on KITTI Dataset
3.3.2. Ablation Study
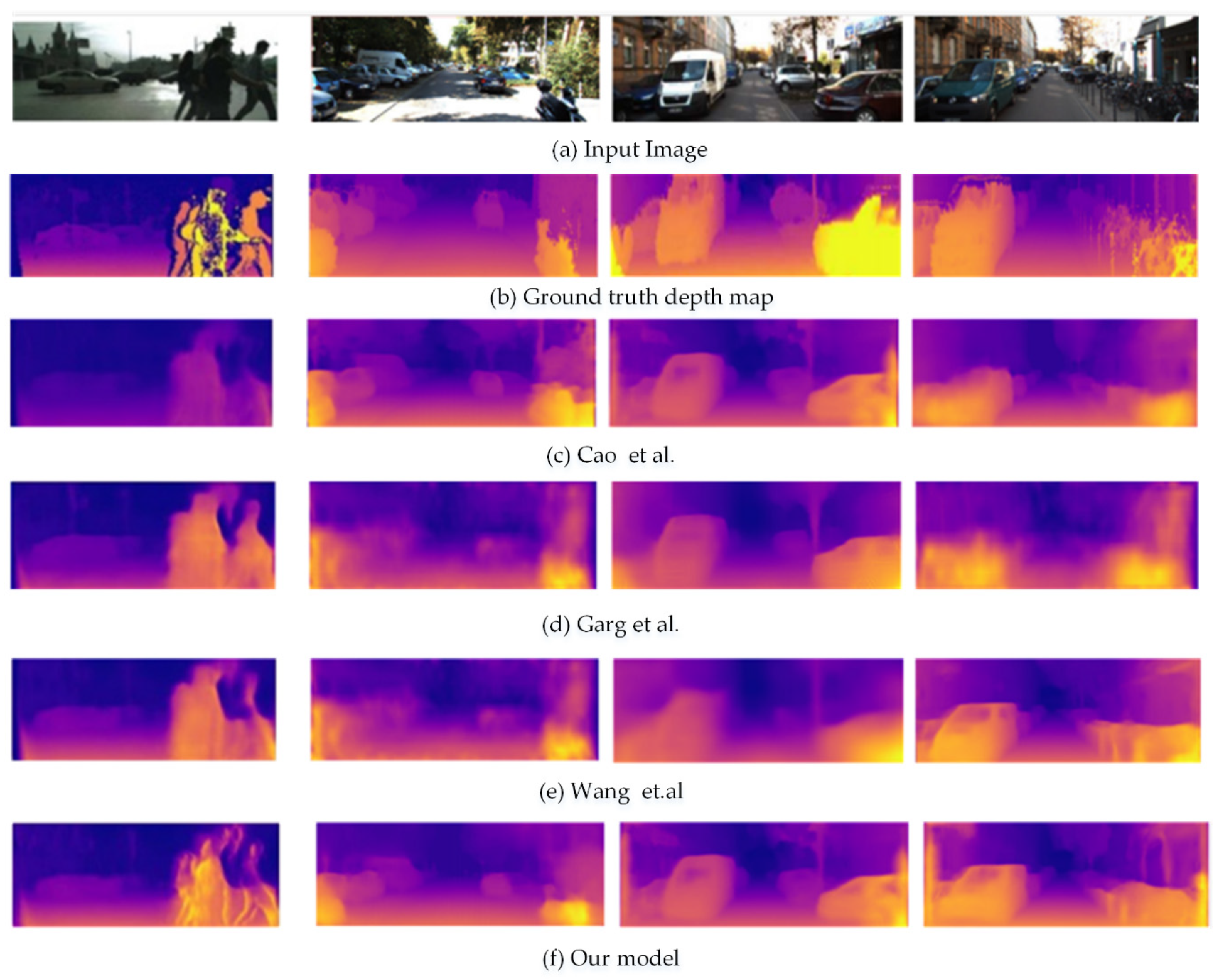
3.3.3. Generalizing to Other Datasets
3.3.4. Result on a Real Scene
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shangjie, J.; Bin, L.; Jun, L.; Yun, Z. Real-time detection of vehicle targets based on drones. Bullet. Sur. Map. 2017, 1, 164–168. [Google Scholar]
- Zhenqiang, B.; Aihua, L.; Zhiqiang, C.; Meng, Y. Research progress of deep learning in visual localization and three-dimensional structure recovery. Laser Optoelectron. Prog. 2018, 55, 050007. [Google Scholar]
- Jiang, G.; Jin, S.; Ou, Y.; Zhou, S. Depth Estimation of a Deformable Object via a Monocular Camera. Appl. Sci. 2019, 9, 1366. [Google Scholar] [CrossRef]
- Tongneng, H.; Jiageng, Y.; Defu, C. Monocular image depth estimation based DenseNet. Comput. Meas. Cont. 2019, 27, 233–236. [Google Scholar]
- Noah, S.; Steven, M.S.; Richard, S. Skeletal Graphs for Efficient Structure from Motion. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Anchorage, AK, USA, 24–26 June 2008; pp. 45–56. [Google Scholar]
- Zhang, R.; Tsai, P.S.; Cryer, J.E.; Shah, M. Shape from Shading: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 690–706. [Google Scholar] [CrossRef]
- Nayar, S.; Nakagawa, Y. Shape from Focus. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 824–831. [Google Scholar] [CrossRef]
- Favaro, P.; Soatto, S. A Geometric Approach to Shape from Defocus. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 406–417. [Google Scholar] [CrossRef]
- Shuanfeng, Z. Study on Driver Model Parameters Distribution for Fatigue Driving Levels Based on Quantum Genetic Algorithm. Open Cybern. Syst. J. 2015, 9, 1559–1566. [Google Scholar]
- Shuanfeng, Z.; Liang, L.; Guanghua, X.; Jing, W. Quantitative diagnosis of a spall-like fault of a rolling element bearing by empirical mode decomposition and the approximate entropy method. Mech. Syst. Sign. Process. 2013, 40, 154–177. [Google Scholar]
- Cang, Y.; He, H.; Qiao, Y. Measuring the Wave Height Based on Binocular Cameras. Sensors 2019, 19, 1338. [Google Scholar] [CrossRef]
- He, L.; Yang, J.; Kong, B.; Wang, C. An Automatic Measurement Method for Absolute Depth of Objects in Two Monocular Images Based on SIFT Feature. Appl. Sci. 2017, 7, 517. [Google Scholar] [CrossRef]
- Silberman, N.; Hoiem, D.; Kohli, P.; Fergus, R. Indoor segmentation and support inference from rgbd images. In Proceedings of the European Conference on Computer Vison, Florence, Italy, 7–13 October 2012; pp. 746–760. [Google Scholar]
- Saxena, A.; Sun, M.; Ng, A.Y. Make3d: Learning 3d scene structure from a single still image. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 824–840. [Google Scholar] [CrossRef]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth map prediction from a single image using a multi-scale deep network. arXiv 2014, arXiv:1406.2283. [Google Scholar]
- Cao, Y.; Wu, Z.; Shen, C. Estimating depth from monocular images as classification using deep fully convolution residual network. arXiv 2016, arXiv:1605.02305. [Google Scholar]
- Li, N.B.; Shen, N.C.; Dai, N.Y.; Hengel, A.V.D.; He, M. Depth and surface normal estimation from monocular images using regression on deep features and hierarchical CRFs. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1119–1127. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Liu, F.; Shen, C.; Lin, G. Deep Convolutional Neural Fields for Depth Estimation from a Single Image. arXiv 2014, arXiv:1411.6387. [Google Scholar]
- Roy, A.; Todorovic, S. Monocular Depth Estimation Using Neural Regression Forest. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 5506–5514. [Google Scholar]
- Sunok, K.; Sunghwan, C.; Kwanghoon, S. Learning depth from a single images using visual-depth words. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec, QC, Canada, 27–30 September 2015; pp. 1895–1899. [Google Scholar]
- Wenjie, L.; Alexander, G.S.; Raquel, U. Efficient deep learning for stereo matching. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 5695–5703. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The KITTI Vision Benchmark Suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Cordts, M.; Omran, M.; Ramos, S.; Rehfeld, T.; Enzweiler, M.; Benenson, R.; Franke, U.; Roth, S.; Schiele, B. The cityscapes dataset for semantic urban scene understanding. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 3354–3361. [Google Scholar]
- Garg, R.; BG, K.G.; Carneiro, G.; Reid, I. Unsupervised CNN for single view depth estimation: Geometry to the rescue. arXiv 2016, arXiv:1603.04992. [Google Scholar]
- Xie, J.; Girshick, R.; Farhadi, A. Deep3d: Fully automatic 2d-to-3d video conversion with deep convolution neural networks. arXiv 2016, arXiv:1604.03650. [Google Scholar]
- Zhou, T.; Brown, M.; Suavely, N.; Lowe, D.G. Unsupervised learning of depth and ego-motion from video. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6612–6619. [Google Scholar]
- Wang, C.; Buenaposada, J.M.; Zhu, R.; Lucey, S. Learning depth from monocular videos using direct methods. arXiv 2017, arXiv:1712.00175. [Google Scholar]
- Wang, C.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Hirschm, H. Stereo Processing by Semiglobal Matching and Mutual Information. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 30, 328–341. [Google Scholar] [CrossRef]
- Peris, M. Realistic CG Stereo Image Dataset with Ground Truth Disparity Maps. Tech. Rep. IEICE PRMU 2012, 111, 117–118. [Google Scholar]



| Layer | Channel I/O | Kernel_Size | Stride | Num_Layers | Num_Blocks/Skip | Scale | Input |
|---|---|---|---|---|---|---|---|
| Conv1 | 3/64 | 7 | 2 | 64 | RGB | ||
| Pool 1 | 64/64 | 3 | Conv1 | ||||
| Resblock_1 | 64/256 | 64 | 3 | Pool 1 | |||
| Resblock_2 | 256/512 | 128 | 4 | Resblock_1 | |||
| Resblock_3 | 512/1024 | 256 | 6 | Resblock_2 | |||
| Resblock_4 | 1024/2048 | 512 | 3 | Resblock_3 | |||
| Upconv5 | 2048/512 | 3 | 1 | 512 | 2 | Resblock_4 | |
| Contact5 | 512/512 | Resblock_3 | Upconv5 | ||||
| Iconv5 | 512/512 | 3 | 1 | 512 | Contact5 | ||
| Upconv4 | 512/256 | 3 | 1 | 256 | 2 | Iconv5 | |
| Contact4 | 256/256 | Resblock_2 | Upconv4 | ||||
| Iconv4 | 256/256 | 3 | 1 | 256 | Contact4 | ||
| Upconv3 | 256/128 | 3 | 1 | 128 | 2 | Iconv4 | |
| Contact3 | 128/128 | Resblock_1 | Upconv3 | ||||
| Iconv3 | 128/128 | 3 | 1 | 128 | Contact3 | ||
| Disp3 | 128/2 | 3 | 1 | 2 | Iconv3 | ||
| Udisp3 | 2/2 | 2 | Disp3 | ||||
| Upconv2 | 128/64 | 3 | 1 | 64 | 2 | Iconv3 | |
| Contact2 | 64/64 | Pool 1 | Upconv2 | ||||
| Iconv2 | 64/64 | 3 | 1 | 64 | Contact2 | ||
| Disp2 | 64/2 | 3 | 1 | 2 | Iconv2 | ||
| Udisp2 | 2/2 | 2 | Disp2 | ||||
| Upconv1 | 64/32 | 3 | 1 | 32 | 2 | Iconv2 | |
| Contact1 | 32/32 | Conv1 | Upconv1 | ||||
| Iconv1 | 32/32 | 3 | 1 | Contact1 | |||
| Disp1 | 32/2 | 3 | 1 | 2 | Iconv1 | ||
| Udisp1 | 2/2 | 2 | Disp1 | ||||
| Upconv0 | 32/16 | 3 | 1 | 16 | 2 | Iconv1 | |
| Contact0 | 16/16 | Udisp1 | Upconv0 | ||||
| Iconv0 | 16/16 | 3 | 1 | 16 | Contact0 | ||
| Disp0 | 16/2 | 3 | 1 | 2 | Iconv0 |
| Method | Supervised | Error (Lower is Better) | Accuracy (Higher is Better) | ||||
|---|---|---|---|---|---|---|---|
| REL | RMSE | Log RMSE | |||||
| Eigen et al. [15] | Yes | 0.203 | 6.307 | 0.282 | 0.702 | 0.890 | 0.958 |
| Cao et al. [16] | Yes | 0.202 | 6.523 | 0.275 | 0.678 | 0.895 | 0.965 |
| Garg et al. [25] | No | 0.208 | 6.856 | 0.283 | 0.678 | 0.885 | 0.957 |
| Xie et al. [26] | No | 0.189 | 6.642 | 0.254 | 0.752 | 0.904 | 0.961 |
| Wang et al. [27] | No | 0.159 | 5.789 | 0.234 | 0.796 | 0.923 | 0.963 |
| Our model | No | 0.135 | 5.446 | 0.215 | 0.895 | 0.979 | 0.986 |
| Method | Supervised | Error (Lower is Better) | Accuracy (Higher is Better) | ||||
|---|---|---|---|---|---|---|---|
| REL | RMSE | Log RMSE | |||||
| Our model (No pyramid) | No | 0.352 | 6.056 | 0.395 | 0.752 | 0.889 | 0.926 |
| Our model (VGG-16) | No | 0.452 | 8.976 | 0.556 | 0.646 | 0.735 | 0.806 |
| Our model (loss of ) | No | 0.396 | 7.152 | 0.465 | 0.672 | 0.796 | 0.845 |
| Our model (loss of ) | No | 0.383 | 7.096 | 0.452 | 0.684 | 0.806 | 0.850 |
| Our model (no skip) | No | 0.362 | 6.758 | 0.425 | 0.696 | 0.854 | 0.895 |
| Our model | No | 0.135 | 5.446 | 0.215 | 0.895 | 0.979 | 0.986 |
| Method | Supervised | Error (Lower is Better) | Accuracy (Higher is Better) | ||||
|---|---|---|---|---|---|---|---|
| REL | RMSE | Log RMSE | |||||
| Eigen et al. [15] | Yes | 0.417 | 8.526 | 0.403 | 0.692 | 0.899 | 0.948 |
| Cao et al. [16] | Yes | 0.462 | 9.972 | 0.456 | 0.656 | 0.887 | 0.945 |
| Garg et al. [25] | No | 0.443 | 8.326 | 0.398 | 0.662 | 0.885 | 0.932 |
| Xie et al. [26] | No | 0.410 | 8.125 | 0.378 | 0.683 | 0.895 | 0.938 |
| Wang et al. [27] | No | 0.387 | 7.895 | 0.354 | 0.704 | 0.899 | 0.946 |
| Our model | No | 0.328 | 7.529 | 0.348 | 0.751 | 0.924 | 0.962 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, T.; Zhao, S.; Geng, L.; Xu, Q. Unsupervised Monocular Depth Estimation Based on Residual Neural Network of Coarse–Refined Feature Extractions for Drone. Electronics 2019, 8, 1179. https://doi.org/10.3390/electronics8101179
Huang T, Zhao S, Geng L, Xu Q. Unsupervised Monocular Depth Estimation Based on Residual Neural Network of Coarse–Refined Feature Extractions for Drone. Electronics. 2019; 8(10):1179. https://doi.org/10.3390/electronics8101179
Chicago/Turabian StyleHuang, Tao, Shuanfeng Zhao, Longlong Geng, and Qian Xu. 2019. "Unsupervised Monocular Depth Estimation Based on Residual Neural Network of Coarse–Refined Feature Extractions for Drone" Electronics 8, no. 10: 1179. https://doi.org/10.3390/electronics8101179
APA StyleHuang, T., Zhao, S., Geng, L., & Xu, Q. (2019). Unsupervised Monocular Depth Estimation Based on Residual Neural Network of Coarse–Refined Feature Extractions for Drone. Electronics, 8(10), 1179. https://doi.org/10.3390/electronics8101179





