A Fast GMPPT Algorithm Based on PV Characteristic for Partial Shading Conditions
Abstract
:1. Introduction
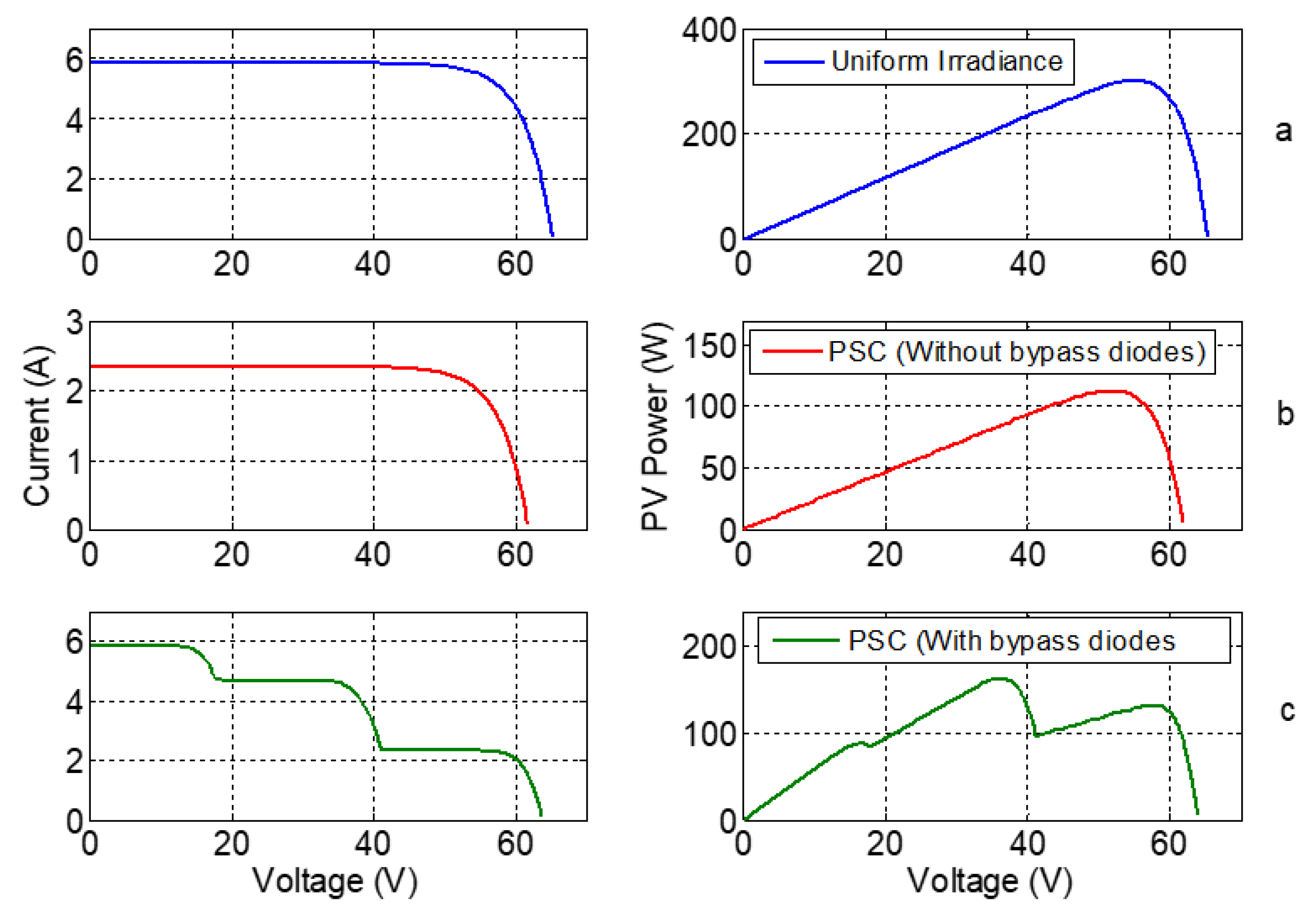
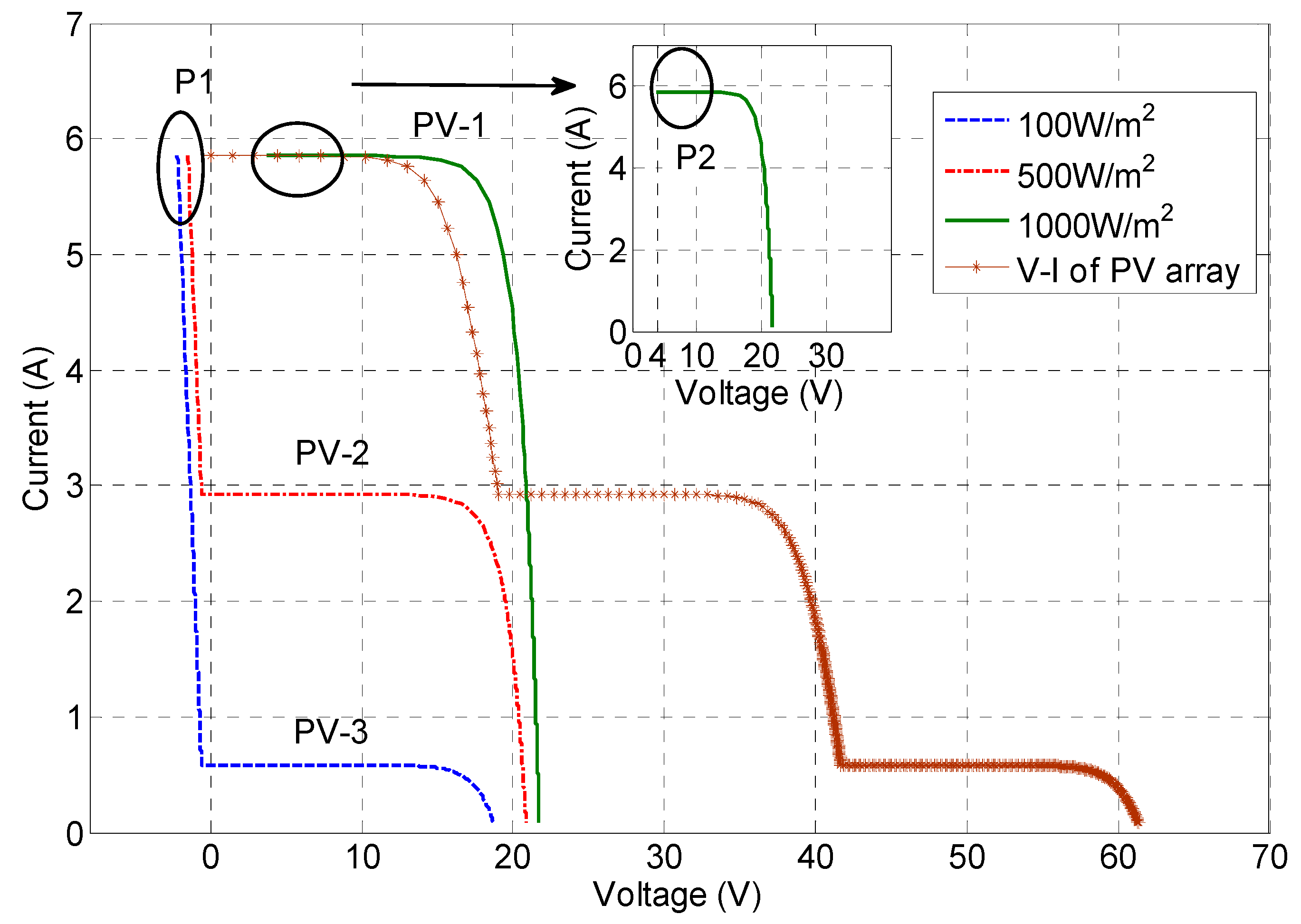
2. PV Characteristic in PSC
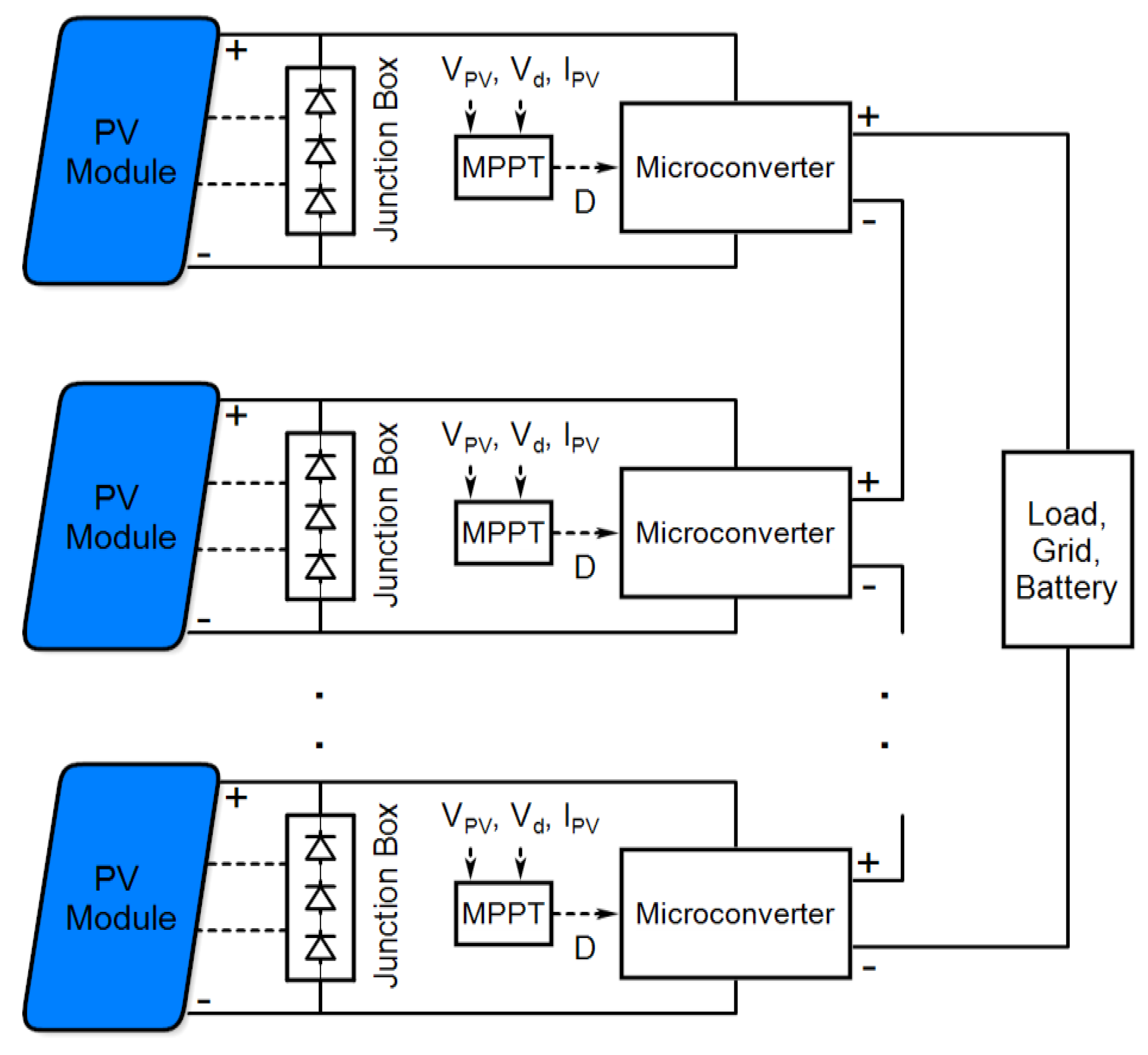
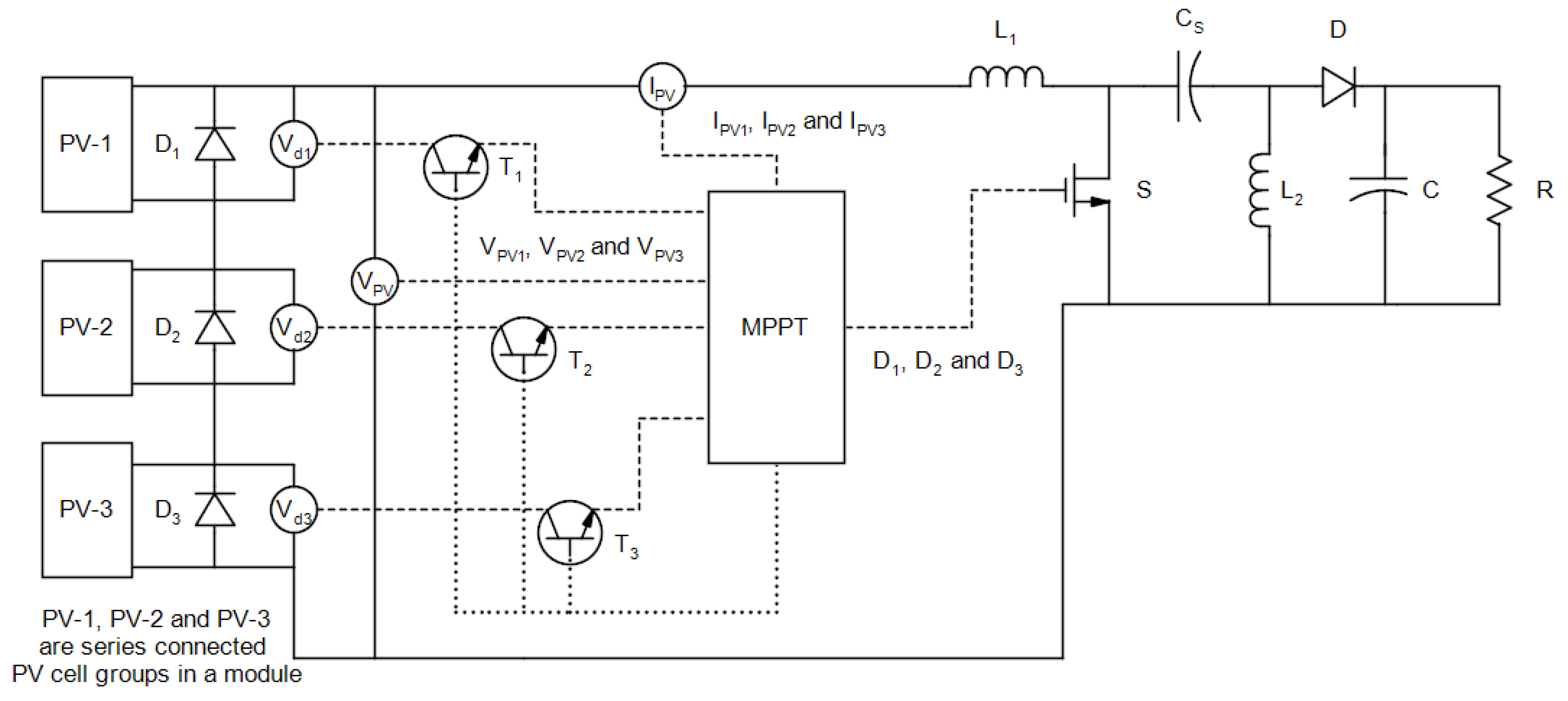
3. Materials and Methodology
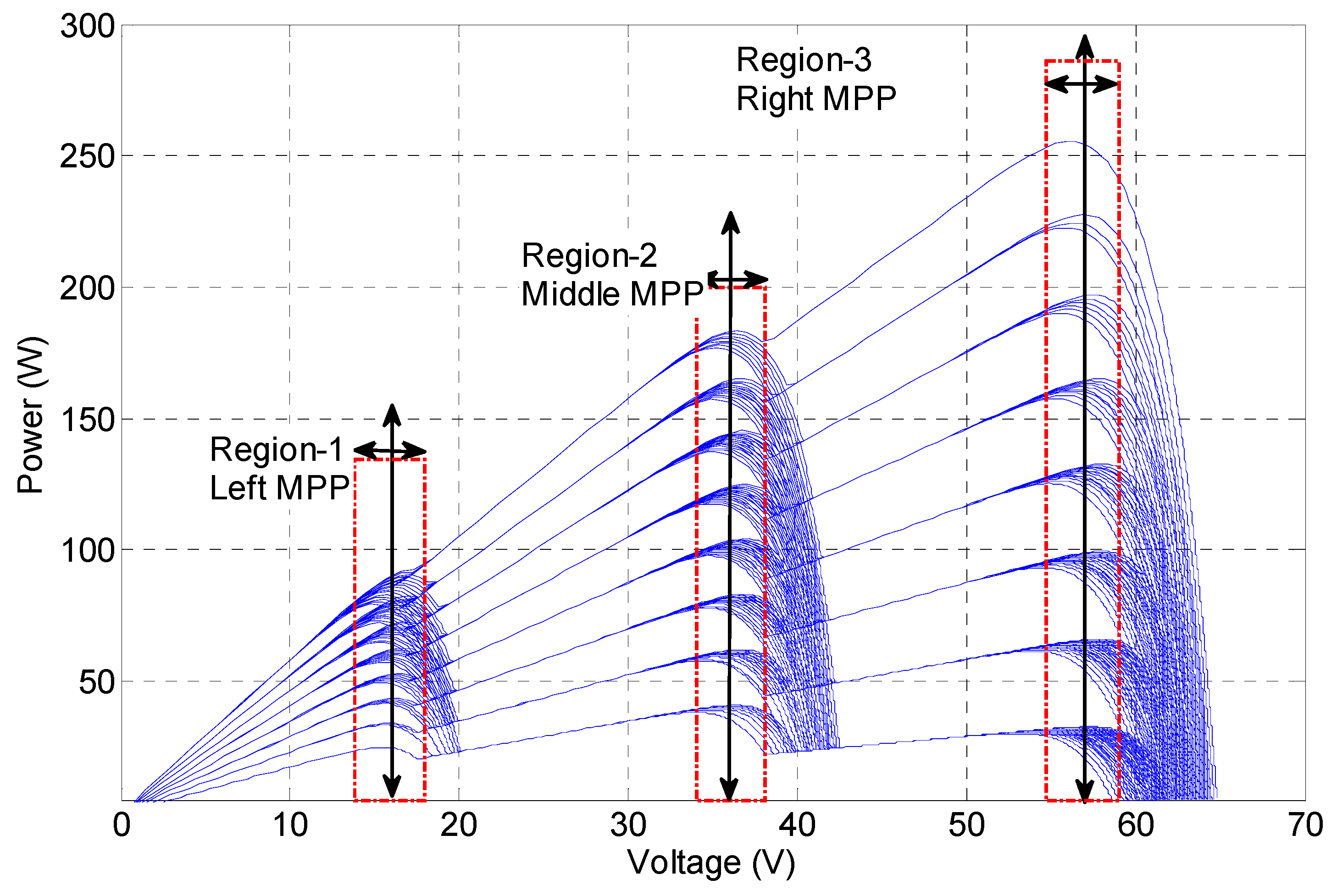
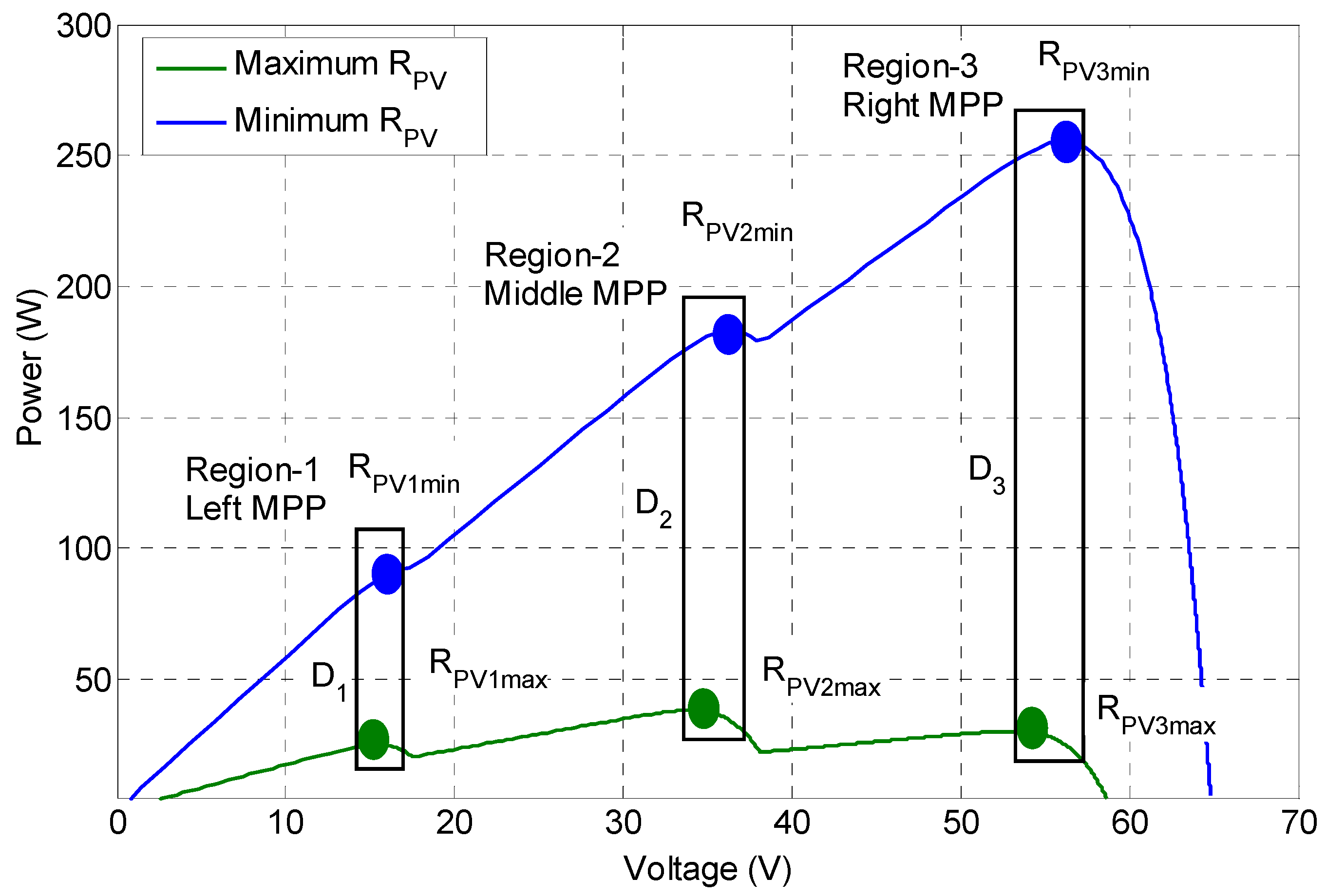
3.1. Preliminary Analyses for Power-Voltage Curve under PSCs
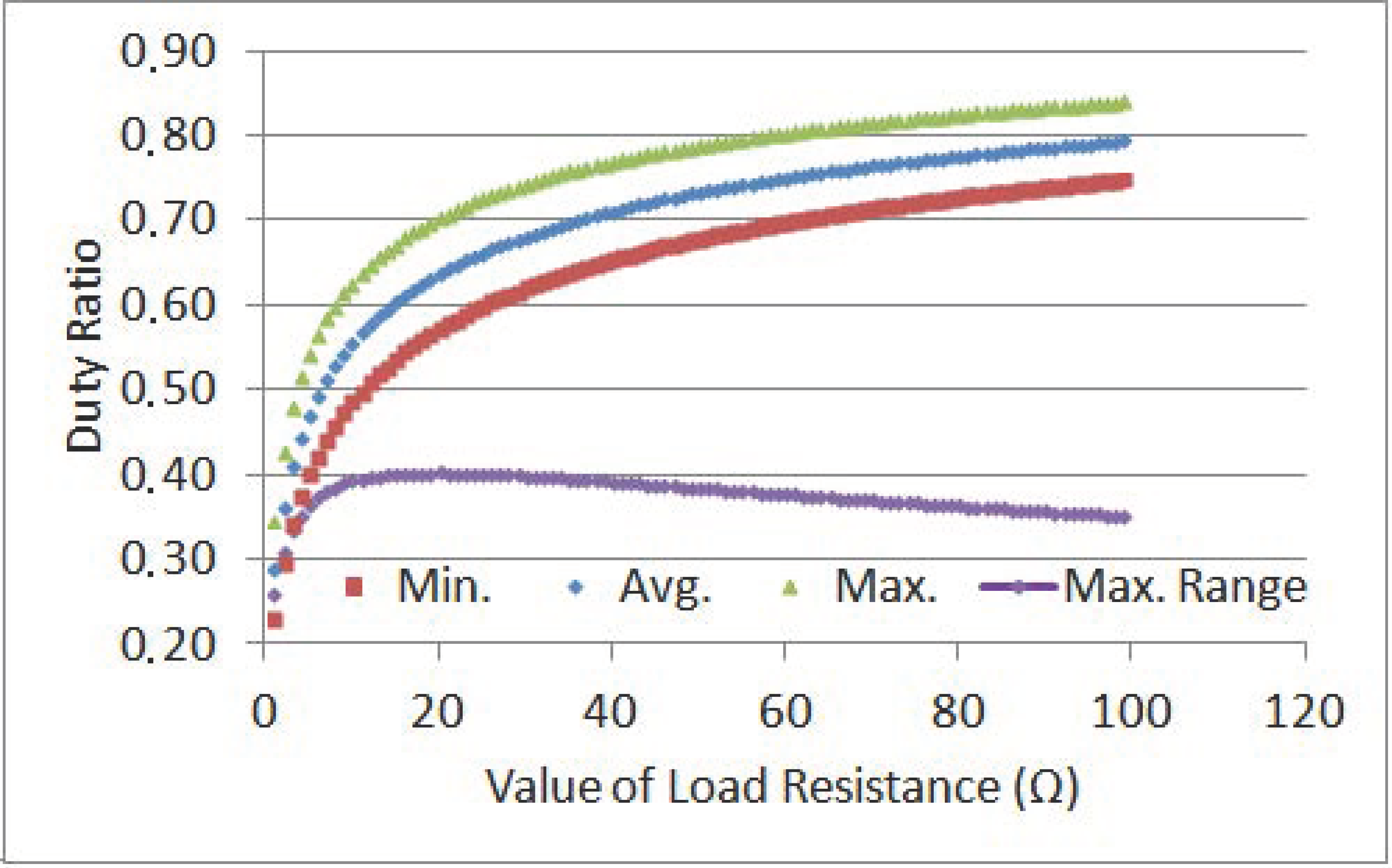
3.2. Duty Ratio and Load Characteristic
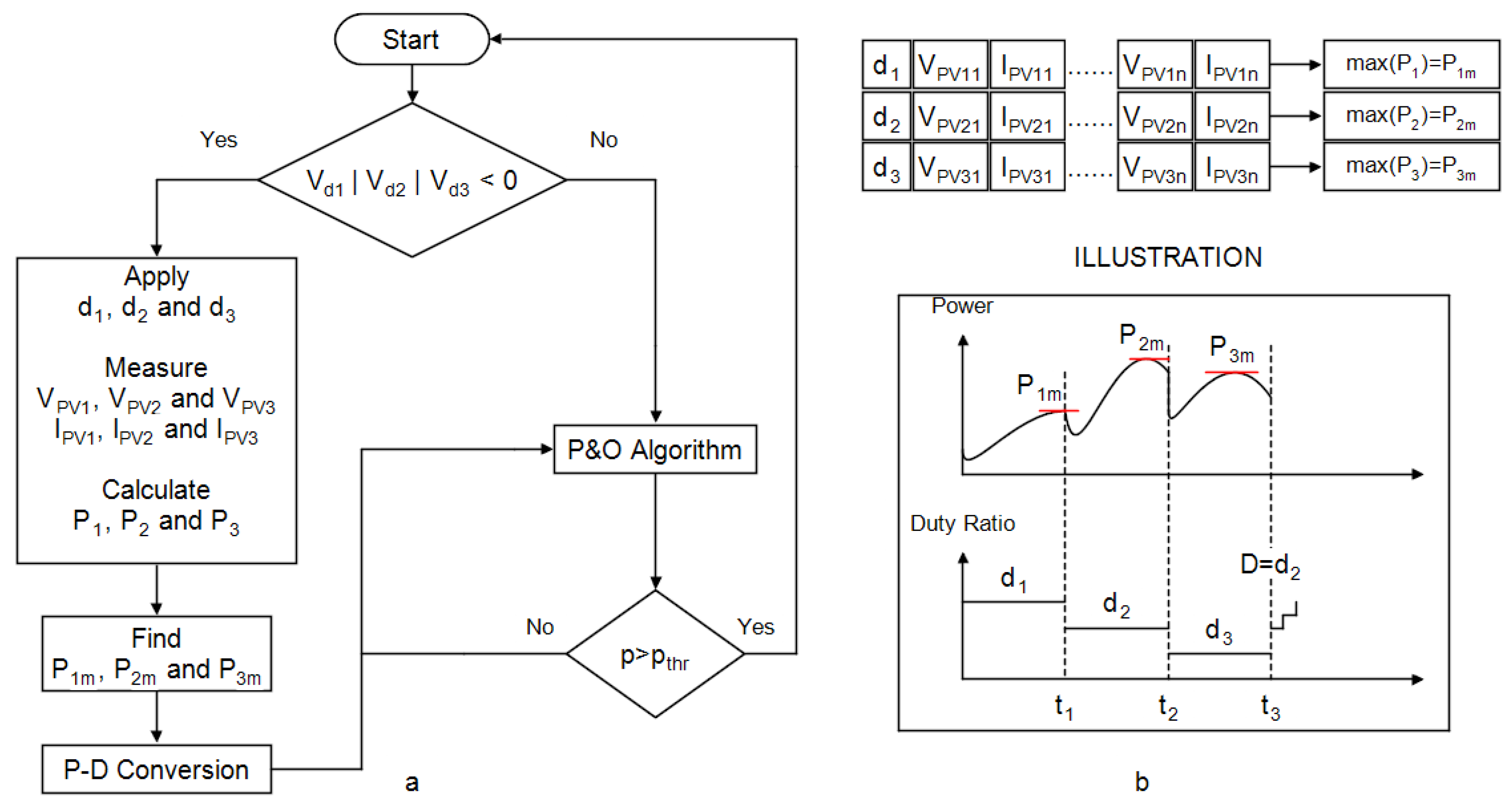
3.3. Proposed Algorithm
4. Performance of the Proposed Algorithm
4.1. Simulation Results
4.2. Experimental Results
4.3. Evaluation of the Proposed Algorithm
5. Conclusions
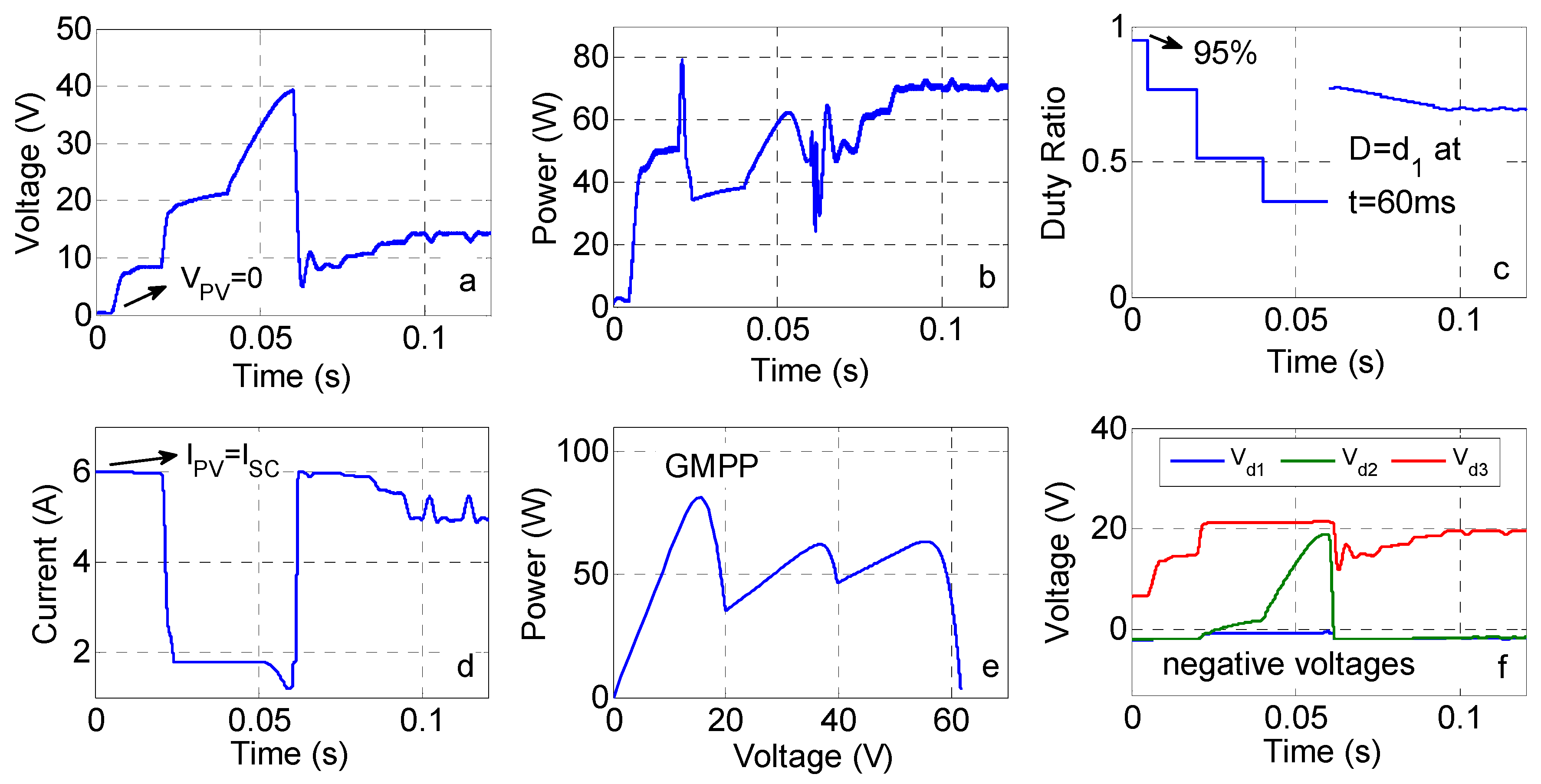
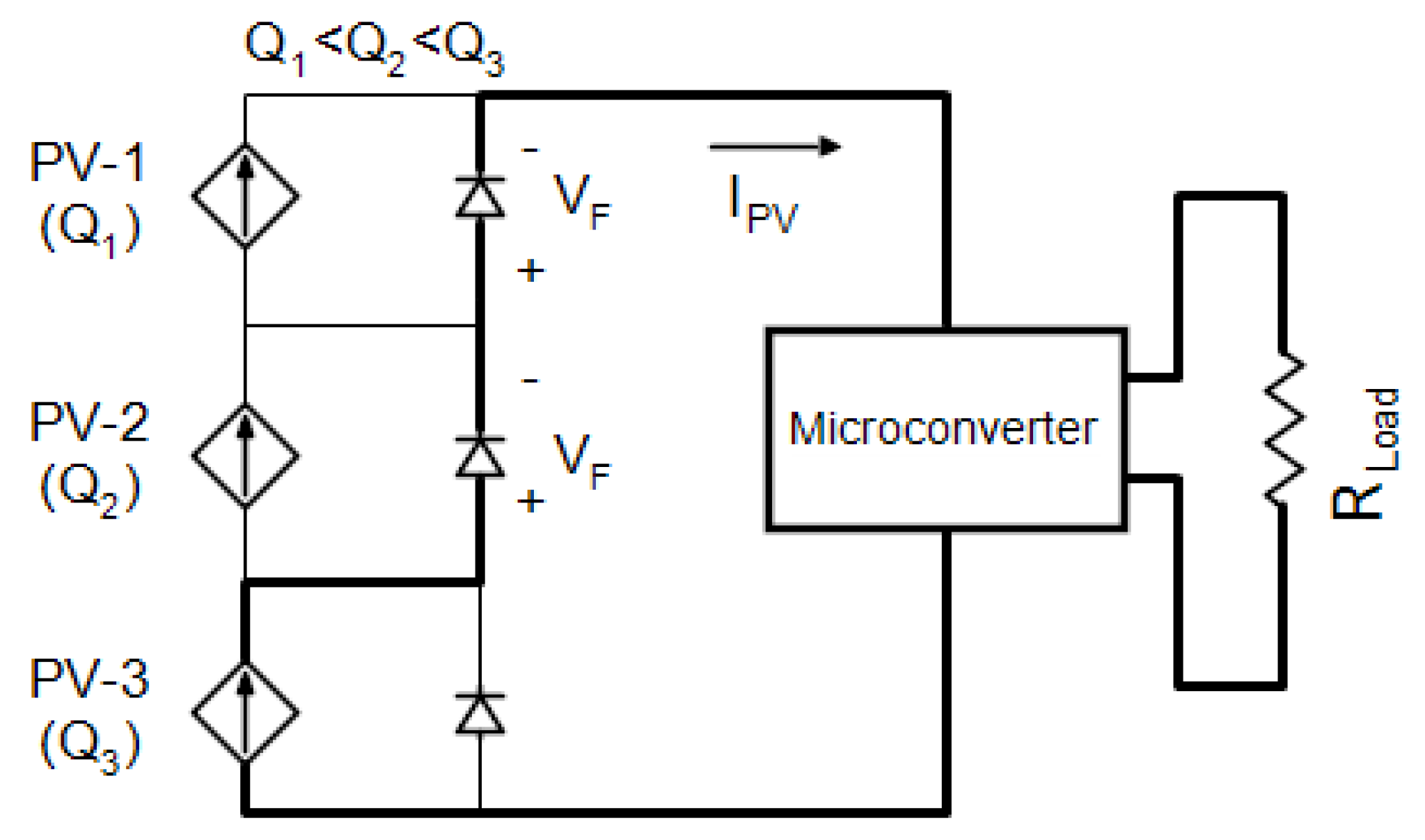
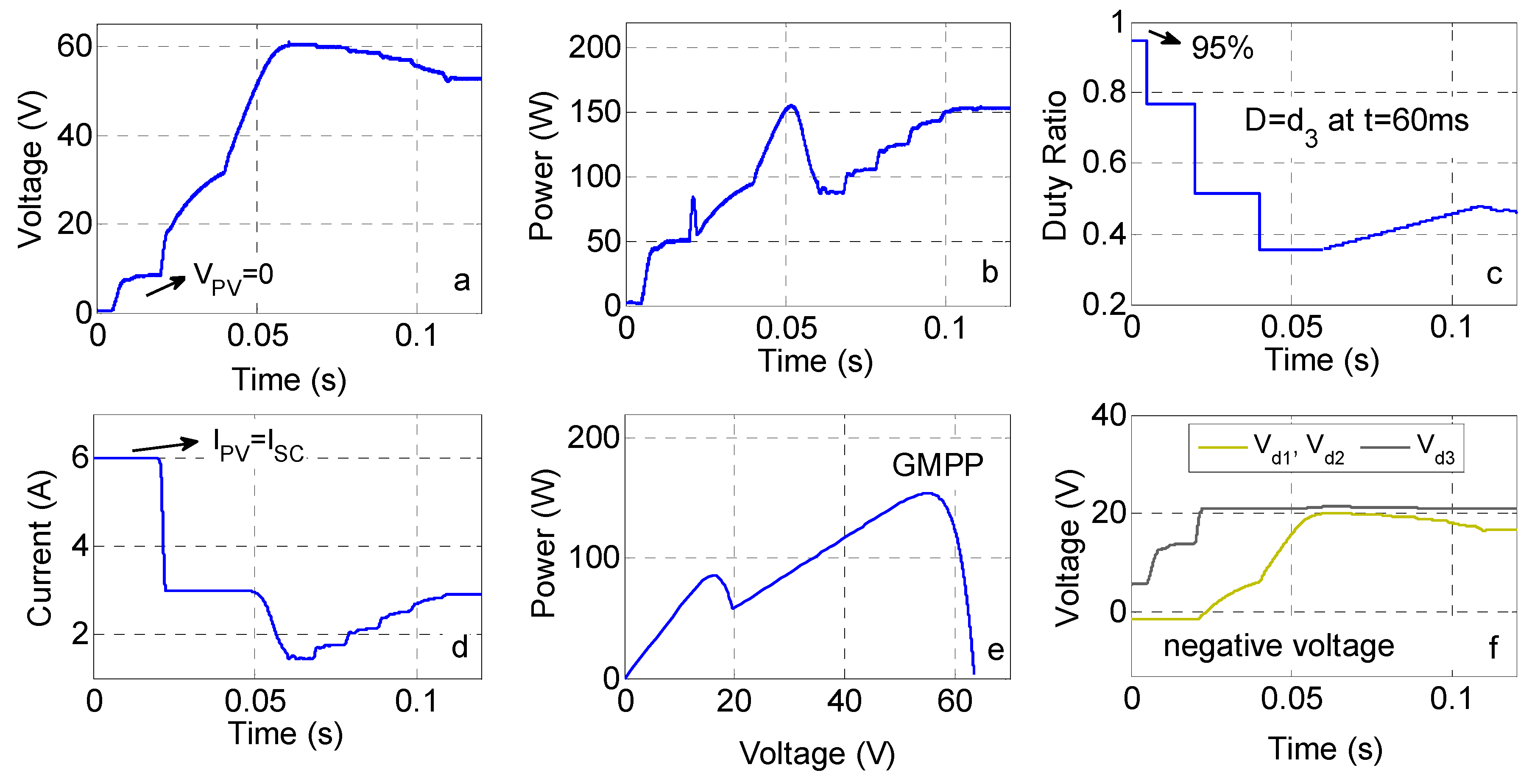
- Voltage values of the bypass diodes are checked in order to detect partial shading. If one of the bypass diodes has a negative voltage value, it can be understood that partial shading occurs. However, the voltages of bypass diodes have to be measured under a specified condition. If the maximum value of duty ratio is set to its maximum value, the current of the module is equal to SCC of the module that satisfies the specified condition. It is also worth noting that there is no need to know the SCC of the module.
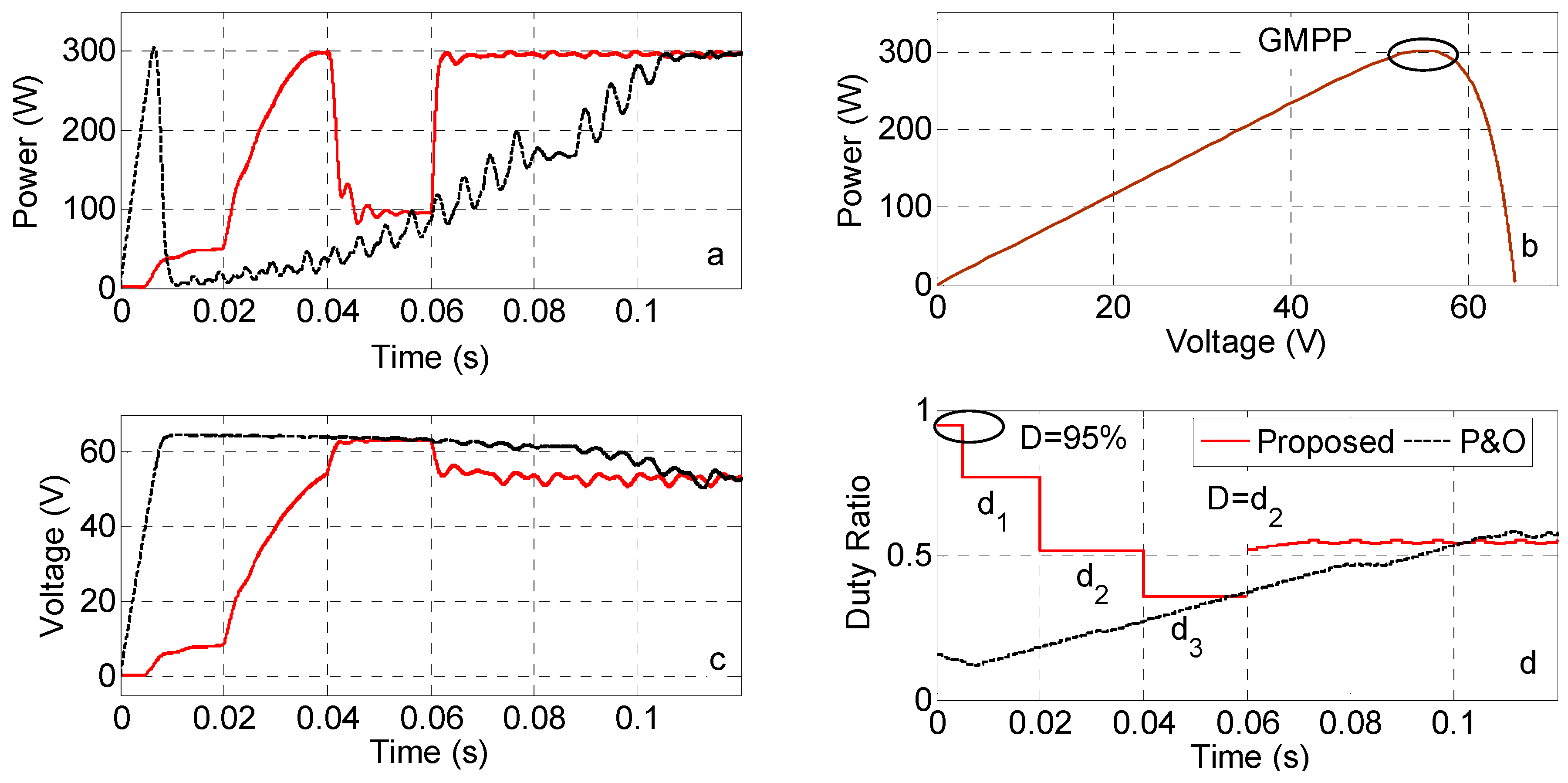
- A contribution presented is about the determination the maximum available duty range in a buck-boost converter topology. It is shown that GMPPs are clustered in a limited duty ratio interval. This interval is approximately 40% for buck-boost converter topology. However, the proposed algorithm does not use a classical scanning procedure. It uses the duties ratios calculated, which are in this limited interval, so as to reach the vicinity of the GMPP. As maximum power is stored for each duty ratios MPP (for all MPPs), it is guaranteed to track GMPP for all shading cases.
- The proposed algorithm has low system dependency and it realizes a fast tracking when compared with the compared studies, which is verified by different simulation and experiments.
- It is verified by the simulation and experimental studies that the proposed algorithm can be used instead of P&O algorithm with a variable step size approach.
- The proposed algorithm is very simple and it leads to the low computational burden. Thus, it can be implemented by a low cost microcontroller. It is expected to have good performance in module based DC power optimizers (micro converter), since a module has limited bypass diodes.
Funding
Conflicts of Interest
References
- Renewables Global Status Report. 2015. Available online: http://www.ren21.net/wp-content/uploads/2015/07/REN12-GSR2015_Onlinebook_low1.pdf (accessed on 1 December 2015).
- Esram, T.; Chapman, P.L. Comparison of photovoltaic array maximum power point tracking techniques. IEEE Trans. Energy Convers. 2007, 22, 439–449. [Google Scholar] [CrossRef]
- Liu, F.; Duan, S.; Liu, F.; Liu, B.; Kang, Y. A variable step size INC method for PV systems. IEEE Trans. Ind. Electron. 2008, 55, 2622–2628. [Google Scholar]
- Noguchi, T.; Togashi, S.; Nakamoto, R. Short-current pulse-based maximum-power-point tracking method for multiple photovoltaic-and-converter module system. IEEE Trans. Ind. Electron. 2002, 49, 217–223. [Google Scholar] [CrossRef]
- Masoum, M.A.S.; Dehbonei, H.; Fuchs, E.F. Theoretical and experimental analyzes of photovoltaic systems with voltage and current based maximum power point tracking. IEEE Trans. Energy Convers. 2002, 17, 514–522. [Google Scholar] [CrossRef]
- Kobayashi, K.; Takano, I.; Sawada, Y. A study of a two stage maximum power point tracking control of a photovoltaic system under partially shaded insolation conditions. Sol. Energy Mater. Sol. Cells 2006, 90, 2975–2988. [Google Scholar] [CrossRef]
- Tey, K.S.; Mekhilef, S. Modified incremental conductance algorithm for photovoltaic system under partial shading conditions and load variation. IEEE Trans. Ind. Electron. 2014, 61, 53845–53892. [Google Scholar]
- Ahmed, N.A.; Miyatake, M. A novel maximum power point tracking for photovoltaic applications under partially shaded insolation conditions. Electr. Power Syst. Res. 2008, 78, 777–784. [Google Scholar] [CrossRef]
- Patel, H.; Agarwal, V. Maximum power point tracking scheme for PV system operating under partially shaded conditions. IEEE Trans. Ind. Electron. 2008, 55, 1689–1698. [Google Scholar] [CrossRef]
- Nguyen, T.L.; Low, K. A global maximum power point tracking scheme employing direct search algorithm for photovoltaic systems. IEEE Trans. Ind. Electron. 2010, 57, 3456–3467. [Google Scholar] [CrossRef]
- Renaudineau, H.; Houari, A.; Martin, J.P.; Pierfederici, S.; Meibody-Tabar, F.; Gerardin, B. A new approach in tracking maximum power under partially shaded conditions with consideration of converter losses. Sol. Energy 2011, 85, 2580–2588. [Google Scholar] [CrossRef]
- Ji, Y.; Jung, D.; Kim, J.; Kim, J.H.; Lee, T.; Won, C. A real maximum power point tracking method for mismatching compensation in PV array under partially shaded conditions. IEEE Trans. Power Electron. 2011, 26, 1001–1009. [Google Scholar] [CrossRef]
- Kouchaki, A.; Iman-Eini, H.; Asaei, B. A new maximum power point tracking strategy for PV arrays under uniform and non-uniform insolation conditions. Sol. Energy 2013, 91, 221–232. [Google Scholar] [CrossRef]
- Gokmen, N.; Karatepe, E.; Urganlı, G.; Silvestre, S. Voltage band based global MPPT controller for photovoltaic systems. Sol. Energy 2013, 98, 322–334. [Google Scholar] [CrossRef]
- Vincenzo, M.C.D.; Infield, D. New maximum power point tracker for photovoltaic systems exposed to realistic operational conditions. IET Renew. Power Gener. 2014, 8, 629–637. [Google Scholar] [CrossRef]
- Parlak, K.S. FPGA based new MPPT (maximum power point tracking) method for PV (photovoltaic) array system operating partially shaded conditions. Energy 2014, 68, 399–410. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, J.; Huang, J. Global maximum power point tracking algorithm for PV systems operating under partially shaded conditions using the segmentation search method. Sol. Energy 2014, 103, 350–363. [Google Scholar] [CrossRef]
- Murtaza, A.; Chiaberge, M.; Spertino, F.; Boero, D.; Giuseppe, M.D. A maximum power point tracking technique based on bypass diode mechanism for PV arrays under partial shading. Energy Build. 2014, 73, 13–25. [Google Scholar] [CrossRef]
- Tey, K.S.; Mekhilef, S. A fast-converging MPPT technique for photovoltaic system under fast-varying solar irradiation and load resistance. IEEE Trans. Ind. Inform. 2015, 11, 176–186. [Google Scholar]
- Syafaruddin; Karatepe, E.; Hiyama, T. Artificial neural network -polar coordinated fuzzy controller based maximum power point tracking control under partially shaded conditions. IET Renew. Power Gener. 2009, 3, 239–253. [Google Scholar] [CrossRef]
- Zainuri, M.A.A.M.; Radzi, M.A.M.; Soh, A.C.; Rahim, N.A. Development of adaptive perturb and observe fuzzy control maximum power point tracking for photovoltaic boost dc-dc converter. IET Renew. Power Gener. 2014, 8, 183–194. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z. A deterministic particle swarm optimization maximum power point tracker for photovoltaic system under partial shading condition. IEEE Trans. Ind. Electron. 2013, 60, 3195–3206. [Google Scholar]
- Tey, K.S.; Mekhilef, S.; Seyedmahmoudian, M.; Horan, B.; Oo, A.T.; Stojcevski, A. Improved differential evolution-based MPPT algorithm using SEPIC for PV systems under partial shading conditions and load variation. IEEE Trans. Ind. Inform. 2018, 14, 4322–4333. [Google Scholar] [CrossRef]
- Seyedmahmoudian, M.; Horan, B.; Tey, K.S.; Rahmani, R.; Oo, A.M.T.; Mekhilef, S.; Stojcevski, A. State of the art artificial intelligence-based MPPT techniques for mitigating partial shading effects on PV systems–A review. Renew. Sustain. Energy Rev. 2016, 64, 435–455. [Google Scholar] [CrossRef]
- Sundareswaran, K.; Peddapati, S.; Palani, S. MPPT of PV systems under partial shaded conditions through a colony of flashing fireflies. IEEE Trans. Energy Convers. 2014, 29, 463–472. [Google Scholar]
- Jiang, L.L.; Maskell, D.L.; Patra, J.C. A novel colony optimization based maximum power point tracking for photovoltaic systems under partially shaded conditions. Energy Build. 2013, 58, 227–236. [Google Scholar] [CrossRef]
- Daraban, S.; Petreus, D.; Morel, C. A novel MPPT (maximum power point tracking) algorithm based on a modified genetic algorithm specialized on tracking the global maximum power point in photovoltaic systems affected by partial shading. Energy 2014, 74, 374–388. [Google Scholar] [CrossRef]
- Başoğlu, M.E. An enhanced scanning-based MPPT approach for DMPPT systems. Int. J. Electron. 2018, 60, 1100–1113. [Google Scholar] [CrossRef]
- How to Choose a Bypass Diode for a Silicon Panel Junction Box. Available online: https://www.st.com/content/ccc/resource/technical/document/application_note/cc/6a/fe/6d/f6/17/40/3c/DM00034029.pdf/files/DM00034029.pdf/jcr:content/translations/en.DM00034029.pdf (accessed on 2 June 2012).
- Qi, J.; Zhang, Y.; Chen, Y. Modeling and maximum power point tracking (MPPT) method for PV array under partial shading conditions. Renew. Energy 2014, 66, 337–345. [Google Scholar] [CrossRef]
- Başoğlu, M.E.; Çakır, B. Comparisons of MPPT performances of isolated and non-isolated DC-DC converters by using a new approach. Renew. Sustain. Energy Rev. 2016, 112, 1100–1113. [Google Scholar] [CrossRef]
- Başoğlu, M.E. An improved 0.8VOC model based GMPPT technique for module level power optimizers. IEEE Trans. Ind. Appl. 2019, 55, 1913–1921. [Google Scholar] [CrossRef]
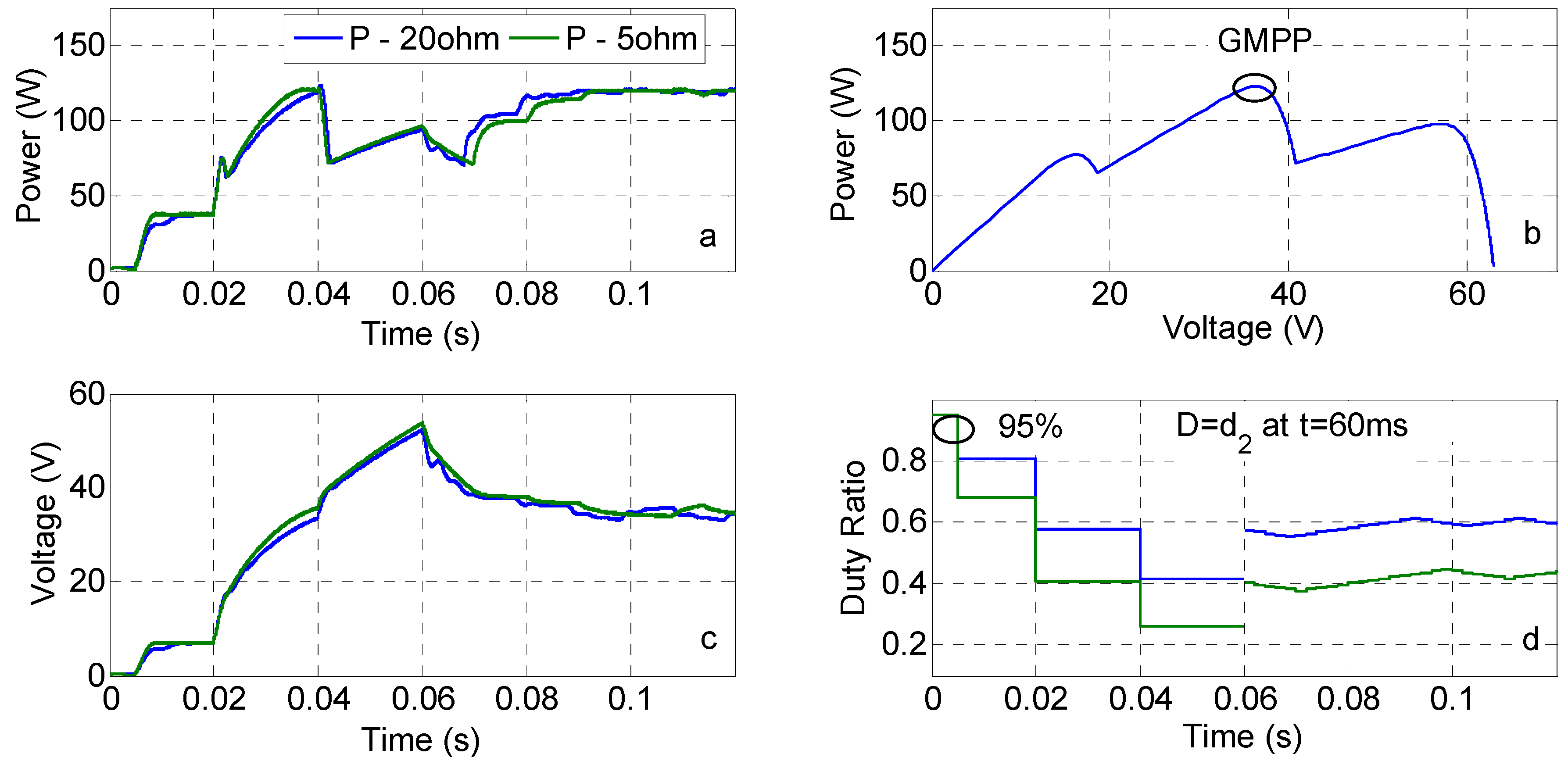

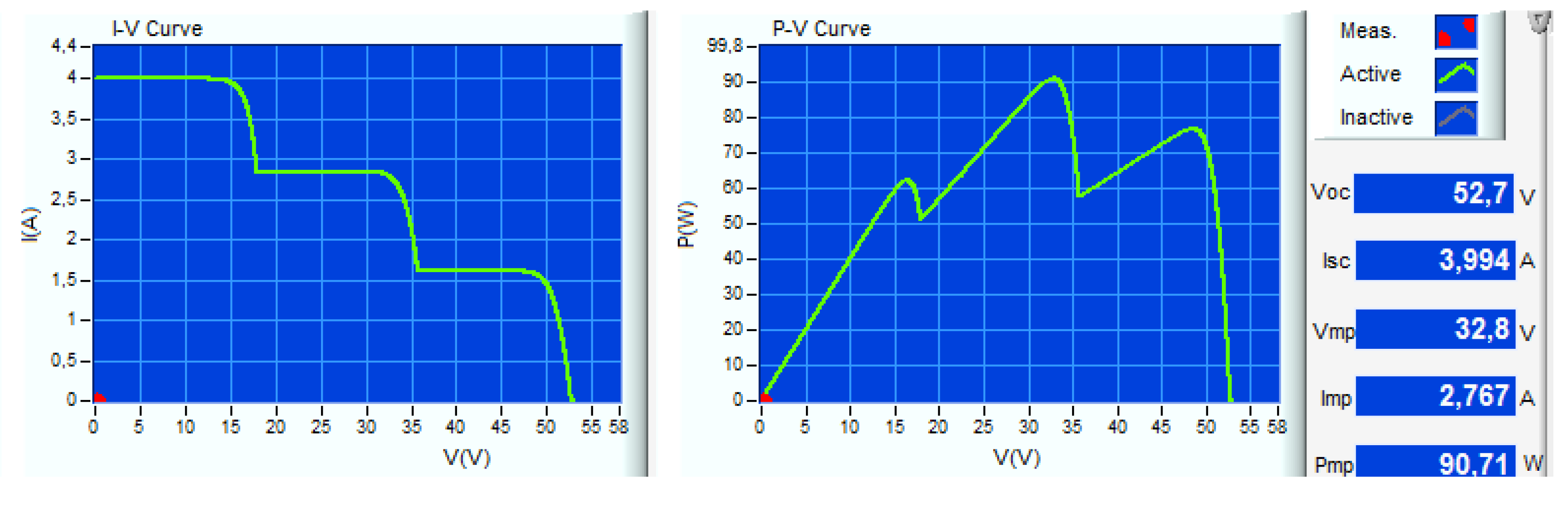
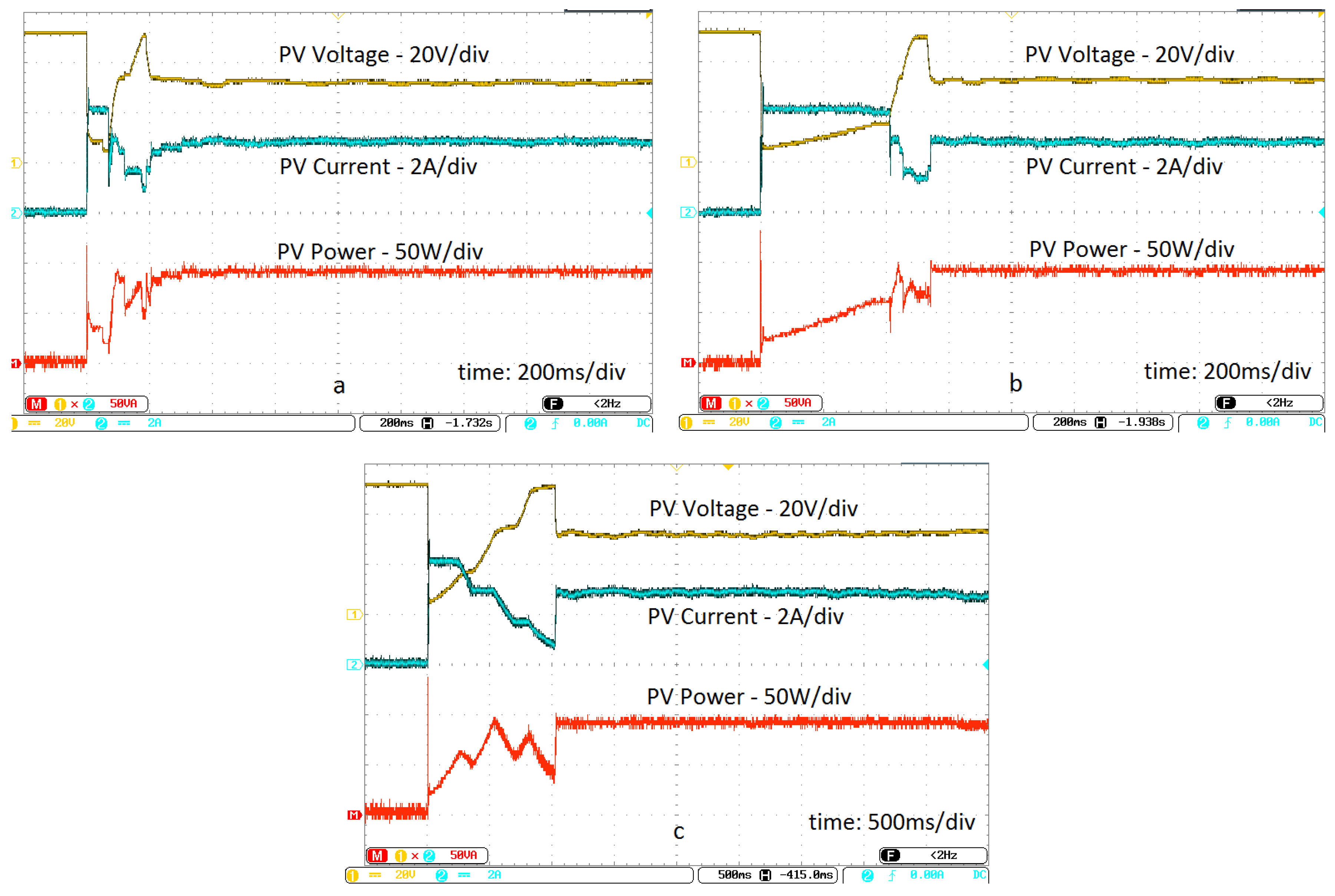
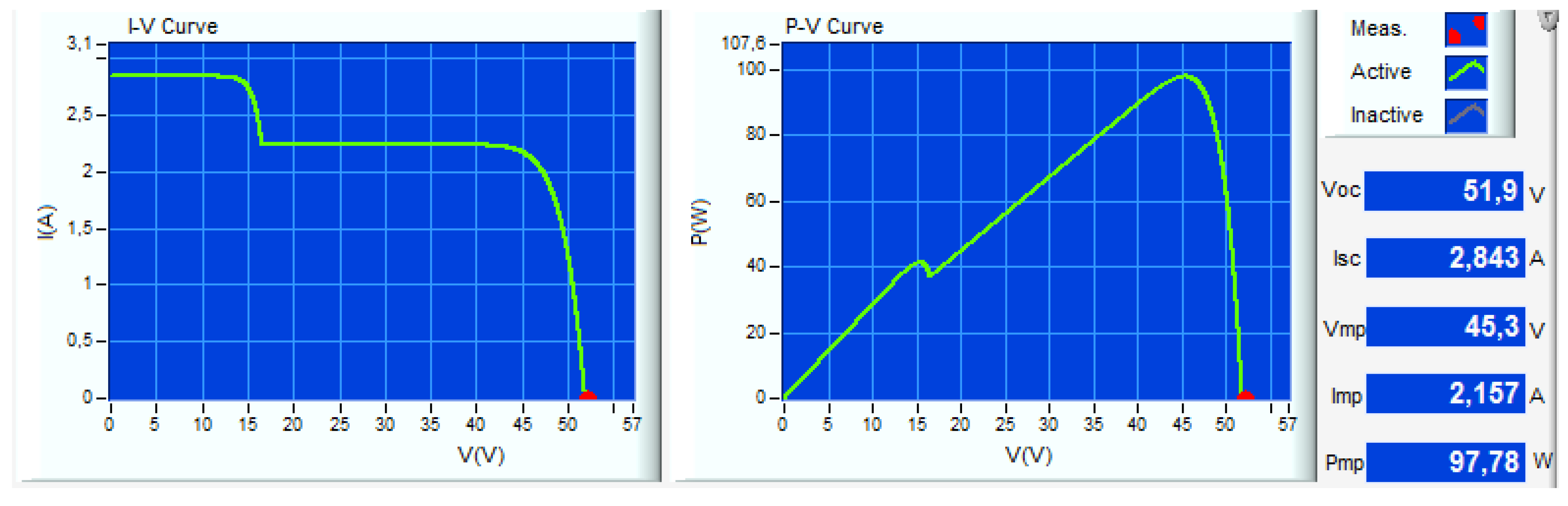
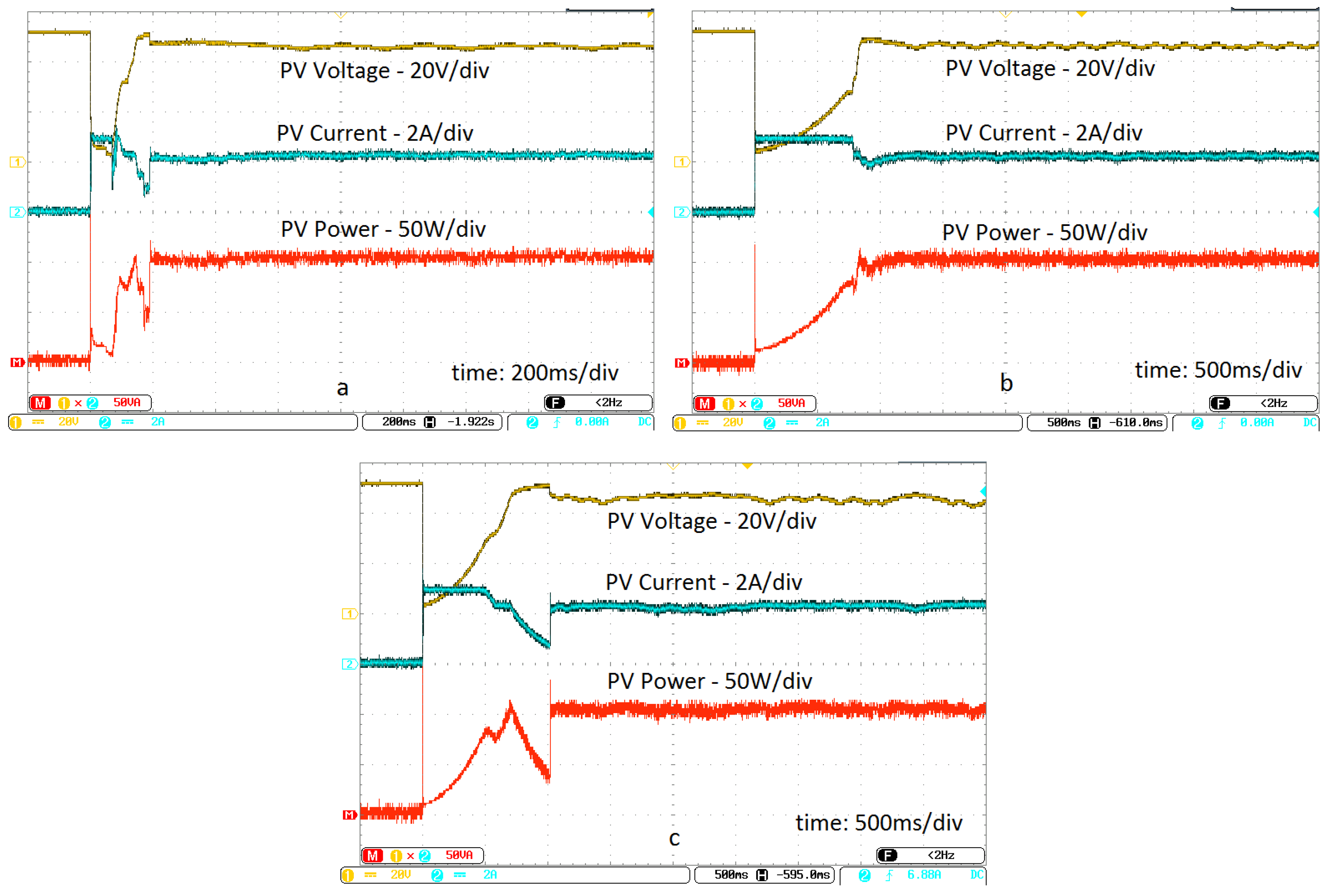
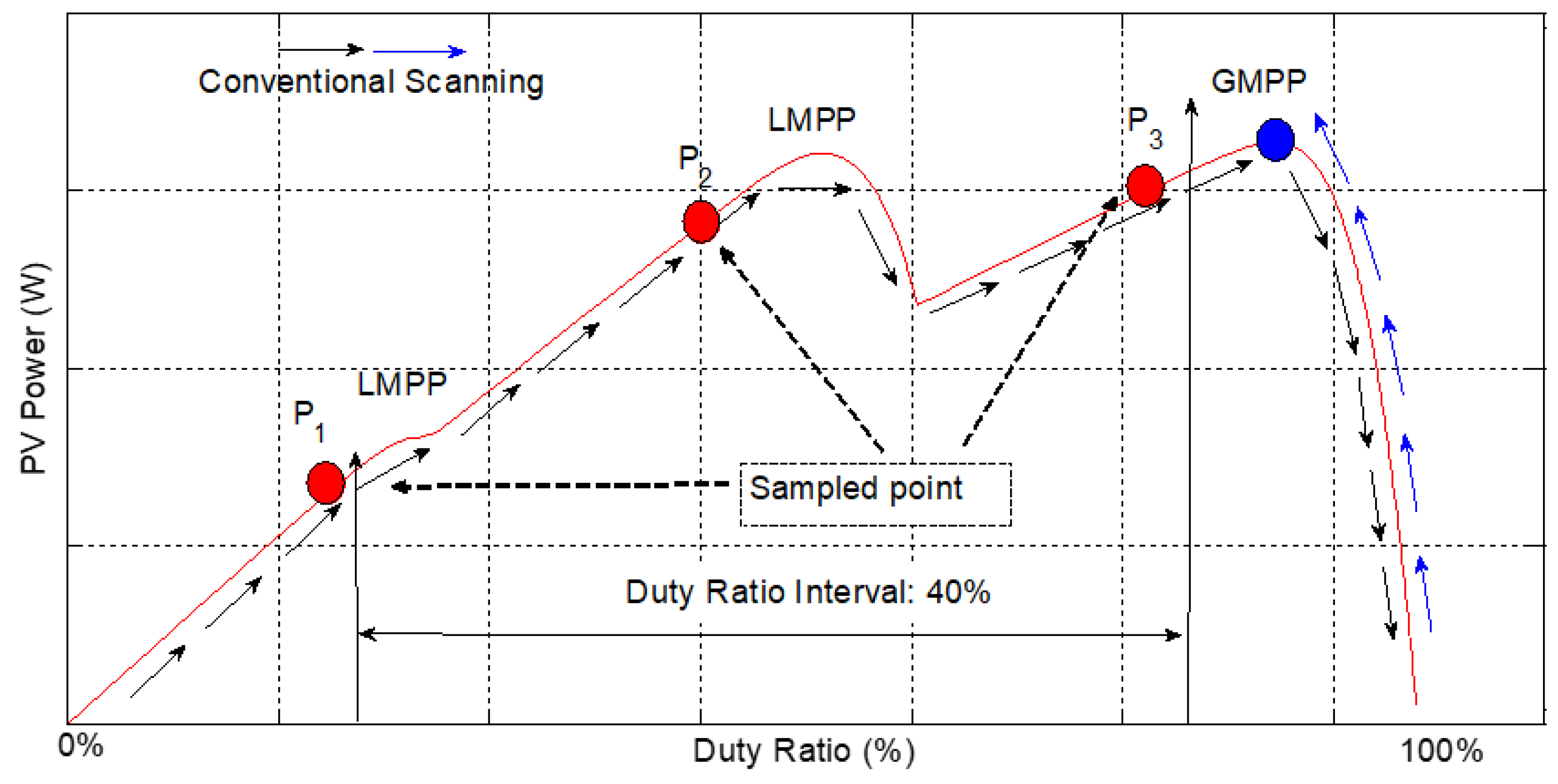
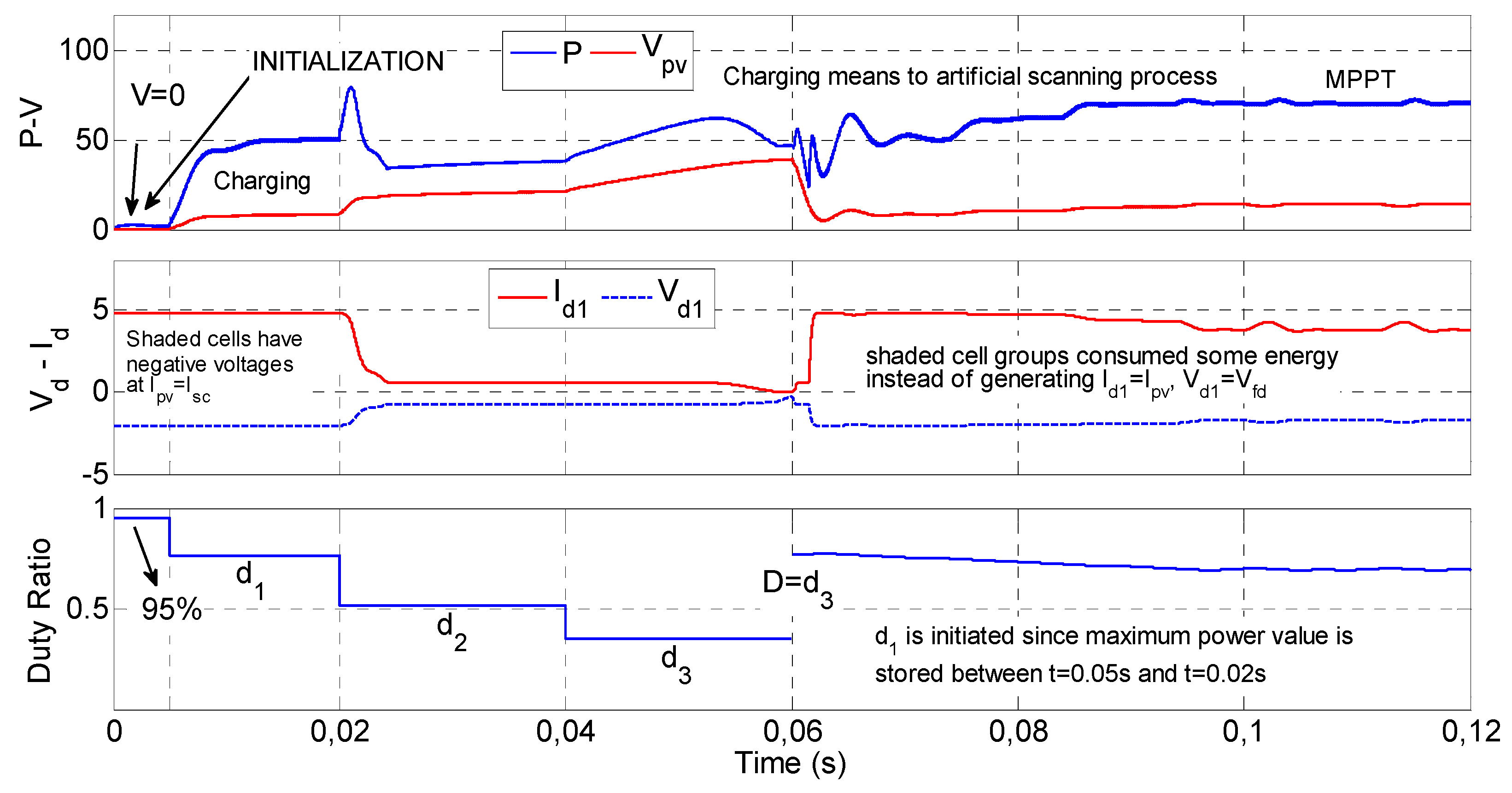
| PV Module @ STC & SEPIC | Feature |
|---|---|
| Short circuit current | 5.85 A |
| Open circuit voltage | 65.2 V |
| Maximum power current | 5.5 A |
| Maximum power voltage | 54.9 V |
| Maximum power | 302 W |
| Bypass diodes | 3 |
| Coupled inductance | 681 µH |
| Input/output capacitor | 1000 µF/100 µF |
| Coupled capacitor | 33 µC |
| Microcontroller | PIC18F452 |
| Current transducer | LTS25-NP |
| Voltage sensing | Voltage divider |
| MOSFET | IRFP450 |
| Diode | MUR860 |
| Switching frequency | 20 kHz |
| Case | Irradiance (kW/m2) | Rload (Ω) | Duty Initialization | ηTR (%) at MPP |
|---|---|---|---|---|
| 1 | 0.2–0.3–1 | 12 | D = d1 | 87.65 |
| 2 | 0.5–0.5–1 | 12 | D = d3 | 99.35 |
| 3 | 1–1–1 | 12 | D = d3 | 98.3 |
| 4 | 0.3–0.6–0.9 | 20 | D = d2 | 99.21 |
| 5 | 0.3–0.6–0.9 | 5 | D = d2 | 99.3 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Başoğlu, M.E. A Fast GMPPT Algorithm Based on PV Characteristic for Partial Shading Conditions. Electronics 2019, 8, 1142. https://doi.org/10.3390/electronics8101142
Başoğlu ME. A Fast GMPPT Algorithm Based on PV Characteristic for Partial Shading Conditions. Electronics. 2019; 8(10):1142. https://doi.org/10.3390/electronics8101142
Chicago/Turabian StyleBaşoğlu, Mustafa Engin. 2019. "A Fast GMPPT Algorithm Based on PV Characteristic for Partial Shading Conditions" Electronics 8, no. 10: 1142. https://doi.org/10.3390/electronics8101142
APA StyleBaşoğlu, M. E. (2019). A Fast GMPPT Algorithm Based on PV Characteristic for Partial Shading Conditions. Electronics, 8(10), 1142. https://doi.org/10.3390/electronics8101142




