4.2. Experimental Data Analysis
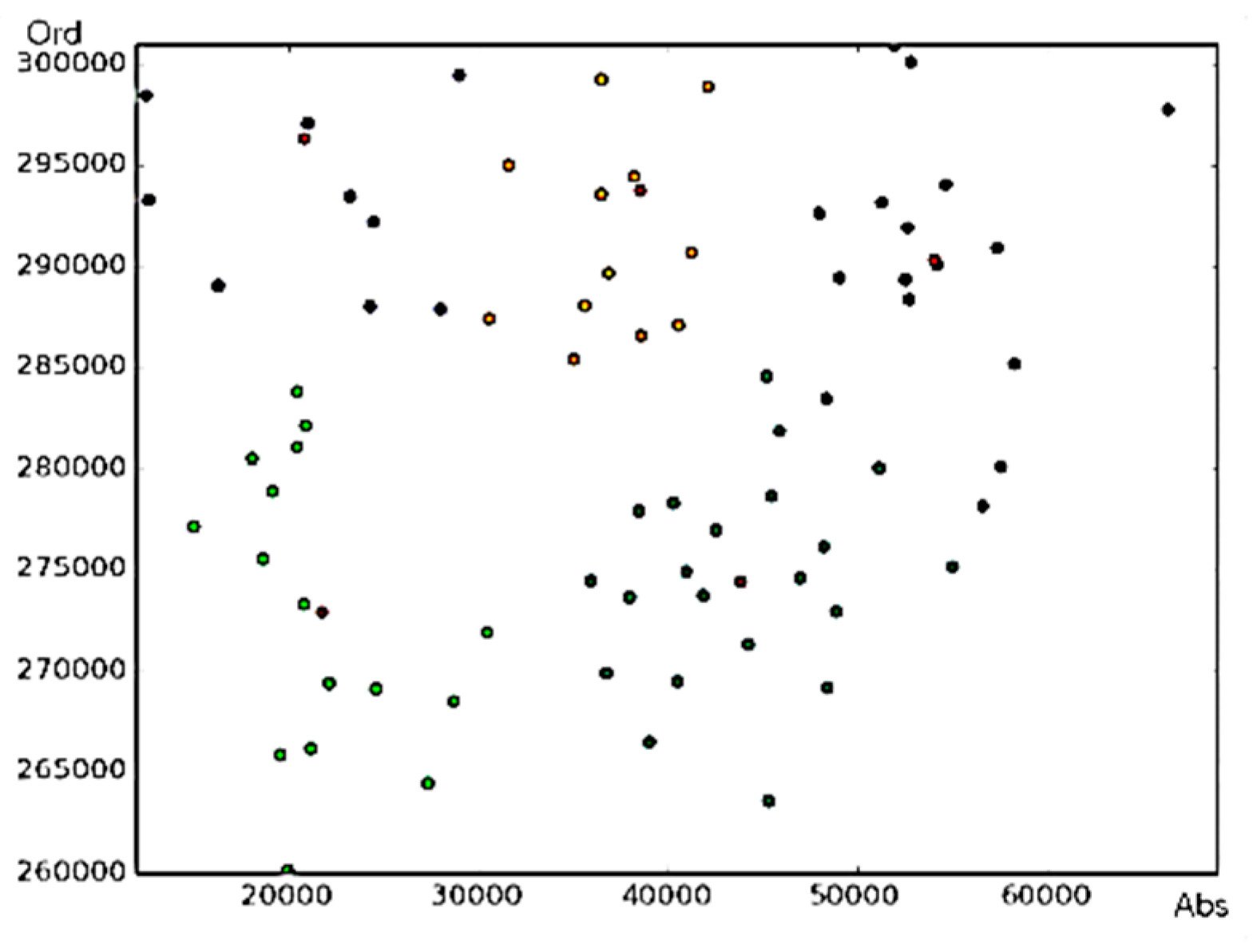
First of all, all the shipments that need to be dispatched that day will be clustered according to the delivery address.The first shipment’s delivery address and the plane coordinates converted from latitude, longitude, and the number of shipments to be delivered for each address are shown in the
Table 1:
In
Table 1 and
Figure 1, Abs is Abscissa, Ord is Ordinate, DM is delivery method, DN is delivery number. In the balanced k-means algorithm below, because the difference between the latitude and longitude of the receiving address is very small, we carried out a reasonable amplification and translation transformation on the data pre-processing, and then converted it into the logical distance calculated in the form of two-dimensional cartesian coordinates, so no specific distance unit is set for it in this paper. Because the latitude and longitude of the delivery addresses in this paper are not very different, the height difference between the delivery addresses is ignored. The specific method is to collect the longitude and latitude coordinates of the address first, convert the collected coordinates into two-dimensional cartesian coordinates, and then calculate the distance information according to the Euclidean distance calculation formula.
The coordinate information in the above table is converted from the latitude and longitude information of the packaged address of the package on the first day of the express center. The cluster analysis is performed by the k-means algorithm in order to obtain
Figure 1.
As can be seen from
Figure 1, all the express items that need to be delivered that day are clustered into five clusters. These clusters were allocated to five couriers for delivery. These five clusters are described in detail below.
As can be seen from the below figure, the receiving addresses in the first category are: Yiyuan, Changbai Sancun, Oriental Home, Shanghai Open University, Fengcheng Sancun-Shanghai Business School, Siping Science Park, Tongji New Village, and Fengcheng Five Villages.
The receiving addresses in the second category are: Cultural Garden, Global Building, Control River Five Village, Oriental Garden, Shuangyang Second Village, Express Center, Guoke Building, Yangpu Park, Wanchang Building, Yangpu Apartment ,Taihong Xinyuan, Environmental Protection Plaza and Huangxing Park.
The receiving addresses in the third category are: Yangpu Station, Democratic Second Village, Donghai Medicine, Yangpu Auto Parts City, Baiyangdian Football Stadium, Yangpu Central Hospital, Express Center, Zhongxuan Liyuan, Dongliaoyang Middle School, Fudan Software Park, Yanji Middle School, Yanji Nursing Home, Neijiang Park, Convenience Market, Guangyuan New Village, Tumen Community, and Shanghai University of Technology.
The receiving addresses in the fourth category are: Liaoyuan Ercun, Yangpu Junior High School, Sanfeng Building, Wuhuan Building, Wentong Building, Double Happiness Home, Yunmu Hotel, Mingyuan Village Community, Shanghai Cigarette Factory, Linyuan, North America Square, Jiangpu Park, Express Center, Huayuan Haoting, Huayuan Haoting, Fenghuang Building, and Tongji Green Park.
The receiving addresses in the fifth category includes: City Business Building, Shuiyuefang, Yinxianggang Community, Bailian Riverside Shopping Center, City Concept Creative Park, Rujia Hotel, Dong Huali, Tianke International Building, Shuyayuan Senior Citizen’s Court, Changxin Xinyuan, Zhenshengli, Shunchengli, Yangpu District People’s Court, Miaojia Shanzhai, Meizhoufang, Express Center, Changyang Chuanggu, Huajing Hotel, Yangpu District Children’s Palace, and Yinhe Court.
In the distribution sequence diagram below, the numbers represent the distribution sequence, and the horizontal and vertical coordinates in the diagram correspond to the data in ordinate
Table 1.
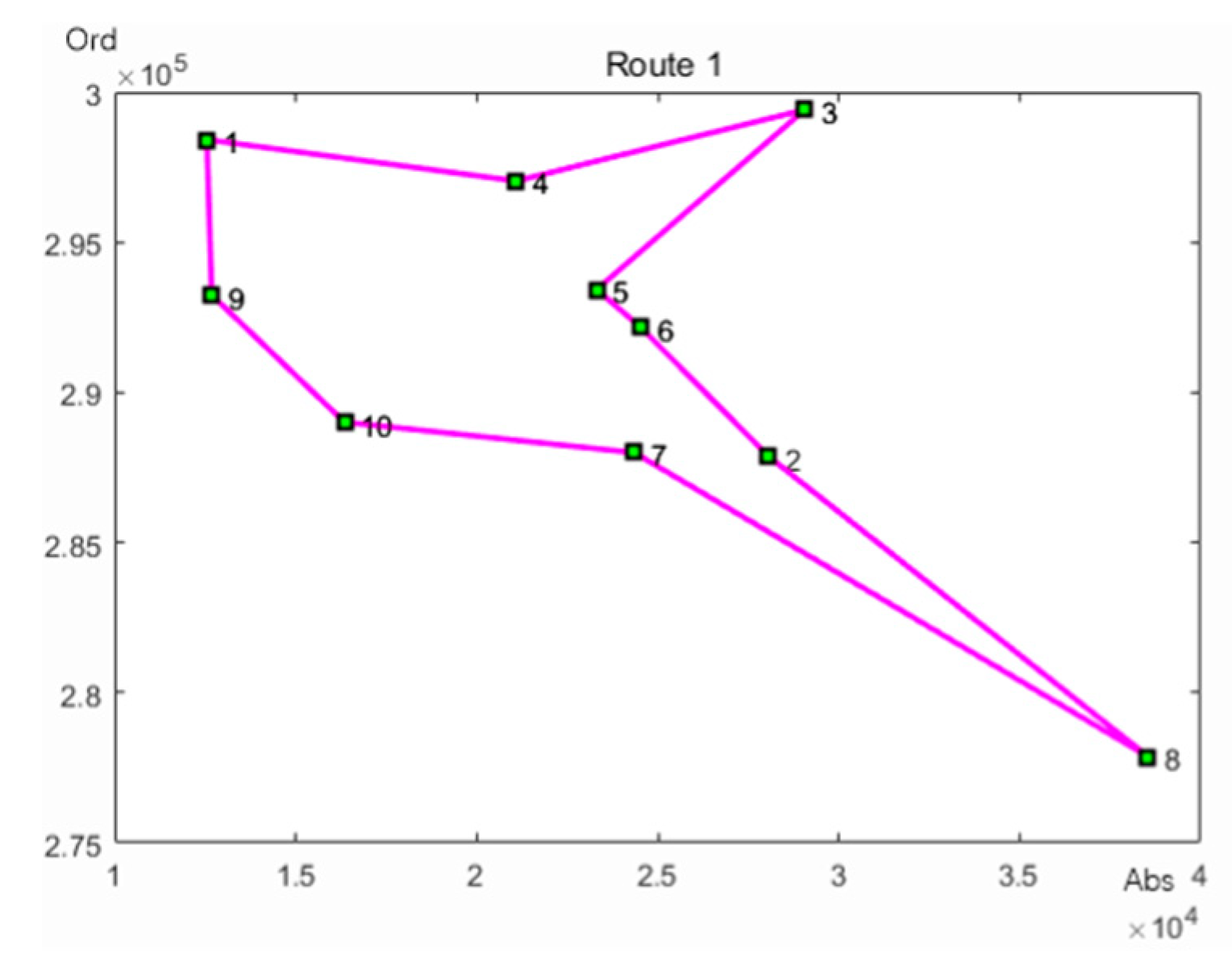
Using the ant colony algorithm to plan the dispatch order of the shipments in the first category.
It can be concluded from
Figure 2 that the delivery order of the first batch of express mail is: Express center to Fengcheng Sancun to Shanghai Business School to Yuyuan to Changbai Sancun to Oriental Home to Shanghai Open University to Siping Science Park to Tongji New Village to Fengcheng Five Village.
Google Maps was used to get the delivery distance of the first shipment, 14.68 km. According to the delivery route of the first batch of express deliveries and the dispatch information in
Table 1, the total delivery time of the first shipment is 4.48 h.
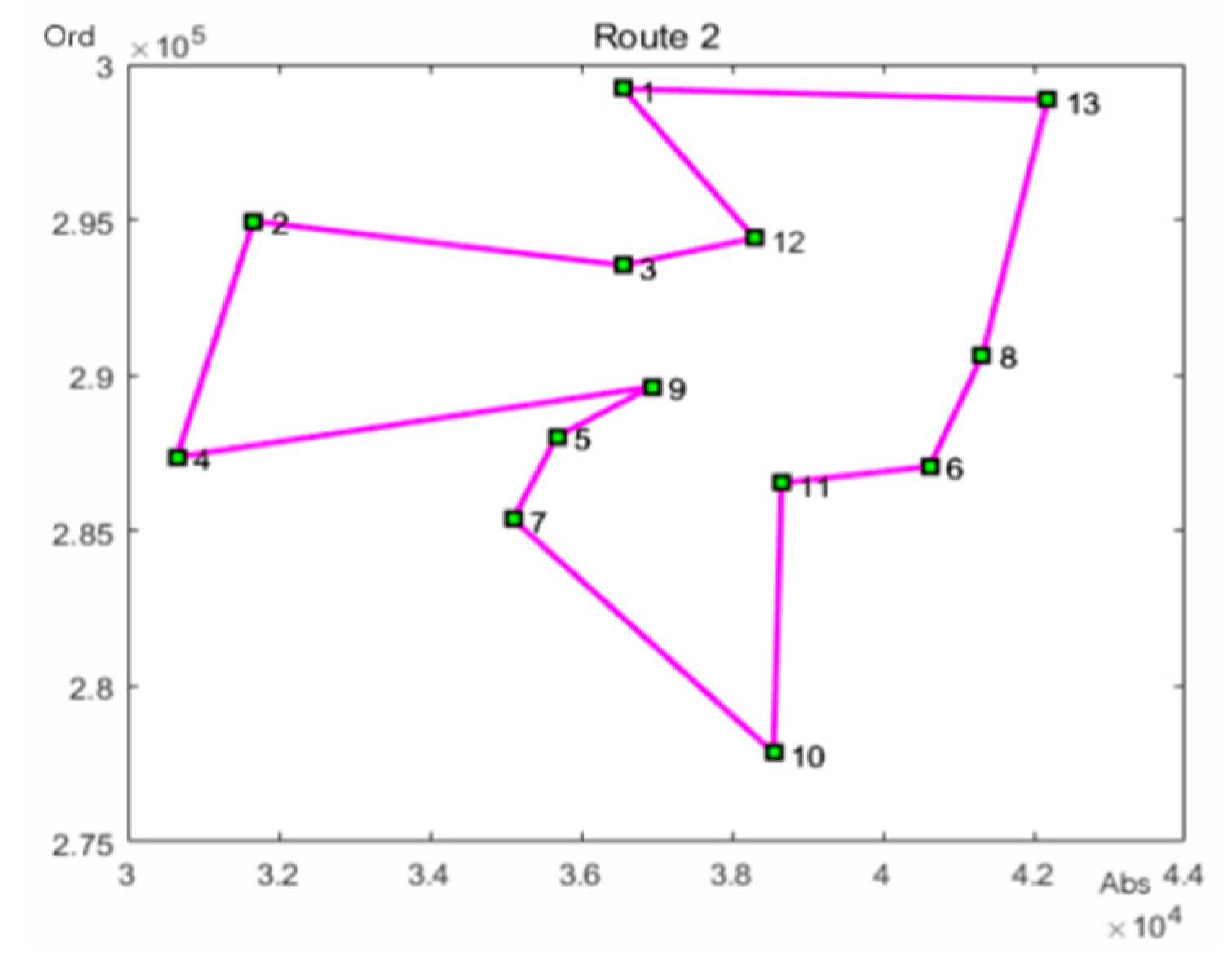
Using the ant colony algorithm to plan the dispatch order of the shipments in the second category:
It can be concluded from
Figure 3 that the delivery order of the second batch of express mail is: Express Center to Guoke Building to Yangpu Park to Taihong Xinyuan to Environmental Protection Plaza to Huangxing Park to Global Building to Jiangjiang Village to Cultural Garden to Oriental Garden to Wanchang Building to Yangpu Apartment to Shuangyang Ercun.
With Google Maps, the delivery distance is 12.4 km for the second shipment. According to the delivery route of the second batch of express deliveries and the dispatch information in
Table 1, the total delivery time of the second batch of express shipments is 5.24 h.
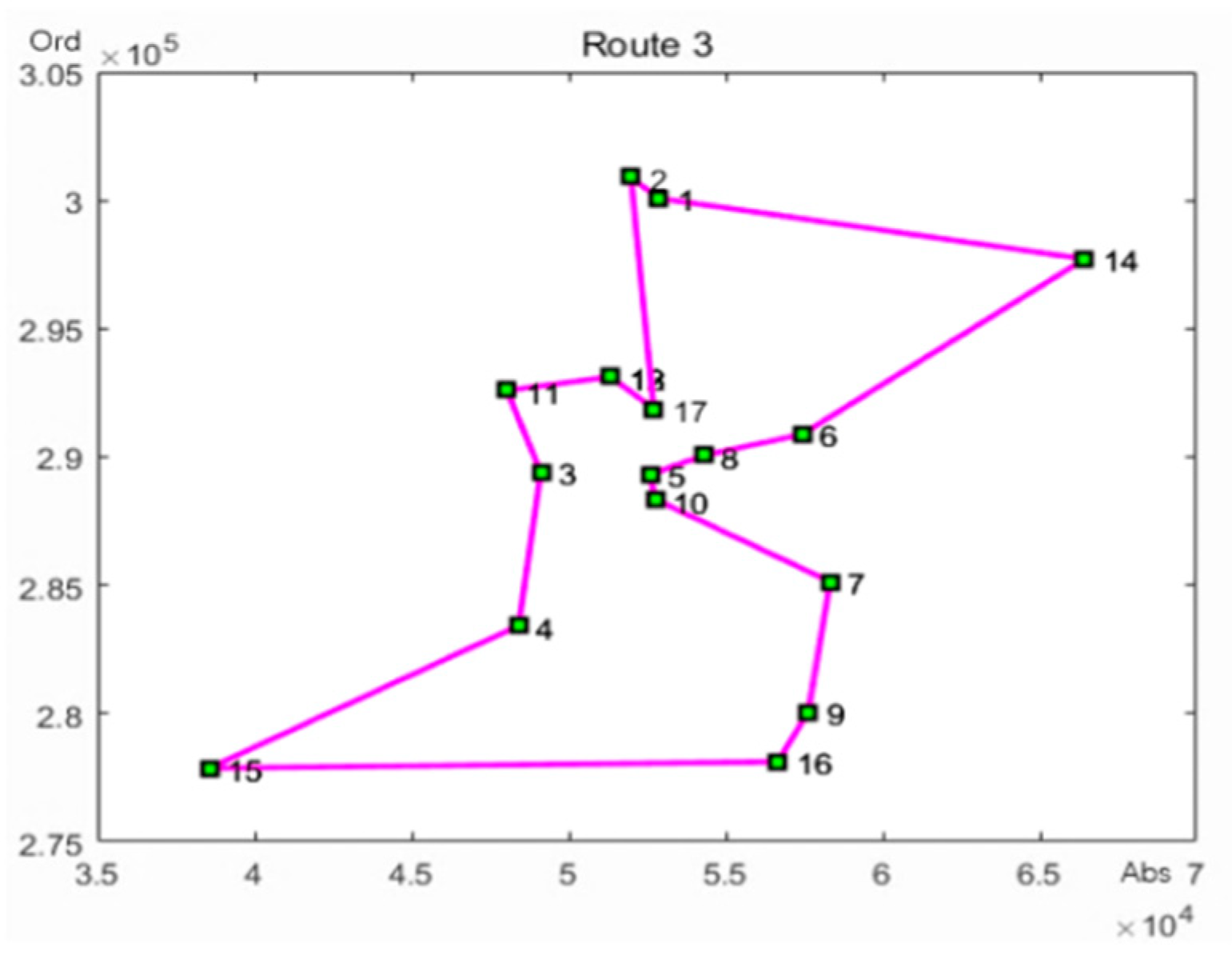
Using the ant colony algorithm to plan the dispatch order of the shipments in the third category:
It can be concluded from
Figure 4 that the order of delivery of the third batch of express mail is: Express Center to Fudan Software Park to Yanji Middle School to Yanji Nursing Home to Neijiang Park to Convenience Market to Guangyuan New Village to Tumen Community to Shanghai University of Technology to Donghai Medicine to Yangpu Auto Parts City to Yangpu Station to Democracy 2 Village to Baiyangdian Football Stadium to Zhongxuan Liyuan to Dongliaoyang Middle School to Yangpu Central Hospital.
With Google Maps, the delivery distance is 15.95 km for the third shipment. According to the delivery route of the third batch of express delivery and the dispatch information in
Table 1, the total delivery time of the third batch of express shipments is 6.11 h.
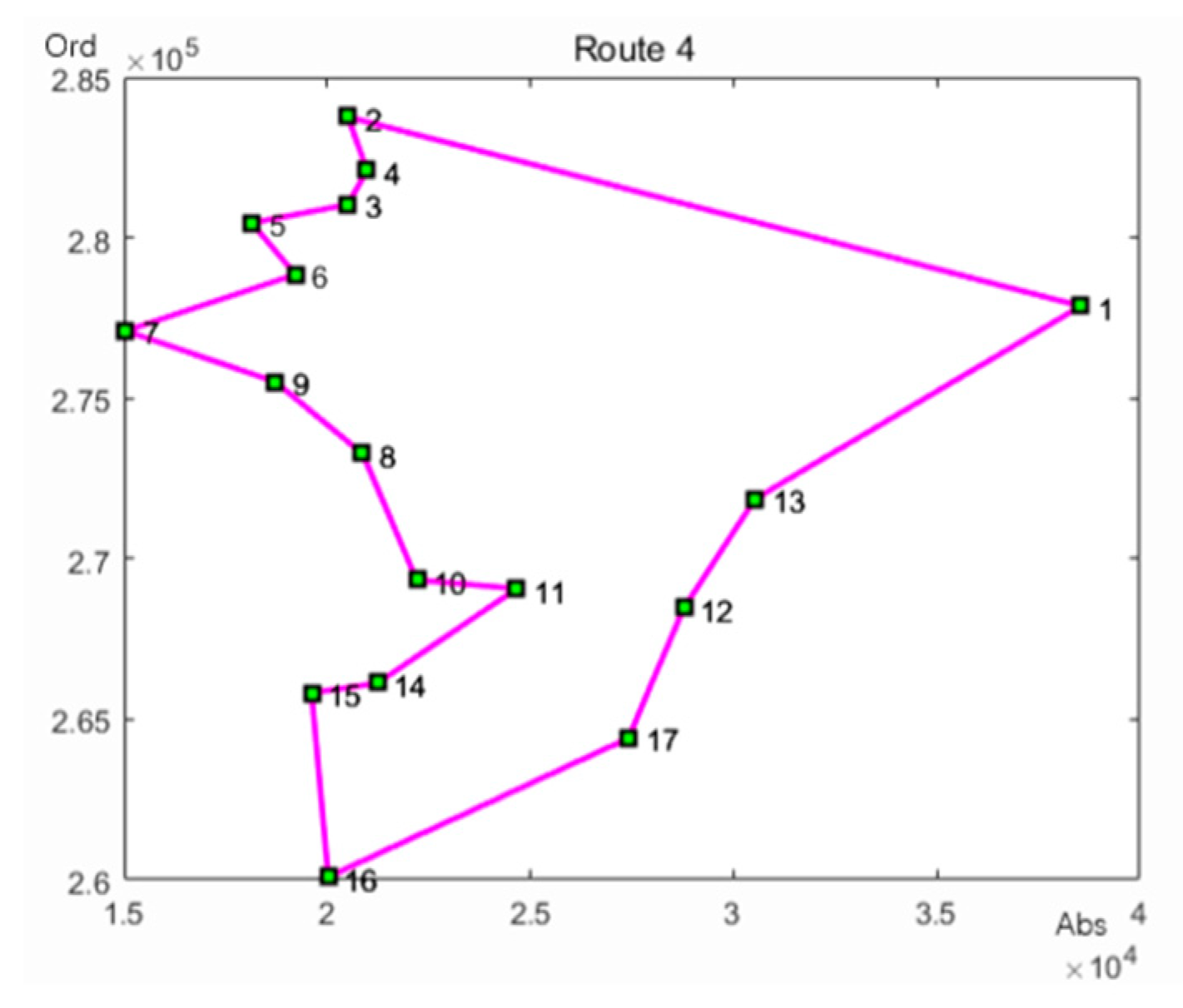
Using the ant colony algorithm to plan the dispatch order of the shipments in the fourth category.
It can be concluded from
Figure 5 that the delivery order of the fourth batch of express mail is: Express center to Huayuan Haoting to Huayuan Haoting to Phoenix Building to Tongji Green Park to Sanfeng Building to Wuhuan Building to Liaoyuan 2 Village to Yangpu Junior High School Wentong Building to Shanghai Cigarette Factory to Linyuan to North America Square to Double Happiness Home to Yunmu Hotel to Mingyuan Village Community to Jiangpu Park.
With Google Maps, the delivery distance is 13.21 km for the fourth shipment. According to the delivery route of the four batches of express delivery and the dispatch information in
Table 1, the total delivery time of the four batches of express shipments is 5.27 h.
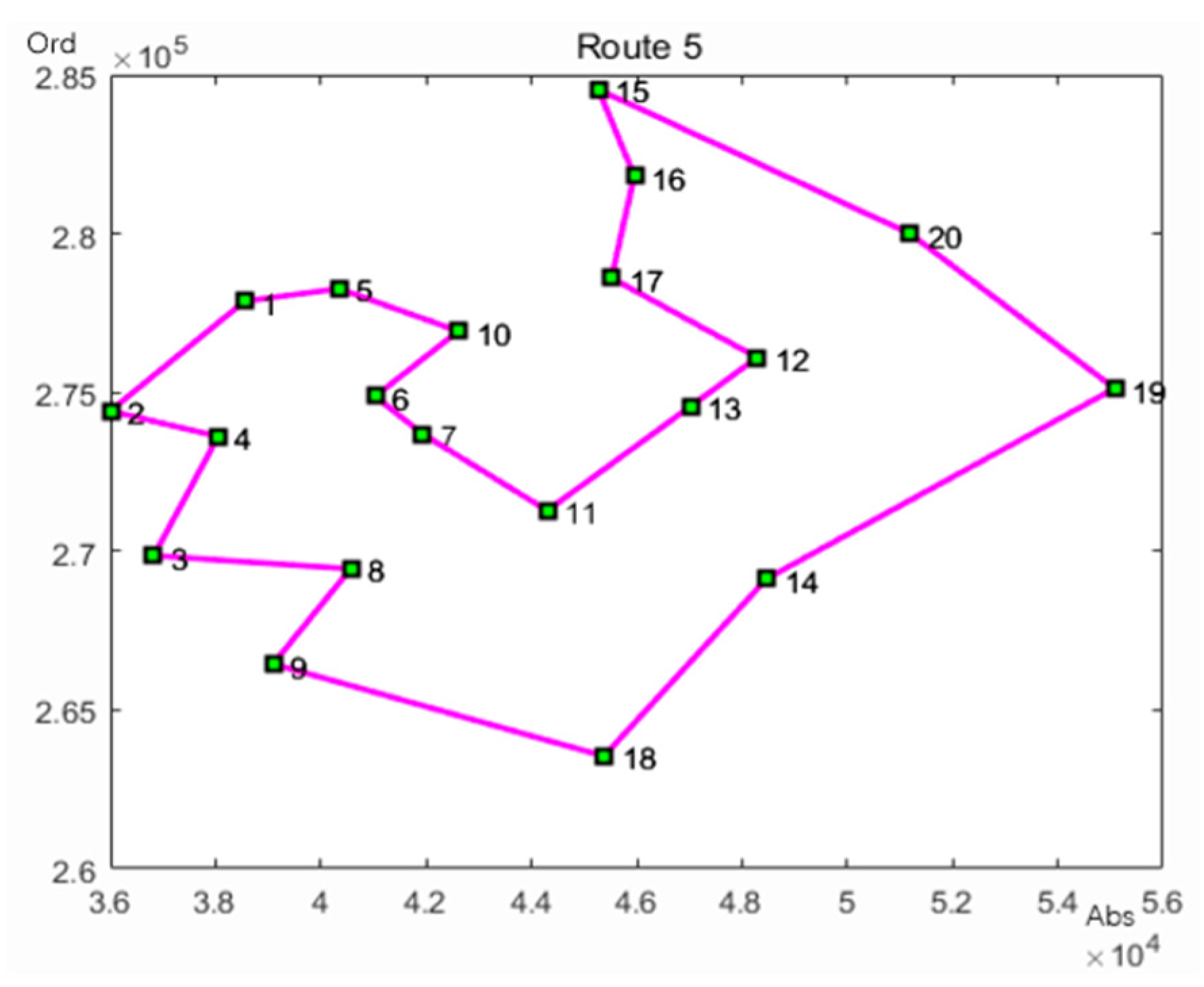
Using the ant colony algorithm to plan the dispatch order of the shipments in the fifth category.
It can be concluded from
Figure 6 that the delivery order of the fifth batch of express mail is: Express center to Changyang Chuanggu to Huajing Hotel to Yangpu District Children’s Palace to Yinheyuan Bailian Riverside Shopping Center to City Business Building to Shuiyuefang to Yinxianggang Community Go to the City Concept Creative Park to the Home Inn to Changxin Xinyuan to Zhenshengli to Shunchengli to Donghuali to Tianke International Building to Shuyayuan Retirement House to Yangpu District People’s Court to Miaojia Village to Meizhou Square.
With Google Maps, the delivery distance is 12.93 km for the fifth shipment. According to the delivery route of the five batch of express delivery and the dispatch information in
Table 1, the total delivery time of the five batch of express shipments is 5.76 h.
The article has calculated the total cost of delivery time for the five batches of couriers obtained on the first day of clustering. The five batches of express mail will be distributed, from the big to the small, to couriers No. 1 to No. 5 according to the delivery time. On the first day, the cumulative time for the courier No. 1 to the courier No. 5 is shown in
Table 2:
Calculated by standard deviation:
The standard deviation of the cumulative time of the five couriers on the first day was: 0.5511.
The above steps were repeated to calculate the total cost of the delivery time of the five batches of express delivery from the second day to the fifteenth day. When assigning a dispatch task according to the dispatch time of the class, the courier class of the day is allocated in descending order of the delivery time cost to the courier who has accumulated the delivery time. Then, the total cost of the delivery time accumulated by the five couriers from the first day to the fifteenth day is calculated, and the standard deviation of the accumulated time of the five couriers is calculated too.
In the below table,
Table 3 shows the accumulated delivery time cost of the first courier in the 15 days.
Table 4 shows the cumulative delivery time cost of the second Courier in the 15 days.
Table 5 shows the cumulative delivery time cost of the third Courier during the 15 days.
Table 6 shows the cumulative delivery time cost of the fourth Courier in the 15 days.
Table 7 shows the cumulative delivery time cost of the sixth Courier in the 15 days.
Table 8 shows the standard deviation of the five couriers’ cumulative delivery time cost in each of the 15 days.
4.3. Discussion of Experimental Results
From the above data, we can get the daily delivery time histogram and the cumulative delivery time standard deviation line chart of each courier.
Since the courier center does not have a good plan for the task assignment of the dispatcher, the courier’s delivery order and route are more uncertain when the mail is delivered. During the data collection, because the couriers chose the delivery route randomly, we have collected the address information and specific income of the couriers, and their actual delivery time cost is temporarily unknown.
According to the task assignment method of this article, the delivery time cost of each courier is obtained, and then the salary will be set proportionally according to the delivery time cost. Next, we compare the changes in the actual income of the dispatchers collected before the experiment with the corresponding indicators of the test delivery time, and then draw a reliable conclusion.
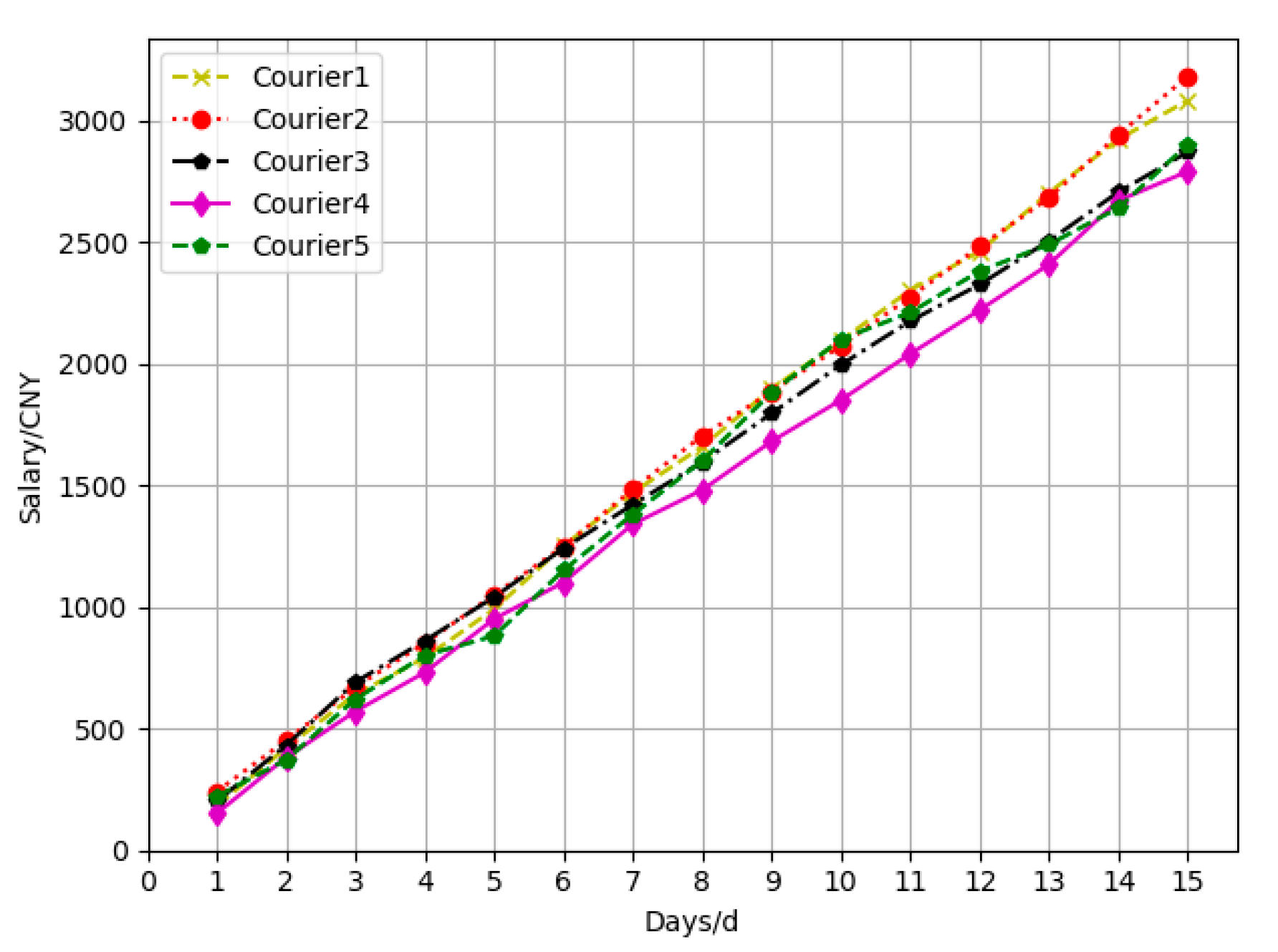
The income of the five couriers in the express delivery center within the same 15 days was collected before the experiment, and a line chart of the difference between the income and income standard was drawn. Then, the income graph and time cost graph was compared and analyzed.
Figure 7 illustrates the change of the accumulated income of five couriers from the express center in the past 15 days.
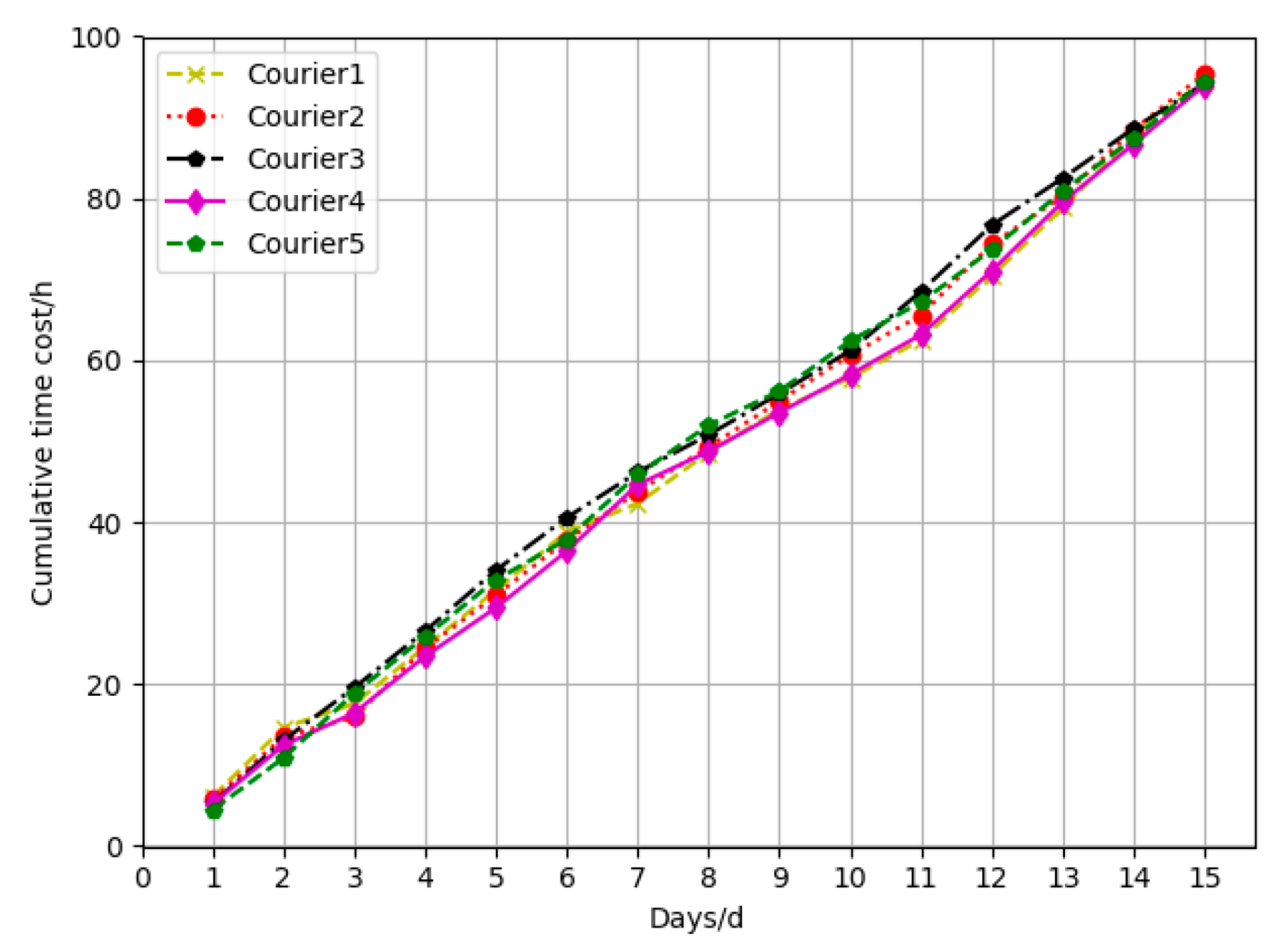
Figure 8 shows the change diagram of the cumulative delivery time cost of five couriers in these 15 days calculated through experiments.
Figure 9 shows the line graph obtained after normalizing the standard deviation of the courier’s accumulated daily income.
Figure 10 is a line graph normalized by the standard deviation of the courier’s cumulative delivery time cost per day.
As can be seen from
Figure 7, the cumulative income between the five couriers in the 15 days from the express center is uneven, and the cumulative income gap between couriers is relatively large. It can be seen from
Figure 8 that the cumulative difference of delivery time cost between five couriers in the 15 days calculated through the experiment is very small, and the income of the couriers is well distributed using the proportion of the delivery time cost. It can be seen from
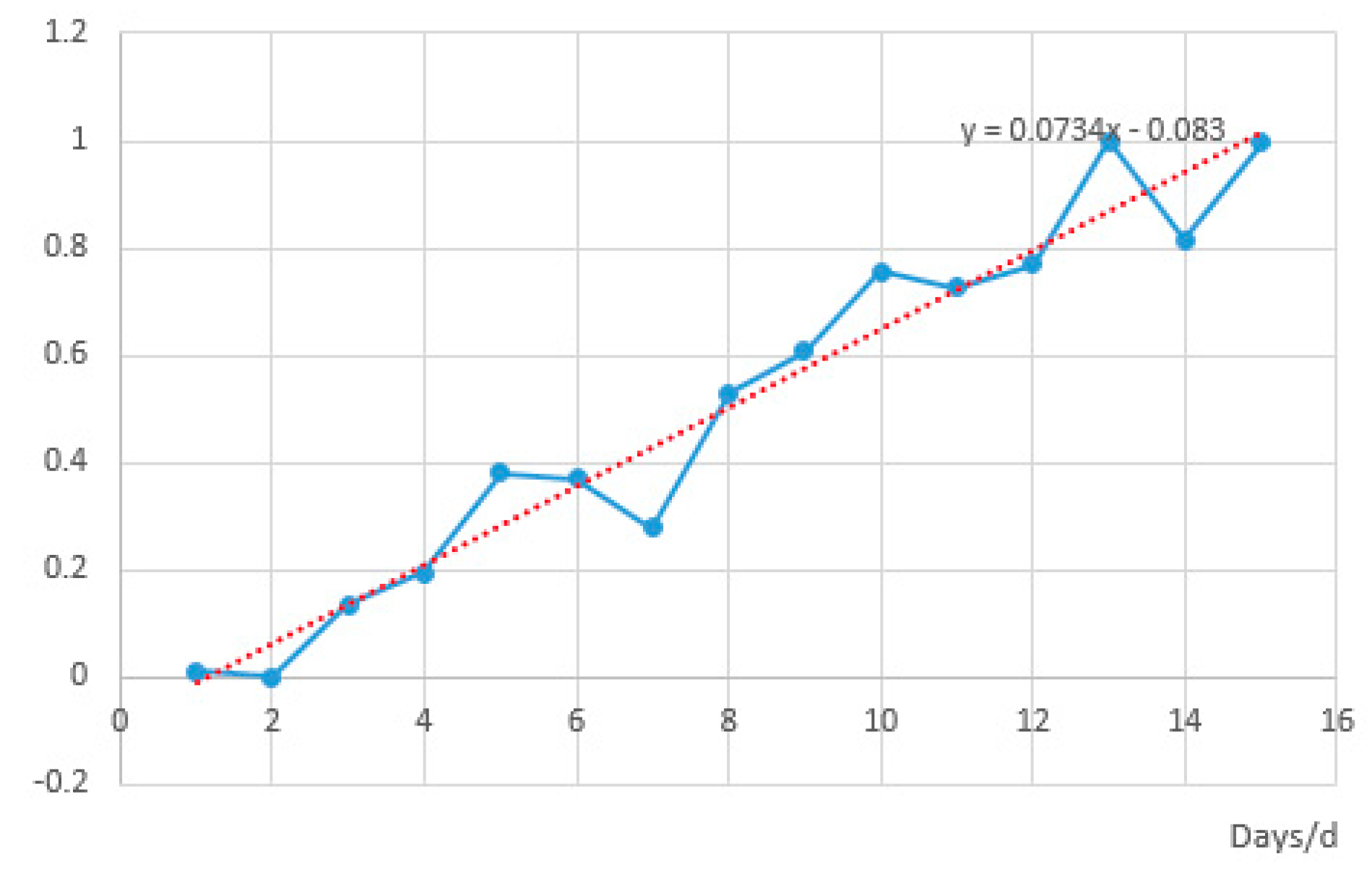
Figure 9 that there is a big difference in the income of the deliverymen according to the statistics of the express center, and the trend line is y = 0.0734x − 0.083. The standard deviation is increasingly larger, and there is no stable trend. As can be seen from
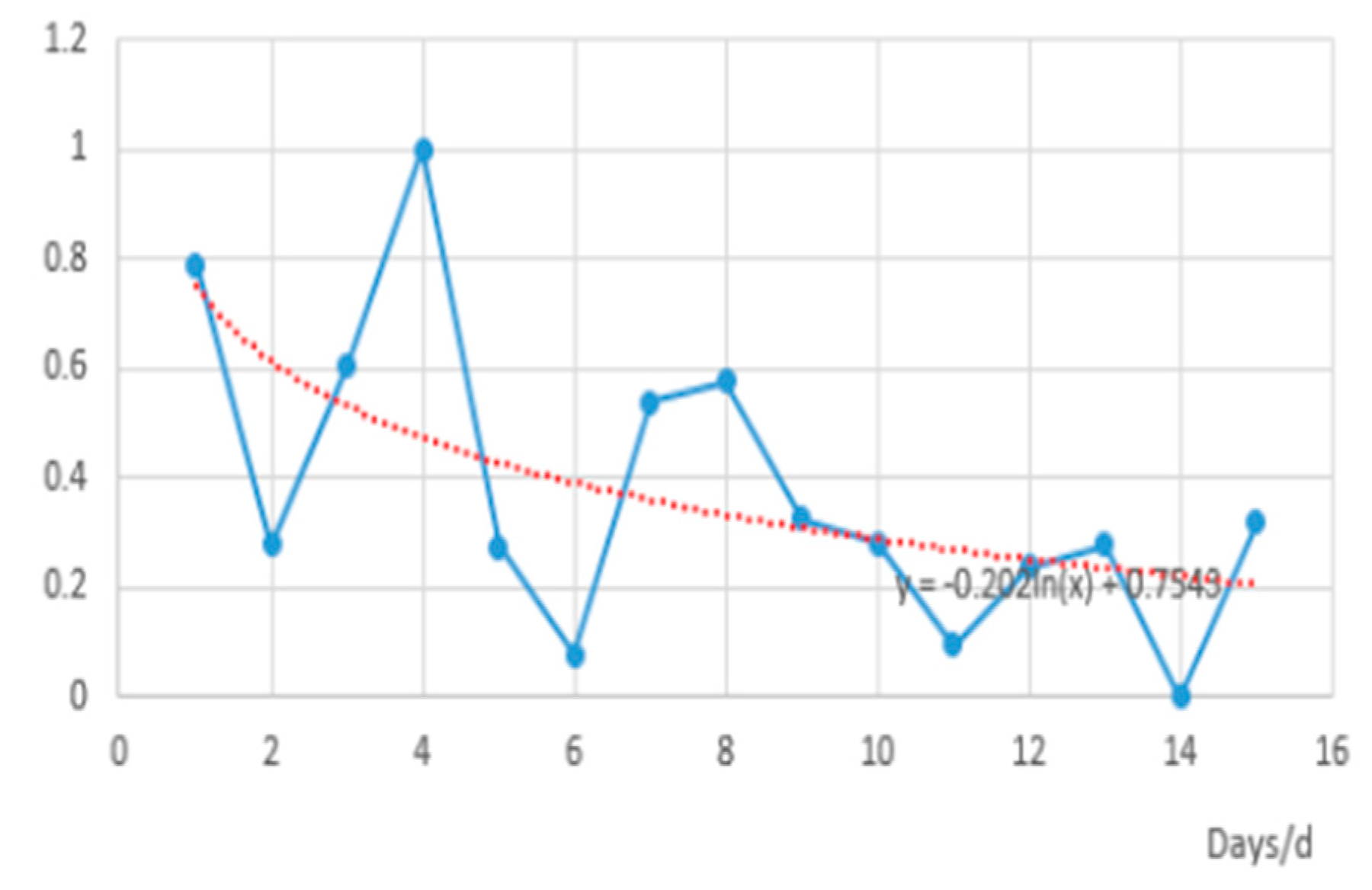
Figure 10, the trend line of the standard deviation of the cumulative delivery time of dispatchers is y = −0.202ln(x) + 0.7543, and the standard deviation gradually decreases and tends to stabilize. The below information can indicate that the task assignment scheme in this paper is better than the previous one, and the task assignment scheme is stable and effective [
7,
52].
4.4. Industrial Applications
According to the experimental results of this paper, it can be seen that the task assignment scheme for the modern logistics terminal is effective and feasible. Therefore, this paper, combined with the real situation of logistics delivery, designed a specific industrial design scheme. The scheme is shown in
Figure 11.
When the express center receives all the express mail that needs to be delivered on that day, it will cluster the express mail according to the longitude and latitude information of the delivery addresses and the balanced k-means algorithm, according to the number of express deliveries and couriers.
After clustering all express items that need to be delivered on that day, the ant colony algorithm is used to regard it as a TSP. The delivery sequence planning is carried out for express items in these classes, respectively, and the optimal delivery sequence of express items in each class is worked out to minimize the delivery distance.
The total delivery time cost of each delivery class is calculated according to the delivery distance in each delivery class and the delivery mode between different addresses and other factors affecting the delivery time. The delivery class is assigned to each courier according to the level of delivery time cost.
Complete the assignment task one day through the above steps, repeat the above steps the next day, and then assign the delivery time cost from low to high to the deliveryman whose cumulative delivery time cost is from high to low. The cycle is one month.
According to the delivery time cost of each type of delivery, combined with the local income status, the delivery staff’s salary is allocated in equal proportion, so as to make the wage gap between the delivery staff very small.