Analysis of Vibration Frequency of Carbon Nanotubes used as Nano-Force Sensors Considering Clamped Boundary Condition
Abstract
1. Introduction
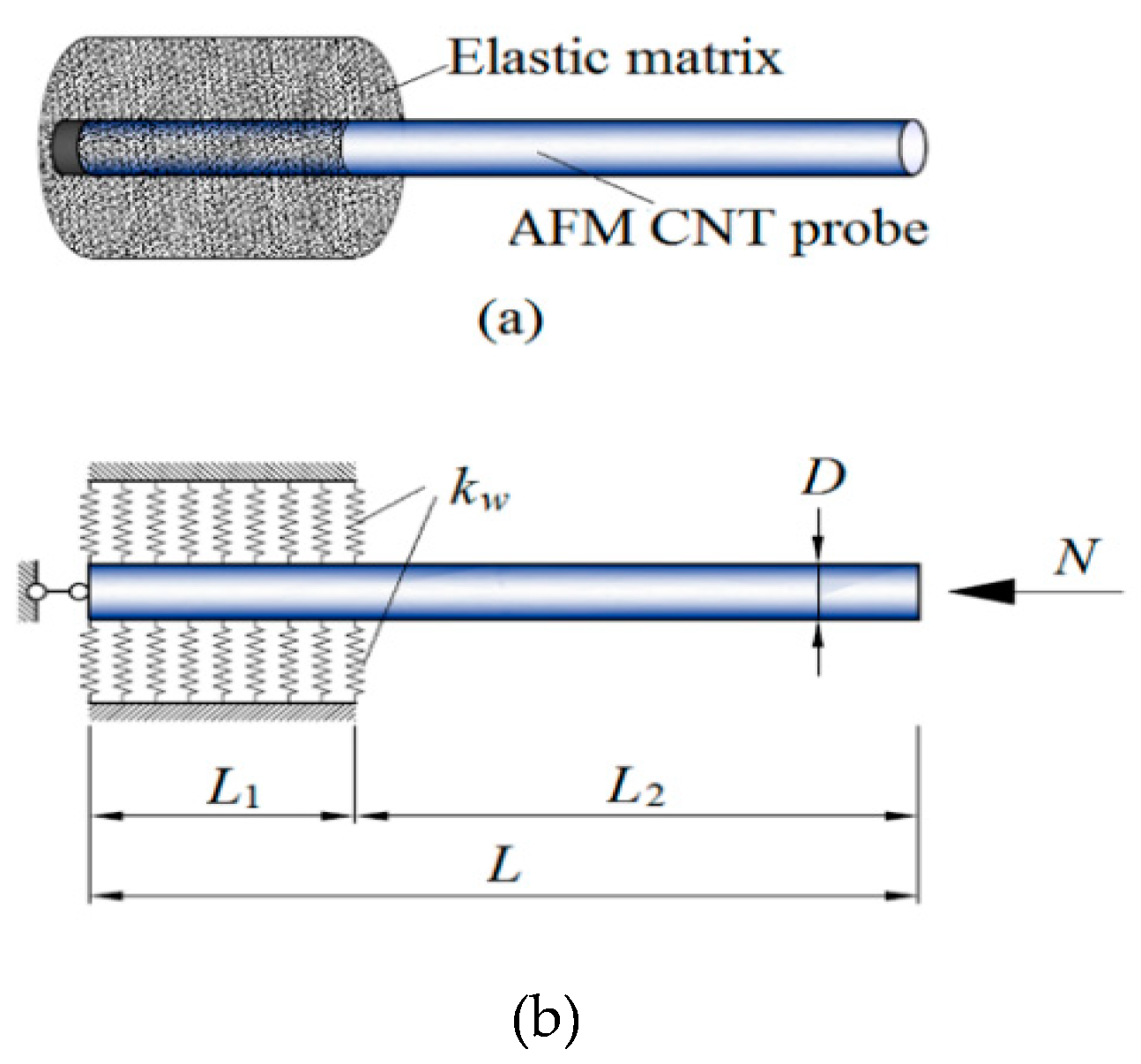
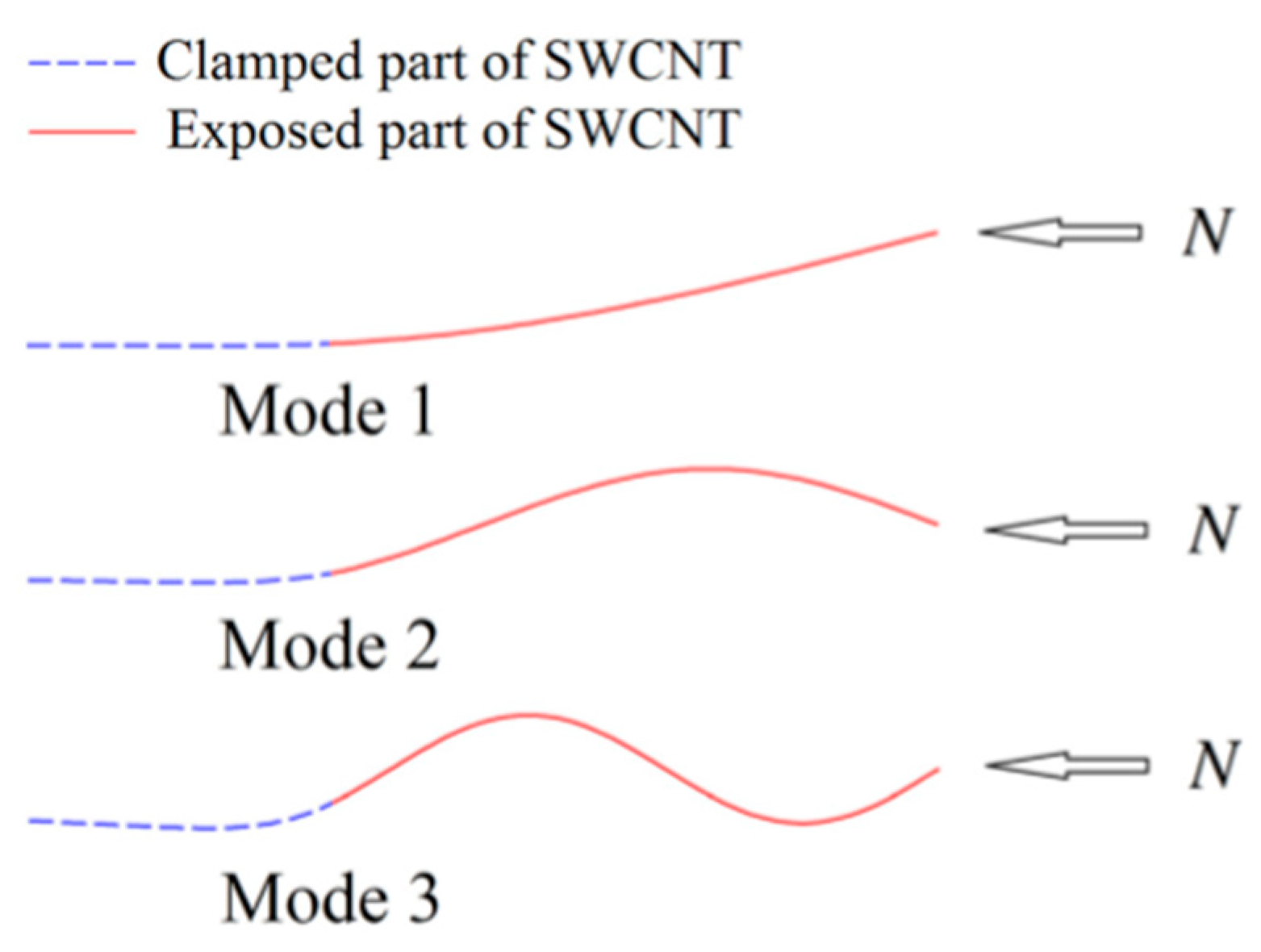
2. Modeling Procedure
2.1. Fundamental Equations
2.2. Solution of Governing Differential Equations
- (1)
- If , we obtainwhereandwhere Aj (j = 1, 2, ⋯, 8) are arbitrary integration constants, which should be determined via boundary conditions.
- (2)
- If , we havewhere
- (3)
- whenwhereFor the exposed part of CNT, the solution of Equation (7) giveswhere
- (1)
- at , for clamped part
- (2)
- at , for exposed part subjected to compressive loading
- (3)
- at the position x1 = L1, which is the connecting position between clamped and exposed parts, the continuous conditions of the vibrational deflection are:
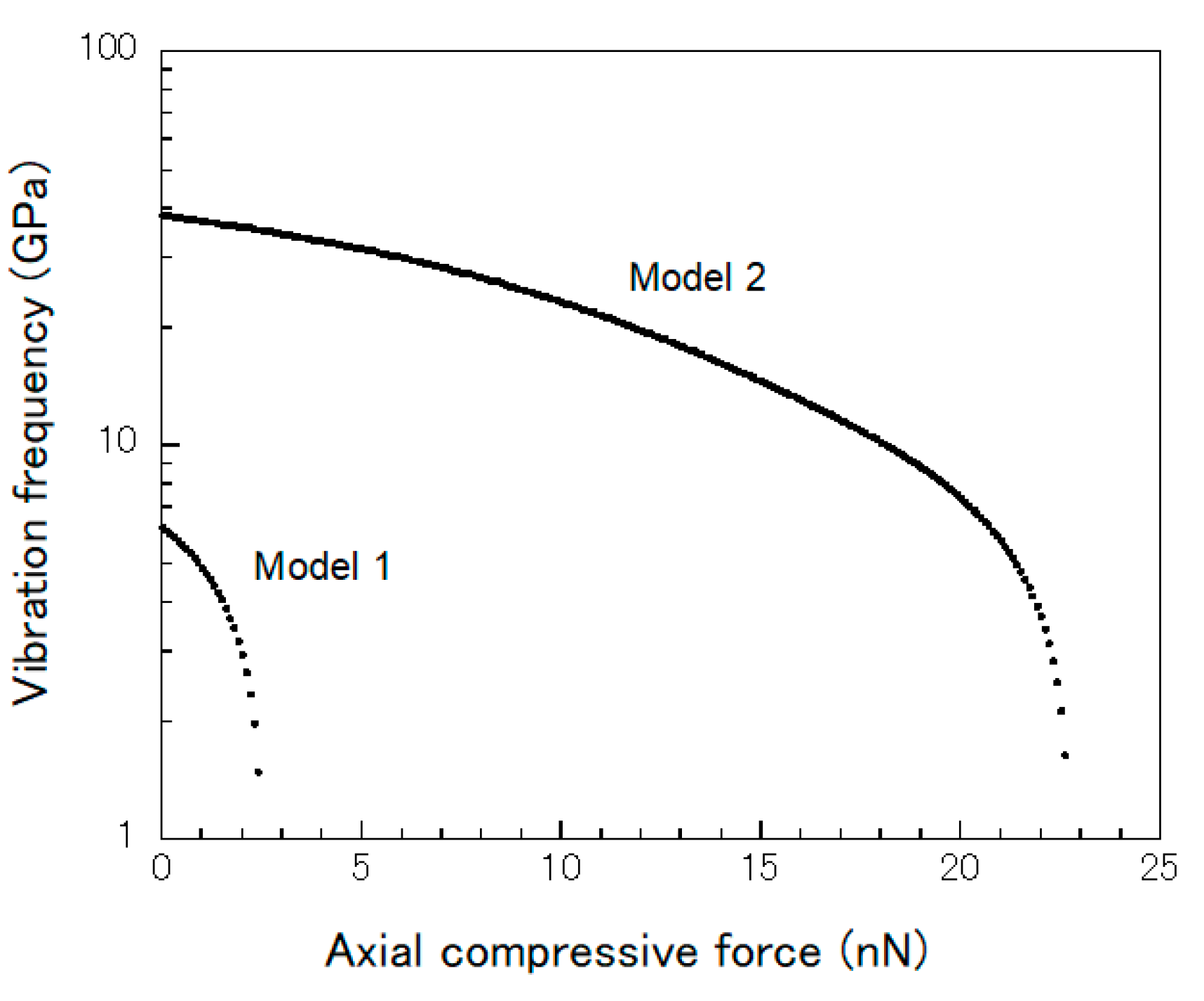
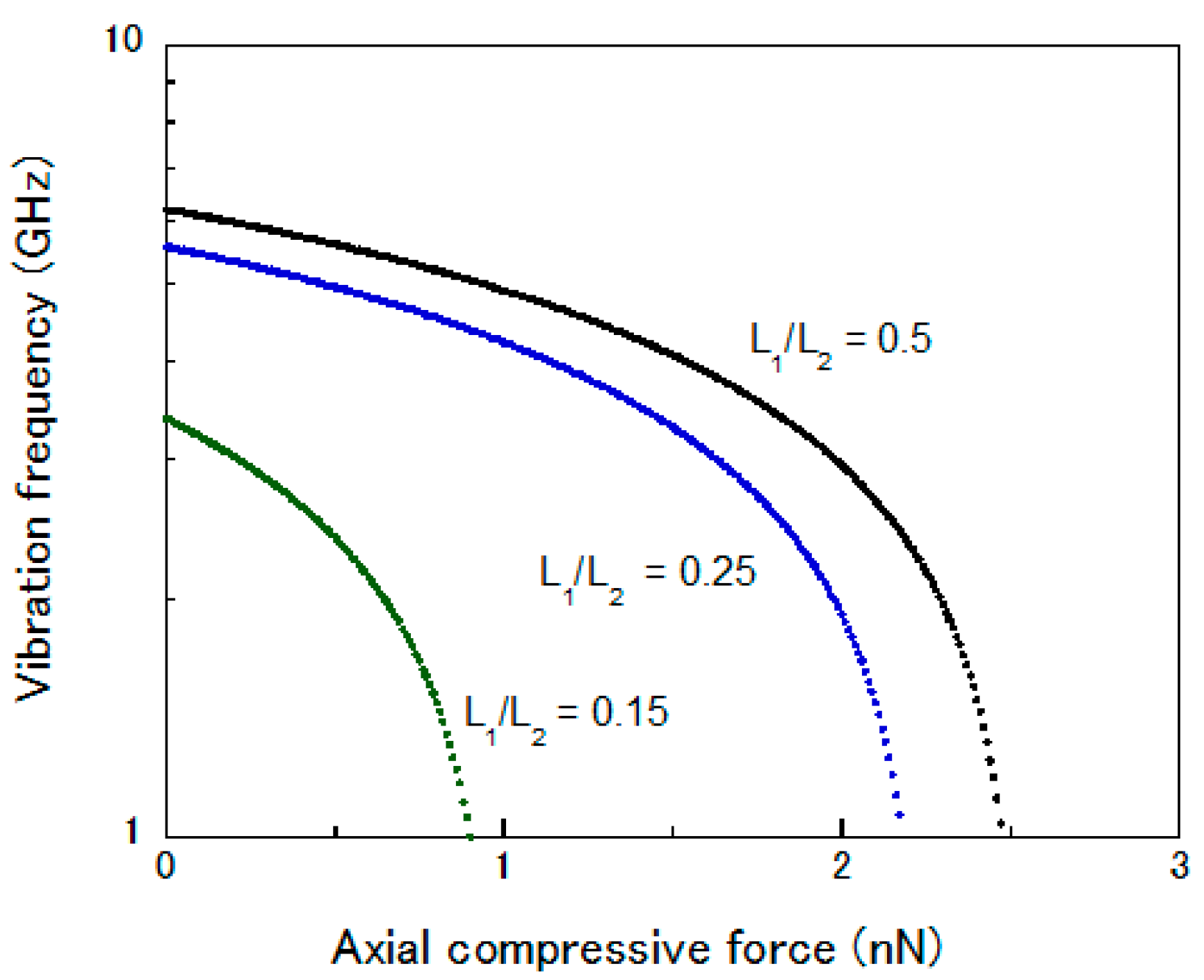
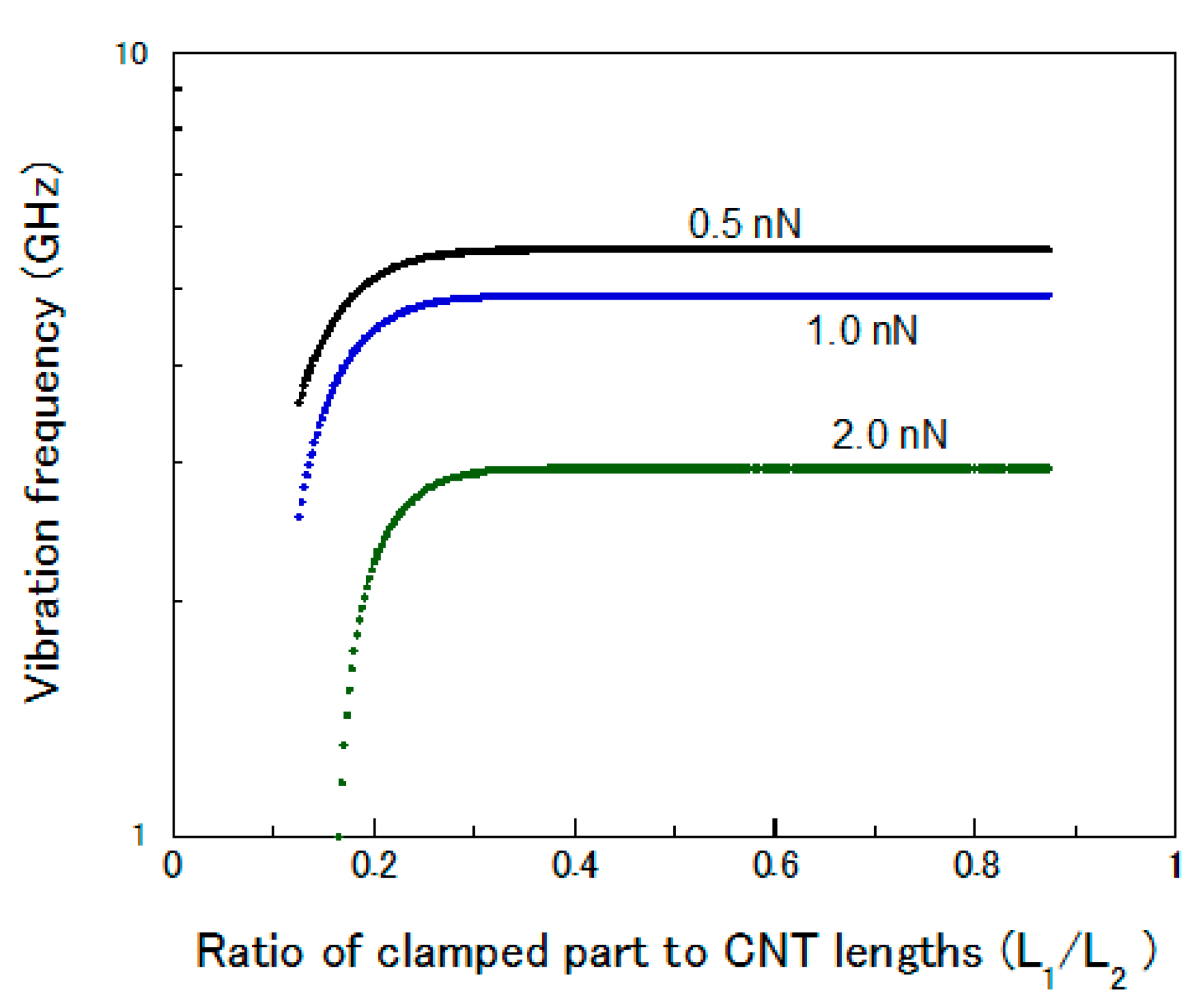
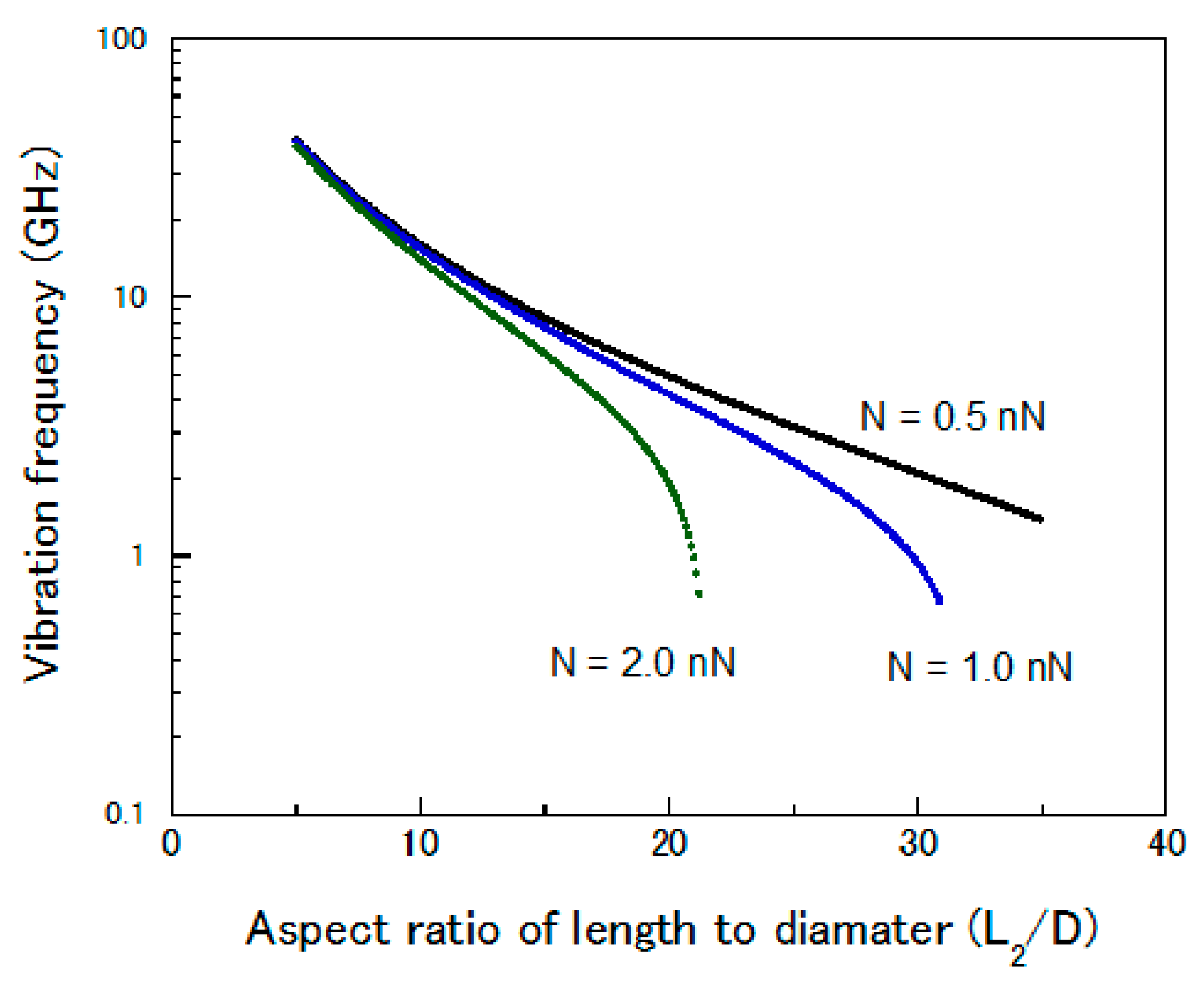
3. Simulation Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Thostenson, E.T.; Renb, Z.; Chou, T.W. Advances in the science and technology of carbon nanotubes and their composites: A review. Compos. Sci. Technol. 2001, 61, 1899–1912. [Google Scholar] [CrossRef]
- Natsuki, T.; Matsuyama, T. Vibration analysis of carbon nanotube-based resonator using nonlocal elasticity theory. Appl. Phys. A. 2015, 120, 1309–1313. [Google Scholar] [CrossRef]
- Martinez, J.; Yuzvinsky, T.D.; Fennimore, A.M.; Zettl, A.; Garcia, R.; Bustamante, C. Length control and sharpening of atomic force microscope carbon nanotube tips assisted by an electron beam. Nanotechnology 2005, 16, 2493–2496. [Google Scholar] [CrossRef]
- Druzhinina, T.S.; Hoeppener, S.; Schubert, U.S. Microwave assisted fabrication of carbon nanotube AFM Tips. Nano Lett. 2010, 10, 4009–4012. [Google Scholar] [CrossRef] [PubMed]
- Irina, V.Z.; Natalia, P.B.; Yuri, N.P.; Lev, V.K. Carbon nanotubes: Sensor properties. A review. Mod. Electron. Mater. 2016, 2, 95–105. [Google Scholar]
- Vera, S.; Suchol, S.; Maggie, H.; Sibo, L.; Timothy, M.S. Carbon nanotube chemical sensors. Chem. Rev. 2019, 119, 599–663. [Google Scholar]
- Strus, M.C.; Raman, A.; Han, C.S.; Nguyen, C.V. Imaging artefacts in atomic force microscopy with carbon nanotube tips. Nanotechnology 2005, 16, 2482–2492. [Google Scholar] [CrossRef]
- Alizadegan, R.; Liao, A.D.; Xiong, F.; Pop, E.; Hsia, K.J. Effects of tip-nanotube interactions on atomic force microscopy imaging of carbon nanotubes. Nano Res. 2012, 5, 235–247. [Google Scholar] [CrossRef]
- Hafner, J.H.; Cheung, C.L.; Oosterkamp, T.H.; Lieber, C.M. High-yield assembly of individual single-walled carbon nanotube tips for scanning probe microscopies. J. Phys. Chem. B 2001, 105, 743–746. [Google Scholar] [CrossRef]
- Lamprecht, C.; Danzberger, J.; Lukanov, P.; Tilmaciu, C.M.; Galibert, A.M.; Soula, B.; Flahaut, E.; Gruber, H.J.; Hinterdorfer, P.; Ebner, A.; et al. AFM imaging of functionalized double-walled carbon nanotubes. Ultramicroscopy 2009, 109, 899–906. [Google Scholar] [CrossRef] [PubMed]
- Wilson, N.R.; Macpherson, J.V. Carbon nanotube tips for atomic force microscopy. Nat. Nanotechnol. 2009, 4, 483–491. [Google Scholar] [CrossRef] [PubMed]
- Wade, L.A.; Shapiro, I.R.; Ma, Z.; Quake, S.R.; Collier, C.P. Correlating AFM probe morphology to image resolution for single-wall carbon nanotube tips. Nano Lett. 2004, 4, 725–731. [Google Scholar] [CrossRef]
- Nguyen, C.V.; Stevens, R.M.D.; Barber, J.; Han, J.; Meyyappan, M.; Sanchez, M.I.; Larson, C.; Hinsberg, W.D. Carbon nanotubes canning probe for profiling of deep-ultraviolet and 193 nm photoresist patterns. Appl. Phys. Lett. 2002, 81, 901–903. [Google Scholar] [CrossRef]
- Chen, L.; Cheung, C.L.; Ashby, P.D.; Lieber, C.M. Single-walled carbon nanotube AFM probes: Optimal imaging resolution of nanoclusters and biomolecules in ambient and fluid environments. Nano Lett. 2004, 4, 1725–1731. [Google Scholar] [CrossRef]
- Choi, N.; Uchihashi, T.; Nishijima, H.; Ishida, T.; Mizutani, W.; Akita, S.; Nakayama, Y.; Ishikawa, M.; Tokumoto, H. Atomic force microscopy of single-walled carbon nanotubes using carbon nanotube tip. Jpn. J. Appl. Phys. 2000, 39, 3707–3710. [Google Scholar] [CrossRef]
- Yan, Y.; Miao, J.; Yang, Z.; Xiao, F.X.; Yang, H.B.; Liu, B.; Yang, Y. Carbon nanotube catalysts: Recent advances in synthesis, characterization and applications. Chem. Soc. Rev. 2015, 44, 3295–3346. [Google Scholar] [CrossRef] [PubMed]
- Eveleens, C.A.; Irle, S.; Page, A.J. How does acetonitrile modulate single-walled carbon nanotube diameter during CVD growth? Carbon 2019, 146, 535–541. [Google Scholar] [CrossRef]
- Hafner, J.H.; Cheung, C.L.; Lieber, C.M. Growth of nanotubes for probe microscopy tips. Nature 1999, 398, 761–762. [Google Scholar] [CrossRef]
- Mori, H.; Ogata, S.; Li, J.; Akita, S.; Nakayama, Y. Plastic bending and shape-memory effect of double-wall carbon nanotubes. Phys. Rev. B 2017, 76, 165405. [Google Scholar] [CrossRef]
- Somada, H.; Yoshikawa, Y.; Nagataki, A.; Hirahara, K.; Nakayama, Y. Energy barrier for disappearance of buckling to form a plastic bend in carbon nanotubes. Jpn. J. Appl. Phys. 2007, 46, 1055–1057. [Google Scholar] [CrossRef]
- Natsuki, T.; Ni, Q.-Q.; Elishakoff, I. Influence of the axial compression on the natural frequency of AFM probes using double-walled carbon nanotubes with different wall lengths. Appl. Phys. A 2013, 110, 1–7. [Google Scholar] [CrossRef]
- Natsuki, T. Theoretical analysis of vibration frequency of graphene sheet used as nanomechanical mass sensor. Electronics 2015, 4, 723–738. [Google Scholar] [CrossRef]
- Yap, H.W.; Lakes, R.S.; Carpick, R.W. Mechanical instabilities of individual multiwalled carbon nanotubes under cyclic axial compression. Nano Lett. 2007, 7, 1149–1154. [Google Scholar] [CrossRef] [PubMed]
- Kuzumaki, T.; Mitsuda, Y. Nanoscale mechanics of carbon nanotube evaluated by nanoprobe manipulation in transmission electron microscope. Jpn. J. Appl. Phys. 2006, 45, 364–368. [Google Scholar] [CrossRef]
- Kutana, A.; Giapis, K.P. Transient deformation regime in bending of single-walled carbon nanotubes. Phys. Rev. Lett. 2006, 97, 245501. [Google Scholar] [CrossRef]
- Farajpour, A.; Rastgoo, A. Influence of carbon nanotubes on the buckling of microtubule bundles in viscoelastic cytoplasm using nonlocal strain gradient theory. Results Phys. 2017, 7, 1367–1375. [Google Scholar] [CrossRef]
- Cheung, C.L.; Hafner, J.H.; Lieber, C.M. Carbon nanotube atomic force microscopy tips: Direct growth by chemical vapor deposition and application to high-resolution imaging. Proc. Natl. Acad. Sci. USA 2000, 97, 3809–3813. [Google Scholar] [CrossRef]
- Yakoboson, B.I.; Brabec, C.J.; Bernholc, J. Nanomechanics of carbon tubes: Instabilities beyond linear response. Phys. Rev. Lett. 1996, 76, 2511–2514. [Google Scholar] [CrossRef]
- Wang, C.Y.; Zhang, Y.Y.; Wang, C.M.; Tan, V.B. Buckling of carbon nanotubes: A literature survey. J. Nanosci. Nanotechnol. 2007, 7, 4221–4247. [Google Scholar] [CrossRef]
- Shima, H. Buckling of carbon nanotubes: A state of the art review. Materials 2012, 5, 47–84. [Google Scholar] [CrossRef] [PubMed]
- Garcia, R.; Herruzo, E.T. The emergence of multifrequency force microscopy. Nat. Nanotechnol. 2012, 49, 217–226. [Google Scholar] [CrossRef] [PubMed]
- Barretta, R.; Luciano, R.; de Sciarra, F.M.; Ruta, G. Simulation of the thermal shock behavior of ultra-high temperature ceramics with the consideration of temperature-dependent crack propagation criterion and interaction between thermal shock cracks evolution and thermal conduction. Eur. J. Mech. A Solids 2018, 72, 268–274. [Google Scholar]
- Apuzzo, A.; Barretta, R.; Faghidian, S.A.; Luciano, R.; de Sciarra, F.M. Free vibrations of elastic beams by modified nonlocal strain gradient theory. Int. J. Eng. Sci. 2018, 133, 99–108. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y.; Li, X. Longitudinal vibration of size-dependent rods via nonlocal strain gradient theory. Int. J. Mech. Sci. 2016, 115, 135–144. [Google Scholar] [CrossRef]
- De Sciarra, F.M. A nonlocal model with strain-based damage. Int. J. Solids Struct. 2009, 46, 4107–4122. [Google Scholar] [CrossRef]
- Barretta, R.; Fabbrocino, F.; Luciano, R.; de Sciarra, F.M. Closed-form solutions in stress-driven two-phase integral elasticity forbending of functionally graded nano-beams. Physica E 2018, 97, 13–30. [Google Scholar] [CrossRef]
- De Sciarra, F.M. On non-local and non-homogeneous elastic continua. Int. J. Solids Struct. 2009, 46, 651–676. [Google Scholar] [CrossRef]
- De Sciarra, F.M. Variational formulations, convergence and stability properties in nonlocal elastoplasticity. Int. J. Solids Struct. 2008, 45, 2322–2354. [Google Scholar] [CrossRef][Green Version]
- De Sciarra, F.M. Novel variational formulations for nonlocal plasticity. Int. J. Plast. 2009, 25, 302–331. [Google Scholar] [CrossRef]
- Shi, J.X.; Natsuki, T.; Lei, X.W.; Ni, Q.-Q. Buckling instability of carbon nanotube atomic force microscope probe clamped in an elastic medium. J. Nanotechnol. Eng. Med. 2012, 3, 020903. [Google Scholar] [CrossRef]
- Yang, H.K.; Wang, X. Torsional buckling of multi-wall carbon nanotubes embedded in an elastic medium. Compos. Struct. 2007, 77, 182–192. [Google Scholar] [CrossRef]
- Natsuki, T.; Ni, Q.-Q.; Endo, M. Stability analysis of double-walled carbon nanotubes as AFM probes based on a continuum model. Carbon 2011, 49, 2532–2537. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Natsuki, T.; Urakami, K. Analysis of Vibration Frequency of Carbon Nanotubes used as Nano-Force Sensors Considering Clamped Boundary Condition. Electronics 2019, 8, 1082. https://doi.org/10.3390/electronics8101082
Natsuki T, Urakami K. Analysis of Vibration Frequency of Carbon Nanotubes used as Nano-Force Sensors Considering Clamped Boundary Condition. Electronics. 2019; 8(10):1082. https://doi.org/10.3390/electronics8101082
Chicago/Turabian StyleNatsuki, Toshiaki, and Kairi Urakami. 2019. "Analysis of Vibration Frequency of Carbon Nanotubes used as Nano-Force Sensors Considering Clamped Boundary Condition" Electronics 8, no. 10: 1082. https://doi.org/10.3390/electronics8101082
APA StyleNatsuki, T., & Urakami, K. (2019). Analysis of Vibration Frequency of Carbon Nanotubes used as Nano-Force Sensors Considering Clamped Boundary Condition. Electronics, 8(10), 1082. https://doi.org/10.3390/electronics8101082




