Shannon Entropy Index and a Fuzzy Logic System for the Assessment of Stator Winding Short-Circuit Faults in Induction Motors
Abstract
1. Introduction
2. Theoretical Background
2.1. Motor Current Signal Analysis (MCSA)
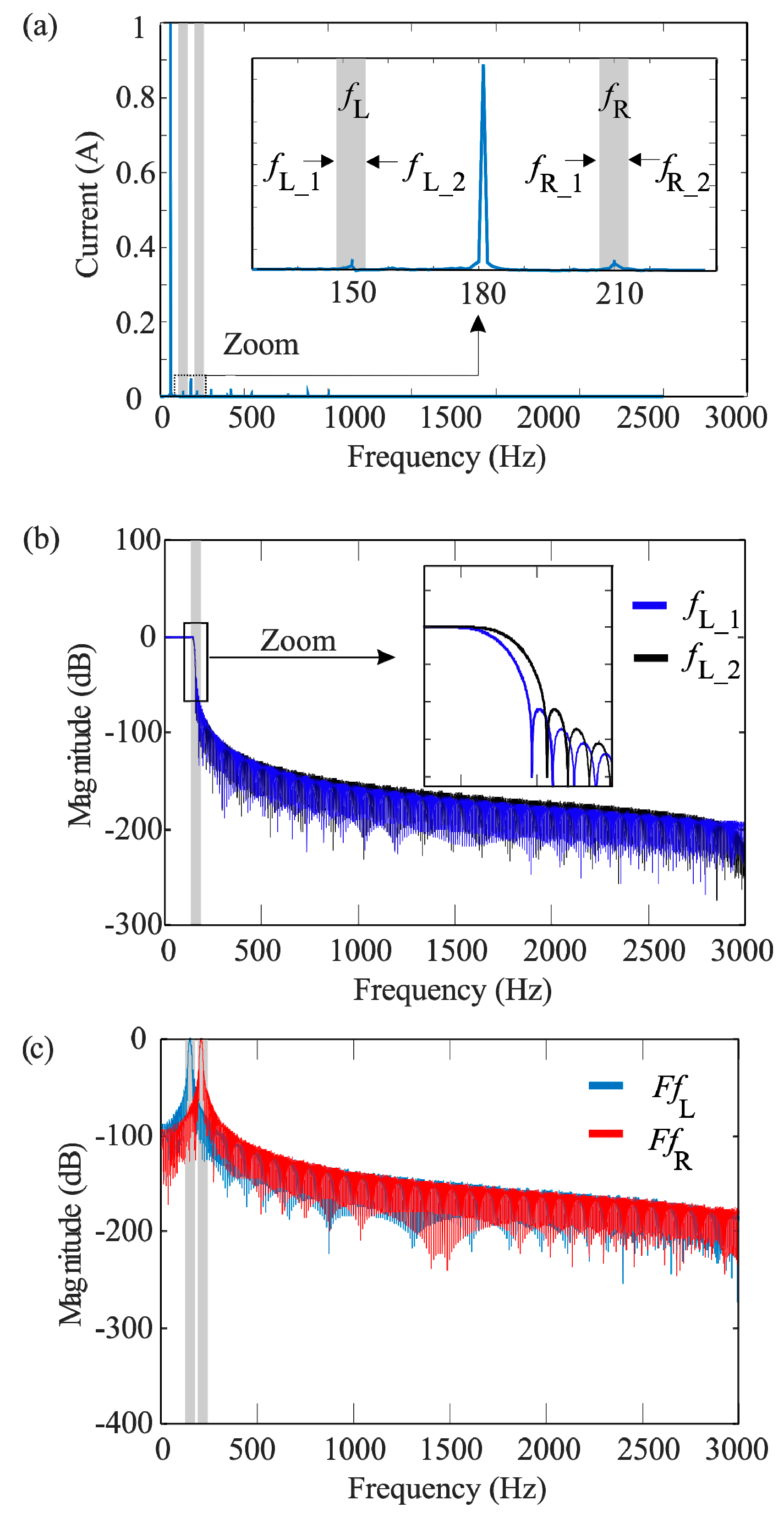
2.2. Brick-Wall Filters
2.3. Fault Indices
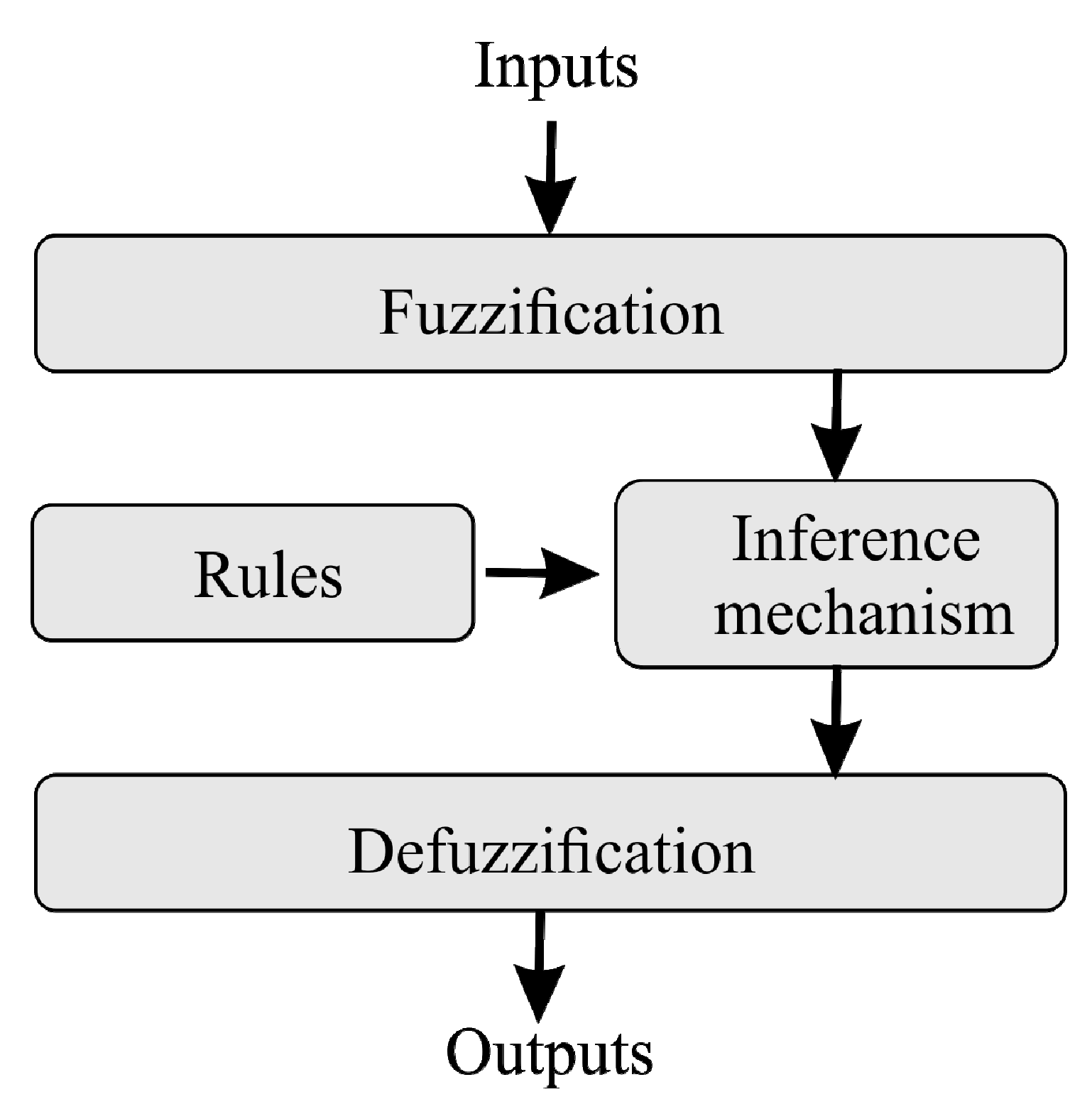
2.4. Fuzzy Logic Systems
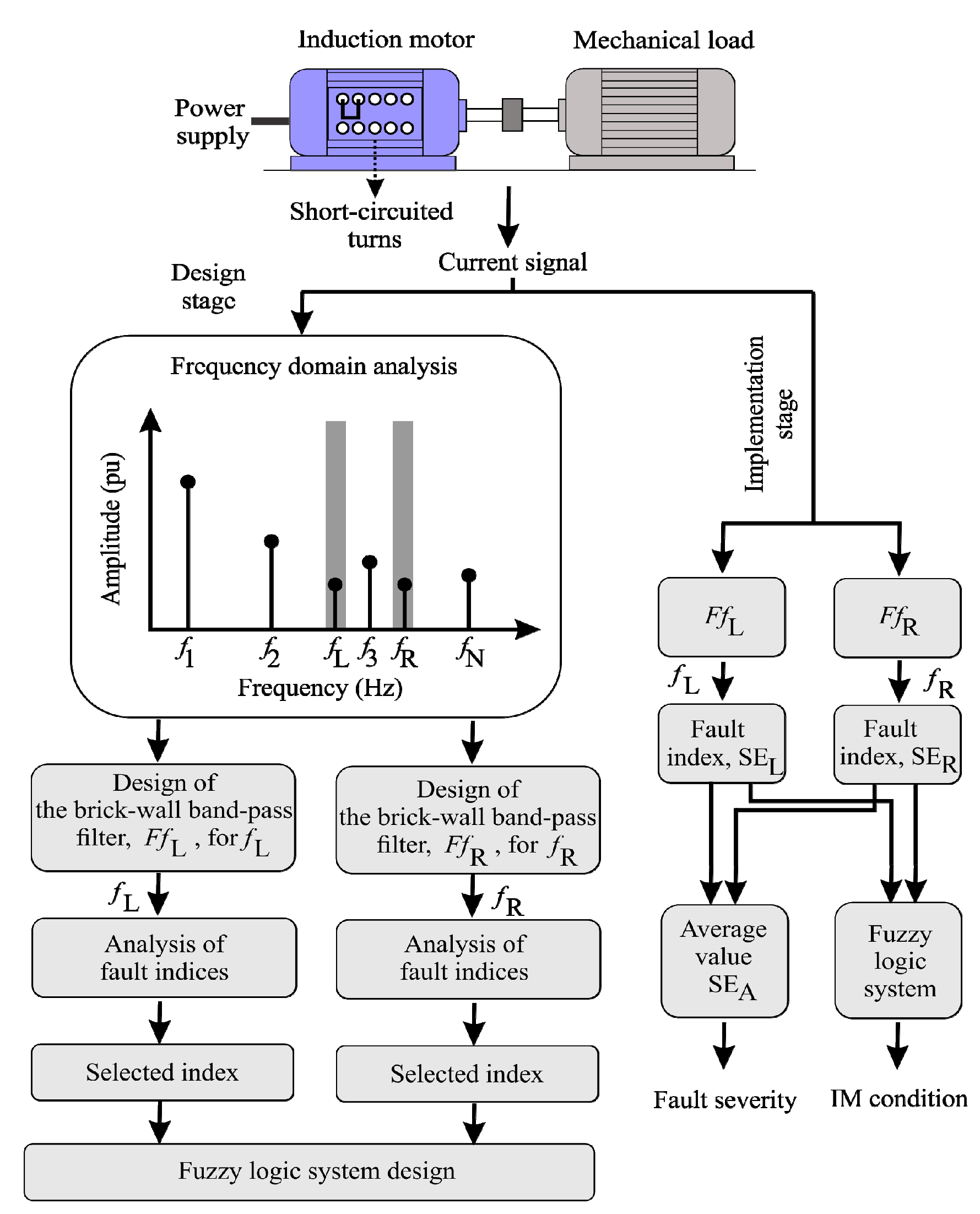
3. Proposed Methodology
4. Experimentation and Results
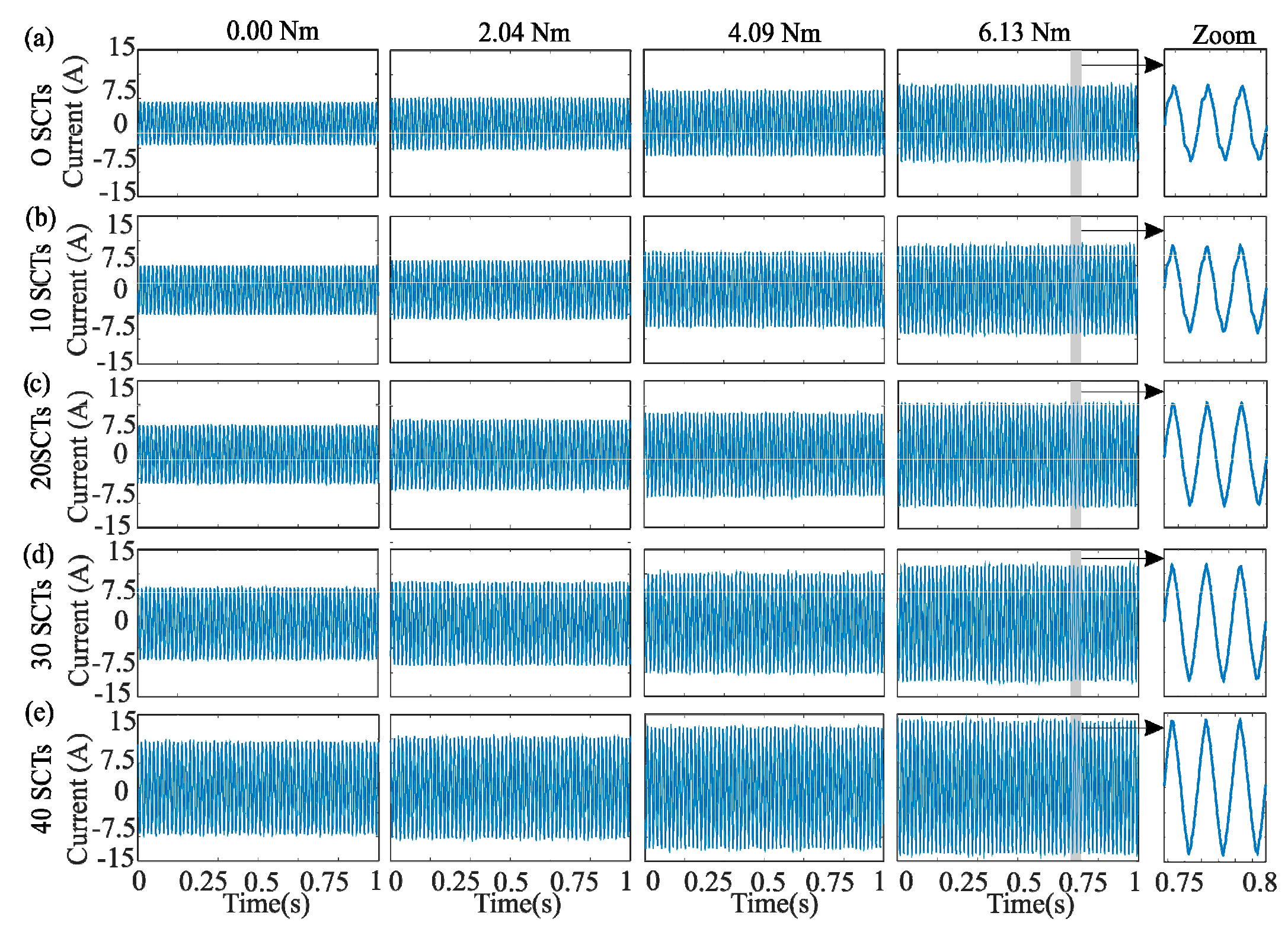
4.1. Experimental Setup
4.2. Results for Real Signals
4.3. Fuzzy Logic System Results
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Glowacz, A. Acoustic-based fault diagnosis of commutator motor. Electronics 2018, 7, 299. [Google Scholar] [CrossRef]
- Singh, A.; Grant, B.; DeFour, R.; Sharma, C.; Bahadoorsingh, S. A review of induction motor fault modeling. Electr. Power Syst. Res. 2016, 133, 191–197. [Google Scholar] [CrossRef]
- Mrizalde, Y.; Hernandez-Callejo, L.; Duque-Perez, O. State of the art and trends in the monitoring, detection and diagnosis of failures in electric induction motors. Energies 2017, 10, 1056. [Google Scholar] [CrossRef]
- Rangari, S.; Suryawanshi, H.; Renge, M. New fault-tolerant control strategy of five-phase induction motor with four-phase and three-phase modes of operation. Electronics 2018, 7, 159. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Valtierra-Rodriguez, M.; Perez-Ramirez, C.A.; Camarena-Martinez, D.; Garcia-Perez, A.; Romero-Troncoso, R.J. Fractal dimension and fuzzy logic systems for broken rotor bar detection in induction motors at start-up and steady-state regimes. Meas. Sci. Technol. 2017, 28, 075001. [Google Scholar] [CrossRef]
- Gyftakis, K.N.; Spyropoulos, D.V.; Kappatou, J.C.; Mitronikas, E.D. A novel approach for broken bar fault diagnosis in induction motors through torque monitoring. IEEE Trans. Energy Convers. 2013, 28, 267–277. [Google Scholar] [CrossRef]
- Florkowski, M.; Furgał, J. Detection of winding faults in electrical machines using the frequency response analysis method. Meas. Sci. Technol. 2004, 15, 2067. [Google Scholar] [CrossRef]
- Bazan, G.H.; Scalassara, P.R.; Endo, W.; Goedtel, A.; Godoy, W.F.; Palácios, R.H.C. Stator fault analysis of three-phase induction motors using information measures and artificial neural networks. Electr. Power Syst. Res. 2017, 143, 347–356. [Google Scholar] [CrossRef]
- Thomson, W.T.; Fenger, M. Current signature analysis to detect induction motor faults. IEEE Ind. Appl. Mag. 2001, 7, 26–34. [Google Scholar] [CrossRef]
- Arthur, N.; Penman, J. Induction machine condition monitoring with higher order spectra. IEEE Trans. Ind. Electron. 2000, 47, 1031–1041. [Google Scholar] [CrossRef]
- Ballal, M.S.; Khan, Z.J.; Suryawanshi, H.M.; Sonolikar, R.L. Adaptive neural fuzzy inference system for the detection of inter-turn insulation and bearing wear faults in induction motor. IEEE Trans. Ind. Electron. 2007, 54, 250–258. [Google Scholar] [CrossRef]
- Ukil, A.; Chen, S.; Andenna, A. Detection of stator short circuit faults in three-phase induction motors using motor current zero crossing instants. Electr. Power Syst. Res. 2011, 81, 1036–1044. [Google Scholar] [CrossRef]
- Drif, M.H.; Cardoso, A.J.M. Stator fault diagnostics in squirrel cage three-phase induction motor drives using the instantaneous active and reactive power signature analyses. IEEE Trans. Ind. Inform. 2014, 10, 1348–1360. [Google Scholar] [CrossRef]
- Glowacz, A.; Glowacz, W.; Glowacz, Z.; Kozik, J. Early fault diagnosis of bearing and stator faults of the single-phase induction motor using acoustic signals. Measurement 2018, 113, 1–9. [Google Scholar] [CrossRef]
- Thomson, W.T. On-line MCSA to diagnose shorted turns in low voltage stator windings of 3-phase induction motors prior to failure. In Proceedings of the Electric Machines and Drives Conference (IEMDC 2001), Cambridge, MA, USA, 17–20 June 2001; pp. 891–898. [Google Scholar]
- Bouzid, M.B.K.; Champenois, G. New expressions of symmetrical components of the induction motor under stator faults. IEEE Trans. Ind. Electron. 2013, 60, 4093–4102. [Google Scholar] [CrossRef]
- Surya, G.N.; Khan, Z.J.; Ballal, M.S.; Suryawanshi, H.M. A simplified frequency-domain detection of stator turn fault in squirrel-cage induction motors using an observer coil technique. IEEE Trans. Ind. Electron. 2017, 64, 1495–1506. [Google Scholar] [CrossRef]
- Asfani, D.A.; Muhammad, A.K.; Purnomo, M.H.; Hiyama, T. Temporary short circuit detection in induction motor winding using combination of wavelet transform and neural network. Expert Syst. Appl. 2012, 39, 5367–5375. [Google Scholar] [CrossRef]
- Devi, N.R.; Sarma, D.V.S.; Rao, P.V.R. Detection of stator incipient faults and identification of faulty phase in three-phase induction motor–simulation and experimental verification. IET Electr. Power Appl. 2015, 9, 540–548. [Google Scholar] [CrossRef]
- Lee, S.H.; Kim, S.; Kim, J.M.; Choi, C.; Kim, J.; Lee, S.; Oh, Y. Extraction of induction motor fault characteristics in frequency domain and fuzzy entropy. In Proceedings of the IEEE International Conference on Electric Machines and Drives, San Antonio, TX, USA, 15 May 2005; pp. 35–40. [Google Scholar]
- Li, J.; Yu, H.; Zhang, L. Application of ensemble empirical mode decomposition on stator inter-turn short-circuit fault in doubly fed induction generators. In Proceedings of the Second International Conference on Mechatronics and Automatic Control, Beijing, China, 20–21 September 2014; pp. 73–83. [Google Scholar]
- Rosero, J.A.; Romeral, L.; Ortega, J.A.; Rosero, E. Short-circuit detection by means of empirical mode decomposition and Wigner–Ville distribution for PMSM running under dynamic condition. IEEE Trans. Ind. Electron. 2015, 56, 4534–4547. [Google Scholar] [CrossRef]
- Sahraoui, M.; Ghoggal, A.; Guedidi, S.; Zouzou, S.E. Detection of inter-turn short-circuit in induction motors using Park–Hilbert method. Int. J. Syst. Assur. Eng. Manag. 2014, 5, 337–351. [Google Scholar] [CrossRef]
- Garcia-Guevara, F.M.; Villalobos-Piña, F.J.; Alvarez-Salas, R.; Cabal-Yepez, E.; Gonzalez-Garcia, M.A. Stator fault detection in induction motors by autoregressive modeling. Math. Probl. Eng. 2016, 2016, 1–7. [Google Scholar] [CrossRef]
- Ghate, V.N.; Dudul, S.V. Optimal MLP neural network classifier for fault detection of three phase induction motor. Expert Syst. Appl. 2010, 37, 3468–3481. [Google Scholar] [CrossRef]
- Valtierra-Rodriguez, M.; Granados-Lieberman, D.; Torres-Fernandez, J.E.; Rodríguez-Rodríguez, J.R.; Gómez-Aguilar, J.F. A new methodology for tracking and instantaneous characterization of voltage variations. IEEE Trans. Instrum. Meas. 2016, 65, 1596–1604. [Google Scholar] [CrossRef]
- Antonino-Daviu, J.A.; Riera-Guasp, M.; Pineda-Sanchez, M.; Pérez, R.B. A critical comparison between DWT and Hilbert–Huang-based methods for the diagnosis of rotor bar failures in induction machines. IEEE Trans. Ind. Appl. 2009, 45, 1794–1803. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2011), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Elbouchikhi, E.; Choqueuse, V.; Amirat, Y.; Benbouzid, M.E.H.; Turri, S. An efficient Hilbert–Huang transform-based bearing faults detection in induction machines. IEEE Trans. Energy Convers. 2017, 32, 401–413. [Google Scholar] [CrossRef]
- Boashash, B.; Khan, N.A.; Ben-Jabeur, T. Time–frequency features for pattern recognition using high-resolution TFDs: A tutorial review. Digit. Signal Process. 2015, 40, 1–30. [Google Scholar] [CrossRef]
- Adeli, H.; Jiang, X. Dynamic fuzzy wavelet neural network model for structural system identification. J. Struct. Eng. 2006, 132, 102–111. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Adeli, H. Synchrosqueezed wavelet transform-fractality model for locating, detecting, and quantifying damage in smart highrise building structures. Smart Mater. Struct. 2015, 24, 065034. [Google Scholar] [CrossRef]
- Jung, J.H.; Lee, J.J.; Kwon, B.H. Online diagnosis of induction motors using MCSA. IEEE Trans. Ind. Electron. 2006, 53, 1842–1852. [Google Scholar] [CrossRef]
- Roscoe, A.J.; Abdulhadi, I.F.; Burt, G.M. Filters for M class phasor measurement units. In Proceedings of the IEEE International Workshop on Applied Measurements for Power Systems (AMPS 2012), Aachen, Germany, 26–28 September 2012; pp. 1–6. [Google Scholar]
- Ramstad, T. Digital methods for conversion between arbitrary sampling frequencies. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 577–591. [Google Scholar] [CrossRef]
- Cabal-Yepez, E.; Valtierra-Rodriguez, M.; Romero-Troncoso, R.J.; Garcia-Perez, A.; Osornio-Rios, R.A.; Miranda-Vidales, H.; Alvarez-Salas, R. FPGA-based entropy neural processor for online detection of multiple combined faults on induction motors. Mech. Syst. Signal Process. 2012, 30, 123–130. [Google Scholar] [CrossRef]
- Mejia-Barron, A.; Valtierra-Rodriguez, M.; Granados-Lieberman, D.; Olivares-Galvan, J.C.; Escarela-Perez, R. The application of EMD-based methods for diagnosis of winding faults in a transformer using transient and steady state currents. Measurement 2018, 117, 371–379. [Google Scholar] [CrossRef]
- Bafroui, H.H.; Ohadi, A. Application of wavelet energy and Shannon entropy for feature extraction in gearbox fault detection under varying speed conditions. Neurocomputing 2014, 133, 437–445. [Google Scholar] [CrossRef]
- Seryasat, O.R.; Honarvar, F.; Rahmani, A. Multi-fault diagnosis of ball bearing using FFT, wavelet energy entropy mean and root mean square (RMS). In Proceedings of the IEEE International Conference on Systems Man and Cybernetics (SMC 2010), Istanbul, Turkey, 10–13 October 2010; pp. 4295–4299. [Google Scholar]
- Kamalapathi, K.; Priyadarshi, N.; Padmanaban, S.; Holm-Nielsen, J.; Azam, F.; Umayal, C.; Ramachandaramurthy, V. A hybrid moth-flame fuzzy logic controller based integrated cuk converter fed brushless DC motor for power factor correction. Electronics 2018, 7, 288. [Google Scholar] [CrossRef]
- Fink, A.; Töpfer, S.; Isermann, R. Nonlinear model-based control with local linear neuro-fuzzy models. Arch. Appl. Mech. 2003, 72, 911–922. [Google Scholar] [CrossRef]
- Nentwig, M.; Mercorelli, P. Throttle valve control using an inverse local linear model tree based on a Fuzzy neural network. In Proceedings of the 7th IEEE International Conference on Cybernetic Intelligent Systems, London, UK, 9–10 September 2008. [Google Scholar] [CrossRef]
- De Silva, C.W. Intelligent Control: Fuzzy Logic Applications; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Passino, K.M.; Yurkovich, S.; Reinfrank, M. Fuzzy Control; Addison-Wesley: Menlo Park, CA, USA, 1998; ISBN 0-201-18074-X. [Google Scholar]

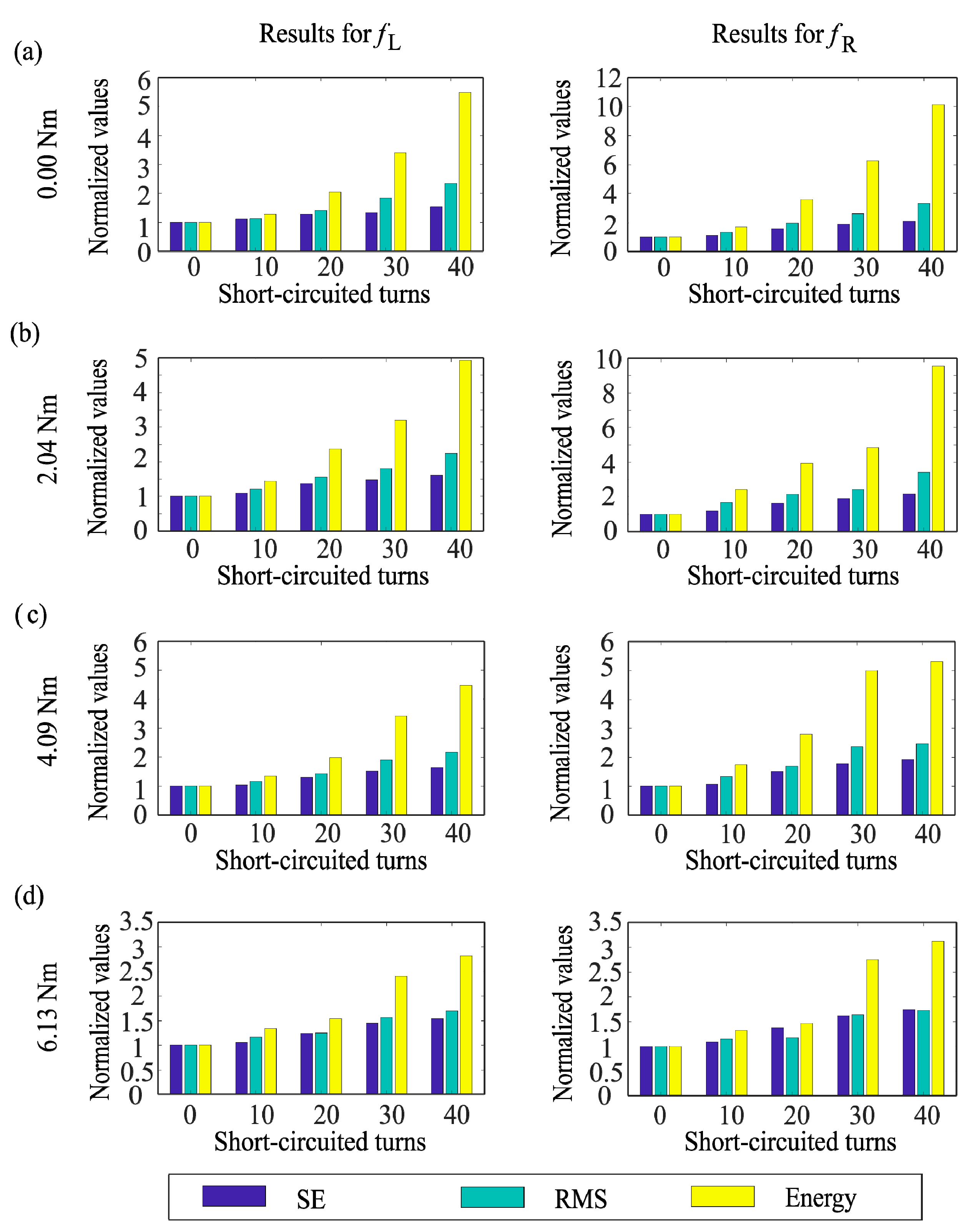
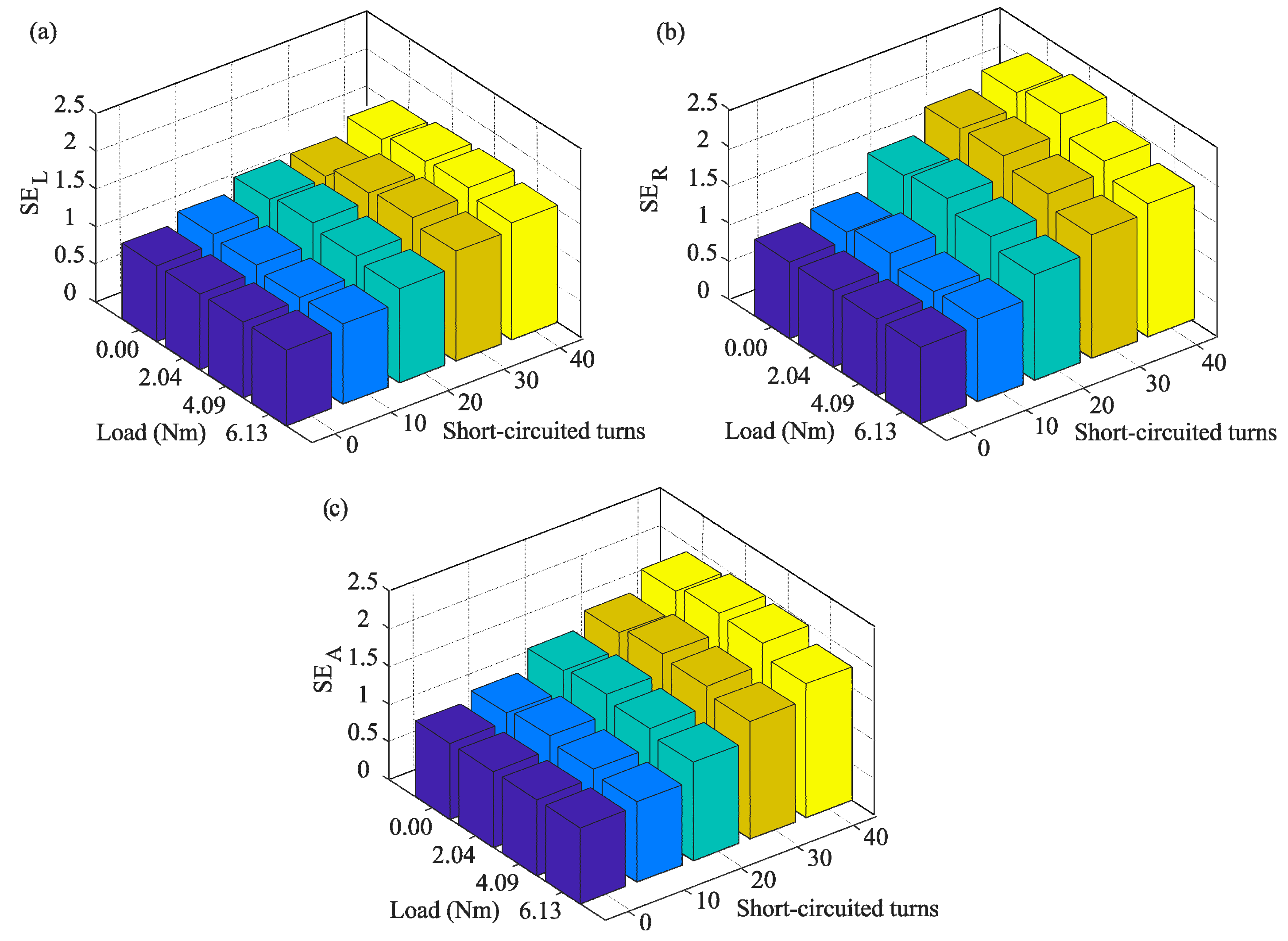
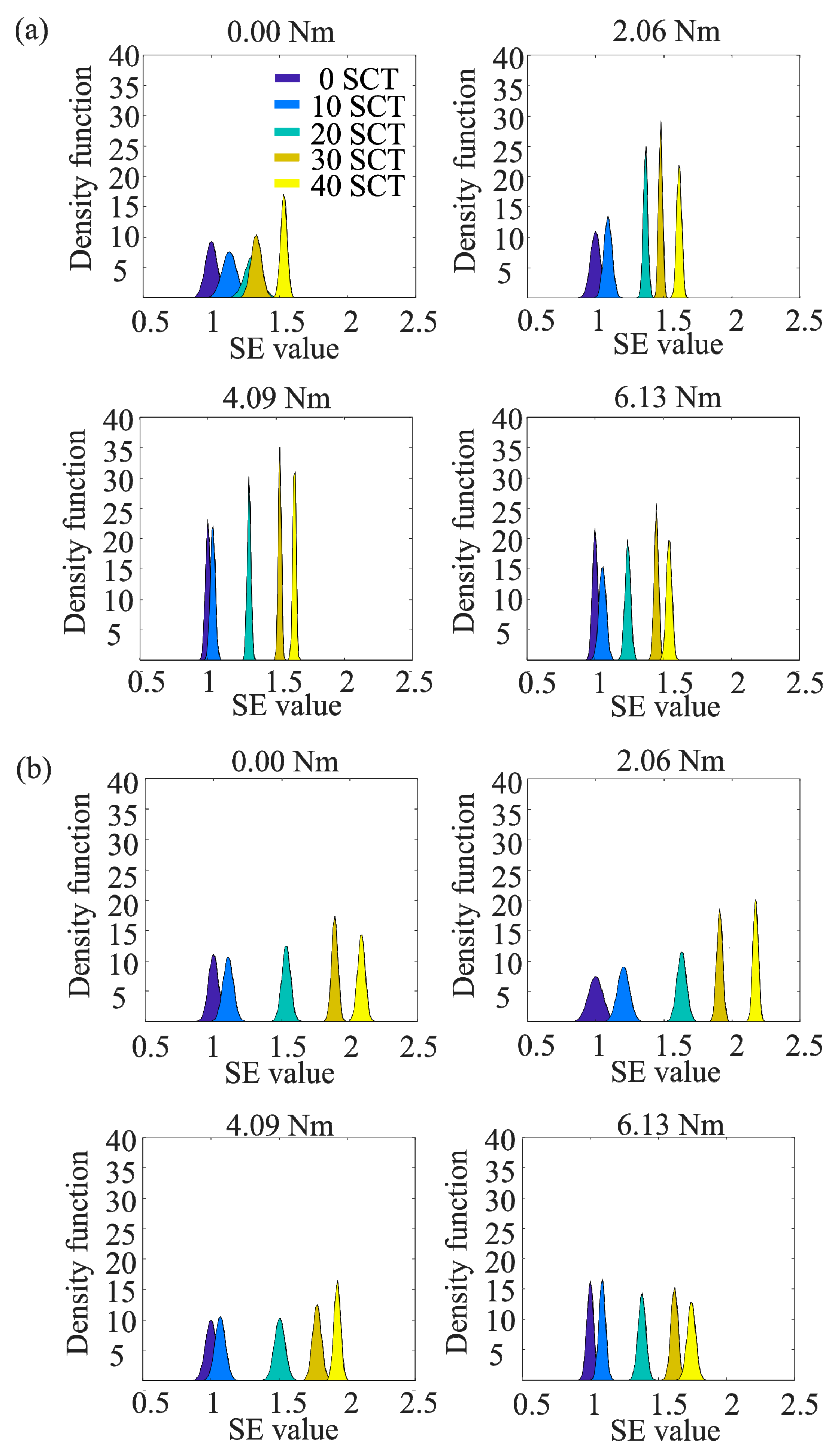
| fL | |||||
| Number of Short-Circuited Turns (μ and σ for SE Values) | |||||
| Load | 0 | 10 | 20 | 30 | 40 |
| 0.00 | 1, 0.1229 | 1.1326, 0.1578 | 1.3051, 0.1720 | 1.3297, 0.1160 | 1.5324, 0.0699 |
| 2.04 | 1, 0.1097 | 1.0916, 0.0890 | 1.3673, 0.0483 | 1.4781, 0.0413 | 1.6144, 0.0533 |
| 4.09 | 1, 0.0516 | 1.0358, 0.0530 | 1.3025, 0.0395 | 1.5279, 0.0335 | 1.6354, 0.0359 |
| 6.13 | 1, 0.0558 | 1.0559, 0.0771 | 1.2410, 0.0613 | 1.4507, 0.0477 | 1.5444, 0.0591 |
| fR | |||||
| Number of Short-Circuited Turns (μ and σ for SE Values) | |||||
| Load | 0 | 10 | 20 | 30 | 40 |
| 0.00 | 1, 0.1082 | 1.1082, 0.1121 | 1.5639, 0.0951 | 1.8904, 0.0696 | 2.0860, 0.0830 |
| 2.04 | 1, 0.1614 | 1.2044, 0.1315 | 1.6318, 0.1035 | 1.9104, 0.0647 | 2.1743, 0.0580 |
| 4.09 | 1, 0.1204 | 1.0683, 0.1135 | 1.5052, 0.1166 | 1.7788, 0.0960 | 1.9281, 0.0727 |
| 6.13 | 0.073833 | 1.0878, 0.0720 | 1.3794, 0.0838 | 1.6181, 0.0786 | 1.7425, 0.0932 |
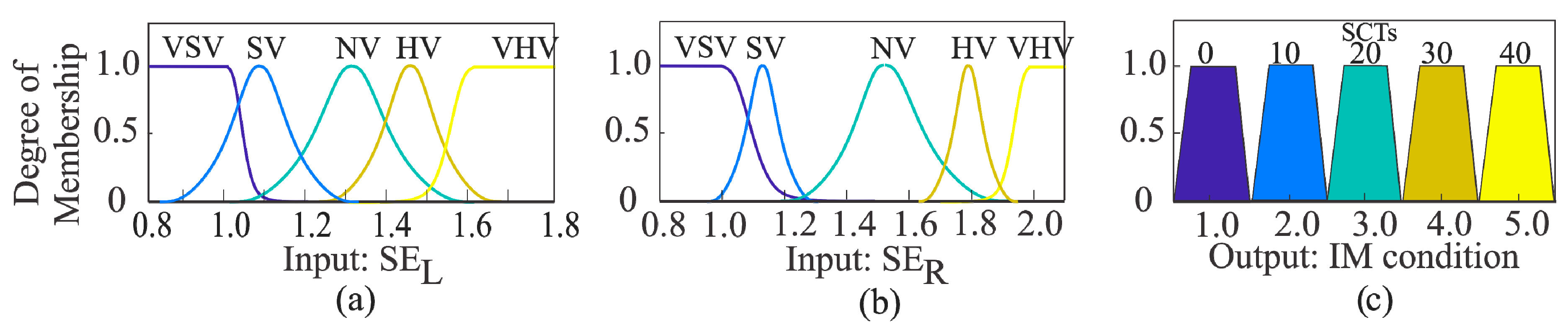
| Inputs | SER | ||||
|---|---|---|---|---|---|
| SEL | VSV | SV | NV | HV | VHV |
| VSV | 0 SCTs | 0 SCTs | 10 SCTs | 20 SCTs | 20 SCTs |
| SV | 0 SCTs | 10 SCTs | 20 SCTs | 20 SCTs | 20 SCTs |
| NV | 10 SCTs | 20 SCTs | 20 SCTs | 20 SCTs | 30 SCTs |
| HV | 20 SCTs | 20 SCTs | 20 SCTs | 30 SCTs | 40 SCTs |
| VHV | 20 SCTs | 20 SCTs | 30 SCTs | 40 SCTs | 40 SCTs |
| IM Condition | 0 SCTs | 10 SCTs | 20 SCTs | 30 SCTs | 40 SCTs | EP (%) |
|---|---|---|---|---|---|---|
| 0 SCTs | 19 | 1 | 0 | 0 | 0 | 95 |
| 10 SCTs | 1 | 19 | 0 | 0 | 0 | 95 |
| 20 SCTs | 0 | 0 | 20 | 0 | 0 | 100 |
| 30 SCTs | 0 | 0 | 0 | 20 | 0 | 100 |
| 40 SCTs | 0 | 0 | 0 | 0 | 20 | 100 |
| Effectiveness | 98% |
| Work | Applied Methods | Domain | Accuracy | Variable Load | Different Fault Severities |
|---|---|---|---|---|---|
| [8] |
| Time | >93% | Yes | Yes |
| [12] |
| Frequency | NR | Yes | No |
| [19] |
| Time-Frequency | NR | No | Yes |
| [23] |
| Frequency | NR | Yes | Yes |
| [24] |
| Time | 95% | No | Yes |
| This work |
| Time | 98% | Yes | Yes |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mejia-Barron, A.; de Santiago-Perez, J.J.; Granados-Lieberman, D.; Amezquita-Sanchez, J.P.; Valtierra-Rodriguez, M. Shannon Entropy Index and a Fuzzy Logic System for the Assessment of Stator Winding Short-Circuit Faults in Induction Motors. Electronics 2019, 8, 90. https://doi.org/10.3390/electronics8010090
Mejia-Barron A, de Santiago-Perez JJ, Granados-Lieberman D, Amezquita-Sanchez JP, Valtierra-Rodriguez M. Shannon Entropy Index and a Fuzzy Logic System for the Assessment of Stator Winding Short-Circuit Faults in Induction Motors. Electronics. 2019; 8(1):90. https://doi.org/10.3390/electronics8010090
Chicago/Turabian StyleMejia-Barron, Arturo, J. Jesus de Santiago-Perez, David Granados-Lieberman, Juan P. Amezquita-Sanchez, and Martin Valtierra-Rodriguez. 2019. "Shannon Entropy Index and a Fuzzy Logic System for the Assessment of Stator Winding Short-Circuit Faults in Induction Motors" Electronics 8, no. 1: 90. https://doi.org/10.3390/electronics8010090
APA StyleMejia-Barron, A., de Santiago-Perez, J. J., Granados-Lieberman, D., Amezquita-Sanchez, J. P., & Valtierra-Rodriguez, M. (2019). Shannon Entropy Index and a Fuzzy Logic System for the Assessment of Stator Winding Short-Circuit Faults in Induction Motors. Electronics, 8(1), 90. https://doi.org/10.3390/electronics8010090








