Efficient Large Sparse Arrays Synthesis by Means of Smooth Re-Weighted L1 Minimization
Abstract
1. Introduction
2. Problem Formulation
3. Smooth Re-Weighted L1 Minimization
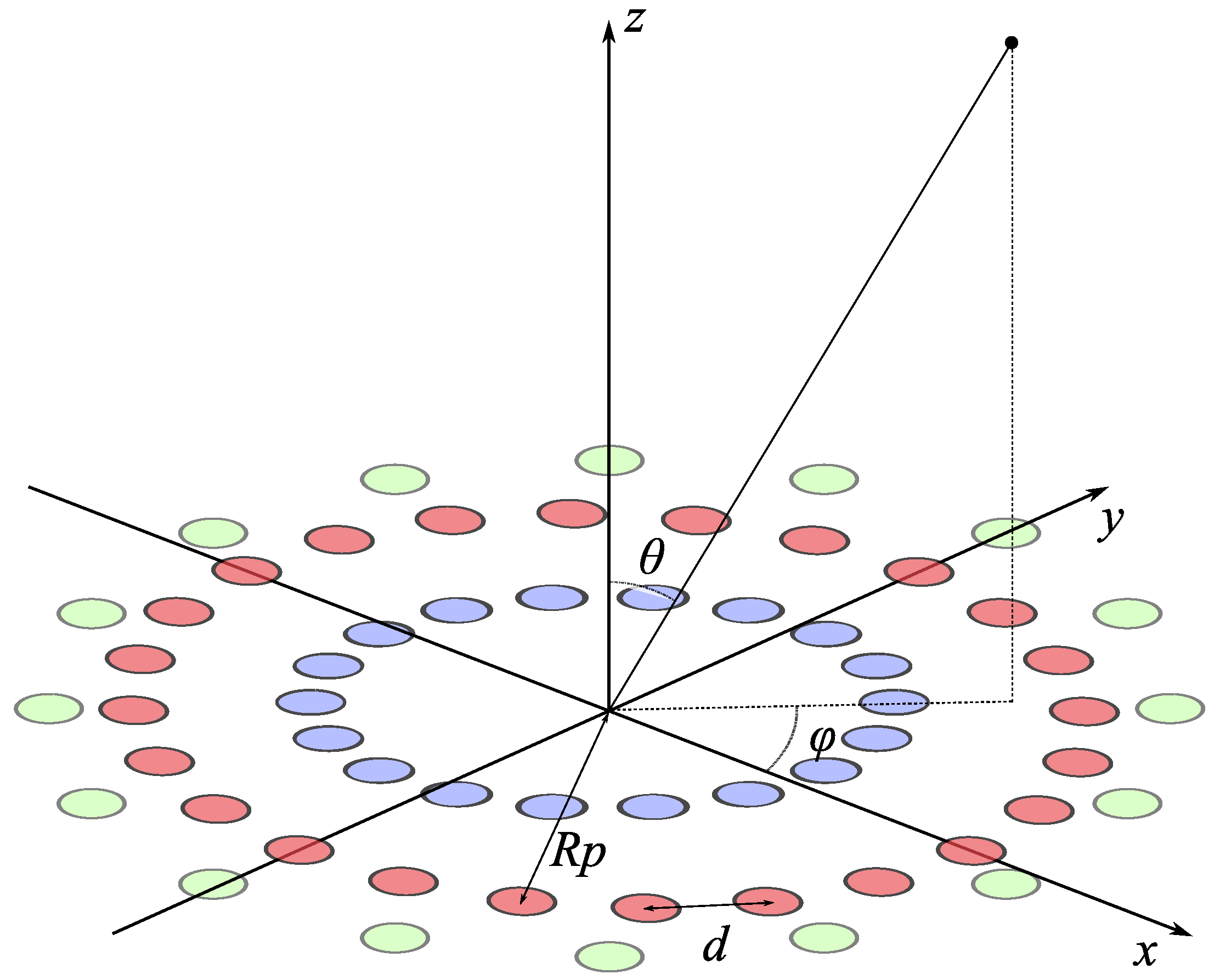
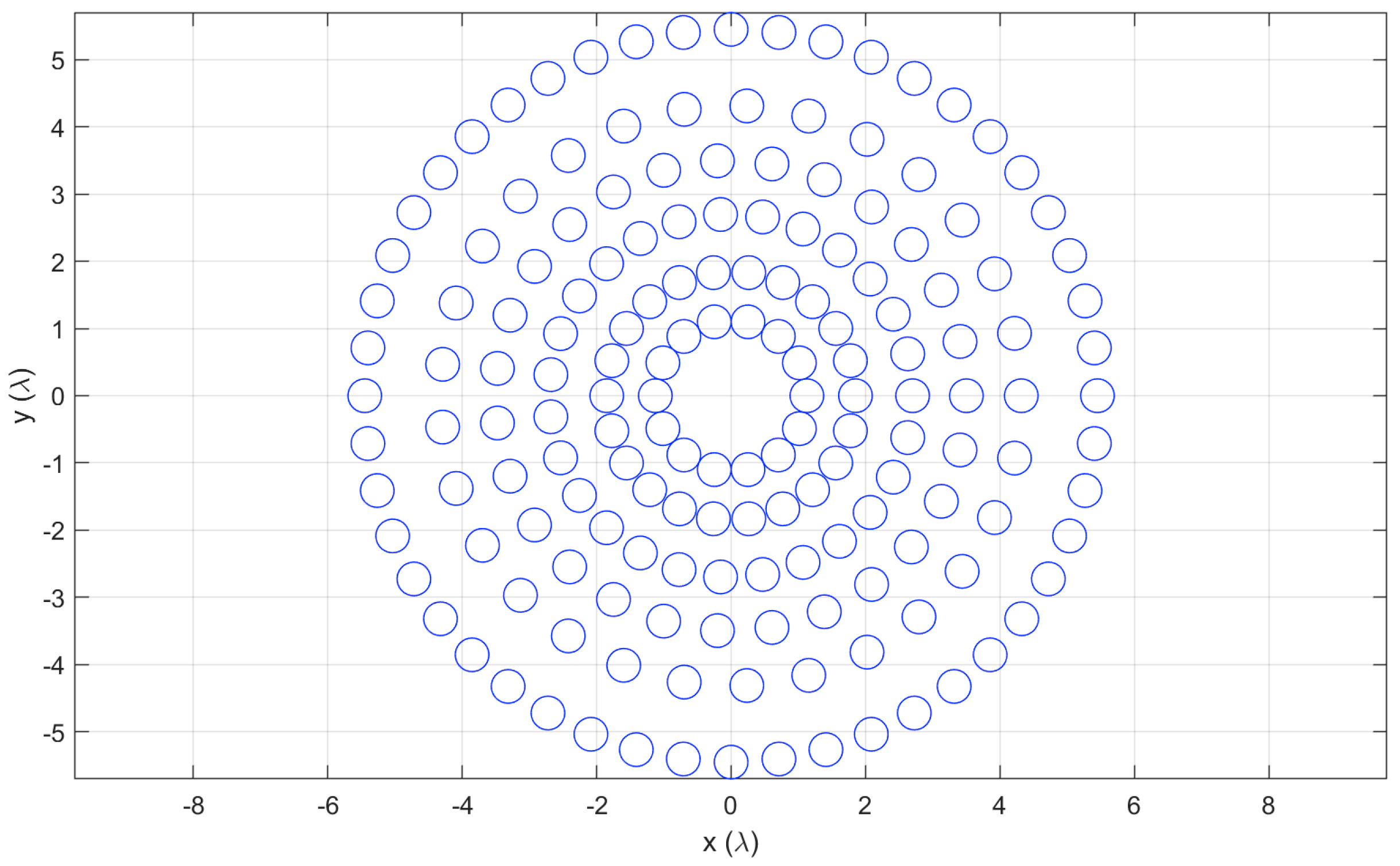
4. Ring Population from the Calculated Excitation
- Choose the values of , , and to use.
- we extract the ring radii and excitations from the sparse vector ;
5. Numerical Examples
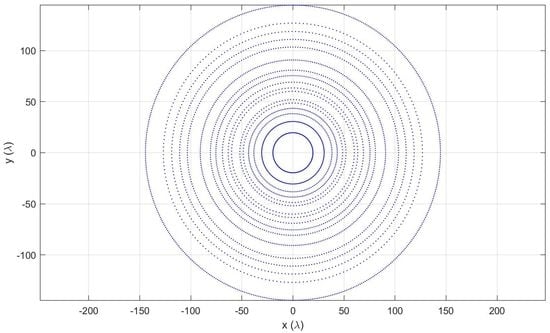
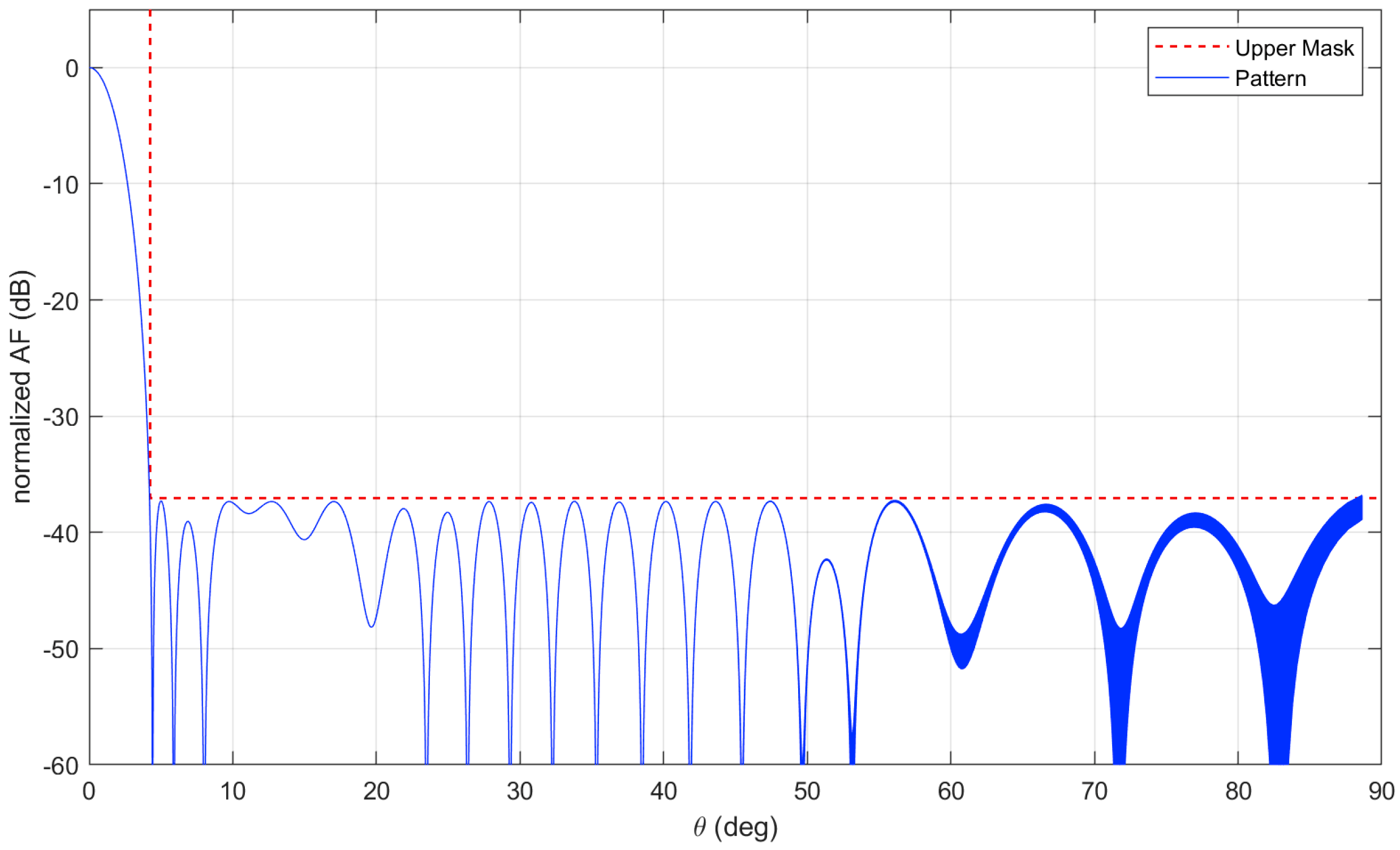
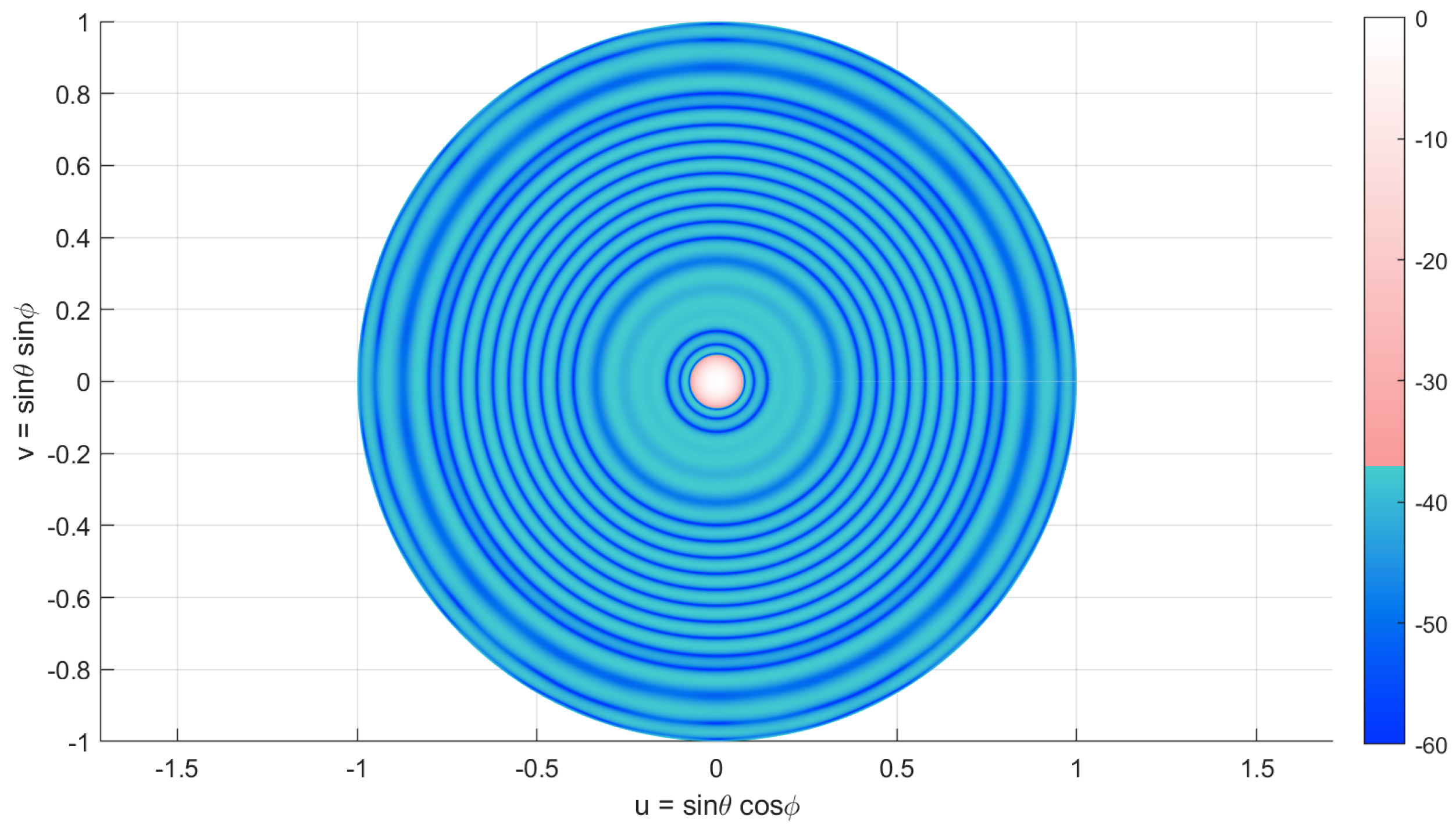
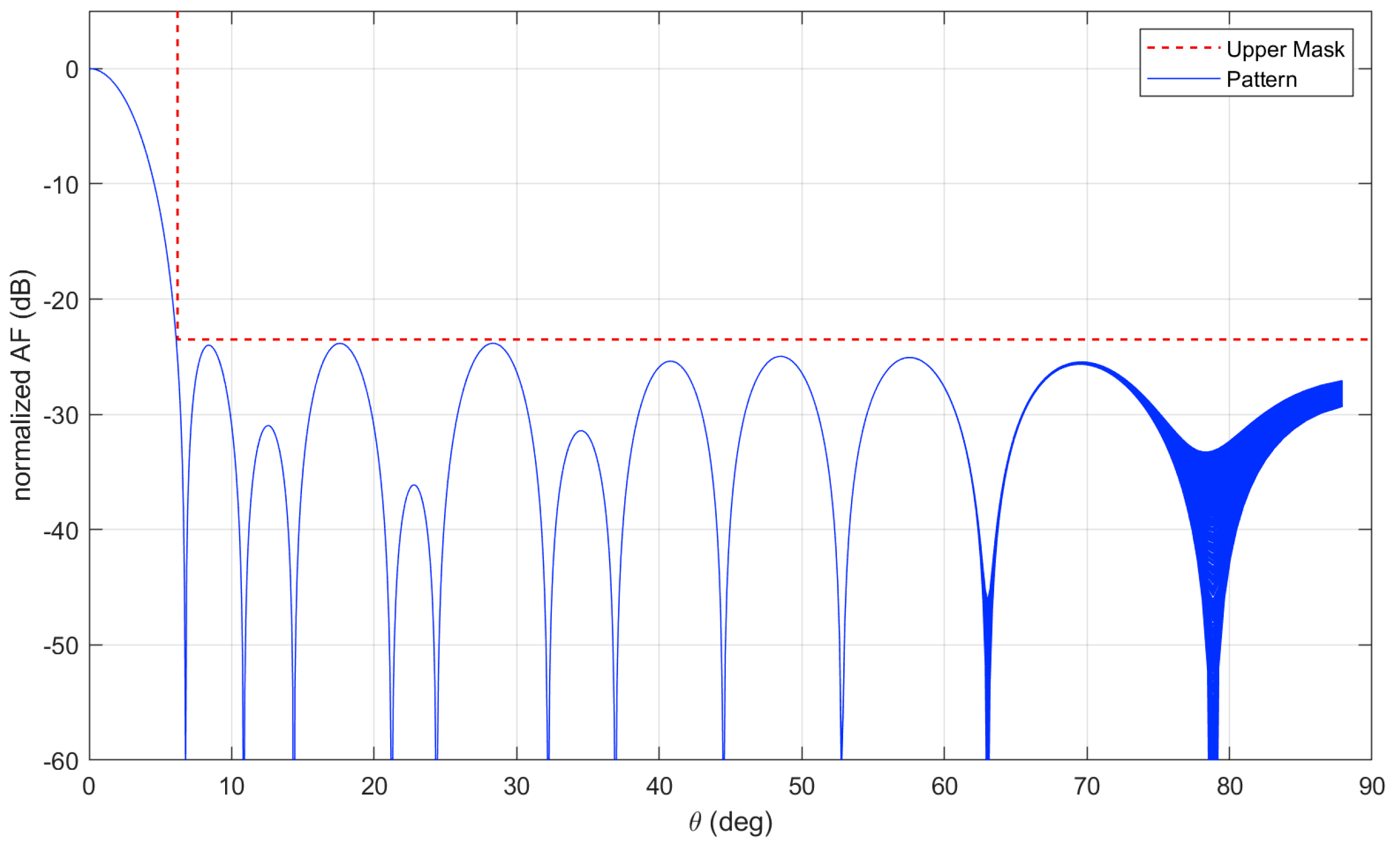
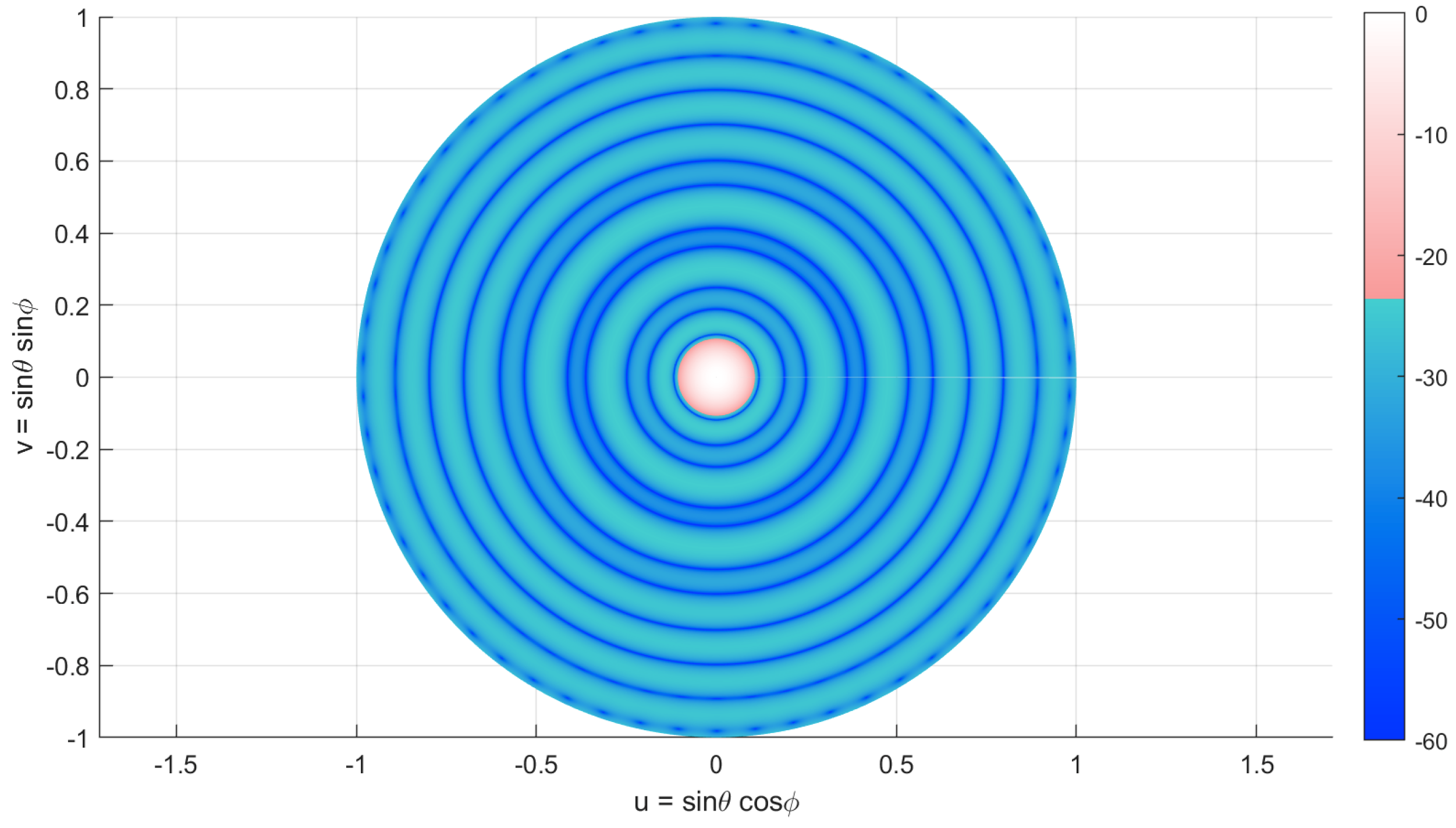
5.1. Large Array with Variable Excitation
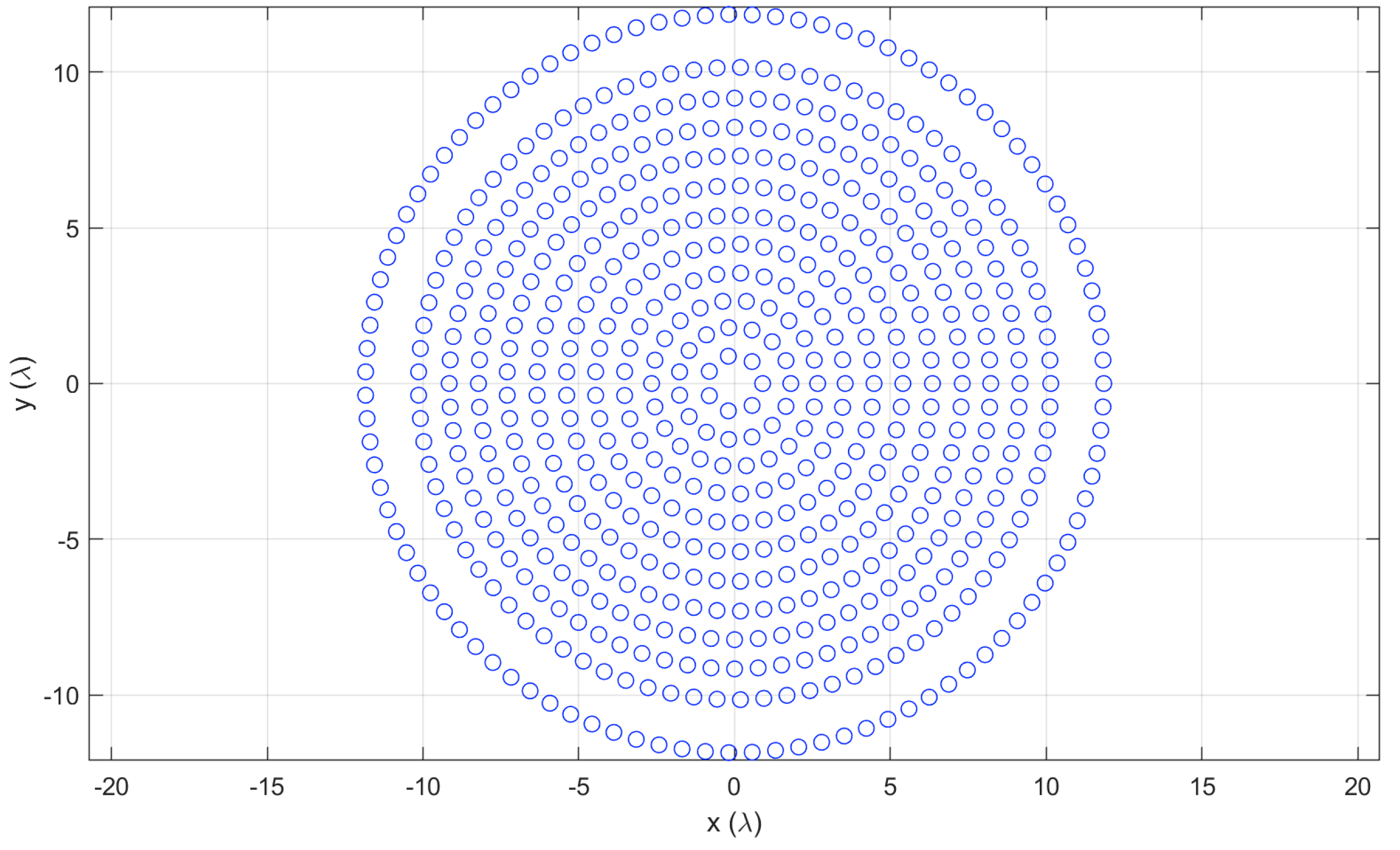
5.2. Small Isophoric Sparse Array
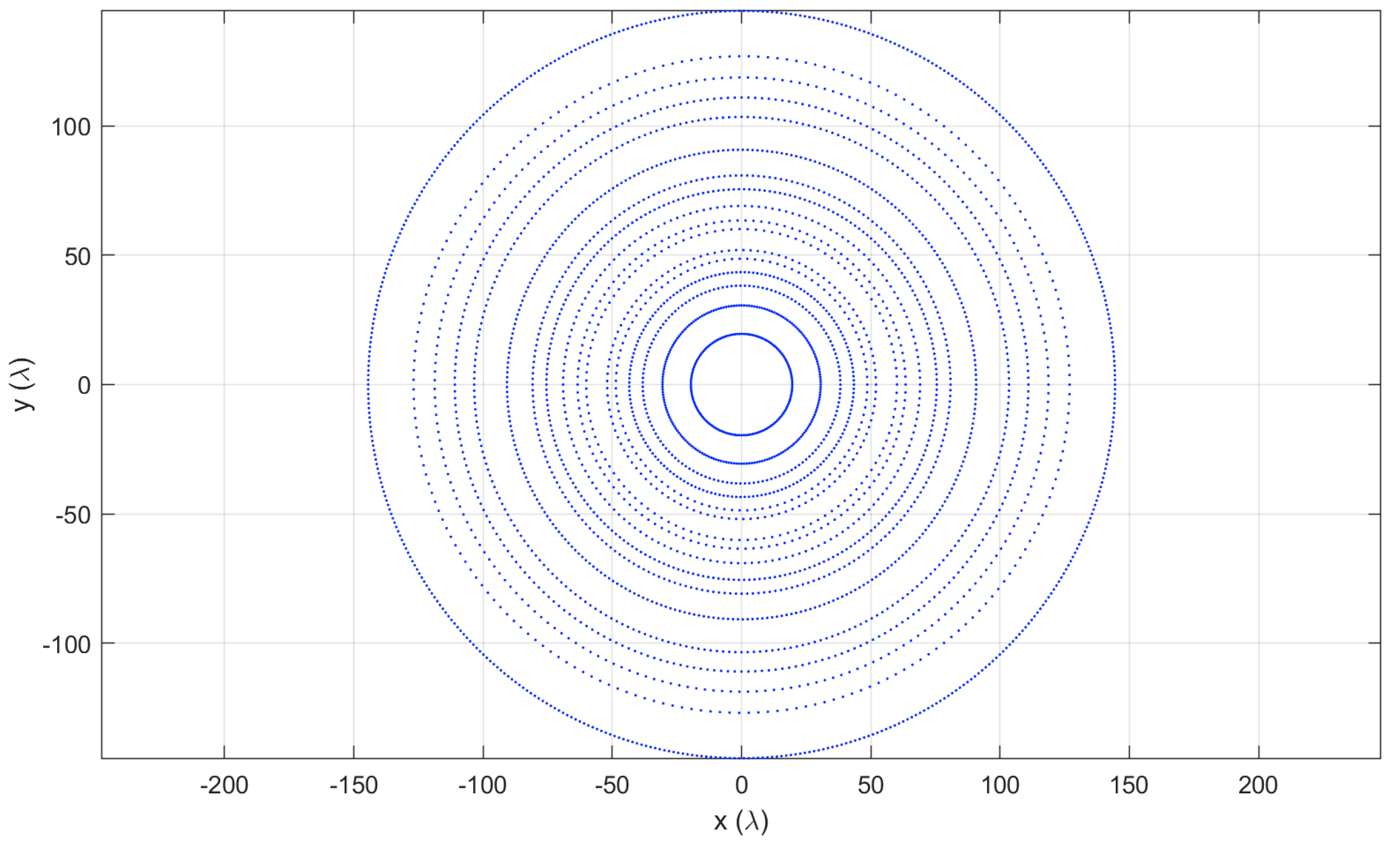
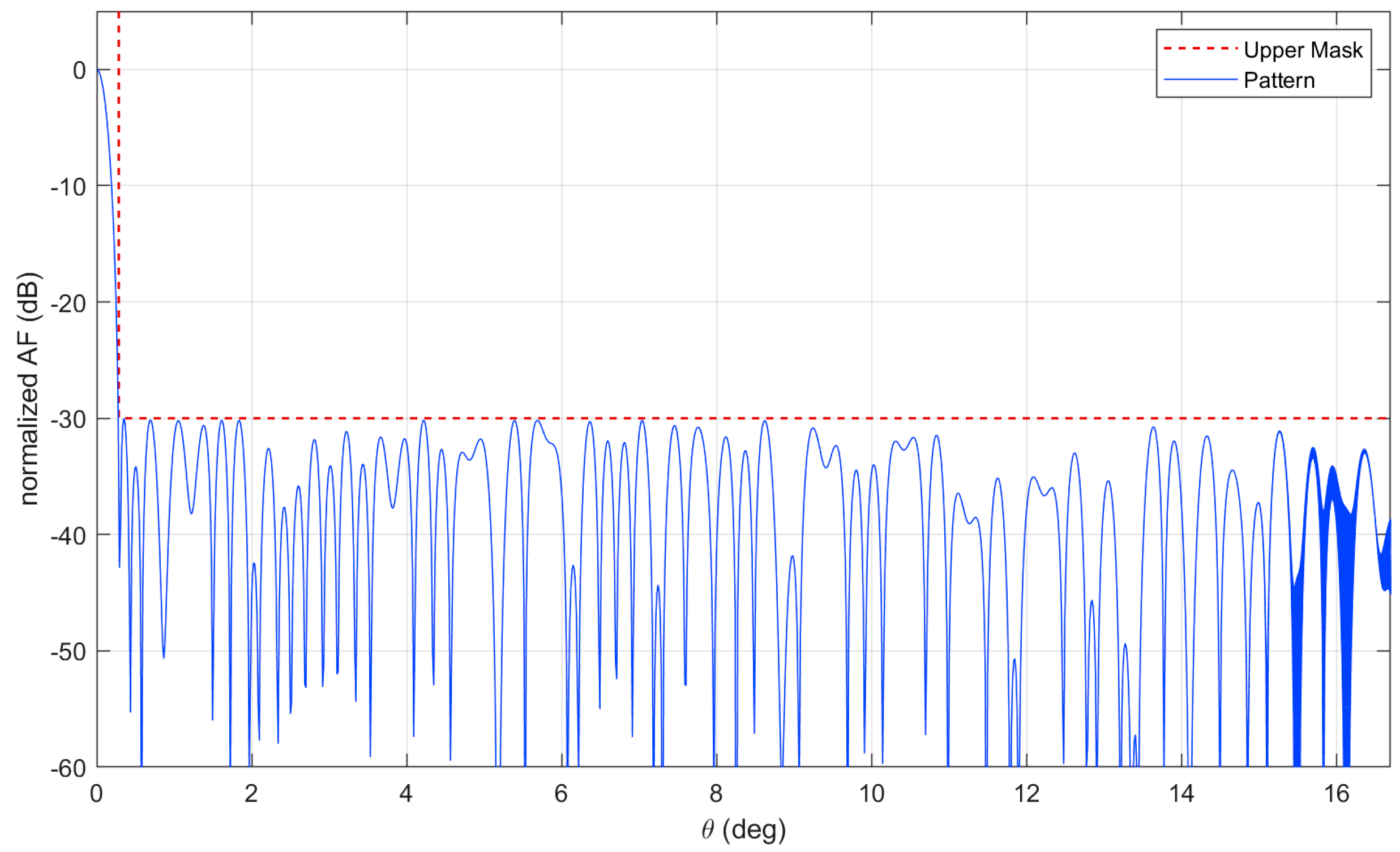
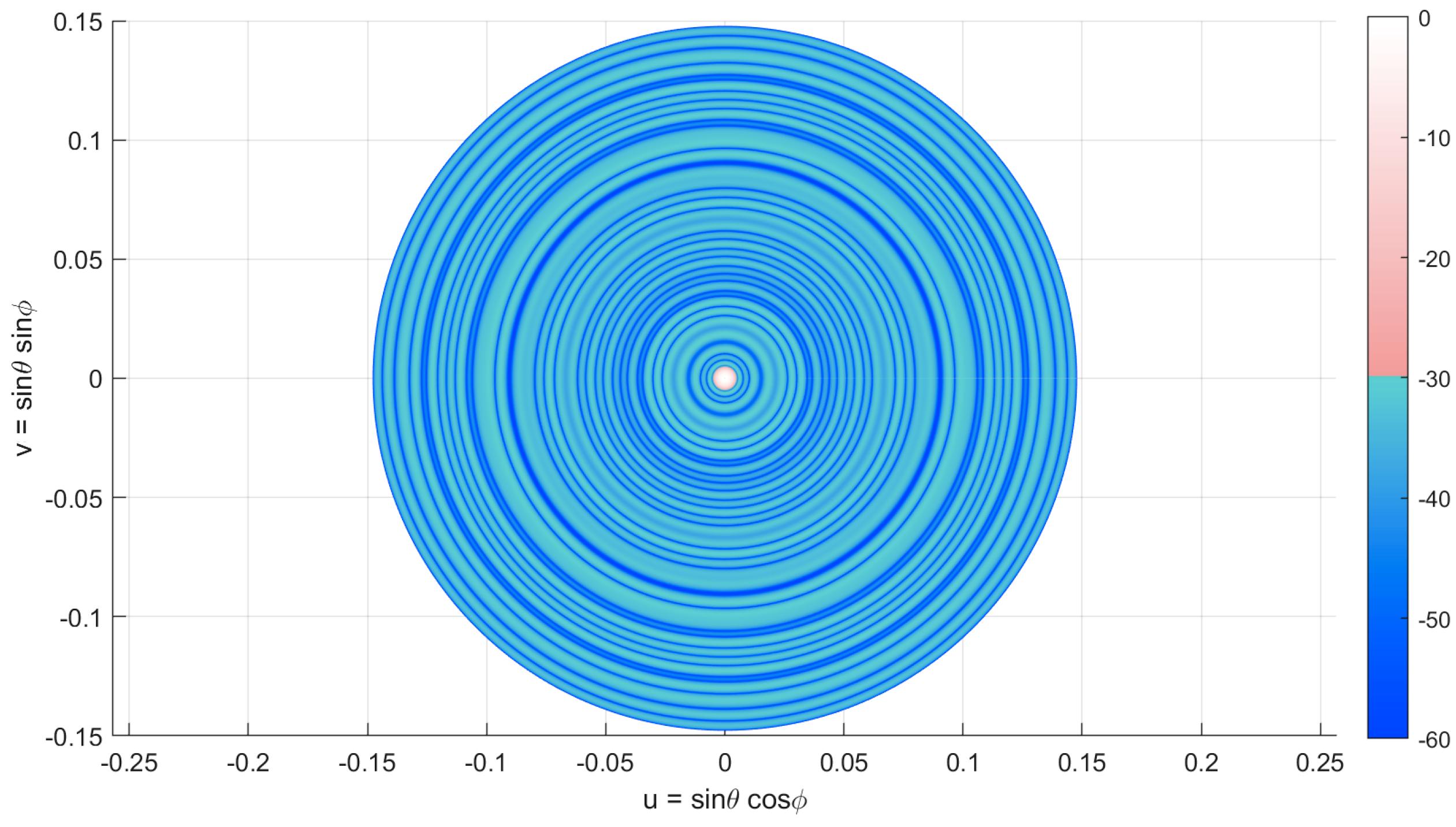
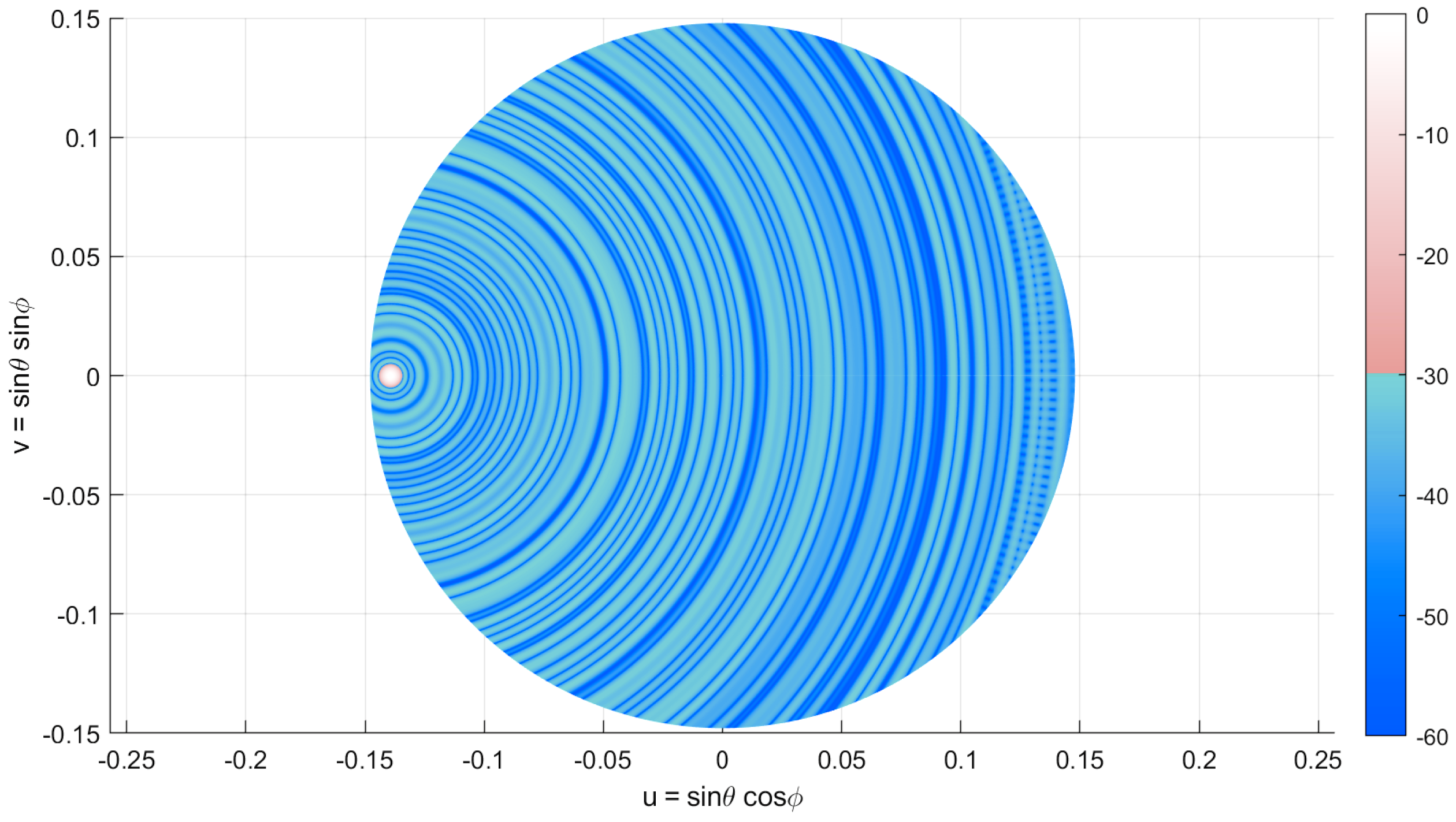
5.3. Very Large Isophoric Sparse Array
6. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Weber, R.H.; Weber, R. Internet of Things; Springer: Berlin, Germany, 2010; Volume 12. [Google Scholar]
- Pinchera, D.; Migliore, M.D.; Schettino, F.; Panariello, G. Antenna Arrays for Line-of-Sight Massive MIMO: Half Wavelength Is Not Enough. Electronics 2017, 6, 57. [Google Scholar] [CrossRef]
- Larsson, E.G.; Edfors, O.; Tufvesson, F.; Marzetta, T.L. Massive MIMO for next generation wireless systems. IEEE Commun. Mag. 2014, 52, 186–195. [Google Scholar] [CrossRef]
- Zhao, D.; Jin, T.; Dai, Y.; Song, Y.; Su, X. A Three-Dimensional Enhanced Imaging Method on Human Body for Ultra-Wideband Multiple-Input Multiple-Output Radar. Electronics 2018, 7, 101. [Google Scholar]
- Haupt, R.L. Thinned arrays using genetic algorithms. IEEE Trans. Antennas Propag. 1994, 42, 993–999. [Google Scholar] [CrossRef]
- Trucco, A.; Omodei, E.; Repetto, P. Synthesis of sparse planar arrays. Electron. Lett. 1997, 33, 1834–1835. [Google Scholar] [CrossRef]
- Bray, M.G.; Werner, D.H.; Boeringer, D.W.; Machuga, D.W. Optimization of thinned aperiodic linear phased arrays using genetic algorithms to reduce grating lobes during scanning. IEEE Trans. Antennas Propag. 2002, 50, 1732–1742. [Google Scholar] [CrossRef]
- Migliore, M.D.; Pinchera, D.; Schettino, F. A simple and robust adaptive parasitic antenna. IEEE Trans. Antennas Propag. 2005, 53, 3262–3272. [Google Scholar] [CrossRef]
- Chen, K.; He, Z.; Han, C.C. A modified real GA for the sparse linear array synthesis with multiple constraints. IEEE Trans. Antennas Propag. 2006, 54, 2169–2173. [Google Scholar] [CrossRef]
- Quevedo-Teruel, O.; Rajo-Iglesias, E. Ant colony optimization in thinned array synthesis with minimum sidelobe level. IEEE Antennas Wirel. Propag. Lett. 2006, 5, 349–352. [Google Scholar] [CrossRef]
- Migliore, M.D.; Pinchera, D.; Schettino, F. Improving Channel Capacity Using Adaptive MIMO Antennas. IEEE Trans. Antennas Propag. 2006, 54, 3481–3489. [Google Scholar] [CrossRef]
- Haupt, R.L. Optimized element spacing for low sidelobe concentric ring arrays. IEEE Trans. Antennas Propag. 2008, 56, 266–268. [Google Scholar] [CrossRef]
- Reyna, A.; Panduro, M.A.; Del Rio, C. Design of concentric ring antenna arrays for isoflux radiation in GEO satellites. IEICE Electron. Express 2011, 8, 484–490. [Google Scholar] [CrossRef]
- Goudos, S.K.; Siakavara, K.; Samaras, T.; Vafiadis, E.E.; Sahalos, J.N. Sparse linear array synthesis with multiple constraints using differential evolution with strategy adaptation. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 670–673. [Google Scholar] [CrossRef]
- Cen, L.; Yu, Z.L.; Ser, W.; Cen, W. Linear aperiodic array synthesis using an improved genetic algorithm. IEEE Trans. Antennas Propag. 2012, 60, 895–902. [Google Scholar] [CrossRef]
- Zhang, L.; Jiao, Y.C.; Chen, B. Optimization of concentric ring array geometry for 3D beam scanning. Int. J. Antennas Propag. 2012, 2012, 625437. [Google Scholar] [CrossRef]
- Manica, L.; Anselmi, N.; Rocca, P.; Massa, A. Robust mask-constrained linear array synthesis through aninterval-based particle SWARM optimisation. IET Microw. Antennas Propag. 2013, 7, 976–984. [Google Scholar] [CrossRef]
- Chen, K.; Chen, H.; Wang, L.; Wu, H. Modified real ga for the synthesis of sparse planar circular arrays. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 274–277. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, S.; Guo, Q.; Li, M. Synthesis of uniformly excited concentric ring arrays using the improved integer GA. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1124–1127. [Google Scholar] [CrossRef]
- Polo-López, L.; Córcoles, J.; Ruiz-Cruz, J.A. Antenna Design by Means of the Fruit Fly Optimization Algorithm. Electronics 2018, 7, 3. [Google Scholar] [CrossRef]
- Leahy, R.M.; Jeffs, B.D. On the design of maximally sparse beamforming arrays. IEEE Trans. Antennas Propag. 1991, 39, 1178–1187. [Google Scholar] [CrossRef]
- Marchaud, F.B.; De Villiers, G.D.; Pike, E.R. Element positioning for linear arrays using generalized Gaussian quadrature. IEEE Trans. Antennas Propag. 2003, 51, 1357–1363. [Google Scholar] [CrossRef]
- Liu, Y.; Nie, Z.; Liu, Q.H. Reducing the number of elements in a linear antenna array by the matrix pencil method. IEEE Trans. Antennas Propag. 2008, 56, 2955–2962. [Google Scholar] [CrossRef]
- Oliveri, G.; Donelli, M.; Massa, A. Linear array thinning exploiting almost difference sets. IEEE Trans. Antennas Propag. 2009, 57, 3800–3812. [Google Scholar] [CrossRef]
- Angeletti, P.; Toso, G. Synthesis of circular and elliptical sparse arrays. Electron. Lett. 2011, 47, 304–305. [Google Scholar] [CrossRef]
- Yang, K.; Zhao, Z.; Liu, Y. Synthesis of sparse planar arrays with matrix pencil method. In Proceedings of the 2011 International Conference on Computational Problem-Solving (ICCP), Chengdu, China, 21–23 October 2011; pp. 82–85. [Google Scholar]
- Bucci, O.M.; Perna, S.; Pinchera, D. Advances in the deterministic synthesis of uniform amplitude pencil beam concentric ring arrays. IEEE Trans. Antennas Propag. 2012, 60, 3504–3509. [Google Scholar] [CrossRef]
- Guo, H.; Guo, C.J.; Qu, Y.; Ding, J. Pattern synthesis of concentric circular antenna array by nonlinear least-square method. Prog. Electromagn. Res. 2013, 50, 331–346. [Google Scholar] [CrossRef]
- Oliveri, G.; Bekele, E.T.; Robol, F.; Massa, A. Sparsening Conformal Arrays Through a Versatile-Based Method. IEEE Trans. Antennas Propag. 2014, 62, 1681–1689. [Google Scholar] [CrossRef]
- Angeletti, P.; Toso, G.; Ruggerini, G. Array antennas with jointly optimized elements positions and dimensions part II: Planar circular arrays. IEEE Trans. Antennas Propag. 2014, 62, 1627–1639. [Google Scholar] [CrossRef]
- Bucci, O.M.; Isernia, T.; Perna, S.; Pinchera, D. Isophoric sparse arrays ensuring global coverage in satellite communications. IEEE Trans. Antennas Propag. 2014, 62, 1607–1618. [Google Scholar] [CrossRef]
- Liu, Y.; You, P.; Zhu, C.; Tan, X.; Liu, Q.H. Synthesis of sparse or thinned linear and planar arrays generating reconfigurable multiple real patterns by iterative linear programming. Prog. Electromagn. Res. 2016, 155, 27–38. [Google Scholar] [CrossRef]
- Bucci, O.; Perna, S.; Pinchera, D. Interleaved Isophoric Sparse Arrays for the Radiation of Steerable and Switchable Beams in Satellite Communications. IEEE Trans. Antennas Propag. 2017, 65, 1163–1173. [Google Scholar] [CrossRef]
- Pinchera, D.; Migliore, M.D. Comparison Guidelines and Benchmark Procedure for Sparse Array Synthesis. Prog. Electromagn. Res. 2016, 52, 129–139. [Google Scholar] [CrossRef]
- Caorsi, S.; Lommi, A.; Massa, A.; Pastorino, M. Peak sidelobe level reduction with a hybrid approach based on GAs and difference sets. IEEE Trans. Antennas Propag. 2004, 52, 1116–1121. [Google Scholar] [CrossRef]
- Donelli, M.; Caorsi, S.; DeNatale, F.; Pastorino, M.; Massa, A. Linear antenna synthesis with a hybrid genetic algorithm. Prog. Electromagn. Res. 2004, 49, 1–22. [Google Scholar] [CrossRef]
- D’Urso, M.; Isernia, T. Solving some array synthesis problems by means of an effective hybrid approach. IEEE Trans. Antennas Propag. 2007, 55, 750–759. [Google Scholar] [CrossRef]
- Bucci, O.M.; Pinchera, D. A generalized hybrid approach for the synthesis of uniform amplitude pencil beam ring-arrays. IEEE Trans. Antennas Propag. 2012, 60, 174–183. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, Z.; Yang, K.; Liu, Q.H. A hybrid optimization for pattern synthesis of large antenna arrays. Prog. Electromagn. Res. 2014, 145, 81–91. [Google Scholar] [CrossRef]
- Bucci, O.M.; Perna, S.; Pinchera, D. Synthesis of isophoric sparse arrays allowing zoomable beams and arbitrary coverage in satellite communications. IEEE Trans. Antennas Propag. 2015, 63, 1445–1457. [Google Scholar] [CrossRef]
- Pinchera, D.; Perna, S.; Migliore, M.D. A Lexicographic Approach for Multi-Objective Optimization in Antenna Array Design. Prog. Electromagn. Res. 2017, 59, 85–102. [Google Scholar] [CrossRef]
- Baraniuk, R.G. Compressive sensing. IEEE Signal Process. Mag. 2007, 24, 118–121. [Google Scholar] [CrossRef]
- Zhang, W.; Li, L.; Li, F. Reducing the number of elements in linear and planar antenna arrays with sparseness constrained optimization. IEEE Trans. Antennas Propag. 2011, 59, 3106–3111. [Google Scholar] [CrossRef]
- Oliveri, G.; Massa, A. Bayesian compressive sampling for pattern synthesis with maximally sparse non-uniform linear arrays. IEEE Trans. Antennas Propag. 2011, 59, 467–481. [Google Scholar] [CrossRef]
- Fuchs, B. Synthesis of sparse arrays with focused or shaped beampattern via sequential convex optimizations. IEEE Trans. Antennas Propag. 2012, 60, 3499–3503. [Google Scholar] [CrossRef]
- Oliveri, G.; Carlin, M.; Massa, A. Complex-weight sparse linear array synthesis by Bayesian compressive sampling. IEEE Trans. Antennas Propag. 2012, 60, 2309–2326. [Google Scholar] [CrossRef]
- Carlin, M.; Oliveri, G.; Massa, A. Hybrid BCS-deterministic approach for sparse concentric ring isophoric arrays. IEEE Trans. Antennas Propag. 2015, 63, 378–383. [Google Scholar] [CrossRef]
- D’Urso, M.; Prisco, G.; Tumolo, R.M. Maximally Sparse, Steerable, and Nonsuperdirective Array Antennas via Convex Optimizations. IEEE Trans. Antennas Propag. 2016, 64, 3840–3849. [Google Scholar] [CrossRef]
- Bencivenni, C.; Ivashina, M.; Maaskant, R.; Wettergren, J. Synthesis of maximally sparse arrays using compressive sensing and full-wave analysis for global earth coverage applications. IEEE Trans. Antennas Propag. 2016, 64, 4872–4877. [Google Scholar] [CrossRef]
- Pinchera, D.; Migliore, M.D.; Lucido, M.; Schettino, F.; Panariello, G. A Compressive-Sensing Inspired Alternate Projection Algorithm for Sparse Array Synthesis. Electronics 2017, 6, 3. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, Q.; Zhang, Y. A hybrid method for the optimal synthesis of 3-D patterns of sparse concentric ring arrays. IEEE Trans. Antennas Propag. 2016, 64, 515–524. [Google Scholar] [CrossRef]
- Pinchera, D.; Migliore, M.D.; Schettino, F.; Lucido, M.; Panariello, G. An Effective Compressed-Sensing Inspired Deterministic Algorithm for Sparse Array Synthesis. IEEE Trans. Antennas Propag. 2018, 66, 149–159. [Google Scholar] [CrossRef]
- Pinchera, D.; Migliore, M.D.; Panariello, G. Synthesis of Large Sparse Arrays Using IDEA (Inflating-Deflating Exploration Algorithm). IEEE Trans. Antennas Propag. 2018, 66, 4658–4668. [Google Scholar] [CrossRef]
- Balanis, C. Antenna Theory: Analysis and Design; Wiley: New York, NY, USA, 2015. [Google Scholar]
- Prisco, G.; D’Urso, M. Maximally sparse arrays via sequential convex optimizations. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 192–195. [Google Scholar] [CrossRef]
- Migliore, M.D. On the sampling of the electromagnetic field radiated by sparse sources. IEEE Trans. Antennas Propag. 2015, 63, 553–564. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming, Version 2.1. 2014. Available online: http://cvxr.com/cvx (accessed on 10 January 2019).
| # | () | ||
|---|---|---|---|
| 1 | 0.9 | 7 | 0.693 |
| 2 | 1.805 | 15 | 1 |
| 3 | 2.665 | 22 | 0.943 |
| 4 | 3.55 | 29 | 0.794 |
| 5 | 4.476 | 37 | 0.72 |
| 6 | 5.403 | 45 | 0.631 |
| 7 | 6.352 | 53 | 0.52 |
| 8 | 7.309 | 61 | 0.464 |
| 9 | 8.222 | 68 | 0.368 |
| 10 | 9.161 | 76 | 0.269 |
| 11 | 10.15 | 85 | 0.277 |
| 12 | 11.85 | 99 | 0.15 |
| # | () | |
|---|---|---|
| 1 | 1.127 | 14 |
| 2 | 1.85 | 22 |
| 3 | 2.7 | 27 |
| 4 | 3.5 | 27 |
| 5 | 4.317 | 29 |
| 6 | 5.45 | 48 |
| # | () | |
|---|---|---|
| 1 | 19.602 | 144 |
| 2 | 30.594 | 192 |
| 3 | 38.25 | 139 |
| 4 | 43.45 | 167 |
| 5 | 48.647 | 103 |
| 6 | 52 | 117 |
| 7 | 60.1 | 119 |
| 8 | 63.45 | 130 |
| 9 | 69.048 | 162 |
| 10 | 75.5 | 238 |
| 11 | 80.84 | 232 |
| 12 | 90.75 | 301 |
| 13 | 103.45 | 272 |
| 14 | 110.95 | 264 |
| 15 | 118.721 | 223 |
| 16 | 126.9 | 215 |
| 17 | 144.459 | 498 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinchera, D.; Migliore, M.D.; Lucido, M.; Schettino, F.; Panariello, G. Efficient Large Sparse Arrays Synthesis by Means of Smooth Re-Weighted L1 Minimization. Electronics 2019, 8, 83. https://doi.org/10.3390/electronics8010083
Pinchera D, Migliore MD, Lucido M, Schettino F, Panariello G. Efficient Large Sparse Arrays Synthesis by Means of Smooth Re-Weighted L1 Minimization. Electronics. 2019; 8(1):83. https://doi.org/10.3390/electronics8010083
Chicago/Turabian StylePinchera, Daniele, Marco Donald Migliore, Mario Lucido, Fulvio Schettino, and Gaetano Panariello. 2019. "Efficient Large Sparse Arrays Synthesis by Means of Smooth Re-Weighted L1 Minimization" Electronics 8, no. 1: 83. https://doi.org/10.3390/electronics8010083
APA StylePinchera, D., Migliore, M. D., Lucido, M., Schettino, F., & Panariello, G. (2019). Efficient Large Sparse Arrays Synthesis by Means of Smooth Re-Weighted L1 Minimization. Electronics, 8(1), 83. https://doi.org/10.3390/electronics8010083