Abstract
This paper shows the topology design of a simple second-order oscillator based on two three-port current conveyors, two resistors, and two grounded capacitors, as well as its modification to a voltage-controlled oscillator (VCO). In comparison with many previous works, the following useful conceptual novelties and improvements were made in this study. Both resistors presented in the topology can be employed to tune of the oscillation frequency by the simultaneous driving of two optocouplers with resistive output stage. The current gain of the current conveyor ensures the control of the oscillation condition. The proposed solution offers advantages (in comparison with many standard so-called single-resistance-controllable types) of improved dependence of the frequency of oscillation (FO) on a driving force (extended tuning of the FO), constant ratio of amplitudes of generated waveforms when the FO is tuned, low complexity (taking into account auxiliary circuitry for optocouplers), and comfortable tuning of the FO by a single control voltage. The oscillator produces waveforms with tunable frequency having a constant 45-degree phase shift between them. The relative sensitivities of the proposed solution achieve typical values for these second-order systems (−0.5). Experimental verification confirmed the expected behavior in the operational band between 1 and 10 MHz tuned by a DC voltage from 1.7 to 5 V. This indicates a significant reduction of the driving force ratio (3:1 in our case) in comparison with standard tuning approaches required for a ratio of 10:1 for FO adjustment. Output amplitudes reached 100 and 150 mV in the observed tunability range with distortion ranging between 0.7 and 3.3%.
1. Introduction
Many recent papers have introduced interesting topologies of oscillators based on various active elements performing so-called single-resistance control of the frequency of oscillation (FO) and single-resistance control of the condition of oscillation (CO) [1]. However, single-resistance-controllable oscillators (SRCOs) [1] have many drawbacks resulting from their natural operation. The overall performance of the oscillator is influenced by adjusting the single integrator. It results in the dependence of the amplitude of one generated signal on the FO and the nonlinear dependence of the FO on the driving resistance value [1]. In some cases, phase shift between generated waves is also influenced because of the fundamental principle of operation. In recent approaches, as little as two resistors can be suitable for FO control (see Table 1); however, there is an issue with the independency of the CO when the inequality of values occurs. This issue is not solved in many works utilizing various active elements [2]. A comparison of known solutions (references [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]) with similar complexity (two active devices from the family of the simplest current conveyors [2] and their modifications) is given in Table 1.

Table 1.
Comparison of solutions of the simplest resistance-controllable oscillators and single-resistance-controllable oscillator (SRCO) types based on two active elements with three-port current conveyors and grounded capacitors.
We may formulate the following conclusions based on the analysis of items in Table 1:
- (a)
- already known solutions lack constant (not varying) amplitudes when the FO is tuned (especially SRCO solutions [3,4,5,6,7,8,9,10,11,12]) or this issue was not analyzed,
- (b)
- many solutions [3,4,5,6,7,8,9,10,11,12,15] where the first resistor serves as the FO control and the second as the CO control are not minimal (an additional resistor with a fixed value is included in the CO and FO relations simultaneously),
- (c)
- the majority of already known solutions provide only inversely proportional square root dependence of the FO on the driving force (value of the single resistor, FO~R−1/2), which limits the tunability to be quite narrow,
- (d)
- solutions combining control by value of passive element (or its replacement) and active parameter (for the CO control, for example) are not studied (only Reference [14] discusses the adjustment of the CO by an active parameter; however, the FO is also tuned by an active parameter (RX)),
- (e)
- solutions implementing two parameters for FO tuning (completely uncoupled from the CO) in order to extend tunability are not proposed (with the exception of Reference [14], where this operation was not verified),
- (f)
- the simple implementation of necessary systems for amplitude gain control circuit (AGC) for amplitude stabilization utilizing electronically (voltage) controlled CO by a specific active parameter is not considered in the majority of solutions summarized in Table 1. Therefore, many topologies have very uncomfortable CO (with a typical form of C1 = C2 or R1 = R2, and their presence is also found in the FO as product of R1R2 and C1C2, see for example solutions in [17,18]). An additional active or passive parameter suitable for the adjustment of CO (not included in the FO relation) should be included, but it cannot be revealed (in these simple solutions having 2 R, 2 C) without the analysis of general (not equal to unity) terminal transfer relations of the active elements (current conveyors).
In particular, the last problem (f) of the simplest published solutions (two active devices, 2 R, 2 C) merits attention because there is significant room for improvement in these previously published solutions, especially concerning specific types of SRCO oscillators.
Some innovative approaches to the FO tunability can be found in topologies where resistor values cannot be used for the FO and the CO adjustment due to the unsuitable form of the characteristic equation. This method supposes the replacement of the negative capacitor (s) with an electronically controllable equivalent for the purposes of FO tunability [16]. However, the complete solution requires additional active devices (one or two) and additional passive elements (two or three). Therefore, such a solution is not minimal and the remaining drawbacks mentioned above still stand (dependence of generated amplitudes on the FO tuning and limited inversely proportional square root dependence of the FO on equivalent capacitance value—not analyzed in Reference [16]).
The controllability of the FO by two values of resistors (completely uncoupled from the CO) is possible in topologies proposed by Soliman [9]. However, three active devices (CCII+ and CCII−) or two dual output CCIIs (not commercially available) are required. The condition of oscillation can also be controlled by two resistors that are not presented in the equation for the FO. Note that the engagement of both resistors (suitability derived from characteristic equations) in References [9,14,17,18] for full employment in FO tuning is not supposed and tested in these works. In addition, the majority of solutions focus on a quadrature type of phase shift; different phase shifts are not expected to be obtained in these structures, but it is possible as shown in our contribution. Work presented by Bajer et al. [19] introduced a new type of Wien oscillator. The FO cannot be simply tuned without impact on the CO if a special matching condition is not fulfilled (unfortunately, the FO adjustment was not tested). Amplitude stabilization (with the exception of many other circuits included in Table 1) is solved by an optocoupler regulating floating resistor.
The goals of our work include the proposal of: (1) improved dependence of the FO on the driving force (extended tuning of the FO) in comparison with standard SRCO types; (2) constant amplitude ratio of generated waveforms when the FO is tuned; (3) using only grounded capacitors in topology; (4) only two active elements, only two capacitors, and two resistors employed in the circuitry; (5) simple implementation of AGC; (6) comfortable tuning of the FO by a single control voltage—a voltage-controlled oscillator (VCO); and (7) constant phase shift (45 degrees) during the tuning of the FO. Point (6) particularly requires the careful selection and testing of known methods for the replacement of the resistor with an electronically controllable equivalent. We selected a rather nonstandard method (optocoupler with resistive output stage) that has not been frequently used for these purposes in the past but brings certain advantages (no significant additional power consumption, not comparable with standard commercially available active devices, good linearity, good frequency features).
The novelty of the presented circuit is revealed by the following features: (a) values of both external resistors presented in a topology of the oscillator topology are suitable for tuning purposes; (b) permitted voltage-controlled linear tuning of frequency that is not possible in the case of many previously published and similar topologies known as single-resistance-controlled methods; (c) no further “dummy” resistors or resistors suitable for the control of the oscillation condition occur in the presented topology; (d) comfortable control of the condition of oscillation by a single active parameter (current gain) independent from frequency; (e) optocouplers with the resistive output stage offer less distorted output waveforms and more precise tuning of the frequency (even when one of the resistors occurs in the floating form) than the field effect transistor (FET), which is not easily applicable in the floating form; and (f) the method of electronic control (voltage driving of optocouplers) improves the ratio of the frequency readjustment (tuning) vs. the driving force ratio.
This paper is organized as follows: Section 1 introduces the topic of resistance-controllable oscillators and provides an overview of significant solutions and their features with respect to our intentions in the above defined goals. Section 2 compares the parameters and available features of the two most similar solutions and our proposal in detail. Section 3 discusses reasons for the selection of the implemented method of resistance control. Section 4 analyses the discussed solution of the oscillator (features of controllability). Section 5 provides a precise explanation of the design and features of the component parameters as well as the experimental results of the circuit behavior when the FO is tuned and their comparison to the expectations and ideal theory. Further methods of the indirect electronic tunability (replacements of resistors) are briefly evaluated and compared in Section 6. Section 7 concludes this work.
2. Detailed Qualitative Comparison of the Most Similar Solutions and the New Proposal
The following section explains the main differences of the newly proposed circuit and the most similar solutions (topologically) already presented. Kumngern et al. [14] proposed a similar topology of the oscillator where the target adjustability of the FO was solved by driving the intrinsic resistance of the input terminal X (RX) by the bias current. This means that external resistors are not present in the solution [14]. Unfortunately, current conveyors with controllable internal resistance RX are not available on the market. The control of the bias current (in order to adjust RX) also has a significant impact on the frequency bandwidth (transfer Y→X), input dynamics, and linearity as well as the output resistance of the current conveyor (unintentional but unavoidable) [20]. Then, the range of RX value can be very limited. This results in a reduced range of FO tunability. Therefore, our contribution, by solving the tunability of the FO with external replacements of both resistors, brings improvement to the common practice (especially owing to the very low ratio of the driving force vs. the ratio of FO readjustability, see Table 2). The CO in Reference [14] also proposes adjusting by the bias current, setting a gain between the X and Z terminals of the current conveyor. Unfortunately, the implementation of the topology as a two-phase oscillator as well as the analysis of the output relation has not been performed and only a single-resistance RX was employed for the FO tuning. This results in an inversely proportional square root dependence of the FO on RX, i.e., limited tunability. Therefore, the full potential of the topology was not revealed and tested in Reference [14]. A very low output amplitude (only slightly more than 20 mV) was also obtained in the results of Reference [14]. Our solution offers a larger output level (amplitudes more than 100 mV). All these aspects (and more details) are clearly visible in Table 2. Lahiri [17] proposed a very similar (topologically) circuit (Figure 1a in Reference [17]), producing output signals in current form. However, the topology also had high-impedance nodes where the output voltages were presented. Several features, compared in Table 2, are similar to those of Reference [14] and our proposal (number of active and passive elements, character of allowed and tested FO dependence). Nevertheless, the range of tested tunability is very narrow (narrow change of resistance value = low ratio of FO readjustability), CO cannot be electronically controlled, and the generated levels are not independent from the tuning process. Other similar solutions (listed in Table 1) do not provide detailed information about the features required for the comparison in Table 2. Therefore, other solutions are not included in this detailed comparison (Table 2).

Table 2.
Comparison of our solution and topologically similar circuits in References [14,17] based on two current conveyors and two grounded capacitors.
3. Implementation of Optocouplers for Control of VCO
Many possible solutions of electronically controllable replacements of resistors are available for designers. Their brief comparison is given in Section 6. We selected the implementation of optocouplers because their applications for purposes of tuning are beneficial in comparison with the standard utilization of unipolar transistors in a triode/ohmic regime (see for example [11,12]). Moreover, the implementation of unipolar transistors in floating connections between nodes is not an easy task (additional active and passive elements are required) [11,12]. The application of optocouplers in oscillators was introduced by Bajer et al. [19] and Biolkova et al. [21]. These devices have been employed to stabilize the amplitude of sine waveforms. Our intentions in this paper are quite different. Optocouplers are expected to be used for tuning purposes (to replace resistors suitable for the FO tuning). The circuit solution in this paper is suited for application of optocouplers more than for unipolar transistors because of the presence of grounded as well as floating resistors intended to tune the FO in the topology.
4. Topology Suitable for Selected Method of FO Control
Figure 1 shows the topology of the oscillator utilizing only two active devices, two grounded capacitors, and two resistors (the most similar solution [14] omits external resistors with full consideration of the issues discussed in a previous text). The negative current conveyor of the second generation (CCII−) [2,22] as well as a positive electronically controllable CCII (ECCII+) [2,22,23,24,25] have identical definitions of two inter-terminal relations—IY = 0, VX = VY—whereas the most important difference rests in the transfer of the current from the X to Z terminals (IZ = −IX for CCII− and IZ = B∙IX for ECCII+). The parameter B represents a generally adjustable current gain. The characteristic equation of this simple oscillator is:
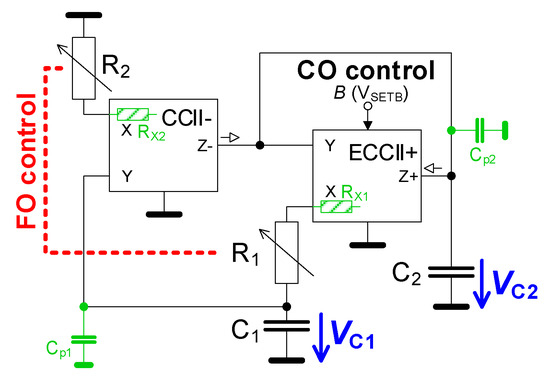
Figure 1.
Simple oscillator employing two current conveyors, two capacitors, and two resistors.
This characteristic equation offers a very beneficial condition for oscillation B ≥ C2/C1. The most important advantage of the solution results from the mutually independent CO and the FO, completely defined by the values of both capacitors and resistors having the typical form of ω0 = (R1R2C1C2)−1/2.
The relation between the generated output voltage levels (amplitudes) can be expressed as:
which can be modified into:
Supposing the equality of both resistors and capacitors (R1 = R2 = R, C1 = C2 = C), the previous relation can be simplified to:
The proposed oscillator theoretically offers a constant level of output amplitudes with a constant ratio of 0.707 between the generated waveforms and a phase shift of 45 degrees, while the FO is tuned by R1 and R2 simultaneously. Note that the controllability of the FO by a single value (R1 or R2) causes amplitude and phase shift changes (when the FO is tuned). Valuable engagement of both resistors for the FO control is not a typical feature in such simple circuitries (Figure 1). This represents a very important finding in comparison with standard SRCOs and other solutions [1,3,4,5,6,7,8,9,10,11,12] tunable by a single parameter value only. Moreover, the dependence of the generated output level on the tuning process (variation of the parameter intended for the FO tuning) presents an unwanted secondary effect of the single-parameter controllability of the FO [26]. It brings additional issues with amplitude limitation and distortion. In our case, this was not an issue.
The most important small-signal parasitic effects of real circuitry (indicated by green color in Figure 1) are easily taken into account in a modified form of Equation (1) where the parasitic (stray) nodal capacitances Cp1, Cp2 (in parallel to C1, C2) and resistances RX1, RX2 of the current input terminals (in X of both current conveyors) are considered:
This equation was gained by the routine analysis of an autonomous circuit including the most important parasitic elements in Figure 1 (indicated by green color). The new CO and FO expressions (difference from ideal CO and FO indicated in superscript *) can be derived from Equation (5a) as follows. The equation for ω0 * (5c) provides the expected values of FO used in Equation (8) and shown in Table 3 when the oscillator is tuned. The relative sensitivity of the FO to the main parameters (R1, R2, C1, C2), in an ideal case derived from (1), reaches a typical value of −0.5. The sensitivities of the FO, including the effect of important parasitic parameters presented in (5c), are: SR1ω0 * = −R1/[2∙(R1 + Rx1)], SR2ω0 * = −R2/[2∙(R2 + Rx2)], SC1ω0 * = −C1/[2∙(C1 + Cp1)], SC2ω0 * = −C2/[2∙(C2 + Cp2)], SRx1ω0 * = −Rx1/[2∙(R1 + Rx1)], SRx2ω0 * = −Rx2/[2∙(R2 + Rx2)], SCp1ω0 * = −Cp1/[2∙(C1 + Cp2)]. In fact, these sensitivities have absolute values lower than those of the ideal case (<0.4 numerically for particular values from our design).

Table 3.
Comparison of ideal, expected, and measured (experimental) FO dependences on driving parameters.
Note that many commercially available types of current conveyors have very high (MΩ) resistances (real parts of voltage inputs and current outputs) at the Y and Z terminals [27] and their inclusion to (5a) does not create a significant effect in comparison with the Cp1,2 and RX1,2 in this case. However, there are solutions where these effects cannot be omitted and full consideration of all parasitic features must be provided for the accurate estimation of behavior at high frequencies and when the value of C1,2 is set in hundreds of pF or lower. The specific values of Cp1,2 for our case are discussed in the next section.
5. Design of Oscillator and Results of Experiments
The initial design of this circuit supposes C1 = C2 = C = 47 pF. Note that this selection (tens of pF) is generally required in combination with resistance values (R1 = R2 = R) in hundreds of Ω for the operation of this and similar oscillators above 1 MHz. However, the values of working capacities are not far from the values of stray capacitances of circuitry including the terminal capacities of active devices (units of pF). The internal value of X terminals of CCIIs (RX1,2) must also be taken into account from Equation (5a) and (5c). The current conveyors used in our topology (Figure 1) are established by current-mode multipliers EL2082 [27] and a high-speed single-input single-output transconductance amplifier known also as a diamond transistor OPA615 [28]. The electronically controllable gain B (proportionally driven by VSETB voltage: B ≅ VSETB for VSETB ≤ 2 V [27]; because B ≅ k∙VSETB, where k = 1 [V−1] is valid for VSETB ≤ 2 V) of EL2082 was set to B = 1 for CCII− operation. The cascade of EL2082 with OPA615 (output inversion of CCII−) creates ECCII+ type where B can be controlled to drive the CO by an external AGC for the amplitude stabilization of the generated waveforms (Figure 2). The main purpose of the AGC consists in the sustentation of unchangeable output levels when the oscillator is tuned. This feature cannot be simply obtained when the CO is set to fulfill an analytically obtained relation because energetic (gain) proportions in the circuit are influenced by tunability. The operation without AGC leads to issues with output waveforms (damage of the shape by nonlinear transfer responses of active devices or even limitation), resulting in high total harmonic distortion (THD) (increased level and amount of higher harmonic components and increased level of spurious combination products) or fading (drop down) of oscillations. Voltage buffers (not included in the simplified schemes), based on the OPA2652 [29] operational amplifier, are added to high-impedance nodes for the impedance separation and subsequent measurement of the circuit on a printed circuit board (PCB) by a low-input-impedance (50 Ω) spectrum analyzer HP4395A and oscilloscope Rigol DS1204B.
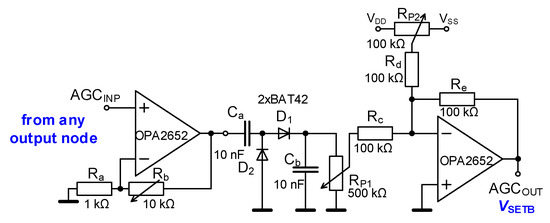
Figure 2.
Simplified topology of AGC circuit for amplitude stabilization.
Expected values of stray/parasitic capacitances are Cp1 = 3 pF and Cp2 = 10 pF (in parallel with C1 and C2) where Cp1 includes the Y terminal capacity 2 pF (CCII−) [27] and input capacity of voltage buffer (1 pF) [29]. The estimated effect of Cp2 supposes a capacity of 5 pF of the Z terminal (CCII−) [27] and the Y, Z terminals (2 + 2 pF) of ECCII+ [28], as well as the input capacity of the voltage buffer (1 pF). Terminal X has an expected input resistance RX1,2 = 95 Ω [27].
FO tuning can be achieved by the variation of R1 and R2 values simultaneously by a dual-channel tandem potentiometer. Our design intention targets tunability in the approximate range of 1–10 MHz. The discussed method (potentiometer) is not very comfortable for standard applications. Many systems produce a DC driving voltage or current (after D/A conversion). Therefore, we seek useful methods of indirect electronic control. The following paragraphs deal with the possible improvement of the circuit to VCO.
The position of the R1 resistor in the topology (Figure 1) of the oscillator requires the implementation of controllable resistance in a floating form. The replacement of R1 by the emulator based on active devices, for example, operational transconductance amplifiers (OTAs) [30,31], brings significant additional power consumption, area, and further complications. Therefore, we selected the optocoupler NSL-32SR3 [32] (photodiode-photoresistor) with very favorable features (frequency bandwidth and linearity) in a grounded or floating form in comparison with many active solutions (unipolar transistors in a linear regime). Our circuit (Figure 1) employs two optocouplers as shown in Figure 3.

Figure 3.
Indirect electronic control of the FO in the oscillator performed by two optocouplers.
The reasons for the presence of Rm1,2 = 910 Ω and Rpot = 2.5 kΩ result from the required transformation (Rm1,2) of the driving voltage VOC to currents with a maximal allowed value (here approximately 1.5 mA per branch, which is approximately more than 10 times lower current consumption than opamp or CCII per single supply branch, for VOC = 5 V—fully positive supply voltage) and the compensation for the slight inequality of the resulting ROC1 and ROC2 (given by fabrication mismatch) for the same driving current. We compensated this effect by the slight inequality of driving currents (IOC1 ≠ IOC2). The threshold voltage Vth ≈ 1.6 V of the optocoupler’s LED was obtained experimentally. The measured frequency features (by vector network analyzer E5071C) of the optocoupler output (ZOC) are introduced in Figure 4 for particular values. Figure 5 shows the dependence of ROC on the driving current and voltage (in accordance with the driving circuitry in Figure 3). The datasheet [32] does not publish these features, but they must be known for the design of applications. Features of the device limit its implementation to systems operating around 10 MHz when the value of ROC is set below 500 Ω. Based on our experiments, the relation between ROC and the driving current IOC can be found empirically as ROC [Ω] ≅ 0.2/IOC [A]. Then ROC can be approximately expressed, in dependence on the driving voltage VOC, as:
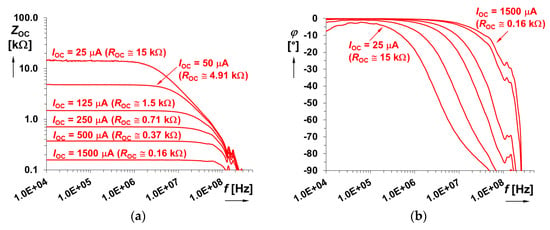
Figure 4.
Frequency responses of the optocoupler output stage impedance: (a) magnitude plots; (b) phase response plots.
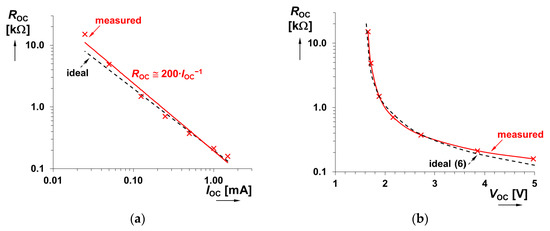
Figure 5.
Dependence of ROC on: (a) driving current IOC; (b) driving voltage VOC.
Neglecting the discussed inequality of IOC1 ≠ IOC2, the ideal equation for the FO (f0i) controlled by the optocoupler can be written as:
Note that this equation supposes the identical behavior of both optocouplers. A more accurate relation (especially for operations with very low values of C1,2; above 1 MHz) for the FO (f0e) can be obtained for real values of parasitic features included in Equation (5c). We expect identical values RX1 = RX2 = RX = 95 Ω (and Cp1 = 3 pF, Cp2 = 10 pF) in the following expression:
The experimental results of the FO of the oscillator in Figure 3, including the AGC from Figure 2, are summarized in Table 3. The implemented optocouplers offer a range of ROC adjustability, from approximately 130 Ω to 2.7 kΩ (IOC varied from 75 μA to 1500 μA) in the ideal case and from 150 Ω to 2.8 kΩ in the measured case, see Table 3 for the detailed results. The expected trace includes the abovementioned parasitic elements. These results are represented graphically in Figure 6a, and the FO dependences for the driving of the oscillator by VOC voltage are shown in Figure 6b. The traces in Figure 6b represent the ideal (Equation (7)), expected (Equation (8), including the nodal parasitics of the circuit), and the additional nodal capacitances (10 pF) expected in the case of the real printed circuit board. Finally, the measured results are very close to the case in which PCB parasitics are considered. The CO for the influenced circuit (as derived in Equation (5b)) is fulfilled theoretically for B ≥ 1.12.

Figure 6.
Dependences of FO on: (a) R1,2 (formed by ROC1,2 only or ROC1,2 influenced by RX1,2 = 95 Ω); (b) VOC (traces obtained from ideal, expected, and measured results).
There are several reasons for the differences between the ideal, expected, and experimental behaviors (results of frequency dependences on VOC in Table 3 and Figure 6b): (a) parasitic elements (capacities) of the active element due to the close values of the working capacitors to the stray capacitances; (b) transit features of active devices (their phase responses are especially important for oscillators—these issues occur at frequencies lower than −3 dB cut-off or transit frequency); (c) Miller effect of the increasing input capacity of active devices (amplifiers) when the gain is varied—the “parasitic capacity” increases with increasing gain of blocks of the circuit; this behavior is not easily predictable and implementable to the design equations; (d) high uncertainties in bands above 1 MHz given by real parasitic features of the PCB (parasitic conductivity, inductance, and capacity) that can be only approximately estimated in the case of capacity—the accuracy and high-frequency (RF) behavior of circuits operating above 1 MHz highly depends on the design and quality of the PCB; and (e) inequality of the driving current of optocouplers (IOC1 ≠ IOC2).
The ideal calculation (ideal values of C1,2 and ROC1,2) supposes a range of the FO tunability of 1.04 MHz→25.27 MHz. Calculations including all important parasitic effects estimate a range of 0.89 MHz→13.32 MHz (R1,2 varied from 247 to 2.88 kΩ). Consideration of the additional PCB effect (+10 pF) leads to a range of 0.75→11.21 MHz. The experimental values follow our expectations because the measured FO yields a range of 1.05→10.30 MHz.
Output amplitudes (VC1 and VC2) reach levels of about 200 mVp-p and 300 mVp-p (based on the setting of the AGC) and they remain almost constant during the tuning process (Figure 7a). Their ratio confirms the validity of Equation (4). The phase shift of both signals is around 45 degrees (Figure 7b). This value was obtained from the oscilloscope in the time-domain measurement by the automatic function evaluating the distance at which signals at both channels cross 0. An example of transient responses for VOC = 4.95 V (f0meas = 10.30 MHz) is shown in Figure 8. Their spectral analysis provided the results shown in Figure 9. The THD varies between approximately 0.7 and 3.3%. Quite high values are given by the low suppression of higher harmonic components of the active device itself (especially by the high-speed device OPA615 [28], only about 35 dBc in MHz bands). Similarly, the implementation of many nonlinear high-speed devices results in a certain presence of somewhat influential intermodulation products (visible in transient responses as superposed fluctuations at peaks of amplitudes as well as some combination products observed in the spectral analysis around the fundamental tone). The overall power consumption of the testbed (including buffers and opamps in AGC) reaches 570 mW (five IC devices, approximately 60 mA of power current per supply branch, ±5 V).

Figure 7.
Effects of the FO tuning on the generated signals: (a) dependence of output levels on the FO, (b) dependence of phase shift on the FO.

Figure 8.
Example of the produced output waveforms in time domain at the end of designed range of the FO adjustment.

Figure 9.
Spectrum of generated waveforms at the end of designed range of the FO adjustment: (a) VC1; (b) VC2.
We replaced values of capacitors in the oscillator in order to demonstrate the maximal available FO in the experimentally tested prototype for a still practically feasible value (C1,2 = 4.7 pF was selected). Then, the value f0 = 25 MHz was set experimentally by VOC = 4.55 V. The results of the spectral analysis are shown in Figure 10 for both output waveforms. Images of the measured prototype are given in Figure 11.

Figure 10.
Spectrum of generated waveforms for C1,2 = 4.7 pF and VOC = 4.55 V: (a) VC1; (b) VC2.

Figure 11.
Measured prototype developed for experimental purposes.
The phase noise evaluation is shown in Figure 12 for VC2 output (these values are actually almost identical for both outputs). The phase noise value was obtained for offset frequency ∆foffset = 10 kHz and 100 kHz (1/1000 and 1/100 of fundamental tone; the oscillator frequency was set to f0 ≅ 10 MHz by VOC = 4.92 V for this test). The phase noise values of 45 and 47 dBc/Hz were obtained for these values of offset frequencies. Note that these are only approximate values due to the limited accuracy of measurement (the noise background is influenced by the resolution-bandwidth (RBW) of the spectrum analyzer that was set to 10 Hz in all cases). The value in the range of 40→70 dBc/Hz is typical for these types of circuits due to the usage of inertial AGC (it solves limitation, shape distortion, THD, and the variation of output levels when f0 is tuned, but its drawback is the higher fluctuation/jitter of output amplitudes). Radio-frequency (GHz)-targeted solutions reach values in the high tens of dBc/Hz (for example >100 dBc/Hz) in dependence on ∆foffset because there is no AGC system in narrow-band tunable oscillators and higher spurious spectral products are filtered. However, this approach cannot be used in base-band or inter-frequency-band oscillators tunable in the f0 range of 10:1 or more. Note that the phase noise and f0 stability (except AGC) also depend on the precision of the construction of the circuit (quality of the PCB, etc.). It may significantly influence overall performances, especially at high frequencies above 1 MHz. The fundamental tone slightly fluctuates in the results shown in Figure 12. The frequency change achieves ±33 kHz (±0.33% at f0 ≅ 10 MHz), which results in a frequency stability of S(f0) = |∆f0/f0| = 6.6 × 10−3 (being within the typical range for active RC oscillators).
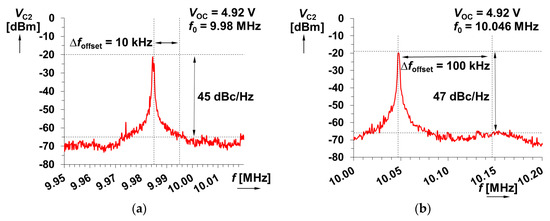
Figure 12.
Spectral analysis for phase noise measurement at VC2: (a) offset frequency 10 kHz; (b) offset frequency 100 kHz.
6. Discussion of Other Methods of Indirect Electronic Control of FO
The position of the resistor R1 is not very beneficial due to the floating (between two nodes) connection to the circuit. The method discussed in the previous paragraphs implemented optocouplers; however, there are also other possibilities that should be briefly discussed (their main advantages and disadvantages). Table 4 reveals their general comparison.

Table 4.
Comparison of the methods for indirect FO tunability (standard potentiometer shown for reference purposes).
The replacement of R1,2 by junction field effect transistors (J-FET) in a triode/ohmic/linear regime [11,12,33,34,35] can be easily applied. However, there are some restrictions. It is not easy to maintain a transistor in a linear regime (VDS < VGS − Vth) even for increasing processed signal levels in nodes where transistors are connected. Transistors behave highly nonlinearly for voltage levels higher than several tens of mV, and nonlinearity increases for increased resistance (rDSon) driven by VGS voltage. The range of the rDSon resistance adjustability can be large (N type J-FET BF245A [36]: 200 Ω→2 kΩ for 0→−2 V); however, the nonlinearity of VDS vs. ID plots plays a significant role, especially for high values of resistances (high VGS). Unfortunately, there is no other way in the IC design practice. One example of J-FET implementation was experimentally tested in our oscillator (Figure 1). Figure 13 illustrates the output level for the VC1 wave that is significantly distorted (THD > 13%) by nonlinearity with increased values of rDSon. The amplitude is not limited but the shape and symmetry of the positive half-wave vs. negative half-wave is significantly damaged. The linearization of the transistor can be provided by two additional resistors [33]; however, the linearization of the floating form of an electronically controllable equivalent is not an easy task (many additional active and passive devices are required) [34,35].

Figure 13.
The example of distorted waveform by nonlinear effects of junction field effect transistors (J-FET) replacing resistors.
Digital potentiometers [37,38,39,40] are widespread parts serving in control and adjustable systems, especially for low-frequency circuits. They have the advantage of simple digital controllability of value; however, many drawbacks limit their practical usability in medium- and high-frequency systems. These issues consist in real parasitic resistance of the middle terminal (wiper), large parasitic capacitances (tens of pF), and therefore very bad frequency features (only tens–hundreds of kHz in many cases). Discontinuous adjustment of the value (based on the number of bits) can be also considered as a drawback for specific applications (the control of amplitude stabilization, for example). Also, the reaction on changes (depending on the construction of specific types and their internal control logic) can be very slow. Therefore, the majority of these devices are unsuitable for the FO tuning in the range presented in this paper.
Similar features are offered by D/A converters (they can establish controllable resistors [41]). However, modern and very fast (Gsps) solutions can be prepared for high-frequency operation. Unfortunately, the power consumption is enormous (power supply currents in hundreds of mA) and the price reaches tens of dollars. This renders this method unsuitable for compact designs and solutions.
Active solutions (a floating resistor can be implemented by two OTAs [30,31]) may have a very good frequency response and fast reaction on changes (adjusting of the driving voltage). However, active solutions (especially OTA-based solutions without linearization [30]) have substantial problems with linearity and dynamical restrictions. The range of the equivalent resistance value can also be very limited (especially in MOS solutions where square laws [42,43] for currents are valid).
The following discussion evaluates the features of the proposed analog solution and direct digital synthesis (DDS). Advantages of DDS are clear: wide bandwidth (hundreds of MHz), simple configurability, stable operation, excellent phase noise (but this parameter is significant for bands starting at hundreds of MHz, not for the bands observed in this paper), immunity to aging of parameters, minimized temperature effects, high accuracy, etc. On the other hand, many DDS chips generate only single-phase waveforms (70–80% of production). The generation of more than one waveform requires the interconnection of several chips or multichannel DDS (conferring a significantly higher power consumption and cost). DDS chips require an external clock generator (additional complication and power consumption) in some cases. The frequency is not continuously tunable. The power current reaches hundreds of mA. A DDS must be equipped with some microcontroller and/or supporting peripheral devices (USB connection, interface, clock generator = additional power consumption), or DDS development boards are used in many designs (several times higher cost). The cost of the complete designed analog oscillator in this paper (elements used in implementation) reaches approximately 30 Euros, the cost of the multichannel DDS (AD9959 for example) chip (with only the chip ready for implementation) reaches 40 Euros, and the cost of the complete operating development board with DDS is several times higher (approximately 350 Euros). Therefore, advantages coming from the utilization of DDS can be overcome by a low-cost solution with acceptable features for the intended application.
The main advantages of the proposed analog solution in comparison to DDS are: (a) simplicity of the resulting circuit and tunability method (an integrated DDS has a much more complex block topology and a higher complexity of internal blocks—it cannot be implemented in discrete form in practice); (b) low cost (for the intended bandwidth—up to low tens of MHz); (c) immediate response of frequency on changes (no delay); (d) no requirement for additional peripheral devices (clock generator, interfaces, etc.); (e) no requirement of programming (the approximate final costs noted above do not take the controlling software for multiphase generation and the tuning of the DDS into account). Of course, there are also disadvantages: (a) influence of temperature and aging effects on frequency stability; (b) low value of phase noise and worse stability (however, this issue is usually not evaluated/solved in the case of similar solutions in studied bands of units—low tens of MHz); (c) the accuracy of frequency setting is influenced by parasitic elements. The proposed device’s power consumption is comparable to that of the DDS (due to low supply voltage of 1.8 V of AD9959, for example), but the supply current is several times lower in comparison to DDS.
Therefore, similar analog solutions are worth investigation at bands where high-speed opamps and other active elements are still competitive (up to several tens of MHz). It really depends on the application and quality of the application to determine whether a digital or analog solution should be selected and, of course, it depends on the budget available for construction.
7. Conclusions
We designed and tested the topology of a sine wave two-phase oscillator with output waveforms having a π/4 phase shift. The phase shift of 45 degrees is suitable as a local source for multiphase generation [1]. It can be further implemented in the modulation process (PSK—phase shift keying) or multistate modulation techniques requiring wideband tunability [44]. The designed circuit brings several benefits: (a) the low number of components (two grounded C, 2R); (b) simple topology using only two three-port active elements; (c) wide tunability (indirectly proportional to the resistance value) of the frequency of oscillations; (d) constant amplitudes when the FO is tuned; (e) simple implementation of the independently controllable (voltage-controlled) condition for oscillation; (f) minimal additional power consumption in comparison with the implementation of full active devices, digital potentiometers, digital-to-analog converters (DACs), etc. for purposes of FO tunability. The experimental tests employing optocouplers at positions of both resistors (floating and grounded) confirmed the intentions and operation of the design in the range from approximately 1 MHz to 10 MHz (ratio 10:1) by driving the control voltage between 1.7 and 5 V (ratio 3:1). So, a large readjustment is not allowed when only a single resistor value is intended to be used for frequency tuning, similar to the method of so-called single-resistance-controlled oscillators [2,3,4,5,6,7,8,9,10,11,12,13]. The output amplitudes sustained 100 and 150 mV (THD between 0.7 and 3.3%) when the frequency of the oscillator was tuned. Sensitivities of proposed solution achieved the standard and low value of −0.5. A possibility of the implementation of the both resistors for tuning purposes and their replacement by suitable electronically controllable equivalents (optocouplers with resistive outputs stage) can be seen as inspiration for many interesting topologies of oscillators (a great overview is available in References [45,46]), where the presented method of tuning can be beneficially implemented.
Author Contributions
Conceptualization, R.S. and J.J.; Methodology, R.S.; Validation, R.S., J.J., and L.L.; Formal Analysis, J.D.; Investigation, R.S. and J.J.; Data Curation, L.L. and J.D.; Writing—Original Draft Preparation, R.S., J.J., L.L., and J.D.; Writing—Review and Editing, R.S., J.J., L.L., and J.D.
Funding
This research was funded by the Czech Ministry of Education through the National Sustainability Program under grant LO1401.
Acknowledgments
Research described in this paper was financed by Czech Ministry of Education in frame of National Sustainability Program under grant LO1401. For research, infrastructure of the SIX Center was used.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Senani, R.; Bhaskar, D.R.; Singh, V.K.; Sharma, R.K. Sinusoidal Oscillators and Waveform Generators Using Modern Electronic Circuit Building Blocks; Springer International Publishing AG: Cham, Switzerland, 2016; pp. 1–622. ISBN 978-3-319-23712-1. [Google Scholar] [CrossRef]
- Senani, R.; Bhaskar, D.R.; Singh, A.K. Current Conveyors: Variants, Applications and Hardware Implementations, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2015; ISBN 978-3-319-08684-2. [Google Scholar] [CrossRef]
- Liu, S.-I. Single-resistance-controlled/voltage-controlled oscillator using current conveyors and grounded capacitors. Electron. Lett. 1995, 31, 337–338. [Google Scholar] [CrossRef]
- Abuelmaatti, M.T.; Ghumaiz, A.-A. Novel CCI-based Single-Element-Controlled Oscillators Employing Grounded Resistors and Capacitors. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1996, 43, 153–155. [Google Scholar] [CrossRef]
- Senani, R.; Singh, V.K. Novel single-resistance-controlled-oscillator configuration using current-feedback-amplifiers. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1996, 43, 698–700. [Google Scholar] [CrossRef]
- Martinez, P.A.; Sabadell, J.; Aldea, C. Grounded resistor controlled sinusoidal oscillator using CFOAs. Electron. Lett. 1997, 33, 346–348. [Google Scholar] [CrossRef]
- Gupta, S.S.; Senani, R. State variable synthesis of single resistance controlled grounded capacitor oscillators using only two CFOAs. IEE Proc. Circuits Devices Syst. 1998, 145, 135–138. [Google Scholar] [CrossRef]
- Gupta, S.S.; Senani, R. State variable synthesis of single resistance controlled grounded capacitor oscillators using only two CFOAs: Additional new realisations. IEE Proc. Circuits Devices Syst. 1998, 145, 415–418. [Google Scholar] [CrossRef]
- Soliman, A.M. Synthesis of grounded capacitor and grounded resistor oscillators. J. Frankl. Inst. 1999, 336, 735–746. [Google Scholar] [CrossRef]
- Khan, A.A.; Bimal, S.; Dey, K.K.; Roy, S.S. Novel RC Sinusoidal Oscillator Using Second-Generation Current Conveyor. IEEE Trans. Inst. Meas. 2005, 54, 2402–2406. [Google Scholar] [CrossRef]
- Bhaskar, D.R.; Senani, R. New CFOA-Based Single-Element-Controlled Sinusoidal Oscillators. IEEE Trans. Inst. Meas. 2006, 55, 2014–2021. [Google Scholar] [CrossRef]
- Gupta, S.S.; Bhaskar, D.R.; Senani, R. New voltage controlled oscillators using CFOAs. AEU—Int. J. Electron. Commun. 2009, 63, 209–217. [Google Scholar] [CrossRef]
- Abuelmaatti, M.T. Identification of a class of two CFOA-based sinusoidal RC oscillators. Analog Integr. Circuits Signal Proc. 2010, 65, 419–428. [Google Scholar] [CrossRef]
- Kumngern, M.; Junnapiya, S. A sinusoidal oscillator using translinear current conveyors. In Proceedings of the IEEE International Asia Pacific Conference on Circuits and Systems (APCCAS), Kuala Lumpur, Malaysia, 6–9 December 2010; pp. 740–743. [Google Scholar] [CrossRef]
- Lahiri, A.; Jaikla, W.; Siripruchyanun, M. Explicit-current-output second-order sinusoidal oscillator using two CFOAs and grounded capacitors. AEU—Int. J. Electron. Commun. 2011, 65, 669–672. [Google Scholar] [CrossRef]
- Lahiri, A.; Gupta, M. Realizations of Grounded Negative Capacitance Using CFOAs. Circuits Syst. Signal Proc. 2011, 30, 143–155. [Google Scholar] [CrossRef]
- Lahiri, A. Current-mode variable frequency quadrature sinusoidal oscillators using two CCs and four passive components including grounded capacitors. Analog Integr. Circuits Signal Proc. 2012, 71, 303–311. [Google Scholar] [CrossRef]
- Chen, H.-P.; Hsien, M.-Y.; Lin, C.-C.; Huang, W.-Y. CFOA-based quadrature oscillator employing grounded capacitors. In Proceedings of the IEEE International Conference on Information Science, Electronics, and Electrical Engineering (ISEEE), Sapporo, Japan, 26–28 April 2014; pp. 470–473. [Google Scholar] [CrossRef]
- Bajer, J.; Lahiri, A.; Biolek, D. Current-mode CCII+ Based Oscillator Circuits using a Conventional and a Modified Wien-Bridge with All Capacitors Grounded. Radioengineering 2011, 20, 245–250. [Google Scholar]
- Sotner, R.; Jerabek, J.; Prokop, R.; Kledrowetz, V.; Polak, J.; Fujcik, L.; Dostal, T. Practically Implemented Electronically Controlled CMOS Voltage Differencing Current Conveyor. In Proceedings of the IEEE 59th International Midwest Symposium on Circuits and Systems (MWSCAS), Abu Dhabi, UAE, 16–19 October 2016; pp. 667–670. [Google Scholar] [CrossRef]
- Biolkova, V.; Bajer, J.; Biolek, D. Four-Phase Oscillators Employing Two Active Elements. Radioengineering 2011, 20, 334–339. [Google Scholar]
- Biolek, D.; Senani, R.; Biolkova, V.; Kolka, Z. Active elements for analog signal processing: Classification, Review and New Proposals. Radioengineering 2008, 17, 15–32. [Google Scholar]
- Surakampontorn, W.; Thitimajshima, W. Integrable electronically tunable current conveyors. IEE Proc. G 1988, 135, 71–77. [Google Scholar] [CrossRef]
- Fabre, A.; Mimeche, N. Class A/AB second-generation current conveyor with controlled current gain. Electron. Lett. 1994, 30, 1267–1268. [Google Scholar] [CrossRef]
- Minaei, S.; Sayin, O.K.; Kuntman, H. A new CMOS electronically tunable current conveyor and its application to current-mode filters. IEEE Trans. Circuits Syst. I 2006, 53, 1448–1457. [Google Scholar] [CrossRef]
- Sotner, R.; Jerabek, J.; Herencsar, N.; Hrubos, Z.; Dostal, T.; Vrba, K. Study of Adjustable Gains for Control of Oscillation Frequency and Oscillation Condition in 3R-2C Oscillator. Radioengineering 2012, 21, 392–402. [Google Scholar]
- Intersil (Elantec). EL2082 CN Current-Mode Multiplier (Datasheet); 1996; 14p. Available online: http://www.intersil.com/data/fn/fn7152.pdf (accessed on 18 August 2018).
- Texas Instruments. OPA615 Wide Bandwidth, DC Restoration Circuit (Datasheet); 2009; 33p. Available online: http://www.ti.com/lit/ds/symlink/opa615.pdf (accessed on 18 August 2018).
- Texas Instruments. OPA2652 SpeedPlus Dual, 700 MHz, Voltage-Feedback Operational Amplifier (Datasheet); 2006; 23p. Available online: https://www.ti.com/lit/ds/symlink/opa2652.pdf (accessed on 18 August 2018).
- Sanchez-Sinencio, E.; Silva-Martinez, J. CMOS transconductance amplifiers, architectures and active filters: A tutorial. IEE Proc. Circuits Devices Syst. 2000, 147, 3–12. [Google Scholar] [CrossRef]
- Geiger, R.L.; Sanchez-Sinencio, E. Active filter design using operational transconductance amplifiers: A tutorial. IEEE Circuits Devices Mag. 1985, 1, 20–32. [Google Scholar] [CrossRef]
- Luna Optoelectronics. NSL-32SR3 Optocoupler (Datasheet); 2016; 2p. Available online: http://lunainc.com/wp-content/uploads/2016/06/NSL-32SR3.pdf (accessed on 18 August 2018).
- Nay, K.; Budak, A. A Voltage-Controlled Resistance with Wide Dynamic Range and Low Distortion. IEEE Trans. Circuits Syst. 1983, CAS-30, 770–772. [Google Scholar] [CrossRef]
- Senani, R. Realisation of linear voltage-controlled resistance in floating form. Electron. Lett. 1994, 30, 1909–1910. [Google Scholar] [CrossRef]
- Senani, R.; Bhaskar, D.R.; Gupta, S.S.; Singh, V.K. A configuration for realising floating, linear, voltage-controlled resistance, inductance and FDNC elements. Int. J. Circuit Theory Appl. 2009, 37, 709–719. [Google Scholar] [CrossRef]
- ON Semiconductor. BF245A/B JFET VHF/UHF Amplifiers N-Channel–Depletion (Datasheet); 2001; 8p. Available online: https://www.onsemi.com/pub/Collateral/BF245A-D.PDF (accessed on 18 August 2018).
- Analog Devices. Choosing the Correct digiPOT for Your Application (Application Note); 2014; 6p. Available online: http://www.analog.com/media/en/news-marketing-collateral/product-selection-guide/Choosing_the_Correct_Digipot.pdf (accessed on 18 August 2018).
- Sevcik, B. Modeling and Signal Integrity Testing of Digital Potentiometers. In Proceedings of the IEEE 17th International Conference Mixed Design of Integrated Circuits and Systems (MIXDES), Wroclaw, Poland, 24–26 June 2010; pp. 570–575. [Google Scholar]
- Lunca, E.; Damian, C.; Petrisor, D.; Postolache, O. Programmable Active Filters Based on Digital Potentiometers. In Proceedings of the IEEE International Conference and Exposition on Electrical and Power Engineering (EPE), Iasi, Romania, 25–27 October 2012; pp. 787–791. [Google Scholar] [CrossRef]
- Pandiev, I.M. Behavioral Modeling of CMOS Digital Potentiometers Using VHDL-AMS. In Proceedings of the IEEE International Power Electronics and Motion Control Conference (PEMC), Varna, Bulgaria, 25–28 September 2016; pp. 940–945. [Google Scholar] [CrossRef]
- Maxim Integrated. DACs vs. Digital Potentiometers: Which Is Right for My Application? 2007; 1p. Available online: https://www.maximintegrated.com/en/app-notes/index.mvp/id/4025 (accessed on 18 August 2018).
- Razavi, B. Design of Analog CMOS Integrated Circuits; McGraw-Hill: New York, NY, USA, 2001; ISBN 978-0072380323. [Google Scholar]
- Gray, P.R.; Hurst, P.J.; Lewis, S.H.; Meyer, R.G. Analysis and Design of Analog Integrated Circuits, 5th ed.; Wiley: Hoboken, NJ, USA, 2009; ISBN 978-0470245996. [Google Scholar]
- Rogers, J.W.M.; Plett, C.; Marsland, I. Radio Frequency System Architecture and Design; Artech House: London, UK, 2013; ISBN 978-1608075379. [Google Scholar]
- Soliman, A.M. Two integrator loop quadrature oscillators: A review. J. Adv. Res. 2013, 4, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Abuelmaatti, M.T. Recent Developments in Current-Mode Sinusoidal Oscillators: Circuits and Active Elements. Arab. J. Sci. Eng. 2017, 42, 2583–2614. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).