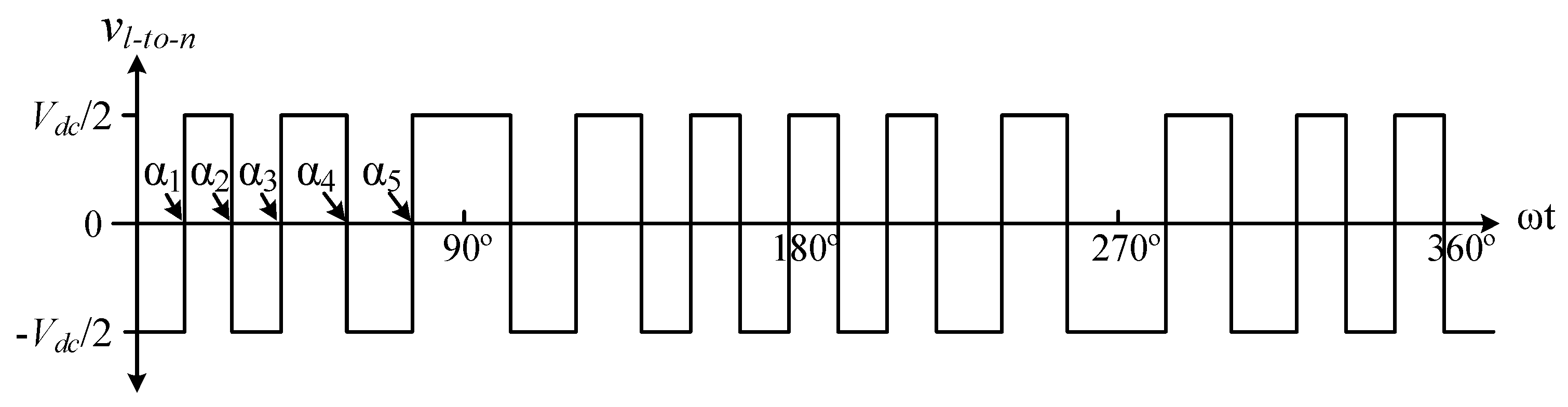1. Introduction
Various modulation schemes have been employed in inverter circuits, such as space vector modulation (SVM), pulse width modulation (PWM), and the selective harmonic elimination method (SHEM). The main feature of the SVM scheme is the fast dynamic response obtained, whereas the SHEM has superior harmonic performance for a given switching frequency. The performance of the best PWM modulation techniques is somewhere between the SVM and SHEM [
1]. On-line application of SHEM to voltage source converters (VSCs) for the elimination of low-order output voltage harmonics, however, has not been reported yet in the literature due to the computational overhead of the digital implementation on processors.
In grid-connected VSCs of either two-level or multilevel types, the SHEM angles can be determined by solving a set of nonlinear algebraic equations. The resulting mathematical model contains sinusoidal terms and the number of equations in the model is equal to the number of switching angles. Two main groups of techniques have been presented in the literature to solve these nonlinear equations. Iterative methods, such as the Newton–Raphson method [
2,
3] and the homotopy algorithm [
4,
5,
6,
7], are given in the first group. Some other iterative numerical techniques have been proposed in [
8,
9,
10,
11], and the Walsh-function-based analytical technique has been adopted in [
12]. In [
13,
14], to find the solutions for all modulation indices, theories of resultants and symmetric polynomials have been employed, which are then used to solve the polynomial equations obtained from transcendental equations. It has been shown in [
13] that such SHEM equations do not have a solution set for some unfeasible modulation index values of the inverter.
In the second group, SHEM is considered as an optimization problem, which is investigated through evolutionary search algorithms. Evolutionary search algorithms have been used to solve various industrial problems in recent years. Easier solutions can be found to these problems by this way as compared to the analytical methods, and in some cases, they constitute the unique way to find a feasible solution [
15]. The global optimum solution can be found by these algorithms for complete elimination of certain harmonics or optimum switching angles can be offered in cases where a feasible solution cannot be found. Some major evolutionary search algorithms which have been applied can be cited as the genetic algorithm (GA) [
16,
17,
18], particle swarm optimization (PSO) [
2,
19,
20], ant colony optimization [
21], the bee algorithm [
22], and the bacterial foraging algorithm [
23].
Until now, SHEM has been applied off-line in industry applications of grid-connected converters by using lookup tables (LUTs). Among these, distribution-type, two-level static synchronous compensator (STATCOM) systems based on a current source converter (CSC) with a variable direct current (DC) link current are reported in [
24,
25,
26], two-level voltage source converter (VSC)-based distribution-type STATCOM systems with variable DC link voltages in [
27], and a transmission-type cascaded multilevel converter-based STATCOM system with constant DC link voltage in [
28,
29]. On the other hand, VSCs with variable DC link voltages are widely used in photovoltaic (PV) and traction applications, in which the modulation index value for the VSC changes in a wide range as the DC link voltage varies. In such applications, the off-line SHEM using LUTs for determination of switching angle sets is disadvantageous primarily due to the stepwise control of the modulation index value resulting in minimization of selected harmonics instead of their elimination, and secondarily due to the infeasible region of the solution space [
30] and the need for a large LUT storage area [
31].
To solve these problems, researchers have searched for an effective way to apply SHEM on-line in order to allow for continuous control of SHEM angles. The generalization ability of an artificial neural network (ANN) has been applied in [
30] to cope with this problem. The switching angles have been calculated beforehand for different DC source values using GA, then the switching angles have been determined for different DC link voltage magnitudes at each phase of the multilevel inverter in real-time by adopting the ANN to train the controller. By this way, the ANN can be used instead of a LUT, thus introducing its inherent capability to generalize the solution space into the problem with proper training. In [
31], another approach was investigated for on-line applications of SHEM, where an analytical procedure was employed for computation of all pairs of valid switching angles in five-level, H-bridge cascaded inverters. Here, a fully analytical calculation is allowed for the switching angles using Chebyshev polynomials and Waring equations. This procedure can be implemented in real-time using either a digital signal controller, a programmable logic device, or a field-programmable gate array (FPGA), as claimed in [
31], due to its limited complexity. On the other hand, digital control techniques applied to voltage source inverters in renewable energy applications were reviewed in [
32]. On-line optimal switching frequency selection for grid-connected voltage source inverters was presented in [
33].
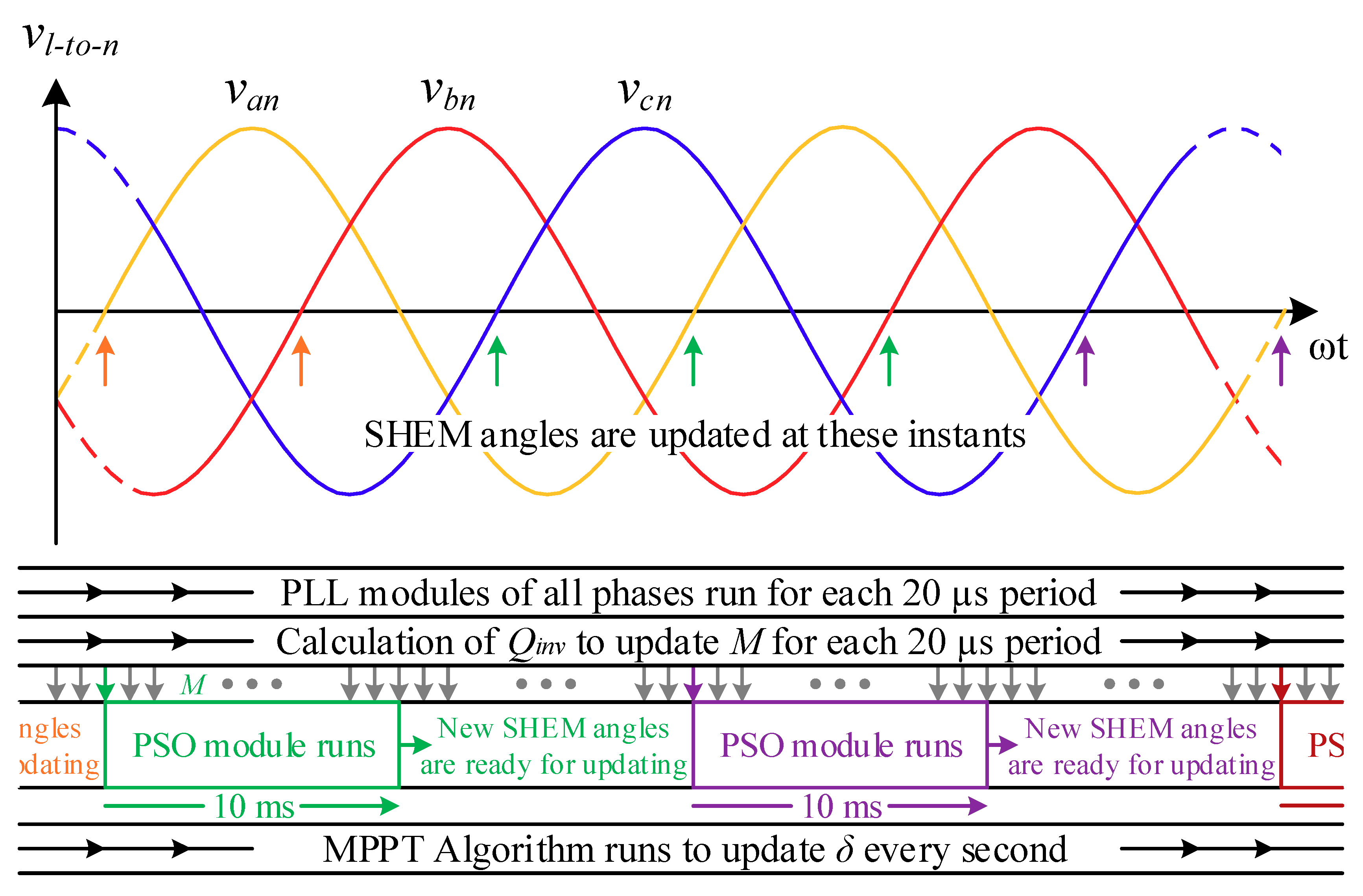
In this paper, calculation of SHEM angles in real-time is described by using a PSO algorithm, specifically developed for this purpose, and a digital computing hardware. An on-line application of SHEM is important especially for grid-connected inverters with variable DC link voltages in order to eliminate all odd-order characteristic power system harmonics up to the 50th. The initialization procedure for the PSO algorithm is generalized to ensure the convergence of the solution to a global optimum by assuming that the modulation index, and hence the inverter’s output voltage, is initially zero. A timing diagram for the on-line application of SHEM is given in the paper, in which the number of SHEM angles, up to 17, is calculated in each half-cycle of the supply voltage waveform, and the firing instants of all power semiconductors of the grid-connected inverter are updated in the next full-cycle. Keeping the switching pattern constant in each full-cycle avoids the generation of DC component and even-order voltage harmonics. The proposed method is verified by a hardware co-simulation work, and the theoretical results are justified in the field on a small-size photovoltaic (PV) supply by calculating on-line seven SHEM angles on a moderately powerful FPGA board. In the prototype PV supply, active power control is implemented by phase shift angle control, reactive power control by variation of the modulation index, and elimination of selected sidekick voltage harmonics (5th, 7th, 11th, 13th, 17th, and 19th) in the inverter’s output phase voltage by SHEM.
2. Problem Description
2.1. Possible Application Areas of SHEM
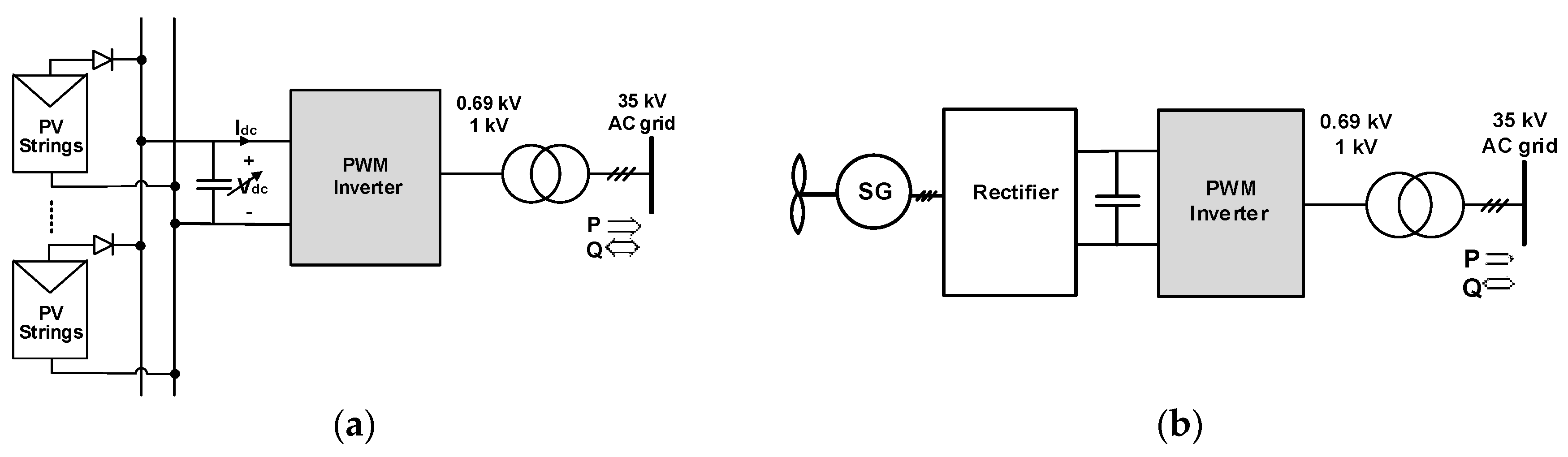
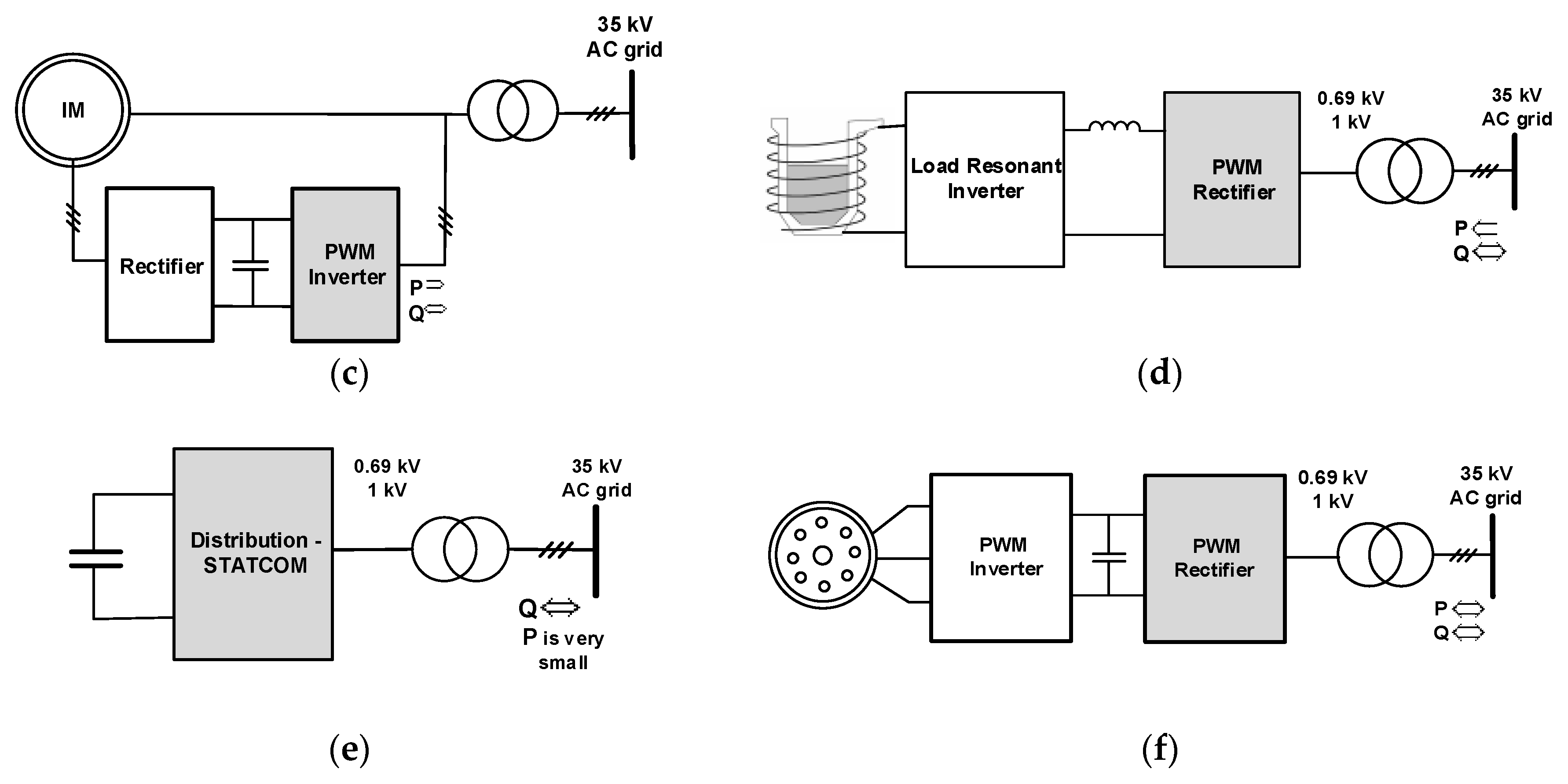
Possible application areas of SHEM are summarized in
Figure 1. The common properties of these applications are: (i) few MVA apparent power rating, (ii) Connection to an available three-phase, medium-voltage grid bus though a dedicated coupling transformer, and (iii) 690 V or 1 kV voltage rating for the grid-side VSC. The application of SHEM is suitable for the gray-shaded converters in
Figure 1. In these three-phase, two-level VSCs, either high voltage insulated gate bipolar transistor (HV-IGBT) type or integrated gate commutated thyristor (IGCT) type power semiconductors are used in practice. IGBTs and IGCTs in these converters can be switched, respectively, in the range of 1.5 kHz and 500 Hz in practical applications because of their relatively high switching losses. SHEM best matches the needs of such applications, i.e., minimum harmonic current distortion on the grid side and high conversion efficiency. In the near future, with the advents in SiC power MOSFET technology, these new power semiconductors can be switched at much higher frequencies in such applications. In the systems shown in
Figure 1a–c, the DC link voltage is variable depending upon the operating condition. In the system in
Figure 1d, the DC link voltage may be kept constant or varies in a narrow range. However, in the systems in
Figure 1e,f, the DC link voltage may be varied only for performance concerns.
In most of these applications, the grid-side inverter or rectifier is connected to the grid by using a dedicated coupling transformer as shown in
Figure 1. If the leakage reactance of the coupling transformer is not sufficiently large for minimization of total demand distortion (TDD), a small series inductor bank may be connected on the converter side of the system. On the other hand, for small-size systems, the grid connection is achieved by using an LCL filter or its derivatives, since an inductance-only filter is not sufficient to suppress high-order harmonic components which are not eliminated by SHEM.
2.2. Switching Techniques for SHEM
Various switching techniques that can be used in the application of SHEM are clearly described in [
34]. Line-to-line converter voltage harmonics can be directly eliminated by the three-phase line-to-line technique (TLL), and line-to-neutral converter output voltage harmonics by the three-phase line-to-neutral techniques (TLN1 and TLN2). In the TLL technique, a 2 times higher switching frequency and a higher DC link voltage are required in comparison with those of the TLN2 technique in order to eliminate the same number harmonics and to give the same grid voltage. Similar conclusions can be drawn also for the TLN1 technique. In view of PV applications with direct power conversion, the TLN1 and TLN2 techniques are more suitable to maintain the maximum power-point voltage,
Vmpp, and hence the DC link voltage of the inverter within an acceptable range, e.g., 600–900 V for thin-film PV arrays. On the other hand, TLN1 differs from the TLN2 technique by the number of harmonics to be eliminated from the voltage waveform. This number is even for the TLN1 technique, whereas it is odd for the TLN2 technique. It can be examined from the line-to-neutral voltage waveform in
Figure 2 that an odd number of notch angles
α1 to
α5 exists, resulting in the elimination of an even number of characteristic power system harmonics, i.e., the 5th, 7th, 11th, and 13th in the line-to-neutral voltage waveform. In SHEM, the first notch angle is always used to control the fundamental voltage component. Triplen harmonics, such as the 3rd, 9th, and 15th, will be cancelled out in line-to-line voltage waveforms although they are present in line-to-neutral voltage waveforms. There will be no even-order characteristic power system harmonics, such as the 2nd, 4th, 6th, 8th, etc., in line-to-neutral voltage waveforms because of the quarter-wave odd symmetry [
24,
27,
35,
36]. The converter’s switching frequency
fc can be expressed as in (1) for TLN1 and TLN2 techniques:
where,
f1 is the frequency of the fundamental component and
N the total number of harmonics to be eliminated, including the fundamental component to be controlled.
If TLN2 were chosen, a higher-order harmonic component, the 13th for N = 4 or the 19th for N = 6 among the sidekick harmonics (the 11th and 13th for N = 4 or the 17th and 19th for N = 6) could not be eliminated. Therefore, in this research work, the TLN1 technique is preferred.
The Fourier series expansion of the line-to-neutral voltage waveform in
Figure 2 gives the magnitude of the
nth characteristic power system harmonic,
, obtained from (2).
where,
n is the odd harmonic order,
Vdc the DC link voltage, and
αk the switching angle for
k = {1, 2, …,
N}.
N transcendental equations with
N unknowns (
α1,
α2, …,
αN) in (3) are then obtained by setting the fundamental voltage component to a prespecified value and equating the remaining
N − 1 harmonics all to zero.
where
X = 3
N − 2 and
α constraints
.
A simultaneous solution of the set of transcendental equations in (3) is necessary to obtain a solution set for α1 to αN. Since these equations are nonlinear, either an iterative method or an evolutionary search algorithm is required.
2.3. Need for On-Line SHEM
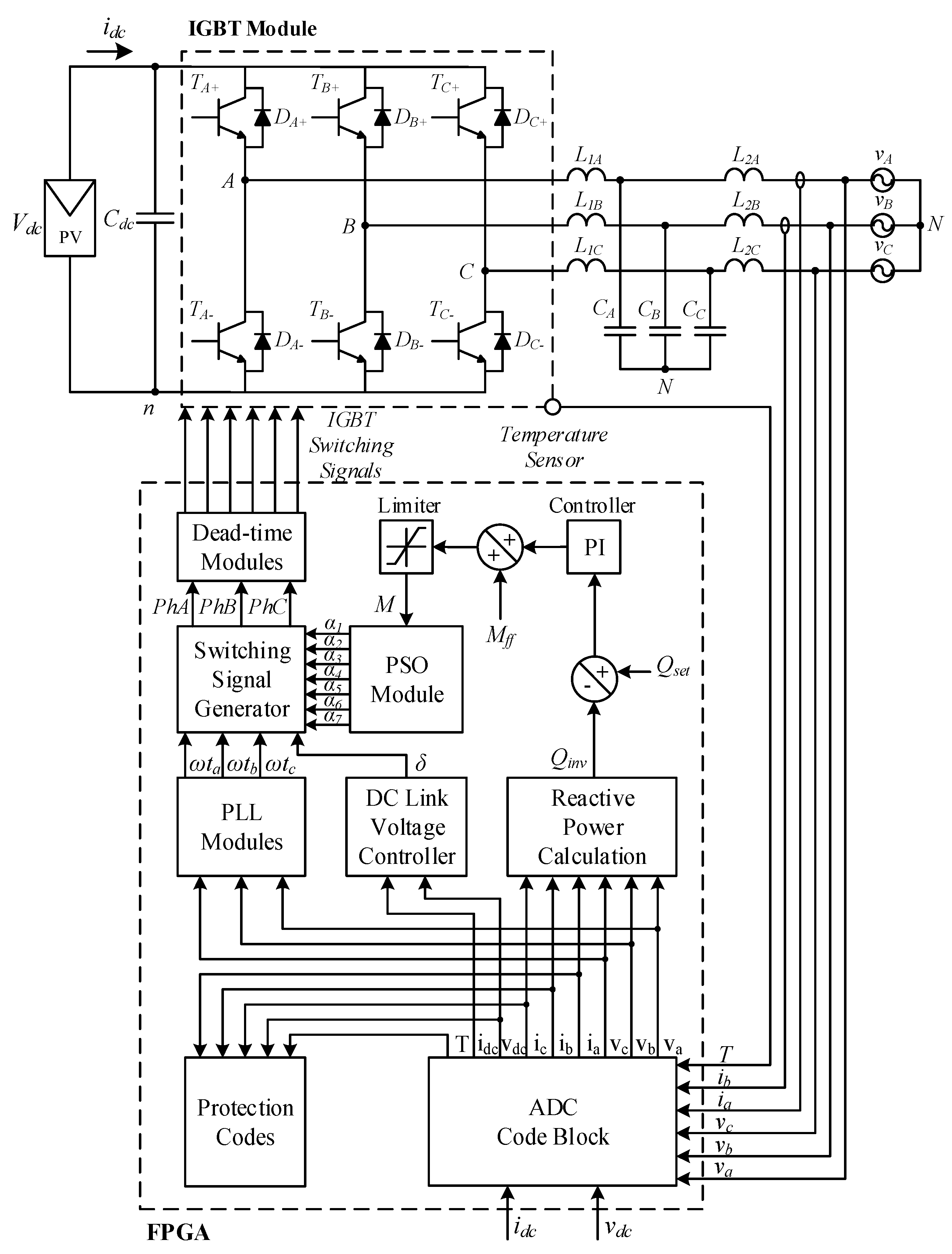
The technical specifications of a three-phase, two-level, and grid-connected VSC with some selected harmonics eliminated by SHEM are assumed to be as follows.
It provides conversion of the desired amount of DC power to AC over a wide DC link voltage range, e.g.,
Vdc = 600 V to 900 V for the thin-film PV systems in
Figure 1a.
Active power control is achieved by controlling the phase shift angle, δ, of the VSC output voltage with respect to the supply voltage.
The reactive power generated or consumed by the VSC should be adjusted to any prespecified value by varying the magnitude of the VSC’s output voltage by controlling the modulation index over the entire operating range.
The need for on-line SHEM is justified by carrying out two case studies as given below.
Case Study I: Constant SHEM Angle Set with Variable DC Link Voltage
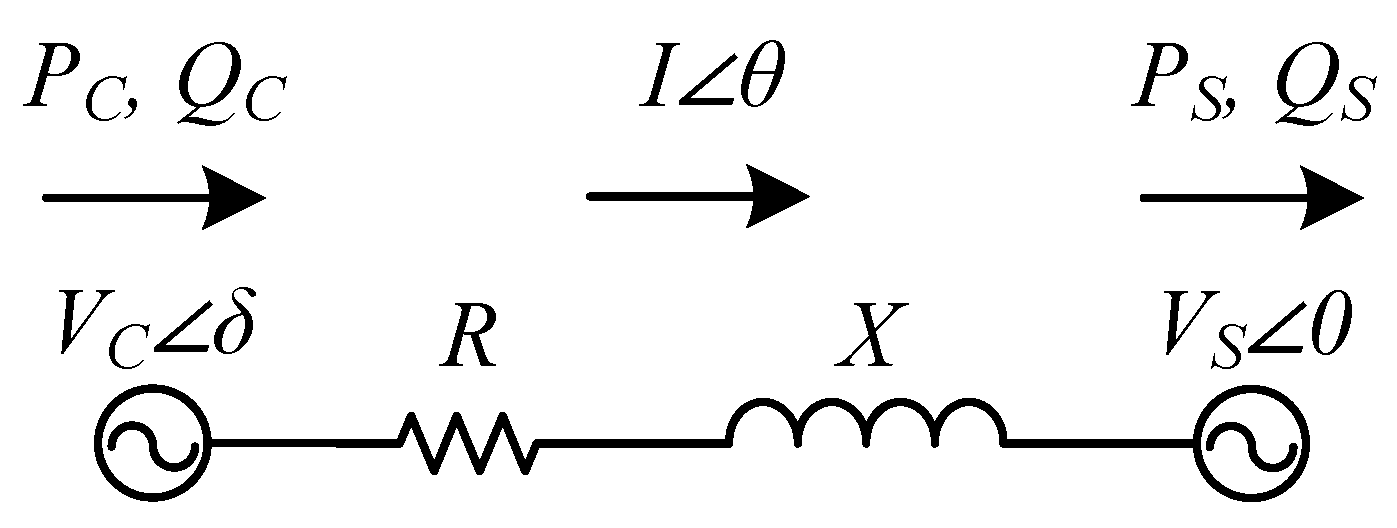
The three-phase, grid-connected VSC can be represented by the single-line diagram shown in
Figure 3.
The output series filter reactor’s internal resistance component,
R, and/or the coupling transformer’s leakage impedance is much smaller than the inductive reactance component,
X, and phase-shift angle,
δ, between the fundamental component of converter voltage,
Vc, and the fundamental component of supply voltage,
Vs, phasors is very small, then
sinδ ≈ δ and
cosδ ≈ 1 [
27,
36]. Under these assumptions, the active and reactive powers generated by the VSC, (
Pc,
Qc), and active and reactive powers consumed by the grid, (
Ps,
Qs), can be approximated by expressions in (4) to (6).
Since
Vs and
X in (6) are constant,
Qs can be adjusted to any preset value only by controlling
Vc. The relationship between the rms value of the fundamental component of the VSC’s output voltage,
Vc, and the variable DC link voltage,
Vdc, is given by the modulation index expression in (7). Since
M is kept constant for a constant SHEM angle set, as
Vdc changes there will be no control on
Vc and hence on
Qs. Therefore, the use of constant SHEM angles in the control system of grid-connected inverters with variable DC link voltages is to be avoided.
Case Study II: Off-line SHEM by the Look-Up Table Method
In order to avoid the drawbacks of constant SHEM angles in the reactive power control of grid-connected inverters with variable DC link voltages, M and hence Vc should be adjusted by using several sets of SHEM angles as Vdc changes. The common approach to this problem is the computation of several SHEM angle sets and their storage in an internal or external random access memory (RAM)/read-only memory (ROM) in the form of (a) LUT(s). This approach makes necessary the discretization of M control range into d number of steps for N number of total harmonics to be controlled over the entire operation range of the resulting system, which yields a d × N LUT. Since M and hence SHEM angles α1 to αN are controlled stepwise instead of by on-line continuous control, the required value of M at any particular operating point will be rounded to the nearest M number stored in the LUT. This may result in a significant error in Vc and hence Qs values when the row number, d, of the LUT is kept low. Therefore, d should be as high as possible. A d × N LUT will be impractical if a huge number of harmonics is to be eliminated.
The effects of the order of a LUT on the discretized values of
M, the corresponding
Vc, and
Qs for unity power factor operation are examined by considering 5 × 7 and 41 × 7 LUTs and the associated results are given in
Table 1 for two different values of DC link voltage (
Vdc (min) = 600 V,
Vdc (max) = 900 V, and
X = 3.14 Ω at 50 Hz). In this paper, theoretical results are verified on a sample small-scale PV system as described in
Section 4. This small-scale prototype is connected to a 400-V, 50-Hz grid. The performance of real-time SHEM in adjusting
M, and hence
Vc to its set value of 230 V in order to bring
Qs =
Qs(set) to zero is also given in
Table 1 for the same problem. As can be understood from the results marked by red colored values in
Table 1,
Vc and
Qs deviate significantly from their set values in the case of a small-sized LUT. Deviations from the set values can be significantly lowered as the size of the LUT increases (marked by yellow color in
Table 1). In order to alleviate the problem arising from the discrete LUT method in variable DC link voltage applications, linear interpolation can be used between consecutive
M steps.
At the present time, with the advances in digital electronics area by using a powerful FPGA module or parallel computing hardware, such as a Graphical Processing Unit (GPU), enormously large SHEM angles can be calculated on-line to control
M continuously. The performance of the on-line SHEM by using a single FPGA module to control seven harmonics is also given in
Table 1 by the green-colored area.
3. Application of PSO to SHEM
In grid-connected PV inverter applications, since the supply frequency is constant (f1 = 50 or 60 Hz), SHEM angles should be updated once in a full-cycle (20 or 16.67 ms) with 2π/3 and 4π/3 phase-shifted signals for the remaining two phases. Therefore, on-line calculation of SHEM angles should be carried out in a total execution time less than a period of grid voltage, i.e., 20 ms for 50 Hz applications. However, variable-frequency alternating current (AC) motor drive applications need lower calculation times when the applied motor frequency is higher than the rated frequency. In this research work, the equations in (3) will be solved by the PSO technique, which is an evolutionary search algorithm.
In order to evaluate the fitness values of each particle at each time frame, a cost function should be formulated as required by the PSO. SHEM equations should be put into a format so that each particle is assigned a real fitness value. Then, boundaries of the solution space are defined, and an initial population of swarms is generated in this solution space. Finally, PSO parameters are set, so that the PSO algorithm is ready to find a feasible global optimum to the optimization problem.
3.1. Particle Swarm Optimization (PSO)
The stochastic population-based optimization technique called particle swarm optimization (PSO) has been developed by Dr. Russell Eberhart and Dr. James Kennedy in 1995 [
37]. It is initialized with a random or heuristic population which consists of particles such as birds, fish, and insects. Each particle in this research work is a vector composed of seven SHEM angles and in order to assess whether it can be a potential global solution or not, it is evaluated with a fitness function. The particles search the problem space via cognitive and social interaction by pursuing the current optimum particles. The personal best location (
pbest) is defined as the coordinates of the particle which is associated with the best personal fitness value acquired so far. The global best location (
gbest), however, is defined as the location with the best fitness value which all of the population has reached. In each time frame, each particle updates its velocity towards its
pbest and
gbest locations. Separate random numbers [
38] are employed to weight the total acceleration terms of local and global searches. The velocity,
vi, and position,
xi, update equations are as given in (8) and (9), respectively.
where,
β is the inertia weight which dictates the velocity of the particles in the next time frame, the acceleration constants
c1 and
c2 are, respectively, the cognition and social factors which are, respectively, related to the diversification and intensification of the search procedure.
rand is chosen as a random number between 0 and 1, which defines the explorative capability of the particle over the search space, and
K is the constriction factor to guarantee the convergence of the algorithm given in (10), which has been found in [
38].
where,
and
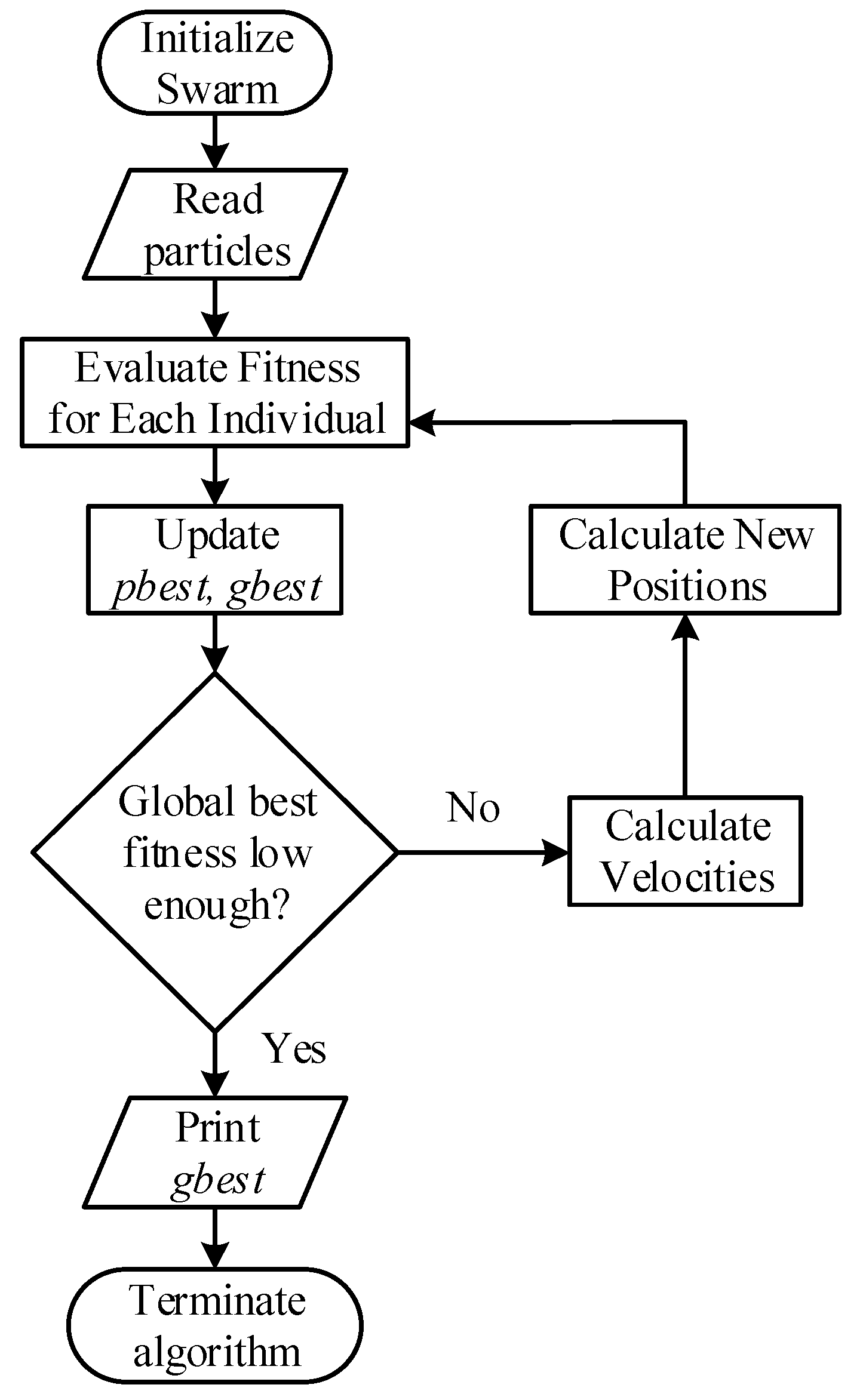
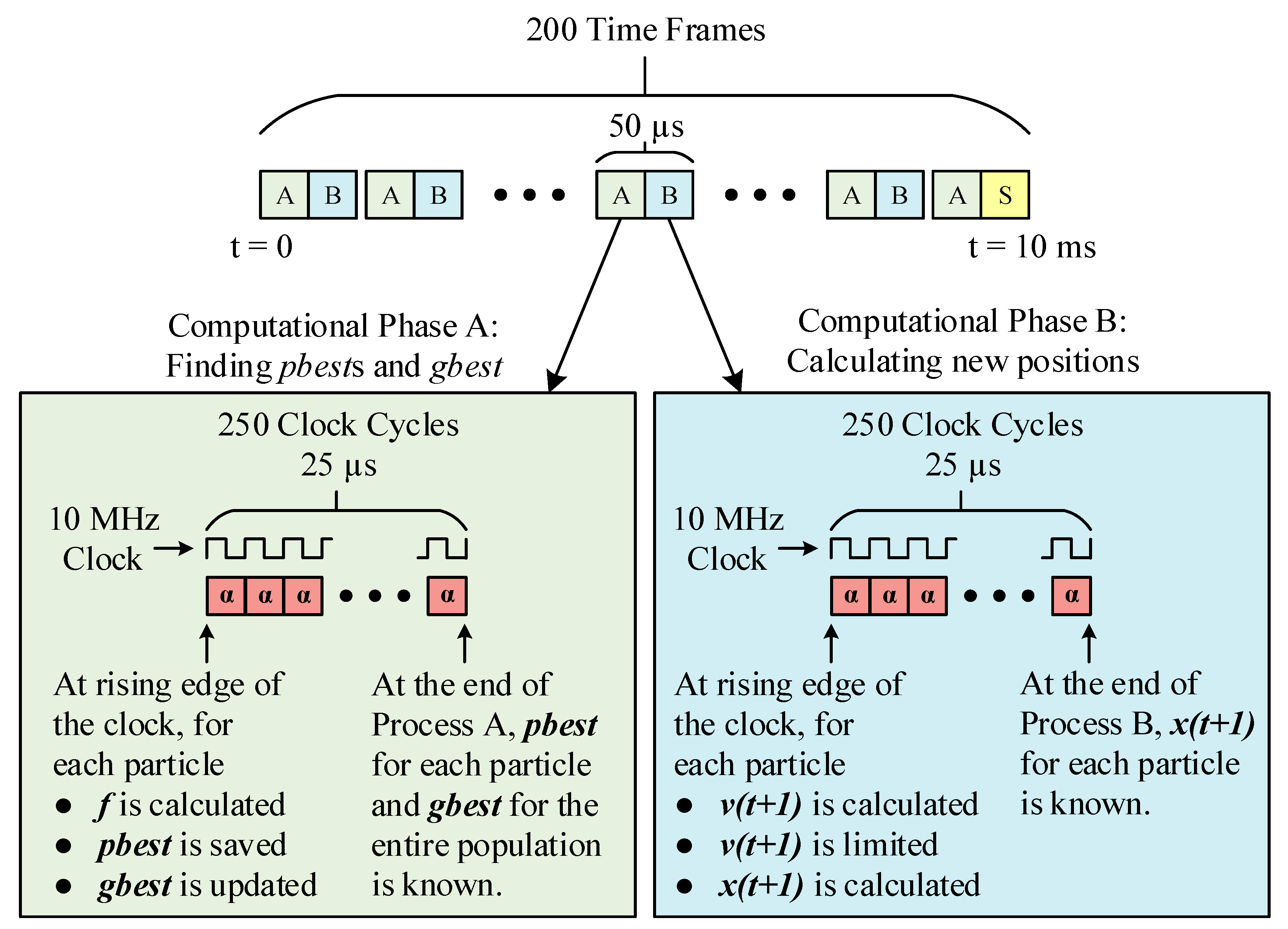
Figure 4 shows the basic flowchart of the PSO algorithm. Whenever the global best fitness,
f, reaches a value less than a prespecified limit, e.g.,
f = 1 × 10
−9 in this application, the algorithm terminates for each PSO calculation window.
3.2. Determination of Cost Function
In this application, the TLN1 technique is chosen to eliminate the six lowest-order sidekick harmonics, given as the 5th, 7th, 11th, 13th, 17th, and 19th, in the output voltage waveform of the inverter since even-order harmonics are not present if an odd quarter-wave symmetric pattern is used, and all triplen harmonics are eliminated in the line-to-line voltages for a three-phase, three-wire system. This results in a switching frequency of 750 Hz. For this sample application, the equation set in (11) is to be solved.
A new set of equations given in (12) is obtained by rearranging equations in (11) and using the
M expression given in (7). The cost function
Tn, and the fitness value,
f, of a SHEM angle set can be expressed by squaring the left hand sides of the equations in (12) and then summing them up as given in (13). In (13),
γ should be set to a value higher than 10 to converge the solution more rapidly. Furthermore,
T1 in (12) has crucial importance in determining
Vc and hence adjusting
Qs to the prespecified set value.
where,
is the peak value of the fundamental line-to-neutral voltage at the inverter output,
Vdc is the DC link voltage,
bn is the peak value of the
nth harmonic component (
n = 5, 7, 11, 13, 17, and 19) as given in (2), and
αk is the SHEM angle to be determined for
k = 1, 2, …, 7.
where
γ and
µ are the penalty values, respectively, for
M and the angle constraint in (14).
µ can be set to 10 for this sample application in order to eliminate invalid SHEM angle sequences rapidly during the on-line application of SHEM.
3.3. Results of the PSO Algorithm
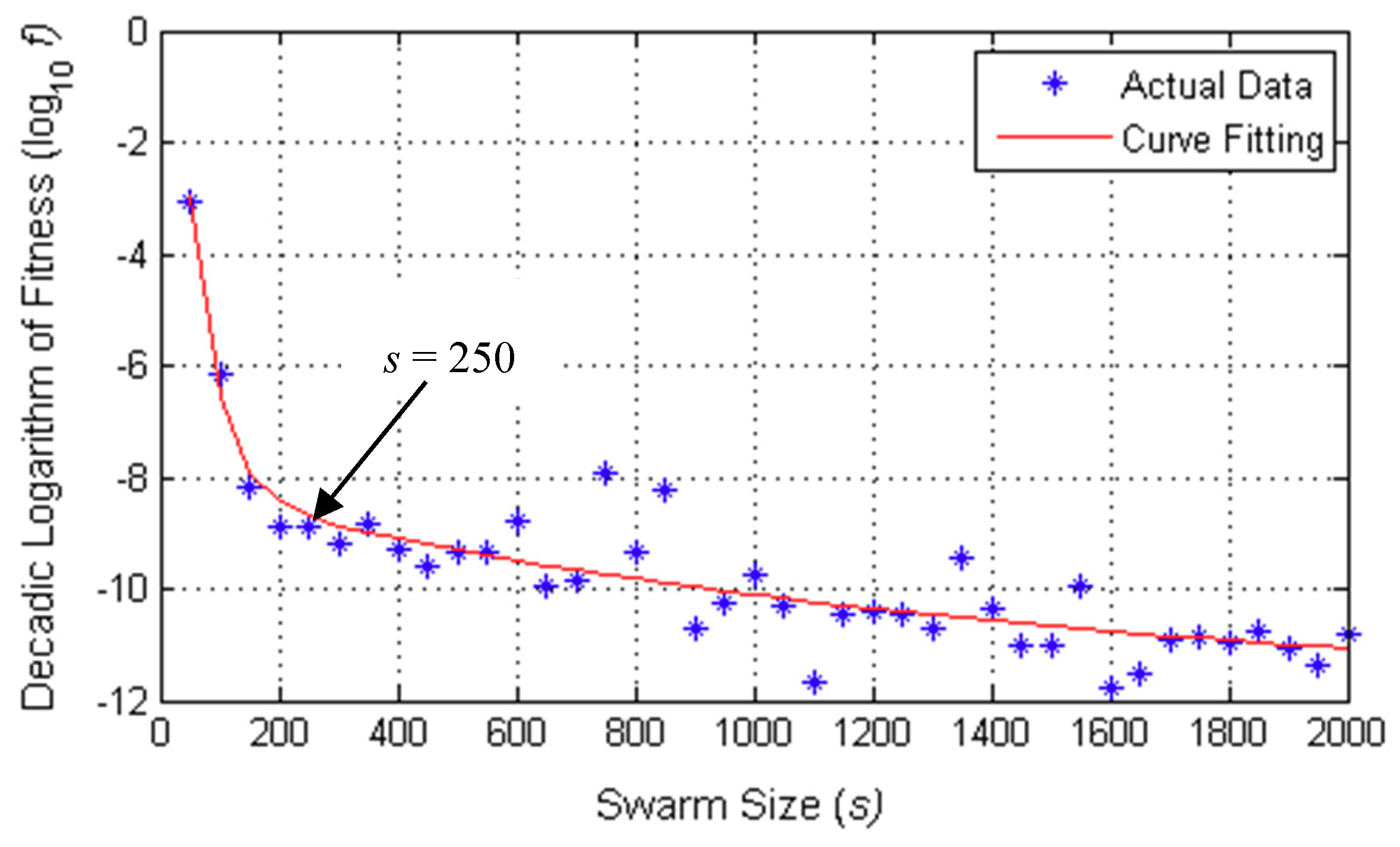
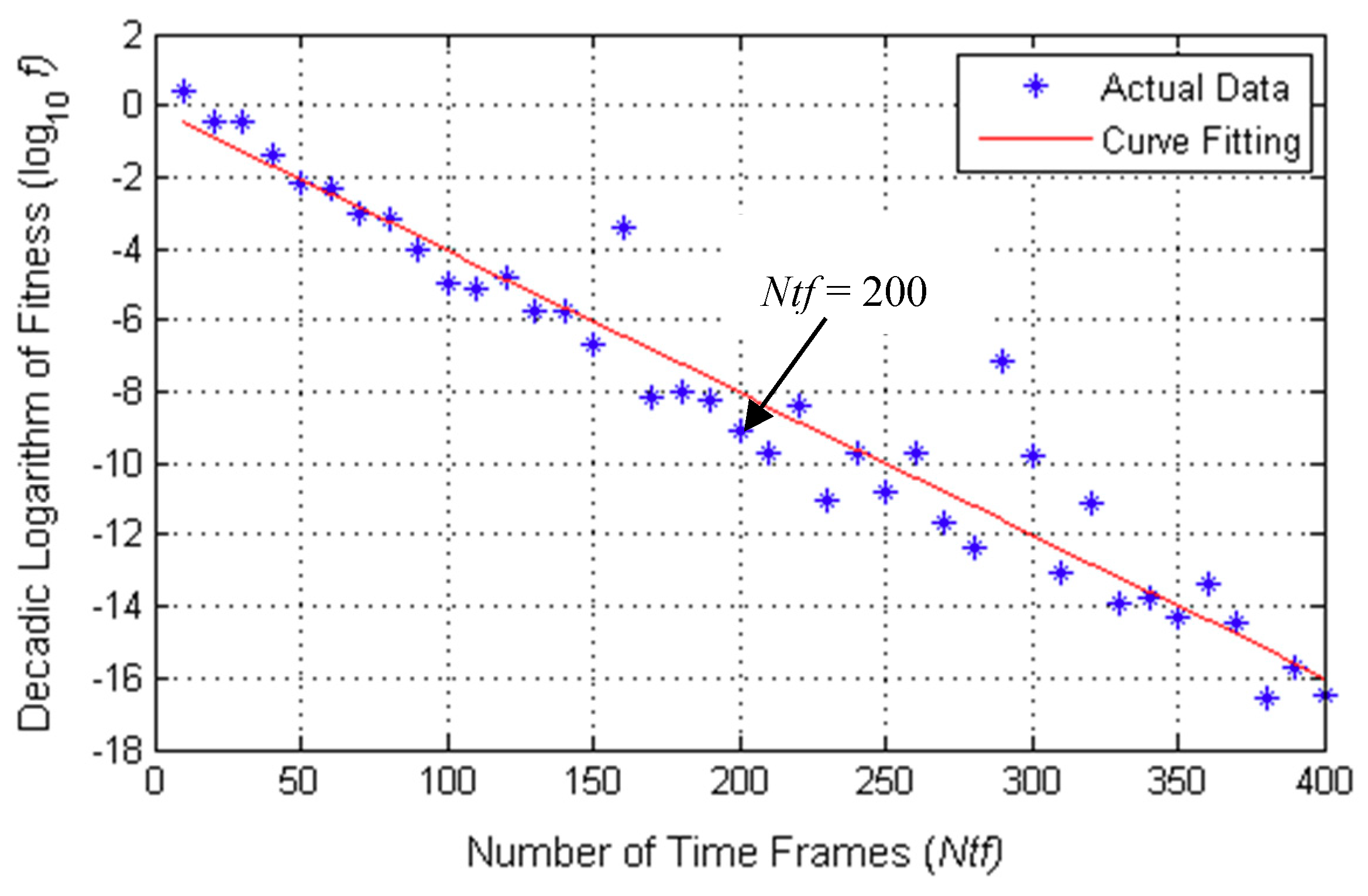
The parameters used in the PSO algorithm are first optimized in the MATLAB environment. Among these, the most important parameters affecting how fast the PSO algorithm converges are the swarm size,
s, and the number of time frames,
Ntf. The variations in fitness value,
f against
s, and
Ntf are given in
Figure 5 and
Figure 6, respectively. The ideal value of
f is zero. From
Figure 5 and
Figure 6, the optimum swarm size and number of time frames are chosen to be
s = 250 and
Ntf = 200, which correspond to a decadic logarithmic error, i.e., log
10 f = −9. The optimized and default values of all parameters used in the PSO algorithm are as given in
Table 2. SHEM angles from
α1 to
α7 are found against
M by running the PSO algorithm in the MATLAB environment with optimized parameters in
Table 2.
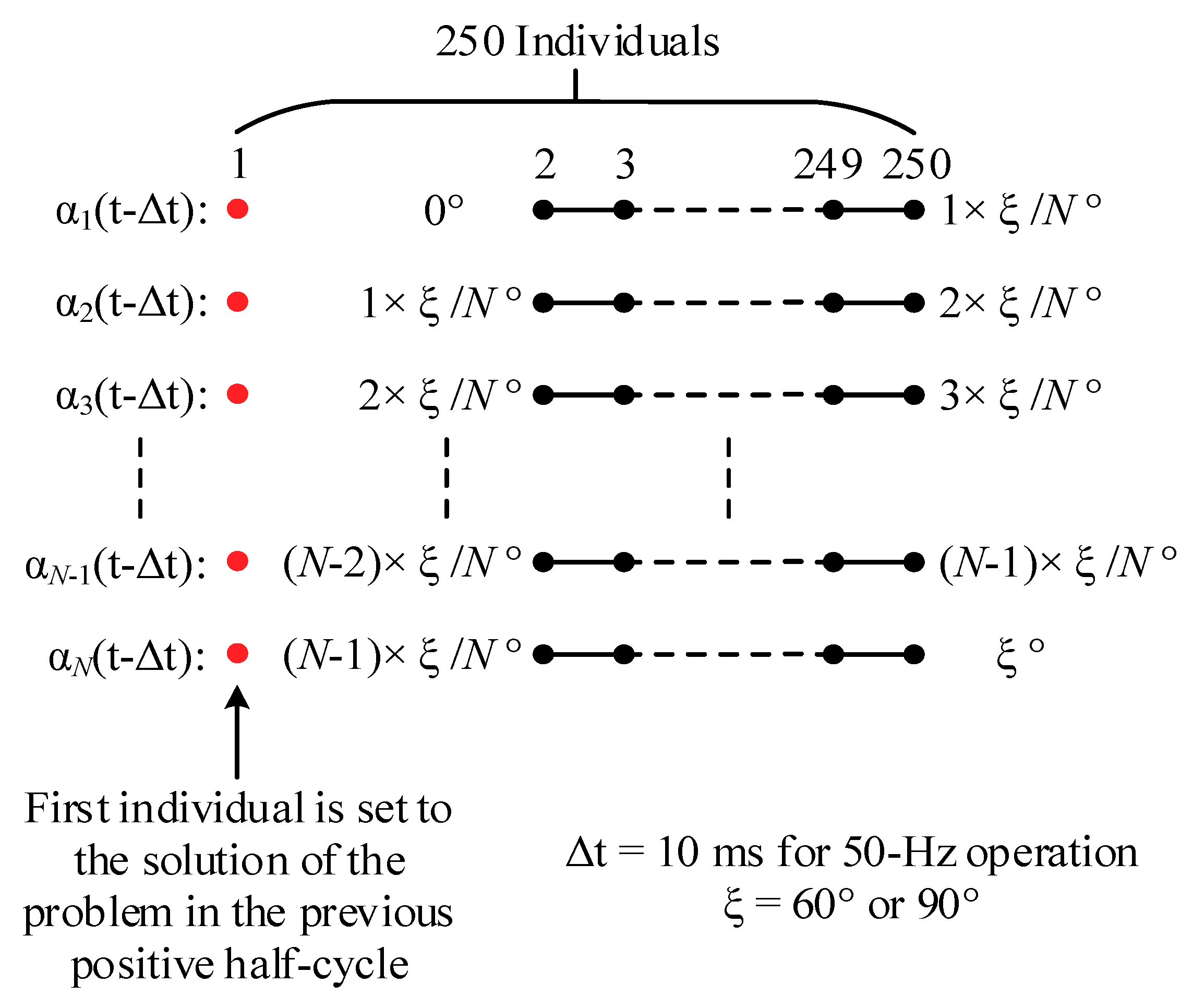
Random initialization of the PSO algorithm at time
t = 0 (at start-up) can be made by utilizing the constraints defined for the problem by equating the initial value of
M and hence the fundamental component of inverter’s output voltage to zero. Randomly chosen initial values usually cause convergence of the solution to a local minimum, especially for large numbers of SHEM angles,
N. When the problem is generalized to eliminate all odd-order power system harmonics up to the 50th according to IEEE Std. 519-2014 [
39] and IEC 61000-4-30 [
40], the initial values of
N number of SHEM angles can be distributed in the range of either,
Case (I) from 0 to ξ = 90°, or
Case (II) from 0 to ξ = 60°,
with respect to the zero crossing point on the rising edge of the fundamental line-to-neutral voltage waveform. Initial values of
N number of SHEM angles can therefore be determined from the first equation in (12) by setting
M to zero as given in (15).
In case (I), the SHEM angles are distributed between 0 and 90°, where the first SHEM angle
α1 is set to zero, and the last angle
αN to 90°. The angles from
α2 to
αN−1 are distributed to
p sections, where
p = (
N + 1)/2, so as to eliminate pairwise the remaining cosine terms in (15). For
N = 7, in the case study,
α1 = 0,
α2 =
α3 = 15°,
α4 = 60°,
α5 =
α6 = 75°, and
α7 = 90°. In order to cancel out the first term (−1) in (15),
α4 is set to 60°. Although the initialization procedure with
M = 0 for case (I) which distributes SHEM angles over the quarter wave from 0 to 90° gives quite accurate results on the PSO algorithm for a low number of harmonics to be eliminated (for
N = 3, 5, 7, and 9), this is not true for
N > 9. However, in case (II), the SHEM angles are distributed between 0 and 60°, i.e., the last SHEM angle should be set to 60°, thus canceling the first term in (15). On the other hand, angles
α1 to
αN-1 are evenly distributed to
p = (
N + 1)/2 sections so as to cancel pairwise the remaining cosine terms. The generalization procedure for initial values of SHEM angles for case (II) is summarized in
Table 3. The initialization procedure in case (II) is simpler and more general than that of case (I).
There may be more than one solution for SHEM angles for any number
N between 3 and 17. As an example, for
N = 7, the optimum values of SHEM angles (
α1,
α2, …
α7) and the corresponding fitness values as a function of
M are obtained by distributing the initial values in the range from 0 to 90° (case (I)) as given in
Table 4. However,
Table 5 shows the optimum values of SHEM angles and fitness values for the same problem when the initial values of those angles are chosen according to the generalized procedure in
Table 3 (case (II)). As can be understood from
Table 4 and
Table 5, the optimum values of SHEM angles are different for the same problem owing to the use of different initial values. Since the
f values are very low, both solutions can be considered to be the global optimum points found by the PSO algorithm.
Much lower
f values could be obtained by using time frames higher than 200 (
Table 2) at the expense of a longer execution time. In this research work, the results given in
Table 4 are used in the implementation.
The control range of M is divided into three subregions:
- (a)
Impractical M values in which the difference between any two consecutive SHEM angles is less than 0.1°. The associated
M values and the critical angles are marked by red color boxes in
Table 4 and
Table 5. As an example, the typical turn-off times for 1700 V 300 A SiC power MOSFET and HV IGBT are nearly 0.27 μs and 1.8 μs, respectively. Deadbands of 0.5 μs and 3 μs can be chosen in the implementation for these power semiconductors. These values for deadbands correspond to ~0.01° and ~0.06° for 50-Hz grid applications, respectively. In higher power applications, IGCT (alternatively ETO) requires a nearly 10-µs deadband, which corresponds to ~0.2°. Therefore, operation at
M ≥ 0.95 is impractical for all power semiconductors.
- (b)
M ≤ 0.10 and 0.9 ≤ M < 0.95 values are not recommended for implementation especially for Si IGBTs, which are marked by yellow color circles in
Table 4 and
Table 5.
- (c)
The remaining M control range in
Table 4 and
Table 5 defines safe operating M values.
In order to justify the usefulness of the PSO algorithm and the generalized initialization procedure in applying SHEM for the elimination of odd-order power system harmonics up to the 50th, optimum SHEM angles have been found for
N = 7, 9, 11, 13, 15, and 17, and sample results corresponding to
M = 0.7 are given in
Table 6. The results of these analyses show that the PSO algorithm can be successfully used in an on-line application of SHEM provided that powerful computing hardware is available for each case.
5. Conclusions
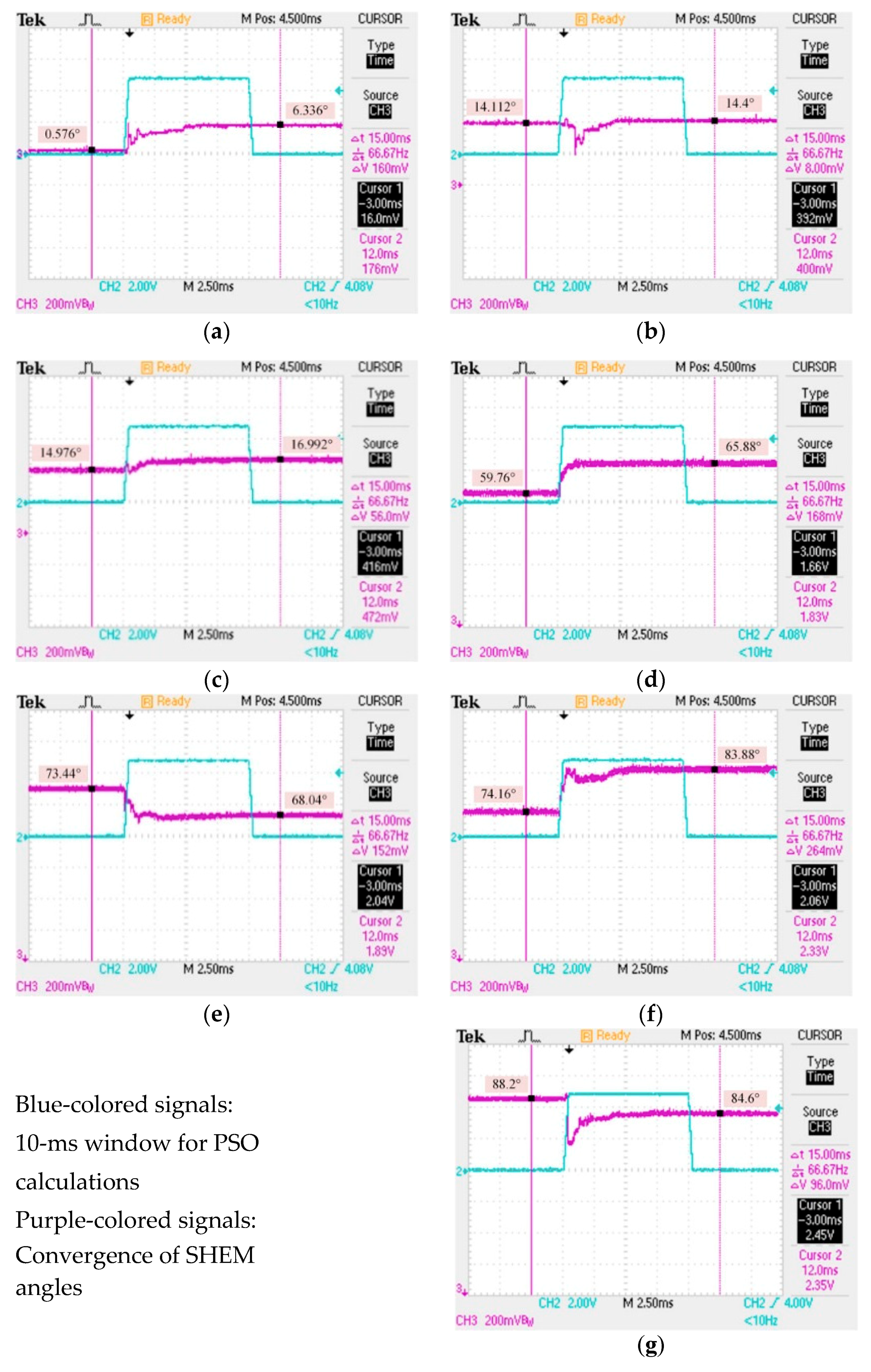
An off-line application of SHEM provides stepwise control of SHEM angles resulting in minimization of the selected harmonic components instead of their elimination. However, in the on-line application, switching angle sets can be continuously controlled by on-line calculation of SHEM angles, resulting in much better harmonic elimination performance and minimization of THDs. As reported in this paper for the first time, the six low, odd-order voltage harmonics of a grid-connected VSI with variable DC link voltage in a small-scale PV supply are eliminated on-line by using the developed PSO algorithm running on am FPGA controller successfully. The global best solution of the PSO algorithm is obtained with 250 individual particles, i.e., switching angle sets, within 200 time frames, resulting in a relatively small fitness value in the range from 10−7 to 10−4 depending on the modulation index, M. For a step change in M, all switching angles converge to the solution within a time period less than one half-cycle of the grid voltage, thus updating the switching instants of power semiconductors in every full-cycle of the output voltage.
In order to eliminate all voltage harmonics up to the 50th continuously and rapidly, very powerful digital computing hardware is needed. This is an important requirement especially for variable frequency traction and industrial AC motor drives, where the motor drive is to be operated frequently at frequencies much higher than the rated frequency. In general, the maximum number of harmonics that can be eliminated or minimized in SHEM applications is dictated by the operational capabilities of power semiconductors employed in the VSC, such as the optimum switching frequency and turn-on and turn-off times. As an example, an SiC power MOSFET, as a wide-band-gap device permits the elimination of a number of harmonics much higher than that of IGBT-based VSCs in an on-line application of SHEM. Each recorded harmonic is the vectorial sum of the harmonic current component injected by the PV supply, and the associated one sinked by the LCL filter from the grid. Therefore, the harmonic current contribution of the prototype system can be assessed only by using a proper measurement and calculation method. On the other hand, the elimination of a much higher number of harmonics at the expense of a higher switching frequency would reduce significantly the size of the LCL filter and hence the amount of low-order harmonics sinked from the grid.