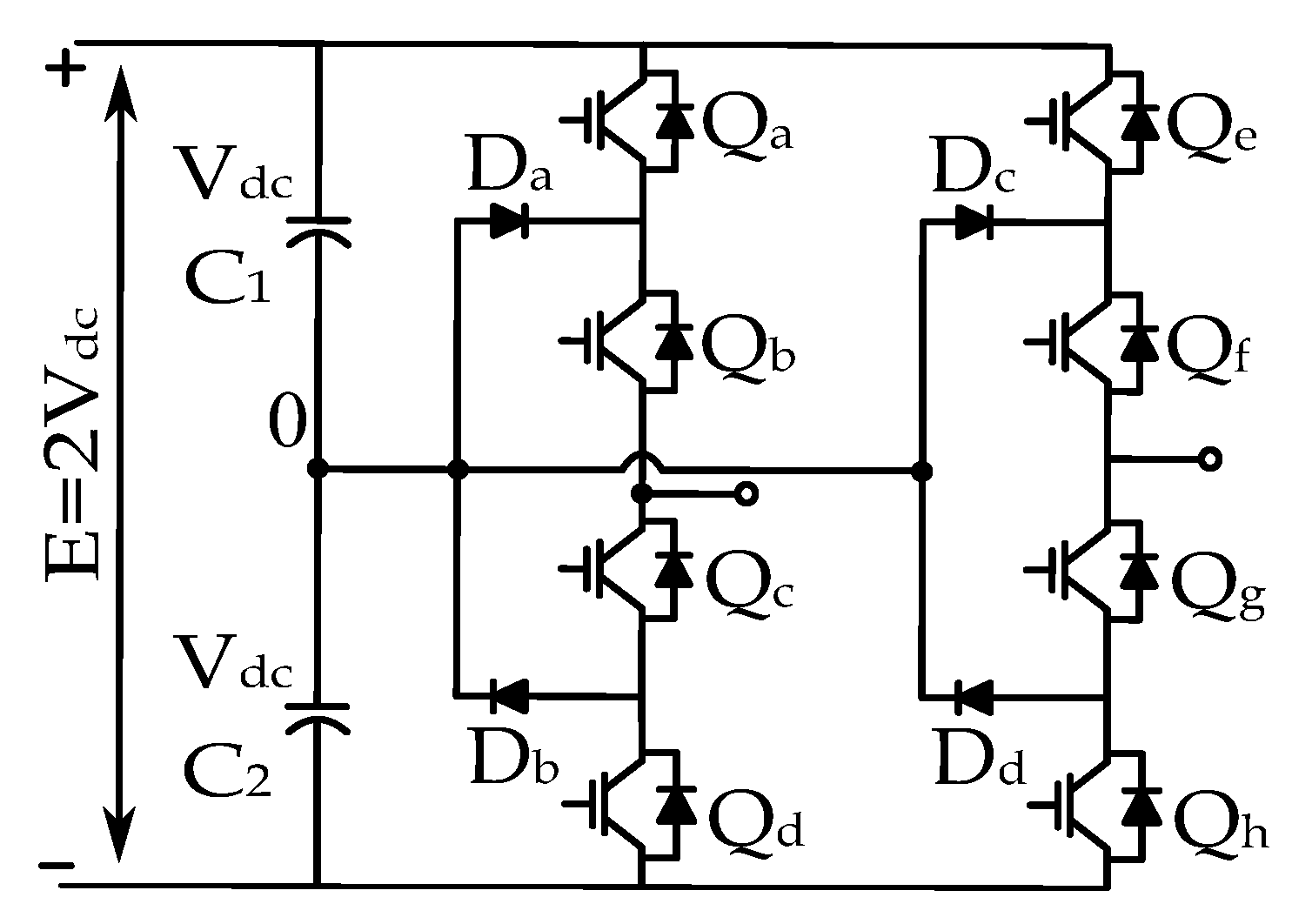
Figure 1.
Five-level NPC converter topology.
Figure 1.
Five-level NPC converter topology.
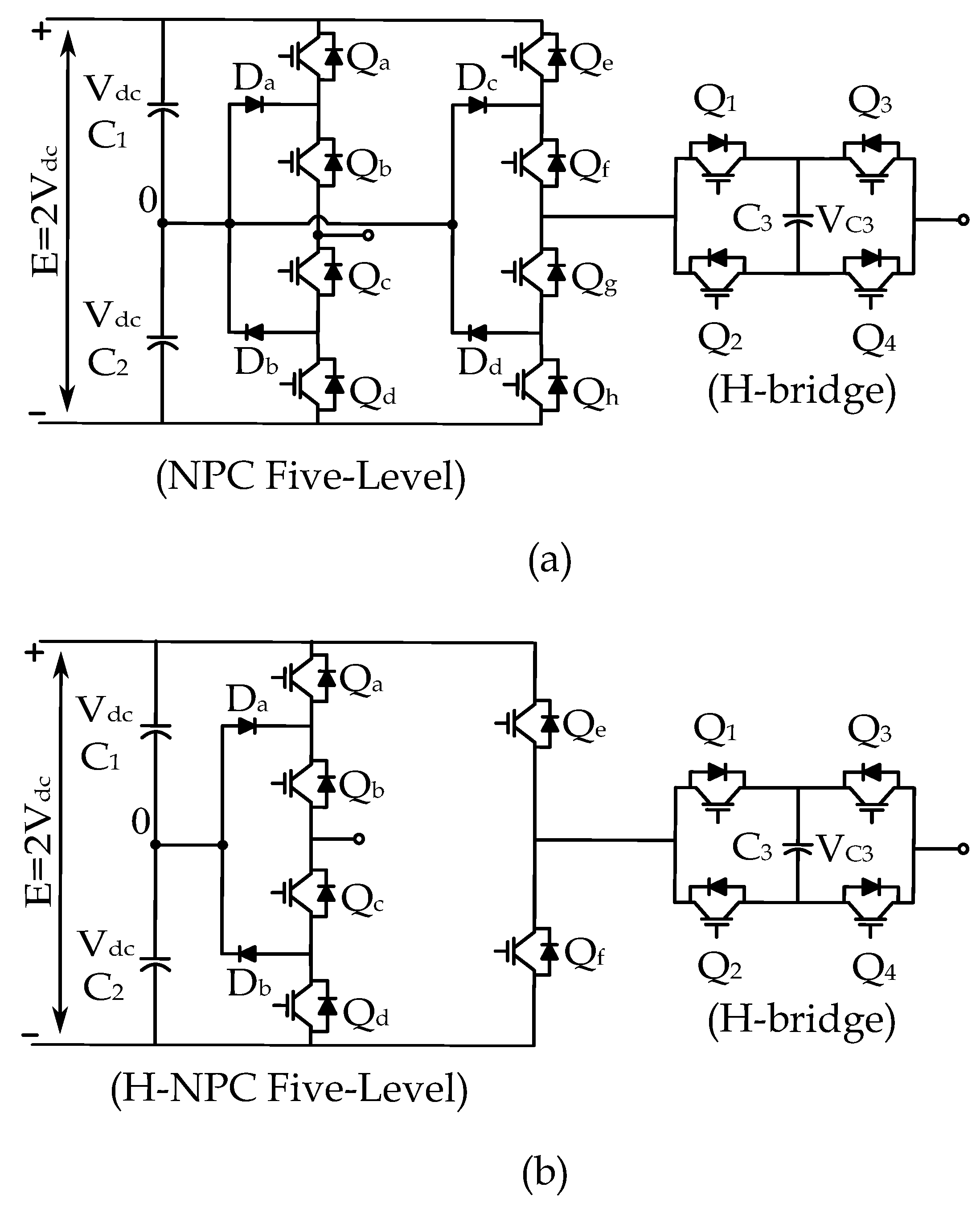
Figure 2.
Five level NPC converter with H-bridge (a) NPC with H-bridge module, and (b) H-NPC with H-bridge module.
Figure 2.
Five level NPC converter with H-bridge (a) NPC with H-bridge module, and (b) H-NPC with H-bridge module.
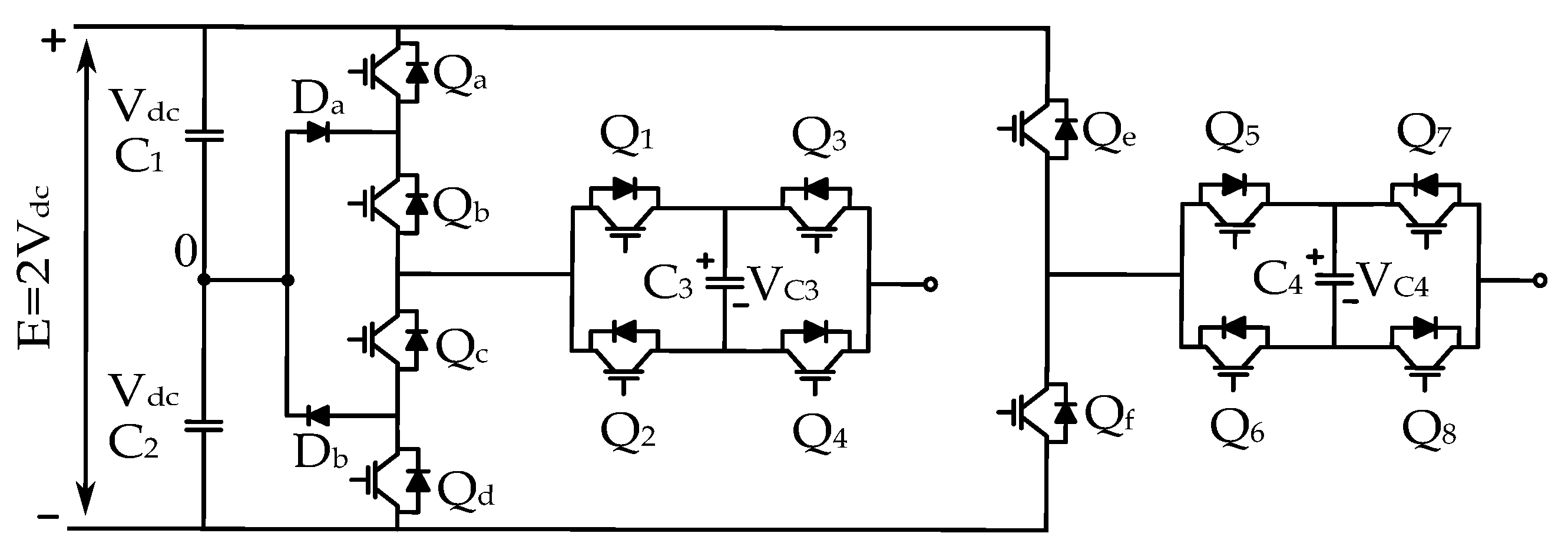
Figure 3.
CHB based converter topology.
Figure 3.
CHB based converter topology.
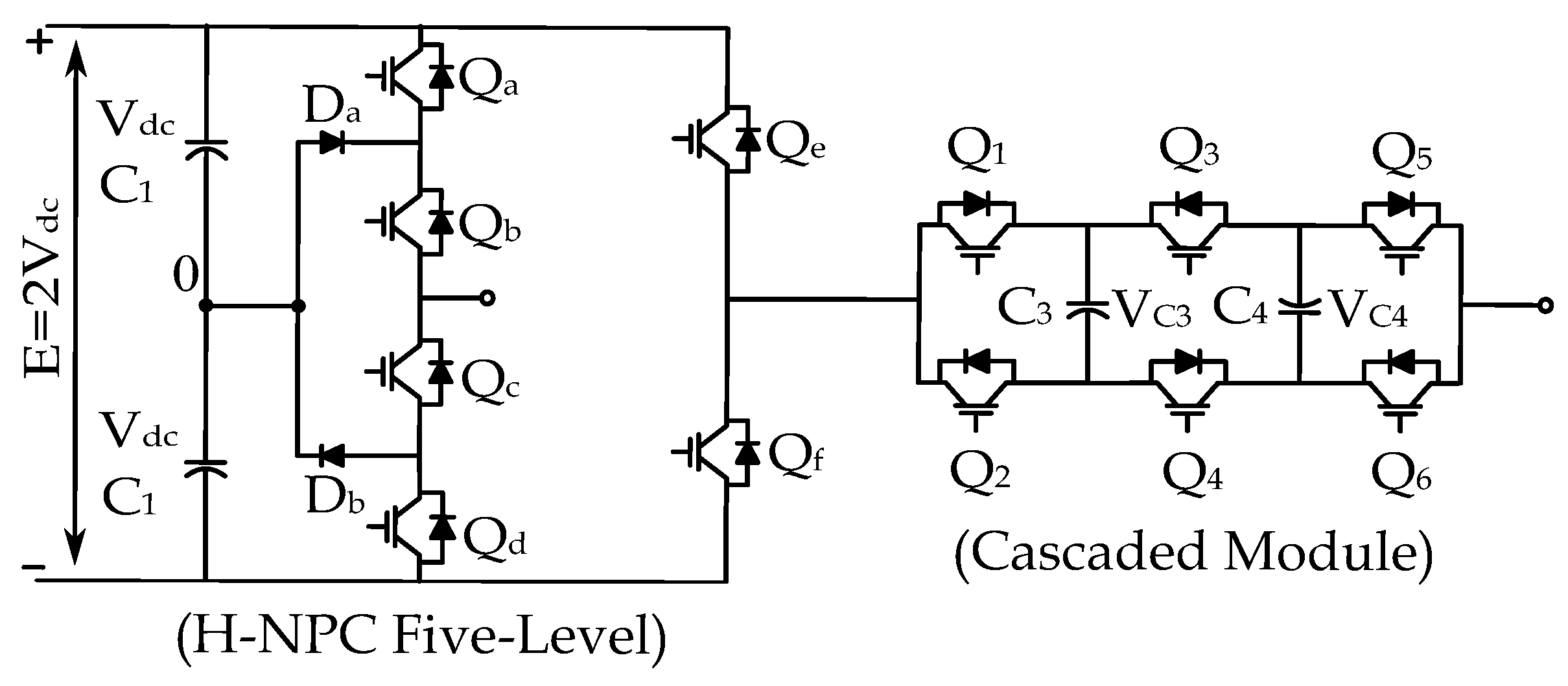
Figure 4.
Five-level H-NPC with cascaded converter module.
Figure 4.
Five-level H-NPC with cascaded converter module.
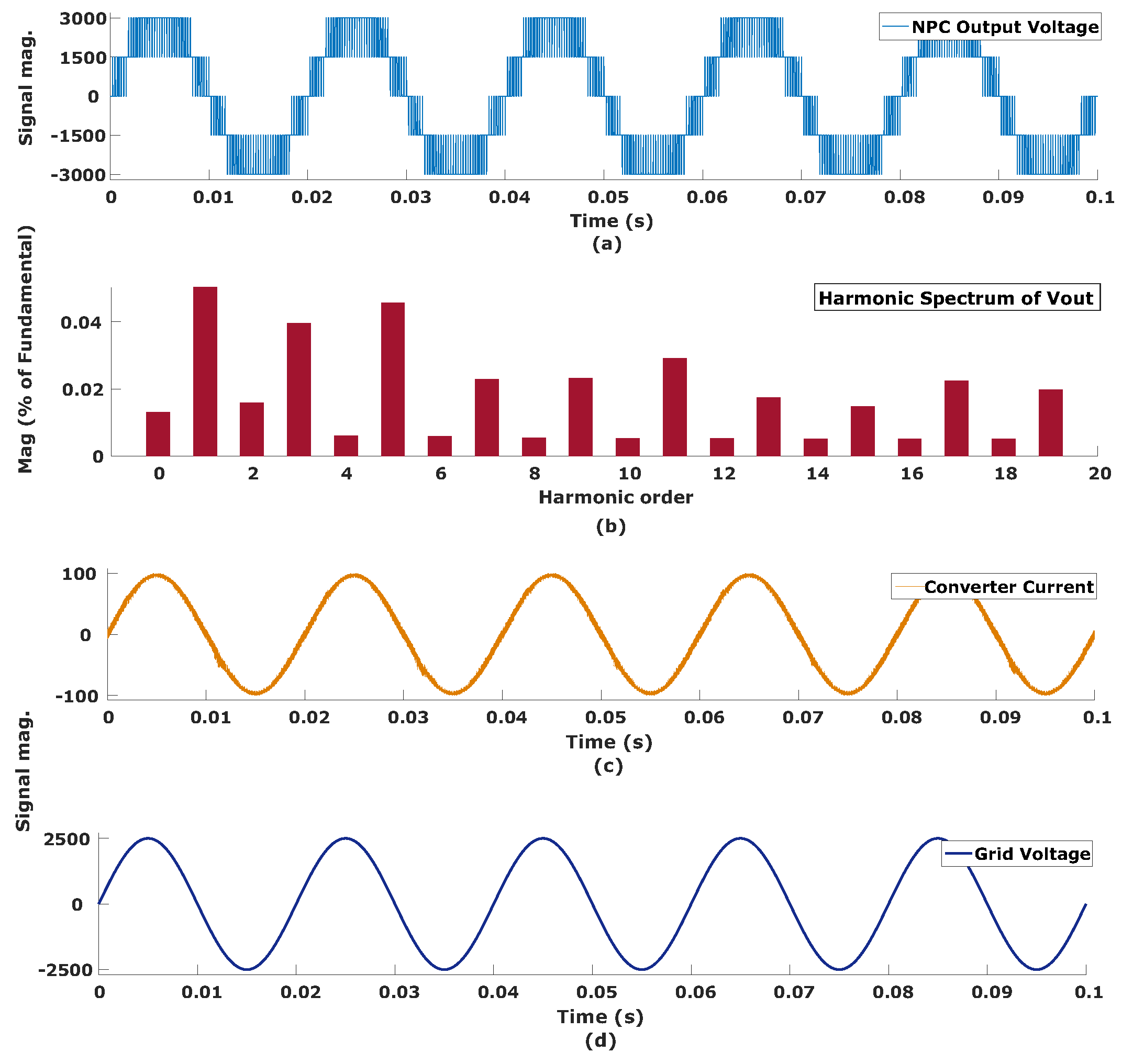
Figure 5.
5-L NPC converter topology (a) output voltage, (b) harmonic spectrum of output voltage, (c) converter current, and (d) grid voltage.
Figure 5.
5-L NPC converter topology (a) output voltage, (b) harmonic spectrum of output voltage, (c) converter current, and (d) grid voltage.
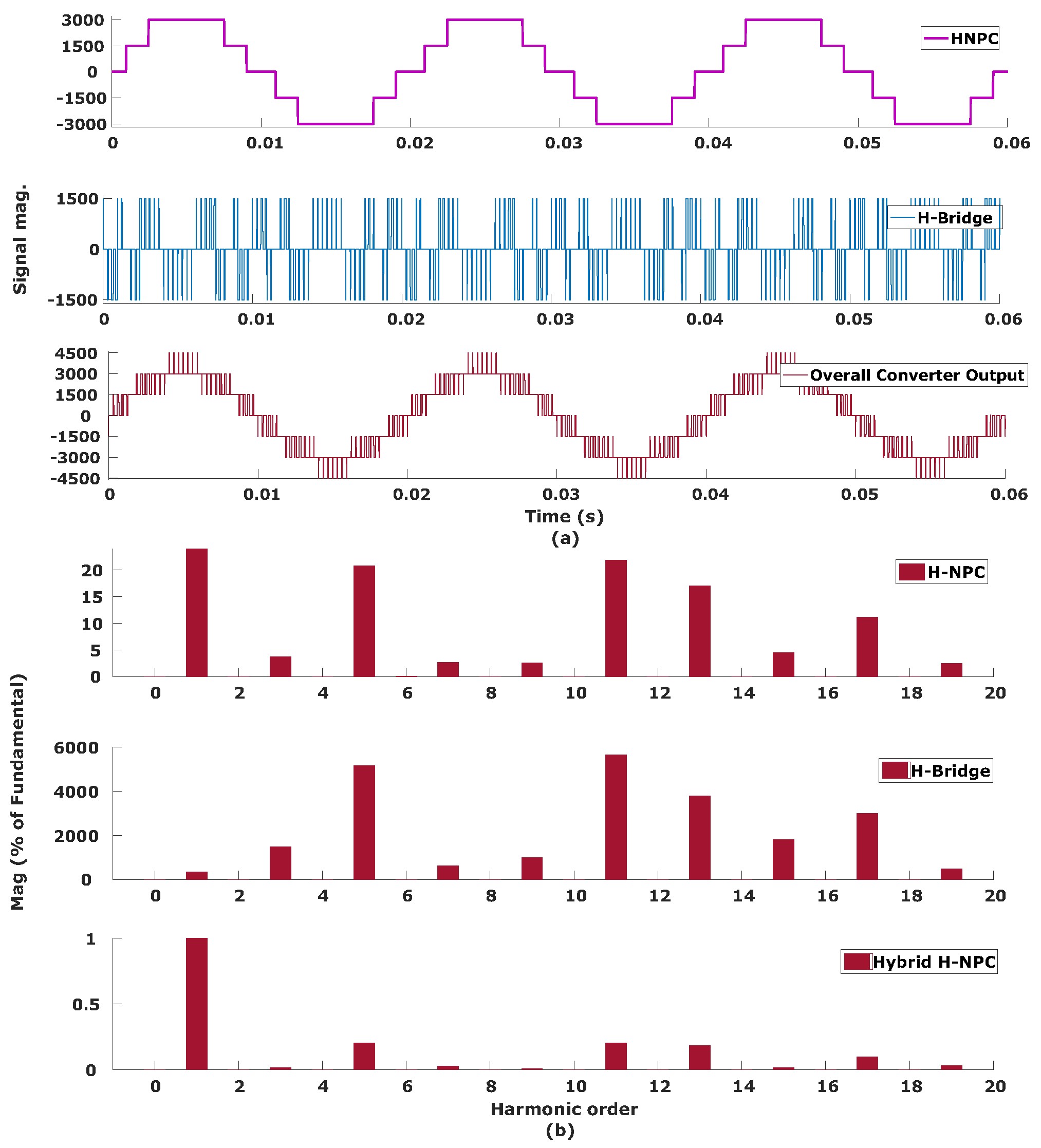
Figure 6.
7-L hybrid H-NPC with H-bridge converter topology (a) output voltage, and (b) harmonic spectrum of output voltage.
Figure 6.
7-L hybrid H-NPC with H-bridge converter topology (a) output voltage, and (b) harmonic spectrum of output voltage.
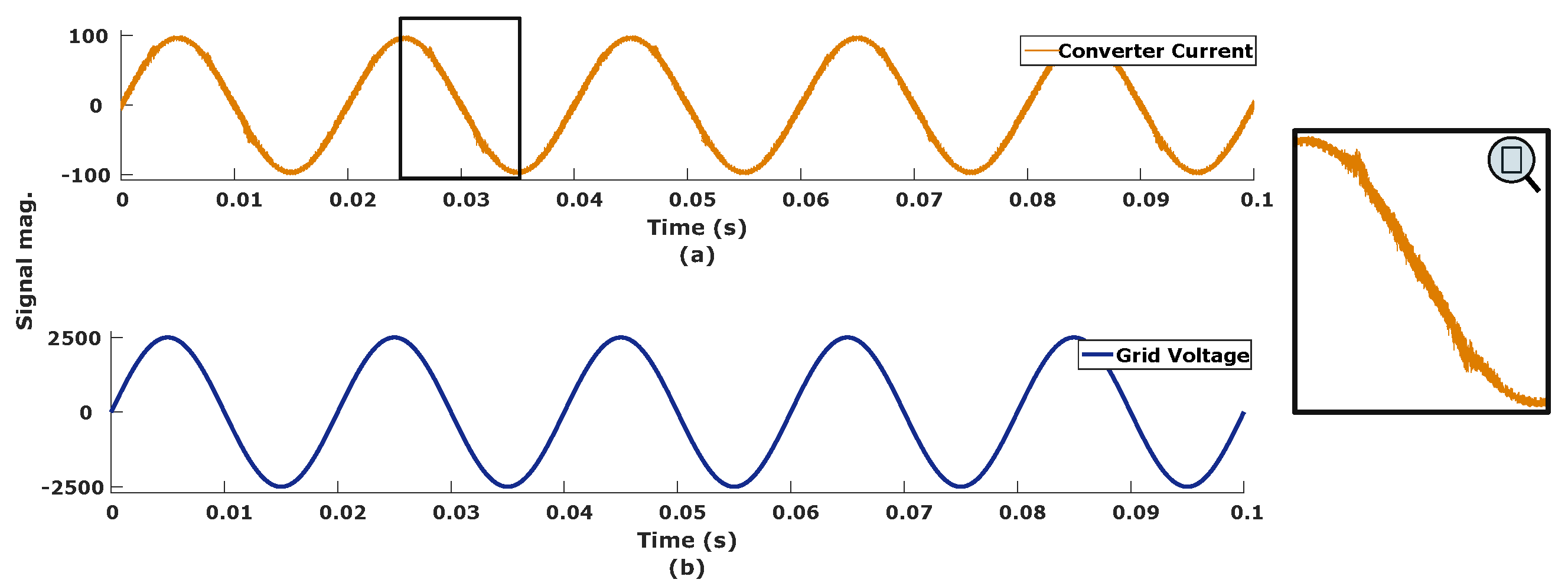
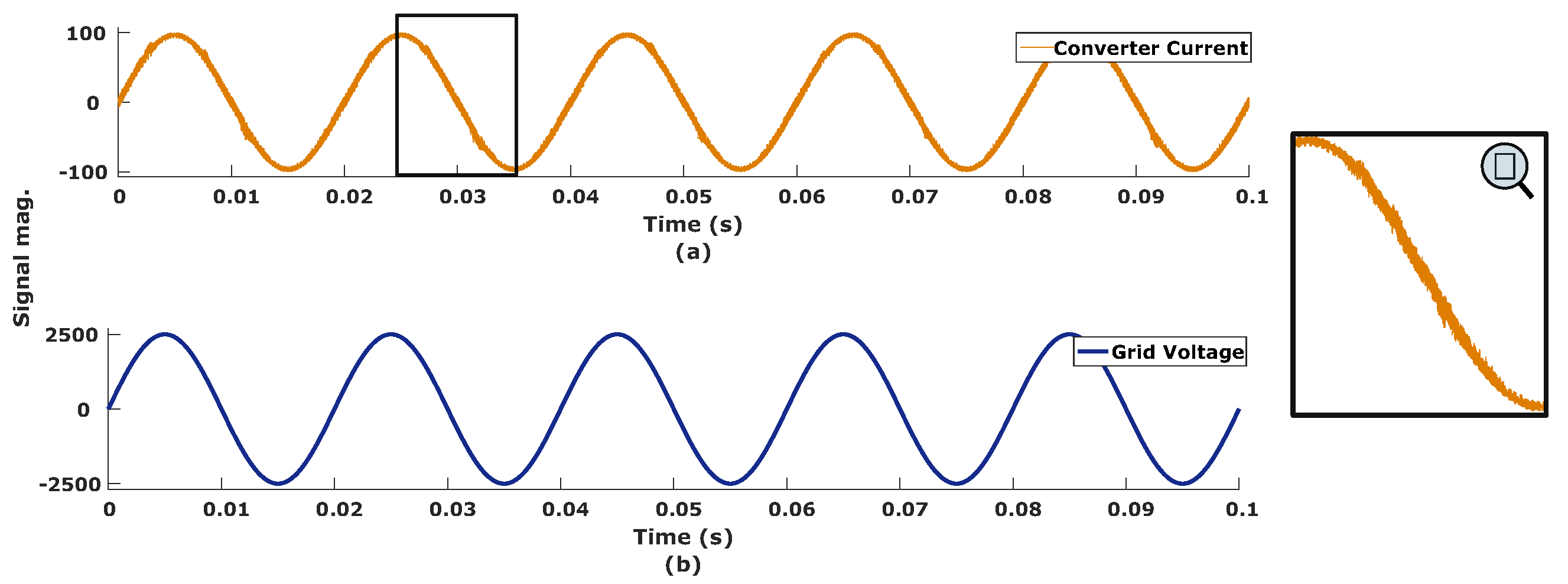
Figure 7.
Converter operating in rectifier mode (a) converter current, and (b) grid voltage.
Figure 7.
Converter operating in rectifier mode (a) converter current, and (b) grid voltage.
Figure 8.
7-L hybrid H-NPC with a cascaded converter topology (a) output voltage, and (b) harmonic spectrum of output voltage.
Figure 8.
7-L hybrid H-NPC with a cascaded converter topology (a) output voltage, and (b) harmonic spectrum of output voltage.
Figure 9.
Converter operating in rectifier mode (a) converter current, and (b) grid voltage.
Figure 9.
Converter operating in rectifier mode (a) converter current, and (b) grid voltage.
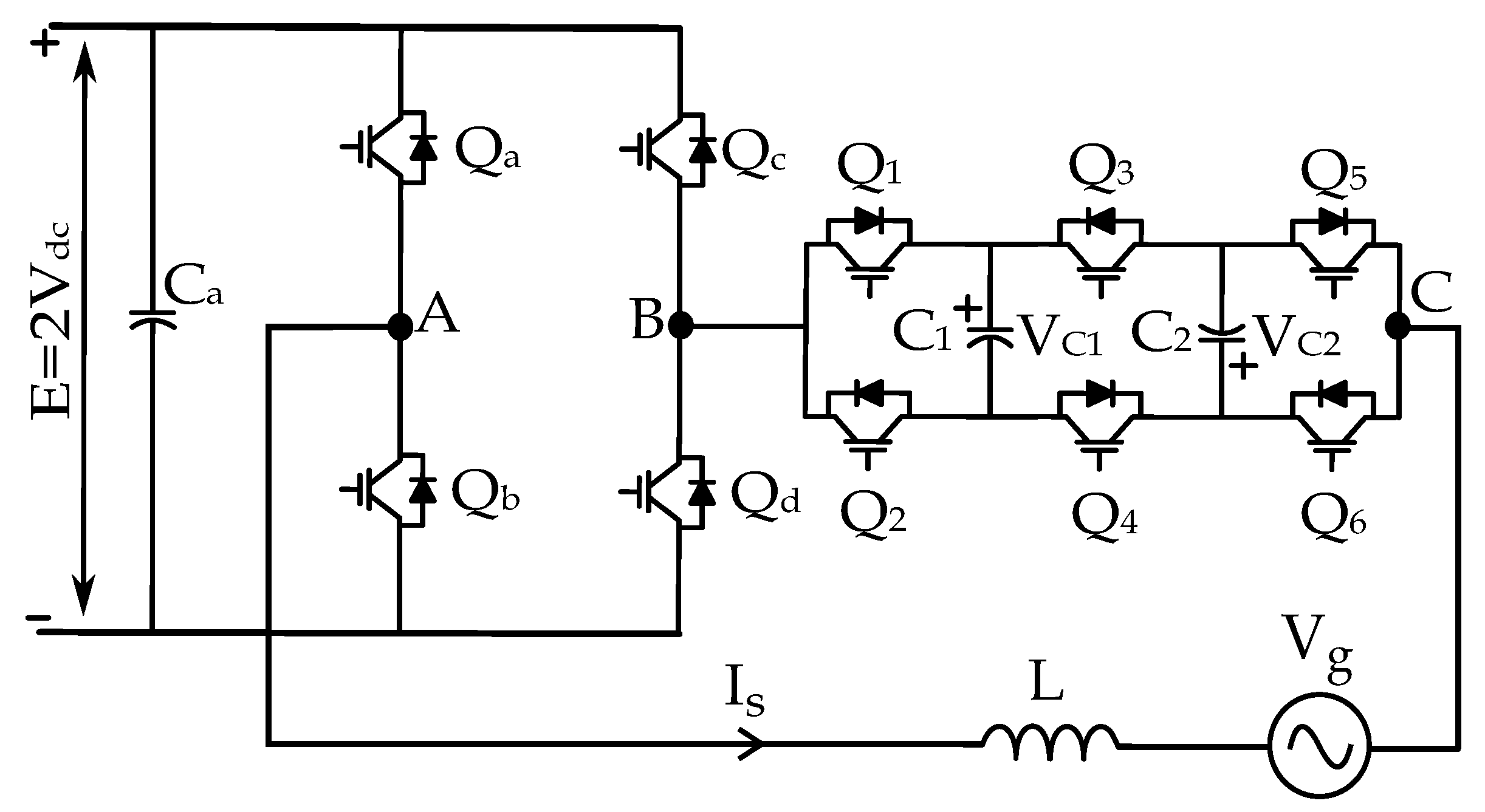
Figure 10.
Proposed AHMMC converter topology.
Figure 10.
Proposed AHMMC converter topology.
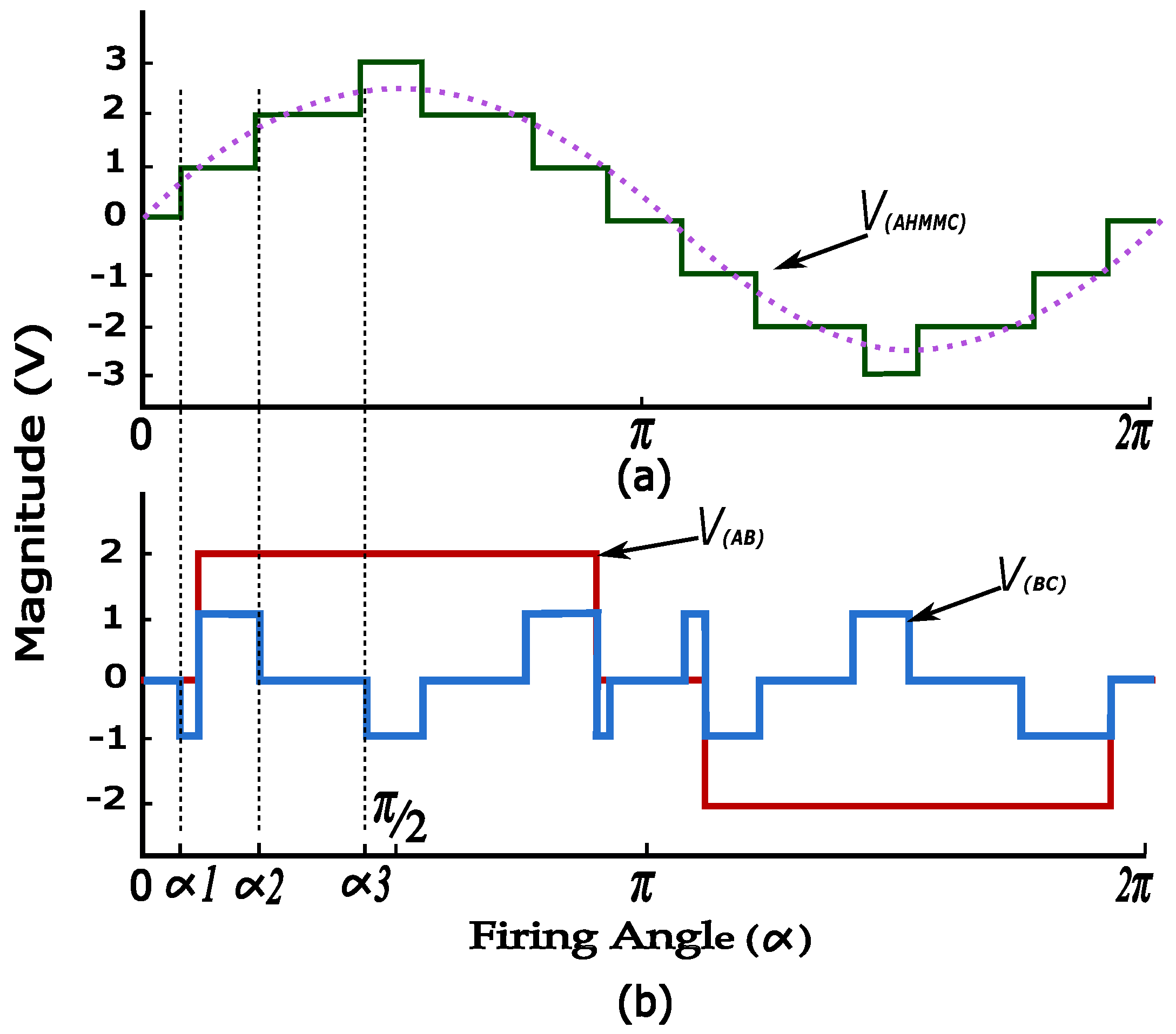
Figure 11.
AHMMC operation mode (a) AHMM output voltage, and (b) H-bridge output voltage and FCCM output voltage .
Figure 11.
AHMMC operation mode (a) AHMM output voltage, and (b) H-bridge output voltage and FCCM output voltage .
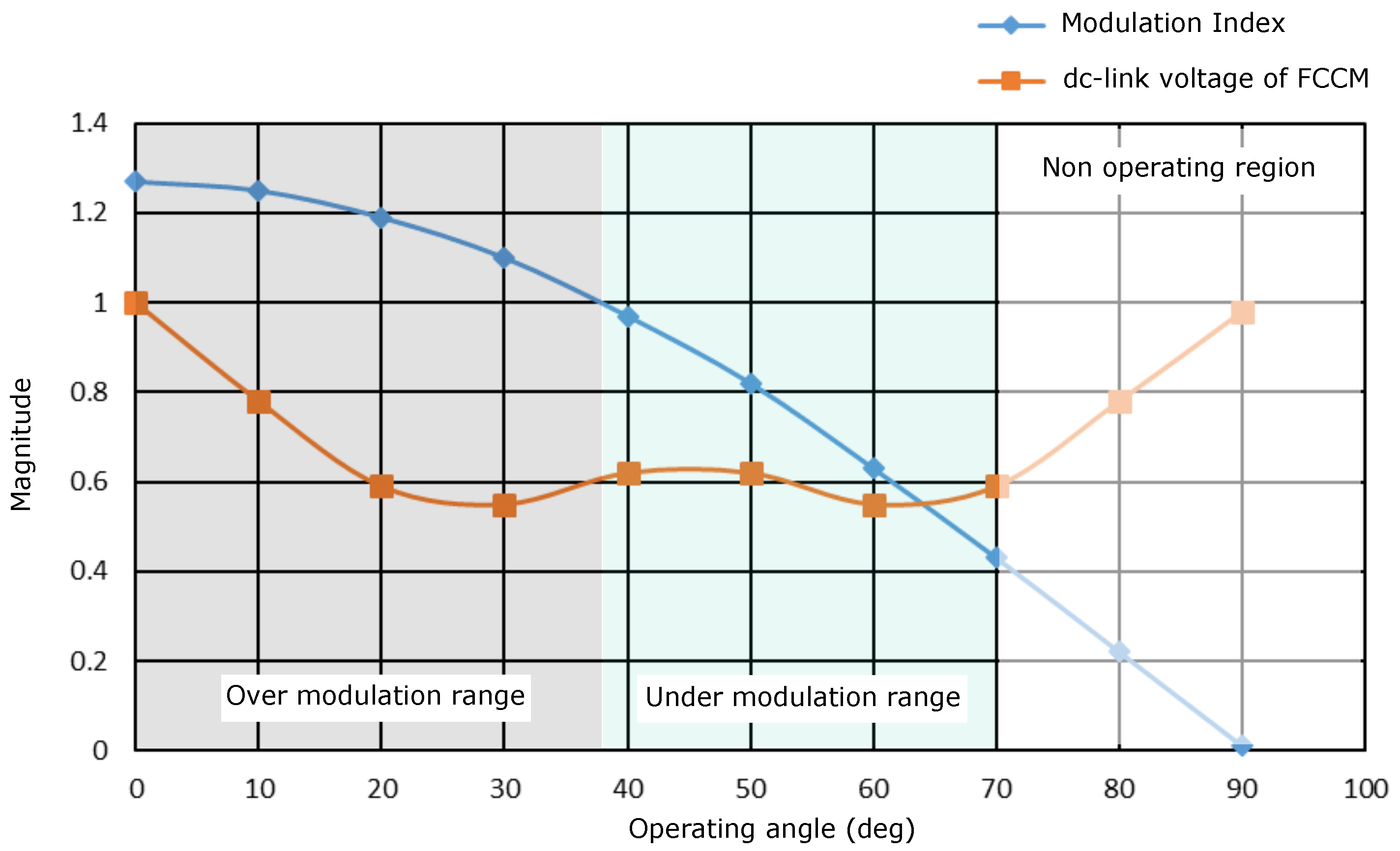
Figure 12.
Modulation index versus dc-link voltage of FCCM.
Figure 12.
Modulation index versus dc-link voltage of FCCM.
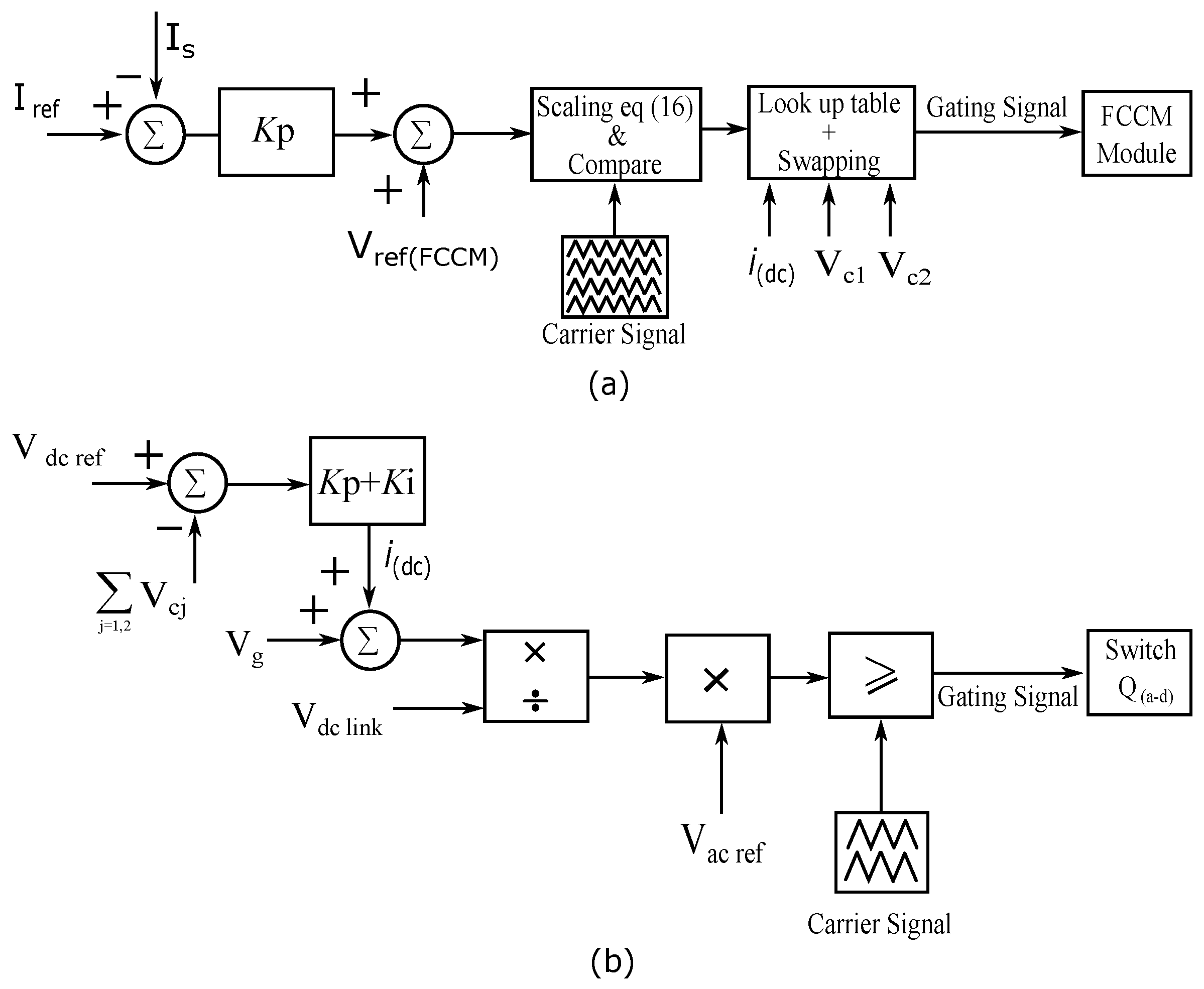
Figure 13.
Corrective control scheme (a) current control loop, and (b) voltage control loop.
Figure 13.
Corrective control scheme (a) current control loop, and (b) voltage control loop.
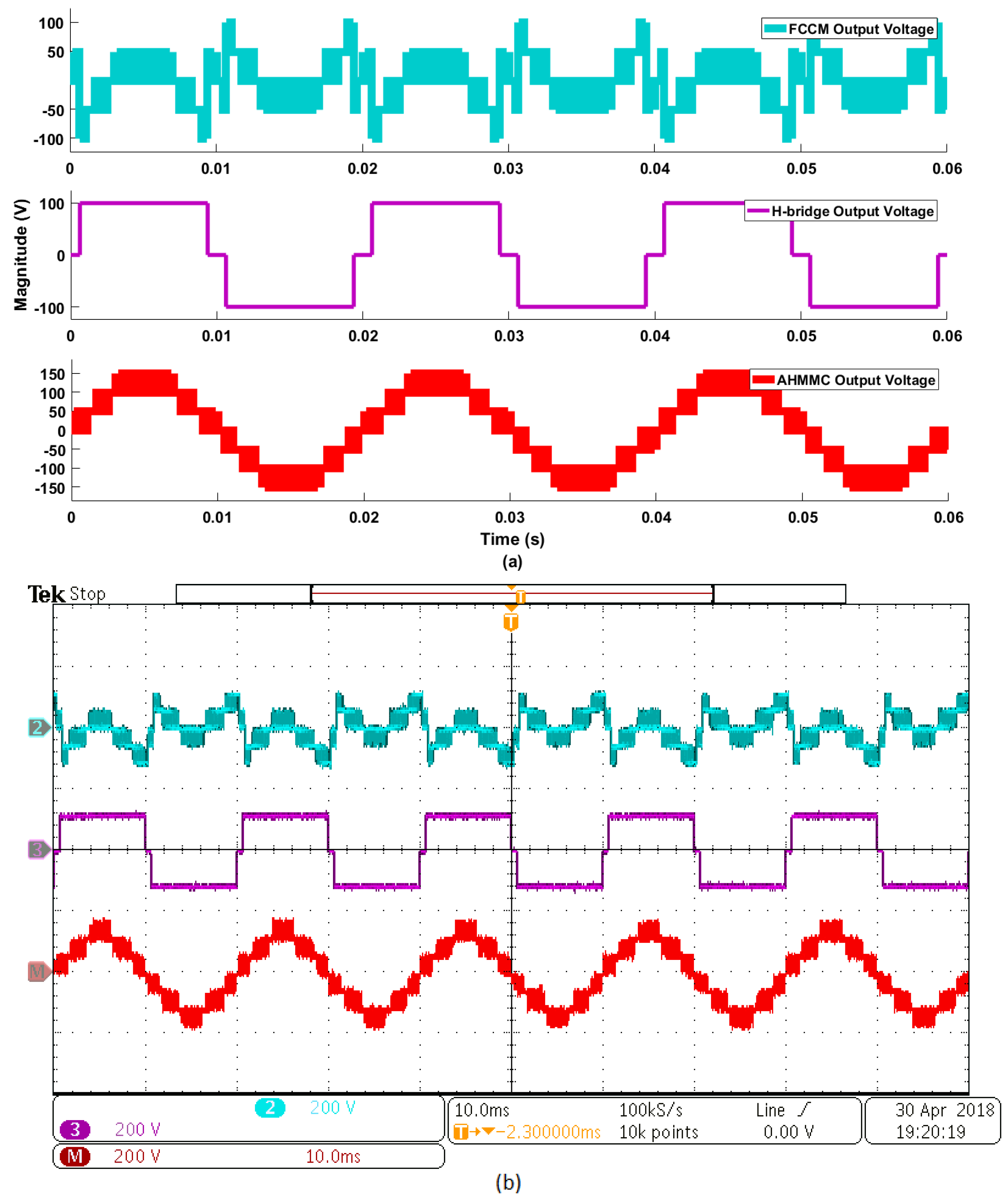
Figure 14.
AHMMC converter output at m = 1.26, (a) simulation validation, and (b) experimental validation, traces channels 2 and 3 (200 V/div).
Figure 14.
AHMMC converter output at m = 1.26, (a) simulation validation, and (b) experimental validation, traces channels 2 and 3 (200 V/div).
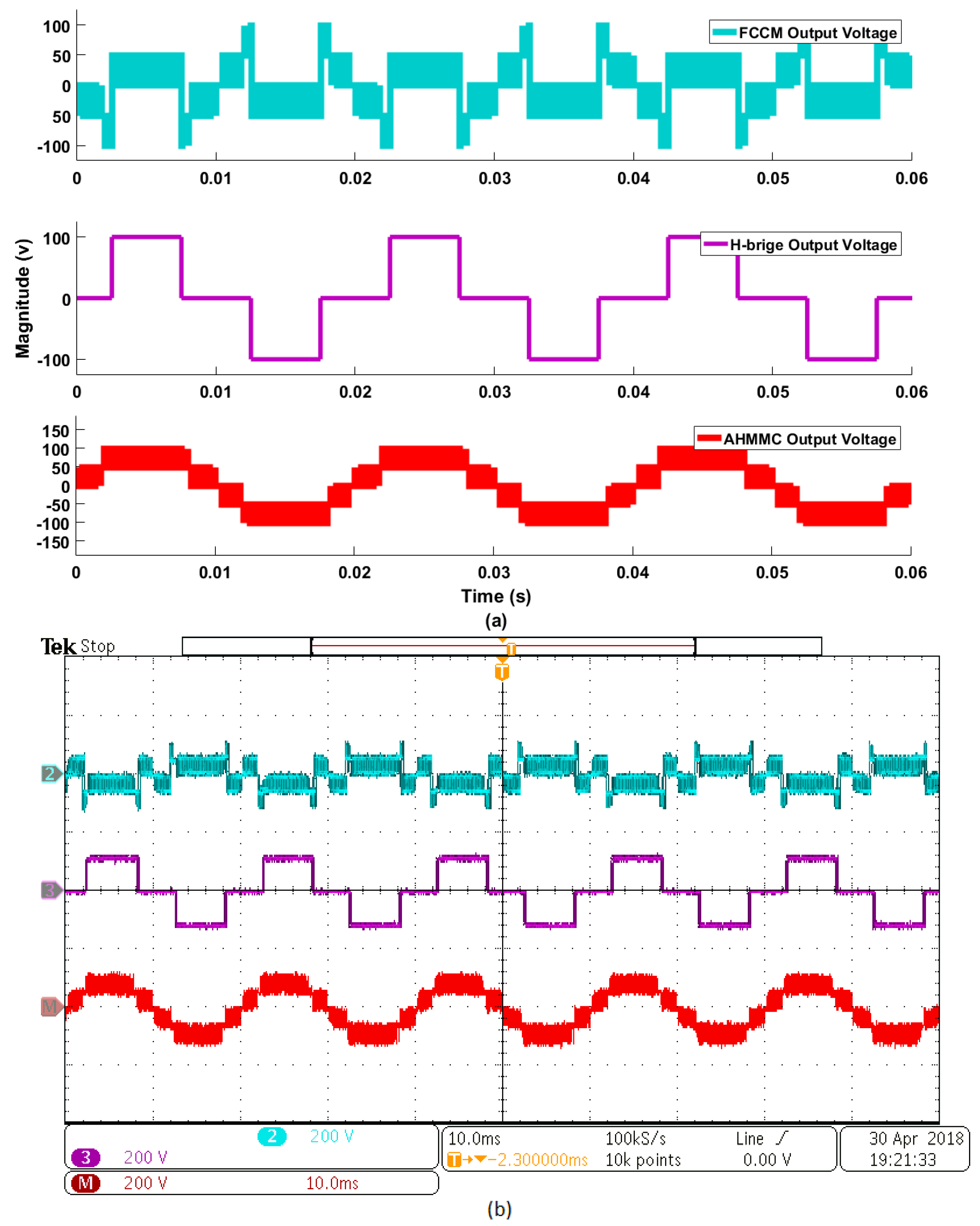
Figure 15.
AHMMC converter output at m = 0.89, (a) simulation validation, and (b) experimental validation, traces chanels 2 and 3 (200 V/div).
Figure 15.
AHMMC converter output at m = 0.89, (a) simulation validation, and (b) experimental validation, traces chanels 2 and 3 (200 V/div).
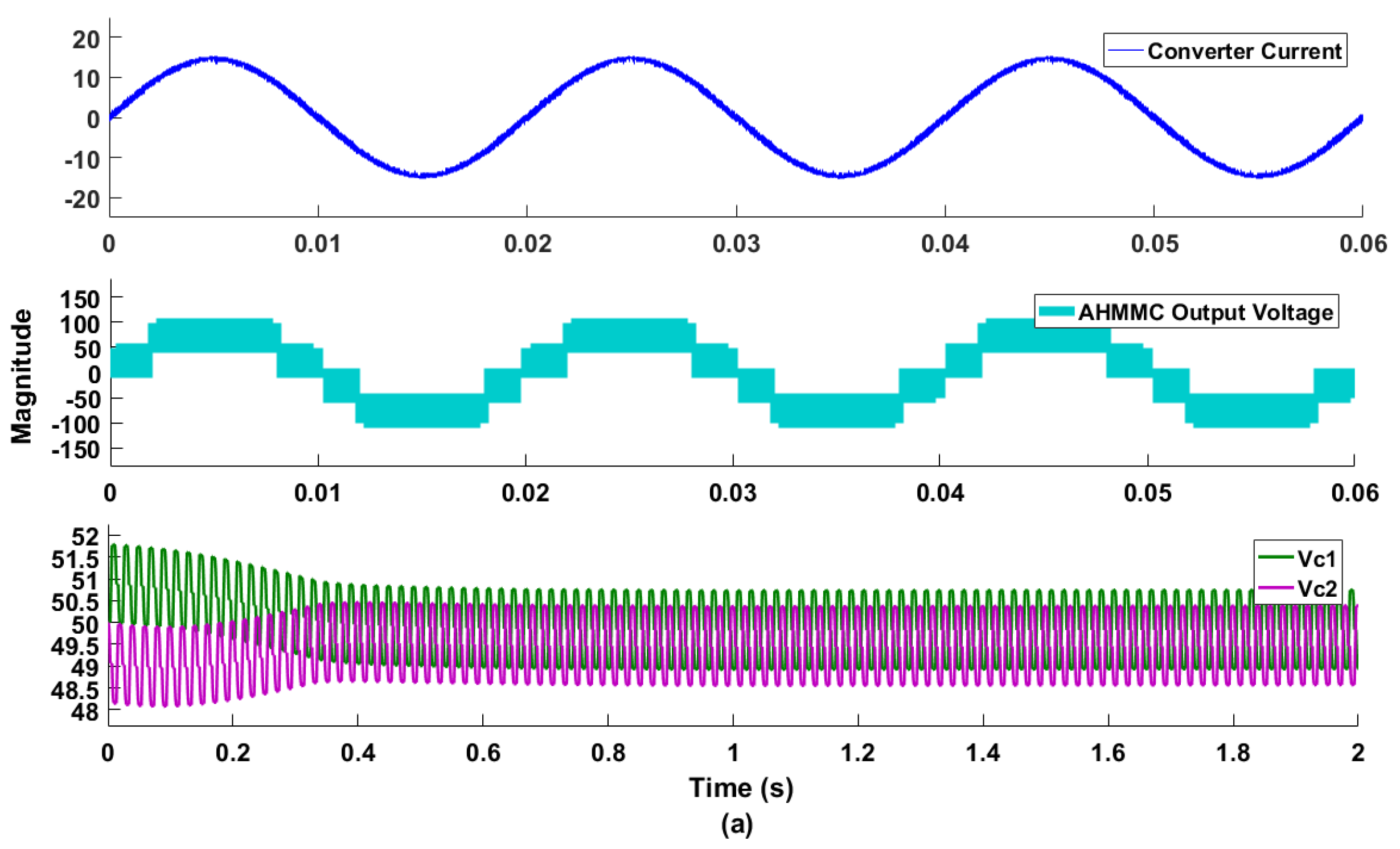
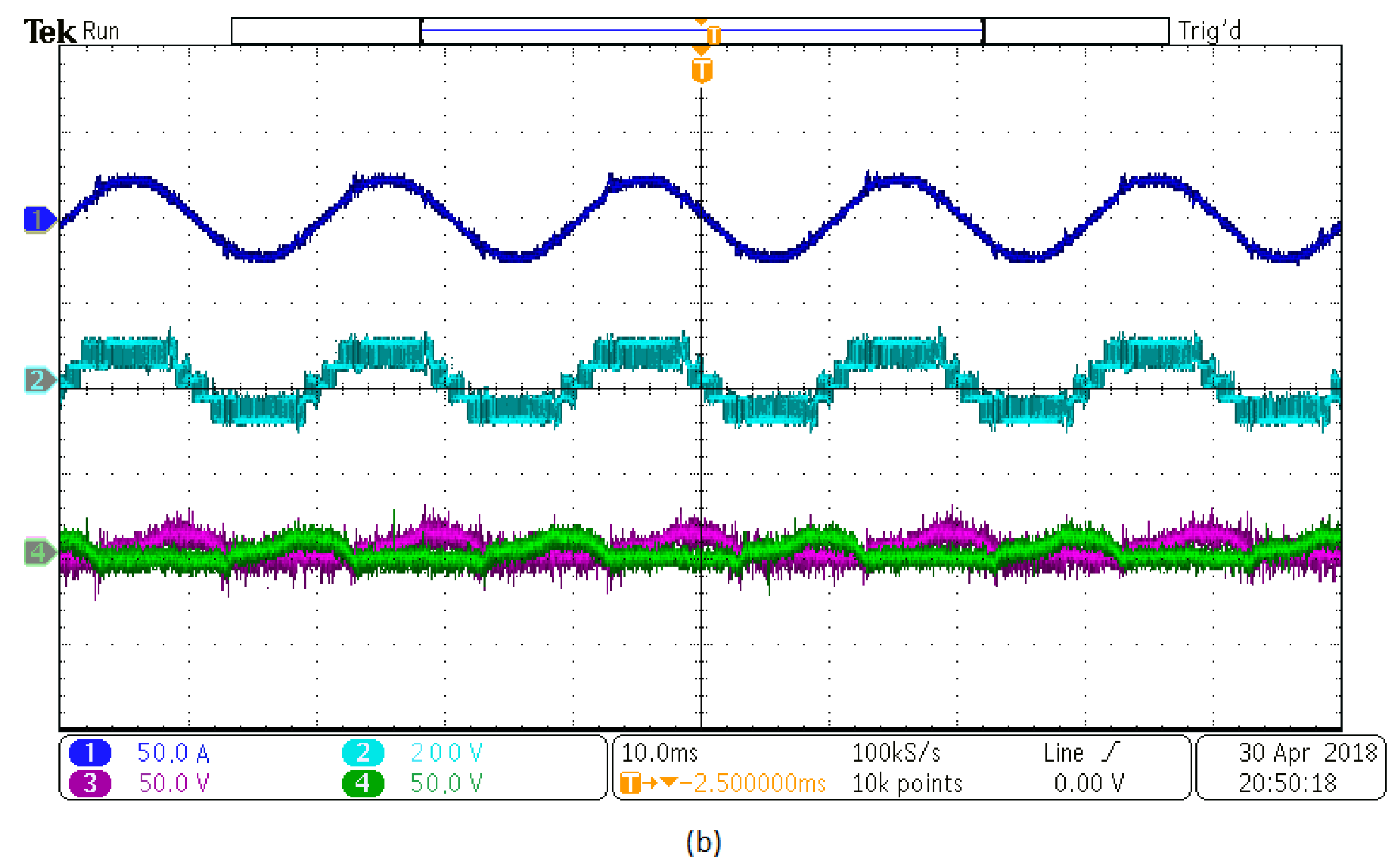
Figure 16.
AHMMC converter output, (a) simulation validation of capacitor voltage balancing togather with a unity power factor, and (b) experimental validation, traces channels 1, 3, 4 (50 V/div), and 2 (200 V/div).
Figure 16.
AHMMC converter output, (a) simulation validation of capacitor voltage balancing togather with a unity power factor, and (b) experimental validation, traces channels 1, 3, 4 (50 V/div), and 2 (200 V/div).
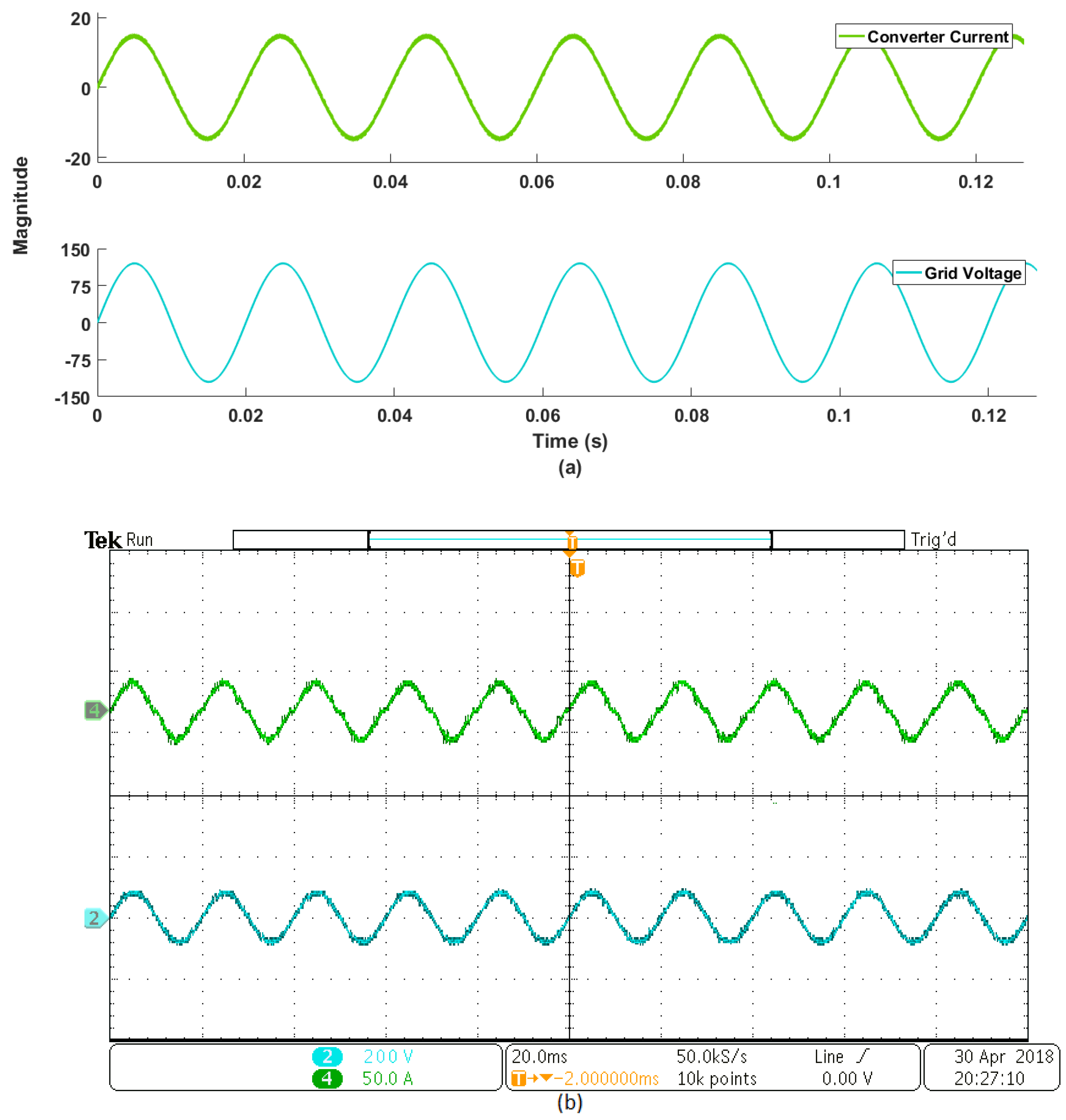
Figure 17.
Low distortion in input current, (a) simulation validation of minimum distorion in current injected to ac main, and (b) experimental validation of minimum distortion in current injected to ac main. traces channels 2 (200 V/div), and 4 (50 A/div).
Figure 17.
Low distortion in input current, (a) simulation validation of minimum distorion in current injected to ac main, and (b) experimental validation of minimum distortion in current injected to ac main. traces channels 2 (200 V/div), and 4 (50 A/div).
Figure 18.
Experimental setup.
Figure 18.
Experimental setup.
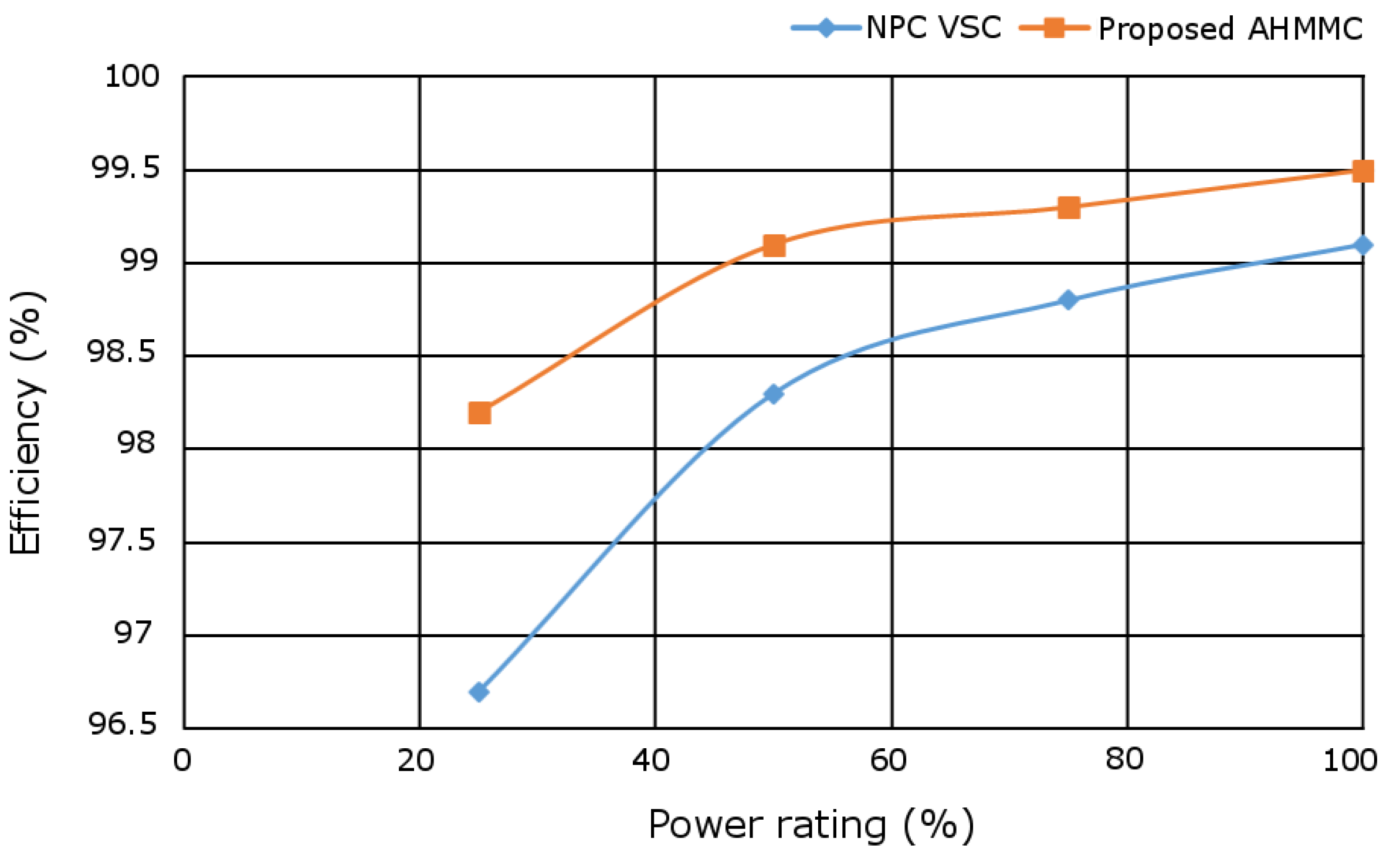
Figure 19.
Converter’s efficency.
Figure 19.
Converter’s efficency.
Table 1.
Simulation Parameters of NPC Converter.
Table 1.
Simulation Parameters of NPC Converter.
| Parameters | Value |
|---|
| Grid Voltage | 1750 V (rms) |
| DC bus Voltage | 3000 V |
| DC link Capacitor | 1500 V |
| Converter Current | 70 Amp (rms) |
| L | 0.6 mH |
| Modulation Depth | 1 |
| 2 kHz |
Table 2.
Simulation parameters of Hybrid H-NPC converter.
Table 2.
Simulation parameters of Hybrid H-NPC converter.
| Parameters | Value |
|---|
| Grid Voltage | 1750 V (rms) |
| DC bus Voltage | 3000 V |
| DC link Capacitor | 1500 V |
| Converter Current | 70 Amp (rms) |
| L | 0.6 mH |
| Modulation Depth | 1.06 |
| H-NPC converter | 350 Hz |
| H-Bridge cell | 2 kHz |
| Cascaded module converter | 2 kHz |
Table 3.
Switching modes of FCCM module.
Table 3.
Switching modes of FCCM module.
| Modes | Switching States | Capacitor | Capacitor | FCCM Output Voltage |
|---|
| - | | | | | | |
|---|
| Table (a) when > 0 |
| 1 | 1 | 1 | 1 | discharge | discharge | |
| 2 | 1 | 1 | 0 | discharge | by pass | |
| 3 | 0 | 1 | 0 | by pass | by pass | 0 |
| 4 | 1 | 0 | 0 | by pass | charge | |
| 5 | 0 | 0 | 0 | charge | charge | |
| Table (b) when > 0 |
| 1 | 1 | 1 | 1 | discharge | discharge | |
| 2 | 0 | 1 | 1 | by pass | discharge | |
| 3 | 1 | 0 | 1 | by pass | by pass | 0 |
| 4 | 0 | 0 | 1 | charge | by pass | |
| 5 | 0 | 0 | 0 | charge | charge | |
Table 4.
AHMMC Converter Output Voltage.
Table 4.
AHMMC Converter Output Voltage.
| Angle | | | |
|---|
| 0 | 0 | 0 |
| 0 | | |
| | | |
| | 0 | |
| | | |
Table 5.
PWM operating conditions.
Table 5.
PWM operating conditions.
| Operating Condition | | | | |
|---|
| is a lower capacitor |
| 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| is a lower capacitor |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 1 |
Table 6.
System parameters of AHMMC.
Table 6.
System parameters of AHMMC.
| Parameter | Value |
|---|
| Inductance | 0.6 mH |
| DC-link Capacitor | 20 F |
| FCCM Switching Frequency | 2 kHz |
| Capacitor Voltage | 50 |
| Grid Voltage | 110 (rms) |
| Current | 14 A (rms) |
| DC-bus Voltage | 100 V |
Table 7.
Current THD of AHMMC operating at differnt power rating.
Table 7.
Current THD of AHMMC operating at differnt power rating.
| Current THD | Power Rating |
|---|
| | 25% | 50% | 100% |
|---|
| Simulation THD | 6.55 | 3.31 | 1.66 |
| Experiment THD | 7.95 | 4.87 | 2.98 |
Table 8.
Component count of converter.
Table 8.
Component count of converter.
| Converter | Components Count |
|---|
| | Active Switches | Diode | Dc-Link Capacitor |
|---|
| NPC | 8 | 4 | 2 |
| HNPC with H-bridge | 10 | 2 | 3 |
| HNPC with cascaded module | 12 | 2 | 4 |
| Proposed AHMMC converter | 10 | - | 3 |
Table 9.
Converter parameter for efficiency comparison.
Table 9.
Converter parameter for efficiency comparison.
| Parameter | Value | |
|---|
| DC bus voltage | | 3 kV | | |
| Grid voltage | | 1.75 kV (rms) | | |
| Modulation index | | Maximum modulation index | | |
| Reactor inductance | | 0.6 mH | | |
| | | | Rise time | Fall time |
| IGBT | 1.7 kV | 2.45 V | 0.29 s | 0.29 s |
| IGBT | 4.5 kV | 2.84 V | 0.35 s | 0.35 s |
Table 10.
Voltage stress on semiconductor devices.
Table 10.
Voltage stress on semiconductor devices.
| Semiconductor Devices | Voltage Stress |
|---|
| | Active Switches | Diode |
|---|
| Half bridge NPC | E/2 | E/2 |
| Half bridge | E/2 | – |
| Cascaded module centre cell | E | – |
| Cascaded module outer cell | E/2 | – |
| Half Bridge (AHMMC) | E | – |
| Cascaded module centre cell | E | – |
| Cascaded module outer cell | E/2 | – |
Table 11.
Converters current THD operating at different power ratings.
Table 11.
Converters current THD operating at different power ratings.
| Converter | Power Rating |
|---|
| | 25% | 50% | 100% |
|---|
| NPC | 5.31 | 2.83 | 1.38 |
| HNPC with H-bridge | 6.71 | 3.43 | 1.73 |
| HNPC with cascaded module | 6.59 | 3.39 | 1.71 |
| Proposed AHMMC | 6.55 | 3.31 | 1.66 |