1. Introduction
Antenna array is a key technology component in various communication systems such as radar, radio-astronomy, remote sensing, satellite communications, and next-generation (fifth generation, 5G) wireless communications [
1], where a very large number (in the hundreds) of radiating elements are particularly used to meet the increasing demands of high radiation performance and reconfigurability [
2]. Conversely, the higher the number of radiating elements in the beam-forming configuration, the higher the probability of failed element(s) will be. This causes abrupt field variations across the aperture of the array, and distortion in the radiation features (e.g., beamwidth, peak sidelobe, and boresight). Therefore, the availability of reliable and effective diagnosis tools for large arrays remains an asset, because manual dismantling and replacement operations consume excessive time and cost, and are even unfeasible in satellite-borne installations. Currently, failure identification in antenna arrays is a theoretical and practical important research domain. Detection of faulty elements in antenna arrays is of great interest in both military and civilian markets. Upcoming technologies adopt active or passive antenna arrays with a large number of elements [
1,
2,
3,
4,
5]. For instance, millimeter-wave transceivers implement multiple-input multiple-output (MIMO) features and beamforming for future 5G applications, as shown in
Figure 1. The block diagram shows the location of the AWMF-0108 in a 5G MIMO system [
6]. The integrated circuit (IC) contents in the circle are the gain and phase control blocks with amplification and RX/TX switching. The first industrial and commercial millimeter-wave quad-core IC transceiver for 5G applications is the AWMF-0108 [
6]. Many compactable antennas were designed for that purpose. Thus, some communication systems will evolve for 5G technology, even before full deployment, which is not expected until 2020. The large number of elements in the planar antenna required by the transceiver must function optimally. Failure in the element(s) causes far-field degradation of antenna systems. The detection of failed elements from field measurements taken from a suitable observation point is very important to re-calibrate the feeding network and to reinstall the needed radiation characteristics by reconfiguring the excitations of the healthy elements [
1,
3]. Testing of antennas is then a necessity when a certain number of elements exhibit fault. Therefore, the fast diagnosis of complex antenna structures is always a fundamental need.
Far-field measurements are a very powerful approach for antenna array testing. The measurement data are sequentially presented for probable failure identification in the array under test (AUT). The matrix method algorithm (MMA) and back propagation algorithm (BPA) are the most commonly used mechanisms to detect the number and corresponding positions of defective elements using a reference antenna (healthy) and the AUT (defective). BPA [
7] was established using the Fourier relationship between radiated far-field and the field situated on the array aperture, and it is applicable to planar antenna arrays. A generalized form of BPA is MMA [
8,
9]. MMA uses linear algebra standard tools to stabilize the inversion matrix, which relates the array aperture field to radiated far-field. However, MMA and BPA demand a large number of measurements, thus causing long post-processing of large arrays. One approach to mitigate the problem is the use of a priori knowledge of the array without failure; consequently, only the defective array elements are identified. The modeled diagnostic problem is solved by employing available customs whose computation time is a little longer than standard methodologies. At this point, it is evident that the total time taken to get the antenna array diagnosed greatly depends on measurement time, with post-processing times having a higher order of magnitude. This is why sparse recovery-based methods require fewer measurement numbers and provide faster antenna array diagnosis.
Recently, compressive sensing emerged rapidly as a potential technique for solving sparse recovery problems [
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20]. Within this context, the appropriateness of compressive sensing in addressing the array diagnosis problem was examined in References [
3,
12,
14,
16,
18,
21]. Evidently, faulty element distribution in array configurations in practice were found to be highly sparse because it accounts for small non-null entries in the excitation vector of the transmit/receive modules. Beginning from that hypothesis,
-norm minimization mechanism was applied successfully to detect failures in planar arrays using a small number of near-field [
9] or far-field [
14] measurements. Conversely, deterministic compressive sparse techniques require a “measurement matrix” to comply with the restricted isometric property (RIP) condition, for which the estimation of large matrices remains an open challenge [
3,
14,
21]. An alternative is the probabilistic compressive sensing approach reported in Reference [
21] to diagnose linear arrays from far-field measurements. However, most of these techniques were not tested experimentally.
In this work, the problem of antenna element excitation level was not examined; however, we estimated field distribution on the array aperture. This helps us identify the modifications of aperture field distribution as a result of factors that cannot be quantified by simple failure of elements, such as different reflections of the array and its feed. The problem faced in getting more information about the AUT is the larger number of unknowns. However, in sparse recovery methods, the required number of measurements increases slowly and logarithmically with the number of unknowns [
10,
11,
12,
13]. Hence, the field reconstruction scheme benefits more in sparse recovery-based mechanisms. Different sparse recovery algorithms used to conduct antenna array diagnosis were unveiled [
14] and compared to the traditional BPA and MMA. In particular, total variation (TV) norm, mixed
norm, and minimization of the
norm were used to proffer solutions to the resulting inversion issues. From the field reconstructed on the antenna aperture, Fuchs et al. [
20] acquired a good antenna diagnosis. The approach was applied to far-field simulation data generated from a 100-element antenna array. The performance of the diagnosis was evaluated and compared to the two standard techniques (BPA and MMA) under different conditions. The approaches were also applied to far-field measurement data of an antenna array with failure to justify the practical applicability of the proposed schemes. Although there were many more works on sparse recovery methods in applied electromagnetics and microwaves involving the diagnosis processes of antenna arrays [
13,
14], experimental data, which are fundamental for testing any procedure, were reported in few of them.
In References [
15,
16,
17,
18,
19,
20], differential scenarios with sparse recovery algorithms were employed to perform antenna diagnosis and retrieve element excitations. Reference [
21] proposed a joint scheme for adaptive diagnosis of antenna arrays using communication signal fusion (radar-communication scheme) and the echoes of probe signals received at the same antenna. This method equally solved the antenna diagnosis problem at low signal-to-noise ratios (SNRs) to ensure optimal performance of smart sensors in wireless sensor networks. Also, Reference [
22] attempted array diagnosis in millimeter waves using compressive sensing. This work considered both full and partial blockage, which occurs from a plethora of particles (such as ice, water droplets, salt, and dirt) and the technique jointly computed the locations of the blocked elements, and the induced phase-shifts and induced attenuation provided the prior knowledge of the angles of departure/arrival. Reference [
23] proposed a deterministic sampling strategy for failure detection in uniform linear arrays via compressed sensing or a sparse recovery approach. This is an extension of the Weyl formula which is basically used for prime numbers. The strategy obtained was good for nonprime number (i.e., valid for any number of array elements). This sampling approach is good for sparse electromagnetic (EM) problems encompassing Fourier matrices. Reference [
24] gives a review of different capacities of sparse recovery by analyzing how compressive sensing can be applied to antenna array synthesis, diagnosis, and processing. Illustrations of a set of applicative examples were given, including direction-of-arrival estimation, along with present challenges and current trends in compressive sensing applications to the solution of innovative and traditional antenna array challenges. In general, compressive sensing generates few unknown numbers; however, it needs a comprehensive array model with exact knowledge of the radiating element patterns to produce useful results. The technique is sparse with respect to the whole array structure, and requires a priori information to recast it as the function of minimization of
norm. However, these techniques are applicable only if the relationships between the data and the unknowns satisfy the restricted isometry property (RIP). To overcome this challenge, the Bayesian compressive sensing (BCS) approach is adopted. This technique was explored in many electromagnetic problems, such as antenna design and synthesis [
25,
26], microwave imaging [
27,
28,
29,
30], and direction-of-arrival estimation [
31,
32,
33]. It is employed in this paper to estimate the number, magnitude, and location of failures in antenna arrays from far-field measurements. The BCS approach was attempted to diagnose large linear arrays [
11], and more recently, planar array configurations [
34]; however, no experimental validation was reported. Hence, there is a need for a more reliable procedure tested experimentally and via simulation, because experiments are fundamental tests of any given procedure.
Specifically, this work is an extension of that described in References [
15,
16]. The BCS method is applied to both the simulated and measured far-field data of a millimeter-wave 100-element microstrip patch antenna array in which failures were added intentionally. A new regularization technique was unveiled and applied to field distribution in order to enhance the efficiency and reliability of antenna array diagnosis. The proposed BCS-based approach is a better choice due to its fast nature and robustness under different noise conditions. The key contributions of this paper are summarized as follows:
The BCS technique was applied to diagnose a millimeter-wave planar array, and the result was compared with other approaches reported in the literature.
The procedure shows high effectiveness and reliability with fewer measurement points compared to the other methods, and is highly robust to additive noisy data. This was validated experimentally and via simulations.
However, some boundary conditions were observed. The BCS-based approach detects diagnostic problems with few measurements, provided prior knowledge of the reference array radiation pattern, and the number of faults is relatively smaller than the array size. The remainder of this paper is arranged as follows:
Section 2 contains the problem formulation of antenna array diagnosis.
Section 3 presents compressed sparse recovery methods. Resolution via the BCS-based approach is given in
Section 4. The numerical simulations are presented in
Section 5. Diagnoses from experimental data are presented and discussed in
Section 6. Finally, some conclusions are drawn in
Section 7.
2. Antenna Array Diagnosis Problem Formulation
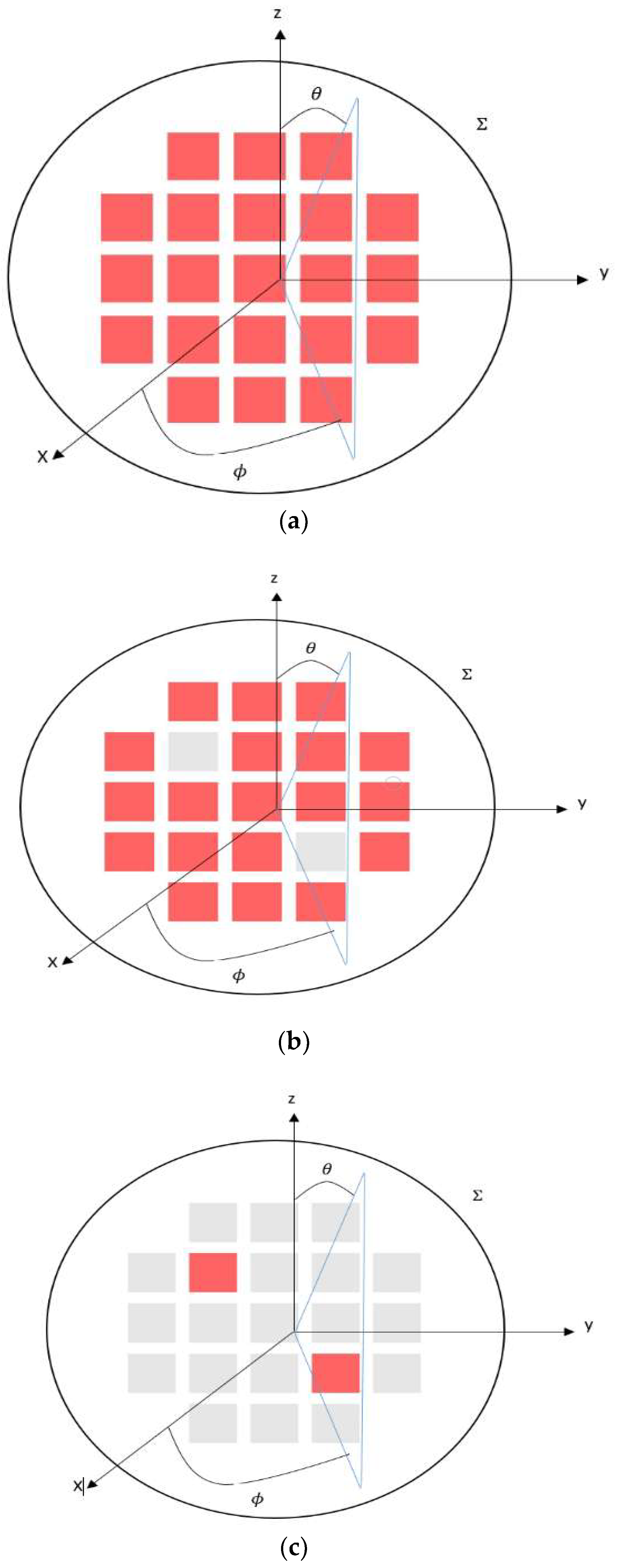
Consider an antenna array in space (
Figure 2a). The antenna radiated far-field is usually quantified by phase and amplitude. The AUT is depicted in
Figure 2b. All the parameters associated with the AUT are marked with superscript “
u”. Specifically,
is the tangential field situated on the antenna aperture, i.e.,
where
and
are the
x and
y planes of the aperture’s electric field, respectively. Far-field
is the measured field on part of the hemispherical surface
at radius
r from the phase center of the AUT, and
, where
D is the diameter. Also, the amplitude and phase of a reference array (RA; array without failures) shown in
Figure 2b are assumed to be available. Associated quantities are marked with superscript “o”.
is the field on the aperture
of the reference array (RA) and
represents the far-field radiation. For the differential antenna (DA) shown in
Figure 2c, the tangential distribution
on the aperture
is equal to the difference between the field distributions of the reference array and the antenna under test, and the corresponding far-field
is expressed as the difference between the fields of reference array (RA) and AUT as
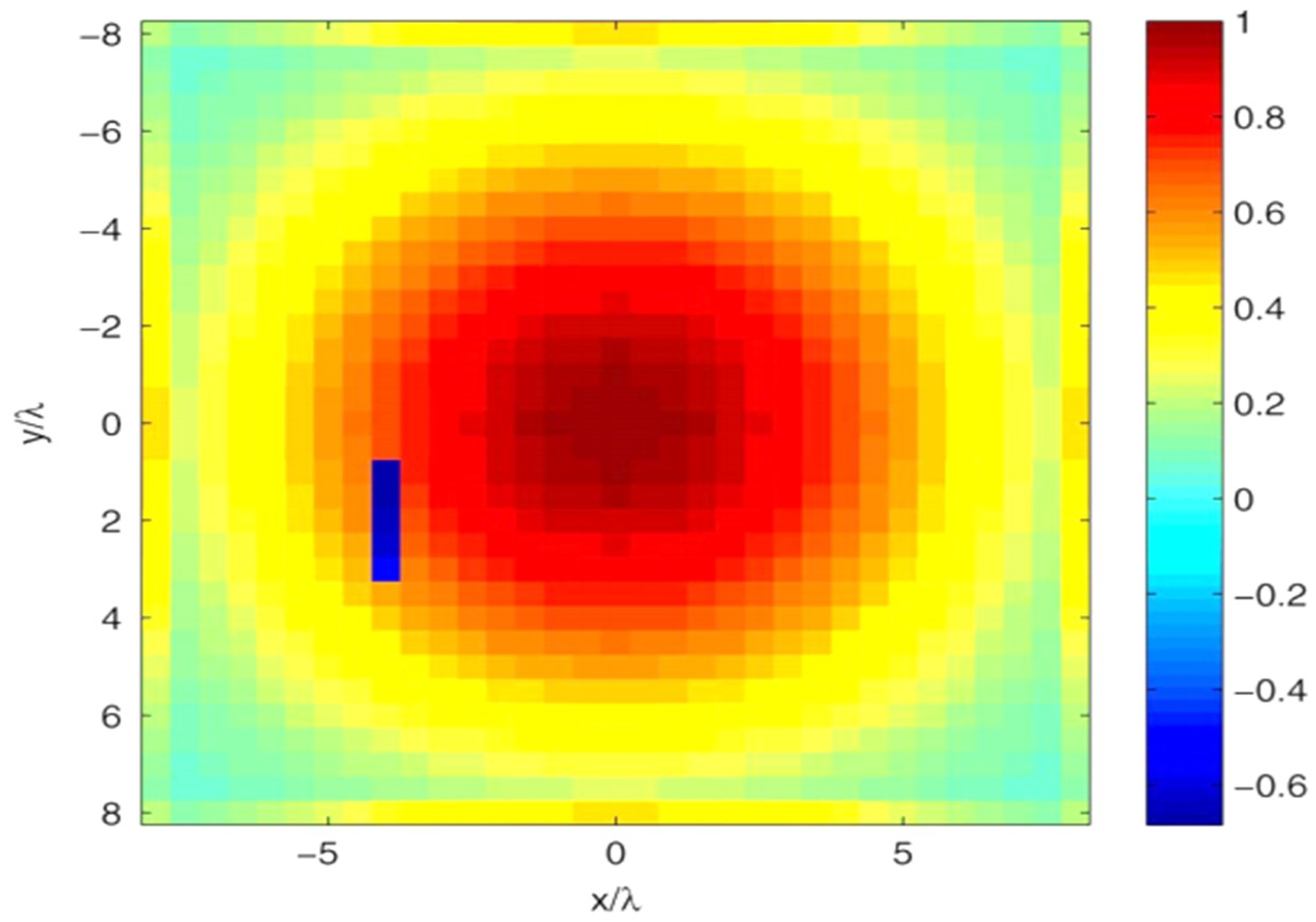
The differential antenna gives a resulting problem in which only the corresponding area to the field modification radiates as a result of failure. By visually monitoring the field distribution on the DA, the identification of faulty elements in the AUT can be observed.
2.1. Number of Far-Field Measurement Points Required
BPA and MMA approaches require a large number of measurement points. In the differential antenna, we assumed the field was localized, i.e., the unknown we wanted to retrieve was very sparse, as shown in
Figure 2c. In practice, there are a fewer number of failures than the overall elements
N. Sparse recovery algorithms estimate
x from a number of measurement points smaller than the number of measurements required by the standard mechanisms. Hence, it is possible to theoretically get a reduction in the number of measurement points. Fuch et al. [
20] demonstrated this using total variation (TV), mixed
norm, and minimization of
. However, better methods/algorithms that require fewer numbers of far-field measurement points for faster array diagnosis are still in demand.
2.2. Signal-to-Noise Ratios (SNRs)
Total variation (TV), mixed norm, and minimization of techniques are the leading compressive techniques, and they exhibit low efficiency and reliability in antenna diagnosis for low SNRs. This drawback fosters the need for a more robust diagnosis procedure in the presence of noisy data.
4. Resolution via Bayesian Compressive Sensing
For a planar antenna configuration of
N elements positioned at coordinates
,
n = 1, …,
N, with error-free excitations
,
n = 1, …,
N, beaming a familiar field
, referencing a noisy case with element failure, the estimated far-field radiation pattern of (AUT) is expressed as
where
for
l = 1, …,
L is the angular location of the
l-th angular sample, and
is the noise effect considered as Gaussian-distributed with zero mean and variance
.
,
n = 1, …,
N, is the failed excitations vector, expressed as
is the failure factor, while
is the rate of failure, and
is the weighting coefficient. From knowledge of the difference in field pattern,
, array failures can be estimated by determining the minimum
vector
which satisfies
The aim is to determine the entries of the “failure” vector
from the prior knowledge of the difference between the field samples in Equation (10) on the AUT and those of the
golden antenna with coefficients
n = 1
. Against the deterministic approaches aimed at retrieving the vector
with minimum
satisfying the condition of Equation (13),
is the
radiation measurement matrix expressed as
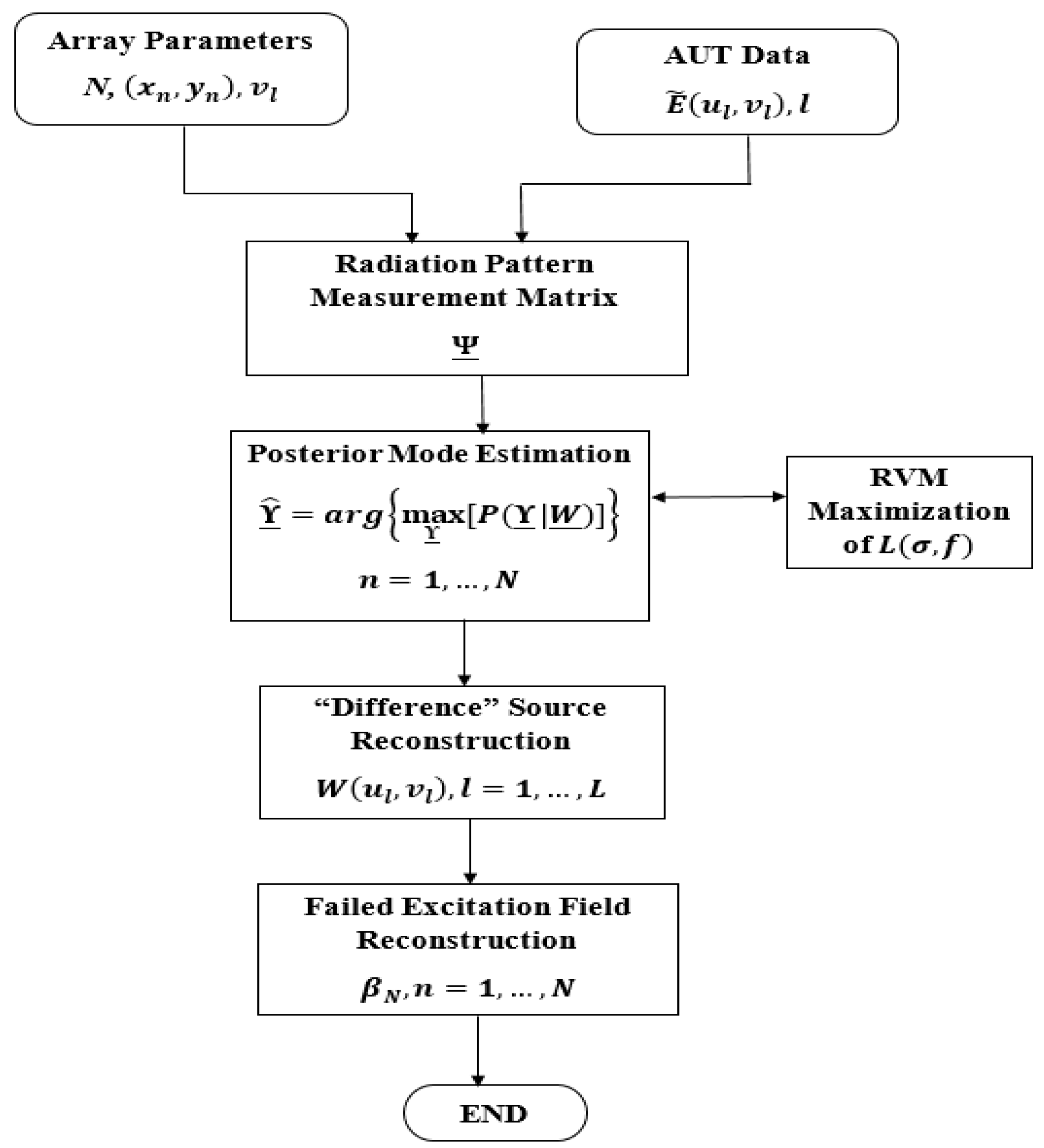
Hence, the BCS technique (summarized in
Figure 2) can be employed to determine the sparsest solution
to the problem
which gives
where
T is the transpose operator, and
and
are the figures that are used to maximize the likelihood function
Equation (11) is computed using RVM [
29], with
, where
.
The implementation of the BCS technique (as shown in
Figure 3) is summarized in Algorithm 1.
| Algorithm 1. Proposed diagnostic procedure |
- a.
Step 1—Array parameter selection and definition of problem: For each element (), accumulate the array field at N measurement points (reference antenna) and randomly sample the AUT field. Appropriate the noise variance and threshold for the maximization of . - b.
Step 2—Radiation pattern measurement matrix definition. Input the parameters of . - c.
Step 3— Posterior mode estimation. Maximize Equation (10) iteratively to estimate using the RVM procedure [ 29]. - d.
Step 4—Source difference reconstruction. Determine for l = 1, …, L. - e.
Step 5—Failed field excitation reconstruction. Determine the vector of failed excitations using Equation (11).
|
5. Simulations and Analysis
Assessing the performance of the BCS algorithm, we consider an RA with
N = 316 with Taylor taper and peak sidelobe level of −25 dB. Assuming a complete failure (
h = 0), the given percentage of failed elements is
. To determine the detection error numerically, the index of detection can be expressed as
where
and
,
n = 1, …,
N, are the real and predicted failure entries of vector
. The uniformly sampled (
k = 316 samples) far-field radiation pattern is within
(u, v) space, with the signal-to-noise ratio
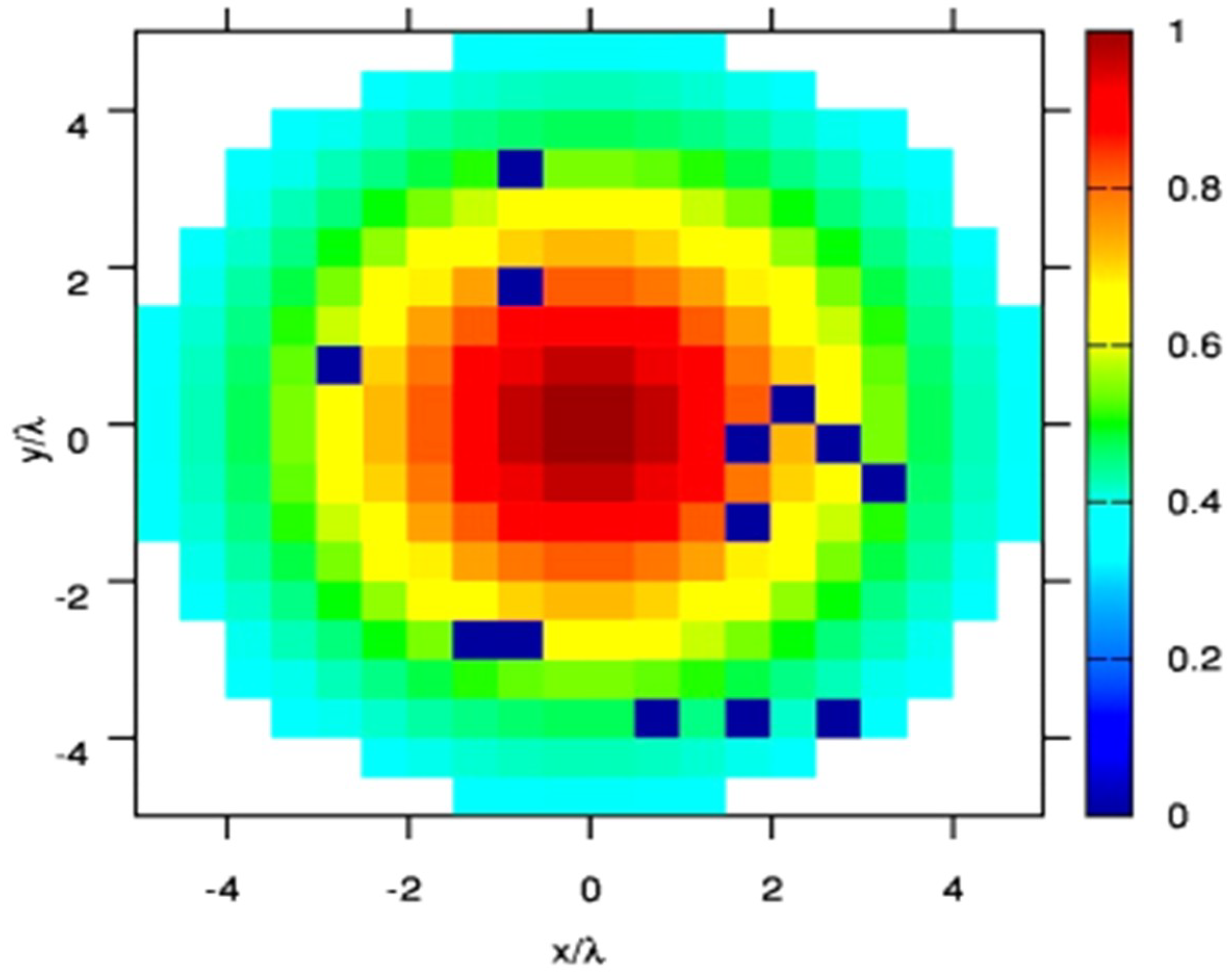
SNR = 30 dB. The configuration of the AUT is presented in
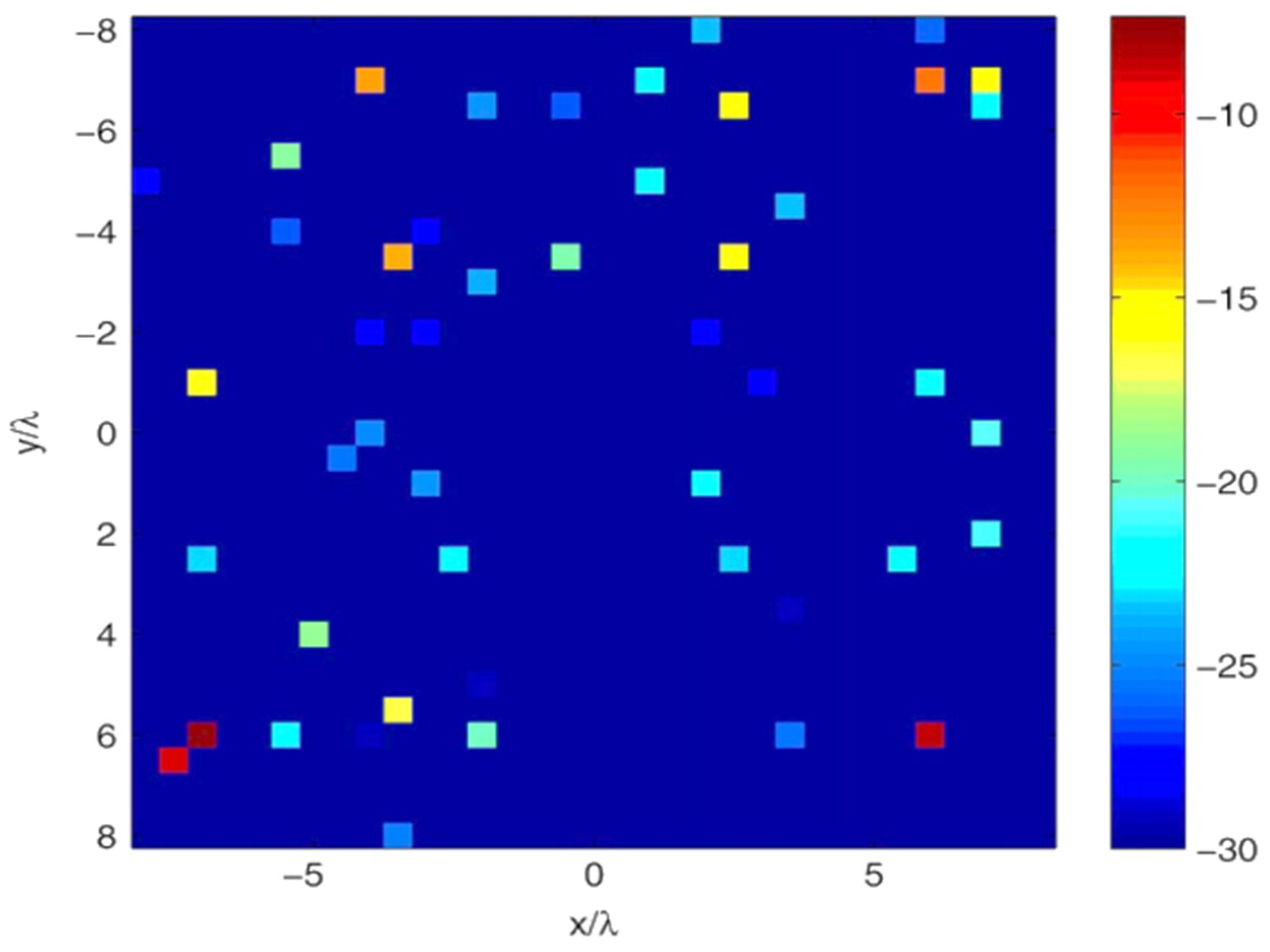
Figure 4, while the excitation coefficients
of the failed array are equally shown.
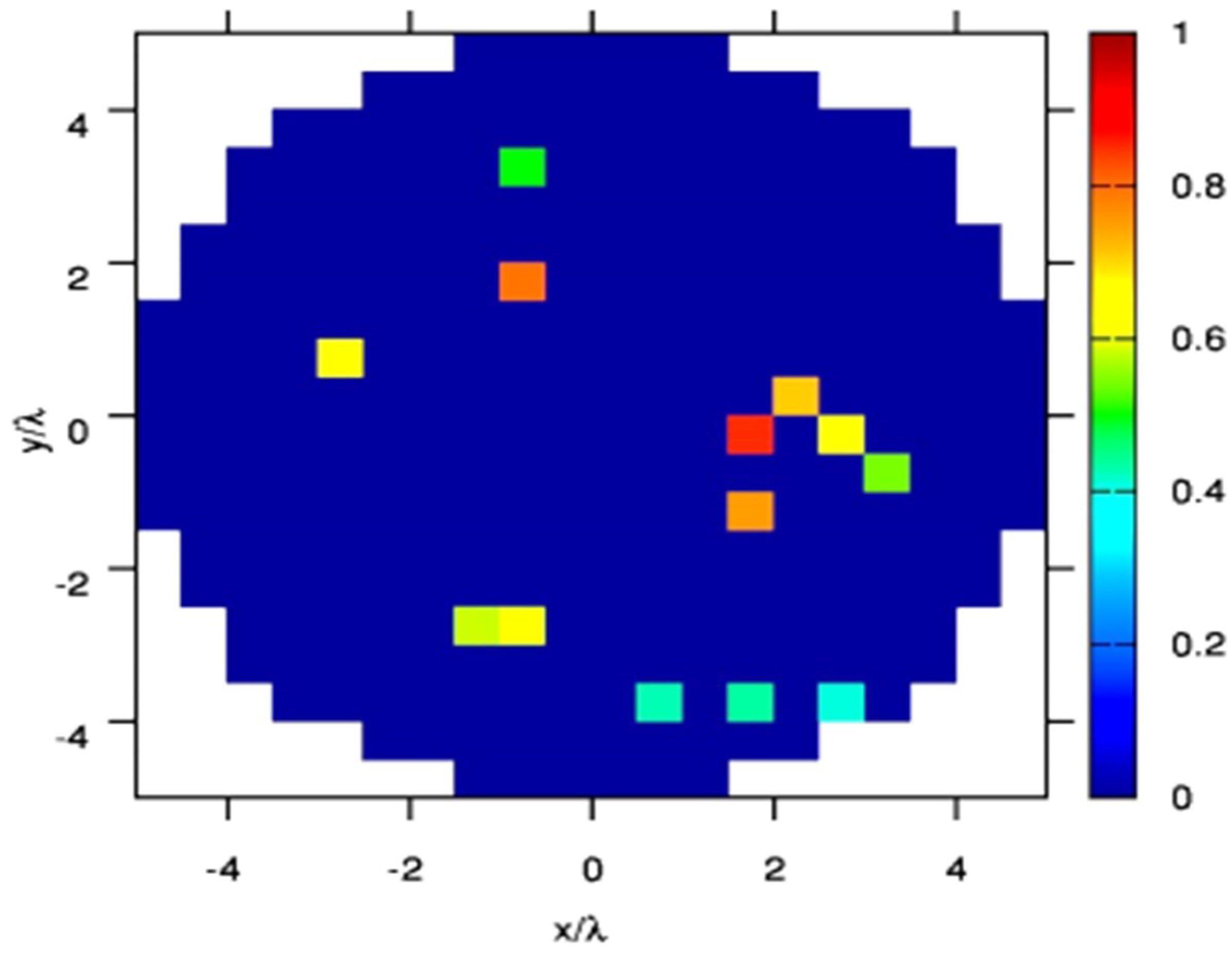
Figure 5 shows
of the failure vector estimated via the proposed technique. As expected, there is good correlation between the location and the number of the real and predicted failed elements. Accuracy of the estimation was ascertained by a very small index of detection figure of
.
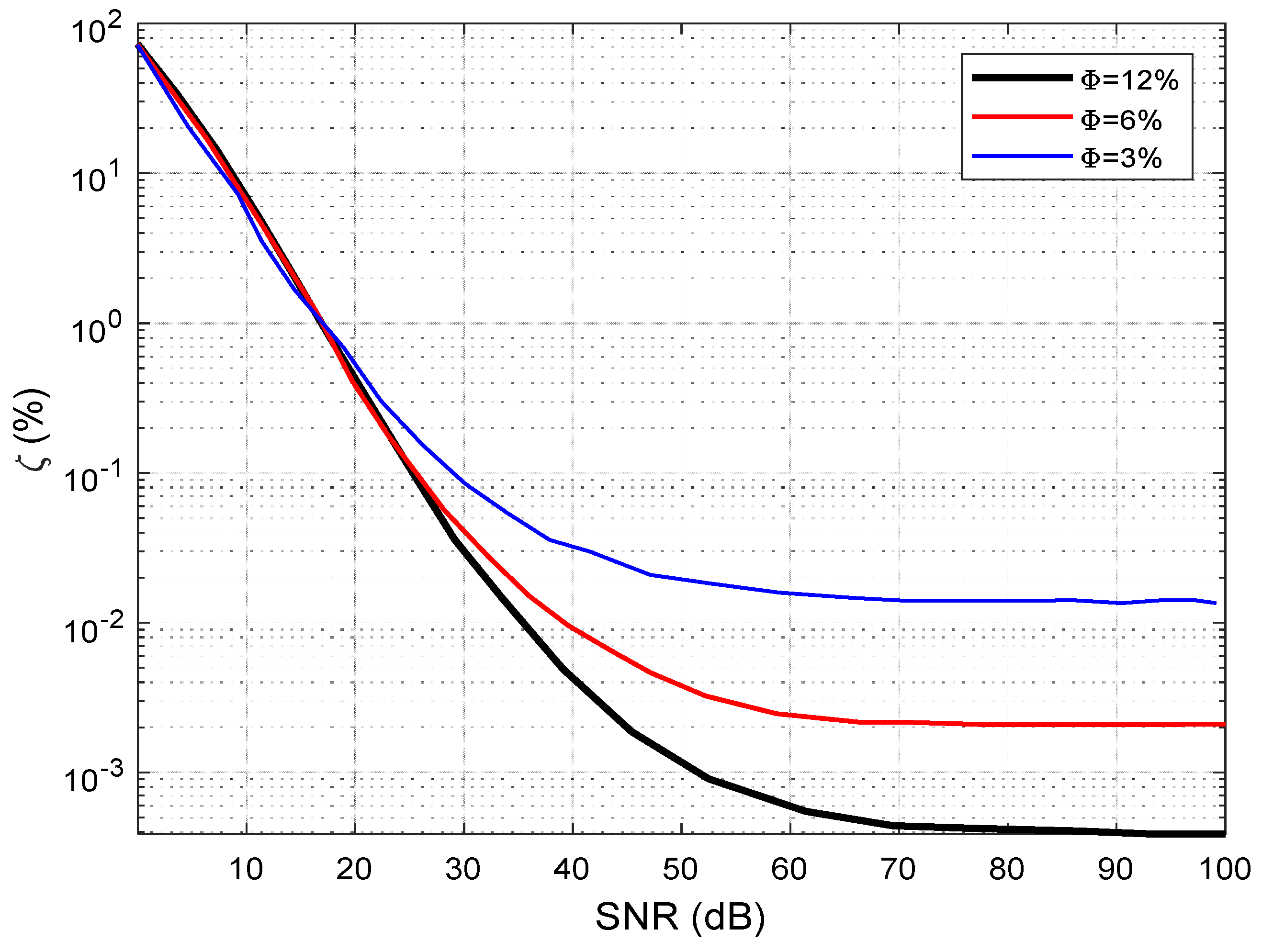
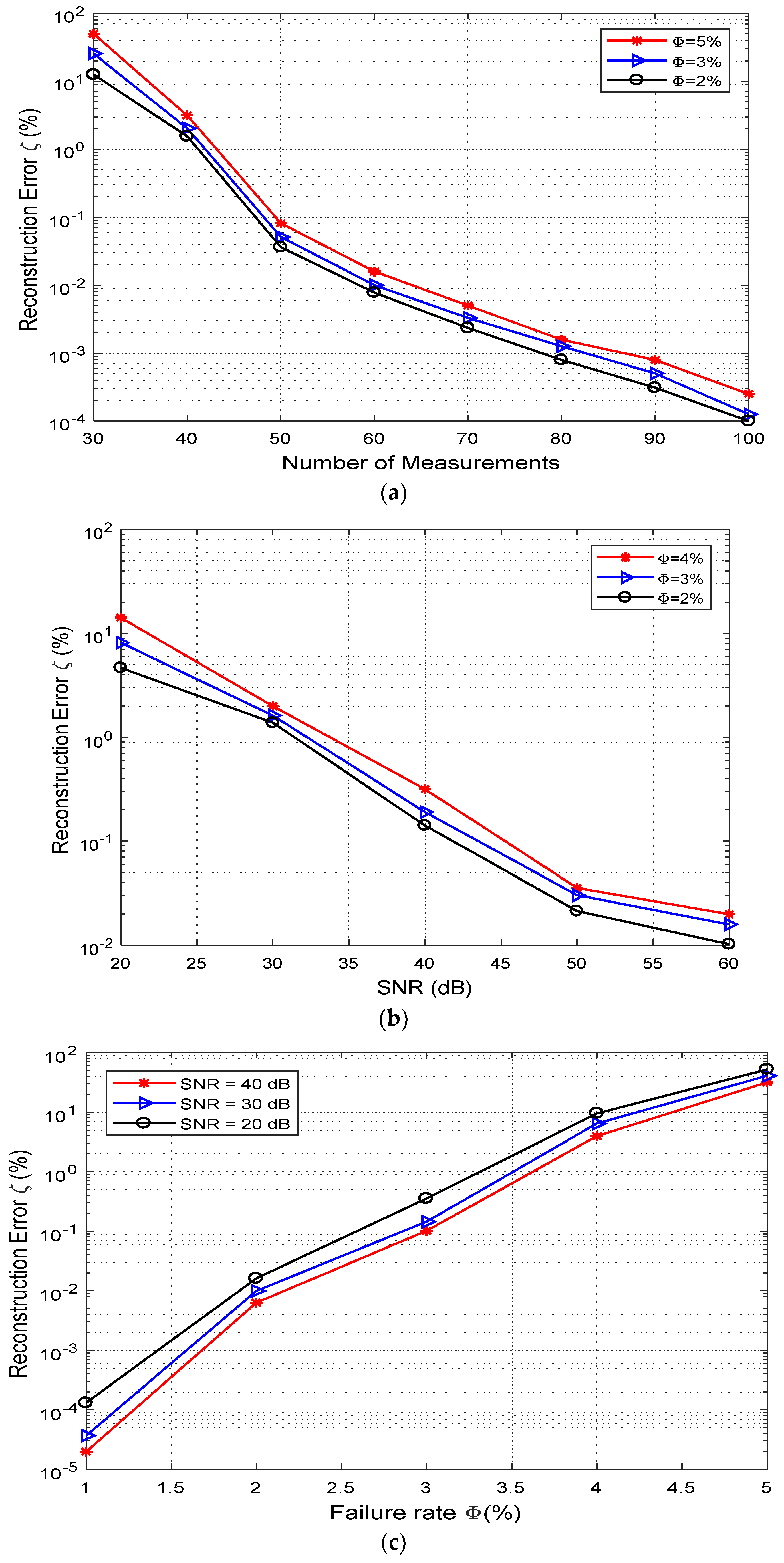
To analyze the impact on performance metrics of the technique of the noise on far-field patterns, we ranged the SNR between 0 dB and 100 dB.
Figure 6 shows the obtained result. The estimation error
is high for low SNRs irrespective of failed element percentage. Also, for higher SNR, the robustness of the approach increases, which shows that the best performances are attained at
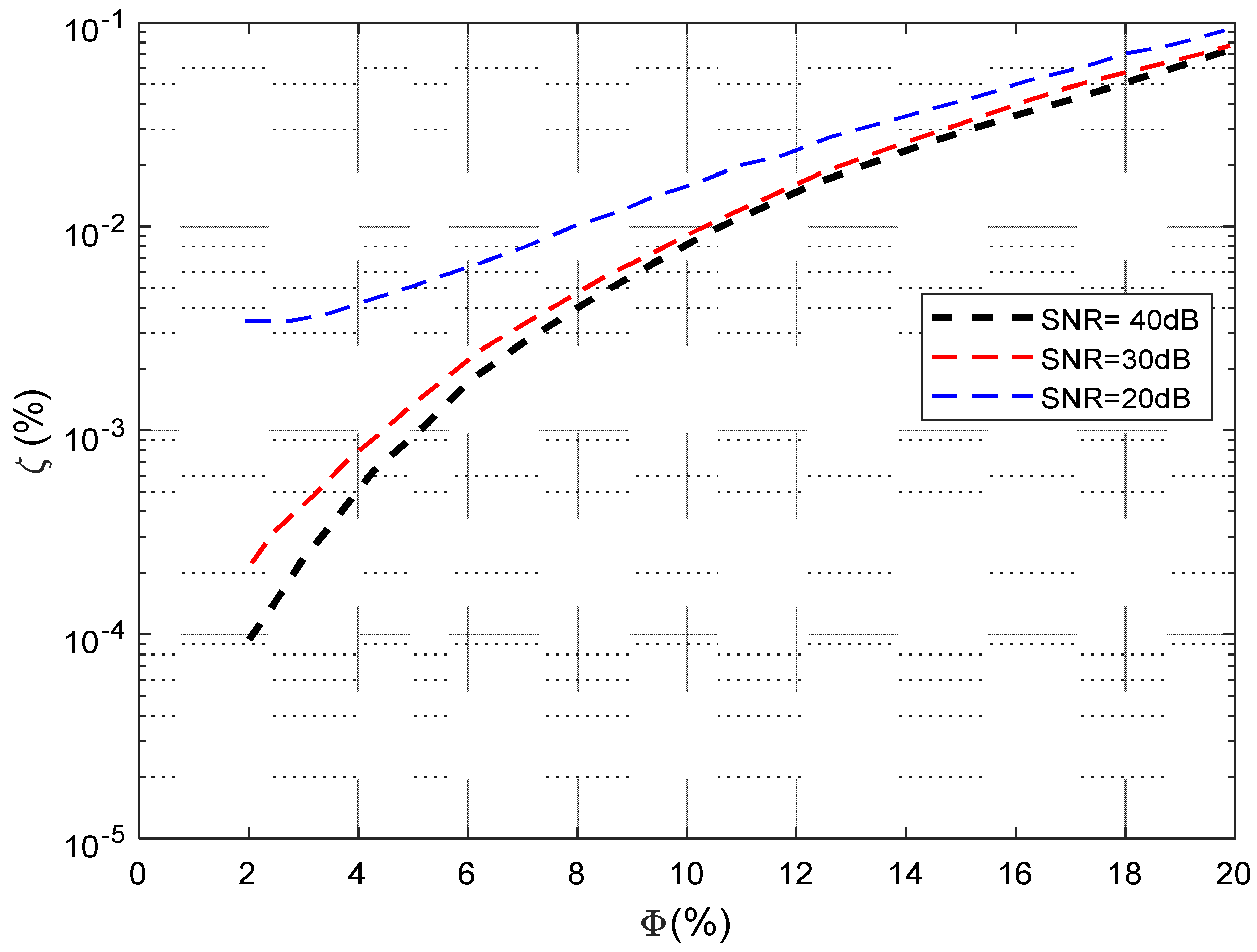
. The impact of the percentage of failed elements on the performance of the method proposed was also assessed by varying the percentage of the failed elements from
to
(see
Figure 7). Expectedly, the performance metrics of the approach reduced for a higher percentage of failed elements, even for very low noise levels. Conversely, the approach achieved a degree acceptable accuracy until about
of damaged elements at any SNR. This result validates the efficiency of the BCS technique in the diagnosis of sparse failures in arrays.
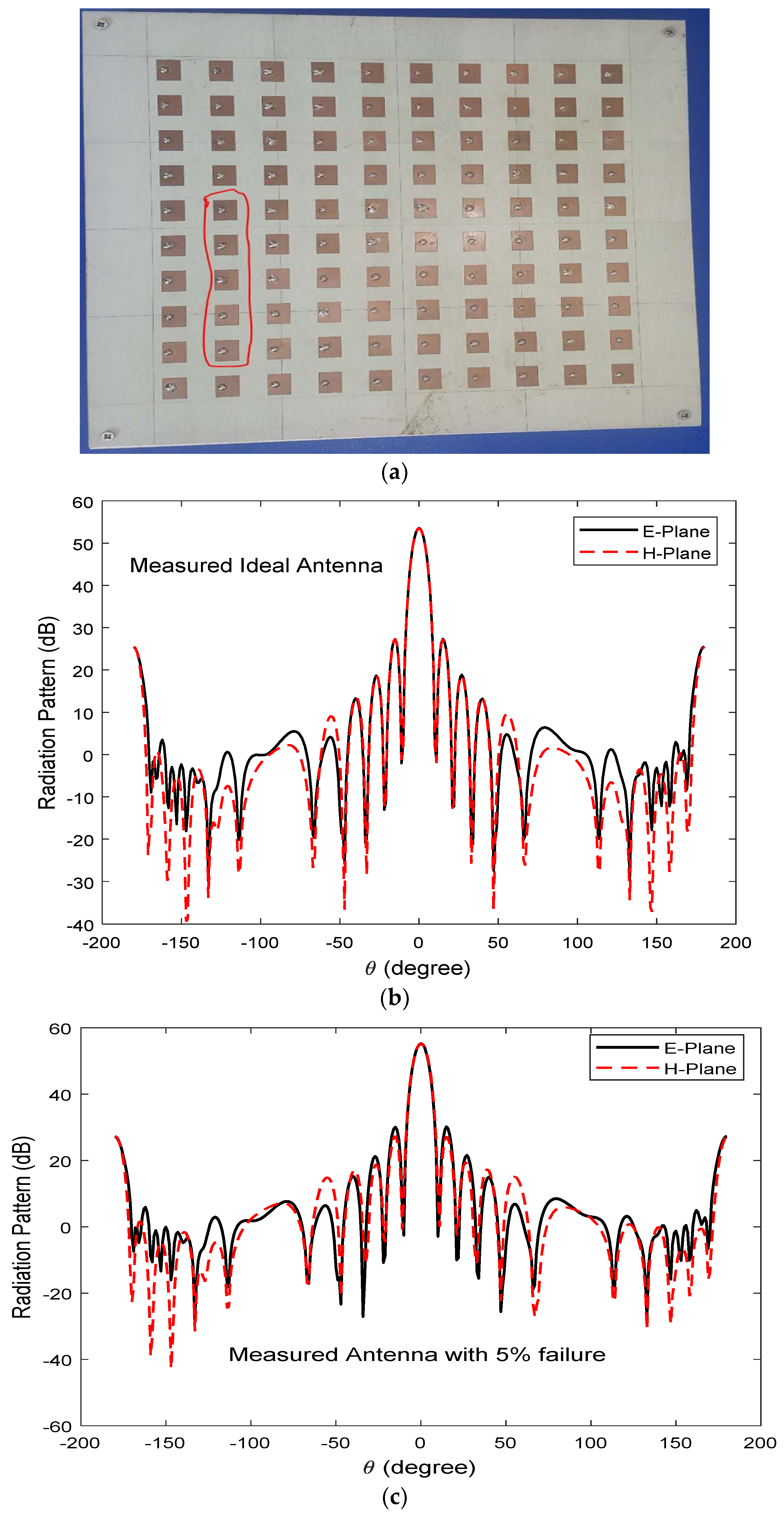
Example Using Full-Wave Simulation Set-Up
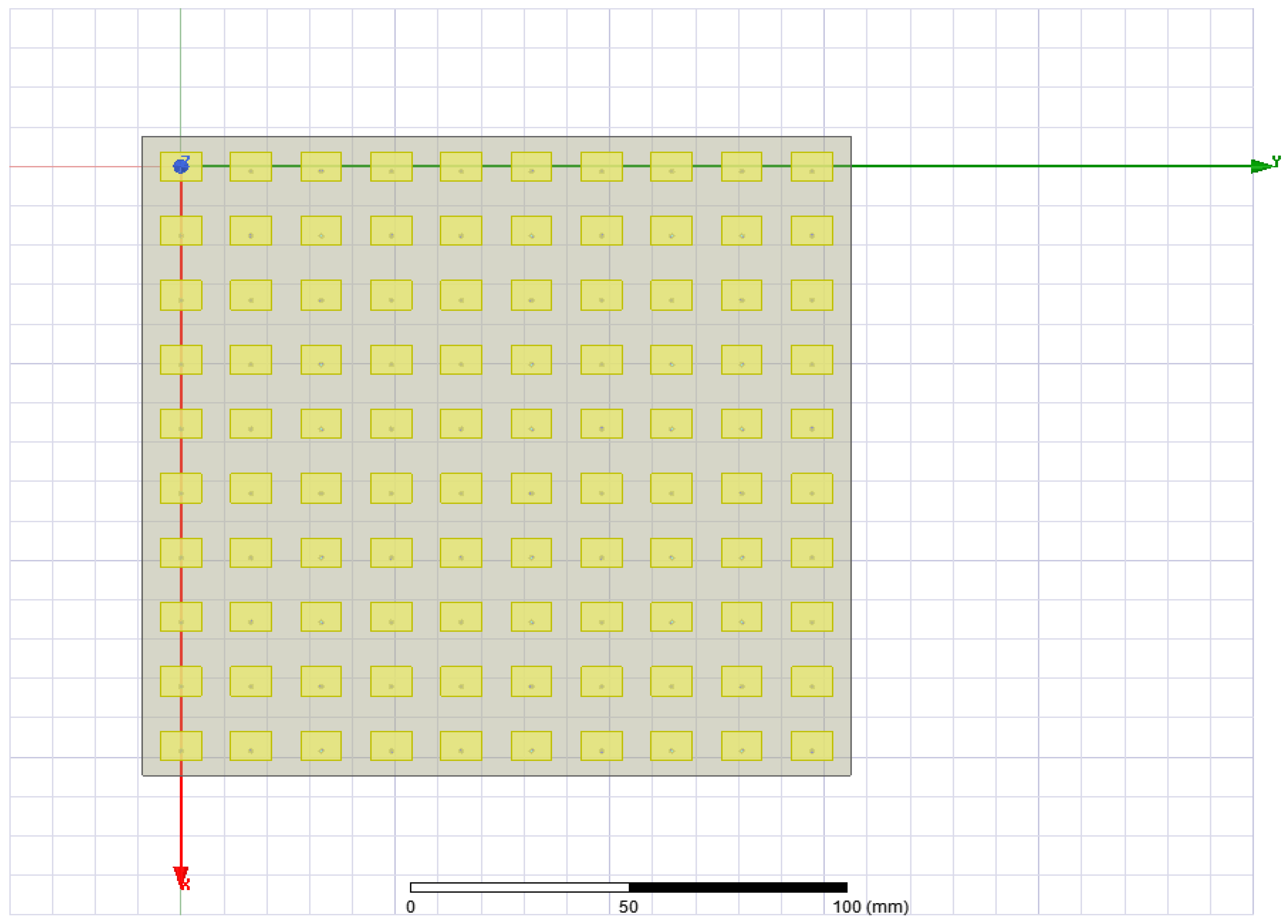
A
microstrip patch antenna array with an aperture size of 31 × 31 mm
2 operating at 28.9 GHz was designed, as shown in
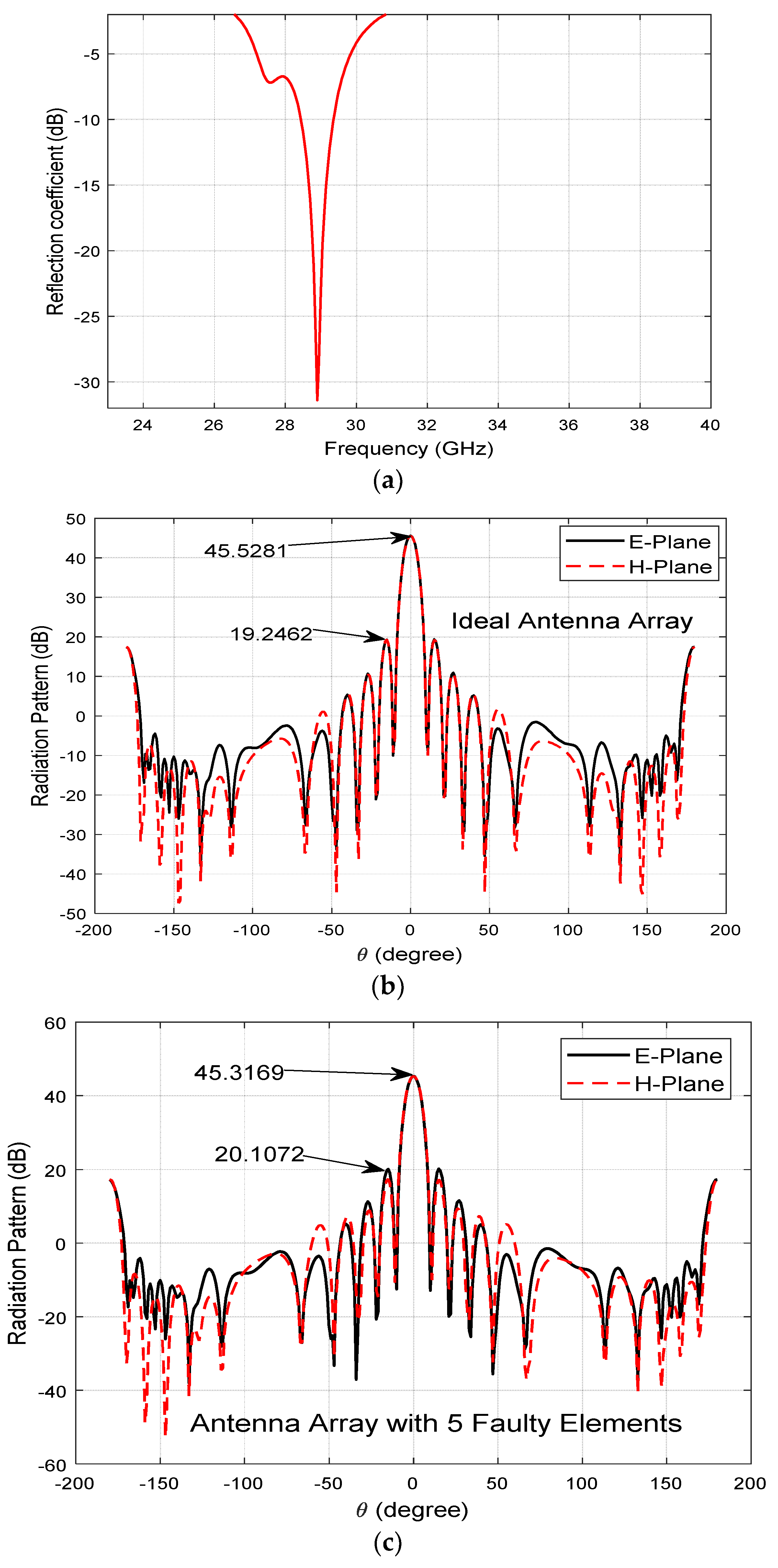
Figure 8. We designed and computed the radiation pattern and S-parameter (
Figure 9) of the antenna using full-wave three-dimensional (3D) EM software Ansys HFSS v. 17. The elements were uniformly spaced along the
x and
y directions. Each element had an excitation port. Practically, measurements are made impure by noise; hence, a Gaussian noise
n was added to the data on both radiation patterns as
, with
. The noise level was determined by signal-to-noise ratio (SNR) defined from the maximum received field magnitude fitting the dynamic measurement range. The noise was estimated as
where
is a Gaussian random vector of mean 0 and standard deviation 1.
The faulty elements cause low gain, high sidelobe level, wider beamwidth, lower front-to-back ratio, and a boresight pointing error. The effects are shown in
Figure 9b. A Rogers 5880 dielectric substrate with 20 mm thickness and 3.48 dielectric constant was used for the antenna design because it has low signal loss, low dielectric loss, low outgassing (which is good for space applications), and cheap circuit fabrication. The total number of elements in the array was 100. The length and width of a single patch were estimated to be 7.4 mm and 9.5 mm, respectively. Elements were uniformly spaced by 8.947 mm and 6.847 mm along
x and
y, respectively.
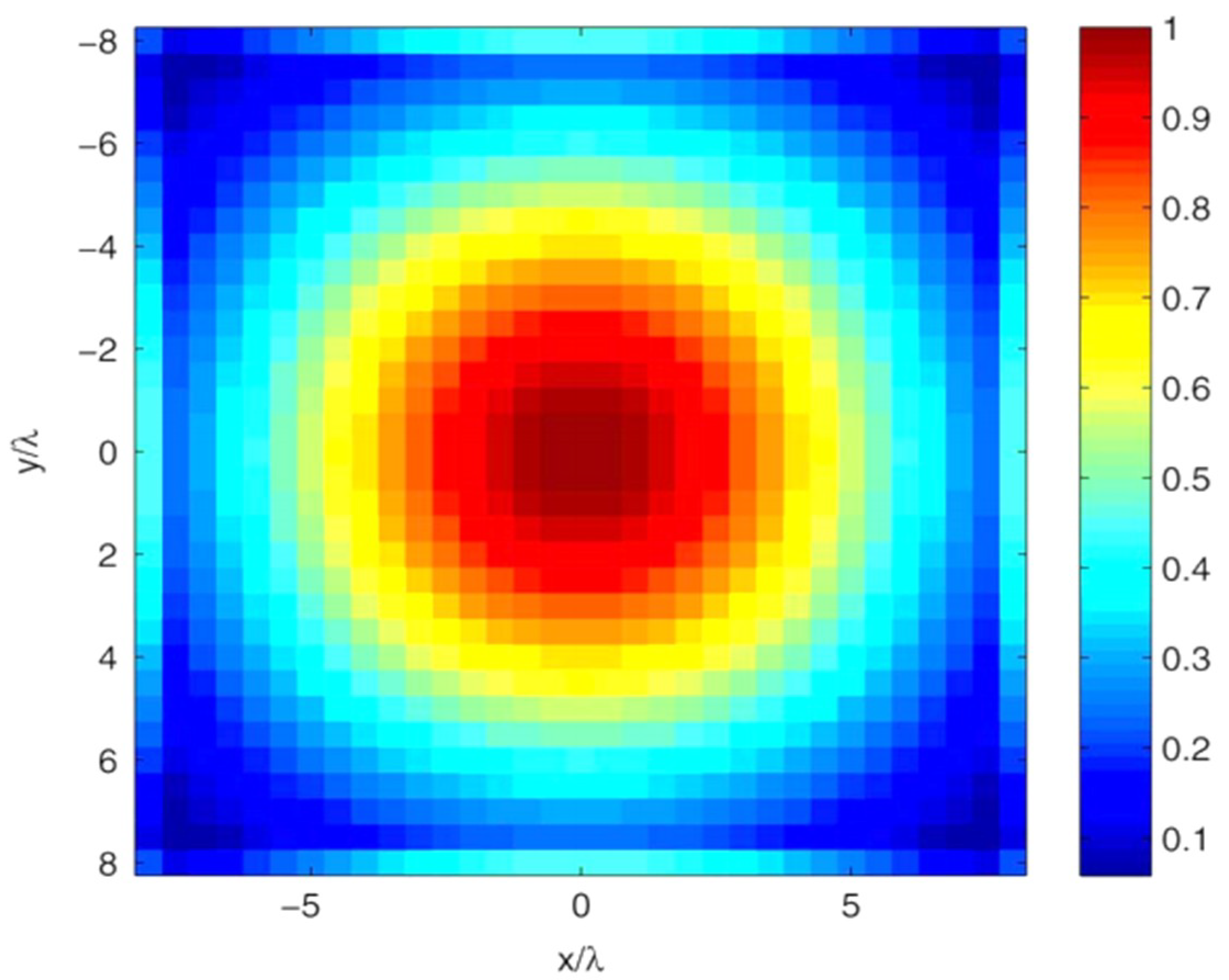
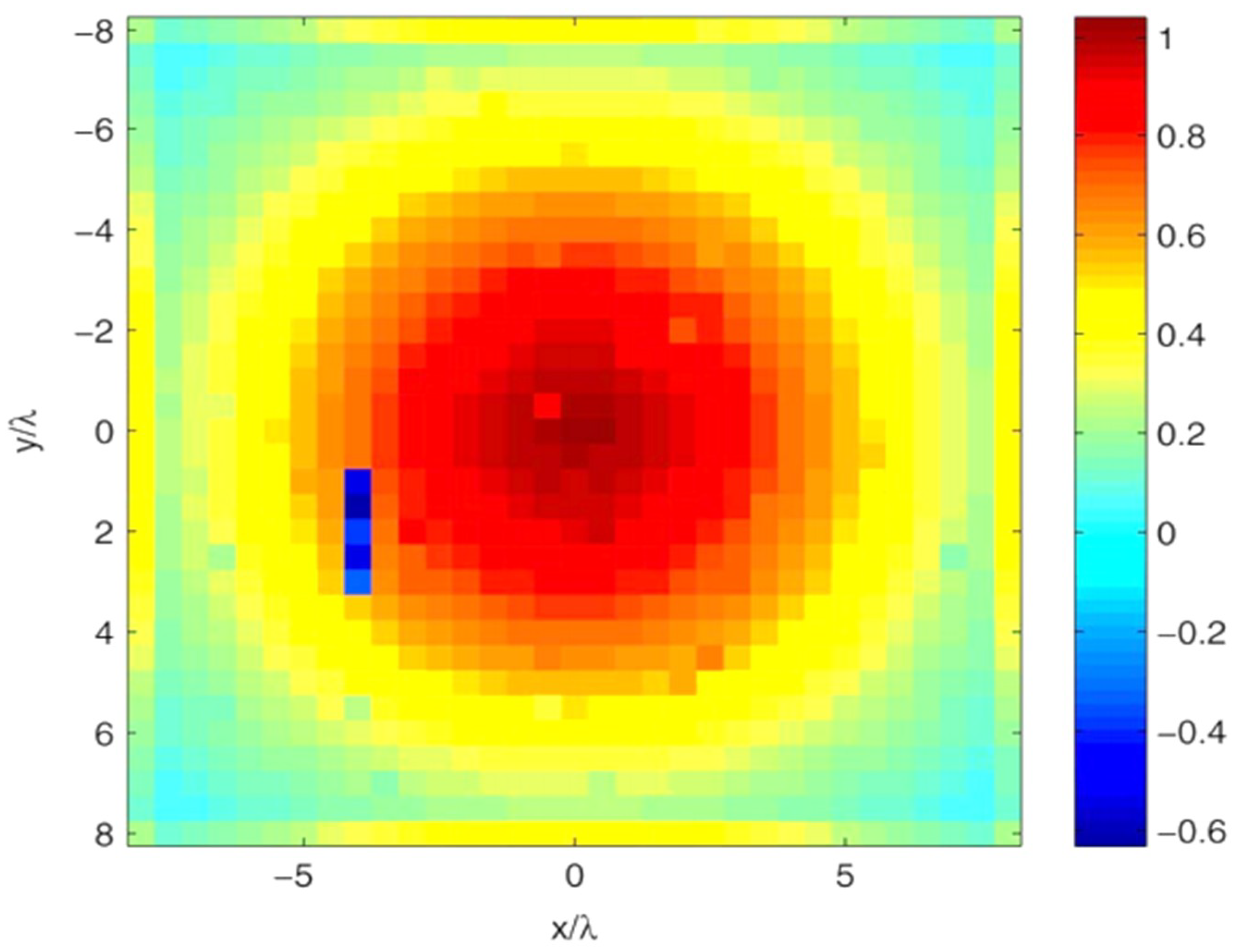
All elements were fed with the same excitation value which equal to one to emulate the array without failure (reference array). Then
K failures (in this case, the estimated percentage of failure rate) were also initiated intentionally by making the excitation equal to zero in order to model the AUT effectively. At first, we considered the reference array, i.e., the array without failures. The excitation coefficients are depicted in
Figure 10, and the reconstructed excitation coefficients are presented in
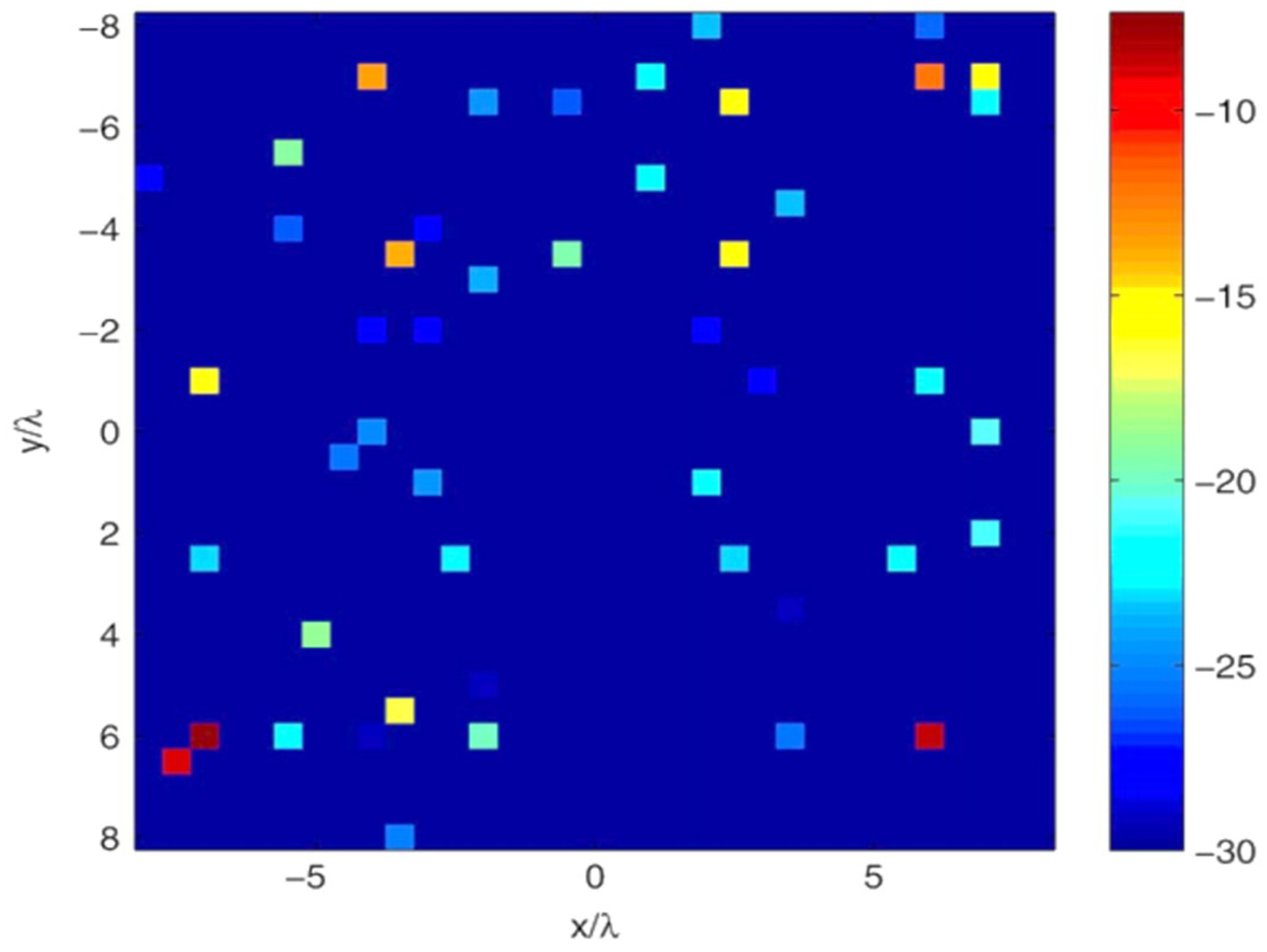
Figure 11. Also, for quantitative knowledge of the error estimated, the computed excitation error in dB is shown in
Figure 12. The result indicates an exact reconstruction in the case of the reference array, and shows a low probability of a false alarm.
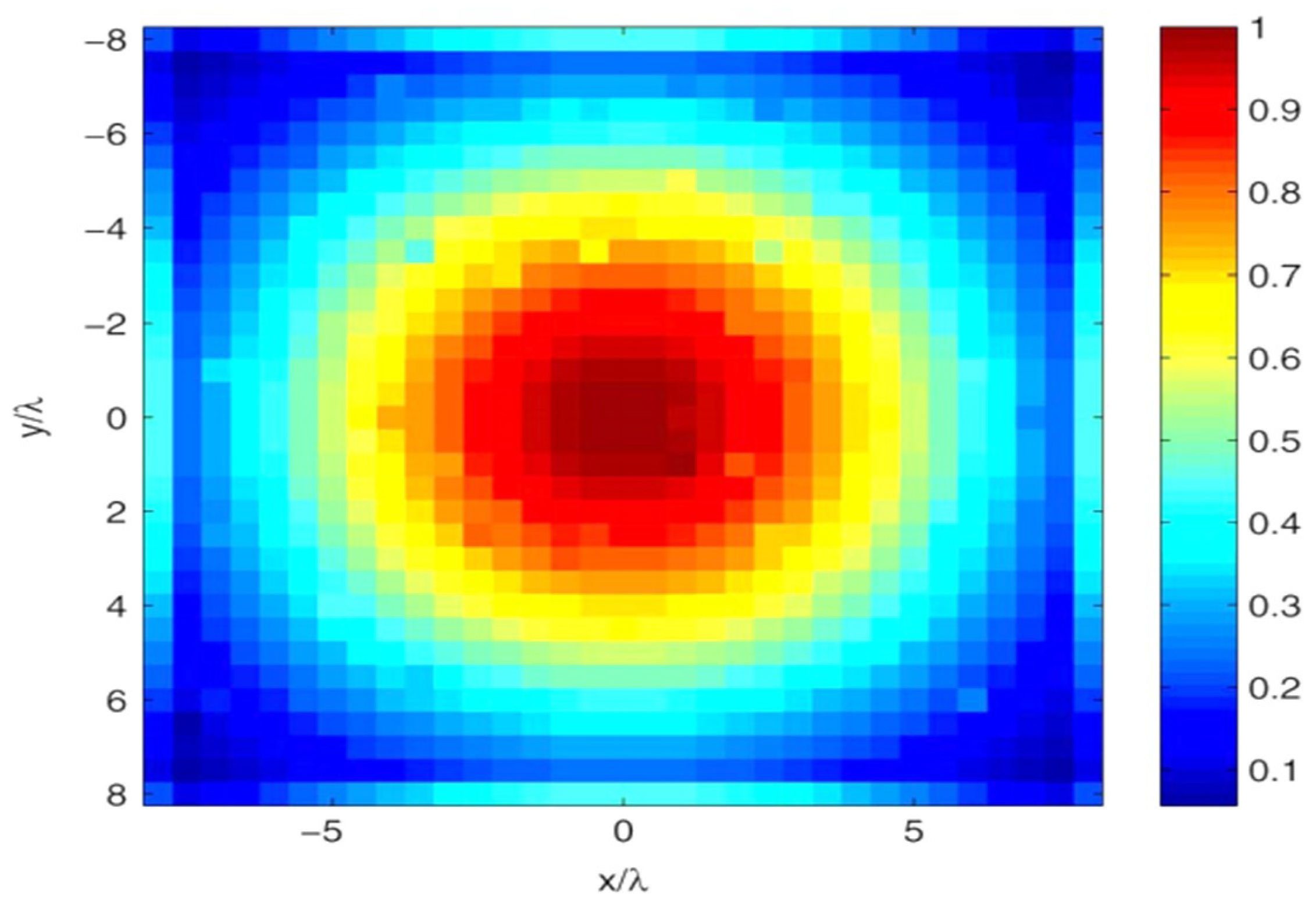
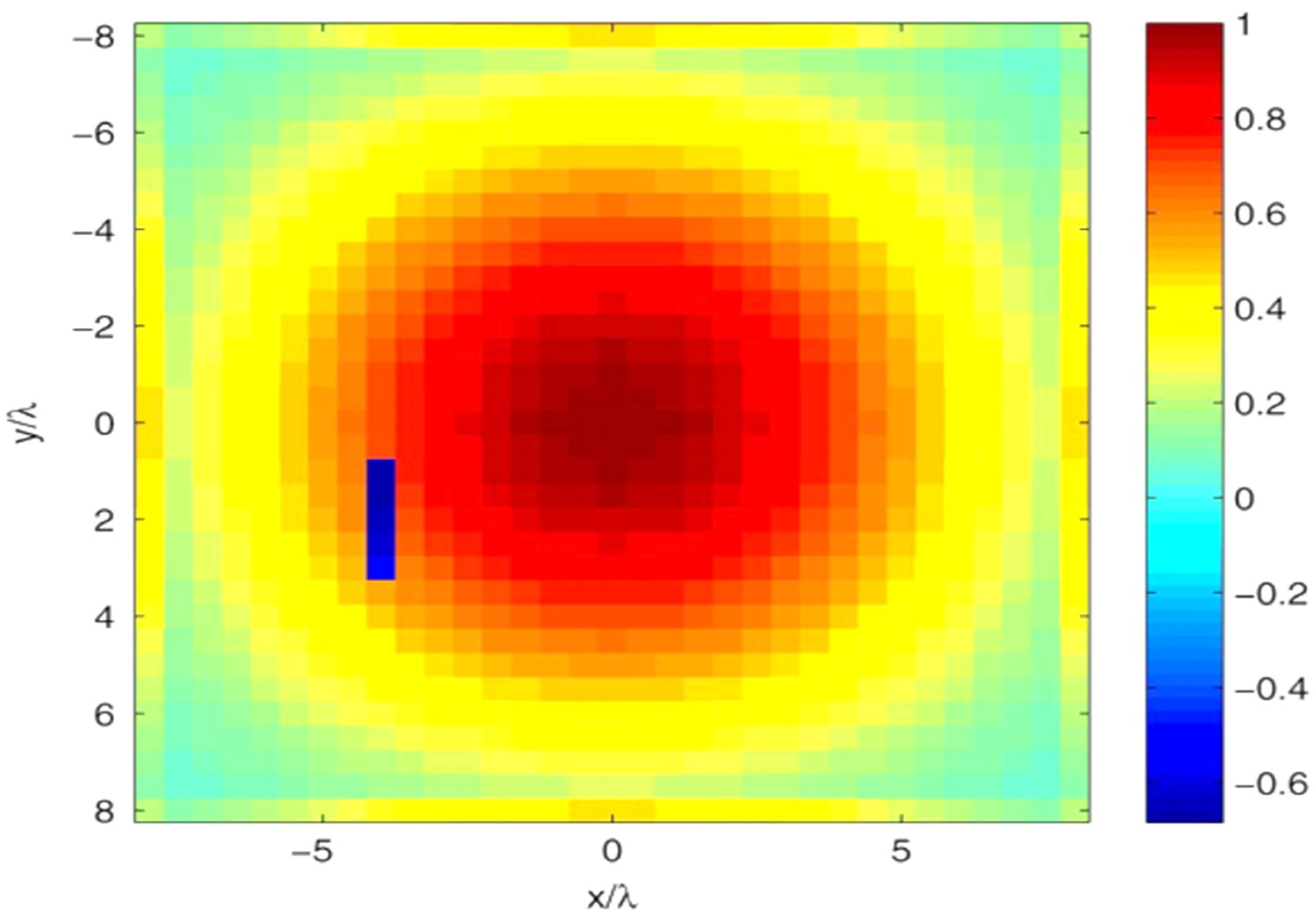
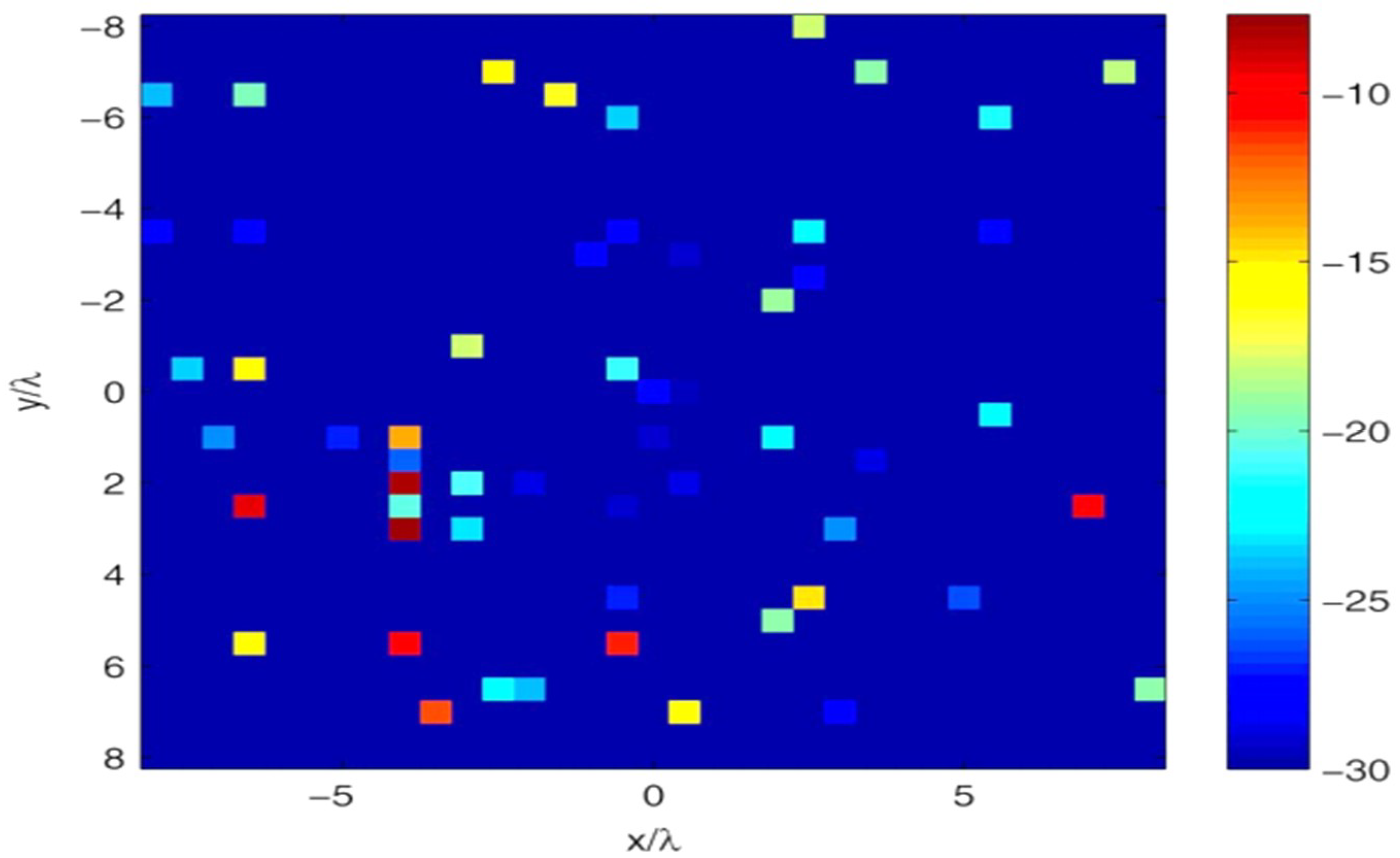
Also, considering an AUT with
K = 5 element failures (
) (elements with zero excitation) because failed elements are usually of small number in practice, the resulted excitation coefficients are presented in
Figure 13, and the estimated excitations by 30 random noisy measurement points are presented in
Figure 14, while the dB excitation error is depicted in
Figure 15. The result is an indication of good estimation of RA excitations and the locations of the faulty elements.