Design And Implementation of Low Area/Power Elliptic Curve Digital Signature Hardware Core
Abstract
:1. Introduction
2. Related Works
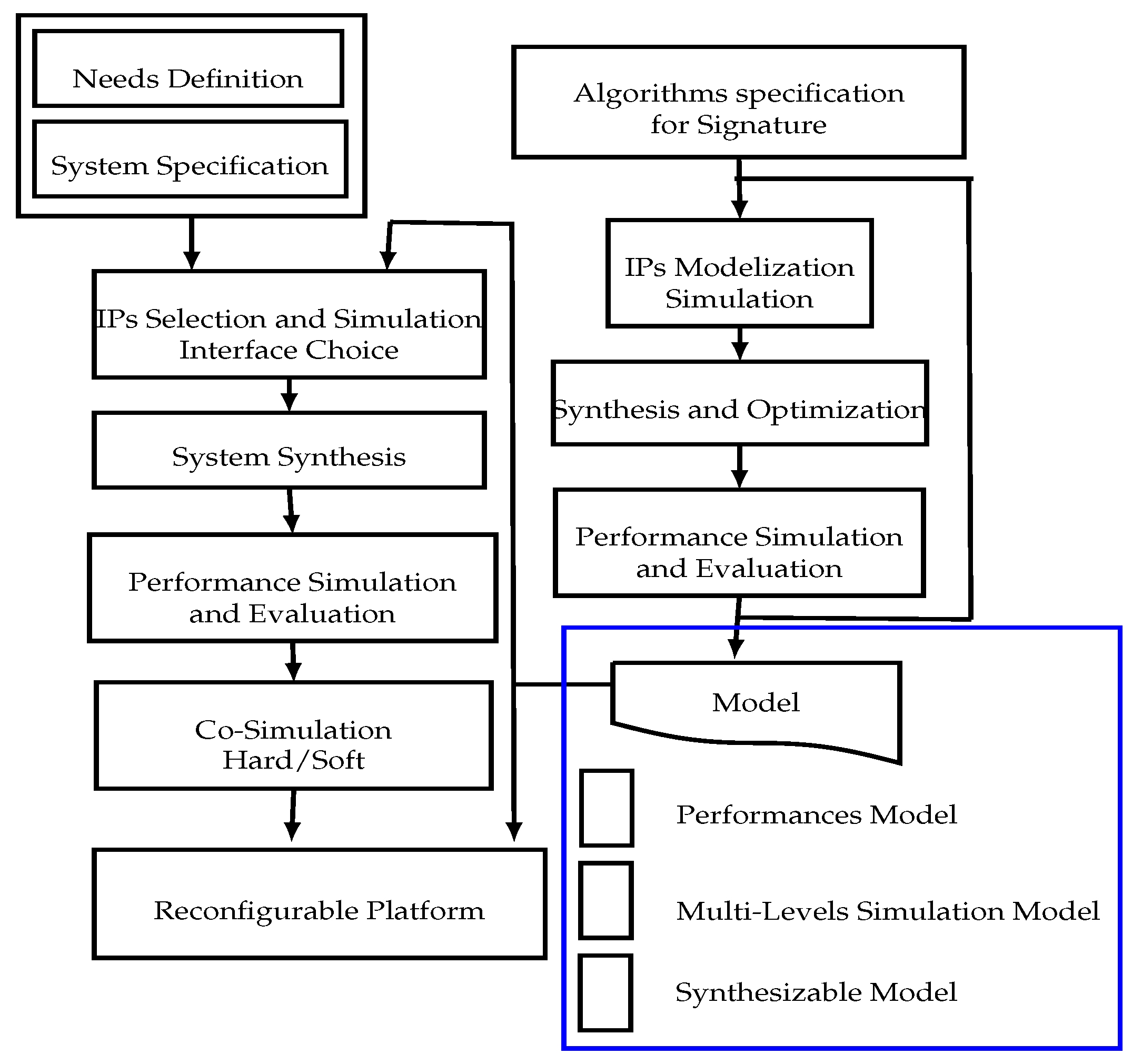
3. ECDSA Processor Methodology and Flow Design
- Select the most suitable algorithms for designing signature IP blocks with respect to the large-scale application’s requirement: a high-security level, a minimum area with maximum throughput and a low consumption.
- Propose RTL (Register Transfer Level) architectural optimizations with the aim of adopting and scaling the signature processor to both the application needs and the platform specifications.
- Propose a hardware verification approach to the proposed signature processor so as to validate and verify RTL implementations. In order to accelerate the verification of the overall architecture, the verification and validation have to apply different co-simulation methods to the used IPs. This can be done thanks to the interfaces between the higher level system environments and the high-performance HDL simulators.
- Definition and specification of algorithms for key generation, signature generation and signature verification,
- Design and modeling of different IP and the choice of a standard interface,
- System-level evaluation of security and throughput performances,
- Logic synthesis of different IPs (SHA-2 IP, ECC IP, RNG IP) and integration on a reconfigurable platform,
- Hardware and software co-simulation of the entire signature processor and performance evaluation.
- The most used algorithms for hash are Message Digest algorithm 5 (MD5) and Secure Hash Algorithm (SHA-0, SHA-1 and SHA-2). Thus, MD5, SHA-1 and SHA-0 have the same size of the message, the word and the block. Furthermore, they have the same number of rounds, except that the size of the MD5 digest (128-bit) is smaller than the SHA 0 and SHA-1 ones (160-bit). Collision has been found in MD5, SHA-0 and SHA-1 with a number of attacks [19], which made them unreliable and unsafe, so not adaptable for the actual cryptographic needs. Since their appearance, the SHA-2 family is the most used hash function thanks to the higher security against attacks due to the larger condensed size and speed.
- Due to their flexibility and enhanced ability to manage keys, asymmetric algorithms, such as the Rivest–Shamir–Adleman-system (RSA) and Elliptic Curve Cryptography (ECC), are the most practical cryptosystems. ECC is based on the algebraic structure of elliptic curves over finite fields. It requires smaller key sizes compared to RSA, which allow it to be more suitable for embedded systems that are low-memory and low-power. Indeed, a 256-bit ECC public key provides comparable security to a 3072-bit RSA public key. It is applicable for encryption/decryption, digital signatures, pseudorandom generators, etc. Based on the Elliptic Curve Discrete Logarithm Problem (ECDLP), ECC is very hard to break.
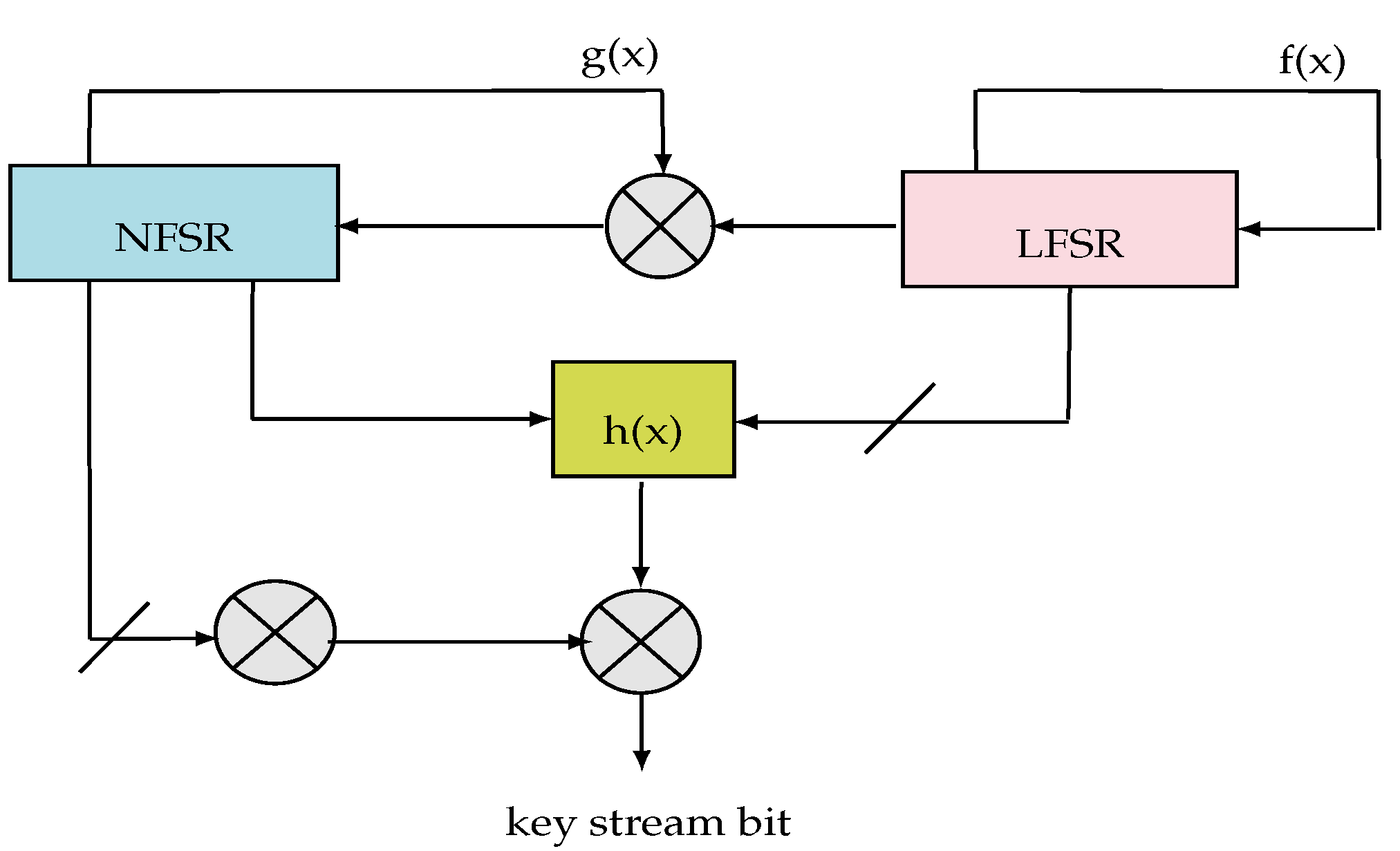
- Key generation is not only needed in symmetric or asymmetric encryption, but also in access codes, passwords, product identification and software authentication. There are several methods for hardware key generation; the best known are the Linear Feed Back Shift Registers (LFSRs), NonLinear Feed Back Shift Registers (NLFSRs), known as grain [20], and the cellular automata, which are an important family of stream cipher generators [21]. The appropriate algorithm in our case is grain-128, because it supports the 128-bit key, and its initial vector is about 96 bits. This encryption is very small and easy to implement in hardware [22]. In addition, it is possible and easy to speed up the hardware design. The grain-128 uses an LFSR to ensure good statistical properties; an NLFSR is used with a non-linear filter to introduce non-linearity. The non-linear filter takes the contribution of the two shift registers.
4. Proposed Hardware Architecture for ECDSA IPs
4.1. Secure Hash Standard 2 IP
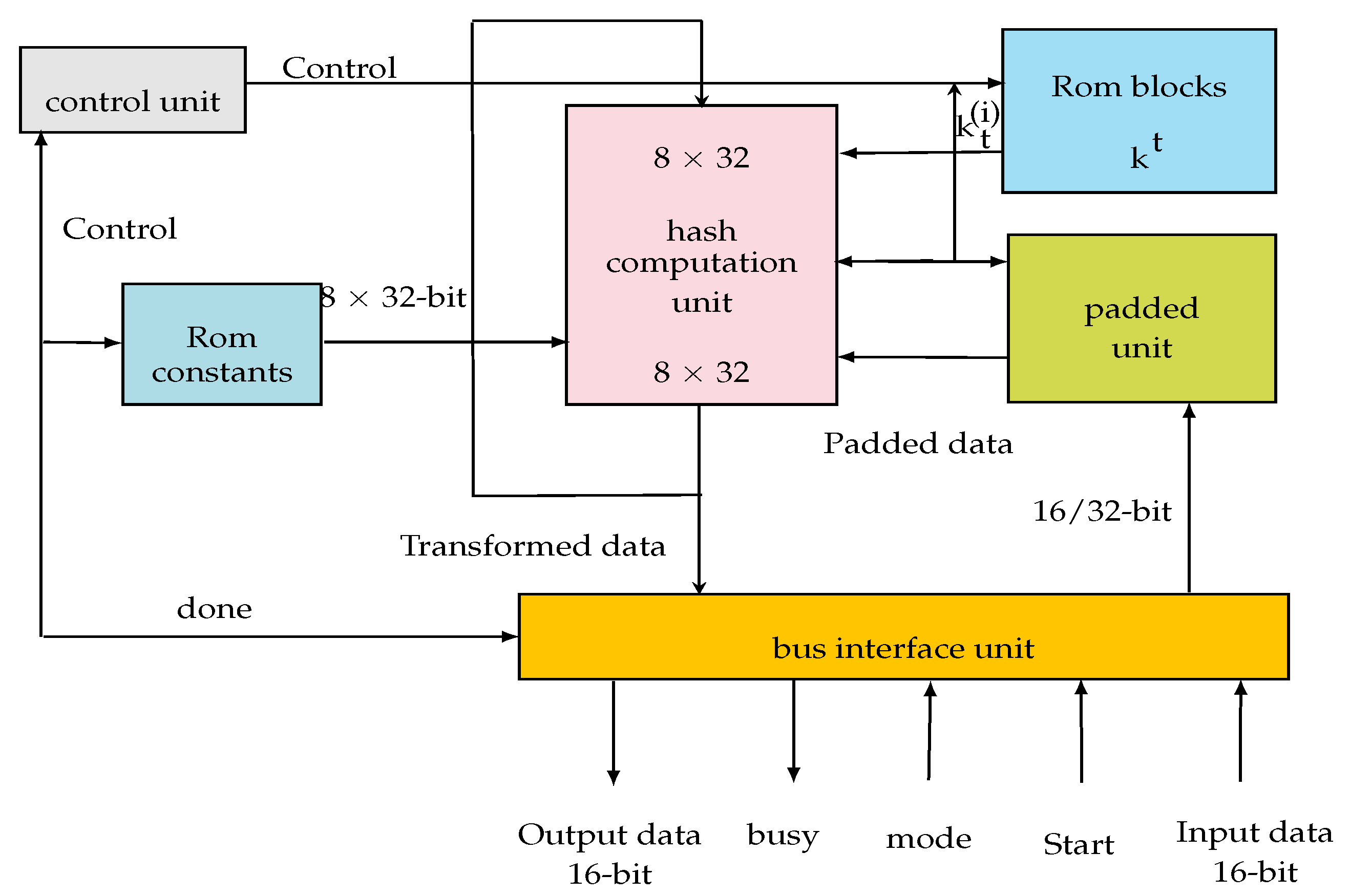
4.1.1. SHA-2 Architecture Design
- The control unit: this is designed to control the data flow in the design, as well as the data transfer between the digest calculation unit (hash computation unit) and the pre-processing unit (padded unit). An FSM is used for this purpose. The control unit coordinates all system operations. It defines the necessary constants and the length of the operation word. It manages the ROM blocks and controls all algebraic and digital logic functions necessary to calculate the digest.
- The pre-processing unit (padded unit): its role is to complete the message in order to make it compatible with the used hash protocols.
- The calculation unit (hash computation unit): this is the digest calculation block. It performs the data transformation functions.
- The input/output interface unit has been designed in order to communicate the processor with the external environment.
4.1.2. SHA-2 Architecture Optimization
- Addition is the most common operation in calculating the message digest. It requires adding a 64-bit operand size. Therefore, it is important for it to be optimized. Thus, in order to have a fast and low area SHA-2 IP, various time-efficient adder architectures have been developed in VHDL [23], such as the Ripple Carry Adder (RCA), the Carry Look-ahead Adder (CLA), the Carry Save Adder (CSaA) and the Carry Selected Adder (CSeA). Being studied in [24] and implemented on FPGA Virtex-II Pro xc2vp7-5ff672, the RCA adder and the CLA are the best in terms of area occupation on the FPGA platform; whereas, the carry select adder is the most speed efficient.
- In each round of the SHA-2, some operations can be calculated independently and the others are dependent. In [24], the authors changed the expressions A, B, C, D, E, F, G and H in order to optimize the SHA-2 design by condensing two cycles (, ) in the same cycle. Thus, the following round can instantly calculate an intermediate value based on the available inputs by storing the intermediate values of Wt and Kt. The data processing time is reduced by half cycles. The processing algorithm will be different since it reduces the number of cycles (divided by two).
- By changing the expressions of A, B, C, D, E, F, G and H, the number of adders increased from 7 to 14. To solve this problem and analyzing the dependency between hash calculations, two methods were proposed, the first used only two adders and the second used three adders. For the first method, only two adders will be used at each stage of the calculation, the two adders are active. In the second method, just three adders are required in two states. It is clear that both methods have the same speed, so, the first method was adopted in order to decrease area occupation.
4.1.3. Simulation and Synthesis Results of the SHA-2 IP
4.2. Elliptic Curves Over Finite Fields
| Algorithm 1: Point Addition and Point Doubling. | |
| Input: | Input: |
| and | |
| Output: | |
| 1. | Output: |
| 2. | 1. |
| 3. | 2. 3. |
| 4. 5. | 4. |
| 6. | 5. |
| 7. | 6. |
| 8. | 7. |
4.2.1. ECC IP Architecture Design
4.2.2. Simulation and Synthesis Results of ECC IP
4.3. Random Number Generator (RNG)
- Finding the appropriate algorithms for random (or pseudorandom) generation of the bit sequences. The period of these algorithms must be long enough,
- Testing the quality of these binary sequences, which means checking the randomness of the generated bit sequences,
- Generating these keys through deterministic algorithms in order to achieve higher speed and efficiency,
- Protecting these pseudorandom generators against the mathematical and the physical attacks.
- Implementing and optimizing these key generation algorithms in hardware with respect to the platform’s requirements.
4.3.1. Security Analyses of PRNG
4.3.2. Implementation and Synthesis Results of the Pseudorandom Number Generators (PRNG).
4.3.3. The grain IP
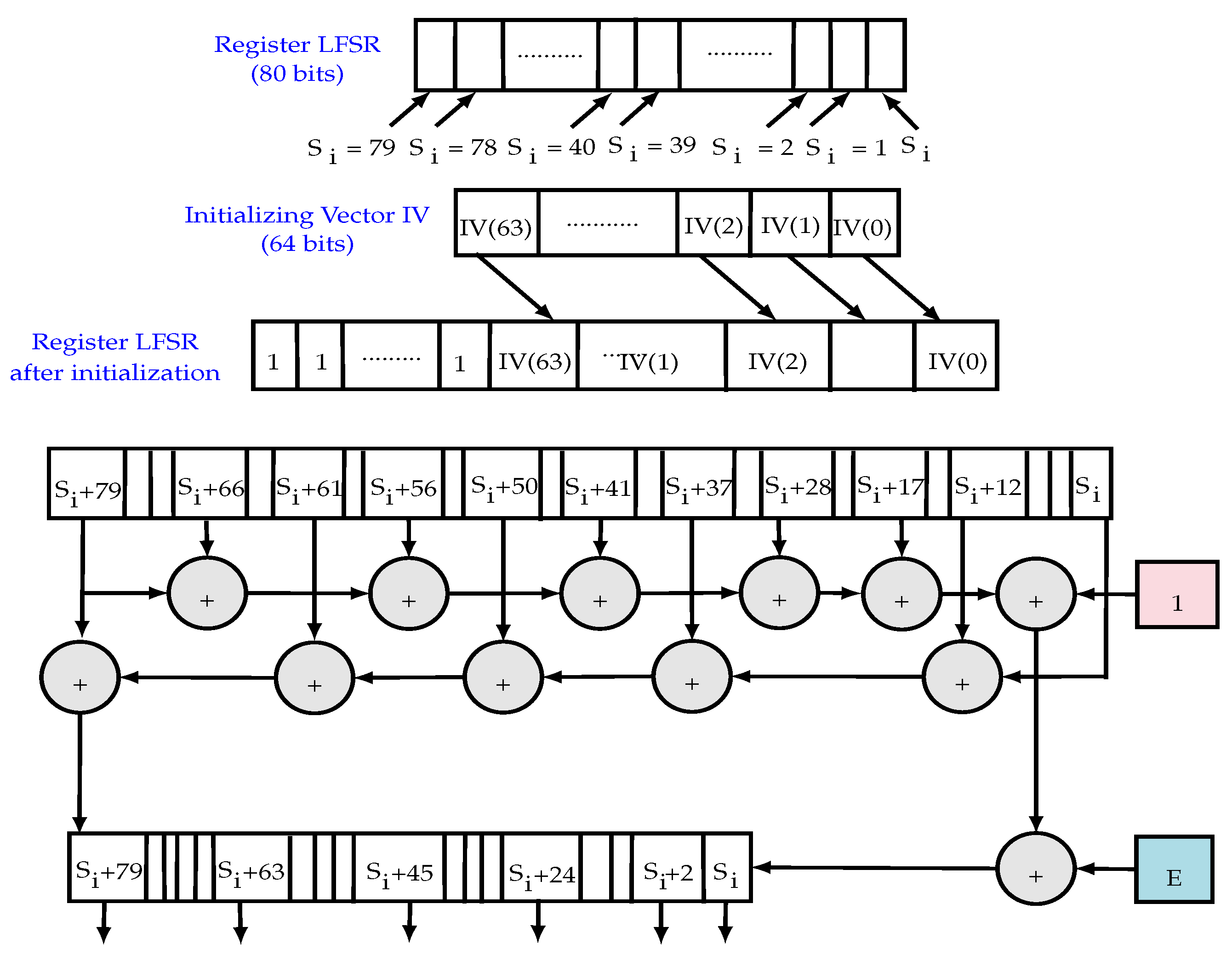
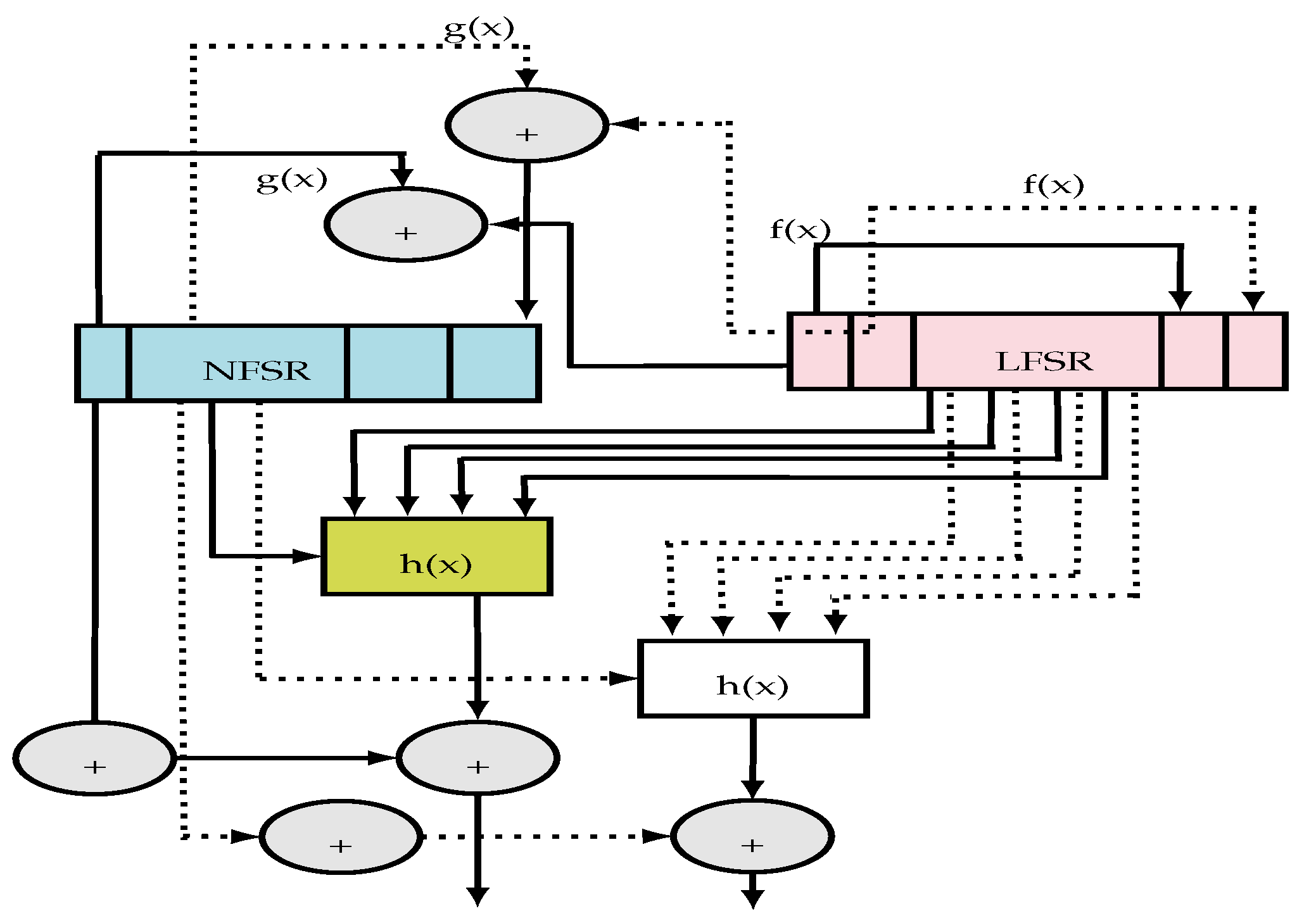
- The LFSR module: based on a sequence () and a linear feedback function. It guarantees a minimum period for the key-stream, so it can be efficiently implemented and it increases significantly the throughput. The polynomial function of the LFSR (feedback polynomial) denoted is a primitive polynomial of degree 80. Figure 6 illustrates the operation of the LFSR block including the register initialization, the polynomial function and the update function.
- The NLFSR module: is a non-linear feedback shift register based on a sequence (). It includes a masked input with the LFSR output in order to balance its state. The NLFSR introduces non-linearity to cipher with the nonlinear output function. It is a filter of a polynomial function .
- The filter module: it is a function of nonlinear output which introduces non-linearity encryption. Based on a nonlinear filtering function () with five input variables, the filter of algebraic degree 3 is selected to be well balanced.
4.3.4. Grain Optimizations
4.3.5. Simulation and Synthesis Results of the Grain IP
5. ECDSA Architecture for Low-Area Low-Power Computing
5.1. Proposed ECDSA Processor Design
| Algorithm 2:Private and Public Key Generation. |
| Input: message m, domain parameters () |
| Output: private key d, public key Q |
| 1. Choice of elliptic curve . |
| 2. Choice of a point of order n. |
| 3. Choice of a big integer d, with . |
| 4. Choice of a point (the Montgomery scalar multiplication). |
| Return private key d and public key Q. |
| Algorithm 3:ECDSA Signature Generation. |
| Input: private key d, message m, domain parameters (), public key |
| Output: signature (r, s) |
| 1. Choice of a random integer k, with . |
| 2. Calculate . |
| 3. Calculate . If , so return to step 1. |
| 4. Calculate . |
| 5. Calculate such that: is cryptographic hash result using SHA-1 or SHA-2 of the message m. |
| 6. Calculate . If , return to step 1. |
| Return (r, s) the signature of the message m |
| Algorithm 4:ECDSA signature verification. |
| Input: a signature , public key, domain parameters (), message m |
| Output: signature verification or rejection |
| 1. Verify that integer r and s are both in . |
| 2. Calculate such that: is cryptographic hash result using SHA-1 or SHA-2 of the message m. |
| 3. Calculate . |
| 4. Calculate and . |
| 5. Calculate . (using the point addition formula on the elliptic curve). |
| 6. If , so signature will be rejected. Else, calculate . |
| 7. Signature will be accepted only if . |
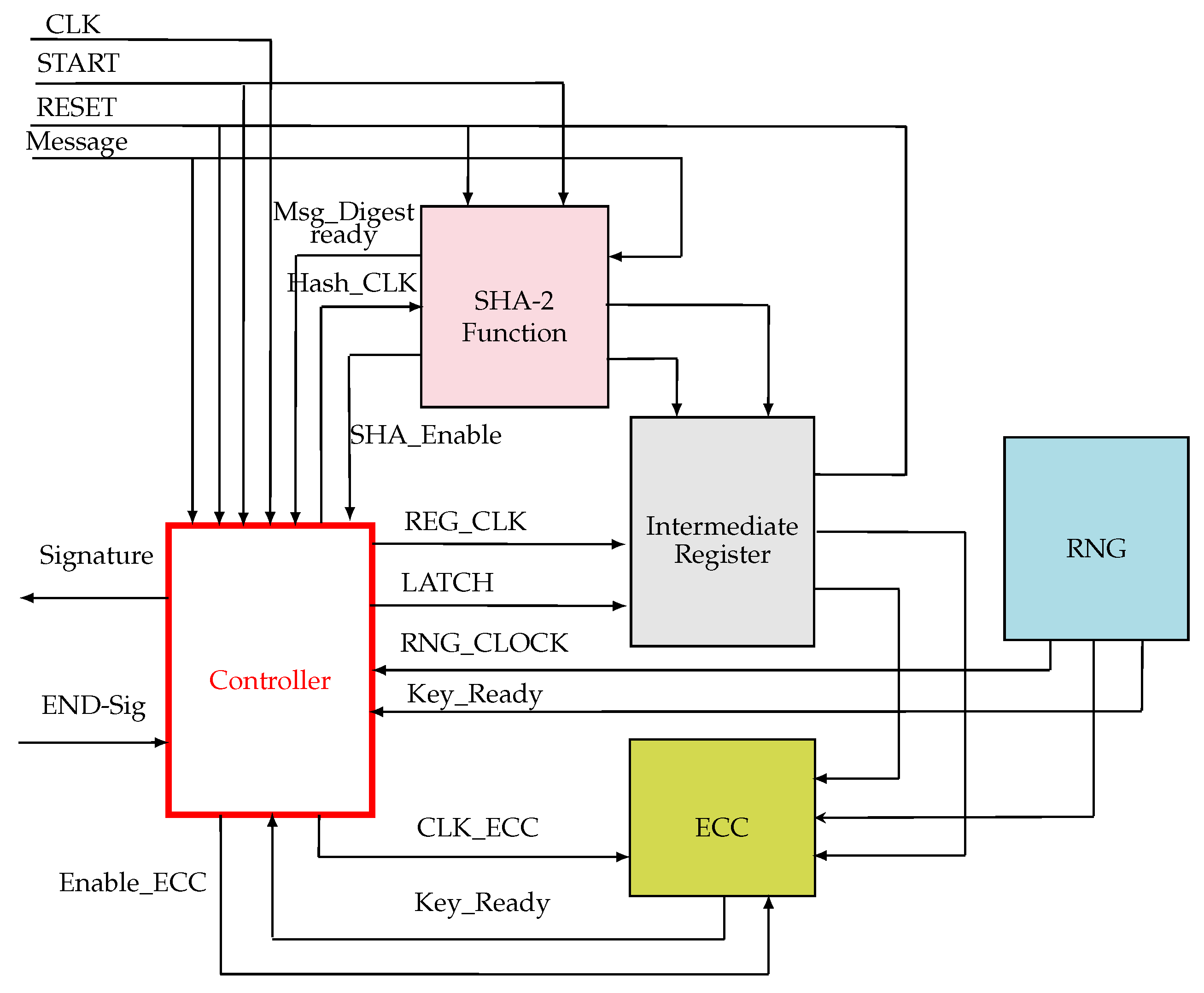
- The ECC unit: it computes the point scalar multiplication based on the Montgomery algorithm which was explained in Section 4.2,
- The SHA-2 function unit: generates hash used in both the signature generation and the signature verification of the message m, it was presented in Section 4.1,
- The PRNG unit: it is a random number generator which generates a random number used as keys during the signing process, it was well detailed in Section 4.3,
- The intermediate register: used to store the intermediate results,
- The controller unit: it generates and sends control signals to all units in order to synchronize them. It is totally responsible of the system management and the data exchange between the different units by the use of the control lines.
- Mode 0: this mode is used for the Key and the signature generation. After the selection of an elliptic curve E(a,b), a point G ∈ E(a,b) of order n and a cryptographically strong random number d which is the private key in the interval [1, n − 1], the controller computes the scalar multiplication using ECC IP: point . It activates the ECC IP by the signals: "Reset-ECC" (enable) and "Start-ECC" (begin the computation). If the signal "End-ECC" = 1, the outputs of the IP-ECC are the coordinates x and y of the public key Q, this is the key generation step. For the signature generation: after selecting a pseudorandom number k, the controller reactivates the ECC-IP as it is mentioned earlier in order to compute . Then, it sends the signal "Start-Red" to the pseudo-Mersenne-reduction block to convert to an integer -conv. After that, the controller tests if -conv = 0, then the step of random number generation will be repeated, else, the controller activates the inversion block, via the signal "Start-Inv", in order to calculate . Here, the inversion and the Mersenne reduction operations are independent, so, they can be done in parallel. Receiving the signal "END-Inv" indicating the end of the inversion, the controller activates the SHA-2 IP. The output of the SHA-2 IP is the message digest e. Receiving the signal "End-SHA2", the controller activates the multiplication operation, by sending the signal "Start-Mul", in order to perform . The Carry Look Ahead Adder (CLA) is used to calculate . The block of multiplication is reactivated to calculate . Computing the second multiplication, the controller tests the value of s, if then return to the step of random number generation, else returns the signature of the message m which is . As it is mentioned, the ECC-IP and the multiplication block are used twice in the Mode 0.
- Mode 1: it is responsible for the signature verification. The inversion block and the SHA-2 IP are reactivated to calculate respectively and . Receiving the signals "End-Inv" and "End-SHA2", the multiplication block is reactivated by the controller to compute firstly and then . After receiving the signal "End-Mul", the controller sends the signal "Start-AddMong" to the Addition-Montgomery block to calculate using the point addition formula on the elliptic curve. The controller tests the value of X: if , so, the signature will be rejected, else, it calculates . Finally, the signature will be accepted only if .
6. Implementation Results of ECDSA and Performance Analyses
7. Security Analyses of ECDSA Processor
- To ensure that one cannot easily solve the discrete logarithm problem and therefore obtain the secret key,
- The hash function used is a one-way collision-resistant hash function.
- The secret key can be obtained using k, r, and s when the generator for k is predictable.
7.1. Fault Injection Attack: No Correctness Check for Input Points
7.2. Restart Attack
8. Conclusions and Future Works
Acknowledgments
Author Contributions
Conflicts of Interest
References
- The FIPS 186-4 Elliptic Curve Digital Signature Algorithm Validation System (ECDSA2VS). Available online: http://csrc.nist.gov/groups/STM/cavp/documents/dss2/ecdsa2vs.pdf (accessed on 18 March 2014).
- Panjwani, B.; Mehta, D.C. Hardware-software Co-design of elliptic curve digital signature algorithm over binary fields. In Proceedings of the International Conference on Advances in Computing, Communications and Informatics (ICACCI), Kochi, India, 10–13 August 2015; pp. 1101–1106. [Google Scholar] [CrossRef]
- Montgomery, P.L. Speeding the pollard and elliptic curve methods of factorization. Math. Comput. 1987, 48, 177–243. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology. Secure hash standard. In Federal Information Processing Standards 180-2; Federal Information Processing Standards Publications (FIPS PUBS): USA, 2002. [Google Scholar]
- Petit, J.; Sabatier, P. Analysis of ECDSA authentication processing in VANETs. In Proceedings of the IEEE 3rd International Conference on New Technologies, Mobility and Security, Cairo, Egypt, 20–23 December 2009; pp. 388–392. [Google Scholar] [CrossRef]
- Khalique, A.; Singh, K.; Sood, S. Implementation of elliptic curve digital signature algorithm. Int. J. Comput. Appl. 2010, 2, 21–27. [Google Scholar] [CrossRef]
- Nabil, G.; Naziha, K.; Lamia, F.; Lotfi, K. Hardware implementation of elliptic curve digital signature algorithm (ECDSA) on Koblitz curves. In Proceedings of the 8th International Symposium on Communication Systems, IEEE Networks and Digital Signal Processing (CSNDSP), Poznan, Poland, 18–20 July 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Belgarric, P.; Fouque, P.A.; Macario-Rat, G.; Tibouchi, M. Side-channel analysis of weierstrass and koblitz curve ecdsa on android smartphones. In Proceedings of the Cryptographers’ Track at the RSA Conference on Topics in Cryptology CT-RSA, San Francisco, CA, USA, 29 February–4 March 2016; Volume 9610, pp. 236–252. [Google Scholar] [CrossRef]
- Biswas, S.; Misic, J. A cross-layer approach to privacy-preserving authentication in wave-enabled vanets. IEEE Trans. Veh. Technol. 2013, 62, 2182–2192. [Google Scholar] [CrossRef]
- Plos, T.; Hutter, M.; Feldhofer, M.; Stiglic, M.; Cavaliere, F. Security-enabled near-field communication tag with flexible architecture supporting asymmetric cryptography. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2013, 21, 1965–1974. [Google Scholar] [CrossRef]
- Gueron, S.; Krasnov, V. Fast prime field elliptic-curve cryptography with 256-bit primes. J. Cryptogr. Eng. 2015, 5, 141–151. [Google Scholar] [CrossRef]
- Pessl, P.; Hutter, M. Curved tags-a low-resource ecdsa implementation tailored for RFID. In Proceedings of the 10th International Workshop, RFIDSec, Revised Selected Papers Radio Frequency Identification: Security and Privacy Issues, Oxford, UK, 21–23 July 2014; Volume 8651, pp. 156–172. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, D.; Zou, X.; Lin, H.; Cheng, J. Design of an elliptic curve cryptography processor for RFID tag chips. Sensors 2014, 14, 17883–17904. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.S.; Xu, Y.; Yen, S.D.; Bi, Y.; Hwang, G.W. Hot carrier injection stress effect on a 65 nm LNA at 70 GHz. IEEE Trans. Devices Mater. Reliab. 2014, 14, 931–934. [Google Scholar] [CrossRef]
- Yuan, J.S.; Bi, Y. Process and temperature robust voltage multiplier design for RF energy harvesting. Microelectron. Reliab. 2014, 55, 107–133. [Google Scholar] [CrossRef]
- Pan, W.; Zheng, F.; Zhao, Y.; Zhu, W.T.; Jing, J. An efficient elliptic curve cryptography signature server with GPU acceleration. IEEE Trans. Inf. Forensics Secur. 2017, 12, 111–122. [Google Scholar] [CrossRef]
- Bi, Y.; Yuan, J.S.; Jin, Y. Beyond the interconnections: Split manufacturing in RF designs. Electronics 2015, 4, 541–564. [Google Scholar] [CrossRef]
- Alasad, Q.; Bi, Y.; Yuan, J.S. E2LEMI: Energy-efficient logic encryption using multiplexer insertion. Electronics 2017, 6, 16. [Google Scholar] [CrossRef]
- Wang, X.; Yin, Y.L.; Yu, H. Finding Collisions in the Full SHA-1. In Proceedings of the 25th Annual International Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2005; Springer; Volume 3621, pp. 17–36. [Google Scholar]
- Hell, M.; Johansson, T. Grain: A stream cipher for constrained environments. Int. J. Wirel. Mob. Comput. 2007, 2, 86–93. [Google Scholar] [CrossRef]
- Kanso, A.A. An efficient cryptosystem Delta for stream cipher applications. Comput. Electr. Eng. 2009, 35, 126–140. [Google Scholar] [CrossRef]
- Mansouri, S.S.; Dubrova, E. An improved hardware implementation of the grain stream cipher. In Proceedings of the 13th Euromicro Conference on Digital System Design: Architectures, Methods, and Tools (DSD), Lille, France, 1–3 September 2010; pp. 433–440. [Google Scholar]
- El hadj youssef, W.; Zeghid, M.; Machhout, M.; Rached, T. Design and performance testing of arithmetic operators library for cryptographic applications. Int. J. Comput. Sci. Eng. Syst. (IJCSES) 2007, 1, 201–212. [Google Scholar]
- Zeghid, M.; Bouallegue, B.; Machhout, M.; Baganne, A.; Tourki, R. Architectural design features of a programmable high throughput reconfigurable SHA-2 Processor. J. Inf. Assur. Secur. 2008, 2, 147–158. [Google Scholar]
- Sghaier, A.; Zeghid, M.; Bouallegue, B.; Baganne, A.; Machhout, M. Area-time efficient hardware implementation of elliptic curve cryptosystem. arXiv, 2015; arXiv:0710.4810 [cs.CR]. [Google Scholar]
- Sutter, G.; Deschamps, J.; Imana, J. Efficient elliptic curve point multiplication using digit-serial binary field operations. IEEE Trans. Ind. Electron. 2013, 60, 217–225. [Google Scholar] [CrossRef]
- Roy, S.; Rebeiro, C.; Mukhopadhyay, D. Theoretical modeling of elliptic curve scalar multiplier on LUT-based FPGAs for area and speed. IEEE Trans. VLSI Syst. 2013, 21, 901–909. [Google Scholar] [CrossRef]
- Liu, S.; Ju, L.; Cai, X.; Jia, Z.; Zhang, Z. High Performance FPGA implementation of elliptic curve cryptography over binary fields. In Proceedings of the IEEE 13th International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom), Beijing, China, 24–26 September 2014; pp. 148–155. [Google Scholar] [CrossRef]
- Khan, Z.U.A.; Benaissa, M. High speed ECC implementation on FPGA over GF(2m). In Proceedings of the International Conference on Field-programmable Logic and Applications (FPL), Lausanne, Switzerland, 2–4 September 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Kerckhoffs, A. La cryptographie militaire. J. Sci. Mil. 1883, IX, 5–38. [Google Scholar]
- Rodrigues, J.M. Transfert sécurisé d’images par combinaison de techniques de compression, cryptage et marquage. Thèse Soutenue, Université Montpellier II, Montpellier, France, 2006. [Google Scholar]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E.; Leigh, S.; Levenson, M.; Vangel, M.; Banks, D.; Heckert, A.; et al. A Statistical Test Suite for Random and Pseudo-Random Number Generator for Cryptographic Applications. Available online: http://nvlpubs.nist.gov/nistpubs/Legacy/SP/nistspecialpublication800-22r1a.pdf (accessed on 19 June 2017).
- Elhadjyoussef, W.; Benhadjyoussef, N.; Machhout, M.; Rached, T. Low power elliptic curve digital signature design for constrained devices. Int. J. Secur. (IJS) 2012, 6, 2. [Google Scholar]
- Ben Hadj Youssef, N.; El Hadj Youssef, W.; Machhout, M.; Tourki, R.; Torki, K. A low-resource 32-bit datapath ECDSA design for embedded applications. In Proceedings of the International Carnahan Conference on Security Technology (ICCST), Rome, Italy, 13–16 October 2014; pp. 1–6. [Google Scholar]
- Knezevic, M.; Nikov, V.; Rombouts, P. Low-latency ECDSA signature verification a road towards safer traffic. Cryptol. ePrint Arch. 2014, 24, 3257–3267. [Google Scholar] [CrossRef]
- Vanstone, S.A. Next Generation Security for Wireless: Elliptic Curve Cryptography, 2003. Available online: http://www8.cs.umu.se/kurser/5DV153/HT14/literature/vanstone2003next.pdf (accessed on 19 June 2017).
- Vaudenay, S. The Security of DSA and ECDSA. In International Workshop on Public Key Cryptography PKC 2003: Public Key Cryptography-PKC; Springer: Berlin/Heidelberg, Germany; Miami, FL, USA, 2003; Volume 2567, pp. 309–323. [Google Scholar]
- Parrilla, L.; Castillo, E.; Morales, P.D.; Garcia, A. Hardware activation by means of PUFs and elliptic curve cryptography in field-programmable devices. Electronics 2016, 5, 5. [Google Scholar] [CrossRef]




| Modules | Cycles | Frequency | Area | Power | Throughput | Efficiency |
|---|---|---|---|---|---|---|
| (MHz) | (Slices) | (mW) | (Mbit/s, Slices) | |||
| Implementation without optimization | ||||||
| SHA-256 | 64 | 77 | 773 | 39 | 308 | 0.398 |
| Implementation with optimizations | ||||||
| SHA-256 | 32 | 73 | 1480 | 50 | 584 | 0.394 |
| Area | Frequency | Time | Power | |
|---|---|---|---|---|
| Slices | MHz | s | mW | |
| ECC over | 9670 | 147.5 | 282.79 | 45 |
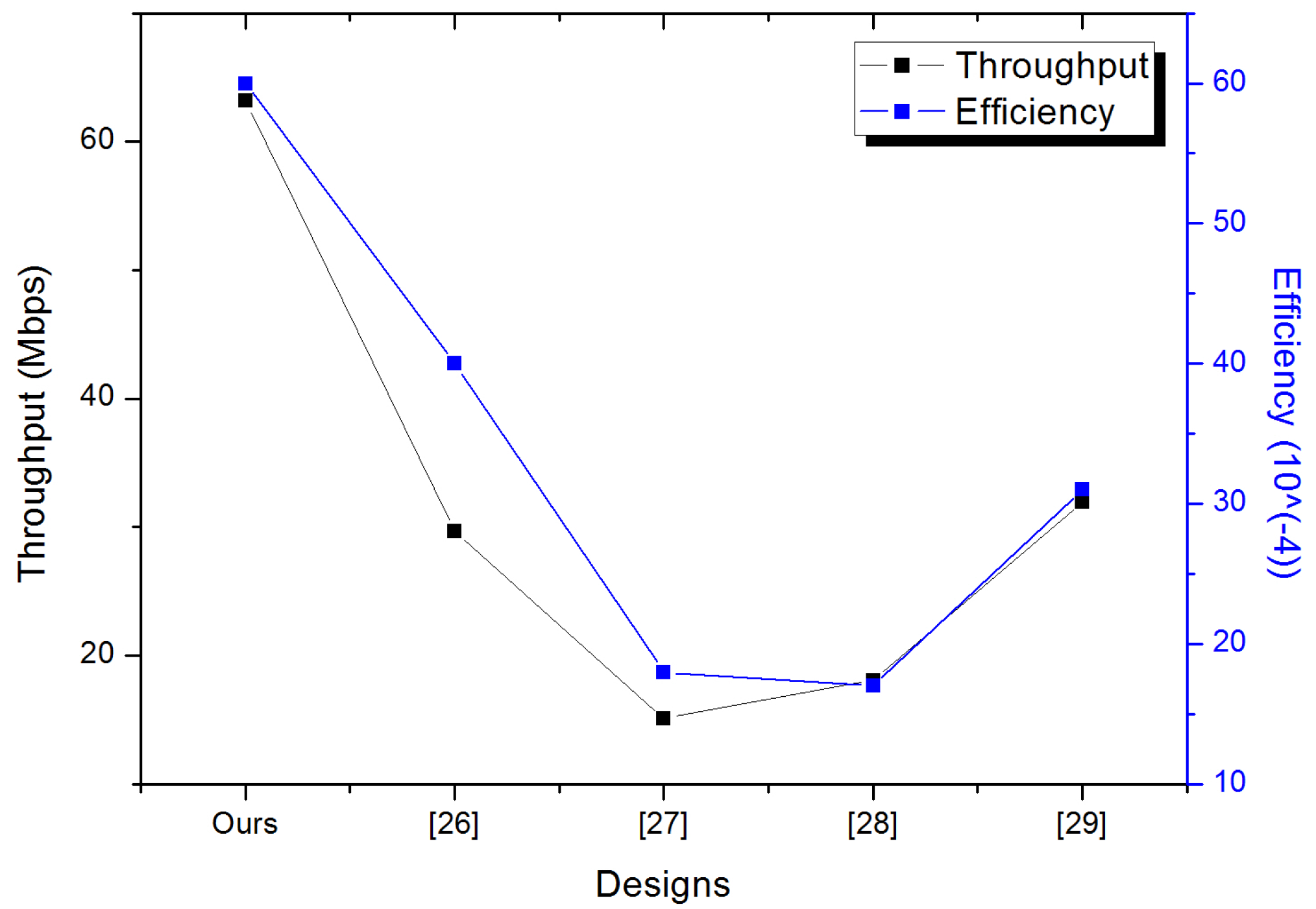
| Designs | Curve | FPGA | Clock | Area | Freq. | Time | Throughput | Efficiency |
|---|---|---|---|---|---|---|---|---|
| Cycles | Slices | (MHz) | (s) | (Mbps) | ||||
| This work | virtex5ML50 | 380 | 9670 | 221 | 2.58 | 63.17 | 0.0060 | |
| ECC [26] | Virtex5 | 1371 | 6150 | 250 | 5.48 | 29.7 | 0.0040 | |
| ECC [27] | Virtex5 | 1414 | 8095 | 131 | 10.70 | 15.1 | 0.0018 | |
| ECC [28] | XC4VLX200 | 1091 | 10,417 | 121 | 9.00 | 18.1 | 0.0017 | |
| ECC [29] | Virtex5 | 780 | 10,363 | 153 | 5.10 | 31.97 | 0.0031 |
| Encryption Algorithms | Key Length (Bit) | Initialization Vector (Bit) |
|---|---|---|
| RC4 | 8-2048 | 8 |
| MUGI | 128 | 128 |
| A5/1 | 64 | 114 |
| W7 | 128 | 128 |
| CA 16 × 16 | 256 | 16 |
| Grain-80 | 80 | 64 |
| Grain-128 [31] | 128 | 96 |
| Statistical TEST | Pseudorandom Number Generators | ||||
|---|---|---|---|---|---|
| A5/1 | W7 | CA | Grain-80 | Grain-128 | |
| Monobit | 0.0026 × | 0.0022 × × | 0.0025 × | 0.0109 × | 0.0178 × |
| Frequency | 0.0028 × | 0.0016 × | 0.0018 × | 0.0101 × | 0.0168 × |
| Runs | 0.0049 × | 0.0046 × | 0.0045 × | 0.0131 × | 0.0196 × |
| Longest-Run | 0.0021 × | 0.0025 × | 0.0010 × | 0.012 × | 0.0182 × |
| Matrix Rank | 0.0012 × | 0.0012 × | 0.0013 × | 0.0102 × | 0.0136 × |
| DFT (Spectral) | 0.0009 × | 0.00095 × | 0.0015 × | 0.0098 × | 0.0112 × |
| Non-overlapping | 0.00085 × | 0.0011 × | 0.0009 × | 0.0095 × | 0.0119 × |
| Template Matching | |||||
| Overlapping Template | 0.00092 × | 0.0027 × | 0.0012 × | 0.0101 × | 0.0123 × |
| Matching | |||||
| Universal Statistical | 0.0023 × | 0.0036 × | 0.0027 × | 0.0125 × | 0.0161 × |
| Linear Complexity | 0.0012 × | 0.0015 × | 0.0017 × | 0.0107 × | 0.0132 × |
| Serial | 0.0035 × | 0.0026× | 0.0031 × | 0.0099 × | 0.0111 × |
| Approximate Entropy | 0.0017 × | 0.0041 × | 0.0021 × | 0.012 × | 0.0143 × |
| Cusums | 0.0011 × | 0.0035 × | 0.0033 × | 0.0112 × | 0.0117× |
| Random Excursions | 0.0027 × | 0.0022 × | 0.0023 × | 0.0108 × | 0.0123 × |
| Random Excursions | 0.0031 × | 0.0033 × | 0.0015 × | 0.0125 × | 0.0135 × |
| Variant | |||||
| PRNG | Frequency | Area | Consumption | Throughput | Efficiency |
|---|---|---|---|---|---|
| (MHz) | (Luts) | (mW) | (Mbps) | ||
| Grain-80 | 230.9 | 355 (3%) | 13.72 | 230.9 | 0.65 |
| Grain-128 | 238.5 | 495 (4%) | 19.22 | 238.5 | 0.48 |
| A5/1 | 250.376 | 110 (1%) | 46.33 | 250.376 | 2.27 |
| W7 | 188.590 | 777 (7%) | 111.77 | 1508.72 | 1.94 |
| CA 16 × 16 | 308.550 | 683 (6%) | 52.75 | 39,622.4 | 58.011 |
| Grain IP | SHA-2 IP | ECC IP | Pseudo- Mersenne- Reduction | Inversion | Multiplication | CLA | Addition Montgomery | |
|---|---|---|---|---|---|---|---|---|
| Key Generation | ON | OFF | OFF | OFF | OFF | OFF | OFF | OFF |
| OFF | OFF | ON | OFF | OFF | OFF | OFF | OFF | |
| Signature Generation | ON | OFF | OFF | OFF | OFF | OFF | OFF | OFF |
| OFF | ON | ON | OFF | OFF | OFF | OFF | OFF | |
| OFF | OFF | OFF | ON | OFF | OFF | OFF | OFF | |
| OFF | OFF | OFF | OFF | ON | ON | OFF | OFF | |
| OFF | OFF | OFF | OFF | OFF | OFF | ON | OFF | |
| OFF | OFF | OFF | OFF | OFF | ON | OFF | OFF | |
| Signature Verification | OFF | ON | OFF | OFF | ON | OFF | OFF | OFF |
| OFF | OFF | OFF | OFF | OFF | ON | OFF | OFF | |
| OFF | OFF | OFF | OFF | OFF | ON | OFF | OFF | |
| OFF | OFF | OFF | OFF | OFF | OFF | OFF | ON |
| FPGA Implementation | |||
|---|---|---|---|
| Designs | Area | Frequency | Power |
| (Slices) | (MHz) | (mW) | |
| SHA-256 | 1480 | 73 | 50 |
| ECC | 9670 | 147.5 | 45 |
| Grain-128 | 495 | 238.5 | 19.22 |
| ECDSA | 18,504 | 107.4 | 105 .7 |
| ASIC Implementation | |||
| Designs | Area cell | Frequency | Total dynamic Power |
| (mm) | (MHz) | (mW) | |
| SHA-256 | 0.023 | 1282 | 18.4070 |
| ECC | 0.121 | 990 | 39 |
| Grain128 | 0.006572 | 1695 | 6.404 |
| ECDSA | 0.257 | 532 | 63.444 |
| FPGA Implementation Results | ||||||||
|---|---|---|---|---|---|---|---|---|
| Design | Platform | Field | Freq. | Area | Time | Power | Through. | Eff. |
| (Bits) | (MHz) | (Slices) | (ms) | (mW) | (Mbps) | |||
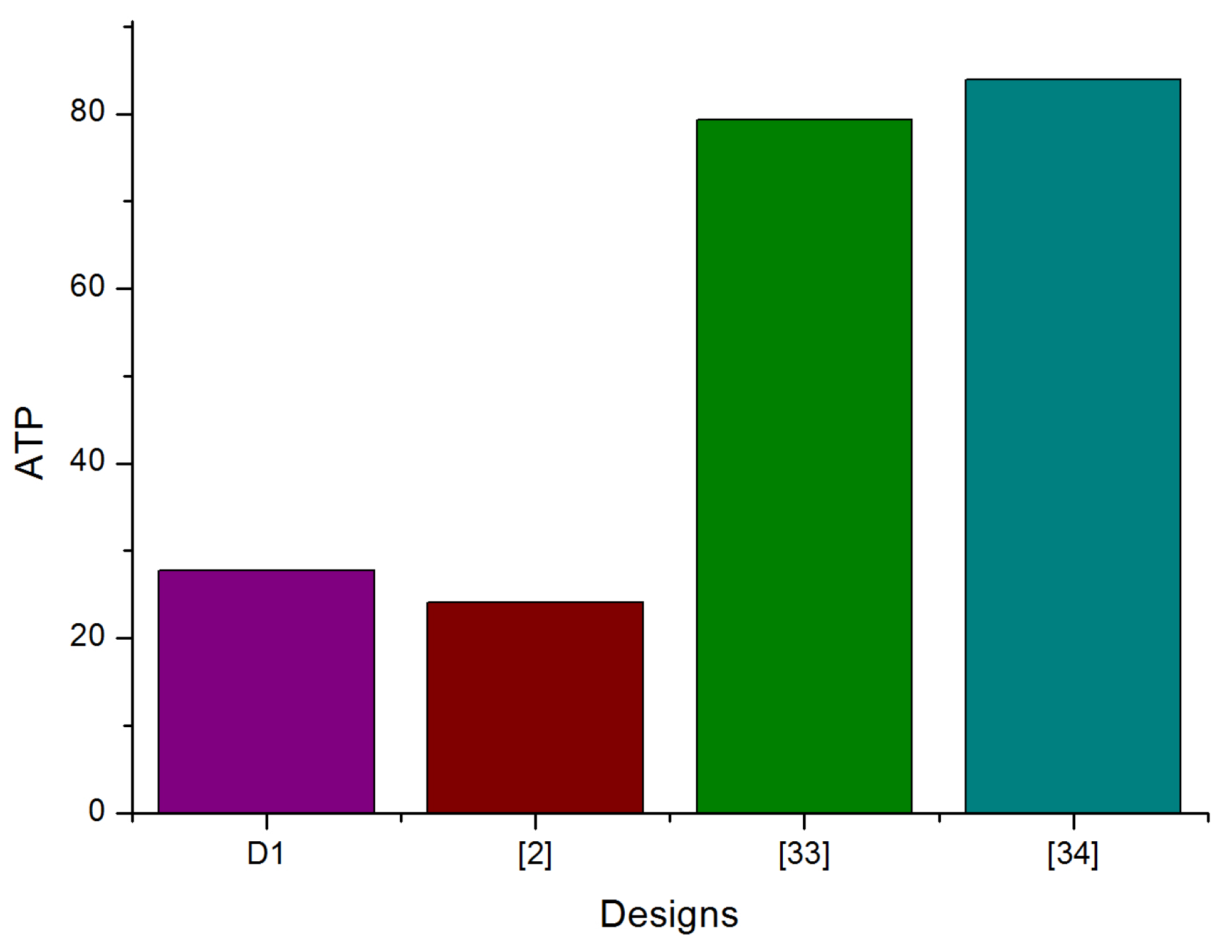
| Virtex-5 | ) | 107.4 | 18,504 | 1.5 | 199.95 | 0.16 | 88 × 10 | |
| [2] | Virtex-6 | 100 | 18,740 | 1.287 | - | - | - | |
| [33] | Virtex-5 | ) | 148.963 | 20,628 | 3.844 | 228 | - | - |
| [34] | Virtex-5 | 195.309 | 23,760 | 3.533 | - | - | - | |
| ASIC Implementation Results | ||||||||
| Design | Platform | Field | Freq. | Area | Power | Through. | Eff. | |
| (Bits) | (MHz) | (mW) | ||||||
| ASIC 45 nm | 532 | 0.257 mm | 63.444 | 0.81 | 3.16 | |||
| [35] | ASIC 45 nm | 500 | 322.1 KGE | - | - | - | ||
| [34] | ASIC 45 nm | 500 | 1.135 mm | - | - | - | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sghaier, A.; Zeghid, M.; Massoud, C.; Mahchout, M. Design And Implementation of Low Area/Power Elliptic Curve Digital Signature Hardware Core. Electronics 2017, 6, 46. https://doi.org/10.3390/electronics6020046
Sghaier A, Zeghid M, Massoud C, Mahchout M. Design And Implementation of Low Area/Power Elliptic Curve Digital Signature Hardware Core. Electronics. 2017; 6(2):46. https://doi.org/10.3390/electronics6020046
Chicago/Turabian StyleSghaier, Anissa, Medien Zeghid, Chiraz Massoud, and Mohsen Mahchout. 2017. "Design And Implementation of Low Area/Power Elliptic Curve Digital Signature Hardware Core" Electronics 6, no. 2: 46. https://doi.org/10.3390/electronics6020046
APA StyleSghaier, A., Zeghid, M., Massoud, C., & Mahchout, M. (2017). Design And Implementation of Low Area/Power Elliptic Curve Digital Signature Hardware Core. Electronics, 6(2), 46. https://doi.org/10.3390/electronics6020046






