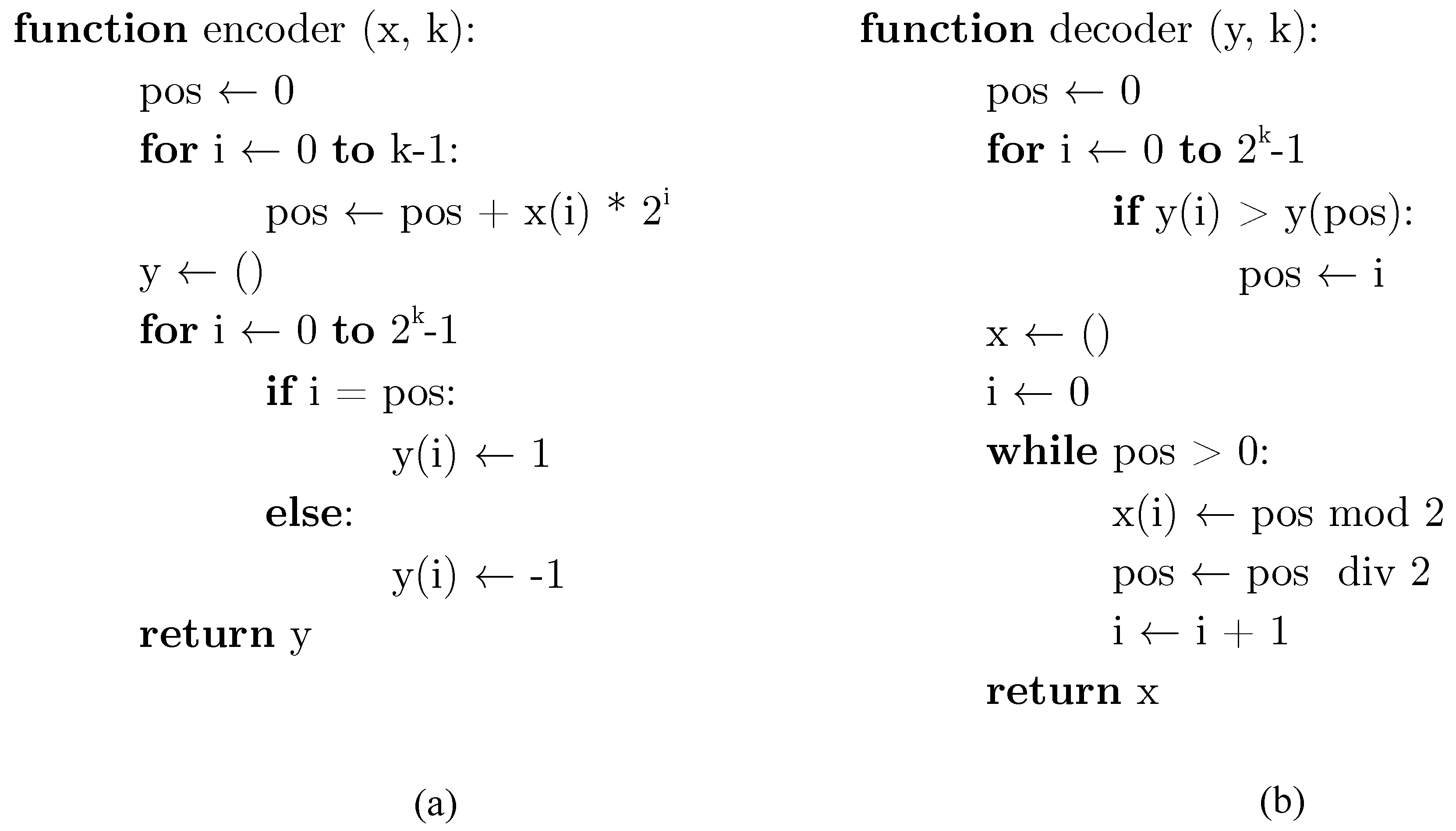A Novel Channel Coding Scheme for RFID Generation-2 Systems

Abstract

Low complexity and efficient algorithms for Radio-Frequency Identification (RFID) are crucial to foster low-cost and energy-saving solutions. With the aim of lowering the complexity of the radio circuitry, and inspired by the superposition codes concept, we propose a novel encoding algorithm for tag-to-reader communication channels of modern RFID systems. We show that the developed scheme—despite the simplicity of its hardware realization—allows a coding gain comparable to the one obtained by the more complex Viterbi decoding of the Miller 4 modulation scheme used in the EPC Generation 2 Class 1 RFID standard. Simulation results prove the effectiveness of the proposed solution for low-cost tags, under different signal-to-noise ratios (SNRs) and interrogation time durations. Although our numerical evaluation mainly focuses on the EPC Generation-2 standard, we believe that the proposed scheme will also be attractive for future Ultra-wideband RFID systems.

1. Introduction

In recent years, systems employing radio frequency identification (RFID) have been growing exponentially [1] as industry realized the potential of this technology when applied to complex manufacturing processes. RFID proved to be an effective and low-cost solution for many key aspects of the so-called “smart factory”, such as asset tracking, supply chain monitoring, inventory control, and access management. As the technology becomes cheaper, it is becoming increasingly prevalent in many applications, and it is widely adopted in other contexts, from mobile payment solutions and passports to virtually any application using the Internet-of-Things (IoT) paradigm [2].

RFID technology consists of multiple tags and at least one reader which exchange information under a specific communication protocol. Depending on the sources of the operating power, tags are usually divided into three categories: passive, semipassive, and active [2,3,4]. Among them, low cost and long life make passive tags an attractive solution despite their limited link budget. In fact, passive tags have no internal power source: the electromagnetic energy transmitted by the reader powers the internal circuit of the tag, and the same energy is also used to reply to the reader. Under this perspective, simple algorithms in the field of RFID technology become fundamental to the development of both low-cost and energy-saving solutions. In particular, energy-efficient solutions could be implemented in RFID systems where tags are made by recyclable materials to be integrated in goods, clothes, and packing. This can be realized by using “green electronics” with recyclable, possibly organic, materials [5].

However, despite the advantages of RFID, there are still some significant issues to be solved, such as the resolution of collisions. The RFID air-interface protocol defines the physical layer, line coding, structure of messages, operating modes, and algorithms for preventing, detecting, and resolving the collisions during communications [6]. Considering a couple of passive tags deployed in the environment, the reader issues a query command and the desired tag replies, ideally leading to a successful identification. Actually, multiple tags are scattered in the range of the reader, increasing the chance that several of them will respond simultaneously, generating a collision.

Hence, one of the current problems with RFID systems is related to the insufficient performance of the anti-collision algorithm, since the wireless RFID environment (e.g., a marketplace) is usually affected by fading noise [7,8], and collisions can significantly degrade the channel efficiency.

RFID anti-collision protocols can be classified into Aloha-based protocols and tree-based protocols. Aloha-based protocols reduce the probability of tag collisions by spreading out tag responses over time, while the latter family of protocols guarantees on the time required to read all tags in the range. Due to their simplicity, Aloha-based protocols were quickly adopted in early RFID systems [9]. A variation of the frame slotted Aloha (FSA) protocol—referred to as Q-algorithm—is used in the widespread UHF EPC Class 1 Generation-2 protocol (hereafter Gen-2 for brevity), which became a standard in 2006 as part of ISO/IEC 18000-6 as amendment 18000-6C [10].

However, the Q-algorithm still shows some drawbacks. For example, all the messages exchanged add a significant overhead on the channel, and its dynamic slot updates require time to converge to the best configuration. Several studies have been carried out in order to improve the performance of Aloha-based protocols in the presence of collisions [11,12,13,14]. However, most of these works depend on the estimation of the tag population in the reader’s range, leveraging on results obtained in the previous time slots. In addition, the authors usually consider ideal air interface conditions, while anti-collision performance highly depends on the physical level of channel noise [15].

Apart from improving the access control mechanism, it is also possible to tackle the collisions at the signal coding level by increasing the robustness of the signal transmitted on the noisy radio channel, so that the receiver is able to correctly reconstruct the original signal, even in case of collisions. Moreover, coding scheme and collision-avoidance protocol are not mutually exclusive; on the contrary, they are complementary approaches that can be combined to increase the overall tag detection probability.

In particular, the current Gen-2 standard supports two types of baseband data encoding schemes prior to the amplitude shift keying (ASK) or phase shift keying (PSK) modulator: a scheme of bi-phase space (FM0) and a Miller baseband data encoding scheme.

A new scheme for the structure of Gen-2 tags [10,16] has been proposed in [8], which includes a channel encoder block based on a convolutional coding scheme and a corresponding decoder block in the receiver system. However, this type of complex decoder impacts the energy efficiency and the cost of passive tags. In [17], the same idea has been further investigated and expanded by considering a turbo coded scheme where an outer convolutional code is serially concatenated to the FM0 and Miller baseband codes, regarded as inner codes.

Since RFID applications require low-cost and low-complexity solutions, we propose a novel Gen-2 modulation scheme inspired by the superposition codes concept and featuring low complexity hardware implementation. Actually, the coding process acts on very short codewords, with a length equal to four bits, and the decoding algorithm may be implemented by an analog comparator which chooses the maximum signal among four. We apply the proposed encoding method to the Gen-2 FM0 modulated signal, with the same code rate of Miller subcarrier modulator.

The proposed scheme has been verified and evaluated through MATLAB simulation of Gen-2 MAC level [18]. Results show that our approach outperforms the more complex Viterbi hard decoding-Miller 4 modulation scheme under different noise levels and interrogation interval conditions, despite the low complexity of the proposed decoder. We have also considered the performance of the Viterbi soft decoding using the same modulation: surprisingly, the performance of our novel and simple decoding algorithm is not far from the best attainable performance for the Miller 4 case.

The rest of the article is organized as follows. Section 2 describes the system model and details the proposed coding and decoding schemes. The simulation environment used for performance evaluation is provided in Section 3, and Section 4 compares the results of the proposed algorithm with the hard and soft Viterbi schemes. Finally, some concluding remarks wrap up and close the article in Section 5.

2. System Model

We consider a single-reader system where the tags are the only interfering entities. As is known, RFID system performance is strongly affected by the amount of channel noise in the return link process. If there is an error in identifying the tag response signal, the system needs to repeat another inventory round. This requires a long time to identify tags information. Thus, we introduce a channel coding algorithm in the Gen-2 system to guarantee high probability of tag identification, while reducing the time spent for the procedure.

The system model consists of the proposed encoder (Section 2.1), placed before the FM0 modulator into the tag as in [8], and the proposed decoding scheme (Section 2.2) implemented inside the reader.

2.1. The Proposed Coding Algorithm

Inspired by the superposition codes concept [19], we developed a simple coding rule that allows a fast soft decoding algorithm which can be easily included in the reader receiver FM0 detector, keeping a significant coding gain. In the FM0 approach, the binary “0” bi-phase space has a transition in the middle of a symbol, whereas the binary “1” does not.

We will focus on the code rate equal to $1/2$, because the decoding performance will be compared with the output of a Miller 4 modulation scheme, decoded by a Viterbi algorithm [8,18].

Let $\mathbf{x}=(x_0,x_2,...,x_{K-1})$ be the encoder input bits, while $\mathbf{y}=(y_0,y_2,...,y_{N-1})$ represents the output, where $K={\log }_2\left(N\right)$, with $K=2,N=4$ in the presented results. The output codeword has all bits equal to zero, except the one whose position corresponds to the binary-to-decimal conversion of the input vector $\mathbf{x}$.

An example of the coding process is shown in Figure 1, and describes the transmission of the codeword $(0,1)$, which may be converted to the decimal number 2 by considering the first bit as the less-significant one. The output of the coder corresponds to the positional codeword, where the bit equal to 1 in the third position (i.e., $y_2$) represents the decimal number 2. Actually, any different univocal mapping can be used, by just considering the constraint to have only one bit different from zero in the output codeword in order to keep the same low decoding complexity.

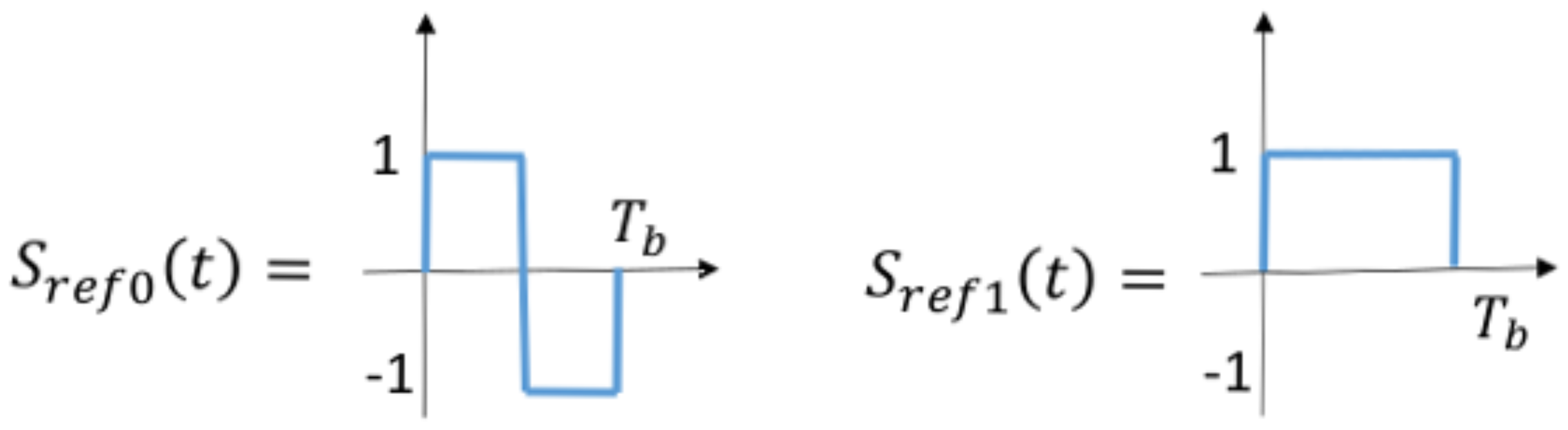
The transmission process ends by modulating the codeword bits of $\mathbf{y}$ by using the reference signal waveforms $S_{ref0}\left(t\right)$ and $S_{ref1}\left(t\right)$ described in Figure 2, producing the transmitted continuous time signal $y\left(t\right)$. The described coder could be simply realized, for instance, by employing a low complexity boolean circuit with two signal inputs and four outputs.

2.2. The Proposed Decoding Algorithm

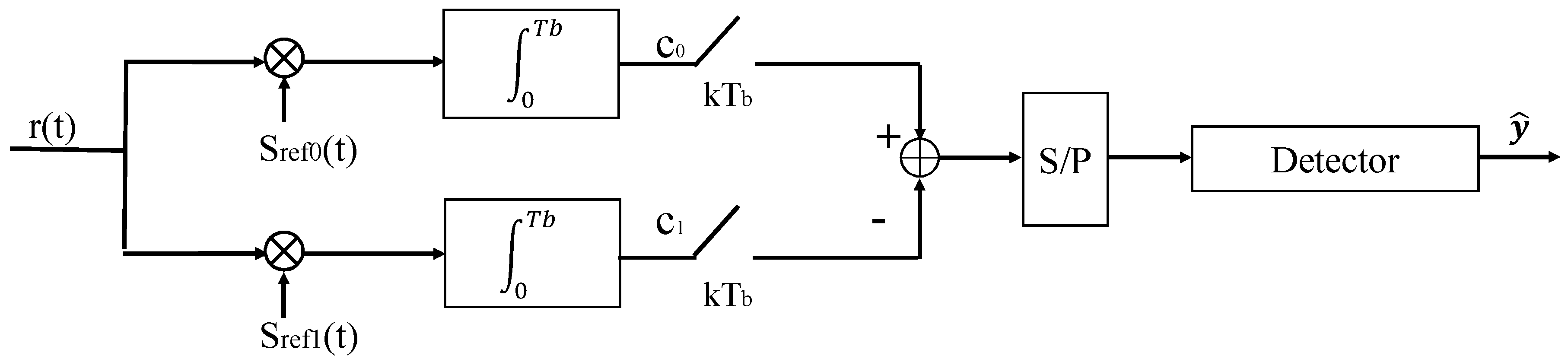
The proposed scheme allows an easy soft decoding detector that finds the maximum of the received codeword and outputs the decimal-to-binary conversion of the position index as decoded string.

Figure 3 shows the proposed receiver architecture—it consists of a signal correlator block followed by the proposed decoder to obtain the estimated output $\widehat{\mathbf{y}}$.

The received signal $r\left(t\right)$ is affected by additive, white, and Gaussian noise (AWGN), slow-fading, and inter-tag interference. We consider—as usual for UHF RFID systems—no inter-symbol interference:

$$r\left(t\right)=\alpha y\left(t\right)+n\left(t\right)+i\left(t\right),$$

(1)

where $y\left(t\right)$ is the transmitted signal, $n\left(t\right)$ represents the AWGN, the attenuation α represents the slow-fading effect, $i\left(t\right)$ the inter-tag interference, while the estimate of the transmitted coded bits is:

$$\widehat{y}\left(i{T}_b\right)=c_0\left(i{T}_b\right)-c_1\left(i{T}_b\right),$$

(2)

where $c_0\left(i{T}_b\right)$ and $c_1\left(i{T}_b\right)$ represent the output of the squared correlation between the received signal $r\left(t\right)$ and, respectively, the FM0 bit waveform $S_{ref0}\left(t\right)$ and $S_{ref1}\left(t\right)$, sampled at the bit timing $T_b$ [20]:

$$c_0\left(i{T}_b\right)={\left|{\int }_{(i-1)T_b}^{i{T}_b}{S}_{ref0}\left(t\right)r\left(t\right)dt\right|}^2$$

(3)

$$c_1\left(i{T}_b\right)={\left|{\int }_{(i-1)T_b}^{i{T}_b}{S}_{ref1}\left(t\right)r\left(t\right)dt\right|}^2$$

(4)

We have considered a square-law non coherent detector, since it is most used in applications because of its simplicity. Anyway, the proposed decoding idea is independent of the particular detector, so it is possible to use, for instance, a more performant coherent detection scheme.

After that, a serial-to-parallel (S/P) converter block outputs the estimate of the transmitted codeword, representing the decoder input as in the following:

$$\widehat{\mathbf{y}}=[\widehat{y}\left(i{T}_b\right),\widehat{y}\left((i-1)T_b\right),...,\widehat{y}\left((i-N+1)T_b\right)]\doteq \left\{\widehat{y}\left((i-j)T_b\right)\right\},$$

(5)

with $j=0,1,...,N-1$.

Finally, the decoder output $\widehat{\mathbf{x}}=(x_0,x_1)$ provided by the detector is the decimal-to-binary conversion of $\arg \left({\max }_j\left(\widehat{\mathbf{y}}\right)\right)$.

It is important to note that the proposed decoding algorithm only uses the outputs of the usual symbol detector, without adding further complexity. A possible hardware implementation could be realized by a comparator which chooses the maximum among $N=4$ different input signals, represented by Equation (5). Moreover, it requires the same robustness against synchronization errors of the common detector.

3. Simulation Environment

Simulations were perfomed at the Medium Access Control (MAC) Gen-2 packet level considering a realistic scenario for performance evaluation. Thus, we have added the proposed codec scheme in the already existing RFID Gen2 MATLAB simulator described in [18], and freely available for download at [21]. The modified MATLAB code is available as supplementary material.

In the simulator, we assume that command packets (Select, Query, and ACKnowledgement) are generated by the reader and broadcast to the tags. Each tag responds individually to the command based on its current status (active/standby). Tags are implemented as independent state machines synchronized to the interrogator Query commands, so the number of tags active in each interrogation round is time-varying.

We assume no error in the downlink, which means that the tags are always able to decode the reader packets. On the other hand, uplink tag packets are corrupted by AWGN channel noise and inter-tag interference; we do not consider inter-symbol interference (ISI), as usual for UHF RFID.

The simulated reader is able to detect all tag collisions, as long as they transmit different RN16 numbers [10,16].

The simulator implements slow fading with Rayleigh distribution for both uplink and downlink channels, with fading coefficients ${\gamma }_T$ and ${\gamma }_R$ exponentially distributed—squared Rayleigh random variables—with unit mean.

According to Gen-2 standards, tag symbols could be coded as either FM0 or Miller. The original implementation in the simulator was based on hard-decision Viterbi and Miller 4 for decoding tag packets. In contrast, our scheme consists of FM0 for coding tag symbols and the proposed codec algorithm. Figure 4 shows the MATLAB code which implements the encoding and decoding functions of the proposed scheme, as described in Section 2. Moreover, in order to enrich the comparison, we added the soft-decision version of the Viterbi decoding scheme as an alternative to the hard one. For both hard and soft decision decoding methods, we set $k/n=1/2$, $N=32$, $K=16$, constraint length $L=2$, and number of states S equal to $2^L=4$.

The setting of the simulation parameters is in line with Wireless Identification and Sensing Platform (WISP) [18], an actual implemented battery-free and programmable RFID sensor device compliant with the EPC Generation 1 protocol RFID platform [22]. The values of the main parameters used for simulations is shown in

Table 1. Setting of the simulation parameters.

Variable	Description	Default Value
BLF	backscatter link frequency	250 kHz
MO	Miller order	4
Tari	data-0 symbol	24 $\mathsf{\mu }$s
EPC	packet length	128 bits
RTcal	reader-to-tag calibration	3.0 × Tari
$T_{Cls}$	duration of a collided query	1.8 ms
$T_{Emp}$	duration of an empty query round	1.1 ms
$T_{IA}$	duration of an invalid ACK query round	2.5 ms
$T_{SF}$	duration of a successful query round	5.0 ms
M	number of listening tags	12

.

4. Simulation Results

The behavior of passive tags in the considered RFID system is cyclical with total period T, including an “on” interval of length $T_{on}$, in which a tag is in operating and able to communicate to reader, and an “off” interval of length $T_{off}$ in which it is in stand-by mode only harvesting energy (voltage restoration interval). Hence, the cycle T for each tag is defined as $T=T_{on}+T_{off}$, and its duration is determined by charge/discharge patterns and in real-world implementations depends on the specific node circuitry.

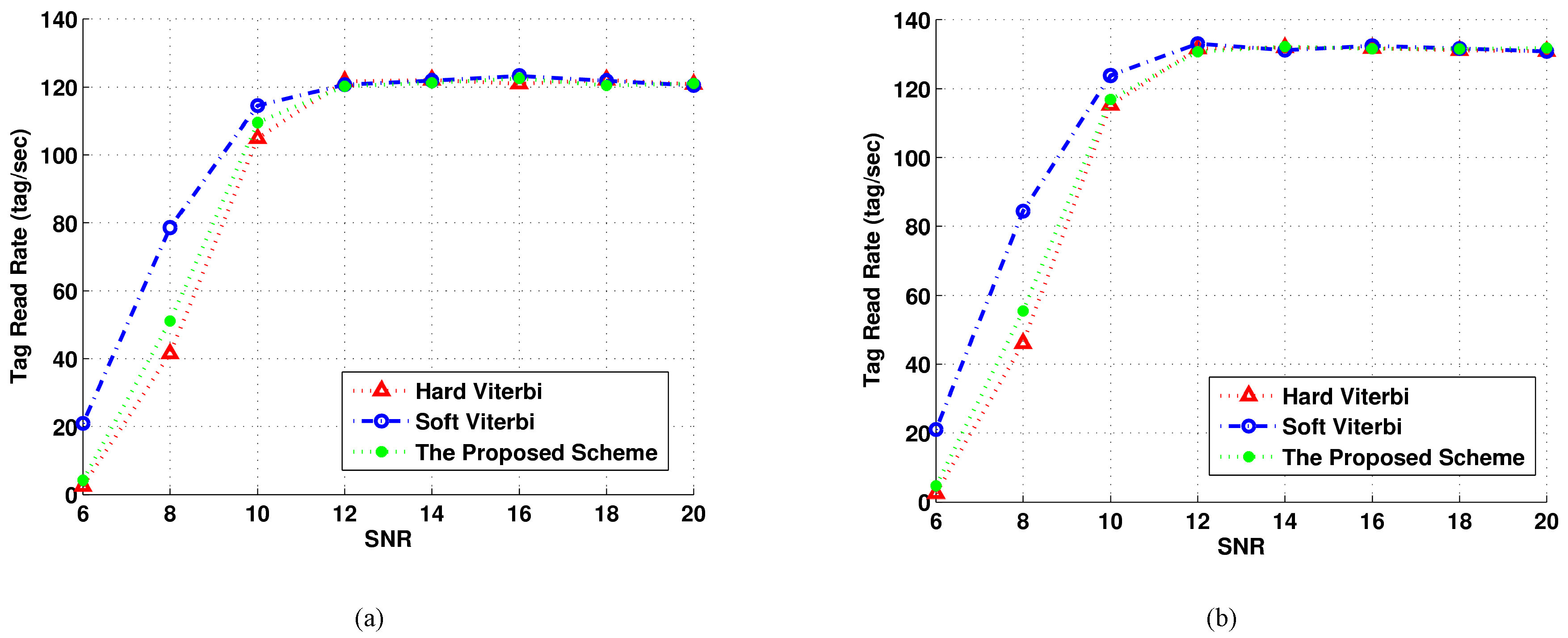
The three different coding schemes (i.e., the proposed algorithm, Hard Viterbi, and Soft Viterbi) have been compared in terms of tag read rate (TRR), defined as the number of successful tag query rounds of length $T_S$ in a unit of time, where $T_s$ is the average number of successful queries that occurs during the interval $T_{on}$.

Figure 5 clearly shows that TRR depends on $T_{on}$/$T_S$: changing the ratio from 5 to 20 provides a read rate gain up to ten tags per second. This is mainly due to the fact that if $T_{on}$ is too small; just a low number of queries might be successful. Moreover, as noted in [18], TRR grows as the ratio increases, but not proportionally: the average rate of successful queries tends to the asymptotic rate as $T_{on}$/$T_S$ reaches a value of about 20–30. This is true not only for the original hard Viterbi scheme, but also for the soft decision algorithm, and most importantly, for our proposed scheme. This means that the behaviour of our approach is similar to those of the other well-established codes.

Looking at the numerical results, as expected, the soft decision Viterbi decoder has the best performance—its applicability in real battery-powered devices is still limited, but here we consider it a performance reference for our system.

It is interesting to note that at lower SNR values (≤10 dB), the proposed soft decoding algorithm performs slightly better with respect to the more complex Viterbi hard decoded scheme. The maximum gain—regardless of the $T_{o}n$/$T_S$ value—is at 6 dB, when our scheme provides a TRR gain of about 10% over the hard solution. This is mainly due to the fact that the proposed scheme (although with a very low hardware complexity) implements a soft decision decoding algorithm, since the comparator implementing the decoder chooses the maximum among the four bit waveforms by looking at the analog output of the receiver correlator.

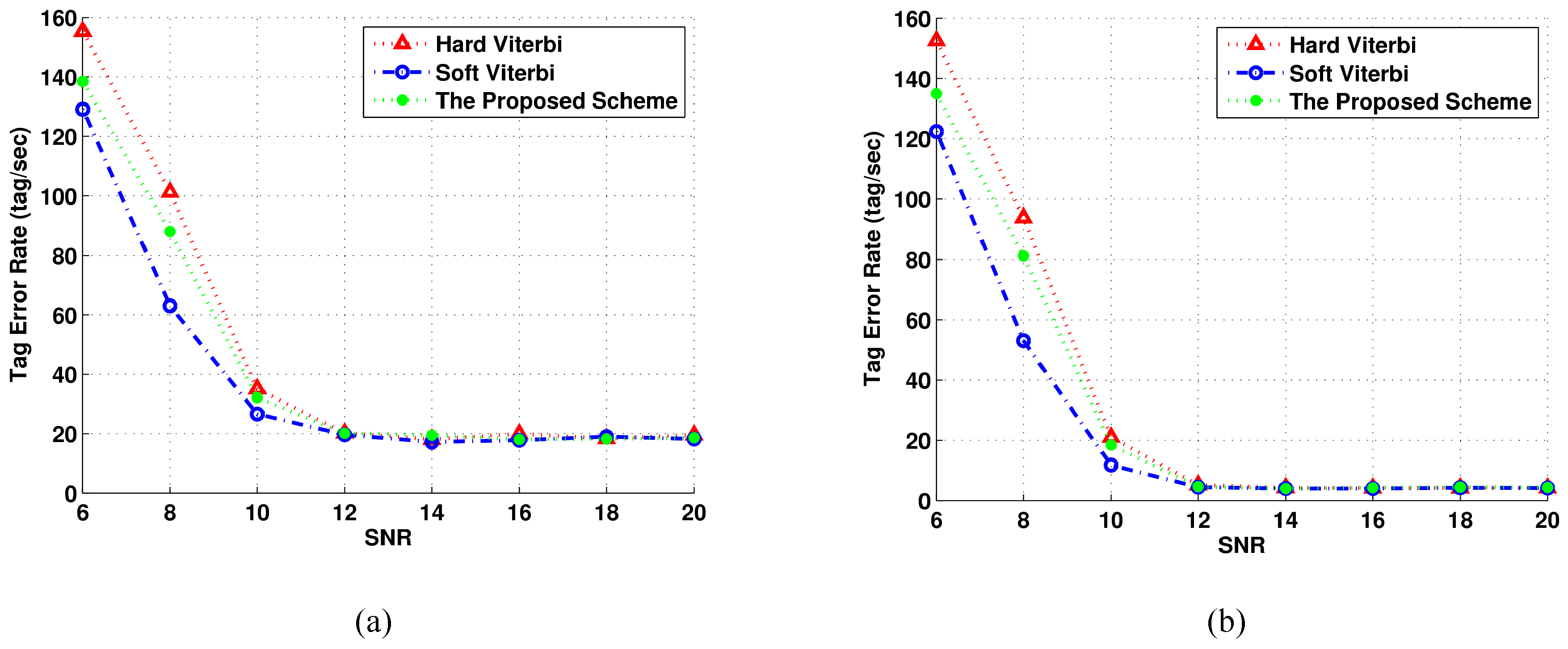
We have also investigated the dual metric of TRR (i.e., the tag error rate (TER) in a unit of time) by considering the number of unsuccessful interrogations. Figure 6 represents the TER performance in the same conditions described above. As expected, at lower SNR values the performance of our approach lays between the soft and the hard Viterbi decoding scheme.

Regarding the complexity, the proposed scheme is comparable to an analog demodulation by maintaining satisfactory performance with respect to the more complex hard-decisioned Viterbi decoder. Actually, the decoder circuit may be implemented in a completely analog manner, by also avoiding the use of more complex analog-to-digital converters.

Moreover, the proposed scheme acts only on a codeword of length equal to just 4 bits, different from the Viterbi decoders that both use a minimum codeword length equal to 32. This can be better appreciated by looking at

Table 2. Computational Complexity Analysis: $S=4$ states of the two Viterbi decoders.

Scheme	Codeword Lenght N	Number of Operations	Number of Comparisons
Soft decision Viterbi	32	$2·S·N$ Euclidean distances	$S·N$
Hard decision Viterbi	32	$2·S·N$ Hamming distances	$S·N$
Proposed scheme	4	-	N

, where both Viterbi decoders shall compute $2·S·N$ distances, with N equal to 32 at least, while the proposed scheme is just an analog demodulator working on four parallel waveforms.

5. Conclusions

In this article, we have proposed a new encoding algorithm for tag-to-reader RFID communication channels. The low-complexity decoder is suitable for RFID applications that require both low-cost and energy-saving solutions, like in battery-powered and passive-based systems.

Despite its simple hardware implementation, the proposed solution has the same performance as a Viterbi hard decoding of the Miller 4 modulation scheme, even better for lower values of the channel signal-to-noise ratio due to the soft decision on the analog output of the receiver correlator. Results obtained through simulations have shown the feasibility and the performance of the proposed solution under different SNR conditions. The evaluation focused on the Gen-2 standard, but we strongly believe that the proposed scheme will be of interest for future UWB RFID research [23], for example by including the new positional encoding concept in a novel line encoder.

Furthermore, the low hardware cost of the decoder could be applied to wireless sensor networks (WSNs), where the energy saving is a crucial design issue, not only for tags but also for readers, as in space applications [24,25].

As an interesting perspective for future research developments, we are looking for more performant decoding schemes by adding a state-dependent coded output, in order to increase the codeword minimum distance. Obviously, the trade-off of getting a higher coding gain with respect to simple hardware realization should be adapted in order to respond to the requirements of different target applications. Further, since the proposed baseband solution may be regarded as an alternative scheme with respect to the FM0 and Miller baseband codes, it could be extended and included in a turbo coded architecture like the one presented in [17], where the FM0 and Miller coded waveforms are treated as inner codes of a turbo coded scheme.