1. Introduction
Array pattern synthesis is of paramount importance for designing modern radar systems, and it is an important and active area of research. Particularly attractive is the use of non-equispaced (or sparse) arrays, by means of which it is possible to reduce the overall number of radiating elements without a significant degradation of the performances with respect to half-wavelength equispaced arrays.
Many efficient synthesis strategies are available in the case of
fixed positions of the radiating elements [
1,
2]. These algorithms take advantage of the linear relationship between the far-field and the unknown (i.e., the excitations of the radiating elements), and, with proper constraints, require the use of fast and efficient local minimizing algorithms.
On the contrary, the efficient synthesis of non-equispaced (or sparse) arrays is an open problem. In fact, the strong nonlinearity of the radiation operator with respect to the array elements’ positions prevents the effectiveness of local minimization algorithms. The use of global minimizing approaches, like evolutionary algorithms, allows to asymptotically obtain an optimal solution of the problem. In spite of the use of hybrid techniques that adopt local minimizers for the convex part of the problem, a strong computational effort is required, in particular when the number of unknowns becomes large. In fact, for a given precision, the computational burden grows exponentially with the number of unknowns [
3].
Besides the use of evolutionary or hybrid algorithms, a number of fast deterministic synthesis techniques, based on the discretization of the current distribution obtained in case of continuous source, have been developed in the last few decades [
4,
5,
6].
Usually in these approaches, the number of radiating elements is fixed, while their positions and excitation coefficients are the output of the synthesis procedure. As a matter of fact, a number of trials is required to identify the minimum number of radiating elements. Consequently, an algorithm able to give the positions, the excitation and the number of radiating elements of the sparse array are of interest.
From a mathematical point of view, we need to identify the (hopefully) sparsest excitation providing a pattern verifying the required specifications in terms of main lobe, side-lobe levels, gain and so on. In the last decade, some dramatic advances have been obtained in the field of Sparse Recovery (SR), mainly pushed by the huge interest toward the Compressed Sensing (CS) theory. Basically, SR and CS deal with
sparse vectors, i.e., vectors having a large number of null (or almost null) elements. The success of SR and CS is due to the availability of efficient algorithms able to solve undetermined linear systems involving sparse unknowns, like the
minimization. Basically, the
minimization promotes the sparsification of the unknown vector [
7,
8,
9,
10].
Based on this behaviour, a number of researchers [
11,
12,
13] have recently used compressive sensing to promote sparsification in array synthesis.
Most of the current implementations of sparse-forcing algorithms in array synthesis problems find a sparse source that mimics a specific pattern, obtained with standard equispaced arrays synthesis techniques. Since the sparse array found by means of these approaches will radiate a pattern that is just an approximation of the specific one chosen, the specifications of the achieved layout could also be an approximation of the desired ones, and the actual performances can be known only a posteriori.
The approach described in this paper overcomes this issue by introducing a new algorithm, the Sparse-Forcing Generalized Alternate Projection (SFGAP). This algorithm is a significant improvement with respect to the CSGAP (Compressive Sensing Generalized Alternate Projections) presented in [
14], and employs a modified generalized alternate projection algorithm [
15] using
norm minimization in order to achieve the excitation and the position of the elements of a sparse array satisfying the synthesis constraints imposed by a power pattern mask. It is worth noting that the use of alternating algorithms, together with
minimization, has been shown to provide very good results in fields different from antenna array synthesis [
16,
17].
In the next section, before the discussion of the SFGAP, we would like to present the less general case of the synthesis of sparse arrays with arbitrary upper masks, by means of minimization: some of the results we will find are exploited to achieve the SFGAP.
2. Sparse Array Synthesis with Arbitrary Upper Masks
In this paragraph, we will preliminarily discuss the synthesis of sparse arrays with arbitrary upper masks; without loss of generality, we will focus on pencil beam patterns.
The sparse array synthesis can be formulated as:
where
N is the number of radiators,
is the vector of their positions,
is the vector of their relative excitations,
is an arbitrary upper mask,
is the maximum size of the linear array, and
is the array factor of the sparse array, with
,
θ being the angular direction with respect to broadside, and
β the free-space wavenumber.
Let us now introduce a dense equispaced position
ν-element vector
in the range
, with a spacing
δ much smaller than
, for instance
, where
λ is the free-space wavelength. Let
be the excitation of such a dense array, and
a
μ-element vector sampling the
u range in which the mask specifications are given; the radiation operator can be expressed as the
matrix
such that
where
is the sampled array factor.
According to the introduced notation, the synthesis of the field radiated by dense equispaced sources in the range
can be achieved by a compressive sensing approach as:
where
is the sampled upper mask and
is the sampled array factor in the direction of the maximum of the main beam.
It is important to underline that the achievement of the “sparse” solution is strictly related to the use of a
norm in Equation (6): it is not possible to use the much more computationally convenient
norm [
18]. Fortunately, there are many available software packages that allow the solution of the aforementioned
minimization problem; in particular, we used CVX (Version 2.1, CVX Research, Inc., Austin, TX, USA) [
19], which permitted an easy and direct coding of the problem in Matlab (R2016, MathWorks, Natick, MA, USA).
Let us now consider the same constraints considered in [
20]. The specifications of this pencil beam are unsymmetrical,
dB for
and
dB for
, with
. The authors of [
20] have employed an hybrid algorithm in order to solve this problem, finding a layout employing 21 radiating elements.
It has to be underlined that the use of values of
out of the range
(i.e., not restricted to the set of real angles) allows to constrain the radiation pattern also out of the visible space. This feature is particularly useful if we want to achieve the beam scanning by means of a linear phase shift of the excitations [
21]: the main beam of the pattern will be unavoidably enlarged by the linear phase scanning process, but the side lobe level will always be lower than the threshold defined by the power pattern mask.
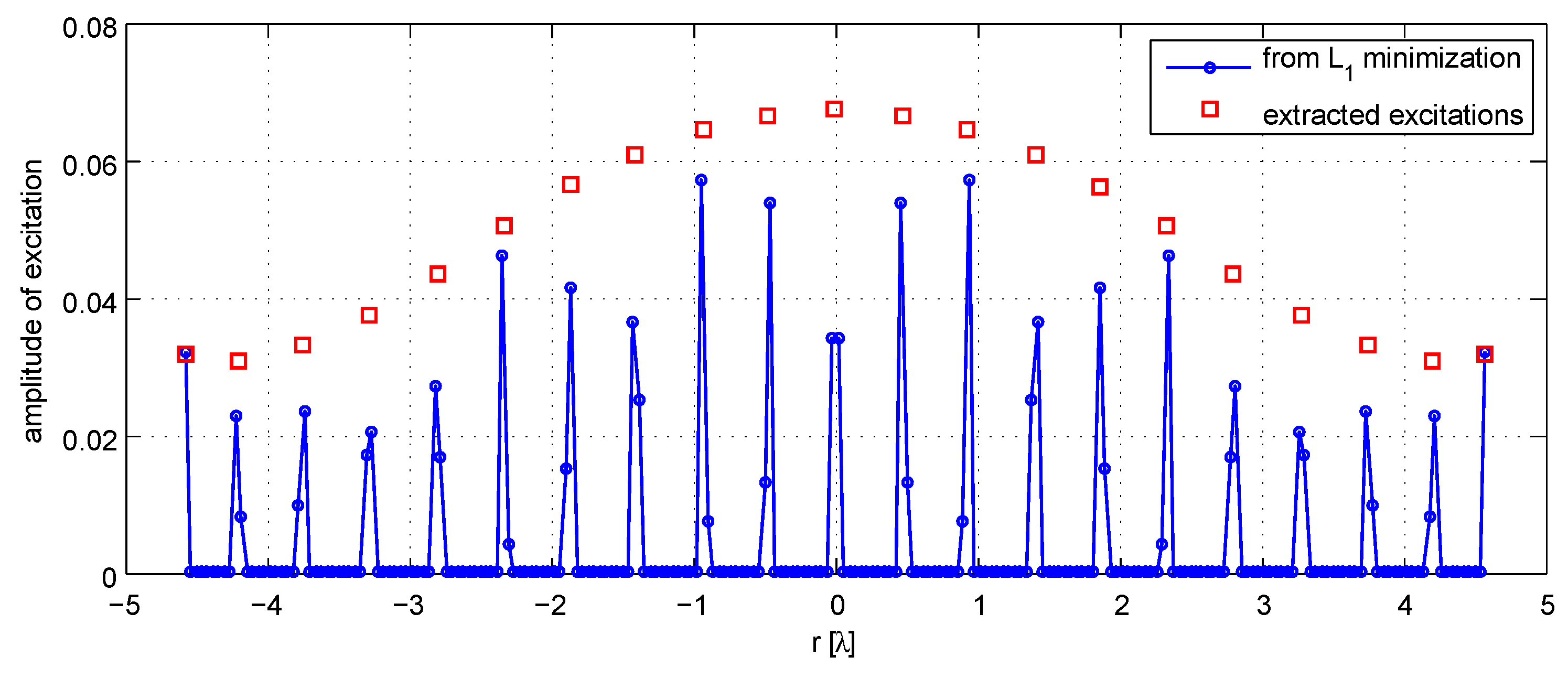
The output of the
minimization is provided in
Figure 1. The achieved excitation vector shows only 40 non null elements, but the interesting fact is that, apart from the first and last sample, the non-null excitations seem to be grouped into adjacent “couples”, and each couple can be substituted by a single element ub a suitable position.
It is evident that the “right” position of excitations has to be taken in an average coordinate between the two points. Let now
and
be the position of two
adjacent samples, of excitation
and
; the chosen position and excitation of the sparse element are then provided by
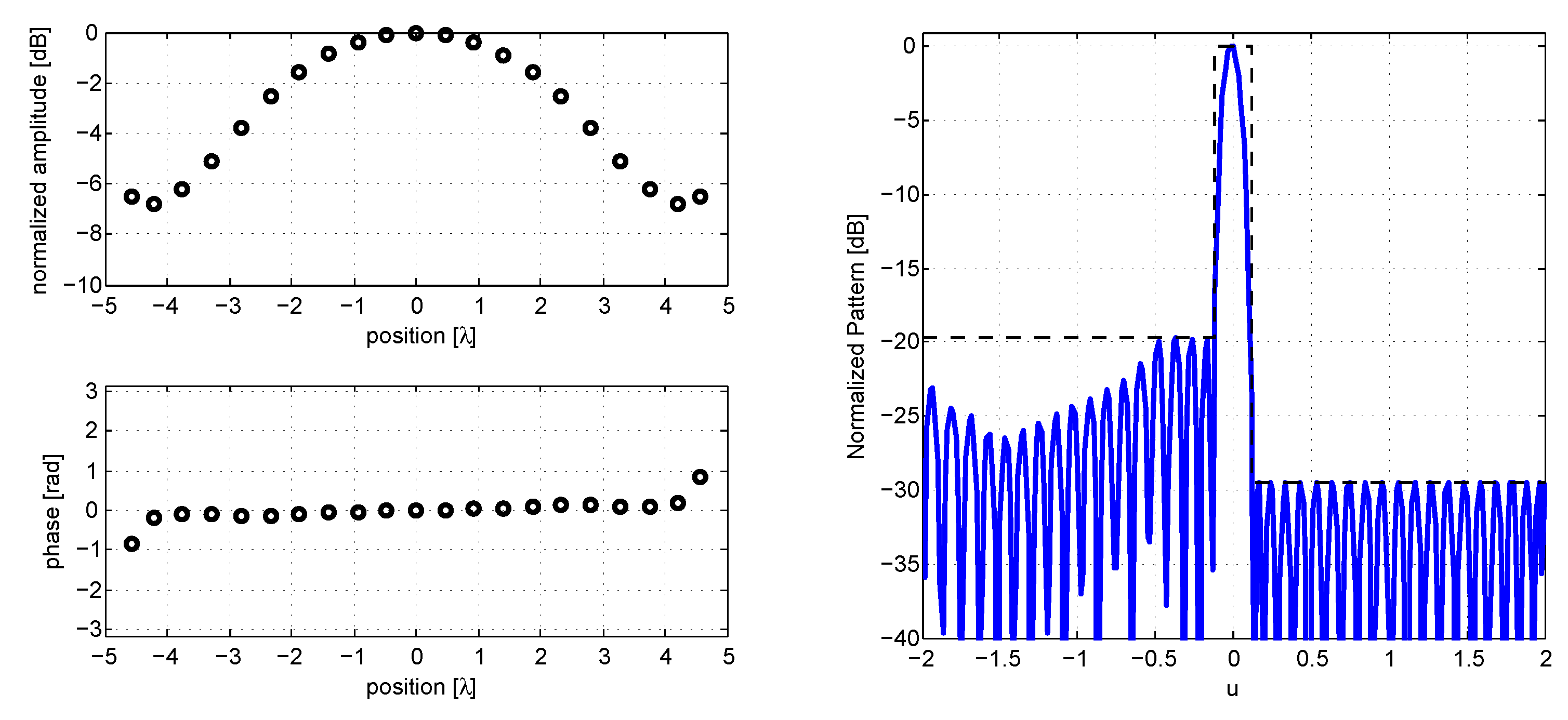
By means of this “clustering”, the overall number of excitations is reduced to 21 (that is the same value obtained by means of a much more cumbersome hybrid algorithm); the clustering in this case has a marginal effect on the the radiated pattern, which does not satisfy the power pattern mask for a fraction of dB; we can then perform a quick optimization of the excitations (always by means of CVX) in order to find the final pattern, which is provided in
Figure 2.
It is of paramount importance to emphasize two main differences with respect to [
12]: first, we use a dense equispaced excitation vector that is sampled in a much coarser way (
) instead of
), with a significant computational advantage; second, by means of the excitations’ clustering, we are able to perform, in most practical cases, a single
minimization, instead of multiple sequential ones, to achieve the desired result. Because of these two differences, the whole computation of the pencil beam pattern, including the final local optimization of the excitations, requires less than 20 s on an office PC running Matlab and CVX with an i5-2310 processor (Intel Corporation, Santa Clara, CA, USA).
We must underline that the simple
minimization is not always capable of providing a sparse solution, particularly if we deal with the synthesis of a pencil beam with a symmetrical level of the sidelobes. To overcome this problem it is possible to use the technique of sequential convex optimizations, similarly to [
12]: in the first step, we solve the problem defined by Equations (6) and (7), and in the successive ones, the non-sparse solution
obtained in step
is employed to build a weighted
norm problem as:
where
and
ϵ is a small constant, of the order of the minimum excitation we want to obtain.
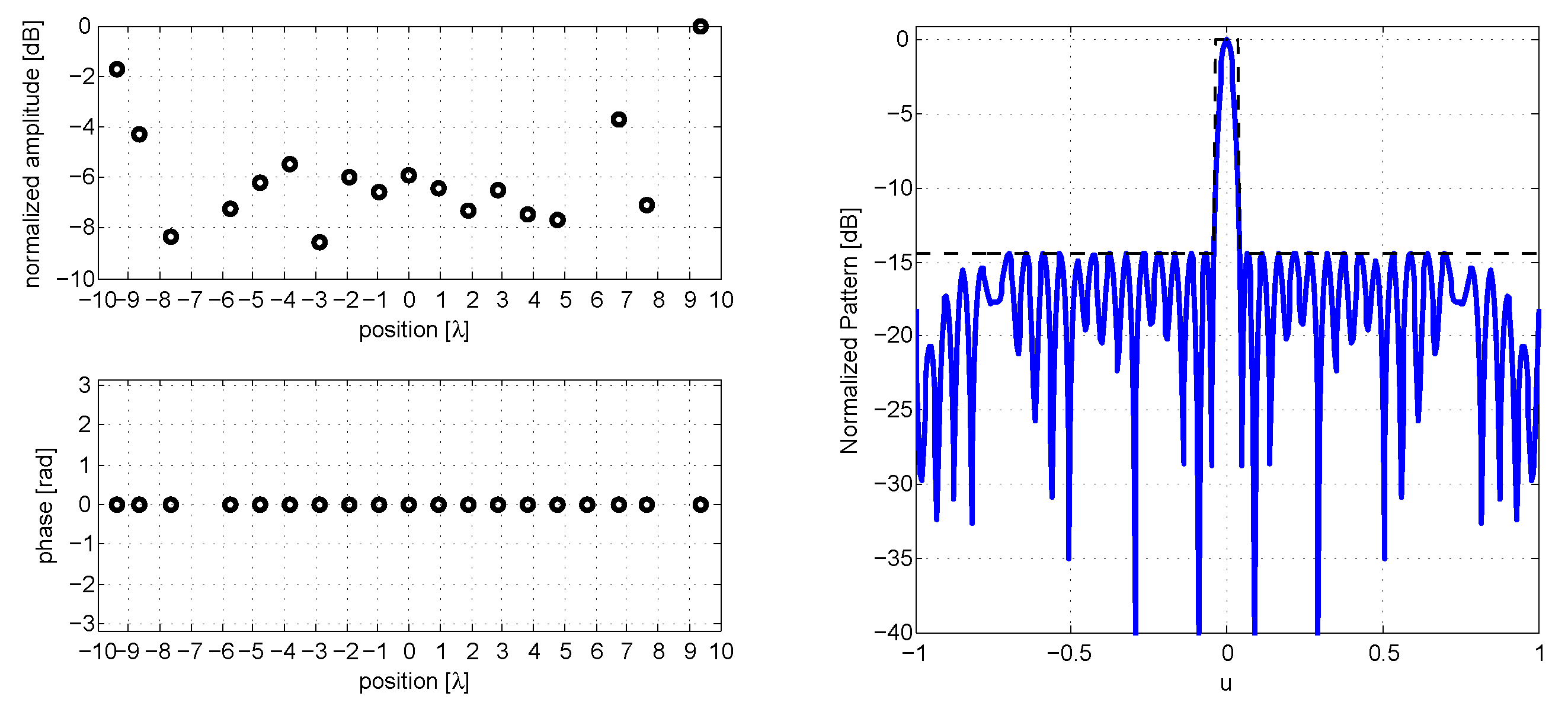
As an example, we can consider the synthesis of a sparse pencil beam array (
dB for
and
); by means of Bayesian compressive sensing [
11], the specification can be met with 24 elements, and almost met with 20 elements; by means of an evolutionary algorithm [
22], it was possible to use 19 radiating elements. With just 15 iterations of the minimization Equations (11)–(13), we are able to achieve a layout employing the same number of elements of the evolutionary approach in
Figure 3, and the specifications are perfectly met.
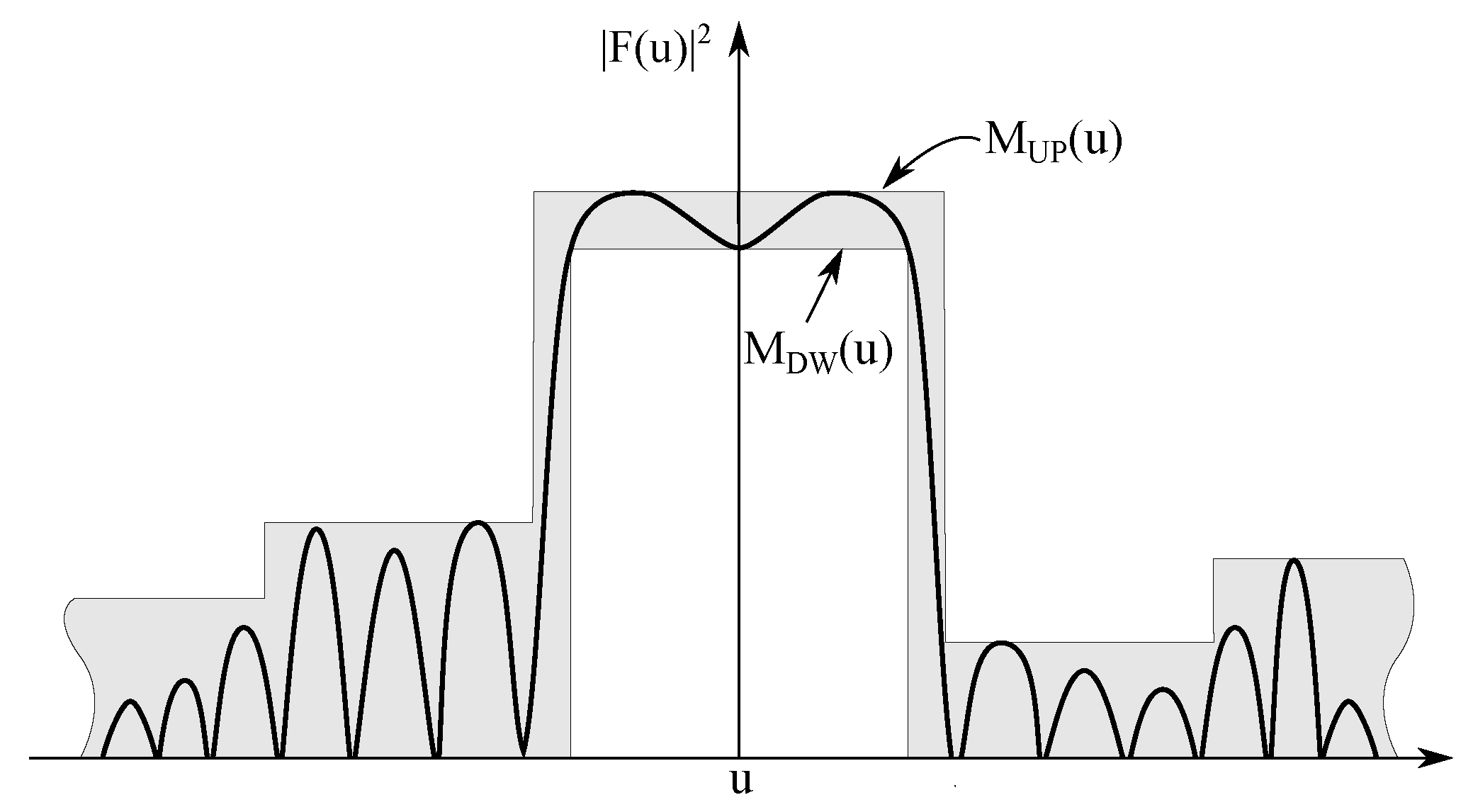
3. The SFGAP Algorithm
The convex nature of the pencil beam synthesis allowed us to obtain a quick and efficient solution by means of a simple
minimization. In general cases, the sparse array pattern synthesis is formulated in terms of an upper and a lower power pattern mask (
Figure 4), as:
Unfortunately, the above formulation does not lead to a convex problem, for which we can rapidly employ the computationally efficient methods of software packages like CVX. Other researchers have employed
minimization approaches for a shaped beam synthesis problem, like in [
12], but, in such approaches, the “shaped part” of the beam, i.e., the part of the beam that is constrained between the upper mask and a non-null lower mask, is usually sought approximating a known or given pattern in amplitude and phase. In the approach that we will discuss in this paper, we just want to define the two power pattern masks without trying to approximate a known function, making the approach more general.
This aim is realized by introducing the SFGAP method.
Let us briefly recall the general principle of the GAP (Generalized Alternate Projections) algorithm [
15]. The GAP achieves the excitation of a fixed element position array by alternatively projecting the solution on two sets: the set of the fields that can be radiated from the fixed positions, and the set of the patterns that belong to the specification’s power pattern mask.
The SFGAP algorithm differs from a standard GAP for two main reasons: first of all, the sources’ positions are taken closely spaced (much less than half the free-space wavelength) within the range in which we want to synthesize the sparse array; second, the projection on the subspace of the field that can be radiated by those closely spaced radiators is constrained by the solution of a convex problem that is similar to the norm minimization that has been employed for the pencil beam case.
Let us now discuss the two projections to be used in SFGAP; according to the notation introduced in the previous paragraph, the projected field
on the mask defined by Equations (14) and (15) can be realized by means of the well-known rule [
1]:
The projection of the field
on the space of the fields that can be radiated by the closely spaced sources can be achieved by a compressive sensing like approach, solving the problem:
where
τ is a proper threshold, the value of which will be discussed in the next paragraph.
While the projection on the set of fields belonging to the power pattern mask does not require any discussion, besides the fact that the set of fields may not be convex because of the presence of the lower mask, the latter projection needs some discussion.
The solutions of Equations (20) and (21) lead to the set of excitations whose norm is below the threshold τ that is as close as possible to the field ; the set defined by Equation (21) is a convex set, and because of the linearity of the relationship (5), also the set of fields , in which we are considering the minimization (20), is convex. Furthermore, it is easy to demonstrate that for .
We also need to underline that, differently from the minimization used in Equations (6) and (7), in this case, we minimize the distance of two fields with a threshold on the maximum norm of the excitation, but, as it will be shown in the following, it leads to a sparse solution as well.
By alternating the projections on the two sets,
and
, we should be able to find a solution belonging to the two sets, but there are two aspects that we should take into account. First, as stated before, the set
can be non-convex: when dealing with the GAP, in these cases, we usually need to pay particular attention to the choice of the starting point of the algorithm. Otherwise, it can be trapped in a local minimum, thus preventing the convergence to a solution belonging to the intersection of the two sets (see
Figure 5a).
Secondly, for a particular choice of
τ, we can not be sure that an intersection of the two sets exists, so we should choose a reasonable value of
τ for the SFGAP to work correctly (see
Figure 5b).
A possible strategy, which in our numerical experiments proved to be very robust, consists of starting the projections with a very low value of
τ; when the algorithm reaches a “trap”, the value of the threshold is increased and the projections start again. In
Figure 5c,d we provide a graphical representation of this behaviour, showing the effect of an increasing value of
τ.
The choice of starting with a low value of the threshold, and then slowly increasing it can surely solve the problem of choosing the correct value of
τ, but it also makes the algorithm less sensitive to the choice of a bad starting point. With reference to
Figure 5b–d, let us consider the sequence of fields
,
and
represented as “points” in which the algorithm has “stopped” when the threshold was, respectively,
,
and
, with
. If the intersection of
and
exists, such a sequence points in the direction of the intersection, so even if we choose a bad starting point (as in
Figure 5a), we would be able to find the solution of the synthesis problem that we are dealing with: we will find the field that fits into the power pattern mask, with the minimum
norm for the excitation.
Obviously, we can not completely avoid the problem of a bad starting point (nor the presence of multiple solutions), but in our numerical trials, we have found that within a few trials of the random starting field, we can reach the sought after solution.
What we need to achieve this desired behaviour is just a proper “increasing” strategy for the threshold. We can not increase it too slowly; otherwise, the synthesis would take too much time. Accordingly, we can not increase it too quickly. Otherwise, we could not find the field with minimum norm for the excitation.
After some numerical testing, we found that a robust yet efficient strategy for obtaining a good value for the threshold can be achieved by evaluating, at each iteration
p, the quantity:
where
is the field belonging to
at iteration
p,
is the field belonging to
at iteration
p, and
is the value of the threshold employed in iteration
p, updated according to:
where
pc is a small integer, and
α and
γ are two constants.
The main idea is to check when the relative decrease of within iterations is lower than α. If this is true, a local minimum of the algorithm is detected, and the value of is increased with a factor that depends on the actual distance of the fields , by means of the multiplicative constant γ.
In our trials, we have found that values of , , and usually lead to a good compromise of speed and accuracy of the overall algorithm. Such values have been used for all of the examples that we provide in the next section.
In summary, the SFGAP algorithm consists of the following steps:
Set the iteration counter , and define a random starting pattern and a value of ;
Increase the iteration counter p and evaluate the projection of the pattern on by Equations (17)–(19);
Calculate the field as the projection of on by Equations (20) and (21);
Evaluate by means of Equation (22), and if , calculate the value of (to be used in the next iteration) according to Equations (23) and (24);
If the termination conditions are met (for instance, a maximum value of iterations and/or a minimum value of is achieved), the algorithm stops; otherwise, go back to step 2.
The starting value of can have a small influence on the quickness of the convergence of the algorithm, since if its value is close to the final value, the overall number of iterations needed to find the solution can be lower, but such a number can be hard to guess, so, in our numerical tests, we have always used as the starting value, leaving to the adaptive increasing rules (23) and (24) the duty of finding the correct value for τ.
It is worth noting that the SFGAP shares some similarities with the CSGAP proposed in [
14]; both of the algorithms are an extension of the generalized alternate projection algorithm, but in the CSGAP at each iteration, we solve the following minimization problem:
where
is the threshold at step
h, which is chosen according to the following rule
,
being the starting value of the threshold. The use of Equations (25) and (26) is very sensitive with respect to the choice of the starting point and of
, making this algorithm much less “stable” and effective with respect to the SFGAP introduced in the present paper. In the following, we will provide some examples of applications of the proposed method.
4. Results
To validate the proposed approach, we will now show the results of some synthesis examples; in particular, we will discuss two sparse arrays, capable of radiating a flat-top beam to be employed—for instance, in a virtual subarray radar architecture [
23].
As the first test case, we will investigate a flat-top synthesized by other researchers [
12,
24,
25] who have tried to minimize the number of feeds required to achieve the pattern with the desired specifications (
for
,
for
), finding that a minimum number of 10 elements is needed.
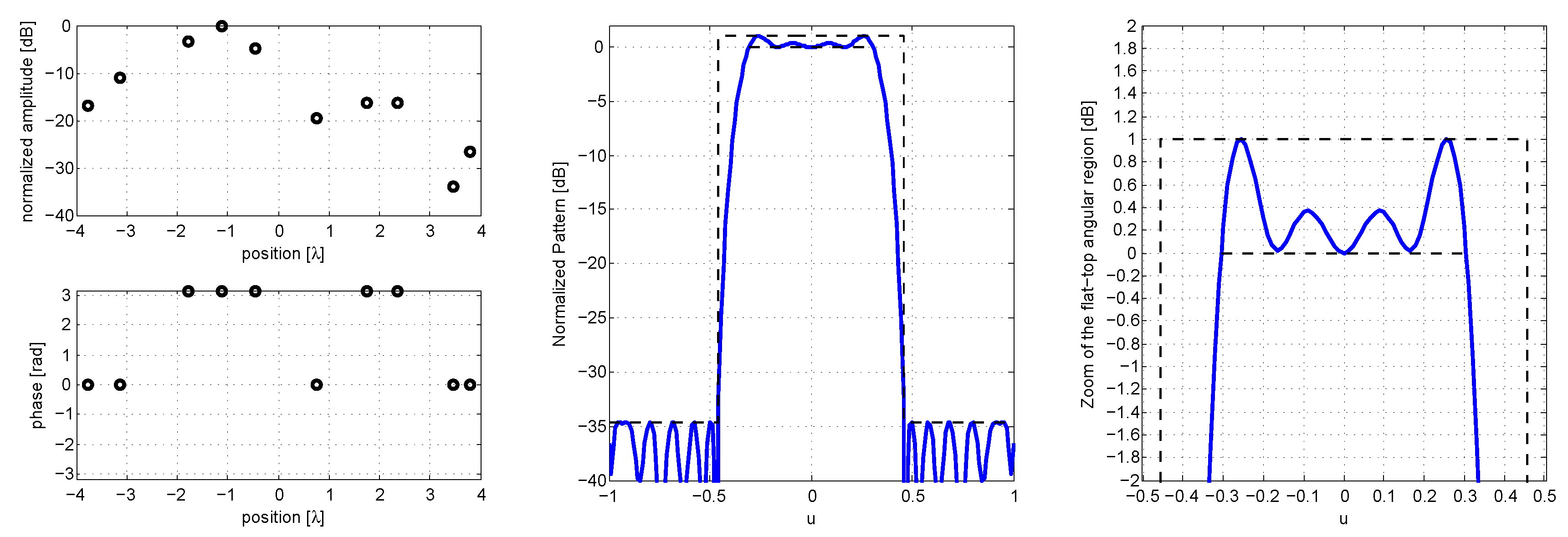
By means of the SFGAP we are also able to find a sparse array with 10 elements, radiating a pattern satisfying the mask constraints (see
Figure 6, providing excitations, overall pattern and a particular of the flat top region), but
without seeking a preliminarily calculated solution, as in the methods employed by other researchers.
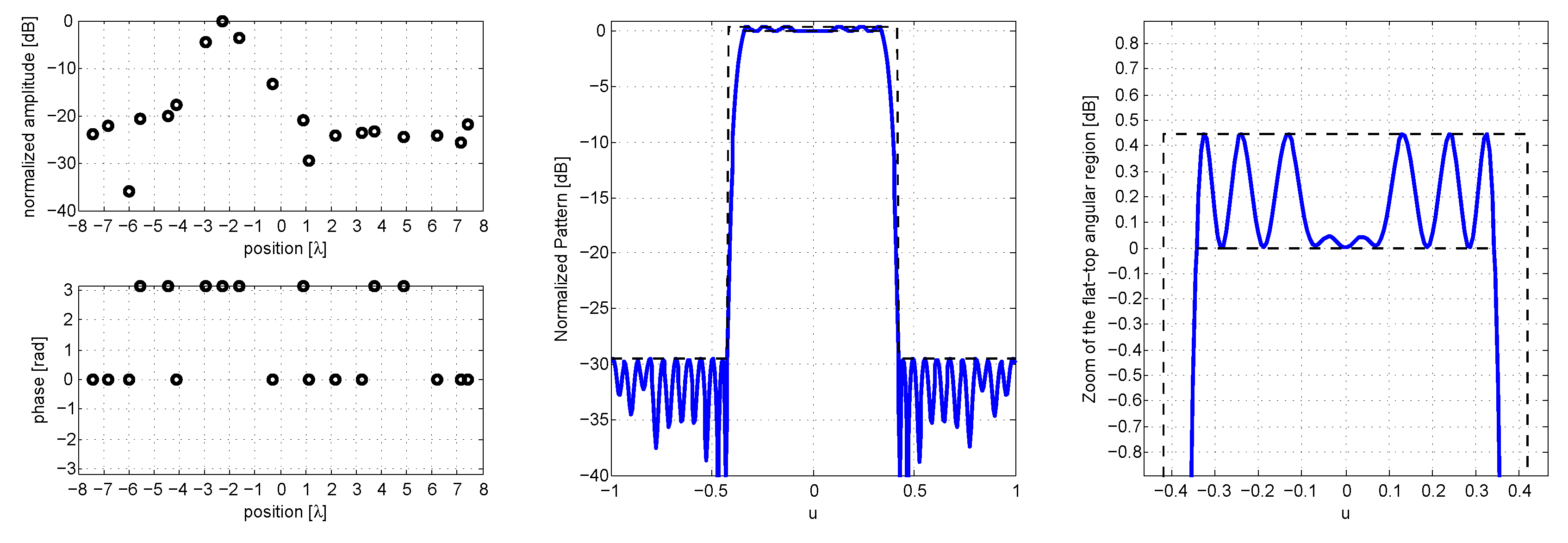
In a second example, we consider the flat-top pattern specifications used in [
26], in particular, the case with 31 radiating elements (
for
,
for
). In our case, the SFGAP is capable of satisfying the same power pattern mask with only 19 radiating elements (see
Figure 7, providing excitations, overall pattern and a particular of the flat top region).
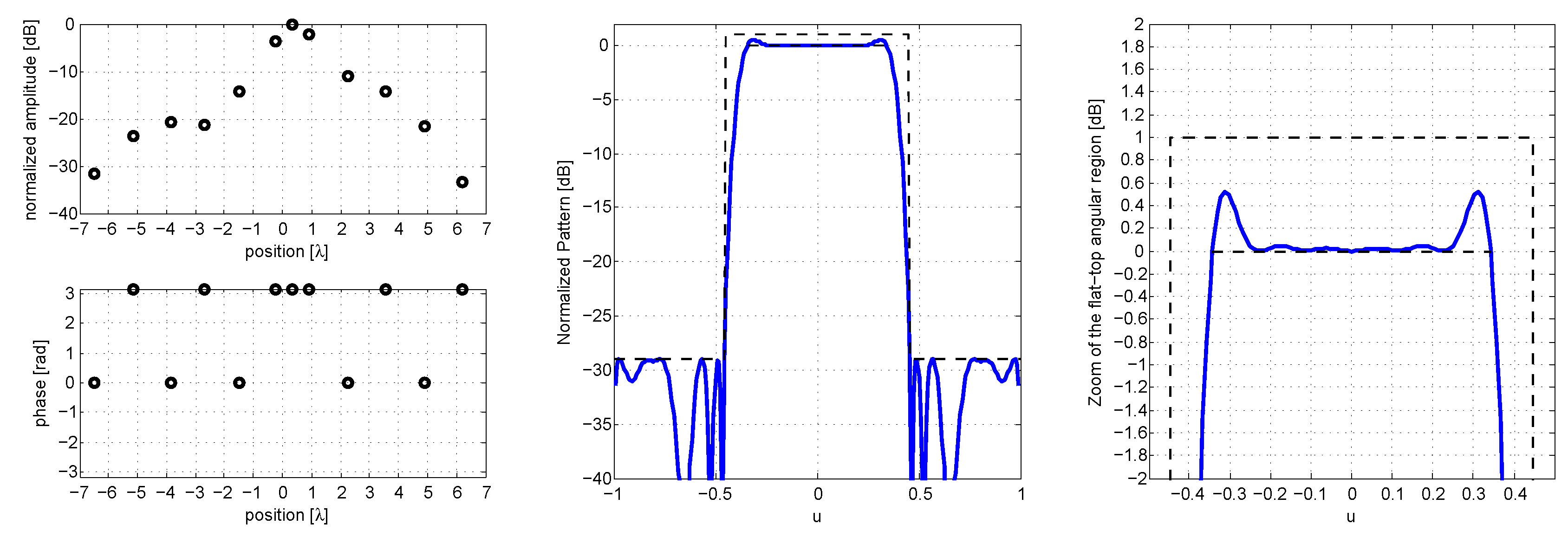
In a third example, we would also like to consider in the synthesis the presence of an element factor; following the specifications used in [
26], in particular, the case with 19 radiating elements (
for
,
for
), with an element factor
that multiplies the array factor in Equation (4). This requires us to multiply all of the columns of matrix
for the sampled vector of the element factor, but this has no other effects on the overall synthesis approach.
The results of the synthesis are provided in
Figure 8 (in which we plot the excitations, the overall pattern and a particular of the flat top region), where we can see that the specifications can be met with 12 elements only, and the ripple is much lower with respect to the specifications (about 0.5 dB instead of 1 dB).
5. Discussion
The results provided in the previous paragraph confirm the good performances of the SFGAP. In particular, we were capable of matching the results provided by other methods that require the preliminary synthesis of a pattern to be sought, and, in other cases, we achieve the satisfaction of the constraints with a much lower number of radiating elements.
In the paper, we have not considered the effect of the mutual coupling among elements; this is a reasonable assumption for sparse arrays, for which the element spacing is usually greater than a half-wavelength, and the main effect of mutual coupling consists in modifying the actual excitation on radiating elements with respect to the imposed voltages on the generators; in this case, once the position of the elements is achieved, it is trivial to calculate the proper compensation of the excitations [
27].
Furthermore, besides the asymmetric pencil beam case (where the power pattern mask was defined in the range
to allow the scanning of the beam in the whole visible range without the appearance of the grating lobes), we have not considered the effect of the scanning of the beam; this could be achieved by simply increasing the range of
u in which we want the satisfaction of the power pattern mask. Furthermore, in such a case, we could also take into account the presence of an element factor (that could change the side lobe level when the beam is scanned) by considering a modified power pattern mask, following the guidelines proposed in [
28].
It also has to be underlined that we may need to try some different random starting patterns , but, in most cases, few trials are sufficient to find a good final result. It is also interesting to observe that different starting points could lead to slightly varied, but equally acceptable, solutions. Generally speaking, these solutions show the same number of radiating elements but a different element spacing or excitation dynamic, so we could exploit this feature of the algorithm in order to have a set of different layouts from which we could choose the one to implement.
Finally, the number of iterations needed to achieve all of the results shown is lower than 100, and the single iteration for these example takes 10 to 20 seconds on an office PC, running Matlab and CVX, with a i5-2310 processor (a low-end processor with respect to current CPUs), Thus, the single synthesis usually takes less than half an hour.