Radar Angle of Arrival System Design Optimization Using a Genetic Algorithm
Abstract
:1. Introduction
2. Background
2.1. Optimization Methods
2.1.1. Particle Swarm Optimization Overview
2.1.2. Invasive Weeds Optimization Overview
2.1.3. Genetic Algorithm Overview
2.2. Optimizations Used in Radar
2.2.1. PSO Used in Radar
2.2.2. IWO Used in Radar
2.2.3. GA Used in Radar
GAs Used to Aid in the Design of Radar Systems
GAs Used to Aid in the Design of Other Systems that Make Use of Radar Data
2.3. Beamforming
2.4. Angle of Arrival Estimation
3. Methods
3.1. Design Parameter Selection Program
3.1.1. Localization Simulator
3.1.2. GA
3.2. Experiments
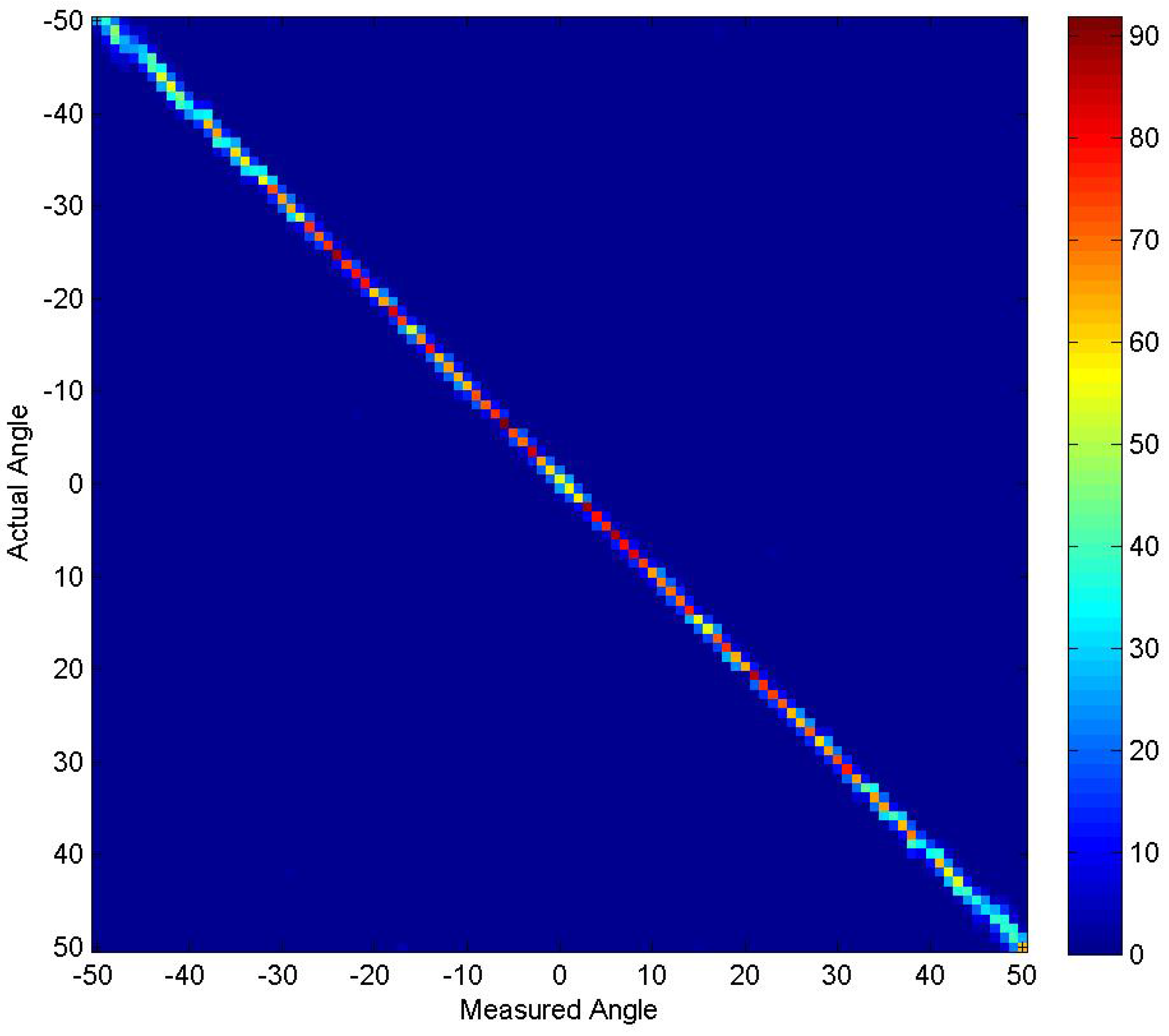
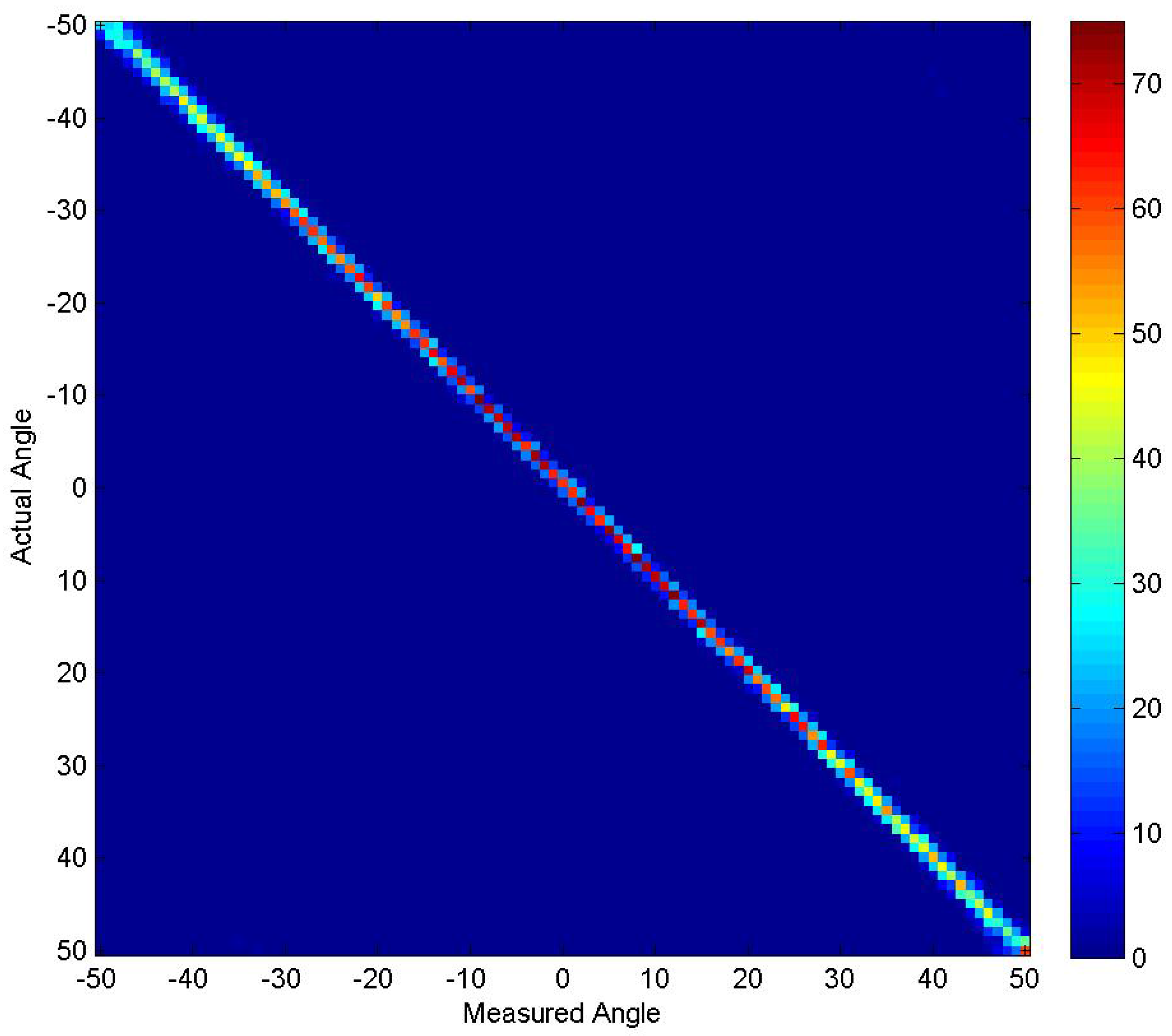
4. Results and Discussion
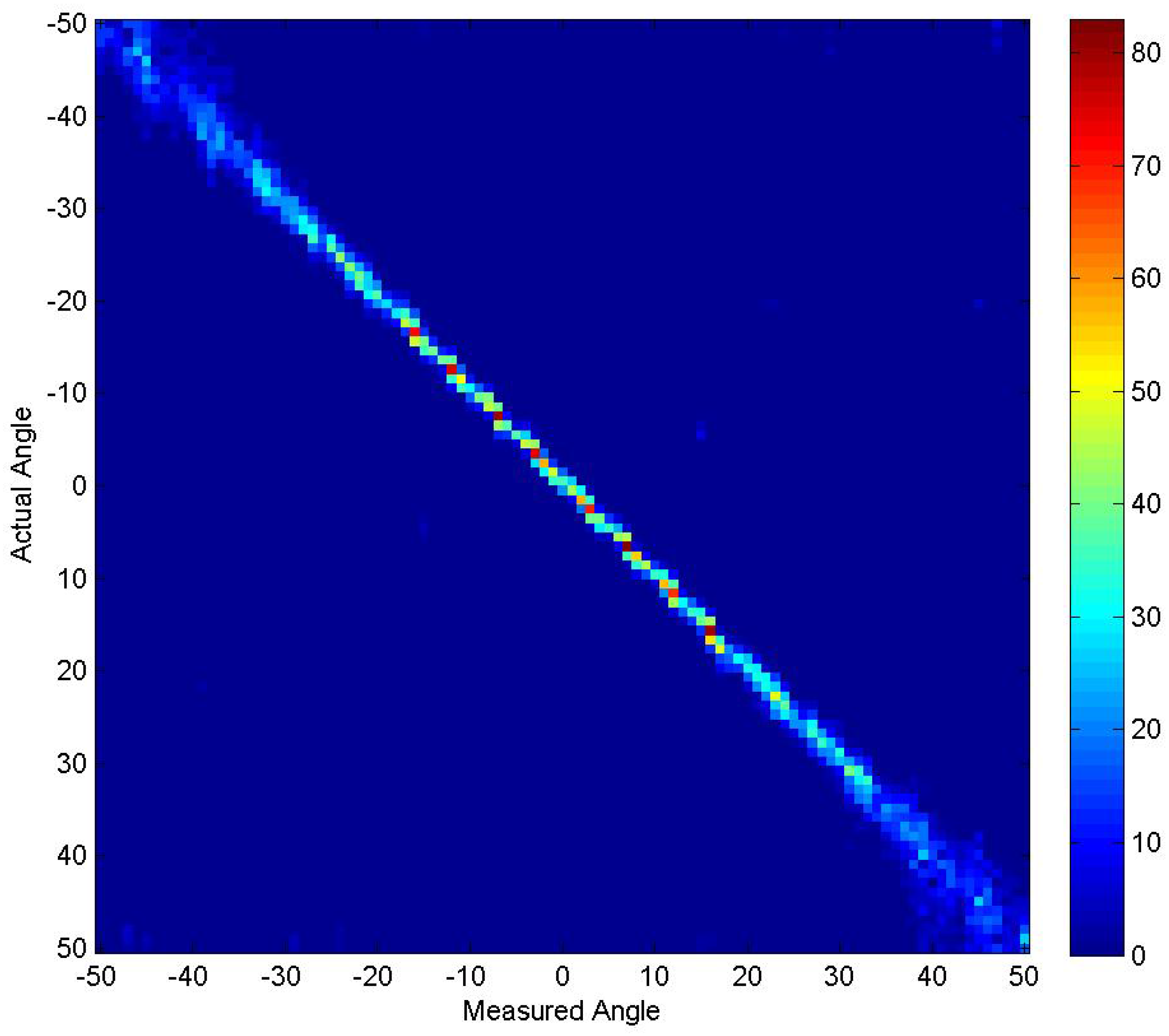
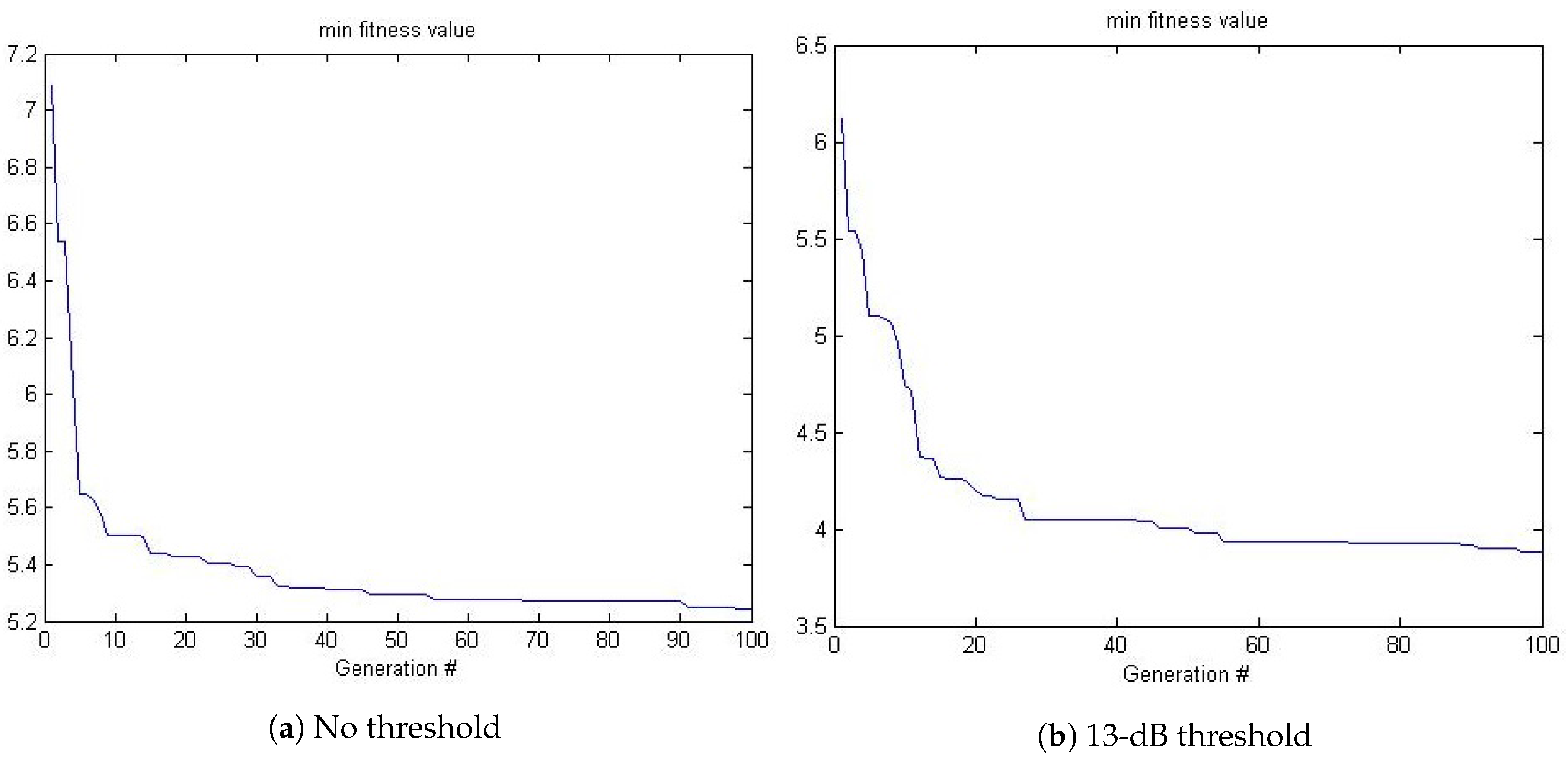
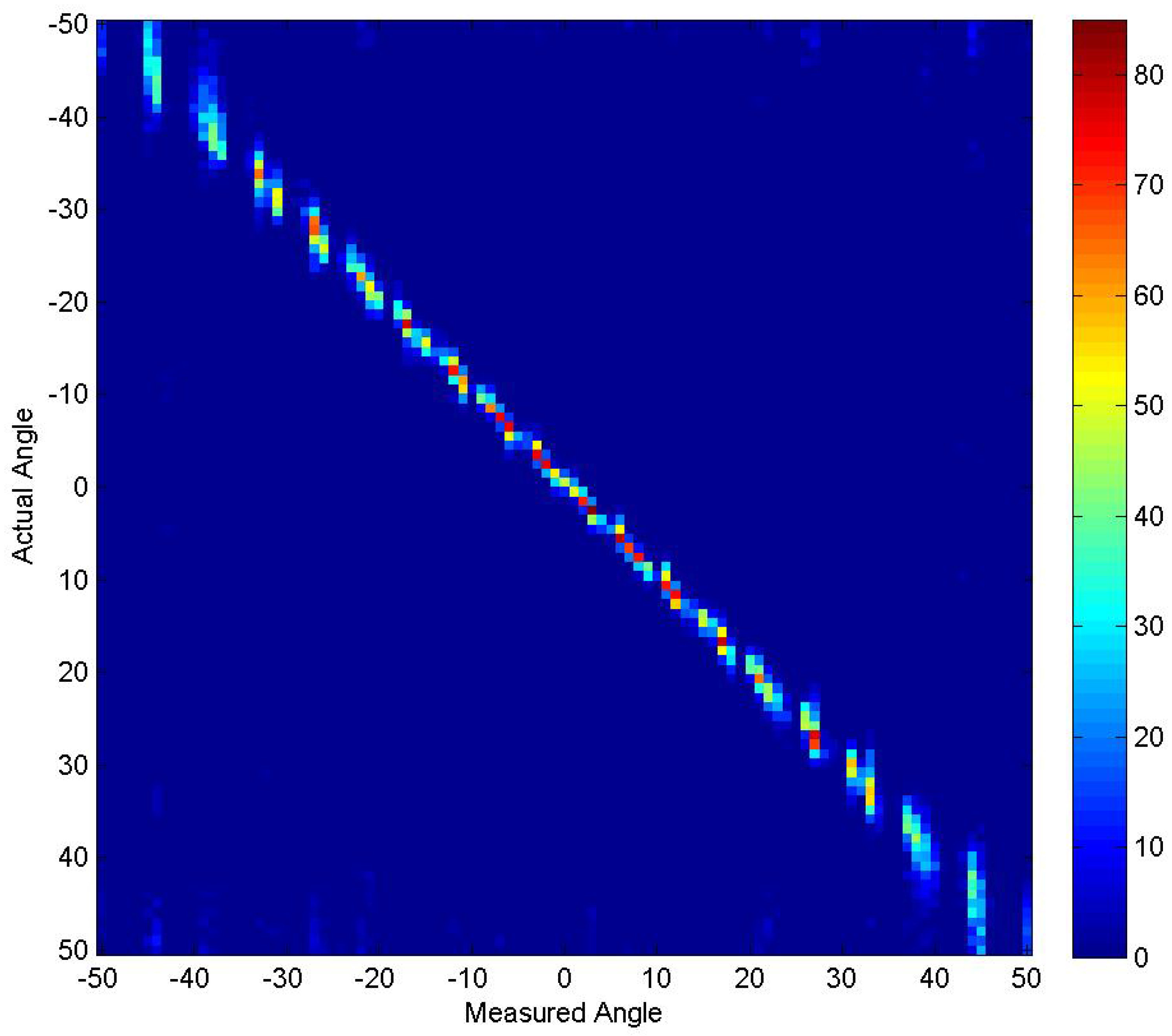
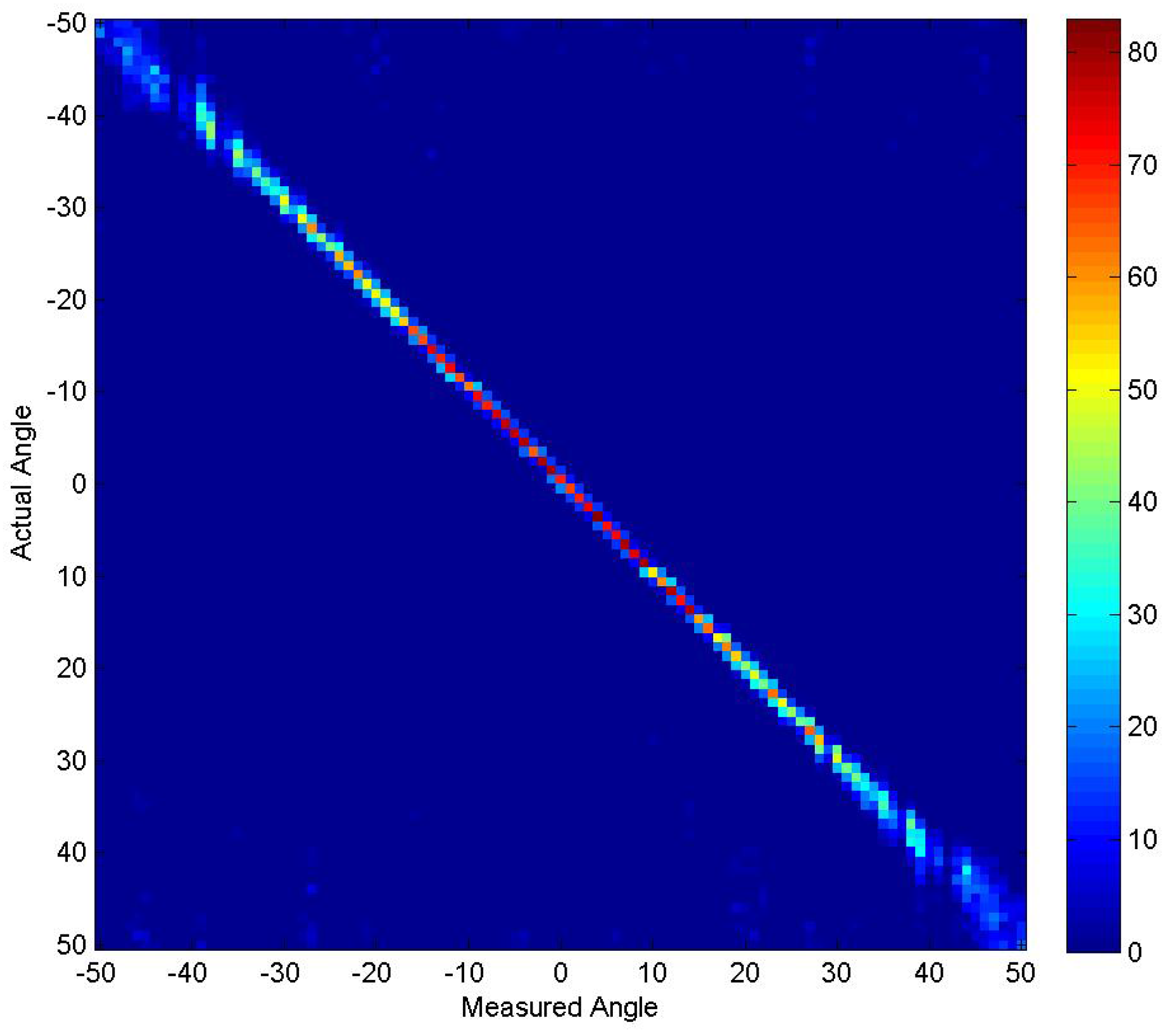
4.1. Experiment 1
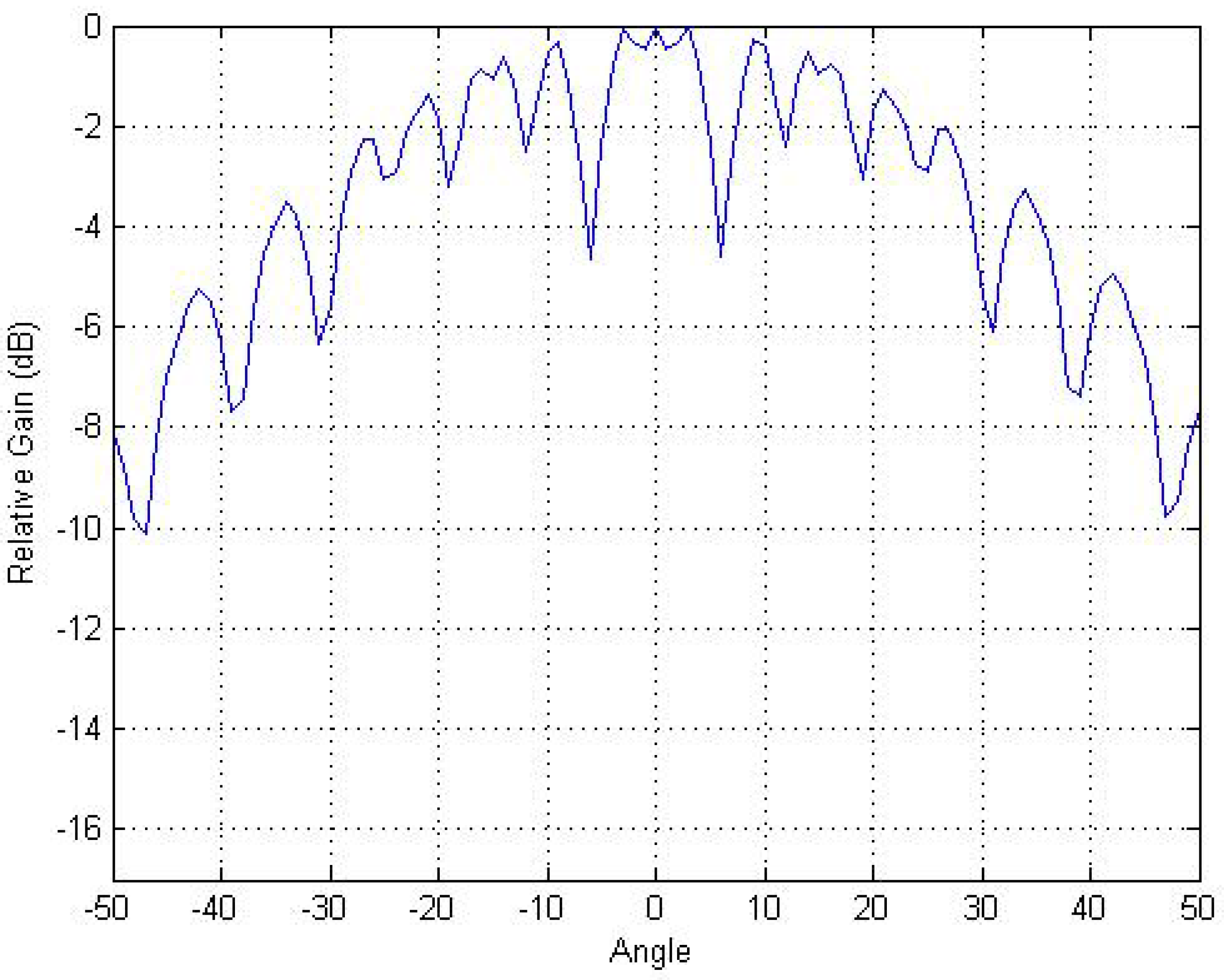
- In both cases, there were some beams that were placed very close together. This occurs a few times in the non-thresholded case where zero and 0.1 degrees are used along with 30.7 and 30.8 degrees. In all likelihood, these beams were not contributing and would have likely been optimized out had the GA continued to run longer.
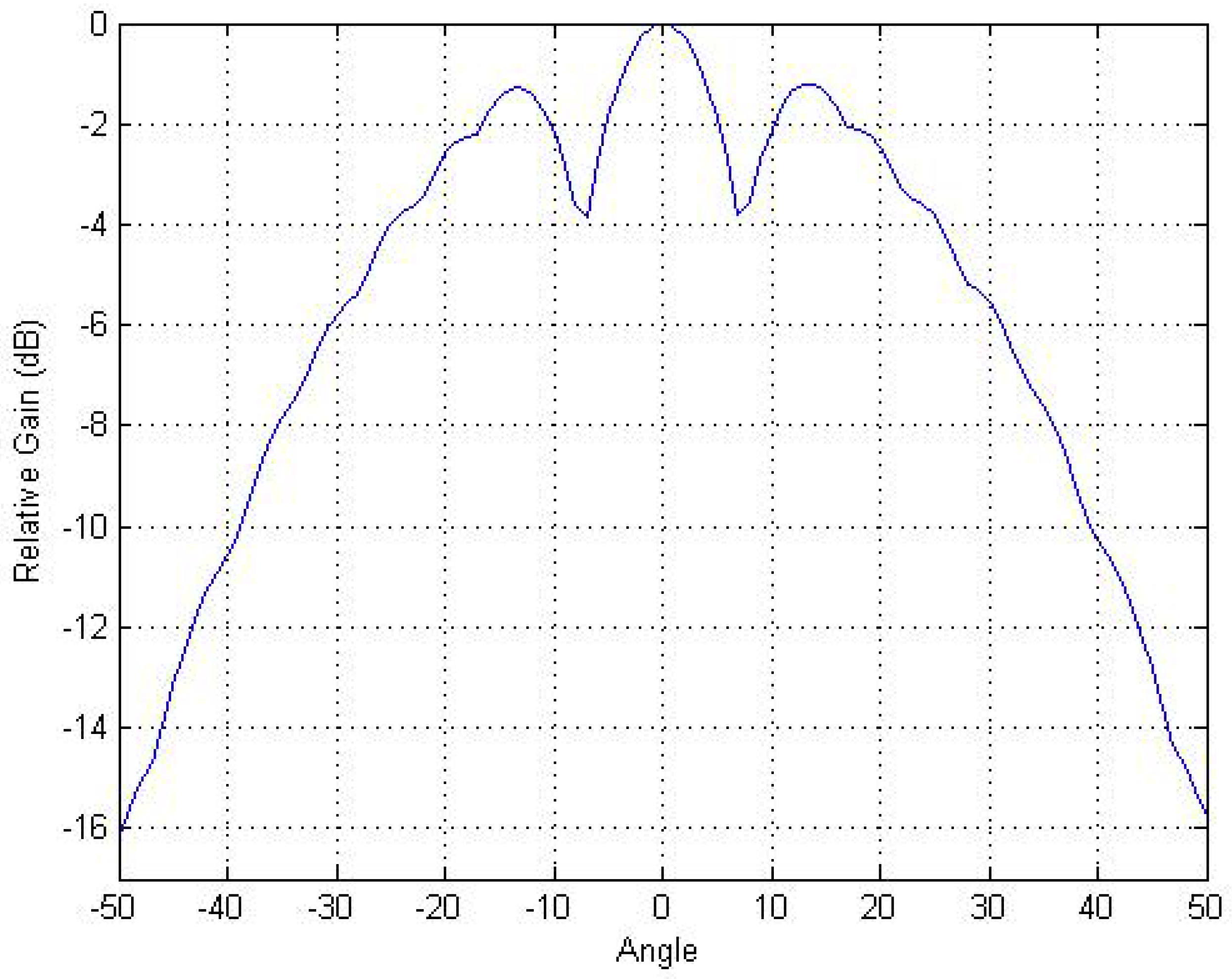
- The steered beams are more predominately steered away from the boresight. In both cases, the first effectively-steered beam occurs at 14 degrees. The GA may have been trying to direct more of the beams in those directions to minimize beam shape loss at those angles. The effect of this choice can be seen in Figure 4 where there are 3-dB dips in the beam pattern around .
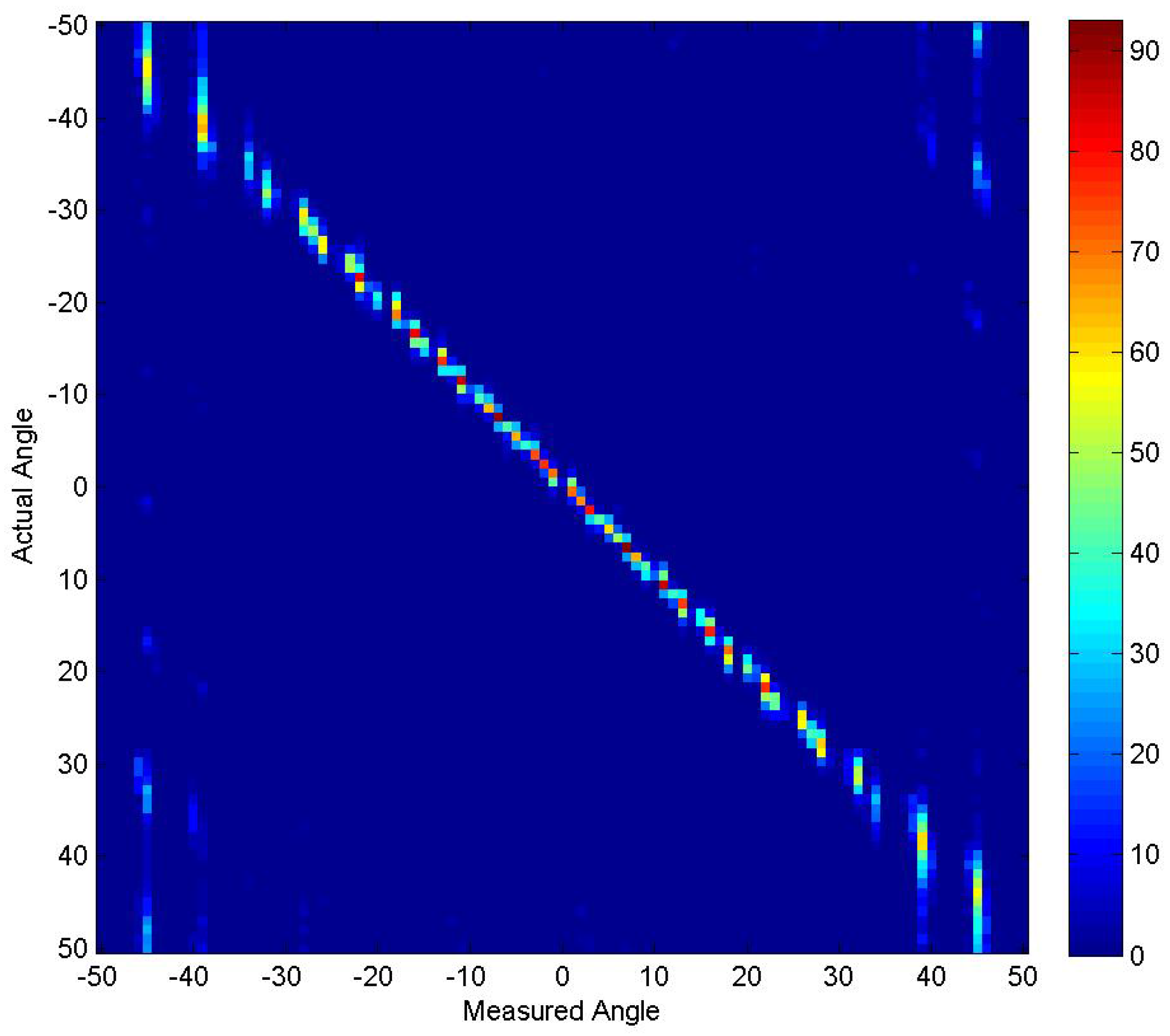
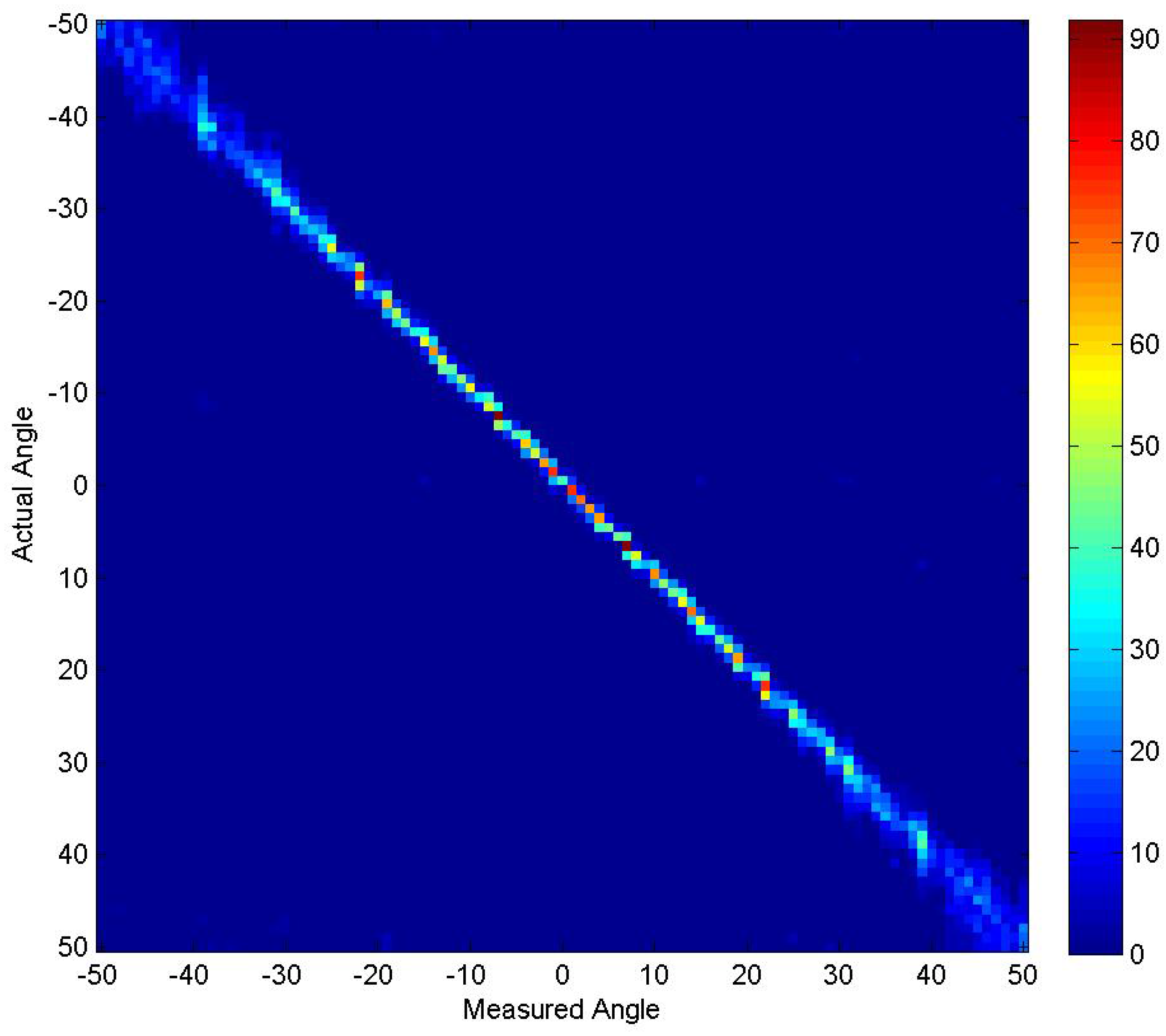
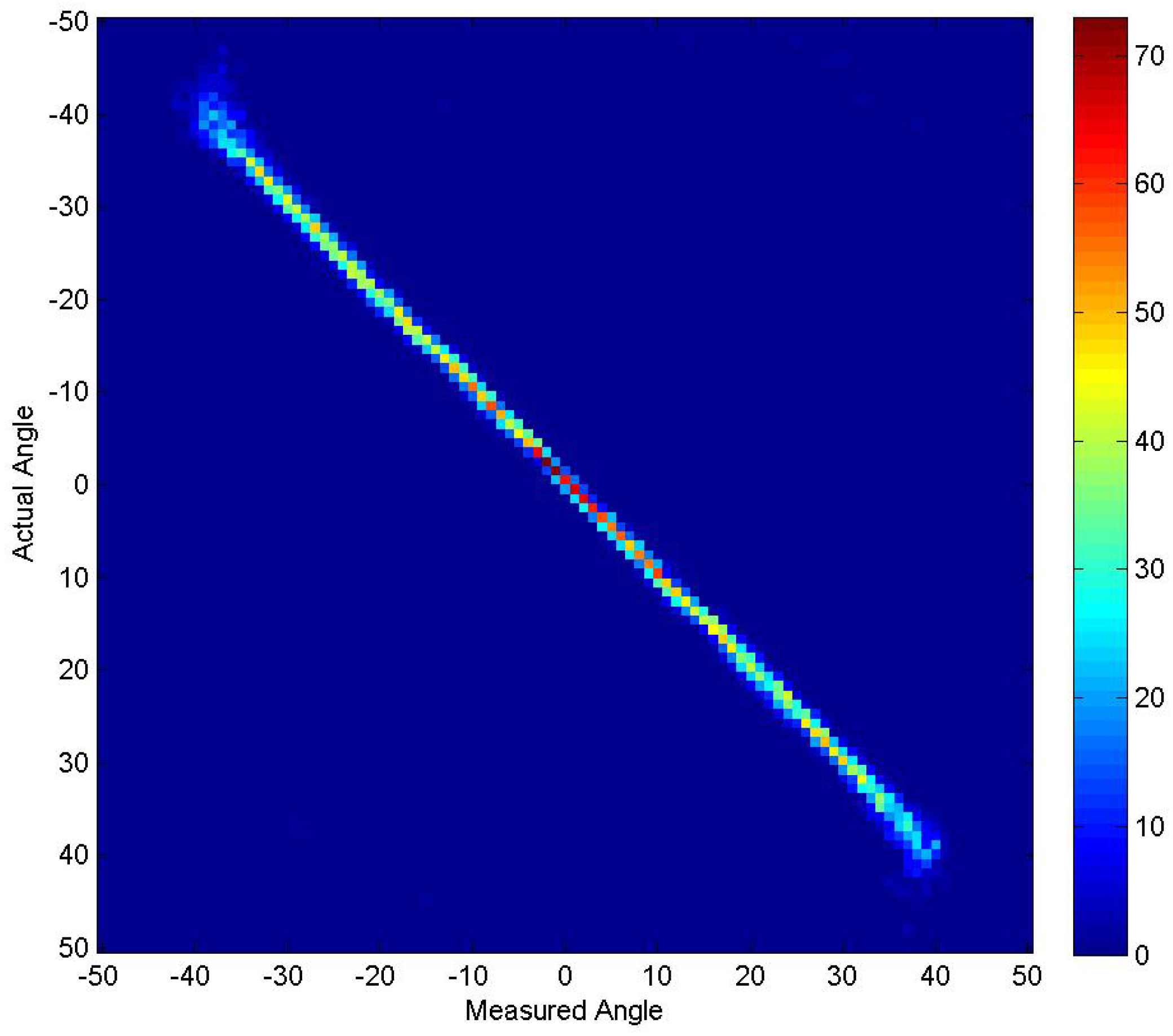
4.2. Experiment 2
4.3. Experiment 3
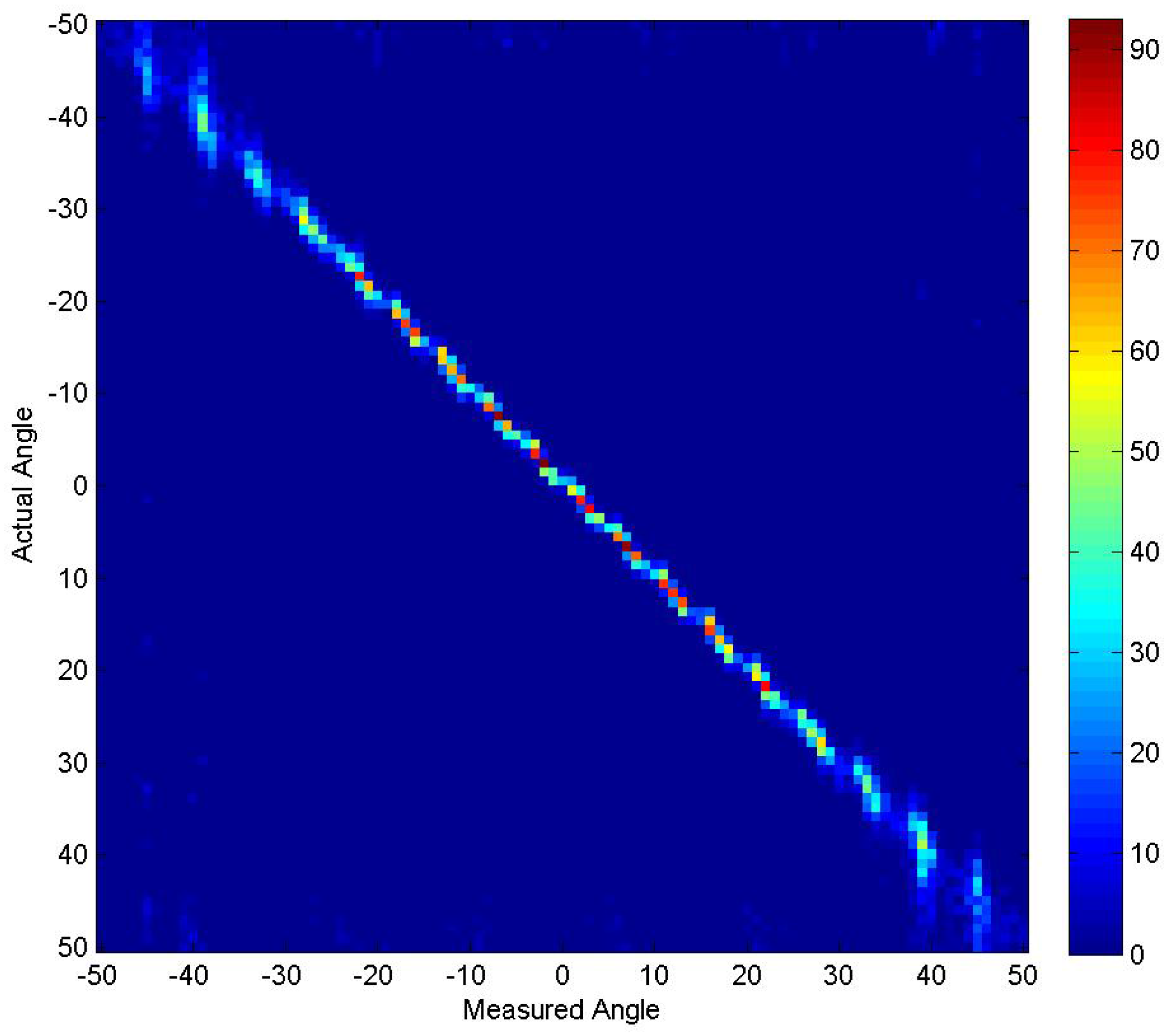
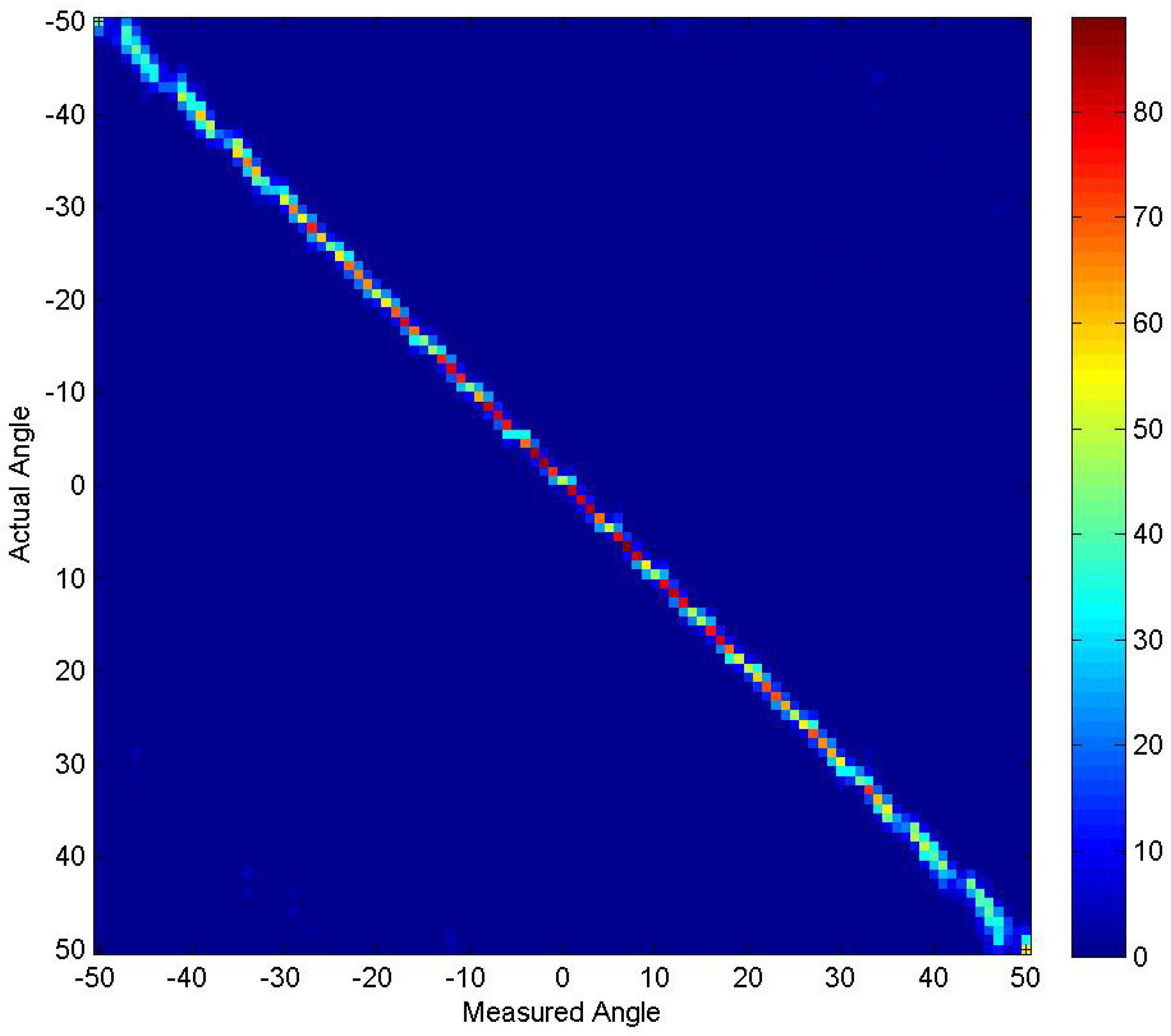
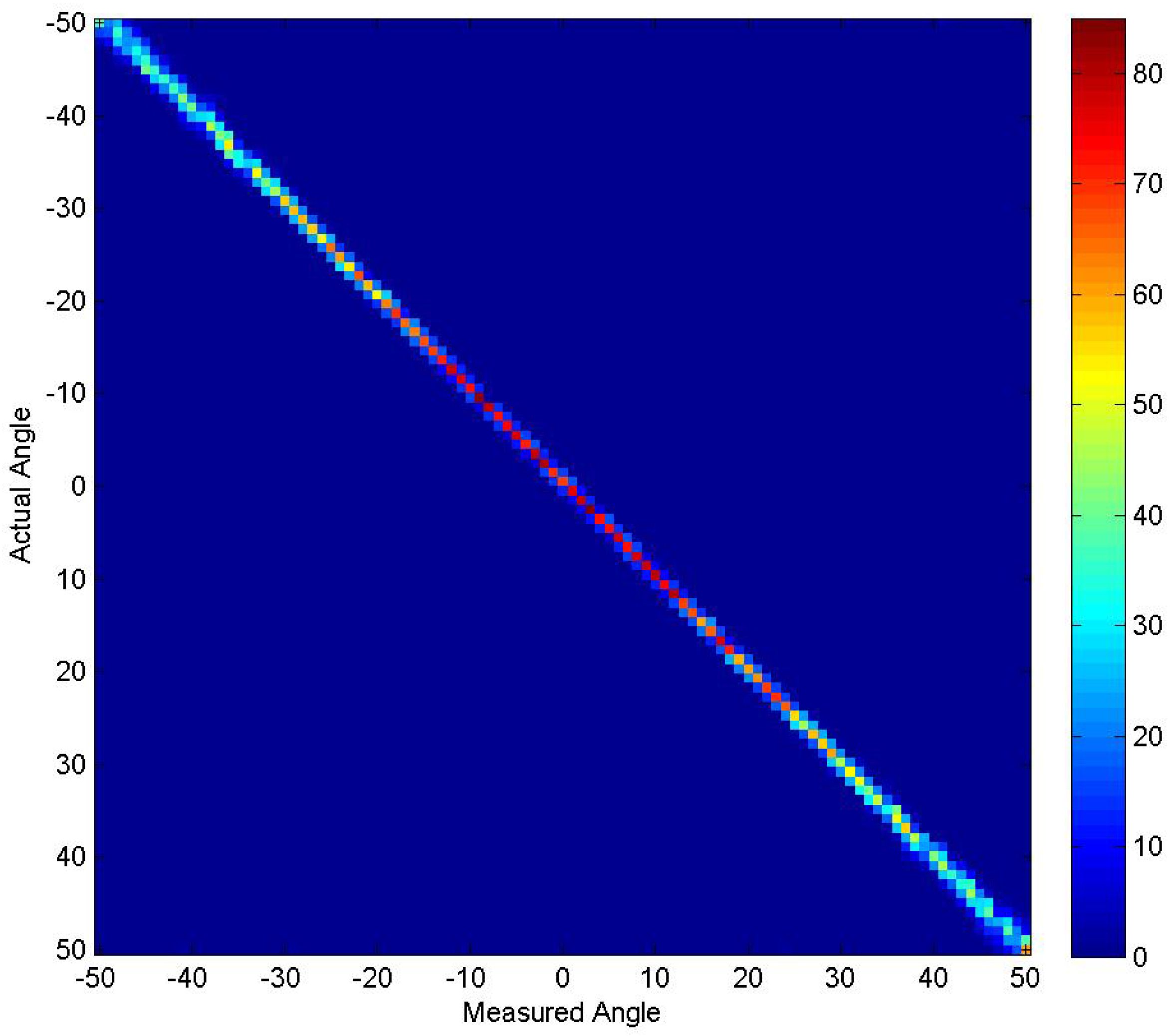
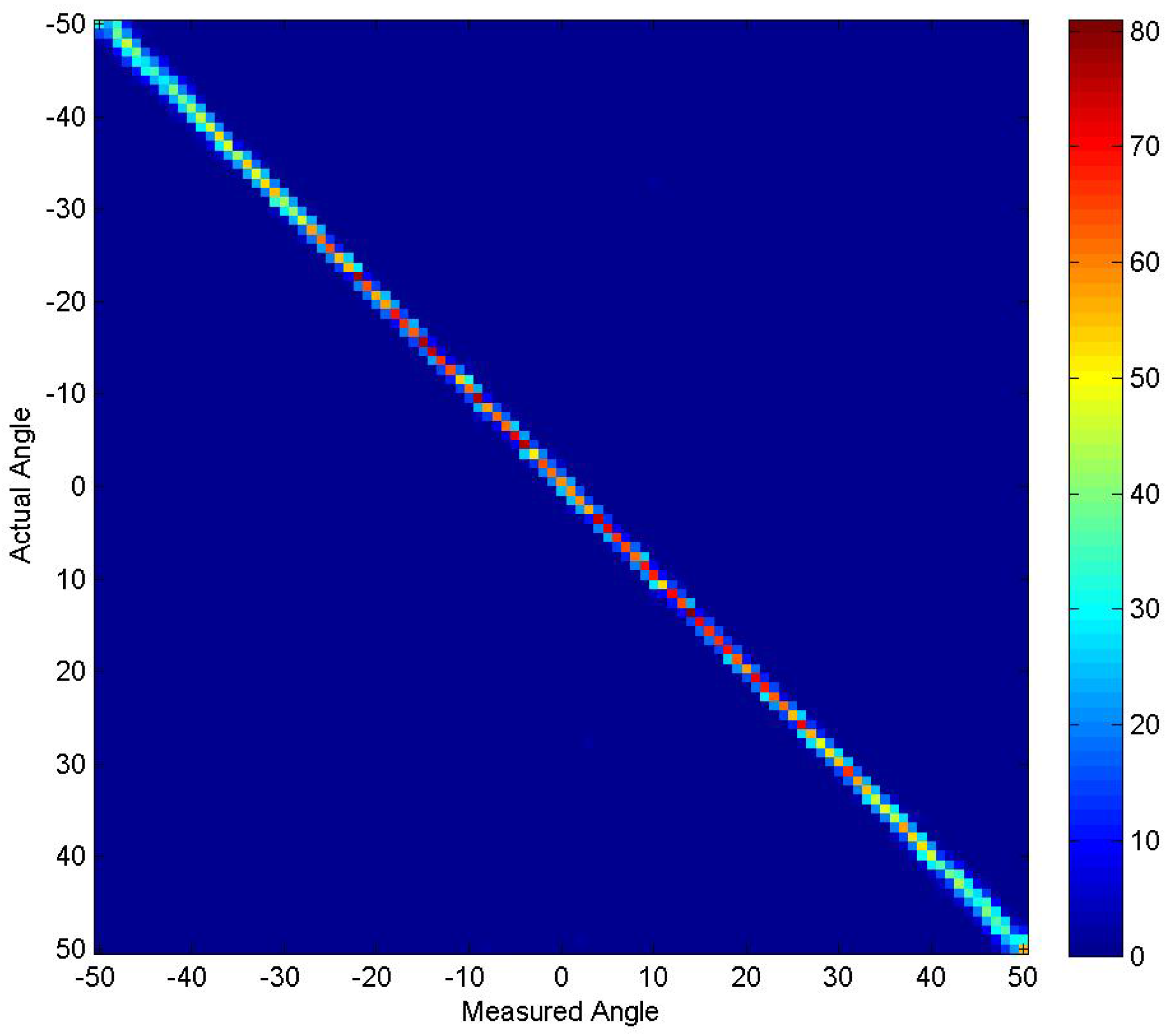
4.4. Experiment 4
4.5. Experiment 5
5. Conclusions
6. Future Work
- The localization simulator uses a specified target SNR at the boresight and calculates what that target’s SNR would be at different angles to the radar. This effectively allows the simulator to evaluate the performance of the system at some given range. The problem with this approach is that it does not allow the user to evaluate system performance at the edge of detection range across the entire field of view. A target with a very low SNR near the edge of the field of view will have a much stronger SNR at the boresight. This can lead the GA to come up with optimization solutions that work well at a particular range, but it may perform very poorly at further ranges. The next step with this evaluation is to modify the simulator to model a target with a given SNR (likely the minimum detectable SNR) across the entire field of view. This would allow the GA to optimize a solution that works the best for the worst case.
- Expanding on the previous item, this approach could be used to optimize parameters that can be configured on the fly for different target SNRs.
- The simulations that were performed only covered a ±50 degree field of view. It is very likely that the solutions the GA came up with have ambiguities outside of that region. Follow up work should be done to analyze these radar parameters with a wider coverage area. It would also be good to see what kind of solutions the GA comes up with when presented with a wider field of view.
- The localization simulator currently only supports localization in the azimuth direction. The program could be expanded to simulate and evaluate performance across both azimuth and elevation. The drawback of doing this is an explosion in computational complexity, which would require the use of far more powerful hardware than what was used for this evaluation.
- This program simulates a target in free space. In an actual radar design, clutter sources at the same range as the target can negatively effect localization performance. Digitally-formed beams with wide beam widths or strong sidelobes are more susceptible to these negative effects. The localization simulator could be updated to model this behavior, which would allow the GA to come up with a solution that works better in cluttered environments.
- The fitness score returned by the objective function in this algorithm is based solely on mean squared error. In an actual radar, there are other design considerations that should be accounted for. For example:
- The number of transmit and receive elements used in a radar design have a significant impact on the cost of the system, the computational resources required to support the signal processing and the power used by the radar. In addition to this, the number of patch elements along with how far apart they are spaced effects the size of the radar, as well, which may be critical to the design of the system.
- The number of beams to digitally form also has a computational cost associated with them, which is not captured by the algorithm. Supporting a large number of digitally-steered beams may not be feasible for some applications.
- The objective function does not take the detectable field of view into consideration when generating a fitness score. This algorithm could be updated to include that design parameter in its fitness score. Solutions that do not meet the desired field of view would be penalized.
Given that these costs are not accounted for, the GA does not consider those impacts when optimizing the radar design parameters. - Some radars use beam spoiling, a process where the transmit beam is widened using digital beamforming techniques. We would like to add beam spoiling capability rather than restrict the number of transmit elements, since this will lower the overall transmit power.
- The reasoning for why the GA frequently chose large element spacings and why it seemed to improve performance is still not well understood. Performing a more detailed analysis of one of these configurations may shed more light on this phenomenon.
Author Contributions
Conflicts of Interest
Abbreviations
| ADIWO | Adaptive Dispersion Invasive Weed Optimization |
| AMBPSO | Adaptive Mutated Boolean PSO |
| AOA | Angle of Arrival |
| CA-CFAR | Cell Averaging CFAR |
| CFAR | Constant False Alarm Rate |
| DRFM | Digital Radio Frequency Memory |
| ESPRIT | Estimation of Signals Parameter Rotational Invariance Technique |
| FIS | Fuzzy Inference System |
| HF | High Frequency |
| GA | Genetic Algorithm |
| GP | Genetic Programming |
| I | In-phase radar signal (see also Q) |
| IMM | Interacting Multiple Model |
| ISL | Integrated Sidelobe Level |
| IWO | Invasive Weed Optimization |
| ML | Maximum Likelihood |
| MPAR | Multi-Mission Phased Array Radar |
| MSE | Mean Square Error |
| MUSIC | MUlitple SIgnal Classification |
| MVDR | Minimum Variance Distortionless Response |
| NN | Neural Network |
| PSO | Particle Swarm Optimization |
| Q | Quadrature radar signal (see also I) |
| RCS | Radar Cross Section |
| RISL | Range Integrated Sidelobe Level |
| RF | Radio Frequency |
| RMS | Root Mean Square |
| SAR | Synthetic Aperture Radar |
References
- San Antonio, G.; Fuhrmann, D.R. Beampattern synthesis for wideband MIMO radar systems. In Proceedings of the 2005 1st IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, Puerto Vallarta, Mexico, 13–15 December 2005; pp. 105–108.
- Bonyadi, M.R.; Michalewicz, Z. Particle swarm optimization for single objective continuous space problems: A review. Evol. Comput. 2016, 25, 1–54. [Google Scholar] [CrossRef] [PubMed]
- Wilke, D.N.; Kok, S.; Groenwold, A.A. Comparison of linear and classical velocity update rules in particle swarm optimization: Notes on diversity. Int. J. Numer. Methods Eng. 2007, 70, 962–984. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Poli, R. Analysis of the publications on the applications of particle swarm optimisation. J. Artif. Evol. Appl. 2008, 2008, 685175. [Google Scholar] [CrossRef]
- Mehrabian, A.R.; Lucas, C. A novel numerical optimization algorithm inspired from weed colonization. Ecol. Inform. 2006, 1, 355–366. [Google Scholar] [CrossRef]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Golberg, D.E. Genetic algorithms in search, optimization, and machine learning. Addion Wesley 1989, 1989, 102. [Google Scholar]
- Mavromatidis, L.E. A review on hybrid optimization algorithms to coalesce computational morphogenesis with interactive energy consumption forecasting. Energy Build. 2015, 106, 192–202. [Google Scholar] [CrossRef]
- Marin, P.; Marsault, X.; Mavromatidis, L.E.; Saleri, R.; Torres, F. Ec-Co-Gen: An evolutionary simulation assisted design tool for energy rating of buildings in early design stage to optimize the building form. In Proceedings of the BS2013, Chambery, France, 26–28 August 2013.
- Jones, G.; Willett, P.; Glen, R.C. Molecular recognition of receptor sites using a genetic algorithm with a description of desolvation. J. Mol. Biol. 1995, 245, 43–53. [Google Scholar] [CrossRef]
- Deaven, D.M.; Ho, K.M. Molecular geometry optimization with a genetic algorithm. Phys. Rev. Lett. 1995, 75, 288. [Google Scholar] [CrossRef] [PubMed]
- Zwickl, D.J. Genetic Algorithm Approaches for the Phylogenetic Analysis of Large Biological Sequence Datasets under the Maximum Likelihood Criterion. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2006. [Google Scholar]
- Hassan, R.; Cohanim, B.; De Weck, O.; Venter, G. A comparison of particle swarm optimization and the genetic algorithm. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Austin, TX, USA, 18–21 April 2005; p. 1897.
- Zaharis, Z.D.; Gotsis, K.A.; Sahalos, J.N. Adaptive beamforming with low side lobe level using neural networks trained by mutated boolean PSO. Prog. Electromagn. Res. 2012, 127, 139–154. [Google Scholar] [CrossRef]
- Zaharis, Z.D.; Yioultsis, T.V. A novel adaptive beamforming technique applied on linear antenna arrays using adaptive mutated boolean PSO. Prog. Electromagn. Res. 2011, 117, 165–179. [Google Scholar] [CrossRef]
- Zaharis, Z.D.; Skeberis, C.; Xenos, T.D. Improved antenna array adaptive beamforming with low side lobe level using a novel adaptive invasive weed optimization method. Prog. Electromagn. Res. 2012, 124, 137–150. [Google Scholar] [CrossRef]
- Roy, G.G.; Das, S.; Chakraborty, P.; Suganthan, P.N. Design of non-uniform circular antenna arrays using a modified invasive weed optimization algorithm. IEEE Trans. Antennas Propag. 2011, 59, 110–118. [Google Scholar] [CrossRef]
- Basak, A.; Pal, S.; Das, S.; Abraham, A. Circular antenna array synthesis with a differential invasive weed optimization algorithm. In Proceedings of the 2010 10th International Conference on Hybrid Intelligent Systems (HIS), Atlanta, GA, USA, 23–25 August 2010; pp. 153–158.
- Basak, A.; Pal, S.; Das, S.; Abraham, A.; Snasel, V. A modified invasive weed optimization algorithm for time-modulated linear antenna array synthesis. In Proceedings of the 2010 IEEE Congress on Evolutionary Computation (CEC), Barcelona, Spain, 18–23 July 2010; pp. 1–8.
- Bhattacharya, R.; Bhattacharyya, T.K.; Saha, S. Sidelobe level reduction of aperiodic planar array using an improved invasive weed optimization algorithm. In Proceedings of the 2011 IEEE Applied Electromagnetics Conference (AEMC), Kolkata, India, 18–22 December 2011; pp. 1–4.
- Pappula, L.; Ghosh, D. Large array synthesis using invasive weed optimization. In Proceedings of the 2013 International Conference on Microwave and Photonics (ICMAP), Dhanbad, India, 13–15 December 2013; pp. 1–6.
- Mallahzadeh, A.R.R.; Oraizi, H.; Davoodi-Rad, Z. Application of the invasive weed optimization technique for antenna configurations. Prog. Electromagn. Res. 2008, 79, 137–150. [Google Scholar] [CrossRef]
- Capraro, C.T.; Bradaric, I.; Capraro, G.T.; Lue, T.K. Using genetic algorithms for radar waveform selection. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008; pp. 1–6.
- Chan, K.C.C.; Lee, V.; Leung, H. Generating fuzzy rules for target tracking using a steady-state genetic algorithm. IEEE Trans. Evol. Comput. 1997, 1, 189–200. [Google Scholar] [CrossRef]
- Lin, Y.; Bhanu, B. Evolutionary feature synthesis for object recognition. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2005, 35, 156–171. [Google Scholar] [CrossRef]
- Kurdzo, J.M.; Palmer, R.D. On the use of genetic algorithms for optimization of a multi-band, Multi-Mission radar network. In Proceedings of the 2011 IEEE RadarCon (RADAR), Kansas City, MO, USA, 23–27 May 2011; pp. 231–236.
- Orfila, A.; Molcard, A.; Sayol, J.M.; Marmain, J.; Bellomo, L.; Quentin, C.; Barbin, Y. Empirical Forecasting of HF-Radar Velocity Using Genetic Algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2875–2886. [Google Scholar] [CrossRef]
- Kristoffersen, S.; Moen, H.J.F. Denial jamming technique development against pulse-doppler radars using genetic algorithms. In Proceedings of the 2008 International Conference on Radar, Rome, Italy, 26–30 May 2008; pp. 253–258.
- Richards, M.A. Fundamentals of Radar Signal Processing; Tata McGraw-Hill Education: New York, NY, USA, 2005. [Google Scholar]
- Li, J.; Stoica, P. Robust Adaptive Beamforming; John Wiley & Sons: Hoboken, NJ, USA, 2005; Volume 88. [Google Scholar]
- Harter, M.; Ziroff, A.; Zwick, T. Three-dimensional radar imaging by digital beamforming. In Proceedings of the 2011 European Radar Conference (EuRAD), Manchester, UK, 12–14 October 2011; pp. 17–20.
- Chang, P.R.; Yang, W.H.; Chan, K.K. A Neural Network Approach to MVDR Beamforming Problem. IEEE Trans. Antennas Propag. 1986, 34, 8190–8192. [Google Scholar]
- Southall, H.; Simmers, J.A.; O’Donnell, T.H. Direction Finding in Phased Arrays with a Neural Network Beamformer. IEEE Trans. Antennas Propag. 1995, 43, 1369–1374. [Google Scholar] [CrossRef]
- Jha, S.; Durrani, T. Direction of arrival estimation using artificial neural networks. IEEE Trans. Syst. Man Cybern. 1991, 21, 1192–1201. [Google Scholar] [CrossRef]
- Shieh, C.S.; Lin, C.T. Direction of Arrival Estimation Based on Phase Differences Using Neural Fuzzy Network. IEEE Trans. Antennas Propag. 2000, 48, 1115–1124. [Google Scholar] [CrossRef]
- Yang, W.H.; Chan, K.K.; Chang, P.R. Complex-valued neural network for direction of arrival estimation—Electronics Letters. Electron. Lett. 1994, 30, 2–3. [Google Scholar] [CrossRef]
- Agatonovic, M.; Stankovic, Z.; Milovanovic, I.; Doncov, N.; Sit, L.; Zwick, T.; Milovanovic, B. Efficient neural network approach for 2D DOA estimation based on antenna array measurements. Prog. Electromagn. Res. 2013, 137, 741–758. [Google Scholar] [CrossRef]
- Lo, T.; Leung, H.; Litva, J. Radial Basis Function Neural Network for Direction-of-Arrivals Estimation. IEEE Signal Process. Lett. 1994, 1, 45–47. [Google Scholar] [CrossRef]
- Zaman, F.; Qureshi, I.M.; Naveed, A.; Khan, J.A.; Asif Zahoor, R.M. Amplitude and directional of arrival estimation: Comparison between different techniques. Prog. Electromagn. Res. B 2012, 39, 319–335. [Google Scholar] [CrossRef]
- Page, R.M. Simultaneous Lobe Comparison, Pulse Echo Locator System. U.S. Patent 2,929,056, 15 March 1960. [Google Scholar]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Viberg, M.; Ottersten, B.; Nehorai, A. Performance analysis of direction finding with large arrays and finite data. IEEE Trans. Signal Process. 1995, 43, 469–477. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Ren, Q.; Willis, A. Fast root MUSIC algorithm. Electron. Lett. 1997, 33, 450–451. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Page, R.M. Accurate Angle Tracking by Radar (Naval Research Laboratory Formal Report RA-3A-222A); Technical Report; Naval Research Laboratory: Washington, DC, USA, 1944. [Google Scholar]

| Parameter Number | Parameter Type | Description |
|---|---|---|
| 1 | Radar | Number of transmit elements in the antenna array |
| 2 | Radar | Number of receive elements in the antenna array |
| 3 | Radar | Array element spacing in terms of the wavelength |
| 4 | Radar | Number of steered beams to use for digital beam-forming |
| 5 | Radar | Steering Angles to be used for digital beam-forming |
| 6 | Radar | Transmit element weighting coefficients to use for beam tapering |
| 7 | Radar | Receive element weighting coefficients to use for beam tapering |
| 8 | Target | Target SNR (specified at boresight) |
| 9 | Simulator | Discrete list of target AOA angles to simulate |
| 10 | Simulator | Number of Monte Carlo simulations to run at each discrete angle |
| 11 | Simulator | Detection SNR threshold. Ignores low SNR detections |
| Parameter Number | Description | Typical Values (Min:Step:Max) |
|---|---|---|
| 1 | Number of transmit elements in the antenna array | 1:1:2 |
| 2 | Number of receive elements in the antenna array | 1:1:6 |
| 3 | Array element spacings in terms of lambda (can be non-uniform) | 0.5:0.01:1.0 |
| 4 | Number of steered beams to use for digital beam-forming | 1:1:10 |
| 5 | Steering angles in degrees to be used for digital beam-forming | 0.1:0.1:60 |
| 6 | Transmit element weighting coefficients to use for beam tapering | 1:1:1 |
| 7 | Receive element weighting coefficients to use for beam tapering | 0.0:0.01:1 |
| Description | Algorithm/Value |
|---|---|
| Initialization Method | Random |
| Objective Function | Localization Simulator MSE |
| Selection Approach | Roulette Wheel Selection (Minimize) |
| Selection Parent Groups | 100 |
| Selection Parents Per Child | 2 |
| Selection Weight | Proportional |
| Elitism Selection Count | 2 |
| Elitism Replacement Policy | Random |
| Crossover Type | One-point |
| Crossover Children Per Parent Group | 2 |
| Mutation Type | Uniform Mutation |
| Mutation Probability | 0.5 (50%) |
| GA Exit Condition | 100 Iterations |
| Experiment Number | Description |
|---|---|
| 1 | Fixed number of elements, element spacing, weights. GA varies the number of beams. |
| 2 | Fixed number beams and weights. GA varies the number of elements and spacing. |
| 3 | Fixed number of elements, element spacing. GA varies the number of beams and weights. |
| 4 | GA varies the number of elements, spacing, weights and the number of beams. |
| 5 | Restricted parameter set GA based on the results from Experiments 1 to 4. |
| Description | Value |
|---|---|
| Number of transmit elements in the antenna array | 2 |
| Number of receive elements in the antenna array | 8 |
| Array element spacings in terms of lambda. | 0.5 |
| Number of steered beams to use for digital beam-forming | 21 |
| Steering angles in degrees to be used for digital beam-forming | 0, ±(5, 10, 15, 20, 25, 30, 35, 40, 45, 50) |
| Receive element weighting coefficients to use for beam tapering | 1 |
| Experiment | (No Threshold) | (13-dB Threshold) |
|---|---|---|
| Baseline | 6.57 | 4.77 |
| Description | Value (No Threshold) | Value (13 dB Threshold) |
|---|---|---|
| Number of transmit elements | 2 | 2 |
| Number of receive elements | 8 | 8 |
| Array element spacings (in lambda) | 0.5 | 0.5 |
| Number of steered beams | 21 | 21 |
| Steering angles in degrees | 0, ±(0.1, 14.7, 19.6, 25.1, 30.7, 30.8, 35.8, 42.9, 51, 59.8) | 0, ±(14.4, 19.5, 23.7, 25.7, 31.4, 36.4, 40.3, 44.8, 52.6, 58.9) |
| Receive element weights | 1 | 1 |
| Fitness score () | 5.24 | 3.88 |
| Description | Value (No Threshold) | Value (13-dB Threshold) |
|---|---|---|
| Number of transmit elements | 1 | 1 |
| Number of receive elements | 8 | 8 |
| RX array element spacings (in lambda) | 0.95, 0.5, 0.99, 0.97, 0.82, 0.9, 0.99 | 0.81, 0.95, 0.98, 0.51, 0.81, 0.5, 0.7 |
| Number of steered beams | 21 | 21 |
| Steering angles in degrees | 0, ±(5, 10, 15, 20, 25, 30, 35, 40, 45, 50) | 0, ±(5, 10, 15, 20, 25, 30, 35, 40, 45, 50) |
| Receive element weights | 1 | 1 |
| Fitness score () | 2.21 | 2.16 |
| Description | Value (No Threshold) | Value (13-dB Threshold) |
|---|---|---|
| Number of transmit elements | 2 | 2 |
| Number of receive elements | 8 | 8 |
| Array element spacings (in lambda) | 0.5 | 0.5 |
| Number of steered beams | 21 | 21 |
| Steering angles in degrees | 0, ±(0.9, 13.3, 19.5, 24.1, 27.3, 28.9, 38.9, 42.3, 48.1, 59.2) | 0, ±(1.1, 6.8, 11.5, 15, 16.9, 20.4, 23, 25, 25.4, 38) |
| Receive element weights | 0.95, 0.32, 0.52, 0.28, 0, 0.32, 0.65, 0.89 | 0.19, 0.13, 0.36, 0.48, 0.98, 0.66, 0.2, 0.27 |
| Fitness score () | 4.06 | 2.85 |
| Description | Value (No Threshold) | Value (13-dB Threshold) |
|---|---|---|
| Number of transmit elements | 1 | 1 |
| Number of receive elements | 8 | 8 |
| Array element spacings (in lambda) | 0.97, 0.6, 0.84, 0.88, 0.77, 0.52, 0.5 | 0.93, 0.77, 0.54, 0.8, 0.51, 0.84, 0.83 |
| Number of steered beams | 21 | 21 |
| Steering angles in degrees | 0, ±(2.8, 9.4, 14.1, 16.4, 21.2, 26.7, 34.2, 42.4, 52, 59.8) | 0, ±(1.5, 7.1, 9.9, 20.5, 26.5, 31.2, 37.8, 43.4, 51.3, 56.8) |
| Receive element weights | 0.92, 0.01, 0.58, 0.75, 0.48, 0.79, 0.01, 0.68 | 0.4, 0.3, 0.29, 0.49, 0.64, 0.4, 0.99, 0.78 |
| Fitness score () | 1.76 | 1.75 |
| Description | Value (No Threshold) | Value (13-dB Threshold) |
|---|---|---|
| Number of transmit elements | 1 | 1 |
| Number of receive elements | 8 | 8 |
| Array element spacings (in lambda) | 0.99, 1.0, 0.79, 0.89, 0.57, 0.66, 0.9 | 0.6, 0.6, 0.88, 0.86, 0.7, 0.85, 0.78 |
| Number of steered beams | 21 | 21 |
| Steering angles in degrees | 0, ±(11.8 13.8 17.5 27.7, 31.5, 36.8, 42, 46.1, 49, 57.8) | 0, ±(4.2, 10.1, 15.5, 18.6, 21.3, 27.6, 33.4, 38.7, 45, 52.4) |
| Receive element weights | 0.82, 0.61, 0.82, 0.06, 0.21, 0.68, 0.44, 0.57 | 0.31, 0.13, 0.16, 0.38, 0.95, 0.84, 0.31, 0.41 |
| Fitness score () | 1.74 | 1.84 |
| Experiment | Parameters Varied | MSE (No Threshold) | MSE (13-dB Threshold) |
|---|---|---|---|
| Baseline | All Fixed | 6.57 | 4.77 |
| Exp. 1 | Number/Angle of Steered Beams | 5.24 | 3.88 |
| Exp. 2 | Number of TX/RX Elements and Their Spacings | 2.21 | 2.16 |
| Exp. 3 | Number/Angle of Steered Beams and Weights | 4.06 | 2.85 |
| Exp. 4 | All | 1.76 | 1.75 |
| Exp. 5 | Element Spacing/Weights and Steering Angles | 1.74 | 1.84 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Egger, N.; Ball, J.E.; Rogers, J. Radar Angle of Arrival System Design Optimization Using a Genetic Algorithm. Electronics 2017, 6, 24. https://doi.org/10.3390/electronics6010024
Egger N, Ball JE, Rogers J. Radar Angle of Arrival System Design Optimization Using a Genetic Algorithm. Electronics. 2017; 6(1):24. https://doi.org/10.3390/electronics6010024
Chicago/Turabian StyleEgger, Neilson, John E. Ball, and John Rogers. 2017. "Radar Angle of Arrival System Design Optimization Using a Genetic Algorithm" Electronics 6, no. 1: 24. https://doi.org/10.3390/electronics6010024
APA StyleEgger, N., Ball, J. E., & Rogers, J. (2017). Radar Angle of Arrival System Design Optimization Using a Genetic Algorithm. Electronics, 6(1), 24. https://doi.org/10.3390/electronics6010024







