Guided Modes in a Double-Well Asymmetric Potential of a Graphene Waveguide
Abstract
:1. Introduction
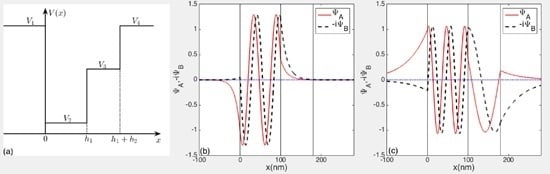
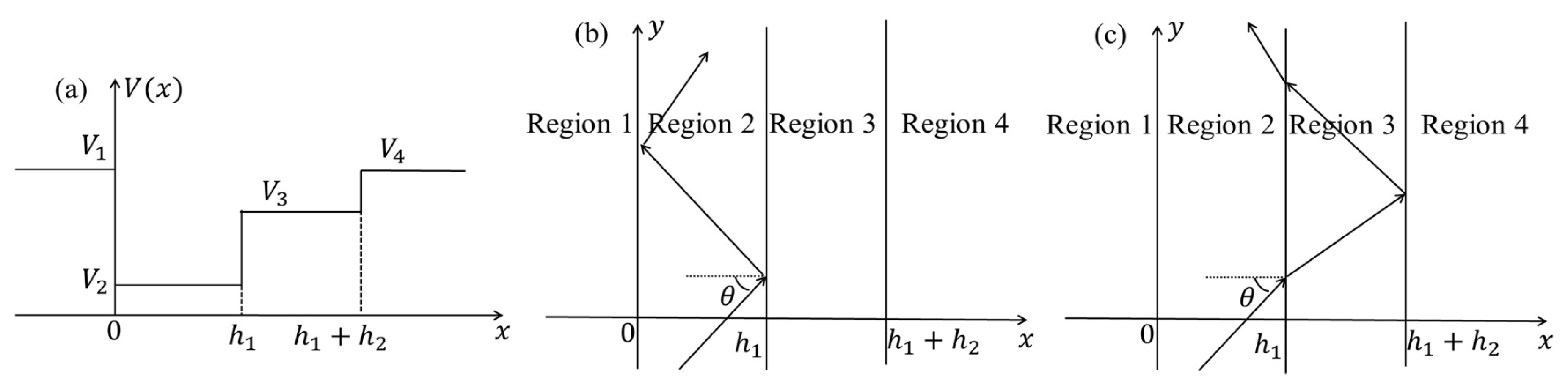
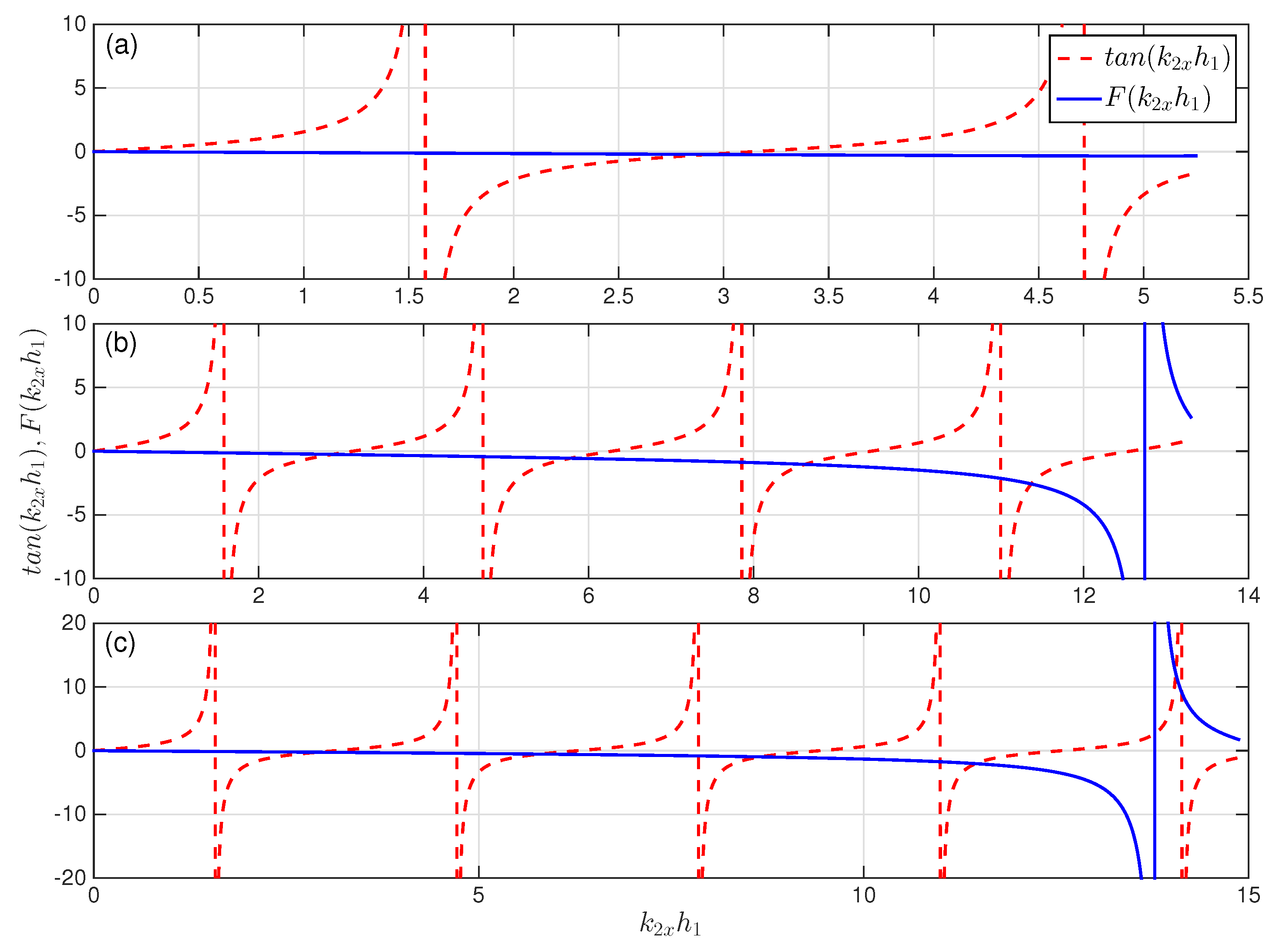
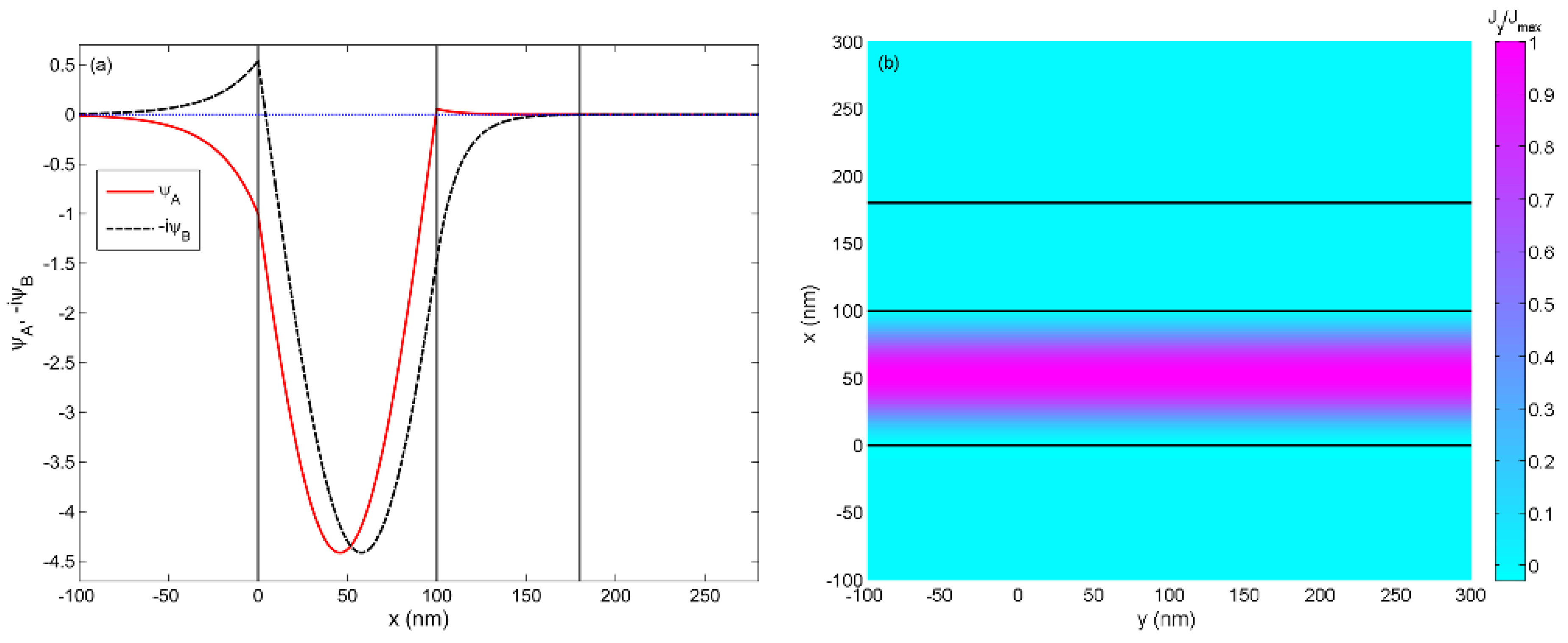
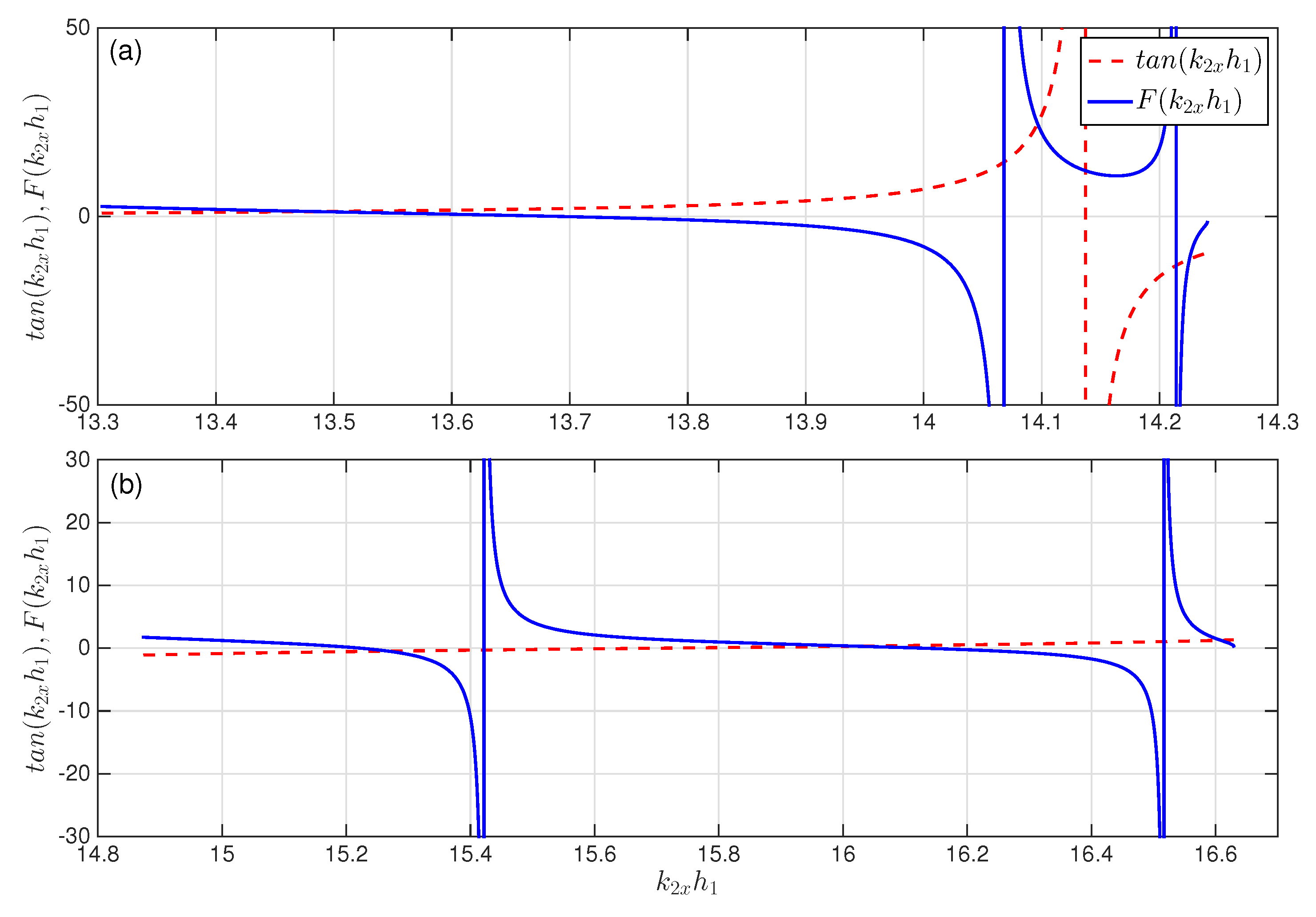
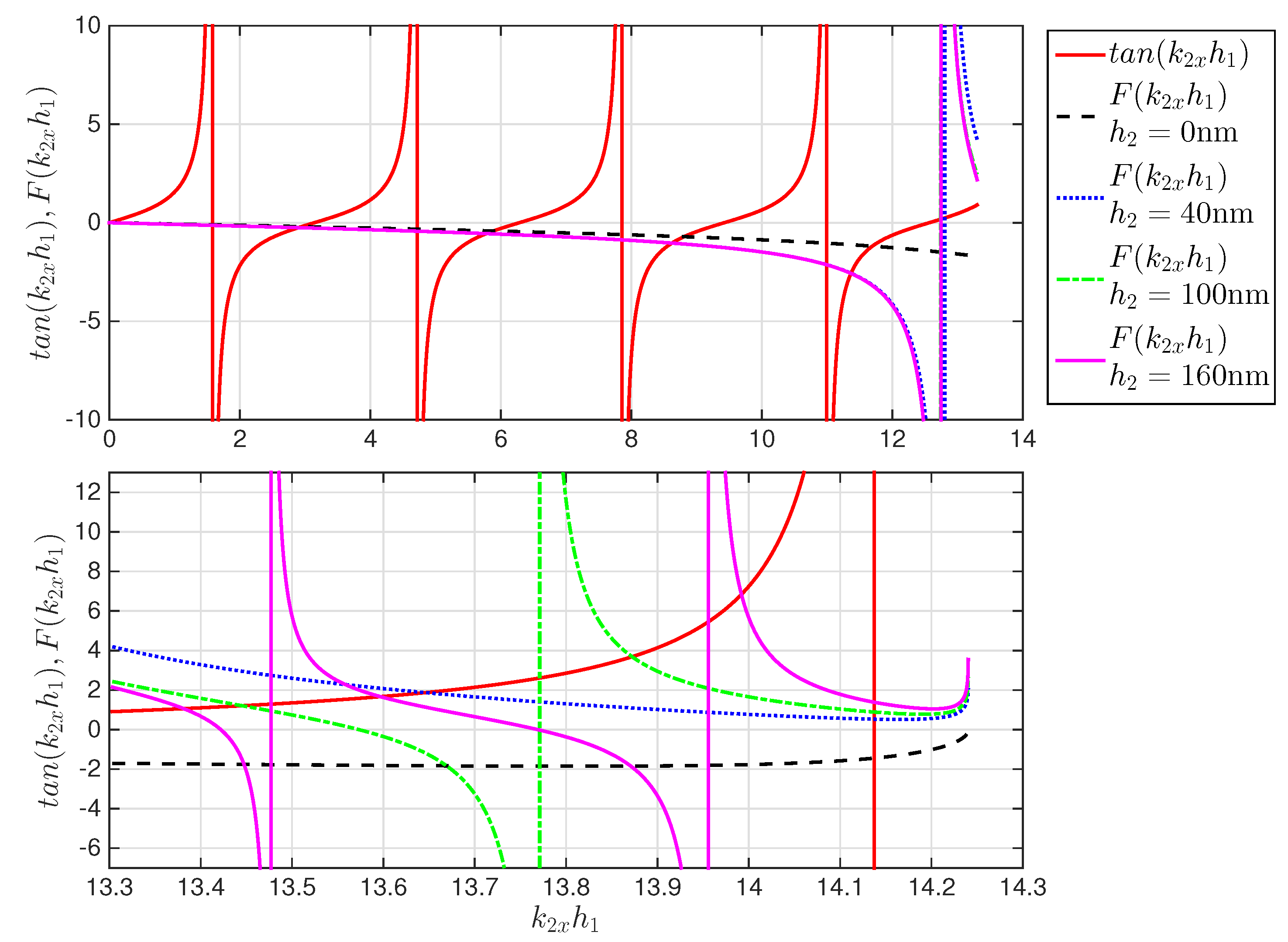
2. Guided Mode and Dispersion Equation for a Double-Well Potential
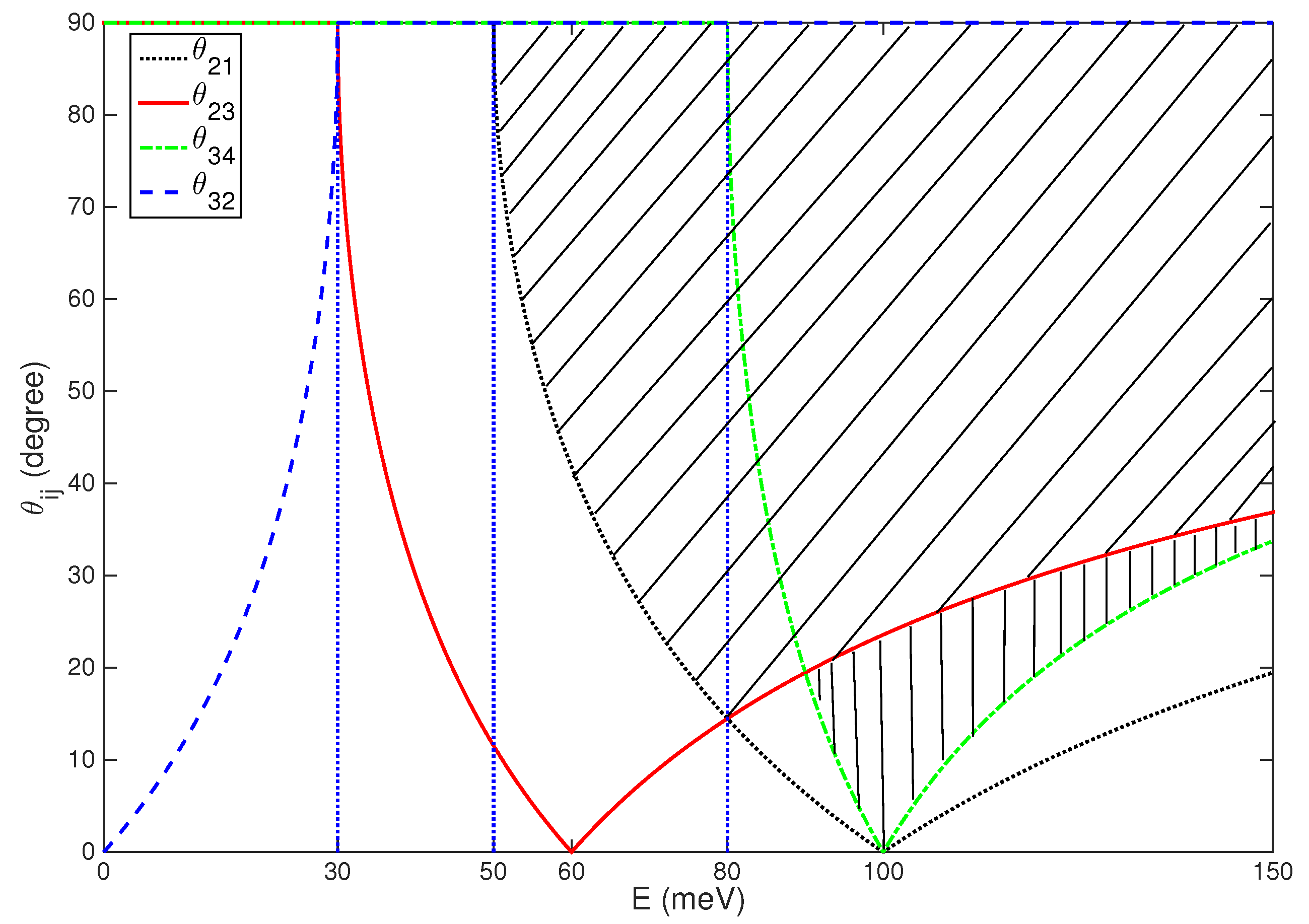
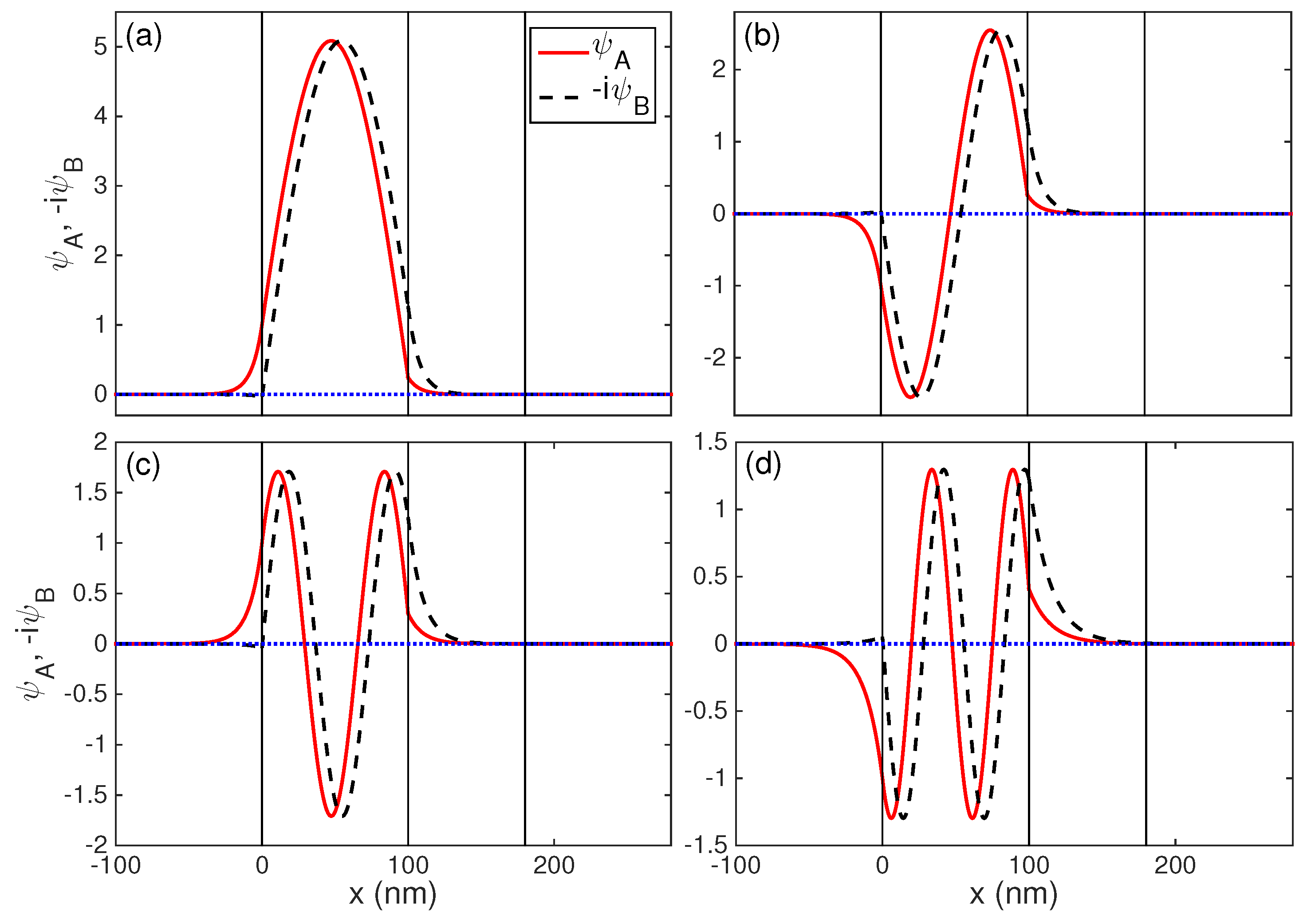
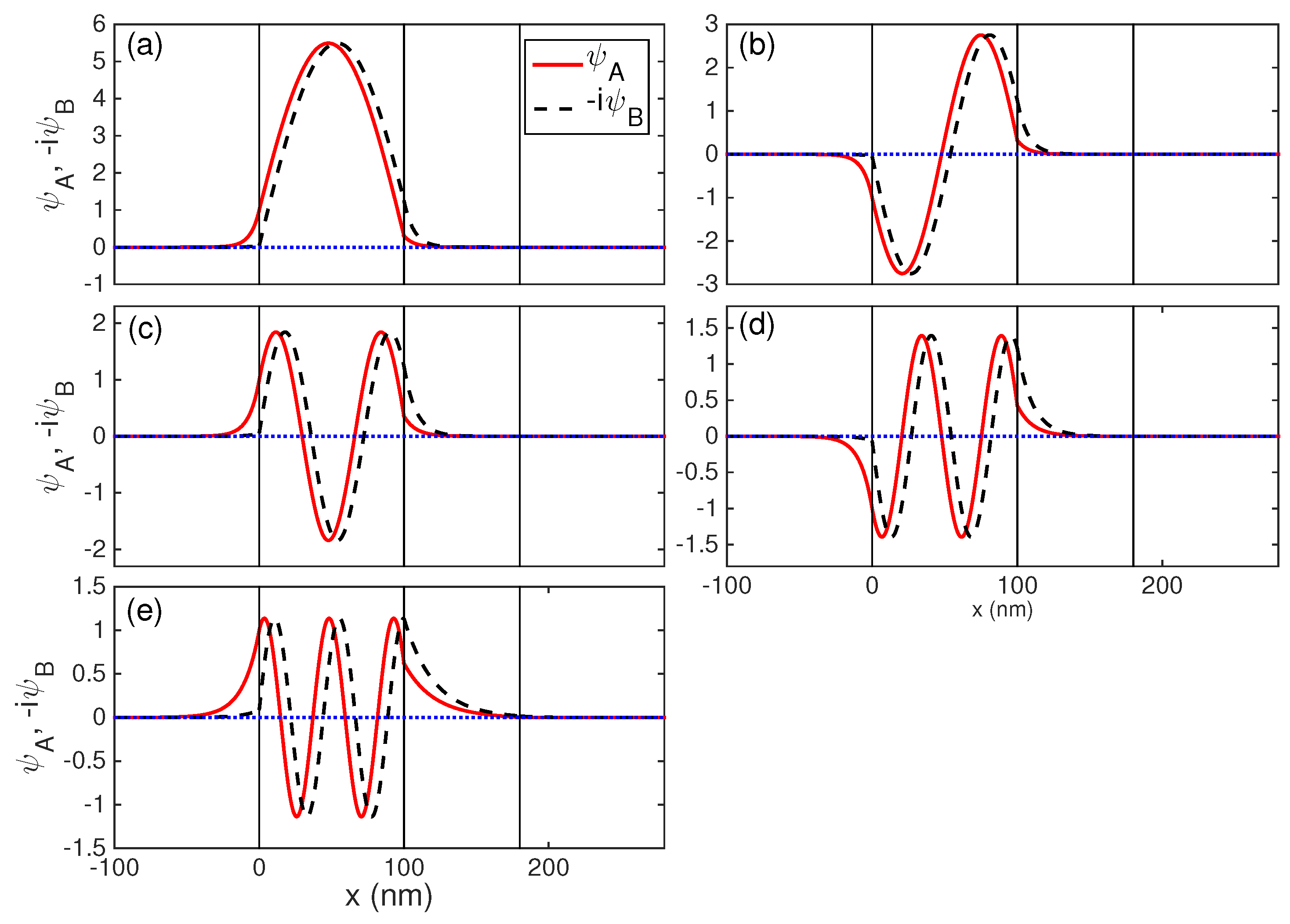
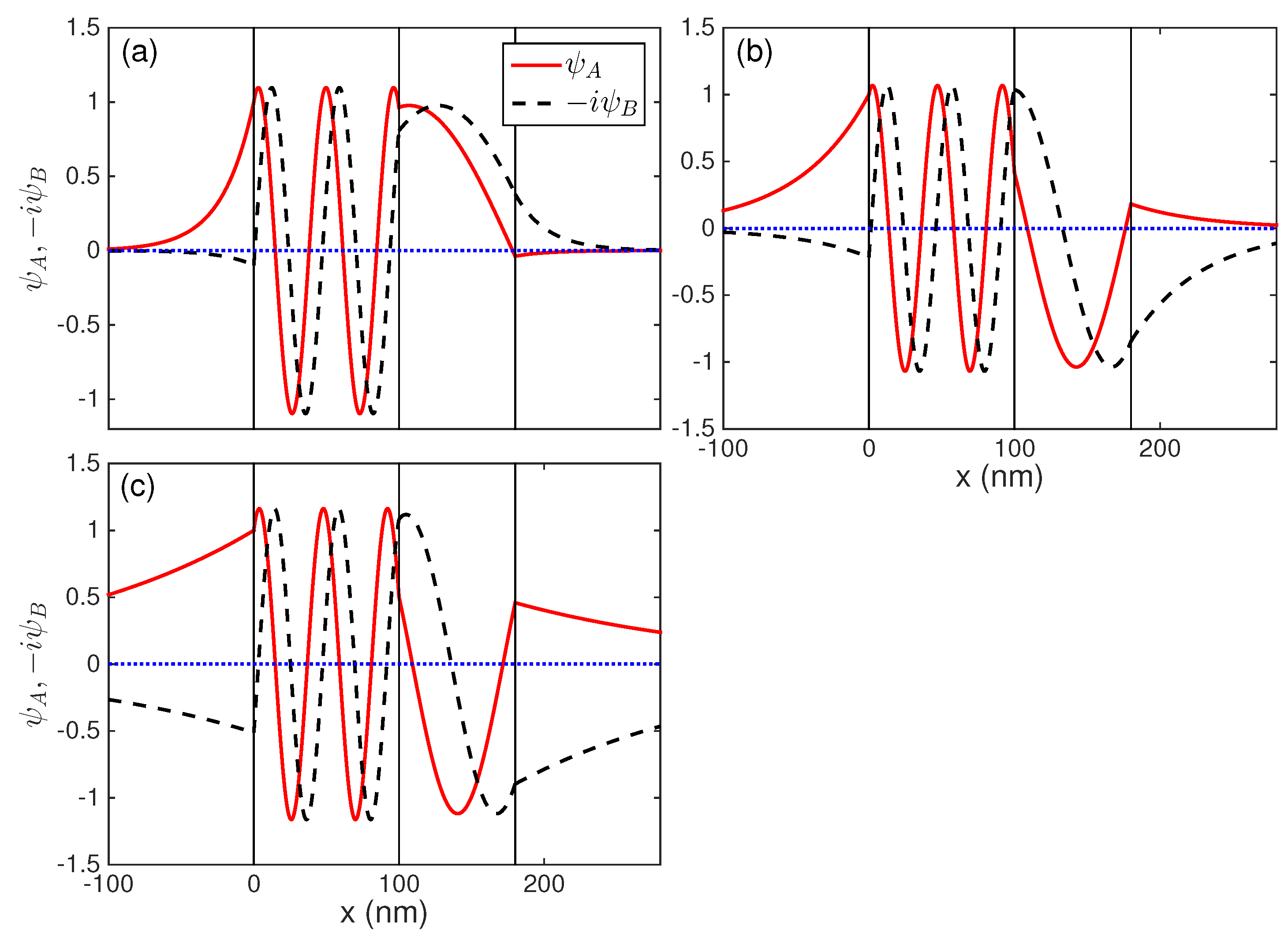
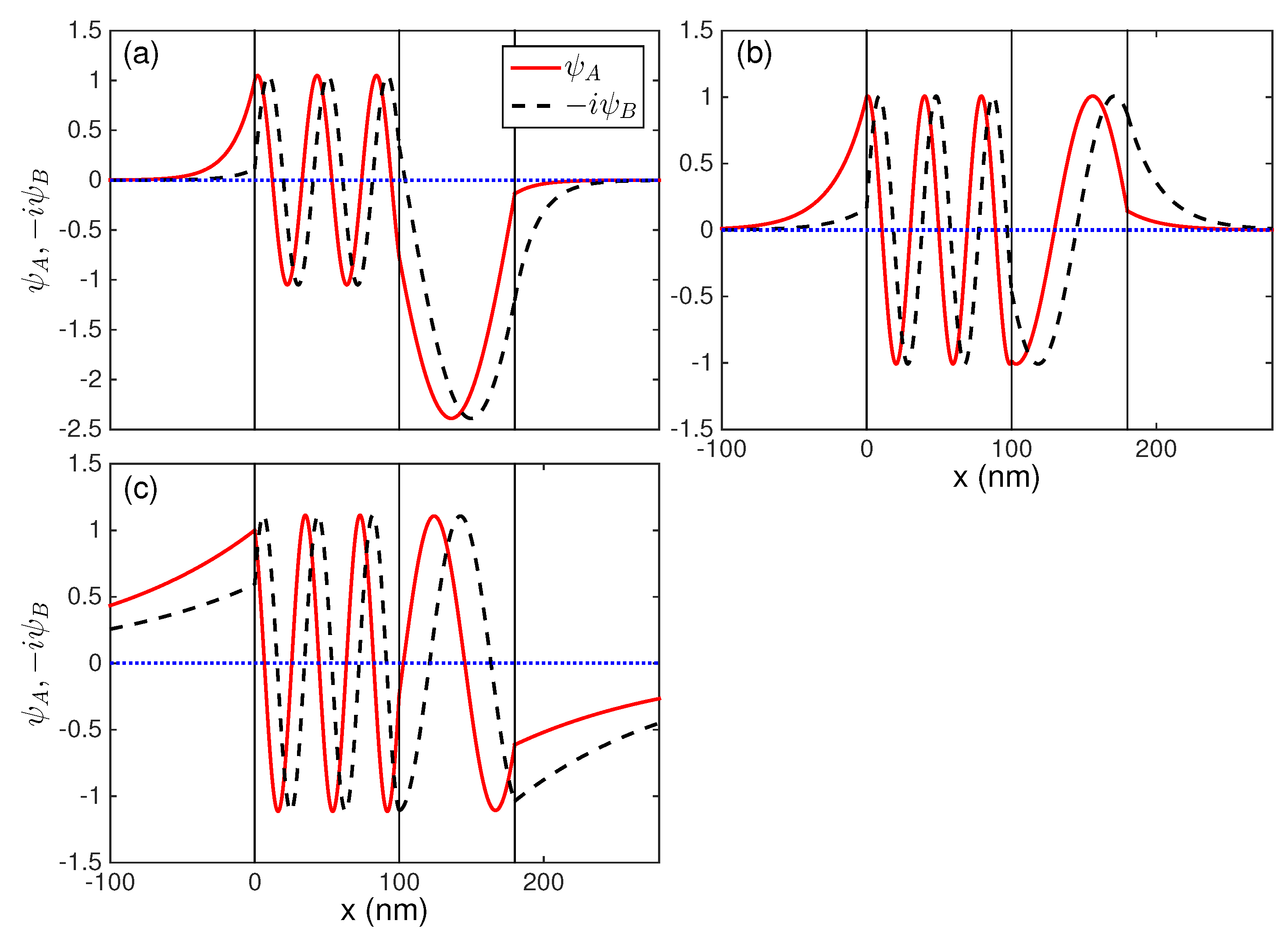
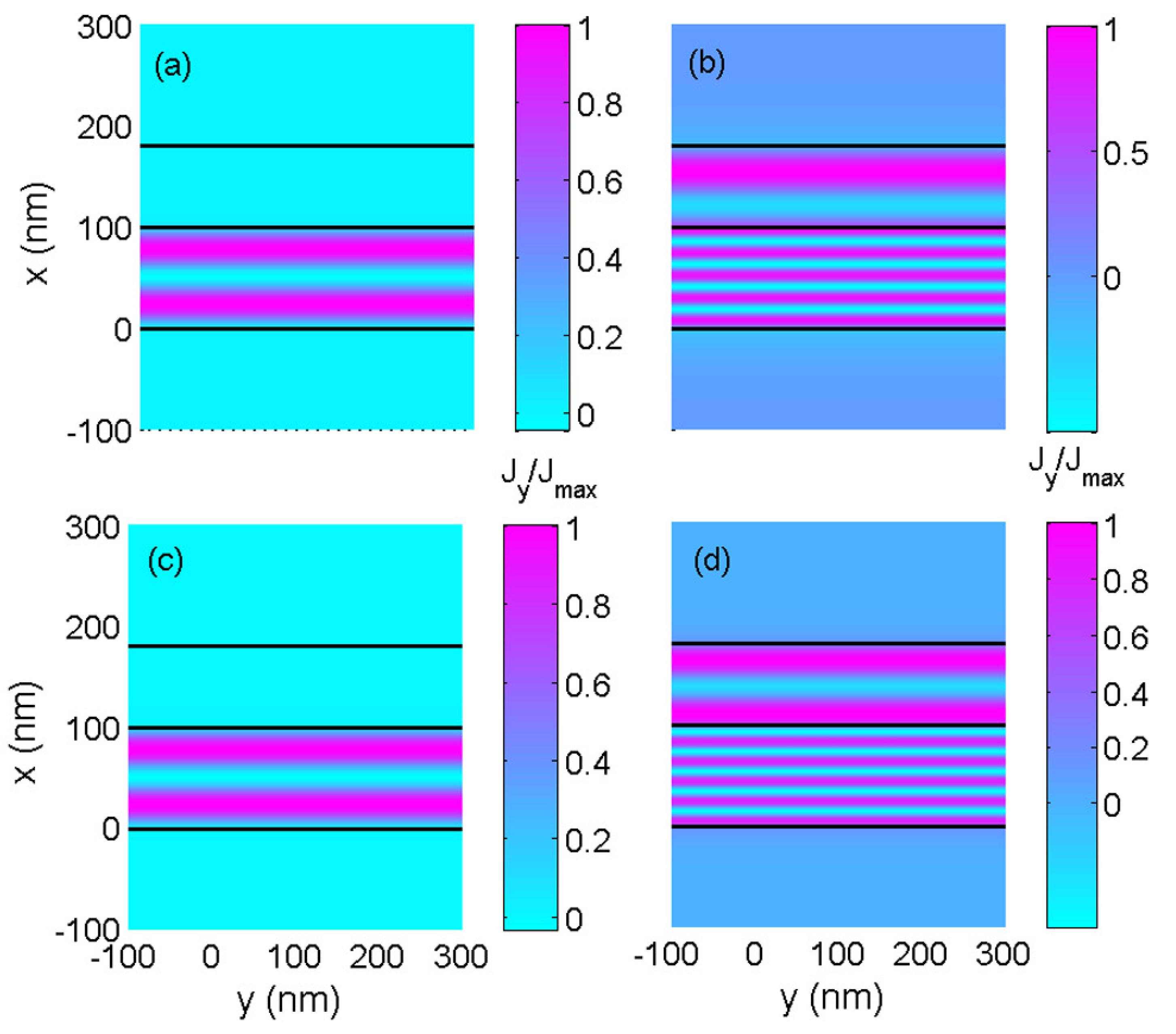
3. Characteristics of the Guided Modes in a Double-Well Potential
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Beenakker, C.; Sepkhanov, R.; Akhmerov, A.; Tworzydło, J. Quantum Goos-Hänchen effect in graphene. Phys. Rev. Lett. 2009, 102, 146804. [Google Scholar] [CrossRef] [PubMed]
- Sharma, M.; Ghosh, S. Electron transport and Goos–Hänchen shift in graphene with electric and magnetic barriers: Optical analogy and band structure. J. Phys. Condens. Matter 2011, 23, 055501. [Google Scholar] [CrossRef] [PubMed]
- Cheianov, V.V.; Fal’ko, V.; Altshuler, B. The focusing of electron flow and a Veselago lens in graphene pn junctions. Science 2007, 315, 1252–1255. [Google Scholar] [CrossRef] [PubMed]
- Park, C.H.; Son, Y.W.; Yang, L.; Cohen, M.L.; Louie, S.G. Electron beam supercollimation in graphene superlattices. Nano Lett. 2008, 8, 2920–2924. [Google Scholar] [CrossRef] [PubMed]
- Asmar, M.M.; Ulloa, S.E. Rashba spin-orbit interaction and birefringent electron optics in graphene. Phys. Rev. B 2013, 87, 075420. [Google Scholar] [CrossRef]
- Ghosh, S.; Sharma, M. Electron optics with magnetic vector potential barriers in graphene. J. Phys. Condens. Matter 2009, 21, 292204. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.M.; He, Y.; Chen, X. Guided modes in graphene waveguides. Appl. Phys. Lett. 2009, 94, 212105. [Google Scholar] [CrossRef]
- He, Y.; Xu, Y.; Yang, Y.F.; Huang, W.D. Guided modes in asymmetric graphene waveguides. Appl. Phys. A 2014, 115, 895–902. [Google Scholar] [CrossRef]
- Ping, P.; Peng, Z.; Liu, J.K.; Cao, Z.Z.; Li, G.Q. Oscillating guided modes in graphene-based asymmetric waveguides. Commun. Theor. Phys. 2012, 58, 765. [Google Scholar] [CrossRef]
- Xu, Y.; Ang, L.K. Guided modes in a triple-well graphene waveguide: Analogy of five-layer optical waveguide. J. Opt. 2015, 17, 035005. [Google Scholar] [CrossRef]
- Williams, J.; Low, T.; Lundstrom, M.; Marcus, C. Gate-controlled guiding of electrons in graphene. Nat. Nanotechnol. 2011, 6, 222–225. [Google Scholar] [CrossRef] [PubMed]
- Myoung, N.; Ihm, G.; Lee, S. Magnetically induced waveguide in graphene. Phys. Rev. B 2011, 83, 113407. [Google Scholar] [CrossRef]
- Huang, W.D.; He, Y.; Yang, Y.F.; Li, C.F. Graphene waveguide induced by gradually varied magnetic fields. J. Appl. Phys. 2012, 111, 053712. [Google Scholar] [CrossRef]
- Hartmann, R.R.; Robinson, N.; Portnoi, M. Smooth electron waveguides in graphene. Phys. Rev. B 2010, 81, 245431. [Google Scholar] [CrossRef]
- Wu, Z.H.; Zhai, F.; Peeters, F.; Xu, H.; Chang, K. Valley-dependent Brewster angles and Goos-Hänchen effect in strained graphene. Phys. Rev. Lett. 2011, 106, 176802. [Google Scholar] [CrossRef] [PubMed]
- Villegas, C.E.; Tavares, M.R.; Hai, G.Q.; Peeters, F. Sorting the modes contributing to guidance in strain-induced graphene waveguides. New J. Phys. 2013, 15, 023015. [Google Scholar] [CrossRef]
- Pereira, V.M.; Neto, A.C. Strain engineering of graphene’s electronic structure. Phys. Rev. Lett. 2009, 103, 046801. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.H. Electronic fiber in graphene. Appl. Phys. Lett. 2011, 98, 082117. [Google Scholar] [CrossRef]
- Pereira, J.M., Jr.; Mlinar, V.; Peeters, F.; Vasilopoulos, P. Confined states and direction-dependent transmission in graphene quantum wells. Phys. Rev. B 2006, 74, 045424. [Google Scholar] [CrossRef]
- Tudorovskiy, T.Y.; Chaplik, A. Spatially inhomogeneous states of charge carriers in graphene. JETP Lett. 2007, 84, 619–623. [Google Scholar] [CrossRef]
- De Martino, A.; Dell’Anna, L.; Egger, R. Magnetic confinement of massless Dirac fermions in graphene. Phys. Rev. Lett. 2007, 98, 066802. [Google Scholar] [CrossRef] [PubMed]
- Low, T.; Guinea, F. Strain-induced pseudomagnetic field for novel graphene electronics. Nano Lett. 2010, 10, 3551–3554. [Google Scholar] [CrossRef] [PubMed]
- Elton, D.M.; Levitin, M.; Polterovich, I. Eigenvalues of a One-Dimensional Dirac Operator Pencil; Annales Henri Poincaré; Springer: Berlin, Germany, 2014; Volume 15, pp. 2321–2377. [Google Scholar]
- Hartmann, R.R.; Portnoi, M. Quasi-exact solution to the Dirac equation for the hyperbolic-secant potential. Phys. Rev. A 2014, 89, 012101. [Google Scholar] [CrossRef]
- Stone, D.; Downing, C.; Portnoi, M. Searching for confined modes in graphene channels: The variable phase method. Phys. Rev. B 2012, 86, 075464. [Google Scholar] [CrossRef]
- Yuan, J.H.; Cheng, Z.; Zeng, Q.J.; Zhang, J.P.; Zhang, J.J. Velocity-controlled guiding of electron in graphene: Analogy of optical waveguides. J. Appl. Phys. 2011, 110, 103706. [Google Scholar] [CrossRef]
- Li, H.D.; Wang, L.; Lan, Z.H.; Zheng, Y.S. Generalized transfer matrix theory of electronic transport through a graphene waveguide. Phys. Rev. B 2009, 79, 155429. [Google Scholar] [CrossRef]
- Pedersen, J.G.; Gunst, T.; Markussen, T.; Pedersen, T.G. Graphene antidot lattice waveguides. Phys. Rev. B 2012, 86, 245410. [Google Scholar] [CrossRef]
- Allen, M.T.; Shtanko, O.; Fulga, I.C.; Akhmerov, A.; Watanabe, K.; Taniguchi, T.; Jarillo-Herrero, P.; Levitov, L.S.; Yacoby, A. Spatially resolved edge currents and guided-wave electronic states in graphene. Nat. Phys. 2016, 12, 128–133. [Google Scholar] [CrossRef]
- Wang, L.G.; Zhu, S.Y. Electronic band gaps and transport properties in graphene superlattices with one-dimensional periodic potentials of square barriers. Phys. Rev. B 2010, 81, 205444. [Google Scholar] [CrossRef]
- Xu, Y.; He, Y.; Yang, Y.F. Transmission gaps in graphene superlattices with periodic potential patterns. Phys. B Condens. Matter 2015, 457, 188–193. [Google Scholar] [CrossRef]
- Xu, Y.; He, Y.; Yang, Y.F.; Zhang, H.F. Electronic band gaps and transport in Cantor graphene superlattices. Superlatt. Microstruct. 2015, 80, 63–71. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008, 103, 064302. [Google Scholar] [CrossRef]
- Tamagnone, M.; Gomez-Diaz, J.; Mosig, J.R.; Perruisseau-Carrier, J. Reconfigurable terahertz plasmonic antenna concept using a graphene stack. Appl. Phys. Lett. 2012, 101, 214102. [Google Scholar] [CrossRef]
- Bouzianas, G.; Kantartzis, N.; Tsiboukis, T. Subcell dispersive finite-difference time-domain schemes for infinite graphene-based structures. IET Microw. Antennas Propag. 2012, 6, 377–386. [Google Scholar] [CrossRef]
- Llatser, I.; Kremers, C.; Cabellos-Aparicio, A.; Jornet, J.M.; Alarcón, E.; Chigrin, D.N. Graphene-based nano-patch antenna for terahertz radiation. Photonics Nanostruct. Fundam. Appl. 2012, 10, 353–358. [Google Scholar] [CrossRef]
- Salonikios, V.; Amanatiadis, S.; Kantartzis, N.; Yioultsis, T. Modal analysis of graphene microtubes utilizing a two-dimensional vectorial finite element method. Appl. Phys. A 2016, 122, 1–7. [Google Scholar] [CrossRef]
- Nayyeri, V.; Soleimani, M.; Ramahi, O.M. Modeling graphene in the finite-difference time-domain method using a surface boundary condition. IEEE Trans. Antennas Propag. 2013, 61, 4176–4182. [Google Scholar] [CrossRef]
- Amanatiadis, S.A.; Kantartzis, N.V.; Tsiboukis, T.D. A loss-controllable absorbing boundary condition for surface plasmon polaritons propagating onto graphene. IEEE Trans. Mag. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Mock, A. Padé approximant spectral fit for FDTD simulation of graphene in the near infrared. Opt. Mater. Express 2012, 2, 771–781. [Google Scholar] [CrossRef]
- Huard, B.; Sulpizio, J.; Stander, N.; Todd, K.; Yang, B.; Goldhaber-Gordon, D. Transport measurements across a tunable potential barrier in graphene. Phys. Rev. Lett. 2007, 98, 236803. [Google Scholar] [CrossRef] [PubMed]
- Brey, L.; Fertig, H. Electronic states of graphene nanoribbons studied with the Dirac equation. Phys. Rev. B 2006, 73, 235411. [Google Scholar] [CrossRef]
- Mhamdi, A.; Salem, E.B.; Jaziri, S. Electronic reflection for a single-layer graphene quantum well. Solid State Commun. 2013, 175, 106–113. [Google Scholar] [CrossRef]
- Allain, P.E.; Fuchs, J. Klein tunneling in graphene: Optics with massless electrons. Eur. Phys. J. B 2011, 83, 301–317. [Google Scholar] [CrossRef]
- He, Y.; Zhang, J.; Li, C.F. Guided modes in a symmetric five-layer left-handed waveguide. J. Opt. Soc. Am. B 2008, 25, 2081–2091. [Google Scholar] [CrossRef]
- Shadrivov, I.V.; Sukhorukov, A.A.; Kivshar, Y.S. Guided modes in negative-refractive-index waveguides. Phys. Rev. E 2003, 67, 057602. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Ang, L.K. Guided Modes in a Double-Well Asymmetric Potential of a Graphene Waveguide. Electronics 2016, 5, 87. https://doi.org/10.3390/electronics5040087
Xu Y, Ang LK. Guided Modes in a Double-Well Asymmetric Potential of a Graphene Waveguide. Electronics. 2016; 5(4):87. https://doi.org/10.3390/electronics5040087
Chicago/Turabian StyleXu, Yi, and Lay Kee Ang. 2016. "Guided Modes in a Double-Well Asymmetric Potential of a Graphene Waveguide" Electronics 5, no. 4: 87. https://doi.org/10.3390/electronics5040087
APA StyleXu, Y., & Ang, L. K. (2016). Guided Modes in a Double-Well Asymmetric Potential of a Graphene Waveguide. Electronics, 5(4), 87. https://doi.org/10.3390/electronics5040087