Stability Analysis of Quantum-Dot Spin-VCSELs
Abstract
:1. Introduction
2. Model and Analysis
3. Results
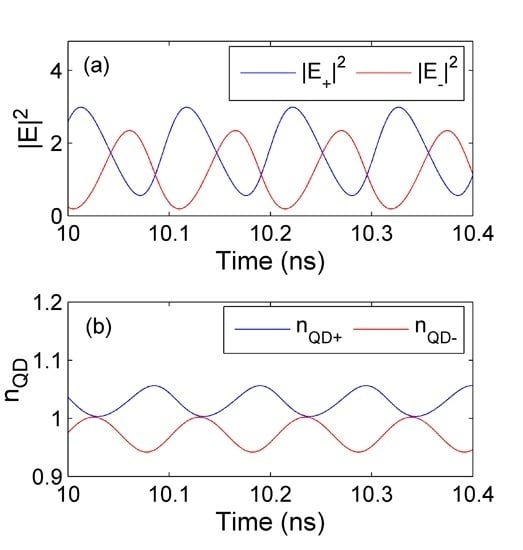
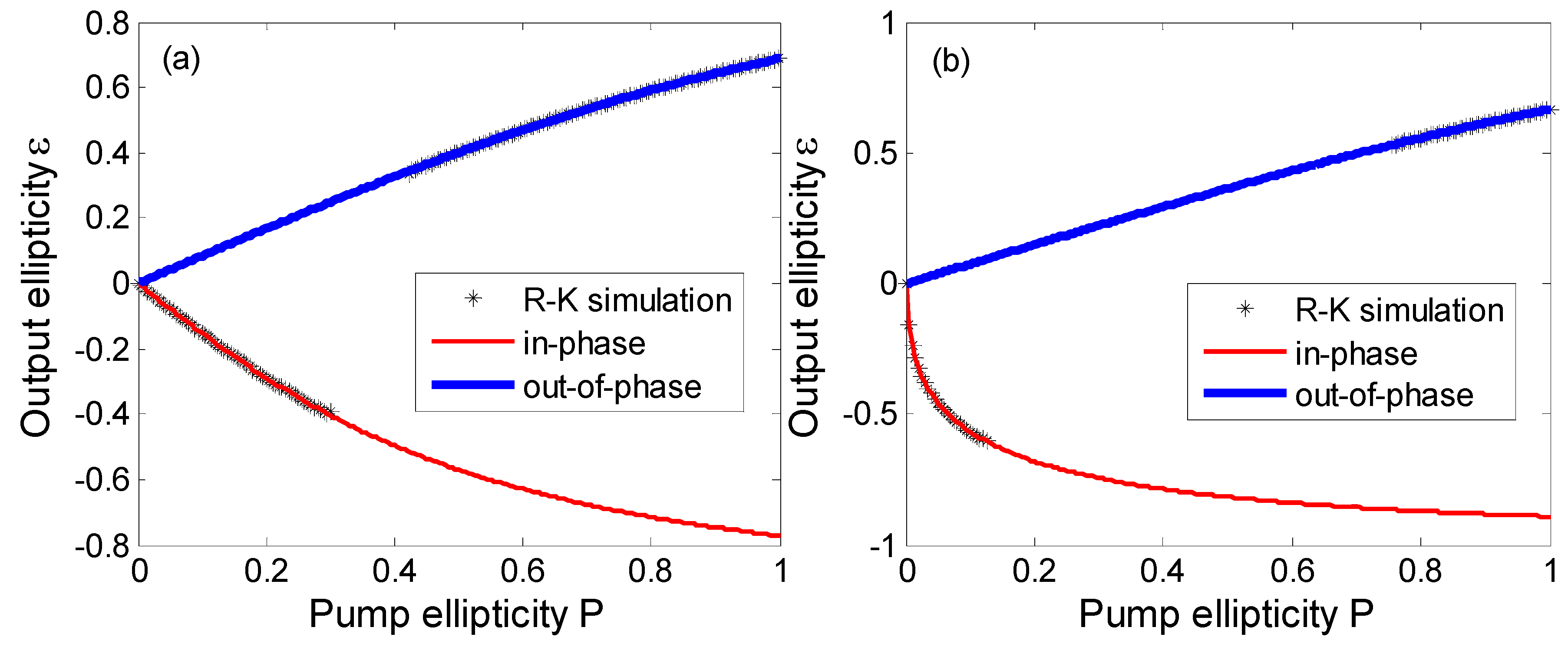
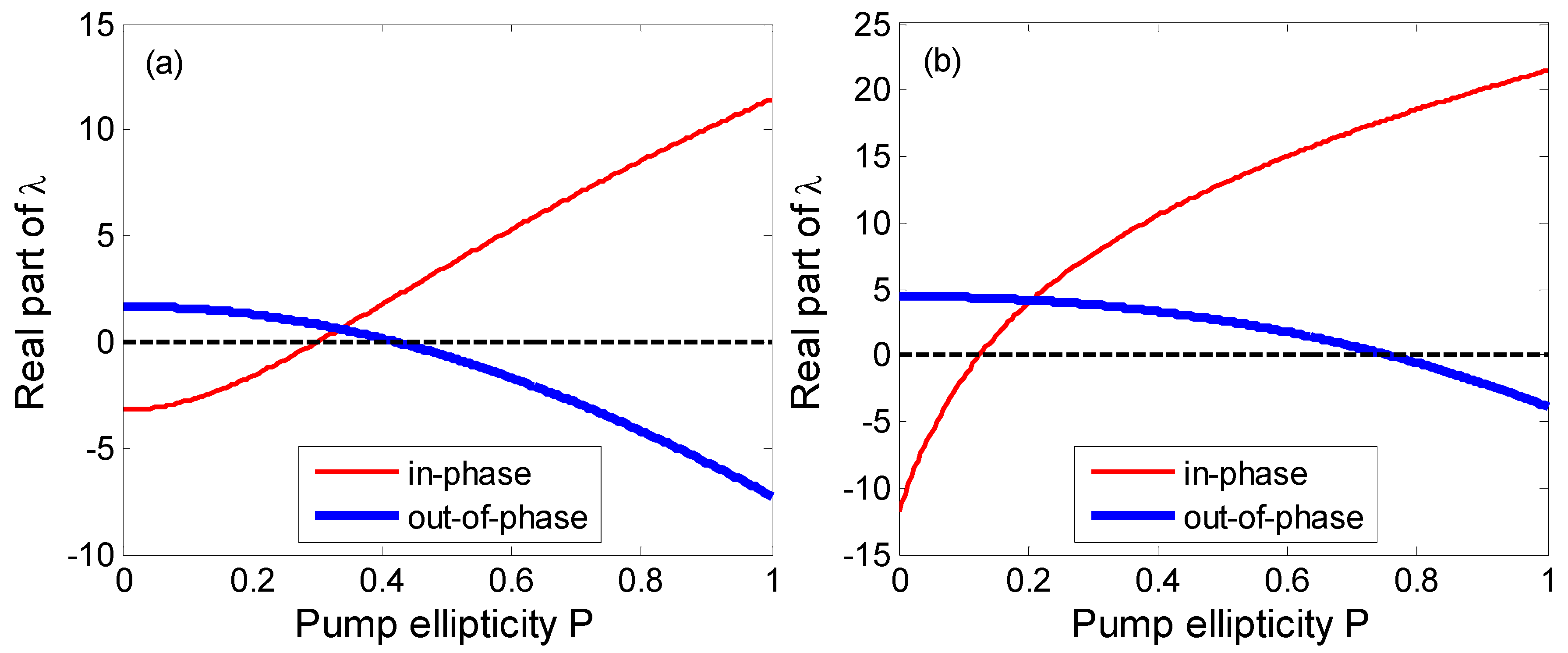
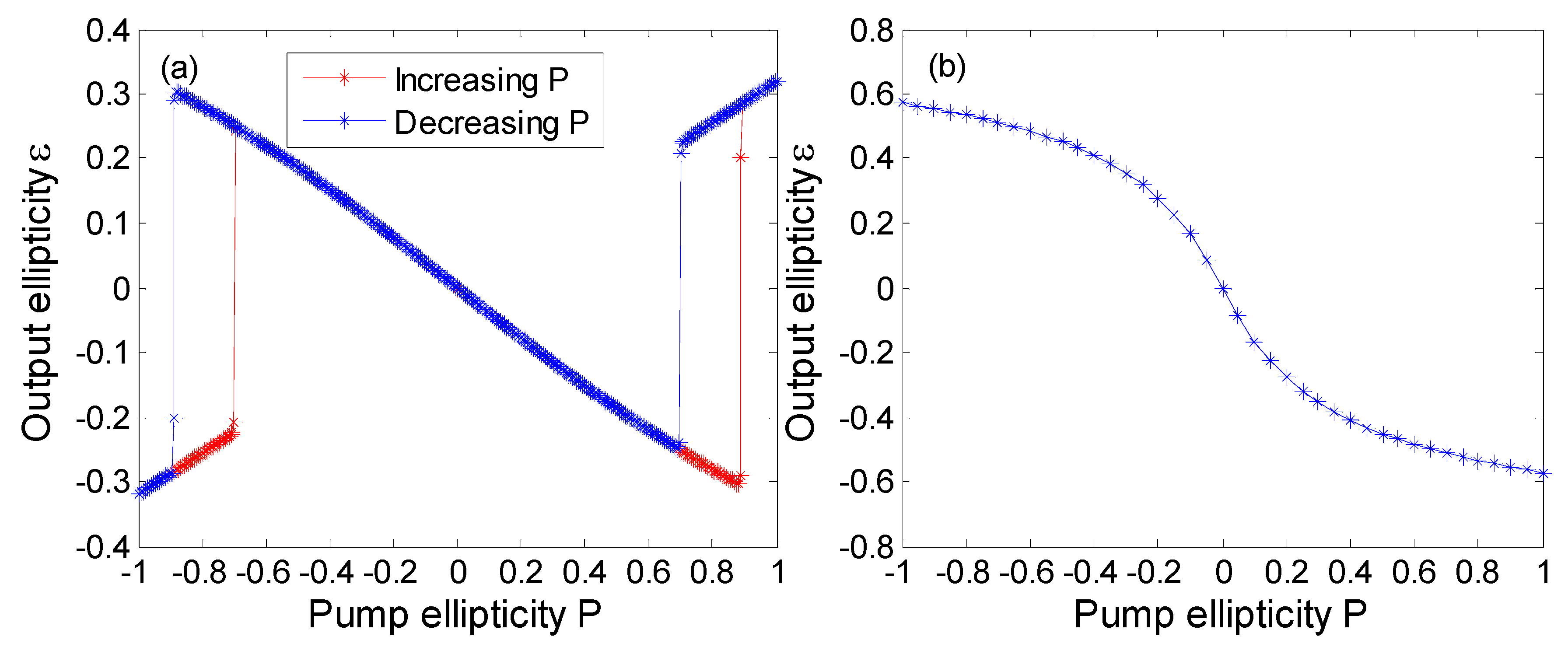
3.1. Results for VCSEL1
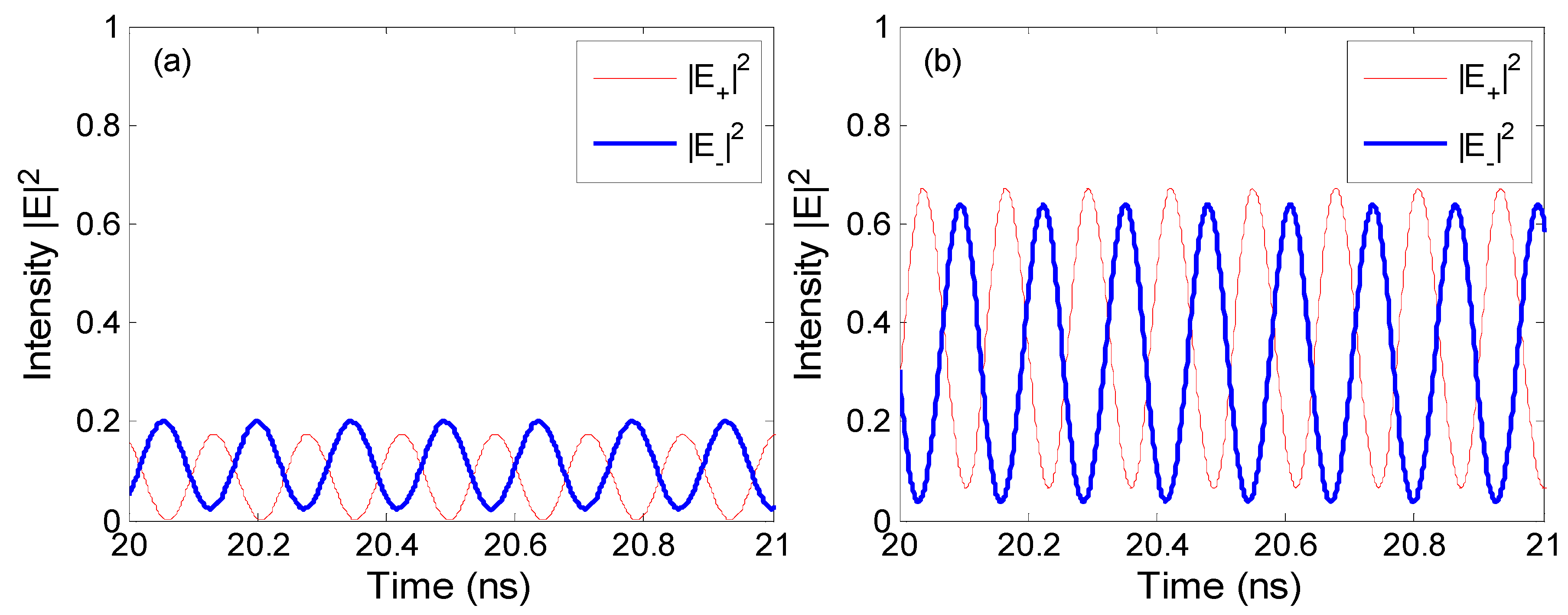
3.2. Results for VCSEL2
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hallstein, S.; Berger, J.D.; Hilpert, M.; Schneider, H.C.; Rühle, W.W.; Jahnke, F.; Koch, S.W.; Gibbs, H.M.; Khitrova, G.; Oestreich, M. Manifestation of coherent spin precession in stimulated semiconductor emission dynamics. Phys. Rev. B 1997, 56, R7076–R7079. [Google Scholar] [CrossRef]
- Ando, H.; Sogawa, T.; Gotoh, H. Photon-spin controlled lasing oscillation in surface-emitting lasers. Appl. Phys. Lett. 1997, 73, 566–568. [Google Scholar] [CrossRef]
- Hendriks, R.F.M.; Van Exter, M.P.; Woerdman, J.P.; Gulden, K.H.; Moser, M. Memory effect for polarization of pump light in optically pumped vertical-cavity semiconductor lasers. IEEE J. Quantum Electron. 1998, 34, 1455–1460. [Google Scholar] [CrossRef]
- Rudolph, J.; Hagele, D.; Gibbs, H.M.; Khitrova, G.; Oestreich, M. Laser threshold reduction in a spintronic device. Appl. Phys. Lett. 2003, 82, 4516–4518. [Google Scholar] [CrossRef]
- Li, M.; Jähme, H.; Soldat, H.; Gerhardt, N.; Hofmann, M.; Ackemann, T. Birefringence controlled room-temperature picosecond spin dynamics close to the threshold of vertical-cavity surface-emitting laser devices. Appl. Phys. Lett. 2010, 97, 191114. [Google Scholar] [CrossRef]
- Gerhardt, N.C.; Hofmann, M.R. Spin-controlled vertical-cavity surface-emitting lasers. Adv. Opt. Technol. 2012, 2012, 268949. [Google Scholar] [CrossRef]
- Žutic, I.; Fabian, J.; Sarma, S.D. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 2004, 76, 323–410. [Google Scholar] [CrossRef]
- Bhattacharya, P.; Basu, D.; Das, A.; Saha, D. Quantum dot polarized light sources. Semicond. Sci. Technol. 2011, 26, 014002. [Google Scholar] [CrossRef]
- Basu, D.; Saha, D.; Wu, C.C.; Holub, M.; Mi, Z.; Bhattacharya, P. Electrically injected InAs/GaAs quantum dot spin laser operating at 200 K. Appl. Phys. Lett. 2008, 92, 091119. [Google Scholar] [CrossRef]
- Saha, D.; Basu, D.; Bhattacharya, P. High-frequency dynamics of spin-polarized carriers and photons in a laser. Phys. Rev. B 2010, 82, 205309. [Google Scholar] [CrossRef]
- Alharthi, S.S.; Orchard, J.; Clarke, E.; Henning, I.D.; Adams, M.J. 1300 nm optically pumped quantum dot spin vertical external-cavity surface-emitting laser. Appl. Phys. Lett. 2015, 107, 151109. [Google Scholar] [CrossRef]
- Oszwałdowski, R.; Gøthgen, C.; Žutić, I. Theory of quantum dot spin lasers. Phys. Rev. B 2010, 82, 085316. [Google Scholar] [CrossRef]
- Lee, J.; Falls, W.; Oszwałdowski, R.; Žutić, I. Mapping between quantum dot and quantum well lasers: From conventional to spin lasers. Phys. Rev. B 2012, 85, 045314. [Google Scholar] [CrossRef]
- Qasaimeh, O. Effect of doping on the polarization characteristics of spin-injected quantum dot VCSEL. Opt. Quantum Electron. 2015, 47, 465–476. [Google Scholar] [CrossRef]
- Qasaimeh, O. Novel closed-form solution for spin-polarization in quantum dot VCSEL. Opt. Commun. 2015, 350, 83–89. [Google Scholar] [CrossRef]
- Alexandropoulos, D.; Al-Seyab, R.K.; Henning, I.D.; Adams, M.J. Instabilities in quantum-dot spin-VCSELs. Opt. Lett. 2012, 37, 1700–1702. [Google Scholar] [CrossRef] [PubMed]
- Adams, M.J.; Alexandropoulos, D. Analysis of quantum-dot spin-VCSELs. IEEE Photon. J. 2012, 4, 1124–1132. [Google Scholar] [CrossRef]
- San Miguel, M.; Feng, Q.; Moloney, J.V. Light-polarization dynamics in vertical cavity surface-emitting lasers. Phys. Rev. A 1995, 52, 1728–1739. [Google Scholar] [CrossRef] [PubMed]
- Gahl, A.; Balle, S.; San Miguel, M. Polarization dynamics of optically pumped VCSELs. IEEE J. Quantum Electron. 1999, 35, 342–351. [Google Scholar] [CrossRef]
- Susanto, H.; Schires, K.; Adams, M.J.; Henning, I.D. Spin-flip model of spin-polarized vertical-cavity surface-emitting lasers: Asymptotic analysis, numerics, and experiments. Phys. Rev. A 2015, 92, 063838. [Google Scholar] [CrossRef]
- Homoyanfour, A.; Adams, M.J. Analysis of SFM dynamics in solitary and optically-injected VCSELs. Opt. Express 2007, 15, 10504–10519. [Google Scholar] [CrossRef]

| Parameter | Symbol | VCSEL1 Value | VCSEL2 Value |
|---|---|---|---|
| Photon decay rate | κ | 250 ns−1 | 250 ns−1 |
| Carrier recombination rate | γn | 1 ns−1 | 1 ns−1 |
| Capture rate into from WL into QD | γo | 400 ns−1 | 400 ns−1 |
| Spin relaxation rate | γj | 10 ns−1 | 10 ns−1 |
| Birefringence rate | γp | 20 ns−1 | 20 ns−1 |
| Dichroism rate | γa | 0 | 0 |
| Linewidth enhancement factor | α | 3 | 4 |
| Normalized gain coefficient | h | 1.1995 | 1.05 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.; Alexandropoulos, D.; Susanto, H.; Henning, I.; Adams, M. Stability Analysis of Quantum-Dot Spin-VCSELs. Electronics 2016, 5, 83. https://doi.org/10.3390/electronics5040083
Li N, Alexandropoulos D, Susanto H, Henning I, Adams M. Stability Analysis of Quantum-Dot Spin-VCSELs. Electronics. 2016; 5(4):83. https://doi.org/10.3390/electronics5040083
Chicago/Turabian StyleLi, Nianqiang, Dimitris Alexandropoulos, Hadi Susanto, Ian Henning, and Michael Adams. 2016. "Stability Analysis of Quantum-Dot Spin-VCSELs" Electronics 5, no. 4: 83. https://doi.org/10.3390/electronics5040083
APA StyleLi, N., Alexandropoulos, D., Susanto, H., Henning, I., & Adams, M. (2016). Stability Analysis of Quantum-Dot Spin-VCSELs. Electronics, 5(4), 83. https://doi.org/10.3390/electronics5040083