A Synthetic Method of Wide-Angle Scanning Sparse Arrays Based on a Hybrid PSO-GA Algorithm

Abstract

To address the issue of traditional Particle Swarm Optimization (PSO) being prone to local optima and insufficient global search capability in sparse phased array optimization, a hybrid optimization algorithm integrating PSO with a Genetic Algorithm (GA) is proposed. Within the PSO framework, the proposed algorithm incorporates the adaptive crossover and mutation operations of the GA to enhance population diversity. It combines an adaptive weighting factor and a constriction factor to balance global exploration and local exploitation capabilities. Furthermore, a density-weighted method is employed to generate a high-quality initial population, thereby accelerating convergence. The proposed algorithm is applied to an 8 × 8 planar sparse array. On the E-plane (φ = 0°) and H-plane (φ = 90°), simulation results indicate that the achieved normalized maximum sidelobe level is −23.14 dB, which is significantly superior to those obtained by standalone PSO and GA. Based on these simulation results, microstrip patch antennas are introduced for array constitution and analysis. Full-wave electromagnetic simulation proves that the proposed sparse array has the ability of wide-angle scanning and low sidelobe. Our work demonstrates that the PSO-GA hybrid algorithm effectively enhances search capability and convergence performance, providing a reliable solution for sparse array design.

1. Introduction

Phased array antennas are characterized by their flexible beam-steering capability and are widely used in radar systems, satellite communications, mobile communications, and other fields. However, since each element is typically backed by a transmit/receive (T/R) module, challenges such as high cost and significant power consumption arise. Sparse phased array antennas mitigate these issues by reducing the number of antenna elements, thereby achieving advantages like weight reduction, compact size, and lower cost. Broadly, sparse phased arrays can be categorized into two types: The first is the sparse array, formed by selectively removing a subset of elements from a uniform array based on specific optimization methods, resulting in a non-uniform array with inter-element spacing constrained to integer multiples of a fundamental unit (typically half a wavelength). The second is the sparse-aperture array, which is realized by directly arranging the elements’ positions, allowing for arbitrary inter-element spacing. However, due to practical constraints such as the physical size of the elements and mutual coupling effects, the element spacing is generally no less than half a wavelength [1].

However, issues such as elevated sidelobe levels and degraded beam directivity necessitate the use of various algorithms to optimize the distribution and excitation of array elements, aiming to achieve performance metrics comparable to those of a full array. In early research, design techniques primarily focused on deriving deterministic sparse array distributions based on analytical formulas or given models. Various methods for deterministic non-uniform array layouts have been proposed to improve sidelobe performance. Such deterministic thinning algorithms can rapidly generate sparse array configurations according to array requirements, yet their results still possess considerable room for further optimization. Later, with advances in computer technology, researchers introduced fast synthesis methods based on numerical approaches, such as the Matrix Pencil Method (MPM) and the Iterative Fourier Technique (IFT) [2,3]. These algorithms offer high computational efficiency and are suitable for the rapid synthesis of regular arrays. Furthermore, several intelligent optimization algorithms have also been applied to the synthesis of sparse phased arrays. These include algorithms with strong global convergence capabilities, such as the Genetic Algorithm (GA) [4], Particle Swarm Optimization (PSO) [5], Differential Evolution (DE) [6], Wolf Pack Algorithm (WPA) [7], and Sparrow Search Algorithm (SSA) [8]. These methods treat the excitation of each element in the array as an independent variable to be optimized. The random search strategy yields favorable optimization results when the array scale is small. However, as the array aperture increases beyond a certain size, the dramatic growth in the dimensionality of the solution space makes it difficult for the original optimization strategies to find a satisfactory solution within a limited time.

To address limitations such as slow convergence, a tendency to fall into local optima, and high computational complexity, researchers have proposed various hybrid algorithms. These methods combine deterministic algorithms to obtain initial values with the global search capability of intelligent optimization algorithms, thereby accelerating convergence for relatively large-scale arrays. For instance, algorithms such as ADSGA [9], DSSDPSO [10], and DS-GA [11] have demonstrated promising results. With advancements in satellite and communication technologies, some researchers have also developed specialized optimization algorithms for specific radar antenna applications. For phased array antennas in Low Earth Orbit (LEO) satellite systems, Kong et al. proposed a hybrid array thinning method that combines a non-iterative algorithm based on amplitude density with a Genetic Algorithm [12]. This approach achieves minimization of the Peak Sidelobe Level (PSLL) under a given thinning ratio while ensuring the main lobe width remains essentially unchanged. For Ka-band large-scale phased arrays, Li et al. introduced a random sparse array synthesis algorithm based on the extreme disturbance method [13]. Through the iterative application of the extreme disturbance rate and the random sparse algorithm, it readily converges to a sparse array configuration meeting the target thinning ratio and yields uniformly distributed thinning results. For multi-beam array antennas, Zhang et al. proposed the Weighted Maximum Power Transfer Efficiency (WMMPTE) method [14], which enables the thinning of multi-beam array antennas such that the number of antenna elements is less than the number of antenna beams. In recent years, array antenna technology has increasingly advanced toward greater intelligence and dynamism. Related research encompasses multiple areas, including reconfigurable array technology, advanced multiple access transmission techniques, and array error calibration methods [15,16,17].

Existing intelligent optimization algorithms still face common challenges in sparse array synthesis, such as susceptibility to local optima, insufficient global search capability, and slow convergence speed. This paper proposes a PSO-GA hybrid optimization algorithm based on the deep integration of particle swarm optimization (PSO) and the genetic algorithm (GA) to address the performance challenges encountered by sparse arrays in wide-angle scanning scenarios, as well as the aforementioned optimization issues. The proposed algorithm incorporates adaptive crossover and mutation operations within the PSO iterative framework, actively injecting diversity after each iteration to structurally avoid premature convergence. It emphasizes enhancing the algorithm’s ability to balance global exploration and local exploitation under large-angle scanning conditions. An adaptive adjustment strategy for crossover and mutation probabilities is designed based on population concentration, and dynamic inertia weights and contraction factors are integrated to achieve a dynamic balance between global exploration and local exploitation, thereby meeting the robustness requirements of directional pattern performance during large-angle scanning. Additionally, a density weighting method is employed to generate the initial element distribution, simulating the suppression effect of amplitude weighting on sidelobes. This approach significantly improves the quality of initial solutions, accelerates the convergence process, and provides an efficient optimization foundation for large-angle scanning applications.

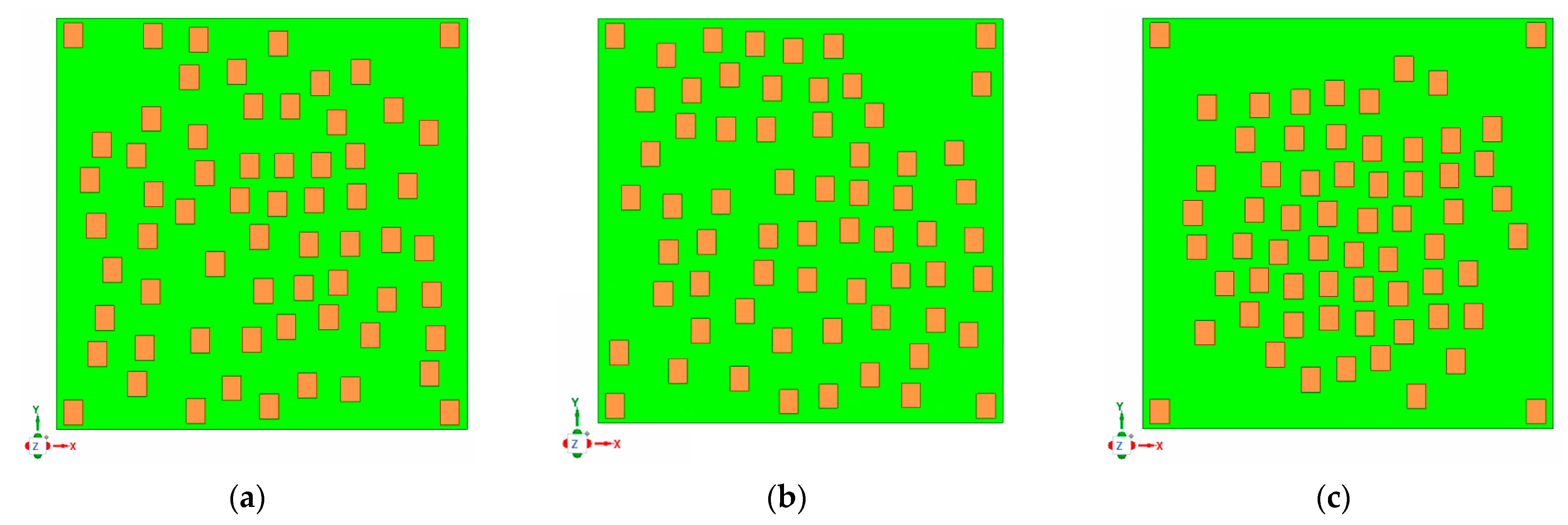
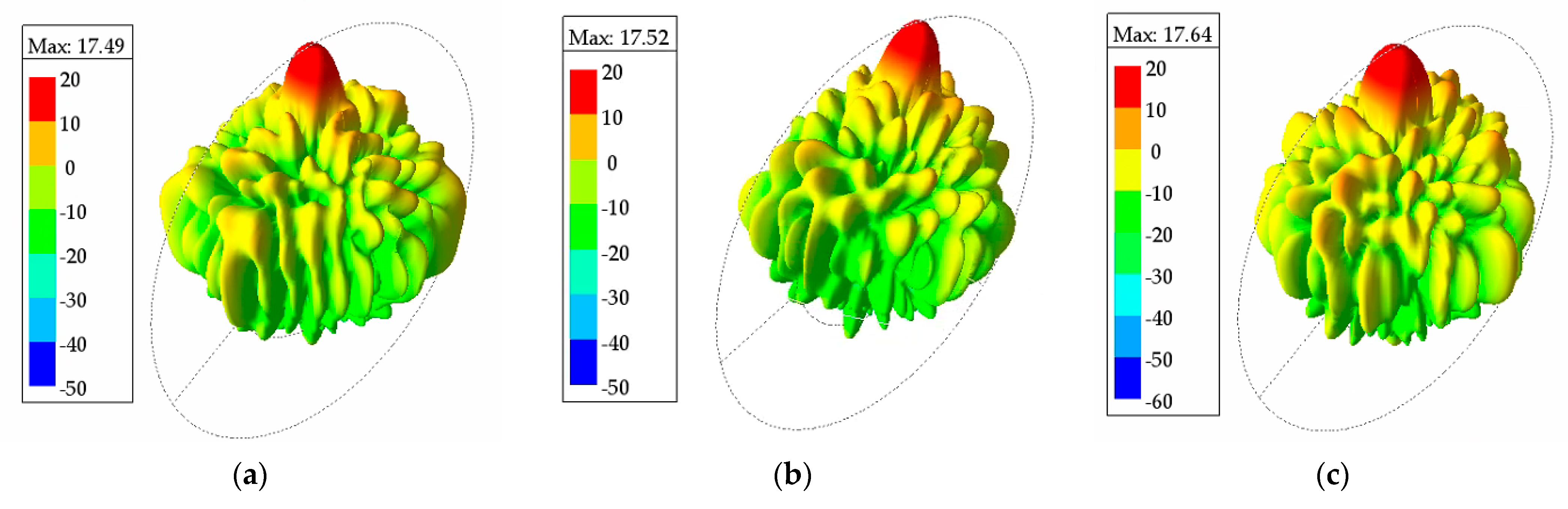
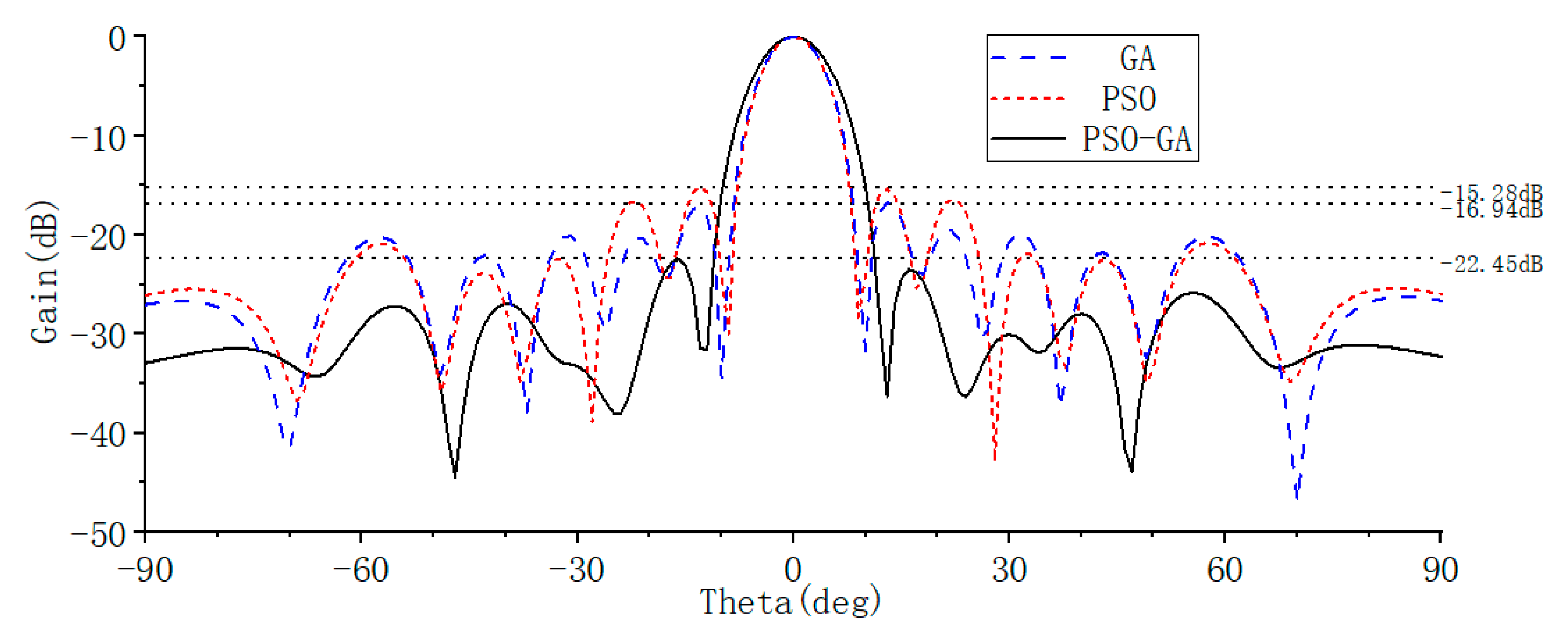
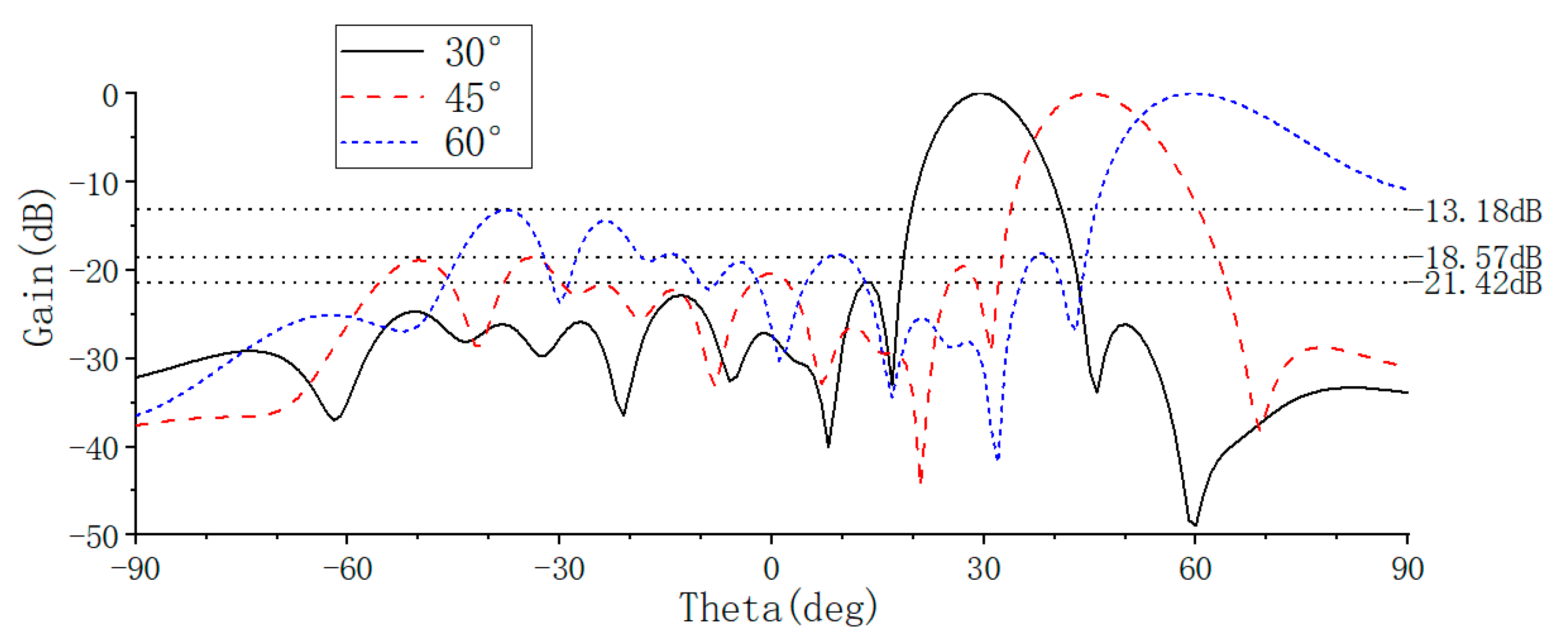
This paper applies the PSO-GA algorithm to optimize the positioning of an 8 × 8 planar sparse array and demonstrates its superiority in enhancing sidelobe suppression and accelerating convergence through numerical simulations and full-wave electromagnetic simulations. This study not only provides an efficient and reliable optimization tool for sparse array layout but also lays the foundation for future solutions to complex problems such as dynamic optimization of reconfigurable arrays and large-scale array synthesis.

2. Array Analysis

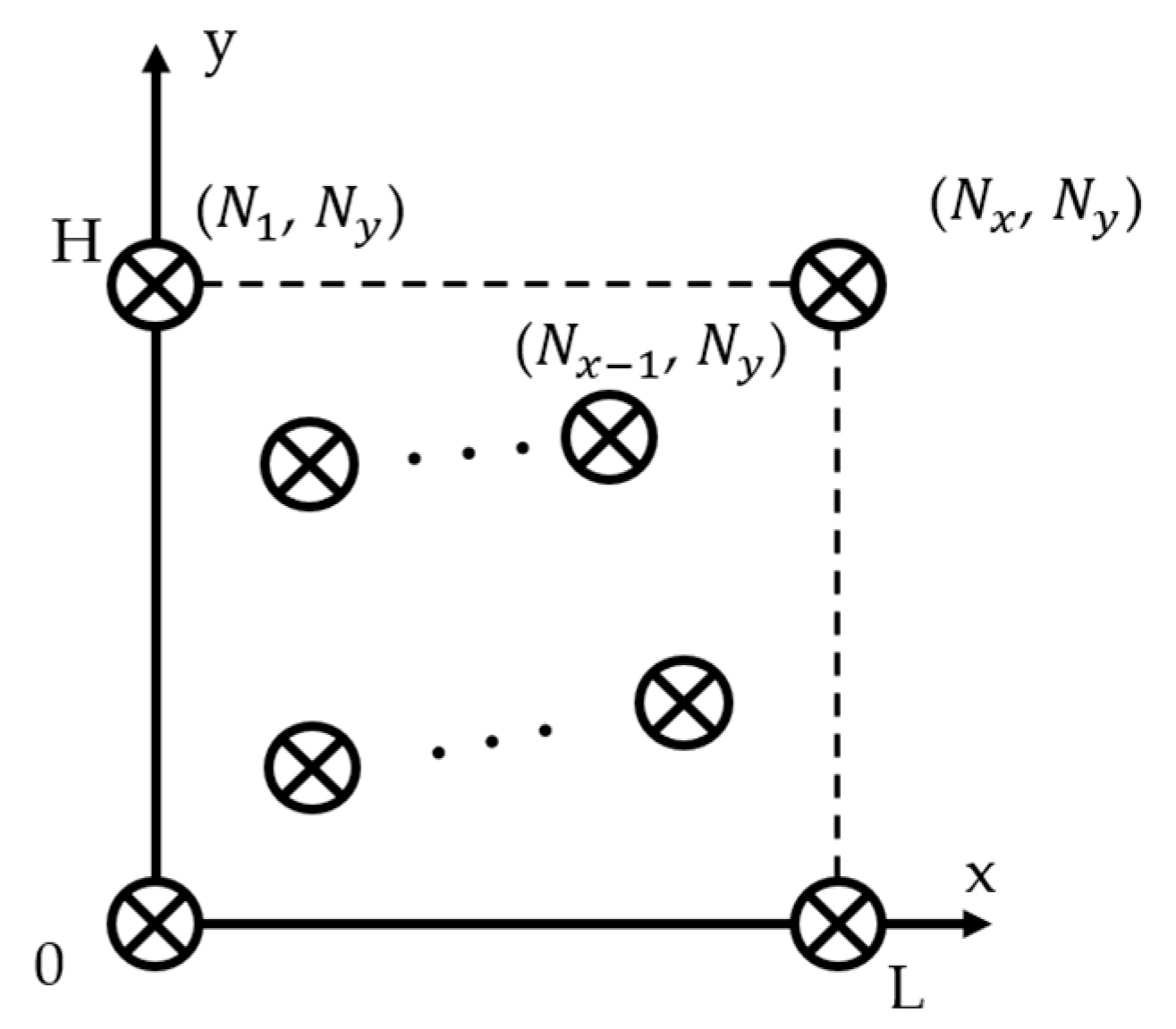
Assume a planar sparse antenna array composed of N × N elements, with an aperture size of L × H. The array is situated in the xoy-plane. Figure 1 illustrates the element layout of this array. To ensure the aperture size of the array antenna remains constant at L × H throughout the design process, the positions of the four corner elements—specifically (1, 1), (1, N), (N, 1), and (N, N)—are fixed at the four corners of the aperture.

For a non-uniform array arranged in the xoy-plane, its far-field radiation pattern can be expressed as the coherent superposition of the radiation fields from each element. The specific expression is:

$$\mathrm{F}(\mathrm{\theta },\mathrm{\phi })=\sum _{\mathrm{m}=1}^{{\mathrm{N}}_x}\sum _{\mathrm{n}=1}^{{\mathrm{N}}_y}\exp [\mathrm{j}{\displaystyle \frac{2\mathrm{\pi }}{\mathrm{\lambda }}}(x_{\mathrm{mn}}(\sin \mathrm{\theta }\cos \mathrm{\phi }-\sin {\mathrm{\theta }}_0\cos {\mathrm{\phi }}_0)+y_{\mathrm{mn}}(\sin \mathrm{\theta }\sin \mathrm{\phi }-\sin {\mathrm{\theta }}_0\sin {\mathrm{\phi }}_0))]$$

(1)

where ${\mathrm{N}}_{\mathrm{x}}$ and ${\mathrm{N}}_{\mathrm{y}}$ represent the array dimensions, ${\mathrm{x}}_{\mathrm{mn}}$ and ${\mathrm{y}}_{\mathrm{mn}}$ denote the coordinates of the array element, and ${\mathrm{\theta }}_0$ and ${\mathrm{\phi }}_0$ specify the beam steering direction.

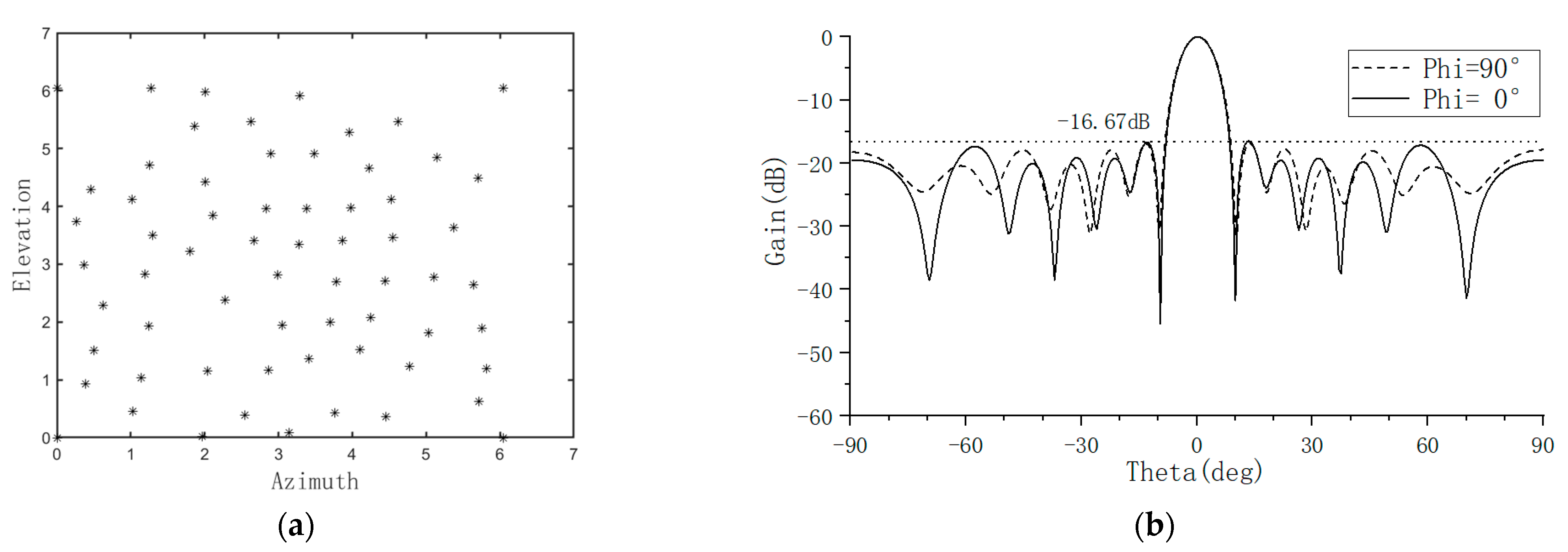
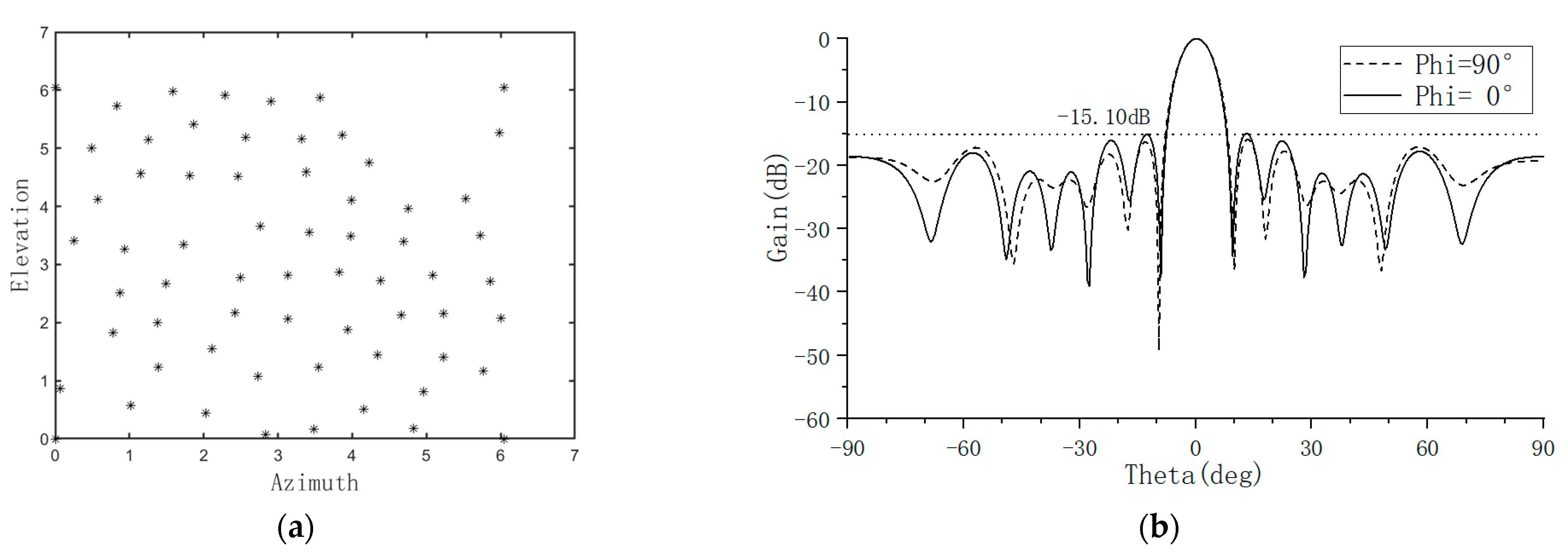
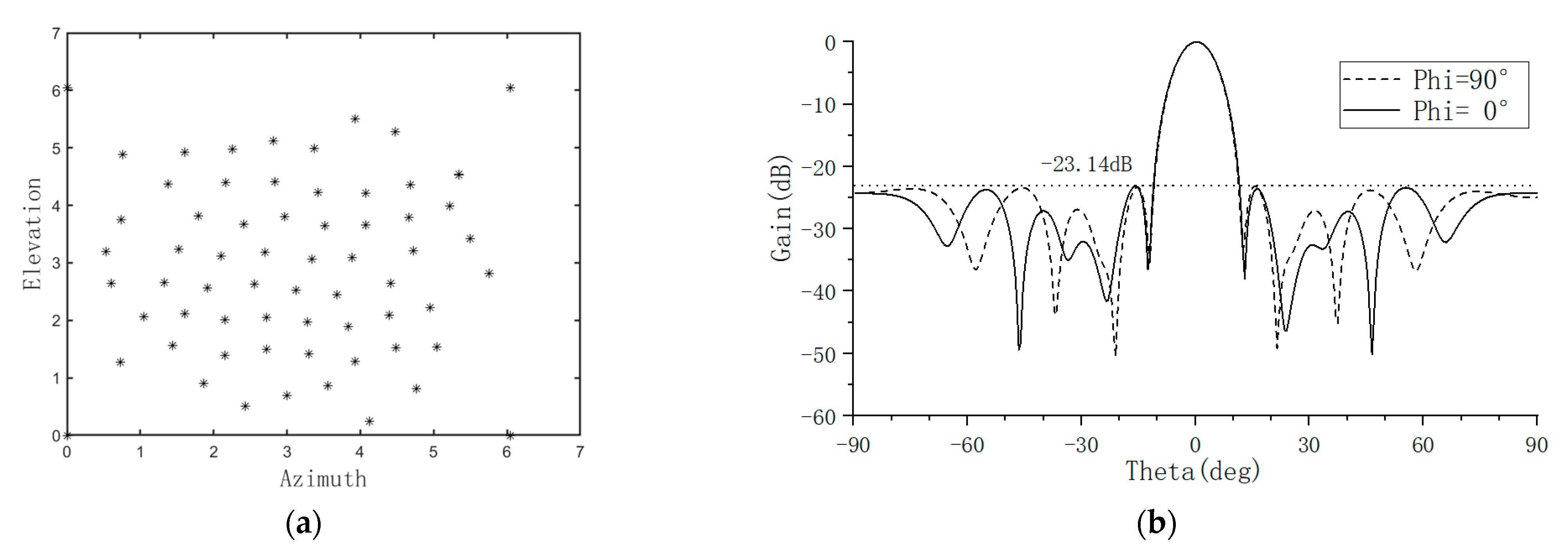
To comprehensively evaluate the array’s sidelobe characteristics, the radiation pattern is analyzed using two orthogonal planes, while azimuth angles are set to 0 and 90 degrees respectively.

This dual-plane analysis method provides a simplified characterization of the array’s three-dimensional radiation characteristics.

Accurate calculation of the sidelobe level requires precise differentiation between the main lobe and the sidelobe regions. First, the radiation pattern is normalized and converted to decibel form:

$${\mathrm{F}}_{\mathrm{dB}} = 20{\log }_{10}({\displaystyle \frac{\left|\mathrm{F}\left(\mathrm{\theta },\mathrm{\phi }\right)\right|}{\max \left|\mathrm{F}\left(\mathrm{\theta },\mathrm{\phi }\right)\right|}} + \mathrm{ϵ})$$

(2)

where ϵ is a minimal constant introduced to prevent computational anomalies. The boundaries of the main lobe region are determined using a peak search algorithm: starting from the maximum value of the pattern and extending bilaterally until the pattern values begin to decrease monotonically. After excluding the identified main lobe region, the maximum value within the remaining area is taken as the peak sidelobe level for that specific observation plane. The peak sidelobe levels of the two planes are defined as follows:

$${\mathrm{SLL}}_1 = \max \left({\mathrm{F}}_{\mathrm{dB}}\left(\mathrm{\phi }= 0°\right)\right)$$

(3)

$${\mathrm{SLL}}_2=\max \left({\mathrm{F}}_{\mathrm{dB}}\left(\mathrm{\phi }=90°\right)\right)$$

(4)

The maximum sidelobe level is expressed as:

$$\mathrm{MSLL} = \left|{\mathrm{SLL}}_1\right| + \left|{\mathrm{SLL}}_2\right|$$

(5)

Based on MSLL, the fitness function value Q can be expressed as:

$$\mathrm{Q} = {\displaystyle \frac{\mathrm{M}\mathrm{SLL}-\min \left(\mathrm{M}\mathrm{SLL}\right)}{\max \left(\mathrm{M}\mathrm{SLL}\right)-\min \left(\mathrm{M}\mathrm{SLL}\right)}}$$

(6)

This comprehensive metric not only reflects the array’s sidelobe suppression capability in the two principal planes but also provides a well-defined objective for the optimization algorithm.

3. A Hybrid PSO-GA Algorithm

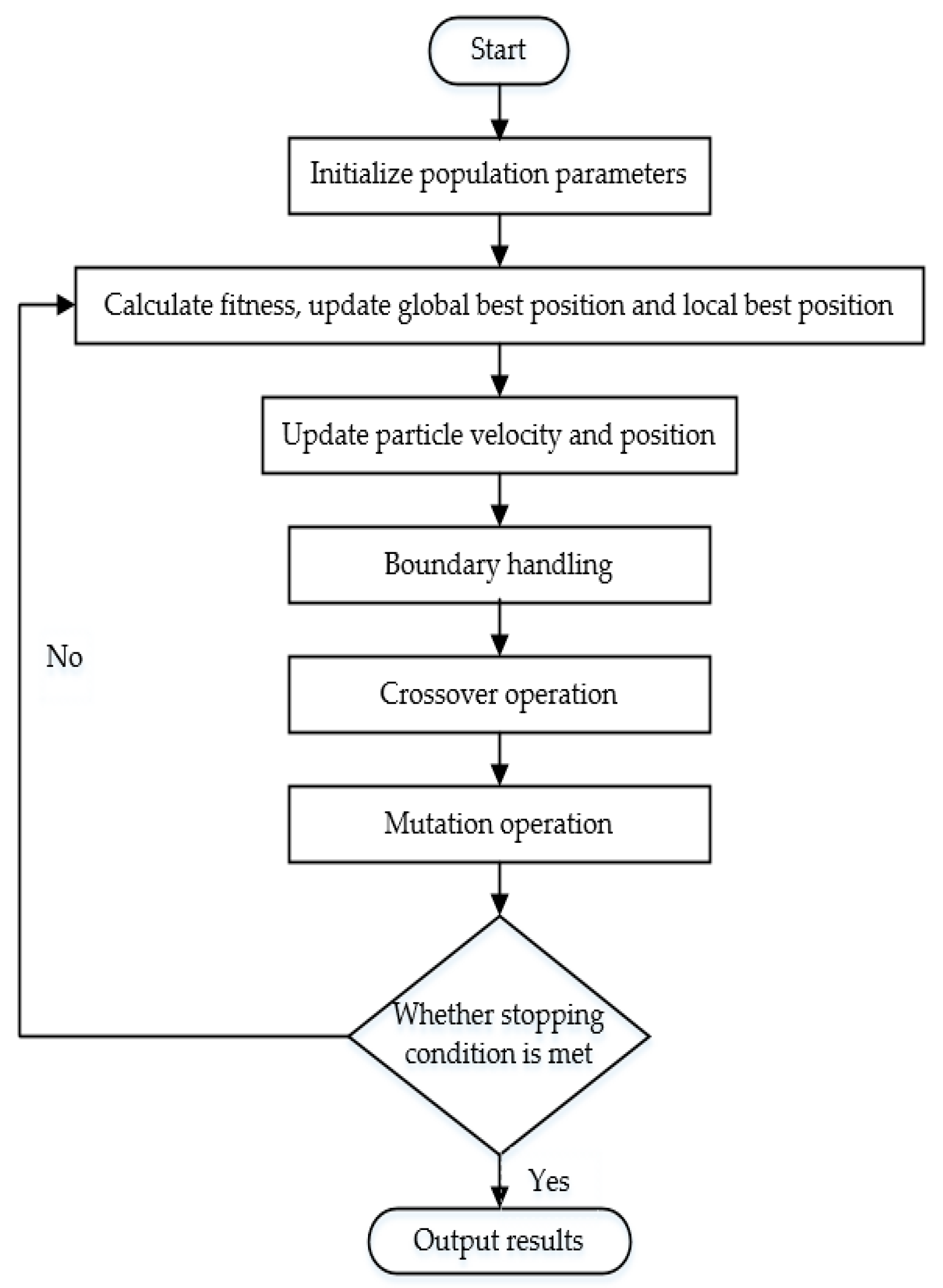
To enhance the global search capability of the PSO algorithm, adaptive crossover and adaptive mutation operations are introduced into the PSO framework. The velocity and position updates in Particle Swarm Optimization cause particles to converge toward their individual historical best positions and the global best position. This behavior can lead to a rapid decline in population diversity and premature convergence. To address this, introducing crossover and mutation operations can reintroduce diversity, helping the population escape potential local optima while preserving the current search direction and offering new opportunities for global exploration. As illustrated in Figure 2, the crossover and mutation operations are incorporated after the standard PSO procedure, forming the PSO-GA hybrid algorithm. The specific procedural steps are as follows:

(1)

Initialization: A swarm of particles is randomly generated. Each particle is assigned a position, representing the coordinates of an array element, and a velocity, which determines the rate at which the position is updated.

(2)

Individual Evaluation: The fitness function value is computed for each particle.

(3)

Update of Individual and Global Best Positions: The individual best position and the global best position are updated based on the current fitness values and historical optimal positions. Positions corresponding to higher fitness values are identified as the optimal positions.

(4)

Update of Particle Velocity and Position: The velocity and position of each particle are adjusted according to its individual best position, the global best position, along with specific weighting factors and stochastic components.

(5)

Crossover Operation: Selected particles from the population are randomly paired. With a crossover probability ${\mathrm{P}}_{\mathrm{c}}$, portions of their position vectors are exchanged, resulting in the creation of new offspring particles.

(6)

Mutation Operation: For each particle in the population, one or more elements of its position vector are randomly altered with a mutation probability ${\mathrm{P}}_{\mathrm{m}}$, replacing them with other permissible position values.

(7)

Boundary Handling: Particles whose positions or velocities exceed the predefined feasible bounds are identified and adjusted to ensure they remain within the specified constraints.

(8)

Iterative Update: The process of updating individual and global best positions, along with particle velocities and positions, is repeated iteratively until a stopping criterion is met (e.g., the maximum number of iterations is reached, or the particle movement converges within a specified tolerance).

(9)

Termination Condition: The algorithm terminates when predefined conditions are satisfied, such as reaching the maximum iteration count or achieving convergence in the objective function value.

Figure 2. Flowchart of the proposed PSO-GA hybrid algorithm.

Figure 2. Flowchart of the proposed PSO-GA hybrid algorithm.

Furthermore, the crossover and mutation operations employ dynamic probabilities, which are determined by the following specific formulae:

$${\mathrm{P}}_{\mathrm{c}}=\left\{\begin{array}{c}{\mathrm{k}}_1{\displaystyle \frac{{\mathrm{fit}}_{\max }}{{\mathrm{fit}}_{\max }-{\mathrm{fit}}_{\min }}},{\displaystyle \frac{{\mathrm{fit}}_{\mathrm{ave}}}{{\mathrm{fit}}_{\max }}} > \mathrm{a},{\displaystyle \frac{{\mathrm{fit}}_{\min }}{{\mathrm{fit}}_{\max }}}> \mathrm{b}\\ {\mathrm{k}}_1 , \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right.$$

(7)

$${\mathrm{P}}_{\mathrm{m}}=\left\{\begin{array}{c}{\mathrm{k}}_2{\displaystyle \frac{{\mathrm{fit}}_{\max }}{{\mathrm{fit}}_{\max }-{\mathrm{fit}}_{\min }}},{\displaystyle \frac{{\mathrm{fit}}_{\mathrm{ave}}}{{\mathrm{fit}}_{\max }}} > \mathrm{a},{\displaystyle \frac{{\mathrm{fit}}_{\min }}{{\mathrm{fit}}_{\max }}} > \mathrm{b}\\ {\mathrm{k}}_2 , \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right.$$

(8)

Formulas (7) and (8) determine the concentration of a population based on its maximum fitness value fitmax, minimum fitness value fitmin, and average fitness value fitave. The thresholds a and b are set to balance the algorithm’s global exploration and local exploitation capabilities. Drawing on the design experience of the adaptive genetic algorithm [18], parameter a is used to assess the overall convergence trend of the population: when the ratio of average fitness to maximum fitness, fitave/fitmax, is greater than a, it indicates that the population has not fully converged and there is still room for exploration. Parameter b evaluates population diversity: when the ratio of minimum fitness to maximum fitness, fitmin/fitmax, is greater than b, it indicates that some dispersion remains in the population. In this study, a = 0.5 and b = 0 are selected to facilitate the algorithm’s triggering of crossover and mutation during the early stages of evolution, thereby enhancing global exploration. As the population converges, the probabilities of crossover and mutation adaptively decrease, shifting the focus toward local exploitation to effectively balance the search process.

The introduction of adaptive crossover and mutation operations into the PSO algorithm may lead to a reduction in convergence speed. To address this issue, an adaptive weighting strategy and a constriction factor are incorporated [19,20]. Furthermore, a density-weighted method is employed to generate the initial population [21], aiming to improve the initial fitness function values and thereby enhance the algorithm’s convergence performance. The specific details are as follows:

Adaptive Weighting: This strategy dynamically adjusts the search weight based on the convergence state of the particles, aiming to achieve a balance between local exploitation and global exploration. The formula for the adaptive weight is given by

$$\mathrm{w}=\left\{\begin{array}{c}{\mathrm{w}}_{\min }-\left({\mathrm{w}}_{\max }-{\mathrm{w}}_{\min }\right){\displaystyle \frac{\mathrm{f}-{\mathrm{f}}_{\min }}{{\mathrm{f}}_{\mathrm{avg}}-{\mathrm{f}}_{\min }}} ,\mathrm{f} \le {\mathrm{f}}_{\mathrm{avg}}\\ {\mathrm{w}}_{\max } ,\mathrm{f}>{\mathrm{f}}_{\mathrm{avg}}\end{array}\right.$$

(9)

where f is the fitness value. In optimization algorithms, the inertia weight w is a crucial parameter. A higher inertia weight facilitates global exploration, whereas a lower inertia weight enhances local exploitation. Therefore, a dynamic inertia weight strategy can be adopted, which employs a larger inertia weight during the initial stages of the search and gradually decreases it thereafter, thereby better adapting to the problem-solving process requirements.

Constriction Factor: The constriction factor ensures eventual convergence of the particle trajectories while enabling effective exploration of different regions, leading to high-quality solutions. The formula for the constriction factor is as follows:

$$\mathrm{\Phi } ={\displaystyle \frac{2}{\left|\left(2 - \mathrm{C} - \sqrt{{\mathrm{C}}^2- 4\mathrm{C}}\right)\right|}},\mathrm{C} = {\mathrm{c}}_1 + {\mathrm{c}}_2$$

(10)

where ${\mathrm{c}}_1$ is the individual learning factor, and ${\mathrm{c}}_2$ is the social learning factor. By incorporating the constriction factor into the velocity update formula, the equation can be expressed as:

$${\mathrm{v}}_{\mathrm{i}}^{\mathrm{d}} = \mathrm{\Phi }\left[\mathrm{w}{\mathrm{v}}_{\mathrm{i}}^{\mathrm{d}-1} +{ \mathrm{c}}_1{\mathrm{r}}_1\left({\mathrm{p}}_{\mathrm{i}}^{\mathrm{d}} -{ \mathrm{x}}_{\mathrm{i}}^{\mathrm{d}}\right) +{ \mathrm{c}}_2{\mathrm{r}}_2\left({\mathrm{g}}_{\mathrm{i}}^{\mathrm{d}} - {\mathrm{x}}_{\mathrm{i}}^{\mathrm{d}}\right)\right]$$

(11)

Among them, ${\mathrm{v}}_{\mathrm{i}}^{\mathrm{d}}$ is the velocity of particle i in the d-th generation, ${\mathrm{r}}_1$ and ${\mathrm{r}}_2$ are two random numbers uniformly distributed in the interval [0, 1], ${\mathrm{p}}_{\mathrm{i}}^{\mathrm{d}}$ is the individual optimal position found by particle i until the d-th generation, ${\mathrm{g}}_{\mathrm{i}}^{\mathrm{d}}$ is the global optimal position found by the entire particle swarm until the d-th generation, and ${\mathrm{x}}_{\mathrm{i}}^{\mathrm{d}}$ is the current position of particle i in the d-th generation. The constriction factor in the Particle Swarm Optimization algorithm is a key parameter that controls the velocity adjustment of particles. During each iteration, the particle velocity update formula incorporates the constriction factor. By modulating the value of this factor, the movement step size of particles within the search space can be controlled, thereby influencing the overall search process of the algorithm.

Density-Weighted Method: This method simulates the amplitude weighting of a uniform full array by varying the density of array elements, aiming to reduce the sidelobes in the radiation pattern. Typically, regions closer to the center of the array exhibit higher element density and smaller average inter-element spacing, while areas farther from the center have lower element density and larger average inter-element spacing. Consequently, the density-weighted method can be utilized to generate the initial population, thereby improving the initial fitness values and accelerating the convergence speed.

Assume that the normalized amplitude weighting of the uniform full array is denoted as A(m,n), and the operational state of an element is represented by S(m,n). Let k be a parameter controlling the sparsity of the array. Then, S(m,n) can be expressed as:

$$\mathrm{S}\left(\mathrm{m},\mathrm{n}\right)=\left\{\begin{array}{c}1 \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}<\mathrm{A}\left(\mathrm{m},\mathrm{n}\right)\times \mathrm{k}\\ 0 \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\ge \mathrm{A}(\mathrm{m},\mathrm{n})\times \mathrm{k}\end{array}\right.$$

(12)

where rand denotes a uniformly distributed random number between 0 and 1. The parameter k can be derived from the sparsity ratio $\mathrm{\eta }$ and the amplitude weighting function A(m,n). The specific formula is as follows:

$$\mathrm{k} ={\displaystyle \frac{\mathrm{\eta } \times \mathrm{M} \times \mathrm{N}}{\sum _{\mathrm{m}=1}^{\mathrm{M}}\sum _{\mathrm{n}=1}^{\mathrm{N}}\mathrm{A}(\mathrm{m},\mathrm{n})}}$$

(13)

In this paper, a sparsity ratio $\mathrm{\eta }$ of 0.5 is adopted, and the normalized amplitude weighting function is defined as:

$$\mathrm{A}\left(\mathrm{m},\mathrm{n}\right) = {\cos }^2({\displaystyle \frac{\mathrm{m} - 0.5\mathrm{M}}{\mathrm{M}}}\times \mathrm{\pi }){\cos }^2({\displaystyle \frac{\mathrm{n} - 0.5\mathrm{N}}{\mathrm{N}}}\times \mathrm{\pi })$$

(14)

4. Theoretical Analysis and Full Wave Simulation

To validate the effectiveness of the proposed PSO-GA hybrid algorithm, theoretical analysis was conducted on a planar sparse array with two-dimensional position optimization. A comprehensive comparative analysis was performed from multiple perspectives, including the array layout, radiation pattern performance, and full-wave electromagnetic simulation results.

4.1. Theoretical Analysis Based on Different Algorithms

During the MATLAB 2024 (Matrix Laboratory) simulation of the sparse array, all elements were assumed to be isotropic. A 12 × 12 uniform array was thinned, retaining only 64 active elements. The array layout was situated in the xoy-plane with an inter-element spacing of 0.55λ. For the Genetic Algorithm, the crossover probability Pc was set to 0.8, the mutation probability Pm to 0.05, the offspring population size NP to 64, and the maximum number of iterations was set not to exceed 400.

Figure 3, Figure 4 and Figure 5 present the optimized 8 × 8 array element layouts and the corresponding normalized radiation patterns obtained by the GA, PSO, and PSO-GA algorithms, respectively. It can be observed that the PSO-GA algorithm achieves a maximum sidelobe level (SLL) of −23.14 dB, which outperforms the GA result of −16.67 dB and the PSO result of −15.10 dB. The array configuration synthesized by the hybrid algorithm exhibits a denser distribution of elements near the center and a sparser distribution towards the edges. Correspondingly, its radiation pattern demonstrates a well-defined main lobe and significantly suppressed sidelobe levels.

4.2. Simulation Validation Based on Full Wave Simulation

To further verify the practical applicability of the algorithm, a physical antenna element was introduced for array construction, and the sparse array was analyzed through electromagnetic simulation using High-Frequency Structure Simulator (HFSS). During the simulation, a rectangular microstrip patch antenna, shown in Figure 6, was employed as the array element.

The antenna was designed with a center frequency of 10 GHz. Rogers RT/duroid 5880 (tm) was selected as the substrate, which has a relative permittivity of 2.2 and a thickness h of 1.6 mm. A 50-Ω coaxial line was used for feeding. The specific parameters of the rectangular microstrip patch are as follows: patch width W = 11.9 mm, patch length L = 9.1 mm, feed position Xf = 3.13 mm, and ground plane size of 16.5 mm × 16.5 mm. A schematic diagram of the 8 × 8 sparse array model is shown in Figure 7.

Figure 8 further displays the three-dimensional polarized radiation pattern of the sparse array obtained from the electromagnetic simulation software. Figure 9 illustrates the radiation pattern characteristics of the sparse array at a 0° scanning angle. It can be observed that the electromagnetic simulation results are in good agreement with those from the MATLAB numerical simulation. The configuration optimized by the PSO-GA hybrid algorithm achieves a favorable balance between main lobe width and sidelobe suppression, thereby validating the effectiveness and robustness of the proposed algorithm for the sparse layout synthesis of planar arrays.

Figure 10 illustrates the scanning directions of an 8 × 8 sparse array optimized using a PSO-GA hybrid algorithm for various beam orientations. It can be seen that at scanning angles of 30°, 45°and 60°, the shapes of the main lobe of the directional pattern remain good, and the average sidelobe is effectively suppressed, indicating that the proposed design can still maintain stable radiation performance under different beam directions and has good beam scanning ability.

A comparison of the radiation performance parameters for the sparse arrays synthesized by the GA, PSO, and PSO-GA algorithms is presented in

Table 1. Summary of Optimization Results for 8 × 8 Sparse Array.

Array Algorithm	Main Lobe Gain/dB	Peak Sidelobe Level/dB	Half Power Beamwidth/(dB)
GA	17.49	−16.94	8.19
PSO	17.52	−15.28	9.34
PSO-GA	17.64	−22.45	9.78

. Compared to the variety optimized by the PSO algorithm, the hybrid algorithm achieves a main lobe gain increase of 0.12 dB, a reduction in the Peak Sidelobe Level (PSLL) of 7.11 dB, and a half-power beamwidth (HPBW) broadening of approximately 0.4°. The simulation results demonstrate that the sparse array obtained by the hybrid algorithm effectively suppresses the sidelobes while maintaining radiation characteristics comparable to those of sparse arrays of the same aperture size synthesized by individual algorithms.

5. Discussion

In this paper, a synthetic method of wide-angle scanning sparse arrays based on a hybrid PSO-GA algorithm is proposed. The PSO-GA algorithm has the advantages of global optimum searching capability, a balance between global exploration and local exploitation, high convergence efficiency, and is more applicable to sparse array design. By applying the algorithm to the positional synthesis of an 8 × 8 planar sparse array, both theoretical analysis and numerical simulation demonstrate that the sparse array based on PSO-GA exhibits a significant advantage in maximum sidelobe suppression and wide-angle scanning compared to the classical GA and PSO algorithms. Future work will focus on extending its application to large-scale arrays and multi-objective optimization scenarios.