Reliability Assessment of Power System Microgrid Using Fault Tree Analysis: Qualitative and Quantitative Analysis

Abstract

Renewable energy sources account for approximately one-quarter of the total electric power generating capacity in the United States. These sources increase system complexity, with potential negative impacts caused by their inherent variability. A microgrid, a decentralized local grid, offers an excellent solution for integrating these sources into the system’s generation mix in a cost-effective and efficient manner. This paper presents a comprehensive fault tree analysis for the reliability assessment of microgrids, ensuring their safe operation. In this work, fault tree analysis of a microgrid in grid-tied mode with solar, wind, and battery energy storage systems is performed, and the results are reported. The analyses and calculations are performed using the Relyence software suite. The fault tree analysis was performed using various calculation methods, including exact (conventional fault tree analysis), simulation (Monte Carlo simulation), cut-set summation, Esary–Proschan, and cross-product. Once these analyses were completed, the results were compared with the ‘exact’ method as the base case. Critical risk measures, such as unavailability, conditional failure intensity, failure frequency, mean unavailability, number of failures, and minimal cut-sets, were documented and compared. Importance measures, such as marginal or Birnbaum, criticality, diagnostic, risk achievement, and risk reduction worth, were also computed and tabulated. Details of all cut-sets and the probability of failure are presented. The calculated importance measures would help microgrid operators focus on events that yield the greatest system improvements and maintain an acceptable range of risk levels to ensure safe operation and improved system reliability.

1. Introduction

Technological breakouts in renewable energy sources (RESs) and the decrease in energy storage prices have exponentially led to increased system installations. Microgrid-decentralized local grids are the logical solution to decentralization and decarbonization in this new era. The US Department of Energy defines a microgrid as ‘a group of interconnected loads and distributed energy resources within clearly defined electrical boundaries that act as a single controllable entity with respect to the grid. A microgrid (MG) can connect and disconnect from the grid to enable it to operate in both grid-connected or island mode’ [1]. Distributed generators (DGs) in the microgrid, typically RES, are intermittent and can be challenging, as these irregular power generators can disrupt the conventional operation of the utility grid (UG). Power fluctuations due to this erratic generation over considerable time periods must be mitigated since they can cause blackouts or other cascading problems.

Battery energy storage systems (BESSs) will reduce intermittency by installing RESs in large numbers or by installing grid-sized batteries as MGs are composed of multiple vulnerable components that must be integrated and optimized for interoperability and security. The failure of a critical component can initiate a cascade of failures, leading to the isolation of a part of the MG, and in extreme cases, blackouts. The conventional grid’s reliability is relatively high; therefore, introducing intermittent renewable sources will reduce grid reliability. System-integrated RES reliability studies are needed to ensure the integrity of MG safety-critical systems by assessing them at the component level due to their high uncertainty and variability. These assessments are vital to ensure dependable MG operation, which will benefit MG and utility grid (UG) owners by increasing revenue, power quality, and energy yield.

The challenges associated with renewable energy sources (RESs) have been recognized for decades [2,3], yet the lack of comprehensive field reliability data has limited quantitative assessment. Photovoltaic (PV) systems have been widely studied in stand-alone, stand-alone with BESS, and grid-connected modes. Early works applied failure mode and effect analysis (FMEA) and fault tree analysis (FTA) [2], while subsequent studies employed quantitative reliability evaluations for large-scale PV systems, considering both grid-connected and islanded operation [4]. Reliability, availability, and maintainability (RAM) analyses provided probabilistic models for PV subassemblies [5], and FTA using exponential probability density functions helped identify critical components to improve reliability and reduce maintenance costs [6]. Fuzzy reasoning Petri nets combined with FTA have also been used to analyze mechanical subsystems, enhancing fault prevention strategies [7]. While these studies advanced PV reliability assessment, they largely focus on PV systems in isolation and do not consider their integration within a larger microgrid environment.

Wind turbines (WTs) similarly require detailed reliability quantification. Approaches such as FTA, failure mode, effects, and criticality analysis (FMECA), event sequence analysis, and structural reliability methods have been applied [8]. Operational and maintenance cost assessments alongside RAM analyses have further informed subsystem reliability [9]. Binary decision diagrams (BDDs) have been used to optimize maintenance scheduling and identify critical components in offshore turbines [10,11], and the power law process has been implemented to evaluate generators, gearboxes, and converters [12]. FTA has also been employed to assess critical subassemblies in offshore WT farms [13]. Despite these advances, studies often rely on limited field data, focus on subsystems in isolation, and rarely account for interactions within a complete microgrid framework.

Battery energy storage systems (BESSs) are increasingly integrated into power grids to enhance flexibility and support ancillary services [14,15]. Reliability models for AC/DC converters and battery modules have been proposed [16], while FTA has been applied to identify failure modes in Li-ion batteries [17,18]. Nonetheless, existing analyses do not fully integrate BESS reliability with PV and wind systems in a grid-tied microgrid, limiting operational insights for combined RES and storage networks.

Microgrid-level studies address the broader integration of RES, power electronic interfaces, and operational contingencies. Reliability assessments considering cyber–physical interdependencies [19], weather conditions, lifecycle management, and load profiles [20,21] have been performed, alongside economic evaluations of radial distribution networks using constrained nonlinear optimization [22]. Analytical frameworks for operational transitions, such as islanded mode, have been proposed [23], and studies on reliability metrics for European markets under varying RES penetration exist [24,25]. However, many of these works consider small-scale microgrids, focus primarily on islanded operation, or omit the critical role of power electronic converters and inverters. Studies using Monte Carlo simulations often address only isolated operation modes without evaluating grid-tied interactions [26].

Although existing research has significantly advanced the reliability assessment of renewable energy systems, several critical gaps remain. First, most prior studies have analyzed individual subsystems in isolation—such as PV [2,3,4,5,6,7], wind [8,9,10,11,12,13], or BESS [14,15,16,17,18]—without adequately addressing the interactions and interdependencies among them when integrated into a grid-tied microgrid. This reductionist approach overlooks failure propagation pathways across different subsystems, leading to incomplete reliability insights. Second, while microgrid-level studies [19,20,21,22,23,24,25,26] have attempted to incorporate multiple components, they often suffer from narrow scopes, focusing only on small-scale microgrids, single operation modes (typically islanded), or limited sets of components. Critical elements such as the utility grid interface, loads, and power electronic converters—which play pivotal roles in real-world operations—are frequently simplified or omitted altogether. Third, methodological limitations persist: the majority of studies rely on a single reliability assessment technique (e.g., FTA, RAM analysis, Monte Carlo simulation), which restricts the robustness of conclusions and provides limited guidance on the relative merits of alternative approaches.

To address these limitations, the present study develops a comprehensive fault tree model that integrates photovoltaics (PV), wind turbines (WTs), battery energy storage systems (BESSs), utility grid (UG), and load components into a single grid-tied microgrid framework. This holistic representation captures the true interdependencies between renewable sources, storage, load, and grid support, enabling a more realistic evaluation of system reliability under practical operating conditions. Unlike prior subsystem-specific or islanded-only analyses, our framework reflects the operational complexity of modern microgrids, including transitions between grid-tied and stand-alone modes.

Moreover, this study applies and compares multiple complementary reliability assessment methods, namely, exact fault tree analysis, Monte Carlo simulation, cut-set summation, cross-product, and the Esary–Proschan approximation (EP). While exact FTA provides benchmark accuracy, it is computationally intensive for complex systems with large numbers of components and cut-sets. Approximate and simulation-based methods, such as Monte Carlo and Esary–Proschan, offer alternative means of estimating system reliability with different trade-offs between accuracy and computational effort. By applying all these methods to the same microgrid model, this study (i) validates the consistency of results across approaches, (ii) highlights the strengths and weaknesses of each method, and (iii) offers practical guidance on method selection for reliability assessment of microgrids of varying size and complexity.

In achieving this, the present work not only overcomes the limitations of subsystem-focused or method-specific studies but also provides a comprehensive, validated, and practically useful framework for microgrid reliability analysis.

In this work, the authors have developed a comprehensive fault tree model of a microgrid incorporating photovoltaic (PV) systems, wind turbines, battery energy storage systems (BESSs), the utility grid (UG), and load components, thereby capturing the full operational and structural complexity often omitted in prior studies. To ensure a robust evaluation, the fault tree is analyzed using multiple solution methods, ranging from basic method to approximate and simulation-based techniques, enabling a balanced assessment of accuracy and computational efficiency. Furthermore, a range of availability metrics is calculated to complement reliability analysis, providing a more practical measure of the microgrid’s sustained performance under real-world operating conditions. The study also derives important measures that emphasize the physical aspects of the microgrid, quantifying the contribution of each subsystem to overall risk and system resilience. Finally, minimal cut-set analysis is employed to identify the most critical failure pathways, offering direct insights for targeted reliability improvements. Collectively, this integrated methodology advances beyond existing work by delivering a holistic and comparative framework for microgrid reliability and availability assessment.

The paper proceeds as follows. In Section 2, FT basics and the FTs for each assembly are developed. The analysis of results is presented in Section 3. Conclusions and future work are addressed in the final section.

The remainder of the paper is organized as follows. Section 2 presents the FT model development and the associated qualitative interpretation of the system logic; quantitative approaches used to evaluate and solve the FT are described in Section 3; Section 4 documents the reliability and availability indices reported in this work; and diagnostic analysis based on minimal cut-sets and importance measures to identify structurally critical components and dominant contributors to the top event are presented in Section 5. Section 6 discusses the numerical results, including interpretation of differences among solution methods, while conclusions and future work are addressed in the final section.

2. Fault Tree Models

FTA analysis is a top-down failure analysis based on Boolean logic and is a directed acyclic graph with events and gates as nodes. The authors of [27,28] reviewed FTA basics, applications, modeling, methods, and analysis. Vesely et al. [29] wrote a reactor safety study report discussing the basics and importance of FTA. The characteristics of the FTA discussed in [30] identify it as the best choice to determine the reliability of complex systems such as an MG. 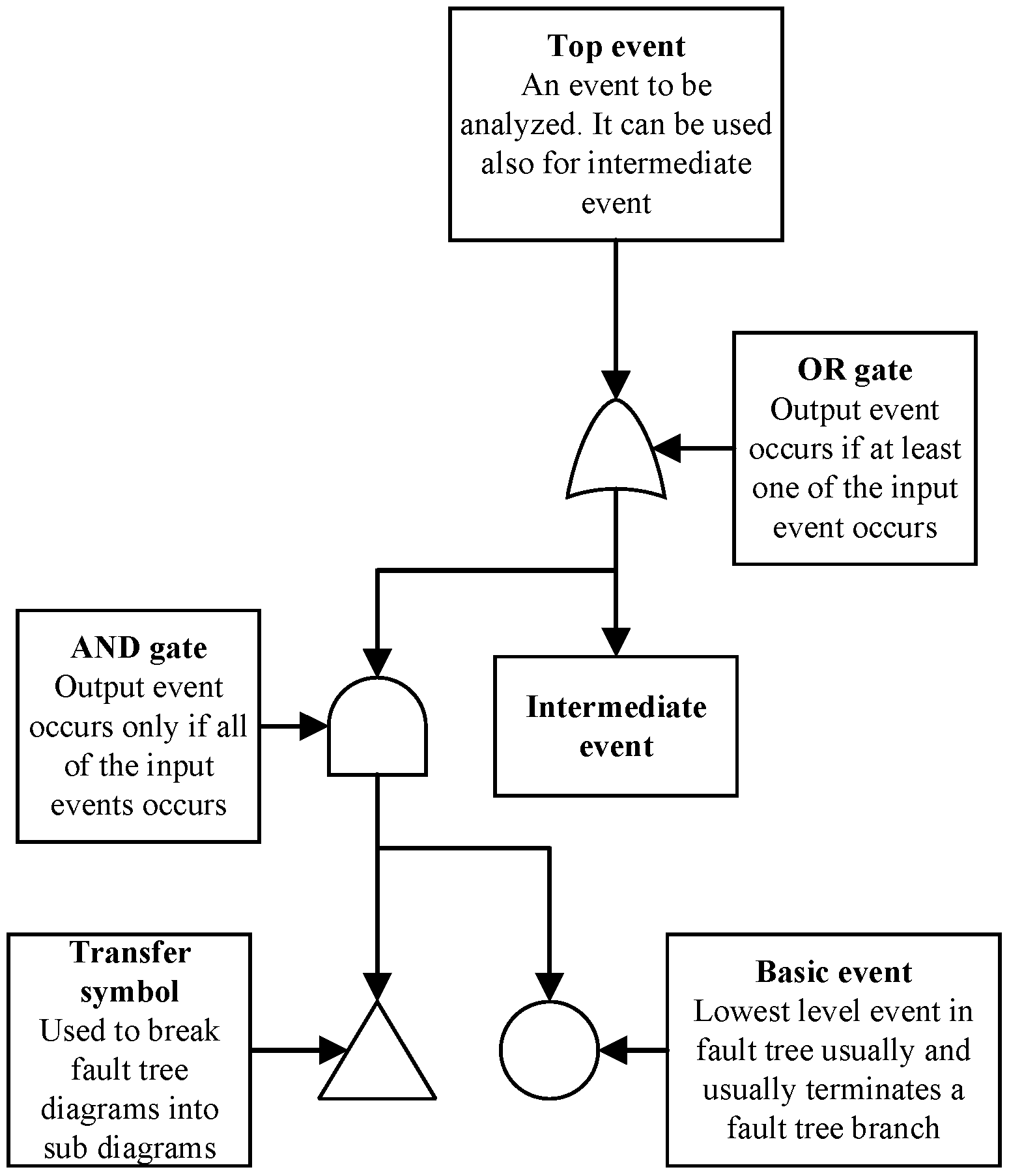Figure 1 shows the general structure of a typical fault tree diagram with gates and event descriptions used in this work.

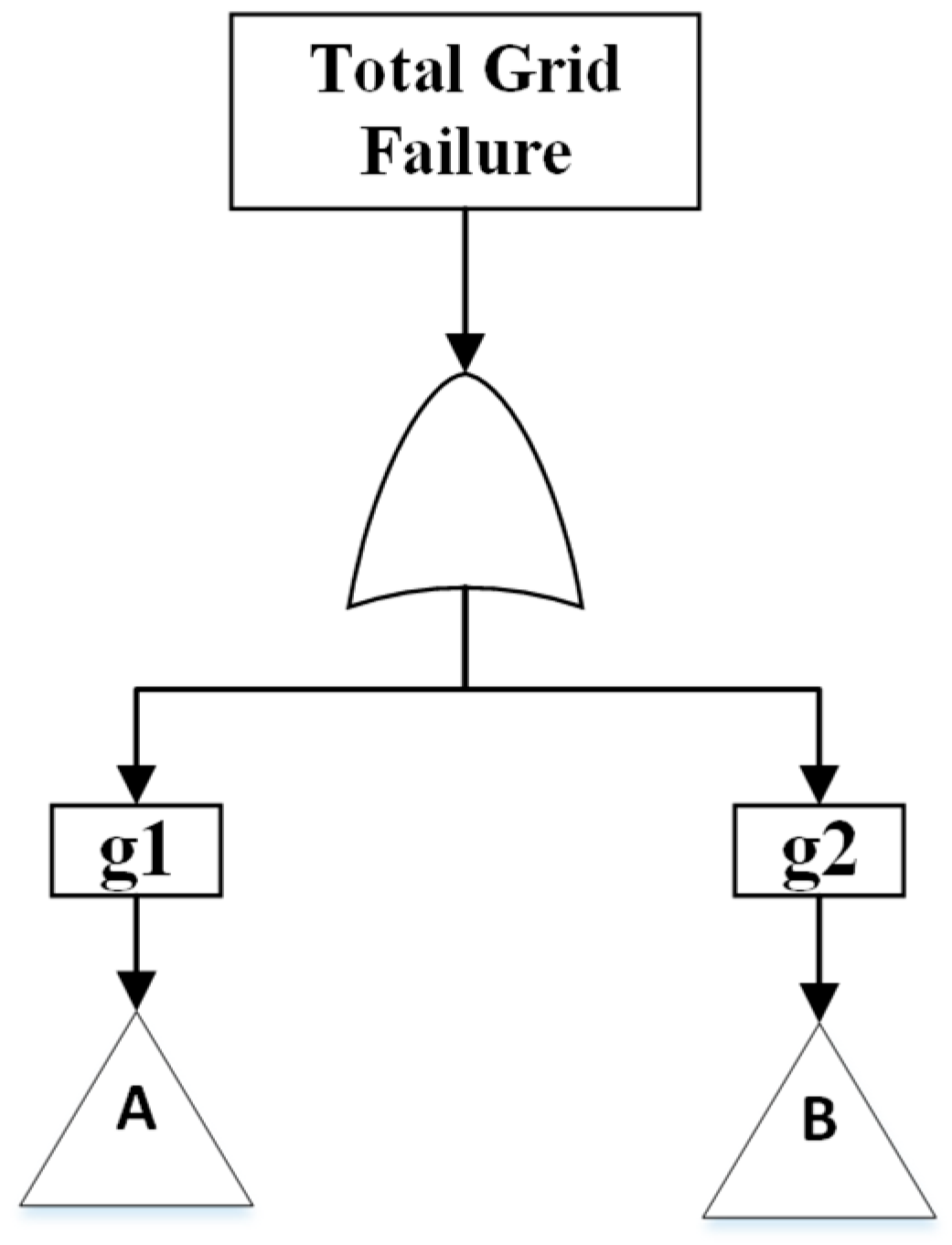
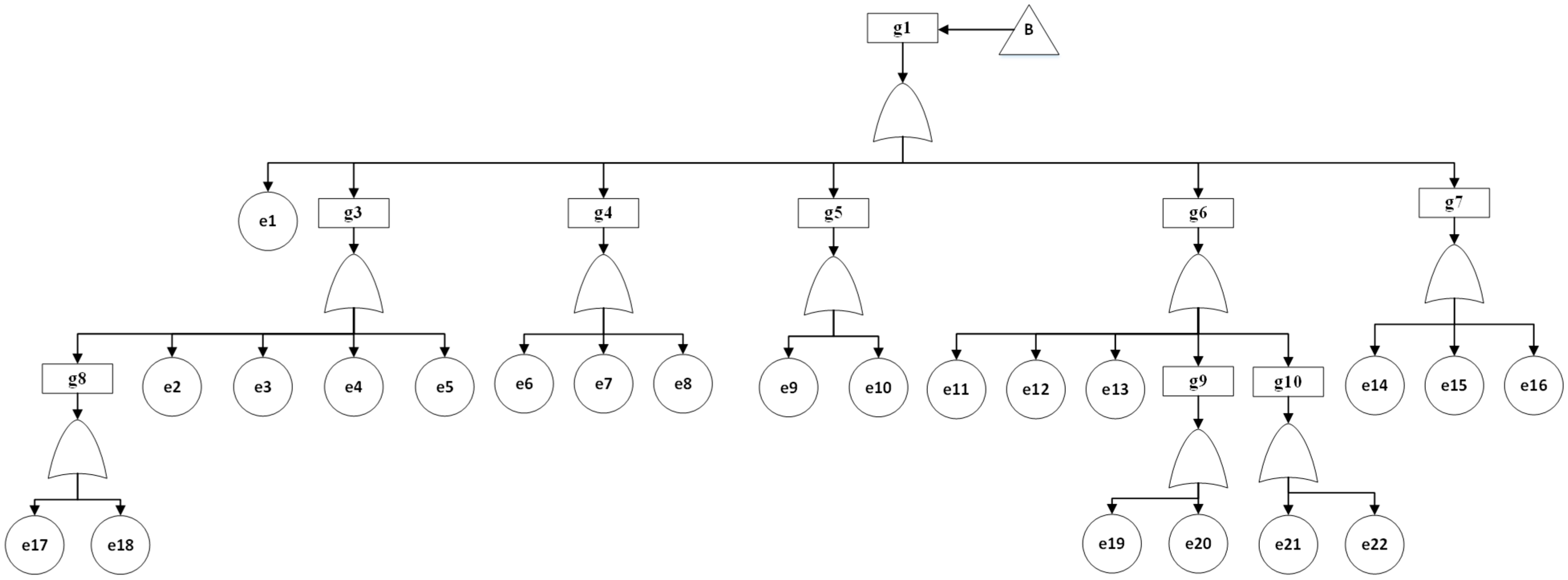
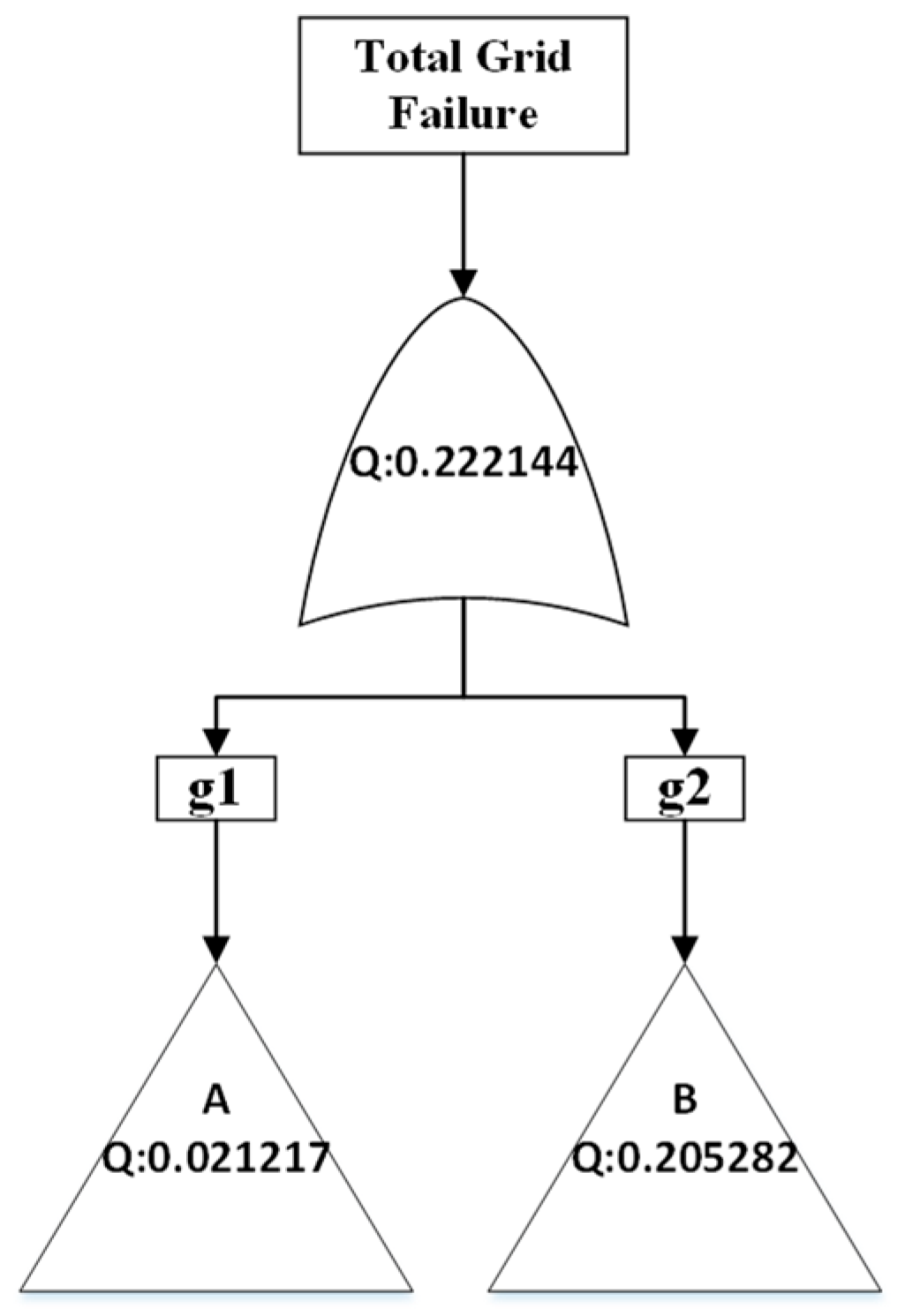
The top view of the FT model of the entire system considered in this work is shown in Figure 2. The top event of this FT is the failure of the total system. The FT for the grid is divided into two major subsystems, namely, utility grid (g1) and microgrid (g2).

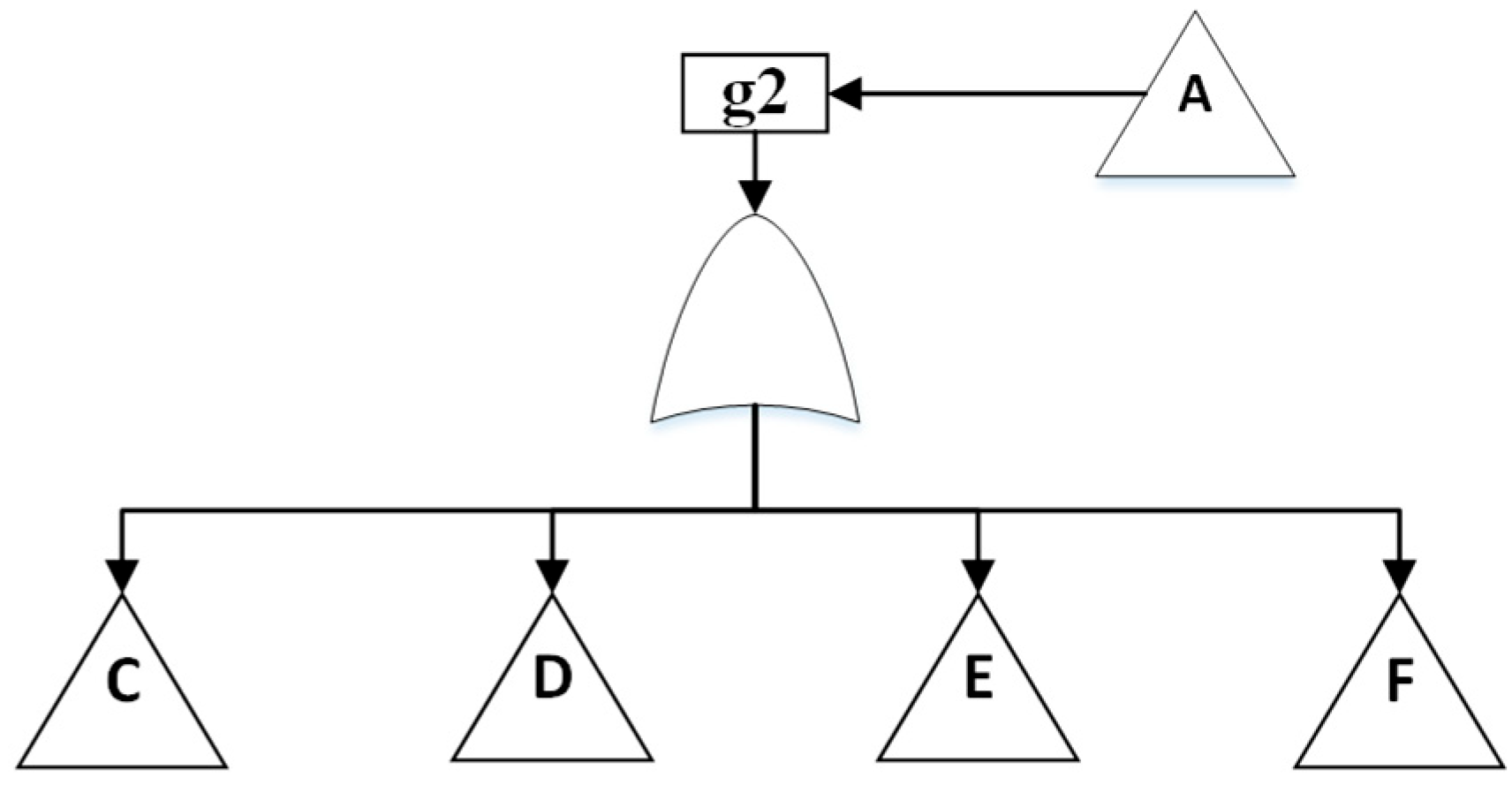
The proposed MG model (g2) has four subassemblies: PV farm (C), wind farm (D), BESS (E), and load (F), where C-F represent transfer trees derived from the fault tree. The top view of the MG FT model and its subassemblies is shown in Figure 3.

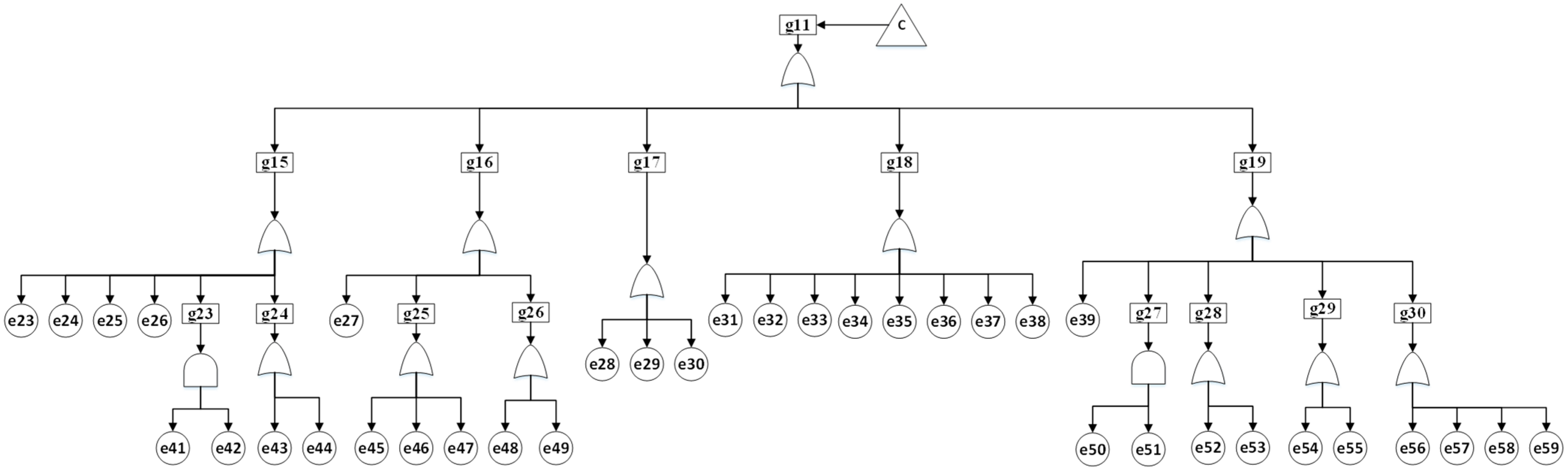
The PV system shown in transfer tree ‘C’ itself has five subassemblies (g15–g19), as depicted in Figure 4. A detailed RAM (Reliability, Availability, and Maintainability) analysis was performed for PV systems in [5]. However, based on the PV reliability block diagram in [5] and drawing failure and repair rate data from [2,5,20], a more comprehensive FT model of the PV farm is developed in the present work as shown in Figure 4. The associated logic gate and basic event codes and their failure probability are shown in

Table 1. Logic gates of PV system failure.

Codes	Logic Gates	Q	Codes	Logic Gates	Q
g2	MG	0.20528	g23	External Conditions	2.32 × 10−12
g11	PV Farm MG	0.08792	g24	V and I Fluctuation	5.00 × 10−5
g15	PV Module	2.15 × 10−4	g25	PV Converter Components	9.26 × 10−7
g16	Converter	9.20 × 10−5	g26	External conditions	9.00 × 10−5
g17	PV Storage	1.70 × 10−7	g27	Switch	1.62 × 10−9
g18	Inverter	0.083	g28	Circuit Breaker	2.37 × 10−7
g19	BOS	0.00506	g29	Grid Connection	1.19 × 10−7
			g30	DC Combiner	0.00506

and

Table 2. Basic events of PV cell failure.

Codes	Basic Events	Q	Codes	Basic Events	Q	Codes	Basic Events	Q
e23	PV Cell	2.13 × 10−7	e35	PV Inverter Filter	0.0026	e48	PV Improper Arrangement	4.50 × 10−5
e24	PV Cell Junction Box	5.50 × 10−5	e36	PV Inverter DC Breaker	0.00606	e49	PV Switching Regulator	4.50 × 10−5
e25	PV Cell Improper Distribution	5.50 × 10−5	e37	PV Inverter AC Breaker	0.00606	e50	PV DC Switch	4.16 × 10−9
e26	PV Improper Wiring	5.50 × 10−5	e38	PV Inverter Communication	0.02459	e51	PV AC Switch	0.38824
e27	PV Converter	1.05 × 10−6	e39	PV BOS Diode	9.00 × 10−7	e52	PV AC Ckt Breaker	1.19 × 10−7
e28	PV Battery failure	6.27 × 10−8	e41	PV Temperature	1.55 × 10−6	e53	PV Diff Ckt Breaker	1.19 × 10−7
e29	PV Charge Controller	1.03 × 10−7	e42	PV Insolation	1.50 × 10−6	e54	PV Grid Protector	1.19 × 10−7
e30	PV Control Unit	3.84 × 10−9	e43	PV Voltage Fluctuations	2.50 × 10−5	e55	PV DC Coupler	3.55 × 10−13
e31	PV Inverter Module	1.90 × 10−8	e44	PV Current Fluctuations	2.5 × 10−5	e56	PV Disconnector Switch	1.00 × 10−4
e32	PV Inverter Capacitor	0.00886	e45	PV Converter Diode	9.00 × 10−7	e57	PV DC Combiner Fuse	2.00 × 10−5
e33	PV Inverter IGBT	0.01134	e46	PV Converter Capacitor	1.03 × 10−8	e58	PV String Monitoring Box	0.00489
e34	PV Inverter Cooling Fan	0.02635	e47	PV Converter IGBT	1.52 × 10−8	e59	PV DC Combiner Main Cable	4.83 × 10−5

. Details of the PV module subsystems are as follows.

PV system operating life depends on the materials used and the manufacturing process. Therefore, it is important to model that dependency in reliability analysis. In the PV module subsystems, the basic event PV cell (g15) is based on the corrosion of the materials, which is one of the major factors influencing PV output. To model the degradation of the PV module due to temperature and insolation effects, the intermediate event external conditions (g23) is included. Other minor factors that can affect the PV output are Discoloration, By-Pass diode failure, Encapsulant failure, PV module open and short circuits, Hot-spot failure, and delamination. However, due to the lack of field data, these events or factors are not included in the PV FT model. However, as more data becomes available, this model can readily be updated and utilized.

FT model for the PV converter includes basic events like ‘PV converter (e27)’, which represents failure from improper manufacturing due to external factors like the improper arrangement and switching regulator.

Based on the architectural design, PV farms can have three inverter systems, namely central, micro, and string. To simplify the FT model in this study, the authors examined a central inverter system and discovered that the most critical component in the proposed MG model is the inverter cooling fan with a failure probability of 0.2597%. If unmonitored, a malfunction in this component can lead to failure of the PV inverter, which will eventually lead to the MG’s failure; therefore, a maintenance schedule must be rigorous.

The balance of system (BOS) generally includes all non-modular components of a PV system, including structural elements such as mounting and tracking systems, electrical infrastructure such as DC/AC cabling, and switchgear, as well as ancillary components like foundations, enclosures, monitoring equipment, and, in some cases, cooling or ventilation systems of the PV system and contributes to 10–50% of purchasing and installation costs. Failure of BOS non-modular components is responsible for the failure of 54% of the PV systems [5]. So, it is extremely important that BOS be included as a part of the reliability analysis. The FT model of the BOS considered in this study is shown in subtree (g19). The proposed PV model is illustrated below in Figure 4, and its associated logic gate and basic event codes, and their corresponding failure probability are shown in Table 1 and Table 2.

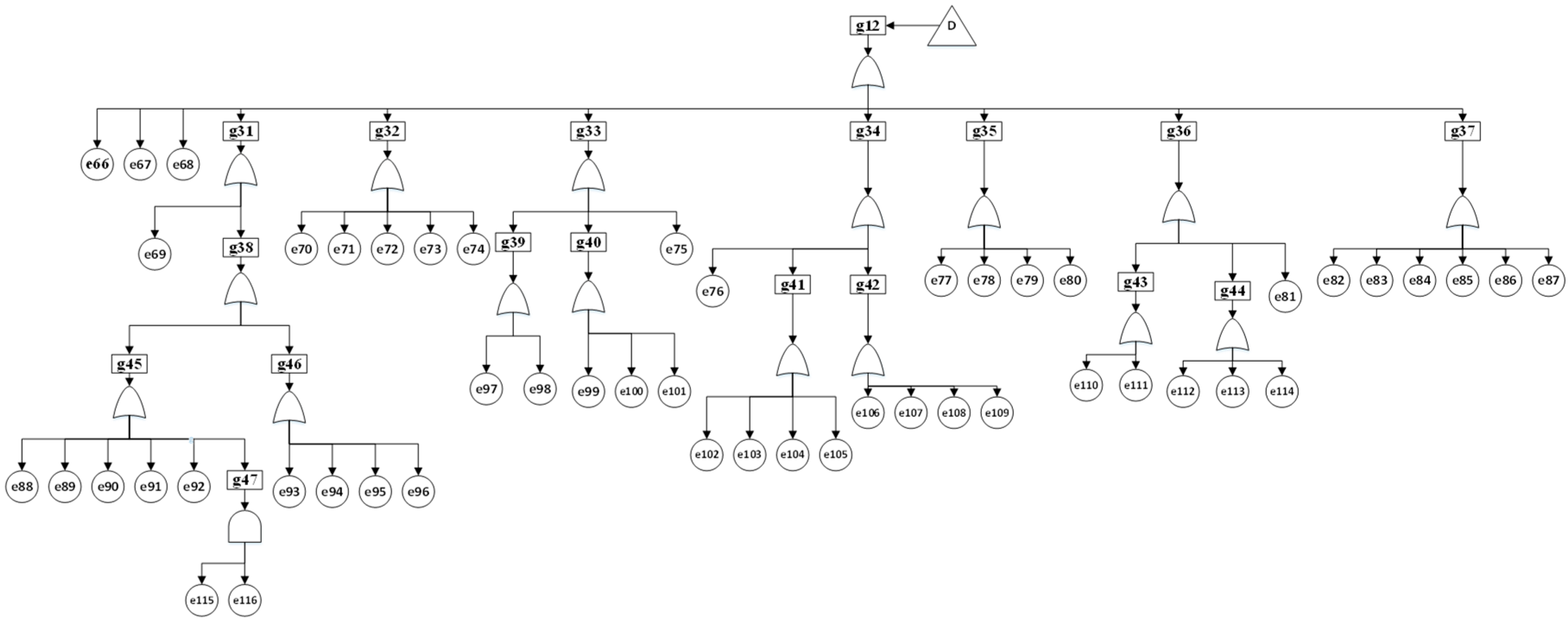
The wind turbine is the most installed RES in the world; the size and complexity of the WTs continue to grow. For failproof and cost-effective WTs operation, reliability assessment is an imperative technology. The FTA model for WT is developed with seven assemblies: generator (g31), support structure (g33), gearbox (g34), blades (g36, g44), control system (g46), hydraulic system (g35), and electrical components (g32). Failures in the WT can occur from electrical or mechanical causes; the model is developed using both physical and electronic components. The proposed WT model has seven subassemblies and three basic events. The proposed WT model is illustrated below in Figure 5, and its associated logic gate, basic event codes, and their corresponding unavailability are shown in

Table 3. Logic gates of WT failure.

Codes	Logic Gates	Q	Codes	Logic Gates	Q
g12	Wind Farm MG	0.10489	g39	WT Tower	0.011928
g31	Generator	0.01054	g40	WT Weather	0.017348
g32	WT Electrical Components	1.00 × 10−3	g41	WT Faulty Bearings	0.022347
g33	WT Support Structure	0.03273	g42	WT External Factors	0.002537
g34	WT Gearbox	0.02623	g43	WT Rotor System	0.007958
g35	WT Hydraulic System	1.00 × 10−3	g44	WT Blade Loss	0.015331
g36	WT Blades Failure	0.0354	g45	WT Rotor System	0.00463
g37	WT Control System	0.001	g46	WT Bearing failure	0.005833
g38	WT Rotor and Stator	0.01044	g47	Heating	5.08 × 10−6

and

Table 4. Basic events of WT failure.

Codes	Basic Events	Q	Codes	Basic Events	Q	Codes	Basic Events	Q
e66	WT Yaw System	0.00124	e83	WT Failure from Meteorological	6.00 × 10−5	e100	WT Strong Wind	0.004988
e67	WT Nacelle	4.30 × 10−5	e84	WT Control System Switches	5.30 × 10−6	e101	WT Storm	0.005485
e68	WT Cooling System	2.80 × 10−5	e85	WT UPS	1.70 × 10−6	e102	WT Bearing Corrosion	0.011928
e69	WT Wire Fault	1.00 × 10−4	e86	WT Control System Sensors Failure	7.00 × 10−7	e103	WT Bearing Wear and Tear	0.00995
e70	WT Feeder Cables	8.35 × 10−4	e87	WT Control Cables	5.00 × 10−7	e104	WT Gear tooth pitting	3.00 × 10−4
e71	WT Lightning Protection Systems	1.58 × 10−4	e88	WT Rotor Blade	3.57 × 10−4	e105	WT Bearing Degradation	3.00 × 10−4
e72	WT Electrical Protection System	3.90 × 10−6	e89	WT Rotor Hub	1.36 × 10−4	e106	WT Failure by Pressure	1.00 × 10−3
e73	WT Capacitor Bank	1.30 × 10−6	e90	WT Rotor Brake System	1.95 × 10−4	e107	WT Failure from High Temperature	2.40 × 10−4
e74	WT Power Electronic Converter	1.10 × 10−6	e91	WT Rotor Pitch System	3.38 × 10−4	e108	WT Metal Fatigue	3.00 × 10−4
e75	WT Maintenance	0.00377	e92	WT Rotor Synchronization	0.0036	e109	WT Design Defects	1.00 × 10−3
e76	WT Dirt in the gearbox	0.00144	e93	WT Rotor Bearing	0	e110	WT Rotor Hub	0.002736
e77	WT Hydraulic Piping	8.46 × 10−4	e94	WT Generator Bearing	0	e111	WT Rotor Bearings	0.005236
e78	WT Hydraulic Motor and Pump	1.33 × 10−4	e95	WT Bearing Cracks	0	e112	WT Blade Loss	0.004679
e79	WT Hydraulic Oil	2.08 × 10−5	e96	WT Bearing Asymmetry	0.00583	e113	WT Loss of a Blade Fragment	0.007124
e80	WT Rotation Union	1.00 × 10−7	e97	WT Foundation Strength	0.00499	e114	WT Partial Blade Loss	0.003603
e81	WT Blade Structural Loss	0.01252	e98	WT Tower Welding	0.00698	e115	WT Rotor Sensor	0.007055
e82	WT Controller	9.32 × 10−4	e99	WT Lightning	0.00698	e116	WT Rotor High Temperature	7.20 × 10−4
						e149	WT Transformer	1.00 × 10−7

.

As stated, faults in WT generators can occur because of electrical or mechanical causes. Some of the most frequent events are open or short circuits in the stator or rotor winding, overheating, bearing failures from cracks or asymmetry, synchronization failures, accumulation of ice and dirt on blades, and manufacturing defects [11]. As such, it is important to include these cases in the FT analysis. The WT generator FT model used in this study is shown as subtree g31, and the WT electronic component model is shown to be represented by g32.

From extreme weather conditions, manufacturing defects, fatigue, or corrosion, WT support structures and blades can fail, so they must be included in the reliability analysis. By considering weather conditions, an extensive FTA model is proposed in [31] for the assessment of WT failure modes and their effects on public safety. For modeling purposes of this work, the WT support structures subsystem’s basic events are taken from [31,32]. To model the FT for WT blade failures, basic events and reliability data are drawn from [10,11,31], and a simple model of that is presented in subtree g36.

The gearbox is another most vulnerable component in a WT. Gearbox failure has been extensively studied and documented because it can lead to considerable turbine downtimes and unplanned maintenance issues, increasing electricity costs. The most probable causes for WT gearbox failures are wear and tear, fatigue, corrosion, abrasion, design defect, excessive pressure, and degradation. A simple FT model for WT gearbox failure is shown in subtree g34. Simple FT models for the WT hydraulic system failure are shown in g35, and the WT control system is shown in g37. Basic events and failure data for these models are drawn from [8,10,13,32,33].

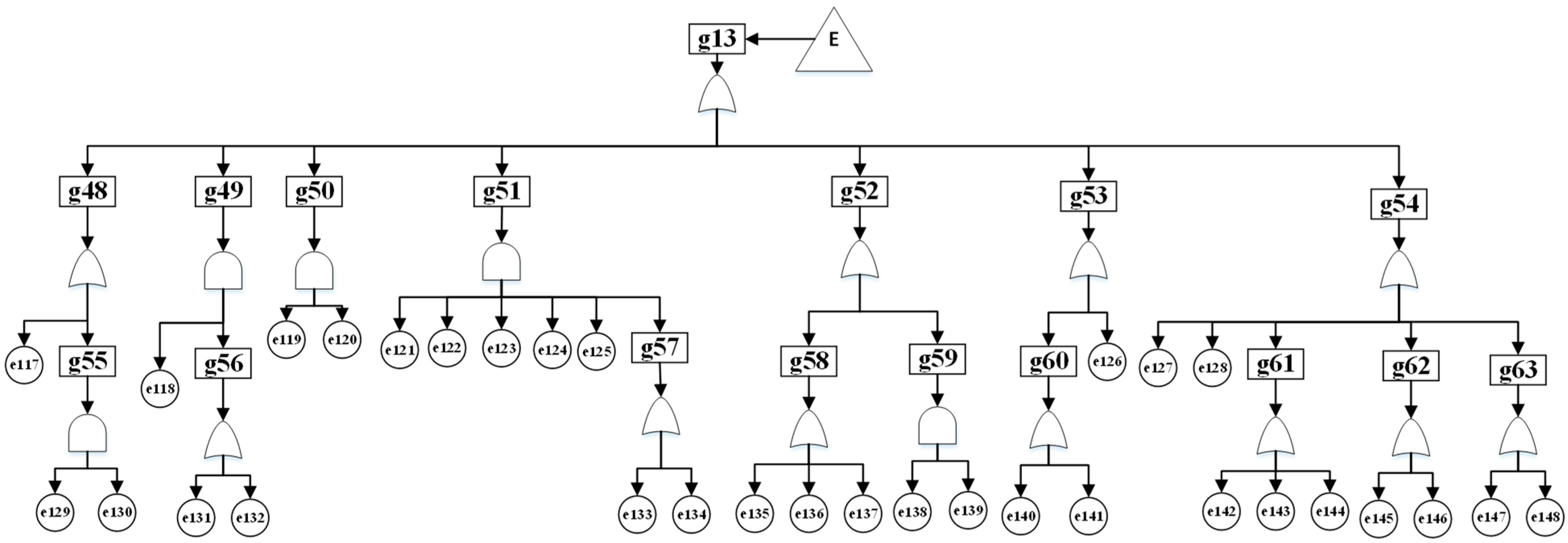
To reduce intermittency from the RES and provide ancillary services to MG and UG, BESS is included. Little to no work went into the reliability analysis of the energy storage, which typically involves Li-ion batteries in MGs. To build the FT model for the BESS basic events, failure, and repair rate data are taken from [17,18,34,35]. There are seven subtree events in the BESS FT model. The proposed FTA model for the BESS is illustrated in Figure 6, and its associated logic gate, basic event codes, and their corresponding failure probabilities are shown in

Table 5. Logic gates of BESS failure.

Codes	Logic Gates	Q	Codes	Logic Gates	Q
g13	BESS MG	0.012885	g55	BESS Module Structural Failure	9.52 × 10−7
g48	BESS Explosion	0.00135	g56	BESS Charging Module Diodes	0.00459
g49	BESS Battery Charging	8.90 × 10−7	g57	BESS DC-AC Converter	0.022151
g50	BESS Rupture by Pressure	3.41 × 10−6	g58	BESS internal Short Circuit	3.43 × 10−5
g51	BESS Electronic Components	1.07 × 10−18	g59	BESS High Temperature	1.09 × 10−5
g52	BESS High Temperature	4.53 × 10−5	g60	BESS high rate of discharge	0.010029
g53	BESS High Discharge rate	0.011493	g61	BESS Controller components failure BESS	9.26 × 10−7
g54	BESS charge controller (CC)	8.13 × 10−6	g62	BESS CC circuit	1.10 × 10−6
			g63	BESS CC regulator	6.00 × 10−6

and

Table 6. Basic events of BESS failure.

Codes	Basic Events	Q	Codes	Basic Events	Q
e117	BESS Single Module Explosion	0.001349	e133	BESS DC-AC Converter (IGBT-based)	0.013902
e118	BESS Low Capacity	1.94 × 10−4	e134	BESS DC-AC Converter (MOSFET-based)	0.008365
e119	BESS Overpressure	3.43 × 10−4	e135	BESS Manufacturing Defect	5.04 × 10−6
e120	BESS Stuck cell vent	0.00995	e136	BESS Wire short	7.20 × 10−6
e121	BESS MOSFET	0.002467	e137	BESS Seal	2.21 × 10−5
e122	BESS IGBT	0.001059	e138	BESS Fuse	0.006519
e123	BESS Capacitor	0.004141	e139	BESS Switch	0.001679
e124	BESS Filter	5.00 × 10−7	e140	BESS String Short	0.002876
e125	BESS Converter	0.00896	e141	BESS Ground	0.007174
e126	BESS Forced Discharge	0.001479	e142	BESS CC diode	9.00 × 10−7
e127	BESS Charge controller	1.03 × 10−7	e143	BESS CC capacitor	1.03 × 10−8
e128	BESS Control Unit	3.84 × 10−9	e144	BESS CC IGBT	1.52 × 10−8
e129	BESS Module Vent Clogging	7.06 × 10−4	e145	BESS CC switch	1.00 × 10−7
e130	BESS Explosion	0.001349	e146	BESS CC fuse	1.00 × 10−6
e131	BESS Improper Installation	0.00457	e147	BESS CC transistor	1.00 × 10−6
e132	BESS Diode failure at the same time	2.10 × 10−5	e148	BESS CC switching internal transistor circuit	5.00 × 10−6

.

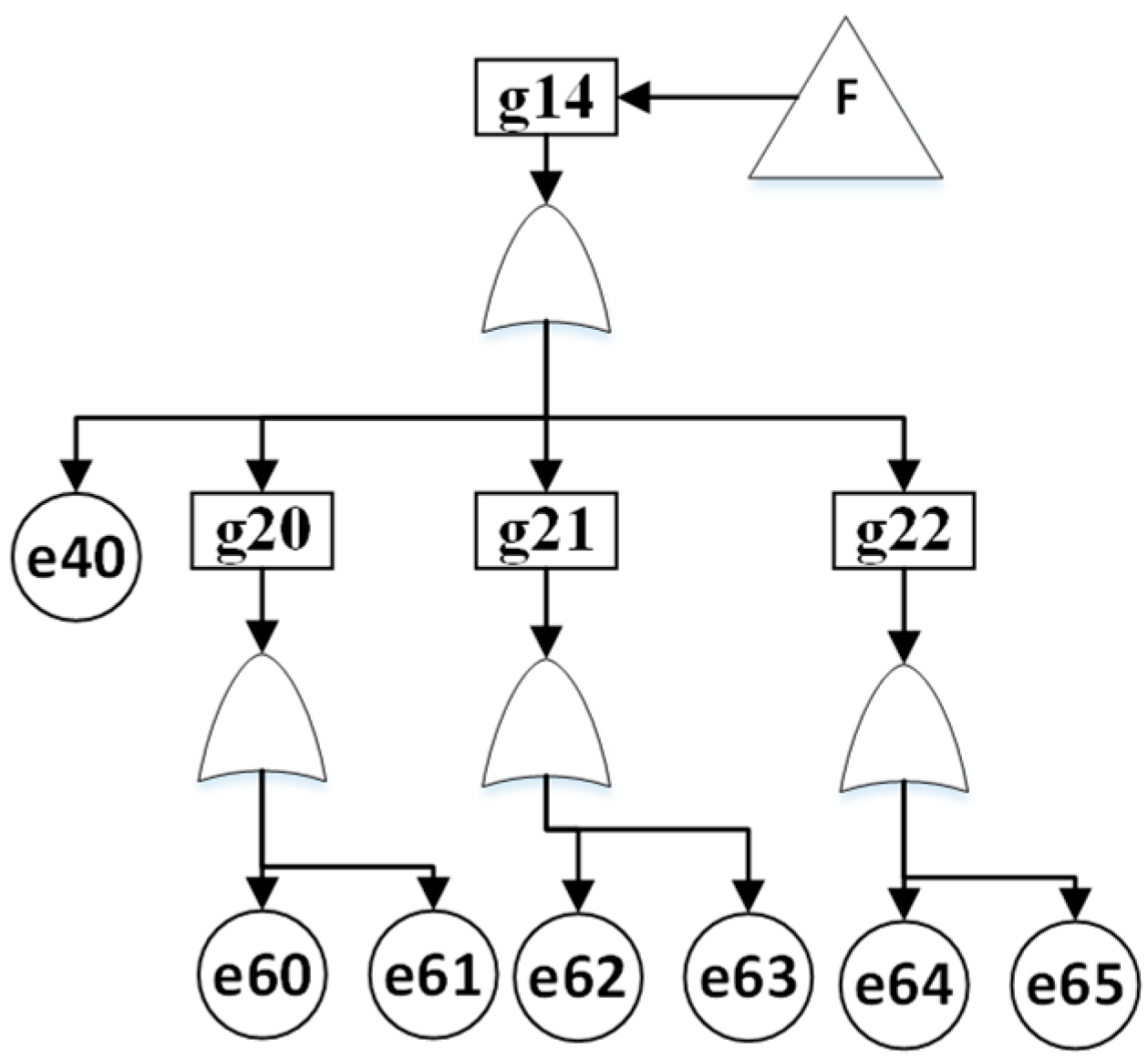
A simple load FTA model is presented in Figure 7. The associated basic event and logic gate codes and failure probability are shown in

Table 7. Logic gates of MG load failure.

Codes	Logic Gates	Q
g14	Load MG	0.013867
g20	Device MG-1	5.10 × 10−6
g22	Load Failure MG-1	3.67 × 10−6
g21	Load circuit breaker MG-1	0.003504

and

Table 8. Basic events of MG load failure.

Codes	Basic Events	Q
e40	Load power loss	0.010391
e60	Device switch	1.00 × 10−7
e61	Device Fuse	5.00 × 10−6
e62	Load Circuit breaker overload	0.001559
e63	load circuit breaker tripping	0.001948
e64	Load failure from natural events	2.62 × 10−6
e65	Load failure from manmade	1.05 × 10−6

.

Previous peer-reviewed literature has determined that the conventional power grid has been extensively studied using FTA. Failure occurrence is rare in distribution systems; in this study, a simple FT model for the utility grid’s distribution end is developed. Authors of the present work used a methodology similar to previous models. The proposed utility grid FT model has five intermediate events and one basic event as shown in Figure 8. Specifically, the FT models for UG transformers (g3), natural (e7) and manmade events (e6), transmission lines (g5), switchgear equipment (g6), and other key components like capacitor banks (e15) and voltage regulators (e16) are included in the model as shown in Figure 8. Basic events and parameter data for this reliability evaluation of the utility grid are drawn from [20,21,36,37,38,39,40]. The associated basic events and logic gate codes with their failure probability are shown in

Table 9. Logic gates of UG failure.

Codes	Logic Gates	Q	Codes	Logic Gates	Q
g1	UG	0.02122	g6	UG Switch Gear	0.01447
g3	UG Transformers	4.56 × 10−4	g7	UG Other Components	2.53 × 10−5
g4	UG Events	0.00628	g8	UG Transformer Type	3.62 × 10−5
g5	UG Transmission Line	5.61 × 10−5	g9	UG Disconnect Switch	1.70 × 10−5
			g10	UG Circuit Breaker	0.0142

and

Table 10. Basic events of UG failure.

Codes	Basic Events	Q	Codes	Basic Events	Q	Codes	Basic Events	Q
e1	UG Substation	3.57 × 10−5	e8	Failure of the equipment in the utility grid	0.002617	e15	UG Capacitor bank	1.28 × 10−5
e2	UG Moisture in transformer oil	6.00 × 10−5	e9	UG single-phase transmission line	2.93 × 10−5	e16	UG Voltage Regulator	1.10 × 10−6
e3	UG Stress on the transformer	3.00 × 10−5	e10	UG Three-phase transmission line	2.68 × 10−5	e17	UG Three-phase transformer	2.09 × 10−5
e4	UG Transformer Lightning strike	1.95 × 10−4	e11	UG switchgear Fuse	3.15 × 10−5	e18	UG Single-phase transformer	1.52 × 10−5
e5	UG Transformer Insulation	1.35 × 10−4	e12	UG switchgear recloser	1.34 × 10−4	e19	UG Disconnecting switch failing to close	1.48 × 10−5
e6	Manmade faults	0.001049	e13	UG sectionalizer	9.00 × 10−5	e20	UG Disconnecting switch failing to remain closed	2.23 × 10−6
e7	Natural events in the utility grid	0.002627	e14	UG Cable pole components	1.13 × 10−5	e21	UG Circuit breaker failing to close (at the point of common coupling)	0.008107
						e22	UG Circuit breaker failing to remain closed (at the point of common coupling)	0.006141

.

3. Reliability Evaluation Methods

Qualitative analysis of the analytical procedures was used to compute the failure probability of the top events. In this work, the comprehensive reliability analysis of the MGs is implemented using five different methods of FT as discussed in the next section.

3.1. Exact Method

The exact or basic method uses graphic binary logic to analyze the system’s risk and safety issues. The basic fault tree and logic symbols that link the events together, often called gates, are usually represented by Boolean logic operators, as shown in Figure 1. In the ‘exact’ method, after the system is defined and the FT diagram is constructed, the analysis starts at the top level by identifying the main undesired event, referred to as the top event. The basic events are connected to the top-level event through a single logic gate or a combination of gates, which describe the relationship between the input event and the outcomes. An analysis is performed using Boolean logic to identify the basic-level events that will lead to the failure of the top event. This process is repeated until all lowest-level events are identified and documented. This technique is widely accepted and applied for cross-disciplinary systems and is the only identified technique for generating the likelihood of complex systems failure. Human error, hardware, and software failures can be included in the analysis, depending on the necessity of both quantitative and qualitative analysis. Constructing and analyzing the FT with this type of top event (total system) can be cumbersome for a large-scale complex system. Sophisticated computer software is needed to perform the FTA in this case, as a manual FTA assumes that all basic events are independent. This assumption creates an unrealistic analysis; however, the necessary software is expensive and uses a large quantity of computational power. In this work, the authors address this issue by identifying and implementing different techniques for the FTA that use less computational power while maintaining the accuracy at an acceptable level. Results demonstrate the effectiveness of the proposed methods and establish the versatility and availability of cost-effective options for reliability analysis.

Using the exact FT method, the MG unreliability (Q) in this study was computed as 0.222144, yielding a reliability of 77.7856% after 1000 simulated hours, as shown in Figure 9. The exact method has also been applied for MG risk analysis in previous studies [19,20,21,22,23,24,25,26,41,42,43].

3.2. Monte Carlo Simulation Method

Monte Carlo simulation is one of the popular methods for solving engineering problems. This method has been used in reliability analysis using probability distributions of component failure and repair data to simulate the system’s random behavior over time. If an FT is complex, i.e., when it has several basic events and interconnections, the Monte Carlo simulation is preferred and the obtained results are adequately accurate; however, such simulation runs use excessive amounts of computational power. The fundamentals and the mathematical background of the Monte Carlo simulation and its application to reliability analysis are extensively documented in [44,45,46]. Significant research has been performed on the reliability evaluation of MG’s using Monte Carlo simulations, the most popular of which are found in [47,48,49,50,51,52].

Using the Monte Carlo simulation engine in the ‘relyence’ FTA suite [53], and with the number of simulation iterations set to 20,000, authors have performed a reliability analysis of the MG in the grid-tied mode for 1000 simulated hours of operation. The results of the Monte Carlo simulation for 20,000 iterations are shown in Figure 10 with an unreliability of 0.218909, which reports a reliability of 78.1091%.

3.3. Cut-Set Approximation Methods

A cut-set is an important concept in FT analysis. A cut-set is a combination of basic events whose simultaneous occurrence will cause the top event failure. A minimal cut-set is the smallest combination that can cause the top event. The probability of a cut-set is calculated by taking the intersection of all sets in the set (unless the events belong to a disjoint event group or a common cause failure group). The probability of the top gate failing is the probability of the union of all cut-sets and is calculated by the following equation:

$$\begin{array}{ll}P\left(Top Gate\right)=& P\left({\displaystyle \bigcup _{i=1}^n}{E}_i\right)\\ & ={\displaystyle \sum _{i=1}^n}P\left(E_i\right)\\ & -{\displaystyle \sum _{i<j}}P\left(E_i\cup { E}_j\right)\\ & + {\displaystyle \sum _{i<j<k}}P\left(E_i\cap { E}_{j }\cap { E}_k\right)-\cdots +{\left(-1\right)}^{n+1}\ast P\left({\displaystyle \bigcap _{i=1}^n}{E}_{i }\right)\end{array}$$

(1)

where $\left\{E_1, E_2, E_3,\dots , E_n\right\}$ are the cut-sets. As seen from the formula, the number of terms increases exponentially with the number of cut-sets. So, calculating the probability of failure of the top gate is impractical for the FT with a large number of cut-sets. Cut-set approximation methods like cut-set summation, cross-product, and Esary–Proschan address this issue particularly when the event probabilities are low.

3.3.1. Cut-Set Summation

Cut-set summation (CSS) is a popular method for analyzing systems with components that have small failure probabilities; it saves time and computational power while providing acceptable results. This method is an optimal choice for risk analysis of the MGs and the utility grid. CSS assumes that the simultaneous occurrence of multiple minimal cut-sets is rare. In the CSS method, the probability of a top event occurring is the sum of the probabilities of its minimal cut-sets. The steps involved in the CSS method are as follows:

(1)

Documenting all failure modes for the top event in terms of component sets.

(2)

Checking if the component set belongs to the minimal cut-sets. If a component from the identified set is deleted, it will no longer trigger the top event.

(3)

Computing the failure probability of the system by the union, or adding, of all set probabilities. As calculating the full union using the inclusion–exclusion principle is computationally expensive, the formula is truncated (by only using the first sum from Equation (1)) to improve efficiency. The probability of failure at the top gate is calculated by the following equation:

$$P\left(Top Gate\right)=P\left({\displaystyle \bigcup _{i=1}^n}{E}_i\right)\approx {\displaystyle \sum _{i=1}^n}P\left(E_i\right)$$

(2)

Evaluating an equation with increasingly higher degrees, such as when the first-order minimal cut-sets contain one basic event and so on, takes more time and computational power to calculate. Several algorithms are proposed to obtain cut-sets from the FTs in minimal computation time, making the CSS method feasible. While many algorithms are available to obtain the minimal cut-sets, the method of cut-sets (MOCUS) [54] is the most popular option; while it performs well for smaller FTs, it has limitations as FT size increases. This method is popular in the fields of aviation and space studies and has also been used to evaluate the reliability of DC power distribution networks [55], biochemical reaction networks [56], non-directional networks [57], and the composite power system reliability of the IEEE 6 bus, 14 bus, and single area IEEE RTS 96 systems [58], which demonstrates its feasibility. Authors in this work have adopted the CSS method for reliability and risk analysis of the MG, and the results demonstrate the method’s effectiveness. When using the cut-set summation method after 1000 simulated hours of operation, the unreliability is computed to be 0.249862, and the reliability is 75.0138% (Figure 11).

3.3.2. Cross-Product Method

The cross-product method (CP) uses minimal cut-sets to approximate the gate probabilities, and is similar to the CSS method. In this method, cut-sets are obtained by MOCUS, and multiple occurrences of minimal cut-sets are rare above a specified order. A cross-product order ‘m’ is used to account for the order of product terms to overcome the CSS method’s drawbacks. A higher order of the cross-product can be specified to improve the accuracy of the results, but it increases the calculations’ complexity, increasing the computational cost. The probability of failure of the top gate using the cross-product for order three is given by the following equation:

$$\begin{array}{ll}P\left(Top Gate\right)=& P\left({\displaystyle \bigcup _{i=1}^n}{E}_i\right)\\ & \approx {\displaystyle \sum _{i=1}^n}P\left(E_i\right)-{\displaystyle \sum _{i<j}}P\left(E_i\cup { E}_j\right)+ {\displaystyle \sum _{i<j<k}}P\left(E_i\cap { E}_{j }\cap { E}_k\right)\end{array}$$

(3)

Depending on the value of ‘n’, the value of the probability of failure varies as follows:

When n = 1, the cross-product method reduces to the CSS method. For higher orders of ‘n’ the truncation alternates between overestimating and underestimating the exact probability. If ‘n’ is odd, the approximation yields an upper bound, whereas if ‘n’ is even, it yields a lower bound of the exact system failure probability.

The cross-product method is popular in aerospace, defense, medical, and nuclear power plants, all of which have safety-critical systems. This method is programmed into commercial reliability software suites like Relyence [53], Isograph [59], Reliasoft [60], and Weibull++ [61], indicating its popularity.

Authors of the present work utilized bibliographical search tools to obtain peer-reviewed journal articles that examine the cross-product method for MG reliability analysis; however, little to no relevant research data were found.

When n = 1, the results from the cross-product method (Figure 12) are similar to the cut-set summation method: the unreliability is 0.249862, and the reliability is 75.01385%.

When n = 2, the unreliability is computed to be 0.22171, and the reliability is 77.829% (Figure 13), which is less than that from the cut-set summation method.

When n = 3, the unreliability is 0.223740, and the reliability is 77.626% (Figure 14), which is greater than when n = 2.

For the proposed FT, an n value of 2 yielded the closest result when compared with the basic method, with minimal computational time.

3.3.3. Esary–Proschan Method

Esary and Proschan (1963) proposed a reliability analysis technique for coherent systems using minimal cut-sets (respective path) and lower bounds of reliability (respective upper bounds) [62]. Upper and lower bounds for the system calculation are shown in [63]. Esary and Proschan (1970) extended the research to include the components of maintenance and interdependency by including the lower cut minimal bound and comparing it with system reliability [64]. The method proposed in [62] became widely popular for reliability analysis due to its simplicity in calculations, and is only applicable for non-identical components. The method proposed in [64] solved the non-identical component problem, by which risk analysis can be performed for maintaining interdependent components. When performing the reliability analysis using the Esary–Proschan (EP) method, the assumption is made that it produces conservative results and that all cut-sets are independent, such as when coherent fault trees do not contain the NOT logic. The probability of failure for the top event is calculated by the following equation:

$$\begin{array}{ll}P\left(Top Gate\right)=& P\left({\displaystyle \bigcup _{i=1}^n}{E}_i\right)=P\left({\left({\displaystyle \bigcap _{i=1}^n}{E}_i^{\prime }\right)}^{\prime }\right)=1-P\left({\displaystyle \bigcap _{i=1}^n}{E}_i^{\prime }\right)\\ & \approx 1-{\displaystyle \prod _{i=1}^n}P\left(E_i^{\prime }\right)=1-{\displaystyle \prod _{i=1}^n}(1-P(E_i))\end{array}$$

(4)

If all the cut-sets have some common events, the Esary–Proschan method top gate failure probability is calculated by the following equation:

$$P\left(Top Gate\right)\approx \left(1-\prod _{i=1}^n\left(1-{P(E}_i^{*}\right)\right)\left(\prod _{j=1}^{k}P\left(e_j\right)\right)$$

(5)

where $\left\{e_1, e_2, e_3,\dots , e_k\right\}$ are the common events in every set and ‘${(E}_i^{*})$’ is the cut-set of ‘$E_i$’ without any common events.

The efficiency of the reliability calculations for coherent systems like MG will be improved by using a minimal path upper bound and a minimal cut lower bound. These bounds are derived for the independent components in [63] by coupling the newly derived bounds with the upper and lower bounds proposed in [62]. Using both exact and approximation (EP) methods, the system reliability analysis was reported in [65], comparing the logical concepts from exact methods and probability calculations from the approximation. Compared to the exact, or basic method, EP is computationally manageable for assessing the reliability of small-scale systems. The EP method employs algebraic manipulations and approximations, which reduce the computational cost; however, when this method is applied to a large-scale system, the computational cost increases as the number of minimal cut-sets increases. Even with these shortcomings, EP performs better than the basic method, and error bounds from the approximation increase, which decreases the efficiency of the method. The use of the EP method is popular in aerospace, automotive, commercial, and defense applications. Industrial-scale reliability software suites like Relyence [53], Isograph [59], Reliasoft Blocksim [60] provide the FTA module with EP preinstalled, demonstrating the effectiveness of the method and its applicability towards safety-critical systems. As stated earlier, the EP method works well with maintained interdependent systems, which makes it suitable for MGs. The authors have implemented the EP method for the MG’s reliability analysis to substantiate the FTA’s versatility and reduce the computational cost. An extensive peer-reviewed literature search suggests this may be the first attempt at implementing the EP method for the risk analysis of an MG.

As there are no basic common events in the cut-sets, the common basic event factor is zero in this case; therefore, the unreliability (Figure 15) is equal to the value in the cut-set summation method.

4. Availability Metrics

Several availability metrics listed in

Table 11. Availability metrics definitions.

Availability Metrics	Formula		Definition
Unavailability	$U\left(t\right)={\displaystyle \frac{MTTR }{MTTR+MTBF}}$	(6)	The probability that the component is in a failed state at time ‘t.’
	($U$(t) = Unavailability at time ‘t’, MTTR = mean time to repair, MTBF = mean time between failures).
	If A(t) is the availability at time ‘t’.
	$A\left(t\right)+U\left(t\right)=1$	(7)
	If $U$(t) is the unavailability at time ‘t,’ for the repairable component or system.
	$A\left(t\right)\le U\left(t\right)$
	For a non-repairable system.
	$A\left(t\right)=U\left(t\right)$	(8)
Conditional Failure Intensity	$\lambda \left(t\right)={\displaystyle \frac{\omega \left(t\right)}{1-U\left(t\right)}}$	(9)	The probability that the system or component will experience a failure at time ‘t’, given it was operating at time ‘t’.
	If U(t) << 1, then
	$\lambda \left(t\right)\ne f\left(t\right) and \lambda \left(t\right)=\omega \left(t\right)$
	If f(t) is the failure rate for non-repairable components or systems, and constant failure rates.
	$\lambda \left(t\right)=f\left(t\right)$	(10)
	General case
	$\lambda \left(t\right)\ne f\left(t\right)$
Failure Frequency (or) Unconditional failure intensity	$\omega \left(t\right)=\lambda \left(t\right)\left[1-U\left(t\right)\right]$	(11)	The probability that the system or component will experience a failure at time ‘t’, given that the system is operating at time zero.
Mean Unavailability	$\overline{\mathsf{\omega }}\left(t\right)={\displaystyle \sum _{i=1}^N}\overline{{⍵}_i}$	(12)	The proportion of time during which the system or component is unavailable for use.
	(N = Number of minimal cut-sets, i = individual component)
Expected Number of Failures	$n={\displaystyle \frac{Total time \left(t\right)}{MTBF}}$	(13)	Total number of failed components after time ‘t’.

were calculated for 1000 h of simulated system operation. A wide range of availability metrics exists in the reliability analysis, and those presented in this paper are the most common and popular for risk analysis of safety-critical systems.

The calculated availability metrics for the basic method are comparable to those of the linear aging model, as shown in Figure 16 [66]. The linear aging model evaluates the implications of the aging phenomenon on the reliability of a component, in which the component’s performance deteriorates with age. The performance deterioration can range from negligible to noticeable, depending on the component. With an optimized maintenance schedule, the stress on the component can be reduced, improving the system’s reliability.

5. Reliability Diagnostics: Cut-Sets and Importance Measures

5.1. Cut-Sets

After determining the minimal cut-sets for the FT, the failure probability is calculated for the components in each identified MCS and documented in decreasing order to provide insight into the vulnerable components for the operators. Using the basic method for 1000 h of operation, the minimal cut-sets of the top twenty critical components and their probability of failure are listed as shown in Figure 17. These calculated cut-sets will provide MG and UG operators with valuable insight into the most vulnerable components of the system, allowing them to target those areas for improvement.

5.2. Importance Measures

There are two classes of importance measures in reliability analysis: structural importance measures (SI) and reliability importance measures (RI). The importance of a component is assessed in the SI [67] based on the FT; structure’s position; however, it does not consider the reliability of the component or the system. RI measures take both position and reliability of the component into account, making them more efficient. In the quantitative analysis of the FTA proposed by the authors, RI measures are mathematically calculated and documented. This analysis will allow the MG and the UG operators to identify critical parts, thus allowing them to emphasize the importance of those parts and optimize their maintenance schedules. Furthermore, based on discrete basic events and top event probabilities, importance measures will help the MG operators in ranking the events in terms of reduced likelihood of occurrence to improve the system’s performance. Manual calculations of the importance measures are manageable with a simple FT; however, as the tree size increases, calculations will become cumbersome. Advanced reliability software suites will easily perform these calculations without constraints on the size of the FT. Calculating different importance measures will provide a comprehensive view of the MG system’s vulnerable areas for the operators, thereby improving overall reliability and ensuring safe operation. Importance measures considered in this work and their significance are listed in

Table 12. Importance measures definitions and significance.

Importance Measure	Definition	Formula		Significance
Marginal or Birnbaum Importance Factor (MIF)	The first calculated importance factor is the marginal or Birnbaum importance factor [68]. If the probability (P), top event (T), and basic event (E), then MIF measures the increase in the probability of ‘T’ due to the occurrence of ‘E’. It is the difference between the P(T) (given P(E) = 1) and P(T) (given P(E) = 0).	$MIF=P\left(T|\mathrm{P}\left(\mathrm{E}\right)=1\right)-\mathrm{P}\left(\mathrm{T}|\mathrm{P}\left(\mathrm{E}\right)=0\right)$	(14)	This importance measure assists MG operators with identifying the most vulnerable components in the system, demonstrating that higher value metrics equal higher system-critical components. (One drawback of the MIF is that it does not take the probability of the basic event ‘E’ occurring directly into account, which can lead to a high MIF value for rare events).
Criticality Importance Factor (CIF)	By modifying the MIF and taking the occurrence of event ‘E’ into account, CIF is calculated by multiplying the MIF and P(E) divided by P(T).	$CIF=MIF\ast {\displaystyle \frac{P\left(E\right)}{P\left(T\right)}}$	(15)	This importance factor measures the impact of the specific component reliability on the system’s overall probability of failure. This metric helps MG owners optimize their maintenance schedule by identifying critical parts as a priority for maintenance.
Diagnostic or Fussell-Vesely Importance Factor (DIF)	The Diagnostic or Fussell-Vesely Importance Factor is a measure of the probability that the top event, or system, has failed given one minimal cut-sets occurrence or failure of one critical component.	$DIF=P\left(E\right)\ast {\displaystyle \frac{P\left(T|\mathrm{P}\left(\mathrm{E}\right)=1\right)}{P\left(T\right)}}$	(16)	The diagnostic importance factor (DIF) allows for the development and optimization of diagnostic activities, as it identifies the most probable failure events.
Risk Achievement Worth (RAW)	Risk achievement worth (RAW), or the top increase sensitivity, is a measure to sense the increase in the probability of the top event ‘T’, given the probability of the basic event ‘E’ occurrence is ‘1’.	$RAW={\displaystyle \frac{P\left(T|\mathrm{P}\left(\mathrm{E}\right)=1\right)}{P\left(T\right)}}$	(17)	This measure highlights the basic events that will have the greatest impact on the system, or top event, helping grid operators develop a prevention strategy that focuses on critical system failures.
Risk Reduction Worth (RRW)	Risk reduction worth (RRW), or top decrease sensitivity, is a measure of the reduction in the probability of top event ‘T’, given the basic event ‘E’ does not occur (P(E) = 0).	$RRW={\displaystyle \frac{P\left(T\right)}{P\left(T|\mathrm{P}\left(\mathrm{E}\right)=0\right)}}$	(18)	This measure helps MG owners track improvement in the areas of most concern, such as reducing the failure probability of vulnerable components, given an aggressive maintenance strategy in place.

.

Xing [69] compares seven RI measures: RAW, RRW, DIF, CIF, MIF, conditional probability (CP), and improvement potential (IP). Reported results demonstrate that RAW and MIF may be erroneous in developing a maintenance schedule; however, these measures help identify the susceptible components and assist MG owners in improving overall system reliability. Results from [69] show that DIF is the most promising measure for safety-critical systems, such as the utility grid and MG, which require aggressive maintenance strategies. For risk assessment of nuclear power plants, a dynamic assessment is used for model-based simulations in [70], and RI measures are used for the qualitative analysis. FTA is applied for the reliability analysis of the IEEE test system in [38]. NRAW (network risk achievement worth) and NRRW (network risk reduction worth), which are the modified versions of the conventional RAW and RRW, are used as importance measures in the system. RI measures in the electric transmission systems are used in [71] to evaluate transmission components with promising results, demonstrating their effectiveness. The versatile nature of RI is demonstrated by its use in applications across multiple disciplines involving safety-critical systems, including spacecraft performance analysis [72], making it ideal for MG assessment. For the present work, various reliability importance measures of the MG are calculated for 1000 h of simulated operation. In total, there are 149 basic and intermediate events in the proposed FTA model.

Since not all of the importance measures rank the basic events in the same way, MG operators can choose an importance measure depending on the requirements. Taking an average of the proposed importance measures is also an effective way in the solution process.

Figure 18 shows a heatmap of the normalized importance measured for the top 20 events and gates. Each column corresponds to a specific measure, and the color intensity indicates respective magnitudes.

6. Analysis and Discussion

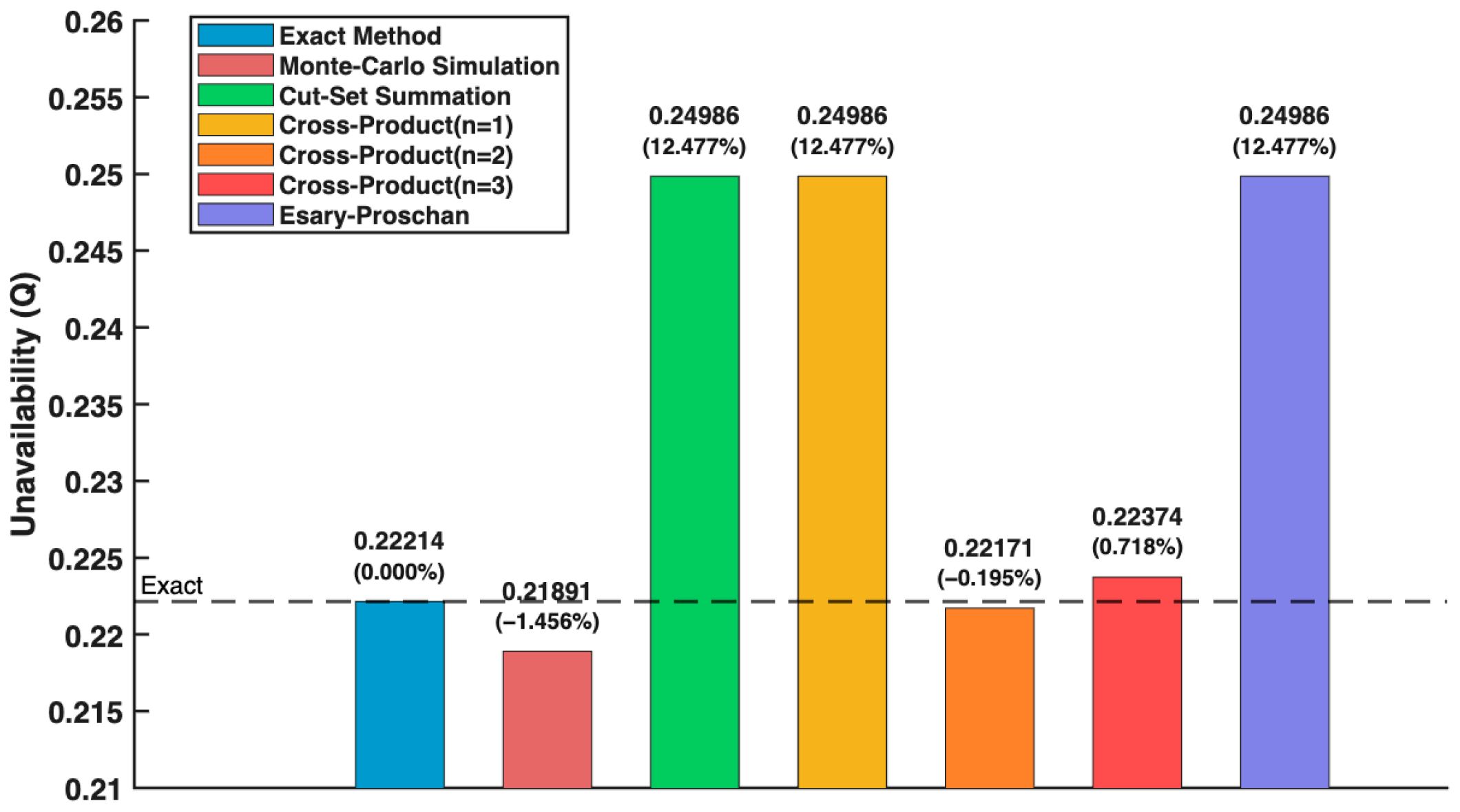
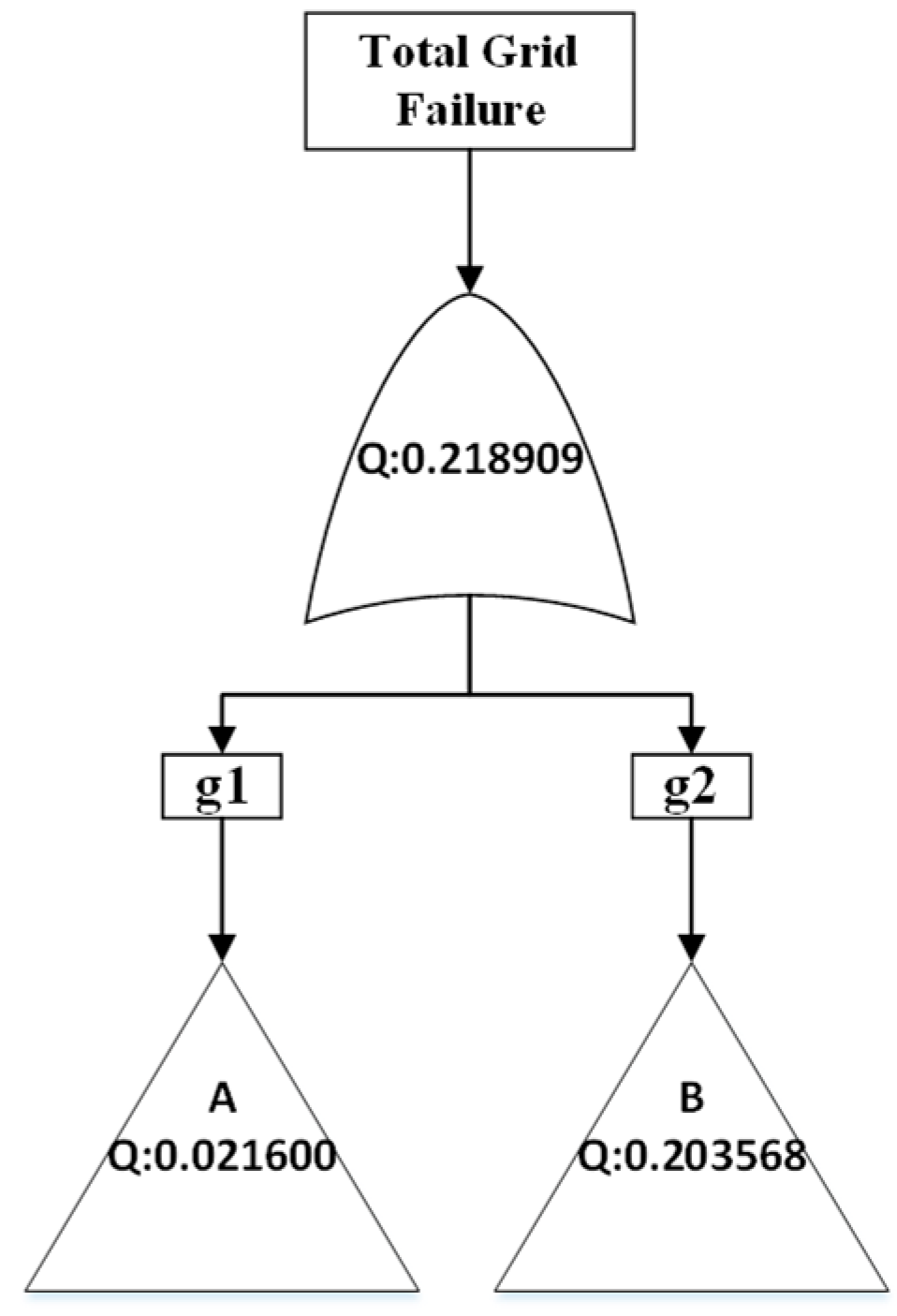
The probability of total system failure was calculated using different methods. As shown in Figure 19, results are largely consistent across all methods and align with theoretical expectations discussed previously. The exact method serves as the baseline for comparison (Q = 0.22214) of all other methods. The Monte Carlo simulation results closely match those of the exact method, with a value of Q = 0.21891, deviating by only −1.456%, confirming that the stochastic simulation can be effectively used to calculate system reliability metrics for the system considered in this work. As previously discussed, exact and Monte Carlo simulation methods are extensively used in FT analysis. These methods are robust, but can be computationally intensive, especially for a complex system like MG, which has several independent events from different renewable sources.

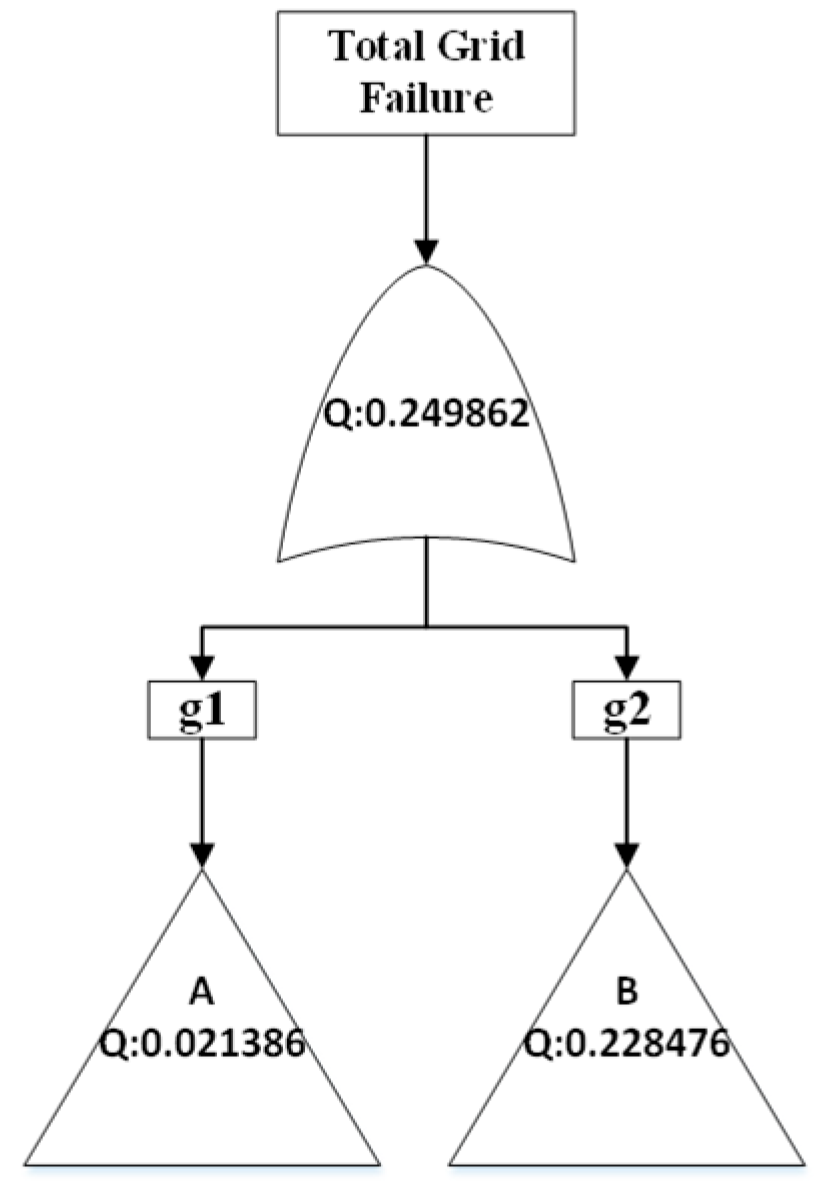
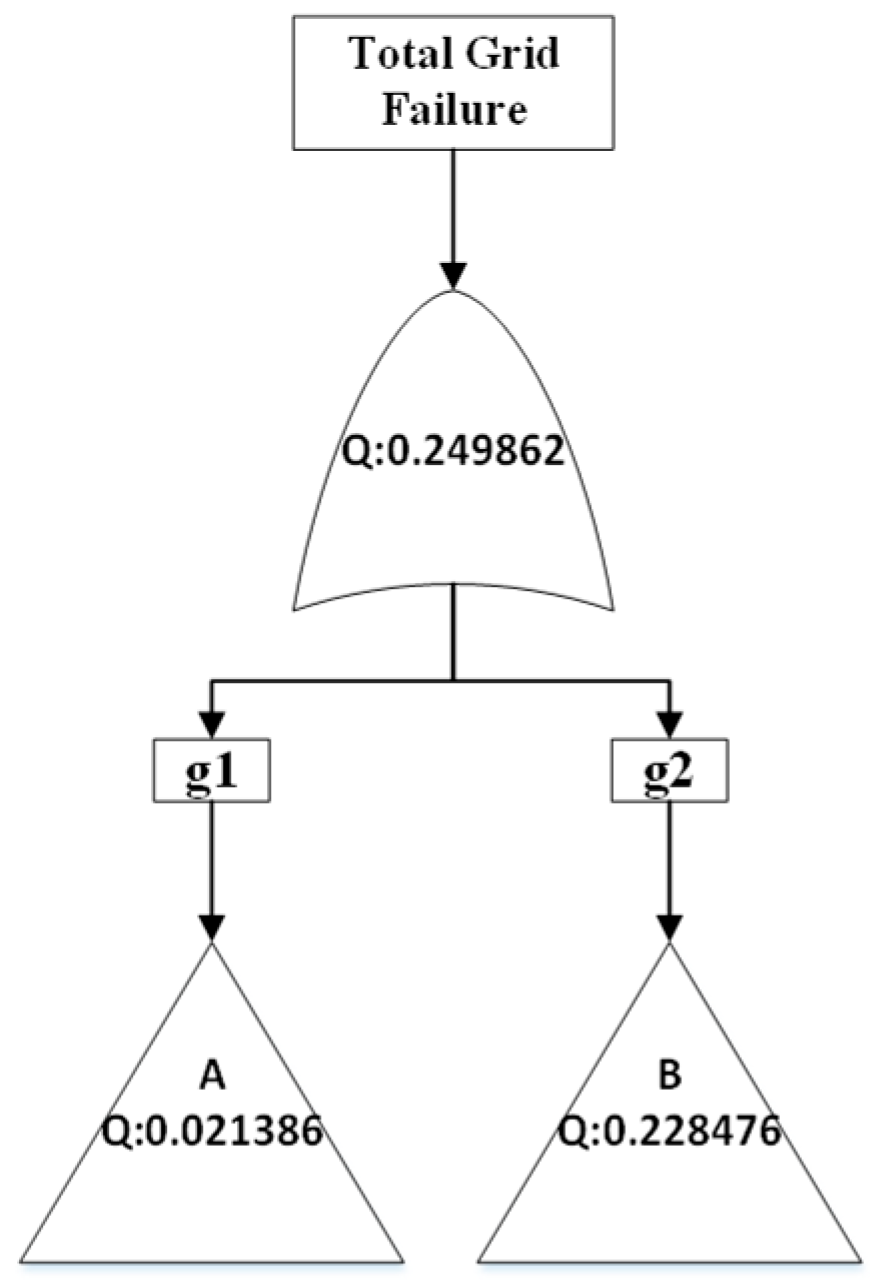
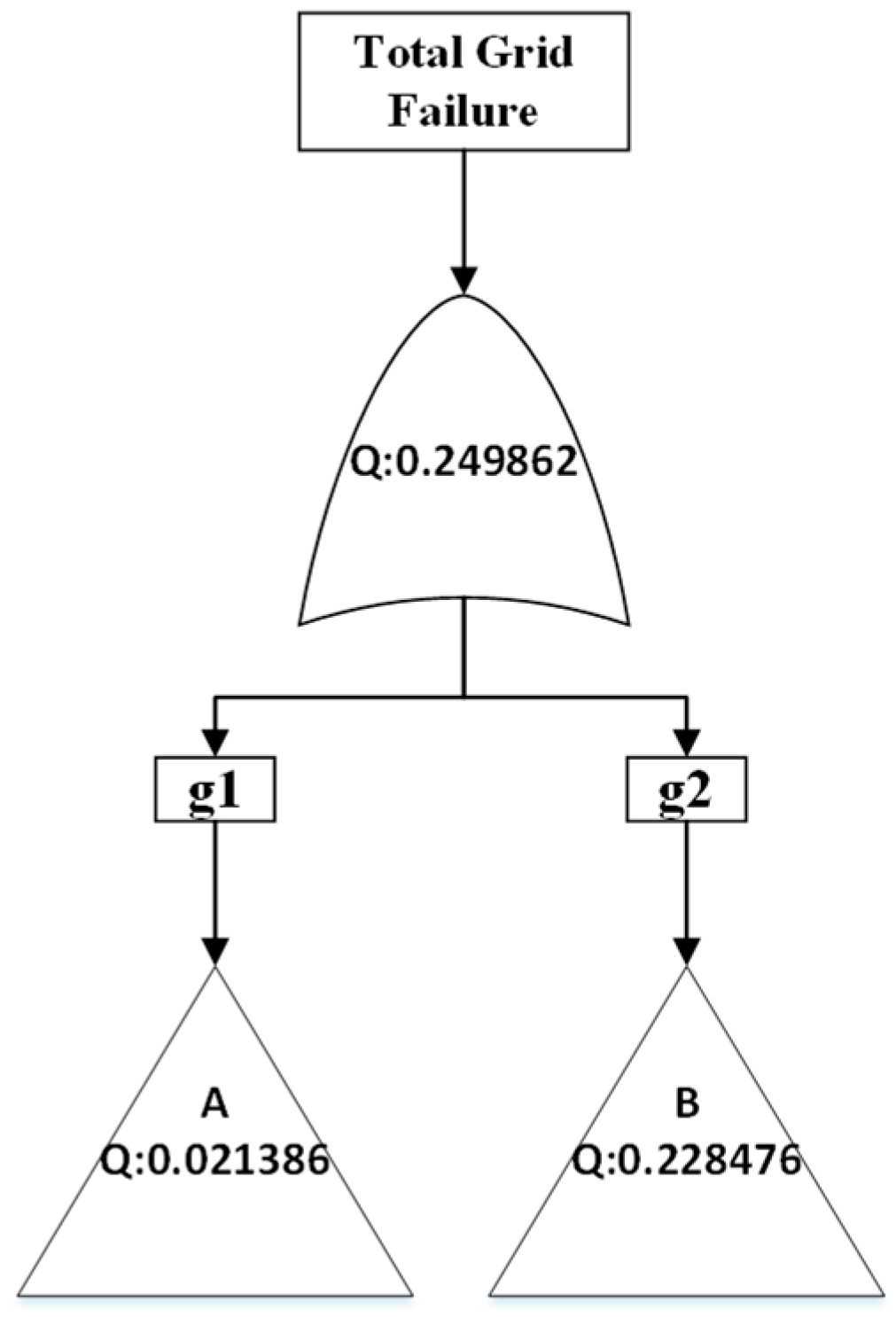
Cut-set approximation methods provide faster alternatives while offering results within valid ranges. The CSS method in this case yields a failure probability of 0.24986, representing a +12.477% deviation from the base case. This is expected, as the CSS method uses the first sum from Equation (1). The CSS method is the fastest of the approximation methods, but it is also the most inaccurate and provides an upper bound for the failure probability of the top gate.

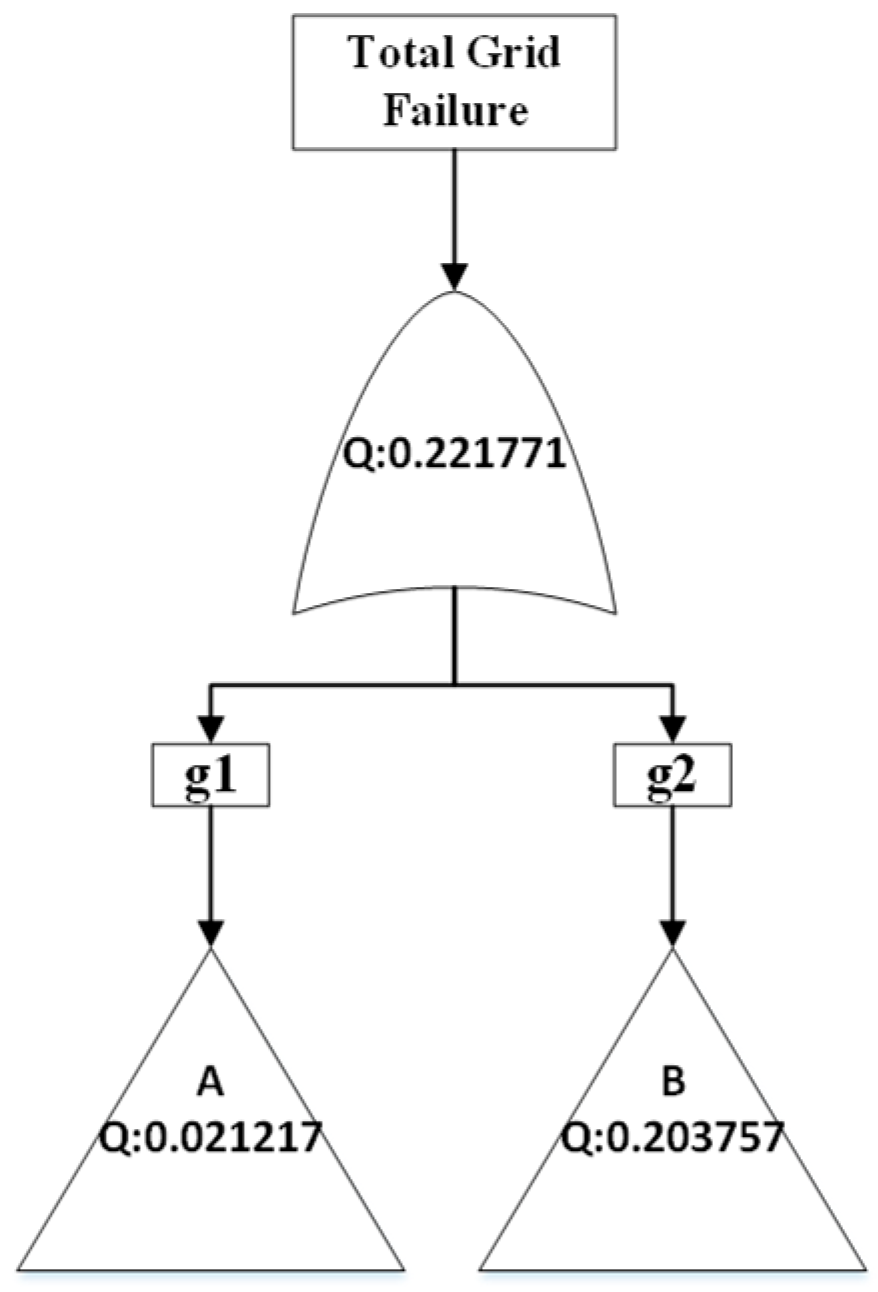
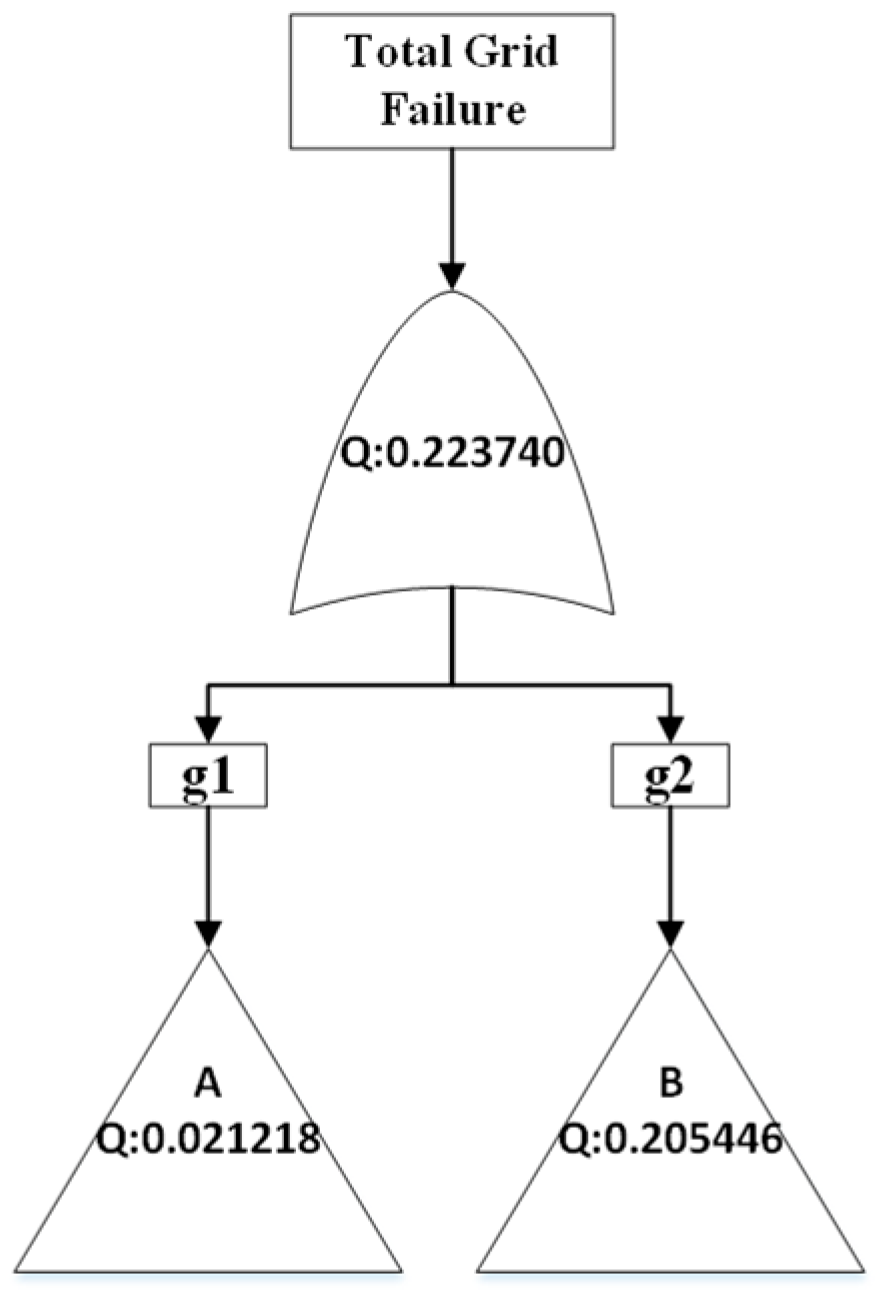
The cross-product approximation method for n = 1 results is the same as the CSS method, which matches the theoretical descriptions discussed above. For instance, n = 2 produced Q = 0.22171 (deviation of −0.195% from exact method), and n = 3 produced Q = 0.22374 (deviation of +0.718%). These values are in proximity to the exact method, thus proving to be efficient alternatives for large fault trees.

Both the CSS and Esary–Proschan methods yielded identical results because MG’s FT cut-sets are mutually exclusive (they share no common components), and the rare-event approximation ensures that the higher-order intersection terms in the inclusion–exclusion expansion contribute insignificantly. So, Esary–Proschan’s expression simplifies the CSS method.

Flexibility to choose between multiple methods is essential for MG operators, as the size and complexity of FT’s vary widely and the morel complexity can vary substantially across systems and operating conditions. The exact method remains the benchmark for verifying approximation methods, but it may become computationally intractable for larger systems due to cut-set interactions, so it is most suitable for small-to-moderate FTs where the number of events or cut-sets is manageable. The EP method provides a computationally efficient solution for identifying dominant vulnerabilities in the system, such as points of failure at point of common coupling or primary distribution transformers. This method is effective when the top event of the FT (loss of power to critical loads) can be represented through a coherent and monotone structure dominated by OR gates and the objective is to obtain conservative bounds with moderate computational effort. The CSS method is recommended when minimal cut-sets can be identified and the overlap remains manageable. CSS provides higher accuracy when compared to first-order approximations and is effective for grid-tied MGs where minimal structural vulnerabilities drive the top event. The CP method is recommended when minimal cut-sets are available, cut-set overlaps are non-negligible, and full inclusion–exclusion principle to all orders is computationally expensive. High renewable energy systems introduce stochastic intermittency and time-dependent constraints, such as the State-of-Charge for BESS, and non-exponential failure distributions and environmental correlations (e.g., solar irradiance). The Monte Carlo simulation method is an indispensable tool to represent these effects because it can track chronological operations and accommodate arbitrary failure distributions or correlated environmental scenarios. While the computational overhead of the Monte Carlo simulation method is higher than that of analytical counterparts, it offers a level of operational realism that is otherwise unattainable. For MG owners, the choice to use the Monte Carlo simulation method represents a pragmatic trade-off: accepting a higher computational cost in exchange for the modeling fidelity required to manage the dynamic nature of modern renewable configurations.

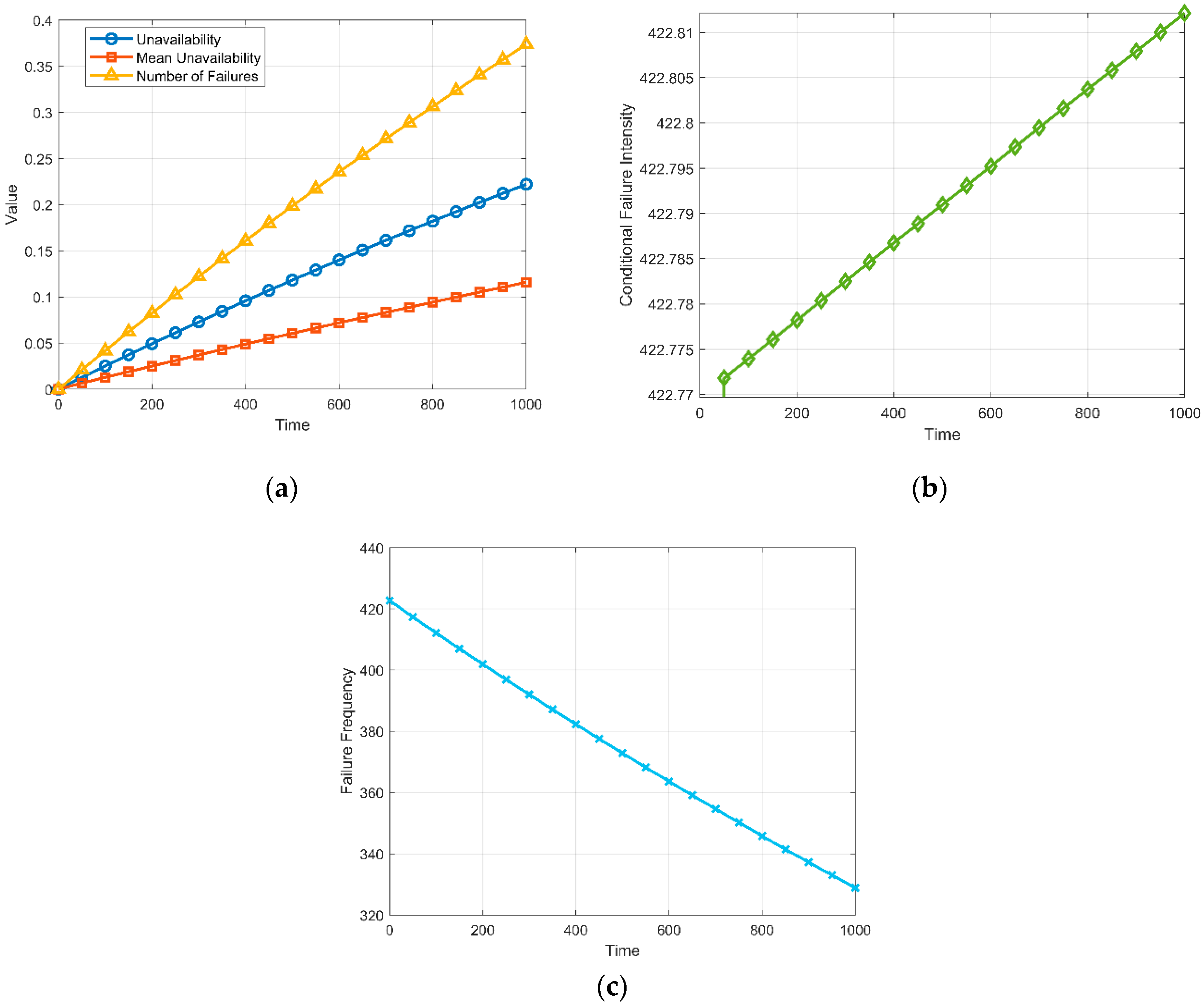
Availability metrics plotted in Figure 16a exhibit a steady increasing trend over time, which is consistent with the reliability theory. These trends validate the expected degradation of system reliability with operating time. The CIF (Figure 16b) remains almost constant around 422.77–422.81 with a slight upward variation, which is the typical expected trend for FT’s modeled under rare-event exponential failure distributions. The failure frequency (Figure 16c) shows a decreasing trend (422.77 to 328.89) over the simulated duration. The observed trend is consistent with the theoretical assumptions, as time progresses, fewer working components remain to contribute to new failures, reducing the failure frequency.

Reliability indices, such as SAIFI (System Average Interruption Frequency Index), SAIDI (System Average Interruption Duration Index), and CAIDI (Customer Average Interruption Duration Index), are well-documented in MG reliability studies. These indices are system-level and customer-focused, so they provide no insight into the contribution of individual components to overall unreliability. By contrast, the importance measures proposed in this work quantify the sensitivity of the system’s probability of failure to changes in the reliability of specific components. This is particularly important for MG operators, as the proposed measures in this work will enable them to identify internal vulnerabilities and optimize their maintenance schedules, thereby enhancing MG reliability.

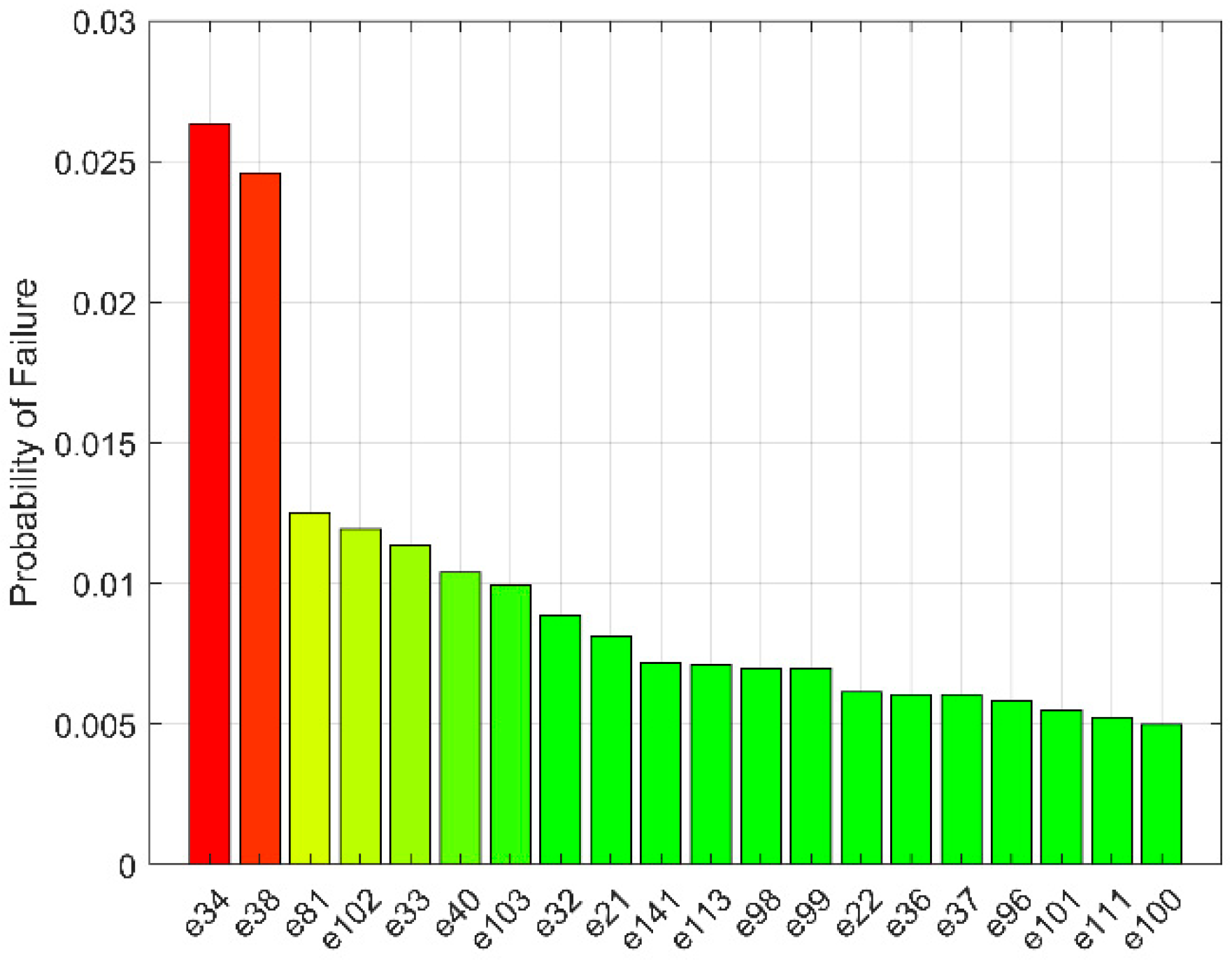
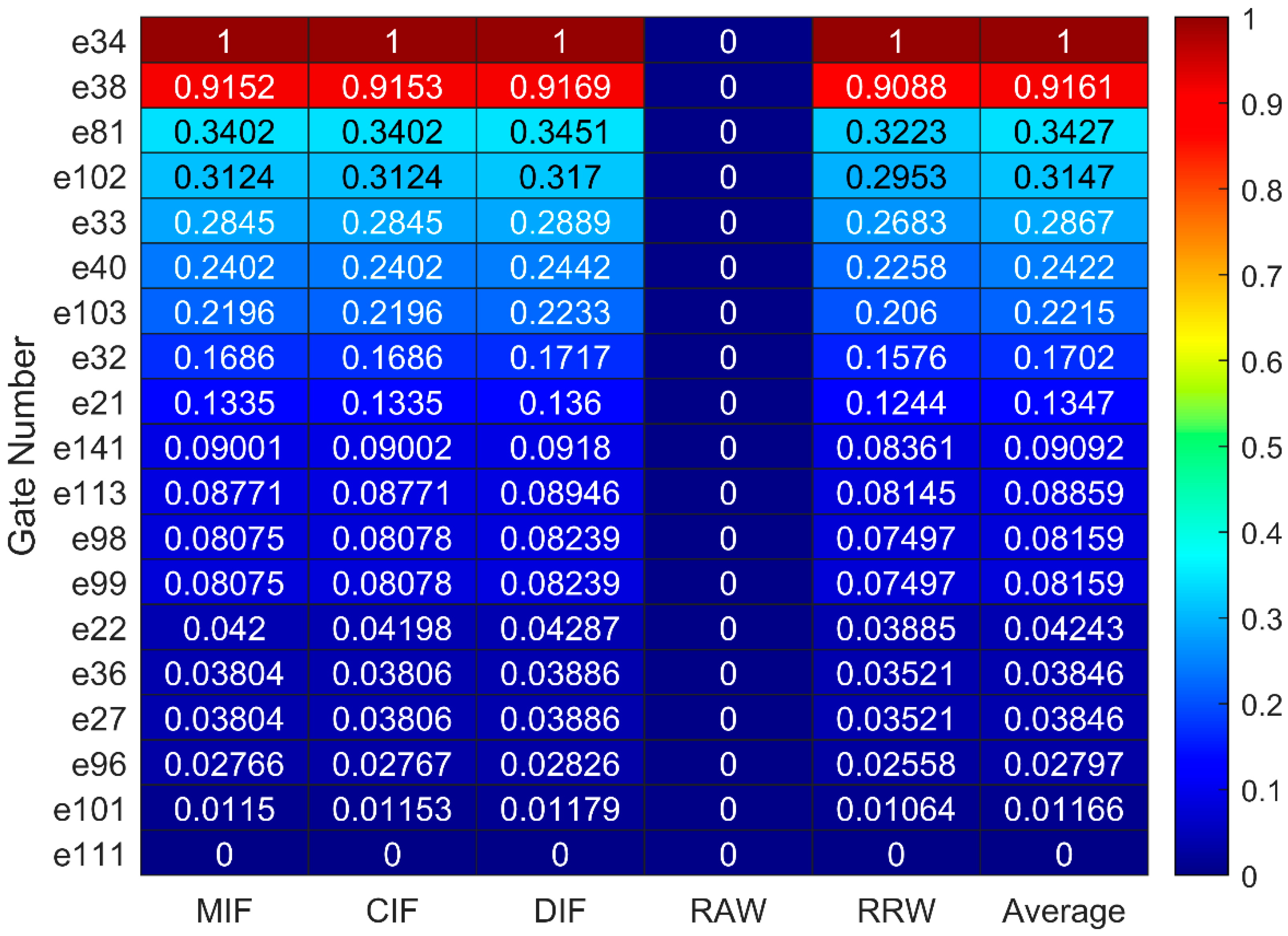
Figure 18 presents the normalized heatmap of the calculated importance measured for the top 20 events in the MG FT. Consistent results between the cut-set probabilities presented in Figure 17 and the calculated importance measures provide strong validation of the results. The same events, such as e34, e38, e81, e102, and e33, emerge as most significant when evaluated for cut-set probabilities and importance measures. This confirms that the importance measures used in this work effectively capture the component-level vulnerabilities in the system. A large subset of dominant events exhibits the same value for RAW (4.501591), because the failure of each component is assumed to lead to the same single, critical top event (total system failure). This trend is expected given the tree structure is dominated by OR-gate logic, where the failure of a basic event directly propagates through the OR structure forcing the occurrence of top event with certainty, i.e., $P\left(T|E_i=1\right)\approx 1$, which yields $RAW \left(E_i\right)\approx {\displaystyle \frac{1}{P\left(T\right)}}={\displaystyle \frac{1}{0.222144}}\approx 4.501591,$ yielding identical RAW values for the dominant events. In contrast, events located within subsystems connected through AND-gate logic do not force the top event with certainty, so RAW value deviates from the dominant event value. For instance, PV DC switch (e50) yields a RAW value of 2.359441, while weaker contributors approach a value of 1.0. To visualize the impact of the measures, a heatmap is presented in Figure 18, with normalized values (where the normalization scales for each measure range from 0 to 1) making the results comparable despite differences in magnitude. It helps the operators to identify the most vulnerable components without distortion from scale differences.

Combined, the results from the proposed system offer a comprehensive and reliable approach for MG reliability assessment. By integrating multiple methods so that operators can choose an appropriate method based on FT size, availability metrics, and importance measures, providing component-level insights, this work proposes a robust methodology that balances computational efficiency with accuracy, providing MG operators with a flexible and practical reliability toolkit for safe and reliable operation.

7. Summary and Conclusions

In this work, an FT-based reliability assessment of a composite (MG and UG) system is presented. Qualitative and quantitative analyses are performed based on a set of generic failure information.

Five different methods were implemented to minimize the computational cost and demonstrate the versatile nature of the FTA approach. Popular availability metrics are presented to help grid operators gain an overall view of both system reliability and unavailability. An important feature of the proposed method is that deficiencies in the system can be readily identified with calculated importance measures, which helps in assisting the MG operators in optimizing maintenance schedules and developing preventive strategies. Cut-set components with the probability of failure for the MG components were documented for further analysis. As more data becomes available, the proposed FT approach will be updated to help further researchers and grid operators improve the system’s performance and increase its reliability.

Future work includes a failure mode and effects analysis (FMEA) and an economic risk assessment to predict failure modes of the critical components and their impact on system performance to enhance the reliability of the system further. Modern MGs are networked, and thus are vulnerable to cyberattacks. Cyberattacks cannot be modeled with the conventional FT. Authors in [73] have proposed an FMEA worksheet for the risk assessment of MG cyber components. Nevertheless, the traditional FMEA has drawbacks in prioritizing the critical components, so authors are currently working on a fuzzy-based FMEA method that can address the drawbacks of the traditional method.