A Novel Sliding-Mode Control Strategy Based on Exponential Reaching Law for Three-Phase AC/DC Converter

Abstract

The control design of three-phase AC/DC converters is particularly challenging, as their dynamic behavior is governed by complex nonlinear interactions and strong coupling among system variables, conventional Proportional–Integral (PI) controllers often suffer from sluggish transient responses and limited immunity to interference. To address these issues, Sliding-Mode Control (SMC) is widely adopted for its robustness against parameter uncertainties and rapid dynamic performance. However, the chattering phenomenon inherent in traditional SMC near the sliding surface remains a critical challenge. To improve the dynamic performance of sliding-mode control, this work introduces a redesigned exponential reaching law into the control framework. The proposed strategy is implemented in a voltage–current cascaded (double closed-loop) structure, where the improved reaching law is embedded in the outer DC-link voltage loop and the inner loop regulates the grid currents in the synchronous dq frame. By modifying the reaching dynamics, the proposed approach effectively weakens chattering phenomena while enabling faster convergence of the system states. Comprehensive validation was conducted using Matlab/Simulink simulations and experimental prototypes. The results demonstrate that, compared to PI control and traditional exponential reaching law-based SMC, the proposed strategy significantly mitigates chattering while delivering superior static stability and faster dynamic response.

1. Introduction

Three-phase AC/DC converters are critical for enabling bidirectional power transfer and ensuring low harmonic currents, which effectively improves grid reliability and mitigates non-technical losses [1,2]. It plays an important role in renewable energy, energy storage systems, motor drives [3], and DC transmission systems [4,5]. In such systems, efficient power conversion often needs cascaded converter stages. For example, to connect low-voltage renewable sources (e.g., photovoltaic panels) to a common DC bus or the grid, as a common configuration, high-gain DC-DC converters serve as the pre- or subsequent stage of the AC/DC converter. Consequently, investigating advanced topologies—such as high-boost interleaved [5] or soft-switched SEPIC structures [6]—is vital for optimizing system regulation and overall efficiency. The control objective of a three-phase AC/DC converter centers on two core priorities: first, maintaining the DC-link voltage at its predefined setpoint (which serves as the foundational power supply for subsequent load circuits), and second, enhancing power quality by mitigating harmonics in the grid-side current—since excessive grid-side current harmonics can disrupt the normal operation of power grid equipment and reduce the efficiency of energy transmission.

In the field of three-phase AC/DC converter control, different strategies have been introduced to address power decoupling requirements. One representative approach is voltage-oriented control, which achieves independent control of active and reactive power components by aligning the control reference with the grid voltage, while direct power control (DPC) focuses on fast dynamic regulation by directly manipulating power variables. In addition, model predictive control (MPC) has attracted increasing attention due to its ability to handle system constraints and multivariable dynamics. The traditional VOC control strategy applies the pulse width modulation (PWM) to control the active and reactive power to track their reference values, and the overall control consists of a voltage outer loop and a current inner loop using proportional–integral (PI) controllers [7], but the method relies on the selection of the PI parameters, which will be limited in dynamic performance. The DPC strategy requires a switching table to control the active and reactive power [8], but it is difficult to construct a perfect switching table, which will affect the steady state performance of the system. MPC operates by explicitly utilizing a system model to predict future behavior, allowing control decisions to be generated directly without relying on modulation processes, while simultaneously accounting for system parameters, operational constraints, and control objectives. Ref. [9] designs a cost function and determines the minimal cost function by constantly seeking the optimal state, but it requires a high level of model accuracy and requires a lot of time to compute.

Sliding-mode control (SMC) is widely acknowledged for its strong robustness against external disturbances, concise control structure, high control precision, and fast finite-time convergence characteristics [10,11]. It is frequently employed in handling nonlinear systems, including motor control of electric vehicles [12,13,14]; converters [15,16]; and active power filters [17,18]. SMC is an effective nonlinear control method that regulates system dynamics through the design of an appropriate sliding surface. With the designed control law, the system trajectories reach the sliding surface in finite time and then evolve toward the target equilibrium state. Three-phase AC/DC converters inherently possess strong nonlinear coupling, making robust control design a challenging task. Although SMC has been shown to enhance system robustness, many reported works apply it exclusively to the inner current loop, while the outer voltage loop continues to rely on conventional PI control [19]. This control configuration effectively strengthens input current regulation but remains inadequate for achieving robust output voltage control. Consequently, voltage outer-loop control schemes based on extended state observers (ESOs) have been developed to address this issue [20], incorporating model uncertainty into ESOs and second-order sliding-mode (SOSM) control to suppress disturbances and uncertainty. Also some scholars have used the SMC strategy in the outer voltage loop to track the active power reference and the MPC strategy in the inner current loop [21]. As a result, both the stability margin and dynamic behavior of the system are significantly enhanced. Furthermore, Lu et al. developed a resonant super-twisting SMC strategy combined with a reduced generalized proportional–integral observer, aiming to improve system performance under uncertainties [22]. In this control framework, proportional regulation derived from the proposed theory is applied in the outer voltage loop to stabilize the DC-link voltage, whereas the RST-SMC controller is employed in the inner loop for converter current control. This scheme effectively enhances outer-loop performance under load disturbances and parameter uncertainties, while simultaneously ensuring fast and stable regulation of the inner loop. Moreover, in SMC design, the selection of an appropriate reaching law is crucial, as it directly influences the convergence speed toward the sliding surface and the level of system chattering [23]. Therefore, there are a lot of scholars researching the selection of reaching law, proposed many new reaching law instead of the traditional reaching law for control [24,25,26], resulting in faster system stabilization and improved control accuracy. In [27], an integral sliding-mode PFC controller using O-spline-based modulation was proposed to achieve fixed switching frequency and reduced chattering. In [28], chattering mitigation was realized for a semi-bridgeless boost PFC converter through an adaptive sliding surface with a variable hysteresis band.

For the proposed control strategy, voltage regulation and current control are achieved via two interconnected loops, both based on SMC principles. By replacing traditional PI regulators, this strategy improves robustness to system disturbances and allows for accurate tracking of the reference value for the DC-link voltage across different operating scenarios. Additionally, distinct reaching laws are employed in the SMC-based outer voltage regulation loop and inner current control loop to further optimize the system’s dynamic response and robustness. To showcase the performance merits of the proposed method, it is assessed in comparison with two widely used control schemes: a PI-based voltage–current cascaded control structure and a cascaded SMC scheme utilizing a conventional reaching law. Both steady-state and dynamic operational scenarios are considered for the comparative assessment of the proposed method and the aforementioned schemes. Simulation and experimental findings demonstrate that the proposed controller delivers a faster dynamic response, retains low total harmonic distortion (THD) during steady-state operation, and shows enhanced performance when subjected to load step disturbances.

This paper is structured to sequentially introduce the modeling, control design, and performance evaluation of the three-phase AC/DC converter. The converter’s mathematical model is first constructed in Section 2. Section 3 is dedicated to designing a voltage–current double closed-loop SMC strategy based on an improved exponential reaching law, alongside an analysis of its stability properties, and the associated overall control block diagram is presented here. For clarity, the “SMC strategy based on exponential reaching law” in the title refers to this voltage–current cascaded (double closed-loop) realization for the three-phase AC/DC converter. The validity of the proposed control method is subsequently verified in Section 4 and Section 5 via comprehensive simulation and experimental comparisons with two traditional control strategies. Finally, concluding comments are summarized in Section 6.

2. Three-Phase AC/DC Converter Model

Figure 1 illustrates the configuration of the three-phase AC/DC converter considered in this study. The converter is supplied by a balanced three-phase AC source, represented by phase voltages e_a, e_b, and e_c. Each phase is connected to the converter through an AC-side filter composed of inductors with identical inductance L and associated parasitic resistance R. On the DC side, a capacitor C is employed to stabilize the DC-link voltage, while a resistive load R_L is connected to the output to represent the power consumption of the system.

To improve the clarity of the manuscript and help readers understand the mathematical formulations, we have included a summary table of the symbols used in the paper.

Table 1. Summary of Symbols and Corresponding Definitions.

Symbols	Definition
s	Sliding surface function
Udc	DC-link voltage
$U_{dc}^{*}$	DC-link voltage reference
ε	Coefficient for the voltage outer-loop sliding-mode reaching law
k	Coefficient for the voltage outer-loop sliding-mode reaching law
a	Adaptive coefficient to ensure a is in the range (0, 1)
δ	Boundary-layer width for the sliding-mode action
sat(s)	Saturation function used to replace the discontinuous sign function in sliding-mode control
ed, eq	d,q-axis voltage component in the synchronous dq reference frame
id, iq	d,q-axis current component in the synchronous dq reference frame
ud, uq	d,q-axis control input
R, L, C	Resistance, inductance and capacitance value in the converter circuit
w	Grid angular frequency

lists the symbols and their corresponding definitions, which will serve as a reference for the mathematical expressions and control design throughout the manuscript.

Under ideal grid operating conditions, the three-phase voltages exhibit complete symmetry in both amplitude and phase, e_a + e_b + e_c = 0, ia + i_b + i_c = 0.

In the three-phase AC/DC converter, the two switches of any one bridge arm cannot be conducted at the same time, otherwise, a short circuit may be caused.

First define a switching function as S_k, k = a, b, c.

$$S_k=\left\{\begin{array}{l}1 (\mathrm{up} \mathrm{bridge} \mathrm{on}, \mathrm{low} \mathrm{bridge} \mathrm{off})\\ 0 (\mathrm{up} \mathrm{bridge} \mathrm{off}, \mathrm{low} \mathrm{bridge} \mathrm{on})\end{array}\right.$$

(1)

According to the topology of Figure 1 and Kirchhoff’s current law, this analysis leads to the following mathematical description of the DC-link current in the three-phase AC/DC converter.

$$C{\displaystyle \frac{d{u}_{dc}}{dt}}=i_a{S}_a+i_b{S}_b+i_c{S}_c-{\displaystyle \frac{v_{dc}}{R_L}}$$

(2)

For the three-phase AC/DC converter, its dynamic mathematical equations are deduced within the three-phase stationary reference frame by examining the circuit topology shown in Figure 1. By utilizing Kirchhoff’s voltage law and integrating the relational expression given in (2), the system model can be established, and it is presented as follows.

$$\left\{\begin{array}{l}L{\displaystyle \frac{d{i}_a}{dt}}=-R{i}_a+e_a-(S_a-{\displaystyle \frac{S_a+S_b+S_c}{3}})v_{dc}\\ L{\displaystyle \frac{d{i}_b}{dt}}=-R{i}_b+e_b-(S_b-{\displaystyle \frac{S_a+S_b+S_c}{3}})v_{dc}\\ L{\displaystyle \frac{d{i}_c}{dt}}=-R{i}_c+e_c-(S_c-{\displaystyle \frac{S_a+S_b+S_c}{3}})v_{dc}\end{array}\right.$$

(3)

For control-oriented modeling, the three-phase circuit equations of the AC/DC converter are converted into the synchronous dq reference frame through an equal-power transformation, which leads to the following mathematical formulation.

$$\left\{\begin{array}{l}L{\displaystyle \frac{d{i}_d}{dt}}=-R{i}_d-s_d{v}_{dc}+\omega L{i}_q+e_d\\ L{\displaystyle \frac{d{i}_q}{dt}}=-R{i}_q-s_q{v}_{dc}-\omega L{i}_d+e_q\\ C{\displaystyle \frac{d{u}_{dc}}{dt}}={\displaystyle \frac{3}{2}}{i}_d{s}_d+{\displaystyle \frac{3}{2}}{i}_q{s}_q-{\displaystyle \frac{v_{dc}}{R_L}}\end{array}\right.$$

(4)

In the synchronous dq reference frame, e_d and e_q represent the grid-side voltage components along the direct and quadrature axes, respectively. The corresponding current components, i_d and i_q, describe the active and reactive current behavior of the converter in the same coordinate system. The switching actions of the power converter are characterized by the unipolar binary switching functions s_d and s_q, while ω denotes the fundamental angular frequency of the grid.

3. Design of Proposed Sliding-Mode Control

During actual operation, a three-phase AC/DC converter faces multiple disturbances, such as parameter uncertainties and load fluctuations. When confronted with these disturbances, traditional PI control strategies are unable to simultaneously guarantee unity power factor operation and stable adjustment of the DC-link voltage to match its reference level. For SMC configuration, the exponential-type reaching law is usually represented as the following expression.

$$\stackrel{·}{s}=-\epsilon \mathrm{sgn}(s)-ks,\epsilon >0,k>0$$

(5)

where s is the sliding surface function.

Nevertheless, the use of the sign function induces oscillations around the sliding surface, which leads to chattering phenomena in the system. To mitigate this problem, an improved exponential reaching law is developed and expressed as:

$$\stackrel{·}{s}=-\epsilon {\left|s\right|}^a·\mathrm{sgn}(s)-ks$$

(6)

where ε and k are voltage outer loop sliding-mode reaching law coefficients and both ε and k are greater than zero, a is an adaptive coefficient and a can be expressed as:

$$a=1-\alpha {\displaystyle \frac{U_{dc}}{U_{dc}^{*}}}$$

(7)

where U_dc is the DC-link voltage, and $U_{dc}^{*}$ is the DC-link voltage reference value. To ensure that the proposed reaching law is well-defined and non-singular, the design is selected such that 0 < a < 1; this can be ensured by choosing (where U_dc,max is the admissible upper bound of the DC-link voltage), or by saturating a within [a_min, a_max]⊂(0, 1) in implementation.

Notably, when 0 < a < 1, the nonlinear term |s| a grows sublinearly for large |s| (avoiding excessive switching gain), while it decays more slowly than |s| as |s|→0, which helps preserve corrective action close to the sliding surface.

Chattering reduction is achieved by substituting the discontinuous sign function with a continuous saturation function sat(s), which also promotes smoother convergence toward the sliding surface.

$$sat(s)=\left\{\begin{array}{l}1,s>\delta \\ {\displaystyle \frac{s}{\delta }},-\delta \le s\le \delta \\ -1,s<-\delta \end{array}\right.$$

(8)

The boundary-layer width is regulated by the parameter δ, which plays a key role in shaping the behavior of the control action around the sliding surface.

Considering bounded disturbances, the sliding variable converges to an ultimate bound given by lim sup ∣s(t)∣ ≤ max (δ, D/(k + ε/δ). Therefore, a smaller δ improves steady-state accuracy but increases sensitivity to noise, whereas a larger δ enhances chattering suppression at the expense of steady-state precision. In this study, δ is selected empirically to balance voltage regulation accuracy and smooth control action.

Instead of relying on a discontinuous switching function, the use of the saturation function sat(s) enables gradual control variation, thereby reducing chattering effects. In practical implementation, the adaptive coefficient a is constrained within predefined upper and lower bounds to prevent excessively fast variation and possible amplification of measurement noise. This bounded adaptation ensures smooth control action and reliable operation in digital control systems without affecting the stability analysis. the controller behaves as a high-gain linear controller while the system trajectory remains within the boundary layer, and functions as an ideal relay once the trajectory moves outside this region.

The reaching law expression obtained after improvement is:

$$\stackrel{·}{s}=-\epsilon {\left|s\right|}^a\cdot sat(s)-ks$$

(9)

Remark (Reachability and convergence): For ∣s∣ > δ, sat(s) = sgn(s); hence

$$\left|\dot{s}\right|=-\epsilon {\left|s\right|}^a-k\left|s\right|$$

(10)

and the reaching condition

$$s\dot{}=-\epsilon {\left|s\right|}^{a+1}-k{s}^2<0$$

(11)

holds for any s≠0, guaranteeing that the trajectory reaches the boundary layer ∣s∣ ≤ δ. For ∣s∣ ≤ δ, sat(s) = s/δ and

$$\dot{s}=-(k+\epsilon |s{|}^a/\delta )s$$

(12)

Implying asymptotic convergence inside the boundary layer with reduced chattering, Furthermore, for ∣s∣ > δ,

$${\displaystyle \frac{d\left|s\right|}{dt}}=-\epsilon {\left|s\right|}^a-k\left|s\right|\le -\epsilon {\left|s\right|}^a$$

(13)

For 0 < a < 1, the reaching time to enter ∣s∣ ≤ δ, admits the explicit upper bound.

$$t_r\le {\displaystyle \frac{1}{k(1-a)}}\ln \left({\displaystyle \frac{\epsilon +k|s(0){|}^{1-a}}{\epsilon +k{\delta }^{1-a}}}\right)$$

(14)

Which provides a rigorous analytical support for the “accelerated convergence” claim. Computational cost comparison: relative to the traditional exponential reaching law (5), the improved law (9) adds only the evaluation of ∣s∣, the fractional power ∣s∣^a, and the saturation sat(s) (a few comparisons and one division by δ within the boundary layer). Both reaching laws remain O(1) per control update, and the additional arithmetic is marginal compared with the overall converter control computations (e.g., PLL, coordinate transformations, and PWM generation). Therefore, the proposed reaching law improves chattering/convergence performance with negligible computational overhead.

To clearly distinguish the proposed reaching law from existing exponential reaching laws, including the representative approach in Ref. [26], a concise comparison is provided in

Table 2. Comparative Characteristics of Different Exponential-Type Reaching Laws.

Item	Traditional Exponential Law	Exponential Law in Ref. [26]	Proposed Law (This Work)
Reaching law form	−ε sgn(s) − ks	Exponential-type reaching law	−ε∣s∣asat(s) − ks
Switching function	sgn(s)	sgn(s)	sat(s)
Switching gain	Constant	State-dependent (fixed design)	State-dependent with adaptive exponent (a)
Online adaptivity	No	No	Yes
Boundary layer	Not explicit	Not explicit	Explicit
Typical application	General SMC	Power converters	Outer voltage loop of AC/DC converters

, highlighting differences in mathematical structure, adaptivity mechanism, boundary-layer treatment, and intended application.

The proposed reaching law is particularly advantageous in outer-loop voltage regulation of cascaded AC/DC converters, where operating conditions (load demand, DC-link voltage reference, and grid-side disturbances) vary over a wide range. In such scenarios, a fixed-parameter exponential reaching law may either induce excessive chattering or sacrifice convergence speed. By contrast, the adaptive exponent and explicit boundary-layer structure of the proposed law allow fast reaching under large errors and smooth regulation near steady state, while maintaining low computational burden.

Compared with the conventional reaching law, the proposed scheme yields a noticeably improved dynamic behavior. As shown by the state trajectories in Figure 2, the constant-rate reaching law produces pronounced oscillations, whereas the proposed reaching law significantly attenuates chattering effects.

Relative to the commonly used exponential reaching law, the proposed method accelerates the system’s convergence toward the sliding surface while simultaneously reducing chattering.

According to the Lyapunov stability principle, the stability of the system under the improved exponential convergence mechanism is examined through Lyapunov stability analysis, it can be denoted as:

$$V_1={\displaystyle \frac{1}{2}}{s}^2$$

(15)

The derivative of V₁ is expressed as:

$$\stackrel{·}{V_1}=s\stackrel{·}{s}$$

(16)

Combined with (6), it can be obtained:

$$\stackrel{·}{V_1}=-s\cdot \epsilon {\left|s\right|}^a\cdot sat(s)-k{s}^2$$

(17)

It can be seen that the derivative of V₁ is always less than zero, proving the stability of the system. This result also explicitly confirms the standard sliding reachability condition $s\dot{s}<0$, providing theoretical support for the proposed reaching law. In particular, because s sat(s) > 0 for all s ≠ 0, one directly has ${\dot{V}}_1<0$ for s ≠ 0, which explicitly confirms the standard sliding reachability condition $s\dot{s}<0$.

The sliding mold surface is selected when using a sliding mold controller as:

$$s=u_{dc}^{*}-u_{dc}$$

(18)

The derivation of (18) is obtained:

$$\stackrel{·}{s}={\displaystyle \frac{d{u}_{dc}^{*}}{dt}}-{\displaystyle \frac{d{u}_{dc}}{dt}}=-{\displaystyle \frac{d{u}_{dc}}{dt}}$$

(19)

This can be obtained by combining (4) and (19):

$$\stackrel{·}{s}={\displaystyle \frac{u_{dc}}{C{R}_L}}-{\displaystyle \frac{3}{2C}}(s_d{i}_d+s_q{i}_q)$$

(20)

Combining with (9) and (21), it can be obtained as:

$$\epsilon |s{|}^a\cdot sat(s)+ks={\displaystyle \frac{3}{2C}}(s_d{i}_d+s_q{i}_q)-{\displaystyle \frac{u_{dc}}{C{R}_L}}$$

(21)

From (21), the active current is given as:

$$i_d=\left[\epsilon |s{|}^a\cdot sat(s)+ks-{\displaystyle \frac{3}{2C}}{s}_q{i}_q+{\displaystyle \frac{u_{dc}}{C{R}_L}}\right]{\displaystyle \frac{2C}{3s_d}}$$

(22)

When the three-phase AC/DC converter system is stabilized, it can be available that i_q = 0, e_q = 0, di_d/dt = 0, di_q/dt = 0. Therefore, it can be concluded from (4) that the system is stabilized at the time of e_d-Ri_d = s_dv_dc, −ωLi_q = s_qv_dc, which can be obtained by substituting into (22) and finishing:

$$i_d=\left[\epsilon |s{|}^a\cdot sat(s)+ks+{\displaystyle \frac{u_{dc}}{C{R}_L}}\right]{\displaystyle \frac{2C{u}_{dc}}{3(e_d-R{i}_d)}}$$

(23)

The system has $i_d^{*}$ = i_d at a steady state, and the value of the current tracking command is found to be:

$$i_d^{*}=\left[\epsilon |s{|}^a\cdot sat(s)+ks+{\displaystyle \frac{i_L}{C}}\right]{\displaystyle \frac{2C{u}_{dc}}{3(e_d-R{i}_d)}}$$

(24)

A cascaded SMC framework is implemented to link voltage regulation with current tracking. Specifically, the outer voltage loop determines the appropriate d-axis current reference required for voltage stabilization, whereas the inner current loop employs sliding-mode regulation to minimize the discrepancy between the reference and the measured current, thereby achieving coordinated voltage–current control.

Regarding the design of the current inner-loop controller, the core goal of this control scheme is to make the d-axis current i_d and q-axis current i_q of the AC-link quickly follow their corresponding reference signals—specifically the d-axis reference signal i_dref and q-axis reference signal i_qref. S is the sliding surface:

$$S=\left[\begin{array}{l}{s}_1\\ s_2\end{array}\right]=\left[\begin{array}{l}{i}_{derf}-i_d\\ i_{qref}-i_q\end{array}\right]$$

(25)

Once the system’s motion trajectory arrives at the sliding surface, a restrictive condition is applied to the sliding variable so as to keep the system’s dynamic behavior bounded to this surface throughout the subsequent movement, and the simultaneous derivatives of both sides of (24) can be obtained as (25), the equivalent control law u_eq can be obtained by substituting (4) into (25):

$$\stackrel{·}{S}=\left[\begin{array}{l}{\stackrel{·}{s}}_1\\ {\stackrel{·}{s}}_2\end{array}\right]=\left[\begin{array}{l}{\stackrel{·}{i}}_{derf}-{\stackrel{·}{i}}_d\\ {\stackrel{·}{i}}_{qref}-{\stackrel{·}{i}}_q\end{array}\right]$$

(26)

$$u_{eq}=\left[\begin{array}{l}{u}_{eqd}\\ u_{eqq}\end{array}\right]=\left[\begin{array}{l}-R{i}_d+\omega L{i}_q+e_d\\ -R{i}_q-\omega L{i}_d+e_q\end{array}\right]{\displaystyle \frac{1}{v_{dc}}}$$

(27)

Design switching control law u_sw is:

$$u_{sw}=-\left[\begin{array}{l}{\epsilon }_1\cdot sat(s_1)+k_1{s}_1\\ {\epsilon }_2\cdot sat(s_2)+k_2{s}_2\end{array}\right]{\displaystyle \frac{1}{v_{dc}}}$$

(28)

where ε₁ and k₁ are the d-axis switching term coefficients of the current inner loop and both ε₁ and k₁ are greater than zero, ε₂ and k₂ are the q-axis SMC switching term coefficients of the current inner loop and both ε₂ and k₂ are greater than zero. Choosing the right coefficients can ensure that the system reaches stability quickly. The reaching-law parameters ε and k determine the convergence behavior of the sliding variable according to $s\dot{}=-\epsilon sat(s)-ks$. where larger values of ε or k accelerate convergence but increase control activity. The boundary-layer width δ influences the trade-off between chattering suppression and steady-state accuracy, while the adaptive parameter α regulates the sensitivity of the reaching law to the voltage tracking error.

Consequently, the control law is formulated as:

$$u=\left[\begin{array}{l}{u}_d\\ u_q\end{array}\right]=u_{eq}+u_{sw}$$

(29)

Assume the Lyapunov function:

$$V_2={\displaystyle \frac{1}{2}}{S}^{T}S$$

(30)

Derive both sides of it simultaneously and relate it to (4), where stable operation can be obtained by considering i_dref to be zero:

$$\stackrel{·}{V_2}=s_1\stackrel{·}{s_1}+s_2\stackrel{·}{s_2}=-{\displaystyle \frac{s_1}{L}}({\epsilon }_1\cdot sat(s_1)+k_1{s}_1)-{\displaystyle \frac{s_2}{L}}({\epsilon }_2\cdot sat(s_2)+k_2{s}_2)$$

(31)

From the coefficients ε₁, k₁, ε₂, k₂ are all greater than zero, the derivatives of V₂ are all less than zero when s₁ and s₂ are not zero. The system is proved to be stable by the Lyapunov stability criterion. The organization and interconnection of the control components implemented in the system are illustrated in Figure 3, offering a clear view of the overall control strategy.

4. Simulation Verification and Analysis

To assess the operational effectiveness of the proposed control approach, a three-phase AC/DC power converter was modeled and emulated using Simulink under a range of operating conditions. This power converter is equipped with three distinct control schemes, specifically: conventional PI control, SMC using a traditional reaching law, and SMC integrated with the improved reaching law. All simulation experiments were conducted with identical system configurations and parameter values to guarantee an unbiased comparison. The core parameters of the converter employed in these simulation experiments are listed in

Table 3. Parameters selected for simulation.

Parameters	Value
Phase voltage/Vabc	220 V
Gird frequency/f	50 Hz
Switching frequency/fs	10 kHz
Load resistance/RL	50 Ω
Parasitic resistance/R	0.1 Ω
Filter capacitor/C	3.3 mF
Filter inductance/L	4 mH

.

The simulation is conducted using a grid-level phase voltage (V_abc = 220) in order to evaluate the proposed control strategy under operating conditions representative of practical three-phase grid-connected converters

The total duration of the simulation is set to 0.6 s, and the load R_L at the output is changed from 50 Ω to 25 Ω at 0.3 s.

For clarity and reproducibility, the performance indices used to evaluate the DC-link voltage regulation are defined as follows. The settling time (also referred to as the adjustment time) is defined as the time required for the DC-link voltage to enter and remain within ±2% of its steady-state value following the load step. The voltage drop is defined as the maximum instantaneous deviation of the DC-link voltage below its steady-state value during the transient response. The RMS tracking error and the peak-to-peak voltage ripple are evaluated over a steady-state time window after transient effects have decayed, using identical evaluation windows for all control strategies.

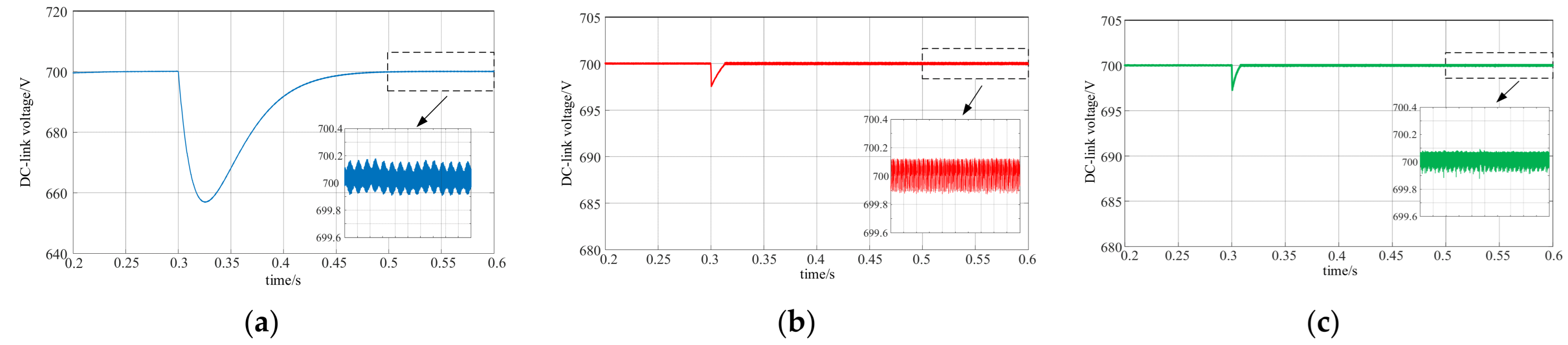
Figure 4 illustrates the DC-link output voltage waveforms obtained under the three control schemes. All the control approaches that were assessed can maintain the DC-link voltage near its preset reference level. However, the SMC scheme enhanced by the improved reaching law demonstrates superior regulation effectiveness and robustness, distinguishing it from the remaining two strategies. DC-link voltage reaches stabilization faster and with a smaller voltage overshoot based on improved reaching law control.

Figure 5 presents the response waveforms corresponding to the three control strategies. As shown in Figure 5a, the DC-link output voltage settles at approximately 0.2 s, accompanied by a voltage drop of about 40 V during the transient process. In Figure 5b, the voltage reaches steady state at around 0.013 s, with a transient voltage drop of approximately 2.5 V. Similarly, Figure 5c indicates that the DC-link voltage stabilizes within about 0.008 s, while the output voltage drop remains around 2.5 V. The comparative simulation results demonstrate that the three-phase converter employing the improved reaching-law-based SMC exhibits strong robustness and effectively suppresses system chattering.

In addition, a supplementary simulation of the reaching dynamics with bounded disturbances is provided in Figure 6 The results show that the sliding variable converges into the boundary-layer region and remains within the predicted ultimate bound, which validates the theoretical analysis under practical implementation conditions.

The dynamic waveforms of the A-phase grid voltage and current obtained using three distinct control approaches are presented in Figure 7. In all cases, the grid current follows the phase of the corresponding grid voltage, indicating correct power factor regulation. However, noticeable differences appear in the transient response: both the PI-based scheme and the SMC with a traditional reaching law exhibit slower stabilization, whereas the improved reaching-law-based SMC achieves a much faster settling process, reflecting superior dynamic performance.

The active power responses corresponding to different control implementations are illustrated in Figure 8. Under PI-based regulation, the system requires a relatively extended period to settle to a stable operating point. When SMC with a conventional reaching law is applied, the active power variation becomes smoother and the stabilization process is moderately improved. A further enhancement is achieved by introducing the improved reaching law, which significantly shortens the regulation time and enables the active power to reach a steady state more rapidly.

Figure 9 presents a comparison of the grid-side current harmonic factors under the three control strategies. The corresponding performance indices for the different control methods are summarized in

Table 4. Comparison of Dynamic and Harmonic Performance Under Different Control Strategies.

Simulation Parameters	PI Control	Traditional SMC	Improved SMC
Voltage Drop (V)	40	2.5	2.5
Adjustment Time (s)	0.2	0.013	0.008
Chatter Voltage (V)	0.25	0.2	0.15
Current THD (%)	3.04	2.57	1.70

.

The comparative results reveal that the proposed control strategy achieves a lower level of harmonic distortion, reduces adverse interactions with the power grid, and maintains a more stable operating condition for the overall system. Additional tests were performed by varying the filter inductance L, parasitic resistance R and DC-link capacitance C within ±20% of their nominal values. Under these parameter variations, the proposed control strategy preserved stable operation and consistent dynamic and steady-state performance trends, demonstrating robustness against system uncertainties.

5. Experimental Verification and Analysis

In order to verify the effectiveness of the proposed control strategy, the rectifier experimental platform was built as shown in Figure 10. The experiment uses a rapid control prototype (RCP) to control, the controller uses DSP TMS320F28335, the RCP systems only need to build the control algorithm model in Matlab/Simulink, download to the controller to achieve the control process.

Due to the nature of the experimental setup, an electronic DC load was used in this study. While electronic DC loads provide precise control over current and voltage, they may not fully reflect the complex characteristics of real-world loads, which typically include additional parasitic elements such as inductance, capacitance, and varying resistance. These factors can influence the controlled system’s performance, including its stability, transient response, and power quality. Despite this, the experimental results offer valuable insights into the proposed control method’s performance under the controlled conditions of the electronic DC load.

The parameters of the rectifier device developed for performance tests and the voltage loop and current loop parameters of the three different control methods used are shown in

Table 5. Parameters selected for experiment.

Parameters	Value	Parameters	Value
Phase voltage/Vabc	50 V	Parasitic resistance/R	0.1 Ω
Gird frequency/f	50 Hz	Filter capacitor/C	680 μF
Switching frequency/fs	10 kHz	Load resistance/RL	150/75 Ω
Filter inductance/L	4 mH	DC output voltage/Vdc	150 V
Voltage loop	PI Control (kpv = 0.35, kiv = 5.5)	Current loop	PI Control (kpdc = kpqc = 20, kidc = kiqc = 2)
	Traditional SMC (ε = 20, k = 50)		Traditional SMC (ε1 = ε2 = 50)
	Improved SMC (ε = 25, k = 50)		Improved SMC (ε1 = ε2 = 30, k1 = k2 = 10)

. Compared with the simulation study, the experimental system operates at a reduced voltage level, as indicated by the parameters in Table 5. The passive component values, including the DC-link capacitance, are scaled accordingly to preserve comparable normalized dynamic behavior under laboratory operating conditions.

To ensure a fair comparison, the outer voltage-loop dynamics of the PI controller, the conventional SMC, and the proposed SMC were designed to exhibit comparable response characteristics. The voltage-loop bandwidth was selected within a similar range for all control strategies, corresponding to a comparable DC-link voltage settling time.

The system behavior under a sudden load variation is evaluated using three different control strategies, as depicted in Figure 10, where the load resistance is reduced from 150 Ω to 75 Ω. The abrupt increase in load demand initially causes a transient deviation in the DC-link voltage. Under PI-based control, a noticeable voltage sag is observed during this transition. In contrast, when SMC is applied, the DC-link voltage recovers rapidly and converges to a new operating point. This fast restoration performance, observed in Figure 11b,c, can be attributed to the sliding surface being constructed directly from the system model, which enhances disturbance rejection capability. In addition, Figure 11a–c present the corresponding active power and grid-side A-phase voltage and current waveforms for the three control modes, indicating that their dynamic behaviors are largely comparable.

An experimental study was carried out to analyze the response of various control strategies to adjustments in the DC-link voltage command, as depicted in Figure 12 and Figure 13. Throughout this test, the preset reference voltage was raised from 150 V to 180 V. Experimental findings indicate that each control strategy can regulate the DC-link voltage to approach the new target level, which verifies their fundamental voltage regulation performance when facing step changes in the reference signal. With the proposed improved SMC strategy, the system reaches the new steady state within 0.085 s, which is significantly faster than the 0.113 s required by the traditional SMC and the 0.25 s achieved by the PI control. This represents a reduction in response time of approximately 25%. Figure 12 further illustrates the grid-side operating characteristics of the three control strategies by depicting the associated active power as well as the A-phase voltage and current waveforms.

The behavior of the three control strategies during a downward adjustment of the DC-link voltage reference is presented in Figure 13, reflecting their transient responses and steady-state regulation capability. Although all methods are capable of regulating the DC-link voltage to the target value, the PI-controlled system exhibits a noticeable voltage drop and requires a longer settling time when the reference voltage decreases. This steady-state deviation arises because the PI controller parameters are tuned to ensure satisfactory performance at a voltage reference of 180 V and remain fixed during operation. As a result, these parameters are no longer optimal when the reference voltage is reduced to 150 V, leading to a slower system response.

To further quantitatively assess the steady-state performance, the DC-link voltage ripple under this operating scenario is assessed and tabulated in

Table 6. Quantitative Comparison of Steady-State Voltage Ripple and Current Harmonics.

Parameters	PI Control	Traditional SMC	Improved SMC
Voltage Ripples	0.030 V	0.011 V	0.009 V
Current THD	5.35%	4.20%	3.12%

. The quantitative data show that the control strategies employing the improved sliding-mode formulation yield significantly smaller voltage ripple amplitudes. This finding aligns with the earlier analyzed current quality results, which verifies the excellent steady-state regulation performance of the proposed approach.

6. Conclusions

This paper introduces a sliding-mode control strategy based on a redesigned exponential reaching law for three-phase AC/DC converters, implemented in a voltage–current cascaded (double closed-loop) framework (outer DC-link voltage loop and inner current loop). Guided by the defined control goals and parameter benchmarks, the proposed approach facilitates the design of the reaching dynamics and control gains to meet the targeted control performance. In real-world operation, the system encounters multiple transient disturbances, such as voltage fluctuations and load demand changes. Unlike traditional PI controllers with fixed parameters—which struggle to adjust to dynamic operating environments—the SMC sliding surface is constructed using the system’s mathematical model, enabling more precise and rapid tracking of reference signals and load fluctuations.

It should be emphasized that the use of SMC for improved robustness compared with PI control is well established in the literature; in this work, PI control and conventional reaching-law-based cascaded SMC are adopted as benchmark baselines to highlight the incremental benefit of the redesigned reaching law.

Simulation and experimental findings that compare the proposed approach with traditional reaching-law-based SMC and PI control show that, when facing the same operational demand changes, the proposed strategy delivers a notably quicker dynamic response for the DC-link voltage. Specifically, in simulation (Table 2), the proposed method achieved an adjustment time of 0.008 s (vs. 0.013 s for conventional SMC and 0.2 s for PI), reduced the current THD to 1.70% (vs. 2.57% and 3.04%), and lowered the chatter voltage to 0.15 V (vs. 0.20 V and 0.25 V). In experiments (Table 4), the DC-link voltage ripple was reduced to 0.009 V (vs. 0.011 V and 0.030 V) and the current THD was reduced to 3.12% (vs. 4.20% and 5.35%). Moreover, during a DC-link reference step (150 V to 180 V), the proposed method reached the new steady state within 0.085 s, which was faster than 0.113 s (traditional SMC) and 0.25 s (PI), as reported in the experimental results. These results confirm that the proposed control approach offers distinct benefits in DC-link voltage regulation speed, steady-state ripple, and current quality (THD), underscoring its fitness for real-world three-phase AC/DC converter deployments.