Hierarchical Hybrid Control and Communication Topology Optimization in DC Microgrids for Enhanced Performance
Abstract
1. Introduction
- (1)
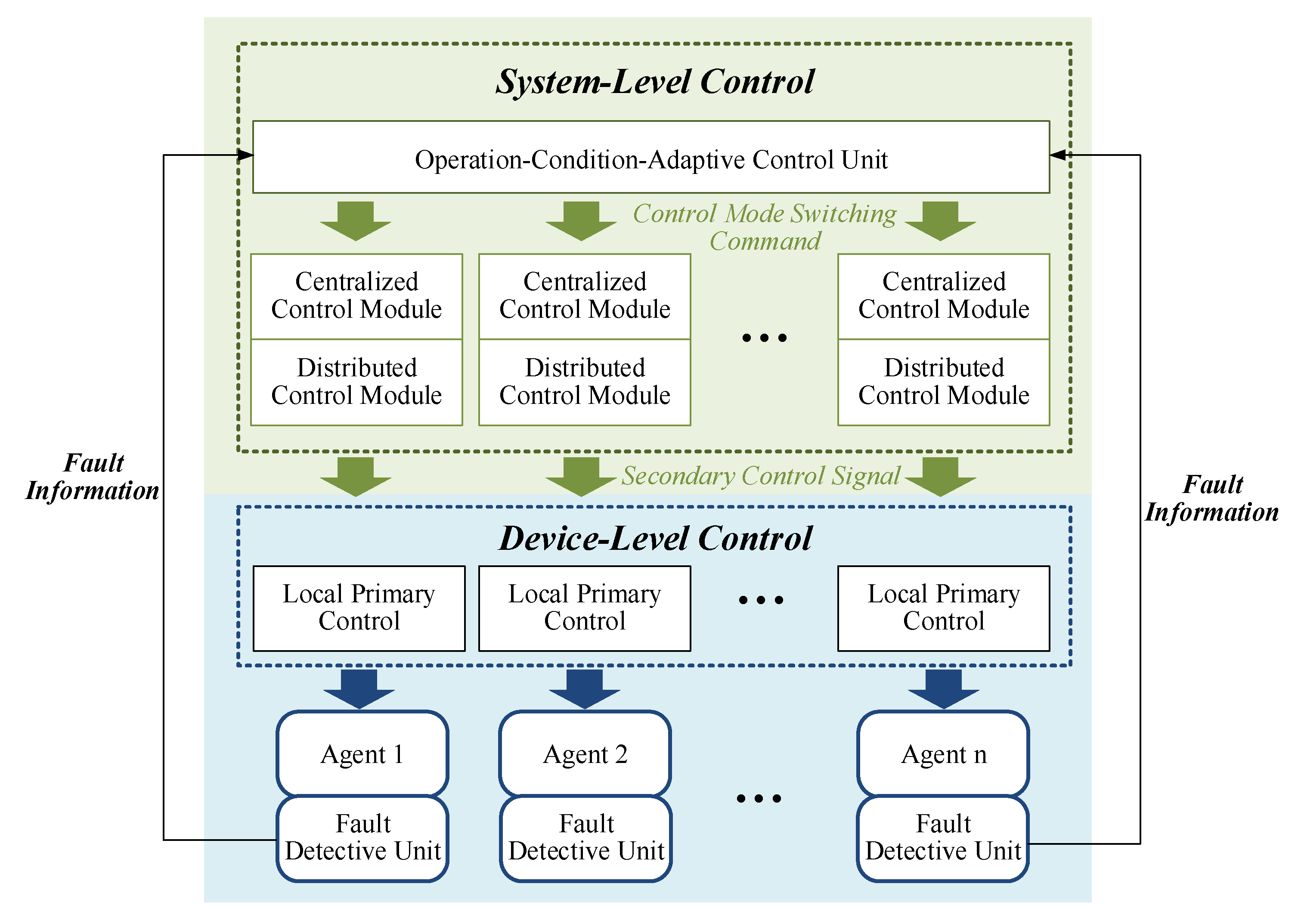
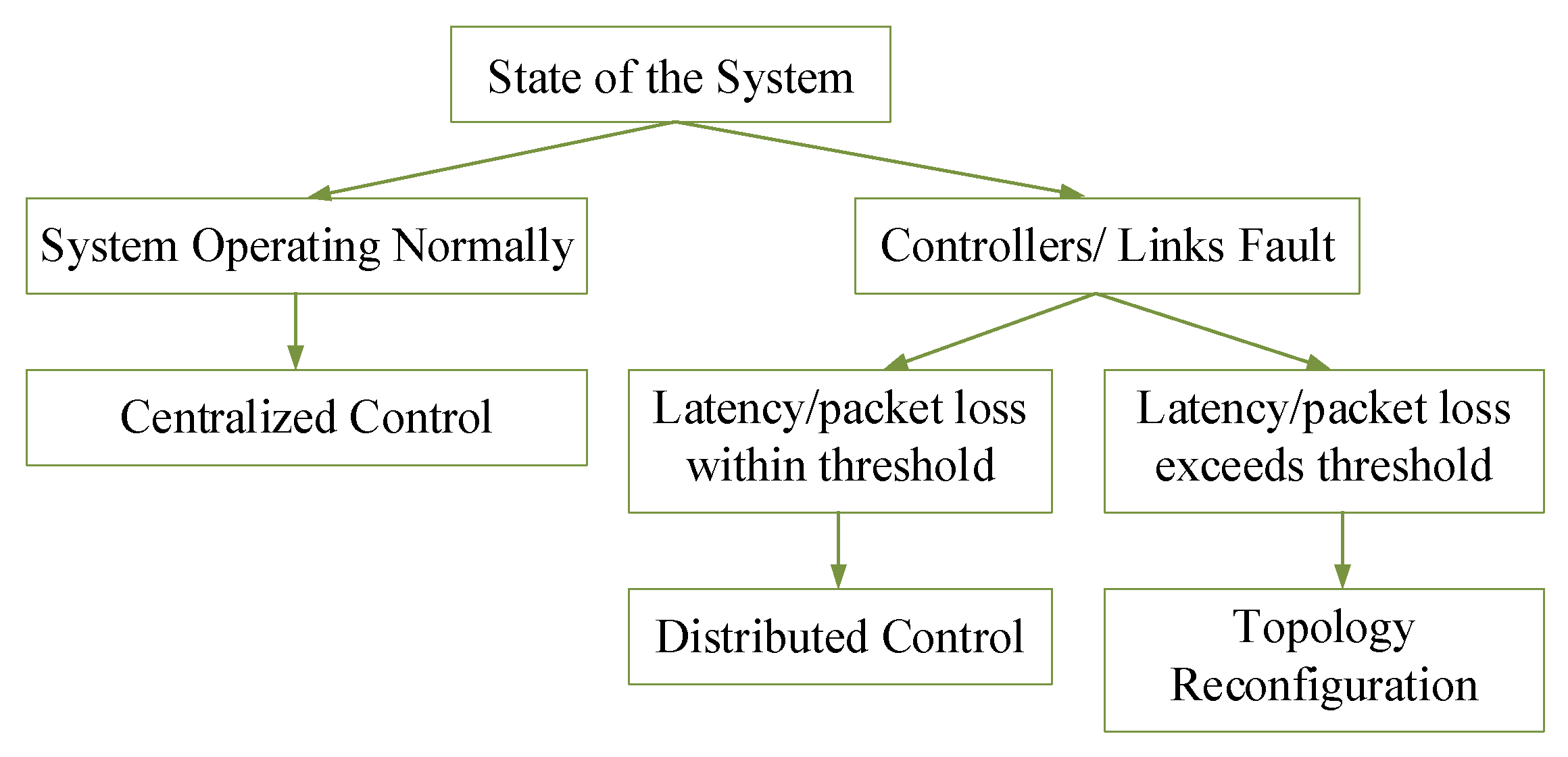
- Capitalizing on the complementary advantages of different control methods, an operation-condition-adaptive hierarchical control (OCAHC) strategy is proposed. The proposed strategy exhibits higher reliability than conventional centralized control under communication device failures, while achieving superior control performance compared to traditional distributed control during normal operating conditions. By incorporating a fault-detection logic module, the OCAHC framework enables automatic switching under different operating conditions, thereby ensuring enhanced control performance.
- (2)
- To address the trade-off between control performance and communication costs in consensus algorithms, a distributed communication topology optimization model is proposed. The proposed planning model formulates communication cost minimization as the objective function, subject to constraints including communication intensity, algorithm convergence rate, and control performance metrics. The model can incorporate various practical operational constraints during the offline planning phase, meeting the communication topology design requirements for distributed systems.
- (3)
- During the topology generation process, an optimization strategy is proposed based on node-degree computation and equivalent topology reduction to accelerate the convergence of the optimization algorithm.
2. Limitations of Conventional Control Methods
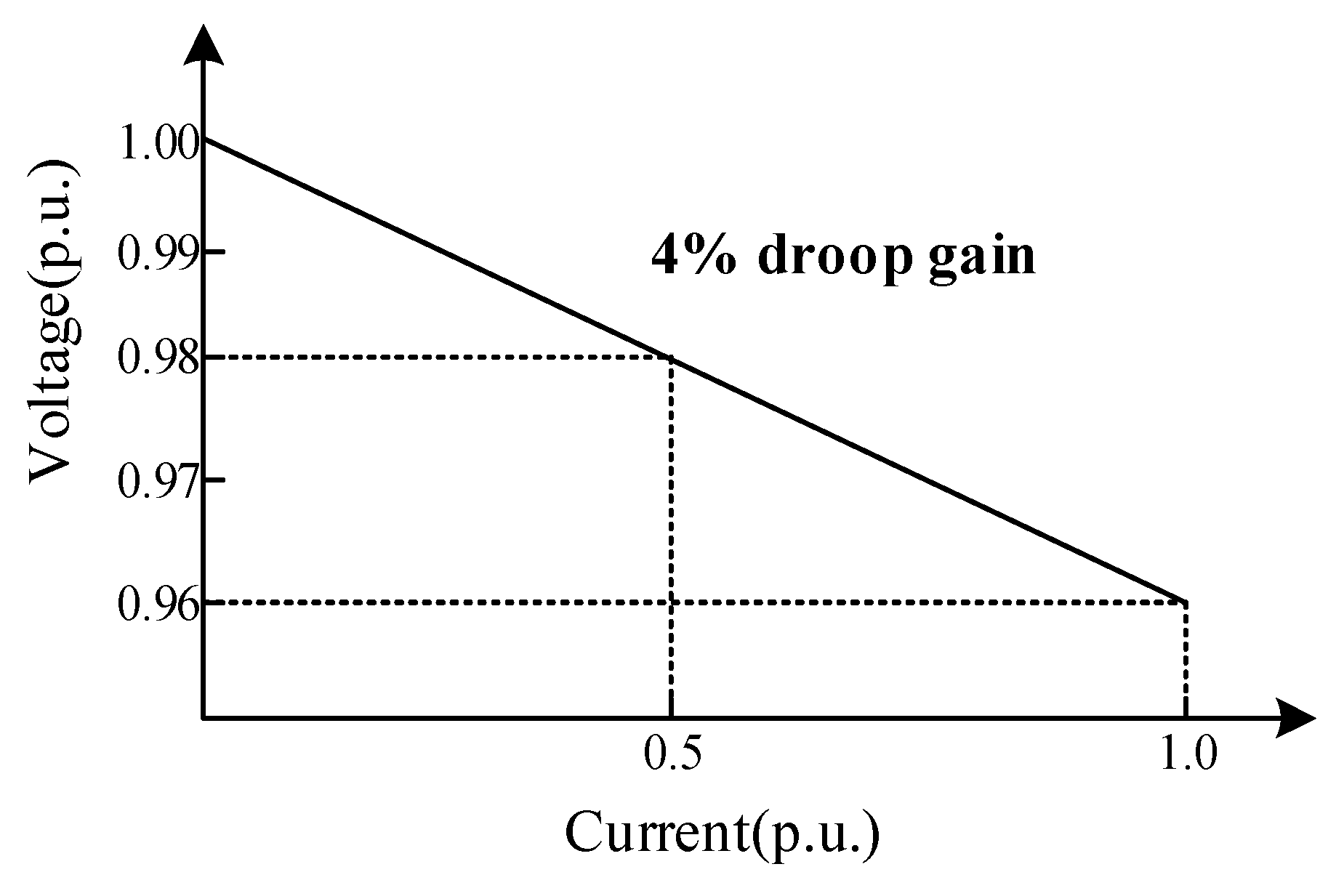
2.1. Droop Control
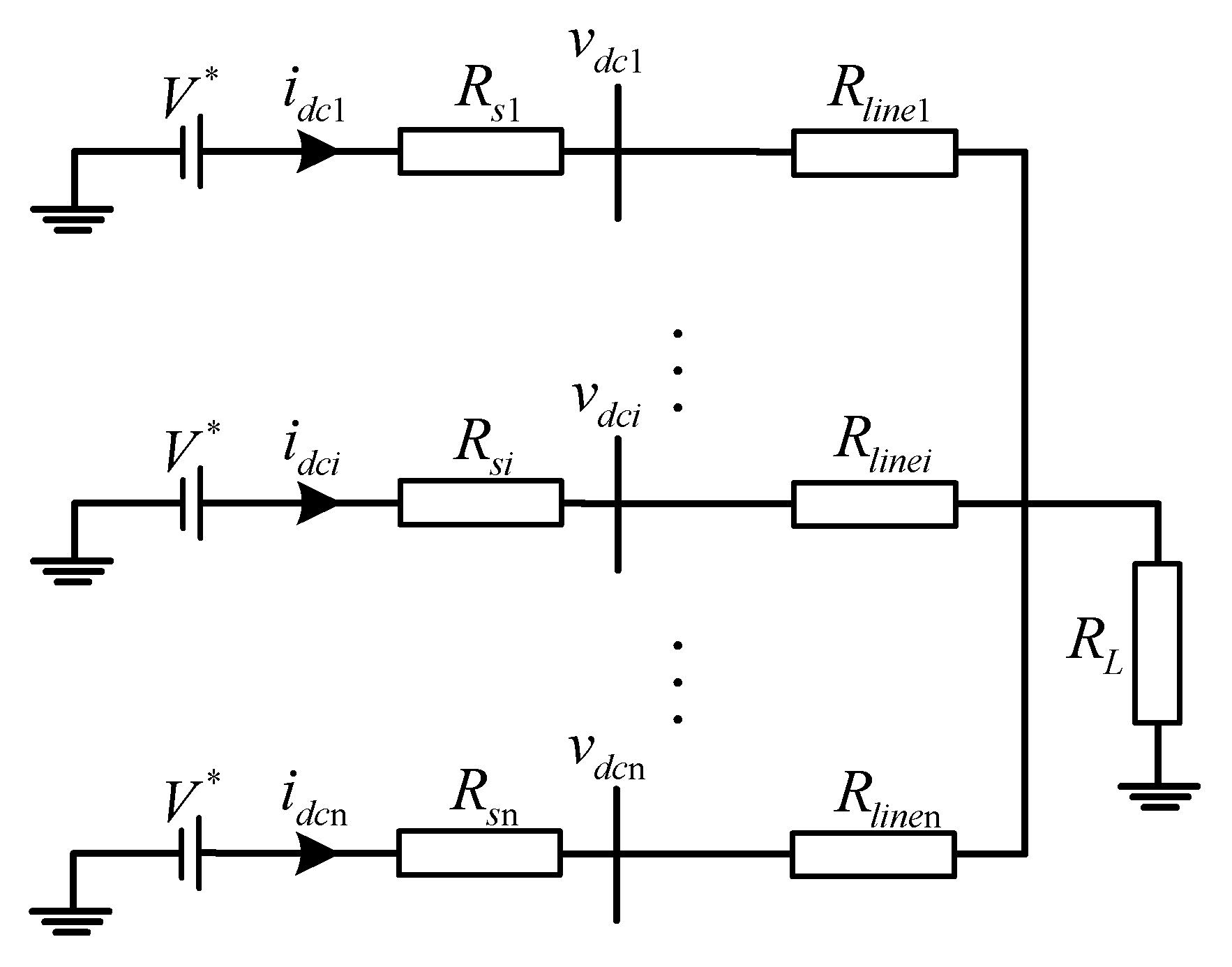
2.2. Centralized Control Strategy
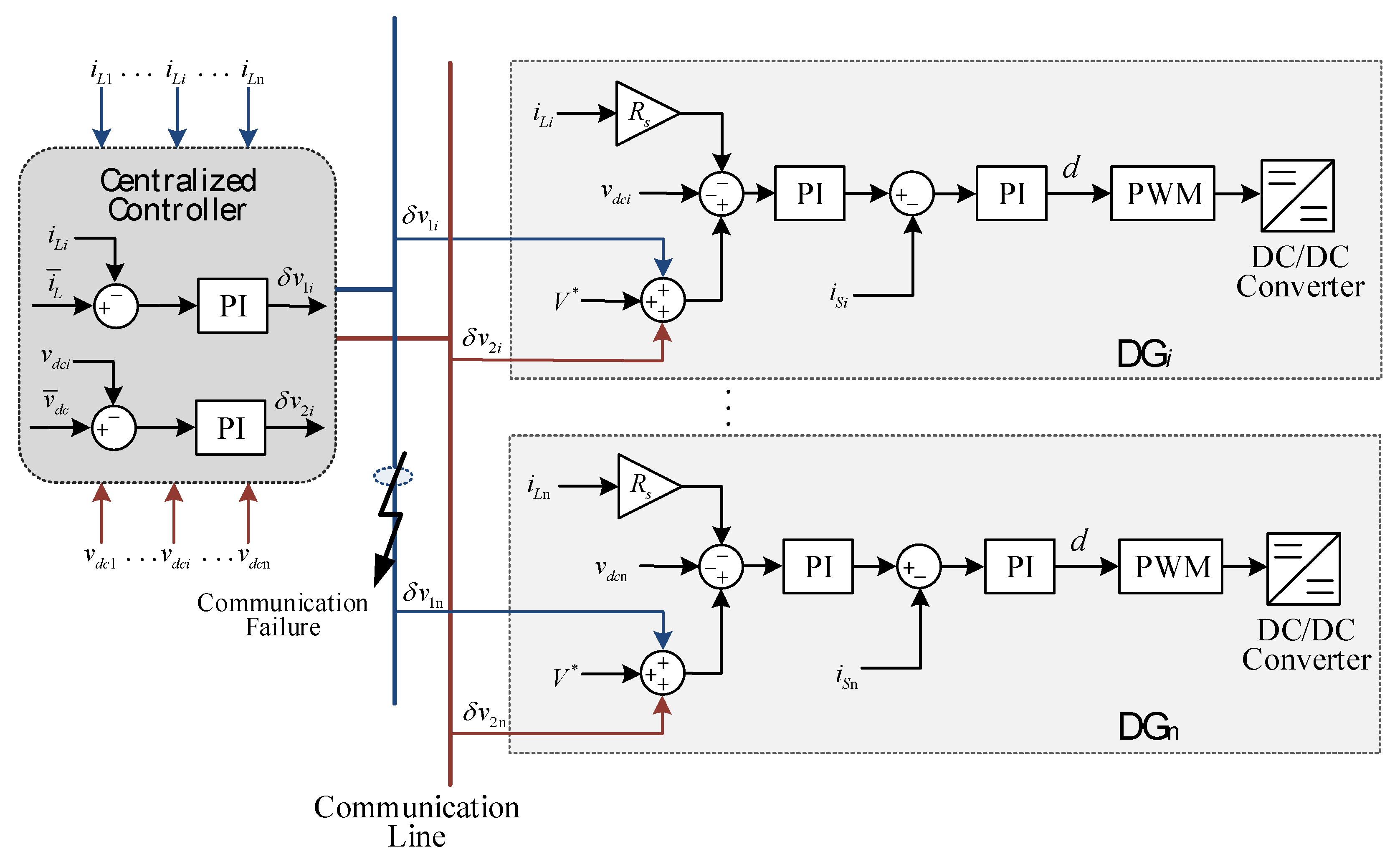
3. Operation-Condition-Adaptive Hierarchical Control
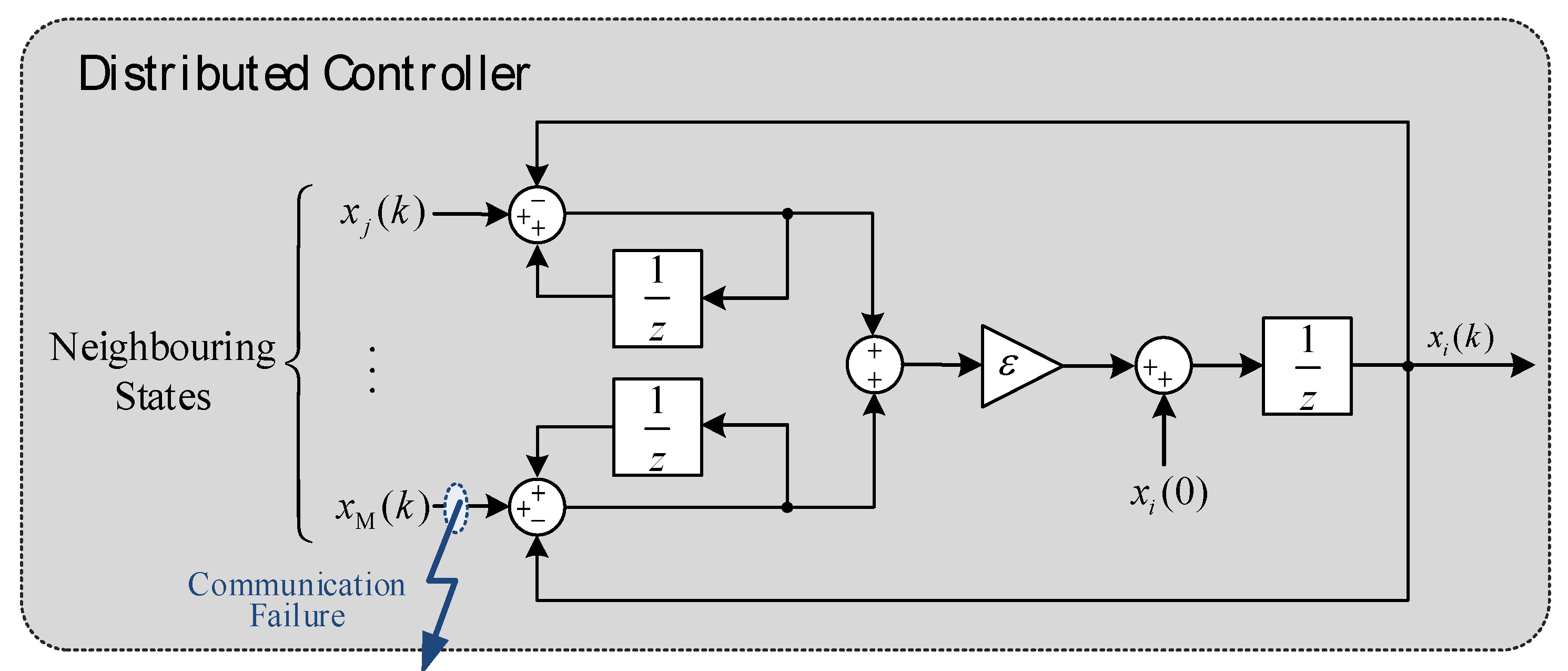
4. Distributed Control Strategy
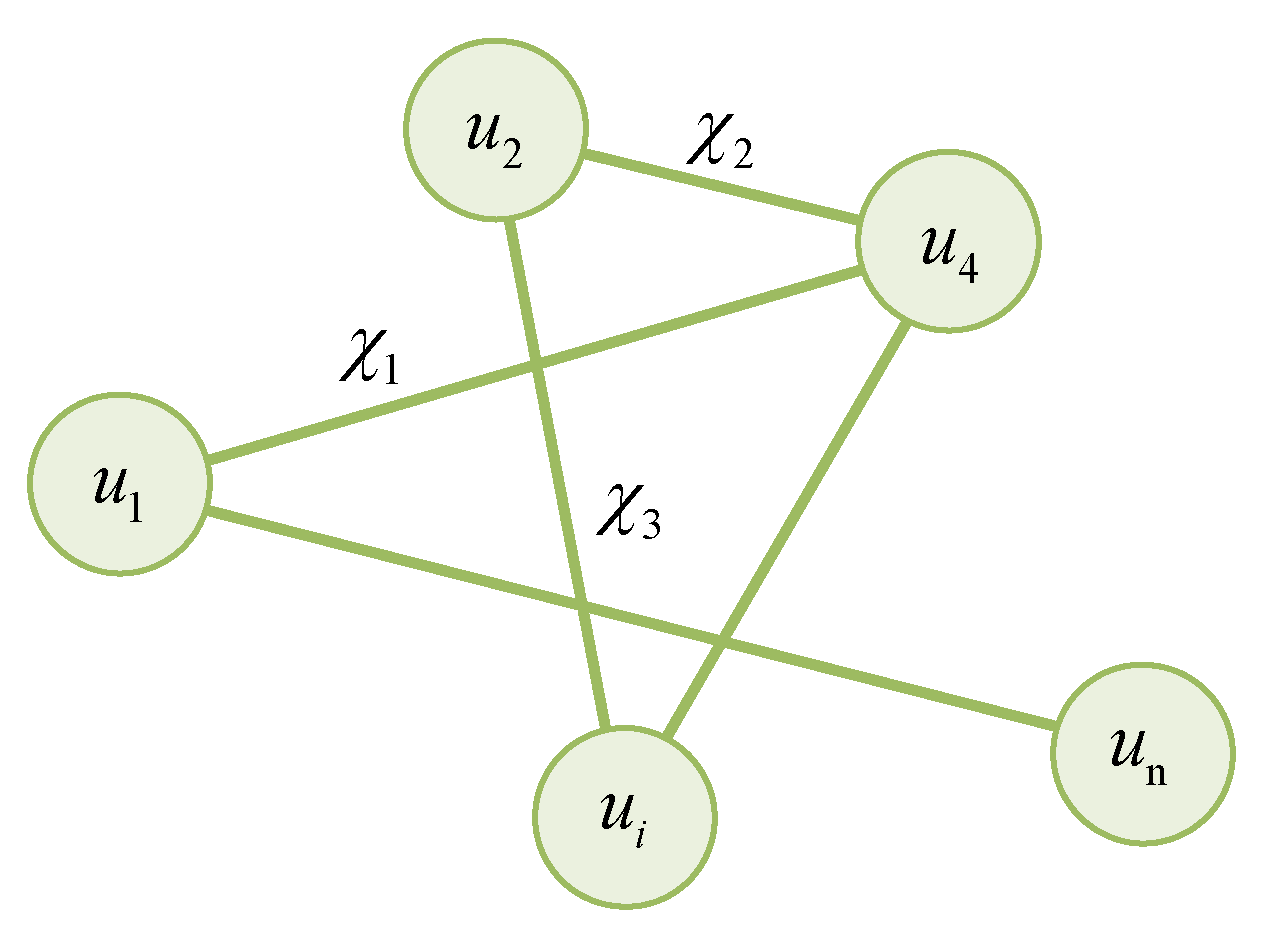
4.1. Graph Theory
4.2. Control Strategy Design
4.3. Communication Topology Optimization
4.3.1. Objective Function
4.3.2. Convergence Conditions
4.3.3. N-1 Resilient Topology Constraints
4.3.4. Control Performance Constraints
4.3.5. Communication Link Reliability Constraint
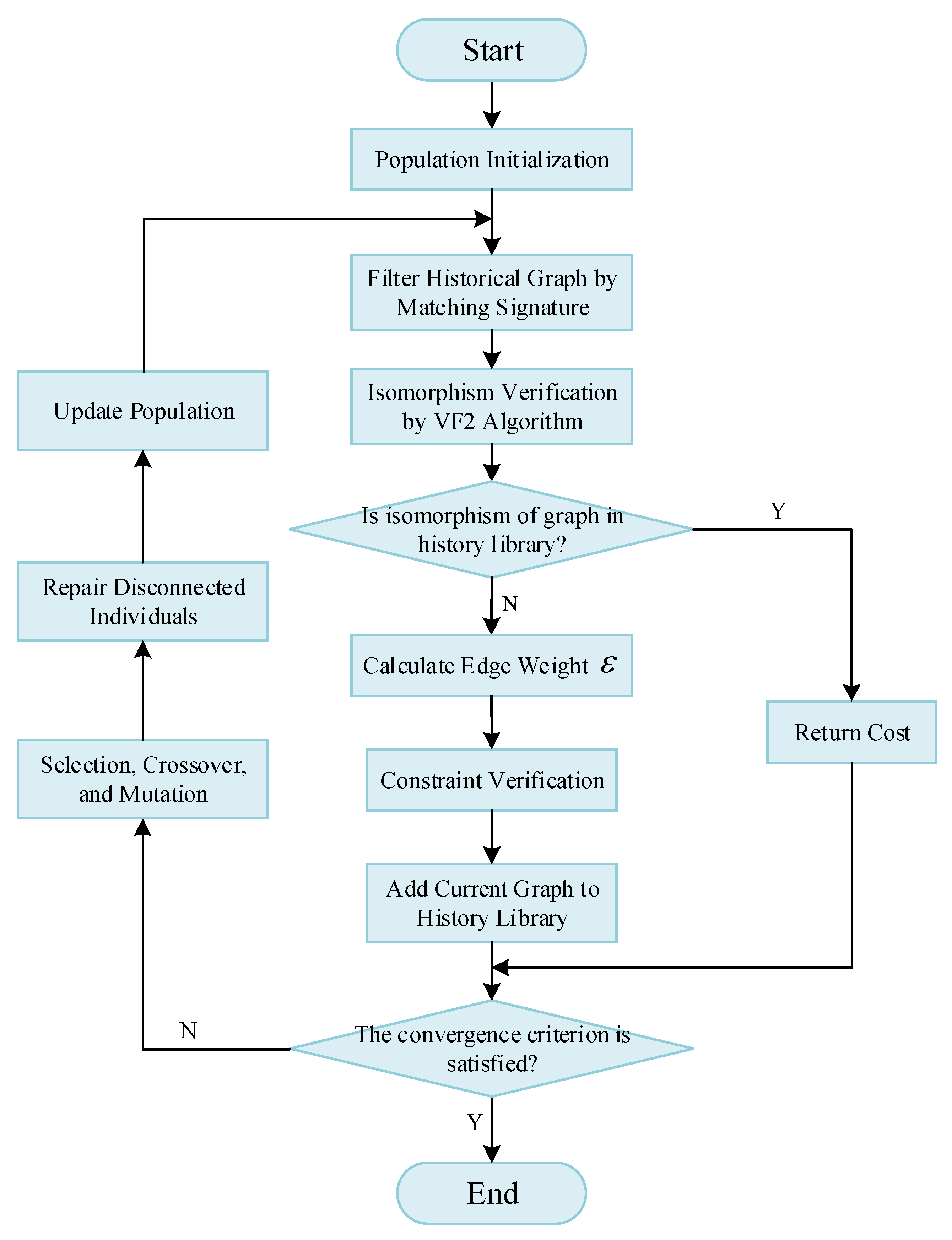
4.3.6. Efficient Solving Strategy for Planning Models
5. Reliability Analysis and MTBF Assessment
6. Case Study
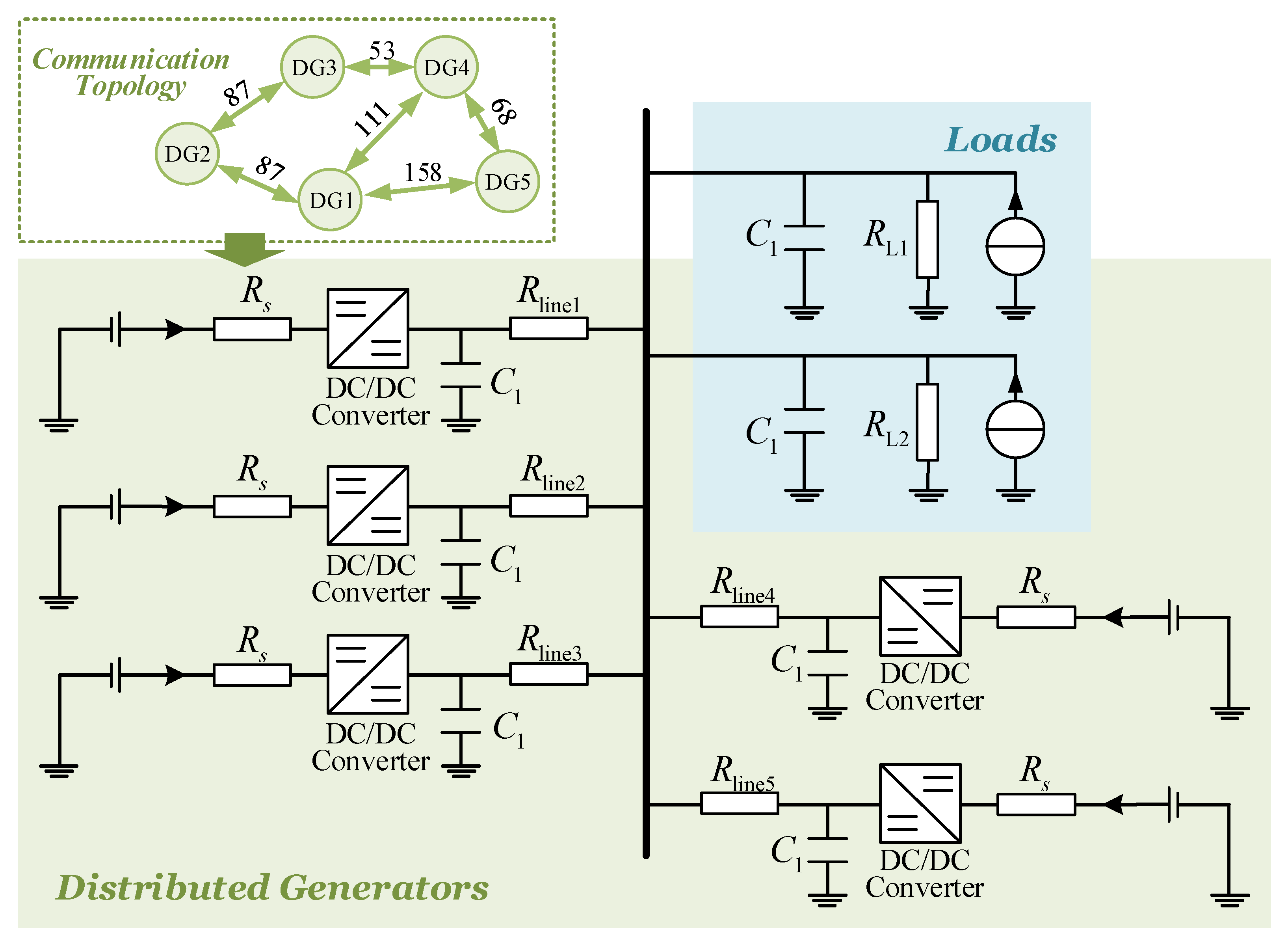
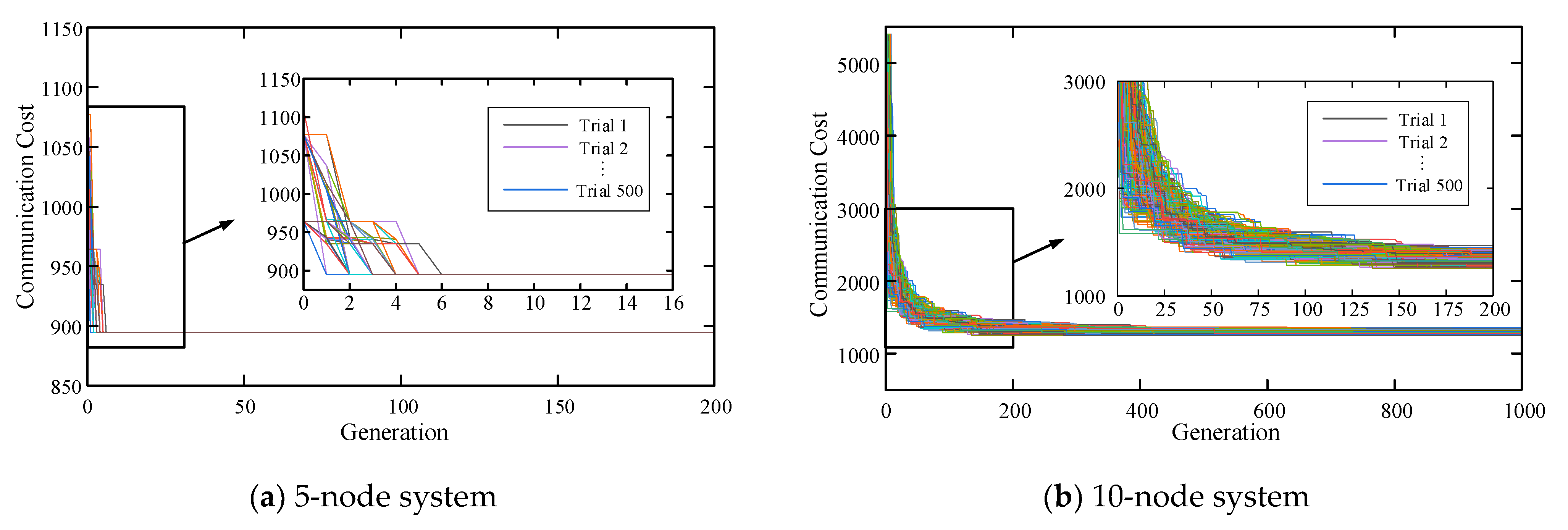
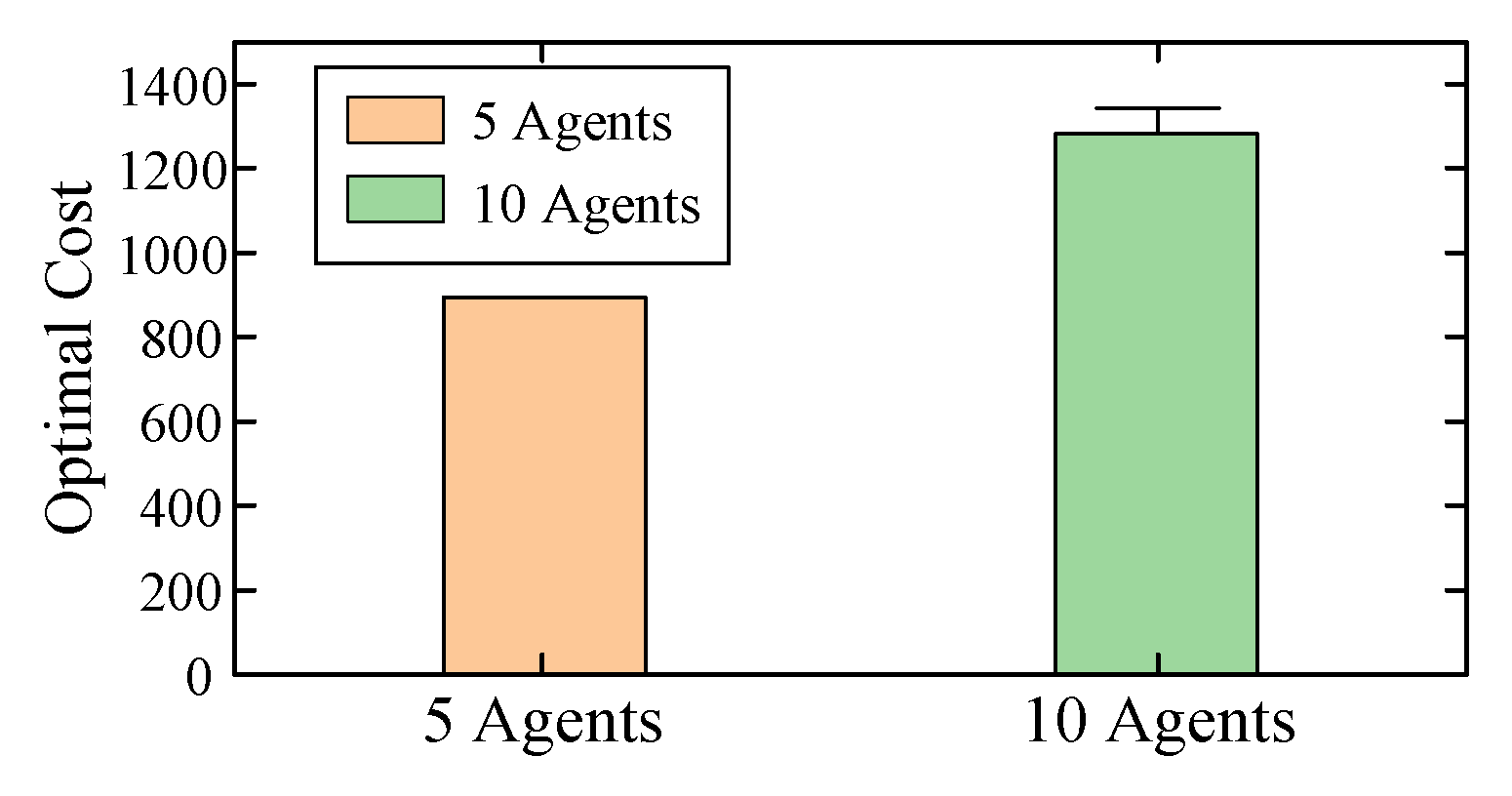
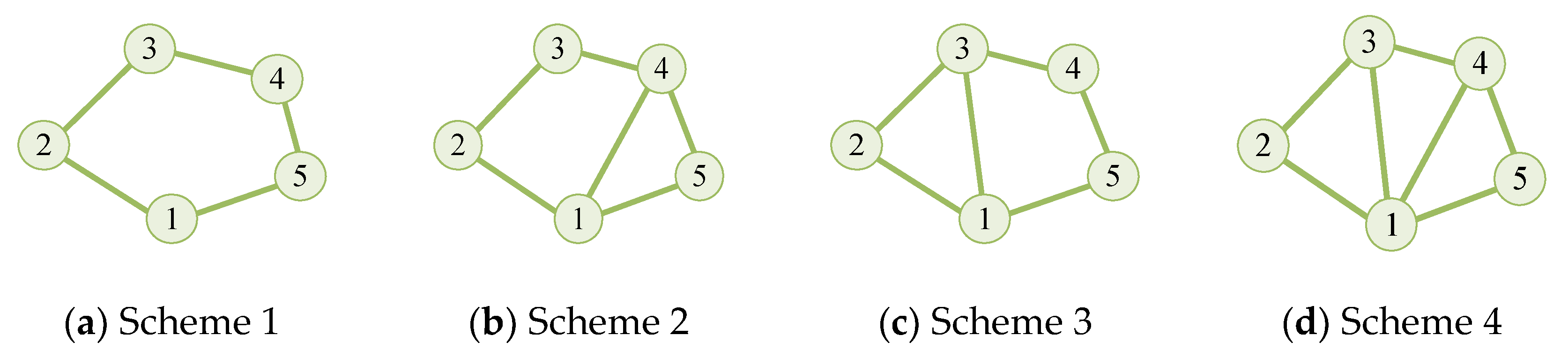
6.1. Analysis of Topology Planning
6.2. Performance of Conventional Control Method
6.3. Validation of Proposed Method
6.3.1. N-1 Condition
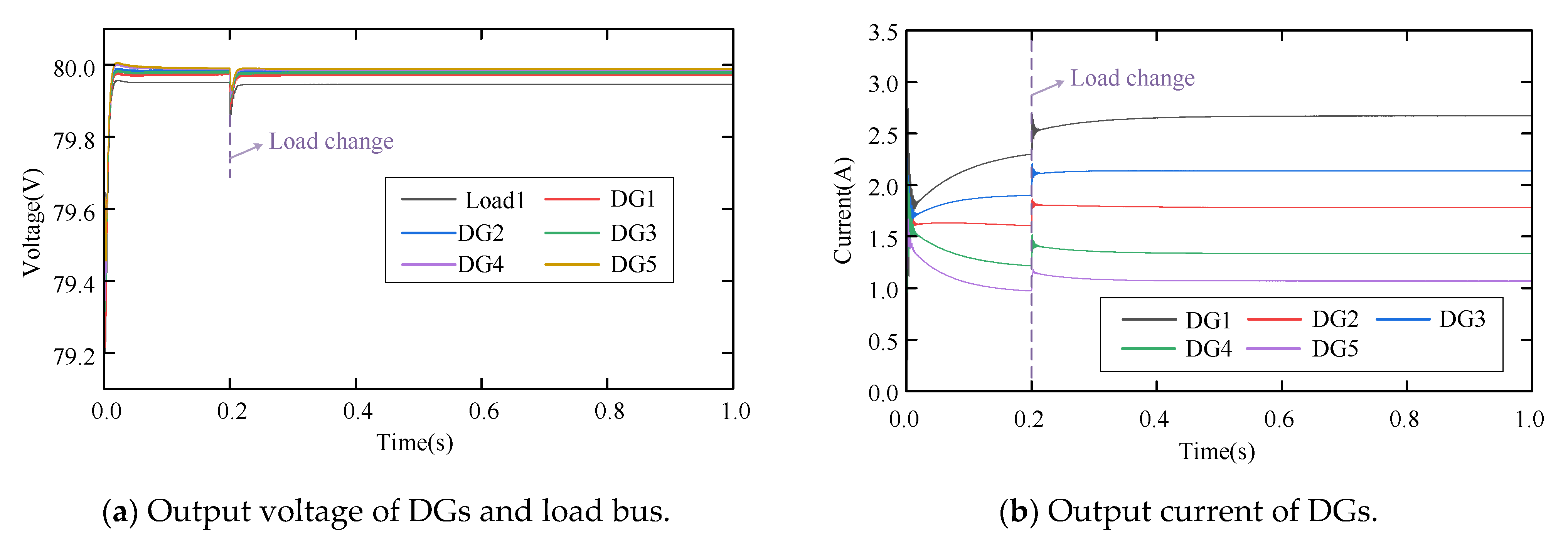
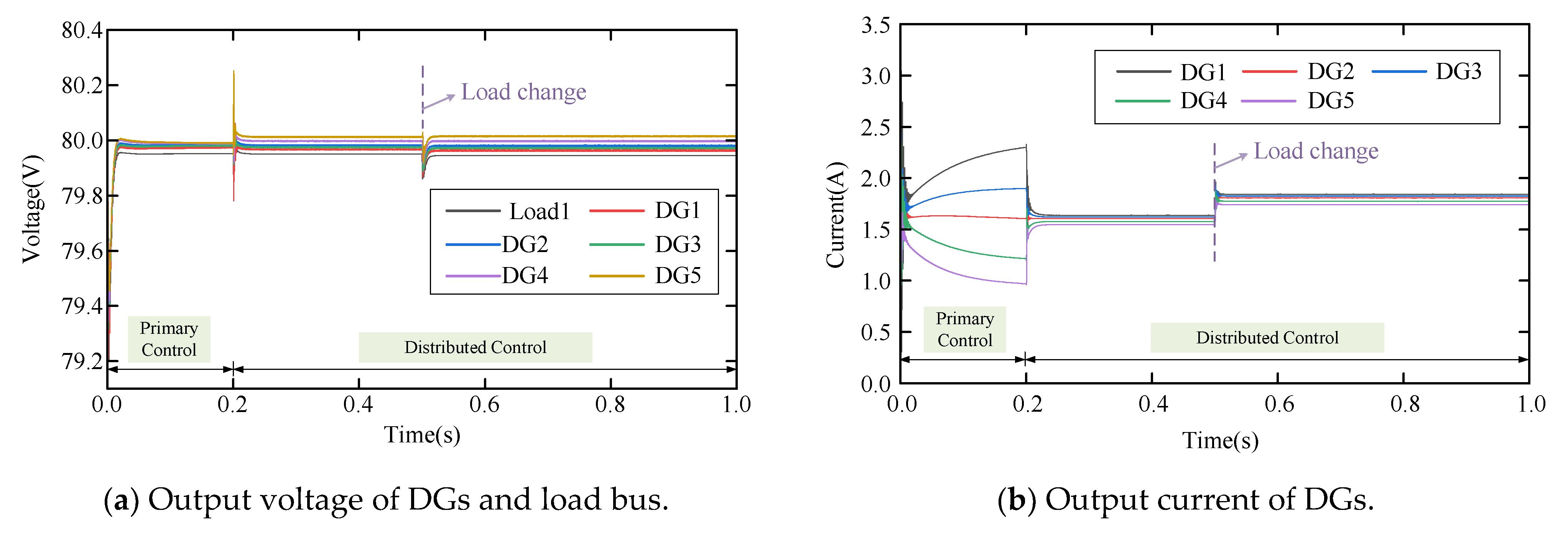
6.3.2. Step-Varying Load
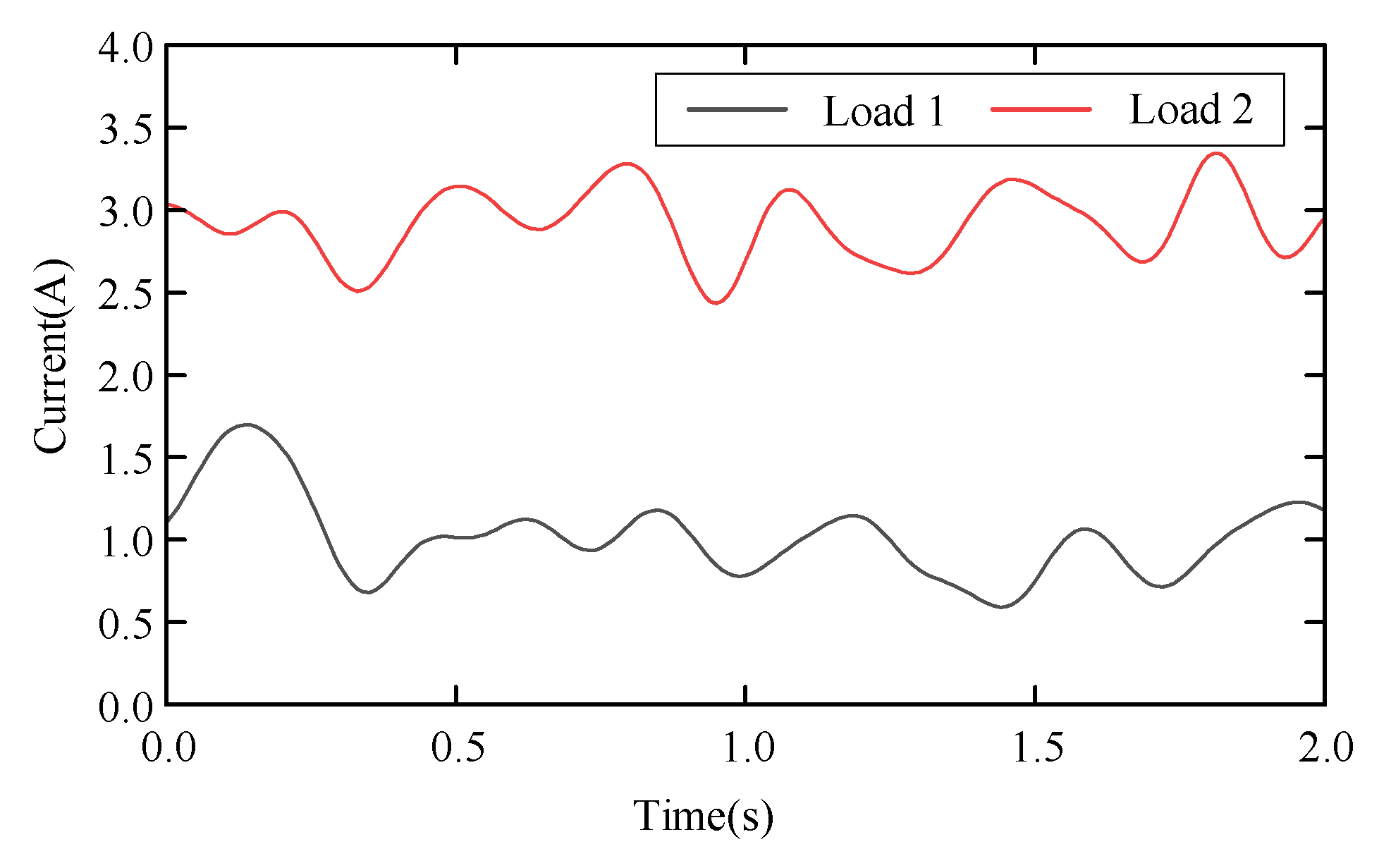
6.3.3. Slow-Varying Load
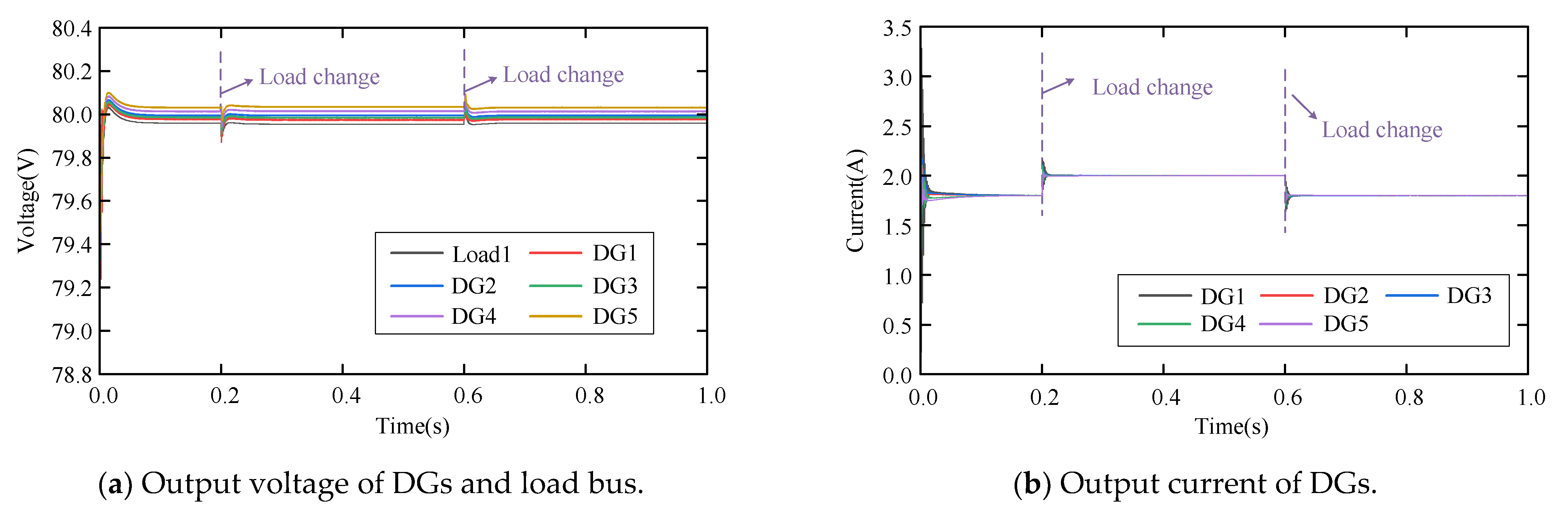
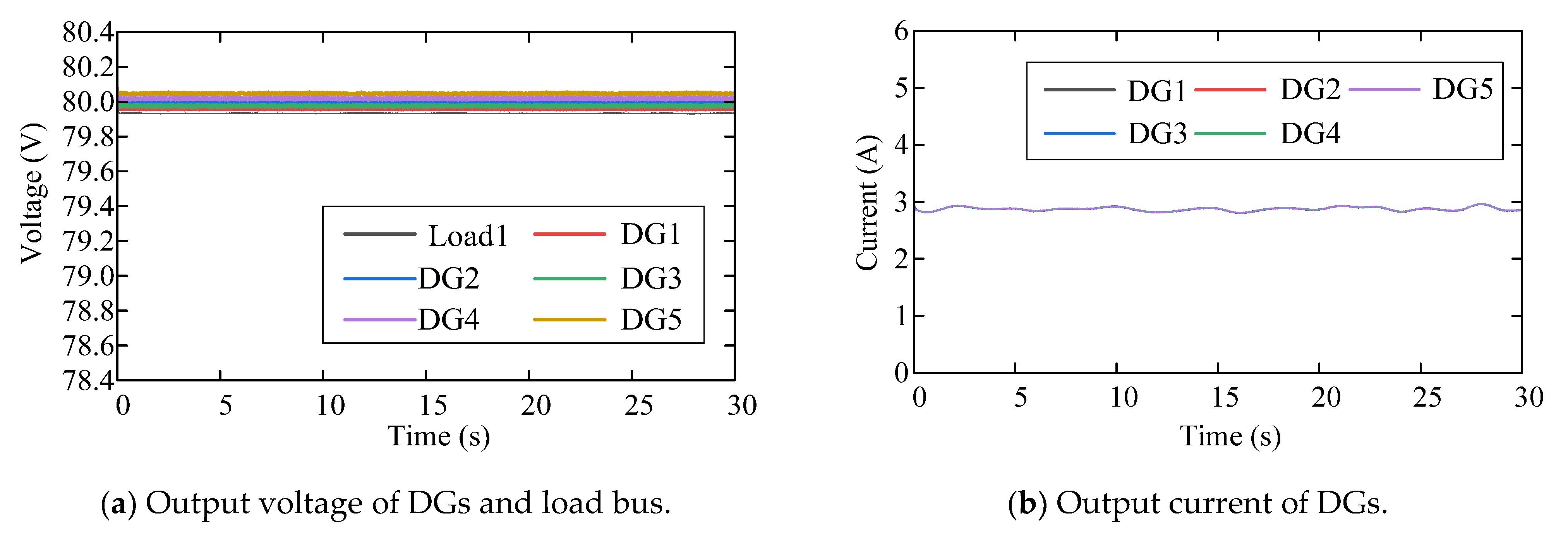
6.3.4. Long-Term Load Variation
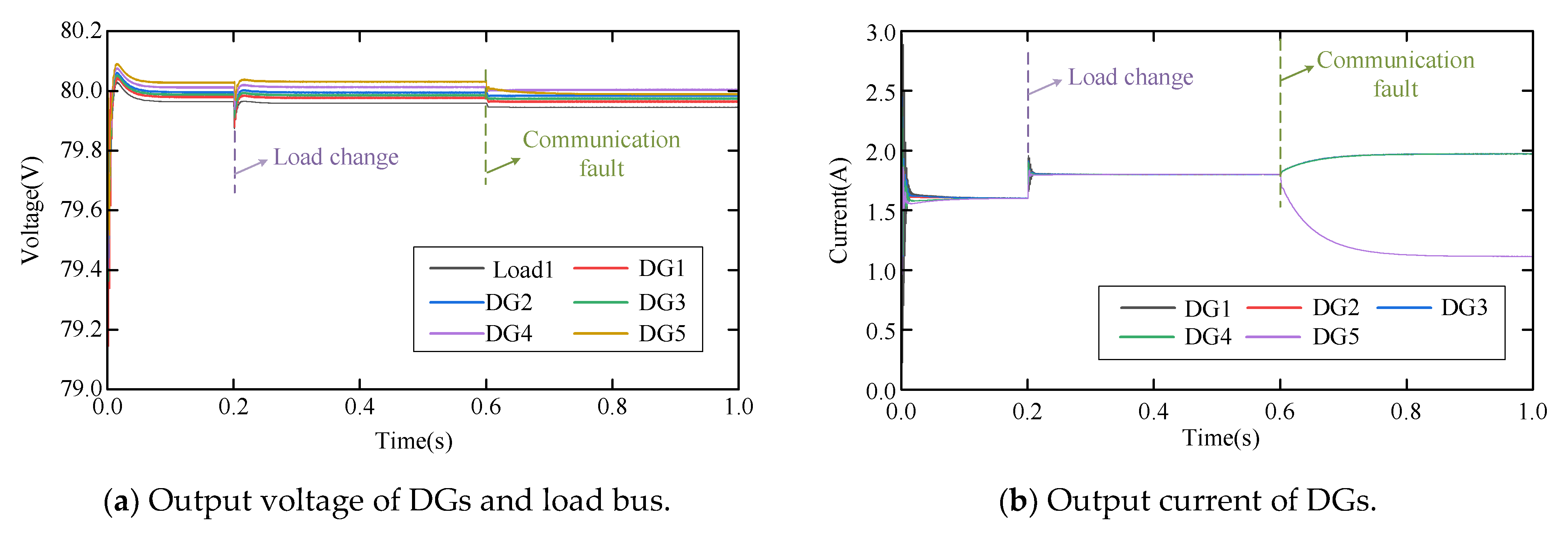
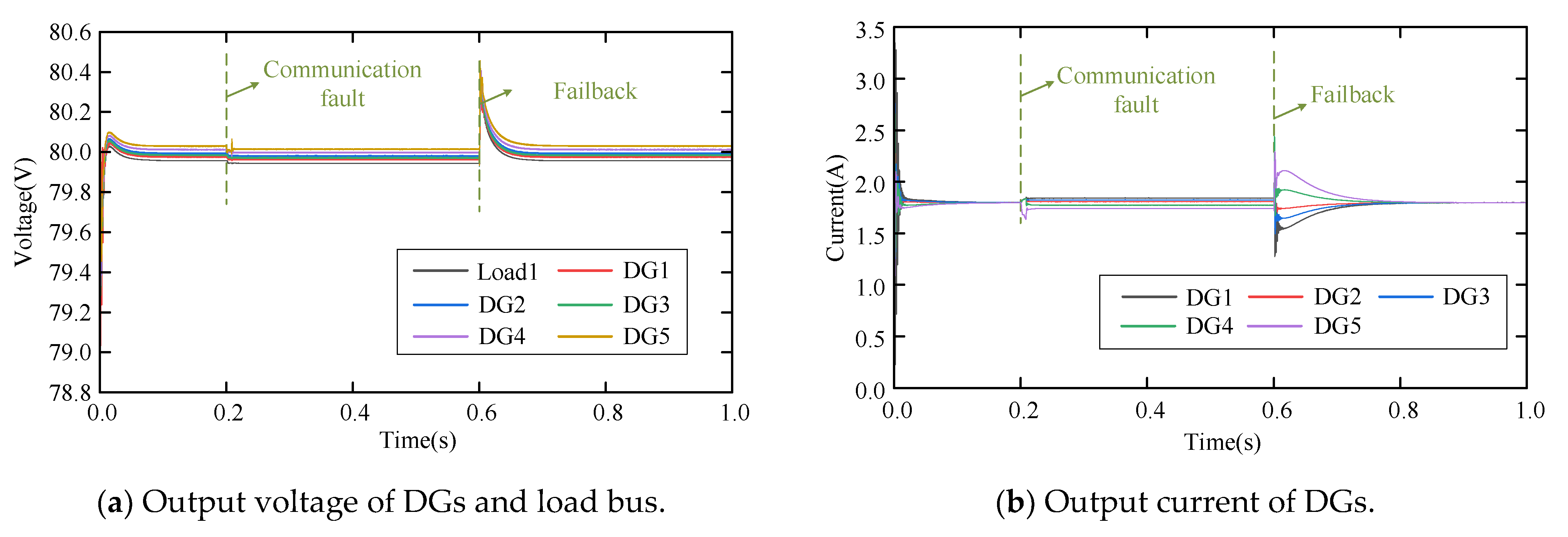
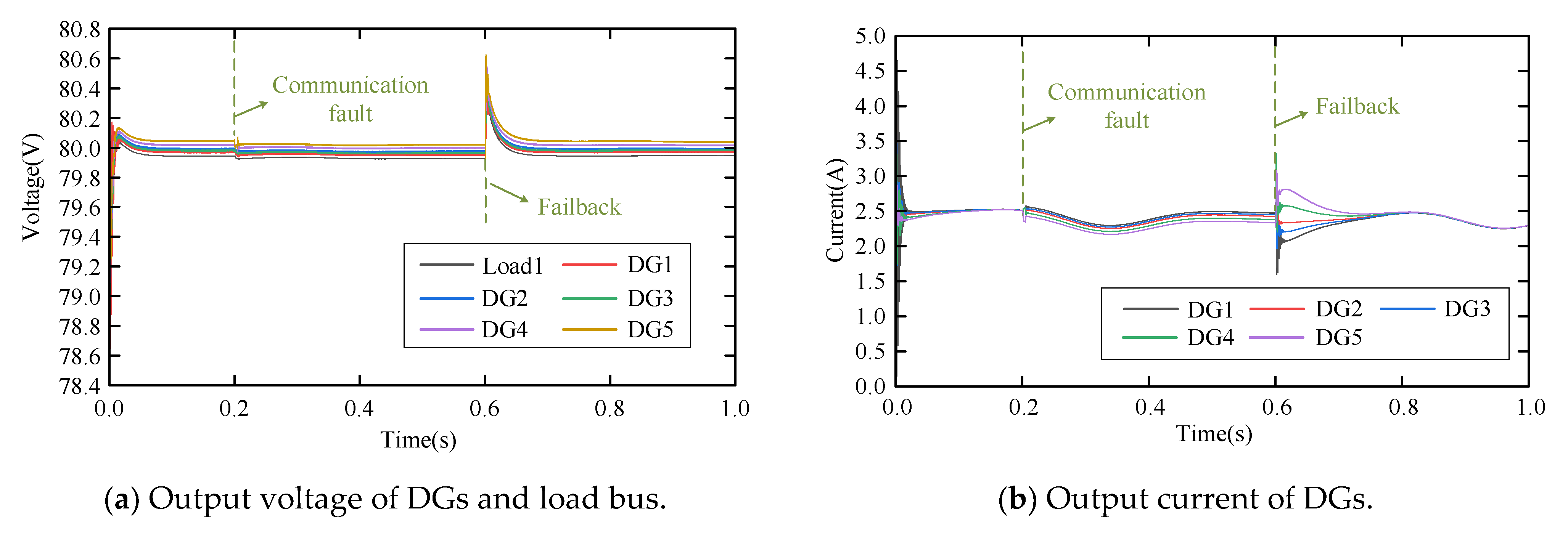
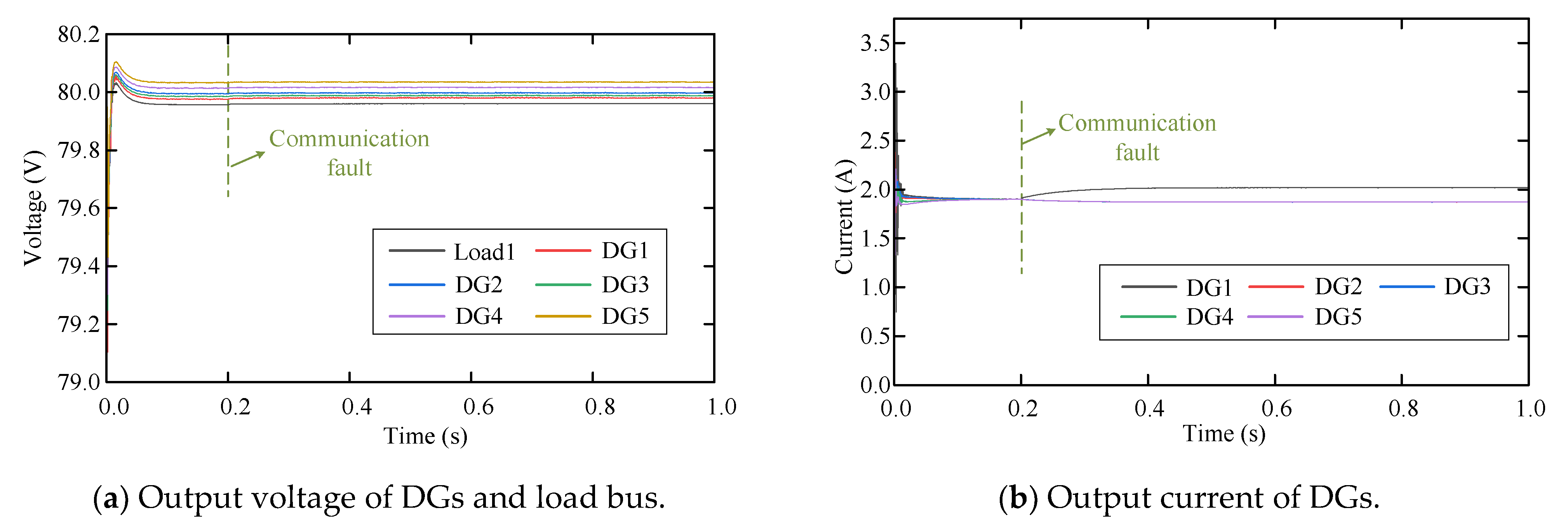
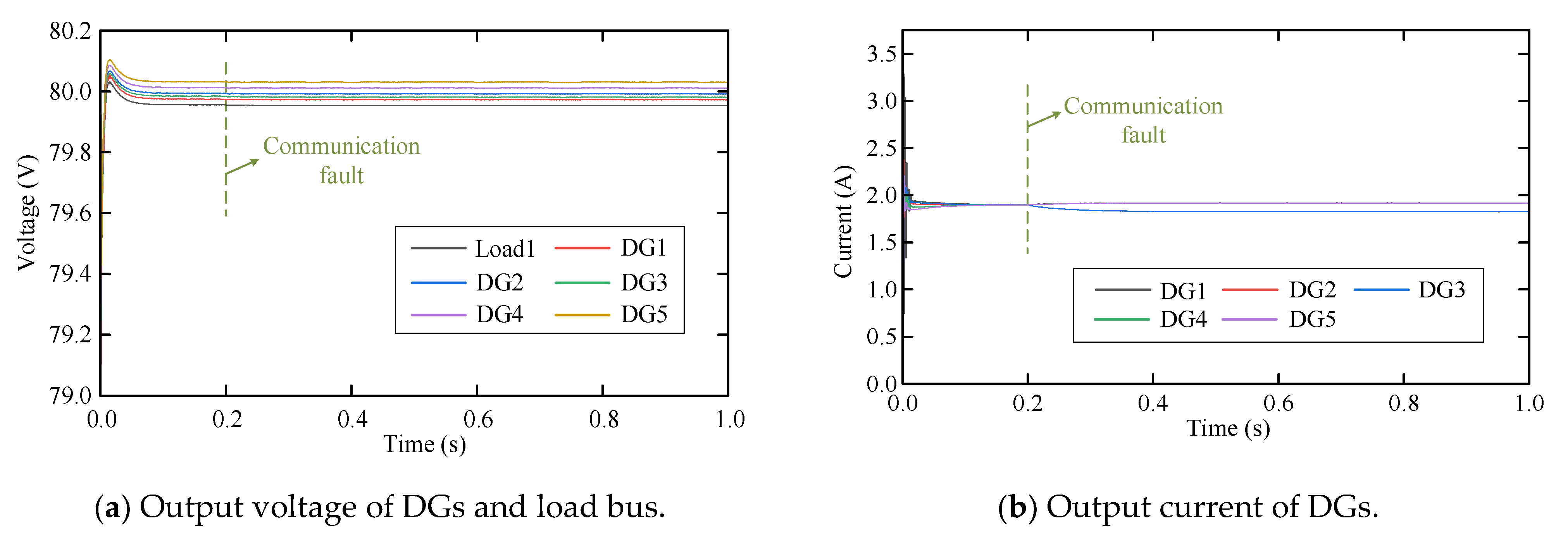
6.3.5. Validation of Fault Detection Logic
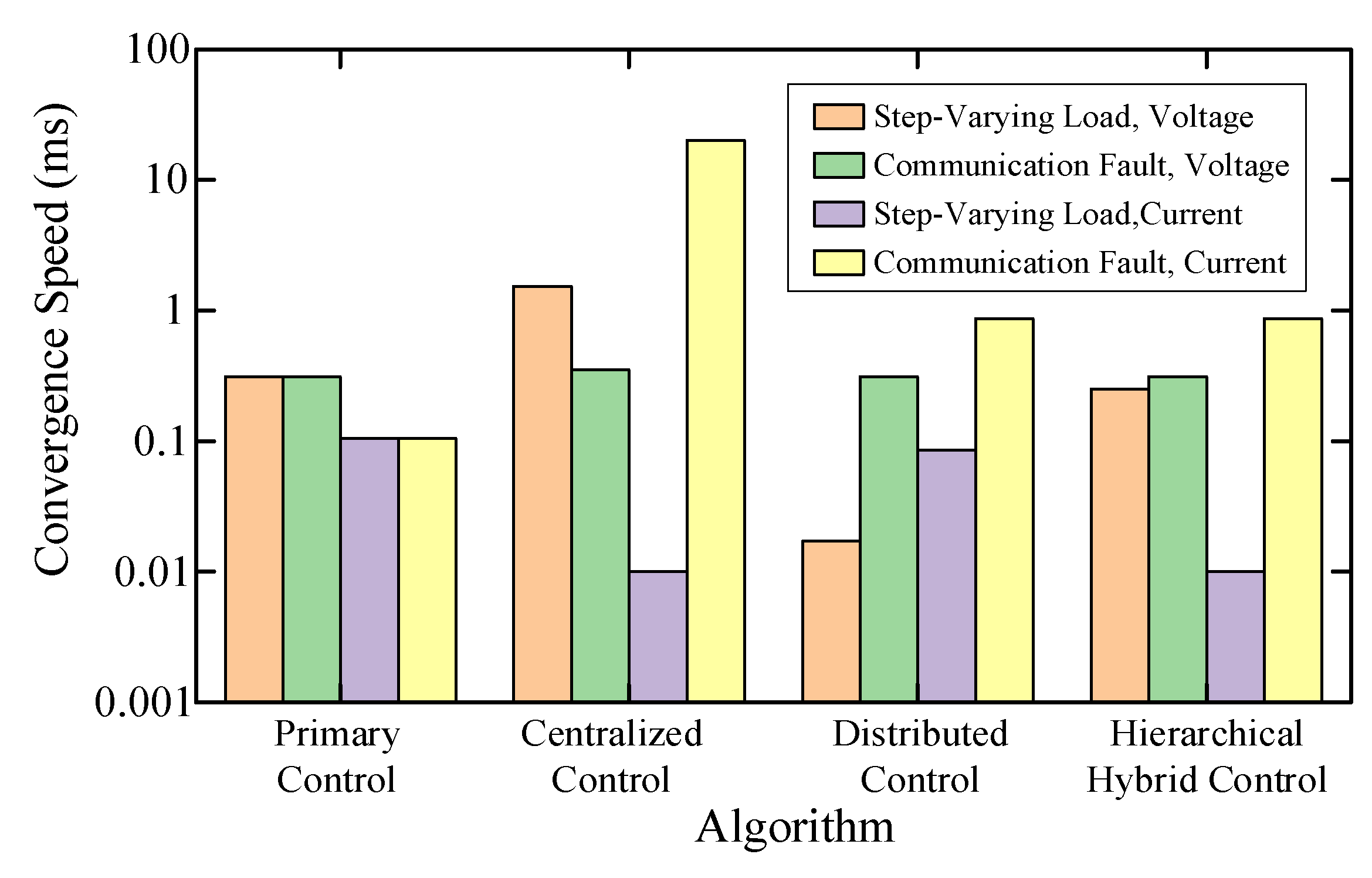
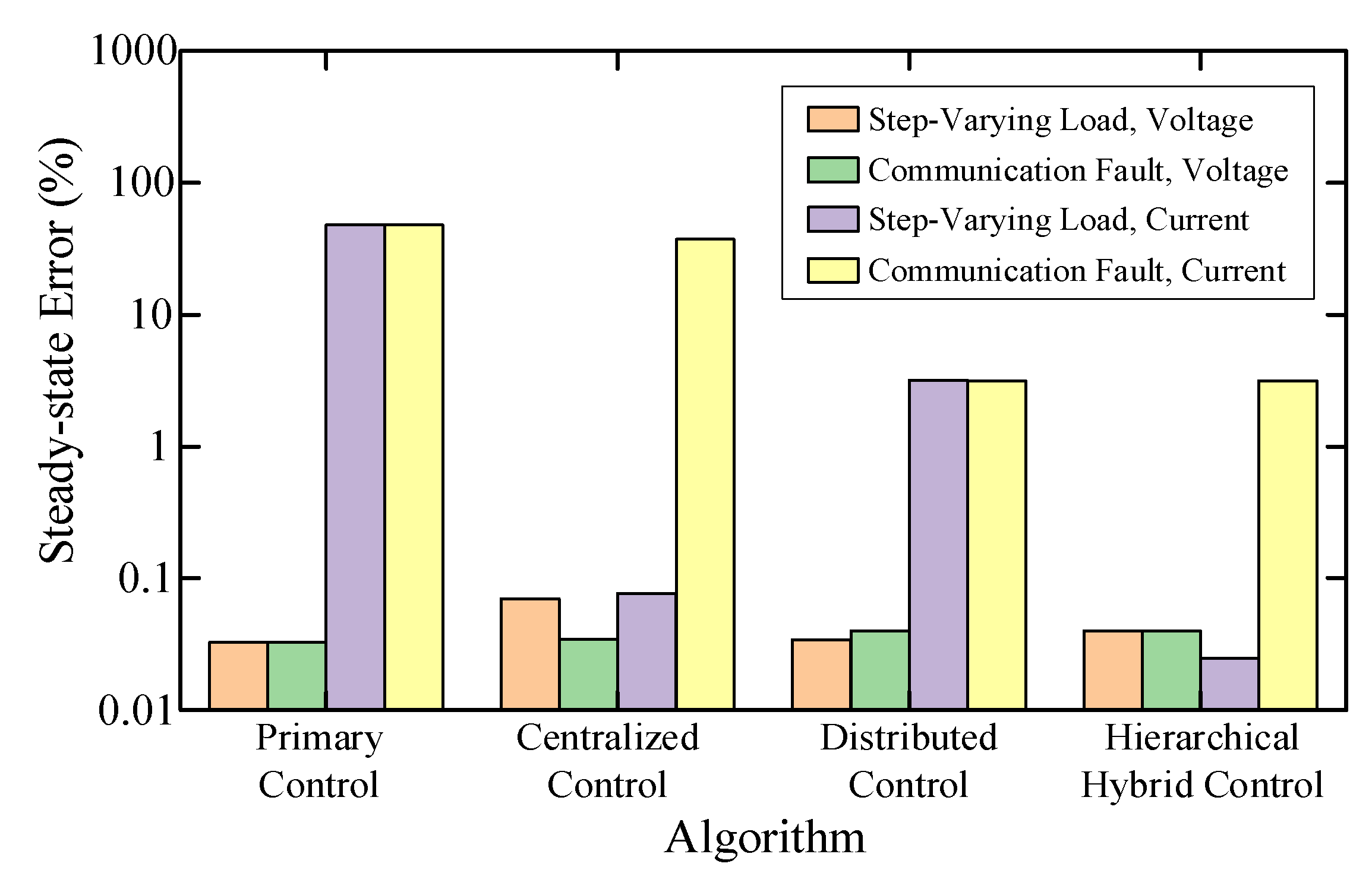
6.3.6. Overall Performance
6.3.7. Scalability and Robustness Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Yang, Y.; Li, Q.; Gao, W.; Qian, F.; Song, L. Economic optimization of microgrids based on peak shaving and CO2 reduction effect: A case study in Japan. J. Clean. Prod. 2021, 321, 128973. [Google Scholar] [CrossRef]
- Dou, Y.; Chi, M.; Liu, Z.; Wen, G.; Sun, Q. Distributed Secondary Control for Voltage Regulation and Optimal Power Sharing in DC Microgrids. IEEE Trans. Control Syst. Technol. 2022, 30, 2561–2572. [Google Scholar] [CrossRef]
- Cucuzzella, M.; Trip, S.; De Persis, C.; Cheng, X.; Ferrara, A.; Van Der Schaft, A. A Robust Consensus Algorithm for Current Sharing and Voltage Regulation in DC Microgrids. IEEE Trans. Control Syst. Technol. 2019, 27, 1583–1595. [Google Scholar] [CrossRef]
- Gao, F.; Kang, R.; Cao, J.; Yang, T. Primary and secondary control in DC microgrids: A review. J. Mod. Power Syst. Clean Energy 2019, 7, 227–242. [Google Scholar] [CrossRef]
- Tah, A.; Das, D. An Enhanced Droop Control Method for Accurate Load Sharing and Voltage Improvement of Isolated and Interconnected DC Microgrids. IEEE Trans. Sustain. Energy 2016, 7, 1194–1204. [Google Scholar] [CrossRef]
- Mohammed, N.; Callegaro, L.; Ciobotaru, M.; Guerrero, J.M. Accurate power sharing for islanded DC microgrids considering mismatched feeder resistances. Appl. Energy 2023, 340, 121060. [Google Scholar] [CrossRef]
- Mokhtar, M.; Marei, M.I.; El-Sattar, A.A. Improved Current Sharing Techniques for DC Microgrids. Electr. Power Compon. Syst. 2018, 46, 757–767. [Google Scholar] [CrossRef]
- Peyghami, S.; Mokhtari, H.; Davari, P.; Loh, P.C.; Blaabjerg, F. On Secondary Control Approaches for Voltage Regulation in DC Microgrids. IEEE Trans. Ind. Appl. 2017, 53, 4855–4862. [Google Scholar] [CrossRef]
- Wan, Q.; Zheng, S. Distributed cooperative secondary control based on discrete consensus for DC microgrid. Energy Rep. 2022, 8, 8523–8533. [Google Scholar] [CrossRef]
- Chen, Y.; Wan, K.; Zhao, J.; Yu, M. Accurate consensus-based distributed secondary control with tolerance of communication delays for DC microgrids. Int. J. Electr. Power Energy Syst. 2024, 155, 109636. [Google Scholar] [CrossRef]
- Meng, L.; Dragicevic, T.; Roldan-Perez, J.; Vasquez, J.C.; Guerrero, J.M. Modeling and Sensitivity Study of Consensus Algorithm-Based Distributed Hierarchical Control for DC Microgrids. IEEE Trans. Smart Grid 2016, 7, 1504–1515. [Google Scholar] [CrossRef]
- Chen, X.; Gao, S.; Zhang, S.; Zhao, Y. On topology optimization for event-triggered consensus with triggered events reducing and convergence rate improving. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 1223–1227. [Google Scholar] [CrossRef]
- Xu, T.; Tan, Y.Y.; Gao, S.; Zhan, X. Interaction topology optimization by adjustment of edge weights to improve the consensus convergence and prolong the sampling period for a multi-agent system. Appl. Math. Comput. 2025, 500, 129428. [Google Scholar] [CrossRef]
- MathWorks. What Is Droop Control? Available online: https://www.mathworks.com/discovery/droop-control.html (accessed on 5 August 2025).
- Lu, X.; Guerrero, J.M.; Sun, K.; Vasquez, J.C. An improved droop control method for dc microgrids based on low bandwidth communication with dc bus voltage restoration and enhanced current sharing accuracy. IEEE Trans. Power Electron. 2014, 29, 1800–1812. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Liu, J.; Wu, Y.; Sun, C. Bipartite finite-time consensus of multi-agent systems with intermittent communication via event-triggered impulsive control. Neurocomputing 2024, 598, 127970. [Google Scholar] [CrossRef]
- Heinzelman, W.B.; Chandrakasan, A.P.; Balakrishnan, H. An application-specific protocol architecture for wireless microsensor networks. IEEE Trans. Wirel. Commun. 2002, 1, 660–670. [Google Scholar] [CrossRef]
- Xiao, L.; Boyd, S. Fast linear iterations for distributed averaging. Syst. Control. Lett. 2004, 53, 65–78. [Google Scholar] [CrossRef]
- Esrafilian, O.; Bayerlein, H.; Gesbert, D. Model-aided deep reinforcement learning for sample-efficient UAV trajectory design in IoT networks. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Jiang, X.; Bunke, H. Optimal quadratic-time isomorphism of ordered graphs. Pattern Recognit. 1999, 32, 1273–1283. [Google Scholar] [CrossRef]
- OEIS Foundation Inc. Sequence A000088: Number of Graphs on n Unlabeled Nodes. In the On-Line Encyclopedia of Integer Sequences. Available online: https://oeis.org/A000088 (accessed on 5 August 2025).
- Manso, B.A.S.; Leite da Silva, A.M.; Milhorance, A.; Assis, F.A. Composite reliability assessment of systems with grid-edge renewable resources via quasi-sequential Monte Carlo and cross-entropy techniques. IET Gener. Transm. Distrib. 2024, 18, 326–336. [Google Scholar] [CrossRef]
- Shu, H.; Dong, H.; Zhao, H.; Xu, C.; Yang, Y.; Zhao, X. Reliability analysis of electrical system in ±800 kV VSC-DC converter station. Electr. Power Autom. Equip. 2023, 43, 119–126. (In Chinese) [Google Scholar] [CrossRef]

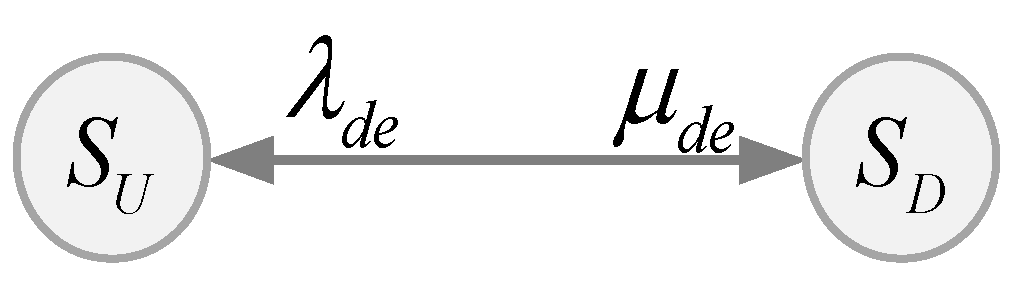
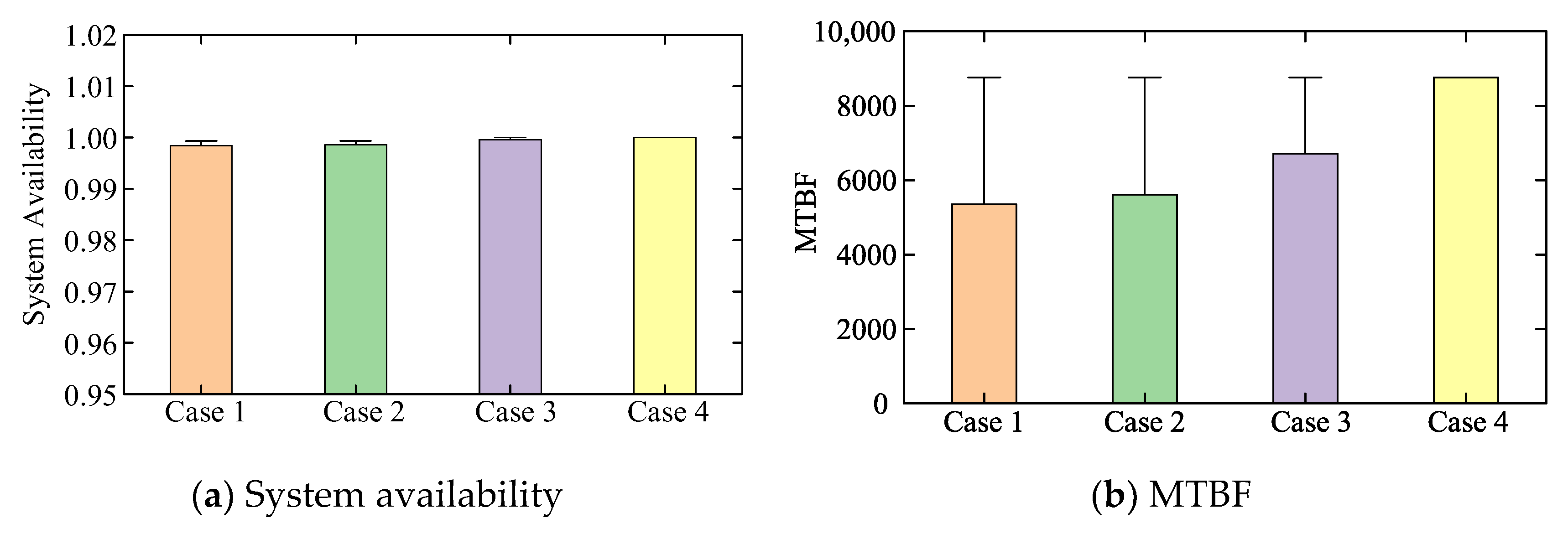


| Reference | Control Performance | Qualitative Topology Analysis | Topology Planning Model | N-1 Constraint | Communication Energy Consumption | Communication Link Reliability |
|---|---|---|---|---|---|---|
| [2] | √ | × | × | × | × | × |
| [10] | √ | × | × | × | × | × |
| [11] | √ | √ | × | × | × | × |
| [12] | √ | √ | × | × | √ | × |
| [13] | √ | √ | × | × | √ | × |
| Number of Agent(s) | Number of Labeled Graph(s) | Number of Non-Isomorphic Graph(s) |
|---|---|---|
| 1 | 20 = 1 | 1 |
| 2 | 21 = 2 | 2 |
| 3 | 23 = 8 | 4 |
| 4 | 26 = 64 | 11 |
| 5 | 210 = 1024 | 34 |
| 6 | 215 = 32,768 | 156 |
| 7 | 221 = 2,097,152 | 1044 |
| 8 | 228 = 268,435,456 | 12,346 |
| 9 | 236 = 68,719,476,736 | 274,668 |
| 10 | 245 = 35,184,372,088,832 | 12,005,168 |
| Case 1 | Case 2 | Case 3 | Case 4 | |
|---|---|---|---|---|
| Availability (Analytical Results) | 0.9974 | 0.9976 | 0.9996 | 1.0000 |
| Availability (MC Results) | 0.9984 | 0.9986 | 0.9996 | 1.0000 |
| MTBF (MC Results)/h | 5352.60 | 5609.50 | 6711.40 | 8760.00 |
| System Parameters | Value |
|---|---|
| Vrated | 80 V |
| Rs | 0.010 Ω |
| C1 | |
| Rline1 | 0.010 Ω |
| Rline2 | 0.020 Ω |
| Rline3 | 0.015 Ω |
| Rline4 | 0.030 Ω |
| Rline5 | 0.040 Ω |
| RL1 | 20 Ω |
| RL2 | 20 Ω |
| TCA | |
| time step |
| From Bus | To Bus | Distance/m |
|---|---|---|
| DG1 | DG2 | 87 |
| DG1 | DG3 | 134 |
| DG1 | DG4 | 111 |
| DG1 | DG5 | 158 |
| DG2 | DG3 | 87 |
| DG2 | DG4 | 64 |
| DG2 | DG5 | 111 |
| DG3 | DG4 | 53 |
| DG3 | DG5 | 100 |
| DG4 | DG5 | 68 |
| Control Parameters | Value |
|---|---|
| Kic | 97 |
| Kpc | 1 |
| Kiv | 800 |
| Kpv | 4 |
| Kisc | 8 |
| Kpsc | 0.4 |
| Kisv | 80 |
| Kpsv | 0.4 |
| Unit Cost | Value | Unit Cost | Value |
|---|---|---|---|
| Celec | 0.15 (USD/kWh) | Ctm | 3 (USD) |
| Cctr | 70 (USD) | mra | 0.1 |
| Csw | 30 (USD) | mre | 0.05 |
| Cgw | 55 (USD) | 50 (nJ/bit) | |
| Cnd | 10 (USD) | 50 (nJ/bit) | |
| Cfd | 20 (USD) | 5 (nJ/bit) | |
| Cs | 50 (USD) | 10 () | |
| Cca | 1.20 (USD/m) | 0.0013 () |
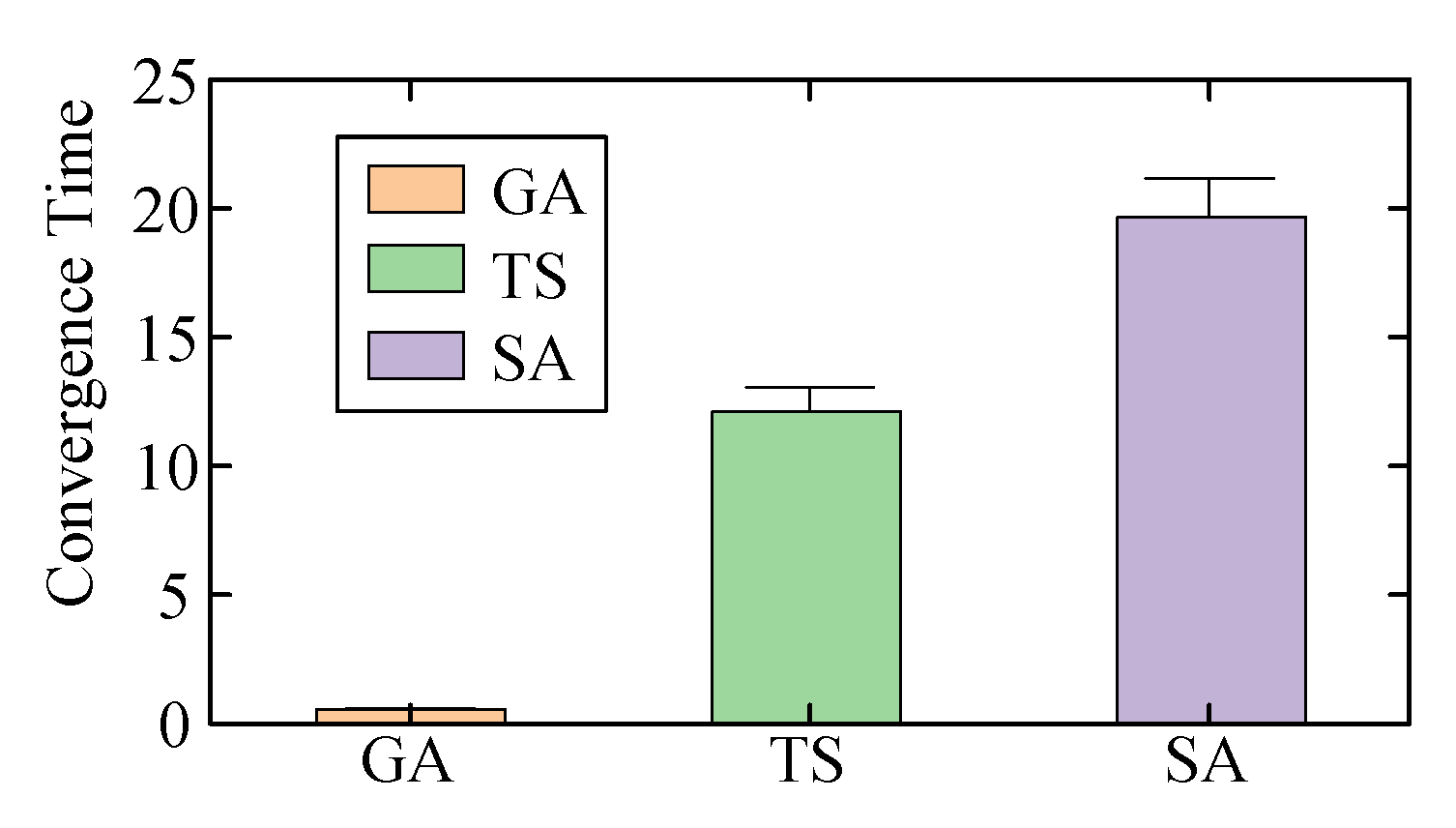
| Number of Agents | Convergence Speed/s (with Isomorphic Graph Recognition) | Convergence Speed/s (without Isomorphic Graph Recognition) |
|---|---|---|
| 5 | 0.4607 | 0.6122 |
| 10 | 25.9661 | 58.1719 |
| 15 | 365.7051 | 921.1013 |
| 20 | 4603.6499 | 17,021.6014 |
| 25 | 7854.5825 | 63,264.7821 |
| Statistical Characteristics | Value |
|---|---|
| 894.35 | |
| 1.36 | |
| 100% |
| Scheme 1 | Scheme 2 | Scheme 3 | Scheme 4 | |
|---|---|---|---|---|
| Unit Power Consumption | 749.22 | 894.35 | 1000.81 | 1145.93 |
| MTBF/h | 6711.40 | 8745.10 | 8745.10 | 8760.00 |
| Marginal Cost | - | 0.0714 | 0.1228 | 0.1937 |
| Cost–Benefit Ratio | 0.1116 | 0.1023 | 0.1142 | 0.1308 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Houari, A.; Guan, L.; Saim, A. Hierarchical Hybrid Control and Communication Topology Optimization in DC Microgrids for Enhanced Performance. Electronics 2025, 14, 3797. https://doi.org/10.3390/electronics14193797
Tang Y, Houari A, Guan L, Saim A. Hierarchical Hybrid Control and Communication Topology Optimization in DC Microgrids for Enhanced Performance. Electronics. 2025; 14(19):3797. https://doi.org/10.3390/electronics14193797
Chicago/Turabian StyleTang, Yuxuan, Azeddine Houari, Lin Guan, and Abdelhakim Saim. 2025. "Hierarchical Hybrid Control and Communication Topology Optimization in DC Microgrids for Enhanced Performance" Electronics 14, no. 19: 3797. https://doi.org/10.3390/electronics14193797
APA StyleTang, Y., Houari, A., Guan, L., & Saim, A. (2025). Hierarchical Hybrid Control and Communication Topology Optimization in DC Microgrids for Enhanced Performance. Electronics, 14(19), 3797. https://doi.org/10.3390/electronics14193797







