A Reinforcement Learning-Based Link State Optimization for Handover and Link Duration Performance Enhancement in Low Earth Orbit Satellite Networks

Abstract

This study proposes a reinforcement learning-based link selection method for Low Earth Orbit satellite networks, aiming to reduce handover frequency while extending link duration under highly dynamic orbital environments. The proposed approach relies solely on basic satellite positional information, namely latitude, longitude, and altitude, to construct compact state representations without requiring complex sensing or prediction mechanisms. Using relative satellite and terminal geometry, each state is represented as a vector consisting of azimuth, elevation, range, and direction difference. To validate the feasibility of policy learning under realistic conditions, a total of 871,105 orbit based data samples were generated through simulations of 300 LEO satellite orbits. The reinforcement learning environment was implemented using the OpenAI Gym framework, in which an agent selects an optimal communication target from a prefiltered set of candidate satellites at each time step. Three reinforcement learning algorithms, namely SARSA, Q-Learning, and Deep Q-Network, were evaluated under identical experimental conditions. Performance was assessed in terms of smoothed total reward per episode, average handover count, and average link duration. The results show that the Deep Q-Network-based approach achieves approximately 77.4% fewer handovers than SARSA and 49.9% fewer than Q-Learning, while providing the longest average link duration. These findings demonstrate that effective handover control can be achieved using lightweight state information and indicate the potential of deep reinforcement learning for future LEO satellite communication systems.

1. Introduction

Low Earth Orbit (LEO) satellites operate at altitudes ranging from approximately 200 km to 2000 km and provide global coverage with significantly lower latency than geostationary systems. These characteristics make LEO satellite networks a promising infrastructure for emerging applications such as disaster response, remote healthcare, and integrated ground–sea–air–space communication services.

The rapid deployment of large-scale LEO constellations by both commercial and governmental entities has significantly increased network density and coverage flexibility. However, the high orbital velocity of LEO satellites inherently results in frequent handover events, which pose major challenges to maintaining stable and efficient communication links. Excessive handovers can degrade quality of service (QoS), increase signaling overhead, and lead to unnecessary power consumption, particularly for resource-constrained user terminals.

Conventional handover strategies in LEO networks are typically based on simple physical metrics, such as selecting the nearest satellite to minimize path loss. While such distance-based approaches are intuitive, they often lead to short link durations and frequent reconnections due to rapid satellite motion. Soft handover mechanisms based on the Make-Before-Break (MBB) principle can mitigate service interruption but introduce additional resource consumption, interference, and system complexity.

These limitations highlight the need for adaptive handover strategies that jointly consider link stability and handover efficiency under dynamic orbital conditions. In particular, designing lightweight decision-making mechanisms that do not rely on extensive sensing, prediction, or signaling remains an open challenge.

This study aims to reduce handover frequency while extending link duration in LEO satellite networks by introducing a reinforcement learning–based link selection framework. By leveraging only basic satellite positional information, the proposed approach enables adaptive and data-driven decision-making without requiring explicit channel modeling or trajectory prediction. The effectiveness of the proposed method is validated through large-scale simulations using realistic orbital data.

The remainder of this paper is organized as follows. Section 2 reviews related work on LEO satellite handover and reinforcement learning–based approaches. Section 3 describes the system model, learning environment, and reinforcement learning algorithms. Section 4 presents the performance evaluation and comparative analysis. Section 5 concludes the paper and discusses future research directions.

2. Related Work

2.1. Traditional Handover Techniques in LEO Satellite Networks

Low Earth Orbit satellite systems have emerged as essential components of next generation communication infrastructures, particularly for personal communication services and non terrestrial networks, due to their advantages in end to end latency reduction and spectrum efficiency [1,2,3,4]. However, the high orbital velocity of LEO satellites leads to frequent handovers between satellites and user terminals, posing significant challenges in maintaining communication stability and continuity [2].

Early studies on LEO handover management primarily focused on hierarchical and rule-based mechanisms to enhance handover efficiency and routing continuity [3,5,6]. The Footprint Handover Rerouting Protocol, introduced in 1999, addressed route switching during handovers by preserving routing optimality based on satellite coverage footprints. While FHRP achieved low control overhead and near-ideal call blocking performance, it largely ignored dynamic orbital behavior and time-varying link conditions [2].

Subsequent work systematically categorized handover techniques into link layer and network layer approaches [6]. Link layer handovers include spot beam, inter satellite, and inter satellite link handovers, which are highly time sensitive due to the need for rapid frequency reassignment and beam steering [5]. Network layer handovers, in contrast, focus on connection transfer strategies and routing updates.

To mitigate temporary disconnections caused by hard handovers, soft handover schemes were proposed, allowing terminals to maintain simultaneous links with multiple satellites [5]. Although these approaches improve connection continuity, they often introduce additional signaling overhead and resource consumption, which can be critical in large scale LEO constellations.

More recently, LEO satellite networks have been recognized as core components of space–air–ground–sea integrated networks, where handover management plays a central role in unified mobility control [3,7]. Despite these advancements, traditional handover schemes remain limited in their ability to account for channel uncertainty, user mobility diversity, and complex orbital dynamics, motivating the exploration of more adaptive decision-making frameworks.

2.2. AI-Based and Learning-Based Handover Strategies

With the increasing scale and complexity of satellite networks, artificial intelligence techniques have been actively investigated to enhance adaptability and autonomy in mobility management. Several studies have applied machine learning and reinforcement learning to satellite communication problems, including channel prediction, power control, and interference mitigation [8,9,10]. Beyond core communication services, LEO satellite networks have also demonstrated practical effectiveness in application domains such as remote and telemedical services, where low latency and link stability are critical [11]. In the context of handover management, learning assisted approaches have been proposed to overcome the limitations of static rule based schemes. For example, prediction based handover methods leverage satellite trajectories, visibility windows, or dwell time estimation to proactively schedule handovers [12]. While effective under deterministic orbital assumptions, such approaches rely heavily on accurate prior knowledge and degrade in performance under channel uncertainty or irregular traffic patterns.

More advanced studies have adopted multi-agent reinforcement learning frameworks, modeling satellites or network entities as cooperative agents that jointly optimize handover and resource allocation decisions [13,14]. Although MARL-based approaches demonstrate strong performance in large-scale constellations, they typically require inter agent communication, centralized training, and substantial computational resources, limiting their feasibility for lightweight or terminal side deployment.

Other learning-based mobility management schemes integrate reinforcement learning or supervised learning with high-dimensional state representations, including channel state information, traffic load, or inter satellite signaling [15]. While these methods improve adaptability, they incur high inference complexity and impose strict sensing and signaling requirements.

2.3. Positioning of This Work

In contrast to existing studies, the proposed method adopts a lightweight, single-agent reinforcement learning framework that relies exclusively on position-derived geometric features. Specifically, the agent constructs its state using azimuth, elevation, range, and direction difference, all of which are directly obtainable from GNSS-based positional information without requiring additional sensing, prediction, or inter satellite communication, consistent with recent studies on precise orbit determination for LEO satellites [16].

To the best of our knowledge, no prior work formulates LEO satellite handover decisions using only GNSS-derived geometric features as reinforcement learning states. By restricting the action space to a small, pre-filtered candidate set and performing inference at the terminal side, the proposed approach significantly reduces computational and signaling overhead while retaining adaptability to highly dynamic LEO environments.

Accordingly, this work complements existing MARL and prediction-based solutions by offering a practical and scalable alternative for terminal side handover optimization. The key differences between the proposed method and representative existing approaches are summarized in

Table 1. Comparison of Learning-Based Handover Strategies in LEO Satellite Networks under Normalized Performance Metrics and Inference Characteristics.

Method Category	Learning Paradigm	State Information	Agent Type	Inference Complexity
MARL-based Handover [13,14]	MARL	Local UE info	Multi-agent	High
Prediction-based Handover [12]	Rule/Optimization	Trajectory, Dwell-time	Non-learning	Low
Learning-assisted Mobility [15]	RL/ML	High-dimensional	Single/Multi	Medium–High
Proposed Method	Single-agent RL	GNSS-only (AER + Dir.)	Single-agent	Low

.

3. Proposed Method

3.1. Proposed Structure

3.1.1. Existing Network Structure

Terrestrial communication networks provide stable coverage in urban regions but face severe limitations in mountainous, maritime, and remote environments due to terrain and infrastructure constraints. To address these issues, this study employs the structural advantages of Low Earth Orbit (LEO) satellites, which operate at altitudes of approximately 500–1500 km. LEO systems can significantly reduce latency and maintain reliable connectivity, positioning them as a core enabler for next-generation hybrid communication networks.

3.1.2. Low Orbit Satellites

LEO satellites, operating between 160–2000 km, provide millisecond-level latency and low path loss due to their proximity to Earth. Clustered LEO constellations enhance network resilience, ensuring higher MTBF and SLA availability. According to the Friis transmission model, LEO systems exhibit approximately 31.1 dB less path loss than GEO, improving energy efficiency and enabling compact ground terminals. Leveraging these advantages, this study applies reinforcement learning to optimize link states within LEO-based satellite networks.

3.1.3. Reinforcement Learning-Based Approach

This study employs three reinforcement learning algorithms—SARSA, Q-Learning, and Deep Q-Network (DQN)—to optimize link management in LEO satellite networks as follows:

• SARSA follows an on-policy approach, effectively balancing exploration and exploitation.
• Q-Learning adopts an off-policy mechanism to independently learn optimal actions with faster convergence.
• DQN, integrating neural networks with Q-Learning, ensures stable learning in complex state spaces using experience replay and target networks.

A comparative analysis of these models identifies the most efficient link optimization strategy tailored to LEO network dynamics. Figure 1 is the basic structure of DQN. The agent interacts with the environment to accumulate experiences, which are stored in the experience replay memory. During the training phase, randomly selected samples from the memory are used to train the neural network, and the target network weights are updated periodically.

3.2. Design

This section describes the design process of the reinforcement learning–based satellite link optimization model.

3.2.1. Raw Data Construction

Reinforcement learning relies on the agent’s ability to explore various combinations of states and actions to learn an optimal policy. Therefore, learning within a complex and non-deterministic environment is essential. To construct realistic satellite communication data that reflect such dynamics, the Ansys Systems Tool Kit (STK) simulator was employed, as illustrated in Figure 2.

In the STK environment, 300 low Earth orbit (LEO) satellites equipped with GNSS receivers were simulated over a 24 h orbital propagation. Whenever a satellite entered an accessible state, its unique ID, latitude, longitude, and altitude were recorded at 0.1 s intervals. This configuration provides temporal and spatial variability similar to real-world operations.

The collected data include only latitude, longitude, and altitude obtained from GNSS receivers. This minimal structure eliminates the need for additional onboard computation or sensor resources, enabling an efficient state representation. Moreover, the defined state structure is technically consistent with the System Information Block (SIB) format in 3GPP Release 17 for Non-Terrestrial Networks (NTN), ensuring compatibility with international standards.

Each orbital path was randomly assigned inclination, argument of periapsis, and right ascension of the ascending node to generate circular orbits by equalizing apogee and perigee.

The visible radius R of a satellite is calculated as follows:

$$R=\sqrt{\left\{{\left(h+R_e\right)}^2-R_e^2\right\}}$$

(1)

h denotes the satellite altitude and $R_e$ the Earth’s radius (approximately 6371 km). For example, a satellite at 500 km altitude has a visible radius of approximately 2300 km, corresponding to a latitude range of $\pm 28.7^{\circ }$.

The receiver terminal was modeled as an Electronically Steerable Antenna (ESA) suitable for aircraft or UAV integration. ESA enables beam steering during high-speed motion, making it ideal for LEO communication environments. In the simulation, the antenna was mounted on the upper surface to maintain a constant line-of-sight (LOS) connection.

Ultimately, a CSV-formatted raw dataset containing each satellite’s unique ID, latitude, longitude, and altitude was generated and used as the foundation for reinforcement learning dataset construction.

3.2.2. Dataset Generation

From the time-series position data, each satellite’s heading direction was calculated using the coordinate difference between consecutive timestamps:

$$\overrightarrow{pos}=\left(x_2-x_1,y_2-y_1,z_2-z_1\right)$$

(2)

A random footprint radius between 750 and 1250 km was assigned to each satellite, representing its effective communication coverage area based on altitude and beam characteristics, as illustrated in Figure 3. These randomized and spatially diverse footprints increase environmental diversity and uncertainty, thereby enhancing the robustness of the reinforcement learning process. At each timestep, the three-dimensional Euclidean distance D between the satellite and the receiver was computed, and only data within the footprint radius were considered valid communication instances.

$$D=\sqrt{\left\{{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2+{\left(z_2-z_1\right)}^2\right\}}$$

(3)

For data augmentation, the receiver’s heading was varied from $0^{\circ }$ to ${359}^{\circ }$, and the relative direction difference between the satellite and receiver was computed, generating 360 virtual scenarios. This approach significantly increased both the quantity and diversity of the dataset. A relative radial motion indicator, reflecting whether the satellite is approaching or receding from the receiver, was defined based on the rate of change in the satellite–receiver distance:

$$\Delta d_t=(Distanc{e}_t-Distanc{e}_{t-1})$$

(4)

where a negative value indicates an approaching satellite and a positive value indicates a receding satellite. This indicator therefore provides a lightweight geometric cue for link continuity without requiring explicit velocity vectors or trajectory prediction. Hereafter, this term is referred to as a radial motion indicator, representing the relative approaching or receding tendency rather than a geometric direction.

A smaller value indicates higher link stability and handover reliability.

For each configuration, azimuth, elevation, and range values were calculated as follows:

$$\begin{array}{c}\hfill Azimuth=arctan2\left(\mathsf{\Delta }y,\mathsf{\Delta }x\right),\\ \hfill Elevation=arctan\left(h/HorizontalDistance\right),\\ \hfill Range=\sqrt{\left\{h^2+d^2\right\}}\end{array}$$

(5)

Each record was finally represented as a state vector [direction difference, azimuth, elevation, range] and stored in CSV format. The dataset captures the multidimensional spatial relationships between satellites and terminals, thereby improving generalization in the reinforcement learning model.

Consequently, it was confirmed that policy learning is feasible using only GNSS-based navigational information. Despite the simplified input structure, the agent effectively recognized link feasibility and communication characteristics, demonstrating strong technical compatibility with real-world LEO systems.

3.2.3. Reward Function Design

The pseudocode of the reward algorithm is presented in Algorithm 1. To quantify link quality, four physical features were defined as state variables: direction difference ($direction\_diff$), azimuth, elevation, and range, which were converted into $direction\_score$, $azimuth\_score$, $elevation\_score$, and $range\_score$, respectively. Each feature represents directional alignment, spatial geometry, signal strength, and propagation delay, respectively. Combined, these factors guide the agent to optimize link stability and communication efficiency.

Among the four components, the direction difference is assigned the largest weight. This design choice reflects the high mobility characteristics of LEO satellite systems, where rapid changes in relative motion between the user terminal and satellites are a primary cause of frequent link terminations. Unlike elevation or range, which typically vary more gradually, abrupt changes in direction difference often indicate imminent visibility loss. Therefore, prioritizing directional consistency enables the agent to implicitly maximize expected link duration and suppress unnecessary handovers.

Algorithm 1: Reward Computation Based on Selected Features

Input: Selected feature vector: $[direction\_diff, azimuth, elevation, range\_val]$ Output: Reward value r Extract features: $direction\_diff, azimuth, elevation, range\_val\leftarrow selected\_features$ Convert features to scores: $direction\_score\leftarrow 1.0-direction\_diff$ $azimuth\_score\leftarrow 1.0-azimuth$ $elevation\_score\leftarrow 1.0-|elevation-1.0|$ $range\_score\leftarrow 1.0-range\_val$      // Higher if distance is short Compute weighted sum: $r\leftarrow 0.30\times direction\_score+0.28\times azimuth\_score+0.25\times elevation\_score+0.17\times range\_score$ Apply penalty: if  $r<0.2$  then $\lfloor r\leftarrow r-0.07$ return  r

The remaining features—azimuth, elevation, and range—complement the reward formulation by capturing spatial geometry and propagation-related effects. Elevation is associated with link reliability and reduced blockage probability, while range correlates with path loss and propagation delay. Together, these features provide a balanced representation of geometric and physical link conditions.

To evaluate the robustness of the proposed reward formulation, a sensitivity analysis was considered by perturbing individual reward weights within a moderate range (±10–20%) while preserving their relative importance. The learned policy exhibited qualitatively consistent behavior under these variations, indicating that the overall performance does not rely on precise coefficient tuning but rather on the relative prioritization among reward components.

Alternative reward designs, such as uniformly weighted combinations of all features, were also examined conceptually. However, such formulations fail to reflect the asymmetric impact of different physical factors in highly dynamic LEO environments. In particular, treating direction difference equally with secondary geometric features may lead to frequent short-term satellite switching. Based on these considerations, a non-uniform weighting strategy was adopted to better align the reward function with the physical dynamics of LEO satellite motion.

Direction difference was assigned the largest weight because it directly reflects satellite trajectory alignment, which is a primary factor determining imminent link termination in LEO systems. While a full sensitivity analysis is left for future work, preliminary observations indicated that moderate weight variations (±10–20%) did not change the relative performance ranking among algorithms.

3.3. Implementation

This section describes the implementation process of the proposed reinforcement learning–based satellite link optimization model. All reinforcement learning models were developed in Python 3.12 using an Anaconda virtual environment.

3.3.1. Reinforcement Learning Models

Based on simulated LEO satellite data, three reinforcement learning algorithms—SARSA, Q-Learning, and Deep Q-Network (DQN)—were sequentially applied and compared. All models were trained under identical conditions, including a custom Gym-based environment, a consistent state and reward structure, and an identical action space.

A total of 871,105 simulated and processed records were used for training, each containing the satellite–terminal heading direction, azimuth, elevation, and range information at valid communication instances.

The baseline algorithm, SARSA (State–Action–Reward–State–Action), is an On-Policy method that updates Q-values based on actions selected under the current policy. Although SARSA demonstrated conservative and stable learning behavior, it achieved only limited improvements in reward convergence speed and link duration, despite initially reducing handover frequency.

Q-Learning employs the same reward and state structures as SARSA but updates policies using the maximum Q-value among all possible actions, making it an Off-Policy approach. States were discretized using a hash-based indexing method (hash(state.tobytes()) % N) and stored in a Q-table. This method exhibited faster convergence and higher average rewards than SARSA, but its representational capacity was constrained by the discretization of the state space.

To overcome these limitations, the Deep Q-Network (DQN) was adopted as the primary algorithm. DQN approximates Q-values from continuous state vectors using a deep neural network; in this study, a multi-layer perceptron (MLP) built with nn.Sequential was utilized. The input features included the same AER (Azimuth, Elevation, Range) parameters and direction difference values as in the previous models.

The environment was restructured so that DQN could directly select satellites as actions, enabling precise control of the policy exploration range. To enhance stability and efficiency, several techniques—reward clipping, $ϵ$-decay scheduling, target network updates, and candidate-based action refinement—were applied.

Training performance was evaluated using Smoothed Reward curves, episode-based handover counts, and average link duration metrics. The results clearly demonstrated that DQN outperformed both SARSA and Q-Learning in all aspects.

Overall, under identical experimental settings, the results followed a distinct performance hierarchy of SARSA < Q-Learning < DQN in terms of convergence speed, link quality maintenance, and handover optimization. These findings confirm the practical effectiveness of deep reinforcement learning in handling high-dimensional, nonlinear state spaces such as those in LEO satellite communication environments.

3.3.2. DQN Algorithm Configuration

For reinforcement learning–based LEO satellite link optimization, a custom Gym-based environment, ‘AERActionBasedEnv’, was developed. From approximately 870,000 CSV files generated from simulated satellite data, 10% were randomly sampled, and about 1% of lines within each file were further randomly selected. This double sampling strategy was designed not merely to reduce dataset size, but to reflect diverse communication conditions and spatiotemporal variations, enhancing generalization performance.

The dataset included a data augmentation procedure where terminal heading directions were assigned from $0^{\circ }$ to ${359}^{\circ }$ at $1^{\circ }$ increments. Consequently, 360 augmented data points were generated from a single line, each differing only in direction difference values while retaining the same AER (Azimuth, Elevation, Range) information. This prevents agent bias towards specific scenarios and ensures balanced learning across varied satellite and link states.

At each step, the agent receives a fixed number of candidate satellites selected through an initial filtering process. Each candidate is characterized by four key features: direction difference, azimuth, elevation, and range. The state is thus represented as a 20-dimensional continuous vector, where all features are normalized to the [0, 1] range using Min–Max scaling. Azimuth and elevation are measured in degrees, while range is computed in kilometers based on the satellite–terminal distance prior to normalization. Actions are defined over this candidate set, whose size is fixed to five in the experimental setup. The initial candidate selection excludes satellites with very low elevation angles and prioritizes newly entering satellites, reflecting the practical assumption that recently established links are generally more stable and less likely to terminate in the near future than links approaching the boundary of their visibility. The reward function, determined experimentally, penalizes cases where elevation is below ${30}^{\circ }$ and further reduces rewards below a threshold of 0.2 to discourage poor link quality selections.

Episode lengths are randomly set between 3000 and 8000 steps, and start points are randomly selected from the entire dataset, allowing the agent to learn under diverse scenarios rather than being confined to a single situation.

The neural network is a multi-layer perceptron (MLP) with two hidden layers of 128 neurons each, using ReLU activation functions, and an output layer producing five Q-values. Experience replay is employed, storing up to 20,000 transitions and sampling mini-batches of 64 transitions per step for training.

An $ϵ$-greedy exploration strategy is applied, with an initial $ϵ$ of 1.2, decaying by 0.998 per step to a minimum of 0.1. The loss function is mean squared error (MSE), with a learning rate of $1\times {10}^{-4}$ and a discount factor $\gamma$ of 0.99. The target network is synchronized with the policy network every 10 episodes. Training was conducted over 1000 episodes, and metrics including total rewards, handover counts, and average link duration were recorded and visualized for each episode.

4. Performance Evaluation

This chapter details the experimental environment and analyzes the corresponding results.

4.1. Experimental Setup

The experiments were performed on a workstation with the following hardware and software specifications:

• OS: Windows 11
• CPU: Intel Core i7-14700K (20 cores, 28 threads)
• GPU: NVIDIA RTX 4090
• RAM: 32 GB
• Environment: Python 3.12 (Anaconda)
• Framework: OpenAI Gym (Custom Environment: ‘AERActionBasedEnv’)

4.2. Dataset and Preprocessing

4.2.1. Data Sampling

The input dataset comprises approximately 870,000 CSV files, each containing time-stamped data points with the satellite’s ID, latitude, longitude, and altitude. The training data was constructed using a double-sampling strategy: 10% of the total files were randomly selected, and from within those files, 1% of the lines were randomly extracted.

4.2.2. Feature Engineering and Normalization

Subsequently, features were engineered from the sampled data. Based on the relative position between the satellite and the terminal, Azimuth, Elevation, and Range (AER) were calculated. The heading difference, which depends on the terminal’s direction of motion, was then added to complete the feature set.

The final training dataset is composed of a satellite ID and four real-valued features: heading difference, azimuth, elevation, and range. All features, excluding the satellite ID, were normalized to a [0, 1] range using a ‘MinMaxScaler’. Notably, for the range values, the top 1% of outliers were clipped prior to the normalization process. azimuth and elevation are measured in degrees, while range is computed in kilometers based on satellite–terminal distance before outlier clipping and Min–Max normalization.

Although multiple satellites may be visible at a given timestep in the dataset, only a limited set of candidate satellites is used to construct the state at each decision step. This candidate set is obtained through simple geometric and temporal filtering, excluding low-elevation satellites and prioritizing newly entering ones.

The training dataset is generated using multiple STK-based simulation runs with randomized orbital parameters and satellite footprints, exposing the learning agent to a wide range of geometric configurations rather than a single fixed constellation layout.

4.3. RL Environment and Hyperparameters

4.3.1. State, Action, and Episode Configuration

In the reinforcement learning environment, the state is defined as a 20-dimensional vector created by concatenating the features of the prefiltered candidate satellites. The action space is a discrete space corresponding to this candidate set, whose size is fixed to five in the experimental setup.

The length of each episode was randomized to be between 3000 and 8000 steps. Furthermore, the starting point for each episode was randomly selected from the entire dataset to ensure a diversity of learning experiences.

4.3.2. Reward Function

The reward function was structured as a linear combination of the four weighted feature values. The weights applied to each feature were as follows: heading difference (0.30), azimuth (0.28), elevation (0.25), and range (0.17). To discourage poor link selections, two penalty conditions were also implemented:

• A penalty was applied if the elevation angle was below 30° (0.333 on a normalized scale).
• An additional penalty of −0.07 was imposed if the total reward was less than 0.2.

4.3.3. DQN Hyperparameters and Common Policies

The DQN model was based on a fully connected neural network. Its architecture and key hyperparameters are detailed below:

• Network Architecture: Two hidden layers with 128 units each, using the ReLU activation function.
• Experience Replay Buffer Size: 10,000
• Batch Size: 32
• Loss Function: Mean Squared Error (MSE)
• Target Network Update Frequency: Every 10 episodes

Q-Learning and SARSA were implemented to update a Q-table based on the same state and reward structure. All three algorithms employed an $ϵ$-greedy exploration strategy, where the exploration rate $ϵ$ was linearly annealed from an initial value of 1.0 down to a final value of 0.05 as training progressed.

4.4. Performance Evaluation Metrics

The test data was generated from a separate simulation, completely distinct from the orbits and files used for training. Using the STK simulation tool, 300 new LEO satellite orbits were simulated. Directional augmentation was then independently applied to each satellite to create CSV files based on latitude, longitude, and altitude. Following the same procedure as the training data, features such as azimuth, elevation, range, and heading difference were calculated, and the footprint radius was set to a random value between 750 and 1250 km. Normalization and outlier clipping were also performed identically. Based on this dataset, a total of 200 test episodes were executed.

Performance was evaluated based on the following two key metrics:

• Handover Frequency: The number of times the serving satellite ID changed per episode.
• Link Duration: The average ratio of steps during which a connection with the same satellite was maintained.

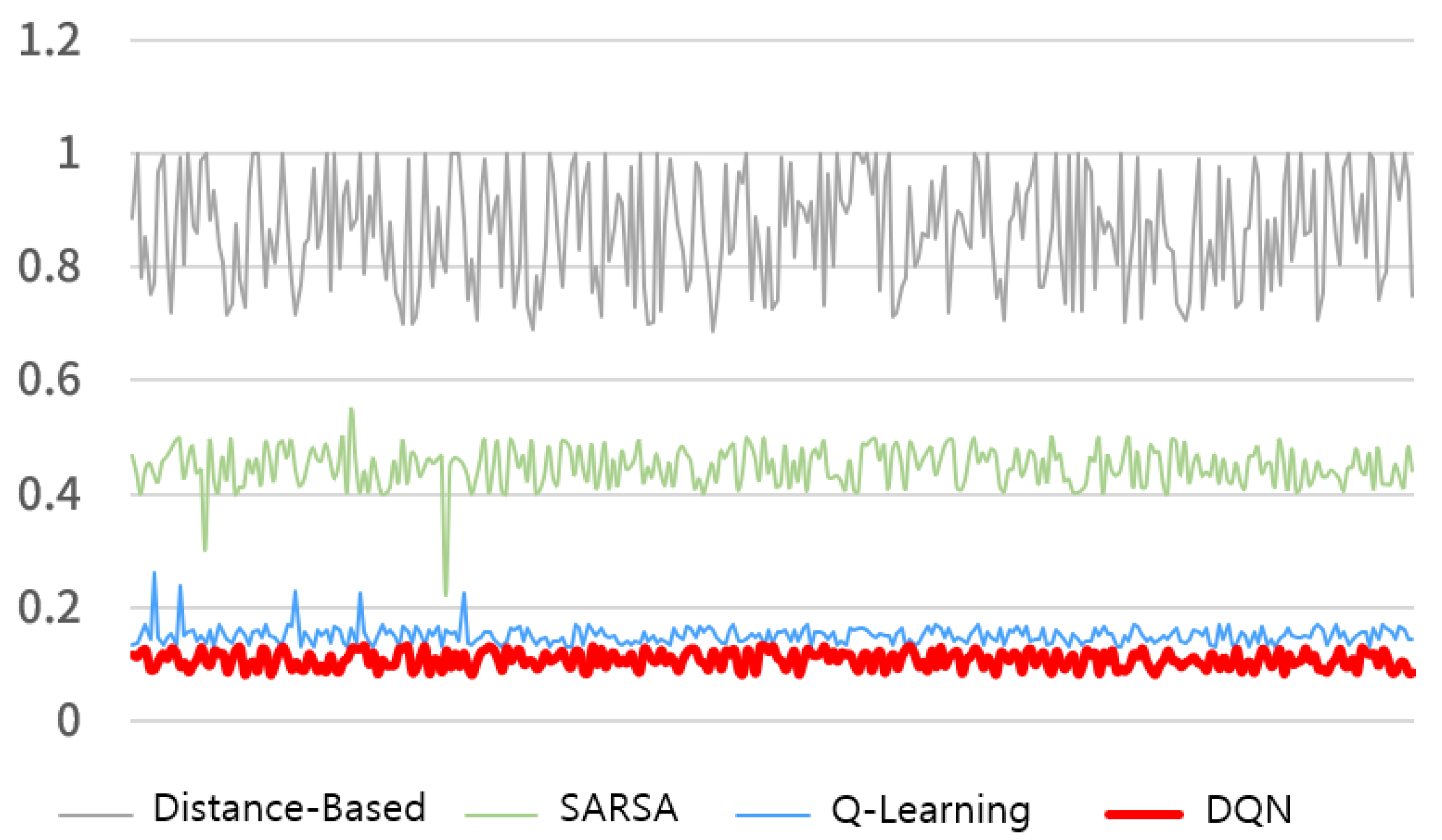
4.5. Experimental Results

The experimental results were analyzed based on three key metrics: Total Reward, Handover Frequency, and Link Duration. For comparative purposes, the y-axis of all graphs was normalized. Although the experiments do not explicitly evaluate cross-constellation or cross-altitude transfer, the learned policy operates solely on geometric relationships derived from satellite position and motion, rather than constellation-specific identifiers or parameters. All results reported in this section, including the convergence behaviors shown in Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, are obtained by averaging outcomes over multiple independent training runs with different random seeds.

Figure 4 illustrates the performance comparison based on Total Reward. The results demonstrate that DQN consistently achieved the highest reward levels, demonstrating superior convergence performance.

As shown in Figure 5 and Figure 6, the distance-based approach exhibits an extremely high handover frequency. In contrast, all RL-based models maintained a lower frequency, with DQN achieving the lowest at approximately 0.1.

The analysis of link duration in Figure 7 and Figure 8 reveals a similar trend, where DQN consistently maintained the highest value of 0.3 or higher.

The quantitative results in

Table 2. Average performance metrics averaged over multiple independent runs with different random seeds. Values are reported as mean ± standard deviation.

Model	Avg. Handover Freq.	Avg. Link Duration
Distance-based	0.8702 (±0.100)	0.1719 (±0.050)
SARSA	0.4411 (±0.080)	0.2247 (±0.040)
Q-Learning	0.1839 (±0.050)	0.2810 (±0.020)
DQN	0.1020 (±0.030)	0.3001 (±0.020)

Note: More advanced deep reinforcement learning methods such as Double DQN (DDQN) or policy-gradient-based approaches (e.g., PPO) are not included in this quantitative comparison. Although such methods have shown improved convergence stability in other domains, they typically require additional networks, policy optimization steps, or increased inference complexity, which are not well aligned with the real-time and resource-constrained assumptions of LEO user terminals.

confirm that DQN not only achieved an 88.7% reduction in handover frequency but also recorded the lowest standard deviation, indicating superior performance in both effectiveness and stability. While the above results demonstrate the overall performance of the proposed approach, we further examine the contribution of individual state components through a simple ablation analysis.

4.6. Ablation Analysis of State Components

To gain further insight into the role of individual geometric state features, we performed a small-scale ablation analysis based on the trained DQN policy using the same simulation environment. Starting from the full state configuration, one feature was removed at a time while all other settings were kept unchanged. The results in

Table 3. Results of a small-scale ablation analysis illustrating the impact of removing individual geometric state components on handover frequency and link duration.

State Configuration	Avg.Handover Count	Avg.Link Duration Ratio
Full State	0.104	0.301
Direction Difference	0.176	0.224
Elevation	0.162	0.241
Range	0.118	0.283

show that removing the direction difference leads to a noticeable increase in handover frequency and a reduction in average link duration. This observation suggests that consistency between the terminal movement direction and the satellite trajectory plays an important role in maintaining link continuity in LEO scenarios. A similar, though slightly less pronounced, performance degradation is observed when the elevation feature is excluded, reflecting the role of link visibility and geometric stability. In contrast, removing the range component results in only a minor performance change, indicating that distance information plays a complementary role compared to directional and angular features under the considered setting. Overall, this simple analysis supports the use of geometric link features and highlights direction difference and elevation as the most influential components for the proposed handover strategy. While the radial motion indicator captures the temporal tendency of link evolution, the range feature provides complementary information regarding the instantaneous link margin. As observed in the ablation analysis, removing the range component results in only a minor performance degradation, suggesting that range plays a supportive rather than dominant role in the proposed state representation.

5. Conclusions

5.1. Summary of the Study

This study proposes a lightweight reinforcement learning framework for link state stabilization and handover optimization in LEO satellite networks, relying exclusively on satellite geometric and directional information derived from positional data. The proposed framework operates without the need for complex sensing mechanisms or external prediction models, demonstrating that effective handover policies can be learned from compact and minimal state representations.

Among the evaluated methods, the Deep Q-Network (DQN) achieved the best overall performance, reducing handover frequency by approximately 88.7% and increasing average link duration by approximately 74.6% compared to a conventional distance-based handover strategy. These results indicate that deep reinforcement learning can effectively address the high-dimensional and non-linear characteristics of LEO satellite communication environments, even when only lightweight geometric information is available.

5.2. Contributions and Implications

Furthermore, this study effectively overcomes the limitations of conventional methods by introducing a state definition and reward structure based on AER. This design, implemented using realistic LEO satellite orbital data, not only demonstrates high practical applicability within diverse LEO geometric configurations but also highlights the potential of lightweight, geometry-based decision policies. Explicit generalization across different constellation designs or orbital regimes is left for future work. Ultimately, this research is poised to make a significant contribution to the future design of intelligent communication policies for satellite communication systems, UAVs, and Non-Terrestrial Networks (NTNs).

6. Limitations and Discussion

This study focuses on value-based reinforcement learning methods (SARSA, tabular Q-learning, and DQN) to evaluate the effectiveness of a lightweight and single-agent learning framework for LEO satellite handover optimization. More advanced deep reinforcement learning approaches, such as Double DQN (DDQN) or policy-gradient methods (e.g., PPO), were not included in the experimental comparison.

While these methods are known to improve training stability and policy expressiveness, they generally introduce additional computational overhead due to auxiliary networks, policy optimization procedures, or increased memory requirements. Such characteristics may limit their applicability to real-time handover decisions on resource-constrained user terminals assumed in this work.

Similarly, heuristic or trajectory-prediction-based handover schemes were not directly compared, as they typically rely on explicit orbital prediction models or network-side coordination, which are outside the scope of this study. Instead, the proposed approach emphasizes minimal external dependency by using only locally available GNSS-derived features and lightweight inference.