An Integrated Scattering Cancellation and Modification Approach for Broadband RCS Reduction of Array Antenna
Abstract
1. Introduction
- (1)
- A hybrid approach integrating scattering cancellation with array-level modification techniques for broadband RCSR design of array antennas is proposed, which supports array scale expansion.
- (2)
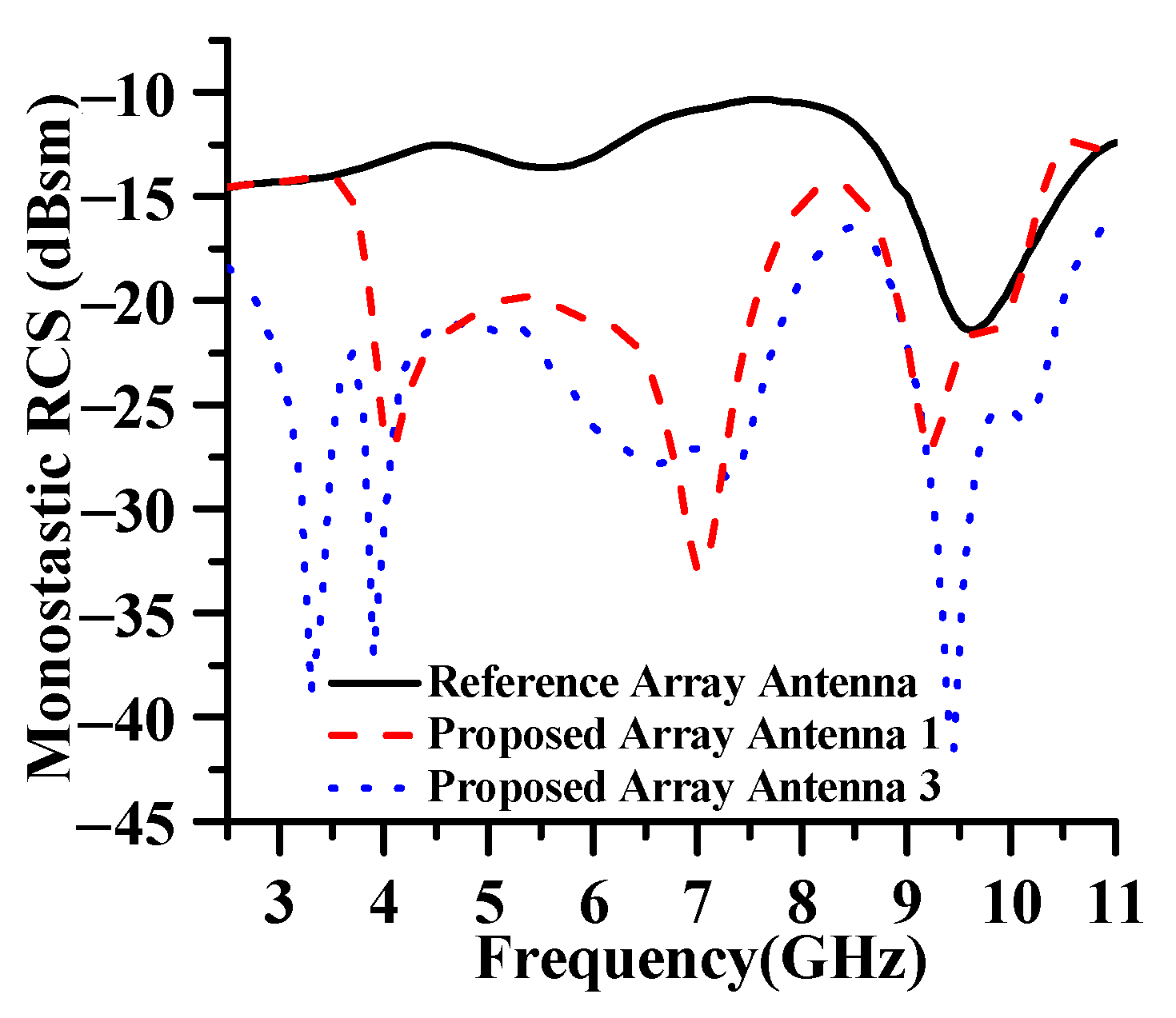
- A 2 × 2 low-RCS array antenna is obtained from 2.5 to 11 GHz (126%), with an average RCSR of 10.3 dB and a peak RCSR of 22 dB. A 4 × 4 low-RCS array antenna is also obtained from 2.5 to 10.5 GHz (123%), with an 8 dB mean RCSR value and 23 dB peak RCSR value, verifying the universality of the design method.
2. Theoretical Analysis
2.1. Scattering Cancellation Theory
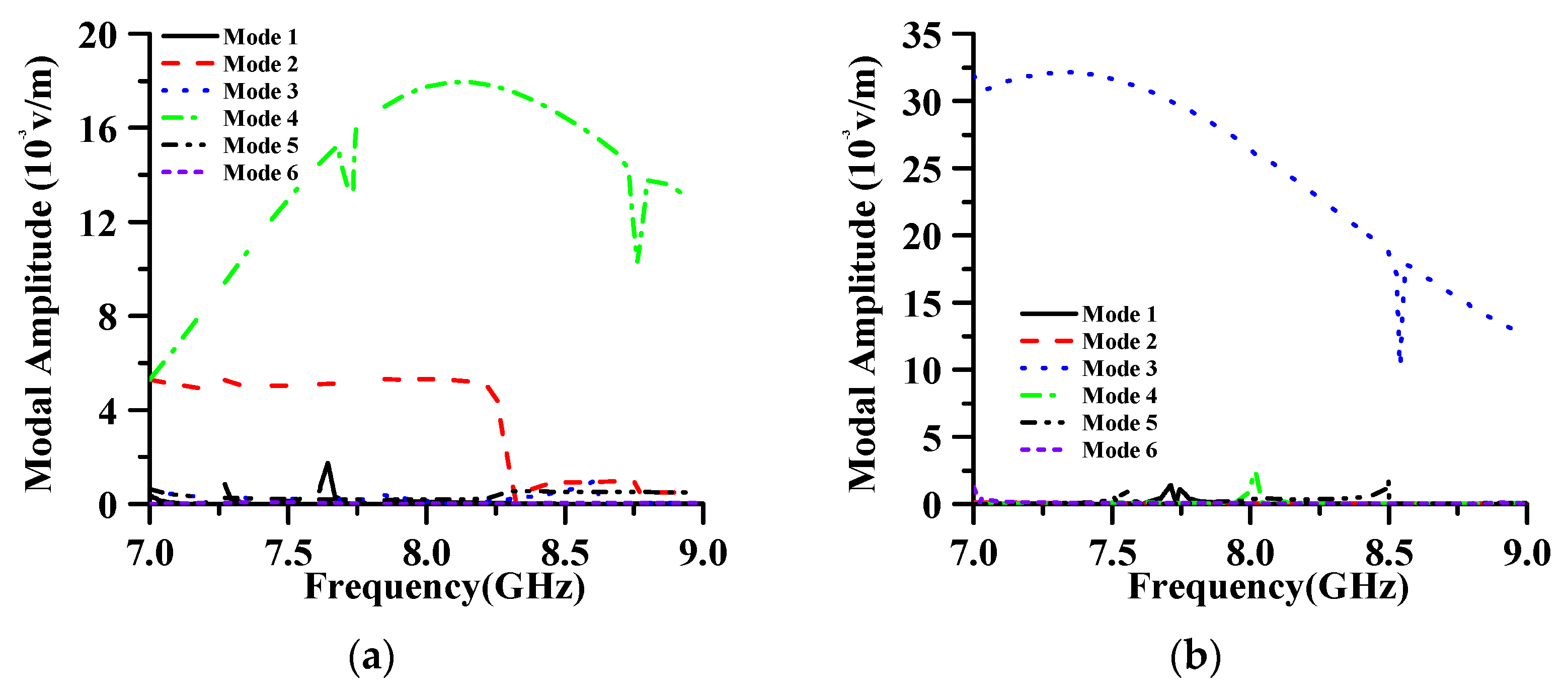
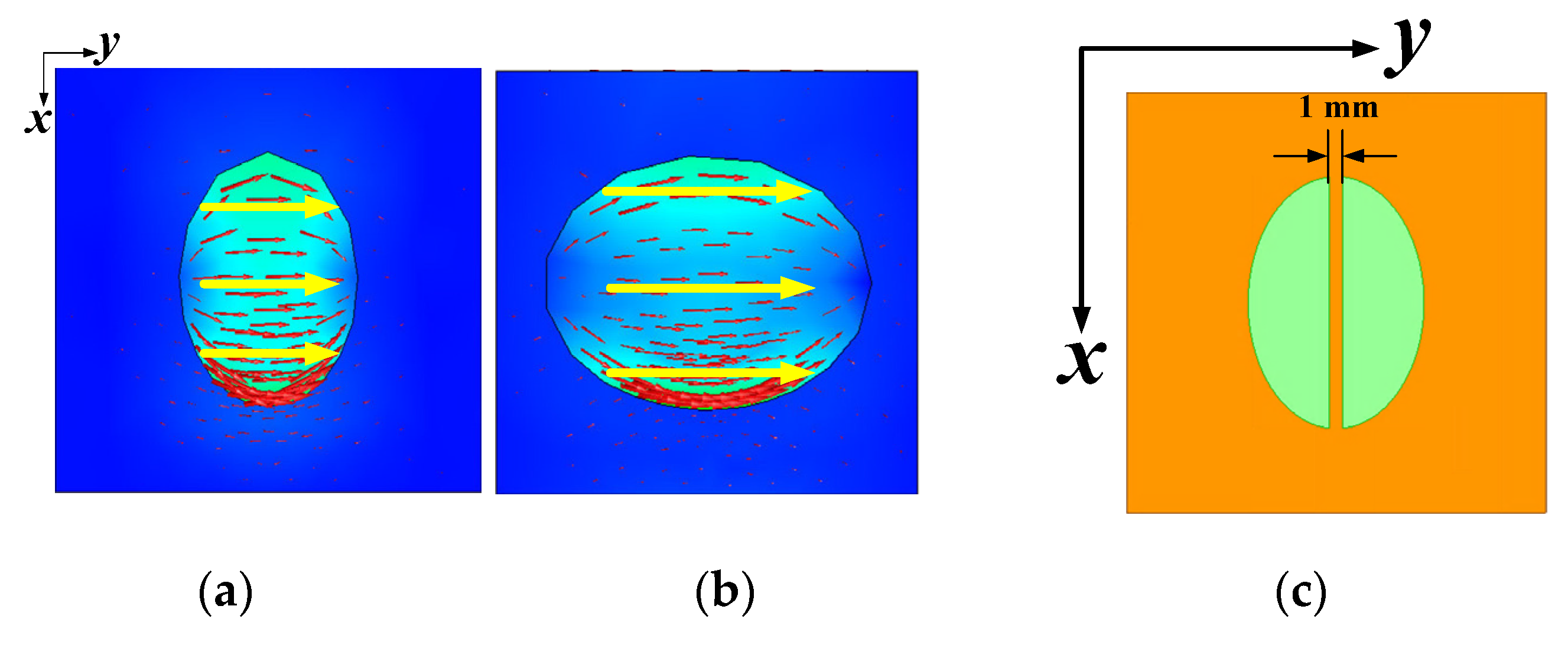
2.2. Characteristic Mode Theory
3. Broadband RCSR Design of Array Antenna
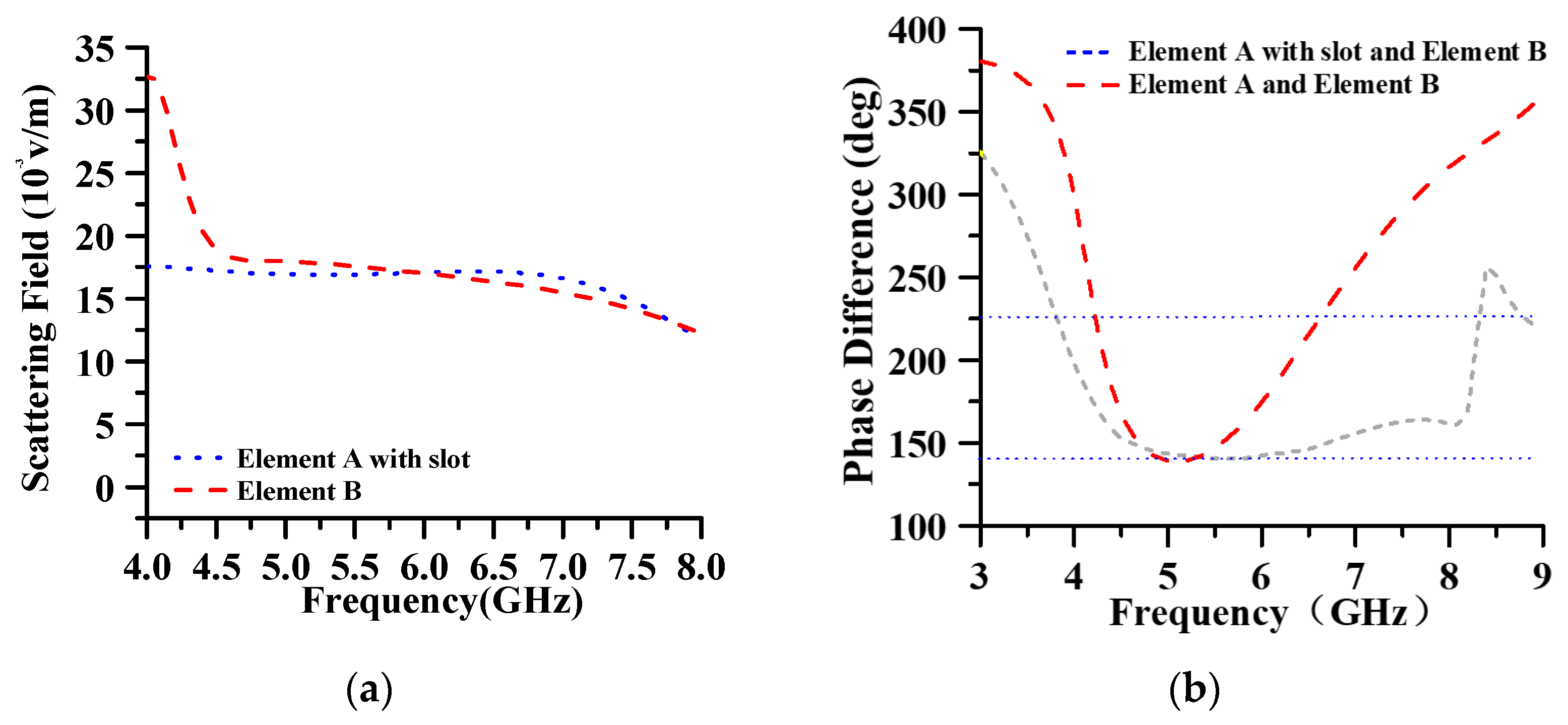
3.1. RCSR Design Based on Scattering Cancellation
3.1.1. Scattering Cancellation Element Design Based on Reshaping Patch
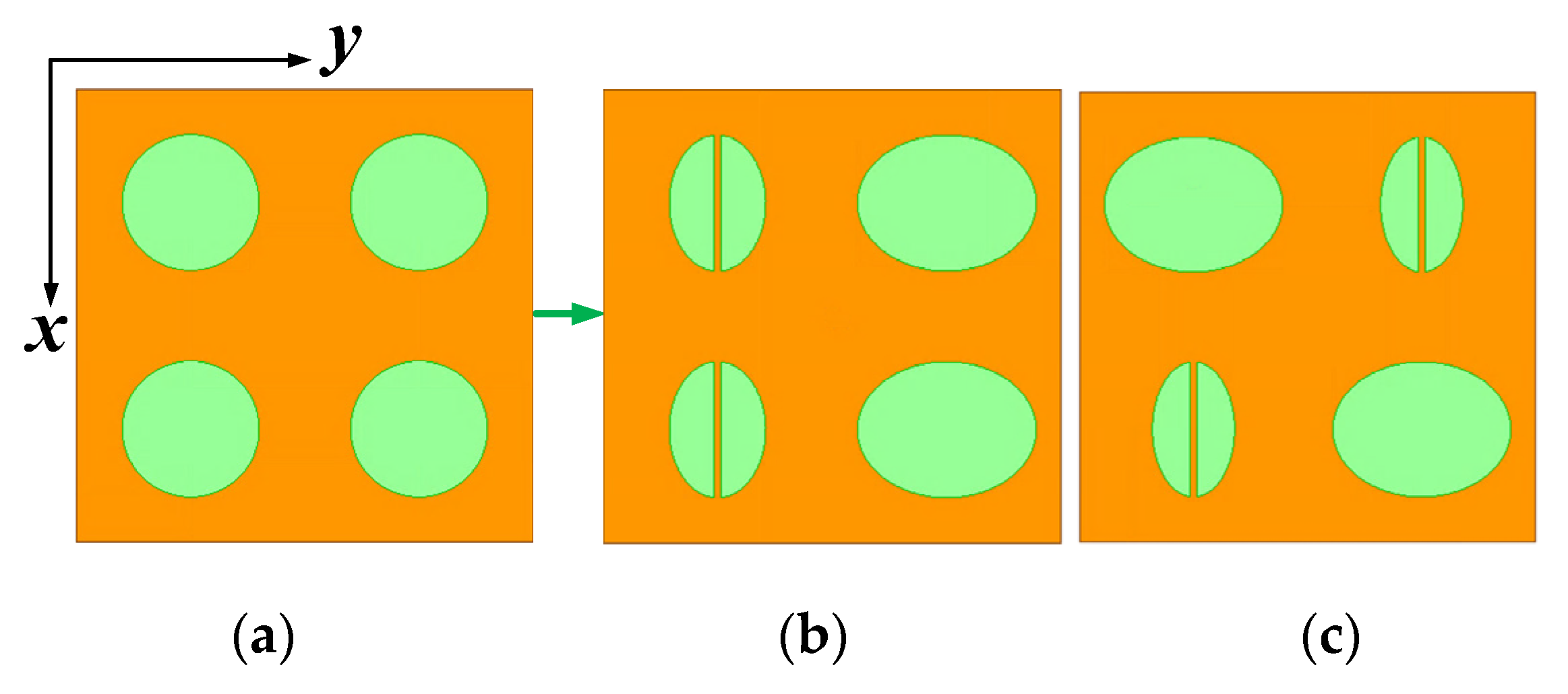
3.1.2. Scattering Cancellation Array Design
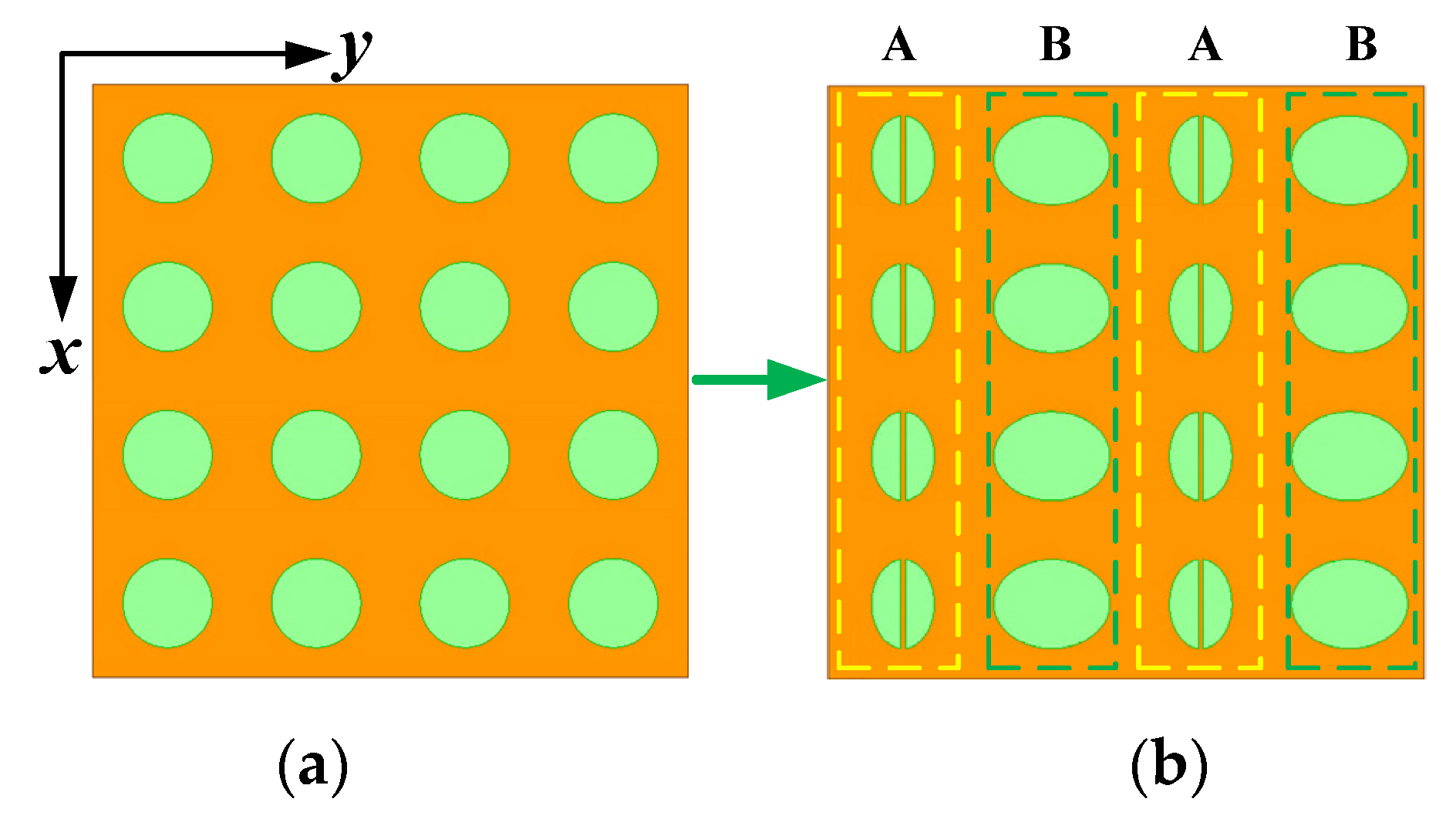
3.2. RCSR Design Based on Array-Level Shape Modification
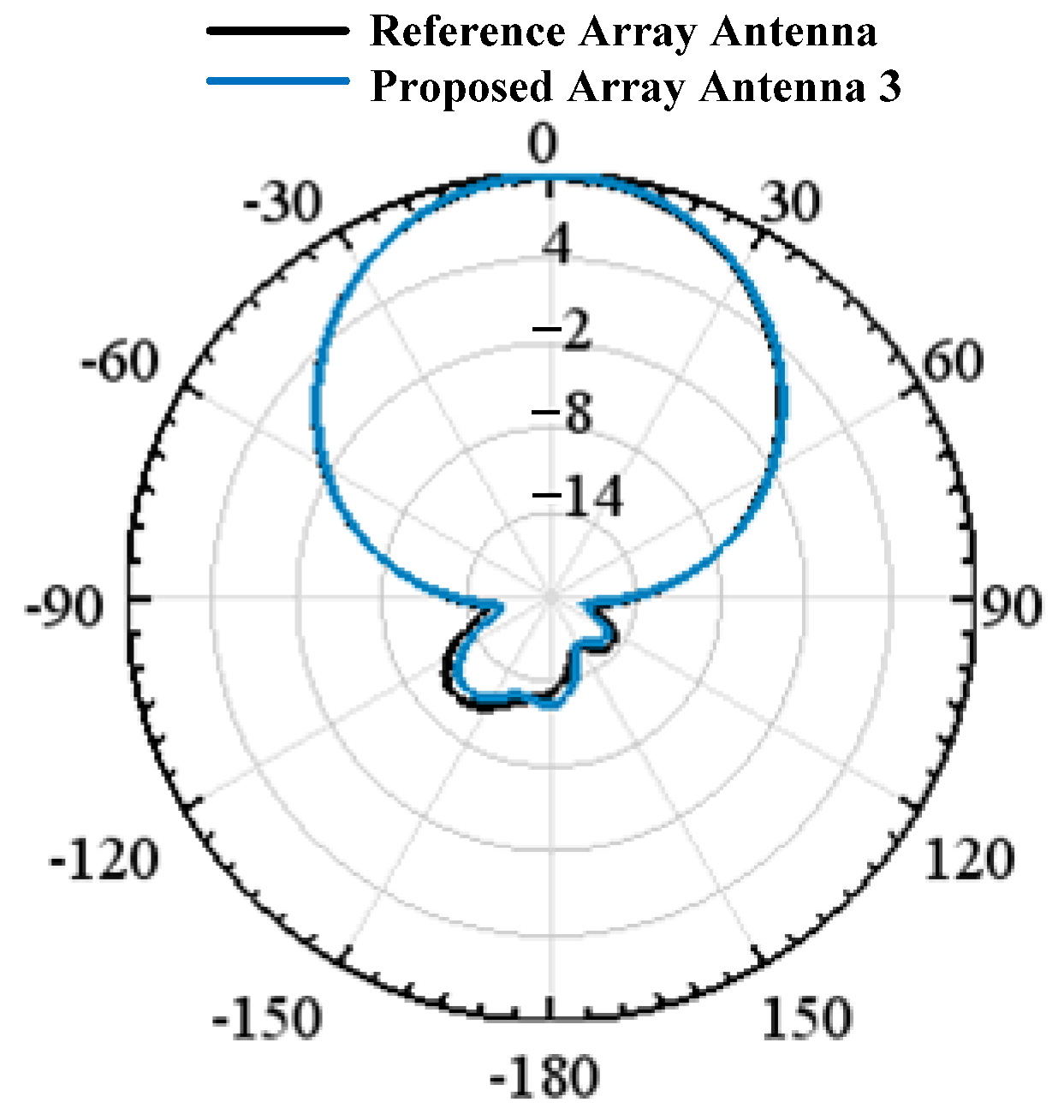
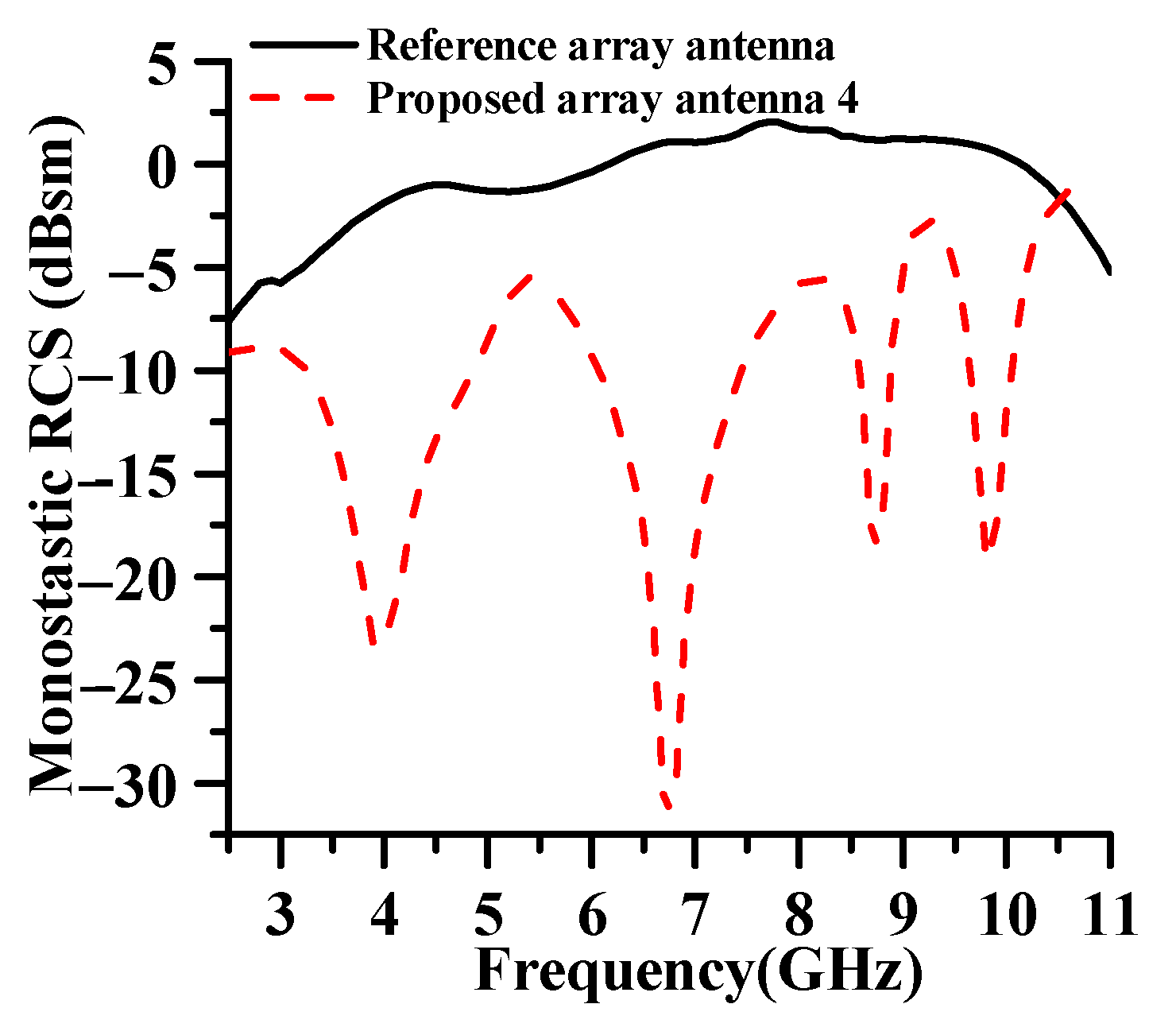
3.3. Design Verification of 4 × 4 Array Antenna
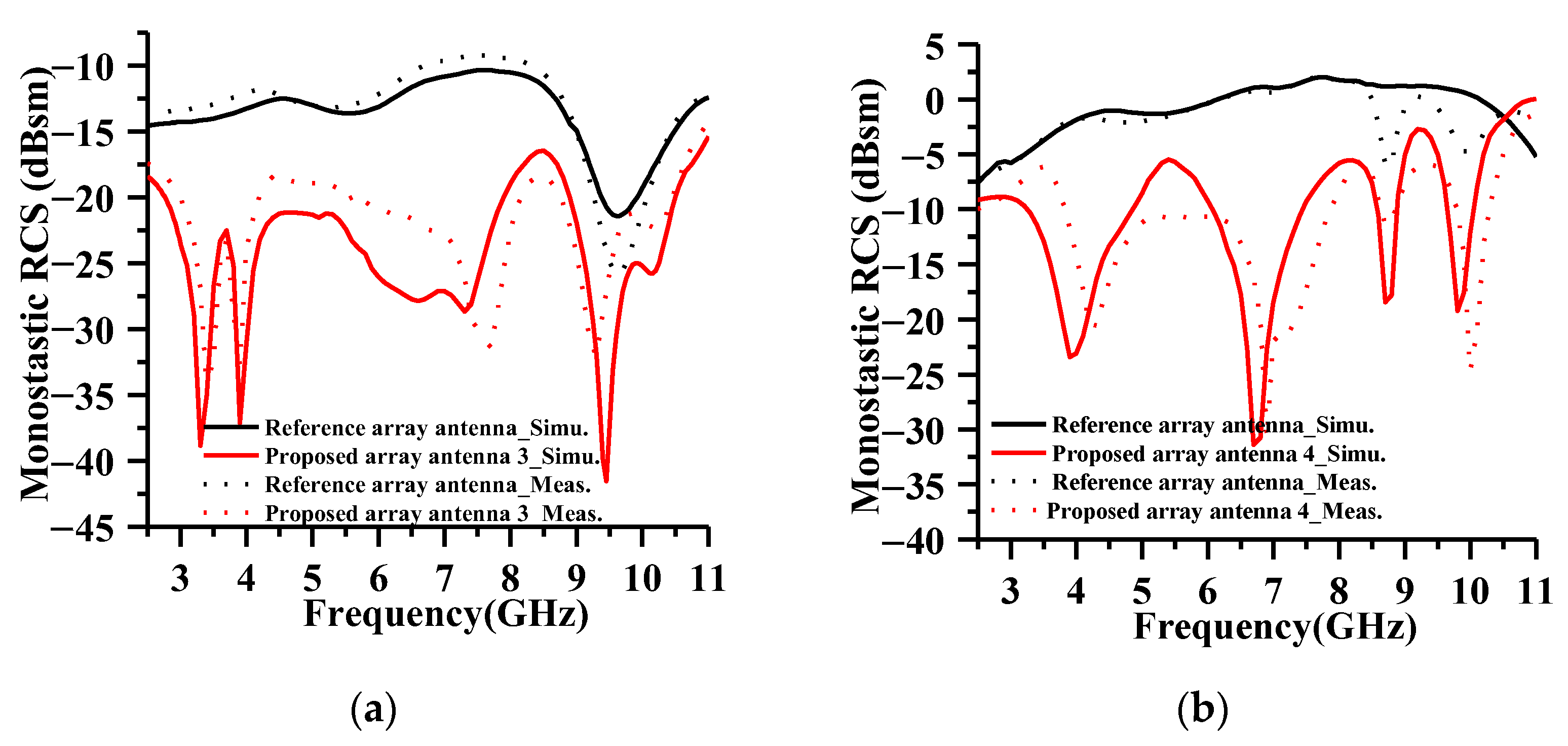
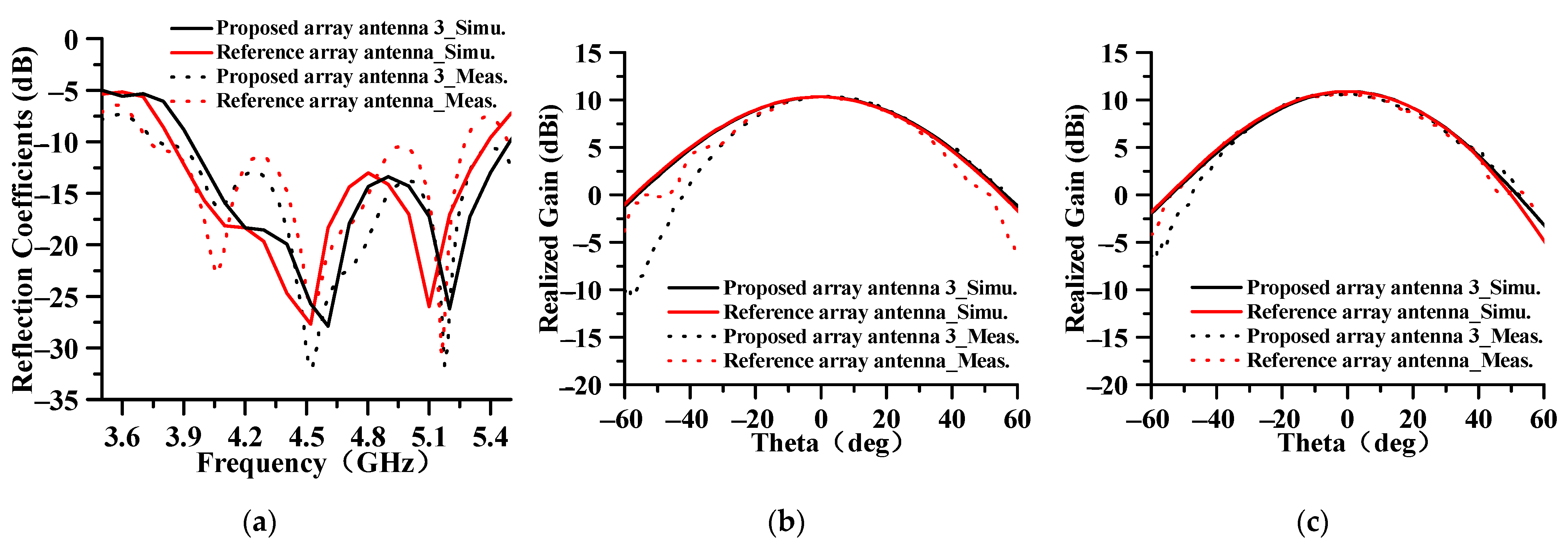
4. Test and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, H.; Li, T.; Jidi, L.; Gao, K.; Li, Q.; Qiao, J.; Li, S.; Cao, X.; Cui, T. From Metasurface to Low-RCS Array Antenna: A Fast and Efficient Route to Design Stealthy Array Antennas. IEEE Trans. Antennas Propag. 2023, 71, 4075–4084. [Google Scholar] [CrossRef]
- Li, Y.-Q.; Zhang, H.; Fu, Y.-Q.; Yuan, N.-C. RCS Reduction of Ridged Waveguide Slot Antenna Array Using EBG Radar Absorbing Material. IEEE Antennas Wirel. Propag. Lett. 2008, 7, 473–476. [Google Scholar] [CrossRef]
- Chen, J.-X.; Wang, X.-F.; Yang, L.-L.; Wang, X.-R.; Gu, X.-F.; Yang, W.-W. Asymmetrical Low-RCS FSS-Based Antenna for Tri-Band Shared-Aperture Array. IEEE Antennas Wirel. Propag. Lett. 2024, 23, 1563–1567. [Google Scholar] [CrossRef]
- Huang, H.; Omar, A.A.; Shen, Z. Low-RCS and Beam-Steerable Dipole Array Using Absorptive Frequency-Selective Reflection Structures. IEEE Trans. Antennas Propag. 2020, 68, 2457–2462. [Google Scholar] [CrossRef]
- Li, Y.; Wang, R.; Ren, P.; Xu, B.; Xiang, Z. Radar Cross Section Reduction of Microstrip Array Antenna Using FSS. In Proceedings of the 2023 IEEE 11th Asia-Pacific Conference on Antennas and Propagation (APCAP), Guangzhou, China, 19–22 November 2023; pp. 1–2. [Google Scholar] [CrossRef]
- Al-Nuaimi, M.K.T.; Huang, G.-L.; Whittow, W.G.; Chen, R.-S.; Wong, S.-W. Realization of Single-Layer Fourier Phased Metasurfaces for Wideband RCS Reduction. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 1179–1183. [Google Scholar] [CrossRef]
- Wu, H.; Wang, M.; Wang, J.; Liu, F. A Broadband Circularly Polarized Low RCS Metasurface Antenna Array. In Proceedings of the 2025 2nd International Conference on Electronic Engineering and Information Systems (EEISS), Nanjing, China, 23–25 May 2025; pp. 1–4. [Google Scholar] [CrossRef]
- Yang, H.; Li, T.; Liao, J.; Gao, K.; Li, Q.; Li, S.; Cao, X. Ultrawideband Low-RCS Array Antenna Based on Double-Layer Polarization Conversion Metasurface. IEEE Antennas Wirel. Propag. Lett. 2024, 23, 4069–4073. [Google Scholar] [CrossRef]
- Qi, Y.; Yang, F.; Chen, K.; Chen, Y.; Hu, J.; Yang, S. Low-Scattering Broadband Phased Array With Polarization-Selective Metasurface Using Characteristic Mode Analysis. IEEE Trans. Antennas Propag. 2025, 73, 2979–2989. [Google Scholar] [CrossRef]
- Yang, H.; Liao, J.; Li, T.; Gao, K.; Li, Z.; Guo, Z.; Cong, L.; Cui, T. An Efficient Design Method for Metasurface Antenna with Low in-Band RCS and Reconfigurable Scattering Fields. IEEE Trans. Antennas Propag. 2025, 73, 9553–9558. [Google Scholar] [CrossRef]
- Ran, D.; Guo, Q.; Jing, S.; Wang, L.; Xu, L.; Zang, T. An Integrated Antenna Array with New Windmill-Arranged AMC Units for RCS Reduction. IEEE Antennas Wirel. Propag. Lett. 2025, 1–5. [Google Scholar] [CrossRef]
- Xue, J.; Gong, S.; Jiang, W.; Hong, T. Wideband low RCS antenna based on absorbing surface and microstrip resonators. In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, CA, USA, 9–14 July 2017; pp. 1917–1918. [Google Scholar] [CrossRef]
- Li, P.-F.; Qu, S.-W.; Yang, S.; Hu, J. In-Band SCS Reduction of Microstrip Phased Array Based on Impedance Matching Network. IEEE Trans. Antennas Propag. 2022, 70, 330–340. [Google Scholar] [CrossRef]
- Zhao, C.; Jiang, W.; Hu, W.; Gao, Y. In-Band RCS Reduction Method for the Vivaldi Array Antennas Based on the Manipulation of the Antenna Mode Scattering Field. IEEE Trans. Antennas Propag. 2024, 72, 4687–4692. [Google Scholar] [CrossRef]
- Jia, Y.; Li, S.; Luo, J.; Shi, G.; Liu, Z.X.; Li, Z.; Liu, Y. In-Band RCS Reduction of Circularly Polarized Microstrip Antenna Array Based on a Novel Feed Network. IEEE Trans. Antennas Propag. 2024, 72, 2181–2188. [Google Scholar] [CrossRef]
- Zhao, J.; Peng, X.; Zheng, Y.; Lu, Y.; Sun, J.; Gao, X. Design of Zero-Backtracking Antenna Array with Wide-angle Low-RCS Performance. In Proceedings of the 2024 14th International Symposium on Antennas, Propagation and EM Theory (ISAPE), Hefei, China, 23–26 October 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Yue, X.; Liu, J.; Li, Z. Analysis of Scattering Mechanism of Dual-port Antennas and a Low-RCS Array Design. In Proceedings of the 2025 IEEE MTT-S International Wireless Symposium (IWS), Xi’an, China, 19–22 May 2025. [Google Scholar] [CrossRef]
- Yang, Z.; Gao, Y.; Hu, W.; Jiang, W. Design of Wideband Wide-angle Low-RCS Quasi-Conformal Array Based on Unit Equivalent Reactance Regulation and Arrangement Optimization. IEEE Trans. Antennas Propag. 2025, 1. [Google Scholar] [CrossRef]
- Jiang, W.; Gong, S.X.; Li, Y.; Zhang, K.Z. Novel microstrip antenna array with low RCS. In Proceedings of the 2014 3rd Asia-Pacific Conference on Antennas and Propagation, Harbin, China, 26–29 July 2014; pp. 447–449. [Google Scholar] [CrossRef]
- Fan, Q.; Wang, Y.; Yuan, J.; Li, Z. Ultra-wideband Low RCS Conformal Patch Array Antenna with a Modified Ground Plane. In Proceedings of the 2023 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Qingdao, China, 14–17 May 2023; pp. 1–3. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, Y.; Yang, S. In-Band Radar Cross-Section Reduction of Slot Antenna Using Characteristic Modes. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1166–1170. [Google Scholar] [CrossRef]
- Liu, Y.; Du, B.; Jia, D. Ultra-wide band radar cross section reduction for ring-shaped microstrip antenna based on characteristic mode analysis. Microw. Opt. Technol. Lett. 2021, 63, 1538–1546. [Google Scholar] [CrossRef]
- Shi, G.; Jia, Y.; Liu, Y. Theoretic Study of Antenna Scattering Problems Based on Characteristic Modes and Its Application In Reducing Antenna Scattering. IEEE Trans. Antennas Propag. 2023, 71, 2098–2109. [Google Scholar] [CrossRef]
- Jia, Y.; Luo, J.; Ren, X.; Shi, G.; Liu, Y. Design of Low-RCS Vivaldi Antenna Based on Characteristic Mode Analysis. IEEE Antennas Wireless Propag. Lett. 2024, 23, 1246–1250. [Google Scholar] [CrossRef]
- Han, J.; Jia, D.; Du, B.; Han, G. Design of Broadband Low-RCS Array Antennas Based on Characteristic Mode Cancellation. Electronics 2023, 12, 1536. [Google Scholar] [CrossRef]
- Singh, B.; Dar, U.R.; Zarger, M.M.; Rajput, A. Low RCS Antenna Array Design Using Checkerboard Arrangement of Antenna Elements. In Proceedings of the 2024 IEEE Microwaves, Antennas, and Propagation Conference (MAPCON), Hyderabad, India, 9–13 December 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Gao, K.; Cao, X.; Gao, J.; Li, T.; Yang, H.; Li, S. Low-RCS Metasurface Antenna Array Design With Improved Radiation Performance Using Odd- and Even-Mode Analysis. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 421–425. [Google Scholar] [CrossRef]
- Gou, Y.; Chen, Y.; Yang, S. RCS Reduction for Wideband Antenna Array. In Proceedings of the 2021 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting (APS/URSI), Singapore, 4–10 December 2021; pp. 1307–1308. [Google Scholar] [CrossRef]
- Huo, K.; Gao, Y.; Jiang, W. An Ultra-Wideband Low-Scattering Tightly-Coupled Dipole Array. In Proceedings of the 2024 IEEE 12th Asia-Pacific Conference on Antennas and Propagation (APCAP), Nanjing, China, 22–25 September 2024; pp. 1–2. [Google Scholar] [CrossRef]
- Gu, P.; Cao, Z.; He, Z.; Ding, D. Design of Ultrawideband RCS Reduction Metasurface Using Space Mapping and Phase Cancellation. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 1386–1390. [Google Scholar] [CrossRef]
- Stutzman, W.L.; Thiele, G.A. Antenna Theory and Design, 3rd ed.; John Weily: Hoboken, NJ, USA, 2012. [Google Scholar]
- Liu, Y.; Du, B.; Jia, D. Design of Broad-Angle Low-RCS Microstrip Antenna for Dual-Polarization Using Characteristic Mode Analysis. Electronics 2025, 14, 2121. [Google Scholar] [CrossRef]
- Zhong, S. Antenna Theory and Techniques, 1st ed.; Publishing House of Electronics Industry: Beijing, China, 2011. (In Chinese) [Google Scholar]
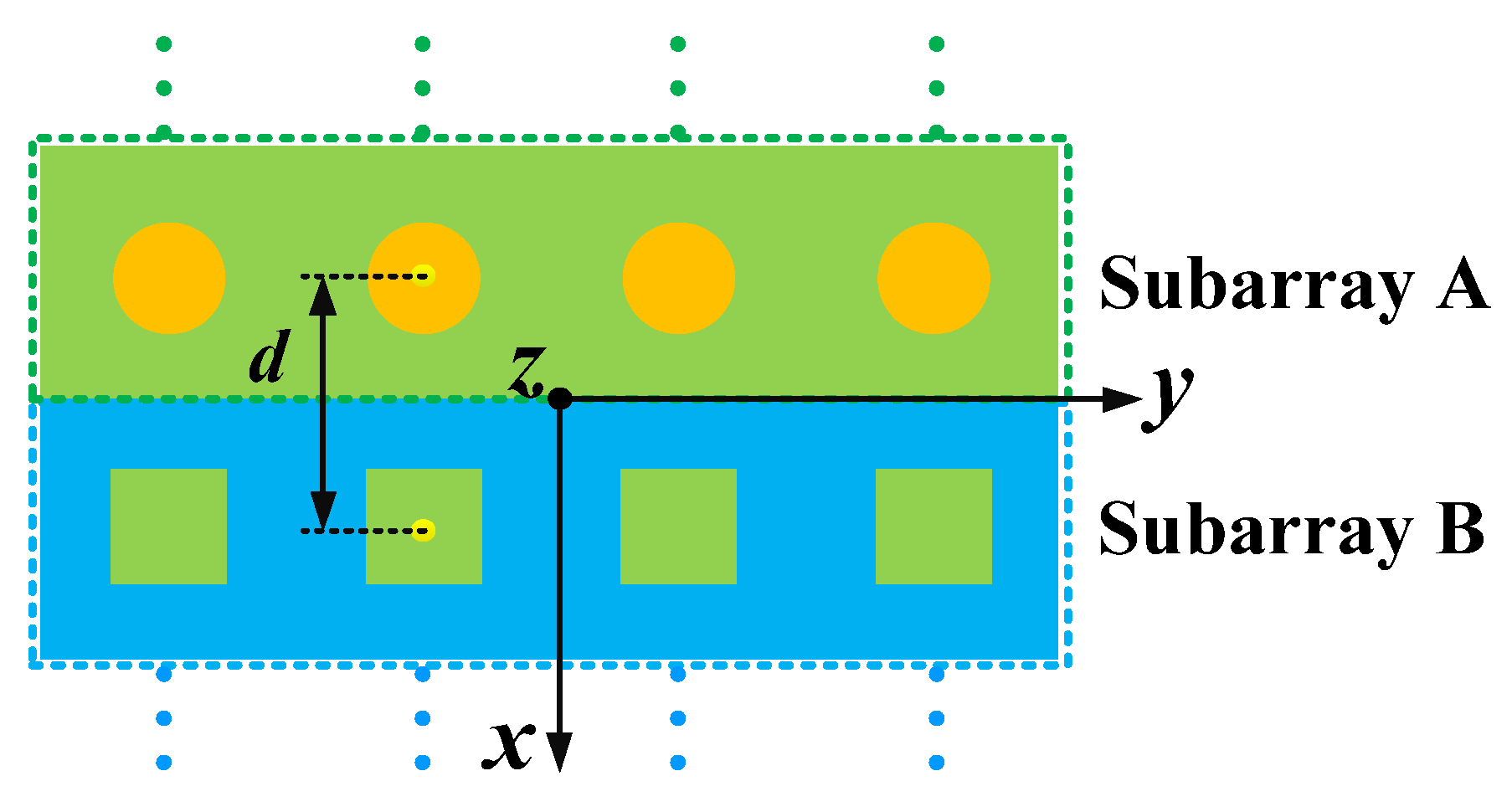
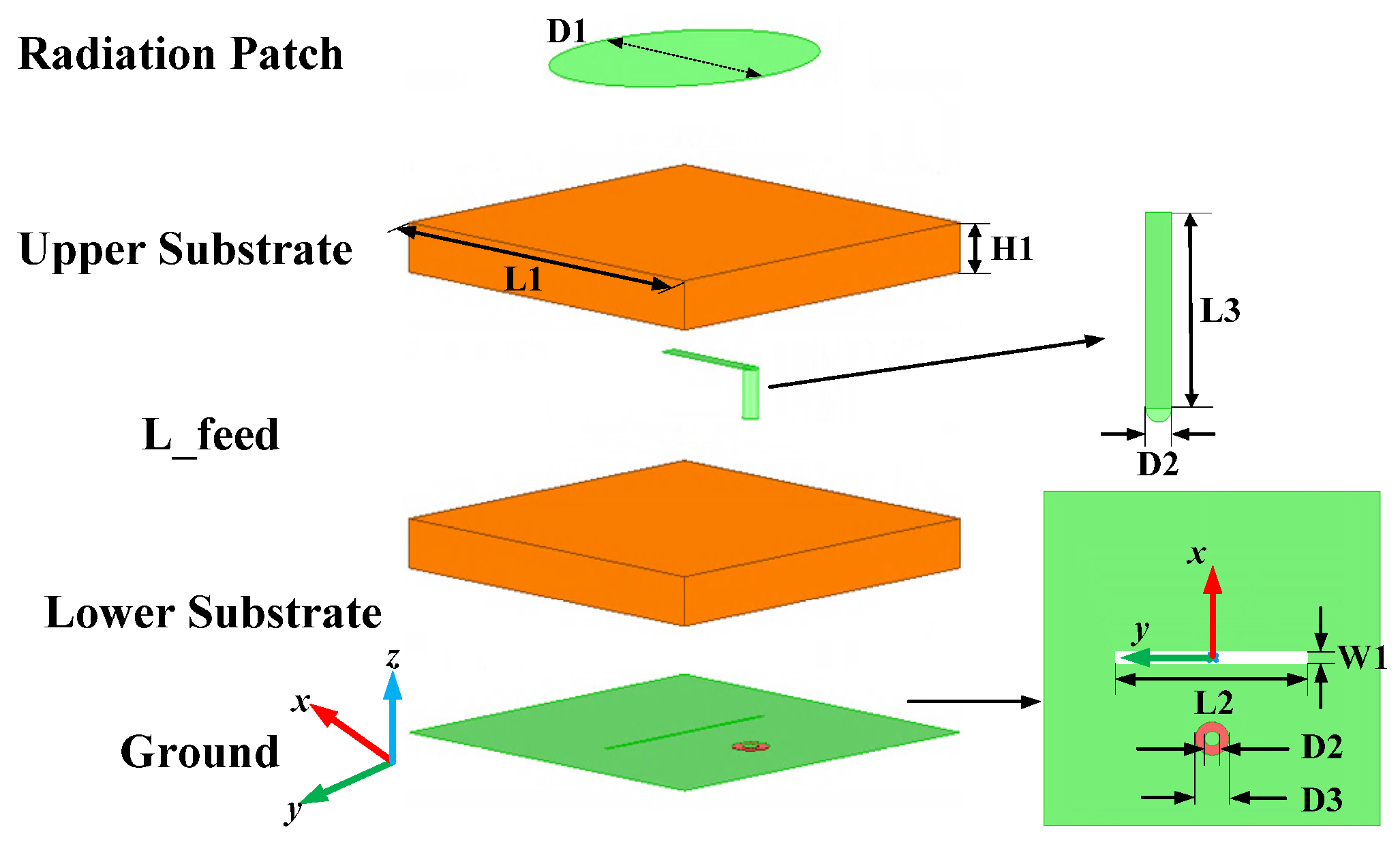
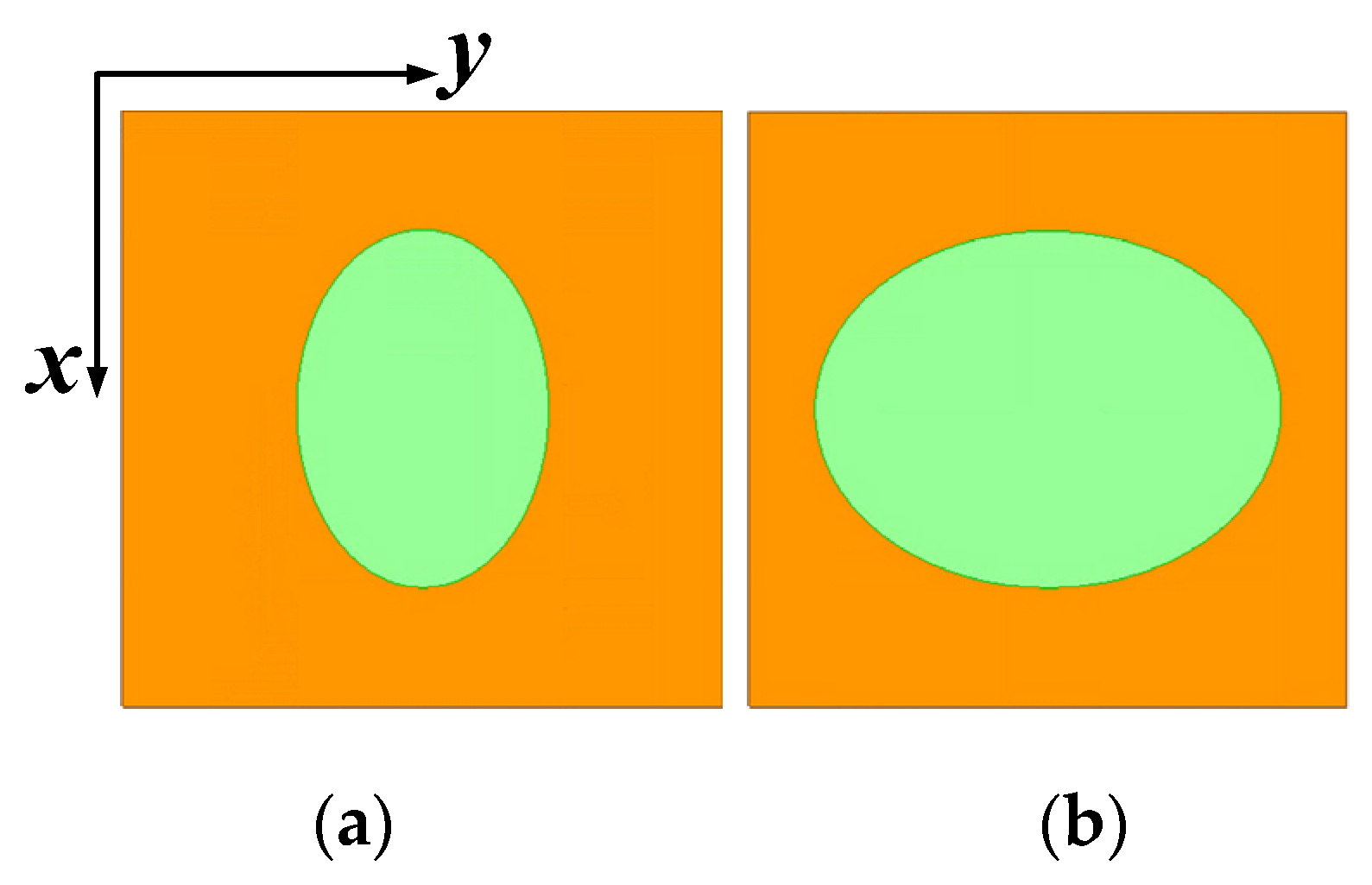
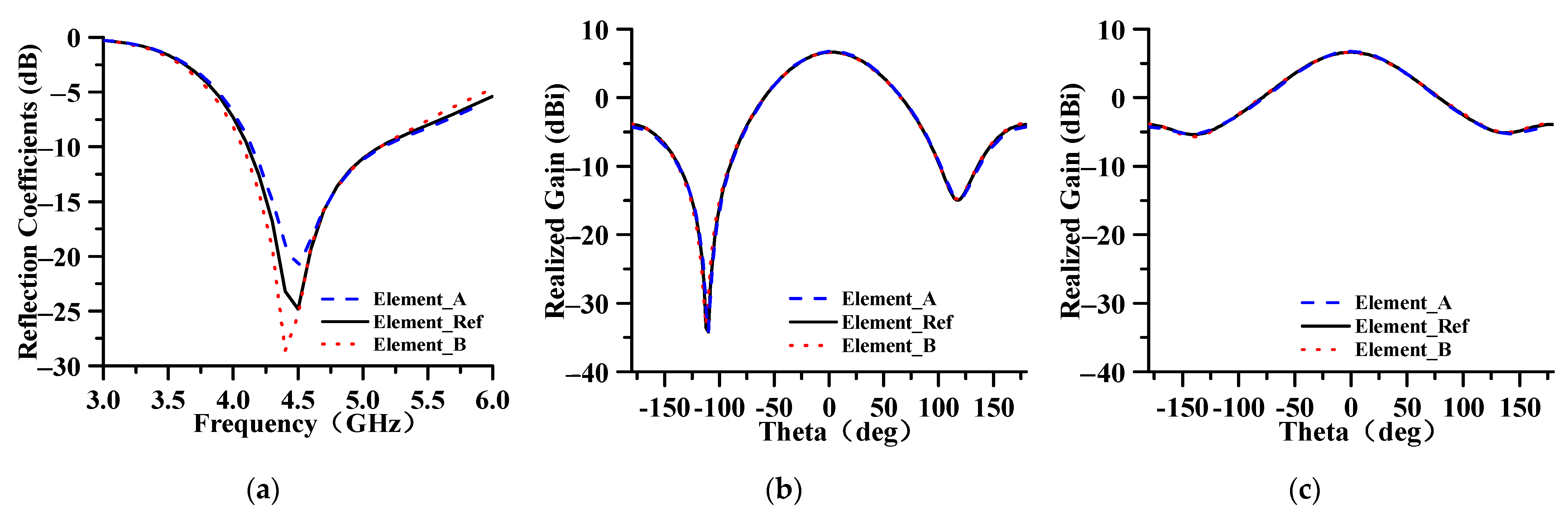

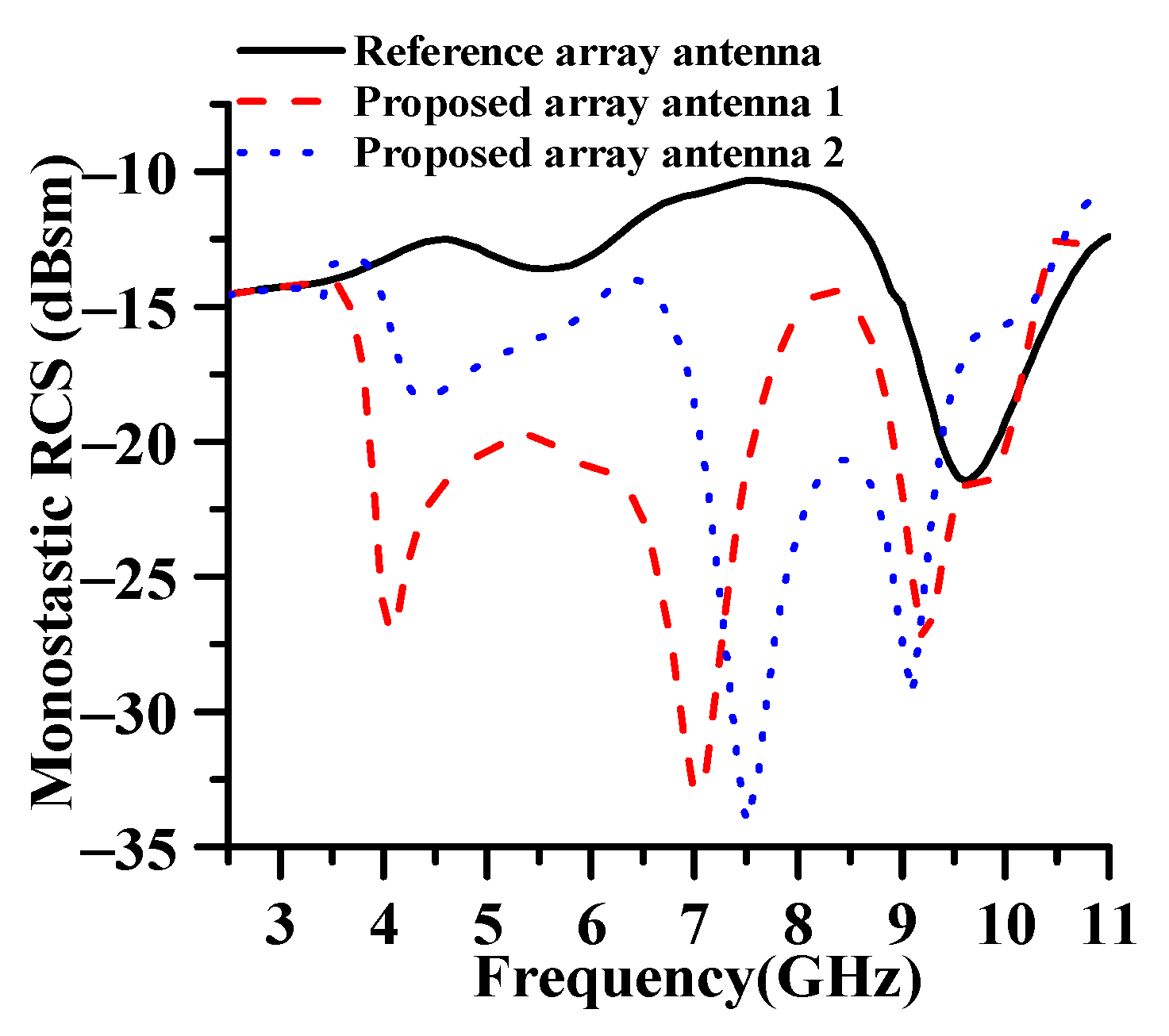
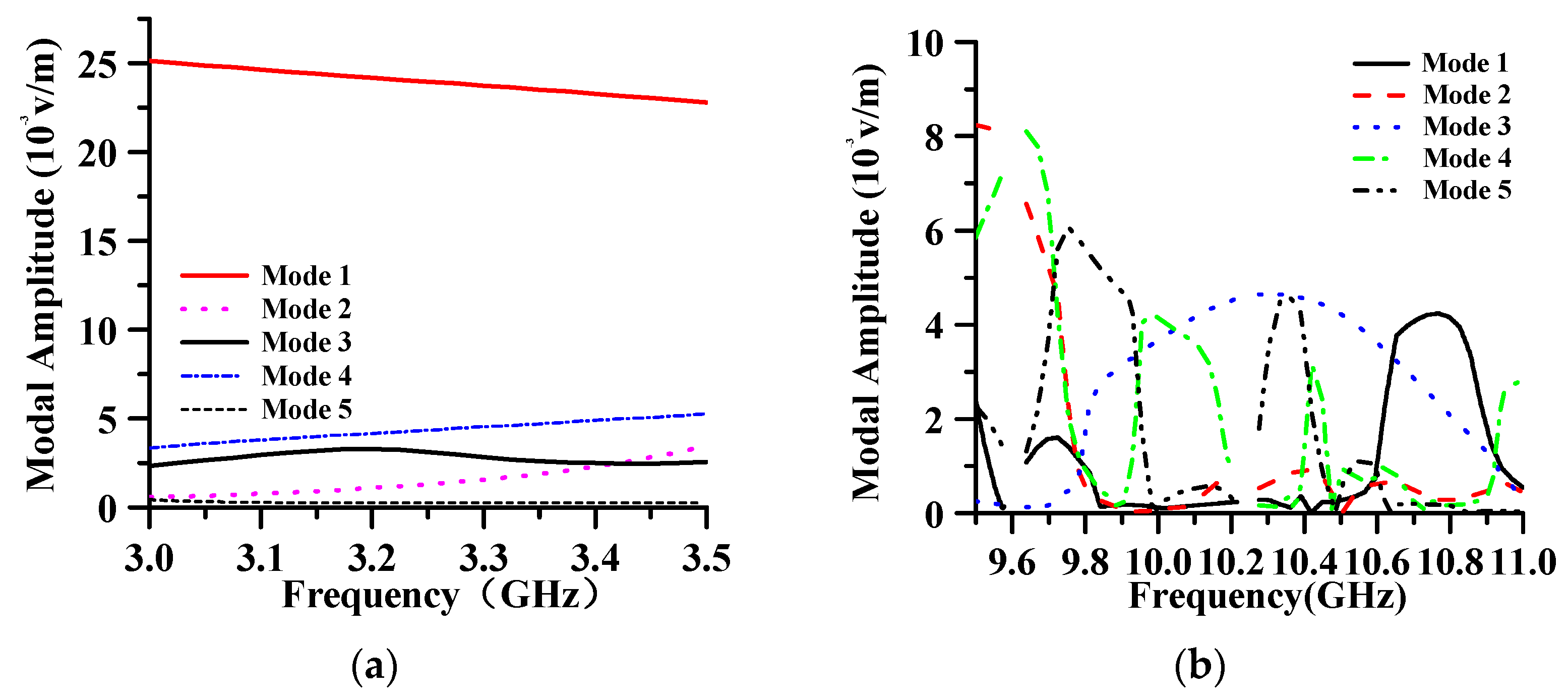
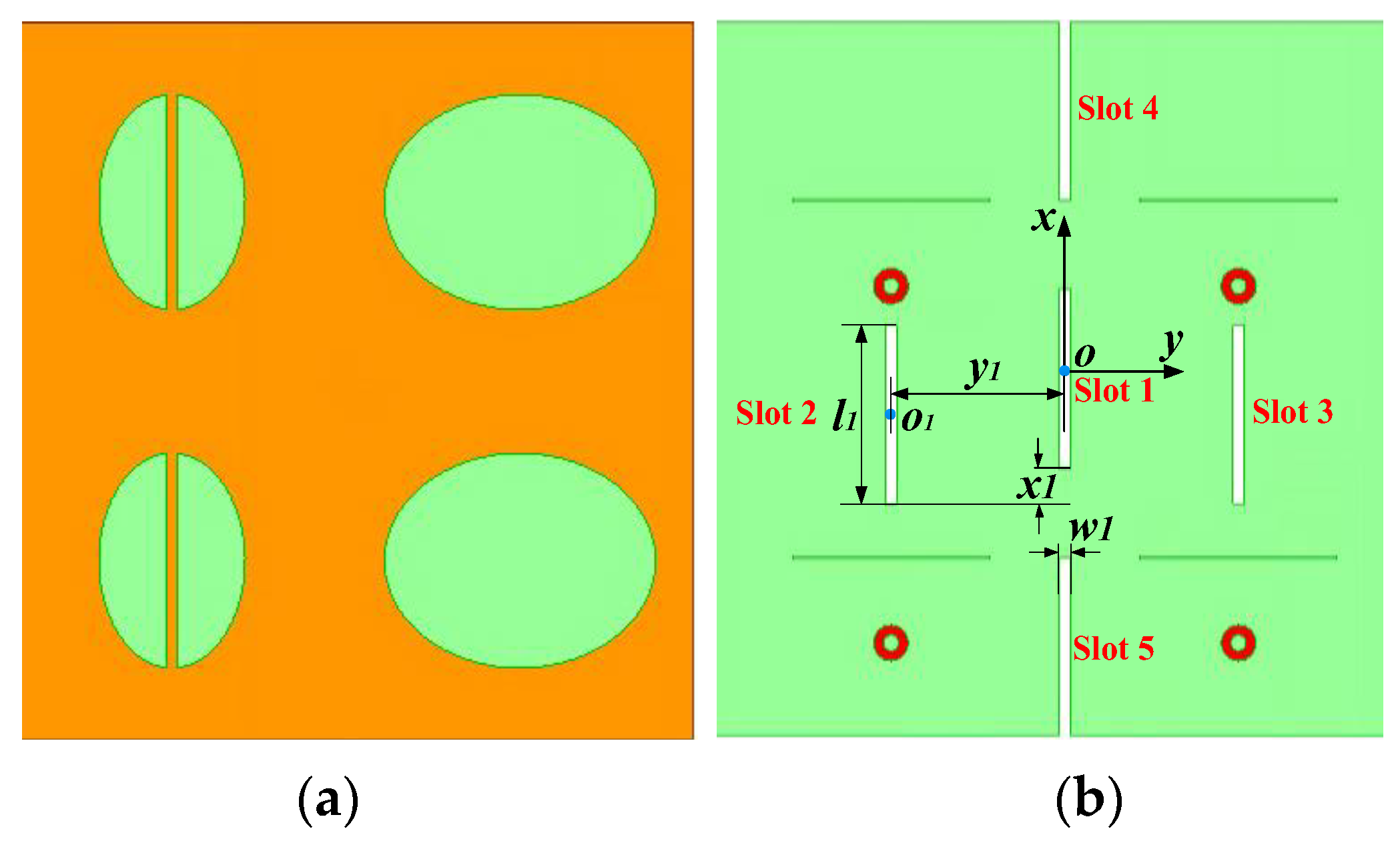

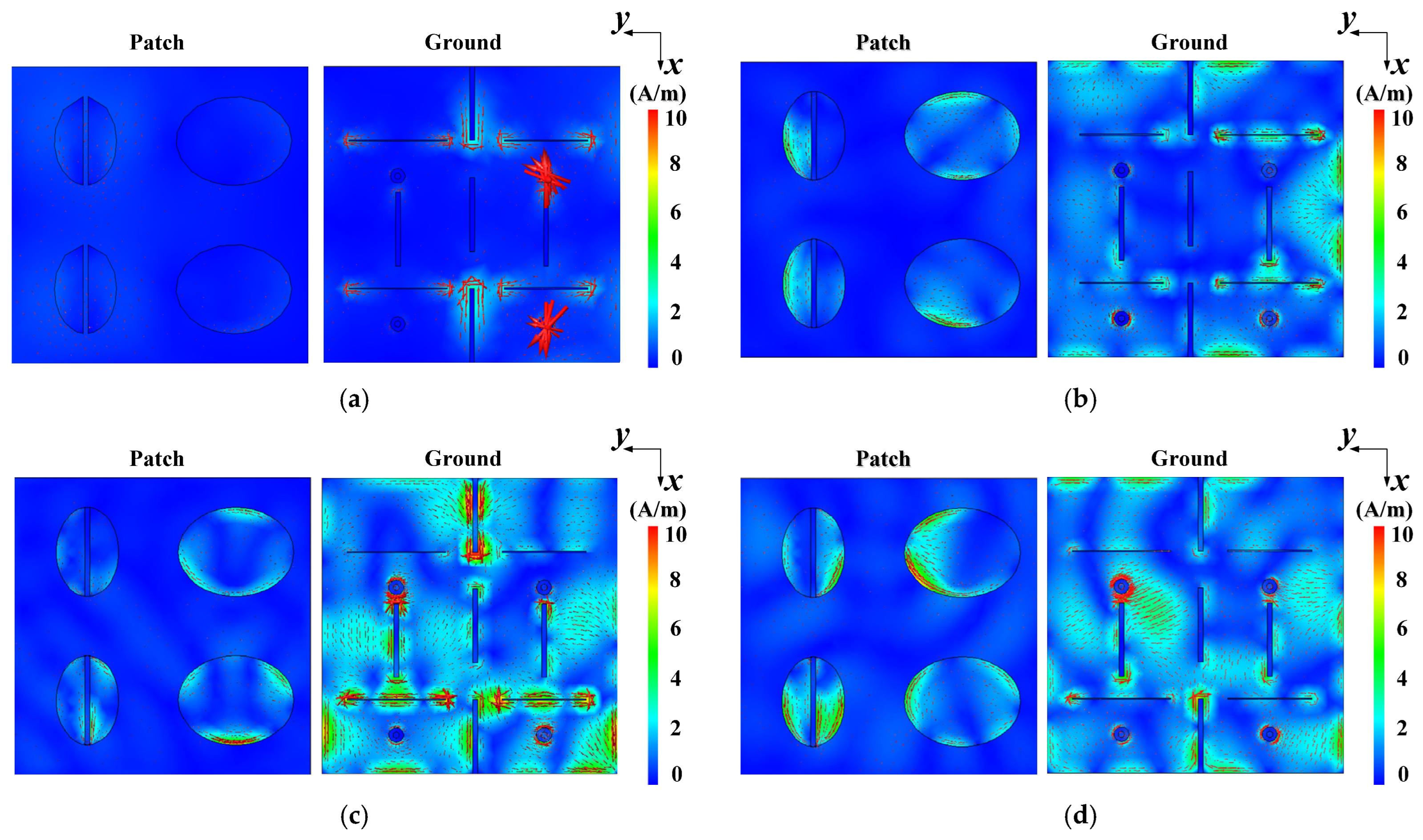
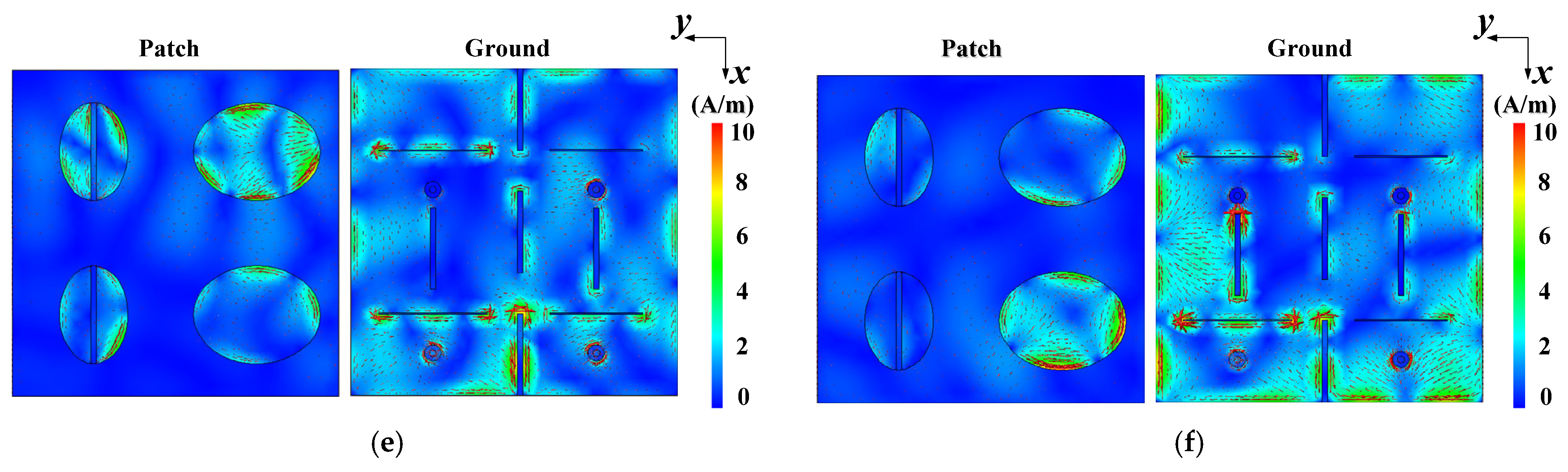
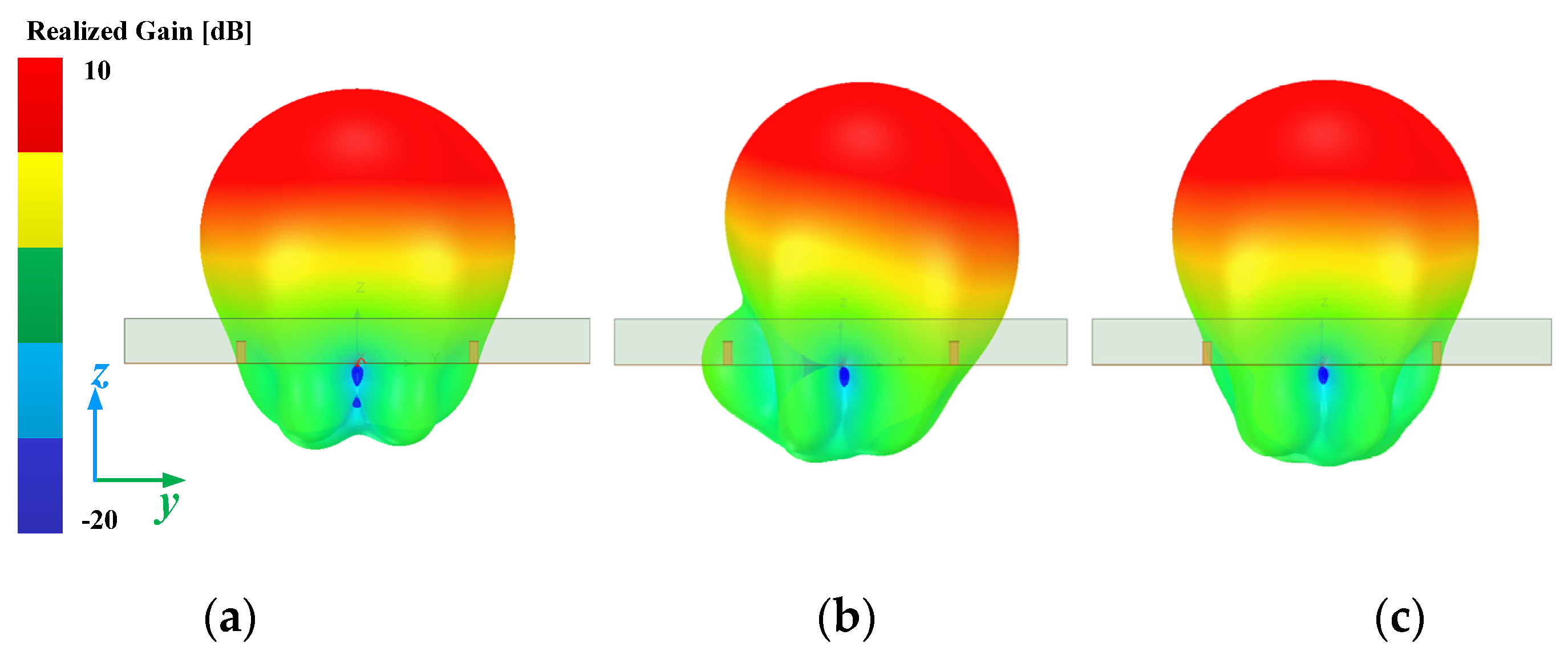


| Parameters | Value/mm |
|---|---|
| D1 | 18 |
| D2 | 1.3 |
| D3 | 3 |
| H1 | 3 |
| L1 | 30 |
| L2 | 17 |
| L3 | 10 |
| W1 | 0.3 |
| X1 | 7.2 |
| Paired Elements | Bandwidth/GHz |
|---|---|
| 0.9 and 1.1 | / * |
| 0.8 and 1.2 | 4.64–5.35 |
| 0.7 and 1.3 | 4.26–6.52 |
| Array | RCSR Band (GHz)/RB* (%) | RCSR Mean Value (dB) | RCSR Peak Value (dB) | Method |
|---|---|---|---|---|
| Proposed 1 | 3.5–9.5/92 | 6 | 20 | Scattering Cancellation |
| Proposed 3 | 2.5–11/126 | 12 | 24 | Scattering Cancellation + Array-level Modification |
| Array Arrangement | RCSR Band (GHz)/RB* (%) | RCSR Mean Value (dB) | RCSR Peak Value (dB) |
|---|---|---|---|
| ABAB | 2.5–10.5/123 | 9 | 32.5 |
| ABBA | 2.6–10.3/119 | 7.3 | 31.4 |
| BAAB | 3.6–10.7/99 | 6.1 | 21.5 |
| BABA | 3.5–10.7/101 | 6.6 | 23 |
| Ref. | Electrical Size (λ02) | Array Configuration | OB* (GHz)/RB* (%) | Gain Variation (dB) | RCSR Band (GHz)/RB* (%) | RCSR Mean Value (dB) | RCSR Peak Value (dB) | RCSR Angle Range (°) | Method |
|---|---|---|---|---|---|---|---|---|---|
| [5] | 1.0 × 1.0 | 2 × 2 | 4.3/− | 0 | 9–11/20 | 5 | 15 | − | FSS |
| [8] | 1.1 × 1.1 | 2 × 2 | 6.7–7.6/13 | +0.3 | 6–16/91 | − | 32 | − | PCM |
| [9] | − | 10 × 10 | 6–18/100 | 0 | 6–24/120 | 10 | 30 | ±20° | MS + CMA |
| [10] | 3.3 × 3.3 | 8 × 8 | 4.6–5.25/13.2 | − | 4.0–6.0/40 | 10 | 15 | − | MS |
| [11] | 3.3 × 3.3 | 4 × 4 | 8.8–12/30.8 | 0 | 7–13/60 | 10 | 21 | 0° | AMC |
| [12] | 3.3 × 3.3 | 1 × 1 | 8.5–10.4/20 | − | 3.2–15/130 | − | 16 | − | Resonator + MS |
| [17] | 5 × 5 | 10 × 10 | 9.7–10.2/5 | − | 9.6–10.4/8 | 12 | 20 | ±40° | Active Cancellation |
| [18] | − | 8 × 8 | 10–11.75/16.1 | 0 | 5–12/82.3 | 9 | 25 | 0° | Unit Equivalent Reactance Regulation |
| [19] | 1.3 × 1.3 | 2 × 2 | 4.3/- | −0.7 | 4–16/120 | − | 26 | ±10° | Shape Modification |
| [27] | 2.0 × 2.0 | 4 × 4 | 5.05–5.42/7 | +2.0 | 5.1–6.9/30 | 6 | 20 | ±60° | Scattering Cancellation |
| This work | 1.0 × 1.0 | 2 × 2 | 3.76–5.45/37 | 0 | 2.5–11/126 | 10.3 | 22 | ±15° | Scattering Cancellation + Array-level Modification Using CMA |
| 2.0 × 2.0 | 4 × 4 | 3.8–5.3/31.1 | 0 | 2.5–10.5/123 | 8.0 | 24 | ±15° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Liu, Y.; Du, B.; Jia, D.; Han, X. An Integrated Scattering Cancellation and Modification Approach for Broadband RCS Reduction of Array Antenna. Electronics 2026, 15, 108. https://doi.org/10.3390/electronics15010108
Liu Y, Du B, Jia D, Han X. An Integrated Scattering Cancellation and Modification Approach for Broadband RCS Reduction of Array Antenna. Electronics. 2026; 15(1):108. https://doi.org/10.3390/electronics15010108
Chicago/Turabian StyleLiu, Yakun, Biao Du, Dan Jia, and Xuchen Han. 2026. "An Integrated Scattering Cancellation and Modification Approach for Broadband RCS Reduction of Array Antenna" Electronics 15, no. 1: 108. https://doi.org/10.3390/electronics15010108
APA StyleLiu, Y., Du, B., Jia, D., & Han, X. (2026). An Integrated Scattering Cancellation and Modification Approach for Broadband RCS Reduction of Array Antenna. Electronics, 15(1), 108. https://doi.org/10.3390/electronics15010108






