Enhancing Out-of-Distribution Detection Under Covariate Shifts: A Full-Spectrum Contrastive Denoising Framework
Abstract
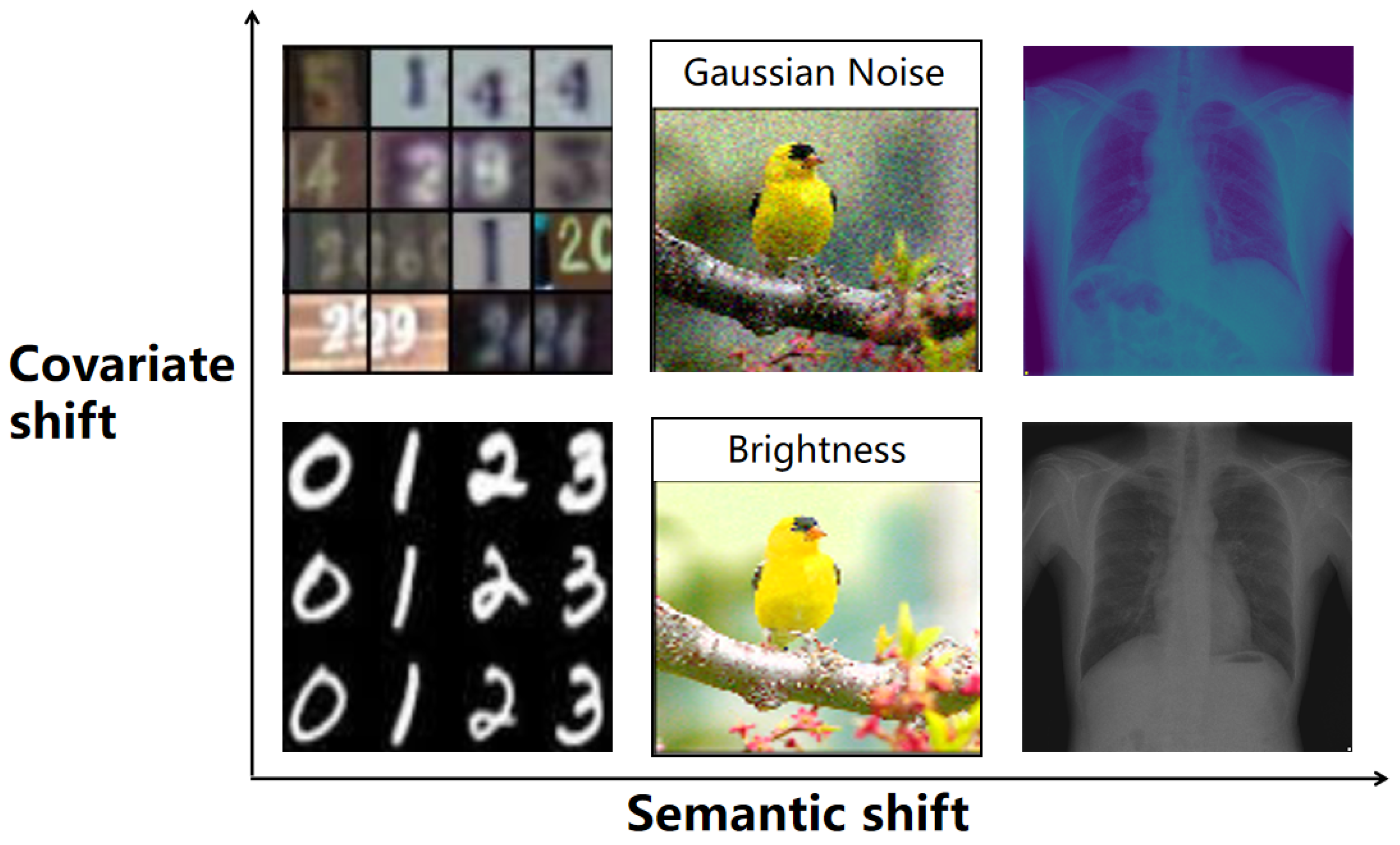
1. Introduction
- We propose the Full-Spectrum Contrastive Denoising (FSCD) framework, which integrates semantic boundary initialization with fine-tuning, significantly improving OOD detection performance in scenarios with covariate shifts.
- We propose the dual-level perturbation augmentation (DLPA) and feature contrastive denoising (FCD) modules to simulate complex covariate shifts and enable more granular differentiation of samples, thereby enhancing the model’s adaptability to distributional variations.
- The effectiveness and superiority of FSCD are validated through extensive experiments on multiple datasets, demonstrating its advantages over existing approaches in full-spectrum out-of-distribution detection and providing new insights for future research.
2. Related Works
2.1. Out-of-Distribution Detection
2.2. Solutions to Covariate Shifts
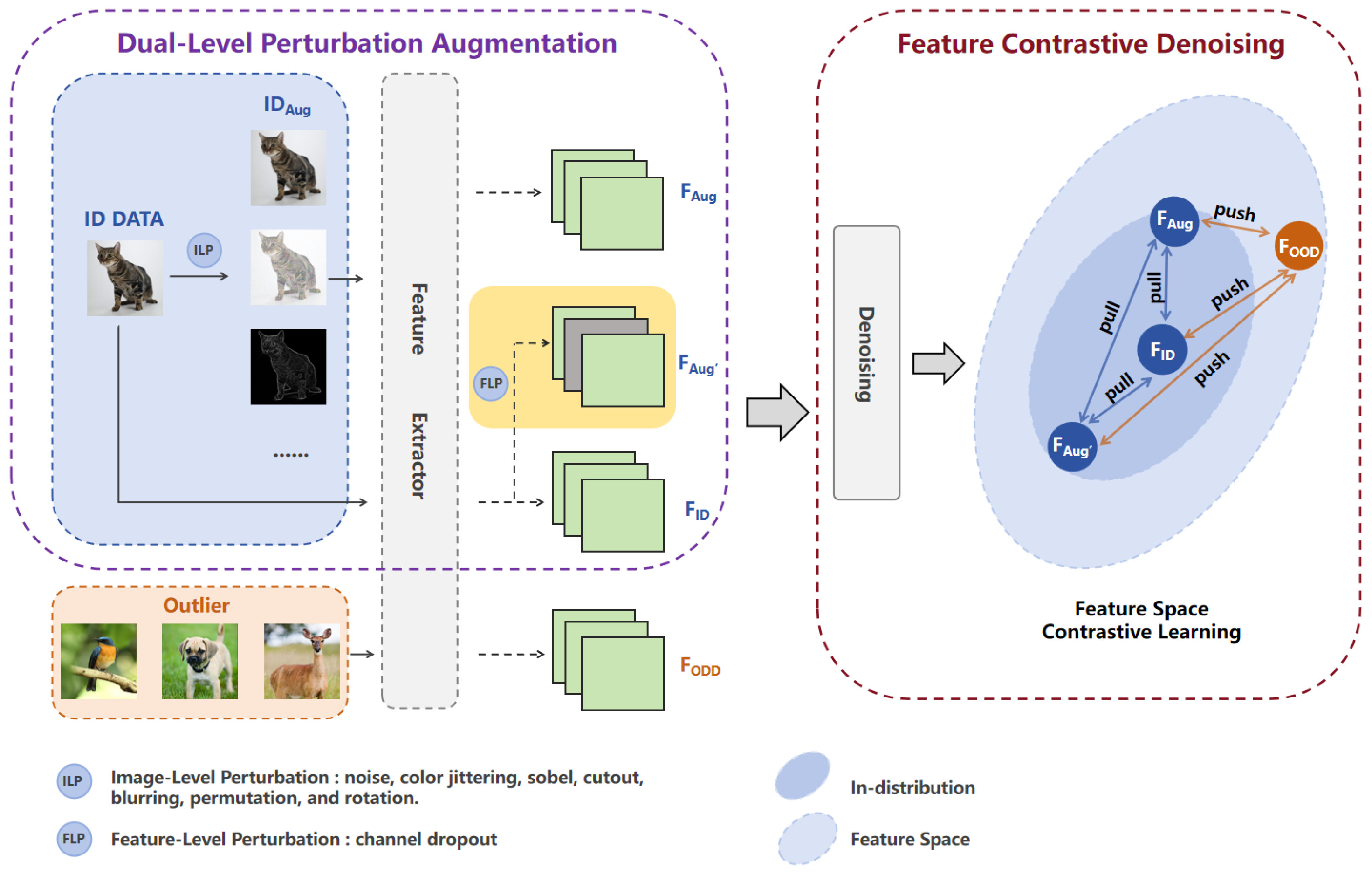
3. Proposed Method
3.1. Overall Architecture
3.2. Semantic Boundary Initialization Stage
3.3. Fine-Tuning Stage
3.3.1. Dual-Level Perturbation Augmentation Module
3.3.2. Feature Contrastive Denoising Module
4. Experiments
4.1. Datasets
4.2. Experimental Settings
4.3. Evaluation Metrics
4.4. Results and Analysis
4.5. Effectiveness of the Modules
4.6. Impact of Backbone Networks
4.7. Influence of Hyperparameters
5. Limitations and Future Research Directions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Nguyen, A.; Yosinski, J.; Clune, J. Deep neural networks are easily fooled: High confidence predictions for unrecognizable images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 427–436. [Google Scholar]
- Hendrycks, D.; Gimpel, K. A baseline for detecting misclassified and out-of-distribution examples in neural networks. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017; pp. 1–12. [Google Scholar]
- Cui, P.; Wang, J. Out-of-distribution (OOD) detection based on deep learning: A review. Electronics 2022, 11, 3500. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, J.; Wang, P.; Wang, H.; Lin, Y.; Zhang, H.; Sun, Y.; Du, X.; Zhou, K.; Zhang, W.; et al. OpenOOD v1.5: Enhanced Benchmark for Out-of-Distribution Detection. In Proceedings of the NeurIPS 2023 Workshop on Distribution Shifts: New Frontiers with Foundation Models, New Orleans, LA, USA, 15 December 2023. [Google Scholar]
- Yang, J.; Zhou, K.; Liu, Z. Full-spectrum out-of-distribution detection. Int. J. Comput. Vis. 2023, 131, 2607–2622. [Google Scholar] [CrossRef]
- Hsu, Y.C.; Shen, Y.; Jin, H.; Kira, Z. Generalized odin: Detecting out-of-distribution image without learning from out-of-distribution data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 10951–10960. [Google Scholar]
- Long, X.; Zhang, J.; Shan, S.; Chen, X. Rethinking the Evaluation of Out-of-Distribution Detection: A Sorites Paradox. Adv. Neural Inf. Process. Syst. 2024, 37, 89806–89833. [Google Scholar]
- Averly, R.; Chao, W.L. Unified out-of-distribution detection: A model-specific perspective. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–3 October 2023; pp. 1453–1463. [Google Scholar]
- Yang, W.; Zhang, B.; Russakovsky, O. Imagenet-Ood: Deciphering Modern Out-of-Distribution Detection Algorithms. In Proceedings of the 12th International Conference on Learning Representations, International Conference on Learning Representations 2024, Vienna Austria, 7–11 May 2024. [Google Scholar]
- Yang, J.; Wang, P.; Zou, D.; Zhou, Z.; Ding, K.; Peng, W.; Wang, H.; Chen, G.; Li, B.; Sun, Y.; et al. Openood: Benchmarking generalized out-of-distribution detection. Adv. Neural Inf. Process. Syst. 2022, 35, 32598–32611. [Google Scholar]
- Hendrycks, D.; Mazeika, M.; Dietterich, T. Deep Anomaly Detection with Outlier Exposure. arXiv 2018, arXiv:1812.04606. [Google Scholar]
- Papadopoulos, A.A.; Rajati, M.R.; Shaikh, N.; Wang, J. Outlier exposure with confidence control for out-of-distribution detection. Neurocomputing 2021, 441, 138–150. [Google Scholar] [CrossRef]
- Zhang, J.; Inkawhich, N.; Linderman, R.; Chen, Y.; Li, H. Mixture outlier exposure: Towards out-of-distribution detection in fine-grained environments. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Paris, France, 2–3 October 2023; pp. 5531–5540. [Google Scholar]
- Choi, H.; Jeong, H.; Choi, J.Y. Balanced energy regularization loss for out-of-distribution detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Paris, France, 2–3 October 2023; pp. 15691–15700. [Google Scholar]
- Xu, K.; Chen, R.; Franchi, G.; Yao, A. Scaling for Training Time and Post-hoc Out-of-distribution Detection Enhancement. In Proceedings of the International Conference on Learning Representations, Vienna Austria, 7–11 May 2024. [Google Scholar]
- Liang, S.; Li, Y.; Srikant, R. Enhancing the reliability of out-of-distribution image detection in neural networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018; pp. 1–12. [Google Scholar]
- Liu, W.; Wang, X.; Owens, J.; Li, Y. Energy-based out-of-distribution detection. Adv. Neural Inf. Process. Syst. 2020, 33, 21464–21475. [Google Scholar]
- Sun, Y.; Guo, C.; Li, Y. React: Out-of-distribution detection with rectified activations. Adv. Neural Inf. Process. Syst. 2021, 34, 144–157. [Google Scholar]
- Hendrycks, D.; Basart, S.; Mazeika, M.; Zou, A.; Kwon, J.; Mostajabi, M.; Steinhardt, J.; Song, D. Scaling Out-of-Distribution Detection for Real-World Settings. In Proceedings of the International Conference on Machine Learning, PMLR, Baltimore, MD, USA, 17–23 July 2022; pp. 8759–8773. [Google Scholar]
- Krumpl, G.; Avenhaus, H.; Possegger, H.; Bischof, H. Ats: Adaptive temperature scaling for enhancing out-of-distribution detection methods. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 1–6 January 2024; pp. 3864–3873. [Google Scholar]
- Karunanayake, N.; Seneviratne, S.; Chawla, S. ExCeL: Combined Extreme and Collective Logit Information for Out-of-Distribution Detection. arXiv 2023, arXiv:2311.14754. [Google Scholar]
- Zhang, S.; Zhang, X.; Wan, S.; Ren, W.; Zhao, L.; Shen, L. Generative adversarial and self-supervised dehazing network. IEEE Trans. Ind. Inform. 2023, 20, 4187–4197. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Hu, E.; Wang, A.; Shiri, B.; Lin, W. VNDHR: Variational Single Nighttime Image Dehazing for Enhancing Visibility in Intelligent Transportation Systems via Hybrid Regularization. IEEE Trans. Intell. Transp. Syst. 2025, 2025, 1–15. [Google Scholar] [CrossRef]
- Tack, J.; Mo, S.; Jeong, J.; Shin, J. Csi: Novelty detection via contrastive learning on distributionally shifted instances. Adv. Neural Inf. Process. Syst. 2020, 33, 11839–11852. [Google Scholar]
- Gwon, K.; Yoo, J. Out-of-distribution (OOD) detection and generalization improved by augmenting adversarial mixup samples. Electronics 2023, 12, 1421. [Google Scholar] [CrossRef]
- Wei, T.; Wang, B.L.; Zhang, M.L. EAT: Towards Long-Tailed Out-of-Distribution Detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 15787–15795. [Google Scholar]
- Feng, S.; Wang, C. When an extra rejection class meets out-of-distribution detection in long-tailed image classification. Neural Netw. 2024, 178, 106485. [Google Scholar] [CrossRef]
- Sohn, K.; Berthelot, D.; Carlini, N.; Zhang, Z.; Zhang, H.; Raffel, C.A.; Cubuk, E.D.; Kurakin, A.; Li, C.L. Fixmatch: Simplifying semi-supervised learning with consistency and confidence. Adv. Neural Inf. Process. Syst. 2020, 33, 596–608. [Google Scholar]
- Yang, L.; Qi, L.; Feng, L.; Zhang, W.; Shi, Y. Revisiting weak-to-strong consistency in semi-supervised semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 7236–7246. [Google Scholar]
- Zhao, H.; Gallo, O.; Frosio, I.; Kautz, J. Loss functions for image restoration with neural networks. IEEE Trans. Comput. Imaging 2016, 3, 47–57. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Hull, J.J. A database for handwritten text recognition research. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 550–554. [Google Scholar] [CrossRef]
- Xiao, H. Fashion-mnist: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Cimpoi, M.; Maji, S.; Kokkinos, I.; Mohamed, S.; Vedaldi, A. Describing textures in the wild. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3606–3613. [Google Scholar]
- Cao, K.; Wei, C.; Gaidon, A.; Arechiga, N.; Ma, T. Learning imbalanced datasets with label-distribution-aware margin loss. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Le, Y.; Yang, X. Tiny imagenet visual recognition challenge. CS 231N 2015, 7, 3. [Google Scholar]
- Zhou, B.; Lapedriza, A.; Khosla, A.; Oliva, A.; Torralba, A. Places: A 10 million image database for scene recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 1452–1464. [Google Scholar] [CrossRef] [PubMed]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Santa Cruz, B.G.; Bossa, M.N.; Sölter, J.; Husch, A.D. Public COVID-19 x-ray datasets and their impact on model bias–a systematic review of a significant problem. Med. Image Anal. 2021, 74, 102225. [Google Scholar] [CrossRef]
- Wang, L.; Lin, Z.Q.; Wong, A. Covid-net: A tailored deep convolutional neural network design for detection of covid-19 cases from chest x-ray images. Sci. Rep. 2020, 10, 19549. [Google Scholar] [CrossRef]
- Winther, H.B.; Laser, H.; Gerbel, S.; Maschke, S.K.; Hinrichs, J.B.; Vogel-Claussen, J.; Wacker, F.K.; Höper, M.M.; Meyer, B.C. COVID-19 Image Repository. 2020. Available online: https://figshare.com/articles/dataset/COVID-19_Image_Repository/12275009 (accessed on 8 February 2025). [CrossRef]
- Yang, X.; He, X.; Zhao, J.; Zhang, Y.; Zhang, S.; Xie, P. Covid-ct-dataset: A ct scan dataset about COVID-19. arXiv 2020, arXiv:2003.13865. [Google Scholar]
- RSNA. RSNA Pediatric Bone Age Challenge; RSNA: Oak Brook, IL, USA, 2017. [Google Scholar]
- Torralba, A.; Fergus, R.; Freeman, W.T. 80 million tiny images: A large data set for nonparametric object and scene recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1958–1970. [Google Scholar] [CrossRef]
- Lee, K.; Lee, K.; Lee, H.; Shin, J. A simple unified framework for detecting out-of-distribution samples and adversarial attacks. Adv. Neural Inf. Process. Syst. 2018, 31, 1–11. [Google Scholar]
- Wang, H.; Li, Z.; Feng, L.; Zhang, W. Vim: Out-of-distribution with virtual-logit matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 4921–4930. [Google Scholar]
- Chen, Y.; Wu, Y.; Wang, T.; Zhang, S.; Zhu, D.; Liu, C. Mitigating covariance overfitting in out-of-distribution detection through intrinsic parameter learning. Knowl.-Based Syst. 2025, 316, 113318. [Google Scholar] [CrossRef]


| Dataset | MSP | EBO | MDS | ViM | SEM | IPL | FSCD |
|---|---|---|---|---|---|---|---|
| -DIGITS (Training ID: MNIST; Covariate-shifted ID: USPS and SVHN) | |||||||
| notMNIST | 32.54 | 25.49 | 79.10 | 85.91 | 96.74 | 95.32 | 96.28 |
| FashionMNIST | 39.71 | 37.64 | 60.42 | 66.45 | 80.20 | 79.28 | 80.79 |
| Mean (Near-OOD) | 36.12 | 31.56 | 69.76 | 76.18 | 88.47 | 87.29 | 88.54 |
| Texture | 64.34 | 65.02 | 72.42 | 70.32 | 74.45 | 73.97 | 74.73 |
| CIFAR-10 | 52.22 | 50.95 | 67.96 | 63.23 | 69.29 | 70.33 | 71.09 |
| Tiny-ImageNet | 52.94 | 51.89 | 64.31 | 62.34 | 67.54 | 67.64 | 68.10 |
| Places365 | 50.22 | 48.95 | 65.42 | 65.32 | 67.63 | 65.49 | 67.91 |
| Mean (Far-OOD) | 54.93 | 54.20 | 67.53 | 65.30 | 69.73 | 69.36 | 70.46 |
| Mean (Average) | 48.66 | 46.66 | 68.27 | 68.93 | 75.98 | 75.34 | |
| -OBJECTS (Training ID: CIFAR-10; Covariate-shifted ID: CIFAR-10-C and ImageNet-10) | |||||||
| CIFAR-100 | 70.17 | 63.85 | 72.05 | 70.12 | 74.70 | 73.19 | 75.91 |
| Tiny-ImageNet | 72.92 | 67.97 | 72.94 | 73.24 | 76.76 | 76.31 | 77.65 |
| Mean (Near-OOD) | 71.55 | 65.91 | 72.50 | 71.68 | 75.73 | 74.75 | 76.78 |
| MNIST | 66.98 | 54.55 | 77.04 | 73.45 | 75.69 | 73.13 | 74.82 |
| FashionMNIST | 73.78 | 76.50 | 80.33 | 81.01 | 79.40 | 80.04 | 80.33 |
| Texture | 74.18 | 68.63 | 72.02 | 73.40 | 79.69 | 77.41 | 79.72 |
| CIFAR-100-C | 74.12 | 68.37 | 68.13 | 73.32 | 78.89 | 79.86 | 80.01 |
| Mean (Far-OOD) | 72.27 | 67.01 | 74.38 | 75.30 | 78.42 | 77.61 | 78.72 |
| Mean (Average) | 72.03 | 66.65 | 73.75 | 74.09 | 77.52 | 76.66 | |
| -COVID (Training ID: BIMCV; Covariate-shifted ID: ActMed and Hannover) | |||||||
| CT-SCAN | 11.31 | 13.14 | 81.21 | 89.23 | 99.51 | 95.69 | 97.33 |
| XRayBone | 32.08 | 77.80 | 78.72 | 90.37 | 94.97 | 95.00 | 96.12 |
| Mean (Near-OOD) | 21.70 | 45.47 | 79.96 | 89.80 | 97.24 | 95.35 | 96.73 |
| MNIST | 24.89 | 99.91 | 80.81 | 98.32 | 100.00 | 98.75 | 99.80 |
| CIFAR-10 | 41.12 | 45.23 | 77.05 | 46.30 | 52.50 | 68.93 | 72.40 |
| Texture | 22.63 | 34.95 | 89.84 | 82.80 | 90.94 | 87.43 | 91.24 |
| Tiny-ImageNet | 30.26 | 32.69 | 81.99 | 79.32 | 83.42 | 82.29 | 83.75 |
| Mean (Far-OOD) | 29.73 | 53.20 | 82.42 | 76.69 | 81.72 | 84.35 | 86.80 |
| Mean (Average) | 27.05 | 50.62 | 81.60 | 81.06 | 86.89 | 88.02 | |
| Dataset | MSP | EBO | MDS | ViM | SEM | IPL | FSCD |
|---|---|---|---|---|---|---|---|
| -DIGITS (Training ID: MNIST; Covariate-shifted ID: USPS and SVHN) | |||||||
| notMNIST | 67.33 | 63.97 | 90.60 | 92.23 | 98.54 | 97.28 | 97.72 |
| FashionMNIST | 82.40 | 81.57 | 88.84 | 89.05 | 94.38 | 95.73 | 96.23 |
| Mean (Near-OOD) | 74.87 | 72.77 | 89.72 | 90.64 | 96.46 | 96.51 | 96.97 |
| Texture | 94.40 | 94.47 | 95.81 | 96.01 | 96.12 | 95.26 | 96.78 |
| CIFAR-10 | 87.26 | 86.36 | 91.74 | 90.52 | 92.06 | 91.75 | 93.10 |
| Tiny-ImageNet | 87.51 | 86.72 | 90.71 | 90.13 | 91.58 | 91.03 | 92.09 |
| Places365 | 67.11 | 65.41 | 76.64 | 73.12 | 77.61 | 77.64 | 78.12 |
| Mean (Far-OOD) | 84.07 | 83.24 | 88.73 | 87.45 | 89.34 | 88.92 | 90.02 |
| Mean (Average) | 81.00 | 79.75 | 89.06 | 88.51 | 91.72 | 91.45 | |
| -OBJECTS (Training ID: CIFAR-10; Covariate-shifted ID: CIFAR-10-C and ImageNet-10) | |||||||
| CIFAR-100 | 88.28 | 83.51 | 89.42 | 82.93 | 90.64 | 89.66 | 91.86 |
| Tiny-ImageNet | 90.04 | 86.30 | 89.96 | 83.57 | 91.86 | 90.97 | 92.00 |
| Mean (Near-OOD) | 89.16 | 84.91 | 89.69 | 83.25 | 91.25 | 90.31 | 91.93 |
| MNIST | 52.66 | 34.14 | 65.31 | 60.33 | 76.61 | 74.07 | 74.58 |
| FashionMNIST | 90.15 | 89.80 | 92.28 | 90.47 | 93.14 | 92.25 | 93.02 |
| Texture | 93.34 | 89.51 | 88.46 | 90.55 | 95.48 | 95.11 | 96.30 |
| CIFAR-100-C | 89.74 | 85.54 | 82.97 | 90.27 | 92.07 | 91.73 | 93.14 |
| Mean (Far-OOD) | 81.47 | 74.75 | 82.25 | 82.91 | 89.33 | 88.29 | 89.26 |
| Mean (Average) | 84.04 | 78.13 | 84.73 | 83.02 | 89.97 | 88.97 | |
| -COVID (Training ID: BIMCV; Covariate-shifted ID: ActMed and Hannover) | |||||||
| CT-SCAN | 52.92 | 53.34 | 94.31 | 88.90 | 99.80 | 97.84 | 99.80 |
| XRayBone | 76.95 | 91.68 | 96.67 | 97.84 | 98.95 | 98.70 | 99.46 |
| Mean (Near-OOD) | 64.94 | 72.51 | 95.49 | 93.37 | 99.37 | 98.27 | 99.63 |
| MNIST | 1.07 | 95.90 | 81.11 | 97.27 | 100.00 | 98.26 | 99.70 |
| CIFAR-10 | 8.73 | 9.77 | 61.14 | 18.74 | 11.27 | 38.21 | 46.03 |
| Texture | 11.43 | 13.14 | 85.50 | 57.21 | 64.71 | 83.01 | 86.66 |
| Tiny-ImageNet | 7.42 | 7.65 | 77.94 | 45.31 | 31.19 | 69.38 | 70.31 |
| Mean (Far-OOD) | 7.16 | 31.62 | 76.42 | 54.63 | 51.79 | 48.14 | 75.68 |
| Mean (Average) | 26.42 | 45.25 | 82.78 | 67.55 | 67.65 | 64.85 | |
| Dataset | MSP | EBO | MDS | ViM | SEM | IPL | FSCD |
|---|---|---|---|---|---|---|---|
| -DIGITS (Training ID: MNIST; Covariate-shifted ID: USPS and SVHN) | |||||||
| notMNIST | 99.97 | 99.99 | 78.83 | 66.34 | 10.93 | 15.68 | 11.01 |
| FashionMNIST | 99.90 | 99.98 | 94.68 | 93.78 | 68.63 | 67.10 | 65.30 |
| Mean (Near-OOD) | 99.93 | 99.98 | 86.75 | 80.06 | 39.78 | 41.39 | 38.16 |
| Texture | 94.89 | 98.40 | 87.46 | 92.34 | 90.90 | 90.02 | 89.72 |
| CIFAR-10 | 98.01 | 99.62 | 95.47 | 93.60 | 91.57 | 90.39 | 90.04 |
| Tiny-ImageNet | 97.98 | 99.58 | 96.20 | 96.18 | 93.39 | 93.30 | 92.17 |
| Places365 | 98.68 | 99.65 | 98.06 | 98.02 | 94.15 | 95.74 | 92.33 |
| Mean (Far-OOD) | 97.39 | 99.31 | 94.30 | 95.04 | 92.50 | 92.36 | 91.07 |
| Mean (Average) | 98.24 | 99.54 | 91.78 | 90.04 | 74.93 | 75.37 | |
| -OBJECTS (Training ID: CIFAR-10; Covariate-shifted ID: CIFAR-10-C and ImageNet-10) | |||||||
| CIFAR-100 | 89.44 | 83.84 | 86.28 | 82.44 | 86.96 | 84.31 | 84.24 |
| Tiny-ImageNet | 88.22 | 81.58 | 87.45 | 87.32 | 86.59 | 96.17 | 85.55 |
| Mean (Near-OOD) | 88.83 | 82.71 | 86.87 | 84.89 | 86.77 | 90.24 | 84.89 |
| MNIST | 93.54 | 92.23 | 84.59 | 90.12 | 99.70 | 95.39 | 94.81 |
| FashionMNIST | 88.08 | 72.40 | 77.17 | 75.32 | 93.72 | 78.62 | 76.51 |
| Texture | 85.64 | 75.57 | 72.98 | 70.92 | 82.15 | 79.38 | 72.60 |
| CIFAR-100-C | 87.26 | 83.64 | 85.53 | 89.32 | 83.92 | 83.02 | 82.17 |
| Mean (Far-OOD) | 88.63 | 80.96 | 80.07 | 81.42 | 89.87 | 84.10 | 81.52 |
| Mean (Average) | 88.70 | 81.54 | 83.33 | 82.57 | 88.84 | 86.15 | |
| -COVID (Training ID: BIMCV; Covariate-shifted ID: ActMed and Hannover) | |||||||
| CT-SCAN | 99.80 | 97.35 | 99.39 | 12.56 | 2.24 | 9.06 | 8.72 |
| XRayBone | 97.00 | 42.00 | 100.00 | 23.35 | 14.50 | 14.17 | 10.07 |
| Mean (Near-OOD) | 98.40 | 69.67 | 99.69 | 17.96 | 8.37 | 11.62 | 9.39 |
| MNIST | 98.30 | 0.35 | 100.00 | 1.69 | 0.00 | 1.24 | 0.78 |
| CIFAR-10 | 96.32 | 94.67 | 98.02 | 89.61 | 85.58 | 85.94 | 82.09 |
| Texture | 98.39 | 87.06 | 56.38 | 40.85 | 27.57 | 28.40 | 13.28 |
| Tiny-ImageNet | 97.78 | 92.73 | 92.11 | 73.96 | 44.99 | 45.92 | 45.70 |
| Mean (Far-OOD) | 97.70 | 68.70 | 86.63 | 51.38 | 39.54 | 40.38 | 35.46 |
| Mean (Average) | 97.93 | 69.03 | 90.98 | 40.34 | 29.15 | 30.78 | |
| Dataset | MNIST | USPS | SVHN | CIFAR-10 | ImageNet-10 | CIFAR-10-C |
|---|---|---|---|---|---|---|
| MSP | 99.6 | 60.2 | 22.1 | 94.3 | 80.0 | 52.3 |
| MDS | 99.0 | 61.4 | 29.1 | 95.1 | 82.2 | 50.4 |
| SEM | 99.4 | 75.2 | 40.2 | 94.2 | 85.7 | 61.5 |
| Ours | 99.8 | 76.0 | 40.0 | 95.3 | 85.7 | 63.2 |
| Pretraining | Fine-Tuning | AUROC | AUPR | FPR95 | ACC | |||
|---|---|---|---|---|---|---|---|---|
| DLPA | FCD | |||||||
| Image Level | Feature Level | Contrastive Learning | Denoising | |||||
| ✓ | 49.61 | 81.05 | 93.23 | 47.01 | ||||
| ✓ | ✓ | ✓ | ✓ | 83.37 | 59.26 | 74.57 | 38.23 | |
| ✓ | ✓ | ✓ | ✓ | 74.45 | 89.73 | 75.01 | 58.82 | |
| ✓ | ✓ | ✓ | ✓ | 75.32 | 90.26 | 75.97 | 59.71 | |
| ✓ | ✓ | ✓ | ✓ | 51.32 | 82.77 | 92.18 | 49.48 | |
| ✓ | ✓ | ✓ | ✓ | 76.21 | 91.84 | 73.66 | 60.13 | |
| ✓ | ✓ | ✓ | * | 75.94 | 90.21 | 75.20 | 59.34 | |
| ✓ | ✓ | ✓ | ✓ | ✓ | 76.49 | 92.34 | 73.43 | 60.44 |
| Model | Method | AUROC | AUPR | FPR95 |
|---|---|---|---|---|
| ResNet-18 | MSP | 72.03 | 84.04 | 88.70 |
| EBO | 66.65 | 78.13 | 81.54 | |
| MDS | 73.75 | 84.73 | 82.33 | |
| ViM | 74.09 | 83.02 | 82.57 | |
| SEM | 77.52 | 89.97 | 88.84 | |
| Ours | 78.07 | 90.15 | 82.65 | |
| DenseNet-100 | MSP | 75.92 | 87.44 | 85.23 |
| EBO | 67.60 | 82.91 | 77.95 | |
| MDS | 77.68 | 86.36 | 79.00 | |
| ViM | 75.60 | 86.81 | 82.04 | |
| SEM | 79.85 | 92.07 | 86.51 | |
| Ours | 81.03 | 92.27 | 74.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, D.; Sheng, B.; Li, X. Enhancing Out-of-Distribution Detection Under Covariate Shifts: A Full-Spectrum Contrastive Denoising Framework. Electronics 2025, 14, 1881. https://doi.org/10.3390/electronics14091881
Pan D, Sheng B, Li X. Enhancing Out-of-Distribution Detection Under Covariate Shifts: A Full-Spectrum Contrastive Denoising Framework. Electronics. 2025; 14(9):1881. https://doi.org/10.3390/electronics14091881
Chicago/Turabian StylePan, Dengye, Bin Sheng, and Xiaoqiang Li. 2025. "Enhancing Out-of-Distribution Detection Under Covariate Shifts: A Full-Spectrum Contrastive Denoising Framework" Electronics 14, no. 9: 1881. https://doi.org/10.3390/electronics14091881
APA StylePan, D., Sheng, B., & Li, X. (2025). Enhancing Out-of-Distribution Detection Under Covariate Shifts: A Full-Spectrum Contrastive Denoising Framework. Electronics, 14(9), 1881. https://doi.org/10.3390/electronics14091881






