A Two-Stage Fault Reconfiguration Strategy for Distribution Networks with High Penetration of Distributed Generators
Abstract
1. Introduction
- Establishing a rapid power restoration reconfiguration model, in which different handling strategies are applied to various types of DGs during fault recovery by adding specific constraint conditions, handled based on the Big-M method, that account for the fault ride-through, improving the load recovery percentage for areas that have lost power supply;
- Proposing a fast solution algorithm for the reconfiguration model based on an AdaBoost-enhanced decision tree, which accelerates the solving process while maintaining the same accuracy;
- Establishing a post-recovery optimal reconfiguration model by assessing system stability using a linearized static voltage stability index, modeling the uncertainty of DG output and load power based on fuzzy mathematics theory, and applying fuzzy chance constraint transformation to facilitate the model’s solution.
2. The Impacts of DGs on Distribution Network Fault Recovery
2.1. Analysis of the Support Capability of DGs
2.1.1. Fault Ride-Through Characteristics of DGs
2.1.2. Handling Strategies for Different Types of DGs During Fault Recovery
- (1)
- Directly decommissioned type
- (2)
- Fault ride-through type
2.2. Analysis of the Output Uncertainty of DGs
- (1)
- Photovoltaic generation
- (2)
- Wind turbine generation
- (3)
- Conventional DGs
2.3. Two-Stage Fault Reconfiguration Strategy for Distribution Networks with DGs
3. Rapid Power Restoration Strategy
3.1. Rapid Power Restoration Reconfiguration Model Considering FRT Capability of DGs
3.1.1. Objective Function of Rapid Power Restoration Reconfiguration Model
3.1.2. Constraints of Rapid Power Restoration Reconfiguration Model
- (1)
- DG output power constraint
- (2)
- Radial network constraint
- (3)
- Other constraints
3.2. Fast Solution Algorithm for Rapid Power Restoration Reconfiguration Model
3.2.1. Fast Solution Algorithm Based on Decision Trees
3.2.2. Steps of Solution Algorithm
- (1)
- Establishment of the instance library
- (2)
- Construction of the knowledge base sample set
- (3)
- Training of the inference machine based on the decision tree
3.2.3. AdaBoost-Enhanced Decision Tree
- (1)
- Assume there are n training samples, where the i-th sample has a feature label Xi and a decision result Yi. Set the initial weight of each sample as D0,i = 1/n.
- (2)
- Iteratively train decision trees based on the CART algorithm to obtain m weak classifiers. In the CART algorithm, the Gini index is used as the criterion for node splitting [36].
- (3)
4. Post-Recovery Optimal Reconfiguration Strategy
4.1. DG and Load Uncertainty Models
4.1.1. Fuzzy Representation of Uncertainty Parameters
4.1.2. Transformation of Fuzzy Chance Constraints
4.2. Optimization Objective of Post-Recovery Optimal Reconfiguration Model
4.3. Constraints of Post-Recovery Optimal Reconfiguration Model
5. Case Study
5.1. Case Study Model Description
5.2. Analysis of Calculation Results for the Rapid Power Recovery Stage
5.3. Analysis of Calculation Results for the Post-Recovery Optimal Reconfiguration Stage
5.4. Analysis of Comparison with Other Methods
5.4.1. Comparison of Reconfiguration Results of Different Methods
5.4.2. Comparison of Load Recovery Speed of Different Methods
5.4.3. Comparison of Algorithm Methods, Considering Different Factors
- (1)
- The factor of DG fault ride-through
- (2)
- The factor of the uncertainty of DGs and loads
5.5. Analysis of the Practicality of the Proposed Method
- Limited adaptability of current reconfiguration schemes
- 2.
- Slow computation and infeasibility under complexity
- 3.
- Neglect of DG support capabilities
- 4.
- Lack of consideration of post-fault operational risks
6. Conclusions
- The proposed rapid power restoration reconfiguration model takes into account different types of DG behaviors during fault recovery, including the fault ride-through capability of DGs. After a fault occurs, it can effectively leverage the DGs’ support capability for distribution networks and improve the load recovery percentage, thereby enhancing the restoration of lost load.
- In the rapid power restoration strategy, the AdaBoost-enhanced improved decision tree algorithm offers faster computation speeds than traditional optimization methods, enhancing its ability to meet fault response requirements in practical engineering applications.
- In the post-recovery optimal reconfiguration strategy, the reconfiguration model simultaneously considers load restoration and system stability as optimization objectives, and accounts for the uncertainty of DGs’ output and load power, in order to enhance the long-term operational stability of the system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
- (1)
- Power flow constraints
- (2)
- Line operation safety constraints
- (3)
- Node voltage constraints
- (4)
- Energy storage operation constraints
Appendix A.2
- (1)
- Power flow constraints
- (2)
- Line operation safety constraints
- (3)
- Node voltage constraints
- (4)
- Energy storage operation constraints
Appendix B
Appendix B.1. IEEE 69-Bus Distribution Network System with DGs
| Equipment | Connected Node | Rated Active Power (kW) | Equipment | Connected Node | Rated Active Power (kW) |
|---|---|---|---|---|---|
| DG1 | 5 | 800 | DG5 | 42 | 200 |
| DG2 | 9 | 400 | DG6 | 48 | 100 |
| DG3 | 19 | 250 | DG7 | 63 | 800 |
| DG4 | 32 | 250 |
| Equipment | Connected Node | Capacity (MWh) | Upper Limit of Charging and Discharging Power (MW) | Charging and Discharging Efficiency |
|---|---|---|---|---|
| Energy storage 1 | 4 | 1.2 | 0.45/0.45 | 90%/90% |
| Energy storage 2 | 51 | 1 | 0.3/0.3 | 90%/90% |
| Type of Load | Connected Nodes | Weight Factor |
|---|---|---|
| Primary load | 6, 8, 21, 51 | 100 |
| Secondary load | 12, 17, 33, 42, 49, 64 | 10 |
| Tertiary load | The rest of the nodes | 1 |

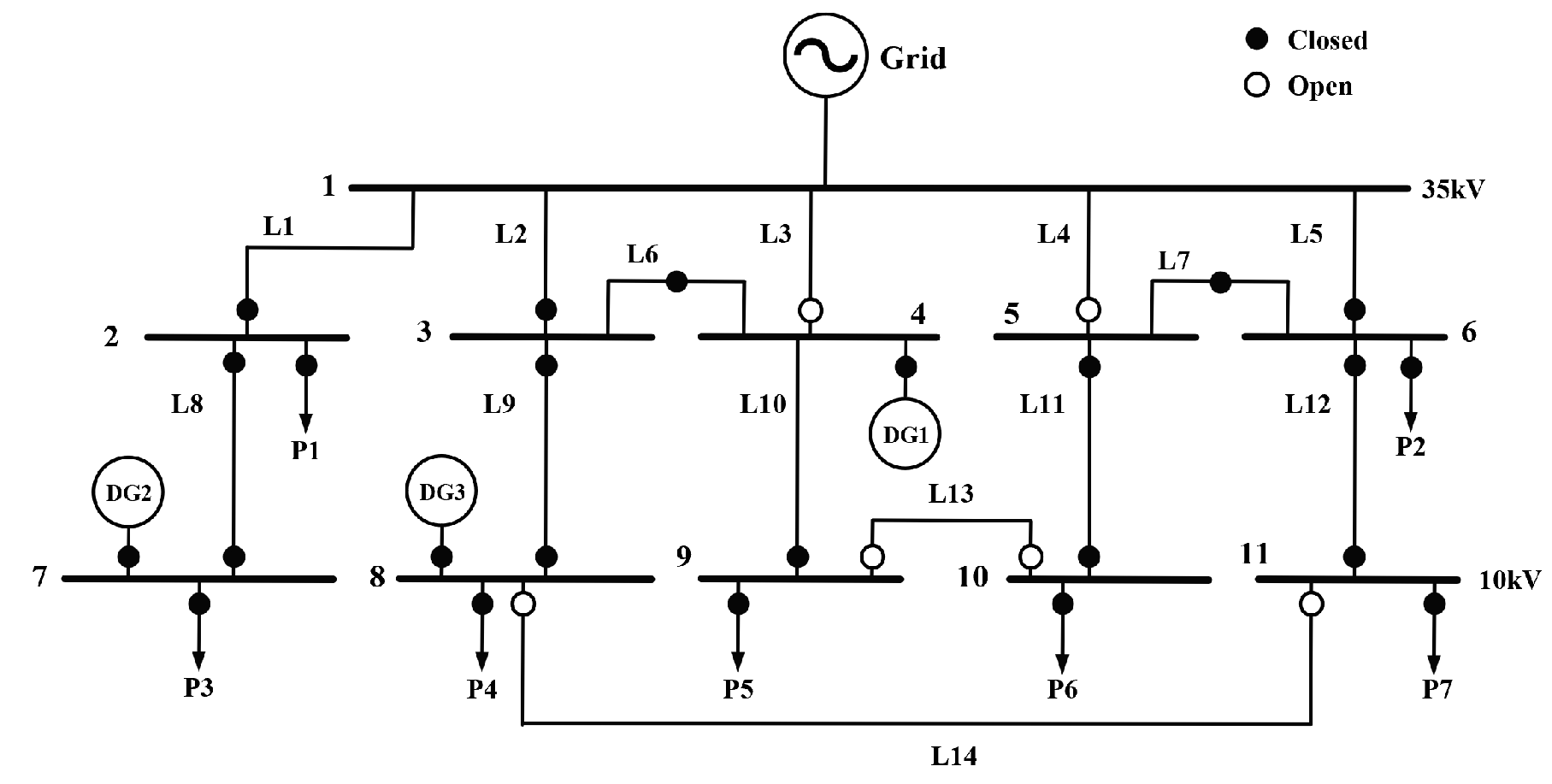
Appendix B.2. 11-Bus Distribution Network System with DGs
| Equipment | Connected Node | Rated Active Power (MW) |
|---|---|---|
| DG1 | 4 | 4 |
| DG2 | 7 | 10.6 |
| DG3 | 8 | 5 |
| Equipment | Connected Node | Power (MW) | Weight Factor |
|---|---|---|---|
| P1 | 2 | 2.14 MW + j0.35 MVar | 100 |
| P2 | 6 | 1.89 MW + j0.96 MVar | 100 |
| P3 | 7 | 4.29 MW + j1.34 MVar | 100 |
| P4 | 8 | 5.93 MW + j4.27 MVar | 10 |
| P5 | 9 | 6.34 MW + j4.71 MVar | 1 |
| P6 | 10 | 4.16 MW + j1.35 MVar | 1 |
| P7 | 11 | 7.85 MW + j2.23 MVar | 1 |
References
- Morales-Munoz, A.; Freijedo, F.D.; Pugliese, S.; Liserre, M. Selective Virtual Impedance for Overcurrent Limitation in Grid-Forming Inverters Under Asymmetrical Faults. In Proceedings of the 2024 IEEE 15th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Luxembourg, 23–26 June 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Liyanage, C.; Nutkani, I.; Meegahapola, L. A Comparative Analysis of Prominent Virtual Synchronous Generator Strategies Under Different Network Conditions. IEEE Open Access J. Power Energy 2024, 11, 178–195. [Google Scholar] [CrossRef]
- Shobug, M.A.; Chowdhury, N.A.; Hossain, M.A.; Sanjari, M.J.; Lu, J.; Yang, F. Virtual Inertia Control for Power Electronics-Integrated Power Systems: Challenges and Prospects. Energies 2024, 17, 2737. [Google Scholar] [CrossRef]
- Li, J.; Mo, H.; Sun, Q.; Wei, W.; Yin, K. Distributed Optimal Scheduling for Virtual Power Plant with High Penetration of Renewable Energy. Int. J. Electr. Power Energy Syst. 2024, 160, 110103. [Google Scholar] [CrossRef]
- Taheri, S.I.; Salles, M.B.C.; Costa, E.C.M. Optimal Cost Management of Distributed Generation Units and Microgrids for Virtual Power Plant Scheduling. IEEE Access 2020, 8, 208449–208461. [Google Scholar] [CrossRef]
- ALAhmad, A.K.; Verayiah, R.; Shareef, H. Long-Term Optimal Planning for Renewable Based Distributed Generators and Battery Energy Storage Systems toward Enhancement of Green Energy Penetration. J. Energy Storage 2024, 90, 111868. [Google Scholar] [CrossRef]
- Nsaif, Y.M.; Lipu, M.S.H.; Ayob, A.; Yusof, Y.; Hussain, A. Fault Detection and Protection Schemes for Distributed Generation Integrated to Distribution Network: Challenges and Suggestions. IEEE Access 2021, 9, 142693–142717. [Google Scholar] [CrossRef]
- Karimi, A.; Nayeripour, M.; Abbasi, A.R. Coordination in Islanded Microgrids: Integration of Distributed Generation, Energy Storage System, and Load Shedding Using a New Decentralized Control Architecture. J. Energy Storage 2024, 98, 113199. [Google Scholar] [CrossRef]
- Behbahani, M.R.; Jalilian, A.; Bahmanyar, A.; Ernst, D. Comprehensive Review on Static and Dynamic Distribution Network Reconfiguration Methodologies. IEEE Access 2024, 12, 9510–9525. [Google Scholar] [CrossRef]
- Zidan, A.; Khairalla, M.; Abdrabou, A.M.; Khalifa, T.; Shaban, K.; Abdrabou, A.; El Shatshat, R.; Gaouda, A.M. Fault Detection, Isolation, and Service Restoration in Distribution Systems: State-of-the-Art and Future Trends. IEEE Trans. Smart Grid 2017, 8, 2170–2185. [Google Scholar] [CrossRef]
- Shen, F.; Wu, Q.; Xue, Y. Review of Service Restoration for Distribution Networks. J. Mod. Power Syst. Clean Energy 2020, 8, 1–14. [Google Scholar] [CrossRef]
- Zarei, S.F.; Parniani, M. A Comprehensive Digital Protection Scheme for Low-Voltage Microgrids with Inverter-Based and Conventional Distributed Generations. IEEE Trans. Power Deliv. 2017, 32, 441–452. [Google Scholar] [CrossRef]
- Musarrat, M.N.; Fekih, A.; Islam, M.R. An Improved Fault Ride Through Scheme and Control Strategy for DFIG-Based Wind Energy Systems. IEEE Trans. Appl. Supercond. 2021, 31, 1–6. [Google Scholar] [CrossRef]
- Bagherzadeh, L.; Shayeghi, H.; Pirouzi, S.; Shafie-khah, M.; Catalão, J.P.S. Coordinated Flexible Energy and Self-Healing Management According to the Multi-Agent System-Based Restoration Scheme in Active Distribution Network. IET Renew. Power Gener. 2021, 15, 1765–1777. [Google Scholar] [CrossRef]
- Ye, Z.; Chen, C.; Chen, B.; Wu, K. Resilient Service Restoration for Unbalanced Distribution Systems With Distributed Energy Resources by Leveraging Mobile Generators. IEEE Trans. Ind. Inform. 2021, 17, 1386–1396. [Google Scholar] [CrossRef]
- Shi, X.; Zhang, H.; Wei, C.; Li, Z.; Chen, S. Fault Modeling of IIDG Considering Inverter’s Detailed Characteristics. IEEE Access 2020, 8, 183401–183410. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, W.; Zhang, Y.; Zhang, H. An Improved Fault Recovery Strategy for Active Distribution Network Considering LVRT Capability of DG. In Proceedings of the 8th Renewable Power Generation Conference (RPG 2019), Shanghai, China, 24–25 October 2019; pp. 1–7. [Google Scholar]
- Li, C.; Xi, Y.; Lu, Y.; Liu, N.; Chen, L.; Ju, L.; Tao, Y. Resilient Outage Recovery of a Distribution System: Co-Optimizing Mobile Power Sources with Network Structure. Prot. Control Mod. Power Syst. 2022, 7, 32. [Google Scholar] [CrossRef]
- Lin, C.; Chen, C.; Bie, Z.; Li, G. Post-disaster Load Restoration Method for Urban Distribution Network with Dynamic Uncertainty and Frequency-Voltage Control. Autom. Electr. Power Syst. 2022, 46, 56–64. [Google Scholar]
- Shi, X.; Ke, Q.; Lei, J.; Yuan, Z. Fault Reconfiguration of Distribution Networks with Soft Open Points Considering Uncertainties of Photovoltaic Outputs and Loads. J. Phys. Conf. Ser. 2020, 1578, 012205. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, G.; Zhu, J. Resilience Improvement Model of Distribution Network Based on Two-Stage Robust Optimization. Electr. Power Syst. Res. 2023, 223, 109559. [Google Scholar] [CrossRef]
- Kanojia, S.S.; Suthar, B.N. Voltage Stability Index: A Review Based on Analytical Method, Formulation and Comparison in Renewable Dominated Power System. IJAPE 2024, 13, 508. [Google Scholar] [CrossRef]
- Moradi, M.H.; Abedini, M. A Combination of Genetic Algorithm and Particle Swarm Optimization for Optimal Distributed Generation Location and Sizing in Distribution Systems with Fuzzy Optimal Theory. Int. J. Green Energy 2012, 9, 641–660. [Google Scholar] [CrossRef]
- Bi, C.Q.; Chen, J.J.; Wang, Y.X.; Feng, L. Fuzzy Credibility Chance-Constrained Multi-Objective Optimization for Multiple Transactions of Electricity–Gas–Carbon under Uncertainty. Electr. Power Syst. Res. 2025, 238, 111089. [Google Scholar] [CrossRef]
- Xiao, G.; Liu, H.; Nabatalizadeh, J. Optimal Scheduling and Energy Management of a Multi-Energy Microgrid with Electric Vehicles Incorporating Decision Making Approach and Demand Response. Sci. Rep. 2025, 15, 5075. [Google Scholar] [CrossRef] [PubMed]
- Fan, G.; Peng, C.; Wang, X.; Wu, P.; Yang, Y.; Sun, H. Optimal Scheduling of Integrated Energy System Considering Renewable Energy Uncertainties Based on Distributionally Robust Adaptive MPC. Renew. Energy 2024, 226, 120457. [Google Scholar] [CrossRef]
- Arjomandi-Nezhad, A.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M.; Safdarian, A.; Dehghanian, P.; Wang, F. Modeling and Optimizing Recovery Strategies for Power Distribution System Resilience. IEEE Syst. J. 2021, 15, 4725–4734. [Google Scholar] [CrossRef]
- Kong, F.; Guo, T.; Zhang, X. Design of Active Fault Diagnosis and Repair System for Active Distribution Networks Based on Decision Tree Algorithm. In Proceedings of the 6th International Conference on Information Technologies and Electrical Engineering, Hunan, China, 3–5 November 2023; Association for Computing Machinery: New York, NY, USA, 2024; pp. 759–764. [Google Scholar]
- Wang, Q.; Meng, L. Distribution Network Fault Reconfiguration with Distributed Generation Based on Ant Colony Algorithm. Adv. Mater. Res. 2013, 732–733, 1328–1333. [Google Scholar] [CrossRef]
- Rebollal, D.; Carpintero-Rentería, M.; Santos-Martín, D.; Chinchilla, M. Microgrid and Distributed Energy Resources Standards and Guidelines Review: Grid Connection and Operation Technical Requirements. Energies 2021, 14, 523. [Google Scholar] [CrossRef]
- IEEE Std 1547-2018 (Revision of IEEE Std 1547-2003); IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. IEEE: New York, NY, USA, 2018; pp. 1–138. [CrossRef]
- Li, H.; Deng, C.; Zhang, Z.; Liang, Y.; Wang, G. An Adaptive Fault-Component-Based Current Differential Protection Scheme for Distribution Networks with Inverter-Based Distributed Generators. Int. J. Electr. Power Energy Syst. 2021, 128, 106719. [Google Scholar] [CrossRef]
- Xu, C.; Dong, S.; Zhu, J. Description Method of Radial Constraints for Distribution Network Based on Disconnection Condition of Power Supply Loop. Autom. Electr. Power Syst. 2019, 43, 82–94. [Google Scholar]
- Ding, W.; Chen, Q.; Dong, Y.; Shao, N. Fault Diagnosis Method of Intelligent Substation Protection System Based on Gradient Boosting Decision Tree. Appl. Sci. 2022, 12, 8989. [Google Scholar] [CrossRef]
- Shan, W.; Li, D.; Liu, S.; Song, M.; Xiao, S.; Zhang, H. A Random Feature Mapping Method Based on the AdaBoost Algorithm and Results Fusion for Enhancing Classification Performance. Expert Syst. Appl. 2024, 256, 124902. [Google Scholar] [CrossRef]
- Han, Y.; Xu, K.; Qin, J. Based on the CART Decision Tree Model of Prediction and Classification of Ancient Glass-Related Properties. Highlights Sci. Eng. Technol. 2023, 42, 18–27. [Google Scholar] [CrossRef]
- Hu, H.; Siala, M.; Hebrard, E.; Huguet, M.-J. Learning Optimal Decision Trees with MaxSAT and Its Integration in AdaBoost. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, International Joint Conferences on Artificial Intelligence Organization, Yokohama, Japan, 11–17 July 2020; pp. 1170–1176. [Google Scholar]
- Chen, S.; Shen, B.; Wang, X.; Yoo, S.-J. A Strong Machine Learning Classifier and Decision Stumps Based Hybrid AdaBoost Classification Algorithm for Cognitive Radios. Sensors 2019, 19, 5077. [Google Scholar] [CrossRef] [PubMed]
- Aboshady, F.M.; Pisica, I.; Zobaa, A.F.; Taylor, G.A.; Ceylan, O.; Ozdemir, A. Reactive Power Control of PV Inverters in Active Distribution Grids With High PV Penetration. IEEE Access 2023, 11, 81477–81496. [Google Scholar] [CrossRef]
- Bhutta, M.S.; Sarfraz, M.; Ivascu, L.; Li, H.; Rasool, G.; ul Abidin Jaffri, Z.; Farooq, U.; Ali Shaikh, J.; Nazir, M.S. Voltage Stability Index Using New Single-Port Equivalent Based on Component Peculiarity and Sensitivity Persistence. Processes 2021, 9, 1849. [Google Scholar] [CrossRef]



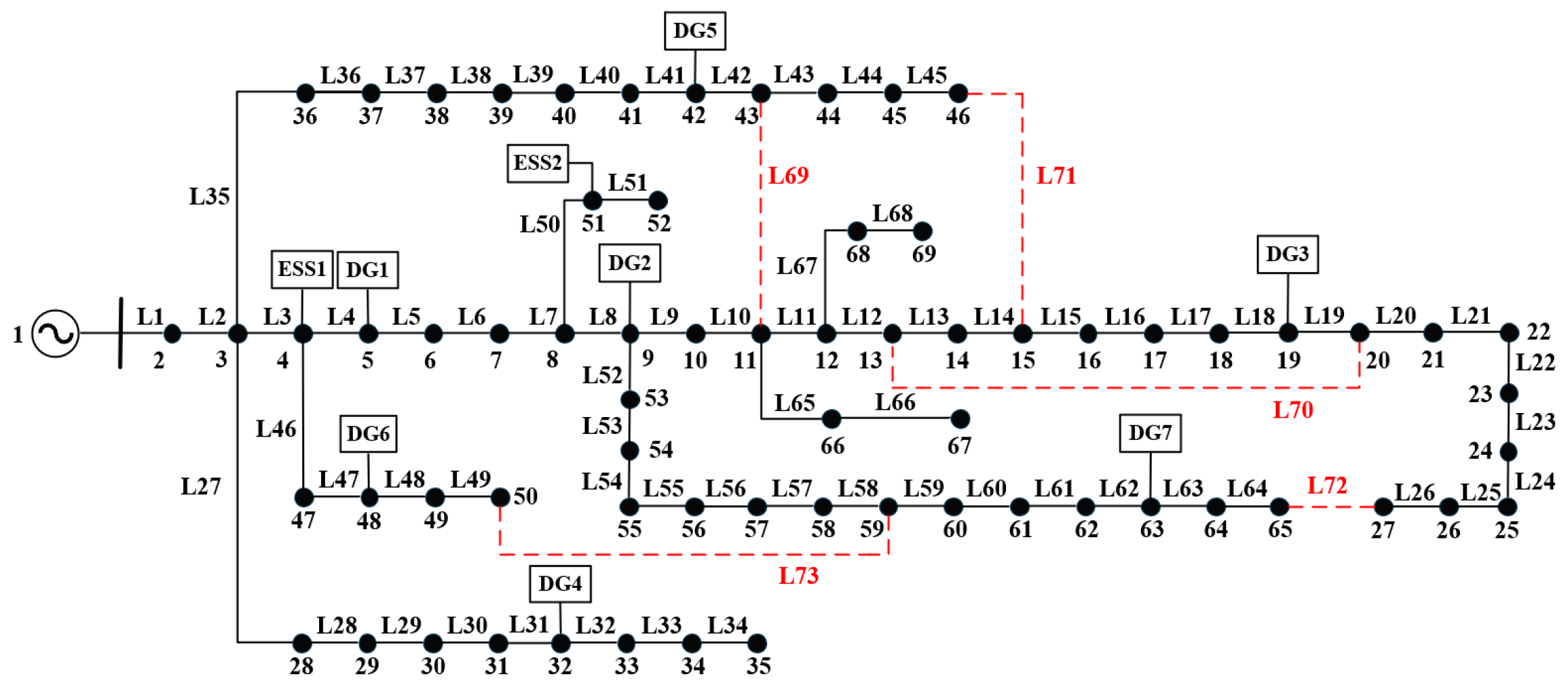


| Case Number | Faulty Line |
|---|---|
| 1 | L3 |
| 2 | L10 |
| 3 | L5 and L18 |
| 4 | L38 and L64 |
| 5 | L48; DG6 fault ride-through operation |
| 6 | L62; DG7 fault ride-through operation |
| Case Number | Faulty Line |
|---|---|
| 1 | L2 |
| 2 | L9 |
| 3 | L3 and L10 |
| 4 | L4; DG1 fault ride-through operation |
| Case Number | Reconfiguration Operation | Load Recovery Percentage | ||
|---|---|---|---|---|
| Primary Load | Secondary Load | Tertiary Load | ||
| 1 | L69 is closed | 100% | 100% | 90.57% |
| 2 | L71 is closed | 100% | 100% | 100% |
| 3 | L69 and L72 are closed | 100% | 100% | 81.33% |
| 4 | L69 and L72 are closed | 100% | 100% | 100% |
| 5 | L73 is closed | 100% | 100% | 93.04% |
| 6 | L72 is closed | 100% | 100% | 95.48% |
| Case Number | Reconfiguration Operation | Load Recovery Percentage | ||
|---|---|---|---|---|
| Primary Load | Secondary Load | Tertiary Load | ||
| 1 | L11 is closed | 100% | 100% | 100% |
| 2 | L14 is closed | 100% | 100% | 100% |
| 3 | L12 and L13 are closed | 100% | 100% | 100% |
| 4 | L11 is closed | 100% | 100% | 100% |
| Case Number | Reconfiguration Operation | Loss of Load (MWh) | |
|---|---|---|---|
| 1 | L69 is closed | −0.8898 | 1.4664 |
| 2 | L69 is closed | −0.9264 | 0.4602 |
| 3 | L72 and L73 are closed | −0.9479 | 1.2070 |
| 4 | L69 and L72 are closed | −0.9251 | 0.6349 |
| Case Number | Reconfiguration Operation | Loss of Load (MWh) | |
|---|---|---|---|
| 1 | L11 is closed | −0.9984 | 0 |
| 2 | L14 is closed | −0.9919 | 0 |
| 3 | L12 and L13 are closed | −0.9919 | 0 |
| ω1/ω2 | Reconfiguration Operation | Loss of Load (MWh) | |
|---|---|---|---|
| 0.1/0.9 | L72 and L73 are closed | −0.9479 | 1.2070 |
| 0.4/0.6 | L72 and L73 are closed | −0.9479 | 1.2070 |
| 0.9/0.1 | L72 and L73 are closed | −0.9479 | 1.2070 |
| Case Number | Reconfiguration Results of Conventional Mathematical Optimization | Reconfiguration Results of Ordinary Decision Trees | Reconfiguration Results of AdaBoost-Enhanced Decision Trees |
|---|---|---|---|
| 1 | L69 is closed | L69 is closed | L69 is closed |
| 2 | L71 is closed | L71 is closed | L71 is closed |
| 3 | L69 and L72 are closed | L70 and L73 are closed | L69 and L72 are closed |
| 4 | L69 and L72 are closed | L71 and L72 are closed | L69 and L72 are closed |
| 5 | L73 is closed | L73 is closed | L73 is closed |
| 6 | L72 is closed | L72 is closed | L72 is closed |
| Case Number | Solving Time of Conventional Mathematical Optimization (s) | Solving Time of AdaBoost-Enhanced Decision Trees (s) |
|---|---|---|
| 1 | 25.6861 | 0.2426 |
| 2 | 23.5707 | 0.2815 |
| 3 | 27.7653 | 0.2328 |
| 4 | 24.3391 | 0.3042 |
| 5 | 22.9184 | 0.2436 |
| 6 | 25.5102 | 0.2761 |
| 7 | Non-convergence | 0.2591 |
| Case Number | Considering Uncertainty | Without Considering Uncertainty | ||
|---|---|---|---|---|
| Loss of Load (MWh) | Loss of Load (MWh) | |||
| 1 | −0.8898 | 1.4664 | −0.8898 | 1.4664 |
| 2 | −0.9264 | 0.4602 | −0.9264 | 0.4712 |
| 3 | −0.9479 | 1.2070 | −0.8425 | 1.5457 |
| 4 | −0.9251 | 0.6349 | −0.9251 | 0.7266 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Li, Y.; Liu, J.; Xiang, X.; Sheng, F.; Zhu, X.; Fang, Y.; Wu, Z. A Two-Stage Fault Reconfiguration Strategy for Distribution Networks with High Penetration of Distributed Generators. Electronics 2025, 14, 1872. https://doi.org/10.3390/electronics14091872
He Y, Li Y, Liu J, Xiang X, Sheng F, Zhu X, Fang Y, Wu Z. A Two-Stage Fault Reconfiguration Strategy for Distribution Networks with High Penetration of Distributed Generators. Electronics. 2025; 14(9):1872. https://doi.org/10.3390/electronics14091872
Chicago/Turabian StyleHe, Yuwei, Yanjun Li, Jian Liu, Xiang Xiang, Fang Sheng, Xinyu Zhu, Yunpeng Fang, and Zhenchong Wu. 2025. "A Two-Stage Fault Reconfiguration Strategy for Distribution Networks with High Penetration of Distributed Generators" Electronics 14, no. 9: 1872. https://doi.org/10.3390/electronics14091872
APA StyleHe, Y., Li, Y., Liu, J., Xiang, X., Sheng, F., Zhu, X., Fang, Y., & Wu, Z. (2025). A Two-Stage Fault Reconfiguration Strategy for Distribution Networks with High Penetration of Distributed Generators. Electronics, 14(9), 1872. https://doi.org/10.3390/electronics14091872






