Abstract
Accurate indoor localization is essential for Internet of Things (IoT) systems and autonomous navigation in the 6G communication system. However, achieving precision in environments affected by signal multipath effects and interference remains a challenge for 6G communication systems. We employ a Residual Neural Network (ResNet) augmented with channel and spatial attention mechanisms to enhance indoor localization performance using time-domain data. Through extensive experimentation, our models, when equipped with an attention mechanism, can achieve accurate location under 20% interference. Numerical results show that the ResNet with a Channel Local Attention Block (CLAB) can reduce the localization error by about 12% even when the interference is high. Similarly, the ResNet with a Spatial Local Attention Block (SLAB) can also improve the localization accuracy. While a ResNet combining both CLAB and SLAB can reduce the position error to about 7 cm.
1. Introduction
Positioning technology plays a crucial role in modern 6G information processing, with applications ranging from indoor navigation to environmental monitoring [1,2]. From a research perspective, positioning methods can generally be categorized into two types: frequency-domain and time-domain. Frequency-domain methods typically extract positioning information by analyzing the frequency characteristics of signals. In contrast, time-domain methods directly utilize the temporal characteristics of signals, such as time delay estimation for positioning. Frequency-domain methods involve analyzing signals in terms of their frequency content, and they make it easier to isolate frequencies and remove noise. However, the time resolution is poor for these methods. On the contrary, time-domain methods provide better time resolution because they analyze the signal directly as it varies over time. Nevertheless, the methods suffer from poor frequency discrimination as well as being noise-sensitive. Existing literature has extensively explored these two approaches, each demonstrating unique advantages and limitations [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17].
By means of the frequency-domain, in 2021, Wu introduced a deep learning approach called Structured Intra-Attention Bidirectional Recurrent (SIABR) for CSI-based (Channel State Information) 3D THz indoor localization, which improved stability and performance in challenging conditions [3]. In 2022, Shubham introduced a novel approach to address the localization challenge in IEEE 802.11ay WLAN systems, specifically tailored for indoor environments. The proposed method integrates advanced signal processing with machine learning techniques, utilizing Doppler and angular domain analysis to effectively differentiate between multipath signals. This differentiation is based on variations in range, velocity, and angular orientation of reflected signals [4].
In 2023, Pu proposed an indoor Wi-Fi localization scheme that extracts both spatial and temporal features from signal data. By incorporating a fusion neural network, the proposed method significantly enhanced signal reconstruction accuracy, as demonstrated by numerical evaluations [5]. In the same year, Alitaleshi introduced a hybrid approach that integrates an autoencoder-based learning framework with a two-dimensional convolutional neural network (2D-CNN). This method achieved superior performance in terms of both positioning accuracy and floor-level estimation [6]. In 2024, Zhou developed a cost-efficient indoor positioning system leveraging 5G downlink multibeam signals. The system demonstrated strong performance in multi-floor environments, achieving a root-mean-square positioning error of under 1.5 m. These results highlight its potential for practical deployment in mobile localization applications [7]. In 2024, Wan proposed a novel deep learning model for solving the MIMO positioning problem, which incorporated two types of attention mechanisms and an improved training scheme to further enhance positioning accuracy [8]. Later, Stavros presented a positioning system that extracted and processed CSI from a single Access Point (AP) to localize commercial smartphones [9]. In the same year, Chiu explored 6G technology for indoor positioning, focusing on accuracy and reliability using Convolutional Neural Networks (CNNs) with CSI at terahertz frequencies and advanced AI algorithms, which achieved centimeter-level accuracy [10].
By means of the time-domain, in 1999, Chiu employed a site-specific model to analyze the performance of millimeter-wave Binary Phase-Shift Keying (BPSK) systems with single cochannel interference. Impulse responses for different room types were computed via the shooting and bouncing rays technique. The Bit Error Rates (BER) and carrier-to-interference ratios were calculated, with findings indicating that interference was more significant in rooms with plasterboard-wall partitions compared to those with concrete-wall partitions [11]. An attention-assisted Ultra-Wideband (UWB) ranging error compensation algorithm was proposed by He in 2023, enabling the reevaluation of the significance of extracted UWB channel characteristics across different environments. This approach enhanced the performance of the Deep Neural Network (DNN) model [12]. In 2024, Lv proposed a dual-channel neural network to accurately recognize Non-Line-Of-Sight (NLOS) and Line-Of-Sight (LOS) signals in UWB positioning systems. By integrating both time-domain and time–frequency-domain features, the network processed UWB Channel Impulse Response (CIR) signals using a combination of CNN, Time Convolutional Networks (TCNs), and self-attention, achieving high classification accuracy across various complex environments and enhancing positioning performance [13]. In 2024, Carlos compared classical fingerprinting with Decision Tree Regressor (DTR)-based algorithms to improve indoor localization in 5G and WiFi environments. This paper demonstrated how machine learning enhanced robustness when radio maps were incomplete during training and discussed the benefits of technology fusion for precise positioning. [14]. In 2024, Gao proposed a paradigm of Localization-oriented Digital Twins (LocDT) with a compound architecture of seven sub-DT layers to characterize the 6G Integrated-Localization-And-Communication (ILAC) feature. LocDT started from a physical environment sublayer to mirror 6G signal interactions within a real-world scenario, along with an ILAC baseband sublayer and a channel frequency polar-coordinate image construction method to provide finer-grained fingerprints [15].
In 2025, Sun constructed a high-precision indoor positioning system by integrating Wi-Fi round-trip time, magnetic field sensing, and pedestrian dead reckoning. Numerical results demonstrated that the proposed fusion model achieved a localization accuracy ranging from 0.64 to 0.91 m [16]. In the same year, Lu proposed an ultra-wideband positioning approach based on a novel position fingerprinting technique and a parallel convolutional neural network. The proposed scheme achieved a mean absolute error of just 0.173 m, indicating high precision in indoor localization tasks [17]. However, we notice that the accuracy of existing methods decreases under high noise and interference, and the CLAB and SLAB mechanisms effectively overcome this problem. Experimental results have demonstrated improvements in stability and anti-interference capabilities.
To the best of our knowledge, there has been no research on a time-domain positioning system using ResNet with Channel Local Attention Block (CLAB) and Spatial Local Attention Block (SLAB). This paper first introduces ResNet with CLAB and SLAB for localization by means of time-domain data. The distinctive features of this work include the following:
- We employ the time-domain approach using the ResNet to effectively leverage channel information, further enhancing the accuracy of the localization results;
- We introduce two advanced attention mechanisms, CLAB and SLAB, that significantly boost model performance, elevating its effectiveness to a new level;
- Existing localization methods often struggle under severe noise and interference, leading to significant accuracy degradation. This paper addresses such limitations by integrating CLAB and SLAB into the ResNet framework, enhancing noise robustness. Experimental results show that under 20% Gaussian noise and an additional 20% interference, our proposed method reduces RMSE by up to 56.5% compared to baseline ResNet, clearly demonstrating superior stability and accuracy in harsh environments.
2. Channel Modeling and Indoor Positioning System
2.1. Channel Modeling
In the context of the 6G terahertz communication channel model, the ray-tracing method is employed to determine the loss and frequency response characteristics. The frequency response of the channel is mathematically expressed as follows:
The term denotes the phase shift delay associated with the corresponding path. This equation encapsulates the channel frequency response as the superposition of multiple propagation paths, each contributing with a distinct amplitude attenuation and phase shift, which collectively influence the received signal. is the total number of paths, f is the frequency, and A is the amplitude of the k-th ray.
The shooting and bouncing ray technique is used to transmit a triangular ray tube. As each ray tube interacts with the environment, the system determines whether the receiver lies within a reflected ray tube. If so, the signal from the ray tube is treated as originating from an equivalent source. The system assesses whether a ray encounters an obstacle. When an interaction occurs, it is classified as either a reflection or a transmission. If reflection occurs, the reflection count is increased, and the newly reflected ray is added to the stack; otherwise, the transmitted ray is added without changing the reflection count. This process iterates until all ray tubes are processed. In the simulation, reflections are limited to six bounces to capture a realistic set of detectable rays, while diffraction is constrained to a single instance, as power attenuation is significant beyond the first diffraction event. The carrier frequency is set to 120 GHz with a bandwidth of 14 GHz. The coordinate system uses a three-dimensional model, with the x-y plane representing the horizontal plane and the z-axis representing the height above the ground.
Once the frequency response is obtained, the inverse Fourier transform is applied in wideband systems to convert the frequency-domain data into time-domain data. The inverse Fourier transform of is applied to obtain the time-domain impulse response:
where represents the impulse response of the channel. The integral accumulates contributions from all frequency components, reconstructing the temporal behavior of the signal propagation. The impulse response is fundamental in characterizing channel-induced distortions, including multipath effects and delay spread, which are critical for the design and optimization of high-frequency wireless communication systems. The primary focus of this research is on time-domain processing using CIR to enhance the accuracy of indoor positioning. CIR provides detailed multipath characteristics essential for precise localization. The system collects impulse responses from terahertz wireless sensors, which capture spatial patterns within the indoor environment. The channel characteristics are extracted from the CIR to provide sufficient available information for localization. The extracted characteristics are the first path amplitude, time of arrival for the first path, channel impulse response power, root mean square delay spread, and Received Signal Strength Indicator (RSSI) [7]. This CIR matrix is converted into an image format for neural network processing.
2.2. Indoor Positioning Framework
The proposed indoor positioning framework, as illustrated in Figure 1, is based on a terahertz wireless sensor framework, which operates in both offline and online phases. The localization system consists of six blocks: signal and interference input, channel, positioning device, fingerprint generator, localization server, and position estimation output. The positioning device is typically a mobile device such as a smartphone or an IoT sensor. This device collects the 6G signal and sends the gathered data to the server for location processing.
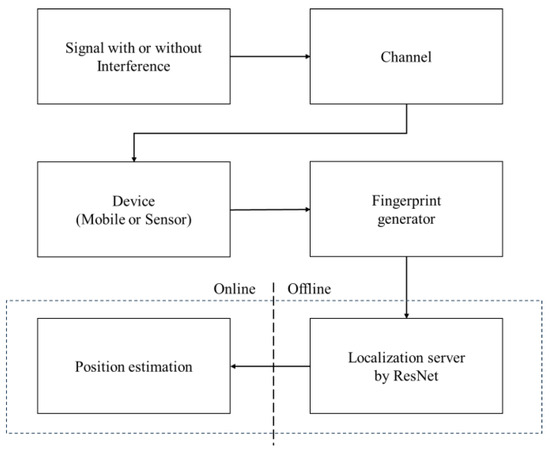
Figure 1.
Indoor positioning framework.
The fourth block is the fingerprint generator block. A database of pre-collected signals is created across the environment to generate the fingerprint data. The same set of CIR features described in Section 2.2 is used for training and evaluation. Cartesian coordinates transformation is applied to enhance positioning accuracy.
The localization server is the most important block of the system. In this research, we use ResNet to process the fingerprint and estimate the positions based on the processed data. In other words, the processed data are used to train the ResNet, enabling it to learn spatial patterns and associate them with physical locations. Given the computationally intensive nature of training, adequate data and processing resources are required to ensure the system’s accuracy and robustness. The CIR features are shuffled and split into the training and testing datasets. The training process utilizes ResNet to map the CIR features to spatial coordinates, improving indoor positioning performance by addressing the associated challenges posed by multipath effects and environmental variations. The offline phase is dedicated to data preprocessing and training ResNet, while the online phase estimates positions in real time based on the processed data.
3. ResNet with SLAB and CLAB
3.1. ResNet for Positioning Tasks
ResNets are designed to address the challenges arising from deeper architectures, particularly the vanishing gradient problem. ResNet introduces residual connections that allow the network to learn the identity function, making it easier to train deeper networks by mitigating gradient issues. For this paper, a modified ResNet architecture, as shown in Figure 2, is employed for position prediction based on the CIR and time-domain data. The ResNet architecture is composed of a feature input layer followed by several residual convolution blocks, each designed to refine the feature representations progressively. The structure is described as follows:
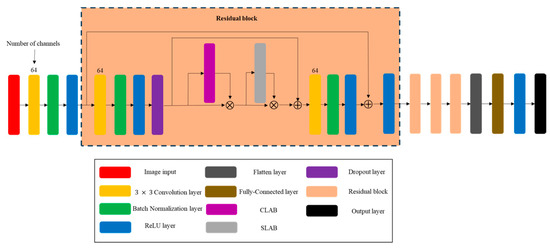
Figure 2.
ResNet with CLAB and SLAB.
- Input Layer: The input layer is set up to handle complex inputs. It receives features from the data and then processes them through the 3 × 3 convolutional layer with 64 filters, a batch normalization layer, and a Rectified Linear unit (ReLu);
- Residual Blocks: The network consists of four residual blocks, each containing:
- (a)
- Convolution Layer: A kernel size of 3 × 3 with 64 filters is employed to extract features;
- (b)
- Batch Normalization: Applied to stabilize training;
- (c)
- ReLU Activation: Introduced to add non-linearity;
- (d)
- Dropout: Regularization to prevent overfitting. The dropout rate is 0.2;
- (e)
- Addition Layer: This layer enables the network to learn residuals by adding the input of the block to its output.
- Fully Connected Layers: After the residual blocks, the output is processed through a series of fully connected layers that reduce the dimensionality before producing the final 2-output layer, corresponding to the x- and y-coordinates.
- Output Layer: The final output layer, with 2 neurons, predicts the position.
The residual convolution block function defines the structure of each residual block, where the key feature is the addition layer that allows the network to learn both the transformed features and the residuals, facilitating deeper network training.
One of the primary objectives of this paper is to evaluate the noise and interference resilience of ResNet models in the context of indoor positioning. Since real-world positioning tasks often involve noisy data and interference, it is crucial to assess how well these models perform in such conditions. ResNet has good noise resilience due to its residual connections, which allow the network to maintain stable performance even in the presence of noise. By incorporating residual blocks, the ResNet architecture is designed to learn both the underlying patterns and the noise, improving its ability to generalize in noisy environments. Additionally, the inclusion of dropout and batch normalization in both architectures helps prevent overfitting and stabilizes training, which is particularly important when dealing with noisy inputs. Note that only using the average strategy could weaken the salient features; thus, we use max-pooling to gather other important information about distinctive object features to infer attention maps. The sigmoid activation layer is used to obtain the probability of which channel to focus on. In other words, CLAB is designed to focus on which channel is important for the given input feature map.
3.2. Channel Local Attention Block (CLAB)
CLAB is designed to refine channel-wise feature representation by leveraging information. As shown in Figure 3, CLAB first applies average pooling and max pooling along the spatial dimensions of the input feature map (), producing two-channel descriptors of size . These pooled features encode different aspects of the channel information. The pooled features are processed through a convolutional layer with a ReLU activation function, followed by another convolutional layer to generate a refined channel representation. The output is then passed through a sigmoid activation function to produce a channel attention map of size . This attention map is used to emphasize informative channels, improving the network’s ability to capture meaningful features [18,19]. Note that only using the average strategy could weaken the salient features; thus, we use max-pooling to gather other important information about distinctive object features to infer attention maps. The sigmoid activation layer is used to obtain the probability of which channel to focus on. In other words, CLAB is designed to focus on which channel is important for the given input feature map.

Figure 3.
Channel local attention block (CLAB).
3.3. Spatial Local Attention Block (SLAB)
SLAB is designed to enhance spatial feature representation by capturing spatial dependencies. As shown in Figure 4, SLAB begins by applying both average pooling and max pooling along the channel dimension of the input feature map (), generating two spatial feature maps of size . These two maps are then concatenated to form a unified spatial representation. The concatenated feature map is processed through a convolutional layer, followed by a sigmoid activation function to generate a spatial attention map of size . This spatial attention map highlights essential regions in the feature map, allowing the network to focus on significant spatial features.
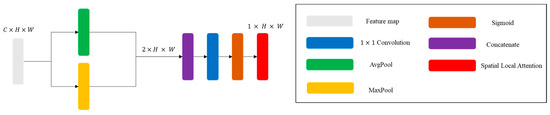
Figure 4.
Spatial local attention block (SLAB).
SLAB applies average-pooling and max-pooling operations and concatenates them along the channel dimension to produce the feature maps. The feature maps are passed through the final sigmoid activation layer to produce the probability of where to focus. In other words, SLAB is designed to identify the most important positions in the given input feature map.
Finally, a cascade structure, where channel attention is applied first, followed by spatial attention. This sequential configuration encourages the model to pre-select informative feature maps and subsequently refine them spatially, enhancing localization accuracy even in complex indoor environments.
4. Numerical Results
Figure 5 is the layout of the environment. A typical laboratory with is simulated to test the positioning algorithm. CIR data from terahertz sensors is collected to extract the fingerprint. The dataset includes data from 289 receiving antennas, 3 transmitters, and 1024 frequency points, spanning a frequency range from 120 GHz to 130.23 GHz, with a frequency resolution of 0.01 GHz. The half-wave dipoles are used for transmitting and receiving antennas. The maximum number of reflections is set to 5, and the number of diffractions is 1. The CIR data are measured 200 times per receiver, with data from 289 receiving antennas, resulting in a significant dataset for training the model. The CIR features are extracted, normalized, and reshaped for model convergence. A database of pre-collected signals is created across the environment to generate fingerprint data. The fingerprint data includes the first path amplitude, time of arrival of the first path, channel impulse response power, root mean square delay spread, and RSSI from CIR. These features are normalized to standardize the input, thereby improving model training.
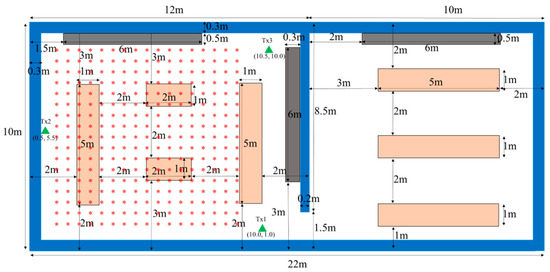
Figure 5.
Laboratory layout. The green triangles denote transmitters. * denotes receviers.
There are three metal bookcases, with a height of 2 m, and seven desks with a height of 0.7 m in the laboratory. Three transmitters, of 1 m tall, located at Tx1(10, 1) m, Tx2(0.5, 5.5) m and Tx3(10.5, 10) m are used to transmit the signal. 289 receivers, all 1 m in height, are uniformly distributed from (1, 1) m to (9, 9) m as shown in Figure 5. The Adam optimizer is used for training, including 200 epochs with a mini-batch size of 128, and an initial learning rate of 0.002. The training is conducted on a GPU. L2 regularization and gradient clipping are employed to improve performance.
This paper primarily focuses on the time-domain to assess the accuracy of position prediction models for indoor positioning systems. The errors in predicted positions are typically computed as the Euclidean distance between the predicted and actual positions at each time point. The overall positioning error across all data points can be represented by the Root Mean Square Error (RMSE), which is calculated as follows:
where N denotes the total number of data points. and are the predicted x- and y-coordinates of the i-th data point. and are the true x- and y-coordinates of the i-th data point. The RMSE provides a more intuitive understanding of the error, with units equivalent to those of the original data (e.g., meters), making it suitable for real-world applications. Lower RMSE values indicate better accuracy, and the RMSE is particularly useful for understanding how well the model generalizes its predictions.
In this section, we analyze the numerical results obtained from four different models under various noise conditions. The four models include the ResNet, ResNet with CLAB, ResNet with SLAB, and ResNet with CLAB and SLAB. The evaluation is based on RMSE, which measures the positioning accuracy of each model. The networks are trained with 10% noise. Figure 6 shows the RMSE performance under different noise levels. Table 1 provides a summary of the results for different noise levels.
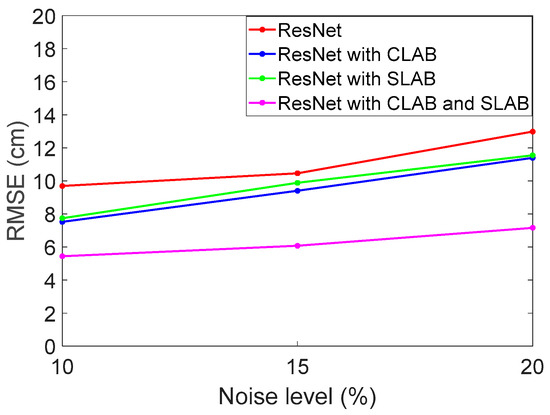
Figure 6.
The RMSE versus noise levels without interference.

Table 1.
RMSE (m) performance under different noise levels.
As shown, the ResNet with CLAB model outperforms ResNet in all noise scenarios, demonstrating its ability to improve feature selection. For a 10% noise level, RMSE is reduced from 0.0969 m to 0.0752 m, achieving a 22.4% improvement. However, the performance gain varies more significantly with different noise levels.
Next, the ResNet with the SLAB model consistently achieves lower RMSE values compared to the baseline ResNet, indicating that spatial attention enhances feature extraction and improves noise robustness. For a 10% noise level, RMSE is reduced from 0.0969 m to 0.0774 m, reflecting a 20.2% improvement. For a 15% noise level, RMSE reduction is 5.5%, showing that SLAB remains effective at moderate noise levels. This indicates that SLAB is particularly effective in reducing errors under varying noise conditions, likely due to its ability to capture spatial dependencies more effectively.
Lastly, the ResNet with CLAB and SLAB models achieves the lowest RMSE values under all noise conditions, verifying that the combination of spatial and channel attention mechanisms results in superior performance. Compared to ResNet, RMSE reductions of 43.9%, 42%, and 44.8% are observed at 10%, 15%, and 20% noise levels, respectively. From Table 1, it is evident that integrating both attention mechanisms, CLAB and SLAB, significantly enhances positioning accuracy. The RMSE can be reduced to 7 cm.
Figure 7 illustrates the RMSE variation over epochs without additional interference sources for different models under a 15% noise level. The results indicate that all models experience an initial sharp decline in RMSE, followed by stabilization as training progresses. The ResNet model with CLAB and SLAB mechanisms achieves the lowest RMSE and demonstrates the best convergence stability, suggesting that combining both channel and spatial attention mechanisms effectively enhances feature extraction and noise resilience. In brief, it has been observed that the standalone CLAB and SLAB models show improvement over the baseline ResNet. Additionally, the hybrid model outperforms both, confirming the complementary benefits of integrating both attention mechanisms. We are currently developing tools to visualize the learned attention weights from CLAB and SLAB in different indoor scenes. Preliminary results show that CLAB tends to emphasize frequency-domain feature channels that correspond to dominant signal components. SLAB highlights regions that spatially align with the anchor point, likely correlating with areas of signal strength variation due to multipath effects.
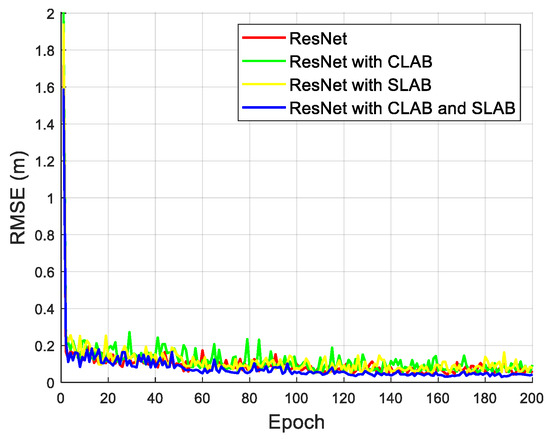
Figure 7.
The RMSE versus epoch without interference.
In some wireless communication systems, interference may come from multiple independent radio sources. The impact of these interference sources can be approximated as a Gaussian distribution. As a result, we use 20% Gaussian interference to evaluate our model. Figure 8 shows the RMSE performance with 20% interference under different noise levels.
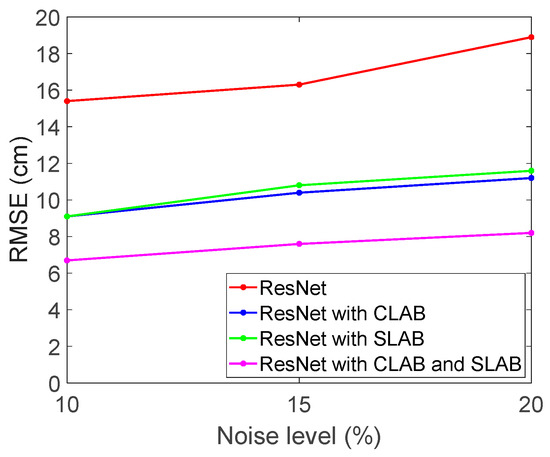
Figure 8.
The RMSE versus noise levels with interference.
Table 2 presents the RMSE performance under different noise levels with an additional 20% interference. The results also indicate that both CLAB and SLAB mechanisms contribute to reducing the RMSE value. Compared to Table 1, the presence of interference significantly increases the RMSE across all models, indicating that interference degrades positioning accuracy. Nevertheless, ResNet integrated with the CLAB and SLAB model still achieves the best performance, demonstrating its robustness against interference.

Table 2.
RMSE (m) performance with 20% interference under different noise levels.
In the 10% noise scenario, RMSE for ResNet increases from 0.0969 m (Table 1) to 0.1546 m (Table 2) due to interference, reflecting the impact of interference. However, applying CLAB or SLAB reduces RMSE, and their combination, CLAB and SLAB, achieves the lowest RMSE at 0.0673, an improvement of 50.5% compared to the baseline ResNet. At the 15% noise level, RMSE for the baseline ResNet rises from 0.1046 m (Table 1) to 0.1631 m (Table 2), further confirming the negative effect of interference. Even so, the CLAB and SLAB mechanisms still provide improvements by reducing RMSE to 0.0768, achieving a 54.3% improvement over the baseline ResNet. At 20% noise, RMSE degradation is most pronounced, with ResNet increasing from 0.1298 m (Table 1) to 0.1898 m (Table 2). Despite this, ResNet with CLAB and SLAB still effectively suppresses the error, achieving an RMSE of 0.0825 m, which represents a 56.5% improvement compared to ResNet. The above results demonstrate that both CLAB and SLAB effectively mitigate noise interference, and their combination provides the most significant improvement in positioning accuracy. The findings highlight the importance of integrating spatial and channel attention mechanisms in challenging environments.
Figure 9 presents the RMSE versus epoch results for the same models under a 15% noise level, with an additional 20% interference source. Compared to Figure 7, the RMSE values are generally higher in the initial training phase due to the added interference, which introduces additional challenges in learning accurate feature representations. However, as training progresses, RMSE stabilizes, with the ResNet model incorporating CLAB and SLAB still achieving the best overall performance. The gap between the baseline ResNet and the models utilizing attention mechanisms widens, highlighting that attention-based architectures are more robust against interference. Notably, the hybrid CLAB and SLAB model not only achieves lower RMSE but also maintains a more stable convergence trend, indicating its superior capacity to mitigate interference effects while preserving localization accuracy. As shown in Figure 7 and Figure 9, models equipped with CLAB and SLAB exhibit faster and more stable convergence trends compared to the baseline ResNet. In particular, the hybrid model with both CLAB and SLAB not only achieves the lowest RMSE but also shows less fluctuation during training, indicating better learning stability and robustness to noise and interference. The loss consistently decreases within the first 50 epochs and stabilizes afterwards, suggesting that our attention-augmented architectures can converge effectively and reliably.
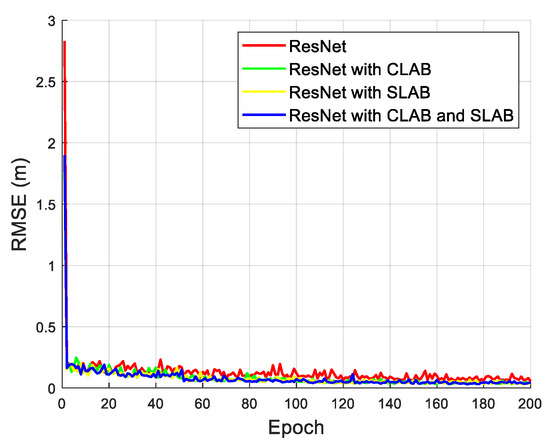
Figure 9.
The loss function versus epoch with interference.
In relation to the overall training duration for deep learning, our experiments are conducted on the same hardware configuration: a personal computer equipped with a 3.8 GHz Intel Core i7 processor, 64 GB RAM, and an NVIDIA RTX 4060 12 GB GPU. The training time for the baseline ResNet model is approximately 150 minutes. In comparison, the ResNet with CLAB requires an average of 155 min, and the model with SLAB needs the training time to approximately 160 min. The model with both CLAB and SLAB needs the training time to approximately 165 min. The computation time for training each model is shown in Table 3. Although training requires several hours, once the models are trained, they can perform inference in less than 1 s, making the proposed method suitable for real-time indoor localization applications.

Table 3.
Computation Time for training each model.
5. Conclusions
A ResNet neural network architecture with channel and spatial attention is proposed for indoor positioning by using time-domain data. ResNet’s deeper architecture with residual connections provides a powerful alternative for handling noisy data. Simulation results demonstrate that incorporating CLAB yields an improvement in RMSE, making it an effective approach for enhancing 6G indoor positioning accuracy. The channel attention SLAB mechanism also contributes to performance improvement. These findings highlight the potential of attention-enhanced ResNet models for improving localization precision in noisy environments. By incorporating either CLAB or SLAB into the ResNet architecture, the positioning error can be reduced to as low as approximately 7 cm. Moreover, the results of this study will offer insights into the relative strengths of these models in noise resilience and positioning accuracy, which are crucial for the success of real-world positioning systems.
While our method demonstrates strong performance in simulated indoor environments using ray-traced CIR data, certain limitations remain. Real-world deployment may introduce practical challenges such as hardware variability across different devices and environmental dynamics due to moving objects or changes in room layout. These factors could affect the model’s generalization ability. Addressing these challenges will require further validation of real-world data and potentially the application of domain adaptation techniques such as transfer learning. Future research could explore global channel and spatial attention mechanisms to further optimize the localization performance.
Author Contributions
Conceptualization, E.H.L.; Data curation, C.-E.C.; Formal analysis, E.H.L.; Funding acquisition, E.H.L.; Investigation, E.H.L.; Methodology, P.-H.C.; Project administration, C.-C.C.; Resources, H.-Y.W.; Software, H.-Y.W.; Supervision, C.-C.C.; Validation, P.-H.C.; Visualization, C.-E.C.; Writing—original draft, H.-Y.W.; Writing—review & editing, P.-H.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jiang, W.; Zhou, Q.; He, J.; Habibi, M.A.; Melnyk, S.; El-Absi, M.; Han, B.; Di Renzo, M.; Schotten, H.D.; Luo, F.-L.; et al. Terahertz Communications and Sensing for 6G and Beyond: A Comprehensive Review. IEEE Commun. Surv. Tutor. 2024, 26, 2326–2381. [Google Scholar] [CrossRef]
- Mukherjee, A.; Goswami, P.; Khan, M.A.; Manman, L.; Yang, L.; Pillai, P. Energy-Efficient Resource Allocation Strategy in Massive IoT for Industrial 6G Applications. IEEE Internet Things J. 2021, 8, 5194–5201. [Google Scholar] [CrossRef]
- Fan, S.; Wu, Y.; Han, C.; Wang, X. SIABR: A Structured Intra-Attention Bidirectional Recurrent Deep Learning Method for Ultra-Accurate Terahertz Indoor Localization. J. Sel. Areas Commun. 2021, 39, 2226–2240. [Google Scholar] [CrossRef]
- Khunteta, S.; Chavva, A.K.R.; Agrawal, A. AI-Based Indoor Localization Using mmWave MIMO Channel at 60 GHz. ITU J. Future Evol. Technol. 2022, 3, 243–251. [Google Scholar] [CrossRef]
- Pu, Q.; Chen, Y.; Zhou, M.; Ng, J.K.-Y.; Zhang, J. PaCNN-LSTM: A Localization Scheme Based on Improved Contrastive Learning and Parallel Fusion Neural Network. IEEE Trans. Instrum. Meas. 2023, 72, 2511011. [Google Scholar] [CrossRef]
- Alitaleshi, A.; Jazayeriy, H.; Kazemitabar, J. EA-CNN: A Smart Indoor 3D Positioning Scheme Based on Wi-Fi Fingerprinting and Deep Learning. Eng. Appl. Artif. Intell. 2023, 117, 105509. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, L.; Ruan, Y.; Zhou, T.; Chen, R. IMPos: Indoor Mobile Positioning with 5G Multibeam Signals from a Single Base Station. IEEE Internet Things J. 2024, 11, 20743–20756. [Google Scholar] [CrossRef]
- Wan, R.; Chen, Y.; Song, S.; Wang, Z. CSI-Based MIMO Indoor Positioning Using Attention-Aided Deep Learning. Commun. Lett. 2024, 28, 53–57. [Google Scholar] [CrossRef]
- Eleftherakis, S.; Santaromita, G.; Rea, M.; Costa-Pérez, X.; Giustiniano, D. SPRING+: Smartphone Positioning From a Single WiFi Access Point. Trans. Mob. Comput. 2024, 23, 9549–9566. [Google Scholar] [CrossRef]
- Chiu, C.C.; Wu, H.Y.; Chen, P.H.; Chao, C.E.; Lim, E.H. 6G Technology for Indoor Localization by Deep Learning With Attention Mechanism. Appl. Sci. 2024, 14, 10395. [Google Scholar] [CrossRef]
- Chiu, C.-C.; Wang, C.-P. Performance of Millimeter-Wave BPSK System With Single Cochannel Interference. IEICE Trans. Commun. 1999, E82-B, 2049–2054. [Google Scholar]
- He, X.; Mo, L.; Wang, Q. An Attention-Assisted UWB Ranging Error Compensation Algorithm. Wirel. Commun. Lett. 2023, 12, 421–425. [Google Scholar] [CrossRef]
- Lv, H.; Feng, J.; Shou, H.; Zhang, J.; Cui, T.; Mei, Z. UWB Localization Based on Dual-Channel Neural Network and Total Least Square Method. Sensors J. 2024, 24, 3477–3487. [Google Scholar] [CrossRef]
- Álvarez-Merino, C.S.; Khatib, E.J.; Luo-Chen, H.Q.; Muñoz, A.T.; Moreno, R.B. Evaluation and Comparison of 5G, WiFi, and Fusion With Incomplete Maps for Indoor Localization. IEEE Access 2024, 12, 51893–51903. [Google Scholar] [CrossRef]
- Gao, K.; Wang, H.; Lv, H.; Liu, W. Localization-Oriented Digital Twinning in 6G: A New Indoor-Positioning Paradigm and Proof-of-Concept. Trans. Wirel. Commun. 2024, 23, 10473–10486. [Google Scholar] [CrossRef]
- Sun, M.; Wang, Y.; Zheng, N.; Chen, G.; Li, Z.; Bi, J.; Yang, H. Smartphone-Based Indoor Localization System Using Wi-Fi RTT/Magnetic/PDR Based on an Improved Particle Filter. IEEE Trans. Instrum. Meas. 2025, 74, 9507616. [Google Scholar] [CrossRef]
- Lu, H.; Shao, W.; Jin, J.; Liu, Y.; Luo, Y.; Feng, M.; Zou, H. Ultra-Wideband Indoor Positioning Based on New Fingerprint with Missing CIR Data and Parallel CNN Model. IEEE Wirel. Commun. Lett. 2025, 14, 761–765. [Google Scholar] [CrossRef]
- Li, Y.; Mavromatis, S.; Zhang, F.; Du, Z.; Sequeira, J.; Wang, Z.; Zhao, X.; Liu, R. Single-Image Super-Resolution for Remote Sensing Images Using a Deep Generative Adversarial Network with Local and Global Attention Mechanisms. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3000224. [Google Scholar] [CrossRef]
- Wang, J.; Wang, B.; Wang, X.; Zhao, Y.; Long, T. Hybrid Attention-Based U-Shaped Network for Remote Sensing Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5612515. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).