Metric-Based Meta-Learning Approach for Few-Shot Classification of Brain Tumors Using Magnetic Resonance Images
Abstract
1. Introduction
- We introduce a novel metric-based meta-learning approach that is designed for effective few-shot MR image classification tasks with advanced vision transformer techniques.
- The research highlights that meta-learning algorithms are inherently suited for few-shot learning, enabling models to efficiently learn new tasks with minimal training data, unlike traditional machine learning methods that typically require large datasets.
- A comprehensive comparative analysis is conducted against multiple state-of-the-art models, demonstrating the proposed framework’s effectiveness in handling data-limited scenarios and enhancing robustness in medical image analysis.
2. Literature Review
2.1. Brain MRI Classification
2.2. Vision Transformer
2.3. Meta-Learning-Based Methods
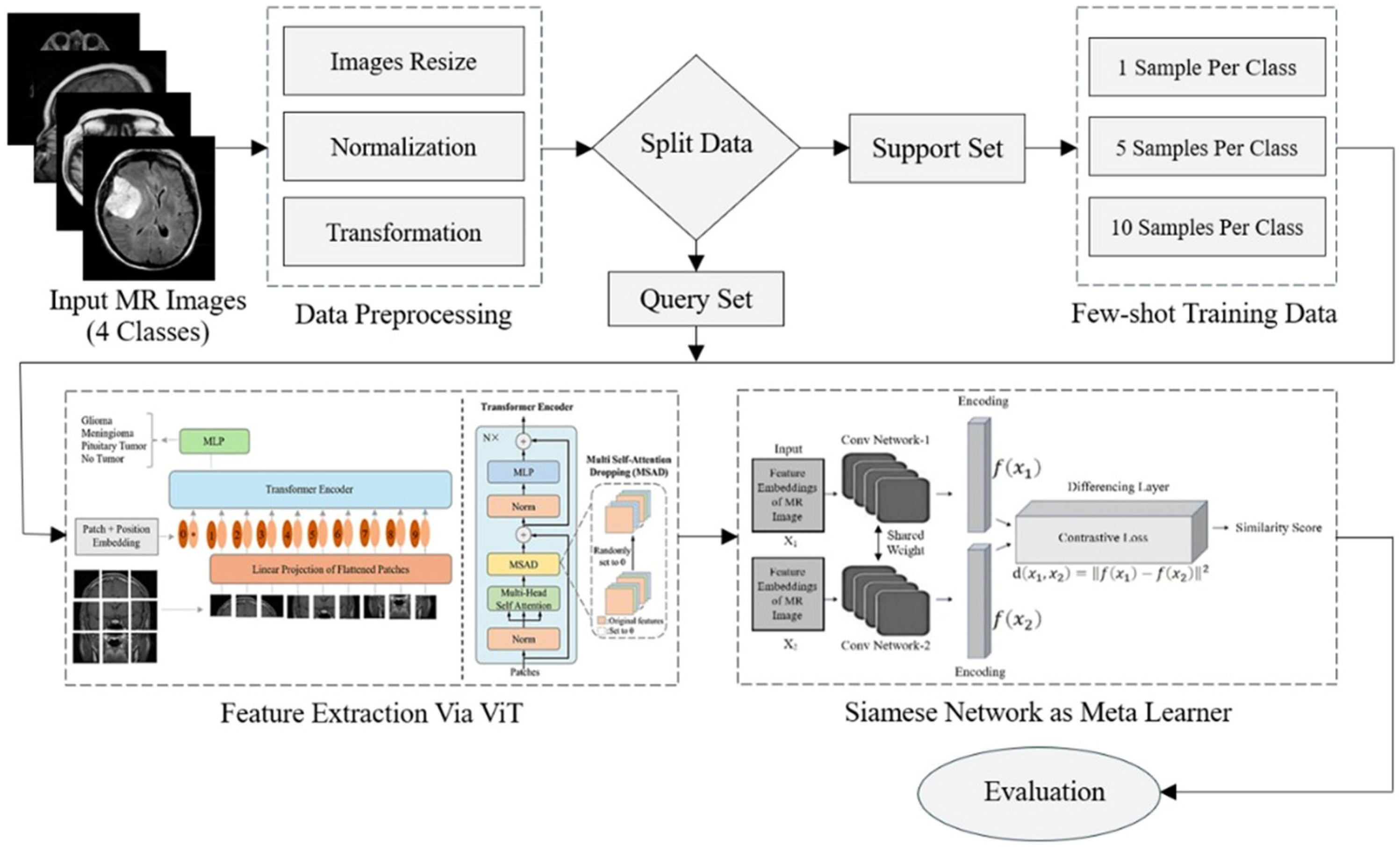
3. Research Methodology
3.1. Preprocessing
3.2. Feature Extraction
3.3. Siamese Network as Meta-Learner
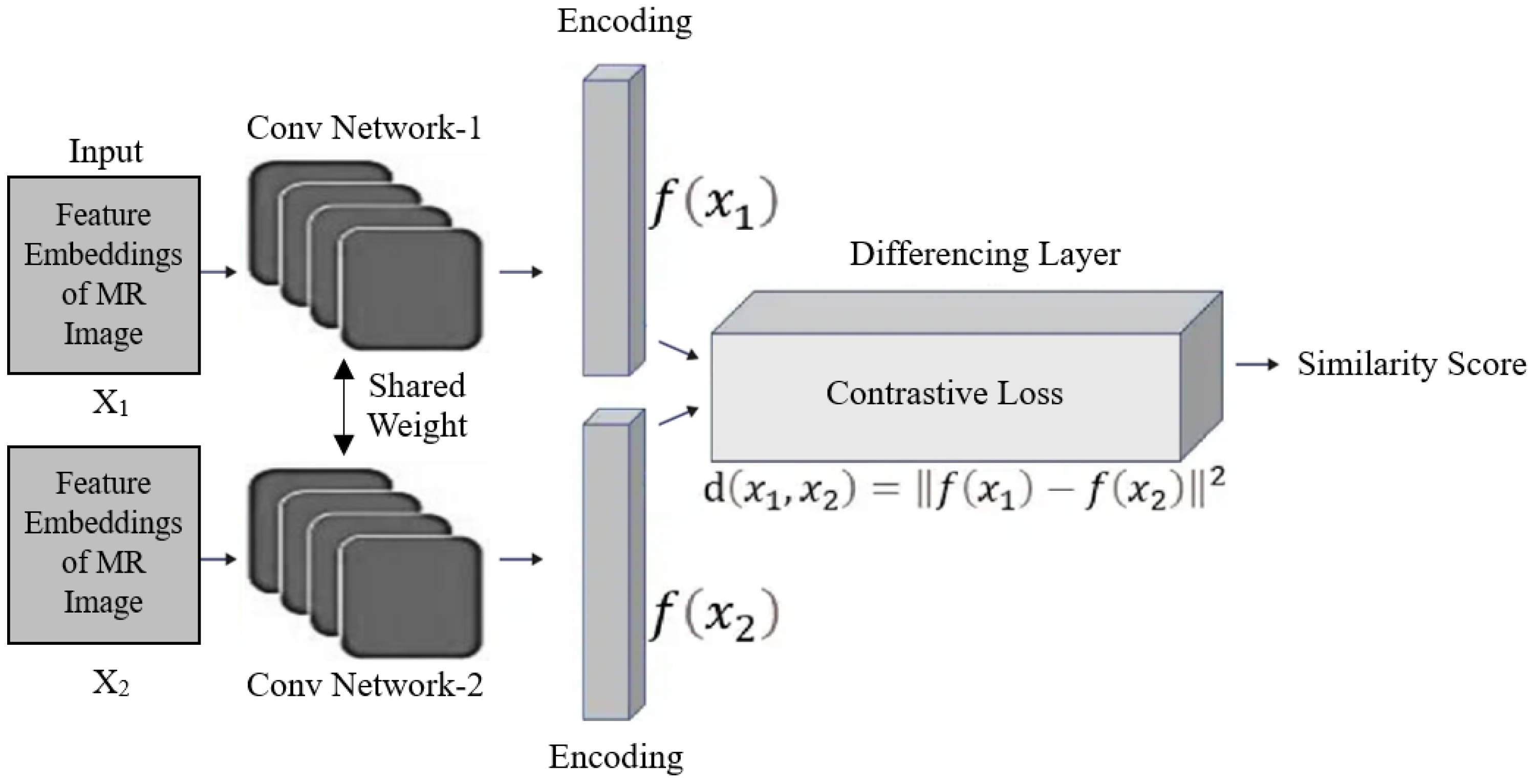
3.4. Few-Shot Classification
4. Experimental Results
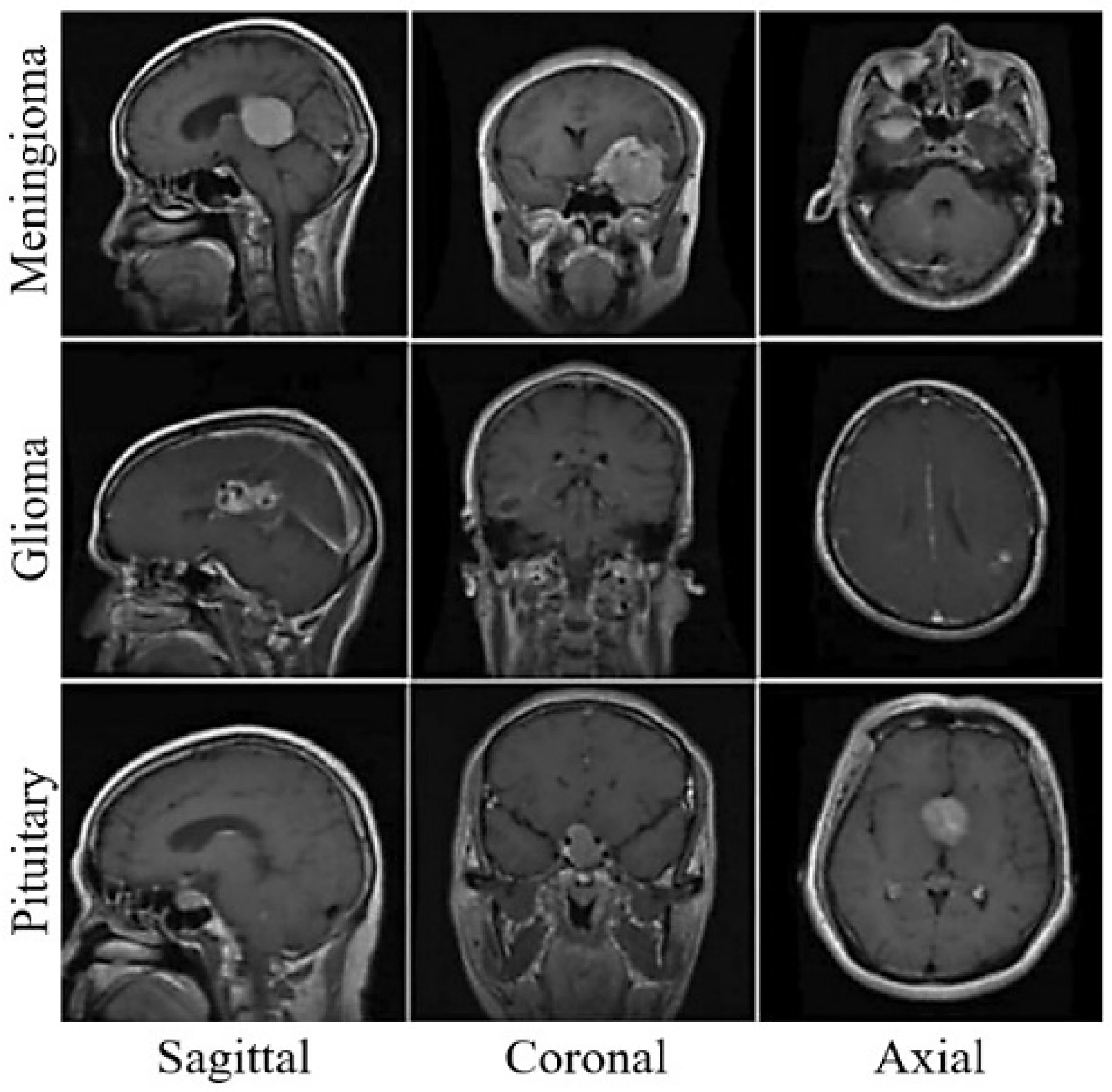
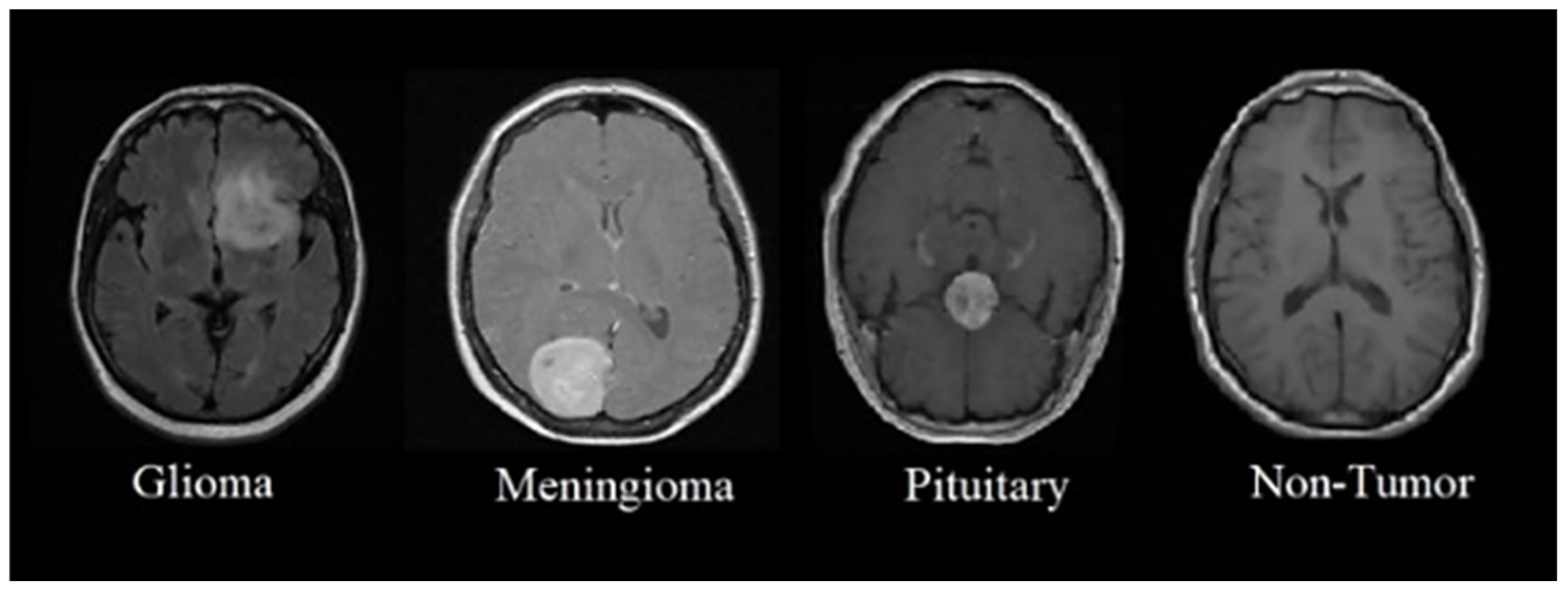
4.1. Dataset
4.2. Model Implementation
4.3. Training Details
4.4. Evaluation Metrics
4.5. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chinnam, S.K.R.; Sistla, V.; Kolli, V.K.K. Multimodal attention-gated cascaded u-net model for automatic brain tumor detection and segmentation. Biomed. Signal Process. Control 2022, 78, 103907. [Google Scholar]
- Deeksha, K.; Deeksha, M.; Girish, A.V.; Bhat, A.S.; Lakshmi, H. Classification of brain tumor and its types using convolutional neural network. In Proceedings of the 2020 IEEE International Conference for Innovation in Technology (INOCON), Bangluru, India, 6–8 November 2020; pp. 1–6. [Google Scholar]
- Rasool, M.; Ismail, N.A.; Boulila, W.; Ammar, A.; Samma, H.; Yafooz, W.M.; Emara, A.-H.M. A hybrid deep learning model for brain tumour classification. Entropy 2022, 24, 799. [Google Scholar] [CrossRef] [PubMed]
- Wen, P.Y.; Packer, R.J. The 2021 who classification of tumors of the central nervous system: Clinical implications. Neuro-oncology 2021, 23, 1215–1217. [Google Scholar] [CrossRef]
- Abd El-Wahab, B.S.; Nasr, M.E.; Khamis, S.; Ashour, A.S. Btc-fcnn: Fast convolution neural network for multi-class brain tumor classification. Health Inf. Sci. Syst. 2023, 11, 3. [Google Scholar] [CrossRef]
- Mokri, S.; Valadbeygi, N.; Grigoryeva, V. Diagnosis of glioma, menigioma and pituitary brain tumor using mri images recognition by deep learning in python. EAI Endorsed Trans. Intell. Syst. Mach. Learn. Appl. 2024, 1, 1–9. [Google Scholar]
- Ciceri, T.; Casartelli, L.; Montano, F.; Conte, S.; Squarcina, L.; Bertoldo, A.; Agarwal, N.; Brambilla, P.; Peruzzo, D. Fetal brain mri atlases and datasets: A review. NeuroImage 2024, 292, 120603. [Google Scholar] [CrossRef]
- Roozpeykar, S.; Azizian, M.; Zamani, Z.; Farzan, M.R.; Veshnavei, H.A.; Tavoosi, N.; Toghyani, A.; Sadeghian, A.; Afzali, M. Contrast-enhanced weighted-t1 and flair sequences in mri of meningeal lesions. Am. J. Nucl. Med. Mol. Imaging 2022, 12, 63. [Google Scholar]
- Louis, D.N.; Perry, A.; Wesseling, P.; Brat, D.J.; Cree, I.A.; Figarella-Branger, D.; Hawkins, C.; Ng, H.; Pfister, S.M.; Reifenberger, G. The 2021 who classification of tumors of the central nervous system: A summary. Neuro-oncology 2021, 23, 1231–1251. [Google Scholar] [CrossRef]
- Gull, S.; Akbar, S. Artificial intelligence in brain tumor detection through mri scans: Advancements and challenges. Artif. Intell. Internet Things 2021, 1, 241–276. [Google Scholar]
- Bakas, S.; Reyes, M.; Jakab, A.; Bauer, S.; Rempfler, M.; Crimi, A.; Shinohara, R.T.; Berger, C.; Ha, S.M.; Rozycki, M. Identifying the best machine learning algorithms for brain tumor segmentation, progression assessment, and overall survival prediction in the brats challenge. arXiv 2018, arXiv:1811.02629. [Google Scholar]
- Archana, R.; Jeevaraj, P.E. Deep learning models for digital image processing: A review. Artif. Intell. Rev. 2024, 57, 11. [Google Scholar] [CrossRef]
- Nassar, S.E.; Yasser, I.; Amer, H.M.; Mohamed, M.A. A robust mri-based brain tumor classification via a hybrid deep learning technique. J. Supercomput. 2024, 80, 2403–2427. [Google Scholar] [CrossRef]
- Mohammed, F.A.; Tune, K.K.; Assefa, B.G.; Jett, M.; Muhie, S. Medical image classifications using convolutional neural networks: A survey of current methods and statistical modeling of the literature. Mach. Learn. Knowl. Extr. 2024, 6, 699–735. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. Squeezenet: Alexnet-level accuracy with 50x fewer parameters and <0.5 mb model size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An extremely efficient convolutional neural network for mobile devices. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6848–6856. [Google Scholar]
- Chauhan, P.; Lunagaria, M.; Verma, D.K.; Vaghela, K.; Diwan, A.; Patole, S.; Mahadeva, R. Analyzing brain tumour classification techniques: A comprehensive survey. IEEE Access 2024, 12, 136389–136407. [Google Scholar] [CrossRef]
- Safdar, K.; Akbar, S.; Gull, S. An automated deep learning based ensemble approach for malignant melanoma detection using dermoscopy images. In Proceedings of the 2021 International Conference on Frontiers of Information Technology (FIT), Islamabad, Pakistan, 13–14 December 2021; pp. 206–211. [Google Scholar]
- Mahesh, T.; Vinoth Kumar, V.; Vivek, V.; Karthick Raghunath, K.; Sindhu Madhuri, G. Early predictive model for breast cancer classification using blended ensemble learning. Int. J. Syst. Assur. Eng. Manag. 2024, 15, 188–197. [Google Scholar] [CrossRef]
- Gull, S.; Akbar, S.; Khan, H.U. Automated detection of brain tumor through magnetic resonance images using convolutional neural network. BioMed Res. Int. 2021, 2021, 3365043. [Google Scholar] [CrossRef]
- Hassan, N.M.; Hamad, S.; Mahar, K. Mammogram breast cancer cad systems for mass detection and classification: A review. Multimed. Tools Appl. 2022, 81, 20043–20075. [Google Scholar] [CrossRef]
- Bhardawaj, F.; Jain, S. Cad system design for two-class brain tumor classification using transfer learning. Curr. Cancer Ther. Rev. 2024, 20, 223–232. [Google Scholar] [CrossRef]
- Işık, G.; Paçal, İ. Few-shot classification of ultrasound breast cancer images using meta-learning algorithms. Neural Comput. Appl. 2024, 36, 12047–12059. [Google Scholar] [CrossRef]
- Gharoun, H.; Momenifar, F.; Chen, F.; Gandomi, A.H. Meta-learning approaches for few-shot learning: A survey of recent advances. ACM Comput. Surv. 2024, 56, 1–41. [Google Scholar] [CrossRef]
- Zhang, C.; Cui, Q.; Ren, S. Few-shot medical image classification with maml based on dice loss. In Proceedings of the 2022 IEEE 2nd International Conference on Data Science and Computer Application (ICDSCA), Dalian, China, 28–30 October 2022; pp. 348–351. [Google Scholar]
- Huisman, M.; Van Rijn, J.N.; Plaat, A. A survey of deep meta-learning. Artif. Intell. Rev. 2021, 54, 4483–4541. [Google Scholar] [CrossRef]
- Fu, M.; Wang, X.; Wang, J.; Yi, Z. Prototype bayesian meta-learning for few-shot image classification. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 7010–7024. [Google Scholar] [CrossRef]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the International conference on machine learning, Sydney, Australia, 6–11 August 2017; PMLR. pp. 1126–1135. [Google Scholar]
- Yeung, M.; Sala, E.; Schönlieb, C.-B.; Rundo, L. Unified focal loss: Generalising dice and cross entropy-based losses to handle class imbalanced medical image segmentation. Comput. Med. Imaging Graph. 2022, 95, 102026. [Google Scholar] [CrossRef]
- Koch, G.; Zemel, R.; Salakhutdinov, R. Siamese neural networks for one-shot image recognition. In Proceedings of the ICML Deep Learning Workshop, Lille, France, 10 July 2015; pp. 1–30. [Google Scholar]
- Vinyals, O.; Blundell, C.; Lillicrap, T.; Wierstra, D. Matching networks for one shot learning. Adv. Neural Inf. Process. Syst. 2016, 19, 1–9. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R. Prototypical networks for few-shot learning. Adv. Neural Inf. Process. systems 2017, 30, 1–11. [Google Scholar]
- Sung, F.; Yang, Y.; Zhang, L.; Xiang, T.; Torr, P.H.; Hospedales, T.M. Learning to compare: Relation network for few-shot learning. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1199–1208. [Google Scholar]
- Yan, J.; Feng, K.; Zhao, H.; Sheng, K. Siamese-prototypical network with data augmentation pre-training for few-shot medical image classification. In Proceedings of the 2022 2nd International Conference on Frontiers of Electronics, Information and Computation Technologies (ICFEICT), Wuhan, China, 19–21 August 2022; pp. 387–391. [Google Scholar]
- Pal, A.; Xue, Z.; Befano, B.; Rodriguez, A.C.; Long, L.R.; Schiffman, M.; Antani, S. Deep metric learning for cervical image classification. IEEE Access 2021, 9, 53266–53275. [Google Scholar] [CrossRef]
- Jiang, H.; Gao, M.; Li, H.; Jin, R.; Miao, H.; Liu, J. Multi-learner based deep meta-learning for few-shot medical image classification. IEEE J. Biomed. Health Inform. 2023, 27, 17–28. [Google Scholar] [CrossRef]
- Ramanarayanan, S.; Palla, A.; Ram, K.; Sivaprakasam, M. Generalizing supervised deep learning mri reconstruction to multiple and unseen contrasts using meta-learning hypernetworks. Appl. Soft Comput. 2023, 146, 110633. [Google Scholar] [CrossRef]
- Sun, Q.; Liu, Y.; Chua, T.-S.; Schiele, B. Meta-transfer learning for few-shot learning. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 403–412. [Google Scholar]
- Jia, J.; Feng, X.; Yu, H. Few-shot classification via efficient meta-learning with hybrid optimization. Eng. Appl. Artif. Intell. 2024, 127, 107296. [Google Scholar] [CrossRef]
- Pachetti, E.; Colantonio, S. A systematic review of few-shot learning in medical imaging. Artif. Intell. Med. 2024, 156, 102949. [Google Scholar] [CrossRef] [PubMed]
- Bateni, P.; Barber, J.; Van de Meent, J.-W.; Wood, F. Enhancing few-shot image classification with unlabelled examples. In Proceedings of the 2022 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2022; pp. 2796–2805. [Google Scholar]
- Shin, J.; Kang, Y.; Jung, S.; Choi, J. Active instance selection for few-shot classification. IEEE Access 2022, 10, 133186–133195. [Google Scholar] [CrossRef]
- Valero-Mas, J.J.; Gallego, A.J.; Rico-Juan, J.R. An overview of ensemble and feature learning in few-shot image classification using siamese networks. Multimed. Tools Appl. 2024, 83, 19929–19952. [Google Scholar] [CrossRef]
- Zeng, W.; Xiao, Z.-Y. Few-shot learning based on deep learning: A survey. Math. Biosci. Eng. 2024, 21, 679–711. [Google Scholar] [CrossRef]
- Liu, Q.; Tian, Y.; Zhou, T.; Lyu, K.; Xin, R.; Shang, Y.; Liu, Y.; Ren, J.; Li, J. A few-shot disease diagnosis decision making model based on meta-learning for general practice. Artif. Intell. Med. 2024, 147, 102718. [Google Scholar] [CrossRef]
- Al-Khuzaie, M.I.M.; Al-Jawher, W.A.M. Enhancing brain tumor classification with a novel three-dimensional convolutional neural network (3d-cnn) fusion model. J. Port Sci. Res. 2024, 7, 254–267. Available online: https://jport.co/index.php/jport/article/view/255 (accessed on 12 December 2024). [CrossRef]
- Pereira, S.; Pinto, A.; Alves, V.; Silva, C.A. Brain tumor segmentation using convolutional neural networks in mri images. IEEE Trans. Med. Imaging 2016, 35, 1240–1251. [Google Scholar] [CrossRef]
- Shamshad, N.; Sarwr, D.; Almogren, A.; Saleem, K.; Munawar, A.; Rehman, A.U.; Bharany, S. Enhancing brain tumor classification by a comprehensive study on transfer learning techniques and model efficiency using mri datasets. IEEE Access 2024, 12, 100407–100418. [Google Scholar] [CrossRef]
- Khaliki, M.Z.; Başarslan, M.S. Brain tumor detection from images and comparison with transfer learning methods and 3-layer cnn. Sci. Rep. 2024, 14, 2664. [Google Scholar] [CrossRef]
- LAROUI. A hybrid machine learning method for image classification. Int. J. Comput. Digit. Syst. 2024, 15, 1–16. [Google Scholar]
- Mohanty, B.C.; Subudhi, P.K.; Dash, R.; Mohanty, B. Feature-enhanced deep learning technique with soft attention for mri-based brain tumor classification. Int. J. Inf. Technol. 2024, 16, 1617–1626. [Google Scholar] [CrossRef]
- Sharif, M.I.; Li, J.P.; Khan, M.A.; Kadry, S.; Tariq, U. M3btcnet: Multi model brain tumor classification using metaheuristic deep neural network features optimization. Neural Comput. Appl. 2024, 36, 95–110. [Google Scholar] [CrossRef]
- Ghaffari, M.; Sowmya, A.; Oliver, R. Automated brain tumor segmentation using multimodal brain scans: A survey based on models submitted to the brats 2012–2018 challenges. IEEE Rev. Biomed. Eng. 2020, 13, 156–168. [Google Scholar] [CrossRef]
- Menze, B.H.; Jakab, A.; Bauer, S.; Kalpathy-Cramer, J.; Farahani, K.; Kirby, J.; Burren, Y.; Porz, N.; Slotboom, J.; Wiest, R.; et al. The multimodal brain tumor image segmentation benchmark (brats). IEEE Trans. Med. Imaging 2015, 34, 1993–2024. [Google Scholar] [CrossRef]
- University of Pennsylvania. Multimodal Brain Tumor Segmentation Challenge 2017. 2017. Available online: https://www.med.upenn.edu/sbia/brats2017.html (accessed on 12 March 2025).
- University of Pennsylvania. Multimodal Brain Tumor Segmentation Challenge 2018. 2018. Available online: https://www.med.upenn.edu/sbia/brats2018/data.html (accessed on 10 March 2025).
- Gull, S.; Akbar, S.; Naqi, S.M. A deep learning approach for multi-stage classification of brain tumor through magnetic resonance images. Int. J. Syst. Technol. 2023, 33, 1745–1766. [Google Scholar] [CrossRef]
- Remzan, N.; Tahiry, K.; Farchi, A. Advancing brain tumor classification accuracy through deep learning: Harnessing radimagenet pre-trained convolutional neural networks, ensemble learning, and machine learning classifiers on mri brain images. Multimed. Tools Appl. 2024, 83, 82719–82747. [Google Scholar] [CrossRef]
- Reddy, C.K.K.; Reddy, P.A.; Janapati, H.; Assiri, B.; Shuaib, M.; Alam, S.; Sheneamer, A. A fine-tuned vision transformer based enhanced multi-class brain tumor classification using mri scan imagery. Front. Oncol. 2024, 14, 1400341. [Google Scholar] [CrossRef]
- Wang, J.; Lu, S.-Y.; Wang, S.-H.; Zhang, Y.-D. Ranmerformer: Randomized vision transformer with token merging for brain tumor classification. Neurocomputing 2024, 573, 127216. [Google Scholar] [CrossRef]
- Goceri, E. Vision transformer based classification of gliomas from histopathological images. Expert Syst. Appl. 2024, 241, 122672. [Google Scholar] [CrossRef]
- Krishnan, P.T.; Krishnadoss, P.; Khandelwal, M.; Gupta, D.; Nihaal, A.; Kumar, T.S. Enhancing brain tumor detection in mri with a rotation invariant vision transformer. Front. Neuroinformatics 2024, 18, 1414925. Available online: https://www.frontiersin.org/journals/neuroinformatics/articles/10.3389/fninf.2024.1414925 (accessed on 15 August 2024). [CrossRef] [PubMed]
- Srinivas, B.; Anilkumar, B.; Devi, N.; Aruna, V. A fine-tuned transformer model for brain tumor detection and classification. Multimed. Tools Appl. 2024, 12, 1573–7721. [Google Scholar] [CrossRef]
- Dutta, T.K.; Nayak, D.R.; Pachori, R.B. Gt-net: Global transformer network for multiclass brain tumor classification using mr images. Biomed. Eng. Lett. 2024, 14, 1069–1077. [Google Scholar] [CrossRef] [PubMed]
- Singh, K.; Malhotra, D. Iram–net model: Image residual agnostics meta-learning-based network for rare de novo glioblastoma diagnosis. Neural Comput. Appl. 2024, 36, 21465–21485. [Google Scholar] [CrossRef]
- Rafiei, A.; Moore, R.; Jahromi, S.; Hajati, F.; Kamaleswaran, R. Meta-learning in healthcare: A survey. SN Comput. Sci. 2024, 5, 791. [Google Scholar] [CrossRef]
- Lu, L.; Cui, X.; Tan, Z.; Wu, Y. Medoptnet: Meta-learning framework for few-shot medical image classification. IEEE/ACM Trans. Comput. Biol. Bioinform. 2024, 21, 725–736. [Google Scholar] [CrossRef]
- Tian, Y.; Zhao, X.; Huang, W. Meta-learning approaches for learning-to-learn in deep learning: A survey. Neurocomputing 2022, 494, 203–223. [Google Scholar] [CrossRef]
- Monteiro, J.P.; Ramos, D.; Carneiro, D.; Duarte, F.; Fernandes, J.M.; Novais, P. Meta-learning and the new challenges of machine learning. Int. J. Intell. Syst. 2021, 36, 6240–6272. [Google Scholar] [CrossRef]
- Vettoruzzo, A.; Bouguelia, M.R.; Vanschoren, J.; Rögnvaldsson, T.; Santosh, K. Advances and challenges in meta-learning: A technical review. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 4763–4779. [Google Scholar] [CrossRef]
- Ali, M.D.; Saleem, A.; Elahi, H.; Khan, M.A.; Khan, M.I.; Yaqoob, M.M.; Khattak, U.F.; Al-Rasheed, A. Breast cancer classification through meta-learning ensemble technique using convolution neural networks. Diagnostics 2023, 13, 2242. [Google Scholar] [CrossRef]
- Verma, A.; Singh, V.P. Hsadml: Hyper-sphere angular deep metric based learning for brain tumor classification. In Proceedings of the Satellite Workshops of ICVGIP 2021, Singapore, 27 November 2022; Springer Nature: Singapore, 2022; pp. 105–120. [Google Scholar]
- Singh, J. Figshare. J. Pharmacol. Pharmacother. 2011, 2, 138–139. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Chen, Y.; Li, Y.; Mao, F.; He, Y.; Xue, H. Self-supervised learning for few-shot image classification. In Proceedings of the ICASSP 2021–2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 1745–1749. [Google Scholar] [CrossRef]
- Singh, R.; Bharti, V.; Purohit, V.; Kumar, A.; Singh, A.K.; Singh, S.K. Metamed: Few-shot medical image classification using gradient-based meta-learning. Pattern Recognit. 2021, 120, 108111. [Google Scholar] [CrossRef]
- Jantzen, J.; Norup, J.; Dounias, G.; Bjerregaard, B. Pap-smear benchmark data for pattern classification. Nat. Inspired Smart Inf. Syst. (NiSIS 2005) 2005, 1–9. [Google Scholar]
- Spanhol, F.A.; Oliveira, L.S.; Petitjean, C.; Heutte, L. A dataset for breast cancer histopathological image classification. IEEE Trans. Biomed. Eng. 2016, 63, 1455–1462. [Google Scholar] [CrossRef]
- Zou, J.; Ma, X.; Zhong, C.; Zhang, Y. Dermoscopic image analysis for isic challenge 2018. arXiv 2018, arXiv:1807.08948. [Google Scholar]
- Sekhar, A.; Gupta, R.K.; Sethi, A. Few-shot histopathology image classification: Evaluating state-of-the-art methods and unveiling performance insights. Comput. Vis. Pattern Recognit. 2024, 2408, 13816. [Google Scholar]
- Acevedo, A.; Merino, A.; Alférez, S.; Molina, Á.; Boldú, L.; Rodellar, J. A dataset of microscopic peripheral blood cell images for development of automatic recognition systems. Data Brief 2020, 30, 105474. [Google Scholar] [CrossRef]
- Kather, J.N.; Krisam, J.; Charoentong, P.; Luedde, T.; Herpel, E.; Weis, C.-A.; Gaiser, T.; Marx, A.; Valous, N.A.; Ferber, D.; et al. Predicting survival from colorectal cancer histology slides using deep learning: A retrospective multicenter study. PLoS Med. 2019, 16, e1002730. [Google Scholar] [CrossRef]
- Wang, X.; Peng, Y.; Lu, L.; Lu, Z.; Bagheri, M.; Summers, R.M. Chestx-ray8: Hospital-scale chest x-ray database and benchmarks on weakly-supervised classification and localization of common thorax diseases. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Lee, J.D.M.C.K.; Toutanova, K. Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Tummala, S.; Kadry, S.; Bukhari, S.A.; Rauf, H.T. Classification of brain tumor from magnetic resonance imaging using vision transformers ensembling. Curr. Oncol. 2022, 29, 7498–7511. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Huang, S.; Xu, Y. Inceptr: Micro-expression recognition integrating inception-cbam and vision transformer. Multimed. Syst. 2023, 29, 3863–3876. [Google Scholar] [CrossRef]
- Bromley, J.; Guyon, I.; LeCun, Y.; Säckinger, E.; Shah, R. Signature verification using a” siamese” time delay neural network. Adv. Neural inf. Process. Syst. 1993, 6, 737–744. [Google Scholar] [CrossRef]
- Kingma, D.P.J.B. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Nickparvar, M. Brain Tumor Mri Dataset. 2021. Available online: https://www.kaggle.com/datasets/masoudnickparvar/brain-tumor-mri-dataset?select=Training (accessed on 24 November 2024).

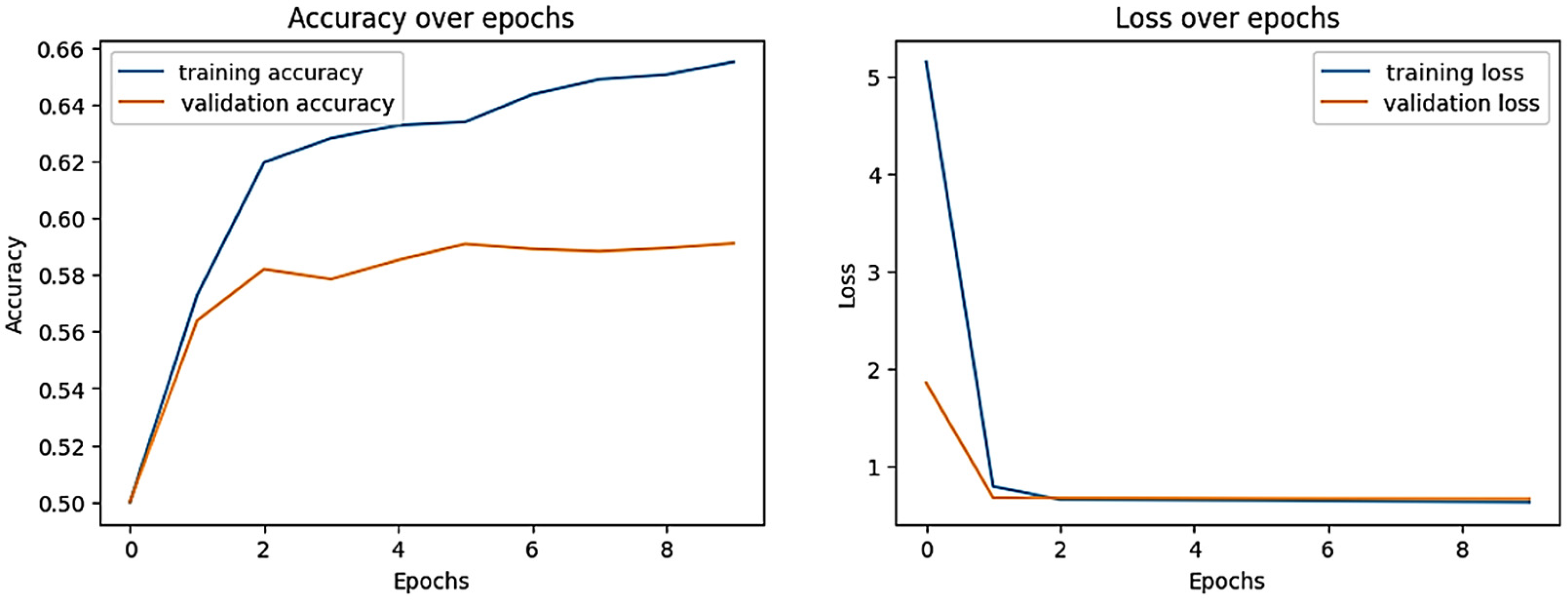
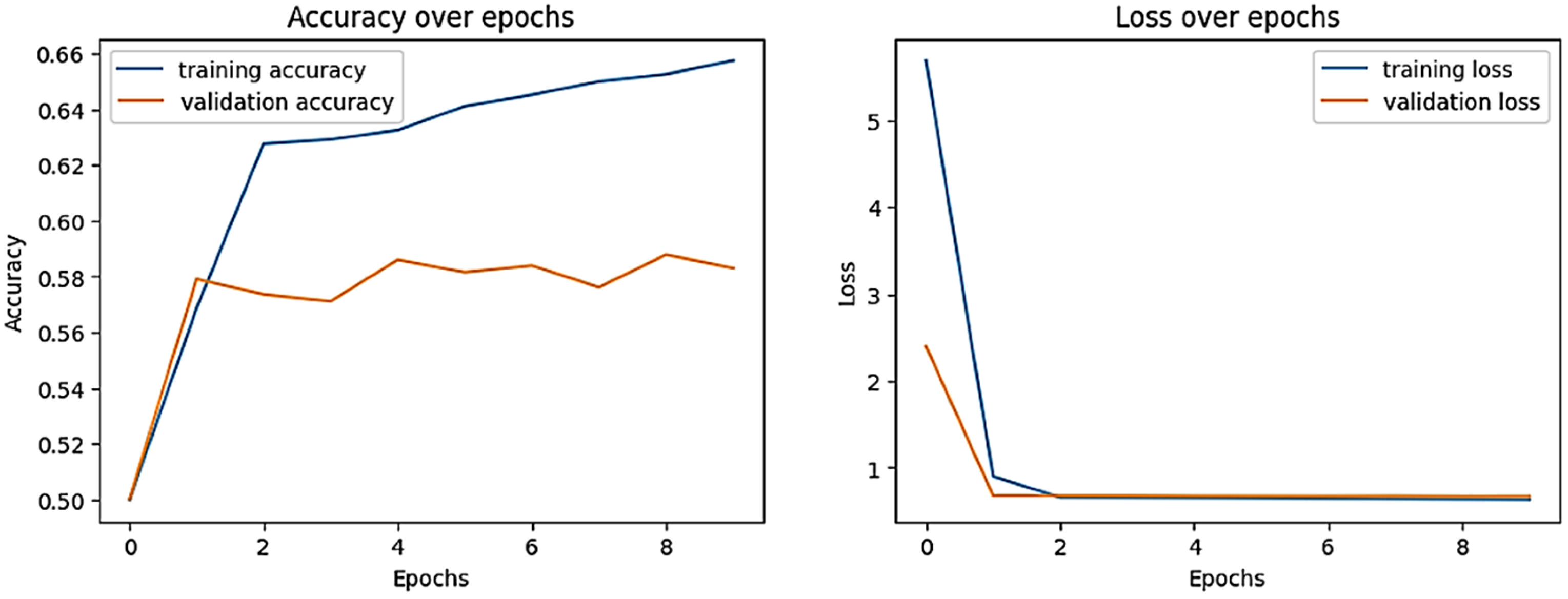
| Dataset Classes | Support Set | Query Set | Total Images of Each Class |
|---|---|---|---|
| Glioma Tumor | 1321 | 300 | 1621 |
| Meningioma Tumor | 1339 | 306 | 1645 |
| Pituitary Tumor | 1457 | 300 | 1757 |
| No Tumor | 1595 | 405 | 2000 |
| Total Images | 5712 | 1311 | 7023 |
| Parameters | Description |
|---|---|
| Input Image Size | 224 224 pixels |
| Patch Dimension | 16 |
| Embedding Size | 768 |
| Network Depth | 12 layers |
| Attention Heads | 12 |
| MLP Layer Size | 1024 |
| Batch Capacity | 32 |
| Dropout Rate | 0.1 |
| Total Epochs | 10 |
| Optimization Method | Adam |
| Regularization | 0.01 weight decay |
| Learning Rate | 0.001 |
| Proposed Methods | Accuracy | Specificity | Sensitivity | Precision | F1-Score |
|---|---|---|---|---|---|
| ViT (4-way 1-shot) | 0.12 | 0.35 | 0.06 | 0.10 | 0.27 |
| ViT (4-way 5-shot) | 0.45 | 0.40 | 0.13 | 0.20 | 0.09 |
| ViT (4-way 10-shot) | 0.49 | 0.48 | 0.25 | 0.31 | 0.17 |
| ViT + MAML (4-way 1-shot) | 0.29 | 0.58 | 0.18 | 0.09 | 0.30 |
| ViT + MAML (4-way 5-shot) | 0.35 | 0.39 | 0.12 | 0.23 | 0.16 |
| ViT + MAML (4-way 10-shot) | 0.50 | 0.67 | 0.14 | 0.17 | 0.13 |
| ViT + matching network (4-way 1-shot) | 0.89 | 0.62 | 0.15 | 0.35 | 0.43 |
| ViT + matching network (4-way 5-shot) | 0.60 | 0.57 | 0.28 | 0.48 | 0.56 |
| ViT + matching network (4-way 10-shot) | 0.60 | 0.49 | 0.37 | 0.52 | 0.27 |
| ViT + Siamese network (4-way 1-shot) | 0.05 | 0.20 | 0.39 | 0.27 | 0.35 |
| ViT + Siamese network (4-way 5-shot) | 0.09 | 78.60 0.32 | 0.73 | 62.32 0.16 | 0.21 |
| ViT + Siamese network (4-way 10-shot) | 60.11 0.95 | 0.09 | 47.73 0.05 | 0.15 | 53.86 0.19 |
| Existing Methods | Accuracy | Specificity | Sensitivity | Precision | F1-Score |
|---|---|---|---|---|---|
| CNN-based model [22] | |||||
| 4-way 1-shot | 39.66% | 65.13% | 36.00% | 42.18% | 38.84% |
| 4-way 5-shot | 52.76% | 62.81% | 52.35% | 54.66% | 52.48% |
| 4-way 10-shot | 55.00% | 68.76% | 51.53% | 55.51% | 53.44% |
| Deep learning model based on CNN layers [60] | |||||
| 4-way 1-shot | 22.88% | 49.00% | 25.00% | 05.72% | 09.31% |
| 4-way 5-shot | 23.34% | 57.00% | 25.00% | 05.84% | 09.46% |
| 4-way 10-shot | 34.63% | 68.12% | 31.50% | 19.63% | 23.38% |
| Proposed method (ViT+ Siamese network) | |||||
| 4-way 1-shot | 50.00% | 58.39% | % | 39.48% | |
| 4-way 5-shot | 58.30% | 74.60% | 62.32% | 50.19% | |
| 4-way 10-shot | 60.11% | 47.73% | 53.86% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gull, S.; Kim, J. Metric-Based Meta-Learning Approach for Few-Shot Classification of Brain Tumors Using Magnetic Resonance Images. Electronics 2025, 14, 1863. https://doi.org/10.3390/electronics14091863
Gull S, Kim J. Metric-Based Meta-Learning Approach for Few-Shot Classification of Brain Tumors Using Magnetic Resonance Images. Electronics. 2025; 14(9):1863. https://doi.org/10.3390/electronics14091863
Chicago/Turabian StyleGull, Sahar, and Juntae Kim. 2025. "Metric-Based Meta-Learning Approach for Few-Shot Classification of Brain Tumors Using Magnetic Resonance Images" Electronics 14, no. 9: 1863. https://doi.org/10.3390/electronics14091863
APA StyleGull, S., & Kim, J. (2025). Metric-Based Meta-Learning Approach for Few-Shot Classification of Brain Tumors Using Magnetic Resonance Images. Electronics, 14(9), 1863. https://doi.org/10.3390/electronics14091863






