Swarm Intelligent Car-Following Model for Autonomous Vehicle Platoon Based on Particle Swarm Optimization Theory
Abstract
1. Introduction
2. Models and Methods
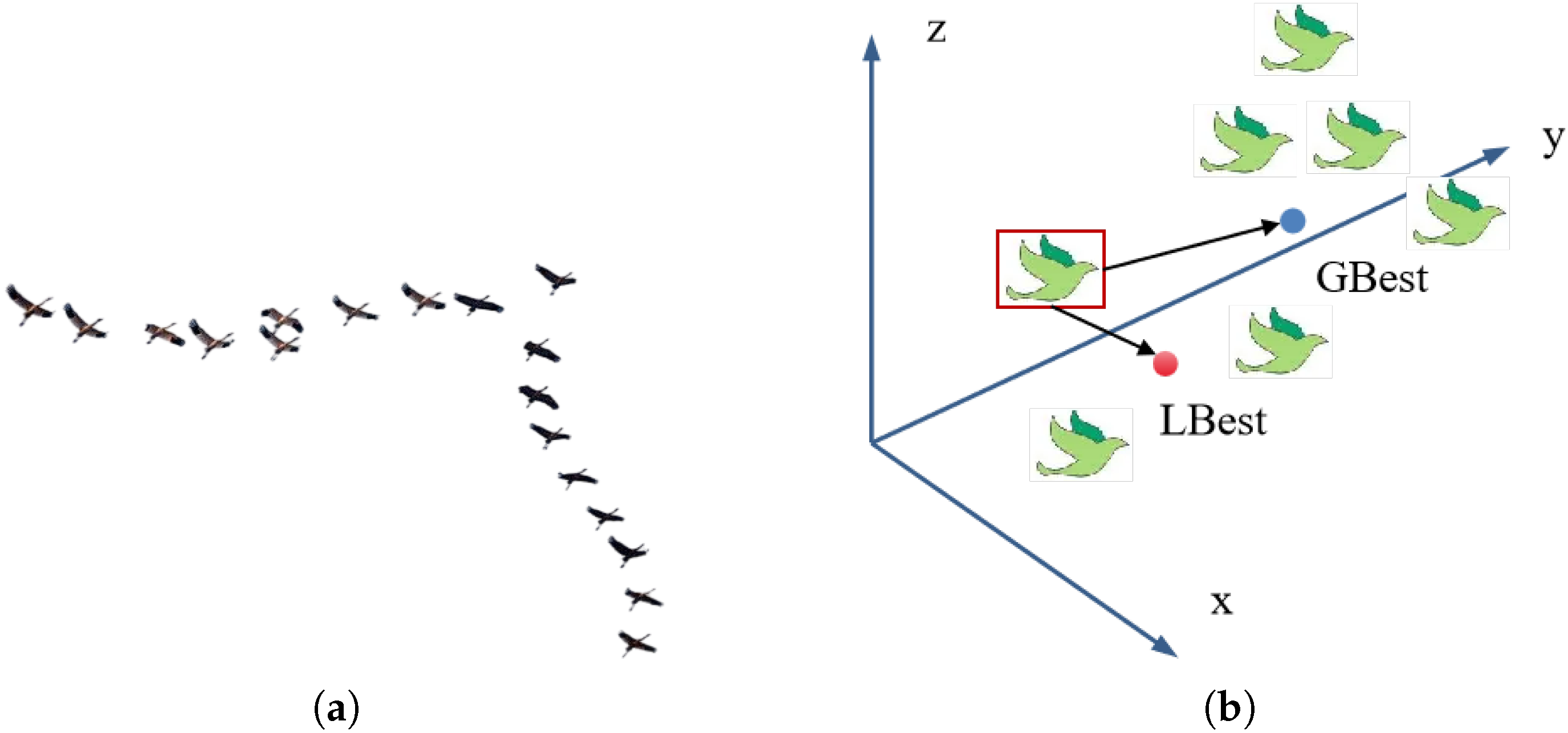
2.1. PSO Principle
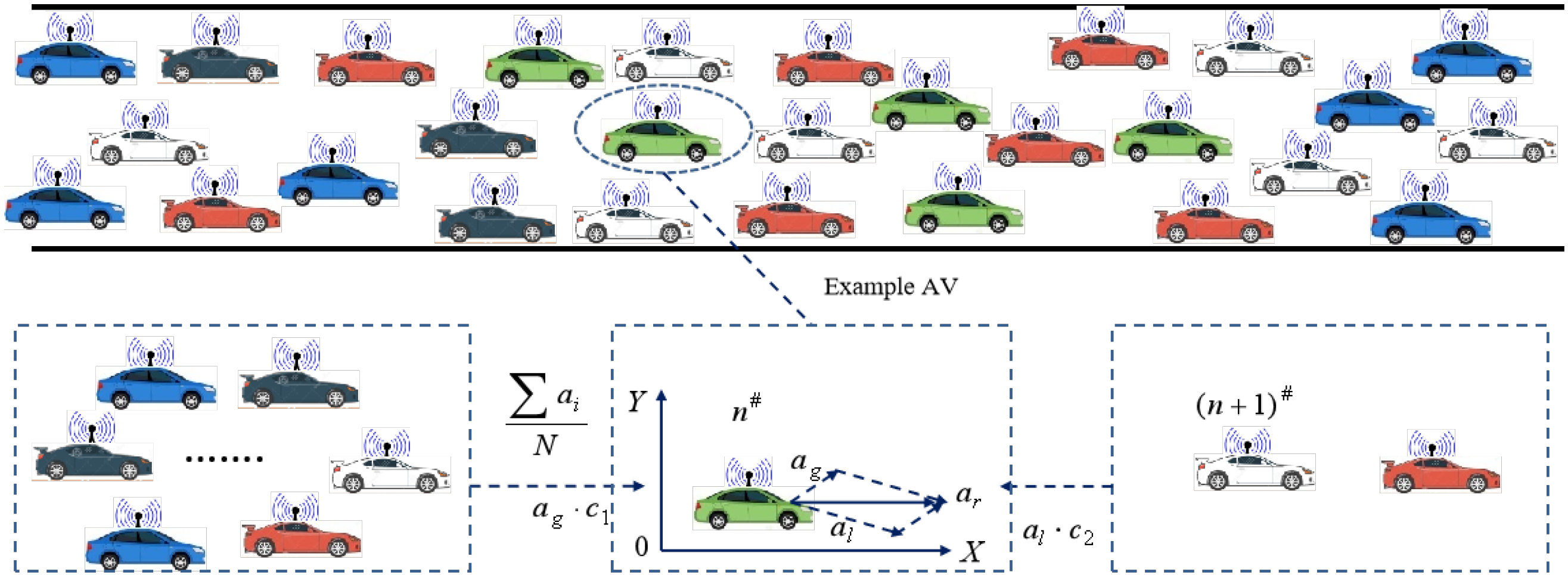
2.2. Particle Behavior Analysis of AV Platoon
2.3. Fitness Function for AV Platoon Motion
2.4. Local Optimal Acceleration Term
2.5. Global Optimal Acceleration Term
2.6. The AV-PSO Model Acceleration Expression
2.7. The AV-PSO Model Motion Expression
3. Model Analysis
3.1. Stability Conditions Analysis
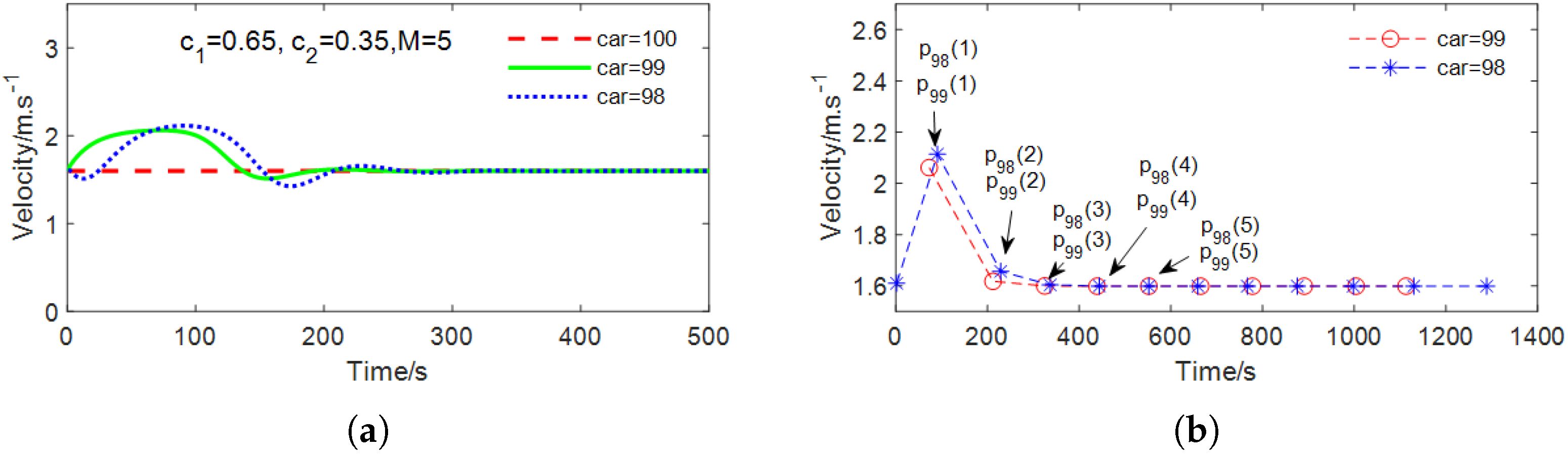
3.2. Stability State Verification
3.3. Peak Value Comparison with Bando Model
4. Simulation
4.1. Simulation Setup
4.2. Simulation Control Flow Chart
- (1)
- Initialization
- (2)
- Create two-dimensional Gbest vector:
| Algorithm 1 Create two-dimensional Gbest vector the AV |
|
- (3)
- Assign the best particle(AV) to the Gbest:
| Algorithm 2 AV-PSO Motion Update |
|
4.3. Car-Following Behavior and Characteristics
4.3.1. Group II: Middle AV
4.3.2. Group III: Tail AV
4.4. Exploration of Influence of Learning Factors on Traffic System Stability
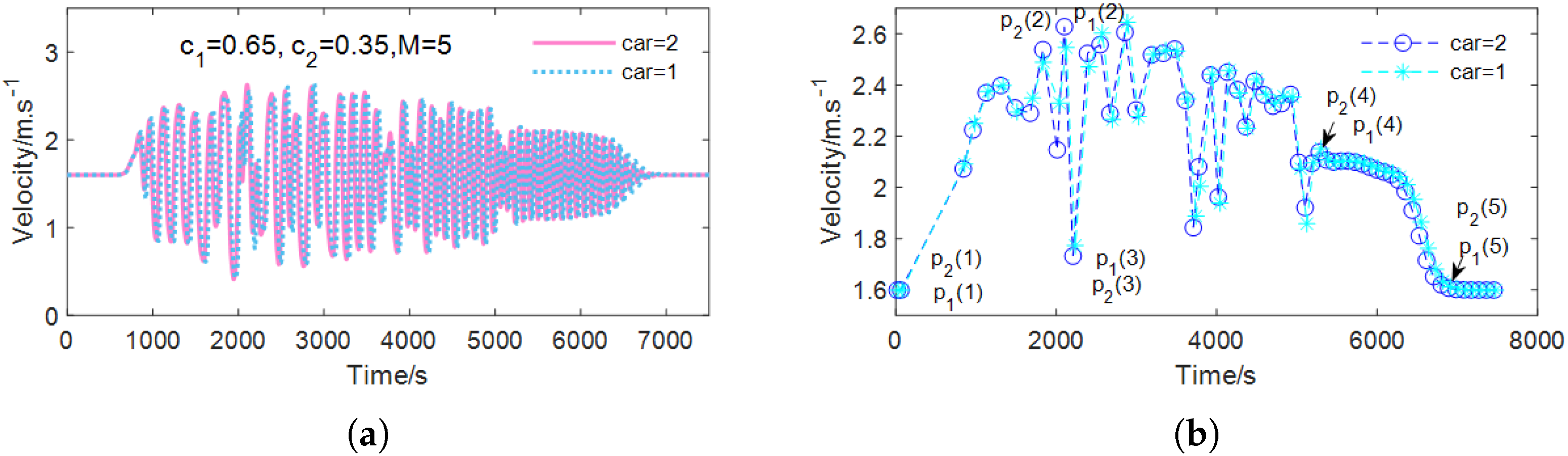
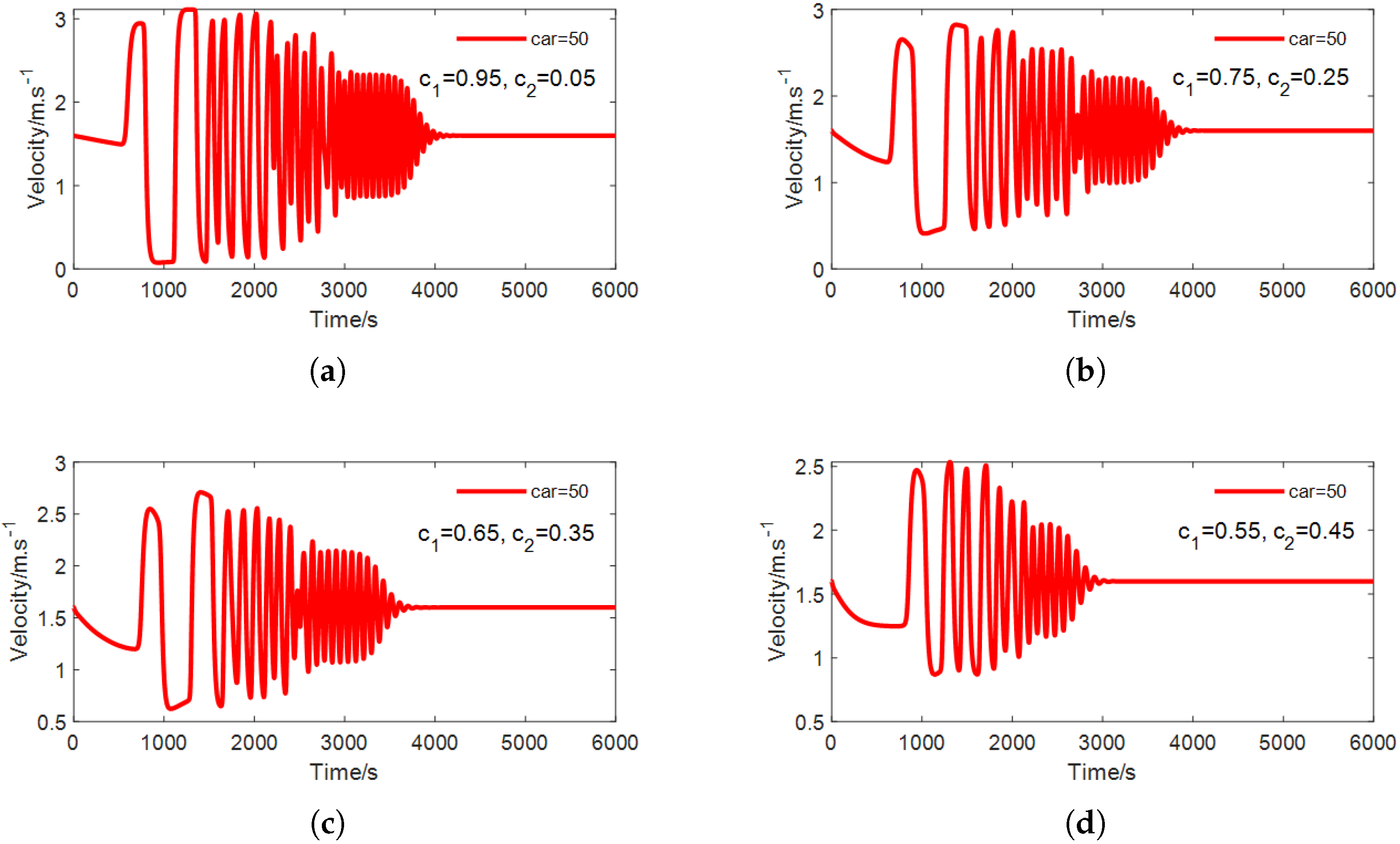
4.4.1. Typical Velocity Profiles
- (1)
- Amplitude of Oscillations: There is a decrease in the amplitude of oscillations, which contributes to a more stable velocity profile characterized by diminished extreme fluctuations.
- (2)
- Convergence Time: The convergence time decreases, implying that the system attains a stable velocity more expeditiously.
- (3)
- Number of Oscillations: A reduction in the number of oscillations is noted, signaling a smoother transition to a stable state with fewer velocity fluctuations.
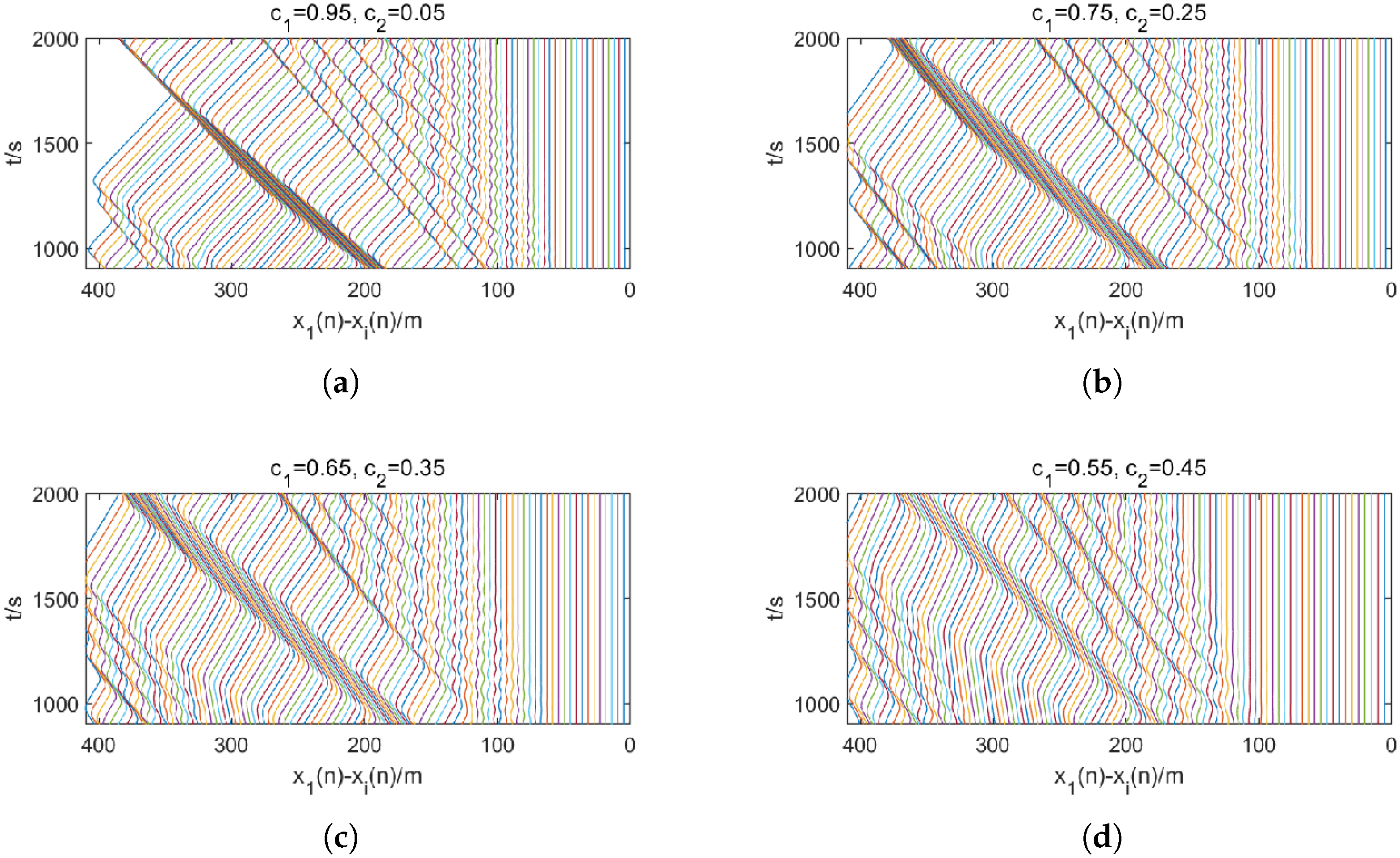
4.4.2. Time-Spatial Graph
4.5. Influence of Viewing Field M on Stability of AV Platoon System
4.5.1. Trends in AV Acceleration
- (1)
- Local Optimal Acceleration (Red Dashed Line): This strategy manifests minimal oscillatory behavior across all the evaluated horizons (, , , ), symbolizing a conservative tactic focusing on stability during vehicle‘s speed adjustments. The near-zero acceleration values signify a steady adherence to uniform velocity, underscoring a cautious operational mode irrespective of horizon length.
- (2)
- Global Optimal Acceleration (Blue Dotted Line): Exhibiting significant oscillations across all horizons, this strategy reflects an assertive optimization approach aimed at swift vehicular speed adjustments for traffic flow optimization. The oscillatory nature varies with horizon length; oscillations are more frequent in shorter horizons and less frequent but larger in longer horizons, reaching up to ±1.5 m/s2. This dynamic nature seeks to rapidly enhance traffic flow but may occasionally compromise stability, particularly in scenarios with extended horizons.
- (3)
- Weighted Acceleration (Green Solid Line): This strategy presents a judicious balance between conservative and assertive approaches, demonstrating moderate oscillations conducive to both responsiveness and stability. Through integrating elements of both the local and global optimal accelerations, it aims to offer a pragmatic solution for dynamic traffic management. The consistent oscillatory behavior across various horizons, maintained within a range of ±1 m/s2, underscores its adaptability and robustness in varying traffic conditions.
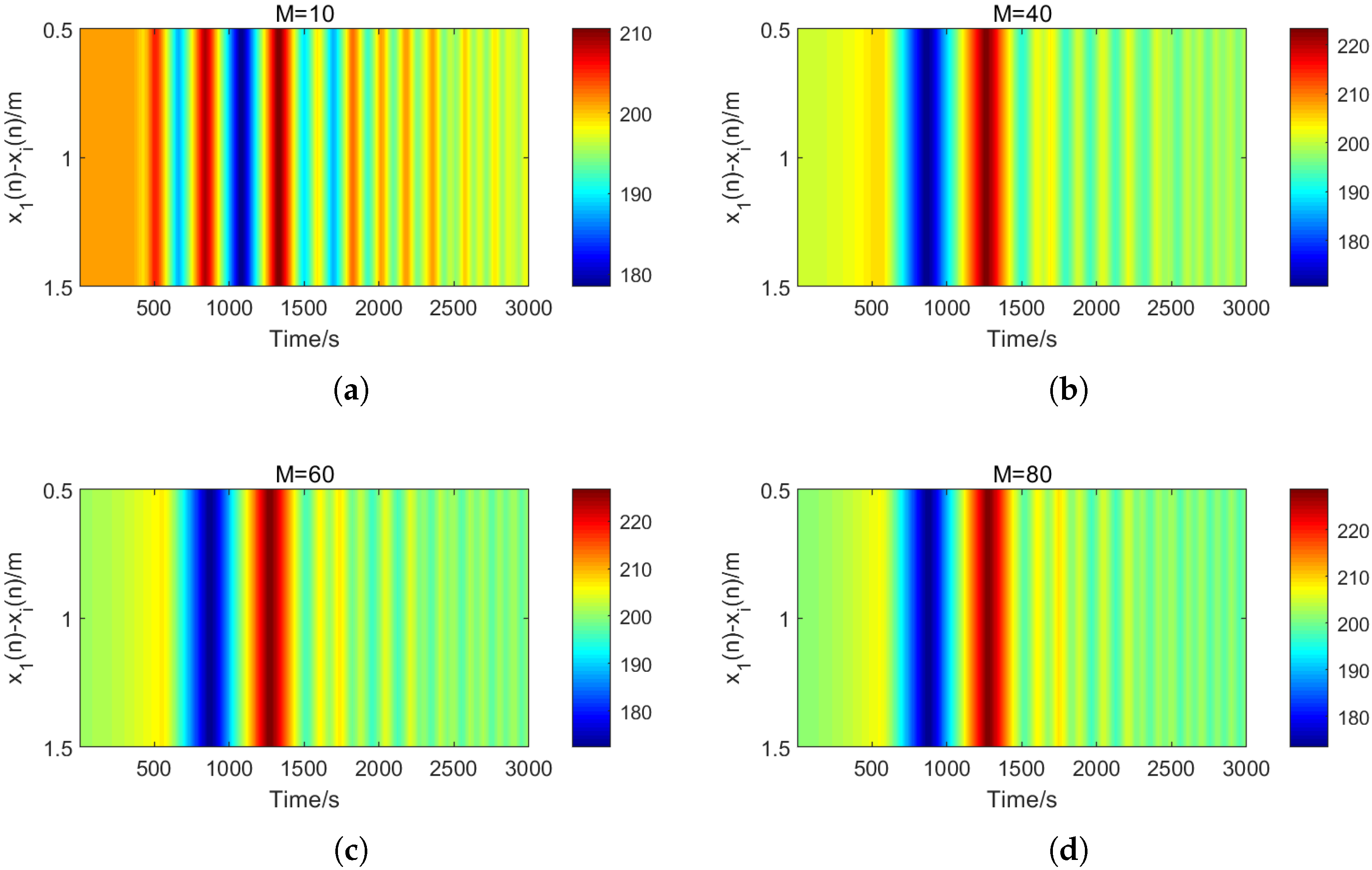
4.5.2. Time-Spatial Spectrum Graph
5. Discussion & Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AV | Autonomous Vehicle |
| PSO | Particle Swarm Optimization |
| CFM | Car-Following Model |
| GHR | Gazis–Herman–Rothery |
| OVM | Optimal Velocity Model |
| IDM | Intelligent Driver Model |
| CF | Car Following |
| AI | Artificial Intelligence |
| ACO | Ant Colony Optimization |
| OVF | Optimal Velocity Function |
| V2X | Vehicle-to-Everything |
| QPSO | Quantum PSO |
| ITS | Intelligent Transportation Systems |
References
- Han, J.; Wang, X.; Wang, G. Modeling the Car-Following Behavior with Consideration of Driver, Vehicle, and Environment Factors: A Historical Review. Sustainability 2022, 14, 8179. [Google Scholar] [CrossRef]
- Ahmed, H.U.; Huang, Y.; Lu, P. A Review of Car-Following Models and Modeling Tools for Human and Autonomous-Ready Driving Behaviors in Micro-Simulation. Smart Cities 2021, 4, 314–335. [Google Scholar] [CrossRef]
- Pipes, L.A. An perational nalysis of Traffic Dynamics. J. Appl. Phys. 1953, 24, 274–281. [Google Scholar] [CrossRef]
- Zhai, C.; Wu, W.; Xiao, Y. Modeling Continuous Traffic Flow with the Average Velocity Effect of Multiple Vehicles Ahead on Gyroidal Roads. Digit. Transp. Saf. 2023, 2, 124. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, Y.; Tong, W.; Gu, Z.; Cheng, Q. Car-following Models for Human-driven Vehicles and Autonomous Vehicles: A Systematic Review. J. Transp. Eng. Part A Syst. 2023, 149, 04023075. [Google Scholar] [CrossRef]
- Han, J.; Shi, H.; Chen, L.; Li, H.; Wang, X. The Car-Following Model and Its Applications in the V2X Environment: A Historical Review. Future Internet 2022, 14, 14. [Google Scholar] [CrossRef]
- Jia, D.; Sun, J.; Sharma, A.; Zheng, Z.; Liu, B. Integrated Simulation Platform for Conventional, Connected and Automated Driving: A Design from Cyber–physical Systems Perspective. Transp. Res. Part C Emerg. Technol. 2021, 124, 102984. [Google Scholar] [CrossRef]
- Newell, R.E. The General Circulation of the Atmosphere and its Effects on the Movement of Trace Substances. J. Geophys. Res. 1963, 68, 3949–3962. [Google Scholar] [CrossRef]
- Bando, M.; Hasebe, K.; Nakayama, A.; Shibata, A.; Sugiyama, Y. Dynamical Model of Traffic Congestion and Numerical Simulation. Phys. Rev. E 1995, 51, 1035. [Google Scholar] [CrossRef]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested Traffic States in Empirical Observations and Microscopic Simulations. Phys. Rev. E 2000, 62, 1805. [Google Scholar] [CrossRef]
- Zhang, T.T.; Jin, P.J.; McQuade, S.T.; Bayen, A.; Piccoli, B. Car-Following Models: A Multidisciplinary Review. IEEE Trans. Intell. Veh. 2024, 1–26. [Google Scholar] [CrossRef]
- Montanino, M.; Punzo, V. On String Stability of A Mixed and Heterogeneous Traffic Flow: A Unifying Modelling Framework. Transp. Res. Part B Methodol. 2021, 144, 133–154. [Google Scholar] [CrossRef]
- Kikuchi, S.; Chakroborty, P. Car-following Model Based on Fuzzy Inference System. Transp. Res. Rec. 1992, 1365, 82–91. [Google Scholar]
- Hao, H.; Ma, W.; Xu, H. A Fuzzy Logic-based Multi-agent Car-following Model. Transp. Res. Part C Emerg. Technol. 2016, 69, 477–496. [Google Scholar] [CrossRef]
- Chen, L.; Hu, X.; Tang, B.; Cheng, Y. Conditional DQN-based Motion Planning with Fuzzy Logic for Autonomous Driving. IEEE Trans. Intell. Transp. Syst. 2020, 23, 2966–2977. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Y.; Shi, X.; Qiu, F. A Decision-making Strategy for Car Following Based on Naturalist Driving Data via Deep Reinforcement Learning. Sensors 2022, 22, 8055. [Google Scholar] [CrossRef]
- Axenie, C.; Scherr, W.; Wieder, A.; Torres, A.S.; Meng, Z.; Du, X.; Sottovia, P.; Foroni, D.; Grossi, M.; Bortoli, S.; et al. Fuzzy Modelling and Inference for Physics-aware Road Vehicle Driver Behaviour Model Calibration. Expert Syst. Appl. 2024, 241, 122590. [Google Scholar] [CrossRef]
- Dougherty, M. A Review of Neural Networks Applied to Transport. Transp. Res. Part C Emerg. Technol. 1995, 3, 247–260. [Google Scholar] [CrossRef]
- Pomerleau, D.A. Progress in Neural Network-Based Vision for Autonomous Robot Driving. In Proceedings of the Proceedings of the Intelligent Vehicles92 Symposium, Detroit, MI, USA, 29 June–1 July 1992; pp. 391–396. [Google Scholar] [CrossRef]
- Chen, L.; Lin, S.; Lu, X.; Cao, D.; Wang, F.Y. Deep Neural Network Based Vehicle and Pedestrian Detection for Autonomous Driving: A Survey. IEEE Trans. Intell. Transp. Syst. 2021, 22, 3234–3246. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, B.; Qiu, Q.; Li, H.; Guo, H.; Wang, B. Graph-based Multi Agent Reinforcement Learning for On-ramp Merging in Mixed Traffic. Appl. Intell. 2024, 54, 6400–6414. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, M.; Feng, L. A Swarm Intelligent Model for AVs Based on Vicsek and OV Model. In Proceedings of the 2024 4th International Conference on Control Theory and Applications (ICoCTA), Hangzhou, China, 18–20 October 2024; pp. 101–105. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95-international conference on neural networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle Swarm Optimization Algorithm: An Overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Han, W.H. A New Simple Micro-PSO for High Dimensional Optimization Problem. Appl. Mech. Mater. 2012, 236, 1195–1200. [Google Scholar] [CrossRef]
- Wang, X.; Yao, W. A Discrete Particle Swarm Optimization Algorithm for Dynamic Scheduling of Transmission Tasks. Appl. Sci. 2023, 13, 4353. [Google Scholar] [CrossRef]
- Kourepinis, V.; Iliopoulou, C.; Tassopoulos, I.X.; Aroniadi, C.; Beligiannis, G.N. An Improved Particle Swarm Optimization Algorithm for the Urban Transit Routing Problem. Electronics 2023, 12, 3358. [Google Scholar] [CrossRef]
- Lo, S.C. A Particle Swarm Optimization Approach to Solve the Vehicle Routing Problem with Cross-Docking and Carbon Emissions Reduction in Logistics Management. Logistics 2022, 6, 62. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, J.; Fan, H.; Zhang, T.; Gao, J.; Yang, P. New Method of Traffic Flow Forecasting Based on Quantum Particle Swarm Optimization Strategy for Intelligent Transportation System. Int. J. Commun. Syst. 2021, 34, e4647. [Google Scholar] [CrossRef]
- Gad, A.G. Particle Swarm Optimization Algorithm and its Applications: A Systematic Review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Tan, L.; Zhu, K.; Yi, J. Vehicle Route Planning of Diverse Cargo Types in Urban Logistics Based on Enhanced Ant Colony Optimization. World Electr. Veh. J. 2024, 15, 405. [Google Scholar] [CrossRef]
- Zhang, L.; Feng, L.; Zhang, M.; Ji, G.; Yang, L. Abnormal Communication Internet-connected Vehicle Platoon Dynamical Modelling and Characteristics Study. Phys. A Stat. Mech. Its Appl. 2024, 651, 130012. [Google Scholar] [CrossRef]




| 0.015 | 2.4335 | 23.95 | 0.9850 | 2.4335 | 23.95 | 20 | 2.4335 | 23.95 |
| 0.030 | 1.9453 | 39.21 | 1.1820 | 2.1164 | 33.85 | 40 | 1.9814 | 38.08 |
| 0.045 | 1.6203 | 49.37 | 1.2805 | 1.9870 | 37.91 | 60 | 1.6710 | 47.78 |
| 0.060 | 1.3883 | 56.62 | 1.3790 | 1.8724 | 41.49 | 80 | 1.4447 | 54.85 |
| 0.075 | 1.2144 | 62.05 | 1.4775 | 1.7704 | 44.68 | 100 | 1.2724 | 60.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L. Swarm Intelligent Car-Following Model for Autonomous Vehicle Platoon Based on Particle Swarm Optimization Theory. Electronics 2025, 14, 1851. https://doi.org/10.3390/electronics14091851
Zhang L. Swarm Intelligent Car-Following Model for Autonomous Vehicle Platoon Based on Particle Swarm Optimization Theory. Electronics. 2025; 14(9):1851. https://doi.org/10.3390/electronics14091851
Chicago/Turabian StyleZhang, Lidong. 2025. "Swarm Intelligent Car-Following Model for Autonomous Vehicle Platoon Based on Particle Swarm Optimization Theory" Electronics 14, no. 9: 1851. https://doi.org/10.3390/electronics14091851
APA StyleZhang, L. (2025). Swarm Intelligent Car-Following Model for Autonomous Vehicle Platoon Based on Particle Swarm Optimization Theory. Electronics, 14(9), 1851. https://doi.org/10.3390/electronics14091851






