Fuzzy PDC-Based LQR Sliding Neural Network Control for Two-Wheeled Self-Balancing Cart
Abstract
1. Introduction
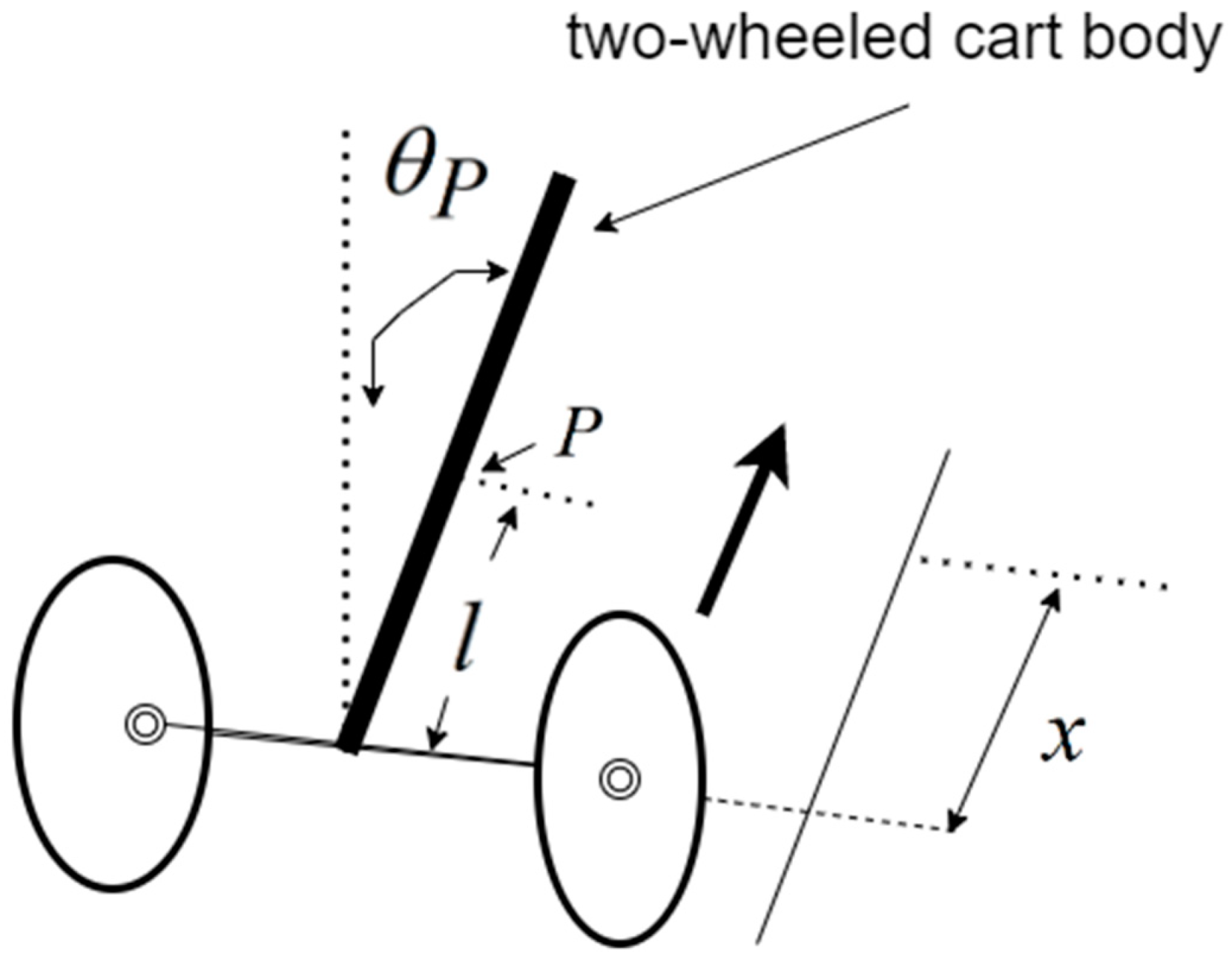
2. Two-Wheeled Self-Balancing Cart Mathematical Model
- : the horizontal displacement of the center, O, of the chassis of the cart;
- : the mass of the vehicle body (kg);
- : the distance from center of mass to center of chassis (m);
- : the moment of inertia of the vehicle body when rotating around the center of mass ();
- : the angle between the vehicle body and the vertical direction (rad);
- : the wheel mass (kg);
- : the radius of the wheel (m);
- : the output torque of the right wheel motor ();
- : the output torque of the left wheel motor ();
- : the moment of inertia of the wheel ();
- : the gravity acceleration magnitude (9.8 ).
3. LQR Controller Design
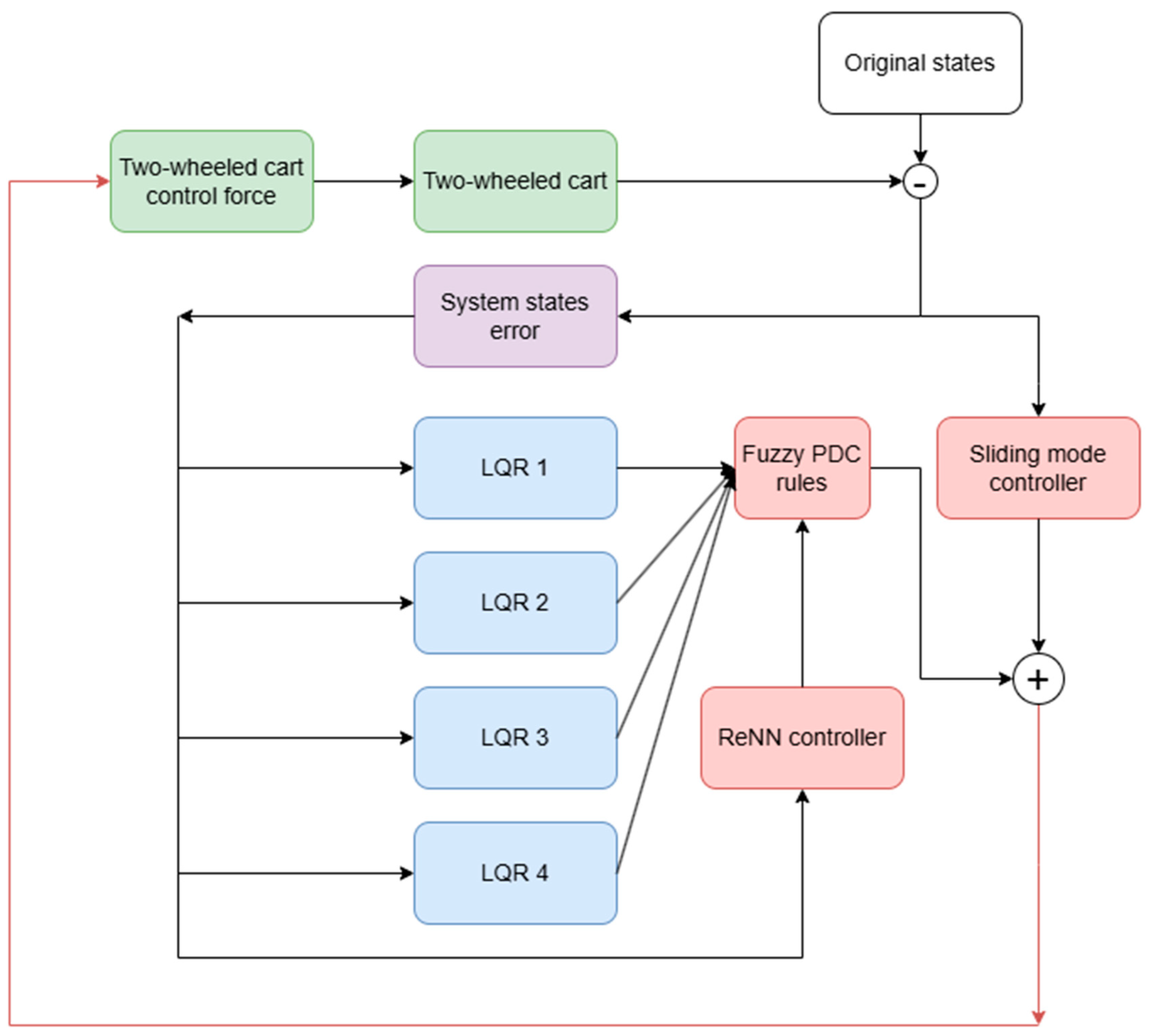
4. Fuzzy PDC-Based Sliding Neural Network Design
4.1. Sliding Controller Design
4.2. Fuzzy PDC-Based LQR Controller Design
4.3. Neural Network Controller Design
- (a)
- Input Layer: Each node within this layer is related to the net input and net output values, which are, respectively, denoted as and .
- (b)
- Hidden Layer: Each node in this layer performs activation using the ReLU function, which is defined as [22,23,24,25,26,27,28]. The derivative of the ReLU is 1 when the input number is greater than zero; otherwise, it is equal to 0. The ReLU will be used as the activation function for the j-th node of the i-th input.
- (c)
- Output Layer: It consists of two nodes, one for LQR and the other for the sliding mode controller, which is responsible for performing the key operation of calculating the percentage of the two controllers. Among these nodes, we have a specific node labeled , which learns and memorizes the optimal percentage output by monitoring all input system states signals. This summation process is represented by the following equation:
- : The link weight denoting the strength of the output action corresponding to the output of the j-th column in relation to the k-th rule.
- : The j-th input to the node of layer.
- : The total number of output nodes.
- : The k-th column output of the ReNN controller.
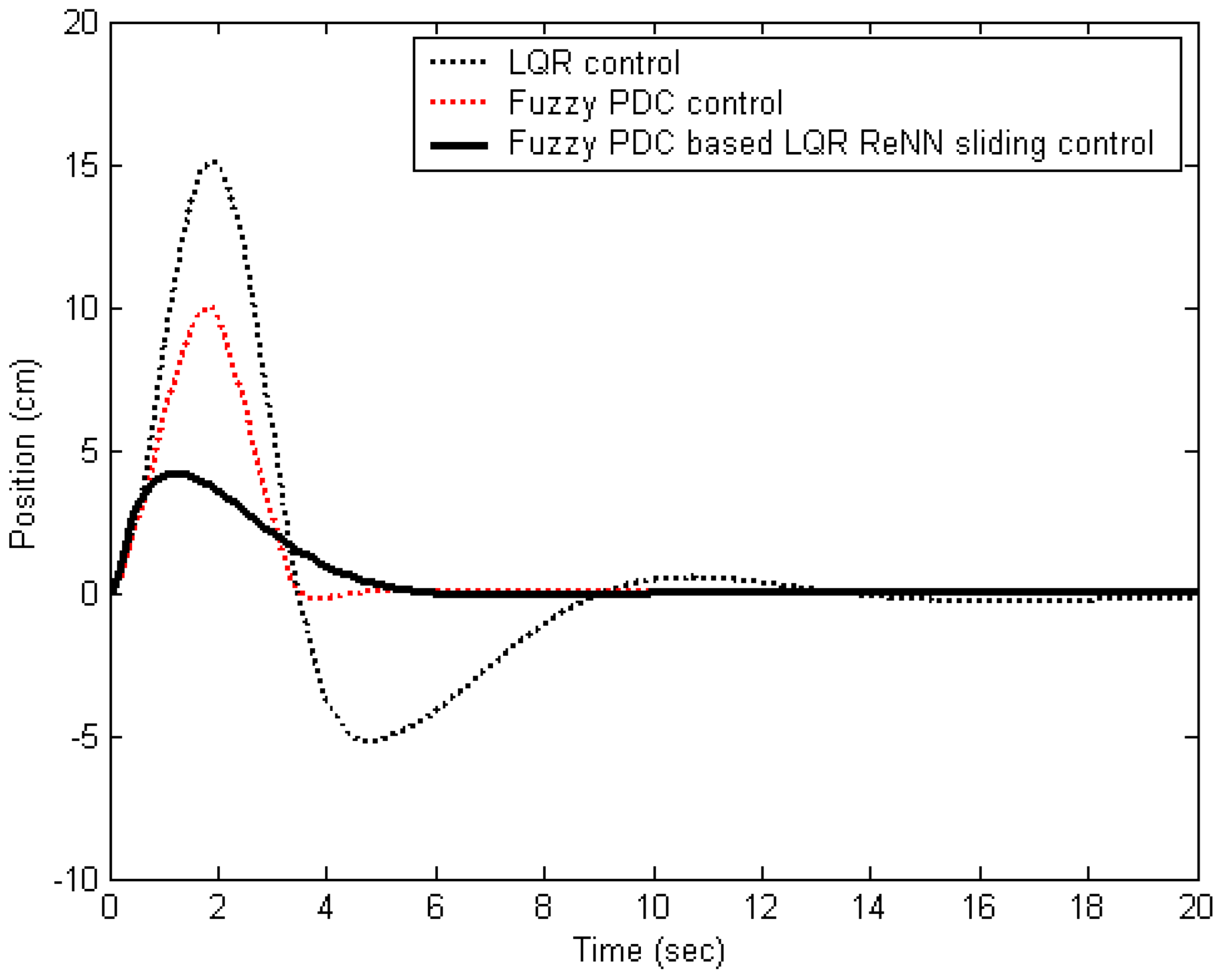
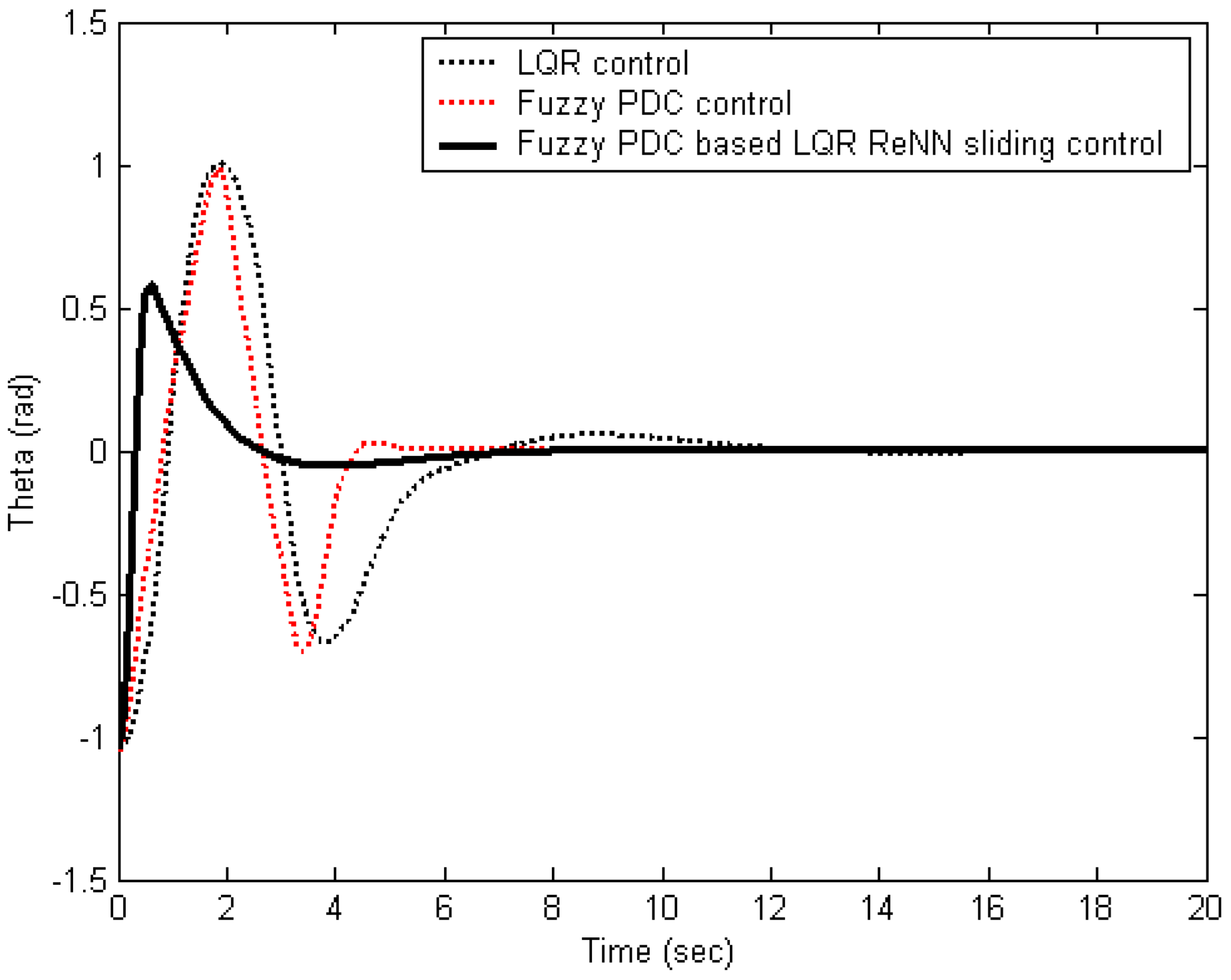
5. Simulation Results
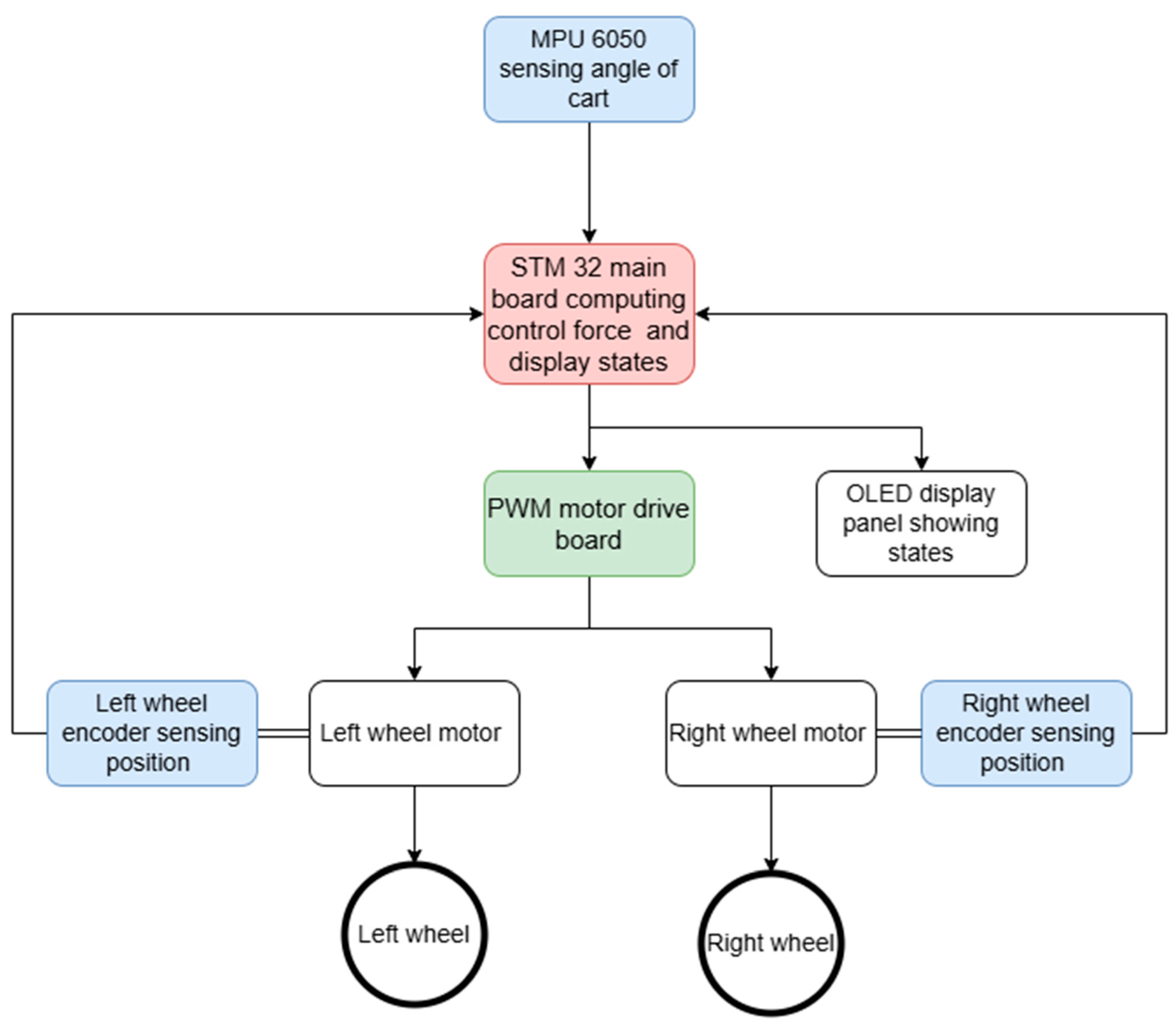
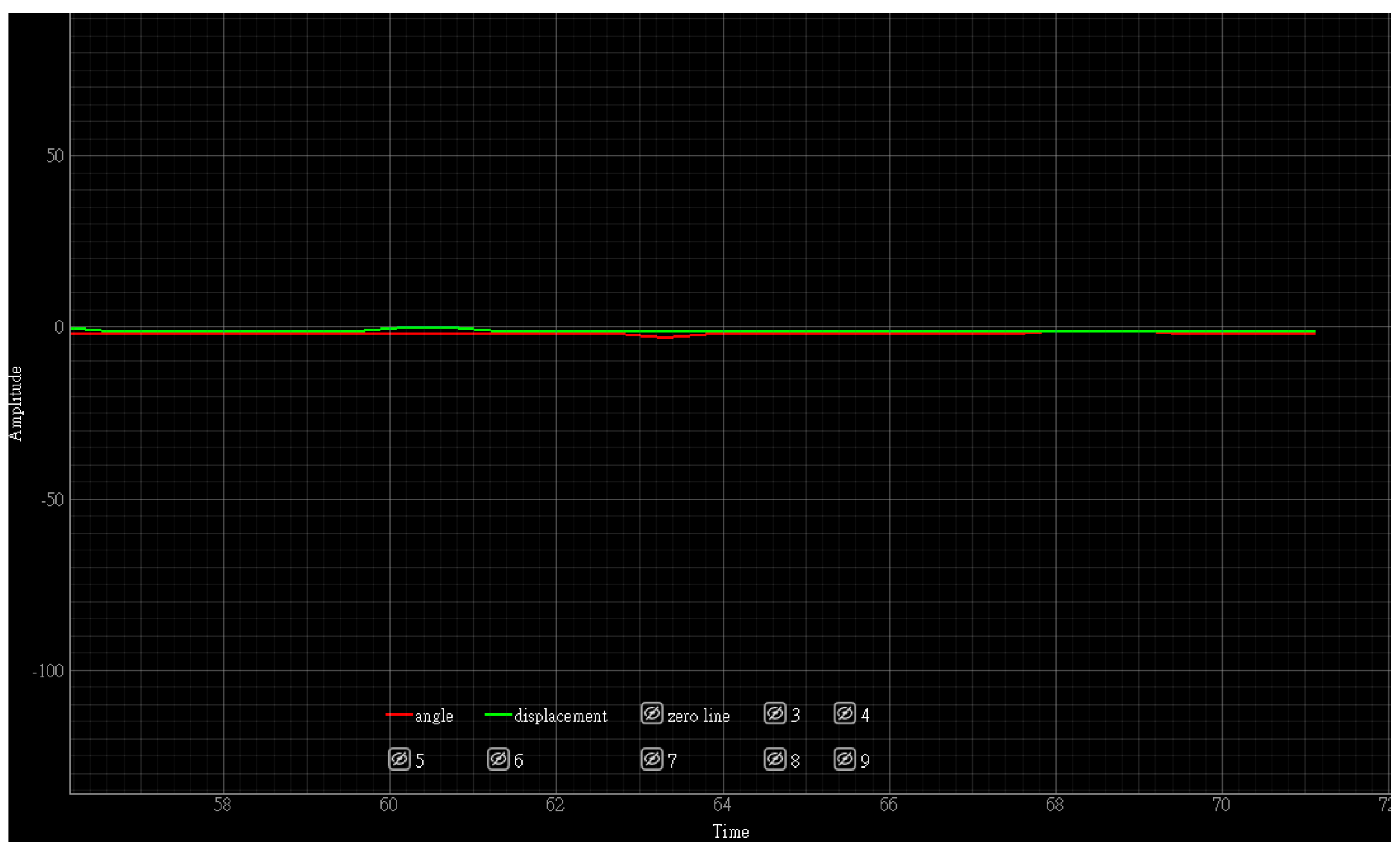
6. Experiment Results
7. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, H.O.; Tanaka, K.; Griffin, M.F. An Approach to Fuzzy Control of Nonlinear Systems: Stability and Design Issues. IEEE Trans. Fuzzy Syst. 1996, 4, 14–23. [Google Scholar]
- Lin, C.M.; Mon, Y.J. A Fuzzy-PDC-Based Control for Robotic Systems. Inf. Sci. 2001, 137, 135–155. [Google Scholar] [CrossRef]
- Pal, D.; Chatterjee, A.; Rakshit, A. Robust-Stable Quadratic-Optimal Fuzzy-PDC Controllers for Systems with Parametric Uncertainties: A PSO Based Approach. Eng. Appl. Artif. Intell. 2018, 70, 38–51. [Google Scholar]
- Alshammari, B.; Ben Salah, R.; Kahouli, O.; Kolsi, L. Design of Fuzzy TS-PDC Controller for Electrical Power System via Rules Reduction Approach. Symmetry 2020, 12, 2068. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prantice-Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Edwards, C.; Spurgeon, S.K. Sliding Mode Control: Theory and Applications; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Zhang, Z.; Yang, X.; Wang, W.; Chen, K.; Cheung, N.C.; Pan, J. Enhanced Sliding Mode Control for PMSM Speed Drive Systems Using a Novel Adaptive Sliding Mode Reaching Law Based on Exponential Function. IEEE Trans. Ind. Electron. 2024, 71, 11978–11988. [Google Scholar] [CrossRef]
- Ma, S.; Zhao, J.; Xiong, Y.; Wang, H.; Yao, X. Sliding-Mode Control of Linear Induction Motor Based on Exponential Reaching Law. Electronics 2024, 13, 2352. [Google Scholar] [CrossRef]
- Ge, S.S.; Hang, C.C.; Lee, T.H.; Zhang, T. Stable Adaptive Neural Network Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 13. [Google Scholar]
- Zheng, C.; Hu, C.; Yu, J.; Wen, S. Saturation Function-Based Continuous Control on Fixed-Time Synchronization of Competitive Neural Networks. Neural Netw. 2024, 169, 32–43. [Google Scholar] [CrossRef]
- Tam, P.; Ros, S.; Song, I.; Kang, S.; Kim, S. A Survey of Intelligent End-to-End Networking Solutions: Integrating Graph Neural Networks and Deep Reinforcement Learning Approaches. Electronics 2024, 13, 994. [Google Scholar] [CrossRef]
- Li, M.; Xu, J.; Wang, Z.; Liu, S. Optimization of the Semi-Active-Suspension Control of BP Neural Network PID Based on the Sparrow Search Algorithm. Sensors 2024, 24, 1757. [Google Scholar] [CrossRef]
- Simon, J. Fuzzy Control of Self-Balancing, Two-Wheel-Driven, SLAM-Based, Unmanned System for Agriculture 4.0 Applications. Machines 2023, 11, 467. [Google Scholar] [CrossRef]
- Tsai, C.-C.; Huang, H.-C.; Lin, S.-C. Adaptive Neural Network Control of a Self-Balancing Two-Wheeled Scooter. IEEE Trans. Ind. Electron. 2010, 57, 1420–1428. [Google Scholar] [CrossRef]
- Nghia, V.B.V.; Van Thien, T.; Son, N.N.; Long, M.T. Adaptive Neural Sliding Mode Control for Two Wheel Self Balancing Robot. Int. J. Dynam. Control 2022, 10, 771–784. [Google Scholar] [CrossRef]
- Mon, Y.-J. Tikhonov-Tuned Sliding Neural Network Decoupling Control for an Inverted Pendulum. Electronics 2023, 12, 4415. [Google Scholar] [CrossRef]
- Hu, Y.; Su, H.; Zhang, L.; Miao, S.; Chen, G.; Knoll, A. Nonlinear Model Predictive Control for Mobile Robot Using Varying-Parameter Convergent Differential Neural Network. Robotics 2019, 8, 64. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Cheng, Y.; Cheng, Y.; Zhang, Q.; Lu, K. Nonlinear Model Predictive Control (NMPC) based shared autonomy for bilateral teleoperation in CFETR Remote Handling. Nuclear Eng. Technol. 2024, 56, 4437–4445. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Z.; Chen, H.; Zhang, Y.; Zhang, D.; Peng, C. Trajectory Tracking Control of a Skid-Steer Mobile Robot Based on Nonlinear Model Predictive Control with a Hydraulic Motor Velocity Mapping. Appl. Sci. 2023, 14, 122. [Google Scholar] [CrossRef]
- Grasser, F.; D’Arrigo, A.; Colombi, S.; Rufer, A.C. JOE: A Mobile, Inverted Pendulum. IEEE Trans. Ind. Electron. 2002, 49, 107–114. [Google Scholar] [CrossRef]
- Wheeltec Inc. Two-Wheeled Self Balancing Cart Technical Development Manual; Wheeltec Inc.: Dongguan, China, 2025; Available online: www.wheeltec.net (accessed on 20 April 2025).
- Kwakernaak, H.; Sivan, R. Linear Optimal Control Systems; Wiley-Interscience: New York, NY, USA, 1972; Volume 1, p. 608. [Google Scholar]
- Wang, M.; He, X.; Li, X. Self-Triggered Impulsive Control for Lyapunov Stability of Nonlinear Systems in Discrete Time. IEEE Trans. Cybern. 2024, 54, 4852–4858. [Google Scholar] [CrossRef]
- Fei, W.; Dai, W.; Li, C.; Zou, J.; Xiong, H. On Centralization and Unitization of Batch Normalization for Deep ReLU Neural Networks. IEEE Trans. Signal Process. 2024, 72, 2827–2841. [Google Scholar] [CrossRef]
- Liang, X.; Xu, J. Biased ReLU Neural Networks. Neurocomputing 2021, 423, 71–79. [Google Scholar] [CrossRef]
- Barbu, A. Training a Two-Layer ReLU Network Analytically. Sensors 2023, 23, 4072. [Google Scholar] [CrossRef] [PubMed]
- Sooksatra, K.; Rivas, P. Dynamic-Max-Value ReLU Functions for Adversarially Robust Machine Learning Models. Mathematics 2024, 12, 3551. [Google Scholar] [CrossRef]
- Mathworks Inc. MATLAB R14 User’s Manual; Mathworks Inc.: Natick, MA, USA, 2004; Available online: https://www.mathworks.com/ (accessed on 20 April 2025).
- TeraSoft Inc. MATLAB R 14 User’s Manual; TeraSoft Inc.: Taipei, Taiwan, 2004; Available online: https://www.terasoft.com.tw/ (accessed on 20 April 2025).
- STMicroelectronics. STM32F103xx Reference Manual; ST Microelectronics: Geneva, Switzerland, 2025; Available online: https://www.st.com.cn/content/st_com/zh.html (accessed on 20 April 2025).








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mon, Y.-J. Fuzzy PDC-Based LQR Sliding Neural Network Control for Two-Wheeled Self-Balancing Cart. Electronics 2025, 14, 1842. https://doi.org/10.3390/electronics14091842
Mon Y-J. Fuzzy PDC-Based LQR Sliding Neural Network Control for Two-Wheeled Self-Balancing Cart. Electronics. 2025; 14(9):1842. https://doi.org/10.3390/electronics14091842
Chicago/Turabian StyleMon, Yi-Jen. 2025. "Fuzzy PDC-Based LQR Sliding Neural Network Control for Two-Wheeled Self-Balancing Cart" Electronics 14, no. 9: 1842. https://doi.org/10.3390/electronics14091842
APA StyleMon, Y.-J. (2025). Fuzzy PDC-Based LQR Sliding Neural Network Control for Two-Wheeled Self-Balancing Cart. Electronics, 14(9), 1842. https://doi.org/10.3390/electronics14091842





