SOH Estimation Model Based on an Ensemble Hierarchical Extreme Learning Machine
Abstract
1. Introduction
- (1)
- Innovative Health Indicator System: We propose a new feature extraction framework based on constant-current charging time and charging current area. This reduces the need for extensive historical data while enhancing the model’s ability to capture complex degradation dynamics.
- (2)
- Ensemble I-HELM Model for Robustness: We introduce an ensemble of 80 HELM sub-models that reduces the volatility associated with single-model predictions. This ensemble structure improves the model’s robustness and accuracy in scenarios with inconsistent battery degradation.
- (3)
- Practical Applicability for Battery Reuse: Our model is specifically designed to support battery reuse industries, with applications in energy storage system optimization and second-life battery management, enabling cost reduction and more informed decision-making for battery repurposing.
2. Related Work
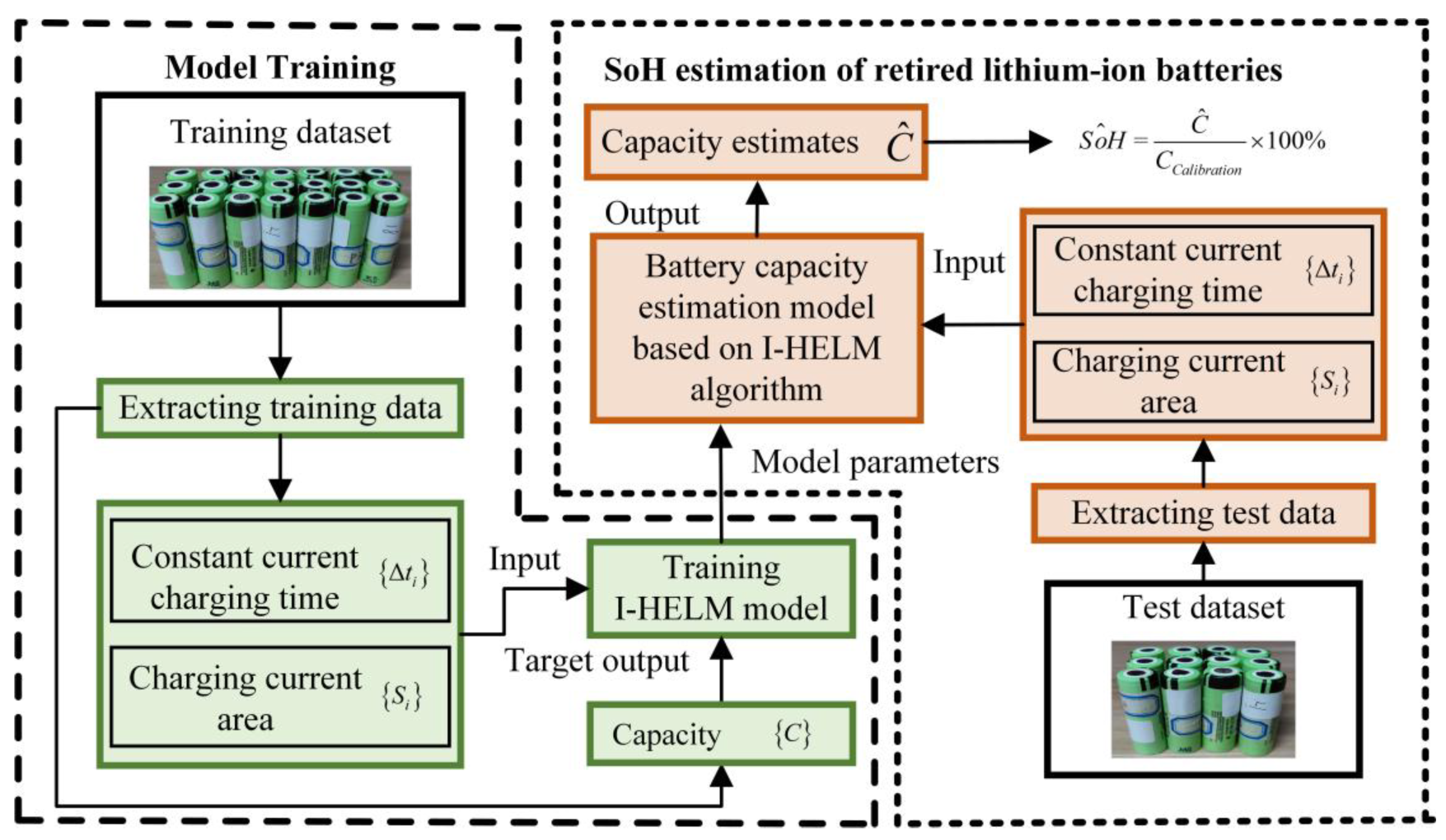
3. SOH Estimation Model for Retired Lithium-Ion Batteries Based on I-HELM
3.1. Hierarchical Extreme Learning Machine
3.2. I-HELM Algorithm Framework
4. Experimental Design
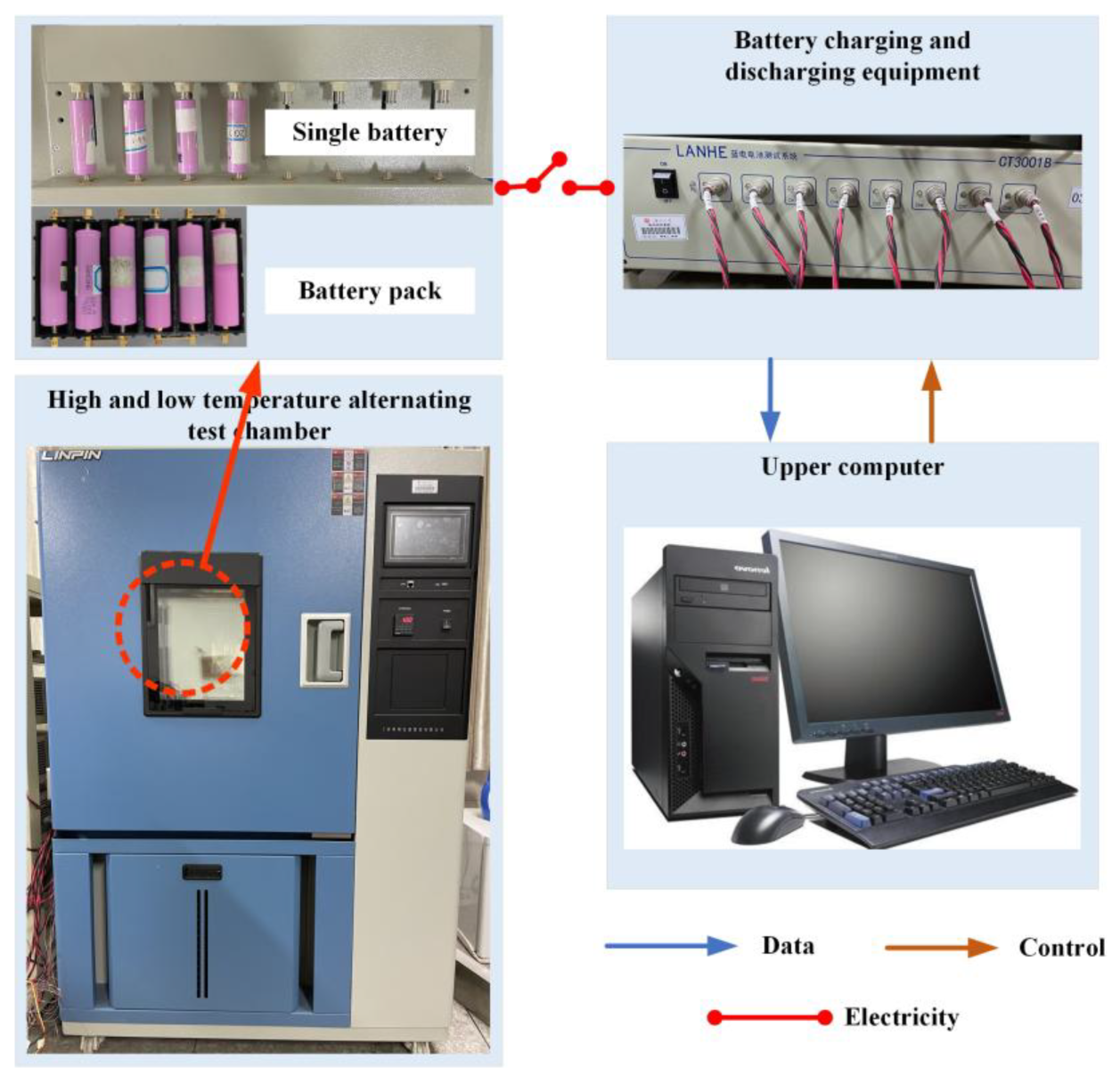
4.1. Experimental Setup and Equipment
- (1)
- A temperature cycling chamber for controlling environmental temperature from −20 °C to 50 °C.
- (2)
- Multi-channel battery charge/discharge equipment with a voltage range of 0–100 V, current range of 0–50 A, and maximum power ratings of 3000 W for charging and 5000 W for discharging.
- (3)
- A computer control system, responsible for programming charge/discharge cycles, real-time monitoring, and storing experimental data.
4.2. Battery Health Indicator Analysis
- (1)
- Capacity value. A battery’s SOH is typically defined by Equation (2). In this study, the SOH estimation is directly characterized by capacity, which serves as a key indicator of battery degradation.
- (2)
- Constant-current charging time feature extraction. Constant-current charging time refers to the duration it takes for a retired battery to charge under constant-current mode, from the start of charging until the voltage reaches the cut-off voltage. The method for extracting the constant-current charging time is described in Equation (3).
- (3)
- Charging current area feature extraction. Charging current area refers to the area under the current curve during the entire charging process of the retired battery in an energy storage system. The method for extracting this feature is given by Equation (4).
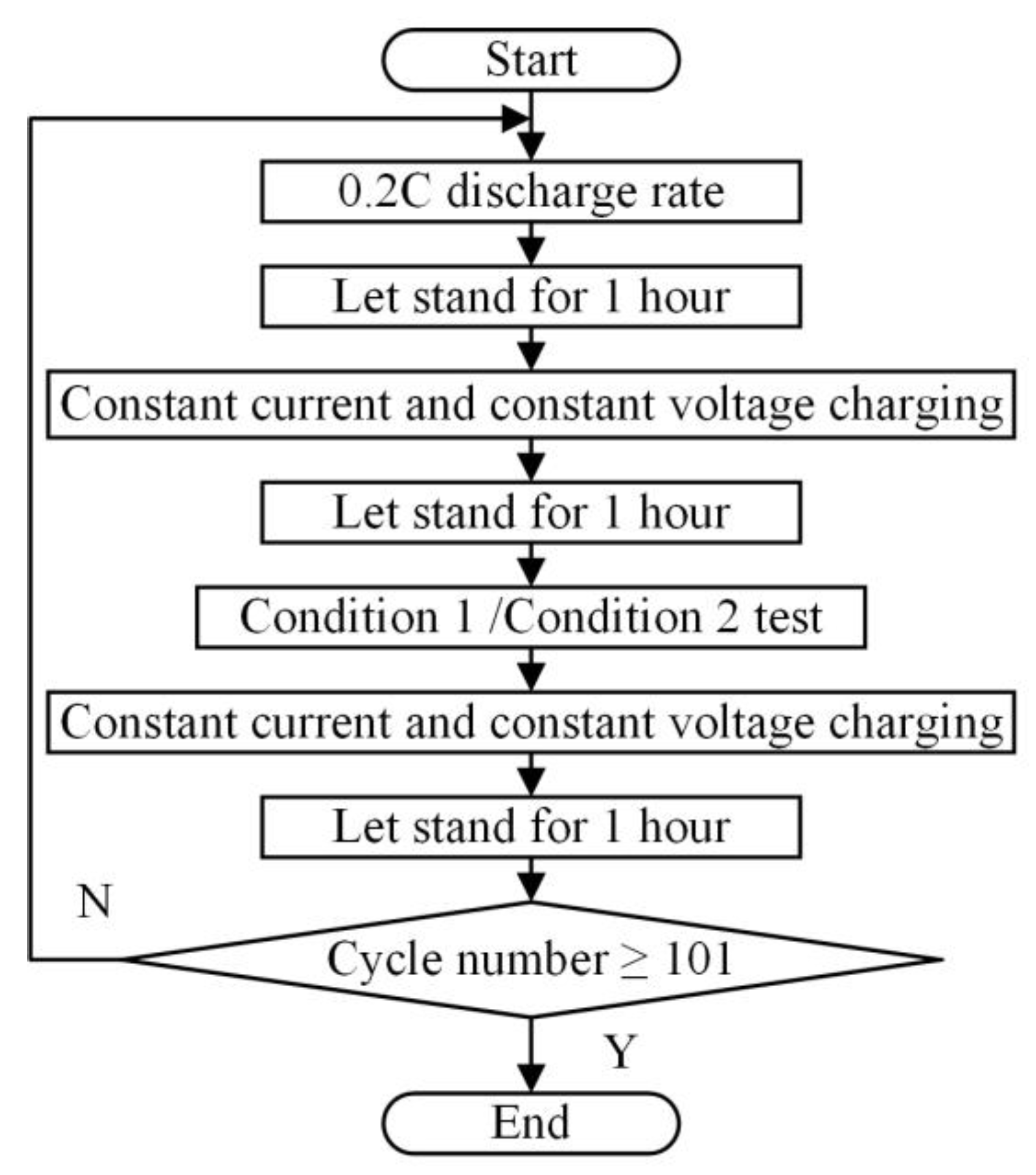
4.3. Experimental Procedure
- (1)
- Temperature setting and initial discharge. The temperature in the high/low-temperature test chamber was set to 24 °C. The batteries were discharged at a 0.2 C rate until reaching the cut-off voltage (2.75 V for Samsung cells, 2.5 V for Panasonic cells, and 16.5 V for battery packs). After discharge, the batteries rested for 1 h.
- (2)
- Energy storage condition testing. First, the batteries were charged at a 0.5 C rate until reaching the full charge voltage (4.2 V for cells, 25.2 V for packs). They then underwent constant voltage charging until the cut-off current (168 mA for Panasonic cells, 130 mA for Samsung cells and packs), followed by 1 h of rest. Next, the batteries were discharged under the corresponding energy storage condition (Condition 1 or Condition 2) to the cut-off discharge voltage and rested for 1 h. Finally, the batteries were charged again under constant current and voltage, followed by 1 h of rest.
- (3)
- Capacity testing. The batteries were discharged as described in Step 1, and discharge capacity data were recorded.
- (4)
- Repetition. Steps (1) through (3) were repeated until 101 cycles were completed under each condition.
5. Results and Discussions
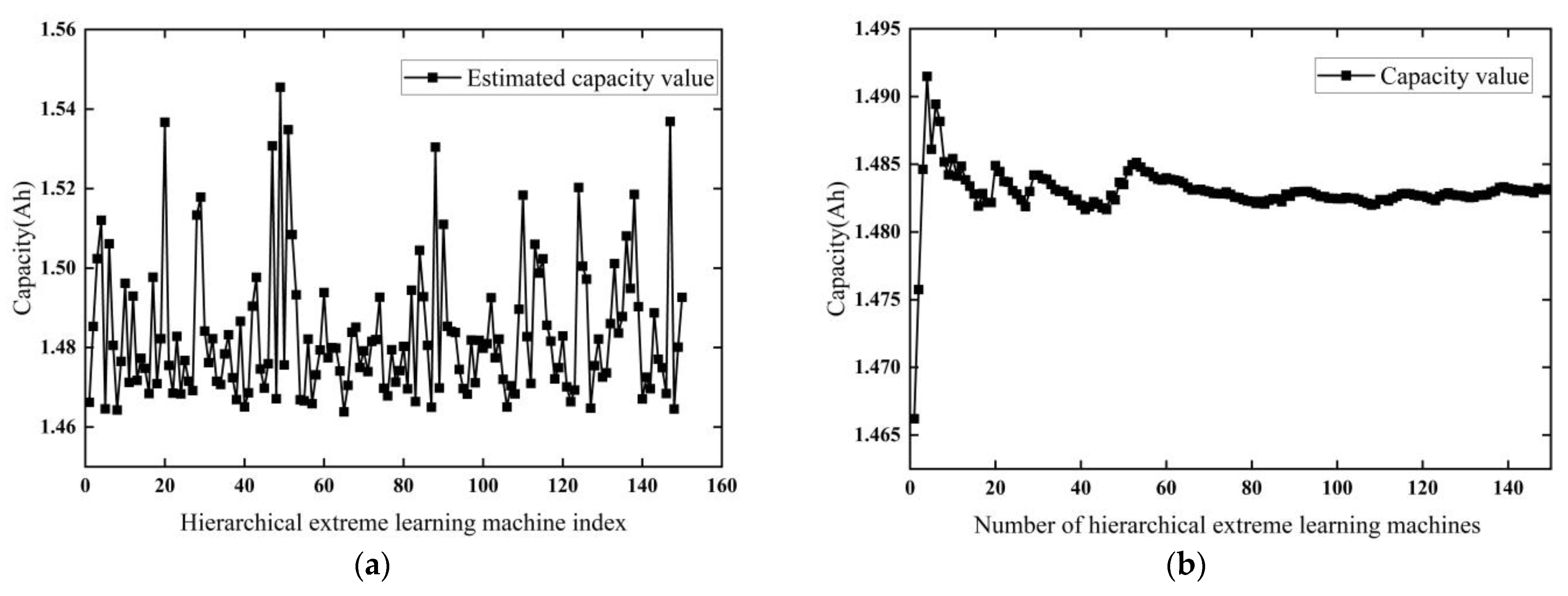
5.1. Analysis of I-HELM Model Integration
5.2. SOH Estimation of Different Retired Lithium-Ion Batteries
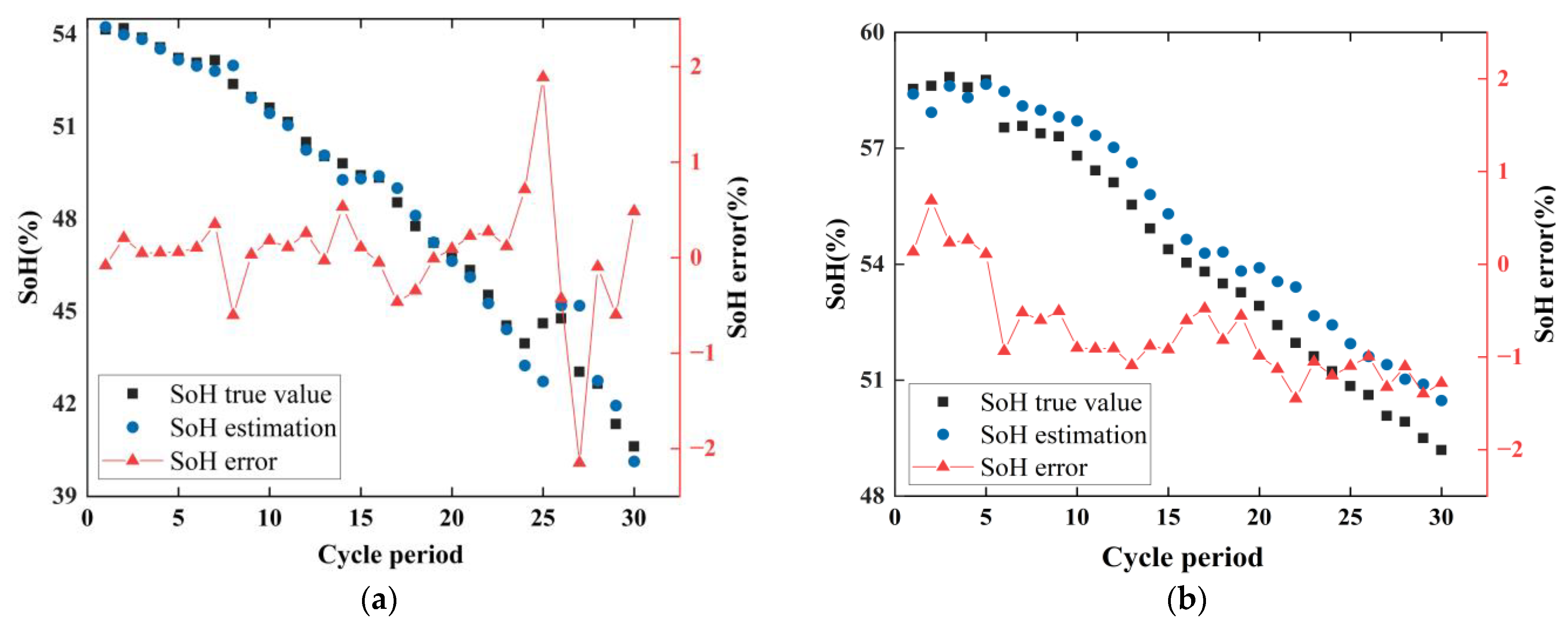
5.2.1. SOH Estimation of Samsung Retired Individual Cells
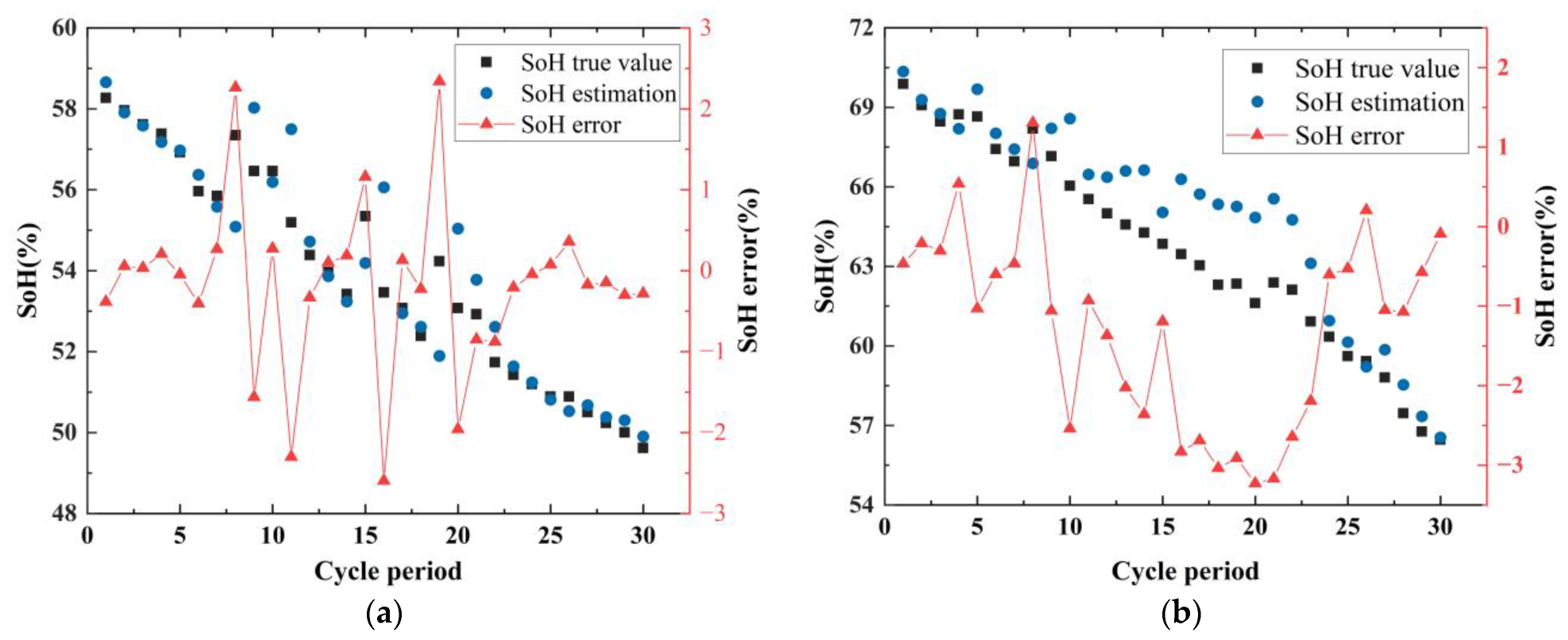
5.2.2. Estimation of SOH of Samsung’s Retired Battery Packs
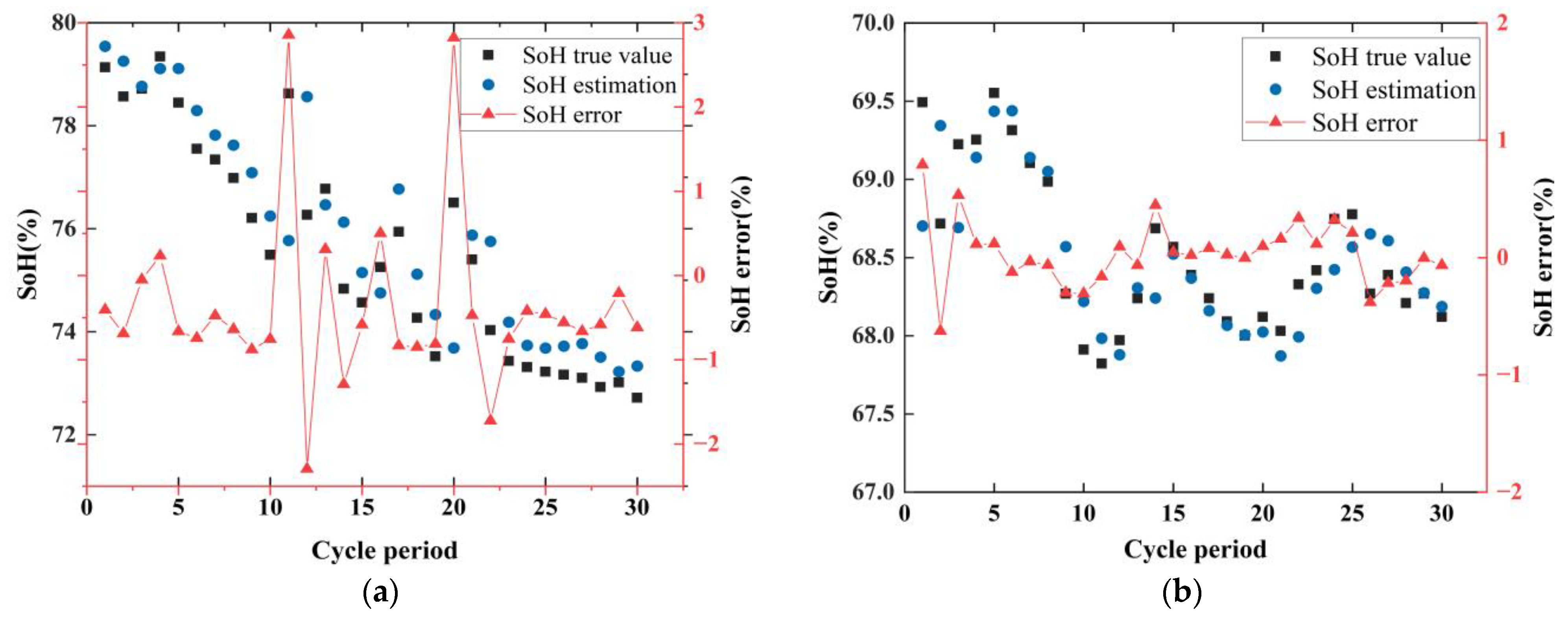
5.2.3. SOH Estimation for Panasonic Retired Battery Cells
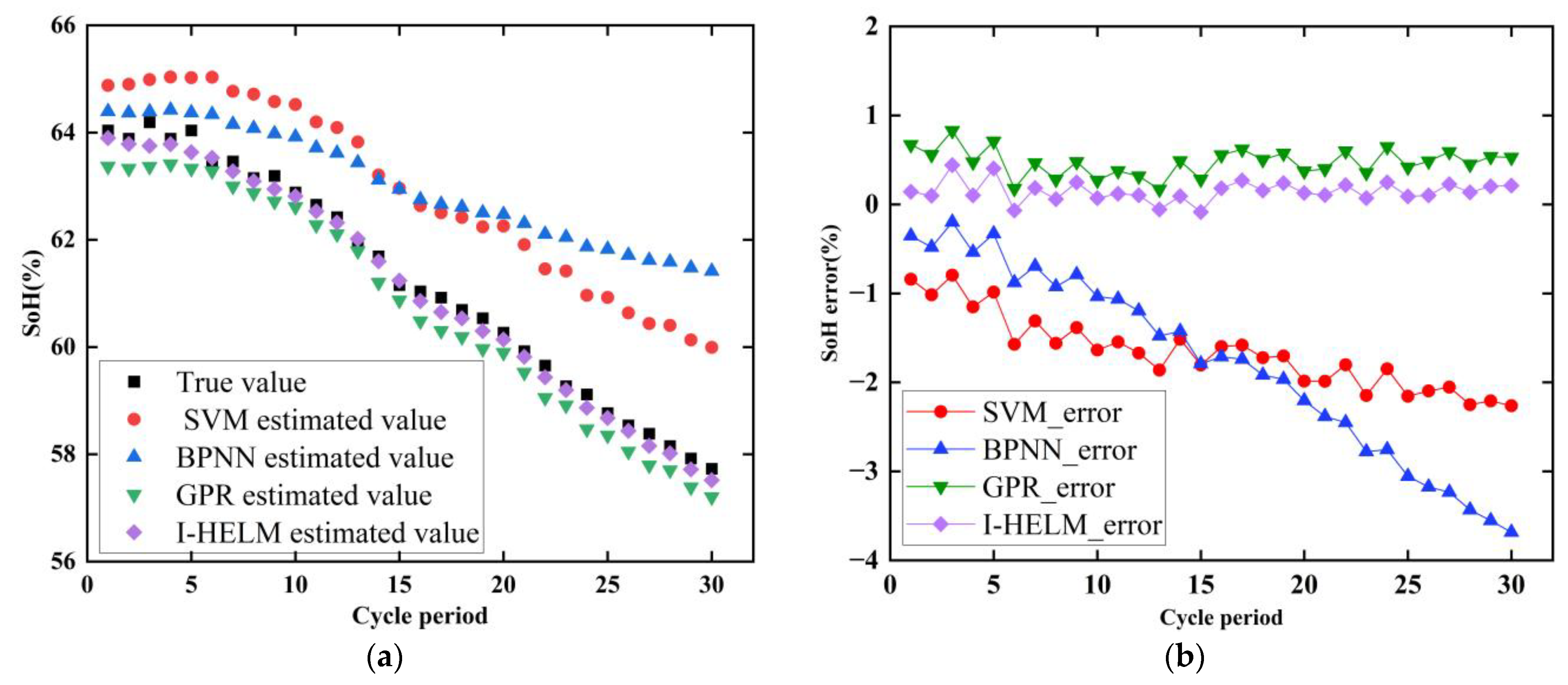
5.3. Comparison of I-HELM with Traditional Machine Learning Algorithms for SOH Estimation
6. Conclusions and Plans
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Diouf, B.; Avis, C. The potential of Li-ion batteries in ECOWAS solar home systems. J. Energy Storage 2019, 22, 295–301. [Google Scholar] [CrossRef]
- Ren, D.; Feng, X.; Liu, L.; Hsu, H.; Lu, L.; Wang, L.; He, X.; Ouyang, M. Investigating the relationship between internal short circuit and thermal runaway of lithium-ion batteries under thermal abuse condition. Energy Storage Mater. 2021, 34, 563–573. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Z.; Zhang, L.; Liu, P.; Zhang, Z. A novel consistency evaluation method for series-connected battery systems based on real-world operation data. IEEE Trans. Transp. Electrif. 2021, 7, 437–451. [Google Scholar] [CrossRef]
- Vermeer, W.; Mouli, G.R.C.; Bauer, P. A comprehensive review on the characteristics and modeling of lithium-ion battery aging. IEEE Trans. Transp. Electrif. 2022, 8, 2205–2232. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y. Prognostics and health management of Lithium-ion battery using deep learning methods, A review. Renew. Sustain. Energy Rev. 2022, 161, 112282. [Google Scholar] [CrossRef]
- Chen, L.; Wang, H.; Liu, B.; Wang, Y.; Ding, Y.; Pan, H. Battery state-of-health estimation based on a metabolic extreme learning machine combining degradation state model and error compensation. Energy 2021, 215, 119078. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, X.; Fu, L.; Zhen, D.; Gu, F.; Ball, A.D. A review on rapid state of health estimation of lithium-ion batteries in electric vehicles. Sustain. Energy Technol. Assess. 2023, 60, 103457. [Google Scholar] [CrossRef]
- Zhang, C.; Tu, L.; Yang, Z.; Du, B.; Zhou, Z.; Wu, J.; Chen, L. A CMMOG-based lithium-battery SOH estimation method using multi-task learning framework. J. Energy Storage 2025, 107, 114884. [Google Scholar] [CrossRef]
- Jiang, L.; Deng, Z.; Tang, X.; Hu, L.; Lin, X.; Hu, X. Data-driven fault diagnosis and thermal runaway warning for battery packs using real-world vehicle data. Energy 2021, 234, 121266. [Google Scholar] [CrossRef]
- Zhang, X.; Hou, J.; Wang, Z.; Jiang, Y. Study of SOC estimation by the ampere-hour integral method with capacity correction based on LSTM. Batteries 2022, 8, 170. [Google Scholar] [CrossRef]
- Mamadou, K.; Lemaire, E.; Delaille, A.; Riu, D.; Hing, S.E.; Bultel, Y. Definition of a state-of-energy indicator (SoE) for electrochemical storage devices: Application for energetic availability forecasting. J. Electrochem. Soc. 2012, 159, A1298. [Google Scholar] [CrossRef]
- Barai, A.; Uddin, K.; Widanalage, W.D.; McGordon, A.; Jennings, P. The effect of average cycling current on total energy of lithium-ion batteries for electric vehicles. J. Power Sources 2016, 303, 81–85. [Google Scholar] [CrossRef]
- Qi, G.; Li, D.; Duan, M.; Guan, W.; Ma, J. Echelon division of battery status considering on-road characteristics of electric buses. China J. Highw. Transp. 2022, 35, 44–54. [Google Scholar]
- Rodriguez-Cea, A.I.; Morinigo-Sotelo, D.; Tinaut, F.V. A procedure for evaluating the SOH of Li-ion batteries from data during the constant voltage charge phase and the use of an ECM with internal resistance. J. Energy Storage 2025, 108, 115074. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.; Li, D.; Wang, K. State-of-health estimation of lithium-ion batteries based on electrochemical impedance spectroscopy: A review. Prot. Control Mod. Power Syst. 2023, 8, 41. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, L.; Zhang, Y.; Wang, X.; Qiao, Y.; Sun, S. Reliable impedance analysis of Li-ion battery half-cell by standardization on electrochemical impedance spectroscopy (EIS). J. Chem. Phys. 2023, 158, 054202. [Google Scholar] [CrossRef]
- Wei, Z.; Sun, X.; Li, Y.; Liu, W.; Liu, C.; Lu, H. A Joint Estimation Method for the SOC and SOH of Lithium-Ion Batteries Based on AR-ECM and Data-Driven Model Fusion. Electronics 2025, 14, 1290. [Google Scholar] [CrossRef]
- Cai, L.; Lin, J.; Liao, X. An estimation model for state of health of lithium-ion batteries using energy-based features. J. Energy Storage 2022, 46, 103846. [Google Scholar] [CrossRef]
- Akbar, K.; Zou, Y.; Awais, Q.; Baig, M.J.A.; Jamil, M. A Machine Learning-Based Robust State of Health (SOH) Prediction Model for Electric Vehicle Batteries. Electronics 2022, 11, 1216. [Google Scholar] [CrossRef]
- Yang, X.; Wang, S.; Xu, W.; Qiao, J.; Yu, C.; Takyi-Aninakwa, P.; Jin, S. A novel fuzzy adaptive cubature Kalman filtering method for the state of charge and state of energy co-estimation of lithium-ion batteries. Electrochim. Acta 2022, 415, 140241. [Google Scholar] [CrossRef]
- Liu, D.; Wang, S.; Fan, Y.; Liang, Y.; Fernandez, C.; Stroe, D.I. State of energy estimation for lithium-ion batteries using adaptive fuzzy control and forgetting factor recursive least squares combined with AEKF considering temperature. J. Energy Storage 2023, 70, 108040. [Google Scholar] [CrossRef]
- Xu, P.; Hu, X.; Liu, B.; Ouyang, T.; Chen, N. Hierarchical estimation model of state-of-charge and state-of-health for power batteries considering current rate. IEEE Trans. Ind. Inform. 2021, 18, 6150–6159. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, K.; Zhu, C.; Zhang, X.; Zhang, D. Co-estimation of state-of-charge and state-of-health for lithium-ion batteries using an enhanced electrochemical model. IEEE Trans. Ind. Electron. 2021, 69, 2684–2696. [Google Scholar] [CrossRef]
- Li, J.; He, S.; Yang, Q.; Ma, T.; Wei, Z. Optimal design of the EV charging station with retired battery systems against charging demand uncertainty. IEEE Trans. Ind. Inform. 2023, 19, 3262–3273. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, H.; Wang, H.; Wu, X. A fast estimation method for state-of-health of retired batteries based on health features. J. Energy Storage 2023, 72, 108677. [Google Scholar] [CrossRef]
- Cai, L.; Lin, J. A charging-feature-based estimation model for state of health of lithium-ion batteries. Expert Syst. Appl. 2024, 238, 122034. [Google Scholar] [CrossRef]
- Gou, B.; Xu, Y.; Feng, X. State-of-health estimation and remaining-useful-life prediction for lithium-ion battery using a hybrid data-driven method. IEEE Trans. Veh. Technol. 2020, 69, 10854–10867. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Z.; Xiong, Q.; Ding, B.; Hou, J.; Luo, D.; Rong, Y.; Li, S. State-of-health estimation and remaining useful life prediction for the lithium-ion battery based on a variant long short term memory neural network. J. Power Sources 2020, 459, 228069. [Google Scholar] [CrossRef]
- Ma, Y.; Shan, C.; Gao, J.; Chen, H. A novel method for state of health estimation of lithium-ion batteries based on improved LSTM and health indicators extraction. Energy 2022, 251, 123973. [Google Scholar] [CrossRef]
- Deng, Z.; Lin, X.; Cai, J.; Hu, X. Battery health estimation with degradation pattern recognition and transfer learning. J. Power Sources 2022, 525, 231027. [Google Scholar] [CrossRef]
- Lin, M.; Yan, C.; Wang, W.; Dong, G.; Meng, J.; Wu, J. A data-driven approach for estimating state-of-health of lithium-ion batteries considering internal resistance. Energy 2023, 277, 127675. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Z.; Su, H. State of health estimation for lithium-ion batteries on few-shot learning. Energy 2023, 268, 126726. [Google Scholar] [CrossRef]
- Lin, C.; Xu, J.; Shi, M.; Mei, X. Constant current charging time based fast state-of-health estimation for lithium-ion batteries. Energy 2022, 247, 123556. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, S.; Yu, C.; Xie, Y. Fernantery state of health estimation and high-adaptability remaining useful life prediction. J. Electrochem. Soc. 2022, 169, 31. [Google Scholar] [CrossRef]
- Wu, L.; Chen, C.; Li, Z.; Chen, Z.; Li, H. The Joint Estimation of SOC-SOH for Lithium-Ion Batteries Based on BiLSTM-SA. Electronics 2025, 14, 97. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, Y.; Wu, J.; Yuan, H.; Guo, F. Lithium-Ion Battery State of Health Estimation Based on Feature Reconstruction and Transformer-GRU Parallel Architecture. Energies 2025, 18, 1236. [Google Scholar] [CrossRef]
- Kasun, L.L.C.; Zhou, H.; Huang, G.; Vong, C.M. Representational learning with ELMs for big data. IEEE Intell. Syst. 2013, 28, 31–34. [Google Scholar]
- Tang, J.; Deng, C.; Huang, G. Extreme learning machine for multilayer perceptron. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 809–821. [Google Scholar] [CrossRef]
- Zhu, W.; Miao, J.; Qing, L.; Huang, G. Hierarchical extreme learning machine for unsupervised representation learning. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015; IEEE: New York, NY, USA, 2015; pp. 1–8. [Google Scholar]
- He, Y.; Pattanadech, N.; Sukemoke, K.; Pan, M.; Chen, L. The State of Health Estimation of Retired Lithium-Ion Batteries Using a Multi-Input Metabolic Gated Recurrent Unit. Energies 2025, 18, 1035. [Google Scholar] [CrossRef]
- Askari, S. Fuzzy C-Means clustering algorithm for data with unequal cluster sizes and contaminated with noise and outliers, Review and development. Expert Syst. Appl. 2021, 165, 113856. [Google Scholar] [CrossRef]
- Chen, L.; He, M.; Wu, S.; Chen, D.; Zhao, M.; Pan, H. Multi-algorithm fusion-based state of energy assessment of retired lithium-ion batteries. J. Energy Storage 2025, 105, 114690. [Google Scholar] [CrossRef]
- Deng, Z.; Xu, L.; Liu, H.; Hu, X.; Wang, B.; Zhou, J. Rapid health estimation of in-service battery packs based on limited labels and domain adaptation. J. Energy Chem. 2024, 89, 345–354. [Google Scholar] [CrossRef]
- Wen, J.; Chen, X.; Li, X.; Li, Y. SOH prediction of lithium battery based on IC curve feature and BP neural network. Energy 2022, 261, 125234. [Google Scholar] [CrossRef]
- Wu, T.; Huang, Y.; Xu, Y.; Jiang, J.; Liu, S.; Li, Z. SOH prediction for lithium-ion battery based on improved support vector regression. Int. J. Green Energy 2023, 20, 227–236. [Google Scholar] [CrossRef]
- Wang, J.; Deng, Z.; Yu, T.; Yoshida, A.; Xu, L.; Guan, G. A Abudula. State of health estimation based on modified Gaussian process regression for lithium-ion batteries. J. Energy Storage 2022, 51, 104512. [Google Scholar] [CrossRef]




| Parameter | Samsung Retired Batteries | Panasonic Retired Batteries |
|---|---|---|
| Nominal capacity | 2600 mAh | 3350 mAh |
| Minimum capacity | 2400 mAh | 3250 mAh |
| Standard charging current | 1300 mAh | 1625 mAh |
| Maximum charging current | 2600 mAh | 2400 mAh |
| Maximum discharge current | 5200 mAh | 7200 mAh |
| Nominal voltage | 3.7 V | 3.6 V |
| Charge cut-off voltage | 4.2 V | 4.2 V |
| Discharge cut-off voltage | 2.75 V | 2.5 V |
| Evaluation Indicators | D22 Battery | D26 Battery | D23 Battery | D123 Battery |
|---|---|---|---|---|
| Max AE (%) | 2.1492 | 1.4502 | 2.5959 | 3.2283 |
| MAE (%) | 0.3562 | 0.836 | 0.6716 | 1.44 |
| RMSE (%) | 0.6035 | 0.9111 | 1.0469 | 1.7684 |
| Evaluation Indicators | Pack 1 Battery Pack | Pack 2 Battery Pack |
|---|---|---|
| Max AE (%) | 2.5974 | 0.4408 |
| MAE (%) | 0.4642 | 0.1622 |
| RMSE (%) | 0.681 | 0.1875 |
| Evaluation Indicators | R2 | R19 |
|---|---|---|
| Max AE (%) | 2.8559 | 0.7912 |
| MAE (%) | 0.838 | 0.2022 |
| RMSE (%) | 1.0822 | 0.2787 |
| Method | D26 | Pack 2 | ||||
|---|---|---|---|---|---|---|
| Max AE (%) | MAE (%) | RMSE (%) | Max AE (%) | MAE (%) | RMSE (%) | |
| SVM | 4.3413 | 3.1219 | 3.2337 | 2.2636 | 1.6685 | 1.7177 |
| BPNN | 4.5025 | 2.5257 | 2.79 | 3.6844 | 1.7738 | 2.064 |
| GPR | 2.2546 | 1.2937 | 1.3828 | 0.8288 | 0.4729 | 0.4968 |
| I-HELM | 1.4502 | 0.836 | 0.9111 | 0.4408 | 0.1622 | 0.1875 |
| Method | R19 | ||
|---|---|---|---|
| Max AE (%) | MAE (%) | RMSE (%) | |
| SVM | 1.2242 | 0.6126 | 0.663 |
| BPNN | 0.8145 | 0.2157 | 0.2817 |
| GPR | 1.0382 | 0.2573 | 0.345 |
| I-HELM | 0.7912 | 0.2022 | 0.2787 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Pattanadech, N.; Sukemoke, K.; Chen, L.; Li, L. SOH Estimation Model Based on an Ensemble Hierarchical Extreme Learning Machine. Electronics 2025, 14, 1832. https://doi.org/10.3390/electronics14091832
He Y, Pattanadech N, Sukemoke K, Chen L, Li L. SOH Estimation Model Based on an Ensemble Hierarchical Extreme Learning Machine. Electronics. 2025; 14(9):1832. https://doi.org/10.3390/electronics14091832
Chicago/Turabian StyleHe, Yu, Norasage Pattanadech, Kasian Sukemoke, Lin Chen, and Lulu Li. 2025. "SOH Estimation Model Based on an Ensemble Hierarchical Extreme Learning Machine" Electronics 14, no. 9: 1832. https://doi.org/10.3390/electronics14091832
APA StyleHe, Y., Pattanadech, N., Sukemoke, K., Chen, L., & Li, L. (2025). SOH Estimation Model Based on an Ensemble Hierarchical Extreme Learning Machine. Electronics, 14(9), 1832. https://doi.org/10.3390/electronics14091832






